试验齿轮的弯曲疲劳极限
42CrMo齿轮渗氮处理R-S-N弯曲疲劳性能研究

检测项 目
浅层深 深层深
表1 浅层、深层渗氮后试样1/2齿高处检测结果
层深 /mm 0.35 0.63
表面硬 度 HV
692 628
白亮层深度/mm (≤0.025mm)
0.0096
0.0175
渗层氮化级别 /级(≤3级)
2 3
晶粒度级 别/级 7.0 7.5
54 2018年 第11期
可靠度(%) 方程底数logm 方程常数logC 相关系数R2
弯曲持久疲 劳极限/MPa
疲劳曲线拐点的 应力循环次数Nc
90
6.409
21.656
1.0
437
54095
95
6.409
渗氮处理是指一种在一定 温度下一定介质中使氮原子渗入 工件表层的化学热处理工艺。经 渗氮处理的制品具有优异的耐磨 性、耐疲劳性、耐蚀性及耐高温 的特性,增加钢件的耐磨性、表 面硬度、疲劳极限和抗蚀能力。 依据ISO6336-5标准,在允许的 渗氮层深度范围内,疲劳极限为 一定值,具体影响程度不详。齿 轮的弯曲疲劳强度是评价齿轮承 载能力的一个重要指标,也是齿 轮设计的基础数据,对不同渗氮 层深度齿轮弯曲疲劳寿命以及影 响因素开展研究,以达到提高齿 轮弯曲疲劳强度的目的,进而提 高齿轮的承载能力。
1.试验齿轮 (1)齿轮材料及参数 齿 轮材料为42CrMo(渗氮)。 试验齿轮的参数和精度:模数 m=5m m,螺旋角β =0º,齿宽 b=20m m,压力角α =20º,应力 修正系数Y st=2.0,齿根圆角参
数q s=2.5,齿根圆角表面粗糙度 Rz≤10μm,精度为ISO13281:1995的5级。
452
11
499
机械设计-齿轮习题与参考答案

机械设计-齿轮习题与参考答案编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(机械设计-齿轮习题与参考答案)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为机械设计-齿轮习题与参考答案的全部内容。
习题与参考答案一、单项选择题(从给出的A、B、C、D中选一个答案)1 一般开式齿轮传动的主要失效形式是。
A。
齿面胶合 B。
齿面疲劳点蚀C。
齿面磨损或轮齿疲劳折断 D。
轮齿塑性变形2 高速重载齿轮传动,当润滑不良时,最可能出现的失效形式是。
A. 齿面胶合B. 齿面疲劳点蚀C。
齿面磨损 D. 轮齿疲劳折断3 45钢齿轮,经调质处理后其硬度值约为。
A. 45~50 HRCB. 220~270 HBSC. 160~180 HBS D。
320~350 HBS4 齿面硬度为56~62HRC的合金钢齿轮的加工工艺过程为。
A. 齿坯加工→淬火→磨齿→滚齿 B。
齿坯加工→淬火→滚齿→磨齿C. 齿坯加工→滚齿→渗碳淬火→磨齿D. 齿坯加工→滚齿→磨齿→淬火5 齿轮采用渗碳淬火的热处理方法,则齿轮材料只可能是。
A。
45钢 B。
ZG340-640C。
20Cr D。
20CrMnTi6 齿轮传动中齿面的非扩展性点蚀一般出现在。
A. 跑合阶段 B。
稳定性磨损阶段C。
剧烈磨损阶段 D. 齿面磨料磨损阶段7 对于开式齿轮传动,在工程设计中,一般 .A. 按接触强度设计齿轮尺寸,再校核弯曲强度B. 按弯曲强度设计齿轮尺寸,再校核接触强度C。
只需按接触强度设计D。
只需按弯曲强度设计8 一对标准直齿圆柱齿轮,若z1=18,z2=72,则这对齿轮的弯曲应力。
A。
σF1>σF2 B. σF1<σF2 C。
机械设计练习题_(6)

1、为什么轮齿的弯曲疲劳裂纹首先发生在齿根受拉伸一侧?解题要点:(1)齿根弯曲疲劳强度计算时,将轮齿视为悬臂梁,受载荷后齿根处产生的弯曲应力最大。
(2)齿根过渡圆角处尺寸发生急剧变化,又由于沿齿宽方向留下加工刀痕产生应力集中。
(3)在反复变应力的作用下,由于齿轮材料对拉应力敏感,故疲劳裂纹首先发生在齿根受拉伸一侧。
2、有一闭式齿轮传动,满载工作几个月后,发现硬度为200~240HBS 的齿轮工作表面上出现小的凹坑。
试问:(1)这是什么现象?(2)如何判断该齿轮是否可以继续使用?(3)应采取什么措施?解题要点:(1)已开始产生齿面疲劳点蚀,但因“出现小的凹坑”,故属于早期点蚀。
(2)若早期点蚀不再发展成破坏性点蚀,该齿轮仍可继续使用。
(3)采用高粘度的润滑油或加极压添加剂于没中,均可提高齿轮的抗疲劳点蚀的能力。
3、一对齿轮传动,如何判断大、小齿轮中哪个齿面不易产生疲劳点蚀?哪个轮齿不易产生弯曲疲劳折断?并简述其理由。
解题要点:(1) 大、小齿轮的材料与热处理硬度及循环次数N 不等,通常21HP HP σσ>, 而21H H σσ=,故小齿轮齿面接触强度较高,则不易出现疲劳点蚀。
(2)比较大、小齿轮的111Sa Fa FP Y Y σ与222Sa Fa FP Y Y σ,若111Sa Fa FP Y Y σ<222Sa Fa FP Y Y σ,则表明小齿的弯曲疲劳强底低于大齿轮,易产生弯曲疲劳折断;反之亦然。
4、图为两级斜齿圆柱齿轮减速器,已知条件如图所示。
试问: (1) 低速级斜齿轮的螺旋线方向应如何选择才能使中间 轴Ⅱ上两齿轮所受的轴向力相反?(2) 低速级小齿轮的螺旋角β2应取多大值,才能使 轴Ⅱ轴上轴向力相互抵?解题要点:(1)轴Ⅱ上小齿轮为左旋;Ⅲ轴上大齿轮为左旋。
(2)若要求Ⅱ轴上轮1、2的轴向力能互相抵消,则必须满足下式: F a1=F a2即 12122211t a n t a n ,t a n t a nββββt t t t F F F F == 由中间轴的力矩平衡,得222211dF d F t t = 则 1121211212t a n c o s /513cos /175tan tan tan ββββββ⨯⨯===d d F F t t 得1438.015sin 513175sin 2=︒⨯⨯=β 则 2161827.82'''︒=︒=β5、今有两对斜齿圆柱齿轮传动,主动轴传递的功率P 1=13kW ,n 1=200r/min ,齿轮的法面模数m n =4mm ,齿数z 1=60均相同,仅螺旋角分别为9°与18°。
圆柱齿轮传动强度的计算

圆柱齿轮传动的强度计算1 直齿圆柱齿轮传动的强度计算1.齿面接触疲劳强度计算为了保证在预定寿命内齿轮不发生点蚀失效,应进行齿面接触疲劳强度计算。
因此,齿轮接触疲劳强度计算准则为:齿面接触应力σH小于或等于许用接触应力σHP,即σH≤σHP赫兹公式由于直齿轮在节点附近往往是单对齿啮合区,轮齿受力较大,故点蚀首先出现在节点附近。
因此,通常计算节点的接触疲劳强度。
图a表示一对渐开线直齿圆柱齿轮在节点接触的情况。
为了简化计算,用一对轴线平行的圆柱体代替它。
两圆柱的半径ρ1、ρ2分别等于两齿廓在节点处的曲率半径,如图b所示。
由弹性力学可知,当一对轴线平行的圆柱体相接触并受压力作用时,将由线接触变为面接触,其接触面为一狭长矩形,在接触面上产生接触应力,并且最大接触应力位于接触区中线上,其数值为式中σH-接触应力(Mpa)Fn-法向力(N)L-接触线长度(mm)rS-综合曲率半径(mm);±-正号用于外接触,负号用于内接触ZE-材料弹性系数(),,其中E1、E2分别为两圆柱体材料的弹性模量(MPa);m1、m2分别为两圆柱体材料的泊松比。
上式表明接触应力应随齿廓上各接触点的综合曲率半径的变化而不同,且靠近节点的齿根处最大(图c、d)。
但为了简化计算,通常控制节点处的接触应力。
节点处的参数(1)综合曲率半径由图可知,,代入rE公式得式中:,称为齿数比。
对减速传动,u=i;对增速传动,u=1/i。
因,则有(2)计算法向力(3)接触线长度L引入重合度系数Ze,令接触线长度将上述参数代入最大接触应力公式得接触疲劳强度计算公式令,称为节点区域系数。
则得(1) 齿面接触疲劳强度的校核公式齿面接触疲劳强度的校核公式为(2) 齿面接触疲劳强度设计公式设齿宽系数,并将代入上式,则得齿面接触疲劳强度的设计公式式中:d1-小齿轮分度圆直径(mm);ZE-材料弹性系数(),按下表查取;注:泊松比m1=m2=0.3Z H-节点区域系数,考虑节点处轮廓曲率对接触应力的影响,可由下左图查取。
齿轮齿面接触强度及齿根弯曲强度核算
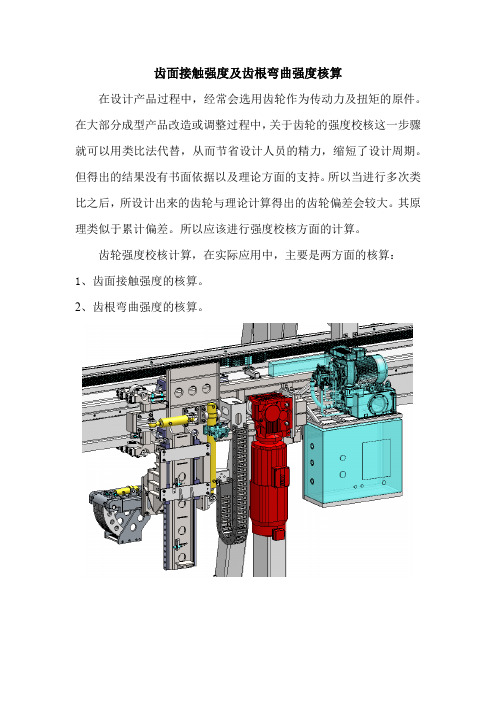
齿面接触强度及齿根弯曲强度核算在设计产品过程中,经常会选用齿轮作为传动力及扭矩的原件。
在大部分成型产品改造或调整过程中,关于齿轮的强度校核这一步骤就可以用类比法代替,从而节省设计人员的精力,缩短了设计周期。
但得出的结果没有书面依据以及理论方面的支持。
所以当进行多次类比之后,所设计出来的齿轮与理论计算得出的齿轮偏差会较大。
其原理类似于累计偏差。
所以应该进行强度校核方面的计算。
齿轮强度校核计算,在实际应用中,主要是两方面的核算:1、齿面接触强度的核算。
2、齿根弯曲强度的核算。
1.齿面接触强度核算-分度圆直径计算参考文献:在初步设计齿轮时,根据齿面接触强度,可按照下列公式估算齿轮传动的尺寸。
(机械设计手册P14-133)a≥A a(μ±1)·√KT1ψaσHP23①d1≥A d·√KT1ψdσHP2·μ±1μ3②公式①为两齿轮中心距的计算;公式②为齿轮分度圆直径的计算。
由于本次计算的是齿轮齿条传动。
所以,中心距a= d1/2其中:d1为齿轮分度圆直径,只需要核算齿轮分度圆直径d1首先,要确定公式②中各个符号代表的含义及数值选取。
d1—齿轮分度圆直径;A d—常系数;K—载荷系数;μ—齿数比;σHP—许用接触应力;ψd—齿宽系数;T1—电机减速机输出扭矩;d1:齿轮分度圆直径,待求;A d:常系数值;A d值在表14-1-65中,通过螺旋角角度β的数值求得。
齿轮的螺旋角β=11.655°,则A d = 756。
载荷系数K,常用值K=1.2~2(机械设计手册P14-133),当载荷平稳,齿宽系数较小,轴承对称布置,轴的刚性较大,齿轮精度较高(6级以上),以及齿轮的螺旋角较大时取较小值;反之取较大值。
根据对比后的结果在K的常用范围内选取。
此次选择K=1.8(载荷平稳,齿宽系数较小,轴为非对称分布,轴的刚性不大,齿轮精度不高)u:传动比。
当齿轮之间为外啮合的时候,选取“+”;当齿轮之间为内啮合的时候,选取“-”,本次计算为齿轮齿条,不影响计算结果。
机械设计练习题_(6)

1、为什么轮齿的弯曲疲劳裂纹首先发生在齿根受拉伸一侧解题要点:(1)齿根弯曲疲劳强度计算时,将轮齿视为悬臂梁,受载荷后齿根处产生的弯曲应力最大。
(2)齿根过渡圆角处尺寸发生急剧变化,又由于沿齿宽方向留下加工刀痕产生应力集中。
(3)在反复变应力的作用下,由于齿轮材料对拉应力敏感,故疲劳裂纹首先发生在齿根受拉伸一侧。
2、有一闭式齿轮传动,满载工作几个月后,发现硬度为200~240HBS 的齿轮工作表面上出现小的凹坑。
试问:(1)这是什么现象(2)如何判断该齿轮是否可以继续使用(3)应采取什么措施解题要点:(1)已开始产生齿面疲劳点蚀,但因“出现小的凹坑”,故属于早期点蚀。
(2)若早期点蚀不再发展成破坏性点蚀,该齿轮仍可继续使用。
(3)采用高粘度的润滑油或加极压添加剂于没中,均可提高齿轮的抗疲劳点蚀的能力。
3、一对齿轮传动,如何判断大、小齿轮中哪个齿面不易产生疲劳点蚀哪个轮齿不易产生弯曲疲劳折断并简述其理由。
解题要点:(1) 大、小齿轮的材料与热处理硬度及循环次数N 不等,通常21HP HP σσ>, 而21H H σσ=,故小齿轮齿面接触强度较高,则不易出现疲劳点蚀。
(2)比较大、小齿轮的111Sa Fa FP Y Y σ与222Sa Fa FP Y Y σ,若111Sa Fa FP Y Y σ<222Sa Fa FP Y Y σ,则表明小齿的弯曲疲劳强底低于大齿轮,易产生弯曲疲劳折断;反之亦然。
4、图为两级斜齿圆柱齿轮减速器,已知条件如图所示。
试问: (1) 低速级斜齿轮的螺旋线方向应如何选择才能使中间轴Ⅱ上两齿轮所受的轴向力相反(2) 低速级小齿轮的螺旋角β2应取多大值,才能使 轴Ⅱ轴上轴向力相互抵 解题要点:(1)轴Ⅱ上小齿轮为左旋;Ⅲ轴上大齿轮为左旋。
(2)若要求Ⅱ轴上轮1、2的轴向力能互相抵消,则必须满足下式: F a1=F a2即 12122211tan tan ,tan tan ββββt t t t F F F F == 由中间轴的力矩平衡,得222211d F d F t t = 则 1121211212tan cos /513cos /175tan tan tan ββββββ⨯⨯===d d F F t t 得1438.015sin 513175sin 2=︒⨯⨯=β 则 2161827.82'''︒=︒=β5、今有两对斜齿圆柱齿轮传动,主动轴传递的功率P 1=13kW ,n 1=200r/min ,齿轮的法面模数m n =4mm ,齿数z 1=60均相同,仅螺旋角分别为9°与18°。
考研机械设计-7

考研机械设计-7(总分:100.00,做题时间:90分钟)一、计算题(总题数:25,分数:100.00)1.已知下图(a)所示零件的极限应力点C的位置,工作应力为σmax (σm ,σa )。
试在该图上标出按三种应力变化的规律,即r=σmin /σmax =c、σm =c及σmin =c时,对应于点C的极限应力点,并指出该点处于破坏区还是安全区。
(分数:4.00)__________________________________________________________________________________________ 正确答案:()解析:解题要点:(1)当r=σmin /σmax =c时,在题图(b)中,连接OC并延长,交于极限应力曲线A"E"S上的点C 1,则点C 1为极限应力点,且位于塑性安全区。
(2)当σm =c时,自点C作横坐标的垂线,交A"E"S于点C 2 (极限应力点),且位于疲劳安全区。
(3)当σmin =c时,自点C作与横坐标轴呈45°角的斜线交A"E"S于C 3点(极限应力点),且位于疲劳安全区。
2.已知某钢材的力学性能为σ-1 =500MPa,σs =1000MPa,σ0 =800MPa。
(1)试按比例绘制该材料的简化疲劳极限应力图;(2)由该材料制成的零件,承受非对称循环应力,其应力循环特性r=0.3,工作应力σmax =800MPa,零件的有效应力集中系数k σ =1.49,零件的尺寸系数εσ =0.83,表面状态系数β=1,按简单加载情况在下图中标出工作应力点及对应的极限应力点;(3)判断该零件的强度是否满足要求。
(分数:4.00)__________________________________________________________________________________________ 正确答案:()解析:解题要点:(1)绘制材料的简化疲劳极限应力图。
第4章 齿轮传动

2.按照齿轮齿面硬度的不同 软齿面齿轮传动:一对啮合齿轮只要有一个 齿轮的齿面硬度≤350HBW 硬齿面齿轮传动:一对啮合齿轮两个齿轮的 齿面硬度均>350HBW
重庆大学机械工程学院
作者: 陈德淑
4.1.2 齿轮传动的特点
1.优点:
①传动比准确、传动平稳。 ②圆周速度大,高达300 m/s。 ③传递功率范围大,从几瓦到10万千瓦。 ④效率高(η 0.99)、使用寿命长、工作安全可靠。 2.缺点
疲劳极限的主要影响因素有材料成分,力学性能, 热处理及硬化层深度、硬度梯度,结构,残余应力, 材料的纯度和缺陷等。
重庆大学机械工程学院
作者: 陈德淑
4.4 直齿圆柱齿轮传动的强度计算
4.4.1 直齿圆柱齿轮传动的几何尺寸计算
1.基本参数
①齿数—— z ②模数—— m ③压力角---α
④齿顶高系数:ha*
如忽略摩擦力影响,轮齿齿廓在节点啮合时相互作
用的总压力为法Fn向力 Fn ,其方向沿啮合线。
重庆大学机械工程学院
作者: 陈德淑
为了计算轮齿强度,设计轴和轴承,有必要分析轮齿上的作用力。
各作用力的方向如图
圆周力
Ft
2T1 d1
O2
O2
Байду номын сангаас
α ω2
α
(从动)
径向力 Fr1 = Fr2 = Ft tan
法向力 Fn Ft / cos
重庆大学机械工程学院
作者: 陈德淑
4.3 齿轮常用材料和试验齿轮的疲劳极限
4.3.1 齿轮常用材料
针对齿轮的各种失效形式,为了确保齿轮在预期寿命内能 正常工作,选择齿轮材料及热处理方法时应考虑: 1)齿轮表面要有较高的硬度和耐磨性;以提高齿面抗点蚀、 抗磨损、抗胶合及抗塑性变形的能力。
齿轮材料及热处理质量检验的一般规定齿轮材料及热处理质量检验要求
齿轮材料及热处理质量检验的一般规定齿轮材料及热处理质量检验要求(一)(GB/T8539-2000)4齿轮材料及热处理质量检验要求4.1一般原则不同材料、不同热处理工艺所得到的σHlim(接触疲劳极限)、σFlim(弯曲疲劳极限)和σFE(σFE=σFlim·Y ST)见图1~图14。
图中的各材料质量等级的定义为:ML表示对齿轮加工过程中材料质量及热处理工艺的一般要求;MQ表示对有经验的制造者在一般成本下可以达到要求的等级;ME表示必须具有高可靠度制造过程控制才能达到的等级;MX表示对淬透性及金相组织有特殊考虑的调质合金钢的质量要求。
4.2齿轮材料及热处理检验要求本条所列要求已经过实际应用验证,作为推荐性文件提出。
根据各自的经验或需要,齿轮制造厂家也可采用其他的方法或数据。
但应由齿轮供需双方对细节达成协议,尤其是大型齿轮的场合。
4.2.1铸钢、结构钢(图1、图2)由于这些钢材无一定化学成分要求,冶练方法也不明确,因此MQ线位于强度下限(ML,即MQ=ML)。
该类结构钢只用于轻载齿轮和次要齿轮。
当钢材生产可达到高档要求或经过实际验证时,亦可采用ME线数据。
4.2.2黑心可锻铸铁(图3、图4)这类材料通常用于小型轻载齿轮。
热处理工艺控制得当时,可提高材料性能。
从可靠性考虑,MQ线位于下限(ML),若经过实用验证,也可采用ME线数据。
4.2.3其他材料(图5~图14)其他材料的质量及热处理检验要求列于表1~表6。
表1铸铁材料(灰口及球墨铸)(图3、图4)序号项目灰口铸铁球墨铸铁ML MQ ME ML MQ ME1 化学成分不检验100%检验提交铸造合格证100%检验提交铸造合格证2 冶炼不规定电炉或相当设备不检验电炉或相当设备3 力学性能只提供HB值要求σb或HB,针对同炉号独立的试样做检验报告不规定检验σs(σ0.2),σb,δ5,φ(代表性试样)靠近实际轮齿部位检验HB4 石墨形态规定但不必检验只担供HB值限制基体组织规定位不必检验铁素体含量≤5%不检验5 焊补在轮齿部位不允许焊补,其他部位只能在认可工艺下进行,焊补后应进行去应力退火处理不允许焊补6 去应力退火不规定推荐500~530℃,对于灰口合金铸铁530~560℃保温适当时间不规定推荐500~560℃保温适当时间7 内部缩孔(裂纹)不检验检验气孔、裂纹、砂眼,限制缺陷为检验检验气孔、裂纹、砂眼,限制缺陷8 表面裂纹不检验着色渗透探伤不检验不允许有裂纹,100%经磁粉或着色渗透探伤,大批量产表2非表面硬化调质钢(铸件)(图6、图8)表3非表面硬化调质钢(锻件或轧材)(图5、图7)表4表面硬化调质钢——经火焰及感应淬火(锻造、轧制或铸造)(图10、图12)表6表面硬化钢——经渗碳(碳氮共渗)(锻打或轧制)(图9、图11)9有效硬化层深度(按GB/T9450检验)有代表性试样检查或类似齿轮的同模数齿块试样的齿宽中部位于齿顶圆以下的齿顶高上检查,本指标关系到齿面接触强度。
齿轮接触强度与弯曲强度

1. 齿轮接触强度计算1.1齿轮接触的计算应力βανεννπσK K K K uu bd F Z Z Z MPa E E R L FH A t E H red H1)(1111222121±⋅=-+-= 式中:A K —工况系数; νK —动载系数;αH K —接触强度的端面载荷分配系数;βK —齿向载荷分布系数;H Z —节点域系数;E Z —弹性系数; εZ 一重合度系数;1.1.1工况系数A K由于齿轮的载荷特性为工作稳定状况下,故取工况系数为A K =1.0. 1.1.2动载系数νK由于=15.96m/s齿轮重合度再根据《机械设计手册》图8-32与8.33得;)=1.48-0.44(1.48-1.22)=1.361.1.3端面载荷分配系数αH K查表8-120得21εαZ C K H H ∙=其中H C 查图8-34为0.865. 1.1.4齿向载荷分布系数βK查图8.35可得βK =1.13. 1.1.5节点域系数H Z式中:错误!未找到引用源。
为端面分度圆压力角;错误!未找到引用源。
为基圆螺旋角;错误!未找到引用源。
为端面啮合角;经计算最后得到H Z =2.254 1.1.6弹性系数E Z带入各值后,得E Z =189.87错误!未找到引用源。
1.1.7重合度系数εZ与1.13的分母约去,不需考虑。
最后得到理论接触应力为:MPaZ mm mm N Z MPa H 67.124413.11865.036.11208.2208.3776.1572.7627.5265287.189254.2=⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯=εεσ1.2 接触疲劳极限lim Hσ' W R V L N H HZ Z Z Z Z lim lim σσ=' 式中: 'H l i m σ表示计算齿轮的接触疲劳极限;H l i m σ表示试验齿轮的接触疲劳极限;N Z 表示接触强度的寿命系数;L Z 表示润滑剂系数;V Z 表示速度系数;R Z 表示光洁度系数;W Z 表示工作硬化系数。
基于42CrMo_齿轮的弯曲疲劳试验研究

Journal of Mechanical Strength2023,45(2):474-480DOI :10.16579/j.issn.1001.9669.2023.02.030∗20210810收到初稿,20210917收到修改稿㊂河北省高等学校科学技术研究项目(QN2019203),唐山市科技创新团队培养计划项目(18130216A,20130204D),唐山市科技重大专项(19140203F)资助㊂∗∗王嘉军,男,1997年生,河北承德人,汉族,华北理工大学机械工程学院在读硕士生,主要研究方向为先进制造技术㊁机械故障诊断㊂∗∗∗裴未迟,男,1975年生,河北唐山人,汉族,华北理工大学机械工程学院副教授,博士,硕士研究生导师,主要研究方向为先进制造技术㊁机械故障诊断㊂基于42CrMo 齿轮的弯曲疲劳试验研究∗RESEARCH ON BENDING FATIGUE TEST BASED ON 42CRMO GEAR王嘉军∗∗㊀裴未迟∗∗∗㊀纪宏超㊀龙海洋㊀王志涛(华北理工大学机械工程学院,唐山063210)WANG JiaJun ㊀PEI WeiChi ㊀JI HongChao ㊀LONG HaiYang ㊀WANG ZhiTao(College of Mechanical Engineering ,North China University of Technology ,Tangshan 063210,China )摘要㊀42CrMo 属于超高强度钢,其具备较高的强度,材料淬透性能好,淬火后的变形量小,大量地应用于牵引用的大齿轮㊁承压主轴㊁连杆等传动件材料,弯曲疲劳试验对齿轮疲劳寿命预测具有重要意义㊂首先,通过齿轮弯曲疲劳试验,获得了应力比R =0.1时交变载荷作用下的齿轮弯曲疲劳试验数据,得到了齿轮弯曲疲劳强度P-S-N 曲线和拟合曲线关系式,以及不同可靠度下齿轮所能承受弯曲的疲劳极限值㊂随后,采用有限元方法对齿轮弯曲疲劳试验进行了数值模拟,得到了齿轮齿根处的静力学强度和理论计算值对比,分析表明数值模拟所得结果与理论分析结果基本一致,可以作为弯曲疲劳试验疲劳寿命仿真的基础㊂最后,通过弯曲疲劳寿命试验试验值与数值模拟结果对比,结果表明,疲劳寿命试验值与可靠度在84.1%时数值模拟得到的弯曲疲劳寿命基本一致,验证了数值模拟的准确性,因此能够有效预测42CrMo 齿轮的弯曲疲劳寿命㊂关键词㊀齿轮㊀弯曲疲劳㊀疲劳寿命㊀P-S-N 曲线中图分类号㊀TH133.3㊀Abstract ㊀42CrMo is a kind of ultra-high strength steel,which has high strength,good hardenability and small deformation after quenching.It is widely used in driving materials such as large gears,bearing spindle and connecting rod used in traction.Bending fatigue test is of great significance for fatigue life prediction of gears.First of all,the bending fatigue test data of gearunder alternating load at stress ratio R =0.1were obtained,the P-S -N curve of gear bending fatigue strength and the fitting curve relation were obtained,and the fatigue limit value of gear under different reliability was obtained.Then the finite element methodwas used to simulate the bending fatigue test of gear.The static strength at the root of the gear tooth is compared with the theoretical value,and the analysis shows that the numerical simulation results are basically consistent with the theoretical analysis results,which can be used as the basis of fatigue life simulation of bending fatigue test.Finally,the experimental values of the bending fatigue life test are compared with the numerical simulation results.The results show that the fatigue life test values are basically consistent with the numerical simulation results when the reliability is 84.1%,which verifies the accuracy of the numerical simulation and can effectively predict the bending fatigue life of 42CrMo gear.Key words㊀Gear ;Bending fatigue ;Fatigue life ;P-S-N curveCorresponding author :PEI WeiChi ,E-mail :pwc @ ,Tel :+86-315-8805440The project supported by the Hebei Provincial Higher Education Science and Technology Research Project (No.QN2019203),the Tangshan Science and Technology Innovation Team Training Project (No.18130216A,20130204D),and the Tangshan Science and Technology Major Project (No.19140203F).Manuscript received 20210810,in revised form 20210917.0㊀引言㊀㊀齿轮弯曲疲劳试验研究其主要目的在于研究其齿轮抗弯曲的能力,即齿轮在工作运转的过程中不断地承受重复载荷且不会造成疲劳破坏;其主要特征是齿根位置由于在反复的周期疲劳载荷的作用下出现疲劳裂纹,而伴随着裂纹的扩展将导致齿根受力面积将不断减小,最终沿着齿根断裂造成齿轮失效[1-3]㊂㊀第45卷第2期王嘉军等:基于42CrMo齿轮的弯曲疲劳试验研究475㊀㊀关于齿轮方向的研究已有将近百年的历史㊂早在1931年,国外就开始了有关齿轮的弯曲疲劳试验的研究,而随着国际工业水平的发展与进步,弯曲疲劳试验的研究不断取得阶段性成果㊂我国有关齿轮方面的研究起步相对较晚,但也在上一世纪七十年代开始起步,至今也有五十年左右的历史㊂2010年郑州机械研究所的祁倩[4]对42CrMo齿轮在高应力水平下,同种材料的齿轮软齿面和硬齿面进行弯曲疲劳试验研究,并且依据试验结果获取了该齿轮的P-S-N曲线㊂2016年郑州机械研究所的马威[5]对18CrNiMo7-6的齿轮以试验法和有限元分析法为基础,并且依据试验结果获取了R-S-N曲线㊂以上研究的齿轮材料或型号与本试验所选齿轮有所不同,所以参考价值有限,有必要单独研究该型号齿轮㊂研究42CrMo合金钢经渗碳0.9~1.1mm后的疲劳性能,随后通过数理统计方法对试验数据分析和处理,得到了P-S-N拟合曲线关系式并绘制疲劳试验P-S-N曲线[6]㊂1㊀齿轮弯曲疲劳试验㊀㊀齿轮在运转啮合的过程中承受交变应力的作用,轮齿表面加工刻痕或内部缺陷等部位,有可能因交变应力的作用引发微小裂纹㊂分散的微小裂纹逐渐汇聚形成宏观裂纹㊂宏观裂纹在轮齿上的缓慢扩展,导致轮齿横截面逐渐缩小,当横截面缩小到一定程度时,轮齿会因无法再承受动载荷导致轮齿断裂[7]㊂齿轮因交变应力发生的失效,属于齿轮的疲劳失效㊂齿轮弯曲疲劳试验是依据试验所得弯曲疲劳寿命数据,绘制齿轮材料的S-N曲线,进而测定该材料下齿轮的疲劳极限的方法[8]㊂1.1㊀试验齿轮及设备㊀㊀本次试验所选用的齿轮材料为42CrMo,其生产工艺为锻造毛坯-正火-粗车-调质-精车-剃齿-渗碳淬火-磨齿,齿轮渗碳层有效硬化层厚度为0.9~1.1mm,表面硬度HRC58~62,齿轮的基本参数如表1所示㊂表1㊀42CrMo齿轮参数Tab.1㊀42CrMo gear parameters齿数Teeth模数Modulus/mm压力角Pressure angle/(ʎ)齿宽Tooth width/mm 2062025试验所采用的是非运转式单向高频共振弯曲疲劳试验机,具体型号为通用的PLG200电磁激励共振性疲劳试验机,其特点是用压头来代替两齿轮啮合所承受的载荷施加到齿面上,振动波形输出的失真度低㊁频率范围广(最高可实现500Hz)㊁试验可控性强,试验效率高㊂在室温下进行试验,不考虑润滑和温度等条件对齿轮疲劳寿命的影响㊂其固有频率如式(1)所示f=C/m/2π(1)式中,C为机械共振系统总刚度,N/m;m为机械共振系统质量,kg㊂试验标准采用GB/T14230 2021标准来执行,采用单齿加载的方式来进行,试验采用成组法来获取齿轮的S-N曲线㊂弯曲疲劳试验如图1所示㊂图1㊀齿轮弯曲疲劳试验Fig.1㊀Bending fatigue test of gear1.2㊀试验失效判定准则㊀㊀42CrMo齿轮弯曲疲劳试验终止,其判定准则如下[9]:(1)齿根处出现肉眼可见的疲劳裂纹㊂(2)施加载荷或载荷下降5%~10%;沿齿根发生轮齿断裂㊂(3)循环寿命次数超过3ˑ106,判定越出㊂1.3㊀试验应力转换㊀㊀在试验过程中,载荷的施加是通过上压头对轮齿表面施加脉动循环载荷㊂载荷是周期性不断变化的,其中最小的载荷不能为0,以避免试验过程中冲击过大或者导致机器不稳定造成设备损伤㊂既循环应力(应力比)R=S min/S maxʂ0,故应力比选择R=0.1㊂试验选择用工程应用中危险截面常选用的平截面法中的30ʎ切线法㊂获取齿轮在轮齿齿顶面上载荷作用点E的位置,如图2所示㊂根据国标GB/T3480 3.2021给齿轮加载位置和相关参数,可得齿根处的应力,如式(2)所示σᶄF=FtY FE Y SE/(bmY ST YδrelT Y RelTY X)(2)图2㊀齿轮加载位置判定Fig.2㊀Determination of gear loading position㊀476㊀机㊀㊀械㊀㊀强㊀㊀度2023年㊀式中,Y FE为载荷作用于E点时的齿形系数,参照GB/T3480.3 2021给出计算公式㊂关于齿轮系数,如公式(3)所示[10]7-23Y FE=6(h FEm n)cosαFEn(s Fn mn)2cosαn(3)式中,m n为齿轮模数为6mm;αn为20ʎ的分度圆上法向压力角;依据GB/T3480.3 2021齿轮加载位置判定如图2所示,可得αFEn=28.10ʎ㊁h FE=9.83㊁S Fn= 11.01㊂将上述的参数代入公式(3)中可得到公式为Y FE=6(9.836)cos28.10ʎ(11.016)2cos20ʎ(4)式中,Y S为应力修正系数,需要与齿形系数Y F联合使用,对于分度圆角度为20ʎ的齿轮,齿形系数公式为Y S=(1.2+0.13L)q s11.21+2.3/L=1.4839(5)式中,L为齿根危险截面处齿厚与弯曲力臂的比值,ρF 从图2中测量可知为4.0㊂L=S Fnh FE=11.019.83=1.120q s=S Fn2ρF=11.012ˑ4.0=1.37625(6)㊀㊀依据国标进行选择Y ST=2,YδrelT=0.95,Y RelT= 1.04,Y X=0.95,将参数代入到公式(2)中可得σᶄF=Ftˑ2.4174ˑ1.48394325ˑ6ˑ2ˑ0.95ˑ1.04ˑ0.95(7)㊀㊀由于考虑到试验的限制性,将本试验预定应力比R=0.1代入,将实际齿根处应力σᶄF进行换算为应力比R=0时的脉动循环应力σF,应力转换公式,如式(8)所示σF=(1-r)σᶄFσb-r FσᶄF σb+350()(8)式中,σb为材料的实际抗拉强度1131MPa㊂将预定好试验的5个载荷水平的应力值代入到公式(7)与公式(8)中,得到应力值转换,如表2所示㊂表2㊀载荷水平转换表Tab.2㊀Load level conversion table载荷Load/kN2522191613σᶄF/MPa318.50280.28242.06203.81165.56σF/MPa292.95257.12221.14186.02150.742㊀疲劳试验及数据处理2.1㊀试验准备过程㊀㊀在弯曲疲劳试验正式开始之前,首先要确定试验的应力水平㊂从试验样品中选2个做静强度试验,根据静强度来确定试验中的最高应力水平为σF1= 292.95MPa,试验选择5个载荷级别㊂其中σF1= 292.95MPa,σF2=257.12MPa,σF3=221.14MPa,σF4=186.02MPa,σF5=150.74MPa㊂对试验齿轮进行编号处理从01㊁02㊁03㊁ ㊁010,共10个试验齿轮,每个应力水平选取8个试验点,即每个齿轮选择4个轮齿样品点,每个样品点之间间隔4个轮齿,降低两个样品点之间会受到相邻试验取样点的影响㊂2.2㊀试验结果㊀㊀本次弯曲疲劳试验共选择五个载荷级别,其中σF1=292.95MPa,σF2=257.12MPa,σF3=221.14 MPa,σF4=186.02MPa,σF5=150.74MPa㊂与之对应的五组载荷下的疲劳寿命次数如表3所示㊂表3㊀不同载荷下的疲劳寿命Tab.3㊀Fatigue life under different loads103cycle序号No.I II III IV V 186.6402.21331.62308.7104 294.2472.41917.52818.7104 3164.7616.82328.53103.3104 4166.1804.42632.93451.2104 5173.4838.22771.53914.8104 6282.5966.13154.84118.1104 7304.41216.93402.24478.6104 8376.31667.93812.35375.2104根据GB/T14230 2021中,关于某一循环寿命N L的寿命经验分布函数的关系表达式为[11]P(N L)=i-0.3n+0.4(9)式中,n为试验点总数;i为试验序号㊂失效概率如表4所示㊂表4㊀寿命累计失效概率表Tab.4㊀Life cumulative failure probability table 序号No.12345678失效概率Failure probability0.080.20.320.440.560.680.80.92 2.3㊀S-N曲线的数据分布处理㊀㊀现有的试验结果表明,关于齿轮弯曲疲劳寿命的概率分布是符合正态分布以及对数正态概率分布,试验中的应力及寿命对数化,如表5所示㊂本试验利用对数正态分布函数来确定齿轮弯曲疲劳寿命,公式为[10]7-23f(N)=lgeNσN2πe-(lg N-μ)22σN2(10)式中,μ为对数寿命平均值;σN为总体的对数寿命标准差;N为齿轮疲劳寿命㊂失效概率为50%的对数寿命,如㊀第45卷第2期王嘉军等:基于42CrMo齿轮的弯曲疲劳试验研究477㊀㊀lg N50=μ(11)㊀㊀而在某一应力水平下,获取到试验的弯曲疲劳试验寿命为N1,N2,N3, ,N n,则对数寿命的平均值,如x=1nðn i=1lg N i(12)表5㊀应力对数和寿命对数Tab.5㊀Log of stress and life序号No.应力和寿命取对数Log of stress and life5.68 5.55 5.40 5.23 5.021 1.134 1.291 1.410 1.465 1.6122 1.145 1.307 1.447 1.485 1.6123 1.201 1.333 1.466 1.495 1.6124 1.202 1.360 1.478 1.505 1.6125 1.206 1.364 1.484 1.518 1.6126 1.255 1.378 1.496 1.523 1.6127 1.263 1.401 1.504 1.532 1.6128 1.284 1.433 1.515 1.550 1.612总体寿命的平均值μ的估计值选择样本寿命的平均值,如lg N50=1nðn i=1lg N i(13)㊀㊀通过对上式的联立求取试验应力水平下的均值疲劳寿命,将获取的五组应力水平对应的N50都计算出来,将所得数据进行拟合得到失效50%时的疲劳寿命曲线㊂2.4㊀S-N曲线拟合㊀㊀本试验的疲劳寿命满足对数正态分布的,如[12]F(N)=ϕ(ln N-μσ)(14)㊀㊀按照正态分布方程为ϕ-1[(F(N)]=ln N-μσ,其中,Y=ϕ-1[(F(N)],x=ln N,A=1/σ,B=-μ/σ,将公式转换为y=Ax+B,可靠度R=1-F(N),以此反映循环寿命和可靠性之间的关系㊂将试验所得的[ln N i,ϕ-1[F(N i)]]采用最小二乘法的数据拟合方式,最终得到循环寿命在107时不同存活率下的拟合后的P-S-N曲线,如图3所示,所得拟合曲线公式,如表6所示㊂图3㊀P-S-N曲线Fig.3㊀P-S-N curve表6㊀P-S-N拟合曲线关系式Tab.6㊀P-S-N fitting curve relation可靠度Reliability/%y=A lg N+B相关系数Correlation coefficient 50y=-75.31lg N+694.410.969090y=-62.18lg N+586.950.978395y=-59.97lg N+569.030.979899y=-55.41lg N+532.000.9823根据弯曲疲劳试验数据的拟合结果可知,齿轮疲劳的可靠度在50%㊁90%㊁95%㊁99%时的弯曲疲劳应力极限水平分别是167.23MPa㊁151.72MPa㊁149.22 MPa㊁144.10MPa㊂从试验数据发现,齿轮寿命的存活率越高,齿轮所能承受的疲劳极限寿命越低㊂3㊀齿轮弯曲疲劳数值模拟3.1㊀齿轮静力学分析㊀㊀根据相关弯曲疲劳试验的夹具二维图纸,利用SolidWorks设计弯曲疲劳试验的三维模型,如图4所示,试验齿轮的相关参数,如表1所示㊂图4㊀弯曲疲劳试验三维模型Fig.4㊀3D model of bending fatigue test为了降低对关键部位的有限元分析结果精确度和降低分析所需要的时间,对弯曲疲劳试验系统三维模型进行简化分析,只保留齿轮主体作为研究对象㊂而弯曲疲劳试验的数值模拟采用Abaqus有限元分析软件,具体分析情况如下:①编辑材料属性,编辑齿轮材料42CrMo的泊松比0.28及弹性模量212GPa,材料密度设置为7800kg/m3等分析所需材料属性㊂②添加加载力,在齿面上设置为线接触,接触线的面与齿轮基圆相切,通过接触线以集中力的方式将载荷施加在轮齿表面,在加载的时候选取线上的一排结点进行加载㊂③设置约束及边界条件㊂在齿轮内孔表面进行圆柱约束,限制齿轮在x,y,z三个方向转动自由度㊂④网格的选取与划分,齿轮整体的网格类型选用较为简单的四面体等参单元(C3D4),有限元模型如图5所示㊂⑤载荷施加,在齿轮上分别加载竖直向下25kN㊁22kN㊁19kN㊁16kN㊁13kN的载荷;在分析运算后获得齿轮等效应力分布云图以及轮齿受拉侧和受压侧的应㊀478㊀机㊀㊀械㊀㊀强㊀㊀度2023年㊀力分布,提取应力云图,如图6所示㊂以给定最大载荷F =25kN 为例,当轮齿疲劳失效发生时,Mises 等效应力云图,如图6a 所示,该载荷下齿根受压侧和受拉侧的局部放大应力云图如图6b 和图6c 所示㊂由于该弯曲疲劳试验一共分为5组,每组设置不同载荷水平进行,故将不同载荷水平下轮齿发生疲劳失效时齿根的应力值列于表7㊂图5㊀齿轮有限元模型Fig.5㊀Gear finite elementmodel图6㊀F =25kN 轮齿及两侧Mises 等效应力云图Fig.6㊀F =25kN gear tooth and Mises equivalent stress cloud diagram on both sides表7㊀五组载荷下的轮齿应力情况Tab.7㊀Tooth stress under five sets of loads载荷Load /kN 2522191613齿根受压侧应力Tooth root compression side stress /MPa 187.96178.33154.01129.69105.38齿根受拉侧应力Tooth root tension side stress /MPa270.32237.88205.45173.01140.57依据表7中的数据绘制图7,从图7中可以发现,齿根受拉侧和齿根受压侧应力的倍率关系前者是后者的1.3倍左右㊂图7㊀齿根两侧应力水平Fig.7㊀Stress levels on both sides of the root将数值模拟所得的仿真应力值用σmax 来表示,用(σmax -σF )/σF 来表示数值模拟应力与理论计算之间的误差,数值模拟所得齿根受拉侧应力仿真值σmax 与理论计算所得实际齿根应力值σᶄF 与脉动循环应力σF 理论值对比,如表8所示㊂表8㊀五组载荷下齿根弯曲应力理论值与仿真值对比Tab.8㊀Comparison of theoretical value and simulation value of bending stress of tooth root under five sets of loads载荷Load /kN σᶄF /MPaσF /MPa σmax /MPa (σmax -σF )/σF25318.5292.95270.32-8.37%22280.28257.12237.88-8.09%19242.06221.14205.45-7.64%16203.81186.02173.01-7.52%13165.56150.74140.57-7.23%一直以来,都是以齿轮的弯曲应力作为齿轮弯曲疲劳寿命计算的参考,利用静强度的方法来设计齿轮疲劳寿命[13]㊂通过表8中的五组载荷下齿根弯曲应力理论值与仿真值对比分析的数据可以发现,通过数值模拟可以利用有限元仿真结果去验证齿轮弯曲疲劳寿命㊂由图8可知,以齿轮受拉侧的数值模拟应力结果作为进一步疲劳分析的数据基础㊂图8㊀齿根弯曲应力理论值与仿真值对比Fig.8㊀Comparison between theoretical value andsimulation value of tooth root bending stress㊀第45卷第2期王嘉军等:基于42CrMo 齿轮的弯曲疲劳试验研究479㊀㊀3.2㊀齿轮弯曲疲劳分析㊀㊀在Fe-Safe 中需要与材料对应的疲劳特性参数,通过对现有参数进行二次编辑的方法㊂对弯曲疲劳试验所用的42CrMo 齿轮材料,按照其弹性模量E =2.12ˑ105MPa,抗拉强度为1080MPa,在现有的材料库进行编辑设定其参数[14]1-6㊂并通过Matlab 编制载荷谱,其载荷谱如图9所示,作为Fe-Safe 中的载荷历程㊂依据Miner 线性累积损伤理论,当所有应力的寿命损伤率之和等于1时,疲劳破坏将会出现[14]1-6㊂Fe-Safe 软件将会参照这一原则,进行齿轮疲劳破坏的判定,发生疲劳破坏的单元计算终止,未发生损伤的单元运算则继续进行,当循环次数达到所设置的值107时,计算停止㊂图9㊀疲劳试验载荷谱Fig.9㊀Fatigue test load spectrum㊀㊀将疲劳寿命计算的最终结果再次导入Abaqus 中进行处理,得到齿轮对数疲劳寿命云图㊂如图10为可靠度为84.1%时,不同载荷下齿轮对数疲劳寿命云图,结果如表9所示㊂图10㊀可靠度84.1%不同载荷下齿轮对数疲劳寿命云图Fig.10㊀Stress levels on both sides of the root表9㊀可靠度84.1%时齿轮弯曲疲劳寿命Tab.9㊀Gear bending fatigue life table at 84.1%reliability 载荷Load /kN 2522191613试验寿命Testlife 9420047240019175002818700107仿真寿命Simulation life9931135481317538802426610107从图10中,可以发现不同载荷下齿轮对数疲劳寿命云图,当载荷水平在13kN 时是分界值,大于13kN的疲劳寿命小于设定值107,而当载荷水平小于等于13kN 时,齿轮的疲劳寿命可以实现无限循环即超越设定值107㊂由图11可知,可靠度在84.1%时,数值模拟得到的弯曲疲劳寿命与弯曲疲劳试验所得数据对比,可以得出采用Abaqus /Fe-Safe 所求取的疲劳寿命是可以满足设计需求的㊂4㊀结论㊀㊀结合弯曲疲劳试验数据的真实有效性与有限元数值模拟便利㊁经济性的特点,本文研究了基于42CrMo 齿轮弯曲疲劳试验,并取得了以下结论:图11㊀试验与仿真弯曲疲劳寿命对比Fig.11㊀Comparison of bending fatigue life between test and simulation1)通过对42CrMo 齿轮的弯曲疲劳试验研究,获得了42CrMo 齿轮的弯曲应力转换以及弯曲疲劳寿命数据㊂2)根据弯曲疲劳试验寿命数据,得到了42CrMo渗碳齿轮弯曲疲劳强度S-N 曲线以及P-S-N 拟合曲线关系式,以及在循环寿命为107时不同存活率下的齿轮弯曲疲劳寿命的疲劳极限应力值㊂3)利用Abaqus /Fe-Safe 估计的齿轮弯曲疲劳寿命与弯曲疲劳试验做对比,可靠度在84.1%时数值模拟可以满足齿轮弯曲疲劳寿命设计需求㊂㊀480㊀机㊀㊀械㊀㊀强㊀㊀度2023年㊀参考文献(References)[1]㊀裴未迟.重型装备传动齿轮疲劳裂纹演化试验与数值模拟研究[D].北京:北京科技大学,2021:1-5.PEI WeiChi,Experimental and numerical simulation study on fatiguecrack evolution of transmission gear of heavy equipment[D].Beijing:University of Science and Technology Beijing,2021:1-5(In Chinese).[2]㊀陈超朋,阳光武,肖守讷,等.基于疲劳寿命预测的齿轮箱箱体结构优化[J].机械强度,2021,43(2):447-452.CHEN ChaoPeng,YANG GuangWu,XIAO ShouNe,et al.Optimization of gearbox structure based on fatigue life prediction[J].Journal of Mechanical Strength,2021,43(2):447-452(InChinese).[3]㊀王雪婷.离心压缩机齿轮断裂失效机理及对策措施研究[D].广州:华南理工大学,2020:18-19.WANG XueTing.Research on gear fracture failure mechanism andcountermeasures of centrifugal compressor[D].Guangzhou:SouthChina University of Technology,2020:18-19(In Chinese). [4]㊀祁㊀倩.42CrMo调质及表面淬火齿轮齿根弯曲应力的研究[D].郑州:机械科学研究总院,2010:8-9.QI Qian.Study on bending stress of tooth root of42CrMo quenchingand surface quenching gear[D].Zhengzhou:General ResearchInstitute of Mechanical Science,2010:8-9(In Chinese).[5]㊀马㊀威.基于试验与数值模拟技术的齿轮弯曲疲劳特性研究[D].郑州:机械科学研究总院,2016:4-6.MA Wei.Research on gear bending fatigue characteristics based ontest and numerical simulation technology[D].Zhengzhou:GeneralResearch Institute of Mechanical Science,2016:4-6(In Chinese).[6]㊀王明旭,李永祥,秦㊀超,等.A35CrNiMo感应淬火齿轮弯曲疲劳强度试验[J].机械设计与研究,2018,34(6):66-69.WANG MingXu,LI YongXiang,QIN Chao,et al.Bending fatiguestrength test of A35CrNiMo induction hardened gear[J].MachineDesign&Research,2018,34(6):66-69(In Chinese). [7]㊀刘本学,郭沛东,徐科飞,等.基于Ansys Workbench的齿轮弯曲疲劳寿命分析[J].机械设计与制造,2018(2):139-141.LIU BenXue,GUO PeiDong,XU KeFei,et al.Analysis of gearbending fatigue life based on Ansys Workbench[J].MachineryDesign&Manufacture,2018(2):139-141(In Chinese).[8]㊀徐鹤鸣,黄再兴,强㊀磊,等.基于损伤本构的齿轮疲劳模型[J].机械强度,2017,39(2):417-422.XU HeMing,HUANG ZaiXing,QIANG Lei,et al.Gear fatiguemodel with damage constitutive[J].Journal of Mechanical Strength,2017,39(2):417-422(In Chinese).[9]㊀全国齿轮标准化技术委员会.齿轮弯曲疲劳强度试验方法:GB/T14230 2021[S].北京:中国标准出版社,2021:5-14.National Technical Committee on Gear of StandardizationAdministration of China.Test method for bending fatigue strength ofgears:GB/T14230 2021[S].Beijing:Standards Press of China,2021:5-14(In Chinese).[10]㊀全国齿轮标准化技术委员会.直齿轮和斜齿轮承载能力计算第3部分:轮齿弯曲强度计算:GB/T3480.3 2021[S].北京:中国标准出版社,2021:7-23.National Technical Committee on Gear of StandardizationAdministration of China.Calculation of bearing capacity of spur andhelical gears-Part3:Calculation of bending strength of gear teeth:GB/T3480.3 2021[S].Beijing:Standards Press of China,2021:7-23(In Chinese).[11]㊀全国钢标准化技术委员会.金属材料疲劳试验数据统计方案与分析方法:GB/T24176 2009[S].北京:中国标准出版社,2009:4-9.National Technical Committee on Steel of StandardizationAdministration of China.Statistical scheme and analysis method offatigue test data of metal materials:GB/T24176 2009[S].Beijing:Standards Press of China,2009:4-9(In Chinese). [12]㊀刘晓伟.P-S-N曲线估计与疲劳荷载统计建模的贝叶斯方法研究[D].哈尔滨:哈尔滨工业大学,2019:35-43.LIU XiaoWei,Study on P-S-N curve estimation and fatigue loadstatistical modeling based on bayesian method[D].Harbin:HarbinInstitute of Technology,2019:35-43(In Chinese). [13]㊀BONAITI L,BAYOUMI A,CONCLI F,et al.Gear root bendingstrength:A comparison between single tooth bending fatigue testsand meshing gears[J].Journal of Mechanical Design,2021:1-17.[14]㊀WANG W,WEI P,LIU H,et al.Damage behavior due to rollingcontact fatigue and bending fatigue of a gear using crystal plasticitymodeling[J].Fatigue&Fracture of Engineering Materials&Structures,2021:1-6.。
不锈钢齿轮的弯曲疲劳强度极限

不锈钢齿轮的弯曲疲劳强度极限不锈钢齿轮的弯曲疲劳强度极限1. 引言不锈钢齿轮是一种常见的机械传动装置,广泛应用于各种工业领域。
而在这些应用中,齿轮的弯曲疲劳强度极限是决定其使用寿命和可靠性的关键因素之一。
本文将以不锈钢齿轮的弯曲疲劳强度极限为主题,通过对其深入探讨,帮助读者更全面、深刻地了解这一重要参数。
2. 不锈钢简介2.1 不锈钢的特点不锈钢是一种具有耐腐蚀性和耐高温性的合金材料,其主要成分为铁、铬、镍等元素。
不锈钢齿轮由于其抗腐蚀性能、机械性能和可靠性等优势,被广泛应用于食品、化工、船舶等领域。
3. 弯曲疲劳强度极限的定义3.1 弯曲疲劳强度弯曲疲劳强度指的是在一定循环次数下,材料在受到弯曲载荷时发生裂纹的能力,通常以弯曲疲劳极限承载力来表示。
对于不锈钢齿轮来说,其弯曲疲劳强度极限决定了其在使用寿命内能否承受弯曲载荷而不发生裂纹。
4. 影响弯曲疲劳强度的因素4.1 材料性能不锈钢齿轮的弯曲疲劳强度受到材料的力学性能和化学成分的影响。
其中,硬度、弹性模量、塑性和疲劳极限等是影响弯曲疲劳强度的重要因素。
4.2 加工工艺不锈钢齿轮在生产过程中经历了材料的锻造、加工、淬火等工艺。
合理的加工工艺可以提高不锈钢齿轮的弯曲疲劳强度极限,而不当的加工则会导致弯曲疲劳强度降低。
4.3 载荷作用方式不锈钢齿轮在使用过程中承受着不同形式和强度的载荷作用,如交变载荷、冲击载荷等。
载荷作用方式直接影响着齿轮的弯曲疲劳强度极限,不同载荷作用下的弯曲疲劳强度极限有所不同。
5. 不锈钢齿轮的弯曲疲劳寿命评估方法5.1 查表法通过查阅相关表格,可以得到不同材料、不同载荷下的弯曲疲劳强度极限值。
在实际应用中,可以通过实测载荷与查表值相对比,进而评估不锈钢齿轮的弯曲疲劳寿命。
5.2 标准试验法通过将不锈钢齿轮进行标准化试验,测得其在不同载荷条件下的弯曲疲劳寿命,从而评估其弯曲疲劳强度极限。
这种方法相对繁琐,但可以提供更准确的结果。
齿轮疲劳强度计算

######################################################################## ## 渐开线圆柱齿轮疲劳强度计算法## ## ( GB/T3480-97,ISO6336-1996 ) ## ## 2014-03-14 ################郑州机械研究所################ 09:47:49 ##------------------基本输入参数--------------------------小轮总扭矩(N.m)T = 1475.0小轮转速(转/分)RPM1 = 354.0大轮转速(转/分)RPM2 = 91.624实际速比U = 3.8636中心距(mm) A = 275.001法向模数(mm)Mn = 5.0螺旋角(度)β= 11.0法向齿形角(度)αn = 20.0------------------------------------------------------------------------------------------------------小齿轮大齿轮齿轮齿数Z = 22 85总有效齿宽(mm) B = 110.0 110.0变位系数Xn = 0.3886 0.1262齿顶高系数Ha* = 1.0 1.0顶隙系数Cn* = 0.25 0.25------------------齿轮几何参数-----------------------------------------------------------小齿轮大齿轮分度圆直径(mm) D = 112.059 432.955节圆直径(mm) Dp = 113.084 436.917基圆直径(mm) Db = 105.069 405.948顶圆直径(mm) Da = 125.785 444.056根圆直径(mm) Df = 103.445 421.717齿顶厚(mm) Sa = 2.937 4.021滑动率η= 0.991 0.991分度圆线速度(m/s) V = 2.077齿轮精度等级(GB 10095-1988) IQ = 6端面重合度εα= 1.525轴向重合度εβ= 1.336------------------材料及热处理等参数---------------------------------------------------------- 传动类型:减速传动齿轮啮合类型:外啮合螺旋角类型:斜齿修形方式:齿向倒坡或有装配调整小轮材料和热处理类型:渗碳淬火钢大轮材料和热处理类型:渗碳淬火钢设计寿命:10.0 年24小时/每天总设计寿命:86400 小时50 度时润滑油粘度(cSt)= 220.0齿面硬度HB/HRc = 60 58 弹性模量 E = 206000 206000 小齿轮疲劳计算基本载荷(N.m) Tn1 = 1475.0切向力(N) Ft = 26325.456径向力(N) Fr = 9761.02轴向力(N) Fx = 5117.15接触载荷系数(MPa) K = 2.688临界转速比N = 0.038单对齿刚度Cp = 14.543啮合刚度CG = 20.267------------------ 接触强度计算系数--------------------------------------------------------- 使用系数KA = 2.000动载系数Kv = 1.025齿向载荷分布系数KHβ= 1.346齿间载荷分配系数KHα= 1.000节点区域系数ZH = 2.371弹性系数ZE = 189.812重合度系数Zε= 0.810螺旋角系数Zβ= 0.991小齿轮大齿轮寿命系数Znt = 0.896 0.933 润滑系数ZL = 1.057 1.057 速度系数Zv = 0.965 0.965 粗糙度系数Zr = 0.973 0.973 工作硬化系数Zw = 1.000 1.000 尺寸系数Zx = 1.000 1.000 单对齿啮合系数ZBD = 1.000 1.000 ----------------- 弯曲强度计算系数--------------------------------------------------------- 动载系数Kv = 1.025齿向载荷分布系数KFβ= 1.306齿间载荷分配系数KFα= 1.000重合度系数Yε= 0.726螺旋角系数Yβ= 0.908小齿轮大齿轮齿形系数YF = 1.186 1.332应力修正系数YS = 2.235 2.150寿命系数Ynt = 0.880 0.904尺寸系数Yx = 1.000 1.000相对齿根圆角敏感系数Yδrelt = 0.999 1.000相对齿根表面状况系数YRrelt = 1.002 1.002 轮缘系数YBM = 1.000 1.000 齿根圆角半径系数ρF = 0.447 0.450******************** 接触强度计算结果********************************小齿轮大齿轮实验齿轮接触疲劳极限(MPa) σHlim = 1350.00 1350.00 计算齿轮接触极限应力(MPa) σHG = 1199.65 1250.30 许用接触应力(MPa) σHP = 959.72 1000.24 计算接触应力(MPa) σH = 983.65 983.65 计算接触强度安全系数SH = 1.220 1.271 最小接触强度安全系数SHmin = 1.250 1.250 ******************** 弯曲强度计算结果********************************小齿轮大齿轮实验齿轮弯曲疲劳极限(MPa) σFlim = 350.00 350.00 计算齿轮弯曲极限应力(MPa) σFG = 616.33 633.72 许用齿根应力(MPa) σFP = 410.89 422.48 计算齿根应力(MPa) σF = 308.59 333.37 计算弯曲强度安全系数SF = 1.997 1.901 最小弯曲强度安全系数SFmin = 1.500 1.500 --------------------------------------------------------------。
齿轮参考
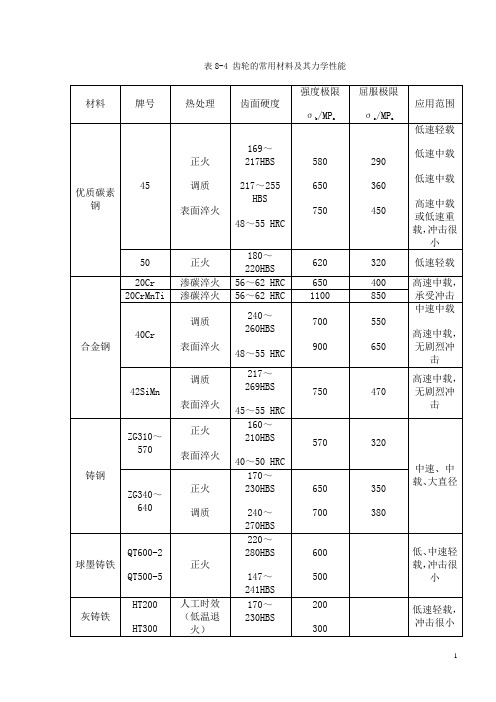
表8-4 齿轮的常用材料及其力学性能2. 许用应力齿轮的许用应力是根据试验齿轮的疲劳极限确定的,与齿轮材料和齿面硬度有关。
齿面接触疲劳许用应力[]minlim H H H S σσ= (8-16)齿根弯曲疲劳许用应力[]minlim F F F S σσ= (8-17)式中:σHlim ——试验齿轮材料的接触疲劳极限,MPa ; 由图8-29查取。
σFlim ——齿轮的弯曲疲劳极限,MPa ;由图8-30查取。
如果齿轮双向长期工作(经常正、反转动的齿轮),σFlim 应取正常值的70% 。
图8-29齿轮材料的接触疲劳强度极σHlim图8-30 齿轮材料的弯曲疲劳强度极σFlimS Hmin,S Fmin——齿面接触疲劳强度的最小安全系数和齿根疲劳弯曲强度的最小安全系数。
S Hmin和S Fmin的值查表8-5。
表8-5 最小安全系数齿轮精度等级的选择,应当根据齿轮的用途、使用条件、圆周速度和功率的大小,合理的确定齿轮的经济技术指标。
8.6.3 渐开线标准直齿圆柱齿轮传动的强度计算1. 齿轮的受力分析和计算载荷(1) 圆柱齿轮传动的受力分析。
在计算齿轮强度时必须首先分析作用在齿轮上的力,如果忽略齿轮齿面之间的摩擦力,在理想情况下,作用在齿面上的力是沿接触线均匀分布且垂直与齿面,常用集中力F n表示,F n称为法向力,由渐开线齿廓啮合特点(见8.2.2节)可知,在传动过程中F n是沿啮合线作用于齿面且保持方向不变。
图8-31表示一直齿圆柱齿轮传动在节点C处的受力情况。
不考虑摩擦力,作用在齿面上的法向力F n可分解为圆周力F t和径向力F r。
图8-31 直齿圆柱齿轮的受力分析各力的计算公式为αααcos2costan21111dTFFFFdTFtntrt====(8-18)式中:T1——为主动轮传递的扭矩,N·mm;d1——主动轮分度圆直径, mm;α——压力角。
如果小齿轮传递的功率为P1(kW),转速为n1(r/min),则11611055.9nPT⨯=(8-19)(2) 计算载荷。
借助直齿轮齿根弯曲疲劳计算公式

思考:
1. 2. 一对齿轮啮合,两齿轮的σH1=σH2吗? 计算σH2时,公式是否代入T2,d2值计算?
3.
从公式说明如何提高轮齿的接触疲劳强度?
12.4.2齿根弯曲疲劳强度
一、确定危险截面: 1.视轮齿为一个悬臂梁; 2.假定Fn作用在齿顶处; 3.危险截面的确定: 采用30°切线法确定。 二、公式推导:
2. 公差组
齿轮的精度指标由4部分组成,即三组公差等级和齿侧间隙。
(1)第Ⅰ公差组(传动的准确性)
要求齿轮在传动时,从动轮在转一圈范围内,其转角误差的最 大值不超过许用值。
(2)第Ⅱ公差组(传动的平稳性)
要求瞬时传动比的变化不超过允许的限度。当齿形或齿距存在 制造误差时,瞬时传动比不为常数,使转速发生波动,从而引 起振动、冲击和噪声。
Ft1
Fn1 n1 Fr2 d1 o1
Ft2
T1
二、计算载荷
由于轴和轴承的变形、传动装 置的制造和安装误差等原因,载荷 沿齿宽的分布并不是均匀的,即出 现载荷集中现象。 各种原动机和工作机的特性不同、 齿轮制造误差以及轮齿变形等原因, 还会引起附加动载荷。精度越低、 圆周速度越高,附加动载荷就越大。 计算载荷:
4.力求材料品种少,便于管理,考虑资源和供应情况。
5.当结构尺寸要求紧凑,耐磨性高时,要采用合金钢。 6.制造单位的设备及技术情况。
12.2 齿轮的精度
1. 精度等级
我国在GB100912-88齿轮精度标准中,将齿轮精度 分为12个等级,按精度高低依次为1~12级。 其中,1、2级是待发展级;3、4、5级为高精度级; 6、7、8级属中等精度级; 9、10、11、12级属于低精度级。 其中一般齿轮传动常用的精度等级为6~9级。
25Cr2Ni4WA合金钢渗碳淬火齿轮的弯曲疲劳试验分析

5 试验 数据 及数 据处 理结 果
6 结束 语
1 本试 验研 究 获得 了完整 的试 验 数据 , 以在 完 ) 可 整 的弯 曲疲 劳 曲线 基 础上 准确求 得 轮齿 弯 曲持 久疲 劳
极限 , 纠正 了 以往采 用 疲 劳 曲线 倾 斜段 外 延 法所 引起
l . 4 —0 9 2 0 4 7.5 90 25 .6 9 121
l . 2 -0 9 8 2 88 78 . 6 4 .7 913 2 2 1 .2 - 9 0 l 85 3 l 0. 5 4 86 50 7 .8
t x m
基节 残 余 变 形 量 平 均 值
图 2 对 数 正 态 分 布 下 的 C- S N 曲线 ( - R- - R=09 - .9 .0 09 )
这 就 存在 置 信 度 的问题 。齿 轮设 计 可 靠 度要 求 不 同 , 其 极 限应 力 值不 同 , 因而 齿 轮 的尺 寸也 不 同。 不 同可 靠 度 时 的极 限应 力 值 , 根据 齿 轮 疲 劳试 验所 得 的应 是 力一 寿命 样 本 , 经分 析 处理 求 得 的 。 因此 , 确定 合 理 的 置信度 和 可靠度 是数 据 分析 的基础 。本次数 据 处理 中 的置 信 度 为 9 %, 5 短寿 命 区 分别 采 用 对数 正 态 分 布拟 合 ; 寿命 区的疲 劳极 限强 度分 布按 正态 分布 处理 , 长 拟 合 出齿 轮 的 Ⅳ曲线方 程 , 即置 信度 一 可靠度 一 疲 劳强度一 寿命 曲 线 方 程 , 而 求 得 具 有 规 定 置 信 度 和 进
9 9 9.9
4.8 7 32
l _ 5l2 - 9l 82 0. 2 l
