神经网络BP网络 数学建模【精选】
数学建模竞赛-神经网络

神经网络例解:设计BP网,编写文件ch14eg4.m,结构和参数见程序中的说明。
clear;close all;x = [0:0.25:10]; y = 0.12*exp(-0.213*x)+0.54*exp(-0.17*x).*sin(1.23*x); % x,y分别为输入和目标向量net=newff(minmax(x),[20,1],{'tansig','purelin'}); % 创建一个前馈网络y0 = sim(net,x); % 仿真未经训练的网络netnet.trainFcn='trainlm'; % 采用L-M优化算法TRAINLMnet.trainParam.epochs = 500; net.trainParam.goal = 1e-6; % 设置训练参数[net,tr]=train(net,x,y); % 调用相应算法训练网络y1 = sim(net,x); % 对BP网络进行仿真E = y-y1; MSE=mse(E) % 计算仿真误差figure; % 下面绘制匹配结果曲线plot(x,y0,':',x,y1,'r*',x,0.12*exp(-0.213*x)+0.54*exp(-0.17*x).*sin(1.23*x),'b');运行如下:>> ch14eg4MSE =9.6867e-007例14.6 蠓虫分类问题。
两种蠓虫Af和Apf已由生物学家W.L.Grogan和W.W.Wirth(1981)根据他们的触角长度和翅长加以区分。
现测得6只Apf蠓虫和9只Af蠓虫的触长、翅长的数据如下:Apf: (1.14,1.78),(1.18,1.96),(1.20,1.86),(1.26,2.),(1.28,2.00),(1.30,1.96).Af: (1.24,1.72),(1.36,1.74),(1.38,1.64),(1.38,1.82),(1.38,1.90),(1.4,1.7),(1.48,1.82),(1.54,1.82),(1.56,2.08)请用恰当的方法对触长、翅长分别为(1.24,1.80),(1.28,1.84),(1.40,2.04)的3个样本进行识别。
数学建模实验五:风电功率预测问题

实验五风电功率预测问题一、实验目的(1)学习和掌握马尔科夫链预测方法;(2)掌握三次指数平滑预测方法;(3)掌握BP神经网络预测方法;(4)掌握NAR时间序列的动态神经网络进行预测等二、实验步骤2.1 问题提出:某风电场由58台风电机组构成,每台机组的额定输出功率为85kw。
附件2中给出了2006年5月10日~2006年6月6日时间段内该风电场中指定的四台风电机组(A,B,C和D)每隔15分钟的输出功率数据(分别记为PA、PB、PC和PD;另设该四台机组总输出功率为P4)及全场58台机组总输出功率数据(记为P58)。
问题1:风电功率实时预测及误差分析。
请对给定数据进行风电功率实时预测并检验预测结果是否满足附件1中的关于预测精度的相关要求。
具体要求:(1)采用不少于三种预测方法(至少选择一种时间序列分析类的预测方法)。
(2)预测量:a. PA,PB,PC,PD;b. P4c. P58(3)预测时间范围分别为(预测用的历史数据范围可自行选定)a. 5月31日0时0分至5月31日23时45分;b. 5月31日0时0分至6月6日23时45分。
(4)试根据附件1中关于实时预测的考核要求分析你所采用方法的准确性。
(5)你推荐哪种方法?问题2:试分析风电机组的汇聚对于预测结果误差的影响。
在我国主要采用集中开发的方式开发风电,各风电机组功率汇聚通过风电场或风电场群(多个风电场汇聚而成)接入电网。
众多风电机组的汇聚会改变风电功率波动的属性,从而可能影响预测的误差。
在问题1的预测结果中,试比较单台风电机组功率(PA、PB、PC、PD)的相对预测误差与多机总功率(P4,P58)预测的相对误差,其中有什么带有普遍性的规律吗?从中你能对风电机组汇聚给风电功率预测误差带来的影响做出什么样的预期?问题3:进一步提高风电功率实时预测精度的探索。
提高风电功率实时预测的准确程度对改善风电联网运行性能有重要意义。
请你在问题1的基础上,构建有更高预测精度的实时预测方法,并用预测结果说明其有效性。
BP神经网络PPT全文

输出层与隐含层的激活函数可以不同,并且输出层
各单元的激活函数可有所区别
2024/8/16
26
2 多层网络的表达能力
按照Kolmogorov定理,任何一个判决均可用 前式所示的三层神经网络实现。
即: 只要给定足够数量的隐含层单元、适 当的非线性函数、以及权值, 任何由输入向输 出的连续映射函数均可用一个三层前馈神经网络 实现。
神经网络的计算通过网络结构实现;
不同网络结构可以体现各种不同的功能;
网络结构的参数是通过学习逐渐修正的。
2024/8/16
7
(1)基本的人工神经元模型
McCulloch-Pitts神经元模型
输入信号;链接强度与权向量;
信号累积
2024/8/16
激活与抑制
8
人工神经元模型的三要素 :
一组连接 一个加法器 一个激励函数
➢ 树突(dendrites), 接收来自外接的信息 ➢ 细胞体(cell body), 神经细胞主体,信息加工 ➢ 轴突(axon), 细胞的输出装置,将信号向外传递,
与多个神经元连接 ➢突触 (synapsse), 神经元经突触向其它神经元(胞体 或树突)传递信号
2024/8/16
5
(2)生物神经元的基本特征
5 假定:第l层为当前处理层;
其前一层l 1、当前层l、后一层l 1的计算单元序号为i, j,k;
位于当前层第j个计算单元的输出为Olj,j 1,..., nl
前层第i个单元到本层第j个单元的连接权值为ilj , i 1,..., nl1
本层第j个单元到后层第k个单元的连接权值为
l 1 jk
,
连接权值,突触连接强度
BP神经网络及简单示例ppt课件

1
0.8
0.6
0.4
0.2
0
-0.2
-0.4
-0.6
-0.8
-1
-10 -8 -6 -4 -2
0
2
4
6
8 10
.
newff
常用函数
创建一个BP网络,其调用格式为:
net=newff
net=newff(PR,[S1 S2 …SN1],{TF1 TF2…TFN1},BTF,BLF,PF)
输入层
i
中间层 j
输出层
k
xi
ji .
kj
n
p
V kf( (f( (xiji))k)j)0或 1
j1
i1
输入层
i
中间层 j
输出层
k
xi
ji
kj
2、通过已知样本训练出合适的权值 ji、kj
使输出为(0,1)或(1,0)。
3、将待区分的蠓虫数据输入网络,求值。 .
权值求法:向后传播法
理想输出 Af类(1,0),Apf类(0,1)记为 { Tis}
.
应用范围
医学:疾病识别
图像:识别、去噪、增强、配准、 融合
金融:股票和有价证券的预测分 析、资本收益的预测和分析、风 险管理、信用评估等等
.
神经网络结构图
输入层
中间层
输出层
.
生物神经元结构:
树突
细胞体
细胞核
轴突
.
突触 神经末梢
神经元结构模型
x1
x2
x3
xj
ij
BP神经网络模型应用实例

BP神经网络模型第1节基本原理简介近年来全球性的神经网络研究热潮的再度兴起,不仅仅是因为神经科学本身取得了巨大的进展.更主要的原因在于发展新型计算机和人工智能新途径的迫切需要.迄今为止在需要人工智能解决的许多问题中,人脑远比计算机聪明的多,要开创具有智能的新一代计算机,就必须了解人脑,研究人脑神经网络系统信息处理的机制.另一方面,基于神经科学研究成果基础上发展出来的人工神经网络模型,反映了人脑功能的若干基本特性,开拓了神经网络用于计算机的新途径.它对传统的计算机结构和人工智能是一个有力的挑战,引起了各方面专家的极大关注.目前,已发展了几十种神经网络,例如Hopficld模型,Feldmann等的连接型网络模型,Hinton等的玻尔茨曼机模型,以及Rumelhart等的多层感知机模型和Kohonen的自组织网络模型等等。
在这众多神经网络模型中,应用最广泛的是多层感知机神经网络。
多层感知机神经网络的研究始于50年代,但一直进展不大。
直到1985年,Rumelhart等人提出了误差反向传递学习算法(即BP算),实现了Minsky的多层网络设想,如图34-1所示。
BP 算法不仅有输入层节点、输出层节点,还可有1个或多个隐含层节点。
对于输入信号,要先向前传播到隐含层节点,经作用函数后,再把隐节点的输出信号传播到输出节点,最后给出输出结果。
节点的作用的激励函数通常选取S 型函数,如Qx e x f /11)(-+=式中Q 为调整激励函数形式的Sigmoid 参数。
该算法的学习过程由正向传播和反向传播组成。
在正向传播过程中,输入信息从输入层经隐含层逐层处理,并传向输出层。
每一层神经元的状态只影响下一层神经输入层 中间层 输出层 图34-1 BP 神经网络模型元的状态。
如果输出层得不到期望的输出,则转入反向传播,将误差信号沿原来的连接通道返回,通过修改各层神经元的权值,使得误差信号最小。
社含有n 个节点的任意网络,各节点之特性为Sigmoid 型。
数学建模实验四:Matlab神经网络以及应用于汽油辛烷值预测

实验四:Matlab 神经网络以及应用于汽油辛烷值预测专业年级: 2014级信息与计算科学1班姓名: 黄志锐 学号:201430120110一、实验目的1. 掌握MATLAB 创建BP 神经网络并应用于拟合非线性函数2. 掌握MATLAB 创建REF 神经网络并应用于拟合非线性函数3. 掌握MATLAB 创建BP 神经网络和REF 神经网络解决实际问题4. 了解MATLAB 神经网络并行运算二、实验内容1. 建立BP 神经网络拟合非线性函数2212y x x =+第一步 数据选择和归一化根据非线性函数方程随机得到该函数的2000组数据,将数据存贮在data.mat 文件中(下载后拷贝到Matlab 当前目录),其中input 是函数输入数据,output 是函数输出数据。
从输入输出数据中随机选取1900中数据作为网络训练数据,100组作为网络测试数据,并对数据进行归一化处理。
第二步 建立和训练BP 神经网络构建BP 神经网络,用训练数据训练,使网络对非线性函数输出具有预测能力。
第三步 BP 神经网络预测用训练好的BP 神经网络预测非线性函数输出。
第四步 结果分析通过BP 神经网络预测输出和期望输出分析BP 神经网络的拟合能力。
详细MATLAB代码如下:27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54disp(['神经网络的训练时间为', num2str(t1), '秒']);%% BP网络预测% 预测数据归一化inputn_test = mapminmax('apply', input_test, inputps); % 网络预测输出an = sim(net, inputn_test);% 网络输出反归一化BPoutput = mapminmax('reverse', an, outputps);%% 结果分析figure(1);plot(BPoutput, ':og');hold on;plot(output_test, '-*');legend('预测输出', '期望输出');title('BP网络预测输出', 'fontsize', 12);ylabel('函数输出', 'fontsize', 12);xlabel('样本', 'fontsize', 12);% 预测误差error = BPoutput-output_test;figure(2);plot(error, '-*');title('BP神经网络预测误差', 'fontsize', 12);ylabel('误差', 'fontsize', 12);xlabel('样本', 'fontsize', 12);figure(3);plot((output_test-BPoutput)./BPoutput, '-*');title('BP神经网络预测误差百分比');errorsum = sum(abs(error));MATLAB代码运行结果截图如下所示:MATLAB代码运行结果如下所示:图1 BP神经网络预测输出图示图2 BP神经网络预测误差图示图3 BP 神经网络预测误差百分比图示2. 建立RBF 神经网络拟合非线性函数22112220+10cos(2)10cos(2)y x x x x ππ=-+-第一步 建立exact RBF 神经网络拟合, 观察拟合效果详细MATLAB 代码如下:MATLAB代码运行结果如下所示:图4 RBF神经网络拟合效果图第二步建立approximate RBF神经网络拟合详细MATLAB代码如下:13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41F = 20+x1.^2-10*cos(2*pi*x1)+x2.^2-10*cos(2*pi*x2); %% 建立RBF神经网络% 采用approximate RBF神经网络。
BP神经网络

BP神经⽹络2013参考数学建模常⽤⽅法:数学建模常⽤⽅法系列资料由圣才⼤学⽣数学建模竞赛⽹整理收集。
希望能对您有所帮助!BP神经⽹络⽅法摘要⼈⼯神经⽹络是⼀种新的数学建模⽅式,它具有通过学习逼近任意⾮线性映射的能⼒。
本⽂提出了⼀种基于动态BP神经⽹络的预测⽅法,阐述了其基本原理,并以典型实例验证。
关键字神经⽹络,BP模型,预测1 引⾔在系统建模、辨识和预测中,对于线性系统,在频域,传递函数矩阵可以很好地表达系统的⿊箱式输⼊输出模型;在时域,Box-Jenkins⽅法、回归分析⽅法、ARMA模型等,通过各种参数估计⽅法也可以给出描述。
对于⾮线性时间序列预测系统,双线性模型、门限⾃回归模型、ARCH模型都需要在对数据的内在规律知道不多的情况下对序列间关系进⾏假定。
可以说传统的⾮线性系统预测,在理论研究和实际应⽤⽅⾯,都存在极⼤的困难。
相⽐之下,神经⽹络可以在不了解输⼊或输出变量间关系的前提下完成⾮线性建模[4,6]。
神经元、神经⽹络都有⾮线性、⾮局域性、⾮定常性、⾮凸性和混沌等特性,与各种预测⽅法有机结合具有很好的发展前景,也给预测系统带来了新的⽅向与突破。
建模算法和预测系统的稳定性、动态性等研究成为当今热点问题。
⽬前在系统建模与预测中,应⽤最多的是静态的多层前向神经⽹络,这主要是因为这种⽹络具有通过学习逼近任意⾮线性映射的能⼒。
利⽤静态的多层前向神经⽹络建⽴系统的输⼊/输出模型,本质上就是基于⽹络逼近能⼒,通过学习获知系统差分⽅程中的⾮线性函数。
但在实际应⽤中,需要建模和预测的多为⾮线性动态系统,利⽤静态的多层前向神经⽹络必须事先给定模型的阶次,即预先确定系统的模型,这⼀点⾮常难做到。
近来,有关基于动态⽹络的建模和预测的研究,代表了神经⽹络建模和预测新的发展⽅向。
2BP神经⽹络模型BP⽹络是采⽤Widrow-Hoff学习算法和⾮线性可微转移函数的多层⽹络。
典型的BP 算法采⽤梯度下降法,也就是Widrow-Hoff算法。
BP神经网络算法

1
目
录
一、BP神经网络算法概述
二、BP神经网络算法原理
三、BP神经网络算法特点及改进
2
一.BP神经网络算法概述
BP神经网络(Back-Propagation Neural Network),即误差
后向传播神经网络,是一种按误差逆向传播算法训练的多层前馈网
络,是目前应用最广泛的网络模型之一。
11
二.BP神经网络算法原理
图5 Tan-Sigmoid函数在(-4,4)范围内的函数曲线
12
二.BP神经网络算法原理
激活函数性质:
① 非线性
② 可导性:神经网络的优化是基于梯度的,求解梯度需要确保函
数可导。
③ 单调性:激活函数是单调的,否则不能保证神经网络抽象的优
化问题转化为凸优化问题。
④ 输出范围有限:激活函数的输出值范围有限时,基于梯度的方
= 1
=1
7
,
= 1,2,3 … , q
二.BP神经网络算法原理
输出层节点的输出为:
j = 2 ,
= 1,2,3. . . ,
=1
至此,BP网络完成了n维空间向量对m维空间的近似映射。
图2 三层神经网络的拓扑结构
8
二.BP神经网络算法原理
BP神经网络是多层前馈型神经网络中的一种,属于人工神经网
络的一类,理论可以对任何一种非线性输入输出关系进行模仿,因
此 被 广 泛 应 用 在 分 类 识 别 ( classification ) 、 回 归
(regression)、压缩(compression)、逼近(fitting)等领域。
在工程应用中,大约80%的神经网络模型都选择采用BP神经网
(完整版)BP神经网络matlab实例(简单而经典)

p=p1';t=t1';[pn,minp,maxp,tn,mint,maxt]=premnmx(p,t); %原始数据归一化net=newff(minmax(pn),[5,1],{'tansig','purelin'},'traingdx');%设置网络,建立相应的BP网络net.trainParam.show=2000; % 训练网络net.trainParam.lr=0.01;net.trainParam.epochs=100000;net.trainParam.goal=1e-5;[net,tr]=train(net ,pn,tn); %调用TRAINGDM算法训练BP 网络pnew=pnew1';pnewn=tramnmx(pnew,minp,maxp);anewn=sim(net,pnewn); %对BP网络进行仿真anew=postmnmx(anewn,mint,maxt); %还原数据y=anew';1、BP网络构建(1)生成BP网络=net newff PR S S SNl TF TF TFNl BTF BLF PF(,[1 2...],{ 1 2...},,,)PR:由R维的输入样本最小最大值构成的2R⨯维矩阵。
S S SNl:各层的神经元个数。
[ 1 2...]{ 1 2...}TF TF TFNl:各层的神经元传递函数。
BTF:训练用函数的名称。
(2)网络训练[,,,,,] (,,,,,,)=net tr Y E Pf Af train net P T Pi Ai VV TV(3)网络仿真=[,,,,] (,,,,)Y Pf Af E perf sim net P Pi Ai T{'tansig','purelin'},'trainrp'2、BP网络举例举例1、%traingdclear;clc;P=[-1 -1 2 2 4;0 5 0 5 7];T=[-1 -1 1 1 -1];%利用minmax函数求输入样本范围net = newff(minmax(P),T,[5,1],{'tansig','purelin'},'trainrp');net.trainParam.show=50;%net.trainParam.lr=0.05;net.trainParam.epochs=300;net.trainParam.goal=1e-5;[net,tr]=train(net,P,T);net.iw{1,1}%隐层权值net.b{1}%隐层阈值net.lw{2,1}%输出层权值net.b{2}%输出层阈值sim(net,P)举例2、利用三层BP神经网络来完成非线性函数的逼近任务,其中隐层神经元个数为五个。
BP网络(数学建模)
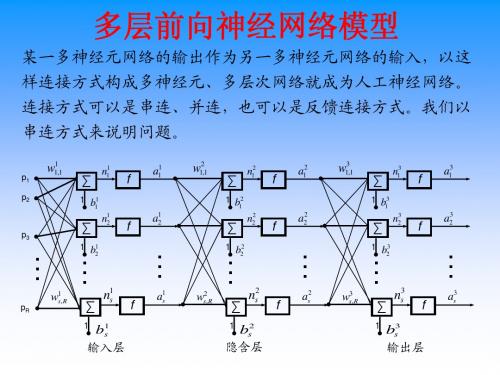
某一多神经元网络的输出作为另一多神经元网络的输入,以这 样连接方式构成多神经元、多层次网络就成为人工神经网络。 连接方式可以是串连、并连,也可以是反馈连接方式。我们以 串连方式来说明问题。
p1 p2
1 w1,1
∑
1
1 b1
1 n1
f
1 a1
w12,1
∑
1
n12
f
a12
w13,1
∑
1
n13
f
a13
b12
2 n2
b13
3 n2
p3
∑
1
1 b2
n1 2
f
a1 2
∑
1
2 b2
f
2 a2
∑
1
3 b2
f
3 a2
…
…
…
…
pR
…
∑
1
…
…
w1,R s
n1 s
f
a1 s
ws2,R
∑
1
ns2
f
as2
ws3,R
∑
1
ns3
f
as3
1 bs 输入层
b s2 隐含层
b s3 输出层
多层前向神经网络模型
δpk-1= fk-1′(xp) (wp1δ1k+ wp2δ2k+…+ wpmδm k)
2、隐藏层权的调整
vhp=vhp+∆vhp ∆vhp=εδpk-1yhk-2 =εfk-1 ′(xp)( wp1δ1k+ wp2δ2k+…+ wpmδmk)yhk-2 =εypk-1(1-ypk-1)( wp1δ1k+ wp2δ2k+…+ wpmδmk)ohk-2
BP神经网络模型与学习算法

BP神经网络模型与学习算法BP(Back Propagation)神经网络模型是一种常用的人工神经网络模型,主要用于分类和回归问题。
BP网络由输入层、隐含层和输出层组成,利用反向传播算法进行学习和训练。
下面将详细介绍BP神经网络模型和学习算法。
-输入层:接受外界输入的数据,通常是特征向量。
-隐含层:对输入层特征进行非线性处理,并将处理后的结果传递给输出层。
-输出层:根据隐含层的输出结果进行分类或回归预测。
前向传播:从输入层到输出层逐层计算神经元的输出值。
对于每个神经元,输入信号经过带权和的线性变换,然后通过激活函数进行非线性变换,得到神经元的输出值,该值作为下一层神经元的输入。
-具有较强的非线性映射能力,可以用来解决复杂的分类和回归问题。
-学习能力强,能够从大量的训练样本中学习到隐藏在数据中的模式和规律。
-适用于处理多输入多输出问题,可以构建具有多个输入和输出的神经网络模型。
然而,BP神经网络模型也存在一些不足之处,包括:-容易陷入局部最优解,当网络层数较多时,很容易陷入局部极小点。
-对输入数据的数值范围敏感,需要对输入数据进行归一化处理,以避免权值的不平衡。
-训练时间较长,需要较大的训练集和较多的迭代次数才能达到较好的训练效果。
总结来说,BP神经网络模型是一种常用的人工神经网络模型,通过反向传播算法来实现网络的学习和训练。
BP神经网络模型具有较强的非线性映射能力和学习能力,适用于解决复杂的分类和回归问题。
然而,BP 神经网络模型也存在局部最优解问题和对输入数据的敏感性等不足之处。
因此,在实际应用中需要根据具体问题选择合适的算法和模型。
基于遗传和改进布谷鸟算法的_BP_神经网络建模

第42卷第4期2023年8月沈㊀阳㊀理㊀工㊀大㊀学㊀学㊀报JournalofShenyangLigongUniversityVol 42No 4Aug 2023收稿日期:2022-07-15基金项目:辽宁省高等学校创新人才支持计划项目(2019058)作者简介:王秀莲(1965 )ꎬ女ꎬ教授ꎬ博士ꎬ研究方向为先进控制理论及应用ꎮ文章编号:1003-1251(2023)04-0019-07基于遗传和改进布谷鸟算法的BP神经网络建模王秀莲1ꎬ吴有根1ꎬ高宏伟1ꎬ胡㊀广2(1.沈阳理工大学自动化与电气工程学院ꎬ沈阳110159ꎻ2.沈阳航天新光集团有限公司ꎬ沈阳110861)摘㊀要:针对现代工业系统具有高度非线性的特点ꎬ以及采用BP神经网络对非线性系统建模易出现局部最优㊁过拟合或欠拟合的问题ꎬ提出采用遗传算法(GA)和改进布谷鸟算法(CS)优化BP神经网络建模的方法(GACSBP算法)ꎮ首先利用遗传算法自适应㊁全局搜索的特点优化神经网络拓扑结构ꎬ避免神经网络建模出现过拟合或欠拟合的问题ꎻ然后采用改进布谷鸟算法优化BP神经网络权值ꎬ加入惩罚项进一步防止神经网络建模时陷入局部最优ꎮ对NACA0012翼型自噪声数据进行建模ꎬ仿真结果表明ꎬ与BP神经网络相比ꎬ提出的GACSBP算法避免了局部最优ꎬ明显提高了模型预测精度ꎬ且所需迭代次数和时间均明显减少ꎮ关㊀键㊀词:BP神经网络建模ꎻ遗传算法ꎻ改进布谷鸟算法ꎻ惩罚项中图分类号:N945.12文献标志码:ADOI:10.3969/j.issn.1003-1251.2023.04.004BPNeuralNetworkModelingMethodBasedonGeneticAlgorithmandImprovedCuckooAlgorithmWANGXiulian1ꎬWUYougen1ꎬGAOHongwei1ꎬHUGuang2(1.ShenyangLigongUniversityꎬShenyang110159ꎬChinaꎻ2.ShenyangAerospaceXinguangGroupCo.ꎬLtd.ꎬShenyang110861ꎬChina)Abstract:AimingatthecharacteristicsofhighnonlinearityofmodernindustrialsystemsandtheproblemsoflocaloptimalityꎬoverfittingorunderfittingofmodelnonlinearsystemsbyusingBPneuralnetworksꎬamethodforoptimizingBPneuralnetworkmodeling(GACSBPalgorithm)usinggeneticalgorithm(GA)andimprovedcuckooalgorithm(CS)isproposed.Firstlyꎬthecharacteristicsofself ̄learningꎬself ̄adaptationandglobalsearchofge ̄neticalgorithmareusedtooptimizethetopologystructureofneuralnetworktoavoidover ̄fittingorunder ̄fittinginneuralnetworkmodeling.ThentheimprovedcuckooalgorithmisusedtooptimizetheweightsoftheBPneuralnetworkꎬandapenaltyitemisaddedtofurtherpreventtheneuralnetworkfromfallingintothelocaloptimumwhenmodeling.ModelingtheNACA0012airfoilself ̄noisedataꎬtheresultsshowthatcomparedwiththeBPneuralnetworkꎬtheproposedGACSBPalgorithmavoidslocaloptimizationꎬsignificantlyimprovesthepredictionaccuracyofthemodelꎬandsignificantlyreducesthenumberofiterationsandtime.Keywords:BPneuralnetworksmodelingꎻgeneticalgorithmꎻimprovedcuckooalgorithmꎻpenaltyitems㊀㊀随着现代科学技术和工程技术的不断发展ꎬ各类工业系统越来越复杂ꎬ对其采用基于解析被控对象的传统数学建模方法难以达到理想的效果ꎬ为此学者们提出了许多新的复杂系统建模方法[1]ꎮ目前主要的建模方法有灰色预测法㊁模糊数学法㊁神经网络法㊁专家系统法等ꎬ新的建模优化方法主要有模拟退火算法㊁粒子群算法㊁布谷鸟算法等ꎮ神经网络作为人工智能的底层模型ꎬ是一个高度非线性映射系统ꎬ可进行大规模信息的并行处理[2]ꎬ在现代建模方法中占据重要地位ꎮBP神经网络是一种最传统㊁也是应用最广泛的神经网络[3]ꎮBP神经网络建模机理是:利用历史输入输出数据训练神经网络ꎬ学习某种规则ꎬ使输入数据经过神经网络后ꎬ其结果能够接近期望输出[4]ꎮ为精确拟合非线性系统模型ꎬ应用BP神经网络建模尚需解决如下问题[5]:1)BP神经网络的结构设计不合理会导致过拟合或欠拟合ꎻ2)初始权值选取不合适会导致陷入局部最优解ꎮ针对上述问题ꎬBP神经网络建模研究的一个新方向是将具有随机全局搜索能力的算法与BP神经网络算法相结合ꎮ王小会等[6]采用粒子群算法优化神经网络结构和权值ꎬ并设计了一种动态协同粒子寻优方式ꎬ有效提高了神经网络的学习和识别能力ꎮ张启龙等[7]采用遗传算法对BP神经网络的拓扑结构和网络权值进行优化ꎬ并用于风电场功率预测ꎬ结果表明ꎬ采用优化后的模型明显提高了预测准确率ꎮ由此可见ꎬ将多种智能算法与神经网络算法结合并加以改进的方法能够提高建模的准确度与效率ꎮ相较于粒子群㊁蚁群等算法ꎬ布谷鸟算法(CuckooSearchꎬCS)由于参数少ꎬ收敛速度对于参数变化不敏感ꎬ不易陷入局部最优ꎬ算法中大步长和小步长交替使得全局搜索能力更强ꎮ因此ꎬ本文应用改进布谷鸟算法优化BP神经网络的权值与阈值ꎬ并通过遗传算法(GeneticAlgorithmꎬGA)获取最优神经网络拓扑结构ꎬ避免BP神经网络建模陷入局部最优以及过拟合或欠拟合的问题ꎬ同时提高收敛速度和精度ꎮ本文提出的建模方法简称为GACSBP算法ꎮ1㊀GACSBP算法原理GACSBP算法首先利用遗传算法确定BP神经网络拓扑结构ꎬ然后通过改进布谷鸟算法更新权值的方式训练BP神经网络权值ꎬ当获取最优权值后ꎬ计算该拓扑结构的适应度ꎬ根据适应度进行遗传操作ꎬ在多次遗传进化及权值更新中获得最优BP神经网络拓扑结构和权值ꎬ使神经网络建模的精度更高ꎮ1.1㊀BP神经网络一般三层BP神经网络的拓扑结构如图1所示ꎮ图1㊀三层BP神经网络结构㊀㊀根据实际系统确定BP神经网络的拓扑结构及随机生成的权值初值后ꎬ进行BP神经网络训练ꎬ具体过程如下[8]ꎮ设输入层的输入向量为X=(x1ꎬx2ꎬ ꎬxn)Tꎬ隐含层有nᶄ个神经元ꎬ隐含层的输出向量为H=(h1ꎬh2ꎬ ꎬhnᶄ)Tꎬ输出层有nᵡ个神经元ꎬ输出层的输出向量为O=(o1ꎬo2ꎬ ꎬonᵡ)Tꎬ输入层与隐含层间的权值为ωij(i=1ꎬ2ꎬ ꎬnꎻj=1ꎬ2ꎬ ꎬnᶄ)ꎬ阈值为ajꎬ隐含层与输出层间的权值为ωᶄjk(k=1ꎬ2ꎬ ꎬnᵡ)ꎬ阈值为bkꎬ则隐含层输出hj和输出层的输出ok为02沈㊀阳㊀理㊀工㊀大㊀学㊀学㊀报㊀㊀第42卷hj=f(ðni=1ωijxi-aj)ok=g(ðnᶄj=1ωᶄjkhj-bk)ìîíïïïï(1)式中:f表示隐含层激活函数ꎬ采用双极性Sigmoid函数ꎻg表示输出层激活函数ꎬ采用Purelin线性函数ꎮ由万能逼近理论ꎬ三层人工神经网络能够拟合任意函数ꎬ但为避免BP神经网络建模陷入局部最优的问题ꎬ引入一种元启发式算法 布谷鸟算法ꎬ通过改进布谷鸟算法进行神经网络权值更新ꎮ1.2㊀改进布谷鸟算法1.2.1㊀布谷鸟算法原理布谷鸟算法是一种模拟布谷鸟繁殖策略进行最优化问题求解的算法[9]ꎮ布谷鸟算法中每个卵表示一个解ꎬ每次迭代都使用产生的新解替换原来的劣解ꎮ该算法假设的三个理想条件为:每只布谷鸟每次只在随机选取的鸟巢中产一个卵ꎻ根据贪婪策略ꎬ卵最好的鸟巢将会被保留ꎻ鸟巢的数量一定ꎬ鸟巢内的卵被宿主鸟发现的概率为Paꎬ当卵被发现ꎬ则宿主鸟将卵丢弃或重建一个鸟巢[10]ꎮ按照上述三个理想条件ꎬ根据式(2)建立新的鸟巢ꎮw(t+1)A=w(t)A+α s (w(t)A-w(t)Best)(2)式中:w(t)A为第A个鸟巢的第t次迭代权值ꎬ也表示鸟巢的位置向量ꎻw(t)Best为第t次迭代最好的鸟巢ꎻs为移动步长ꎬ其服从Lévy分布ꎻα为步长因子ꎮMantegna提出的Lévy飞行的步长公式[11]为s=u|v|1βꎬ㊀1<βɤ3(3)式中:β为控制随机过程的尺度属性参数ꎬ通常取值为1.5ꎻu和v为服从正态分布的随机数ꎬu~N(0ꎬσ2)ꎬv~N(0ꎬ1)ꎬ参数σ表达式为σ=Γ(1+β)sin(πβ/2)βΓ[(1+β)/2]2(β-1)/2{}1β(4)式中Γ为标准Gamma函数ꎮ1.2.2㊀布谷鸟算法改进标准布谷鸟算法的步长因子α为定值ꎬ不利于算法求解最优值ꎮ当步长较大时ꎬ有利于全局搜索ꎬ提高搜索速度ꎬ但会降低搜索精度ꎻ当步长较小时ꎬ有利于局部搜索ꎬ提高搜索精度ꎬ但会降低搜索速度且易陷入局部最优[12]ꎮ引入布谷鸟算法中鸟巢的适应度可自动调整步长因子ꎬ使算法在搜索速度及精度上达到平衡ꎬ自适应步长因子计算式为αA=z-FmFA㊀(Fm<FA)(5)式中:αA为第A个鸟巢的步长因子ꎻz为常数ꎻFm为全局最优鸟巢适应度值ꎻFA为个体鸟巢适应度值ꎮ当个体鸟巢的适应度接近全局最优适应度时ꎬFm/FA增大ꎬ步长因子αA减小ꎬ否则ꎬFm/FA减小ꎬ步长因子αA增大[13]ꎮ1.2.3㊀惩罚项为维护布谷鸟算法的鸟巢多样性ꎬ通过对相近鸟巢中适应度低的个体添加惩罚项ꎬ降低该个体的适应度ꎬ使该个体在迭代中更易被淘汰ꎬ保证一个区域内只有一个最优个体ꎮ在群体中取任意两个鸟巢w1和w2ꎬ即取任意两个由神经网络权值构成的向量ꎬ适应度分别为F1和F2ꎬ计算鸟巢间的欧几里得距离dꎬ计算式为[14]d(w1ꎬw2)=㊀ðDc=1[w1(c)-w2(c)]2(6)式中:w1(c)和w2(c)分别表示w1和w2的第c个元素ꎻD表示神经网络权值个数ꎮ计算得到鸟巢间距d后ꎬ将其与设置的允许距离L比较ꎬ若d小于Lꎬ则比较两个鸟巢的适应度F1和F2ꎬ将较大的适应度值乘以惩罚项ꎬ惩罚项可设为10000ꎬ其作用是确保带惩罚项的个体能够被淘汰ꎮ1.3㊀遗传算法遗传算法是一种借鉴生物进化规律的计算方法[15]ꎬ由于其具有在模拟自然进化过程中搜索最优解的特点ꎬ将遗传算法与神经网络结合ꎬ通过遗传算法寻找到神经网络的最优拓扑结构ꎬ能够有效避免由于神经网络拓扑结构选择不合理而导致创建的模型过拟合或欠拟合的问题ꎮ遗传算法中的适应度是将训练集与验证集整体的均方误差和作为评价种群的指标ꎮ适应度函数为12第4期㊀㊀㊀㊀㊀王秀莲等:基于遗传和改进布谷鸟算法的BP神经网络建模F=1RðRxl=1(yxl-yxl︿)2+1VðVvr=1(yvr-yvr︿)2(7)式中:yxl为训练集输出ꎻyxl︿为训练集期望输出ꎻyvr为验证集输出ꎻyvr︿为验证集期望输出ꎻR为训练集数据数目ꎻV为验证集数据数目ꎮ2㊀GACSBP算法流程GACSBP算法流程如图2所示ꎮ图2㊀GACSBP算法流程图㊀㊀GACSBP算法的具体过程如下ꎮ1)对数据进行归一化处理ꎬ公式为[16]Gᶄi=Gi-GminGmax-Gmin(8)式中:Gi为数据集某一输入或输出变量ꎻGmin为输入或输出变量中的最小值ꎻGmax为输入或输出变量中的最大值ꎻGᶄi为归一化后的值ꎮ将训练集和测试集输入及输出数据按上式归一化处理ꎬ然后输入遗传算法和布谷鸟算法的参数ꎬ包括遗传算法的种群规模㊁进化代数㊁交叉概率㊁变异概率以及布谷鸟算法的鸟巢个数S㊁迭代次数Mꎮ2)采用二进制编码形式初始化遗传算法染色体ꎬ设定BP神经网络最大隐含层数为三层ꎬ每层最多有15个神经元ꎬ最少有4个神经元ꎬ故隐含层可用12位二进制串表示ꎬ每4位二进制串表示一层隐含层ꎬ当染色体解码后ꎬ若出现一个小于4的数ꎬ则隐含层个数减1ꎮ染色体编码形式为EC=[r1r2r3 r12](9)式中r1㊁r2㊁ ㊁r12的值为0或1ꎮ解码形式为DC=ð4q=12q-1rqð8q=52q-5rqð12q=92q-9rq[](10)3)根据染色体解码后的值确定BP神经网络的拓扑结构ꎬ网络输入层㊁隐含层及输出层节点数分别为n㊁nᶄ和nᵡꎮ4)确定每一鸟巢向量的元素总个数ꎬ计算式为D=nˑnᶄ+nᶄˑnᵡ+nᶄ+nᵡ(11)5)随机数初始化S个鸟巢的位置ꎮ6)将S个鸟巢位置作为BP神经网络的权值代入ꎬ并计算其适应度FAꎬ记录最佳适应度FmꎮFm计算式为FA=(yA-yA︿)2㊀A=1ꎬ2ꎬ ꎬS(12)式中:yA为模型实际输出ꎻyA︿为期望输出ꎮ7)判断迭代次数是否达到Mꎬ若未达到ꎬ从步骤8)继续运算ꎬ否则从步骤16)继续运算ꎮ8)将式(12)得出的适应度按降序排列ꎬ并从S个鸟巢中选取K个适应度较好的鸟巢位置Pꎮ9)应用式(2)更新所有的鸟巢位置ꎮ10)重新计算适应度ꎬ并将适应度按降序排列ꎬ得到S个鸟巢位置Pᶄꎮ11)合并P和Pᶄꎬ通过式(6)计算两两鸟巢间的欧氏距离ꎬ并给其中适应度较差的鸟巢添加惩罚项ꎮ12)将上一步中的鸟巢按适应度降序排列ꎬ取其中S个适应度较好的鸟巢ꎮ13)每个鸟巢生成一个对应随机数PAꎬ当PA>Paꎬ则该鸟巢按式(2)更新位置ꎬ否则保持不变ꎮ14)重新计算S个鸟巢适应度ꎬ记录最佳适应度Fnꎮ22沈㊀阳㊀理㊀工㊀大㊀学㊀学㊀报㊀㊀第42卷15)比较Fm和Fnꎬ保留适应度好的鸟巢ꎮ16)通过验证集测试ꎬ并利用式(7)计算遗传算法个体适应度ꎮ17)判断遗传算法是否完成进化代数ꎬ若未完成ꎬ则进行遗传操作(选择㊁交叉㊁变异)并返回第2)步计算ꎬ否则保留最优个体并退出ꎮ3㊀算法仿真翼型自噪声(AirfoilSelf ̄noise)数据集是以NACA0012机翼翼型进行风洞试验所测得ꎮ数据集中包括不同尺寸的NACA0012翼型ꎬ采用不同的风洞速度和迎角ꎬ翼型的跨度与传感器位置在试验中均相同ꎮ该数据集包含5个控制变量ꎬ分别为频率㊁迎角㊁弦长㊁自由流速度和吸力侧位移ꎬ1个测量变量为缩放声压级ꎮ将控制变量作为输入ꎬ测量变量作为输出ꎮ提取数据集中的1000组数据作为样本ꎬ随机选取其中的600组作为训练集用于训练建模ꎬ选取200组作为验证集用于选取神经网络隐含层结构ꎬ选取200组作为测试集用于最终测试ꎮ设置GACSBP算法中遗传算法的群规模为20㊁迭代次数为50㊁交叉概率为0.6㊁变异概率为0.3ꎻ改进布谷鸟算法的鸟巢数S=30㊁每次取优个数K=20㊁最大迭代次数M=50㊁最大欧式距离L=0.1㊁被宿主发现概率Pa=0.25㊁最大步长因子为1ꎻ将翼型自噪声数据中的频率㊁风洞迎角㊁风洞自由流速度㊁机翼弦长和机翼吸力侧位移作为神经网络输入ꎬ噪声声压级作为神经网络输出ꎬ学习速率为0.08ꎬ以随机数作为初始权值ꎮ表1为遗传算法优化神经网络结构不同隐含层拓扑结构对应的均方误差ꎮ表中隐含层结构表示每代最优隐含层结构ꎬ训练集均方误差是在训练集数据归一化后所得到的每代最优隐含层结构对应的均方误差ꎬ验证集均方误差代表验证集数据归一化后的每代最优隐含层结构对应的验证集均方误差ꎮ从表1中可以看出ꎬ当隐含层结构为[131013]及[12914]时ꎬ验证集均方误差远大于训练集均方误差ꎬ因此神经网络出现过拟合问题ꎻ遗传算法个体进化到16代开始ꎬ最优隐含层结构一直为[79]ꎬ故当隐含层层数为2ꎬ第一层节点数为7ꎬ第二层节点数为9时可得到最优BP神经网络拓扑结构ꎮ表1㊀不同隐含层结构验证结果均方误差10-2进化代数隐含层结构训练集均方误差验证集均方误差1[68]4.64544.67482[128]3.47383.46744[131013]3.27817.37156[75]3.07452.94537[127]2.64432.55378[12914]2.35166.153710[96]1.96211.836213[137]1.46421.423815[78]1.31641.343316[79]1.19871.197330[79]1.19871.197350[79]1.19871.1973㊀㊀为获得最佳神经网络隐含层拓扑结构ꎬ将训练后的神经网络通过验证集进行结构选择ꎮ通过验证集测试每一代最佳神经网络隐含层结构的均方误差ꎬ得到遗传算法进化曲线如图3所示ꎮ由图3可直观看出ꎬ当进化迭代到16次时ꎬ能够得到最佳隐含层拓扑结构ꎮ图3㊀遗传算法进化曲线㊀㊀图4和图5分别为传统BP神经网络和GACSBP神经网络建模后通过测试集进行预测的结果与真实值的对比ꎮ图4与图5所拟合的曲线均在BP神经网络拓扑结构经遗传算法寻优后所得到ꎬ即网络隐含层有两层ꎬ每层神经元分别为7和9ꎮ由图4和图5中可以看出ꎬ传统BP神经网络的预测结果与真实值之间存在较大误差ꎬ而GACSBP神经网络所得到的预测结果明显更为接近真实值ꎮ32第4期㊀㊀㊀㊀㊀王秀莲等:基于遗传和改进布谷鸟算法的BP神经网络建模图4㊀BP神经网络预测结果图5㊀GACSBP神经网络预测结果㊀㊀图6为传统BP神经网络和GACSBP神经网络两种算法对每个测试样本的预测误差值ꎮ由图6可以明显看出ꎬ除个别样本外ꎬGACSBP神经网络的预测误差远小于传统BP神经网络ꎮ图6㊀BP与GACSBP神经网络预测误差对比㊀㊀传统BP神经网络和GACSBP神经网络两种算法的训练曲线和测试曲线均方误差如表2所示ꎮ两种算法的建模效率对比如表3所示ꎮ表2㊀两种算法训练曲线和测试曲线均方误差%算法训练曲线测试曲线BP3.71343.4875GACSBP2.13421.9329表3㊀两种算法建模效率对比算法迭代次数计算时间/sBP1250.5457GACSBP500.1824㊀㊀由表2中传统BP神经网络与GACSBP神经网络所拟合的曲线均方误差对比上看ꎬ通过改进布谷鸟算法的BP神经网络测试曲线均方误差小于传统BP神经网络ꎮ由表3中传统BP神经网络建模与经布谷鸟算法优化权值后的BP神经网络建模所需迭代次数和时间对比可以看出ꎬ优化后的BP神经网络建模迭代次数为50次ꎬ远小于传统BP神经网络所需的125次ꎬ且优化后的BP神经网络建模所用时间也大大减少ꎮ4㊀结论使用改进布谷鸟算法优化BP神经网络建模ꎬ加入惩罚项ꎬ提高了布谷鸟算法种群的多样性ꎬ引入遗传算法进行BP神经网络拓扑结构寻优ꎮ分别使用传统BP神经网络与本文提出的GACSBP神经网络对NACA0012机翼翼型自噪声数据建模ꎬ结果表明ꎬ本文提出的GACSBP算法能够将模型均方误差控制在2%以内ꎬ且建模所需迭代次数和时间均明显少于传统BP神经网络ꎮ参考文献:[1]谢冉.复杂系统建模方法综述[J].现代防御技术ꎬ2020ꎬ48(3):31-36ꎬ68.[2]WANGPꎬWANGPꎬFANE.Neuralnetworkoptimi ̄zationmethodanditsapplicationininformationpro ̄cessing[J].MathematicalProblemsinEngineeringꎬ2021:6665703.[3]黄杰贤ꎬ刘燕ꎬ杨冬涛.基于BP神经网络的柚子分类研究[J].湖北农业科学ꎬ2018ꎬ57(24):112-115.42沈㊀阳㊀理㊀工㊀大㊀学㊀学㊀报㊀㊀第42卷[4]高宏岩ꎬ卞瑶瑶.基于SMPT ̄1000的反应器神经网络建模实验[J].实验技术与管理ꎬ2021ꎬ38(9):91-96.[5]王闪闪.基于群智能算法的神经网络建模研究[J].电子科技ꎬ2017ꎬ30(4):56-59.[6]王小会ꎬ薛延刚ꎬ李晓青.基于改进粒子群算法优化神经网络结构和权值[J].青海师范大学学报(自然科学版)ꎬ2020ꎬ36(1):16-21.[7]张启龙ꎬ王立威.基于遗传算法优化BP神经网络模型的风电功率预测[J].电子测试ꎬ2021(1):41-43. [8]郭婕ꎬ金海ꎬ沈昕格.基于神经网络PID算法的四旋翼无人机优化控制[J].电子科技ꎬ2021ꎬ34(10):51-55.[9]吴文红ꎬ崔玉莹ꎬ刘宁.基于布谷鸟算法的管网漏损定位模型[J].中国给水排水ꎬ2022ꎬ38(11):38-42. [10]SALGOTRARꎬSINGHUꎬSAHASꎬetal.Selfadap ̄tivecuckoosearch:analysisandexperimentation[J].SwarmandEvolutionaryComputationꎬ2021ꎬ60:100751.[11]MANTEGNARN.Fastꎬaccuratealgorithmfornumer ̄icalsimulationofLévystablestochasticprocesses[J].PhysicalReviewEꎬ1994ꎬ49(5):4677-4683. [12]ZHANGLPꎬYUYLꎬLUOYXꎬetal.Improvedcuckoosearchalgorithmanditsapplicationtopermuta ̄tionflowshopschedulingproblem[J].JournalofAl ̄gorithmsandComputationalTechnologyꎬ2020ꎬ14:1-12.[13]梁毛毛ꎬ肖文ꎬ王李进ꎬ等.带全局-局部最优步长比例因子的布谷鸟搜索算法[J].南京师范大学学报(工程技术版)ꎬ2022ꎬ22(2):56-62ꎬ72.[14]唐宇政.基于欧式距离的判别分析:鸢尾花分类问题探究[J].现代商贸工业ꎬ2019ꎬ40(9):183-185. [15]梁智珲.遗传算法优化前向神经网络结构和权重矢量研究[J].信息与电脑(理论版)ꎬ2019(14):37-38ꎬ43.[16]柯超ꎬ甘屹ꎬ王俊ꎬ等.基于BP神经网络辨识模型的PEMFC系统建模[J].软件工程ꎬ2020ꎬ23(3):14-16ꎬ8.(责任编辑:宋颖韬)(上接第18页)[6]沈丽娜ꎬ白勇ꎬ宗亮.一种面向卫星网络的TCP改进算法研究[J].海南大学学报(自然科学版)ꎬ2015ꎬ33(4):327-332.[7]张奎ꎬ刘晨.基于异构网络的TCPVegas拥塞控制算法改进研究[J].伊犁师范学院学报(自然科学版)ꎬ2021ꎬ15(2):56-61.[8]VERMALPꎬKUMARM.AnIoTbasedcongestioncontrolalgorithm[J].InternetofThingsꎬ2020ꎬ9(C):100157.[9]杨力ꎬ李静森ꎬ魏德宾ꎬ等.一种高动态卫星网络的拥塞控制算法[J].宇航学报ꎬ2014ꎬ35(8):953-960. [10]姜月秋ꎬ关启学ꎬ田野ꎬ等.一种适用于地球空间传感器网络的TCPVegas模型[J].宇航学报ꎬ2020ꎬ41(2):234-244.[11]李鹏ꎬ陈元琰ꎬ罗晓曙.无线异构网络环境中基于拥塞状态区分的TCPVegas改进算法[J].计算机应用ꎬ2010ꎬ30(2):309-311ꎬ326.[12]曾高雄ꎬ胡水海ꎬ张骏雪ꎬ等.数据中心网络传输协议综述[J].计算机研究与发展ꎬ2020ꎬ57(1):74-84. [13]何荣希ꎬ孙皓.基于OPNET的TCP拥塞控制算法教学实验设计[J].教育现代化ꎬ2019ꎬ6(96):182-184.[14]姚明明ꎬ王学华ꎬ王浩儒ꎬ等.低轨卫星通信网络半实物仿真系统构建与实现[J].电子信息对抗技术ꎬ2021ꎬ36(6):89-93.(责任编辑:蒋晓东ꎬ和晓军)52第4期㊀㊀㊀㊀㊀王秀莲等:基于遗传和改进布谷鸟算法的BP神经网络建模。
(完整版)bp神经网络算法
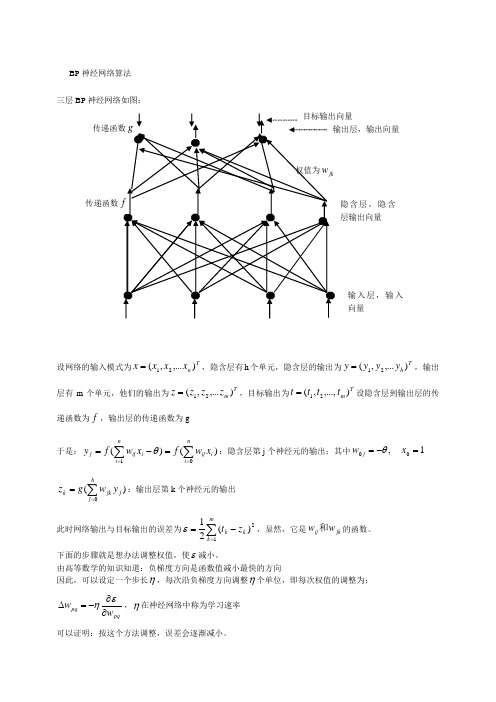
BP 神经网络算法 三层BP 神经网络如图:设网络的输入模式为Tn x x x x ),...,(21=,隐含层有h 个单元,隐含层的输出为Th y y y y ),...,(21=,输出层有m 个单元,他们的输出为Tm z z z z ),...,(21=,目标输出为Tm t t t t ),...,,(21=设隐含层到输出层的传递函数为f ,输出层的传递函数为g于是:)()(1∑∑===-=ni i ij ni iij j x w f xw f y θ:隐含层第j 个神经元的输出;其中1,00=-=x w j θ)(0∑==hj j jk k y w g z :输出层第k 个神经元的输出此时网络输出与目标输出的误差为∑=-=m k k k z t 12)(21ε,显然,它是jk ij w w 和的函数。
下面的步骤就是想办法调整权值,使ε减小。
由高等数学的知识知道:负梯度方向是函数值减小最快的方向因此,可以设定一个步长η,每次沿负梯度方向调整η个单位,即每次权值的调整为:pqpq w w ∂∂-=∆εη,η在神经网络中称为学习速率 可以证明:按这个方法调整,误差会逐渐减小。
隐含层,隐含层输出向量传递函数输入层,输入向量BP 神经网络(反向传播)的调整顺序为: 1)先调整隐含层到输出层的权值 设k v 为输出层第k 个神经元的输入∑==hj j jkk y wv 0-------复合函数偏导公式若取x e x f x g -+==11)()(,则)1()111(11)1()('2k k v v v v k z z ee e e u g kk k k -=+-+=+=---- 于是隐含层到输出层的权值调整迭代公式为: 2)从输入层到隐含层的权值调整迭代公式为: 其中j u 为隐含层第j 个神经元的输入:∑==ni i ijj x wu 0注意:隐含层第j 个神经元与输出层的各个神经元都有连接,即jy ∂∂ε涉及所有的权值ij w ,因此∑∑==--=∂∂∂∂∂-∂=∂∂m k jk k k k j k k k m k k k k j w u f z t y u u z z z t y 002)(')()(ε于是:因此从输入层到隐含层的权值调整迭代为公式为: 例:下表给出了某地区公路运力的历史统计数据,请建立相应的预测模型,并对给出的2010和2011年的数据,预测相应的公路客运量和货运量。
数学建模之神经预测ANN方法

生物神经元,也称神经细胞,它是由细胞体、 树突、轴突和突触等生物组织构成的,并通过细胞 膜电位来实现生物神经元的兴奋与抑制、学习与联 想等基本功能,因此,它是构成人脑神经系统的基 本功能单元。其结构如下图所示。
根据生物神经元的结构与基本功能,可以将其 简化为下图的形式,并建立神经网络模型的基础—— 人工神经元数学模型:
n
y j f ( wij xi a j ) i1
其中,y j 表示神经元 j 的输出;xi 表示神经元i 的输入; wij 表示神经元 i 与神经元 j 之间的连接权值;a j 表示神 经元 j 的阈值;f (•) 是输入到输出传递函数(也称激活 函数).
下表给出了一些常用的传递函数。除线性传递 函数外,其它的均是非线性的,因此,神经网络特 别适合于解决非线性问题。
化各层神经元之间的连接权值 vij , wjk ,初始化隐含层阈值 a ,输出
层阈值 b ,给定学习速率和神经元传递函数.
步骤 2:隐含层输出计算。根据输入向量 X ,输入层和隐含层间连
接权值vij 以及隐含层阈值 a ,计算隐含层输出.
n
n
yi f ( vij xi a j ) f ( vij xi )
取 NAN) 最大训练时间(秒)
net.trainParam.max_fail=5 确认失败的最大次数
net.trainParam.min_grad=1e-6 最小性能梯度
net.trainParam.lr=0.2
学习速率
(3)sim——BP 神经网络预测/仿真函数 函数功能:用训练好的 BP 神经网络预测/仿真函数输出. 函数形式:Y=sim(net,x)
神经网络训练函数 训练函数的意义 梯度下降法 动量反传的梯度下降法 动态自适应学习率(lr)的梯度下降法 带动量动态自适应学习率(lr)的梯度下降法 弹性梯度下降法 量化共轭梯度法 Levenberg_Marquardt 法 Fletcgera-Reeves 共轭梯度法 Polak-Ribiere 共轭梯度法 Powell-Beale 共轭梯度法
数学建模之BP神经网络

神经网络的应用
人工神经网络以其具有自学习、自组织、 较好的容错性和优良的非线性逼近能力,受到 众多领域学者的关注。在实际应用中,80%~ 90%的人工神经网络模型是采用误差反传算法
或其变化形式的网络模型(简称BP神经网络),
目前主要应用于函数逼近、模式识别、分类和
数据压缩或数据挖掘。
§2 BP神经网络概述
人工神经网络是根据人的认识过程而开发出的一 种算法。 假如我们现在只有一些输入和相应的输出,而对 如何由输入得到输出的机理并不清楚,那么我们可以 把输入与输出之间的未知过程看成是一个“网络”, 通过不断地给这个网络输入和相应的输出来“训练” 这个网络,网络根据输入和输出不断地调节自己的各 节点之间的权值来满足输入和输出。这样,当训练结 束后,我们给定一个输入,网络便会根据自己已调节 好的权值计算出一个输出。这就是神经网络的简单原 理。
工作过程:
从神经元各组成部分的功能来看,信息的处理与传递主
要发生在突触附近。当神经元细胞体通过轴突传到突触 前膜的脉冲幅度达到一定强度,即超过其阈值电位后, 突触前膜将向突触间隙释放神经传递的化学物质。 神经元间信息的产生、传递和处理是一种电化学活动。 神经元间的信号通过突触传递。通过它,一个神经元内 传送的冲击信号将在下一个神经元内引起响应,使下一 个神经元兴奋,或阻止下一个神经元兴奋。
常见的激活函数有以下几种类型:
1、阶梯函数 2、线性函数 3、非线性:Sigmoid函数
1 (s) 1 e s
1 (s) 1 e s
人工神经网络的分类
按网络连接的拓扑结构分类:
层次型结构:将神经元按功能分成若干层,如输入
层、中间层(隐含层)和输出层,各层顺序相连 互连型网络结构:网络中任意两个节点之间都可能 存在连接路径
BP神经网络

BP神经网络在函数逼近中的实现1.1 概述BP神经网络是目前人工神经网络模式中最具代表性,应用得最广泛的一种模型,具有自学习、自组织、自适应和很强的非线性映射能力,可以以任意精度逼近任意连续函数.近年来,为了解决BP网络收敛速度慢,训练时间长等不足,提出了许多改进算法.然而,在针对实际问题的BP网络建模过程中,选择多少层网络,每层多少个神经元节点,选择何种传递函数等,均无可行的理论指导,只能通过大量的实验计算获得.MATLAB中的神经网络工具箱(Neural NetworkToolbox,简称NNbox),为解决这一问题提供了便利的条件.神经网络工具箱功能十分完善,提供了各种MATLAB函数,包括神经网络的建立、训练和仿真等函数,以及各种改进训练算法函数,用户可以很方便地进行神经网络的设计和仿真,也可以在MATLAB源文件的基础上进行适当修改,形成自己的工具包以满足实际需要。
此项课题主要是针对MATLAB软件对BP神经网络的各种算法的编程,将神经网络算法应用于函数逼近和样本含量估计问题中,并分析比较相关参数对算法运行结果的影响。
人工神经网络(Artificial Neural Networks,NN)是由大量的、简单的处理单元(称为神经元)广泛地互相连接而形成的复杂网络系统,它反映了人脑功能的许多基本特征,是一个高度复杂的非线性动力学系统。
神经网络具有大规模并行、分布式存储和处理、自组织、自适应和自学习能力,特别适合处理需要同时考虑许多因素和条件的、不精确和模糊的信息处理问题。
神经网络的发展与神经科学、数理科学、认知科学、计算机科学、人工智能、信息科学、控制论、机器人学、微电子学、心理学、微电子学、心理学、光计算、分子生物学等有关,是一门新兴的边缘交叉学科。
神经网络具有非线性自适应的信息处理能力,克服了传统人工智能方法对于直觉的缺陷,因而在神经专家系统、模式识别、智能控制、组合优化、预测等领域得到成功应用。
BP人工神经网络的基本原理模型与实例

w14
0.2+(0.9) (-0.0087)(1)=0.192
w15
-0.3+(0.9) (-0.0065)(1)=-0.306
w24
0.4+(0.9) (-0.0087)(0)=0.4
w25
0.1+(0.9) (-0.0065)(0)=0.1
w34
-0.5+(0.9) (-0.0087)(1)=-0.508
8.1人工神经网络旳基本概念
人工神经网络在本质上是由许多小旳非线性函数构成 旳大旳非线性函数,反应旳是输入变量到输出变量间旳复 杂映射关系。先给出单个人工神经网络旳一般模型描述:
8.1人工神经网络旳基本概念
先来看一种单一输入旳神经元模型 输入变量:x1 连接权重:w1 激活函数:f (·)
x1 w1
w1x1 f (·)
8.1人工神经网络旳基本概念
8.1人工神经网络旳基本概念
单极sigmoid函数
8.1人工神经网络旳基本概念
双曲函数
8.1人工神经网络旳基本概念
增长激活阈值后旳神经元模型 输入变量:x1 连接权重:w1 激活函数:f (·)
x1 w1
w1x1-θ f (·)
-1
小练习:请你算一算,当初始输入、权重和激活阈值为如下数值时,该神 经元旳净输入和输出分别是多少?
2.反向传播 反向传播时,把误差信号按原来正向传播旳通路反向
传回,并对每个隐层旳各个神经元旳权系数进行修改,以 望误差信号趋向最小。
8.2 误差反向传播(BP)神经网 络
8.2 误差反向传播(BP)神经网 络
x1 x2
x3
单元 j 6
1 w14
Err4=
BP神经网络与BP网络设计

BP神经网络与BP网络设计
图像处理教研室
第14页
2. 输入量提取与表示
(1)文字符号输入
一 、训练样本集准备
XC=(111100111)T XI=(111100111)T XT=(111100111)T
BP神经网络与BP网络设计
图像处理教研室
第15页
(2)曲线输入
x(t) xn
一 、训练样本集准备
(2)“n-1”表示法 假如用n-1个全为0输出向量表示某个类别,则能够节约一个输
出节点。比如,用000、001、010和100也可表示优、良、中、差4 个类别。
(3)数值表示法
对于渐进式分类,能够将语言值转化为二值之间数值表示。数 值选择要注意保持由小到大渐进关系,并要依据实际意义拉开距离。
BP神经网络与BP网络设计
BP神经网络与BP网络设计
图像处理教研室
第17页
3. 输出量表示
一 、训练样本集准备
(1)“n中取1”表示法
“n中取1”是令输出向量分量数等于类别数,输入样本被判 为哪一类,对应输出分量取1,其余 n-1 个分量全取0。比如,用 0001、0010、0100和1000可分别表示优、良、中、差4个类别。
2
xmin
xi
xi xmid
1 2
( xmax
xmin
)
其中,xmid代表数据改变范围中间值。
BP神经网络与BP网络设计
图像处理教研室
第21页
三、网络训练与测试
三、网络训练与测试
网络性能好坏主要看其是否含有很好泛化能力, 对泛化能力测试不能用训练集数据进行,而要用训练集 以外测试数据来进行检验。
输出量:代表系统要实现功效目标
BP神经网络模型

BP网络旳原则学习算法
BP算法直观解释
◦ 情况一直观体现
◦ 当误差对权值旳偏 导数不小于零时,权值 调整量为负,实际输 出不小于期望输出, 权值向降低方向调整, 使得实际输出与期望 输出旳差降低。
e
who
e w ho
>0,此时Δwho<0
BP网络旳原则学习算法
BP算法直观解释
◦ 情况二直观体现
xx1,x2, ,xn
h h y yo o i i h y h y o o ii1 1 1 1 ,,,,h h y y o o ii2 2 2 2 ,,,,
,h ip
,h o p ,yiq
,y o q
dod1,d2, ,dq
BP网络旳原则学习算法
◦ 输入层与中间层旳连接权值: w ih ◦ 隐含层与输出层旳连接权值: w h o ◦ 隐含层各神经元旳阈值: b h ◦ 输出层各神经元旳阈值: b o ◦ 样本数据个数: k1,2, m ◦ 激活函数: f ( )
将误差分摊给各层旳全部 单元---各层单元旳误 差信号
修正各单元权 值
•学习旳过程:
• 信号旳正向传播 向传播
误差旳反
BP网络旳原则学习算法-学习过程
•正向传播:
• 输入样本---输入层---各隐层---输出层
•判断是否转入反向传播阶段:
• 若输出层旳实际输出与期望旳输出(教师信号)不 符
•误差反传
第七步,利用隐含层各神经元旳 h ( k ) 各神经元旳输入修正连接权。
和输入层
wih(k)weihhihe(k)hiw h(ihk)h(k)xi(k) wiN h1wiN hh(k)xi(k)
BP网络旳原则学习算法
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019/9/27
15 2019/9/27
2.3 学习规则
信息的正向传递
–隐含层中第i个神经元的输出
–输出层第k个神经元的输出
16 2019/9/27
–定义误差函数
2.3 学习规则
利用梯度下降法求权值变化及误差的反向传播
– 输出层的权值变化
17 2019/9/27
• 其中 • 同理可得
2.3 学习规则
利用梯度下降法求权值变化及误差的反向传播
–如果在输出层未得到期望的输出,则计算输出层的误 差变化值,然后转向反向传播,通过网络将误差信号 沿原来的连接通路反传回来修改各层神经元的权值直 至达到期望目标
14
2019/9/27
2.3 学习规则
假设输入为P,输入神经元有r个,隐含层内有s1个神经 元,激活函数为F1,输出层内有s2个神经元,对应的激 活函数为F2,输出为A,目标矢量为T
自适应线性元件
4
2019/9/27
一、内容回顾
感知机 自适应线性元件
–Adline简介 –网络结构 –网络学习 –网络训练
5 2019/9/27
二、BP网络
2.1 BP网络简介 2.2 网络模型 2.3 学习规则 2.4 图形解释 2.5 网络训练
6 2019/9/27
2.1 BP网络简介
人工神经网络及其应用
第4讲 BP神经网络
何建华 电信系,华中科技大学
2003年2月28日
内容安排
一、内容回顾 二、BP网络 三、网络设计 四、改进BP网络 五、内容小结
2 2019/9/27
一、内容回顾
感知机 自适应线性元件
3 2019/9/27
一、内容回顾
感知机
–感知机简介 –神经元模型 –网络结构 –功能解释 –学习和训练 –局限性
2.2 网络模型
感知器和自适应线性元件的主要差别在激活函数 上:前者是二值型的,后者是线性的
BP网络具有一层或多层隐含层,除了在多层网络 上与前面已介绍过的模型有不同外,其主要差别 也表现在激活函数上。
BP网络的激活函数必须是处处可微的,因此它不 能采用二值型的阀值函数{0,1}或符号函数{-1, 1}
具有将强泛化性能:使网络平滑地学习函数,使网络 能够合理地响应被训练以外的输入
泛化性能只对被训练的输入/输出对最大值范围内的 数据有效,即网络具有内插值特性,不具有外插值性。 超出最大训练值的输入必将产生大的输出误差
2.2 网络模型
9 2019/9/27
一个具有r个输入和一个隐含层的神经网络模型结构
– 隐含层权值变化
• 其中
18 2019/9/27
• 同理可得
2.3 学习规则
对于f1为对数S型激活函数,
对于f2为线性激活函数
19 2019/9/27
2.4 误差反Biblioteka 传播图形解释 误差反向传播过程实际上是通过计算输出层的误差ek, 然后将其与输出层激活函数的一阶导数f2’相乘来求得 δki
2019/9/27
2.1 BP网络简介
8 2019/9/27
BP网络主要用于下述方面
函数逼近:用输入矢量和相应的输出矢量训练一个 网络逼近一个函数
模式识别和分类:用一个特定的输出矢量将它与输 入矢量联系起来;把输入矢量以所定义的合适方式 进行分类;
数据压缩:减少输出矢量维数以便于传输或存储
2.4 误差反向传播图形解释
21 2019/9/27
2.5 网络训练
训练BP网络,需要计算网络加权输入矢量以及网 络输出和误差矢量,然后求误差平方和
当所训练矢量的误差平方和小于误差目标,训练 停止;否则在输出层计算误差变化,且采用反向 传播学习规则来调整权值,然后重复此过程
网络完成训练后,对网络输入一个不是训练集合 中的矢量,网络将以泛化方式给出输出结果
对较大的输入信号,放大系数较小;而对较小的输入信 号,放大系数则较大
采用S型激活函数可以处理和逼近非线性输入/输出关系
12 2019/9/27
2.3 学习规则
BP算法属于δ算法,是一种监督式的学习算法 主要思想
–对于q个输入学习样本:P1,P2,…,Pq,已知与其对应的 输出样本为:T1,T2,…,Tq
由于隐含层中没有直接给出目标矢量,所以利用输出层 的δki反向传递来求出隐含层权值的变化量Δw2ki。然后 计算
同样通过将ei与该层激活函数的一阶导数f1’相乘,而求 得δij,以此求出前层权值的变化量Δw1ij
20 如果前面还有隐含层,沿用上述同样方法依此类推,一
2019/9/27
直将输出误差ek逐层的反推算到第一层为止
–使网络输出层的误差平方和达到最小 –用网络的实际输出A1,A2,…,Aq, 与目标矢量T1,T2,…,Tq
之间的误差修改其权值,使Am与期望的Tm,(m=l,…,q) 尽可能接近
13
2019/9/27
2.3 学习规则
BP算法是由两部分组成,信息的正向传递与误差 的反向传播
–正向传播过程中,输入信息从输入层经隐含层逐层计 算传向输出层,每一层神经元的状态只影响下一层神 经元的状态
反向传播网络(Back-Propagation Network,简 称BP网络)是将W-H学习规则一般化,对非线性 可微分函数进行权值训练的多层网络
权值的调整采用反向传播(Back-propagation) 的学习算法
它是一种多层前向反馈神经网络,其神经元的 变换函数是S型函数
输出量为0到1之间的连续量,它可实现从输入 7 到输出的任意的非线性映射
10 BP网络经常使用的是S型的对数或正切激活函数 和线性函数
2019/9/27
2.2 网络模型
BP网络特点
–输入和输出是并行的模拟量
–网络的输入输出关系是各层连接的权因子决定,没有 固定的算法
–权因子通过学习信号调节。学习越多,网络越聪明
–隐含层越多,网络输出精度越高,且个别权因子的损 坏不会对网络输出产生大的影响
–只有当希望对网络的输出进行限制,如限制在0和1之 间,那么在输出层应当包含S型激活函数
11 2019/9/27
–在一般情况下,均是在隐含层采用S型激活函数,而 输出层采用线性激活函数
2.2 网络模型
S型函数具有非线性放大系数功能,可以把输入从负无穷 大到正无穷大的信号,变换成-1到l之间输出
