模糊聚类分析例子1教学内容
模糊聚类分析PPT课件

A∪Ac U, A∩Ac .
模糊集不再具有“非此即彼”的特点,
这正是模糊性带来的本. 质特征.
12
例:设论域U = {x1, x2, x3, x4, x5}(商品集), 在U上定义两个模糊集: A =“商品质量好”, B =“商品质量坏”,并设
A = (0.8, 0.55, 0, 0.3, 1).
言,需要选取不同的置信水平 (0 1) 来确
定其隶属关系。截集就是将模糊集转化为普
通集的方法。模糊集A 是一个具有游移边界的
集合,它随值的变小而增大,即当1 <2时,
有A1∩A2。
.
14
模糊集的-截集A是一个经典集合,由隶属 度不小于的成员构成.
例:论域U={u1, u2, u3, u4 , u5 , u6}(学生集), 他们的成绩依次为50,60,70,80,90,95,A=“学 习成绩好的学生”的隶属度分别为 0.5,0.6,0.7,0.8, 0.9,0.95,则
并:A∪B的隶属函数为
(A∪B)(x)=A(x)∨B(x);
交:A∩B的隶属函数为
(A∩B)(x)=A(x)∧B(x);
余:Ac的隶属函数为
Ac (x) =. 1- A(x).
10
模糊集的并、交、余运算性质
幂等律:A∪A = A, A∩A = A;
交换律:A∪B = B∪A,A∩B = B∩A;
结合律:(A∪B)∪C = A∪(B∪C),
射,而对于模糊子集的运算,实际上可以转换称为对隶属函数的运算:
AAx 0,AU Ax 1 ABAxB x,ABAx B x AA x 1Ax
ABCC x maxAx, B x ABDDx minAx, B x
.
模糊聚类分析ppt课件

k 1
1 2
m k 1
(
xik
x jk )
m
( xik x jk )
rij
k 1 m
xik .x jk
k 1
5. 求模糊等价矩阵
用上述方法建立起来的模糊矩阵 R ,一般说来只 满足自反性和对称性,不一定满足传递性,即 R 不一 定是模糊等价关系,需要将 R改造成模糊等价矩阵R,
然后再在适当的阈值上进行截取,便可得所需分类。
根据需要可同时选择不同准则分别进行聚类分析,然后 通过综合取交的方法,以做到兼顾多目标,使分类结果更科学。
3、建立数据矩阵
设论域U { x1, x2 ,, xn }为被分类对象, 每个对象又由m 个指标表示其性状:
xi { xi1, xi2 ,, xim } (i 1,2,, n) 则得到原始数据矩阵为 X ( xij )nm .
1, 2,..., m
构造下列形式的F统计量,
r
i
2
ni x x /(r 1)
F i1 r ni
xij
i
x
2
/(n r)
i1 jn1
x x 其中, 为 i x x
m
i
(xk
xk )2
i
与
的距离, xij x i
i 为第
k 1
类中样本
xij 与
i
x 的距离。
F 统计量分子表征类与类之间的距离, 分母表示类内样本间距离,因此 F 值越大,说
改造的方法是将 R 自乘得 R R R2,再自 乘 R2 R2 R4 ,如此继续下去,得 R8 , R16 ……,至某 一步出现 R2k Rk 为止。则 Rk便是一个模糊等价关系。 这个方法是由所谓“传递闭包”理论而来,我们在此 拿来直接应用,不再作详细介绍。
模糊聚类分析实验报告
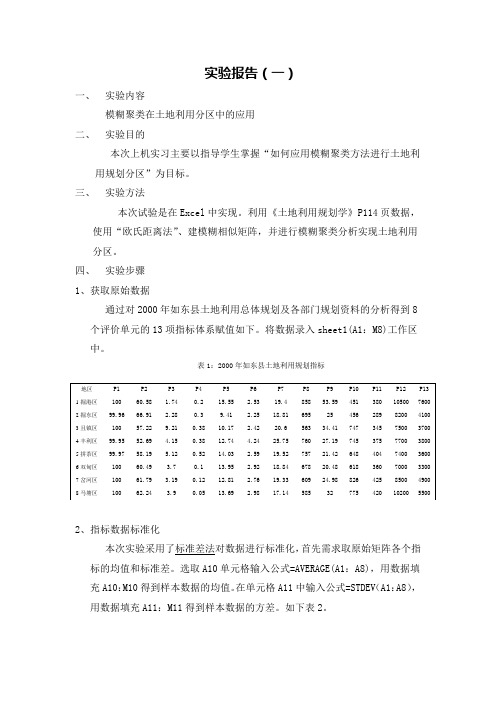
实验报告(一)一、实验内容模糊聚类在土地利用分区中的应用二、实验目的本次上机实习主要以指导学生掌握“如何应用模糊聚类方法进行土地利用规划分区”为目标。
三、实验方法本次试验是在Excel中实现。
利用《土地利用规划学》P114页数据,使用“欧氏距离法”、建模糊相似矩阵,并进行模糊聚类分析实现土地利用分区。
四、实验步骤1、获取原始数据通过对2000年如东县土地利用总体规划及各部门规划资料的分析得到8个评价单元的13项指标体系赋值如下。
将数据录入sheet1(A1:M8)工作区中。
表1:2000年如东县土地利用规划指标2、指标数据标准化本次实验采用了标准差法对数据进行标准化,首先需求取原始矩阵各个指标的均值和标准差。
选取A10单元格输入公式=AVERAGE(A1:A8),用数据填充A10:M10得到样本数据的均值。
在单元格A11中输入公式=STDEV(A1:A8),用数据填充A11:M11得到样本数据的方差。
如下表2。
表2:13个指标值得均值和标准差选取A13单元格输入公式=(A1-A$10)/A$11,并用数据填充A13:M20区域得到标准化矩阵如下表3。
表3:标准化数据矩阵3、求取模糊相似矩阵本次试验是通过欧氏距离法求取模糊相似矩阵。
其数学模型为:mr ij=1−c√∑(x ik−x jk)2k=1选取A23单元格输入公式=SQRT((A$13-A13)^2+(B$13-B13)^2+(C$13-C13)^2+(D$13-D13)^2+(E$13-E13)^2+(F$13-F13)^2+(G$13-G13)^2+(H$13-H13)^2+(I$13-I13)^2+(J$13-J13)^2+(K$13-K13)^2+(L$13-L13)^2+(M$13-M13)^2)求的d11,B23中输入公式=SQRT((A$14-A13)^2+(B$14-B13)^2+(C$14-C13)^2+(D$14-D13)^2+(E$14-E13)^2+(F$14-F13)^2+(G$14-G13)^2+(H$14-H13)^2+(I$14-I13)^2+(J$14-J13)^2+(K$14-K13)^2+(L$14-L13)^2+(M$14-M13)^2)q 求的d12。
模糊聚类分析

模糊聚类分析定义:根据具体的标准和性质对事物进行分类的方法称为聚类分析 根据模糊标准对事物进行分类的方法称为模糊聚类分析基本思想:根据分类对象之间的模糊相似程度来衡量相互的异同程度,进而实现模糊分类。
传统聚类分析VS 模糊聚类分析1. 传统聚类分析: 设有n 个对象12,,...nx x x,每个对象有m 种特性12,,...my y y。
1>首先对每个对象的特性进行数量化:用ijz代表第i 个对象的第j 个性质的数值。
则对象ix 的性质形成的一个向量()12,,...i i im z zz2>考察对象之间相近的程度:引入“欧式距离”和“夹角余弦”。
1欧式距离:设对象()()1212,,...,,,....i i im j j jm ijy x z zz z zz ==则欧式距离为:ijyx -=这与我们所熟知的向量的欧式距离是一样的!2夹角余弦:设α是对象ix和jy之间的夹角,0180α≤≤,则夹角余弦为:(),cos ijijy x yx α=其中:()11,...i j im jm ijy x z zz z =++ix=iy=有了这些基础认识之后,下面我们通过一个例子来说明传统聚类分析 设有5个对象125,,...x x x,不妨设每个对象只有一个性质,数量化后分别为1,2,4.5,6,8.现使用传统聚类法进行聚类。
1 欧式距离:5个对象,共有25c个欧式距离。
计算可得121x x-=133.5x x-= 145x x-= 157x x-= 232.5x x-= 244x x -= 256x x-=341.5x x-=35 3.5x x-=452x x-=根据聚类的思想,差异最小的对象属于一类 从而1x 和2x为一类,并记为1G2 将1G 看成新的对象,其特征值为1x 和2x 的平均值1.5。
此时对象为1345,,,G x x x 。
再次计算欧式距离。
可知34,x x之间的距离最小。
模糊聚类分析实验报告

专业:信息与计算科学 姓名: 学号:实验一 模糊聚类分析实验目的:掌握数据文件的标准化,模糊相似矩阵的建立方法,会求传递闭包矩阵;会使用数学软件MATLAB 进行模糊矩阵的有关运算实验学时:4学时实验内容:⑴ 根据已知数据进行数据标准化.⑵ 根据已知数据建立模糊相似矩阵,并求出其传递闭包矩阵.⑶ (可选做)根据模糊等价矩阵绘制动态聚类图.⑷ (可选做)根据原始数据或标准化后的数据和⑶的结果确定最佳分类. 实验日期:20017年12月02日实验步骤:1 问题描述:设有8种产品,它们的指标如下:x 1 = (37,38,12,16,13,12)x 2 = (69,73,74,22,64,17)x 3 = (73,86,49,27,68,39)x 4 = (57,58,64,84,63,28)x 5 = (38,56,65,85,62,27)x 6 = (65,55,64,15,26,48)x 7 = (65,56,15,42,65,35)x 8 = (66,45,65,55,34,32)建立相似矩阵,并用传递闭包法进行模糊聚类。
2 解决步骤:2.1 建立原始数据矩阵设论域},,{21n x x x X 为被分类对象,每个对象又有m 个指标表示其性状, im i i i x x x x ,,,21 ,n i ,,2,1 由此可得原始数据矩阵。
于是,得到原始数据矩阵为323455654566356542155665482615645565276285655638286384645857396827498673176422747369121316123837X 其中nm x 表示第n 个分类对象的第m 个指标的原始数据,其中m = 6,n = 8。
2.2 样本数据标准化2.2.1 对上述矩阵进行如下变化,将数据压缩到[0,1],使用方法为平移极差变换和最大值规格化方法。
(1)平移极差变换:111min{}max{}min{}ik ik i n ik ik ik i n i n x x x x x ,(1,2,,)k m L显然有01ikx ,而且也消除了量纲的影响。
模糊聚类分析方法

模糊聚类分析方法对所研究的事物按一定标准进行分类的数学方法称为聚类分析,它是多元统 计“物以类聚”的一种分类方法。
载科学技术、经济管理中常常要按一定的标准 (相似程度或亲疏关系)进行分类。
例如,根据生物的某些性状可对生物分类, 根据土壤的性质可对土壤分类等。
由于科学技术、经济管理中的分类界限往往不 分明,因此采用模糊聚类方法通常比较符合实际。
一、模糊聚类分析的一般步骤1、第一步:数据标准化[9](1)数据矩阵设论域U ={X i ,X 2,||l,X n }为被分类对象,每个对象又有m 个指标表示其性状,于是,得到原始数据矩阵为Xm 1X m2bI-Xnm」其中X nm 表示第n 个分类对象的第m 个指标的原始数据(2)数据标准化在实际问题中,不同的数据一般有不同的量纲,为了使不同的量纲也能进行 比较,通常需要对数据做适当的变换。
但是,即使这样,得到的数据也不一定在 区间[0,1]上。
因此,这里说的数据标准化,就是要根据模糊矩阵的要求,将数据 压缩到区间[0,1]上。
通常有以下几种变换: ① 平移•标准差变换X i = {x i1, X i2,川,X m }X i 1X2 1X n2 IHxik -(i 一 1,21 n, k_;HL 2mS k其中-1 n1 n_ 2xkxi , 2(xik~'兀)。
n i 4: n i 4经过变换后,每个变量的均值为 0,标准差为1,且消除了量纲的影响。
但是,再用得到的x k 还不一定在区间[0,1]上。
② 平移•极差变换显然有0乞x ik 乞1,而且也消除了量纲的影响 ③ 对数变换xk- lg x ik (i = 1,n , k; l [L 2 m取对数以缩小变量间的数量级。
2、第二步:标定(建立模糊相似矩阵)设论域U ={为公2,川,人} , X i ={为1必2,川,心},依照传统聚类方法确定相似 系数,建立模糊相似矩阵,x i 与X j 的相似程度用=R(X j ,X j )。
聚类分析及其应用实例ppt课件

Outlines
聚类的思想 常用的聚类方法 实例分析:层次聚类
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
3. 实例分析:层次聚类算法
定义:对给定的数据进行层次的分解
第4 步
➢
凝聚的方法(自底向上)『常用』
思想:一开始将每个对象作为单独的
第3 步
一组,然后根据同类相近,异类相异 第2步 的原则,合并对象,直到所有的组合
并成一个,或达到一个终止条件。 第1步
a, b, c, d, e c, d, e d, e
X3 Human(人) X4 Gorilla(大猩猩) X5 Chimpanzee(黑猩猩) X2 Symphalangus(合趾猿) X1 Gibbon(长臂猿)
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
离差平方和法( ward method ):
各元素到类中心的欧式距离之和。
Gp
Cluster P
Cluster M
Cluster Q
D2 WM Wp Wq
G q
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
凝聚的层次聚类法举例
Gp G q
Dpq max{ dij | i Gp , j Gq}
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
基于模糊C均值的聚类分析

• U = initfcm(cluster_n, data_n); %初始 化模糊分割矩阵
%以下为主循环: • for i = 1:max_iter, • [U, center, obj_fcn(i)] =
stepfcm(data, U, cluster_n, expo); • if display, • fprintf('Iteration count = %d, obj.
基于模糊C均值的聚类分析
1 模糊c均值聚类(FCM)方法
模糊C均值聚类(FCM)方法是一种在已 知聚类数的情况下,利用隶属度函数和迭 代算法将有限的数据集分别聚类的方法。 其目标函数为:
式中, 为样本数; 为聚类数; 为第 个 样本相对于第 个聚类中心的隶属度; 为
第 个类别的聚类中心; 为样本到聚类 中心的欧式距离。聚类的结果使目标函 数 最小,因此,构造如下新的目标函 数:
(2)
这里 , =1,⋯ ,n,是等式的n个约束 式的拉格朗日乘子。对所有输入参量求 导,使式(1)达到最小的必要条件为:
(3)
(4)
由上述两个必要条件,模糊c均值聚类算 法是一个简单的迭代过程。在批处理方 式运行时,FCM采用下列步骤确定聚类中 心 和隶属矩阵 U:
步骤1 用值在0,1间的随机数初始 化隶属矩阵U,使其满足式(2)中的约束 条件。
1735.33; 2421.83; 2196.22; 535.62; 584.32; 2772.9; 2226.49; 1202.69;
2949.16 1692.62 1680.67 2802.88 172.78 2063.54 1449.58 1651.52 341.59 291.02
3244.44 1867.5 1575.78 3017.11 3084.49 3199.76 1641.58 1713.28 3076.62 3095.68
模糊数学-模糊数学基本知识

隶属函数参数化
1. 三角形隶属函数
0
trig ( x;
a,
b,
c)
x a ba
cx
cb
0
xa a xb b xc
cx
trig(x; a,b, c) max(min( x a , c x), 0) ba cb
参数a,b,c确定了三角形MF三个顶点的x坐标。
2. 梯形隶属函数
0
xa
trap(x, a, b, c, d )
g(x;50,20)
bell(x:20,4,50)
❖ (2)模糊子集运算的基本性质
模糊集合间的并、交、补(余)运算 具有如下的性质.
1)幂等律 A~ A~ A~, A~ A~ A~
2)交换律 A~ B~ B~ A~; A~ B~ B~ A~
3)结合律 ( A~ B~) C~ A~ (B~ C~),
论域U上的模糊集A由隶属函数uA来表征, uA的大小反映了x对于模糊子集的从属程度。 模糊子集完全由隶属函数来描述。
❖ 模糊子集的表示方法 (1)向量法
(2)查德表示法 有限集 无限集
模糊集举例 例4 设U={1,2,3,4,5,6}, A表示“靠近4”的数,则 AF (U),各数属于A的程度A(ui) 如表。
经典集合论的例子: 设U={ 红桃,方块,黑桃,梅花 }
V={ A,1,2,3,4,5,6,7,8,9, 10,J, Q, K } 求U×V
解: U×V={ (红桃,A),(红 桃, 2),……,(
梅花, K) }
35
模糊关系论例子: 设有一组学生U:
U={ 张三,李四,王五 } 他们对球类运动V:
( A~ B~) C~ A~ (B~ C~).
模糊聚类案例分析(DOC)

模糊数学方法及其应用论文题目:模糊聚类方法案例分析小组成员:王季光宋申辉兰洁陈倩芸肖仑杨洋吴云峰2013年10 月27 日模糊聚类分析方法1.1距离和相似系数为了将样品(或指标)进行分类,就需要研究样品之间关系。
目前用得最多的方法有两个:一种方法是用相似系数,性质越接近的样品,它们的相似系数的绝对值越接近1,而彼此无关的样品,它们的相似系数的绝对值越接近于零。
比较相似的样品归为一类,不怎么相似的样品归为不同的类。
另一种方法是将一个样品看作P 维空间的一个点,并在空间定义距离,距离越近的点归为一类,距离较远的点归为不同的类。
但相似系数和距离有各种各样的定义,而这些定义与变量的类型关系极大,因此先介绍变量的类型。
由于实际问题中,遇到的指标有的是定量的(如长度、重量等),有的是定性的(如性别、职业等),因此将变量(指标)的类型按以下三种尺度划分: 间隔尺度:变量是用连续的量来表示的,如长度、重量、压力、速度等等。
在间隔尺度中,如果存在绝对零点,又称比例尺度,本书并不严格区分比例尺度和间隔尺度。
有序尺度:变量度量时没有明确的数量表示,而是划分一些等级,等级之间有次序关系,如某产品分上、中、下三等,此三等有次序关系,但没有数量表示。
名义尺度:变量度量时、既没有数量表示,也没有次序关系,如某物体有红、黄、白三种颜色,又如医学化验中的阴性与阳性,市场供求中的“产”和“销”等。
不同类型的变量,在定义距离和相似系数时,其方法有很大差异,使用时必须注意。
研究比较多的是间隔尺度,因此本章主要给出间隔尺度的距离和相似系数的定义。
设有n 个样品,每个样品测得p 项指标(变量),原始资料阵为px x x np n n p p nx x x x x x x x x X X X X 2122221112112121 ⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=其中(1,,;1,,)ij x i n j p ==为第i 个样品的第j 个指标的观测数据。
模糊数学2模糊聚类分析方法模糊综合评判方法

❖ (1)单层次模糊综合评判模型 设X={x1,x2…xn}是综合评判因素所组成集合,
Y={y1,y2…yn}是评语所组成的集合。
R:X→Y rij=µR(xi,yj) 元素rij表示xi符合yj标准的程度。
A=(a1,a2…an)是各评判因素的权重分配,
则评判结果 B=A◦R.
例
我们对于某学校的校园网络一期建设情况进行评判,设包括三个因 素,即硬件建设,软件建设、人员培训,用论域U表示为:
0.38 0.8 0.67
0.49 1375 931源自0.380.80.67
0.93
0.95 0.67 0.94
0.9
0.94 0.67 0.95
1
0.99
0.99 0.45 0.55
0.99
1
0.99 0.45 0.55
0.99
0.45 0.55
0.99
0.45 0.55
1
0.45 0.55
0.45 1
0.49137 5931
0.93
0.9
1 0.67 0.94 0.38
0.38
0.38 0.95 0.94
0.67 1 0.67
0.94 0.67 1
0.8 0.67
0.8 0.67
0.8 0.67
0.67 0.94 0.67 0.95
0.49137 5931
0.38 0.8 0.67
0.49137 5931
较好
40% 30% 10%
可以
10% 20% 30%
不好
0 10% 60%
0.2 R ~
0.7
0.1
0
上表就构成模糊矩阵 R= 0
0.4 0.5 0.1
模糊聚类实验报告

一、实验背景随着大数据时代的到来,数据挖掘技术在各个领域得到了广泛的应用。
聚类分析作为数据挖掘的一种基本方法,通过对数据进行无监督学习,将相似的数据点归为一类,从而揭示数据中的潜在结构和规律。
传统的聚类算法如K-means算法在处理复杂数据时往往存在局限性,而模糊聚类算法能够更好地处理模糊性和不确定性,因此在实际应用中具有更广泛的前景。
二、实验目的1. 理解模糊聚类算法的基本原理和实现方法;2. 掌握模糊C均值(FCM)算法的应用;3. 分析不同参数对聚类结果的影响;4. 对比模糊聚类算法与传统聚类算法的性能。
三、实验内容1. 数据准备选取UCI机器学习库中的鸢尾花(Iris)数据集作为实验数据。
该数据集包含150个样本,每个样本有4个特征,属于3个类别。
2. 模糊C均值算法实现(1)初始化聚类中心:随机选取3个样本作为初始聚类中心。
(2)计算隶属度:根据每个样本与聚类中心的距离,计算其属于各个聚类的隶属度。
(3)更新聚类中心:根据隶属度,计算每个聚类中心的新位置。
(4)重复步骤(2)和(3),直到满足迭代终止条件。
3. 参数设置与调整(1)模糊系数m:m值越大,聚类结果越模糊,m值越小,聚类结果越精确。
实验中分别取m=1.5、m=2.5和m=3.5。
(2)最大迭代次数:设置最大迭代次数为100次。
4. 聚类结果分析(1)对比不同m值下的聚类结果:通过可视化工具展示不同m值下的聚类结果,分析m值对聚类结果的影响。
(2)对比模糊聚类算法与传统K-means算法的性能:通过计算聚类结果的轮廓系数,对比两种算法的性能。
四、实验结果与分析1. 不同m值下的聚类结果当m=1.5时,聚类结果较为模糊,部分样本同时属于多个类别;当m=2.5时,聚类结果较为精确,但仍存在一些样本同时属于多个类别;当m=3.5时,聚类结果最为精确,但部分样本的类别归属存在争议。
2. 模糊聚类算法与传统K-means算法的性能对比通过计算轮廓系数,模糊聚类算法的平均轮廓系数为0.76,而K-means算法的平均轮廓系数为0.54。
模糊聚类分析

模糊聚类分析----96845308-7160-11ec-a68e-7cb59b590d7d聚类分析就是将一个没有类别标记的样本集按照某种准则划分成若干个子集(类),使相似的样本尽可能归为一类,而不相似的样本尽可能划分到不同的类中。
由于在对样本集进行聚类的过程中,没有任何关于类别的先验知识,所以聚类分析属于无监督分类的范畴。
传统的聚类分析是一种硬划分,它严格地将每个待识别对象划分为一个类。
阶级划分的界限是明确的,具有非此即彼的性质。
在现实世界中,无论是一组对象根据其亲和力和相似性形成一个组,还是一个对象是否属于一个类别,其边界往往是不明确的,并且具有“这个和那个”的性质。
对于这种具有不确定性的聚类问题,模糊聚类分析提供了一种强有力的分析工具。
模糊聚类分析能够建立样本对于类别的不确定性描述,表达样本类属的中介性,已经成为聚类分析研究的主流。
粗略来讲,模糊聚类分析方法可分为两类:基于模糊等价关系的聚类方法和基于目标函数的聚类方法。
有时,这两类方法也结合起来使用。
一、数据预处理在模糊聚类分析中,我们称待分类的对象为样本。
要对样本进行合理的分类,首先应考虑样本的各种特性指标(观测数据)。
设有n个被分类对象,即样本集为x={x1,x2,…,xn}每一个xi有m个特性指标,即xi可表示为特性指标向量xi={xi1,xi2,…,xim}其中xij表示第i个样本的第j个特性指标。
于是,n个样本的特性指标矩阵为⎜⎜x21⎜M⎜⎜十、⎜n1x12lx1m⎜x22lx2m⎜xn2lxnm⎜⎜通常,我们也将样本集记为特性指标矩阵的形式,即x=(xij)n×m。
如果M个特征指标的维度和数量级不同,在运行过程中可能会突出一些大数量级特征指标的作用,而一些小数量级特征指标的作用可能会减少甚至被排除,导致每个特征指标的分类缺乏统一的尺度。
因此,为了消除不同特征指标单位和数量级的影响,当特征指标的维度和数量级不同时,通常会提前对各种指标值进行数据标准化(归一化),使每个指标值统一在一个共同的数值特征范围内。
模糊聚类分析例子1

1. 模糊聚类分析模型环境区域的污染情况由污染物在4个要素中的含量超标程度来衡量。
设这5个环境区域的污染数据为1x =(80, 10, 6, 2), 2x =(50, 1, 6, 4), 3x =(90, 6, 4, 6), 4x =(40, 5, 7, 3), 5x =(10, 1, 2, 4). 试用模糊传递闭包法对X 进行分类。
解 :由题设知特性指标矩阵为: *80106250164906464057310124X ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦数据规格化:最大规格化'ij ijjx x M =其中: 12max(,,...,)j j j nj M x x x =00.8910.860.330.560.10.860.6710.60.5710.440.510.50.110.10.290.67X ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦构造模糊相似矩阵: 采用最大最小法来构造模糊相似矩阵55()ij R r ⨯=,10.540.620.630.240.5410.550.700.530.620.5510.560.370.630.700.5610.380.240.530.370.381R ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦利用平方自合成方法求传递闭包t (R )依次计算248,,R R R , 由于84R R =,所以4()t R R =210.630.620.630.530.6310.560.700.530.620.5610.620.530.630.700.6210.530.530.530.530.531R ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦,410.630.620.630.530.6310.620.700.530.620.6210.620.530.630.700.6210.530.530.530.530.531R ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦=8R选取适当的置信水平值[0,1]λ∈, 按λ截矩阵进行动态聚类。
模糊聚类分析法

4.聚类(求动态聚类图)
(1)基于模糊等价矩阵聚类方法 有① 传递闭包法② 布尔矩阵法 (2) 直接聚类法 对上述撤销观测站的问题用基于模 糊等价矩阵的模糊聚类方法进行分 析
注:R是对称矩阵,故只写出它的下三角矩阵
1.000 0.861 0.697 0.861 0.861 R * 0.861 0.994 0.719 0.697 0.688 0.719 1 0.697 1 0.996 0.697 1 0.996 0.697 0.992 1 0.995 0.697 0.922 0.922 1 0.719 1 0.697 0.676 1 0.688 0.688 0.697 1 0.719 0.688 0.697 0.688 1
, 而且也消除了量纲的影响。 ③ 对数变换
显然有
,
取对数以缩小变量间的数量级。
3.建立模糊相似矩阵
建立模糊相似矩阵,主要借用传统聚类的相似系数法、距离法以及其 他方法。相似系数表示两个对象之间的相似程度.
得到模糊相似矩阵R
1.000 0.839 0.528 0.844 0.828 0.702 0.995 0.671 0.431 0.573 0.712 0.839 1.000 0.542 0.996 0.989 0.899 0.855 0.510 0.475 0.617 0.572 0.528 0.542 1.000 0.562 0.585 0.697 0.571 0.551 0.962 0.642 0.568 0.844 0.996 0.562 1.000 0.992 0.908 0.861 0.542 0.499 0.639 0.607 0.828 0.989 0.585 0.992 1.000 0.922 0.843 0.526 0.512 0.686 0.584 0.702 0.899 0.697 0.908 0.922 1.000 0.726 0.455 0.667 0.596 0.511 0.995 0.855 0.571 0.861 0.843 0.726 1.000 0.676 0.489 0.587 0.719 0.671 0.510 0.551 0.542 0.526 0.455 0.676 1.000 0.467 0.678 0.994 0.431 0.475 0.962 0.499 0.512 0.667 0.489 0.467 1.000 0.487 0.485 0.573 0.617 0.642 0.639 0.686 0.596 0.587 0.678 0.487 1.000 0.688 0.712 0.572 0.568 0.607 0.584 0.511 0.719 0.994 0.485 0.688 1.000
模糊聚类分析步骤

根据’• ( 0,1)的不同取值分布不同的类。
注释(1):模糊相似矩阵只具有自反性和对称性,不具有传递性,求 丸截矩阵的 前提是R 是X 上的的模糊等价关系。
所以要先求得R 传递闭包,将模糊相似矩阵 转化为模糊等价矩阵。
原始数据矩阵X=l 1标准化矩阵模糊相似矩阵R ( 1求分类对象的相似度传递闭包法进行聚类(求动态聚类图)等价关系矩阵传递闭包法布尔矩阵法直接聚类法雨量站问题集地区毀置有I】个南量站,比分布图ftS b 10年耒紛條站所测得的年降雨盘列入表1中.现間経费问範希望撤涓几个蔺嵋站”问撇俏@呼雨量站. 而不会太筋的喊少降帕信息?图1南屋站分布图表ft南朮站年向测得的雨原始数据矩阵:>> X^ilsreadf shujian^. s 1SK T 3 ' sheet 1T ,1 B2:K12R )K = 276251152245曲1 4旳25845315S324324 28? 433 232 51] 153 32?J55 2ri 4阳 159349200 243 502 224 432357 410 23S 41 了 344 563 Z81 383 173 401 452 308 520 292 310 479 267 330 1C4 361 384 283 442 25S 4 &4 502 310 410 203 381 420 410 520 31128S221 273 3B2502301482201358303451220 515 257320413228173343175402320285603240402350 43025124330?41132723U27SW9342232320 470 232352292350421252185371» T=b :hi (r>r=0.4S06C.1167 0.(1714 CUP 前D.E532 0L 38 開c0.31i3n” 倒 951. w 口” M95rr.巧in ii 1. 5194 □ .53轨 D.41^1 C.HDCO0. 4475 CL 2&42 01.05170. 1她 I. DODD a. BOW O .滤咒 0L.OODD0. 12471,0X00.4D&3 a. 3soiO.QGtlD. BBrD18819 a .氐 IE l.OQOO 0. B236□. 2&剤□L msC.2P17 U. 1STBa.airi□ .□.6142 D. 4B» o. rsf] 0. 3G9B J. 9269 0. OXG C.GDOd C.42^ a.130B 0. F9L1 a 7559 IL 9266 L.COOOD ・ 69B43. 15530. 0762 C.3417 C.2630J.COOO0r 43T B 1. 0000IL 1581 0.4316u. secaD. 9132LI. Hftib D.时If uo.4ru3J. 91R5LI UL Q/t2 O. 37890.0C3DD. 0835 0. 3450 C. 4-^17 1.00000.2334o. enz0.519r 1.X0C 0. C5f] 0. $3D7J. 25570, B903 0, 7G17 Q* C6SE0. 348$Da. 3466 OL S?6E Q ・ 1649 D_E339 i. iran口” 1Q7BL r l i 口[:c . f : run. 5531n.n. OJQS□r FW33D. 4?72M R=biaod?CY, OL 1]1.0J0U0L 阳孔Q.E1D8 0.1762O . 6138 ixqzu OL 8M.L□.6139 D. dllF □.61^3OL 5?go一fi >SU L_ DDQO a. 6237 LL r :和O. SSB8 0_63&fO L 妙T D.SB33 U.協弱 O L 葩曲 EL 5705 O.610&0i623ri.oajo 0.557 Do. am D.dl99 O L 5164D.63S3 0. 廿 C L 6O8T0.4M3 g 磋OU ⑷0.65^0 L. 000.80D?O.E782 D.6069 0,涮1H6424H4M1CL513S 0L BS8B.0,«2»8 0.=00T1.0000 0, f lflg Ou 67? 8 0.600? 山&)2SO L «0LSO L 57=35 C.424JCL bJb/(1・ £199 u. r f b 七Qi nsp LUIJUU Ol 40'sS D.bBfS u. sru □. &ZI32OLB643 ..H=4] DL B9U?CLM 虫 II. . 'K. OL S C 刿日 ].UOOO 0.6402 U.4SLJ4 □-曲甜D L ESSE C.S130 0. 5333 Q. 5.3 53 0L 506?o. soor C.5 37S0.15452 l.ODOO o. sro3CL 0223O L0OiSE-ML ;0.EME0.8S47 0*66310.6026 tis^i0.4!?^ o.eroa :,J OOO0U1S4 H&245 C.4143饥闊罪o.^asr C. 5124a. ms D.dD32 O L OS'S D.6223 0. C131 1. OOOO Ou 5»52L .BMD 0LB7QE□ ,40930.4M1IL b 赳 bEL H 6430.鸵刈D.SD05U.駁叮a ;bJb2 L DDOD(重要定理:设R F ( X X )是相似关系(即R是自反、对称模糊关系),则e(R) = t(R)即模糊相似关系的传递闭包就是它的等价闭包。
第4章 模糊聚类分析

第8讲 模糊关系(第四章 模糊关系与模糊聚类分析)一、模糊关系1.普通关系(1)直积(笛卡尔积,Descartes)定义4.1给定集合,A B ,由A 中元素和a B 中元素搭配起来的所有元素对构成的集合称为(,)a b b A B 与的直积,或笛卡尔(Descartes)乘积,记作A B ×,即{}(,)|,A B a b a A b B ×=∈∈ 类似地,可定义{}11(,,),1,,n n i i A A x x x A i n Δ××=∈= 211321111,R R R R R R R R R=×=×=×× (2)关系现实世界中存在各种各样的关系。
“父子关系”,“师生关系”,“数的大于等于关系”…,X Y 特点:涉及两个集合,y ,x X y Y ∀∈∈x ,与或者有关系,或者没关系,这就是普通关系。
,X Y X 定义4.2 给定论域,规定一个到的关系R X Y →Y R (记作),对任意y ,x X y Y ∈∈xRy x x ,与有关系,记作,与y c xR y 无关系记作,二者必居其一,且仅居其一。
R X 当时,X Y =称为上的关系。
对元素间的搭配施加某些限制,构成的集合就是A B ×的一个子集,这种联系就是所谓关系。
R X Y ⊆×定义 4.2 (等价定义)若',则称R X 为到的关系。
Y 例4.1 “大于等于“关系,记作“” ≥(,)x y R R ∀∈×,1, (,)0, x y x y x y ≥⎧≥=⎨<⎩例4.2 设表示教室里的全体男同学,Y 表示教室里的全体女同学。
X X Y ×表示什么?任意一个男同学和任意一个女同学组成的有序对构成的集合。
R ,则“同系”关系记为{}(,)|R x y x X y Y x y =∈∈,,且与同属一个系,显然R X Y ⊆×。
工业大数据分析-聚类算法教学讲义

任务6.3聚类算法任务概述聚类分析仅根据在数据中发现的描述对象及其关系的信息,将数据对象分组。
其原理是:组内的对象相互之间是相似的(相关的),而不同组中的对象是不同的(不相关的)。
组内的相似性(同质性)越大,组间差别越大,聚类就越好。
聚类分析可以建立宏观的概念,发现数据的分布模式,是知识发现的基础。
本节以聚类分析中的模糊C均值为例来讲解相关案例实现过程。
模糊聚类分析作为无监督机器学习的主要技术之一,是用模糊理论对重要数据分析和建模的方法。
建立了样本类属性的不确定性描述。
在众多模糊聚类算法中,模糊C均值算法应用最广泛且较为成功。
模糊C均值聚类算法通过优化目标函数得到每个样本点对所有类中心的隶属度,从而决定样本点的类属以达到自动对样本数据进行分群的目的。
●数据格式①不支持设置类属性(输出);②(输入)支持离散型(名词)属性和连续型(数值)属性。
●参数说明图6-3-1模糊C均值参数设置具体说明参见表 6-7:表6-7模糊C均值参数设置本案例使用的数据集是某水厂投药控制系统实时采集的数据信息,数据均为瞬时测量值,包括历史原水水质数据、原水流量数据、沉淀池浊度和混凝剂投加量(PAC耗)数据等,共6166个样本。
数据文件:投药量数据.csv。
数据集说明(共137行,6列),同表6-2。
通过本任务的学习:(1)能够构建聚类算法模型对工业大数据进行分析。
任务实现具体操作如下:步骤1:建模区分别拖入“文件输入”节点、“设置角色”节点和“模糊C均值”节点,构建如下模型,如图6-3-2所示:图6-3-2聚类算法-构建模型步骤2:“文件输入”节点配置,选择工业用水处理投药量数据,具体操作图形如下,如图6-3-3所示:图6-3-3聚类算法-文件输入-文件上传步骤3:点击确定,完成文件输入配置。
对“设置角色”节点配置如下,如图6-3-4所示:图6-3-4聚类算法-设置角色步骤4:“模糊C均值”节点配置如下,如图6-3-5所示:图6-3-5聚类算法-模糊C均值-节点配置步骤5:点击右上角执行按钮,如图6-3-6所示图6-3-6执行模型步骤6:模型运行结果如下,如图6-3-7、图6-3-8和图6-3-9所示:图6-3-7聚类算法-运行结果1图6-3-8聚类算法-运行结果2图6-3-9聚类算法-运行结果3运行结果说明:通过以上图片,完成学习如何进行聚类算法的建模和运行方法,聚类分析仅根据在数据中发现的描述对象及其关系的信息,将数据对象分组。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
模糊聚类分析例子11. 模糊聚类分析模型环境区域的污染情况由污染物在4个要素中的含量超标程度来衡量。
设这5个环境区域的污染数据为1x =(80, 10, 6, 2), 2x =(50, 1, 6, 4), 3x =(90, 6, 4, 6), 4x =(40, 5, 7, 3), 5x =(10, 1, 2, 4). 试用模糊传递闭包法对X 进行分类。
解 :由题设知特性指标矩阵为: *80106250164906464057310124X ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦数据规格化:最大规格化'ij ijjx x M =其中: 12max(,,...,)j j j nj M x x x =00.8910.860.330.560.10.860.6710.60.5710.440.510.50.110.10.290.67X ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦构造模糊相似矩阵: 采用最大最小法来构造模糊相似矩阵55()ij R r ⨯=,10.540.620.630.240.5410.550.700.530.620.5510.560.370.630.700.5610.380.240.530.370.381R ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦利用平方自合成方法求传递闭包t (R )依次计算248,,R R R , 由于84R R =,所以4()t R R =210.630.620.630.530.6310.560.700.530.620.5610.620.530.630.700.6210.530.530.530.530.531R ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦,410.630.620.630.530.6310.620.700.530.620.6210.620.530.630.700.6210.530.530.530.530.531R ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦=8R选取适当的置信水平值[0,1]λ∈, 按λ截矩阵进行动态聚类。
把()t R 中的元素从大到小的顺序编排如下: 1>0.70>0.63>062>053. 依次取λ=1, 0.70, 0.63, 062, 053,得11000001000()0010*******0001t R ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦,此时X 被分为5类:{1x },{2x },{3x },{4x },{5x }0.71000001010()001000101000001t R ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦,此时X 被分为4类:{1x },{2x ,4x },{3x },{5x }0.631101011010()001001101000001t R ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦,此时X 被分为3类:{1x ,2x ,4x },{3x },{5x }0.621111011110()111101111000001t R ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦,此时X 被分为2类:{1x ,2x ,4x ,3x },{5x }0.531111111111()111111*********t R ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦,此时X 被分为1类:{12345,,,,x x x x x }Matlab 程序如下: %数据规格化MATLAB 程序 a=[80 10 6 250 1 6 4 90 6 4 6 40 5 7 3 10 1 2 4]; mu=max(a) for i=1:5 for j=1:4r(i,j)=a(i,j)/mu(j); end end r%采用最大最小法构造相似矩阵r=[0.8889 1.0000 0.8571 0.3333 0.5556 0.1000 0.8571 0.6667 1.0000 0.6000 0.5714 1.0000 0.4444 0.5000 1.0000 0.5000 0.1111 0.1000 0.2857 0.6667]; b=r'; for i=1:5 for j=1:5R(i,j)=sum(min([r(i,:);b(:,j)']))/sum(max([r(i,:);b(:,j)'])); end end R%利用平方自合成方法求传递闭包t (R ) 矩阵合成的MATLAB 函数function rhat=hech(r); n=length(r); for i=1:n for j=1:nrhat(i,j)=max(min([r(i,:);r(:,j)'])); end end求模糊等价矩阵和聚类的程序R=[ 1.0000 0.5409 0.6206 0.6299 0.2432 0.5409 1.0000 0.5478 0.6985 0.5339 0.6206 0.5478 1.0000 0.5599 0.3669 0.6299 0.6985 0.5599 1.0000 0.3818 0.2432 0.5339 0.3669 0.3818 1.0000]; R1=hech (R) R2=hech (R1) R3=hech (R2) bh=zeros(5); bh(find(R2>0.7))=12. 模糊综合评判模型某烟草公司对某部门员工进行的年终评定,关于考核的具体操作过程,以对一名员工的考核为例。
如下表所示,根据该部门工作人员的工作性质,将18个指标分成工作绩效(1U )、工作态度(2U )、工作能力(3U )和学习成长(4U )这4各子因素集。
员工考核指标体系及考核表技能提高 0.1 0.4 0.3 0.1 0.1 培训参与 0.2 0.3 0.4 0.1 0 工作提供0.40.30.20.1请专家设定指标权重,一级指标权重为:()0.4,0.3,0.2,0.1A =二级指标权重为:()10.2,0.3,0.3,0.2A =()20.3,0.2,0.1,0.2,0.2A = ()30.1,0.2,0.3,0.2,0.2A = ()40.3,0.2,0.2,0.3A =对各个子因素集进行一级模糊综合评判得到:()1110.39,0.39,0.26,0.04,0.01B A R ==o ()2220.21,0.37,0.235,0.125,0.06B A R ==o ()3330.15,0.32,0.355,0.125,0.06B A R ==o()4440.27,0.35,0.24,0.1,0.02B A R ==o这样,二级综合评判为:()0.390.390.260.040.010.210.370.2350.1250.060.4,0.3,0.2,0.10.150.320.3550.1250.060.270.350.240.10.2B A R ⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎣⎦o o ()0.28,0.37,0.27,0.09,0.04=根据最大隶属度原则,认为该员工的评价为良好。
同理可对该部门其他员工进行考核。
3. 层次分析模型你已经去过几家主要的摩托车商店,基本确定将从三种车型中选购一种,你选择的标准主要有:价格、耗油量大小、舒适程度和外观美观情况。
经反复思考比较,构造了它们之间的成对比较判断矩阵。
A=1378115531113751111853⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦三种车型(记为a,b,c )关于价格、耗油量、舒适程度和外表美观情况的成对比较判断矩阵为价格 a b c 耗油量 a b c1231/2121/31/21a b c ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦ 11/51/251721/71a b c ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦舒适程度 a b c 外表 a b c1351/3141/51/41a b c ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦ 11/535171/31/71a b c ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦根据上述矩阵可以看出四项标准在你心目中的比重是不同的,请按由重到轻顺序将它们排出。
解:用matlab 求解 层次总排序的结果如下表Matlab 程序如下:clc,clear n1=4; n2=3;a=[1 3 7 8 1/3 1 5 5 1/7 1/5 1 3 1/8 1/5 1/3 1];b1=[1 2 3 1/2 1 2 1/3 1/2 1 ]; b2=[1 1/5 1/2 5 1 7 2 1/7 1 ];b3=[1 3 5 1/3 1 4 1/5 1/4 1 ]; b4=[1 1/5 3 5 1 7 1/3 1/7 1];ri=[0,0,0.58,0.90,1.12,1.24,1.32,1.41,1.45]; % 一致性指标RI [x,y]=eig(a); %x 为特征向量,y 为特征值lamda=max(diag(y));num=find(diag(y)==lamda);w0=x(:,num)/sum(x(:,num));w0 %准则层特征向量CR0=(lamda-n1)/(n1-1)/ri(n1) %准则层一致性比例for i=1:n1[x,y]=eig(eval(char(['b',int2str(i)])));lamda=max(diag(y));num=find(diag(y)==lamda);w1(:,i)=x(:,num)/sum(x(:,num)); %方案层的特征向量CR1(i)=(lamda-n2)/(n2-1)/ri(n2); %方案层的一致性比例endw1CR1, ts=w1*w0, CR=CR1*w0 %ts为总排序的权值,CR为层次总排序的随机一致性比例% 当CR小于0.1时,认为总层次排序结果具有较满意的一致性并接受该结果,否则对判断矩阵适当修改4. 灰色预测GM(1,1)模型某地区年平均降雨量数据如表某地区年平均降雨量数据x i<=hz为旱灾。
预测下一次旱灾发生的时间规定hz=320,并认为(0)()解:初始序列如下(0)x =(390.6,412,320,559.2,380.8,542.4,553,310,561,300,632,540,406.2,313.8,576,587.6,318.5)由于满足(0)()x i <=320的(0)()x i 为异常值,易得下限灾变数列为0hz x = (320,310,300,313.8,318.5)其对应的时刻数列为t = (3,8,10,14,17)建立GM (1,1)模型(1) 对原始数据t 做一次累加,即t(1) = (3,11,21,35,52) (2) 构造数据矩阵及数据向量 (3) 计算a ,ba=-0.2536,b=6.2585 (4) 建立模型y=-24.6774+27.6774*exp(.253610*t) (5) 模型检验(6) 通过计算可以预测到第六个数据是22.0340由于 22.034 与17 相差5.034,这表明下一次旱灾将发生在五年以后。
