第二章数据结构基础
数据结构第二章课后答案

数据结构第二章课后答案数据结构第二章课后答案1. 线性表1.1 数组实现线性表Q1. 请说明线性表的定义,并结合数组实现线性表的特点进行解释。
线性表是由n(n≥0)个数据元素构成的有序序列,其中n表示线性表的长度。
数组实现线性表的特点是使用一组具有相同数据类型的连续存储空间存储线性表中的元素,通过下标访问和操作元素。
A1. 线性表的定义指出,线性表是由若干个数据元素组成的有序序列。
具体地,在数组实现线性表中,我们将元素存储在一组连续的内存空间中,通过下标访问和操作元素。
由于数组的存储空间具有连续性,这样的实现方式可以在O(1)的时间复杂度下进行元素的访问和修改操作。
1.2 链表实现线性表Q2. 请说明链表实现线性表的特点,并与数组实现进行比较。
链表实现线性表的特点是通过指针将线性表中的元素按照节点的形式连接起来,每个节点包含了存储的元素和指向下一个节点的指针。
与数组实现相比,链表的插入和删除操作更为高效,但是访问某个位置的元素需要从头开始遍历,时间复杂度较大。
A2. 链表实现线性表的特点是通过使用节点和指针将线性表中的元素连接起来。
每个节点中包含了一个存储的元素和指向下一个节点的指针。
链表的插入和删除操作的时间复杂度为O(1),因为只需要改变指针的指向即可。
但是,访问某个位置的元素需要从头开始遍历链表,所以时间复杂度为O(n)。
2. 栈和队列2.1 栈的定义和基本操作Q3. 请给出栈的定义和基本操作。
栈是一种特殊的线性表,它只能在表的一端进行插入和删除操作,该端称为栈顶。
栈的基本操作包括入栈(push)和出栈(pop),分别用于将元素压入栈和将栈顶元素弹出。
A3. 栈是一种特殊的线性表,它只能在表的一端进行插入和删除操作。
这个特定的一端称为栈顶,而另一端称为栈底。
栈的基本操作包括入栈(push)和出栈(pop)。
入栈操作将一个元素压入栈顶,出栈操作将栈顶元素弹出。
2.2 队列的定义和基本操作Q4. 请给出队列的定义和基本操作。
《数据结构》课后习题答案(第2版)

《数据结构》课后习题答案(第2版)数据结构课后习题答案(第2版)第一章:基本概念1. 什么是数据结构?数据结构是指数据元素之间的关系,以及相应的操作。
它研究如何组织、存储和管理数据,以及如何进行高效的数据操作。
2. 数据结构的分类有哪些?数据结构可以分为线性结构和非线性结构。
线性结构包括数组、链表、栈和队列;非线性结构包括树和图。
3. 什么是算法?算法是解决特定问题的一系列有序步骤。
它描述了如何输入数据、处理数据,并产生期望的输出结果。
4. 算法的特性有哪些?算法具有确定性、有限性、输入、输出和可行性这五个特性。
5. 数据结构和算法之间的关系是什么?数据结构是算法的基础,算法操作的对象是数据结构。
第二章:线性表1. 顺序表的两种实现方式是什么?顺序表可以通过静态分配或动态分配的方式实现。
静态分配使用数组,动态分配使用指针和动态内存分配。
2. 单链表的特点是什么?单链表由节点组成,每个节点包含数据和一个指向下一个节点的指针。
它的插入和删除操作效率高,但是查找效率较低。
3. 循环链表和双向链表分别是什么?循环链表是一种特殊的单链表,在尾节点的指针指向头节点。
双向链表每个节点都有一个指向前一个节点和后一个节点的指针。
4. 链表和顺序表的区别是什么?链表的插入和删除操作效率更高,但是查找操作效率较低;顺序表的插入和删除操作效率较低,但是查找操作效率较高。
第三章:栈和队列1. 栈是什么?栈是一种特殊的线性表,只能在表的一端进行插入和删除操作。
后进先出(LIFO)是栈的特点。
2. 队列是什么?队列是一种特殊的线性表,只能在表的一端进行插入操作,在另一端进行删除操作。
先进先出(FIFO)是队列的特点。
3. 栈和队列的应用有哪些?栈和队列在计算机科学中有广泛的应用,例如浏览器的前进后退功能使用了栈,操作系统的进程调度使用了队列。
4. 栈和队列有哪些实现方式?栈和队列可以使用数组或链表来实现,还有更为复杂的如双端队列和优先队列。
数据结构第二章:线性表

实现:可用C 实现:可用C语言的一维数组实现
6
V数组下标 0 1
内存 a1 a2
元素序号 1 2
typedef int DATATYPE; #define M 1000 DATATYPE data[M]; 例 typedef struct card { int num; char name[20]; char author[10]; char publisher[30]; float price; }DATATYPE; DATATYPE library[M];
4
{加工型操作 加工型操作} 加工型操作
ClearList( &L ) 初始条件:线性表 L 已存在。 操作结果:将 L 重置为空表。 PutElem( &L, i, &e ) 初始条件:线性表L已存在,1≤i≤LengthList(L)。 操作结果:L 中第 i 个元素赋值同 e 的值 ListInsert( &L, i, e ) 初始条件:线性表 L 已存在,1≤i≤LengthList(L)+1。 操作结果:在 L 的第 i 个元素之前插入新的元素 e,L 的长度增1。 ListDelete( &L, i, &e ) 初始条件:线性表 L 已存在且非空,1≤i≤LengthList(L)。 操作结果:删除 L 的第 i 个元素,并用 e 返回其值,L 的长度减1。 }ADT LIST
3
PriorElem( PriorElem L, cur_e, &pre_e ) 初始条件:线性表 L 已存在。 操作结果:若 cur_e 是 L 中的数据元素,则用 pre_e 返回 它的前驱,否则操作失败,pre_e 无定义。 NextElem( NextElem L, cur_e, &next_e ) 初始条件:线性表 L 已存在。 操作结果:若 cur_e 是 L 中的数据元素,则用 next_e 返 回它的后继,否则操作失败,next_e 无定义。 GetElem( GetElem L, i, &e ) 初始条件:线性表 L 已存在,1≤i≤LengthList(L)。 操作结果:用 e 返回 L 中第 i 个元素的值。 LocateElem( LocateElem L, e, compare( ) ) 初始条件:线性表 L 已存在,compare( ) 是元素判定函数。 操作结果:返回 L 中第1个与 e 满足关系 compare( ) 的元 素的位序。若这样的元素不存在,则返回值为0。 ListTraverse(L, visit( )) ListTraverse 初始条件:线性表 L 已存在,visit( ) 为元素的访问函数。 操作结果:依次对 L 的每个元素调用函数 visit( )。 一旦 visit( ) 失败,则操作失败。
数据结构基础知识

复习提纲第一章数据构造概述根本概念与术语〔P3〕1.数据构造是一门研究非数值计算程序设计问题中计算机的操作对象以及他们之间的关系和操作的学科.2.数据是用来描述现实世界的数字,字符,图像,声音,以及能够输入到计算机中并能被计算机识别的符号的集合2.数据元素是数据的根本单位3.数据对象一样性质的数据元素的集合4.数据构造三方面容:数据的逻辑构造.数据的存储构造.数据的操作.〔1〕数据的逻辑构造指数据元素之间固有的逻辑关系.〔2〕数据的存储构造指数据元素及其关系在计算机的表示( 3 ) 数据的操作指在数据逻辑构造上定义的操作算法,如插入,删除等.5.时间复杂度分析--------------------------------------------------------------------------------------------------------------------1、名词解释:数据构造、二元组2、根据数据元素之间关系的不同,数据的逻辑构造可以分为集合、线性构造、树形构造和图状构造四种类型。
3、常见的数据存储构造一般有四种类型,它们分别是___顺序存储构造_____、___链式存储构造_____、___索引存储构造_____和___散列存储构造_____。
4、以下程序段的时间复杂度为___O(N2)_____。
int i,j,*;for(i=0;i<n:i++) n+1for(j=0;j<n;j++) n+1*+=i;------------------------------------------------------------------------------------------------------------------第二章线性表1.顺序表构造由n(n>=0)个具有一样性质的数据元素a1,a2,a3……,an组成的有穷序列//顺序表构造#define MA*SIZE 100typedef int DataType;Typedef struct{DataType items[MA*SIZE];Int length;}Sqlist,*LinkList;2.单链表(1)链表结点构造//链表的节点构造Typedef struct Node{int data;struct Node *ne*t;} Lnode,*Pnode,*LinkList;(2)结点遍历void TraverseList(LinkList t){LinkList p;while(t){p=t;t=t->ne*tfree(p);}}(3)链表操作算法:初始化、插入、输出、删除void InitList(LinkList *h){*h=(LinkList)malloc(sizeof(LNode));if(!h){print("初始化错误〞);return;}(*h)->ne*t=NULL;}void InsertList(LinkList h,int pos,datatype *){ LinkList p=h,q;int i=0;while(p&&i<pos-1){p=p->ne*t;i++;}if(!p||i>pos-1)print("插入位置出错!!〞);InitList(&q);q->ne*t=NULL;q->data=*;}void DeleteList(LinkList h,int pos){LinkList p=h,q;int i=0;while(p&&i<pos-1){p=p->ne*t;i++;}if(!p||i>pos-1){cout<<〞删除位置错误〞;return;}q=p->ne*t;p->ne*t=q->ne*t;free(q);}-----------------------------------------------------------------------------------------------------------------1、线性表中,第一个元素没有直接前驱,最后一个元素没有直接后驱。
数据结构课件第2章线性表

27
线性表的顺序存储结构适用于数据 元素不经常变动或只需在顺序存取设备 上做成批处理的场合。为了克服线性表 顺序存储结构的缺点,可采用线性表的 链式存储结构。
28
2.3 线性表的链式存储结构
线性表的链式存储表示 基本操作在单链表上的实现 循环链表 双向链表 线性表链式存储结构小结
2.3.1 线性表的链式存储表示 29
2.1.1 线性表的定义
6
一个线性表(linear_list)是 n(n≥0)个具有相同属性的数 据元素的有限序列,其中各元素有着依次相邻的逻辑关系。
线性表中数据元素的个数 n 称为线性表的长度。当 n = 0 时 该线性表称为空表。当 n > 0 时该线性表可以记为:
(a1,a2,a3,…,ai,…,an)
数据域 指针域
结点 data next
31
(2) 线性表的单链表存储结构
通过每个结点的指针域将线性表中 n 个结点按其逻辑顺序链 接在一起的结点序列称为链表,即为线性表 ( a1, a2, a3, …, ai, …, an ) 的链式存储结构。如果线性链表中的每个结点只有一个指针域, 则链表又称为线性链表或单链表 (linked list)。
17
(2) 算法编写
#define OK 1
#define ERROR 0
Int InsList ( SeqList *L, int i, ElemType e ) /*在顺序线性表 L 中第 i 个位置插入新的元素 e。*/ /* i 的合法值为 1≤i ≤L->last+2*/ {
int k; if ( i < 1) ||( i > L->last+2)) /*首先判断插入位置是否合法*/ { printf(“插入位置i值不合法”);
《数据结构》课程课件第二章线性表

Step2:数据域赋值
插入后: Step3:插入(连接)
X q
(1)式和(2)式的顺序颠倒,可以吗?
4、插入元素(在第i个元素之前插入元素e)
为什么时间复杂度不再是O(1)?
第i-1个元素
第i个元素
p
s
新插入元素
5、删除p所指元素的后继元素
P
删除前:
P->next P->next->next
删除:
五、线性表ADT的应用举例
Void mergelist(list La,list Lb,list &Lc)
{ //已知线性表La和Lb中的数据元素按值非递减排列
//归并La和Lb得到新的线性表Lc,Lc中的元素也按值非递减排列
例: 将两个各有n个元素的有序表归并成一个有序表, 其最小的比较次数是( )。 A、n B、2n-1 C、2n D、n-1
三、线性表的ADT
四、线性表的分类
五、线性表ADT的应用举例
例1:已知有线性表L,要求删除所有X的出现
五、线性表ADT的应用举例
例2: 已知有两个分别有序的线性表(从小到大),要 求合并两个线性表,且合并后仍然有序。——归并 方法1: 合并,再排序O((m+n)2)
方法2: 归并,利用分别有序的特点O((m+n))
二、线性表上常见的运算
8、删除 Delete(L,i):删除线性表的第i个元素 删除前 a1 a2 … ai-1 ai ai+1 … an 删除后 a1 a2 … ai-1 ai+1 … an 9、判断是否为空 Empty(L):线性表空,则返回TRUE, 否则FALSE 10、输出线性表 Print(L):输出线性表的各个元素 11、其它操作 复制、分解、合并、分类等
计算机算法基础第三版答案余祥宣

计算机算法基础第三版答案余祥宣《计算机算法基础第三版(余祥宣著)课后习题答案详解》。
要是你正在学习计算机算法,那余祥宣老师编写的《计算机算法基础第三版》肯定不陌生吧。
这本书可是算法学习路上的好帮手呢,不过课后习题有时候会让人有点头疼。
别担心,下面我就来给大家详细讲讲这本书的部分课后习题答案,还会说说为啥是这样解,让咱们一起把算法知识学个透!第一章:算法概述。
习题1:什么是算法?请举例说明。
答案:算法呢,简单说就是解决问题的步骤和方法。
就好比你要做一顿饭,得先买菜、洗菜、切菜,然后再炒菜,这一系列的步骤就是做饭的“算法”。
再比如说,计算两个整数相加,你先把两个数对齐,从个位开始相加,满十进一,这就是加法运算的算法。
原因:算法得有明确的步骤,就像做饭和做加法一样,每一步都清楚该做什么,这样才能得到正确的结果。
而且算法还得是有限的步骤,不能没完没了,不然问题永远解决不了。
习题2:算法有哪些特性?请分别举例解释。
答案:算法有五个特性,分别是有穷性、确定性、可行性、输入和输出。
- 有穷性:就是说算法在执行有限的步骤之后必须结束。
比如说计算1到100的整数和,通过一个循环,从1加到100,加完100就结束了,不会一直加下去。
- 确定性:算法的每一步都必须有明确的定义,不能模糊不清。
例如在一个判断奇数偶数的算法中,规定如果一个数除以2余数为0就是偶数,余数为1就是奇数,这个规则是明确的。
- 可行性:算法的每一步都能够通过有限次的基本运算来实现。
就像你要计算两个数的乘积,通过乘法运算就可以实现,这是可行的操作。
- 输入:算法可以有零个或多个输入。
比如计算圆的面积,需要输入圆的半径这个数据。
- 输出:算法至少有一个输出。
还是计算圆的面积这个例子,输出就是计算得到的圆的面积数值。
原因:这五个特性是算法的基本要求。
有穷性保证了算法不会无限循环下去;确定性让算法的执行结果是可预测的;可行性确保算法能够在实际中实现;输入和输出则明确了算法的处理对象和结果呈现。
数据结构第二章

操作结果:构造一个空线性表L。
Destroylist(&L)
初始条件:线性表L已存在。
操作结果:销毁线性表L。
ClearList(&L)
初始条件:线性表L已存在。 操作结果:将线性表L臵为空表。
四、抽象数据类型线性表的定义
Listempty(L) 初始条件:线性表L已存在。
操作结果:若L为空,则返回TRUE,否则返回FALSE。 ListLength(L) 初始条件:线性表L已存在。 操作结果:返回L中数据元素个数。 GetElem(L,i,&e) 初始条件:线性表L已存在。 操作结果:用e返回L中第i个数据元素的值。 LocateElem(L,e,compare()) 初始条件:线性表L已存在。 操作结果:返回L中第1个与e满足关系compare()的数 据元素的位序。若这样的元素不存在,则返回值为0。
四、抽象数据类型线性表的定义
上述类型定义中的操作均为“原子操作”,利用 这些“原子操作”可以完成其他更复杂操作。 例2-1 设两个线性表LA和LB分别表示两个集合A和B, 现要得到一个新的集合A=A∪B(并)。 此问题可演绎为对线性表作如下操作:
扩大线性表LA,将存在于线性表LB中而不存在于线
性表LA中的数据元素插入到LA中。
四、抽象数据类型线性表的定义
ListInsert(&L,i,e) 初始条件:线性表L已存在,1≼i ≼ ListLength(L)+1 。 操作结果:在L中第i个位臵之前插入新的数据元素e,L 的长度加1。 ListDelete(&L,i,&e) 初始条件:线性表L已存在, 1≼i ≼ ListLength(L) 。 操作结果:删除L的第i个数据元素,并用e返回其值,L 的长度减1。 }ADT List
第二章基本数据结构及其运算

用这种方法查找,每次比较都可抛弃子表一半的 元素,查找效率较高 从该例可看出,数据元素在表中的排列顺序对查 找效率有很大的影响
例2、学生情况登记表信息查询 成绩在90分及以上的学生情况登记表
学 号 970156 970157 970158 970159 970160 970161 970162 970163 970164 … 姓 名 性 别 年龄 20 张小明 男 19 李小青 女 19 赵 凯 男 21 李启明 男 18 刘 华 女 19 曾小波 女 18 张 军 男 20 王 伟 男 19 胡 涛 男 … … … 成绩 86 83 70 91 78 90 80 65 95 … 学 号 姓 名 性别 男 女 男 女 年龄 21 19 19 17 成绩 91 90 95 93 970159 李启明 970161 曾小波 970164 胡 970168 梅 涛 玲
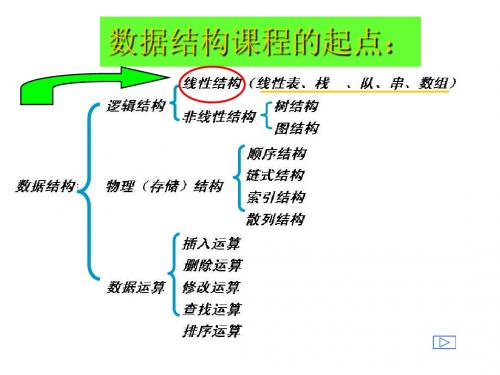
数据结构主要研究和讨论三方面问题:
1、数据元素之间的固有逻辑关系,称为数据的逻辑结构 2、数据元素及其关系在计算机中的存储方式,称为数据的 物理结构或存储结构
3、施加在数据结构上的操作,称为数据结构的运算。数据处 理的本质就是对数据结构施加各种运算,常见的运算有:查找、 排序、插入、删除等。
主要目的是提高数据处理的效率:
§2.1.3 数据结构的图形表示
D中的数据元素用中间标有元素值的方框表示, 称为数据结点(结点);R中的关系用一条有向线段 从前件结点指向后件结点。
例:设数据元素的集合为D = {di |1≤ i≤ 7的整数},画 出对应于下列关系所构成的数据结构的图形
①、R1={(d1,d3),(d1,d7),(d4,d5),(d3,d6),(d2,d4)} ②、R2={(di,dj)|i+j=5} ③、R3={(d2,d3)(d3,d1),(d1,d4),(d4,d6),d6,d5),(d5,d7)}
数据结构基础知识要点

第一章数据结构1.定义数据结构是计算机存储、组织数据的方式.数据结构是抽象数据类型的物理实现.2.数据结构包括如下几个方面:(1)数据元素之间的逻辑关系,即数据的逻辑结构。
(2) 数据元素及其关系在计算机存储器中的存储方式,即数据的存储结构,也称为数据的物理结构。
(3) 施加在该数据上的操作,即数据的运算。
2。
逻辑结构类型(1)集合结构。
交通工具的集合,动物的集合(2) 线性结构。
一对一,综合素质测评产生的学生排名(3)树形结构。
一对多,单位的组织结构图,族谱(4)图形结构.多对多,生产流程、施工计划、网络建设图等3.存储结构类型(1) 顺序存储方法。
数组(2) 链式存储方法。
链表(3) 索引存储方法(4) 散列存储方法4.算法通常把具体存储结构上的操作实现步骤或过程称为算法。
C语言里通常表现为解决问题的步骤程序= 算法(加工数据)+ 数据结构(数据的存储和组织)5.算法的五个特征(1) 有穷性:在有穷步之后结束。
(2)确定性:无二义性.(3)可行性:可通过基本运算有限次执行来实现。
(4)有输入:可有零个或多个.(5)有输出:至少有一个输出。
6.算法分析(1)时间复杂度:(算法的工作量大小)通常把算法中包含基本运算次数的多少称为算法的时间复杂度,也就是说,一个算法的时间复杂度是指该算法的基本运算次数.算法中基本运算次数T(n)是问题规模n的某个函数f(n),记作:T(n)=O(f(n))(2) 空间复杂度:实现算法所需的存储单元多少第二章线性表1.线性表的基本概念线性表是具有相同特性的数据元素的一个有限序列.该序列中所含元素的个数叫做线性表的长度,用n 表示,n≥0。
2。
线性结构的基本特征为:(1) 集合中必存在唯一的一个“第一元素"; (2) 集合中必存在唯一的一个“最后元素”;(3) 除最后一个元素之外,均有唯一的后继(后件); (4) 除第一个元素之外,均有唯一的前驱(前件)。
地理信息系统(第二章 空间数据基础)

有
公共边、结点自动生成 多重叠合、网络分析易
3、不规则三角网结构
不规则三角网(TIN):用一组非叠置的三角形来近
似表示地形的矢量数据三角网。
TIN的基本元素
节点(Node):相邻三角形的公共顶点(x,y,z)。 边(Edge):两个三角形的公共边界,是Tin不光滑性的具体 反映。
面(Face):由最近的三个节点所组成的三角形面,是TIN描
地理现象
地理事物在发生、发展和变化中的外部形式和表面特征。
地理空间数据:
用符号化表示地球表层的地理事物和地理现象的记录。
第一节
地球椭球体
地球体:极半径略短,赤道半径略长,北极略突出、南极略扁平,近似于梨
形的椭球体。
大地球体:由穿越陆地、岛屿的全球静止海平面连片形成,与重力方向处处
正交的,连续的封闭曲面称为大地水准面,由该水准面所包含的形体称为大地球体, 它是地球形体的一级逼近。
第四节
地图投影种类
1、几何投影法
正轴 横轴 斜轴
方位
圆柱
圆锥
方位投影
圆柱投影
圆锥投影
高斯-克吕格(Gauss Kruger)投影
属于横轴等角切椭圆柱投影。中央经线无长度变形。
6°或3°分带投影。中央经线与赤道为互相垂直的直线。
我国国家基本比例尺地形图中的大中比例尺地形图均采用该 投影。包括第13-23带共11个投影带。 内置了直角平面坐标系统:中央经线为X轴,赤道为Y轴,中 央经线与赤道交点为坐标原点。坐标纵轴西移500km。
国际主要椭球参数
椭球名称
德兰勃(Delambre) 埃弗瑞斯(Everest) 贝赛尔(Bessel) 克拉克(Clarke) 克拉克(Clarke) 海福特 (Hayford) 克拉索夫斯基 (Krasovski) 1967年大地坐标系 1975年大地坐标系
R语言—第二章 数据结构与基本运算

析
与
分
据
数
分 析
与
建
2
模
数 据
上面,我们用c()函数首先生成了向量z,c()函数的具体使用方 法详见2.2.1。is.na()返回的结果是前面5个元素都为FALSE, 最后一个是TRUE。这说明前面5个都不是缺失值,最后一个才 是缺失值。
分 析
• 有些统计资料是不完整的。当一个元素或值在统计的时候是 “不可得到”(Not Available)或“缺失值”(missing value)时, 相 关 位 置 可 能 会 被 保 留 并 且 赋 予 一 个 特 定 的NA(not available)值。任何NA的运算结果都是NA. • is.na()函数用来检测数据是否缺失,如果数据缺失,返回 值为TRUE;否则返回FALSE。例如: > z<-c(1:5,NA) #生成向量z > z #返回向量z的结果 [1] 1 2 3 4 5 NA > is.na(z) #识别z向量的值是否有缺失值 [1] FALSE FALSE FALSE FALSE FALSE TRUE
> sqrt(2)^2==2 [1] FALSE
在处理R里的数据时,尤其是在判断时,需要特别注意精度问题。
数 据
分 析
6
与
TRUE
据
建
模
[1] 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
析
与
2.2.1 向量
1 向量赋值
析
与
分
向量是由相同基本类型元素组成的序列,相当于一维数组。如: > x<- c(1,3,5,7,9) #用c()构建向量
数据结构第2章线性表A
在线性表的第i个位臵前插入一个元素的示意图如下:
1 2 3 4 插入25 5 12 1
12
13 21
13
21 24 28 30 42 77
2
3 4 5 6 7 8
24
25
6
7 8
28
30 42 77
9
16
3)删除
删除线性表的第i个位臵上的元素
实现步骤: 将第i+1 至第n 位的元素向前移动一个位臵; 表长减1。 注意:事先需要判断,删除位臵i 是否合法? 应当符合条件:1≤i≤n 或 i=[1, n] 核心语句: for ( j=i+1; j<=n; j++ )
18
2.2.3 顺序表的运算效率分析
时间效率分析:
算法时间主要耗费在移动元素的操作上,因此 计算时间复杂度的基本操作(最深层语句频度) T(n)= O (移动元素次数) 而移动元素的个数取决于插入或删除元素的位臵.
讨论1:若在长度为 n 的线性表的第 i 位前 插入一个元素, 则向后移动元素的次数f(n)为: f(n) = n – i + 1
例2 分析学生情况登记表是什么结构。
学号 姓名 性别 年龄 班级
0406010402
0406010405 0406010406 0406010410 0406010413 :
陈杰
邓博 管杰 黄腾达 李荣智 : : :
2004级计软04-1班
2004级计软04-1班 2004级计软04-1班 2004级计软04-1班 2004级计软04-1班 :
InitList( &L ); DestoryList( &L ); //建空表,初始化 //撤销表,释放内存
2.1节线性数据结构-基本概念-去掉声音效果了

空间复杂度
一个算法的实现在计算机中所占用的存储空间 大致包括三个方面: 1. 指令、常量、变量所占用的存储空间。 2. 输入数据所占用的存储空间。
3. 算法执行时需要的辅助空间。
时间复杂度和空间复杂度的关系
相互矛盾
复习:链表
9.1.1 自己建立结构体类型
学生学籍信息
num 10001 10002 10003 name Zhang xin Wang li Li fang sex M F M age 19 18 18 addr Shanghai Xi’an Beijing
时间复杂度的计算:
程序 例 1: 例 2: {++x;s=0;} for(i=1;i<=n;++i) {++x;s+=x;} 例3: for(j=1;j<=n;++j) 2 for(k=1;k<=n;++k) n+3n {++x;s+=x;} 频度 2 n+2n 时间复杂度 O(1) O(n)
O(n2)
顺序存储结构:用数据元素在存储器中的相对位
置来表示数据元素之间的逻辑关系。
链式存储结构:在每一个数据元素中增加一个
存放地址的指针,用此指针来表示数据元素之间
的逻辑关系。
例
a1 a2 a3 a30
姓 名
刘晓光
马广生 王 民
性别
男
男 男
民 族
汉
回 壮
年龄
16
17 21
其 他
…
张玉华
…
女
…
汉
…
记录
struct Student { int num; char name[20]; char sex; int age; char addr[30]; };
数据结构 第二章__线性表(本)

数据结构与算法华东师范大学计算机系杨沛第二章线性表2.1 线性表的基本概念线性表是具有相同数据类型的数据元素的有限序列。
由n(n≥0)个数据元素k0,k1,…,kn-1组成的线性表记为(k0 ,k1 ,…,kn-1),线性表中包含的数据元素的个数n称为线性表的长度(length),称长度为零的线性表为空的线性表(简称为空表)。
相关概念:表头、表尾、前驱、后继有序线性表:数据元素的相对位置与它们的值有联系。
无序线性表:数据元素的相对位置与它们的值没有联系。
第二章线性表例小于20的质数组成的线性表(2,3,5,7,11,13, 17,19);英文字母表也是线性表,表中每个字母是一个数据元素:(A,B,C,……,Z);2.2 顺序表2.2.1 线性表顺序表(sequential list)就是顺序存贮的线性表,即用一组连续的存贮单元依次、连续地存贮线性表中的结点。
如果每个结点占用s个存贮单元,并假设存放结点ki(0≤i≤n-1)的开始地址为loc(k0),则结点ki的地址loc(ki)可表示成Loc(ki) =loc(k0) + i*s。
2.2 顺序表在C 语言中,可用数组表示线性表:#define MAXN 100int list[MAXN];int n;线性表的结点k 0,k 1,…,k n-1依次存放在数组单元list[0],list[1],…,list[n-1]。
2.2.1 线性表最大表长实际表长线性表2.2 顺序表2.2.1 线性表假设s=sizeof(int),则可得到计算ki的地址的公式,因loc(ki)=&list[i],而&list[i]=&list[0]+i·s,故loc(ki)=&list[0]+i·s。
2.2 顺序表2.2.2 顺序表的操作(1)初始化:初始长度置为0即可(n=0;),数组空间在编译时分配。
(2)顺序表的插入:插入算法的C函数SqListInsert():若插入位置i不在可以插入的位置上,即i<0或i>n,则返回0;若n=MAXN,即线性表已满,此时数组list[]没有多余的存贮单元可以存放新结点,则返回-1;若插入成功,则返回12.2 顺序表实际表长(2)顺序表的插入:int SqListInsert(int list[],int*p_n,int i,int x) {int j;if(i<0||i>*p_n)return(0);//i不是合法的插入位置if(*p_len==MAXN)return(-1);//线性表已满2.2 顺序表for(j=*p_n;j>i;j--)list[j]=list[j-1];//结点右移list[i]=x;(*p_n)++;//表长加1return(1);}2.2 顺序表(2)顺序表的插入:对于存放在数组list[]中的、具有n个结点的顺序表,为了把值为x的结点插在表的位置i(0≤i≤n)上,可调用如下的语句:k=SqListInsert(list, &n, i, x);注:结点移动是本算法的关键操作2.2 顺序表(3)顺序表的删除:删除算法的C函数SqListDelete():在具有n个结点的顺序表中,删除第i(0≤i≤n-1)个位置上的结点,使线性表长度减1,若删除位置不合法,即i<0或i≥n,则返回0;若删除位置合法,即0≤i≤n-1,则删除成功,返回1。
数据结构第2章基础习题-作业

第二章习题一判断题1.线性表的逻辑顺序与存储顺序总是一致的。
×2.顺序存储的线性表可以按序号随机存取。
3.顺序表的插入和删除操作不需要付出很大的时间代价,因为每次操作平均只有近一半的元素需要移动。
×4.线性表中的元素可以是各种各样的,但同一线性表中的数据元素具有相同的特性,因此是属于同一数据对象。
5.在线性表的顺序存储结构中,逻辑上相邻的两个元素在物理位置上并不一定紧邻。
×6.在线性表的链式存储结构中,逻辑上相邻的元素在物理位置上不一定相邻。
7.线性表的链式存储结构优于顺序存储结构。
8.在线性表的顺序存储结构中,插入和删除时,移动元素的个数与该元素的位置有关。
×9.线性表的链式存储结构是用一组任意的存储单元来存储线性表中数据元素的。
10.在单链表中,要取得某个元素,只要知道该元素的指针即可,因此,单链表是随机存取的存储结构。
×11.线性表中每个元素都有一个直接前驱和一个直接后继。
(×)12.线性表中所有元素的排列顺序必须由小到大或由小到小。
(×)13.静态链表的存储空间在可以改变大小。
(×)14.静态链表既有顺序存储结构的优点,又有动态链表的优点。
所以它存取表中第i个元素的时间与i无关。
(×)15.静态链表中能容纳元素个数的最大数在定义时就确定了,以后不能增加。
()16.静态链表与动态链表的插入、删除操作类似,不需要做元素的移动。
()17.线性表的顺序存储结构优于链式结构。
(×)18.在循环单链表中,从表中任一结点出发都可以通过前后的移动操作扫描整个循环链表。
(×)19.在单链表中,可以从头结点开始查找任何一个结点。
()20.在双链表中,可以从任何一结点开始沿同一方向查找到任何其他结点。
(×)二单选题 (请从下列A,B,C,D选项中选择一项)1.线性表是( ) 。
(A) 一个有限序列,可以为空; (B) 一个有限序列,不能为空;(C) 一个无限序列,可以为空; (D) 一个无序序列,不能为空。
数据结构重点知识点

数据结构重点知识点第一章概论1. 数据是信息的载体。
2. 数据元素是数据的基本单位。
3. 一个数据元素可以由若干个数据项组成。
4. 数据结构指的是数据之间的相互关系,即数据的组织形式。
5. 数据结构一般包括以下三方面内容:数据的逻辑结构、数据的存储结构、数据的运算①数据元素之间的逻辑关系,也称数据的逻辑结构,数据的逻辑结构是从逻辑关系上描述数据,与数据的存储无关,是独立于计算机的。
②数据元素及其关系在计算机存储器内的表示,称为数据的存储结构。
数据的存储结构是逻辑结构用计算机语言的实现,它依赖于计算机语言。
③数据的运算,即对数据施加的操作。
最常用的检索、插入、删除、更新、排序等。
6. 数据的逻辑结构分类: 线性结构和非线性结构①线性结构:若结构是非空集,则有且仅有一个开始结点和一个终端结点,并且所有结点都最多只有一个直接前趋和一个直接后继。
线性表是一个典型的线性结构。
栈、队列、串等都是线性结构。
②非线性结构:一个结点可能有多个直接前趋和直接后继。
数组、广义表、树和图等数据结构都是非线性结构。
7.数据的四种基本存储方法: 顺序存储方法、链接存储方法、索引存储方法、散列存储方法(1)顺序存储方法:该方法把逻辑上相邻的结点存储在物理位置上相邻的存储单元里,结点间的逻辑关系由存储单元的邻接关系来体现。
通常借助程序语言的数组描述。
(2)链接存储方法:该方法不要求逻辑上相邻的结点在物理位置上亦相邻,结点间的逻辑关系由附加的指针字段表示。
通常借助于程序语言的指针类型描述。
(3)索引存储方法:该方法通常在储存结点信息的同时,还建立附加的索引表。
索引表由若干索引项组成。
若每个结点在索引表中都有一个索引项,则该索引表称之为稠密索引,稠密索引中索引项的地址指示结点所在的存储位置。
若一组结点在索引表中只对应一个索引项,则该索引表称为稀疏索引稀疏索引中索引项的地址指示一组结点的起始存储位置。
索引项的一般形式是:(关键字、地址)关键字是能唯一标识一个结点的那些数据项。
数据结构(第二章 线性表)

2.2 线性表的顺序存储和实现
顺序表-顺序表定义
由上可知,数据的存储逻辑位置由数组的下标决定。 所以相邻的元素之间地址的计算公式为(假设每个数 据元素占有d个存储单元): LOC(ai)=LOC(ai-1)+d 对线性表的所有数据元素,假设已知第一个数据元 素a0的地址为LOC(a0) ,每个结点占有d个存储 单元, 则第i个数据元素ai的地址为: LOC(ai)=LOC(a0)+i*d 线性表的第一个数据元素的位置通常称做起始位置 或基地址。 在使用一维数组时,数组的下标起始位置根据给定 的问题确定,或者根据实际的高级语言的规定确定。
2.1 线性表抽象数据类型
线性表的分类
顺序存储结构 (元素连续存储、 随机存取结构) 线性表 ADT 链式存储结构 (元素分散存储) 继承 顺序表类 排序顺序表类 继承 单链表类 循环单链表 双链表 继承 排序循环双链表类 排序单链表类
单链表
双链表
循环双链表类
线性表的存储结构
2.2 线性表的顺序存储和实现
线性表的基本操作 求长度:求线性表的数据元素个数。 访问:对线性表中指定位置的数据元素进行存取、替 换等操作。 插入:在线性表指定位置上,插入一个新的数据元素, 插入后仍为一个线性表。 删除:删除线性表指定位置的数据元素,同时保证更 改后的线性表仍然具有线性表的连续性。 复制:重新复制一个线性表。 合并:将两个或两个以上的线性表合并起来,形成一 个新的线性表。 查找:在线性表中查找满足某种条件的数据元素。 排序:对线性表中的数据元素按关键字值,以递增或 递减的次序进行排列。 遍历:按次序访问线性表中的所有数据元素,并且每 个数据元素恰好访问一次。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章数据结构基础2.1 基本概念程序 = 算法 + 数据结构也就是说,计算机按照程序所描述的算法对某种结构的数据进行加工处理。
1.数据结构数据:在计算机领域,指能够被计算机输入、存储、处理和输出的一切信息。
数据项:是数据的最小单位,有时也称为域(field)。
数据记录:是数据处理领域组织数据的基本单位,它由数据项组成。
数据元素:是数据集合中相对独立的单位,也称结点。
它和数据是相对而言的(如一条记录相对于所在文件被认为是数据元素,而它相对于所含的数据项又被认为是数据)。
数据结构:是描述一组数据元素及元素间的相互关系的。
逻辑结构:是指数据元素之间抽象化的相互关系。
存储结构:或称物理结构,是数据的逻辑结构在计算机存储器中的存储形式。
线性结构:每个结点有且只有一个前驱结点和一个后继结点(第一和最后一个结点除外)逻辑结构树型结构:每个结点有且只有一个前驱结点(树根结点除非线性结构外),但可以有任意多个后继结点。
每个结点可以有任意多个前驱结点和任意多个后继结点数据结构顺序存储结构:将数据结构的数据元素按某中顺序存放在计算机存储器的连续存储单元中。
其结构简单,可节省存放指针的空间,但需要连续的存储空间,当数据元素的数目不确定时,会造成存储空间的闲置。
链接存储结构:为数据结构的每个结点元素附加一个数据项,其中存放一个与其相邻接的元素的地址(指针),通过指针找到下一个相关元素的实际存储地址。
每个结点由数据域和指针域组成。
存储结构其存储空间不必连续,在进行插入、删除操作时不必移动结点,但结点指针要占用额外的存储空间。
索引存储结构:将全部记录分别存放在存储器的不同位置,系统为整个记录建立一张索引表,表中登记了每条记录的长度、逻辑记录号和在存储器中位置。
通过索引表来访问记录。
散列存储结构:在记录的存储位置和它的关键字之间建立一个确定的对应关系,使每个关键字和结构中一个唯一的存储位置相对应。
由关键字作某种运算后直接确定元素的地址。
在数据的逻辑结构中,树型结构(1:N)是图型结构(M:N)的特例(M=1),线性结构(1:1)是树型结构(1:N)的特例(N=1)。
一种数据结构可以表示成一种或多种物理结构。
在数据处理过程中,一个恰当的数据结构起着非常重要的作用。
2.算法算法:即解决特定问题的方法。
数值算法:是解决数值问题的算法,主要进行算术运算,如:求解代数方程、求算法种类解数值积分等。
早期的计算机主要用于数值计算。
非数值算法:是解决非数值问题的算法,主要进行比较和逻辑运算,如:排序、查找、插入、删除等。
随着计算机技术的发展,非数值计算的应用越来越广。
有穷性:在执行有限步之后必须终止确定性:所给出的每一计算步骤必须是精确定义的算法准则可行性:要执行的每一计算步骤都可在有限时间内完成输入:一般应具有0个或多个输入信息,它是算法所需的初始数据输出:一般应具有0个或多个输出信息,它是算法对输入信息的运算结果正确性:指在合理的数据输入下,能在有限的运行时间内得到正确的结果。
算法评价运行时间(时间复杂性):指一个算法在计算机上运算所花费的时间占用的存储空间(空间复杂性):指一个算法在计算机存储器中所占用的存储空间简单性:指容易验证其正确性,且便于编写、修改、阅读和调试3.P ascal语言简介整型 integer 一个整型数据占用2个字节的存储单元实型 real 一个实型数据占用4个字节的存储单元简单类型字符型 char 一个字符型数据占用1个字节的存储单元布尔型 boolean 一个布尔型数据(false或true)占用1个字节的存储单元数组:数组中的元素在位置上是顺序排列的,存储结构是顺序存储结构,逻辑结构为线性结构。
(1)数据类型记录:记录中的成分在位置上是顺序排列的,存储结构是顺序存储结构,逻辑结构为线性结构。
结构类型集合:集合与元素的位置无关,存储结构是顺序存储结构,逻辑结构是关系为空(即不存在次序关系)的结构文件:文件中的成分在位置上是顺序排列的,但逻辑结构和存储结构可以有多种不同结构。
指针类型是以存储单元的地址作为其值的一种数据类型,它也是一种整体变量,系统为指针变量分配一个固定的存储单元,一般为2个字节。
指针类型的定义为: ↑类型标识符数组、记录、集合之间的区别(2)语句赋值语句:变量名:=表达式;转向语句: goto 语句标号;调用过程语句:过程名(参数表);退出循环语句: exit;返回语句:return;出错处理语句:error(字符串);复合语句: begin语句1;语句2;…;语句n end;条件语句:if条件then语句1 [else语句2];情况语句:case变量名of常量1:语句1;常量2:语句2;……end;for循环语句:for变量名:=初值to [downto]终值do语句;while循环语句:while条件do语句;repeat循环语句: repeat一组语句until条件;2.2 线性表1. 线性表的逻辑结构线性表:是具有相同特征的数据元素的一个有限序列,除第一个和最后一个元素外,每个元素都只有一个之间前驱和一个直接后驱。
表示为:(a 1,a 2,… a i … a n )逻辑结构:是线性结构。
2. 线性表的存储结构线性表的存储结构有两种: 顺序存储结构 和 链接存储结构 。
顺序表:具有顺序存储结构的线性表 线性链表:具有链接存储结构的线性表单链表:每个结点有一个指针域,有一个头指针h 而无尾指针,表中最后一个结点的指针域是空的。
其结构简单,但查找效率不高(查某结点总要从头开始)线性链表 循环链表:每个结点有一个指针域,有一个头指针h 和一个尾指针r ,表中最后一个结点的指针域不是空的,尾指针指向表的第一个结点。
它形成环行结构,可显著提高查找效率(从任何结点出发都能查到所需结点)。
双向链表:每个结点有两个指针域,一个指向直接前驱,一个指向直接后驱。
它形成双环行结构,可进一步提高查找效率(从某结点出发,既可以向前查又可以向后查)。
单链表循环链表双向链表3. 线性表的运算(1)基本运算插入:在表中任一位置插入一个结点 删除:删除表中任一结点 修改:修改表中给定结点的值 读值:读取表中给定结点的数据求长:计算表中结点的个数清表:清除表中结点,使其成为空表检索:找出表中给定特征的结点排序:按给定要求对表中元素重新排序(2)常用算法举例·顺序表的插入例题: ** 向线性表中第i个元素位置插入一个新元素 **算法步骤:1)检查i值是否超出所允许的范围(1≤i≤n+1),若超出,则进行“超出范围”错误处理;2)将线性表的第i个元素和它后面的所有元素均向后移动一个位置;3)将新元素写入到空出的第I个位置上;4)使线性表的长度增1。
PROCEDURE insertlist(v,n,i,x)BEGINIF (i<1) OR (i>n+1) THEN[FOR j:=n DOWNTO i DOv[j+1]:=v[j];v[i]:=x;n:=n+1 ] 1# 2# 3# 4# 5# 6# 7#8#·顺序表的删除例题: ** 删除线性表中第i个元素 **算法步骤:1)检查i值是否超出所允许的范围(1≤i≤n),若超出,则进行“超出范围”错误处理;2)将线性表的第i个元素后面的所有元素均向前移动一个位置;3)使线性表的长度减1。
1# 2# 3# 4# 5# 6# 7#PROCEDURE deletelist(v,n,i)BEGINIF (i<1) OR (i>n+1) THEN[FOR j:=i TO n-1v[j]:=v[j+1];n:=n-1END;·单链表的插入例题: ** 向单链表中第i 个结点(i ≥0)之后插入一个元素为b 的结点 ** 算法步骤:1)为待插入元素b 分配一个结点(假定是由s 指针变量所指向的结点,即s ↑结点) ,并把b 赋给s ↑结点的值域;2) 如果i=0,则将s ↑结点插入表头后返回; 3) 从单链表中查找第i 个结点;4)若查找成功,则在第i 个结点后插入s ↑结点,。
否则表明值超出单链表的长度,应进行错误处理。
插入前head插入后 head1 2 3 4 5 6 7 1 2 3 4 5 6 7 8插入前插入后PROCEDURE insert(head,i,b) BEGIN; S ↑.data:=b ;i=0 THEN [s ↑.next:= head ; head:=s ; RETURN ]; ; j:=1 ; {用指针P 指向单链表中第j 个结点}While (p< > nil) and (j<i) do j:=j+1; p:=p ↑.next ;p< >nil THEN { 若条件成立,则表明查找成功 }s ↑.next:=p ↑.next ; {使s ↑结点的指针域指向p ↑结点的后继 } p ↑.next:=s ; {使p ↑结点的指针域指向s ↑结点} ELSE error ('error') END;· 单链表的删除例题: ** 在单链表中删除结点d ** 算法步骤:1) 如果单链表为空,则进行出错处理;data next2) 如果表头结点是被删除结点,则删除该结点后返回;3) 从单链表中查找其值等于d 的结点,直到查找结束(成功或失败)为止; 4)若查找成功,则删除被查找到的结点后,否则进行错误处理。
删除前head删除后 head1 2 3 4 5 6 7 1 2 3 4 5 6 7删除前删除后PROCEDURE delete(head,d) BEGINIF head=nil THEN error ('this is a empty list'); head ↑.data =d THENp:=head ; {把表头指针赋给P ,以便删除表头结点后收回该结点} head:=head ↑.next ; {删除表头结点}dispose(p); {系统回收由p 所指向的结点,即原表头结点} RETURN ; {返回}; p:=q ↑.next ;{ P 指向待比较的结点,q 指向p 的前驱结点}While p< > nil doIF p ↑.data=d THEN exit ELSE [q:=p; p:=p ↑.next];p< >nil THENq ↑.next:=p ↑.next ; {删除p ↑结点,即值为d 的结点} dispose(p); {回收p 结点} ELSE error('error') END;结论:在表很长时,采用顺序方式时插入和删除元素的效率很低,只有在很少进行插入和删除运算的情况下,采用顺序表才是合适的。
