第十四章 轴解析
山东菏泽市人教版初中物理九年级第十四章综合知识点总结(含解析)

一、选择题1.如图所示为内燃机四冲程工作示意图,下列说法正确的是()A.一个工作循环的正确顺序是∶甲乙丙丁B.甲图冲程能获得动力C.丙图冲程存在化学能转化为内能的过程D.丁图冲程存在内能转化为机械能的过程D解析:D甲图中两个气阀都关闭,活塞向上运动,所以为压缩冲程,是机械能转化为内能;乙图中进气门打开,活塞向下运行,气缸容积增大,是吸气冲程;丙图中排气门打开,活塞向上运动,气缸容积减小,是排气冲程;丁图中两个气阀都关闭,火花塞点火,活塞向下运动,是做功冲程,此冲程将内能转化为机械能;A.四个冲程的正确顺序是乙甲丁丙,故A错误;B.甲图为压缩冲程,内燃机在做功冲程(丁图)获得动力,故B错误;C.丙图为排气冲程,不存在化学能转化为内能的过程,故C错误;D.丁图为做功冲程,在该冲程中将内能转化为机械能,故D正确。
故选D。
2.2020年11月24日,搭载着“嫦娥五号”探测器的长征五号火箭发射成功,标志着中国“探月工程”第三步拉开序幕,长征五号运载火箭采用无毒,无污染的液氢液氧燃料作推进剂,属于绿色环保大型液体运载火箭,下列说法正确的是()A.液氢燃烧得越充分,其热值就越大B.燃料燃烧产生高温高压的燃气对火箭做功,燃气的内能会增加C.高温高压的燃气推动火箭升空把内能转化成机械能D.通常情况下气态的氢氧是采用高温高压方式进行加注的C解析:CA.热值是燃料的一种特性,它只与燃料的种类有关,与有无充分燃烧无关,故A错误;B.燃气对火箭做功,内能转化为机械能,燃气的内能会减小,故B错误;C.燃气对火箭做功,内能转化为机械能,故C正确;D.令气体液化的方法有两种,一是降低温度,二是压缩体积。
通常情况下气态的氢氧是采用低温、高压进行加注的。
故选C。
3.如图所示,是小普同学跟爷爷学习气功的四个基本动作,由此他联想到热机的四个冲程,以下与排气冲程最相似的是()A.鼻孔吸气B.气沉丹田C.排山倒海D.打完收工D解析:D小普同学跟爷爷学习气功的四个基本动作,鼻孔吸气相当于吸气冲程,气沉丹田相当于压缩冲程,排山倒海时对外做功,相当于做功冲程,打完收工相当于排气冲程。
九年级物理第十四章课后习题答案(详析详解)

九年级物理第十四章课后习题答案(详析详解)【写在前面】“动手动脑学物理”栏目中每一道习题的设计都有很强的目标指向性。
每做一道题我们都要清楚:课本中为什么要设计这样一道题目?某一道题不会做,肯定是因为与这道题相关的某个知识点你没有掌握好,该达到的目标要求你还没有达到。
这就提醒我们需要重新翻书,进一步理解相关的知识内容。
从这一点上说,做好课本上的题目是基础、是达标的关键,大家一定要给予足够的重视。
课本上的习题还没有做好,就盲目地做大量的课外习题,只能是越做越发蒙,降低学习效率。
本资料由辽宁省物理优秀课教师安绍文根据多年的教学实践经验及学生学情实际状况编制而成。
供需要者在教学或学习中参考。
(14-1热机)说明:题目是在有意引导同学们注意观察身边的物理。
通过大脑的搜索和对平时观察的回忆你会发现:原来觉得很神秘的热机,实际上,在生活、生产中的应用随处可见。
分析:关键是要清楚,利用内能做功的机械都是热机。
怎样知道它是否利用内能了?那就要看它是否燃烧燃料了。
热机工作时利用的内能,就是燃料燃烧后所形成的高温高压气体的内能。
提示:按照上面的分析思路,在生活和生产中寻找“能动的”并“燃烧燃料的”机器。
答案:例如生活中:常用的交通工具除了飞机、汽车、摩托车之外,还有火车、轮船也是利用热机提供动力的。
这都属于内燃机。
(注:电动自行车上利用的是电动机,不是热机。
)例如生产中:工地上常看到吊车、推土机、挖掘机、拖拉机里面用的都是热机。
(也都是内燃机。
)再如坦克、火箭里面的发动机都是热机。
(火箭发动机不是内燃机,但属于热机。
)提示:四冲程内燃机的一个工作循环中,曲轴转动两周,活塞往复运动两次。
分析:(1)已知图甲为吸气冲程(此时活塞在曲轴的带动下向下运动),吸气冲程进气门应该打开、排气门应该关闭,由此可断定各图中左侧为进气门,右侧为排气门。
(2)压缩冲程应该是曲轴带动活塞向上运动,只有两个气门就都应该关闭才能使缸内气体被(见下图乙)。
机械设计基础课件第十四章 轴

• • • • • • 轴的功用和类型 轴的材料 轴的结构设计 轴的强度计算 轴的刚度计算 轴的临界转速的概念
轴
第一节 轴的功用和类型
一、轴的功用
● 支撑回转零件,如齿轮、带轮; 传递运动和转矩 ●
二、轴的类型
● 心轴 — 只承受弯矩 按受载 ● 传动轴 — 只承受转矩 ● 转轴 — 既受弯矩、又受转矩 ● 直 轴(光轴、阶梯轴) ●曲 轴
第三节 轴的结构设计
倒角
砂轮越程槽
第三节 轴的结构设计
轴环
第三节 轴的结构设计
• 三、轴上零件的轴向定位和固定 • 定位 - 使轴上零件处于正确的工作位置;
• 固定 - 使轴上零件牢固地保持这一位置。 阶梯轴上截 • 目的 - 防止轴上零件工作时发生轴向蹿动。 面变化处 • 常用的轴向定位和固定方法:
第三节 轴的结构设计
为保证轴上零件紧靠在定位面(轴肩),轴 肩的圆角须大于C1或R。
第三节 轴的结构设计
• 四、改善轴的受力状况,减小应力集中 • 合理布置轴上零件可以改善轴的受力状况。
第三节 轴的结构设计
• 减小应力集中 • 零件截面发生突 然变化的地方, 都会产生应力集 中。合金钢对应 力集中比较敏感, 尤需加以注意。
第四节 轴的强度计算
第四节 轴的强度计算
第四节 轴的强度计算
第四节 轴的强度计算
第四节 轴的强度计算
• 若计算的截面有一个键槽,则将计算出的轴的直 径 d加大4%左右,若两个键槽,则增大8%,然 后圆整成标准直径。 • 对于一般用途的轴,按上述方法设计计算即可。 对于重要的轴,还需进一步的强度校核(如安全 系数法) • 安全系数的校核计算包括疲劳强度和静力强度两 项内容。 • 疲劳强度的校核即计入应力集中、表面状态和绝 对尺寸影响以后的精确校核。 • 静强度校核的目的在于校核轴对塑性变形的抵抗 能力。
数学(文)一轮教学案:第十四章 数系的扩充与复数的引入 Word版含解析

第十四章 数系的扩充与复数的引入考纲展示 命题探究1 复数的定义形如a +b i(a ,b ∈R )的数叫复数,其中实部是a ,虚部是b . 2 复数的分类 3 复数相等的充要条件a +b i =c +d i ⇔a =c 且b =d (a ,b ,c ,d ∈R ). 4 复平面建立直角坐标系来表示复数的平面,叫做复平面.x 轴叫做实轴,y 轴叫做虚轴.实轴上的点表示实数;除原点外,虚轴上的点表示纯虚数.5 复数的几何意义6 复数的模向量OZ →的模r 叫做复数z =a +b i 的模,记作|z |或|a +b i|,则|z |=|a +b i|=r =a 2+b 2(r ≥0,r ∈R ),即复数a +b i 的模表示点Z (a ,b )与原点O 的距离.特别地,b =0时,z =a +b i 是实数a ,则|z |=|a |. 注意点 复数概念的理解的注意事项 (1)两个不全是实数的复数不能比较大小. (2)复平面内虚轴上的单位长度是1,而不是i.(3)复数与向量的关系:复数是数的集合,而向量是有大小和方向的量,二者是不同的概念.为了令复数更好地发挥解决实际问题的作用,所以用向量来表示复数.1.思维辨析(1)复数z =a +b i(a ,b ,∈R )中,虚部为b i.( )(2)在实数范围内的两个数能比较大小,因而在复数范围内的两个数也能比较大小.( )(3)一个复数的实部为0,则此复数必为纯虚数.( ) (4)复数的模就是复数在复平面内对应向量的模.( )答案 (1)× (2)× (3)× (4)√2.实部为-2,虚部为1的复数所对应的点位于复平面的( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限答案 B解析 实部为-2,虚部为1的复数在复平面内对应的点的坐标为(-2,1),位于第二象限.3.在复平面内,已知6+5i 对应的向量为OA →,AB →=(4,5)则OB →对应的复数为________.答案 10+10i解析 由AB →=OB →-OA →得:OB →=OA →+AB →又∵AB →=(4,5) ∴AB →对应的复数为4+5i. ∴OB →对应的复数为:4+5i +6+5i =10+10i.[考法综述] 复数的分类、实部、虚部、复数相等的条件、共轭复数、复数的模都会结合复数的运算一起考查.难度一般不大.命题法1 复数的概念与分类典例1 设i 是虚数单位,复数1+a i2-i 为纯虚数,则实数a 为( )A .2B .-2C .-12D .12 [解析] 解法一:设1+a i2-i =b i(b ∈R 且b ≠0),则1+a i =b i(2-i)=b +2b i ,所以b =1,a =2b =2.解法二:1+a i 2-i =(1+a i )(2+i )(2-i )(2+i )=2-a 5+1+2a 5i ,令2-a 5=0且1+2a5≠0,得a =2.[答案] A【解题法】 与复数概念及分类题型的解题步骤第一步,先把题目中的复数z 的代数形式设出,即设复数z =a +b i(a ,b ∈R ).第二步,把非标准代数形式的复数通过复数的运算法则化为代数形式的标准形式,即化为a +b i(a ,b ∈R )的形式.第三步,紧扣复数的分类: 复数z =a +b i(a ,b ∈R )根据分类列出相应的方程,如:若题目要求该复数是实数,则根据虚部b =0列出相关方程(组).第四步,解方程(组),求得结果. 命题法2 复数相等典例2 若复数z 满足z (2-i)=11+7i(i 为虚数单位),则z 为( )A .3+5iB .3-5iC .-3+5iD .-3-5i[解析] 解法一:令z =a +b i(a ,b ∈R ),则(a +b i)(2-i)=(2a +b )+(2b -a )i =11+7i ,⎩⎪⎨⎪⎧2a +b =11,2b -a =7,解得a =3,b =5,故选A.解法二:z =11+7i 2-i =(11+7i )(2+i )5 =22-7+(14+11)i 5=3+5i. [答案] A【解题法】 复数相等问题的解题策略两复数相等的充要条件,即a +b i =c +d i ⇔⎩⎪⎨⎪⎧a =c ,b =d ,(a ,b ,c ,d ∈R ).解决此类问题的本质就是分离出实部与虚部,使之分别相等,得到方程组,从而解决问题.命题法3 复数的模及几何意义典例3 (1)若复数z 满足i z =2+4i ,则在复平面内,z 对应的点的坐标是( )A .(2,4)B .(2,-4)C .(4,-2)D .(4,2)(2)a 为正实数,i 为虚数单位,⎪⎪⎪⎪⎪⎪a +i i =2,则a =( ) A .2 B . 3 C. 2D .1[解析] (1)由i z =2+4i ,得z =2+4ii =4-2i ,所以z 对应的点的坐标是(4,-2).(2)∵⎪⎪⎪⎪⎪⎪a +i i =|a +i||i|=a 2+1=2,∴a =±3,又a >0,∴a = 3.故选B.[答案] (1)C (2)B【解题法】 与复数几何意义、模有关的解题技巧(1)只要把复数z =a +b i(a ,b ∈R )与向量OZ →对应起来,就可以根据平面向量的知识理解复数的模、加法、减法的几何意义,并根据这些几何意义解决问题.(2)有关模的运算要注意灵活运用模的运算性质. 1.若复数z =i(3-2i)(i 是虚数单位),则z =( ) A .2-3i B .2+3i C .3+2i D .3-2i答案 A解析 因为z =i(3-2i)=2+3i ,所以z =2-3i.2.设i 是虚数单位,则复数2i1-i 在复平面内所对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限 答案 B解析2i1-i=2i(1+i)(1-i)(1+i)=-1+i,其在复平面内所对应的点位于第二象限.3.设复数z1,z2在复平面内的对应点关于虚轴对称,z1=2+i,则z1z2=()A.-5 B.5C.-4+i D.-4-i答案 A解析由题意知:z2=-2+i.又z1=2+i,所以z1z2=(2+i)(-2+i)=i2-4=-5.故选A.4.设z=10i3+i,则z的共轭复数为() A.-1+3i B.-1-3i C.1+3i D.1-3i 答案 D解析z=10i3+i=10i(3-i)(3+i)(3-i)=30i+1032+12=1+3i,z=1-3i,选D.5.已知a,b∈R,i是虚数单位,若a-i与2+b i互为共轭复数,则(a+b i)2=()A.5-4i B.5+4iC.3-4i D.3+4i答案 D解析由a-i与2+b i互为共轭复数,可得a=2,b=1.所以(a+b i)2=(2+i)2=4+4i-1=3+4i.6. i是虚数单位,若复数(1-2i)(a+i)是纯虚数,则实数a的值为________.答案-2解析由题意知,复数(1-2i)(a+i)=a+2+(1-2a)i是纯虚数,则实部a+2=0,虚部1-2a≠0,解得a=-2.7.设复数z 满足z 2=3+4i(i 是虚数单位),则z 的模为________. 答案5解析 设复数z =a +b i ,a ,b ∈R ,则z 2=a 2-b 2+2ab i =3+4i ,a ,b ∈R ,则⎩⎪⎨⎪⎧ a 2-b 2=32ab =4,a ,b ∈R ,解得⎩⎪⎨⎪⎧ a =2b =1或⎩⎪⎨⎪⎧a =-2b =-1,则z=±(2+i),故|z |= 5.8.已知复数z =(5+2i)2(i 为虚数单位),则z 的实部为________. 答案 21解析 由题意,得z =(5+2i)2=25+20i -4=21+20i ,其实部为21.1 复数的加法(1)运算法则:设z 1=a +b i ,z 2=c +d i(a ,b ,c ,d ∈R )是任意两复数,那么z 1+z 2=(a +b i)+(c +d i)=(a +c )+(b +d )i.(2)运算律:交换律、结合律.(3)几何意义:复数z 1+z 2是以OZ 1→,OZ 2→为邻边的平行四边形的对角线OZ →所对应的复数,其中OZ 1→,OZ 2→分别为z 1,z 2所对应的向量.2 复数的减法(1)运算法则:设z 1=a +b i ,z 2=c +d i(a ,b ,c ,d ∈R ),则z 1-z 2=(a +b i)-(c +d i)=(a -c )+(b -d )i.(2)几何意义:复数z 1-z 2是从向量OZ 2→的终点指向向量OZ 1→的终点的向量Z 2Z 1→所对应的复数.3 复数的乘法(1)运算法则:设z 1=a +b i ,z 2=c +d i(a ,b ,c ,d ∈R ),则z 1·z 2=(a +b i)·(c +d i)=(ac -bd )+(ad +bc )i.(2)运算律:交换律、结合律、分配律. 4 共轭复数(1)定义:一般地,当两个复数的实部相等,虚部互为相反数时,这两个复数叫做互为共轭复数.用z 表示z 的共轭复数,若z =a +b i ,则z =a -b i.特别地,实数的共轭复数还是它本身.(2)几何意义:互为共轭复数的两个复数在复平面内所对应的点关于实轴对称.实数和它的共轭复数在复平面内所对应的点重合,且在实轴上.(3)性质:z ·z =(a +b i)·(a -b i)=a 2+b 2=|z |2(a ,b ∈R ). 5 复数的除法运算法则:设z 1=a +b i ,z 2=c +d i(a ,b ,c ,d ∈R ),则z 1z 2=a +b ic +d i =(a +b i )(c -d i )(c +d i )(c -d i )=ac +bd c 2+d 2+bc -adc 2+d 2i(c +d i ≠0),即分子、分母同乘以分母的共轭复数,使分母实数化,以简化运算.注意点 虚数单位i 的周期性计算得i 0=1,i 1=i ,i 2=-1,i 3=-i ,继续计算可知i 具有周期性,且最小正周期为4,故有如下性质(n ∈N ):(1)i 4n =1,i 4n +1=i ,i 4n +2=-1,i 4n +3=-i ; (2)i 4n +i 4n +1+i 4n +2+i 4n +3=0. 1.思维辨析(1)若a ∈C ,则a 2≥0.( ) (2)方程x 2+x +1=0没有解.( ) (3)原点是实轴与虚轴的交点.( ) (4)z =z ⇔z ∈R .( )(5)若z ≠0且z +z =0,则z 为纯虚数.( ) 答案 (1)× (2)× (3)√ (4)√ (5)√2.复数z 满足(z +2)(1+i 3)=2(i 为虚数单位),则z =( ) A .1-i B .1+i C .-1-i D .-1+i答案 D解析 由题意得:(z +2)(1+i 3)=2,(z +2)(1-i)=2,z =21-i-2=1+i -2=-1+i ,故选D.3.已知实数m 是方程x 2+(2+i)x +n +2i =0,n ∈R 的一个根,则m +n =________.答案 -2解析 由题意知:m 2+(2+i)m +n +2i =0, 即m 2+2m +n +(m +2)i =0,由复数相等的条件得⎩⎪⎨⎪⎧m 2+2m +n =0m +2=0,解得:⎩⎪⎨⎪⎧m =-2n =0,即m +n =-2[考法综述] 复数的四则运算法则及其加减法的几何意义(平行四边形法则、三角形法则),尤其除法运算及i 的运算规律为命题热点.命题法 复数的四则运算典例 (1)下面是关于复数z =2-1+i 的四个命题:p 1:|z |=2,p 2:z 2=2i ,p 3:z 的共轭复数为1+i ,p 4:z 的虚部为-1, 其中的真命题为( ) A .p 2,p 3 B .p 1,p 2 C .p 2,p 4D .p 3,p 4(2)已知复数z =3+i (1-3i )2,z -是z 的共轭复数,则z ·z -=________. [解析] (1)z =2(-1-i )(-1+i )(-1-i )=-1-i ,故|z |=2,p 1错误;z 2=(-1-i)2=(1+i)2=2i ,p 2正确;z 的共轭复数为-1+i ,p 3错误;p 4正确.(2)∵z =3+i (1-3i )2=3+i -2-23i =3+i-2(1+3i )=(3+i )(1-3i )-2(1+3i )(1-3i )=23-2i -8=-34+14i ,∴z ·z =⎝⎛⎭⎪⎫-34+14i ⎝ ⎛⎭⎪⎫-34-14i =316+116=14.故填14.[答案] (1)C (2)14【解题法】 复数四则运算中常用技巧 (1)巧用“分母实数化”,求解复数除法运算.复数的除法一般是将分母实数化,即分子、分母同乘以分母的共轭复数再进一步化简.其原理是(a +b i)(a -b i)=a 2+b 2(a 、b ∈R ).(2)巧用“结论”,求解复数的乘方运算.记忆结论(1±i)2=±2i ,1+i 1-i =i ,1-i1+i =-i ,在化简复数的过程中构造出结论的形式,便可直接代入进行计算.1.设复数z 满足1+z1-z =i ,则|z |=( )A .1B . 2 C. 3 D .2答案 A解析 由题意知1+z =i -z i ,所以z =i -1i +1=(i -1)2(i +1)(i -1)=i ,所以|z |=1.2.若a 为实数,且(2+a i)(a -2i)=-4i ,则a =( ) A .-1 B .0 C .1 D .2 答案 B解析 由于(2+a i)(a -2i)=4a +(a 2-4)i =-4i ,所以⎩⎪⎨⎪⎧4a =0a 2-4=-4,解得a =0.故选B. 3.若复数z 满足z1-i=i ,其中i 为虚数单位,则z =( )A .1-iB .1+iC .-1-iD .-1+i答案 A解析 由已知z =i(1-i)=i -i 2=i +1,所以z =1-i.故选A. 4.设i 是虚数单位,则复数i 3-2i =( )A .-iB .-3iC .iD .3i答案 C解析 i 3-2i =-i -2ii 2=-i +2i =i ,选C.5.已知(1-i )2z =1+i(i 为虚数单位),则复数z =( ) A .1+i B .1-i C .-1+i D .-1-i答案 D解析 z =(1-i )21+i =-2i 1+i =-2i (1-i )(1+i )(1-i )=-1-i.6.(1+i )3(1-i )2=( ) A .1+i B .1-i C .-1+i D .-1-i 答案 D解析 (1+i )3(1-i )2=(1+i )2(1+i )(1-i )2=2i (1+i )-2i =-1-i.故选D.7.设i 是虚数单位,z 表示复数z 的共轭复数.若z =1+i ,则z i+i·z =( )A .-2B .-2iC .2D .2i答案 C解析 原式=1+ii +i(1-i)=-(i +i 2)+i(1-i)=1-i +i +1=2. 8.设复数a +b i(a ,b ∈R )的模为3,则(a +b i)(a -b i)=________. 答案 3解析 复数a +b i(a ,b ∈R )的模为a 2+b 2=3,则a 2+b 2=3,则(a +b i)(a -b i)=a 2-(b i)2=a 2-b 2·i 2=a 2+b 2=3.9.若复数z =1+2i ,其中i 是虚数单位,则⎝ ⎛⎭⎪⎪⎫z +1z ·z =________. 答案 6解析 ∵z =1+2i ,∴z =1-2i. ∴⎝ ⎛⎭⎪⎪⎫z +1z ·z =z ·z +1=5+1=6. 10.复数2-2i 1+i =________.答案 -2i解析 2-2i 1+i =(2-2i )(1-i )(1+i )(1-i )=2-2-4i 2=-2i. 已知复数z 满足z =2i 1+3i (i 为虚数单位),则z 的共轭复数的虚部是( )A.32 B .-32 C .-12 D .-12i [错解][错因分析] 对虚部的概念理解不清,将复数z =a +b i(a ,b ∈R )的虚部错误地认为是b i.[正解] z =2i 1+3i =2i (1-3i )(1+3i )(1-3i )=23+2i 4=32+12iz 的共轭复数为32-12i ,∴z 的共轭复数的虚部为-12,故选C. [答案] C [心得体会]………………………………………………………………………………………………时间:45分钟基础组1.[2016·冀州中学期末]设z =1+i(i 是虚数单位),则2z =( ) A .i B .2-i C .1-i D .0答案 C解析 因为2z =21+i =2(1-i )(1+i )(1-i )=1-i ,故选C.2.[2016·衡水中学周测]i 为虚数单位,若a1-i =1+i i ,则a 的值为( )A .iB .-iC .-2iD .2i 答案 C解析 由已知a 1-i =1+i i 得,a i =(1-i)(1+i),a i =2,a =2i =-2i ,故选C.3.[2016·冀州中学月考]设复数z =2-1-i(i 为虚数单位),z 的共轭复数为z ,则在复平面内i z 对应的点的坐标为( )A .(1,1)B .(-1,1)C .(1,-1)D .(-1,-1)答案 C解析 ∵z =2-1-i =-1+i ,∴i z =i(-1-i)=1-i ,其在复平面内对应的点的坐标为(1,-1).4.[2016·武邑中学周测]在复平面内,复数z 和2i2-i 表示的点关于虚轴对称,则复数z =( )A.25+45i B .25-45i C .-25+45i D .-25-45i答案 A解析 由2i 2-i =-25+45i 可知该复数对应的点为⎝ ⎛⎭⎪⎫-25,45,其关于虚轴的对称点为⎝ ⎛⎭⎪⎫25,45,故复数z =25+45i ,故选A.5.[2016·衡水中学月考]已知i 是虚数单位,则2+i3-i =( )A.12-12i B .72-12i C.12+12i D .72+12i答案 C解析 2+i 3-i =(2+i )(3+i )(3-i )(3+i )=5+5i 10=12+12i.6.[2016·枣强中学猜题]若复数z =(2-i)i(其中i 为虚数单位),则z =( )A .2-iB .1+2iC .-1+2iD .1-2i答案 D解析 z =(2-i)i =1+2i ,∴z =1-2i ,选D.7.[2016·衡水中学期中]已知复数z =3+4i ,z 表示复数z 的共轭复数,则|zi |=( )A. 5 B .5 C. 6 D .6答案 B解析 由z =3+4i ,得z =3-4i ,所以|z i |=⎪⎪⎪⎪⎪⎪3-4i i =|(3-4i)(-i)|=|-4-3i|=(-4)2+(-3)2=5.8. [2016·武邑中学期中]复数z =2i 20141-2i (i 是虚数单位)在复平面内的对应点位于( )A .第一象限B .第二象限C .第三象限D .第四象限答案 C解析 ∵i 2014=(i 2)1007=(-1)1007=-1,∴z =2i 20141-2i =-21-2i =-2(1+2i )(1-2i )(1+2i )=-2+2i 3,∴z 在复平面内的坐标为⎝⎛⎭⎪⎫-23,-23,故选C.9.[2016·衡水中学期末]若(1+2a i)i =1-b i ,其中a ,b ∈R ,则|a +b i|=( )A.12+i B . 5 C.52 D .54答案 C解析 因为(1+2a i)i =1-b i ,所以-2a +i =1-b i ,a =-12,b=-1,所以|a +b i|=⎪⎪⎪⎪⎪⎪-12-i =52,选C.10.[2016·衡水二中期中]复数z =1-i ,则1z +z =( ) A.12+32i B .12-32i C.32-32i D .32-12i答案 D解析 ∵z =1-i ,∴1z +z =11-i +1-i =1+i (1-i )(1+i )+1-i =1+i 2+1-i =32-12i ,故选D.11. [2016·枣强中学模拟]设复数z =-1-i(i 为虚数单位),z 的共轭复数为z ,则|(1-z )·z |=( )A.10 B .2 C. 2 D .1 答案 A解析 解法一:|(1-z )·z |=|1-z ||z |=|2+i||-1+i|=22+12·(-1)2+(1)2=10.解法二:|(1-z )·z |=|z -z ·z |=|-1+i -2|=|-3+i|=(-3)2+12=10.12.[2016·衡水二中期末]若a 为实数,i 为虚数单位,2+a i 1+2i =-2i ,则a 等于________.答案 - 2解析 由已知2+a i1+2i =-2i ,得2+a i =-2i(1+2i),即2+a i =-2i +2,∴a =- 2.能力组13.[2016·武邑中学猜题]复数z 1,z 2满足z 1=m +(4-m 2)i ,z 2=2cos θ+(λ+3sin θ)i(m ,λ,θ∈R ),并且z 1=z 2,则λ的取值范围是( )A .[-1,1]B .⎣⎢⎡⎦⎥⎤-916,1 C.⎣⎢⎡⎦⎥⎤-916,7 D .⎣⎢⎡⎦⎥⎤916,7答案 C解析 由复数相等的充要条件可得⎩⎪⎨⎪⎧m =2cos θ4-m 2=λ+3sin θ,化简得4-4cos 2θ=λ+3sin θ,由此可得λ=-4cos 2θ-3sin θ+4=-4(1-sin 2θ)-3sin θ+4=4sin 2θ-3sin θ,因为sin θ∈[-1,1],所以4sin 2θ-3sin θ∈⎣⎢⎡⎦⎥⎤-916,7.14. [2016·冀州中学仿真]已知复数z =1+2i1-i,则1+z +z 2+…+z 2014为( )A .1+iB .1-iC .iD .1答案 C解析 z =1+2i1-i=1+2i (1+i )2=i ,∴1+z +z 2+…+z 2014=1×(1-z 2015)1-z =1-i 20151-i =1-i4×503+31-i=1+i 1-i =(1+i )2(1-i )(1+i )=2i2=i. 15.[2016·武邑中学预测]已知x 1=1-i(i 是虚数单位)是关于x 的实系数一元二次方程x 2+ax +b =0的一个根,则实数a =________,b =________.答案 -2 2解析 由题意,知x 2=1+i 是方程的另一根,因此-a =x 1+x 2=2,a =-2,b =x 1x 2=(1-i)(1+i)=2.16.[2016·衡水二中模拟]已知复数 z =4+2i(1+i )2(i 为虚数单位)在复平面内对应的点在直线x -2y +m =0上,则m =________.答案 -5解析 z =4+2i (1+i )2=4+2i 2i =(4+2i )i2i 2=1-2i ,复数z 在复平面内对应的点的坐标为(1,-2),将其代入x -2y +m =0,得m =-5.。
第十四章轴-资料

2020/5/30
如上图,减速器箱体一般为剖分式,轴上零件安装顺序为:
从左端装齿轮
套筒
左滚动轴承;
右滚动轴承
将轴装在轴承座上
左端盖
右端盖
装带轮
轴端挡圈
2020/5/30
2020/5/30
14-4 轴的强度计算
轴的强度计算概述: 轴的强度计算通常有四种方法:
扭转强度条件 按弯扭合成强度条件 按疲劳强度条件进行精确校核计算
(前三种最常用)
静强度条件进行校核计算 本节主要讲前面二种方法
2020/5/30
一、扭转强度
• 对于只受转矩或以承受转矩为主的传动轴,
(即所受弯矩很小的传动轴)应按扭转强度
2020/5/30
d C3 P n
设计公式 (14-2)
设计公式15-2的应用场合: ① 只受转矩,不受弯矩的传动轴的精确计算。 ② 主要受转矩,弯矩很小的轴,如带轮的 外伸轴。但这时为近似计算, 可用降低许用应力的方法来考虑其影响。 ③ 初步估算轴的最小直径dmin , 并根据dmin进 行结构设计,这是最重要用途。 因为新设计一根轴时一般只知道P和 n 。
2020/5/30
14-3 轴的结构设计
一、轴的结构设计概述: 二、阶梯轴结构设计的几个主要问题:
2020/5/30
㈠、制造安装要求
轴的装配方案---指轴上主要零件的装 配方向、顺序和相互关系。
轴上零件的装配方案不同,则轴的基本形 式就不同。
2020/5/30
便于安装: 为了便于拆装轴上的零件,一 般将轴设计
第十四章第1讲 光的折射 全反射--2025版高考总复习物理

第14章 光
A.水的折射率为sin
1 41°
B.水的折射率为sin
1 49°
C.当他以 α=60°向水面发射激光时,岸上救援人员接收激光光束的方
向与水面夹角小于 60°
D.当他以 α=60°向水面发射激光时,岸上救援人员接收激光光束的方
向与水面夹角大于 60°
返回导航
第14章 光
关键信息
返回导航
第14章 光
解析:光在纤芯和外套的界面上发生全反射,纤芯的折射率比外套的大, A 正确,B 错误;由 v=nc可知,波长越短、频率越高的光的折射率越大, 在光纤中的传播速度越小,C 错误,D 正确。
返回导航
第14章 光
2.(2023·江苏卷)地球表面附近空气的折射率随高度降低而增大,太阳光 斜射向地面的过程中会发生弯曲。下列光路图中能描述该现象的是 ()
返回导航
第14章 光
解析:从表中可得出在 20 ℃时玻璃对这种光的折射率大于水对这种光的折 射率,根据 v=nc可知,这种光在玻璃中的速度小于在水中的速度,故 A 错误; 折射率大小不仅与介质本身有关,还与光的频率(颜色)有关,同一种介质中, 频率越大的光折射率越大,故 B 错误;在 20 ℃温度下,玻璃对这种光的折 射率大于水对这种光的折射率,则这种波长的光从玻璃射入水中,即从光密 介质射向光疏介质时,可能发生全反射,故 C 正确;根据 n=sin1 C知,折射 率大的临界角小,在 20 ℃温度下,水晶对这种光的折射率大于水对这种光 的折射率,因此这种波长的光射入水晶更容易发生全反射,故 D 错误。
sin C=n1得水的折射率 n=sin 419°,A 错误,B 正确;当以 α=60°向水
sin 面发射激光时,入射角为 θ1=30°,设折射角为 θ2,则由 n=sin
机械设计基础 第十四章 联轴器与离合器制动器
键对的轴向位移、径向位移、角位移或综合位移。
②万向联轴器1——主、从动轴的叉状接头;2——十字形连接件;3——轴销;4——中间轴,左右单万向联轴器。
=45°。
允许两轴线夹角αmax单万向联轴器:ω1恒定时,ω4变速,引起惯性力。
双万向联轴器:可使从动轴ω恒定。
条件——中间轴两叉头在同一平面内;两万向联轴器的夹角需相等。
应用:汽车、拖拉机、金属切削机床中。
组成:两个外表面带齿的套连);两个内表面有(螺栓联工作时:转矩有齿轮传递。
14—4 非金属弹性元件挠性联轴器L sd1:10圆锥形孔圆柱形孔短圆柱形孔A12345A A§14—5 牙嵌离合器组成:左摩擦盘(联接主动轴)右摩擦盘(从动轴,可工作原理:依靠接触面上产生的摩擦力矩来传递特点:可平稳的接合、脱开;、多片式摩擦离合器外套筒内套筒内摩擦片主动轴从动轴特点:结构紧凑、轴向压力小,传递转矩大。
应用:机床变速箱、飞机、汽车及起重设备中。
自动离合器自动离合器是能根据机器运转参数(T,n )的变化而自动完成接合和分离动作的离合器。
当传递的转矩达到一定值时,便能自动分离,具有防止摩擦式安全离合器二、离心式离合器套筒1与主动轴连,套筒2与从动轴连,外表面覆着石棉的闸块3,当转速大时,闸块3产生的离心力使闸块压向套筒2,产生摩擦力从而带动从动轴一起转。
相连,1内均有径向叶片,14—8 制动器。
物理九年级上册 第十四章 欧姆定律(篇)(Word版 含解析)

物理九年级上册第十四章欧姆定律(篇)(Word版含解析)一、初三物理第十四章欧姆定律易错压轴题提优(难)1.欣欣利用如图甲所示的电路,探究通过“导体的电流跟电阻的关系”。
实验器材:电源(电压恒为 4.5V),电流表、电压表各一只,开关,三个定值电阻(5Ω、10Ω、15Ω),两只滑动变阻器(甲“10Ω 2A”、乙“20Ω 1A”),导线若干。
(1)用笔画线代替导线完成图甲电路的连接;(_____________)(2)实验中欣欣发现,无论怎样移动滑动变阻器的滑片,两电表的指针始终处于图乙所示的状态,则电路故障可能是_______;(3)排除故障后,多次改变 R的阻值,根据实验数据画出如图丙所示的I-R图像,得到的结论是_______ ;(4)在上述实验中,欣欣用10Ω的电阻替换5Ω的电阻,为了完成实验,他应该将滑动变阻器的滑片向 ______ 端移动(选填“A”或“B”),使电压表示数为______________V;(5)当欣欣改用15Ω的电阻继续实验时,发现无论怎样移动滑动变阻器的滑片,都无法使电压表的示数达到实验要求的值,则欣欣选用的滑动变阻器的规格是______(选填“甲”或“乙”),如果串一个定值电阻就能完成实验,那么这个定值电阻的范围是________;(6)除了更换滑动变阻器的方案以外,欣欣想到原有器材不变,调整定值电阻两端的电压也可以完成实验,他应控制定值电阻两端的电压范围是________。
【答案】定值电阻断路在电压不变时,通过导体的电流与电阻成反比A 2.5 甲2~12Ω 2.7V∼3V【解析】【分析】【详解】(1)[1]将电压表并联在定值电阻的两端,如图所示;(2)[2]乙图中,左表为电压表,示数满偏,说明电压表与电源连通;右边为电流表示为0,说明电路断路或总电阻很大,由此可知,与电压表并联的定值电阻断路了。
(3)[3]由图丙所示图象可知:通过电阻的电流与电阻值的乘积为2.5保持不变,是一个定值,这说明:在电压不变时,电流与电阻成反比。
第14章-轴

设计:潘存云
设计:潘存云
③
④ ⑤⑥ ⑦
中南大学专用
作者: 潘存云教授
二、轴上零件旳定位
轴肩----阶梯轴上截面变化之处。起轴向定位作用。 零件旳轴向定位由轴肩或套筒来实现。
4、5间旳轴肩使齿轮在轴上定位,1、2间旳轴肩使带轮定位,6、7间旳轴肩使右端滚动轴承定位。
套筒
轴肩
设计:潘存云
设计:潘存云
[σ0b]
[σ-1b]
400
对称130循环状态下70旳
40
碳素钢
500
600
许170用弯曲应力75
45
200
95
55
700
230
110
65
800
合金钢
900
270
130
75
300
140
80
1000
330
150
90
铸钢
400
中南大学专用
500
100
50
30
120
70
40 作者: 潘存云教授
举例:计算某减速器输出轴危
轴端挡圈 带轮 轴承盖 套筒 齿轮 滚动轴承
经典 轴系 构造
中南大学专用
设计:潘存云
设计:潘存云
作者: 潘存云教授
一、制造安装要求
为便于轴上零件旳装拆,一般轴都做成从轴端逐 渐向中间增大旳阶梯状。零件旳安装顺序 装零件旳轴端应有倒角,需要磨削旳轴端有砂轮越程槽, 车螺纹旳轴端应有退刀槽。
倒角
取值见P119
840 N m
中南大学专用
作者: 潘存云教授
6) 求F力产生旳弯矩图
a
P231
M 2F FM KaV 4500 0.206
人教版八年级数学--一次函数-直线与坐标轴围成的面积问题(2)

第十四章 第二节
一次函数
一次函数图象与坐标轴围成的面积问题
一、利用解析式求面积
例1 求直线 y 3x 6 与两坐标轴所围 成的三角形的面积。
3 练习1将直线 y 4 x 3 平移,使其经过(4,3)
(1)求平移后的函数解析式 (2)求平移后的函数图象与两坐标轴围成的三角 形面积
思考:
1、在下列直角坐标系中,一次函数
1 y kx 2k 的图象只可能是( 2
)
若一次函数y (m 3) x 2m 5不过 第二象限,求 m的取值范围
若一次函数y x 4的自少,最 值是多少?
一次函数y kx b上 1 x 3时,对应 的函数值为 4 y 6, 求k , b的值?
次函数的解析式。
思考题
如图,一直线过点A(0,4),B(2,0),将 这条直线向左平移与x轴负半轴、y轴负半轴分别 交于点C、D,使DB=DC.求直线CD的函数表达 y 式. 4
A
B
c
0
2
x
D
作业
1、已知一次函数y=kx+8的图象与两坐标轴围成 三角形面积为8,求此一次函数解析式. 2、一次函数y=kx+b的图象过点(3,0),且与 两坐标轴围成的三角形的面积是6,求此一次 函数的解析式. 3、已知一次函数的图象过点(0,-2),且与两 坐标轴截得的直角三角形的面积为3,求这个一
y=kx+b与y轴的交点坐标(0, b b) y=kx+b与x轴的交点坐标( k ,0) y=kx+b(k≠0)与坐标轴围成的图形是 三角形
1 b s b 2 k 1b = 2 k
2
第十四章第3节 能量的转化和守恒 课件(共29张PPT)

第3节 能量的转化和守恒
学习目标
掌握能量的转化和守恒定律。 能举出日常生活中能量守恒的实例。 具备用能量守恒的观点分析物理现象的意识。
新课引入
大家尝试做以下小实验谈谈现象及感受。 (1)来回迅速摩擦双手。 (2)黑塑料袋内盛水,插入温度计后系好袋口,放在阳光下。 (3)将太阳能电池连在小电扇上,并使它对着阳光。 (4)用钢笔杆在头发或毛衣上摩擦后再靠近细碎的纸片。
能量的转化
实验现象和结论: 来回迅速摩擦双手:手会感觉到热。机械能转化为内能。 黑塑料袋内盛水,插入温度计后系好袋口,放在阳光下:光能转化
为内能。 将太阳能电池连在小电扇上,并使它对着阳光:光能转化为电能再
转化为机械能。 用钢笔杆在头发或毛衣上摩擦后再靠近细碎的纸片:机械能转化为
电能。
能量的转化
能量守恒定律
想想议议: 右图是一种设想中的永动机,它通过高
处的水流冲击叶片,叶片的转动用来对 外做功,同时带动抽水器从低处将水抽 到高处,从而循环工作。你能不能从能 量守恒的角度说明它为什么不能一直工 作下去?
能量守恒定律
此“永动机”中,高处的水流冲击叶片转动 对外做功时,因为摩擦等原因,有部分机械 能转化为其他形式的能,从高处流下的水不 可能全部被抽回原高度,根本不会“永动下 去”。在机械能转化的过程中,总会有一部 分能量以热的形式向四周扩散,成为无用的 能量,所以抽水机的机械能会逐渐减小。
课堂练习
【解析】选项A中凡是能量守恒的过程可能发生能量的转化,也可能发生能量的转 移,不符合题意。选项B中摩擦生热的过程是不可逆的。例如钻木取火, 不能用火得到木头,符合题意。选项C中热传递是有方向性的,热量一定 从温度高的物体传向温度低的物体,或从温度高的部分传向温度低的部分 。不符合题意。选项D中由于能量转移或转化是有方向性的,虽然能量守 恒,但是还会产生能源危机,不符合题意。故选B。 易错提醒:能量只能被转移或转化,但是能量转移或转化都是有方向的, 所以即使能量守恒,能源危机依然存在。
机械设计基础 第十四章

(3) 弹性柱销联轴器
如图14-6所示,弹性柱销联轴器(LX型,GB/T5014-2003, 附表5) 是用尼龙柱销将两个半联轴器连接起来。这种联轴器结 构简单,维修安装方便,具有吸振和补偿轴向位移及微量径向 位移和角位移的能力。允许径向位移为0.1~0.25 mm。
图14-6 弹性柱销联轴器
14.1 联轴器 14.1.1 联轴器的功能和分类
联轴器是机械传动中一种常用的轴系部件,它的基本功 用是连接两轴,有时也用于连接轴和其他回转零件,以传递 运动和转矩。有时也可作为一种安全装置用来防止被连接机 件承受过大的载荷,起到过载保护的作用。
联轴器所连接的两轴,由于制造和安装的误差,承载后 的变形以及温度变化、轴承磨损等原因,都可能使被连接的 两轴相对位置发生变化,如图14-1所示。
14.3 制动器
制动器是用来降低机械运转速度或迫使机械停止运转的 装置。制动器通常装在机构中转速较高的轴上,这样所需制 动力矩和制动器尺寸可以小一些。
14.3.1 制动器的类型
制动器的分类有很多种,常见的有以下几种:
按照制动零件的结构特征,制动器可分为带 式、块式、盘式等形式的制动器。
按机构不工作时制动零件所处状态,制动器可 分为常闭式和常开式两种制动器。
图14-3 夹壳联轴器
2. 可移式联轴器
(1) 十字滑块联轴器
如图14-4所示,十字滑块联轴器是由两个端面带槽的半联 轴器1和3以及一个两面具有凸榫的浮动盘2所组成。浮动盘的 两凸榫互相垂直并分别嵌在两半联轴器的凹槽中,凸榫可在 半联轴器的凹槽中滑动。利用其相对滑动来补偿两轴之间的 偏移。
图14-4 十字滑块联轴器
图14-10 牙嵌式安全离合器
新人教版九年级物理第十四章课后习题答案

第十四章第一节《热机》1. 除了飞机、汽车、摩托车之外,你还知道哪些地方用到了热机?你列举的这些热机中哪些是内燃机?2. 在图14.1-6 中,甲为四冲程内燃机吸气冲程的示意图,图中画出了吸气冲程中活塞和曲轴的位置和进气门、排气门的开闭情况。
请在图乙、丙、丁中,分别画出压缩、做功、排气冲程中活塞和曲轴的位置和进气门、排气门的开闭情况。
图14.1-6 画出各冲程中活塞、曲轴的位置以及阀门的开闭情况3. 从能量转化的角度看,一台四冲程内燃机在一个循环中(1)哪个冲程存在着化学能转化为内能的过程?(2)哪个冲程存在着内能转化为机械能的过程?(3)哪个冲程具有很明显的机械能转化为内能的过程?4. 柴油机和汽油机的工作过程有什么相同点,有什么不同点?第十四章第一节《热机》课后习题答案1.轮船、拖拉机、小型农业机械、火车等都用到了热机,这些热机也都是内燃机。
2.图略。
要点提示:压缩冲程进排气门都关闭,活塞向上运动。
做功冲程进排气门都关闭活塞向下运动。
排气冲程进气门闭合,排气门打开活塞向上运动。
3.(1)做功冲程(2)做功冲程(3)压缩冲程4.柴油机和汽油机的相同点:都是燃料在气缸内燃烧;都是将内能转化为机械能的机器;都是由吸气、压缩、做功、排气四个冲程构成一个工作循环,曲轴和飞轮转两周对外做功一次;排气冲程排出废气;启动时都要靠外力先使飞轮和曲轴转动起来。
不同点:燃料不同(汽油、柴油),构造不同(火花塞、喷油嘴);吸气冲程吸入物质不同(汽油和空气混合物,柴油机只吸入空气),缸内气压、与温度高低不同(汽油机低,柴油机高)点火方式不同(汽油机是点燃式,柴油机是压燃式),效率不同(汽油机效率低,柴油机效率高)。
另外汽油机机体轻便,主要用于小汽车、摩托车,柴油机机体笨重,主要用于载重汽车,拖拉机、火车、轮船第十四章第二节《热机的效率》1. 汽油的热值为4.6×107 J/kg。
这个数值究竟有多大?有人通过一个具体例子来认识汽油热值的大小:一个60 kg 的人,从大厦的1 楼步行至第11 楼(走了10 层楼),每层楼的层高为3 m,他克服重力做了多少焦耳的功?如果汽油完全燃烧获得热量的焦耳数和这些功相等,需要汽油的质量是多少?这大约相当于生活中什么物体的质量?2. 如果燃烧干木柴跟燃烧煤油放出的热量相等,干木柴的质量应该等于煤油质量的几倍?请列出相关计算式来说明理由。
1轴对称测
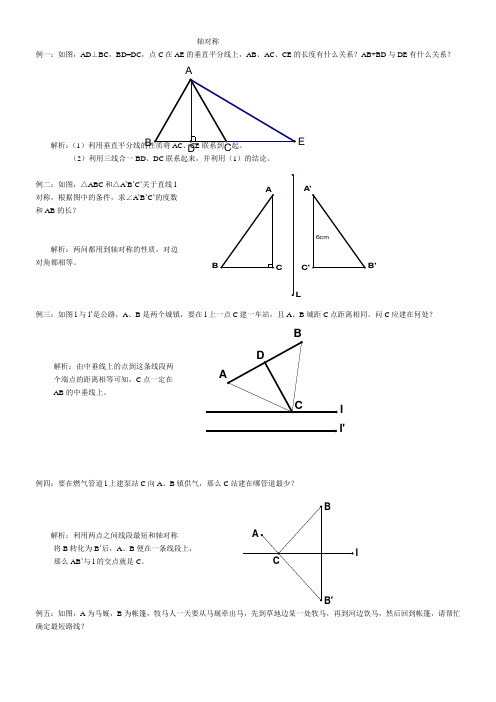
轴对称例一:如图,AD ⊥BC ,BD=DC ,点C 在AE 的垂直平分线上,AB 、AC 、CE 的长度有什么关系?AB+BD 与DE 有什么关系?解析:(1(2)利用三线合一BD 、DC 联系起来,并利用(1)的结论。
例二:如图,△ABC 和△A’B ’C ’关于直线l 对称,根据图中的条件,求∠A ’B ’C ’的度数 和AB 的长?解析:两问都用到轴对称的性质,对边 对角都相等。
例三:如图l与l ’是公路,A 、B 是两个城镇,要在l 上一点C 建一车站,且A 、B 城距C 点距离相同。
问C 应建在何处?解析:由中垂线上的点到这条线段两 个端点的距离相等可知,C 点一定在 AB 的中垂线上。
例四:要在燃气管道l 上建泵站C 向A 、B 镇供气,那么C 站建在哪管道最少?解析:利用两点之间线段最短和轴对称 将B 转化为B ’后,A 、B 便在一条线段上, 那么AB ’与l 的交点就是C 。
例五:如图,A 为马厩,B 为帐篷,牧马人一天要从马厩牵出马,先到草地边某一处牧马,再到河边饮马,然后回到帐篷,请帮忙确定最短路线?B EB'C LBl l'l解析:确定A 关于草地的对称点A ’,B 关于河的对称点B ’,连接A ’ B ’,与河和草地的交点就是最短路程。
例六:如图,在△ABC 中,AB=AC ,点D 在AC 上,且BD=BC=AD ,求△ABC 各角的度数?解析:根据条件找出图形中相等的角,列出方程,根据 参数求解。
例七:如图,AC 和BD 相交与点O , 且AB ∥DC ,OA=OB ,求证OC=OD 。
解析:这道题主要是求出AC=BD, 可以通过平移BD 来完成,使BD=CE , 然后通过倒角使∠A=∠E 。
例八:如图,点D 、E 在△ABC 的边B 、C 上,AB=AC ,AD=AE ,求证:BD=CE 。
解析:这道题不用证全等,利用三线 和一的性质来解决。
例九:如图△ABD 、△AEC 都是等边三角形,求证BE=DC 。
理论力学 第十四章 动荷载解析

三、动荷载的分类
1.惯性荷载 2.冲击荷载 3.振动荷载 4.交变荷载
实验表明:在静载荷下服从虎克定律的材料,只要应力不超 过比例极限 ,在动载荷下虎克定律仍成立且 E静 = E动。
四、本章讨论的动载荷问题:
(1)构件作等加速直线运动和等速转动时的动应力计算; (2)构件在受冲击的动应力计算;
§14-2 等加速直线运动时构件的应力计算
P d
d2 2 st d 2h st 0
d 2 st d st ( 1
42st
2
8h st
st (1
1
2h
st
)
Kd st
1 2h )
st
其中 Kd 1
Fd d P st
1 Kd
2h
st
d Kd st
为冲击动荷系数
Fd Kd P
解决冲击问题,关键在于如何确定动荷系数Kd
图示装有飞轮的轴,飞轮的转速n=100r/min,转动惯
量I=0.5kN.m.s2.轴的直径d=100mm.刹车时使轴在
10秒内均匀减速至停止.求:轴内最大动应力
飞轮与轴的转动角速度:
0
n
30
10
3
角加速度: 1 0
角加速度与角速度方向相反, 按动静y法在飞轮上加惯性力:
Md
10
I
动静法:
达朗伯原理 达朗伯原理认为 处于不平衡状态的物体,存在惯性力,惯性力
的方向与加速度方向相反,惯性力的数值等于加速度与质量的乘 积.只要在物体上加上惯性力,就可以把动力学问题在形式上作为
静力学问题来处理,这就是动静法.
惯性力大小等于质点的质量m与加速度a的乘积,方向与a 的
难点解析沪教版七年级数学第二学期第十四章三角形必考点解析试卷(含答案详解)

沪教版七年级数学第二学期第十四章三角形必考点解析考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、△BDE和△FGH是两个全等的等边三角形,将它们按如图的方式放置在等边三角形ABC内.若BC =5,则五边形DECHF的周长为()A.8 B.10 C.11 D.122、下列三个说法:①有一个内角是30°,腰长是6的两个等腰三角形全等;②有一个内角是120°,底边长是3的两个等腰三角形全等;③有两条边长分别为5,12的两个直角三角形全等.其中正确的个数有().A.3 B.2 C.1 D.03、有下列说法:①轴对称图形的对称轴是任何一对对应点所连线段的垂直平分线;②等腰三角形一腰上的高与底边的夹角与顶角互余;③等腰三角形顶角的平分线是它的对称轴;④等腰三角形两腰上的中线相等.其中正确的说法有( )个.A .1B .2C .3D .44、如图,AB =AC ,点D 、E 分别在AB 、AC 上,补充一个条件后,仍不能判定△ABE ≌△ACD 的是( )A .∠B =∠C B .AD =AE C .BE =CD D .∠AEB =∠ADC5、如图,在ABC 中,40B ∠=︒,60C ∠=°,AD 平分BAC ∠交BC 于点D ,在AB 上截取AE AC =,则EDB ∠的度数为( )A .30°B .20°C .10°D .15°6、如果三角形一边上的中线等于这条边的一半,那么这个三角形一定是( ).A .锐角三角形B .直角三角形C .钝角三角形D .等腰三角形7、如图,ABC ≌DEF ,点B 、E 、C 、F 在同一直线上,若BC =7,EC =4,则CF 的长是( )A.2 B.3 C.4 D.78、如图,∠BAD=90°,AC平分∠BAD,CB=CD,则∠B与∠ADC满足的数量关系为()A.∠B=∠ADC B.2∠B=∠ADCC.∠B+∠ADC=180°D.∠B+∠ADC=90°9、如图,将△OAB绕点O逆时针旋转80°得到△OCD,若∠A的度数为110°,∠D的度数为40°,则∠AOD的度数是()A.50°B.60°C.40°D.30°10、如图,在△ABC和△DEF中,∠A=∠D,AF=DC,添加下列条件中的一个仍无法证明△ABC≌△DEF的是()A.BC=EF B.AB=DE C.∠B=∠E D.∠ACB=∠DFE第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、如图,线段AC 与BD 相交于点O ,∠A =∠D =90°,要证明△ABC ≌△DCB ,还需添加的一个条件是____________.(只需填一个条件即可)2、如图,已知△ABC 中,AB =AC ,将△ABC 沿DF 折叠,点A 落在BC 边上的点E 处,且DE ⊥BC 于E ,若∠A =56°,则∠AFD 的度数为________.3、如图,1AP 为△ABC 的中线,2AP 为△1APC 的中线,3AP 为△2AP C 的中线,……按此规律,n AP 为△1n AP C -的中线.若△ABC 的面积为8,则△n AP C 的面积为_______________.4、如图,在ABC 中,90ACB ∠=︒,DE AB ⊥交BC 的延长线于点E ,若AD DE =,点C 是BE 中点,则B ∠=______°.5、如图,在△ABC中,AB=AC.在AB、AC上分别截取AP,AQ,使AP=AQ.再分别以点P,Q为圆心,以大于12PQ的长为半径作弧,两弧在∠BAC内交于点R,作射线AR,交BC于点D.若BC=6,则BD的长为______________.三、解答题(10小题,每小题5分,共计50分)1、如图,△ABC中,AB=AC,D为BC边的中点,AF⊥AD,垂足为A.求证:∠1=∠22、如图,ADC AEB∠=∠,AD AE=,求证:OB OC=.3、如图,在△ABC中,AB=AC,CD⊥AB于点D,∠A=50°,求∠BCD的度数.4、已知,如图,AB=AD,∠B=∠D,∠1=∠2=60°.(1)求证:△ADE≌△ABC;(2)求证:AE=CE.5、如图,AD,BC相交于点O,AO=DO.(1)如果只添加一个条件,使得△AOB≌△DOC,那么你添加的条件是(要求:不再添加辅助线,只需填一个答案即可);(2)根据已知及(1)中添加的一个条件,证明AB=DC.6、如图,灯塔B 在灯塔A 的正东方向,且75km AB =.灯塔C 在灯塔A 的北偏东20°方向,灯塔C 在灯塔B 的北偏西50°方向.(1)求ACB ∠的度数;(2)一轮船从B 地出发向北偏西50°方向匀速行驶,5h 后到达C 地,求轮船的速度.7、在ABC 中,AC BC =,90ACB ∠=︒,点D 是直线AC 上一动点,连接BD 并延长至点E ,使ED BD =.过点E 作EF AC ⊥于点F .(1)如图1,当点D 在线段AC 上(点D 不与点A 和点C 重合)时,此时DF 与DC 的数量关系是______.(2)如图2,当点D 在线段AC 的延长线上时,依题意补全图形,并证明:2AD AF EF =+.(3)当点D 在线段CA 的延长线上时,直接用等式表示线段AD ,AF ,EF 之间的数量关系是______.8、如图,ABC 是等边三角形,D 点是BC 上一点,2BD CD =,DE AB ⊥于点E ,CE 交AD 于点P .求APE ∠的度数.9、在等边ABC 中,D 、E 是BC 边上两动点(不与B ,C 重合)(1)如图1,,25AD AE BAD =∠=︒,求AEB ∠的度数;(2)点D 在点E 的左侧,且AD =AE ,点E 关于直线AC 的对称点为F ,连接AF ,DF .①依题意将图2补全;②求证:AD DF =.10、探究与发现:如图①,在△ABC 中,∠B =∠C =45°,点D 在BC 边上,点E 在AC 边上,且∠ADE =∠AED ,连接DE .(1)当∠BAD=60°时,求∠CDE的度数;(2)当点D在BC(点B、C除外)边上运动时,试猜想∠BAD与∠CDE的数量关系,并说明理由.(3)深入探究:如图②,若∠B=∠C,但∠C≠45°,其他条件不变,试探究∠BAD与∠CDE的数量关系.-参考答案-一、单选题1、B【分析】证明△AFH≌△CHG(AAS),得出AF=CH.由题意可知BE=FH,则得出五边形DECHF的周长=AB+BC,则可得出答案.【详解】解:∵△GFH为等边三角形,∴FH=GH,∠FHG=60°,∴∠AHF+∠GHC=120°,∵△ABC为等边三角形,∴AB=BC=AC=5,∠ACB=∠A=60°,∵∠AHF=180°-∠FHG-∠GHC=120°-∠GHC,∠HGC =180°-∠C -∠GHC =120°-∠GHC ,∴∠AHF =∠HGC ,在△AFH 和△CHG 中A C AHF HGC FH GH ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△AFH ≌△CHG (AAS ),∴AF =CH .∵△BDE 和△FGH 是两个全等的等边三角形,∴BE =FH ,∴五边形DECHF 的周长=DE +CE +CH +FH +DF =BD +CE +AF +BE +DF ,=(BD +DF +AF )+(CE +BE ),=AB +BC =10.故选:B .【点睛】本题考查了全等三角形的判定与性质,等边三角形的性质,熟练掌握全等三角形的判定方法是解题的关键.2、C【分析】根据三角形全等的判定方法,等腰三角形的性质和直角三角形的性质判断即可.【详解】解:①当一个是底角是30°,一个是顶角是30°时,两三角形就不全等,故本选项错误; ②有一个内角是120°,底边长是3的两个等腰三角形全等,本选项正确;③当一条直角边为12,一条斜边为12时,两个直角三角形不全等,故本选项错误;正确的只有1个,故选:C.【点睛】本题考查了全等三角形的判定定理,等腰三角形的性质和直角三角形的性质,熟练掌握全等三角形的判定定理是解题的关键.3、B【分析】根据轴对称的性质,轴对称图形的概念,等腰三角形的性质判断即可.【详解】解:①轴对称图形的对称轴是任何一对对应点所连线段的垂直平分线,说法正确;②等腰三角形一腰上的高与底边的夹角与底角互余,原说法错误;③等腰三角形的顶角平分线在它的对称轴上,原说法错误;④等腰三角形两腰上的中线相等,说法正确.综上,正确的有①④,共2个,故选:B.【点睛】本题考查了轴对称的性质及等腰三角形的性质,掌握轴对称的性质,轴对称图形的概念,等腰三角形的性质是解题的关键.4、C【分析】根据全等三角形的判定定理进行判断即可.【详解】解:根据题意可知:AB =AC ,A A ∠=∠,若B C ∠=∠,则根据()ASA 可以证明△ABE ≌△ACD ,故A 不符合题意;若AD =AE ,则根据(SAS)可以证明△ABE ≌△ACD ,故B 不符合题意;若BE =CD ,则根据()SSA 不可以证明△ABE ≌△ACD ,故C 符合题意;若∠AEB =∠ADC ,则根据()AAS 可以证明△ABE ≌△ACD ,故D 不符合题意;故选:C .【点睛】本题考查了全等三角形的判定,熟练掌握全等三角形的判定定理是解本题的关键.5、B【分析】利用已知条件证明△ADE ≌△ADC (SAS ),得到∠DEA =∠C ,根据外角的性质可求EDB ∠的度数.【详解】解:∵AD 是∠BAC 的平分线,∴∠EAD =∠CAD在△ADE 和△ADC 中,AE AC EAD CAD AD AD =⎧⎪∠=∠⎨⎪=⎩, ∴△ADE ≌△ADC (SAS ),∴∠DEA =∠C 60=︒,∵40B ∠=︒,∠DEA =∠B +EDB ∠,∴604020EDB ∠=︒-︒=︒;故选:B【点睛】本题考查了全等三角形的性质与判定,解决本题的关键是证明△ADE≌△ADC.6、B【分析】根据题意画出图形,利用等腰三角形的性质及三角形内角和定理即可得到答案.【详解】如图,在△ABC中,CD是边AB上的中线∵AD=CD=BD∴∠A=∠DCA,∠B=∠DCB∵∠A+∠ACB+∠B=180°∴ ∠A+∠DCA+∠DCB+∠B=180即2∠A+2∠B=180°∴∠A+∠B=90°∴∠ACB=90°∴△ABC是直角三角形故选:B【点睛】本题考查了等腰三角形的性质及三角形内角和定理,熟练运用这两个知识是关键.7、B【分析】根据全等三角形的性质可得BC EF =,根据CF EF EC =-即可求得答案.【详解】 解:ABC ≌DEF ,∴BC EF =点B 、E 、C 、F 在同一直线上,BC =7,EC =4,∴CF EF EC =-743BC EC -=-=故选B【点睛】本题考查了全等三角形的性质,掌握全等三角形的性质是解题的关键.8、C【分析】由题意在射线AD 上截取AE =AB ,连接CE ,根据SAS 不难证得△ABC ≌△AEC ,从而得BC =EC ,∠B =∠AEC ,可求得CD =CE ,得∠CDE =∠CED ,证得∠B =∠CDE ,即可得出结果.【详解】解:在射线AD 上截取AE =AB ,连接CE ,如图所示:∵∠BAD =90°,AC 平分∠BAD ,∴∠BAC =∠EAC ,在△ABC 与△AEC 中,AC AC BAC EAC AB AE =⎧⎪∠=∠⎨⎪=⎩, ∴△ABC ≌△AEC (SAS ),∴BC =EC ,∠B =∠AEC ,∵CB =CD ,∴CD =CE ,∴∠CDE =∠CED ,∴∠B =∠CDE ,∵∠ADC +∠CDE =180°,∴∠ADC +∠B =180°.故选:C .【点睛】本题主要考查全等三角形的判定与性质,解答的关键是作出适当的辅助线AE ,CE .9、A【分析】根据旋转的性质求解80,BOD AOC 110,C A 再利用三角形的内角和定理求解1801104030,COD 再利用角的和差关系可得答案.【详解】 解: 将△OAB 绕点O 逆时针旋转80°得到△OCD ,80,BOD AOC∠A 的度数为110°,∠D 的度数为40°,110,1801104030,C A CODAOD803050,故选A【点睛】本题考查的是三角形的内角和定理的应用,旋转的性质,掌握“旋转前后的对应角相等”是解本题的关键.10、A【分析】根据AF=DC求出AC=DF,再根据全等三角形的判定定理逐个判断即可.【详解】解:∵AF=DC,∴AF+FC=DC+FC,即AC=DF,A、BC=EF,AC=DF,∠A=∠D,不符合全等三角形的判定定理,不能推出△ABC≌△DEF,故本选项符合题意;B、AB=DE,∠A=∠D,AC=DF,符合全等三角形的判定定理SAS,能推出△ABC≌△DEF,故本选项不符合题意;C.∠B=∠E,∠A=∠D,AC=DF,符合全等三角形的判定定理AAS,能推出△ABC≌△DEF,故本选项不符合题意;D.∠ACB=∠DFE,AC=DF,∠A=∠D,符合全等三角形的判定定理ASA,能推出△ABC≌△DEF,故本选项不符合题意;故选:A.【点睛】本题考查了全等三角形的判定定理,能熟记全等三角形的判定定理是解此题的关键,注意:全等三角形的判定定理有SAS ,ASA ,AAS ,SSS ,两直角三角形全等还有HL .二、填空题1、答案不唯一,如:AC =DB ,AB =DC ,∠ABC =∠DCB【分析】根据全等三角形的判定条件求解即可.【详解】解:∵∠A =∠D =90°,BC =CB ,∴只需要添加:AC =DB 或AB =DC ,即可利用HL 证明△ABC ≌△DCB ;添加∠ABC =∠DCB 可以利用AAS 证明△ABC ≌△DCB ,故答案为:答案不唯一,如:AC =DB ,AB =DC ,∠ABC =∠DCB .【点睛】本题主要考查了全等三角形的判定,熟知全等三角形的判定条件是解题的关键.2、48°48度【分析】先求出∠ABC 和∠ACB 的度数,再利用直角三角形的性质得出∠BDE 的度数,根据由翻折的性质可得:ADF EDF ∠=∠,最后利用三角形的内角和定理得出结论.【详解】解:∵AB =AC ,∠A =56° ∴18056622ABC ACB ︒-︒∠=∠==︒, ∵DE ⊥BC ,∴90906228BDE ABC ∠=︒-∠=︒-︒=︒,由折叠的性质可得:ADF EDF ∠=∠,∵180BDE ADF EDF ∠+∠+∠=︒,∴18028762ADF EDF ︒-︒∠=∠==︒, ∴∠AFD =180°-∠A -∠ADF =180°-56°-76°=48°,故答案为:48°.【点睛】本题考查了等腰三角形的性质,轴对称的性质,直角三角形的性质及三角形的内角和定理,解题的关键是熟练掌握这些性质.3、312n -【分析】根据三角形的中线性质,可得△1APC 的面积=182⨯,△2AP C 的面积=2182⨯,……,进而即可得到答案.【详解】由题意得:△1APC 的面积=182⨯,△2AP C 的面积=2182⨯,……,△n AP C 的面积=182n ⨯=312n -. 故答案是:312n -.【点睛】 本题主要考查三角形的中线的性质,掌握三角形的中线把三角形的面积平分,是解题的关键. 4、67.5°【分析】连接AE ,先得出∠BAC =12∠BAE ,再根据AD DE =,得出∠BAC =22.5°,最后得出结果.【详解】解:连接AE ,∵点C 是BE 中点,∵∠ACB=90°,∴AC⊥BE,∴AB=AE,∠BAE,∴∠BAC=12∵DE⊥AB,∴∠ADE=90°,∵AD DE,∴∠AED=∠DAE=45°,∴∠BAC=1∠BAE=22.5°,2∴∠B=90°-∠BAC=67.5°.故答案为:67.5°.【点睛】本题考查了线段垂直平分线的性质,等腰三角形的性质及直角三角形的性质,正确作出辅助线是解题的关键.5、3根据题意依据等腰三角形的性质,即可得到BD=12BC,进而分析计算即可得出结论.【详解】解:由题可得,AR平分∠BAC,又∵AB=AC,∴AD是三角形ABC的中线,∴BD=12BC=12×6=3.故答案为:3.【点睛】本题主要考查基本作图以及等腰三角形的性质,注意掌握等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.三、解答题1、见详解.【分析】根据等腰三角形三合一性质以及等边对等角性质得出AD⊥BC,∠B=∠C,根据AF⊥AD,利用在同一平面内垂直同一直线的两直线平行得出AF∥BC,利用平行线性质得出∠1=∠B,∠2=∠C即可.【详解】证明:∵△ABC中,AB=AC,D为BC边的中点,∴AD⊥BC,∠B=∠C,∵AF⊥AD,∴AF∥BC,∴∠1=∠B,∠2=∠C,∴∠1=∠2.【点睛】本题考查等腰三角形性质,平行线的判定与性质,掌握等腰三角形性质,平行线的判定与性质是解题关键.2、证明过程见解析【分析】先证明AEB ADC ≅,得到DB EC =,B C ∠=∠,再证明DOB EOC ≅△△,即可得解;【详解】由题可得,在AEB △和ADC 中,A A AE AD AEB ADC ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴AEB ADC ≅,∴AB AC =,B C ∠=∠,又∵AD AE =,∴DB EC =,在DOB 和EOC △中,B C DOB EOC DB EC ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴DOB EOC ≅△△,∴OB OC =.【点睛】本题主要考查了全等三角形的判定与性质,准确分析证明是解题的关键.3、25°【分析】直接利用等腰三角形的性质得出∠ABC =∠ACB =65°,进而利用三角形内角和定理得出答案.【详解】∵AB =AC ,∠A =50°,∴∠ABC =∠ACB =65°,∵CD ⊥BC 于点D ,∴∠BCD 的度数为:180°−90°−65°=25°.【点睛】此题主要考查了等腰三角形的性质,正确得出∠B 的度数是解题关键.4、(1)见解析;(2)见解析【分析】(1)根据∠1=∠2可推出∠DAE =∠BAC ,然后结合全等三角形的判定定理进行证明;(2)由全等三角形的性质可得AE =AC ,结合∠2=60°可推出△AEC 为等边三角形,据此证明.【详解】(1)证明:∵∠1=∠2∴∠1+BAE ∠=∠2+BAE ∠即∠DAE =∠BAC在△ADE 和△ABC 中DAE BAC AD ABD B ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ADE ≌△ABC (ASA )(2)证明:∵△ADE ≌△ABC∴AE =AC又∵∠2=60°∴△AEC 为等边三角形∴AE =CE【点睛】此题考查了全等三角形的性质和判定,等边三角形的性质和判定,解题的关键是熟练掌握全等三角形的性质和判定方法,等边三角形的性质和判定方法.5、(1)OB =OC (或A D ∠=∠,或B C ∠=∠);(2)见解析【分析】(1)根据SAS 添加OB =OC 即可;(2)由(1)得△AOB ≌△DOC ,由全等三角形的性质可得结论.【详解】解:(1)添加的条件是:OB =OC (或A D ∠=∠,或B C ∠=∠)证明:在AOB ∆和DOC ∆中AO BO AOB COD BO CO =⎧⎪∠=∠⎨⎪=⎩所以,△AOB ≌△DOC(2)由(1)知,△AOB ≌△DOC所以,AB =DC .【点睛】本题主要考查了全等三角形的判定与性质,熟练掌握全等三角形的判定方法是解答本题的关键6、(1)70°;(2)15km/h【分析】(1)根据题意得∠BAC =70°,∠ABC =40°,根据三角形的内角和定理即可求得∠ACB ;(2)根据等腰三角形的判定可得BC=AB=75km ,进而由速度=路程÷时间求解即可.【详解】解:(1)根据题意得∠BAC =70°,∠ABC =40°,∴∠ACB =180°-∠BAC -∠ABC =180°-70°-40°=70°;(2)∵∠BAC =∠ACB =70°,∴BC=AB=75km ,∴轮船的速度为75÷5=15(km/h ).【点睛】本题考查方位角、等腰三角形的判定、三角形的内角和定理,理解方位角,熟练掌握等腰三角形的等角对等边是解答的关键.7、(1)DF DC =(2)见解析(3)2AF EF AD -=【分析】(1)利用边相等和角相等,直接证明EDF BDC ∆∆≌,即可得到结论.(2)利用边相等和角相等,直接证明EDF BDC ∆∆≌,得到DF DC =和EF BC AC ==,最后通过边与边之间的关系,即可证明结论成立.(3)要证明2AF EF AD -=,先利用边相等和角相等,直接证明EDF BDC ∆∆≌,得到DF DC =和EF BC AC ==,最后通过边与边之间的关系,即可证明结论成立.【详解】(1)解:DF DC =90ACD ∠=︒,EF AC ⊥,90ACB EFD ∴∠=∠=︒,在EDF ∆和BDC ∆中,ACB EFD FDE BDC ED BD ∠=∠⎧⎪∠=∠⎨⎪=⎩()EDF BDC AAS ∴∆∆≌,DF DC ∴=.(2)解:当点D 在线段AC 的延长线上时,如下图所示:90ACD ∠=︒,EF AC ⊥,90ACB EFD ∴∠=∠=︒,在EDF ∆和BDC ∆中,ACB EFD FDE BDC ED BD ∠=∠⎧⎪∠=∠⎨⎪=⎩()EDF BDC AAS ∴∆∆≌,DF DC ∴=,EF BC AC ==,=2AF EF AD DF AC AD CD AD ∴+=++=+.(3)解:2AF EF AD -=,如下图所示:90ACD ∠=︒,EF AC ⊥,90ACB EFD ∴∠=∠=︒,在EDF ∆和BDC ∆中,ACB EFD FDE BDC ED BD ∠=∠⎧⎪∠=∠⎨⎪=⎩()EDF BDC AAS ∴∆∆≌,DF DC ∴=,EF BC AC ==,()2AF EF AF AC AF DF AD AF DF AD AD ∴-=-=--=-+=.【点睛】本题主要是考查了三角形全等的判定和性质,熟练利用条件证明三角形全等,然后利用边相等以及边与边之间关系,即可证明结论成立,这是解决该题的关键.8、60APE ∠=︒【分析】由题意易得60ABC ACB ∠=∠=︒,AB AC BC ==,则有30BDE ∠=︒,然后可得BE CD =,进而可证BEC CDA ≌,则有BCE =∠∠CAD ,最后问题可求解.【详解】解:∵ABC 是等边三角形,∴60ABC ACB ∠=∠=︒,AB AC BC ==,∵DE AB ⊥,∴90DEB ∠=︒,∴30BDE ∠=︒,∴2BD BE =,∵2BD CD =,∴BE CD =,∴BEC CDA ≌(SAS ),∴BCE =∠∠CAD ,∵,60APE PAC ACP ACB DAC ACP ∠=∠+∠∠=∠+∠=︒,∴60APE ACB ∠=∠=︒.【点睛】本题主要考查等边三角形的性质、含30度直角三角形的性质及全等三角形的性质与判定,熟练掌握等边三角形的性质、含30度直角三角形的性质及全等三角形的性质与判定是解题的关键.9、(1)85︒;(2)①作图见解析;②证明见解析【分析】(1)等边三角形ABC 中60BAC B C ∠=∠=∠=︒,由AD AE =知ADC AEB ∠=∠,ADC B BAD ∠=∠+∠,进而求出AEB ∠的值;(2)①作图见详解;②ADE B BAD ∠=∠+∠ ,AED C EAC ∠=∠+∠,BAD EAC ∠=∠,点E ,F 关于直线AC 对称,EAC FAC ∠=∠,AE AF AD ==,60FAC DAC BAD DAC ∠+∠=∠+∠=︒,ADF 为等边三角形,进而可得到AD DF =.【详解】解:(1)ABC 为等边三角形85ADC BAD B ∴∠=∠+∠=︒AD AE =85AEB ADC ∴∠=∠=︒.(2)①补全图形如图所示,②证明:ABC 为等边三角形60B C BAC ∴∠=∠=∠=︒AD AE =ADE AED ∴∠=∠ADE B BAD ∠=∠+∠ ,AED C EAC ∠=∠+∠BAD EAC ∴∠=∠点E ,F 关于直线AC 对称EAC FAC ∠=∠∴,AE AF =60FAC DAC BAD DAC ∴∠+∠=∠+∠=︒即60DAF=∠︒AD AF =ADF ∴为等边三角形AD AF ∴=.【点睛】本题考察了等边三角形的判定与性质,等腰三角形的性质,轴对称的性质.解题的关键在于角度的转化.10、(1)30°;(2)∠BAD=2∠CDE,理由见解析;(3)∠BAD=2∠CDE.【分析】(1)根据三角形的外角的性质求出∠ADC,结合图形计算即可;(2)设∠BAD=x,根据三角形的外角的性质求出∠ADC,结合图形计算即可;(3)设∠BAD=x,仿照(2)的解法计算.【详解】解:(1)∵∠ADC是△ABD的外角,∴∠ADC=∠BAD+∠B=105°,∠DAE=∠BAC﹣∠BAD=30°,∴∠ADE=∠AED=75°,∴∠CDE=105°﹣75°=30°;(2)∠BAD=2∠CDE,理由如下:设∠BAD=x,∴∠ADC=∠BAD+∠B=45°+x,∠DAE=∠BAC﹣∠BAD=90°﹣x,∴∠ADE=∠AED=902x︒+,∴∠CDE=45°+x﹣902x︒+=12x,∴∠BAD=2∠CDE;(3)设∠BAD=x,∴∠ADC=∠BAD+∠B=∠B+x,∠DAE=∠BAC﹣∠BAD=180°﹣2∠C﹣x,∴∠ADE=∠AED=∠C+12x,∴∠CDE=∠B+x﹣(∠C+12x)=12x,∴∠BAD=2∠CDE.【点睛】本题考查了三角形内角和和外角的性质,解题关键是熟练掌握三角形内角和和外角性质,通过设参数计算,发现角之间的关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三、 轴的结构设计
轴结构设计的任务——在满足强度、刚度和振动稳 定性的基础上,根据轴上零件的定位要求及轴的加 工、装配工艺性要求,合理地确定轴的结构形状和 全部尺寸。
轴结构设计要求: ①轴和轴上零件要有准确、牢固的工作位置 ②轴上零件装拆、调整方便 ③轴应具有良好的制造工艺性等 ④尽量避免应力集中
40Cr,35CrMo等调制处理; 20CrMnTi渗碳淬火。常用 于高速、 重载,要求结构紧凑,耐磨性好的工况下。
③铸铁(球墨铸铁,高强度铸铁) 流动性好,吸振性耐 磨性强,对应力集中敏感性较低,易得到复杂结构。发动 机曲轴。
3. 轴的毛坯
可用轧制圆钢材、锻造、焊接、铸造等方法获得。 对要求不高的轴或较长的轴,毛坯直径小于150mm时,
可用轧制圆钢材; 受力大,生产批量大的重要轴的毛坯可由锻造提供; 对直径特大而件数很少的轴可用焊件毛坯; 生产批量大、外形复杂、尺寸较大的轴,可用铸造毛
坯。
4、轴的失效形式与设计步骤
失效形式——
因疲劳强度不足而产生的疲劳断裂; 因静强度不足而产生的塑性变形或脆性断裂; 超过允许范围的变形和振动等。
2)零件在轴上的周向定位和固定——
定位方式的选择——考虑传递转矩的大小和性质、零 件对中精度的高低、加工难易等因素。
常用周向定位方法——键、花键、成形、销、过盈配 合等,通称轴毂连接。紧定螺钉也可作周向定位,但 仅用于转矩不大的场合。
3、轴结构的工艺性
轴结构的工艺性——是指轴的结构应尽量简单,有良好的 加工和装配工艺性,以利减少劳动量,提高劳动生产率及 减少应力集中,提高轴的疲劳强度。
注意点——
(1) 为减少加工时换刀时间及装夹工件时间,同一根轴上所 有圆角半径、倒角尺寸、退刀槽宽度应尽可能统一;当 轴上有两个以上键槽时,应置于轴的同一条母线上,以 便一次装夹后就能加工。
(2) 轴上的某轴段需磨削时,应留有砂轮的越程槽;需切 制螺纹时,应留有退刀槽。
(3) 为了去掉毛刺,便于装配,轴端应制出45º倒角。
轴向定位和固定—— ⑥ 弹性挡圈
在轴上切出环形槽(手册),将弹性挡圈嵌入槽中,利用 它的侧面压紧被定位零件的端面,图为轴肩与弹性挡圈 联合使用的情况。这种定位方法工艺性好、装拆方便, 但对轴的强度消弱较大,常用于所受轴向力小的轴。
轴向定位和固定—— ⑦ 锁紧挡圈、紧定螺钉
锁紧挡圈用紧定螺钉固定在轴上,装拆方便,但不能承 受大的轴向力。
轴上零件轴向定位与固定的常用方法—— 轴肩和轴环,轴套(套筒) ,圆螺母,圆锥面,轴端挡板, 弹性挡圈,锁紧挡圈、紧定螺钉等
轴向定位和固定—— ① 轴肩和轴环
轴肩与轴环——由定位面和过度圆角组成。
为保证零件端面能靠紧定位面,轴肩(环)圆角半径r必须 小于零件毂孔的圆角半径R或倒角高度C1; 轴肩(环)高度 h应大于C1和R,为了有足够的强度来承受轴向力,通常 取h=(0.07~0.1)d。轴环宽度b≥1.4h。
心轴——只承受弯矩而不承受转矩的轴,如自行 车轮轴。按轴转动与否,又可分为转动心轴和固 定心轴。
传动轴——指只受转矩不受弯矩或受很小弯矩的 轴,如连接汽车发动机输出轴和后桥的轴。
转轴 传动轴
转轴
转动心轴 固定心轴
提升机
1
2
Motor
×
3
4
×
×
1——传动轴:T
2——转轴:T + M
×
3——转轴:T + M
圆螺母定位装拆方便, 通常用细牙螺纹来增 强防松能力和减小对 轴的强度消弱及应力 集中。
轴向定位和固定—— ④ 圆锥面
将轴与零件的配合面加工成圆锥面,可以实现轴向定位。 圆锥面的锥度小时,所需轴向力小,但不易拆卸,通常 取锥度1:30~1:8。
轴向定位和固定—— ⑤ 轴端挡板
当零件位于轴端时,可用轴端挡板与轴肩、轴套、圆锥 面等的组合,使零件双向固定。挡板用螺钉紧固在轴端 并压紧被定位零件的端面。该方法简单可靠、装拆方便, 但需在轴端加工螺纹孔。
(4) 当采用过盈配合连接时, 配合轴段的零件装入端, 常加工成导向锥面。若 还附加键连接,则键槽 的长度应延长到锥面处, 便于轮毂上键槽与键对 中。
(5) 如果需从轴的一端装入两个过盈配合的零件,则轴上 两配合轴段的直径不应相等,否则第一个零件压入后, 会把第二个零件配合的表面拉毛,影响配合。
4、提高轴的强度的措施
4——心轴 :M
二、材料、毛坯及失效形式
1.对轴材料的性能要求 ①具有足够的强度; ②对应力集中敏感性小; ③良好的加工工艺性和经济性。
具体材料见 p265 表14-2
2. 轴的常用材料 轴的常用材料为碳素钢、合金钢、球墨铸铁,高强度铸
铁。 ①碳素钢 价格便宜,对应力集中敏感性小,应用最广。
如45调制。 ②合金钢 机械强度高,热处理性能好,淬火性好。如
作业:
P280
14.1,14.7
第十四章 轴
一、轴的用途及分类 1、功用 1)支承回转零件;2)传递运动和动力
2、轴的分类 按轴线形状分——直轴、曲轴和软轴。 直轴——
曲轴—— 软轴——
按所受载荷性质分——心轴、转轴和传动轴。
转轴——指既受弯矩又受转矩的轴,转轴在各种 机器中最为常见。
1)改进轴的结构以减少应力集中
(1) 轴上相邻轴段的直径不应相差过大,在直径变化处,尽量用圆角 过渡,圆角半径尽可能大。
(2) 轴上与零件毂孔配合的轴段,在配合边缘会产生较大的应力集中。 可以在轴或轮毂上开卸载槽以及加大配合部分的直径等措施进行 改善。
原则:1)轴的结构越简单越合理 2)装配越简单、方便越合理
1、轴的组 成
轴颈
轴头
轴身
轴颈——轴上被支承部分; 轴头——安装轮毂部分; 轴身——连接轴颈和轴头的部分。
2、零件在轴上的定位和固定
1)零件在轴上的轴向定位和固定
应考虑——零件所受轴向力的大小,轴的制造,轴上零件 装拆的难易程度,对轴强度的影响,工作可靠性等因素。
轴肩
轴环 b
R
D h
C1 d
D h
d
r
r
轴向定位和固定—— ② 轴套(套筒)
轴套适用于轴上两个相距较近零件之间的定位,其两个 端面为定位面,应有较高的平行度和垂直度。为使轴上 零件定位可靠,应使轴段长度比零件毂长短2~3mm。
1
23
4
轴向定位和固定—— ③ 圆螺母
可用圆螺母与轴肩、 1 轴环等的组合实现零 件在轴上的双向定位 2 和固定。
