连续模型优化(约束问题)

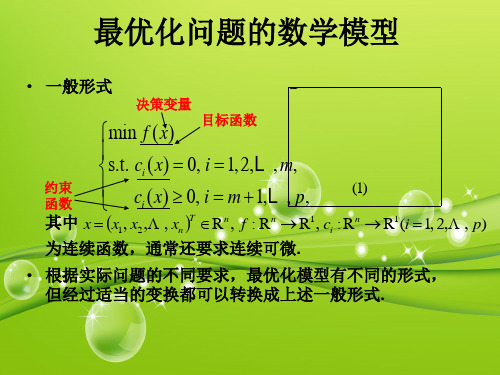
一般形式：
min f ( X ) s.t. AX b
Aeq X beq l X u c(X ) 0 ceq ( X ) 0
❖ 1.求解非线性规划问题的函数fmincon
1.约束中可以有等式约束 2.可以含线性、非线性约束均
输入参数语法：
x = fmincon(fun,x0,A,b) x = fmincon(fun,x0,A,b,Aeq,beq) x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub) x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon, ...)
x1 2x2 2x3 0 x1 2x2 2x3 72
这是2个线性约束，形如 Ax b
这里： A=[-1 -2 -2; 1 2 2 ]; b=[0 72]’;
第三步：提供一个搜索起点，然后调用相 应函数，程序如下：
% 给一个初始搜索点
x0 = [10; 10; 10];
主程序（整体）：
求解方法：主要由于约束条件、目标函数不同而不同
非线性规划的基本解法
惩罚函数法的基本思想：利用原问题的中的约束 函数构造适当的惩罚函数，并和原问题的目标函数 相加，得到带参数的增广目标函数，从而将原问题
转换为一系列无约束非线性规划问题。所以也称序
列无约束极小化技术(Sequential Unconstrained Minimization Technique, SUMT)
*采用黄金分割查找和抛物线插值算法
例2：求解
min f (x) cos(4x 5)
0 x
2
[x,fval]=fminbnd('cos(4*x+5)',0,pi/2) 结果：
x=
1.1062
fval =
-1.0000 表示当x=1.1062时，函数取得最小值-1。
2 fminsearch函数
例子：min f (x) 2(x1 1)2 3(x2 3)2
A b
eq
eq
l X u
注意：约束有线性等式、不等式约束
语法：
x = lsqlin(C,d,A,b) x = lsqlin(C,d,A,b,Aeq,beq) x = lsqlin(C,d,A,b,Aeq,beq,lb,ub) x = lsqlin(C,d,A,b,Aeq,beq,lb,ub,x0) x = lsqlin(C,d,A,b,Aeq,beq,lb,ub,x0,options) [x,resnorm] = lsqlin(...) [x,resnorm,residual] = lsqlin(...) [x,resnorm,residual,exitflag] = lsqlin(...) [x,resnorm,residual,exitflag,output] = lsqlin(...) [x,resnorm,residual,exitflag,output,lambda] = lsqlin(...)
1 fminbnd求单变量函数最小值点 2 fminsearch求多变量函数最小值点 3 fminunc求多变量函数最小值点
1 fminbnd求单变量函数最小值点
x = fminbnd(fun,x1,x2) x = fminbnd(fun,x1,x2,options) x = fminbnd(fun,x1,x2,options,P1,P2,...) [x,fval] = fminbnd(...) [x,fval,exitflag] = fminbnd(...) [x,fval,exitflag,output] = fminbnd(...)
124.3622
最优化问题的解
局部最优解 f(X)
整体最优解
求解无约束最优化
一般形式： min f( X ) 或
max f( X )
标准形式： min f( X )
求解的基本思想 ( 以二元函数为例 )
f (x1 x2 )
连
续
可
微 0
x2
x1
迭代法一般步骤
（1） 选定初始点 X (0)，k=0 （2） 寻找一个合适的方向 P (k)，k=0，1，2，…
lsqnonlin(...)
返回参数说明
resnorm 等于 norm(C*x-d)^2 residual 等于C*x-d
例3：求解x，使得下式最小
10
(2 2k ekx1 ekx2)2
k 1
第一步：编写M文件myfun.m计算向量F
function F = myfun(x) k = 1:10; F = 2 + 2*k-exp(k*x(1))-exp(k*x(2));
❖ 4.非线性最小二乘lsqnonlin
适合模型：
min 1 2
F(X)
2 2
1 2
i
Fi
(
X
)
2
X
s.t. l X u
语法：
x = lsqnonlin(fun,x0) x = lsqnonlin(fun,x0,lb,ub) x = lsqnonlin(fun,x0,lb,ub,options) x = lsqnonlin(fun,x0,options,P1,P2, ... ) [x,resnorm] = lsqnonlin(...) [x,resnorm,residual] = lsqnonlin(...) [x,resnorm,residual,exitflag] = lsqnonlin(...) [x,resnorm,residual,exitflag,output] = lsqnonlin(...) [x,resnorm,residual,exitflag,output,lambda] = lsqnonlin(...) [x,resnorm,residual,exitflag,output,lambda,jacobian] =
fval = 3.1076e-009
exitflag = 1
求解有约束最gi (x) 0(i 1,2,, m)
h j (x) 0( j 1,2,,l)
其中f(x)，gi(x)，hj(x)均是En上的连续函数(i=1,2,…,m; j=1,2,…,l)。
1、编写函数： function f=fun1search(x) %通过fminsearch求极小值的函数 f=2*(x(1)-1)^2+3*(x(2)-3)^2; 2、输入命令求解： [x,fval,exitflag]=fminsearch('fu
n1search',[0 0])
结果：
x= 1.0000 3.0000
例2：求解如下最优化问题.
min f (x) x1x2 x3 s.t 0 x1 2x2 2x3 72
第一步：编写一个M文件返回目标函数f在点 x处的值函数程序
函数myfun.m function f = myfun(x) f = -x(1) * x(2) * x(3);
第二步：为了调用MATLAB函数，必须将模 型中的约束转化为如下形式(<=)。
P (k)为第 k+1 步的搜索方向。
（3） 求出沿 P (k)方向前进的步长 (k )
（4） 得到新的点 X (k+1)， X (k1) X (k) (k) P(k)
检验 X (k+1)是否最优，如果是最优，则迭代结束，
否则 k k 1，转到（2）执行。
Matlab求解无约束非线性最小化
第二步：调用优化函数lsqnonlin
% 给定搜索起点 x0 = [0.3 0.4] ; % 调用求解函数 [x,resnorm] = lsqnonlin('myfun',x0) x=
0.2578 0.2578 resnorm %residual or sum of squares resnorm =
连续模型优化
最优化问题的基本概念 求解无约束最优化 求解有约束最优化
最优化问题的基本概念
许多实际问题都可以归纳为最优化问题, 最优 化模型是数学建模中应用最广泛的模型之一；其 内容包括线性规划、整数线性规划、非线性规划、 动态规划、多目标规划、最优控制等.
最优化问题的一般形式
目标函数
约束条件
可行解域
1、罚函数法
惩罚函数法(SUMT外点法) 障碍函数法(SUMT内点法)
2、近似规划法
Matlab求解有约束非线性最小化
❖ 求解非线性规划问题的函数fmincon ❖ 非负条件下线性最小二乘lsqnonneg ❖ 有约束线性最小二乘lsqlin ❖ 有约束非线性最小二乘lsqnonlin
❖ 1.求解非线性规划问题的函数fmincon
对照约束条件编写myfun1.m
x12 x22 x32 100
x12 10x32 60
x1
x
2 2
x3
80
x13 x22 x3 80
function [c,ceq] = mycon1(x) c(1) = x(1)*x(1)+x(2)*x(2)+x(3)*x(3)-100 c(2) = 60 - x(1)*x(1) + 10*x(3)*x(3) ceq(1) = x(1) + x(2)*x(2) + x(3) - 80 ceq(2) = x(1)^3 + x(2)*x(2) + x(3) - 80
A=[-1 -2 -2; 1 2 2 ]; b=[0 72]’;
% 给一个初始搜索点
x0 = [10; 10; 10]; [x,fval] = fmincon('myfun',x0,A,b)
最后得到如下结果：
x= 24.0000 12.0000 12.0000
fval = -3.4560e+03