经纬度模式调成坐标模式
经纬度转平面坐标

经纬度转平面坐标
1、找到数据为txt格式的经纬度坐标文件,然后打开QGIS主界面;
2、创建矢量图层:打开QGIS,选择Layer-->AddLayer-->AddDelimitedTextLayer菜单;
3、导入文本坐标:弹出创建图层对话框,选择带有坐标的文本文件,选择自定自定义分割符(Customdelimiters),选择空格(Space),在Xfield和Yfield下拉框中选择对应的x、y坐标,然后点击确定;
4、选择坐标系:点击确定之后需要选择坐标系,这里选择WGS84地理坐标系,在Filter搜索框中输入:WGS84选择EPSG:4326的坐标系;
5、另存矢量图层到本地计算机:这时数据就被导入进来了,然后另存数据,选中导入的图层,右键,选择SaveAs;
6、设置导出图层参数:打开另存为对话框,这里导出的格式为ShapeFile。
填写好文件路径和坐标系之后,点击确定就可以导出了,导出后文件会自动加载到QGIS中;
7、打开属性表:右键打开shp图层的属性表;
8、打开字段计算器:打开属性表后开始计算X、Y坐标,点击属性表上面的:字段计算器Calculator;。
关于经纬度坐标转换的方法

关于经纬度坐标转换的方法经纬度是一种地理坐标系统,用来标识地球上其中一点的位置。
经度是指从东经0度到西经180度的范围,纬度是指从南纬0度到北纬90度的范围。
在实际应用中,有时需要进行经纬度坐标转换的操作。
下面将介绍常用的几种经纬度坐标转换的方法。
1.经纬度转换为UTM坐标:UTM坐标是一种常用的地理坐标系统,可以将地球表面分为60个纵向区域,每个区域中有一个横向投影面,将地球表面映射到该投影面上。
将经纬度转换为UTM坐标的方法是先确定所在纵向区域,然后将经纬度转换为该纵向投影面上的坐标。
2.UTM坐标转换为经纬度:将UTM坐标转换为经纬度的方法是先确定所在纵向区域和横向投影面,然后将UTM坐标转换为该投影面上的经纬度。
3.经纬度转换为高斯坐标:高斯坐标是一种常用的地理坐标系统,将地球表面分为带状区域,每个区域中有一个标准纬度和标准经度,将地球表面映射到该区域的平面上。
将经纬度转换为高斯坐标的方法是先确定所在带状区域,然后将经纬度转换为该区域平面上的坐标。
4.高斯坐标转换为经纬度:将高斯坐标转换为经纬度的方法是先确定所在带状区域,然后将高斯坐标转换为该区域平面上的经纬度。
5.经纬度转换为WGS84坐标:WGS84是一种全球地理坐标系统,将地球模型化为一个椭球体,将地球表面映射到该椭球体上。
将经纬度转换为WGS84坐标的方法是先确定椭球体的参数,然后将经纬度转换为该椭球体上的坐标。
6.WGS84坐标转换为经纬度:将WGS84坐标转换为经纬度的方法是先确定椭球体的参数,然后将WGS84坐标转换为该椭球体上的经纬度。
7.经纬度转换为墨卡托坐标:墨卡托坐标是一种平面直角坐标系统,将地球表面映射到一个二维平面上。
将经纬度转换为墨卡托坐标的方法是先确定投影中心点,然后将经纬度转换为该平面上的坐标。
8.墨卡托坐标转换为经纬度:将墨卡托坐标转换为经纬度的方法是先确定投影中心点,然后将墨卡托坐标转换为该平面上的经纬度。
经纬度转换成大地2000坐标 js方法

经纬度转换成大地2000坐标js方法摘要:1.引言2.大地2000坐标介绍3.JS方法实现经纬度转换大地2000坐标4.代码示例及解析5.结论正文:【引言】在地理信息系统(GIS)和相关领域,经纬度坐标与大地2000坐标之间的转换是一项常见任务。
本文将介绍如何使用JavaScript(JS)方法实现这一转换,从而为开发者提供一种实用的解决方案。
【大地2000坐标介绍】大地2000坐标,又称CGCS2000坐标,是我国采用的地理坐标系。
它基于地球椭球体模型,具有高斯克吕格投影和地方投影两种形式。
大地2000坐标系是我国地理信息领域的重要基础,广泛应用于地图制图、导航定位、资源调查等领域。
【JS方法实现经纬度转换大地2000坐标】要实现经纬度坐标到大地2000坐标的转换,可以采用七参数模型、五参数模型等方法。
在JavaScript中,可以通过调用相关库或自行编写函数实现。
以下是一个简单的JS函数示例:```javascriptfunction convertCGCS2000(lat, lng, x, y) {// 七参数模型参数const k = 0.9999;const b = 0.1913;const a = 6378249.1999;// 转换公式const dx = x - lng * Math.cos(lat);const dy = y - lat;const d = Math.sqrt(dx * dx + dy * dy);const z = a * Math.sqrt(1 - k * Math.pow(d, 2));const h = b * Math.tan(lat) * (d * Math.pow(k, 3) / (1 + Math.pow(d, 2)));return [x * k, y * k, z + h];}```【代码示例及解析】上述函数接受经纬度坐标(lat,lng)和大地2000坐标(x,y)作为输入,采用七参数模型进行转换。
经纬度CAD文件如何转换为平面坐标系(CGCS2000-国家2000坐标系)文件
经纬度CAD文件如何转换为平面坐标系(CGCS2000-国家2000坐标系)文件,
附CAD文件转换成kml操作。
1.经纬度CAD文件
如下图中红色标注位置,表示的是经度108.89度,纬度24.96度。
可以看出是一个经纬度文件,不是我们熟悉的坐标文件,好多人就一脸懵逼,特别是新手。
2.转换文件
(1)安装电脑版的奥维地图。
打开如下,点击用户登陆手机端的账户。
(2)在CAD中将经纬度文件转换成DXF文件,因为奥维不能读取DWG。
(3)在奥维中“系统”-“倒入对象”中导入DXF文件。
(4)在弹出的“解析文件”对话框中依次按图进行设置,“CAD坐标”选择“经纬度”,然后“开始解析”,最后点“导入”。
(5)在收藏夹中选择导入的文件,右击,出现对话框中选择“导出”
(6)在导出对话框中,选择导出的格式。
在这里可以选择KML或者DXF格式。
Kml格式是奥维地图的基础格式,经纬度的文件,该格式文件可以直接在奥维里打开,而不需要进行任何设置,区别于DXF格式还需要设置才可以导入奥维。
想要在GPS手簿软件中或者CAD中打开需要选择导出DXF。
(7)选择存放路径
(8)进行到处文件的坐标系设置。
这里注意中央经线根据不同地区对应设置即可,其他不变。
最后点击“确定”后“导出”即可。
(9)成果。
经纬度转直角坐标系误差较小的方法

经纬度转直角坐标系误差较小的方法经纬度是一种用于表示地理位置的坐标系统,而直角坐标系是另一种常用的坐标系统。
在将经纬度转换为直角坐标系时,存在一定的误差。
为了减小这种误差,可以采用以下方法:1. 球面投影方法:球面投影方法通过将地球表面投影到一个平面上,将经纬度坐标转换为直角坐标。
其中,常用的球面投影方法有经纬度度数投影、墨卡托投影等。
这些方法考虑了地球的形状和曲率,可以在一定程度上减小转换误差。
2. 基于椭球体的方法:地球并非完全的球体,而是一个稍微扁平的椭球体。
因此,在转换经纬度为直角坐标时,可以采用基于椭球体的算法。
这些算法引入了椭球体的参数,如长半轴、短半轴等,以更准确地估计转换误差。
3. 采用更精确的坐标转换模型:常用的经纬度转换模型有WGS84和WGK84等。
这些模型基于更精确的测量数据和数学算法,可以提供更准确的经纬度转换结果,从而减小直角坐标系误差。
需要注意的是,虽然可以采用以上方法来减小经纬度转直角坐标系的误差,但完全消除误差是不可能的。
因为经纬度和直角坐标系是两种不同的坐标系统,它们的基本原理和精确度有所差别。
在实际应用中,应根据具体需求选择合适的方法,并对转换结果进行适当的误差估计和修正。
经纬度转直角坐标系误差较小的方法摘要:经纬度转直角坐标系时存在一定误差,而寻找误差较小的方法可以提高转换精度。
本文将介绍两种常用的方法,分别是投影法和四参数法,这两种方法在经纬度转直角坐标系时能够有效降低误差。
正文:经纬度转直角坐标系是在地理信息系统(GIS)、导航、测量等领域中常见的操作。
然而,由于地球的真实形状是椭球体,而不是平面,所以在进行经纬度与直角坐标系之间的转换时往往会引入一定的误差。
为了降低误差,可以采用投影法。
投影法将地球表面的经纬度投影到一个平面上,从而将问题转化为二维平面上的几何计算。
常见的投影方法有墨卡托投影、兰伯托投影和极射投影等。
具体选择哪种投影方法取决于应用需求和研究区域的地理位置。
经纬度转化为xy坐标系公式

经纬度转化为xy坐标系公式地球是一个球体,而我们通常使用的平面坐标系是二维的,因此需要将地球上的经纬度坐标转化为平面坐标系中的xy坐标。
这个转化过程需要用到一些数学公式和地球的基本参数,下面我们来详细介绍一下。
1. 地球的基本参数地球的形状是近似于一个椭球体,因此需要用到椭球体的基本参数来进行坐标转化。
常用的椭球体参数有:a:地球的赤道半径,单位为米。
b:地球的极半径,单位为米。
f:地球扁率,即赤道半径与极半径之差与赤道半径之比。
e:地球的第一偏心率,即椭球体的离心率。
2. 经纬度坐标系经纬度坐标系是地球表面上最常用的坐标系,它是以地球的赤道和子午线为基准线,将地球表面划分为若干个区域,每个区域都有一个唯一的经纬度坐标。
经度是以本初子午线为基准线,从0度到180度东经和从0度到180度西经分别表示东半球和西半球的位置。
纬度是以赤道为基准线,从0度到90度北纬和从0度到90度南纬分别表示北半球和南半球的位置。
3. 经纬度转化为xy坐标系公式将经纬度坐标转化为xy坐标系需要用到以下公式:x = (N + h) * cosφ * cosλy = (N + h) * cosφ * sinλz = (N * (1 - e^2) + h) * sinφ其中,x、y、z分别表示地球上某一点的空间坐标,N表示该点到地球极点的距离,h表示该点的高度,φ表示该点的纬度,λ表示该点的经度。
由于我们需要将地球上的点转化为平面坐标系中的点,因此需要将上述公式进行简化。
假设我们将地球的赤道作为平面坐标系的x轴,将本初子午线作为平面坐标系的y轴,那么可以得到以下公式:x = (R + h) * cosφ * cos(λ - λ0)y = (R + h) * cosφ * sin(λ - λ0)其中,R表示地球的平均半径,λ0表示本初子午线的经度。
4. 代码实现下面是一个简单的Python代码实现,将经纬度坐标转化为xy坐标系:```pythonimport mathdef convert_to_xy(lat, lon, height):a = 6378137.0b = 6356752.3142f = (a - b) / ae = math.sqrt(2 *f - f ** 2)R = a * (1 - e ** 2) / (1 - e ** 2 * math.sin(lat) ** 2) ** 1.5N = a / math.sqrt(1 - e ** 2 * math.sin(lat) ** 2)x = (N + height) * math.cos(lat) * math.cos(lon)y = (N + height) * math.cos(lat) * math.sin(lon)return x, y```5. 总结经纬度坐标系和xy坐标系是地球上最常用的两种坐标系,它们之间的转化需要用到一些数学公式和地球的基本参数。
经纬度转化为xy坐标系

经纬度转化为xy坐标系:
在投影坐标系中,通过格网上的x,y 坐标来标识位置,其原点位于格网中心。
每个位置均具有两个值,这两个值是相对于该中心位置的坐标。
一个指定其水平位置,另一个指定其垂直位置。
这两个值称为x 坐标和y 坐标。
采用此标记法,原点坐标是x = 0 和y = 0。
投影坐标系在二维平面中进行定义与地理坐标系不同,在二维空间范围内,投影坐标系的长度、角度和面积恒定。
投影坐标系始终基于地理坐标系,而后者则是基于球体或旋转椭球体的。
在球面系统中,水平线是等纬度线或纬线,垂直线是等经度线或经线。
经度和纬度值以十进制度为单位或以度、分和秒(DMS) 为单位进行测量。
维度值相对于赤道进行测量,其范围是-90°(南极点)到+90°(北极点)。
经度值相对于本初子午线进行测量。
其范围是-180°(向西行进时)到180°(向东行进时)。
用X 表示经度值并用Y 表示纬度值可能会有帮助。
这样,显示在地理坐标系上定义的数据就如同度是线性测量单位一样。
此方法与普通圆柱投影基本相同。
经纬度与直角坐标转换(MAPGIS转换)

经纬度与直角坐标转换㈠MAPGIS转换⒈实用服务——投影变换——P投影转换——P输入单点投影转换。
⒉原始投影参数设置:坐标系类型——大地坐标或地理坐标;比例尺分母——1;坐标单位:DDDMMSS.SS;椭球面高程、投影面高程、平移X、平移Y均为0。
⒊结果投影参数设置:坐标系类型——投影平面直角投影类型——5:高斯-克吕格[横切椭园柱等角]投影比例尺分母——1坐标单位——米椭球面高程、投影面高程、平移X、平移Y——0投影带类型——根据所给数据源图确定投影带序号——根据投影中心点经度所处的带号确定。
参见下表。
⒋输入格式:如经度119°16′,纬度32°08′,则输入格式为:1191600,320800。
⒌点“投影点”,则结果显示:X=713901.92712,Y=3558951.83797。
㈡利用坐标转换软件打开软件,点击最上部“坐标转换”——换带计算——选择3度或6度带,并在投影参数的中央子午线中填入相应数据(如117)。
选择源坐标类型——大地坐标——度:分:秒;椭球基准——北京54。
输入源坐标格式:如经度119°16′,纬度32°08′,则B=032:08:00,L=119:16:00。
选择目标坐标类型——平面坐标;椭球基准——北京-54坐标系点转换坐标:X=3558951.837925,Y=713901.927116。
3度分带表-----------------------------------------------------------投影区带号中央经度经度范围-----------------------------------------------------------1 3 1.5 -> 4.52 6 4.5 -> 7.53 9 7.5 -> 10.54 12 10.5 -> 13.55 15 13.5 -> 16.57 21 19.5 -> 22.58 24 22.5 -> 25.59 27 25.5 -> 28.510 30 28.5 -> 31.511 33 31.5 -> 34.512 36 34.5 -> 37.513 39 37.5 -> 40.514 42 40.5 -> 43.515 45 43.5 -> 46.516 48 46.5 -> 49.517 51 49.5 -> 52.518 54 52.5 -> 55.519 57 55.5 -> 58.520 60 58.5 -> 61.521 63 61.5 -> 64.522 66 64.5 -> 67.523 69 67.5 -> 70.524 72 70.5 -> 73.525 75 73.5 -> 76.526 78 76.5 -> 79.527 81 79.5 -> 82.528 84 82.5 -> 85.529 87 85.5 -> 88.530 90 88.5 -> 91.531 93 91.5 -> 94.532 96 94.5 -> 97.533 99 97.5 -> 100.534 102 100.5 -> 103.535 105 103.5 -> 106.536 108 106.5 -> 109.537 111 109.5 -> 112.538 114 112.5 -> 115.539 117 115.5 -> 118.540 120 118.5 -> 121.541 123 121.5 -> 124.542 126 124.5 -> 127.543 129 127.5 -> 130.544 132 130.5 -> 133.545 135 133.5 -> 136.546 138 136.5 -> 139.547 141 139.5 -> 142.548 144 142.5 -> 145.549 147 145.5 -> 148.551 153 151.5 -> 154.552 156 154.5 -> 157.553 159 157.5 -> 160.554 162 160.5 -> 163.555 165 163.5 -> 166.556 168 166.5 -> 169.557 171 169.5 -> 172.558 174 172.5 -> 175.559 177 175.5 -> 178.560 180 178.5 -> -178.561 -177 -178.5 -> -175.562 -174 -175.5 -> -172.563 -171 -172.5 -> -169.564 -168 -169.5 -> -166.565 -165 -166.5 -> -163.566 -162 -163.5 -> -160.567 -159 -160.5 -> -157.568 -156 -157.5 -> -154.569 -153 -154.5 -> -151.570 -150 -151.5 -> -148.571 -147 -148.5 -> -145.572 -144 -145.5 -> -142.573 -141 -142.5 -> -139.574 -138 -139.5 -> -136.575 -135 -136.5 -> -133.576 -132 -133.5 -> -130.577 -129 -130.5 -> -127.578 -126 -127.5 -> -124.579 -123 -124.5 -> -121.580 -120 -121.5 -> -118.581 -117 -118.5 -> -115.582 -114 -115.5 -> -112.583 -111 -112.5 -> -109.584 -108 -109.5 -> -106.585 -105 -106.5 -> -103.586 -102 -103.5 -> -100.587 - 99 -100.5 -> - 97.588 - 96 - 97.5 -> - 94.589 - 93 - 94.5 -> - 91.590 - 90 - 91.5 -> - 88.591 - 87 - 88.5 -> - 85.592 - 84 - 85.5 -> - 82.593 - 81 - 82.5 -> - 79.595 - 75 - 76.5 -> - 73.596 - 72 - 73.5 -> - 70.597 - 69 - 70.5 -> - 67.598 - 66 - 67.5 -> - 64.599 - 63 - 64.5 -> - 61.5 100 - 60 - 61.5 -> - 58.5 101 - 57 - 58.5 -> - 55.5 102 - 54 - 55.5 -> - 52.5 103 - 51 - 52.5 -> - 49.5 104 - 48 - 49.5 -> - 46.5 105 - 45 - 46.5 -> - 43.5 106 - 42 - 43.5 -> - 40.5 107 - 39 - 40.5 -> - 37.5 108 - 36 - 37.5 -> - 34.5 109 - 33 - 34.5 -> - 31.5 110 - 30 - 31.5 -> - 28.5 111 - 27 - 28.5 -> - 25.5112 - 24 - 25.5 -> - 22.5 113 - 21 - 22.5 -> - 19.5 114 - 18 - 19.5 -> - 16.5 115 - 15 - 16.5 -> - 13.5 116 - 12 - 13.5 -> - 10.5 117 - 9 - 10.5 -> - 7.5118 - 6 - 7.5 -> - 4.5119 - 3 - 4.5 -> - 1.5120 - 0 - 1.5 -> 1.56度分带表-----------------------------------------------------------投影区代号中央经度经度范围-----------------------------------------------------------1 3 0 -> 62 9 6 -> 123 15 12 -> 184 21 18 -> 245 27 24 -> 306 33 30 -> 367 39 36 -> 428 45 42 -> 489 51 48 -> 5411 63 60 -> 6612 69 66 -> 7213 75 72 -> 7814 81 78 -> 8415 87 84 -> 9016 93 90 -> 9617 99 96 -> 10218 105 102 -> 10819 111 108 -> 11420 117 114 -> 12021 123 120 -> 12622 129 126 -> 13223 135 132 -> 13824 141 138 -> 14425 147 144 -> 15026 153 150 -> 15627 159 156 -> 16228 165 162 -> 16829 171 168 -> 17430 177 174 -> 18031 -177 -180 -> -17432 -171 -174 -> -16833 -165 -168 -> -16234 -159 -162 -> -15635 -153 -156 -> -15036 -147 -150 -> -14437 -141 -144 -> -13838 -135 -138 -> -13239 -129 -132 -> -12640 -123 -126 -> -12041 -117 -120 -> -11442 -111 -114 -> -10843 -105 -108 -> -10244 -99 -102 -> -9645 -93 -96 -> -9046 -87 -90 -> -8447 -81 -84 -> -7848 -75 -78 -> -7249 -69 -72 -> -6650 -63 -66 -> -6051 -57 -60 -> -5452 -51 -54 -> -4853 -45 -48 -> -4255 -33 -36 -> -3056 -27 -30 -> -2457 -21 -24 -> -1858 -15 -18 -> -1259 -9 -12 -> -650 -3 -6 -> 0文件转换(经纬度转直角坐标)1、源文件转化为excel的csv 格式——将文件另存为Csv,保存类型:Csv逗号分隔。
经纬度和平面坐标的相互转换
经纬度与平面坐标得相互转换首先,RTK中测量得坐标,想要再转换成经纬度,很简单,其实不用转。
直接打开所测量得工程,在坐标管理库中有数据导出得功能,可以直接导出来您所测得每一个点得经纬度或者就是把工程文件中得、RTK文件复制出来,用EXCEL表格打开,直接提取经纬度即可。
如果就是别人提供得平面坐标,或者以前测量得原始文件删除了,那就需要通过软件进行转换来获得大地坐标。
GPStool GPS工具箱就是常用得坐标转换软件,已上传到百度网盘。
第一步,打开软件新建作业——起名,保存第二步,设置转换参数源椭球,肯定选择WGS84。
目标椭球,以西安80为例投影参数设置,中心经度,也就就是中央子午线,输入进去,在这里中央子午线得输入格式就是“度、分秒”格式,(举例126度02分03、55秒就输126、020355 注意千万不要输成126、2355 中间得0不能少),其她一般不用。
四参数,校正参数,拟合参数,七参数这四个参数,有哪些,输哪些。
一般都就是四参数+高程拟合参数+校正参数或者七参数+校正参数.这里以校正参数为例,记得使用校正参数一定打勾!转换前坐标设置为大地坐标,格式有多种选择,一般选度或者无格式.度就就是度得格式,举个例子,125度30分,度得格式下,就应该输125、5。
无格式得情况下,就输入125、30或者125、3(末位得0可以不用输)说到这,告诉大家怎么区分“度”与“度、分秒”得区别,当您拿到一些经纬度时,出现43、6579 125、7484这种情况,肯定就就是“度”得格式了,因为度分秒中,分秒不会大于60得.如果所有得经纬度中,小数点后第一位与第三位都小于6,那么基本就可以判断,这就是“度、分秒”得格式。
转换后类型,根据需要,自己选择.经纬度转平面,转换前椭球选择WGS84,类型选择大地坐标,转换后椭球选择80,类型选择平面坐标。
平面转经纬度,转换前椭球选择80,类型选择平面坐标,转换后椭球选择WGS84,类型选择大地坐标。
经纬度转化为xy坐标系公式

经纬度转化为xy坐标系公式经纬度是地球上任何一个点的位置坐标,而我们常用的地图则是平面的xy坐标系。
因此,经纬度与xy坐标系之间的转换就显得尤为重要。
以经纬度转化为xy坐标系公式为标题,本文将介绍经纬度与xy坐标系之间的转换原理与公式。
一、经纬度的基本概念经度是指地球上某个点与本初子午线之间的夹角,通常用东经和西经来表示。
西经表示为负数,东经表示为正数,范围为-180~180度。
纬度是指地球上某个点与赤道之间的夹角,通常用南纬和北纬来表示。
南纬表示为负数,北纬表示为正数,范围为-90~90度。
二、经纬度与xy坐标系的转换原理地球是一个球体,而平面的xy坐标系是二维的,因此需要将地球表面的经纬度转换为平面上的xy坐标系。
在转换时,需要先确定一个基准点,即将地球表面映射到平面上的点,通常选取的是正投影或者高斯投影。
然后,根据经纬度与基准点之间的距离和方向,可以计算出该点在xy坐标系中的坐标。
三、经纬度与xy坐标系的转换公式1. WGS84椭球体下的经纬度转XY坐标系需要将经纬度转换为弧度制,然后根据以下公式计算:X = R * cos(lat) * cos(lon)Y = R * cos(lat) * sin(lon)Z = R * sin(lat)其中,R为地球半径,lat为纬度,lon为经度。
将X和Y坐标平移,使得基准点在原点上,则有:x = X - X0y = Y - Y0其中,X0和Y0为基准点在xy坐标系中的坐标。
2. 高斯投影下的经纬度转XY坐标系高斯投影是一种常用的投影方式,它将地球表面划分成若干个带状区域,每个区域内的地图都可以使用一个平面直角坐标系来表示。
具体转换公式如下:X = N + k0 * E^2 * sin(2 * lat) / 2 + (k5 - k4 + k3 * cos(2 * lat) - k2 * cos(4 * lat) + k1 * cos(6 * lat)) * sin(lon - L0)Y = M + k0 * E^2 * sin(lat) * cos(lat) * (1 + E^2 * cos(lat)^2) / 2 + (k6 - k3 * cos(2 * lat) + k2 * cos(4 * lat) - k1 * cos(6 * lat)) * sin(2 * (lon - L0)) / 2其中,N和M为常数,E为椭球的偏心率,k0~k6为系数,L0为中央经线。
不同经纬度转换坐标方法

不同经纬度转换坐标方法一、经纬度转换为直角坐标系坐标经纬度是地球表面上一个点的位置坐标,而直角坐标系是平面上的坐标系。
为了将经纬度转换为直角坐标系的坐标,可以使用投影算法来实现。
1. 地心经纬度坐标系转换为地心直角坐标系地心经纬度坐标系是以地球中心为原点建立的坐标系,将地球表面上的点投影到地球球面上。
将地心经纬度坐标系转换为地心直角坐标系,可以使用球面转直角坐标变换公式来实现。
2. 大地坐标系转换为地心直角坐标系大地坐标系是以地球表面上某一点为原点建立的坐标系,将地球表面上的点投影到地球球面上。
将大地坐标系转换为地心直角坐标系,可以使用大地坐标系转换为地心经纬度坐标系的公式,再将地心经纬度坐标系转换为地心直角坐标系。
二、直角坐标系转换为经纬度将直角坐标系的坐标转换为经纬度,可以使用反投影算法来实现。
1. 地心直角坐标系转换为地心经纬度坐标系地心直角坐标系是以地球中心为原点建立的坐标系,将地球表面上的点投影到地球球面上。
将地心直角坐标系转换为地心经纬度坐标系,可以使用直角坐标转球面坐标变换公式来实现。
2. 地心直角坐标系转换为大地坐标系地心直角坐标系转换为大地坐标系的方法与地心经纬度坐标系转换为大地坐标系类似,只是在转换过程中需要考虑椭球参数。
三、经纬度转换为平面坐标系坐标在地图制图和测量等应用中,经常需要将经纬度坐标转换为平面坐标系的坐标。
常用的转换方法有以下几种:1. 经纬度转换为UTM坐标UTM坐标是一种平面坐标系,适用于大范围的地图测绘。
将经纬度转换为UTM坐标,可以使用UTM投影算法来实现。
2. 经纬度转换为高斯-克吕格坐标高斯-克吕格坐标是一种平面坐标系,适用于小范围的地图测绘。
将经纬度转换为高斯-克吕格坐标,可以使用高斯投影算法来实现。
四、平面坐标系坐标转换为经纬度将平面坐标系的坐标转换为经纬度,可以使用反投影算法来实现。
1. UTM坐标转换为经纬度将UTM坐标转换为经纬度,可以使用UTM反投影算法来实现。
经纬度坐标系转CGCS2000坐标系步骤
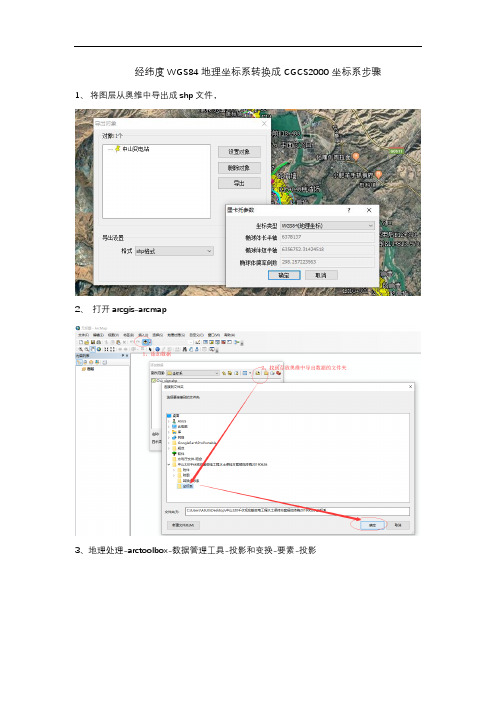
经纬度WGS84地理坐标系转换成CGCS2000坐标系步骤1、将图层从奥维中导出成shp文件,
2、打开arcgis-arcmap
3、地理处理-arctoolbox-数据管理工具-投影和变换-要素-投影
4、WGS84坐标转换为地理坐标系-world-ITRF2000
5、打开ArcCatalog,找到上一步中已经成ITRF2000坐标系的shp文件,单击右键-属性,将图层坐标重新定义成GCGS2000地理坐标系
6、重新打开arcmap,重新打开已经重新定义坐标系的shp文件,按照地理处理-arctoolbox-数据管理工具-投影和变换-要素-投影
7、关于带号计算方法
如果不用带带号的,采用所在区域中央经度,
均为3度带中央经度线
如果前面加带号,采用6度带或三度带带号,
均为三度带带号
8、计算
上一步将GCGS2000地理坐标系转换为GCGS2000投影坐标系后,打开上一步转换成投影坐标系后的shp文件,单击图层,右键属性,常规里,将十进制单位改成米。
再右键单击shp图层,打开属性表,添加字段,添加x,y坐标字段
这里需要注意一个事项,前面我们在选带号是,有带带号,也有没带带号,如果带带号,
那么计算出来的y(对应经度)是8位,如果不带带号,对应的y(对应经度)是6位;
x(对应纬度)是7位,不变。
经纬度坐标系转CGCS2000坐标系步骤
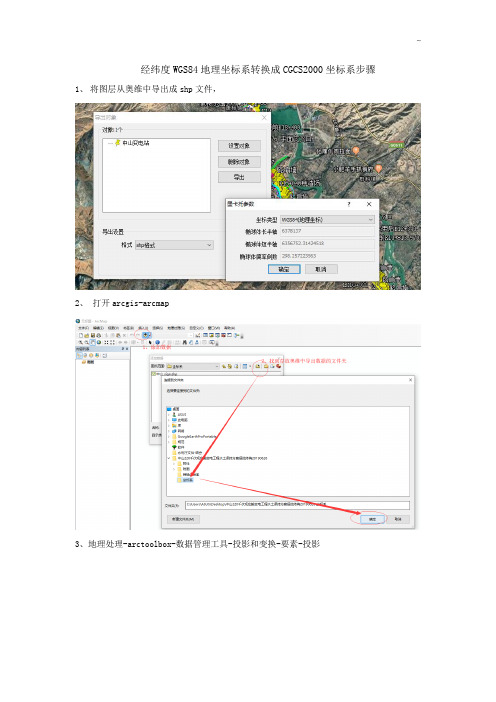
经纬度WGS84地理坐标系转换成CGCS2000坐标系步骤1、将图层从奥维中导出成shp文件,
2、打开arcgis-arcmap
3、地理处理-arctoolbox-数据管理工具-投影和变换-要素-投影
4、WGS84坐标转换为地理坐标系-world-ITRF2000
5、打开ArcCatalog,找到上一步中已经成ITRF2000坐标系的shp文件,单击右键-属性,将图层坐标重新定义成GCGS2000地理坐标系
6、重新打开arcmap,重新打开已经重新定义坐标系的shp文件,按照地理处理-arctoolbox-数据管理工具-投影和变换-要素-投影
7、关于带号计算方法
如果不用带带号的,采用所在区域中央经度,
均为3度带中央经度线如果前面加带号,采用6度带或三度带带号,
均为三度带带号
8、计算
上一步将GCGS2000地理坐标系转换为GCGS2000投影坐标系后,打开上一步转换成投影坐标系后的shp文件,单击图层,右键属性,常规里,将十进制单位改成米。
再右键单击shp图层,打开属性表,添加字段,添加x,y坐标字段
这里需要注意一个事项,前面我们在选带号是,有带带号,也有没带带号,如果带带号,那么计算出来的y(对应经度)是8位,如果不带带号,对应的y(对应经度)是6位;
x(对应纬度)是7位,不变。
经纬度转换坐标系

经纬度转换坐标系从经纬度转换成坐标系的角度讲述,可以从以下几个方面展开:一、引言经纬度是一种用于地理定位的坐标系统,用于描述地球上任意一点的位置。
然而,经纬度并不是常用的坐标系,因此在实际应用中,我们常常需要将经纬度转换成其他常见的坐标系,以方便地理信息的处理和分析。
本文将以人类的视角,详细介绍经纬度转换成坐标系的过程和方法。
二、经纬度的定义和特点经度是指地球上东西方向上的位置,以本初子午线为基准,向东为正值,向西为负值。
纬度是指地球上南北方向上的位置,以赤道为基准,向北为正值,向南为负值。
经纬度的定义使得我们可以准确地定位地球上的任意一点。
三、常见的坐标系1. 地球坐标系:地球坐标系是一种以地球为基准的三维坐标系,常用于地理信息系统(GIS)中。
地球坐标系使用经度、纬度和高程来描述地球上的点的位置。
2. 平面直角坐标系:平面直角坐标系是一种二维坐标系,常用于地图绘制和测量。
平面直角坐标系使用横坐标和纵坐标来描述地图上的点的位置。
3. 投影坐标系:投影坐标系是一种将地球表面上的点投影到平面上的坐标系,常用于地图制作和空间分析。
不同的地图投影方法会产生不同的投影坐标系。
四、经纬度转换成地球坐标系将经纬度转换成地球坐标系的方法有多种,其中最常用的是大地测量学方法。
大地测量学方法基于椭球体模型,通过数学计算,将经纬度转换成地球坐标系中的三维坐标。
五、经纬度转换成平面直角坐标系将经纬度转换成平面直角坐标系的方法也有多种,常用的方法有UTM投影法和高斯投影法。
这些方法通过将地球表面划分成多个投影带,将经纬度转换成平面直角坐标系中的横坐标和纵坐标。
六、经纬度转换成投影坐标系将经纬度转换成投影坐标系的方法也多种多样,具体的方法取决于使用的地图投影方法。
常见的地图投影方法有等经纬度投影法、墨卡托投影法、兰伯特投影法等。
七、总结经纬度是一种用于地理定位的坐标系统,但在实际应用中,我们常常需要将经纬度转换成其他常见的坐标系。
经纬度转换成平面坐标如何实现经度纬度到平面坐标的相互转换

经纬度转换成平面坐标如何实现经度纬度到平面坐标的相互转换如何实现经度纬度到平面坐标的相互转换现在好多人在使用ArcObject的时候都可能需要作经纬度和平面坐标的相互转换。
由于经纬度是球面坐标,平面坐标是X-Y的笛卡尔坐标系统,所以这是一个看起来比较难的问题。
好多人一上来就搬出地图学、地图投影学或者测绘学中的投影公式(如高斯投影或墨卡托投影),又是基准坐标又是角度的搞的人头都大了。
实际上要想实现这个功能非常easy。
ARC Engine中的IPoint就可以进行投影和反投影运算了。
投影过程(C#):/// flatref 投影的坐标系统,这里的54013是世界投影,世界投影所有经纬度都可以转换为平面坐标,但是由于投影面积大失真也会比较大(相当于把整个地球劈成一片片的,然后拉伸最后贴到平面上,失真当然大了)。
当然也可以选择精度更高的平面如:esriSRProjCS_Beijing1954GK_23N 对应数值21483 仅仅把北京附近的地球平面拉伸铺在平面上,由于投影面积变小,所以投影经度提高。
但是由于面积变小,所以有些经度纬度不能转换,比如所美国的精度纬度用北京投影就投不了。
flatref = pfactory.CreateProjectedCoordinateSystem(54013);//没什么说的,标准大地经纬度,可以将X-Y逆投影为经度和纬度earthref = pfactory.CreateGeographicCoordinateSystem((int)esriSRGe oCST ype.esriSRGeoCS_NAD1983);/// 将经纬度点转换为平面坐标。
private IPoint GetProject(double x, double y) {IPoint pt = new PointClass();pt.PutCoords(x, y);IGeometry geo = (IGeometry)pt;geo.SpatialReference = earthref;geo.Project(flatref);return pt;}/// 将平面坐标转换为经纬度。
经纬度CAD文件如何转换为平面坐标系(CGCS2000-国家2000坐标系)文件
经纬度CAD文件如何转换为平面坐标系(CGCS2000-国家2000坐标系)文件,
附CAD文件转换成kml操作。
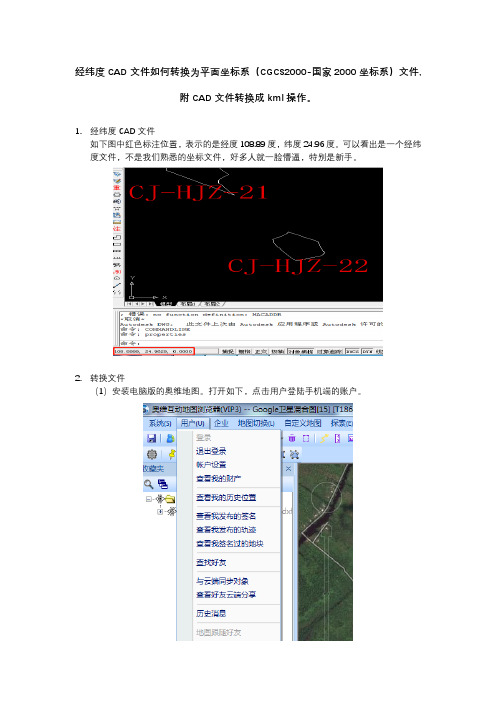
1.经纬度CAD文件
如下图中红色标注位置,表示的是经度108.89度,纬度24.96度。
可以看出是一个经纬度文件,不是我们熟悉的坐标文件,好多人就一脸懵逼,特别是新手。
2.转换文件
(1)安装电脑版的奥维地图。
打开如下,点击用户登陆手机端的账户。
(2)在CAD中将经纬度文件转换成DXF文件,因为奥维不能读取DWG。
(3)在奥维中“系统”-“倒入对象”中导入DXF文件。
(4)在弹出的“解析文件”对话框中依次按图进行设置,“CAD坐标”选择“经纬度”,然后“开始解析”,最后点“导入”。
(5)在收藏夹中选择导入的文件,右击,出现对话框中选择“导出”
(6)在导出对话框中,选择导出的格式。
在这里可以选择KML或者DXF格式。
Kml格式是奥维地图的基础格式,经纬度的文件,该格式文件可以直接在奥维里打开,而不需要进行任何设置,区别于DXF格式还需要设置才可以导入奥维。
想要在GPS手簿软件中或者CAD中打开需要选择导出DXF。
(7)选择存放路径
(8)进行到处文件的坐标系设置。
这里注意中央经线根据不同地区对应设置即可,其他不变。
最后点击“确定”后“导出”即可。
(9)成果。
经纬度转换为平面坐标的方法

经纬度转换为平面坐标的方法在地理信息系统(GIS )中,经纬度是一种常用的地理坐标系统,用于描述地球上的位置。
然而,在一些应用场景中,我们需要将经纬度转换为平面坐标,以便进行距离计算、地图绘制等操作。
本文将介绍几种常用的经纬度转平面坐标的方法,包括投影法和三角测量法。
1. 投影法投影法是将地球表面上的经纬度坐标映射到平面坐标系中的一种方法。
常用的投影方法有墨卡托投影、高斯投影等。
这些投影方法通过一定的数学模型将地球的表面投影到一个平面上,从而将经纬度坐标转换为平面坐标。
1.1 墨卡托投影墨卡托投影是一种等角圆柱投影,将地球表面划分为无数个等距的正方形网格。
在墨卡托投影中,经度和纬度的单位都是度,投影后的平面坐标单位为米。
墨卡托投影的转换公式如下:x =R ⋅θy =R ⋅ln (tan (π4+ϕ2)) 其中,x 和 y 分别表示平面坐标系中的横坐标和纵坐标,R 是地球的平均半径,θ 是经度,ϕ 是纬度。
1.2 高斯投影高斯投影是一种等角圆锥投影,将地球表面划分为无数个等距的椭圆形网格。
在高斯投影中,经度和纬度的单位都是度,投影后的平面坐标单位为米。
高斯投影的转换公式较为复杂,需要根据具体的高斯投影带进行计算。
一般来说,高斯投影的转换可以分为以下几个步骤:1.根据所在地区选择合适的高斯投影带。
2.根据高斯投影带的参数,计算投影中央经线的经度偏移量。
3.计算纬度的带内偏移量。
4. 根据偏移量和经度、纬度的差值,计算平面坐标。
2. 三角测量法三角测量法是通过测量地球上两个点之间的距离和方位角,然后利用三角函数计算出两点之间的平面坐标。
2.1 大地测量学大地测量学是三角测量法的一种应用,用于测量地球上两个点之间的距离和方位角。
大地测量学考虑了地球的椭球形状和重力变化等因素,可以提供更加精确的测量结果。
大地测量学的转换公式较为复杂,需要考虑椭球参数、大地方位角、大地线弧长等因素。
一般来说,大地测量学的转换可以分为以下几个步骤:1.根据椭球参数计算经纬度的弧度值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如何将GARMIN手持GPS的经纬度模式调成坐标模式
方法如下:
1. 进入"主菜单页面"的"设置"子页面中,按动方向键选择“单位”按输入键进入坐标设置的页面,将"位置格式"的选项改为" User UTM Grid "(自定义坐标格式)。
2. 在出现的参数输入页面中输入相关的参数,包括中央经线,投影比例(该数值为1),东西偏差(该数值为500000),南北偏差(该数值为0)。
3. 按下屏幕上的"存储"按钮后,再将"地图基准"(有的机器称之为"坐标系统")的选项改为"User"(自定义坐标系统)。
4. 在出现的参数输入页面中输入相关参数,包括DX,DY,DZ,DA和DF。
其中DA的数值为-108,DF的数值为0.0000005。
按下屏幕上的"存储"按钮后,机器显示的位置将用北京54坐标来表示了。
如果是80坐标,则DA=-3,DF=0。
5. DX,DY,DZ三个参数因地区而异,具体如何求解可以让首先与本地测绘部门去咨询,如果不给的话,可以通过如下方法来求解:
首先知道一个点的已知BJ54坐标(这个他们肯定都有,如果要做工作的话),然后用手持机测此点的坐标(WGS84坐标),通过坐标转换程序,即可求出DX,DY,DZ。
需要注意的是,此程序中的y为6位数,也就是要将Bj54坐标中的前两位(带数)去掉。
如果不知道BJ54坐标的高程,可以输入与WGS84坐标相同的即可。
如果有地形图可以再地形图上面找到一个点(地形图的四角点最好),在选点处查看设置成WGS84坐标的数值和该点的实际(地形图上的数值)进行比较,对数值进行校核,计算出差值,也就是DX、DY、DZ点的参数,就调到准确了。
通过上述设置后,即可将坐标系进行转换,此时手持机中显示的坐标上行为y,下行为x坐标。
知识链接
在大地起始子午面内与 Z轴垂直指向经度 0方向;Y轴与 Z、X轴成右手坐标系;
(3)椭球参数采用IUG 1975年大会推荐的参数,因而可得西安80椭球两个最常用的几何参数为:
长半轴a=6378140±5(m)
短半轴b=6356755.2882(m)
扁率α=1/298.257
第一偏心率平方 =0.00669438499959 第二偏心率平方
=0.00673950181947
椭球定位时按我国范围内高程异常值平方和最小为原则求解参数。
(4)多点定位;
(5)大地高程以1956年青岛验潮站求出的黄海平均水面为基准。
北京54坐标系(BJZ54)
北京54坐标系为参心大地坐标系,大地上的一点可用经度L54、纬度M54和大地高H54定位,它是以克拉索夫斯基椭球为基础,经局部平差后产生的坐标系,其坐标详细定义可参见参考文献[朱华统1990]。
历史
1954年北京坐标系的历史:
新中国成立以后,我国大地测量进入了全面发展时期,在全国范围内开展了正规的,全面的大地测量和测图工作,迫切需要建立一个参心大地坐标系。
由于当时的“一边倒”政治趋向,故我国采用了前苏联的克拉索夫斯基椭球参数,并与前苏联1942年坐标系进行联测,通过计算建立了我国大地坐标系,定名为1954年北京坐标系。
因此,1954年北京坐标系可以认为是前苏联1942年坐标系的延伸。
它的原点不在北京而是在前苏联的普尔科沃。
它是将我国一等锁与原苏联远东一等锁相连接,然后以连接处呼玛、吉拉宁、东宁基线网扩大边端点的原苏联1942年普尔科沃坐标系的坐标为起算数据,平差我国东北及东部区一等锁,这样传算过来的坐标系就定名为1954年北京坐标系。
因此,P54可归结为:
a.属参心大地坐标系;
b.采用克拉索夫斯基椭球的两个几何参数;
c.大地原点在原苏联的普尔科沃;
d.采用多点定位法进行椭球定位;
e.高程基准为1956年青岛验潮站求出的黄海平均海水面;
f.高程异常以原苏联1955年大地水准面重新平差结果为起算数据。
按我国天文水准路线推算而得。
坐标参数
椭球坐标参数:长半轴a=6378245m;短半轴=6356863.0188m;扁率α=1/298.3。
缺点
自P54建立以来,在该坐标系内进行了许多地区的局部平差,其成果得到了广泛的应用。
但是随着测绘新理论、新技术的不断发展,人们发现该坐标系存在如下缺点:
1、椭球参数有较大误差。
克拉索夫斯基椭球差数与现代精确的椭球参数相比,长半轴约大109m。
2、参考椭球面与我国大地水准面存在着自西向东明显的系统性的倾斜,在东部地区大地水准面差距最大达+60m。
这使得大比例尺地图反映地面的精度受到影响,同时也对观测量元素的归算提出了严格的要求。
3、几何大地测量和物理大地测量应用的参考面不统一。
我国在处理重力数据时采用赫尔默特1900~1909年正常重力公式,与这个公式相应的赫尔默特扁球不是旋转椭球,它与克拉索夫斯基椭球是不一致的,这给实际工作带来了麻烦。
4、定向不明确。
椭球短半轴的指向既不是国际普遍采用的国际协议(原点)CIO (Conventional International Origin),也不是我国地极原点JYD1968.0;起始大地子午面也不是国际时间局BIH(Bureau International de I Heure)所定义的格林尼治平均天文台子午面,从而给坐标换算带来一些不便和误差。
为此,我国在1978年在西安召开了“全国天文大地网整体平差会议”,提出了建立属于我国自己的大地坐标系,即后来的1980西安坐标系。
但时至今日,北京54坐标系仍然是在我国使用最为广泛的坐标系。
