2017-2018学年山西省实验中学高一下学期第一次月考数学试题 (1)
2023-2024学年山西省实验中学高一上学期第一次月考化学试题

2023-2024学年山西省实验中学高一上学期第一次月考化学试题1.下列操作或现象与分散质粒子直径无关的是A.熬药后箅渣B.防雾霾戴口罩C.制作玫瑰精油D.森林中的丁达尔2.下列关于纯净物、混合物、电解质、非电解质的正确组合为()3.下列说法正确的是A.在氧化还原反应中,钠原子失去1个电子,铝原子失去3个电子,故钠的还原性小于铝B.阳离子只有氧化性,阴离子只有还原性C.根据树状分类法分析,MgSiO 3属于镁盐、硅酸盐D.《石灰吟》“千锤万凿出深山,烈火焚烧若等闲”,诗文中隐含化学变化且不属于氧化还原反应4.磁流体是电子材料的新秀,它既具有固体的磁性,又具有液体的流动性。
制备时将含等物质的量的硫酸亚铁和硫酸铁的溶液混合,再滴入稍过量的氢氧化钠溶液,随后加入油酸钠溶液,即可生成黑色的、分散质粒子直径在36~55nm之间的磁流体。
下列说法中正确的是()A.该磁流体是一种纯净物B.该磁流体比较稳定C.该磁流体为悬浊液D.该磁流体不能产生丁达尔效应5.将氯化钠溶液通电后灯泡发亮,下列示意图能解释该现象的是A.B.C.D.6.图中“—”表示相连的物质间在一定条件下可以反应,“→”表示甲在一定条件下可以转化为戊,下列四组选项中,符合图示要求的是甲乙丙丁戊7.宏观辨识与微观探析是化学学科核心素养之一。
下列物质性质实验对应的反应方程式书写正确的是A.将稀硫酸滴在铜片上:Cu+2H + =Cu 2+ +H 2↑B.碳酸氢钠溶液中滴加氢氧化钠:HCO +OH - =CO 2↑+H 2 OC.铁片浸入氯化铁溶液中:Fe+Fe 3+ =2Fe 2+D.食醋滴在石灰石上:CaCO 3 +2CH 3 COOH=Ca 2+ +CH 3 COO - +CO 2↑+H 2 O8.下列各组离子在指定溶液中一定能大量共存的是A.能使紫色石蕊溶液变蓝的溶液:K +、Al 3+、Cl -、NOB.无色溶液:K +、H +、SO 、MnOC.含大量SO 的澄清溶液:Mg 2+、Cu 2+、Cl -、NOD.强酸溶液:Na +、Mg 2+、Cl -、CH 3 COO -9. X、Y、Z各代表一种物质,若X+Y=Z+H2O,则X和Y的反应不可能是A.盐和盐的反应B.酸与碱的反应C.碱性氧化物和酸性氧化物反应D.酸性氧化物和碱的反应10.下列各组两种物质在溶液中的反应,可用同一离子方程式表示的是A.Cu(OH) 2和盐酸;Cu(OH) 2和CH 3 COOHB.BaCl 2和Na 2 SO 4;Ba(OH) 2和CuSO 4C.NaHCO 3和NaHSO 4;Na 2 CO 3和NaHSO 4D.NaHCO 3 (过量)和Ca(OH) 2;Ca(HCO 3 ) 2和NaOH(过量)11.下列是实验室常见的气体制取、干燥和收集装置.若用过氧化氢和催化剂二氧化锰制取干燥的氧气,则合理的装置组合为A.B.C.D.12.下列化学方程式中,表示电子转移的方向和数目都正确的是A.B.D. CuSO 4 +SO 2 C. =2NaOH+H 2↑↑+2H 2 O13.氯酸钾与浓盐酸发生如下反应:KClO3+6HCl(浓)=KCl+3Cl2↑+3H2O。
山西省实验中学高一英语下学期第一次月考试题

山西省实验中学2020-2021学年高一英语下学期第一次月考试题考试时间: 90分钟。
试卷满分:100分。
第一部分阅读理解(共两节,满分40分)第一节 (共15小题;每小题2分,满分30分)阅读下列短文,从每题所给的A、B、C和D四个选项中,选出最佳选项。
AThere are dozens of movie recommendation engines on the Web. They're all different, but some are definitely better than others.Rotten TomatoesInstead of telling Rotten Tomatoes which films you like, you can tell it what kind of films you enjoy, which actors you want to see, and other standards to help it find the best movie for you. There's a lot of variability in the quality of Rotten Tomatoes recommendations but it's also a nice way to find the right film for any mood.NetflixNetflix asks you to rate (划分等级) movies to determine which films you'll want to see next. And although it does make it easy to rate movies and it does return huge lists, the ideas it gives you aren't all that strong. It's easy to use, but it's not the best way to get movie recommendations.JinniWhether you want to search for films based on your mood, time available, or reviews, the site has it all. But Jinni's most amazing feature is its semantic (语义的) search. You can enter a term like “films that show Chris Farley yelling” and the site will return films that match your question. Go to use Jinni. You won't regret it!CritickerInstead of just allowing you to rank films, Criticker compares your ratings to those of other users and see how closely your tastes match those of other users. Once the service finds matches, you can view these users' lists and see which movies they like.1.Which one does the author recommend most?A.Rotten Tomatoes. B.Netflix.C.Jinni. D.Criticker.2.What makes Criticker special?A.Comparing users' ratings.B.Ranking your favourite films.C.Offering different standards.D.Finding films based on mood.3.What is the purpose of the text?A.To recommend the best online movies.B.To show how to use movie search engines.C.To introduce several movie search engines.D.To explain how to find the best online moviesB“If y ou are cold, it will warm you; if you are too heated, it will cool you; if you are depressed, it will cheer you; if you are exhausted, it will calm you.” 1)The poem best identifies the passion for tea in Britain. 4)Outside of the United Kingdom, many people refer to afternoon tea as “high tea”. Afternoon tea, also known as low tea, is what most people think of when they hear “high tea”. It involves things like manners, lace (蕾丝) and light meals such as cookies and finger sandwiches. It is typically served in the midafternoon and it wastraditionally served on low tables, hence its two names.A fternoon tea was started in the mid1800s by the Duchess of Bedford. Around that time,2)kerosene (煤油) lamps were introduced into wealthier homes and eating a late dinner (around 8 or 9 p.m.) became fashionable. This increasingly late dinner was one of the only two meals each day, and the other was a midmorning one. The story goes that the Duchess found herself with a “sinking feeling”. This came from hunger during the long wait between meals. She decided to invite friends over for various snacks and tea. The idea of an afternoon tea gathering spread across high society and 3)became a favorite pastime of females for leisure. Later, it spread to other social groups.However, the British working population did not have afternoon tea. They had a meal about midday, and a meal after work, between five and seven o'clock. This meal was called “high tea” or just “tea”. Traditionally eaten early evening, high tea was a substantial(内容充实的)meal that combined delicious sweet food, such as cookies, cakes or tea bread, with heavy food, such as cheese on toast, cold meats and poached eggs on toast. This meal is now often replaced with a supper due to people eating their main meal in the evening rather than at midday. 4.What is the author's purpose of using a poem at the beginning of the passage?A.To introduce a topic.B.To present a puzzle.C.To describe the phenomenon.D.To clarify his writing purpose.5.What led to the appearance of afternoon tea?A.Kerosene lamps were used at home.B.Upper class had more free time.C.Drinking tea makes people feel good.D.Duchess of Bedford was influential in social circle.6.What was the most important feature of afternoon tea in the mid1800s?A.Simple food and tea.B.A ladies' social occasion.C.Being served on low tables.D.Serving time.7.What is the best title for the text?A.A Good TraditionB.Ways of Low TeaC.Traditional Afternoon TeaD.High Tea and Low TeaCSports can help you keep fit and get in touch with nature. However, whether you are on the mountains, in the waves, or on the grassland, you should be aware that your choice of sport might have great influence on the environment.Some sports are resource-hungry. Golf, as you may know, eats up not only large areas of countryside, but also tons of water. Besides, all sorts of chemicals and huge amounts of energy are used to keep its courses(球场)in good condition. This causes major environmental effects. For example, in the dry regions of Portugal and Spain, golf is often responsible for serious water shortage in some local areas.There are many environment-friendly sports. Power walking is one of them that you could take up today. You don't need any special equipment except a good pair of shoes, and you don't have to worry about resources and your purse. Simple and free, power walking can also keep you fit. If you walk regularly, it will be good for your heart and bones. Experts say that 20 minutes of power walking daily can make you feel less anxious, sleep well and have better weight control. Whatever sport you take up, you can make it greener by using environment-friendly equipment and buying products made from recycled materials. But the final goal should be “green gyms”.They are better replacements(代替物)for traditional health clubs and modern sports centers. Members of green gyms play sports outdoors, in the countryside or other open spaces. There is no special requirement for you to start your membership. And best of all, it's free.8. Which of the following is the author most probably in favor of?A. Playing basketball in a gym.B. Motor racing in the desert.C. Cycling around a lake.D. Swimming in a sports center.9. What do we know about golf from the passage?A. It is popular in Portugal and Spain.B. It needs water and electricity to keep its courses green.C. It pollutes the earth with chemicals and wastes.D. It causes water shortages around the world.10. The author uses power walking as an example mainly because _______.A. it uses fewer resourcesB. it improves our healthC. it is an outdoor sportD. it is recommended by experts11. The author writes the passage to _______.A. show us the function of major sportsB. encourage us to go in for green sportsC. discuss the major influence of popular sportsD. introduce different types of environment-friendly sportsDInside Out is one of my favorite Disney movies. The story is about a young girl named Riley who moves from Minnesota to San Francisco with her family and how she deals with her emotions through the move. These five emotions in Riley's brain are Joy, Fear, Anger, Disgust (厌恶) and Sadness. These emotions play a very important role in her life. I can relate because I am an 11-year-old girl and I am very in touch with my emotions and pre-teen feelings.The film is extremely beautiful and you couldn't ask for better direction from Pete Doctor. The use of the right colors for the characters is great. For example, Joy is yellow, Sadness is blue, Disgust is green, Fear is purple and Anger of course is red. Sadness plays a main role in the story and it makes me wonder why we are told not to be sad. I think it's important to be sad when the time comes. The end of the movie pretty much got me and the whole audience (families, couples and even elderly people) in tears and I cried very hard.I recommend this movie for anyone from 8 to 18 because it has enough joy in it for younger kids to like it even though it does have some sad moments. I believe that adults will like it too. And I give it 4 out of 5 stars because it connects to an older audience even though it is designed for a younger audience. I think younger children can see this, but a parent would have to explain some things to them after the movie.12. The author feels connected with the movie because she and the character Riley ______.A. enjoy the same movieB. have the same feelingsC. have the same move experienceD. have a similar family background13. What does the author think of Pete Doctor's job?A. Bad.B. Just so-so.C. Wonderful.D. Disappointing.14. After seeing the movie, the author has a new understanding of ______.A. fearB. sadnessC. angerD. joy15. In the author's eyes, the movie ______.A. won't attract people over 18B. is really unsuitable for childrenC. will be popular among kids and adultsD. can easily be understood by younger kids第二节(共5小题;每小题2分,满分10分)根据短文内容,从短文后的选项中选出能填入空白处的最佳选项,选项中有两项为多余选项。
山西省实验中学2018-2019学年高一(上)期中数学试题(解析版)

2018-2019学年山西省实验中学高一(上)期中数学试卷一、选择题(本大题共10小题,共40.0分)1.已知元素a∈{0,1,2,3},且a∉{1,2,3},则a的值为()A. 0B. 1C. 2D. 3【答案】A【解析】【分析】由题意,根据集合中元素与集合的关系,即可求解,得到答案.【详解】由题意,元素a∈{0,1,2,3},且a∉{1,2,3},∴a的值为0.故选:A.【点睛】本题主要考查了集合中元素与集合的关系的应用,其中解答中牢记集合的元素与集合的关系,合理应用是解答本题的关键,着重考查了推理与论证能力,属于基础题.2.在同一坐标系中,函数y=3x与y=3-x的图象关于()A. 直线对称B. x轴对称C. 直线对称D. y轴对称【答案】D【解析】【分析】由题意,函数与,根据指数函数的图象与性质,即可求解.【详解】由题意,函数与的纵坐标相等时,横坐标相反,∴在同一坐标系中,函数与的图象关于y轴对称,故选:D.【点睛】本题主要考查了指数函数的图象与性质的应用,其中解答中熟记指数函数的运算,以及指数函数的图象与性质是解答的关键,着重考查了分析问题和解答问题的能力,属于基础题.3.设偶函数的定义域为R,当时,是增函数,则的大小关系是()A. >>B. >>C. <<D. <<【答案】A【解析】因为是偶函数,则,由于在单调递增,则,即,故选A。
4.设函数,则的表达式是()A. B. C. D.【答案】B【解析】试题分析:考点:函数求解析式5.下列对应是集合A到集合B上的映射的个数是()(1)A=R,B=N*,对应关系f:对集合A中的元素取绝对值,与B中的元素相对应;(2)A={1,-1,2,-2},B={1,4},对应关系f:f:x→y=x2,x∈A,y∈B;(3)A={三角形},B={x|x>0},对应关系f:对集合A中的三角形求面积,与集合B中的元素对应A. 0B. 1C. 2D. 3【答案】C【解析】【分析】由题意,根据集合A到集合B的映射的概念,逐一判定,即可得到答案.【详解】由题意,对于(1):A中元素0取绝对值后还是0,B中元素全部是正整数,没有对应元素,故不是A到B 上的映射;对于(2):A中四个元素分别平方后所得值,都有B中元素与之对应,故是A到B上的映射;对于(3):A中每个三角形的面积,都有B中的一个正数与之对应,故是A到B上的映射,故选:C.【点睛】本题主要考查了映射的基本概念,其中解答中熟记映射的概念,根据映射的概念合理判定是解答的关键,着重考查了推理与论证能力,属于基础题.6.图中曲线是幂函数在第一象限的图象,已知n取±2,±四个值,则对应于曲线C1,C2,C3,C4的n值依次为( )A. -2,-,,2B. 2,,-,-2C. -,-2,2,D. 2,,-2,-【答案】B【解析】当n大于0时,幂函数为单调递增函数,当n小于0时,幂函数为单调递减函数,并且在x=1的右侧幂指数n自下而上依次增大,故选B.7.已知集合则实数的取值范围是()A. B. C. D.【答案】B【解析】试题分析:,;当时,,解得;当时,由,得,解得;综上所述,实数的取值范围是或,即;故选B.考点:集合的关系.【易错点睛】本题考查集合的运算,属于基础题.在研究集合间的关系时,要注意“”这种特殊情况,否则出现错误.8.已知定义在R上的函数f(x)满足(x1-x2)[f(x1)-f(x2)]>0,设,则()A. B.C. D.【答案】B【解析】【分析】根据题意,由函数单调性的定义分析可得函数f(x)在R上为增函数,又由0<a=0.32<1,b=log20.3<0,c=20.3>1,分析可得答案.【详解】根据题意,定义在R上的函数f(x)满足(x1-x2)[f(x1)-f(x2)]>0,则函数f(x)在R上为增函数,又由0<a=0.32<1,b=log20.3<0,c=20.3>1,则有b<a<c,则f(b)<f(a)<f(c),故选:B.【点睛】本题主要考查了函数的单调性的判定及应用,其中解答中根据题意正确得到函数的单调性,合理利用函数的单调性进行比较是解答的关键,着重考查了分析问题和解答问题的能力,属于基础题.9.已知函数f(2x+1)的定义域为[0,2],则y=f(x)的定义域为()A. B. C. D.【答案】A【解析】【分析】根据题意,可由x∈[0,2]求出2x+1的范围,即得出y=f(x)的定义域.【详解】由题意,函数的定义域为,即0≤x≤2,∴0≤2x≤4,所以1≤2x+1≤5,即y=f(x)的定义域为[1,5].故选:A.【点睛】本题主要考查了抽象函数的定义域的概念及应用,其中解答中熟记函数的定义域的定义,合理利用定义域的定义,列出相应的不等式是解答本题的关键,着重考查了推理与运算能力,属于基础题.10.已知函数y=f(x)的图象与函数y=a x(a>0且a≠1)的图象关于直线y=x对称,记g(x)=f(x)[f(x)+f(2)-1].若y=g(x)在区间上是增函数,则实数a的取值范围是()A. B. C. D.【答案】D【解析】【分析】先表述出函数的解析式然后代入将函数表述出来,然后对底数进行讨论即可得到答案.【详解】已知函数的图象与函数的图象关于直线对称,则,记.当时,若在区间上是增函数,为增函数,令,t∈,要求对称轴,无解;当时,若在区间上是增函数,为减函数,令,t∈,要求对称轴,解得,所以实数a的取值范围是,故选D.【点睛】本题主要考查指数函数与对数函数互为反函数.这里注意指数函数和对数函数的增减性与底数的大小有关,即当底数大于1时单调递增,当底数大于0小于1时单调递减.二、填空题(本大题共4小题,共16.0分)11.已知幂函数f(x)的图象经过点(2,4),则f(x)为______函数.(填奇偶性)【答案】偶【解析】【分析】根据幂函数的概念设出的解析式,然后代点求出,再用函数奇偶性定义判断奇偶性.【详解】因为函数是幂函数,所以可设,又f(2)=4,即2a=4,解得a=2,∴,∴,∴f(x)为偶函数.故答案为:偶.【点睛】本题主要考查了幂函数的基本概念,以及利用定义法判定函数的奇偶性,其中解答中熟记幂函数的基本概念,熟练应用函数奇偶性的定义判定是解答的关键,着重考查了推理与运算能力,属于基础题.12.设函数,则=______.【答案】【解析】【分析】由分段函数的解析式,可得,再由对数恒等式可得所求值.【详解】函数,可得,由,可得,故答案为:.【点睛】本题主要考查了分段函数的求值问题,以及对数恒等式的运用,其中解答中熟记对数的运算公式,合理运算是解答的关键,着重考查了推理与运算能力,属于基础题.13.设函数的定义域是实数集,则实数k的取值范围是______.【答案】[0,)【解析】【分析】函数的定义域为实数集,即恒成立,分和讨论,当时,需二次三项式对应的二次方程的判别式小于0.【详解】∵函数的定义域是实数集,∴对恒不为零,当时,成立;当时,需,解得.综上,使函数的定义域为R的实数的取值范围为.故答案为:.【点睛】本题主要考查了函数的定义域及其求法,其中根据函数的解析式有意义,得到函数的解析式所满足的条件,合理分类讨论求解是解答的关键,着重考查了数学转化思想方法及分类讨论的数学思想方法,是基础题..14.已知对于任意实数x,函数f(x)都满足f(x)+2f(2-x)=x,则f(x)的解析式为______.【答案】【解析】【分析】用2-x换上f(x)+2f(2-x)=x①中的x得到,f(2-x)+2f(x)=2-x②,这样①②联立即可解出f(x).【详解】由题意,因为f(x)+2f(2-x)=x①;∴f(2-x)+2f(x)=2-x②;①②联立解得.故答案为:.【点睛】本题主要考查了函数的解析式的求解,其中解答中根据题意,联立方程组求解是解答本题的关键,着重考查了分析问题和解答问题的能力,属于中档试题.三、解答题(本大题共5小题,共44.0分)15.设全集U=R,集合A={x|-2<x<3},B={y|y=2x-4,x∈A}.试求A∩B,(∁U A)∩B,(∁U A)∩(∁U B).【答案】A∩B=(-2,2),(∁U A)∩B=(-8,-2],(∁U A)∩(∁U B)=(-∞,-8]∪[3,+∞).【解析】【分析】由x∈A得出-2<x<3,从而得出-8<2x-4<2,从而求出集合B,然后进行交集,补集的运算即可.【详解】由题意,集合A中,-2<x<3,∴-4<2x<6,∴-8<2x-4<2;∴B={y|-8<y<2},且A={x|-2<x<3};∴A∩B=(-2,2),∁U A={x|x≤-2,或x≥3},(∁U A)∩B=(-8,-2],∁U B={y|y≤-8,或y≥2},(∁U A)∩(∁U B)=(-∞,-8]∪[3,+∞).【点睛】本题主要考查了描述法、区间表示集合的定义,以及交集和补集的运算,其中解答中熟记集合运算的基本概念,以及运算方法,准确运算是解答的关键,着重考查了推理与运算能力,属于基础题.16.设.(1)在图的直角坐标系中画出f(x)的图象;(2)若f(t)=2,求t值;(3)求函数f(x)的最小值.【答案】(1)见解析;(2)t=-2或t=,或t=2;(3)-1.【解析】【分析】(1)根据分段函数的解析式,分三段画图,即可得到函数的图象;(2)对t分三种情况讨论,得出相应的方程求解,即可得到答案;(3)由(1)中函数的图象,结合图象,即可得到函数的最小值.【详解】(1)f(x)的图象如右边:(2)当t≤-1时,f(t)=-t=2,∴t=-2;当-1<t<2时,f(t)=t2-1=2,解得:t=;当t≥2时,f(t)=t=2,∴t=2,综上所述:t=-2或t=,或t=2.(3)由图可知:当x∈(-1,2)时,f(x)=x2-1≥-1,所以函数f(x)的最小值为-1.【点睛】本题主要考查了分段函数的解析式的应用,以及分段函数的图象的应用,其中解答中分段的函数的解析式,正确画出分段函数的图象是解答本题的关键,着重考查了分析问题和解答问题的能力,属于基础题.17.(1)求(log2125+log425+log85)(log52+log254+log1258)的值;(2)化简【答案】(1)13;(2) .【解析】【分析】(1)利用对数运算性质及其换底公式,即可得出.(2)利用指数幂运算性质,准确化简,即可得出.【详解】(1)原式=(log2125+log25+)(log52+log52+log52)==13.(2)原式===.【点睛】本题主要考查了实数指数幂的运算性质和对数的运算性质和换底公式的应用,其中解答中熟记实数指数幂的运算和对数的运算性质,合理准确运算是解答本题的关键,着重考查了推理与运算能力,属于基础题.18.已知函数.(1)若函数f(x)是R上的奇函数,求m的值;(2)若函数f(x)的值域为D,且D⊆[-3,1],求m的取值范围.【答案】(1)m=1;(2)[-1,1].【解析】【分析】(1))由f(x)是R上的奇函数,得f(0)=0,得,即可求得m的值;(2)首先求出D,再由D⊆[-3,1],得,即可求得,实数m的范围.【详解】(1)∵f(x)是R上的奇函数,∴f(0)=0,∴m-=0,∴m=1,此时为奇函数,满足题意.(2)∵5x>0,∴5x+1>1,∴0<<2,∴-2<-<0,∴m-2<m-<m,∴D=(m-2,m),∵D⊆[-3,1],∴,∴-1≤m≤1,∴m的取值范围为[-1,1].【点睛】本题主要考查了函数的奇偶性的应用,以及函数的单调性的应用,其中解答中合理应用函数的奇偶性,以及函数的单调性,求得函数的值域,列出不等式组是解答本题的关键,着重考查了分析问题和解答问题的额能力,属于中档试题.19.已知函数.(1)若m=0,求函数f(x)的定义域;(2)若函数f(x)的值域为R,求实数m的取值范围;(3)若函数f(x)在区间上是增函数,求实数m的取值范围.【答案】(1){x|x≠0};(2)m≤-4或m≥0;(3).【解析】【分析】(1)直接由对数式的真数大于0,即可求解x的范围,得到答案;(2)由内层函数二次函数的判别式大于等于0,即可求解m的取值范围;(3)由题意可得,函数的对称轴,列出关于的不等式,即可求解.【详解】(1)若m=0,函数f(x)=,其定义域为{x|x≠0};(2)函数f(x)的值域为R,说明t=x2-mx-m能够取到大于0的所有实数,∴△=m2+4m≥0,即m≤-4或m≥0;(3)函数f(x)在区间上是增函数,则函数t=x2-mx-m的对称轴x=,且,解得:.【点睛】本题主要考查了函数的定义域及其求法,考查复合函数的单调性,对应复合函数的单调性,一要注意先确定函数的定义域,二要利用复合函数与内层函数和外层函数单调性之间的关系进行判断,判断的依据是“同增异减”,属于中档题,着重考查了分析问题和解答问题的能力.。
山西省实验中学2022-2023学年高一上学期第一次月考化学试题(解析版)

山西省实验中学2022—2023学年第一学期第一次月考试题高一年级化学可能用到的相对原子质量:C12O16Na23第I卷客观题一、选择题(2分×20=40分每小题只有一个选项符合题意)1.“爆竹声中一岁除,春风送暖入屠苏。
千门万户曈曈日,总把新桃换旧符。
”是王安石的作品《元日》,其中的“屠苏”是一种酒。
下列说法错误的是()A.黑火药是由硫黄、硝石和木炭按照一定比例混合而成B.“屠苏”中不含非电解质C.爆竹爆炸发生了化学变化D.早期的桃符大都是木质的,其主要成分纤维素可以发生水解反应【答案】B【解析】【详解】A.黑火药是由硫黄、硝石和木炭按照一定比例混合而成,故A正确;B.“屠苏”是药酒,含有酒精,酒精是非电解质,故B错误;C.爆竹爆炸生成新物质,发生了化学变化,故C正确;D.早期的桃符大都是木质的,含有纤维素,纤维素是多糖,在一定条件下能发生水解,故D正确;故选:B。
2.下列分散系中分散质直径最小的是A.氢氧化铁悬浊液B.氢氧化铝胶体C.淀粉溶液D.明矾溶液【答案】D【解析】【分析】【详解】A.氢氧化铁悬浊液,浊液的分散质粒子直径大于100nm,B.氢氧化铝胶体,胶体的分散质粒子直径在1~100nm,C.淀粉溶液属于胶体,胶体的分散质粒子直径在1~100nm,D.明矾溶液,溶液在分散质粒子的直径小于1nm,故分散质直径最小的是D,故答案为:D。
3.下列物质在水中的电离方程式书写正确的是A.2-+-3KClO K +Cl +3O = B.++2-33NaHCO =Na +H +CO C.2+2-2424H SO =H +SO D.2+-2Ba(OH)=Ba +2OH 【答案】D 【解析】【详解】A .氯酸钾应该电离出3ClO -,A 错误;B .碳酸氢钠在水中电离出3HCO -,B 错误;C .硫酸电离出2个氢离子2H +,C 错误;D .氢氧化钡电离出钡离子和两个氢氧根离子,D 正确;故选D 。
高一数学第一次月考试题与答案

2017-2018学年度高一数学9月月考试卷本试卷分第Ⅰ卷和第Ⅱ卷两部分,共150分,考试时间120分钟。
学校:___________姓名:___________班级:___________考号:___________分卷I一、选择题(共12小题,每小题5.0分,共60分)1.已知集合M ={x ∈N +|2x ≥x 2},N ={-1,0,1,2},则(∁R M )∩N 等于( ) A . ∅ B . {-1} C . {1,2} D . {-1,0}2.已知集合P ={4,5,6},Q ={1,2,3},定义P ⊕Q ={x |x =p -q ,p ∈P ,q ∈Q },则集合P ⊕Q 的所有真子集的个数为( )A . 32B . 31C . 30D . 以上都不对3.定义A -B ={x |x ∈A ,且x ∉B },若A ={1,2,4,6,8,10},B ={1,4,8},则A -B 等于( ) A . {4,8} B . {1,2,6,10} C . {1} D . {2,6,10}4.下列各组函数中,表示同一个函数的是( ) A .y =x -1和y =B .y =x 0和y =1C .f (x )=x 2和g (x )=(x +1)2 D .f (x )=和g (x )=5.小明骑车上学,开始时匀速行驶,途中因交通堵塞停留了一段时间,后为了赶时间加快速度行驶.与以上事件吻合得最好的图像是( )A .B .C .D .6.下列三个函数:①y =3-x ;②y =;③y =x 2+2x -10.其中值域为R 的函数有( ) A .0个 B .1个 C .2个 D .3个 7.一次函数g (x )满足g [g (x )]=9x +8,则g (x )是( ) A .g (x )=9x +8 B .g (x )=3x +8C .g (x )=-3x -4D .g (x )=3x +2或g (x )=-3x -4 8.下列函数中,在[1,+∞)上为增函数的是( ) A .y =(x -2)2 B .y =|x -1| C .y =D .y =-(x +1)2 9.若非空数集A ={x |2a + ≤x ≤3a -5},B ={x |3≤x ≤ },则能使A ⊆B 成立的所有a 的集合是( ) A . {a | ≤a ≤9} B . {a |6≤a ≤9} C . {a |a ≤9} D . ∅10.若函数f (x )= ,, , ,φ(x )=, , , ,则当x <0时,f (φ(x ))为( ) A . -x B . -x 2C .XD .x 2 11.若函数f (x )=的最小值为f (0),则实数m 的取值范围是( )A . [-1,2]B . [-1,0]C . [1,2]D . [0,2]12.已知函数f (x )=4x 2-kx -8在区间(5,20)上既没有最大值也没有最小值,则实数k 的取值范围是( )A. [160,+∞) B. (-∞,40]C. (-∞,4 ]∪[ 6 ,+∞) D. (-∞, ]∪[8 ,+∞)分卷II二、填空题(共4小题,每小题5.0分,共20分)13.已知M={2,a,b},N={2a,2,b2},且M=N,则有序实数对(a,b)的值为________.14.已知函数y=f(x2-1)的定义域为{x|-2<x<3},则函数y=f(3x-1)的定义域为____________.15.设函数f(x)=, ,, ,若f(f(a))=2,则a=_________.16.已知函数y=f(x)的定义域为{1,2,3},值域为{1,2,3}的子集,且满足f[f(x)]=f(x),则这样的函数有________个.三、解答题(共6小题,,共70分)17.(10分)用单调性的定义证明函数f(x)=2x2+4x在[-1,+∞)上是增函数.18(12分).根据下列函数解析式求f(x).(1)已知f(x+1)=2x2+5x+2;(2)已知f=x3+3-1;(3)已知af(x)+f(-x)=bx,其中a≠± 19(12分).已知集合A={x| ≤x<7},B={x|3<x<10},C={x|x<a}.(1)求A∪B,(∁R A)∩B;(2)若A∩C≠∅,求a的取值范围.20(12分).经市场调查,某超市的一种小商品在过去的近20天内的销售量(件)与价格(元)均为时间t(天)的函数,且销售量近似满足g(t)=80-2t,价格近似满足f(t)=20-|t-10|.(1)试写出该种商品的日销售额y与时间t( ≤t≤ )的函数表达式;(2)求该种商品的日销售额y的最大值与最小值.21(12分).已知函数f(x)=(x-a)2-(a2+1)在区间[0,2]上的最大值为g(a),最小值为h(a)(a∈R).(1)求g(a)和h(a);(2)作出g (a )和h (a )的图像,并分别指出g (a )的最小值和h (a )的最大值各为多少?22(12分).已知函数f (x )的定义域是(0,+∞),当x >1时,f (x )>0,且f (x ·y )=f (x )+f (y ). (1)求f (1)的值;(2)证明:f (x )在定义域上是增函数;(3)如果f (3)=-1,求满足不等式f (x )-f (x - )≥ 的x 的取值范围.2017-2018学年度高一数学9月月考试卷答案解析1.【答案】D【解析】因为M ={1,2},所以(∁R M )∩N ={-1,0},故正确答案为D. 2.【答案】B【解析】由所定义的运算可知P ⊕Q ={1,2,3,4,5}, ∴P ⊕Q 的所有真子集的个数为25-1=31.故选B. 3.【答案】D【解析】A -B 是由所有属于A 但不属于B 的元素组成,所以A -B ={2,6,10}.故选D. 4.【答案】D【解析】A 中的函数定义域不同;B 中y =x 0的x 不能取0;C 中两函数的对应关系不同,故选D. 5.【答案】C【解析】考查四个选项,横坐标表示时间,纵坐标表示的是离开学校的距离,由此知,此函数图像一定是下降的,由此排除A ;再由小明骑车上学,开始时匀速行驶,可得出图像开始一段是直线下降型,又途中因交通堵塞停留了一段时间,故此时有一段函数图像与x轴平行,由此排除D,后为了赶时间加快速度行驶,此一段时间段内函数图像下降的比较快,由此可确定C正确,B不正确.故选C.6.【答案】B【解析】7.【答案】D【解析】∵g(x)为一次函数,∴设g(x)=kx+b,∴g[g(x)]=k(kx+b)+b=k2x+kx+b,又∵g[g(x)]=9x+8,∴9,8,解得3,或3,4,∴g(x)=3x+2或g(x)=-3x-4.故选D.8.【答案】B【解析】y=(x-2)2在[2,+∞)上为增函数,在(-∞,2]为减函数;y=|x-1|= , ,,在[1,+∞)上为增函数,故选B.9.【答案】B 10.【答案】B【解析】x<0时,φ(x)=-x2<0,∴f(φ(x))=-x2.11.【答案】D【解析】当x≤ 时,f(x)=(x-m)2,f(x)min=f(0)=m2,所以对称轴x=m≥ .当x>0时,f(x)=x++m≥ +m=2+m,当且仅当x=,即x=1时取等号,所以f(x)min=2+m.因为f(x)的最小值为m2,所以m2≤ +m,所以 ≤m≤ .12.【答案】C【解析】由于二次函数f(x)=4x2-kx-8在区间(5,20)上既没有最大值也没有最小值,因此函数f(x)=4x2-kx-8在区间(5,20)上是单调函数.二次函数f(x)=4x2-kx-8图像的对称轴方程为x=8,因此8≤5或8≥ ,所以k≤4 或k≥ 6 .13.【答案】(0,1)或(4,)【解析】∵M={2,a,b},N={2a,2,b2},且M=N,∴或即或或4当a=0,b=0时,集合M={2,0,0}不成立,∴有序实数对(a,b)的值为(0,1)或(4,),故答案为(0,1)或(4,).14.【答案】{x| ≤x<3}【解析】∵函数y=f(x2-1)的定义域为{x|-2<x<3},∴-2<x<3.令g(x)=x2-1,则- ≤g(x)<8,故- ≤3x-1<8,即 ≤x<3,∴函数y=f(3x-1)的定义域为{x| ≤x<3}.15.【答案】【解析】若a≤ ,则f(a)=a2+2a+2=(a+1)2+1>0,所以-(a2+2a+2)2=2,无解;若a>0,则f(a)=-a2<0,所以(-a2)2+2(-a2)+2=2,解得a=.故a=.16.【答案】10【解析】∵f[f(x)]=f(x),∴f(x)=x,①若f:{ , ,3}→{ , ,3},可以有f(1)=1,f(2)=2,f(3)=3,此时只有1个函数;②若f:{ , ,3}→{ },此时满足f(1)=1;同理有f:{ , ,3}→{ };f:{ , ,3}→{3},共有3类不同的映射,因此有3个函数;③首先任选两个元素作为值域,则有3种情况.例如选出1,2,且对应关系f:{ , ,3}→{ , },此时满足f(1)=1,f(2)=2.则3可以对应1或2,又有2种情况,所以共有3× =6个函数.综上所述,一共有1+3+6=10个函数.17.【答案】设x1,x2是区间[-1,+∞)上的任意两个实数,且x1<x2,则f(x1)-f(x2)=(2+4x1)-(2+4x2)=2(-)+4(x1-x2)=2(x1-x2)(x1+x2+2).∵- ≤x1<x2,∴x1-x2<0,x1+x2+2>0,∴f(x1)-f(x2)<0,即f(x1)<f(x2),∴f(x)在[-1,+∞)上是增函数.18.【答案】(1)方法一(换元法)设x+1=t,则x=t-1,∴f(t)=2(t-1)2+5(t-1)+2=2t2+t-1,∴f(x)=2x2+x-1.方法二(整体代入法)∵f(x+1)=2x2+5x+2=2(x+1)2+(x+1)-1,∴f(x)=2x2+x-1.(2)(整体代入法)∵f=x3+3-1=3-3x2·-3x·-1=3-3-1,∴f(x)=x3-3x-1(x≥ 或x≤-2).(3)在原式中以-x替换x,得af(-x)+f(x)=-bx,于是得+ - = ,- + =-消去f(-x),得f(x)=.故f(x)的解析式为f(x)=x(a≠± ).19.【答案】(1)因为A={x| ≤x<7},B={x|3<x<10},所以A∪B={x| ≤x<10}.因为A={x| ≤x<7},所以∁R A={x|x<2或x≥7},则(∁R A)∩B={x|7≤x<10}.(2)因为A={x| ≤x<7},C={x|x<a},且A∩C≠∅,所以a>2.20.【答案】(1)y=g(t)·f(t)=(80-2t)·( -|t-10|)=(40-t)(40-|t-10|)=3 4 , ,4 5 ,(2)当 ≤t<10时,y的取值范围是[1 200,1 225],在t=5时,y取得最大值1 225;当 ≤t≤ 时,y的取值范围是[600,1 200],在t=20时,y取得最小值600.综上,第5天,日销售额y取得最大值1 225元;第20天,日销售额y取得最小值600元.21.【答案】( )∵f(x)=(x-a)2-(a2+1),又x∈[ , ],∴当a≤ 时,g(a)=f(2)=3-4a,h(a)=f(0)=-1;当0<a≤ 时,g(a)=f(2)=3-4a,h(a)=f(a)=-(a2+1);当1<a<2时,g(a)=f(0)=-1,h(a)=f(a)=-(a2+1);当a≥ 时,g(a)=f(0)=-1,h(a)=f(2)=3-4a.综上可知g(a)=3 4h(a)=3 4(2)g(a)和h(a)的图像分别为:由图像可知,函数y=g(a)的最小值为-1,函数y=h(a)的最大值为-1.【解析】22.【答案】(1)解令x=y=1,得f(1)=2f(1),故f(1)=0.(2)证明令y=,得f(1)=f(x)+f()=0,故f()=-f(x).任取x1,x2∈( ,+∞),且x1<x2,则f(x2)-f(x1)=f(x2)+f()=f().由于>1,故f()>0,从而f(x2)>f(x1).∴f(x)在(0,+∞)上是增函数.(3)解由于f(3)=-1,而f(3)=-f(3),故f(3)=1.在f(x·y)=f(x)+f(y)中,令x=y=3,得f(9)=f(3)+f(3)=2.故所给不等式可化为f(x)-f(x- )≥f(9),∴f(x)≥f[9(x-2)],∴x≤94.又∴ <x≤94,∴x的取值范围是94.【解析】。
山西省实验中学2020-2021学年高一下学期第一次月考数学试卷及答案

2020-2021学年山西省实验中学高一(下)第一次月考数学试卷一、单选题(共12小题).1.下列说法正确的是()A.若向量,满足||>||,且与同向,则>B.若∥且∥,则∥C.向量与是共线向量,则A,B,C,D四点共线D.非零向量与非零向量满足∥,则向量与方向相同或相反2.若z(1+i)=2i,则z=()A.﹣1﹣i B.﹣1+i C.1﹣i D.1+i3.已知在△ABC中,sin A:sin B:sin C=4:3:2,则cos B等于()A.B.C.D.4.在△ABC中,a=8,B=60°,C=75°,则b=()A.B.C.D.5.已知•=﹣12,||=4,和的夹角为135°,则||为()A.12B.6C.D.36.△ABC的三内角A,B,C所对边的长分别为a,b,c.设向量=(a+c,b),=(b ﹣a,c﹣a),若向量∥,则角C的大小是()A.B.C.D.7.在直角梯形ACBD中,AB∥CD,AD⊥AB,∠B=45°,AB=2CD=2,M为腰BC的中点,则=()A.1B.2C.3D.48.如图,在山根A处测得山顶B的仰角∠CAB=45°,沿倾斜角为30°的山坡向山顶走1000米到达S点,又测得山顶仰角∠DSB=75°,则山高BC为()A.500米B.1000米C.1200米D.1500米9.在△ABC中,三内角A、B、C所对边分别为a、b、c若(b﹣c)sin B=2c sin C且,则△ABC面积等于()A.B.C.D.310.在△ABC中,若=,则△ABC是()A.等腰三角形B.直角三角形C.等腰直角三角形D.等腰三角形或直角三角形11.若函数f(x)=2sin()(﹣2<x<10)的图象与x轴交于点A,过点A的直线l与函数的图象交于B、C两点,则(+)•=()A.﹣32B.﹣16C.16D.3212.设两个向量和,其中λ,m,α为实数.若,则的取值范围是()A.[﹣6,1]B.[4,8]C.(﹣∞,1]D.[﹣1,6]二、填空题(本题共4个小题,每小题4分,共16分,把正确答案填在题中横线上.)13.在△ABC中,BC=x,AC=2,B=45°,若三角形有两解,则x的取值范围是.14.在平行四边形ABCD中,AC与BD交于点O,E是线段OD中点,AE的延长线与CD 交于点F.若,,则=.15.已知=(1,3),=(2+λ,1),且与成锐角,则实数λ的取值范围是.16.在某次军事演习中红方为了准确分析战场形势,在两个相距为的军事基地C和D,测得蓝方两支精锐部队分别在A处和B处,且∠ADB=30°,∠BDC=30°,∠DCA=60°,∠ACB=45°.如图所示,则蓝方这两支精锐部队的距离为.三、解答题(本题共4个小题,共36分,解答应写出文字说明,证明过程或演算步骤.)17.已知平面向量=(1,x),=(2x+3,﹣x),x∈R.(1)若x=2,求在上的投影向量c的坐标;(2)若⊥,求x的值.18.在△ABC中,角A,B,C所对的边分别为a,b,c,cos=,•=3.(1)求△ABC的面积S.(2)若b+c=6,求a的值.19.已知||=1,||=2,与的夹角为120°.(1)求|2+|;(2)求向量2+与向量﹣的夹角θ的余弦值.20.在锐角△ABC中,角A,B,C的对边分别为a,b,c,且2b•cos A=c cos A+a cos C.(1)求角A的大小;(2)若a=,求△ABC的面积S的取值范围.参考答案一、单选题(本题共12个小题,每小题4分,共48分,在每小题给出的四个选项中只有一个是符合题目要求的.)1.下列说法正确的是()A.若向量,满足||>||,且与同向,则>B.若∥且∥,则∥C.向量与是共线向量,则A,B,C,D四点共线D.非零向量与非零向量满足∥,则向量与方向相同或相反解:对于A:向量,满足||>||,且与同向,则>,由于向量是不能比较大小的,故A错误;对于B:若∥且∥(),则∥,故B错误;对于C:向量与是共线向量,则A,B,C,D四点共线或直线AB∥直线CD,故C 错误;对于D:非零向量与非零向量满足∥,则向量与方向相同或相反,故D正确.故选:D.2.若z(1+i)=2i,则z=()A.﹣1﹣i B.﹣1+i C.1﹣i D.1+i解:由z(1+i)=2i,得z==1+i.故选:D.3.已知在△ABC中,sin A:sin B:sin C=4:3:2,则cos B等于()A.B.C.D.解:依题意设a=4k,b=3k,c=2k(k>0),则cos B===.故选:A.4.在△ABC中,a=8,B=60°,C=75°,则b=()A.B.C.D.解:由内角和定理得:A=180°﹣60°﹣75°=45°,根据正弦定理得:=,又a=8,sin A=,sin B=,则b===4.故选:C.5.已知•=﹣12,||=4,和的夹角为135°,则||为()A.12B.6C.D.3解:由题意利用两个向量的数量积的定义可得=cos135°=4•(),解得=6,故选:B.6.△ABC的三内角A,B,C所对边的长分别为a,b,c.设向量=(a+c,b),=(b ﹣a,c﹣a),若向量∥,则角C的大小是()A.B.C.D.解:∵∴(a+c)(c﹣a)=b(b﹣a)∴b2+a2﹣c2=ab2cos C=1∴C=故选:B.7.在直角梯形ACBD中,AB∥CD,AD⊥AB,∠B=45°,AB=2CD=2,M为腰BC的中点,则=()A.1B.2C.3D.4解:以A为原点,AB为x轴,AD为y轴,建立直角坐标系.则:A(0,0),B(2,0),D(0,1),C(1,1),M(.因为AB=2CD=2,∠B=45,所以AD=DC=1,M为腰BC的中点,则M点到AD的距离=(DC+AB)=,M点到AB的距离=DA=所以,,所以=9/4﹣1/4=2.故选:B.8.如图,在山根A处测得山顶B的仰角∠CAB=45°,沿倾斜角为30°的山坡向山顶走1000米到达S点,又测得山顶仰角∠DSB=75°,则山高BC为()A.500米B.1000米C.1200米D.1500米解:依题意,过S点作SE⊥AC于E,SH⊥AB于H,∵∠SAE=30°,AS=1000米,∴CD=SE=AS•sin30°=500米,依题意,在Rt△HAS中,∠HAS=45°﹣30°=15°,∴HS=AS•sin15°,在Rt△BHS中,∠HBS=30°,∴BS=2HS=2000sin15°,在Rt△BSD中,BD=BS•sin75°=2000sin15°•sin75°=2000sin15°•cos15°=1000×sin30°=500米.∴BC=BD+CD=1000米.故选:B.9.在△ABC中,三内角A、B、C所对边分别为a、b、c若(b﹣c)sin B=2c sin C且,则△ABC面积等于()A.B.C.D.3解:∵(b﹣c)sin B=2c sin C由正弦定理可得(b﹣c)b=2c2即b2﹣bc﹣2c2=0∴b=2c∵,由余弦定理可得,=∴c=2,b=4,sin A==则=×=故选:A.10.在△ABC中,若=,则△ABC是()A.等腰三角形B.直角三角形C.等腰直角三角形D.等腰三角形或直角三角形解:∵cos B=,cos A=,∴a2+c2﹣b2=2ac•cos B,b2+c2﹣a2=2bc•cos A,∴===,又=,∴==,即sin A cos A=sin B cos B,∴sin2A=sin2B,又A和B都为三角形的内角,∴2A=2B或2A+2B=180°,即A=B或A+B=90°,则△ABC为等腰三角形或直角三角形.故选:D.11.若函数f(x)=2sin()(﹣2<x<10)的图象与x轴交于点A,过点A的直线l与函数的图象交于B、C两点,则(+)•=()A.﹣32B.﹣16C.16D.32解:由f(x)=2sin()=0可得∴x=6k﹣2,k∈Z∵﹣2<x<10∴x=4即A(4,0)设B(x1,y1),C(x2,y2)∵过点A的直线l与函数的图象交于B、C两点∴B,C两点关于A对称即x1+x2=8,y1+y2=0则(+)•=(x1+x2,y1+y2)•(4,0)=4(x1+x2)=32故选:D.12.设两个向量和,其中λ,m,α为实数.若,则的取值范围是()A.[﹣6,1]B.[4,8]C.(﹣∞,1]D.[﹣1,6]解:由,,,可得,设代入方程组可得消去m化简得,再化简得再令代入上式得(sinα﹣1)2+(16t2+18t+2)=0可得﹣(16t2+18t+2)∈[0,4]解不等式得因而解得﹣6≤k≤1.故选:A.二、填空题(本题共4个小题,每小题4分,共16分,把正确答案填在题中横线上.)13.在△ABC中,BC=x,AC=2,B=45°,若三角形有两解,则x的取值范围是.解:∵在△ABC中,BC=x,AC=2,B=45°,且三角形有两解,∴如图:x sin45°<2<x,解得,∴x的取值范围是,故答案为:.14.在平行四边形ABCD中,AC与BD交于点O,E是线段OD中点,AE的延长线与CD 交于点F.若,,则=.解:∵△DEF∽△BEADF:BA=DE:BE=1:3;作FG平行BD交AC于点G,∴FG:DO=2:3,CG:CO=2:3,∴等于,∵=+==,∴=+=+,故答案为:.15.已知=(1,3),=(2+λ,1),且与成锐角,则实数λ的取值范围是{λ|λ>﹣5,且λ≠﹣}.解:由题意可得>0,且、不共线,∴,求得λ>﹣5,且λ≠﹣,故答案为:{λ|λ>﹣5,且λ≠﹣}.16.在某次军事演习中红方为了准确分析战场形势,在两个相距为的军事基地C和D,测得蓝方两支精锐部队分别在A处和B处,且∠ADB=30°,∠BDC=30°,∠DCA=60°,∠ACB=45°.如图所示,则蓝方这两支精锐部队的距离为a.解:由题意知∠ADC=∠ADB+∠BDC=60°,又因为∠ACD=60°,所以∠DAC=60°.所以AD=CD=AC=a.在△BCD中,∠DBC=180°﹣30°﹣105°=45°,由正弦定理得=,所以BD=CD•=a•=a,在△ADB中,由余弦定理得:AB2=AD2+BD2﹣2AD•BD•cos∠ADB=a2+()2﹣2•a•a•=a2,所以AB=a.故答案为:a.三、解答题(本题共4个小题,共36分,解答应写出文字说明,证明过程或演算步骤.)17.已知平面向量=(1,x),=(2x+3,﹣x),x∈R.(1)若x=2,求在上的投影向量c的坐标;(2)若⊥,求x的值.解:(1)若x=2,则=(1,2),=(7,﹣2),则==(,).(2)若⊥,则=(1,x)•(2x+3,﹣x)=1×(2x+3)+x(﹣x)=0,即x2﹣2x﹣3=0,解得x=﹣1或x=3.18.在△ABC中,角A,B,C所对的边分别为a,b,c,cos=,•=3.(1)求△ABC的面积S.(2)若b+c=6,求a的值.解:(1)在△ABC中,∵cos=,∴cos A=2×﹣1=,A∈(0,π),∴sin A==.又•=3,∴bc×=3,解得bc=5.∴S==2.(2)∵b+c=6,bc=5,∴a2=(b+c)2﹣2bc﹣2bc×cos A=62﹣2×5﹣2×5×=20,解得a=2.19.已知||=1,||=2,与的夹角为120°.(1)求|2+|;(2)求向量2+与向量﹣的夹角θ的余弦值.解:(1)因为=•=,所以.(2)因为=,所以又===﹣1,所以=.20.在锐角△ABC中,角A,B,C的对边分别为a,b,c,且2b•cos A=c cos A+a cos C.(1)求角A的大小;(2)若a=,求△ABC的面积S的取值范围.解:(1)由正弦定理,2b cos A=c cos A+a cos C,所以2cos A sin B=cos A sin C+sin A cos C=sin(A+C)=sin B,∵sin B≠0,∴cos A=,∵0°<A<180°,∴A=60°.(2)由正弦定理,,所求b=2sin B,c=2sin C,所以S=×=sin(B+)×4,=sin B()=,=+,=,=+sin(2B﹣),又因为锐角△ABC是锐角三角形,所以,所以,<2B﹣,所以sin(2B﹣)≤1,所以。
诱导公式解答题15题学生

1.(1)化简:()()()()3tan cos 2sin 2cos sin ⎛⎫---+ ⎪⎝⎭----ππαπαααππα; (2)已知1sin 35⎛⎫+= ⎪⎝⎭πα,求5cos 6⎛⎫+ ⎪⎝⎭πα的值. 【来源】江西省樟树中学2017-2018学年人教A 版高一下学期第一次月考数学(理)试题2.已知角α的终边经过点(P m,sin αα为第二象限. (1)求m 的值;(2)若tan =β()()sin cos 3sin sin 2cos cos 3sin sin ⎛⎫++ ⎪⎝⎭+--παβαβπαβαβ的值. 【来源】【全国百强校】广东省揭阳市第一中学2017-2018学年高一下学期第一次月考数学(理)试题3.已知π40,sin 25<<=αα. (1)求tan α的值;(2)求()()()sin 2cos 2sin cos ⎛⎫+-+ ⎪⎝⎭--++παπααπα的值. 【来源】【全国百强校】广西河池市高级中学2017-2018学年高一下学期第二次月考数学试题4.已知sin =α,且α是第一象限角。
(1)求cos α的值。
(2)求()()3sin 2tan cos ⎛⎫- ⎪⎝⎭++-πααππα的值。
【来源】河南省林州一中(分校部)2017-2018学年下学期高一4月调研考试数学试题5.求证: ()()()tan 2sin 2cos 6tan 33sin cos 22----=-⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭παπαπααππαα. 【来源】河南省林州一中(分校部)2017-2018学年下学期高一4月调研考试数学试题6.(1)计算:191425sin cos 634⎛⎫+-+ ⎪⎝⎭tan πππ (2)求()=f x 的定义域. 【来源】江西省樟树中学2017-2018学年人教A 版高一下学期第一次月考数学(文)试题7.已知sin =α,且α是第一象限角。
(1)求cos α的值。
2019-2020学年山西省太原市实验中学校高一下学期期中考试数学试题

山西省太原市实验中学校2019-2020学年高一下学期期中考试试题一、选择题 ( 每小题3分,共36分) 。
1. sin585°的值为( )A .-22 B.22 C .-32 D .322.若角β的终边经过点P (a ,2a )(a ≠0),则cos β等于( )A .±55 B.255 C .±255 D .-255 3.已知△ABC 中,c =6,a =4,B =120°,则b 等于( )A .76B .219C .27D .274.把函数y =sin x(x ∈R )的图像上所有的点向左平移π6个单位长度,再将所得的图像的横坐标缩短到原来的12倍(纵坐标不变),则最后得到的图像所表示的函数是( )A .y =sin(12x +π6)B .y =sin(12x +π12)C .y =sin(2x +π3)D .y =sin(2x +π6)5.向量BA →=(4,-3),向量BC →=(2,-4),则△ABC 的形状为( )A .等腰非直角三角形B .等边三角形C .直角非等腰三角形D .等腰直角三角形6.若f (x )=tan(x +π4),则( )A .f (0)>f (-1)>f (1)B .f (0)>f (1)>f (-1)C .f (1)>f (0)>f (-1)D .f (-1)>f (0)>f (1)7.设D 为△ABC 所在平面内一点,BC =3CD →,则( ) A.AD →=-13AB →+43AC →B.AD →=13AB →-43AC →C.AD →=43AB →+13AC →D.AD →=43AB →-13AC →8.已知α∈⎝⎛⎭⎫π,32π且sin(α+β)·cos β-cos(α+β)sin β=-45,则tan α2的值是( ) A .3 B .2 C .-2D .-39.在锐角三角形ABC 中,已知A =2C ,则ac 的范围是( )A .(0,2)B .(2,2)C .(2,3)D .(3,2)10.在△ABC 中,M 为边BC 上任意一点,N 为AM 的中点,AN →=λAB →+μAC →,则λ+μ的值为( )A.12B.13C.14D .1 11.函数f (x )=sin(ωx +φ)(ω>0,|φ|<π2)的最小正周期为π,若将其图象向左平移π6个单位长度后,得到函数g (x )的图象,且g (x )为奇函数,则函数f (x )的图象( )A .关于点(π12,0)对称B .关于点(5π12,0)对称C .关于直线x =5π12对称D .关于直线x =π12对称12.若在x ∈[0,π2]上有两个不同的实数满足方程cos2x +3sin2x =k +1,则k 的取值范围是( )A .[-2,1]B .[-2,1)C .[0,1]D .[0,1) 二 、填空题( 每小题4分,共16分) 。
2020山西省实验中学高一10月数学月考题

山西省实验中学2020—2021学年度第一学期第二次月考试题(卷)高一年级数学卷面总分值100分考试时间90分钟命题人:高一数学组审核人:高一数学组第一卷(客观题)一、单选题(本题共8个小题,每小题4分,共32分,在每小题给出的四个选项中只有一个是符合题目要求的.)1.满足条件{1,2,3,4}⊆M ⊆{1,2,3,4,5,6}的集合M 的个数是()A .2B .3C .4D .52.若a <0,-1<b <0,则下列不等式中正确的是()A .a >ab >ab 2B .ab 2>ab >a C .ab >a >ab 2D .ab >ab 2>a3.函数f (x )=|x -2|x 的单调减区间是()A .[1,2]B .[-1,0]C .[0,2]D .[2,+∞)4.若x >2m 2-3是-1<x <4的必要不充分条件,则实数m 的取值范围是()A .[-3,3]B .(-∞,-3]∪[3,+∞)C .(-∞,-1]∪[1,+∞)D .[-1,1]5.若函数f (x )的定义域为[0,3],则函数(2)3f x x 的定义域为()A .-32B .-34C .-32或-34 D.32或-34二、多选题(本题共4个小题,每小题4分,共16分,在每小题给出的四个选项中有多个是符合题目要求的,全部选对得4分,部分选对得2分,有选错的不得.下列选项中所给图象是函数图象的为().下列选项中,能使b a +a b ≥2成立的条件有()>0 B.ab <0 C.a >0,b >0 D.a <0,b <0.下列函数中,满足“对任意x 1,x 2∈(1,+∞),都有112()(f x f x x x --x )=2x B.f (x )=x 2+4x +3x )=-3x +1D .f (x )=x +1x 已知集合2{|0,0}x x ax b a ++=>有且仅有两个子集,则下列选项中结论正确的是()A.224a b -≤B.21+4a b ≥C.若不等式20x ax b +-<的解集为12{|}x x x x <<,则120x x >D.若不等式2x ax b c ++<的解集为12{|}x x x x <<,且12||4x x -=,则1c =第二卷(主观题)三、填空题(本题共4个小题,每小题4分,共16分,把正确答案填在题中横线上.)15.()f x 为(0,)+∞上的增函数,且对任意(0,)x ∈+∞,都有2(())1f f x x+=-,则(1)f =____.16.当11x -≤≤时,不等式2ax 2+2x -3<0恒成立,则实数a 的取值范围是________.A B C D四、解答题(本题共4个小题,共36分,解答应写出文字说明,证明过程或演算步骤.)17.(本小题满分8分)设集合{|121}A x a x a =-<<+,{|03}B x x =<≤,U R =.(1)若a =12,求A B ⋃,()U A C B ⋂;(2)若()U A C B ⋂=∅,求实数a 的取值范围.18.(本小题满分8分)已知关于x 的不等式ax 2-3x +b>0的解集为{x|x<1或x>2}.(1)求a ,b 的值;(2)当c ∈R 时,解关于x 的不等式ax 2-(ac +b )x +bc <0(用c 表示).19.(本小题满分8分)某地发生地质灾害,使当地的自来水受到了污染,某部门对水质检测后,决定在水中投放一种药剂来净化水质.已知每投放质量为m(mg)的药剂后,经过x天该药剂在水中释放的浓度y(mg·L-1)满足y=mf(x),其中f(x)0<x≤4,x>4.当药剂在水中释放的浓度不低于4mg·L-1时称为有效净化;当药剂在水中释放的浓度不低于4mg·L-1且不高于10mg·L-1时称为最佳净化.(1)如果投放的药剂质量为4mg,问自来水达到有效净化一共可持续几天?(2)为了使在7天(从投放药剂算起)之内的自来水达到最佳净化,试确定应该投放的药剂质量m的最小值.。
山西省实验中学2020-2021学年高一第一学期第一次月考化学试题(含答案)

山西省实验中学2020~2021学年高一第一学期第一次月考题化学试题可能用到的相对原子质量: H 1 C 12 N 14 O 16 Na 23 Mg 24 Ca 40Cu 40 Zn 65 S 32 Cl 35.5 Al 27 Ba 137一、选择题(本题包括20 小题,每题2 分,共40 分。
每小题只有一个选项符合题意。
)1.病毒可以通过气溶胶传播,气溶胶属于胶体的一种。
下列关于胶体的叙述,正确的是()A.依据丁达尔效应可将分散系分为溶液、胶体与浊液B.胶体的本质特征是具有丁达尔效应C.雾是气溶胶,在阳光下可观察到丁达尔效应D.溶液中溶质粒子的运动有规律,胶体中分散质粒子的运动无规律,即布朗运动2.我国科学家在世界上第一次为一种名为“钴酞菁”的分子(直径为1.3×10﹣9 m)恢复了磁性。
“钴酞菁”分子结构和性质与人体内的血红素与植物体内的叶绿素非常相似。
下列关于“钴酞菁”分子的说法中正确的是()A.在水中形成的分散系能产生丁达尔效应B.“钴酞菁”分子既能透过滤纸,也能透过半透膜C.分子直径比钠离子小D.在水中所形成的分散系属于悬浊液3.在Zn、ZnO、ZnCO3、盐酸和CaCl2 溶液五种物质中,每两种物质反应能生成ZnCl2 的方法有()A.2 种B.3 种C.4 种D.5 种4.下列分散系最不稳定的是()A.向CuSO4 溶液中加入NaOH 溶液得到的分散系B.向水中加入食盐得到的分散系C.向沸水中滴入饱和FeCl3 溶液得到的红褐色液体D.向NaOH 溶液中通入少量CO2 得到的无色溶液5.对下列物质分类全部正确的是()①纯碱②食盐水③石灰水④烧碱⑤液态氧⑥KClO3A.碱﹣﹣①④B.纯净物﹣﹣③④⑤C.盐﹣﹣①⑥D.混合物﹣﹣②⑤6.下列叙述不正确的是()A.由两种或两种以上元素形成的纯净物称为化合物B.由一种元素组成的纯净物是单质C.由一种物质组成的是纯净物D.含氧元素的化合物称为氧化物7.下列有关物质分类错误的是()A.混合物:生铁、空气、碱石灰B.化合物:烧碱、氧化镁、硫酸C.盐:氯化钠、石灰石、生石灰D.单质:石墨、臭氧、水银8.过滤后的食盐水仍含有可溶性的CaCl2、MgCl2、Na2SO4 等杂质,通过如下几个实验步骤,可制得纯净的食盐水,不正确的操作顺序是()①加入稍过量的Na2CO3 溶液;②加入稍过量的NaOH 溶液;③加入稍过量的BaCl2 溶液;A.③②①⑤④B.③①②⑤④④滴入稀盐酸至无气泡产生;⑤过滤C.②③①⑤④D.①②③⑤④9.若50 滴水正好是m mL,水的密度为1g/mL,1 滴水所含的分子数是()A.m×50×18×6.02×1023 18m ⨯ 6.02 ⨯1023m ⨯ 6.02 ⨯1023 B.50 ⨯18m ⨯ 50 ⨯18C.D.50 6.02 ⨯102310.关于偏二甲肼(C2H8N2)下列叙述中正确的是()A.偏二甲肼的摩尔质量为60g B.6.02 1023 个偏二甲肼分子的质量为60gC.1mol 偏二甲肼的质量为60g·mol-1 D.6g 偏二甲肼含有N A 个偏二甲肼分子11.用N A 表示阿伏德罗常数,下列叙述正确的是()A.标准状况下,22.4 L H2O 含有的分子数为1 N AB.物质的量浓度为0.5mol/L 的K2SO4 溶液中,含有SO4 个数为0.5N A2﹣C.常温常压下,16g O2 含有的氧原子数为1 N AD.通常状况下,1 N A 个SO2 分子占有的体积为22.4L12.把VL 含有MgSO4 和K2SO4 的混合溶液分成两等份,一份加入含a mol NaOH 的溶液,恰好使镁离子完全沉淀为氢氧化镁;另一份加入含b mol BaCl2 的溶液,恰好使硫酸根离子完全沉淀为硫酸钡,则原混合溶液中钾离子的浓度为()A.mol/L B.mol/L C.mol/L D.mol/L13.把500mL 有BaCl2 和KC1 的混合溶液分成5 等份,取一份加入含a mol 硫酸钠的溶液,恰好使Ba2+完全沉淀;另取一份加入含b mol 硝酸银的溶液,恰好使Cl﹣完全沉淀.则该混合溶液中K+浓度为()A.10(b﹣2a)mol•L﹣1 B.5(b-2a)mol•L﹣1C.2(b﹣a)mol•L﹣1 D.10(2a-b)mol•L﹣114.实验室中需要配制2mol/L 的NaCl 溶液950mL,配制时应选用的容量瓶的规格和称取NaCl 的质量分别是()A.950mL 111.2g B.500mL 117.0gC.1000mL 117.0g D.1000mL 111.2g15.同温同压下两个容积相等的贮气瓶,一个装有C2H4,另一个装有C2H2 和C2H6 的混合气体,两瓶内的气体一定具有相同的()A.质量B.原子总数C.碳原子数D.密度16.下列选项中的物质所含指定原子数目一定相等的是()A.温度和压强不同,相同质量的N2O 和CO2 两种气体的总原子数B.等温等压下,相同体积的C2H4 和C2H2、C2H6 的混合气体的总原子数C.等温等压下,相同体积的O2 和O3 两种气体中的氧原子数D.相同物质的量、不同体积的NH3 和CH4 两种气体中的氢原子数17.实验室配制450mL 1mol/L NaOH 溶液,下列有关说法正确的是()A.用托盘天平称取18g NaOH 固体B.容量瓶用蒸馏水洗净后需晾干再使用C.配制过程中玻璃棒的作用主要是搅拌和引流D.定容摇匀后,发现液面下降,继续加水至刻度线18.下列说法正确的是()A.把100mL 3mol•L﹣1 的H2SO4 跟100g H2O 混合,硫酸的物质的量浓度变为1.5mol•L﹣1B.把100g 20%的NaCl 溶液跟100g H2O 混合后,NaCl 溶液的质量分数是10%C.把200mL 3mol•L﹣1 的BaCl2 溶液跟100mL 3mol•L﹣1 的KCl 溶液混合后,溶液中的c(Cl﹣)仍然是3mol•L﹣1D.把100mL 20%的NaOH 溶液跟100mL H2O 混合后,NaOH 溶液的质量分数是10%19.一个密闭容器,中间有一可自由滑动的隔板(厚度不计)将容器分成两部分,当左边充入1mol N2,右边充入一定量的CO 时,隔板处于如图位置(保持温度不变),下列说法正确的是()A.右边与左边分子数之比为4:1B.右侧CO 的质量为5.6 gC.右侧气体密度是相同条件下氢气密度的14 倍D.若改变右边CO 的充入量而使隔板处于容器正中间,保持温度不变,则应充入0.2mol CO20.现有两种硫酸溶液,一种硫酸溶液的物质的量浓度为C1,密度为ρ1;另一种硫酸溶液的物质的量浓度为C2,密度为ρ2,将它们等体积混合后,所得溶液的密度为ρ3,则混合后硫酸的物质的量浓度为()A.B.C.D.二.填空题(26 分)21.仔细分析如图中的实验:A、B、C 试管中的现象如表所示:A B C产生白色沉淀,溶液仍为蓝色产生蓝色沉淀,溶液变为无色产生蓝色沉淀,溶液为无色写出A、B、C 试管中发生反应的化学方程式:A.;B.;C.。
2017-2018学年山西省实验中学七年级(下)期中数学试卷

2017-2018学年山西省实验中学七年级(下)期中数学试卷一、选择题(本大题共10个小题,每小题2分,共20分.每小题的四个选项中只有一个正确答案)1.(2分)计算:2a a 的结果是( )A .aB .2aC .3aD .22a2.(2分)如图,1∠和2∠是对顶角的是( )A .B .C .D .3.(2分)下列运算正确的是( )A .01a =B .21(3)9--=C .632a a a ÷=D .3261()2a a = 4.(2分)肥皂泡的泡壁厚度大约是0.00000071米,数字0.00000071用科学记数法表示为()A .77.110⨯B .60.7110-⨯C .77.110-⨯D .87110-⨯5.(2分)已知,1∠与2∠互为邻补角,1140∠=︒,则2∠的余角的度数为( )A .30︒B .40︒C .50︒D .100︒6.(2分)将一副三角板如图放置,使点A 在DE 上,//BC DE ,45C ∠=︒,30D ∠=︒,则ABD ∠的度数为( )A .10︒B .15︒C .20︒D .25︒7.(2分)下列多项式乘法中可以用平方差公式计算的是( )A .()()a b a b -+-B .(2)(2)x x ++C .()()33x x y y +-D .(2)(1)x x -+8.(2分)周末小丽从家里出发骑单车去公园,因为她家与公园之间是一条笔直的自行车道,所以小丽骑得特别放松.途中,她在路边的便利店挑选一瓶矿泉水,耽误了一段时间后继续骑行,愉快地到了公园.图中描述了小丽路上的情景,下列说法中错误的是( )A .小丽在便利店时间为15分钟B .公园离小丽家的距离为2000米C .小丽从家到达公园共用时间20分钟D .小丽从家到便利店的平均速度为100米/分钟9.(2分)如图,点P 是直线a 外的一点,点A 、B 、C 在直线a 上,且PB a ⊥,垂足是B ,PA PC ⊥,则下列不正确的语句是( )A .线段PB 的长是点P 到直线a 的距离B .PA 、PB 、PC 三条线段中,PB 最短C .线段AC 的长是点A 到直线PC 的距离D .线段PC 的长是点C 到直线PA 的距离10.(2分)如图,在下列条件中:①12∠=∠;②180BAD ADC ∠+∠=︒;③ABC ADC ∠=∠;④34∠=∠,能判定//AB CD 的有( )A .1个B .2个C .3个D .4个二、填空题(本大题共8个小题,每题3分,共24分,)11.(3分)计算2232x xy 的结果是 .12.(3分)计算22222(663)(3)m n m n m m --÷-=13.(3分)如图,直线AB 、CD 相交于点O ,OE 平分AOD ∠,若80BOC ∠=︒,则AOC∠的度数是 ,COE ∠的度数是 .14.(3分)如果23273n ⨯=,则n = .15.(3分)计算:2201820172019-⨯= .16.(3分)如图,将一张长方形纸片ABCD 沿EF 折叠,点D 、C 分别落在D '、C '的位置处,若156∠=︒,则DEF ∠的度数是 .17.(3分)太原市出租车价格是这样规定的:不超过3千米,付车费8元,超过的部分按每千米1.6元收费,已知李老师乘出租车行驶了(3)x x >千米,付车费y 元,则所付车费y 元与出租车行驶的路程x 千米之间的关系式为 .18.(3分)如图,已知GF AB ⊥,12∠=∠,B AGH ∠=∠,则下列结论:①//GH BC ;②D F ∠=∠;③HE 平分AHG ∠;④HE AB ⊥,其中正确的是 (只填序号)三.解答题(本大题共7个小题,共56分,)直滑,19.(16分)计算下列各题:(1)201820(1)3( 3.14)π--+--(2)22(3)x x +-(3)(2)(3)3()x x y x x y +--+(4)(21)(21)x y x y+++-20.(6分)先化简,再求值:[(1)(2)2]x x x++-÷,其中25x=-.21.(6分)(1)如图,利用尺规作图:过点B作//BM AD.(要求:不写作法保留作图痕迹);(2)若直线//DE AB,设DE与M交于点C.试说明:A BCD∠=∠.22.(5分)某公交车每月的支出费用为4000元,每月的乘车人数x(人)与每月利润(利润=收入费用-支出费用)y(元)的变化关系如下表所示(每位乘客的公交票价是固定不变的):(1)在这个变化过程中,是自变量,是因变量;(2)观察表中数据可知,每月乘客量达到人以上时,该公交车才不会亏损;(3)请你估计当每月乘车人数为3500人时,每月利润为多少元?(4)若5月份想获得利润5000元,则请你估计5月份的乘客量需达人.23.(8分)已知:如图,//AB CD,70B∠=︒,20BCE∠=︒,130CEF∠=︒,请判断AB 与EF的位置关系,并说明理由.解:,理由如下://AB CD,B BCD∴∠=∠,()70B∠=︒,70BCD∴∠=︒,()20BCE∠=︒,50ECD∴∠=︒,130CEF∠=︒,。
高一数学第一次月考试题及答案

2017-2018学年度高一数学9月月考试卷本试卷分第Ⅰ卷和第Ⅱ卷两部分,共150分,考试时间120分钟。
学校:___________姓名:___________班级:___________考号:___________一、选择题(共12小题,每小题5.0分,共60分) 1.已知集合M ={x ∈N +|2x ≥x 2},N ={-1,0,1,2},则(∁R M )∩N 等于( ) A . ∅ B . {-1} C . {1,2} D . {-1,0}2.已知集合P ={4,5,6},Q ={1,2,3},定义P ⊕Q ={x |x =p -q ,p ∈P ,q ∈Q },则集合P ⊕Q 的所有真子集的个数为( )A . 32B . 31C . 30D . 以上都不对3.定义A -B ={x |x ∈A ,且x ∉B },若A ={1,2,4,6,8,10},B ={1,4,8},则A -B 等于( ) A . {4,8} B . {1,2,6,10} C . {1} D . {2,6,10}4.下列各组函数中,表示同一个函数的是( ) A .y =x -1和y =x 2−1x+1B .y =x 0和y =1C .f (x )=x 2和g (x )=(x +1)2D .f (x )=(√x)2x和g (x )=(√x)25.小明骑车上学,开始时匀速行驶,途中因交通堵塞停留了一段时间,后为了赶时间加快速度行驶.与以上事件吻合得最好的图像是( )A .B .C .D .6.下列三个函数:①y =3-x ;②y =1x 2+1;③y =x 2+2x -10.其中值域为R 的函数有( ) A .0个 B .1个 C .2个 D .3个 7.一次函数g (x )满足g [g (x )]=9x +8,则g (x )是( ) A .g (x )=9x +8 B .g (x )=3x +8C .g (x )=-3x -4D .g (x )=3x +2或g (x )=-3x -4 8.下列函数中,在[1,+∞)上为增函数的是( ) A .y =(x -2)2 B .y =|x -1| C .y =1x+1D .y =-(x +1)29.若非空数集A ={x |2a +1≤x ≤3a -5},B ={x |3≤x ≤22},则能使A ⊆B 成立的所有a 的集合是( ) A . {a |1≤a ≤9} B . {a |6≤a ≤9}C . {a |a ≤9}D . ∅10.若函数f (x )={x 2,x ≥0,x ,x <0,φ(x )={x ,x ≥0,−x 2,x <0,则当x <0时,f (φ(x ))为( )A . -xB . -x 2C .XD .x 211.若函数f (x )={(x −m )2,x ≤0,x +1x +m,x >0的最小值为f (0),则实数m 的取值范围是( ) A . [-1,2] B . [-1,0] C . [1,2] D . [0,2]12.已知函数f (x )=4x 2-kx -8在区间(5,20)上既没有最大值也没有最小值,则实数k 的取值范围是( )A . [160,+∞)B . (-∞,40]C . (-∞,40]∪[160,+∞)D . (-∞,20]∪[80,+∞)分卷II二、填空题(共4小题,每小题5.0分,共20分) 13.已知M ={2,a ,b },N ={2a,2,b 2},且M =N ,则有序实数对(a ,b )的值为________.14.已知函数y =f (x 2-1)的定义域为{x |-2<x <3},则函数y =f (3x -1)的定义域为____________.15.设函数f (x )={x 2+2x +2,x ≤0,−x 2,x >0,若f (f (a ))=2,则a =_________. 16.已知函数y =f (x )的定义域为{1,2,3},值域为{1,2,3}的子集,且满足f [f (x )]=f (x ),则这样的函数有________个.三、解答题(共6小题,,共70分)17.(10分)用单调性的定义证明函数f (x )=2x 2+4x 在[-1,+∞)上是增函数.18(12分).根据下列函数解析式求f (x ). (1)已知f (x +1)=2x 2+5x +2; (2)已知f (x +1x)=x 3+1x 3-1;(3)已知af (x )+f (-x )=bx ,其中a ≠±119(12分).已知集合A ={x |2≤x <7},B ={x |3<x <10},C ={x |x <a }.(1)求A ∪B ,(∁R A )∩B ;(2)若A ∩C ≠∅,求a 的取值范围.20(12分).经市场调查,某超市的一种小商品在过去的近20天内的销售量(件)与价格(元)均为时间t (天)的函数,且销售量近似满足g (t )=80-2t ,价格近似满足f (t )=20-12|t -10|. (1)试写出该种商品的日销售额y 与时间t (0≤t ≤20)的函数表达式;(2)求该种商品的日销售额y 的最大值与最小值.21(12分).已知函数f (x )=(x -a )2-(a 2+1)在区间[0,2]上的最大值为g (a ),最小值为h (a )(a ∈R ). (1)求g (a )和h (a );(2)作出g (a )和h (a )的图像,并分别指出g (a )的最小值和h (a )的最大值各为多少?22(12分).已知函数f (x )的定义域是(0,+∞),当x >1时,f (x )>0,且f (x ·y )=f (x )+f (y ). (1)求f (1)的值;(2)证明:f (x )在定义域上是增函数;(3)如果f (13)=-1,求满足不等式f (x )-f (x -2)≥2的x 的取值范围.2017-2018学年度高一数学9月月考试卷答案解析1.【答案】D【解析】因为M={1,2},所以(∁R M)∩N={-1,0},故正确答案为D.2.【答案】B【解析】由所定义的运算可知P⊕Q={1,2,3,4,5},∴P⊕Q的所有真子集的个数为25-1=31.故选B.3.【答案】D【解析】A-B是由所有属于A但不属于B的元素组成,所以A-B={2,6,10}.故选D.4.【答案】D【解析】A中的函数定义域不同;B中y=x0的x不能取0;C中两函数的对应关系不同,故选D.5.【答案】C【解析】考查四个选项,横坐标表示时间,纵坐标表示的是离开学校的距离,由此知,此函数图像一定是下降的,由此排除A;再由小明骑车上学,开始时匀速行驶,可得出图像开始一段是直线下降型,又途中因交通堵塞停留了一段时间,故此时有一段函数图像与x轴平行,由此排除D,后为了赶时间加快速度行驶,此一段时间段内函数图像下降的比较快,由此可确定C正确,B不正确.故选C.6.【答案】B【解析】7.【答案】D【解析】∵g(x)为一次函数,∴设g(x)=kx+b,∴g[g(x)]=k(kx+b)+b=k2x+kx+b,又∵g[g(x)]=9x+8,∴{k2=9,kb+b=8,解得{k=3,b=2或{k=−3,b=−4,∴g(x)=3x+2或g(x)=-3x-4.故选D.8.【答案】B【解析】y=(x-2)2在[2,+∞)上为增函数,在(-∞,2]为减函数;y=|x-1|={x−1,x≥1,1−x,x<1在[1,+∞)上为增函数,故选B.9.【答案】B10.【答案】B【解析】x<0时,φ(x)=-x2<0,∴f(φ(x))=-x2.11.【答案】D【解析】当x≤0时,f(x)=(x-m)2,f(x)min=f(0)=m2,所以对称轴x=m≥0.当x>0时,f(x)=x+1x+m≥2√x·1x+m=2+m,当且仅当x=1x,即x=1时取等号,所以f(x)min=2+m.因为f(x)的最小值为m2,所以m 2≤2+m ,所以0≤m ≤2. 12.【答案】C【解析】由于二次函数f (x )=4x 2-kx -8在区间(5,20)上既没有最大值也没有最小值,因此函数f (x )=4x 2-kx -8在区间(5,20)上是单调函数.二次函数f (x )=4x 2-kx -8图像的对称轴方程为x =k8,因此k8≤5或k8≥20,所以k ≤40或k ≥160. 13.【答案】(0,1)或(14,12)【解析】∵M ={2,a ,b },N ={2a,2,b 2},且M =N , ∴{a =2a,b =b 2或{a =b 2,b =2a, 即{a =0,b =1或{a =0,b =0或{a =14,b =12,当a =0,b =0时,集合M ={2,0,0}不成立, ∴有序实数对(a ,b )的值为(0,1)或(14,12),故答案为(0,1)或(14,12). 14.【答案】{x |0≤x <3}【解析】∵函数y =f (x 2-1)的定义域为{x |-2<x <3},∴-2<x <3.令g (x )=x 2-1,则-1≤g (x )<8,故-1≤3x -1<8,即0≤x <3,∴函数y =f (3x -1)的定义域为{x |0≤x <3}.15.【答案】√2【解析】若a ≤0,则f (a )=a 2+2a +2=(a +1)2+1>0, 所以-(a 2+2a +2)2=2,无解; 若a >0,则f (a )=-a 2<0,所以(-a 2)2+2(-a 2)+2=2,解得a =√2. 故a =√2. 16.【答案】10【解析】∵f [f (x )]=f (x ),∴f (x )=x ,①若f :{1,2,3}→{1,2,3},可以有f (1)=1,f (2)=2,f (3)=3,此时只有1个函数; ②若f :{1,2,3}→{1},此时满足f (1)=1; 同理有f :{1,2,3}→{2};f :{1,2,3}→{3}, 共有3类不同的映射,因此有3个函数;③首先任选两个元素作为值域,则有3种情况.例如选出1,2,且对应关系f :{1,2,3}→{1,2},此时满足f (1)=1,f (2)=2.则3可以对应1或2,又有2种情况,所以共有3×2=6个函数. 综上所述,一共有1+3+6=10个函数.17.【答案】设x 1,x 2是区间[-1,+∞)上的任意两个实数,且x 1<x 2,则f (x 1)-f (x 2)=(2x 12+4x 1)-(2x 22+4x 2)=2(x 12-x 22)+4(x 1-x 2)=2(x 1-x 2)(x 1+x 2+2).∵-1≤x 1<x 2,∴x 1-x 2<0,x 1+x 2+2>0,∴f (x 1)-f (x 2)<0,即f (x 1)<f (x 2),∴f (x )在[-1,+∞)上是增函数.18.【答案】(1)方法一 (换元法)设x +1=t ,则x =t -1,∴f (t )=2(t -1)2+5(t -1)+2=2t 2+t -1,∴f (x )=2x 2+x -1.方法二 (整体代入法)∵f (x +1)=2x 2+5x +2 =2(x +1)2+(x +1)-1, ∴f (x )=2x 2+x -1.(2)(整体代入法)∵f (x +1x )=x 3+1x 3-1=(x +1x )3-3x 2·1x -3x ·1x 2-1 =(x +1x )3-3(x +1x )-1,∴f (x )=x 3-3x -1(x ≥2或x ≤-2).(3)在原式中以-x 替换x ,得af (-x )+f (x )=-bx ,于是得{af (x )+f (-x )=bx ,af (-x )+f (x )=-bx.消去f (-x ),得f (x )=bxa−1.故f (x )的解析式为f (x )=ba−1x (a ≠±1).19.【答案】(1)因为A ={x |2≤x <7},B ={x |3<x <10},所以A ∪B ={x |2≤x <10}. 因为A ={x |2≤x <7},所以∁R A ={x |x <2或x ≥7}, 则(∁R A )∩B ={x |7≤x <10}.(2)因为A ={x |2≤x <7},C ={x |x <a },且A ∩C ≠∅,所以a >2. 20.【答案】(1)y =g (t )·f (t )=(80-2t )·(20-12|t -10|) =(40-t )(40-|t -10|)={(30+t )(40−t ),0≤t <10,(40−t )(50−t ),10≤t ≤20.(2)当0≤t <10时,y 的取值范围是[1 200,1 225],在t =5时,y 取得最大值1 225;当10≤t ≤20时,y 的取值范围是[600,1 200], 在t =20时,y 取得最小值600.综上,第5天,日销售额y 取得最大值1 225元;第20天,日销售额y 取得最小值600元. 21.【答案】(1)∵f (x )=(x -a )2-(a 2+1),又x ∈[0,2], ∴当a ≤0时,g (a )=f (2)=3-4a ,h (a )=f (0)=-1; 当0<a ≤1时,g (a )=f (2)=3-4a ,h (a )=f (a )=-(a 2+1); 当1<a <2时,g (a )=f (0)=-1,h (a )=f (a )=-(a 2+1);当a ≥2时,g (a )=f (0)=-1,h (a )=f (2)=3-4a .综上可知g (a )={3−4a,a ≤1,−1,a >1, h (a )={−1,a ≤0,−(a 2+1),0<a <2,3−4a,a ≥2.(2)g (a )和h (a )的图像分别为:由图像可知,函数y =g (a )的最小值为-1, 函数y =h (a )的最大值为-1. 【解析】22.【答案】(1)解 令x =y =1,得f (1)=2f (1),故f (1)=0. (2)证明 令y =1x ,得f (1)=f (x )+f (1x )=0, 故f (1x )=-f (x ).任取x 1,x 2∈(0,+∞),且x 1<x 2, 则f (x 2)-f (x 1)=f (x 2)+f (1x 1)=f (x 2x 1).由于x 2x 1>1,故f (x 2x 1)>0,从而f (x 2)>f (x 1).∴f (x )在(0,+∞)上是增函数.(3)解 由于f (13)=-1,而f (13)=-f (3),故f (3)=1. 在f (x ·y )=f (x )+f (y )中,令x =y =3,得 f (9)=f (3)+f (3)=2.故所给不等式可化为f (x )-f (x -2)≥f (9), ∴f (x )≥f [9(x -2)],∴x ≤94.又{x >0,x −2>0, ∴2<x ≤94,∴x 的取值范围是(2,94].【解析】。
2017-2018学年度第一学期高一第一次月考成绩统计表
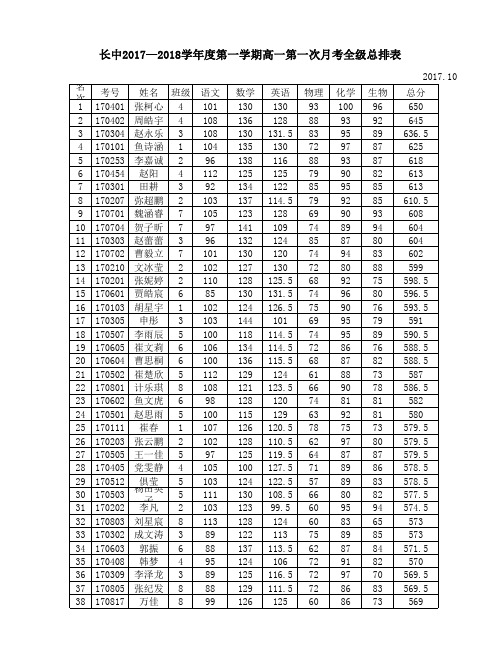
长中2017—018学年度第一学期高一第一次月考全级总排表
2017.10 名次 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 考号 170614 170104 170822 170712 170107 170834 170114 170115 170311 170708 171055 170318 170417 170815 170333 170519 170624 170217 170215 170308 170729 170514 170516 170617 170809 170811 170225 170711 170411 170610 170223 170406 170234 170108 170618 170211 170508 170616 姓名 班级 司梦晨 6 惠嘉康 1 胡叶叶 8 周逸飞 7 鱼朝阳 1 弥田 8 高金枝 1 尚甜甜 1 陈宝玲 3 李阳 7 杨广 10 杨扬 3 宇文雅 4 郭钾 8 黎佳昊 3 于莹莹 5 全宝婷 6 张晨 2 洪亦璇 2 李昭伟 3 解欣 7 陈雪彤 5 景凡 5 李一杰 6 党佳杰 8 尚国梁 8 罗睿青 2 剡心怡 7 梁娜 4 高星 6 曹亚鹏 2 曹锐洋 4 申岩 2 司帅 1 王帅 6 李煜 2 贾文丽 5 尚丁 6 语文 98 96 89 82 102 103 93 97 90 88 100 88 95 94 87 98 101 95 108 93 102 101 99 94 89 87 91 84 84 107 83 100 92 94 92 90 102 91 数学 117 126 117 119 101 126 112 109 107 120 118 101 103 119 113 115 124 92 97 108 120 116 111 113 138 118 114 123 118 125 123 98 111 102 133 113 112 110 英语 114 100 123.5 89.5 109 105.5 101.5 123 113 98.5 76 113 114.5 81.5 86.5 104 114.5 105.5 106.5 101.5 108 113 78 90.5 87 111.5 99 105 72 79.5 84.5 108.5 73 95.5 109.5 67.5 117 76 物理 57 60 67 67 70 48 66 50 58 65 64 61 63 62 80 59 42 69 47 45 56 42 62 55 44 57 65 56 74 50 62 69 80 68 56 70 52 67 化学 73 85 83 90 73 76 86 82 92 87 82 82 87 86 81 72 72 84 84 89 62 70 86 89 88 80 76 76 95 86 78 76 84 86 80 90 55 95 生物 77 68 54 86 78 74 74 71 71 72 89 83 64 84 79 78 72 79 79 85 72 78 84 78 73 65 72 73 73 68 84 62 73 67 42 82 74 73 总分 536 535 533.5 533.5 533 532.5 532.5 532 531 530.5 529 528 526.5 526.5 526.5 526 525.5 524.5 521.5 521.5 520 520 520 519.5 519 518.5 517 517 516 515.5 514.5 513.5 513 512.5 512.5 512.5 512 512
山西省实验中学2022-2023学年高一下学期3月月考化学试题(原卷版)

①
②
③
④
稀硝酸的体积/mL
100
200
300
400
剩余金属 质量/g
18.0
9.6
0
0
NO的体积/mL
2240
4480
6720
V
试通过计算填空:
(1)硝酸 物质的量浓度为____________________。
(2)②中溶解了_______________g Fe。
(3)③中溶解了_______________g Cu。
C.若A为碳单质,则将C通入澄清石灰水中,可能观察到白色沉淀产生
D.工业上,B转化为D的反应条件为点燃
18.为确定某溶液的离子组成,进行如下实验:
①取少量溶液滴加Ba(NO3)2溶液,产生白色沉淀
②然后继续加入稀盐酸至溶液呈酸性,产生无刺激性气味且能使澄清石灰水变浑浊的无色气体;白色沉淀部分溶解
③取上层清液继续滴加Ba(NO3)2溶液至无沉淀时,再滴加AgNO3溶液,产生白色沉淀。
C.氧化性强弱的顺序为O2>Fe3+>S
D.转化过程中参加循环反应的离子只有Fe2+、Fe3+
20.一定温度下,探究铜与稀硝酸的反应,反应过程如图:
下列说法不正确的是
A.过程I中生成气体的离子方程式为3Cu+8H++2NO =3Cu2++2NO↑+4H2O
B 当活塞不再移动时,即使再抽入空气,金属铜屑也不继续溶解
⑥二氧化硫和二氧化氮都能形成酸雨,酸雨的pH等于5.6()
A.①③④B.①②C.①⑤D.①②⑥
13.部分含氮物质的分类与其相应化合价的关系如图所示,下列有关推断不合理的是
山西省实验中学2022-2023学年高一上学期第一次月考数学试卷(含答案)

山西省实验中学2022-2023学年度第一学期第一次月考试题(卷)高一年级数学卷面总分值100分考试时间90分钟命题人:高一数学组审核人:高一数学组第一卷(客观题)一、单选题(本题共8个小题,每小题4分,共32分,在每小题给出的四个选项中只有一个是符合题目要求的.)1.已知集合A={−1,1},B={x∣ax=1},若A∩B=B,则a的取值集合为()A.{1}B.{−1}C.{−1,1}D.{−1,0,1}2.下列存在量词命题是假命题的是()A.存在x∈Q,使2x−x3=0B.存在x∈R,使x2+x+1=0C.有的素数是偶数D.有的有理数没有倒数3.定义集合A,B的一种运算:A⊗B={x∣x=a2−b,a∈A,b∈B},若A= {−1,0},B={1,2},则A⊗B中的元素个数为()A.1B.2C.3D.44.已知x,y,z为非零实数,代数式x|x|+y|y|+z|z|+xyz|xyz|的值所组成的集合是M,则下列判断正确的是()A.4∈MB.2∈MC.0∉MD.−4∉M5.《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架,其中卷第九勾股中记载:“今有邑,东西七里,南北九里,各中开门.出东门一十五里有木.问出南门几何步而见木?”其算法为:东门南到城角的步数,乘南门东到城角的步数,乘积作被除数,以树距离东门的步数作除数,被除数除以除数得结果,即出南门x里见到树,则x=(9×12)×(7×12)15.若一小城,如图所示,出东门1200步有树,出南门750步能见到此树,则该小城的周长的最小值为(注:1里=300步)()A.2√10里B.4√10里C.6√10里D.8√10里6.已知集合A={x∣ax2−(a+1)x+1<0},B={x∣x2−3x−4<0},且A∩B=A,则实数a的取值范围是()A.a≤14B.0<a≤14C.a≥14D.14≤a<1或a>17.如图,抛物线y=ax2+bx+c的对称轴是直线x=1,下列结论:(1)abc> 0;(2)b2−4ac>0;③8a+c<0;(4)5a+b+2c>0,正确的有()A.4个B.3个C.2个D.1个8.某单位周一、周二、周三开车上班的职工人数分别是14,10,8.若这三天中至少有一天开车上班的职工人数是20,则这三天都开车上班的职工人数的最大值是()A.6B.5C.7D.8二、多选题(本题共4个小题,每小题4分,共16分,在每小题给出的四个选项中有多个是符合题目要求的,全部选对得4分,部分选对得2分,有选错的不得分.)9.下列说法正确的是()A.若a>b>0,则1a <1bB.若a>b>0,m>0,则b+ma+m >baC.a>b>0,则a3−b3>a2b−ab2。
山西省实验中学2017-2018学年高一下学期3月月考数学试题 Word版缺答案

山西省实验中学2017—2018学年度高一年级第一次月考题(卷)数学试题命题人:谢桂霞 赵婧一 校对人:谢桂霞 赵婧一说明:1.考生务必将自己所在班级、姓名、准考证号等信息填写在密封线内的相应位置。
2.本试卷分第Ⅰ卷和第Ⅱ卷两部分,共 4 页。
答题时间 90 分钟,满分 100 分。
3.答卷时考生务必用蓝、黑色墨水笔或圆珠笔作答。
第 Ⅰ 卷 客观题 (36 分 )一 、选择题(本题共 12 小题 ,每小题 3 分 ,共 36 分)1.已知532cos =⎪⎭⎫ ⎝⎛+απ,且⎪⎭⎫ ⎝⎛∈232π,πα,则αtan =( ) A.34 B.43 C.43- D.43±2.点 P 从(1,0) 出发,沿单位圆122=+y x 顺时针方向运动32π弧长到达 Q 点,则 Q 的坐标为( ) A.⎪⎪⎭⎫ ⎝⎛-2321, B.⎪⎪⎭⎫ ⎝⎛21-23-, C.⎪⎪⎭⎫ ⎝⎛23-21-, D.⎪⎪⎭⎫ ⎝⎛2123-, 3.已知 tan θ=2,则θθθθ22cos 2-cos sin sin +=( )A .34- B.45 C.43- D.54 4.在△ABC 中,已知 D 是 AB 边上一点,若DB AD 2=,CB CA CD μλ+=,则λμ的值( )A.1B.21C.2D.31 5.函数()x x x f cos 2sin 2+=在区间⎥⎦⎤⎢⎣⎡θ,π32-上的最大值为1 ,则θ的值是( ) A.0 B.3π C.2π D.2-π 6.函数()()⎪⎭⎫ ⎝⎛+=20sin π<,>ϕϖϕϖx x f 的最小正周期为π,且其图象向左平移6π个单位后得到的函数为奇函数,则函数()x f 的图象( )A.关于点⎪⎭⎫ ⎝⎛012,π对称B.关于直线125π=x 对称 C.关于点⎪⎭⎫ ⎝⎛0,125π对称 D.关于直线12x π=对称 7.已知0>ϖ,函数()⎪⎭⎫ ⎝⎛+=4sin πx x f ω在⎪⎭⎫ ⎝⎛,ππ2上单调递减,则ω的取值范围是( ) A.⎥⎦⎤⎢⎣⎡4521, B.⎥⎦⎤⎢⎣⎡4321, C.⎥⎦⎤ ⎝⎛210, D.(]20,8.若 tan2=a ,tan3=b ,tan5=c ,则( )A.a <b <cB.b <c <aC.c <b <aD.c <a <b9.要得到函数x y 2sin 3=的图象,可将函数⎪⎭⎫ ⎝⎛-=42cos 3πx y 的图象( ) A.沿 x 轴向左平移8π个单位长度 B.沿 x 轴向右平移8π个单位长度C.沿 x 轴向左平移4π个单位长度D.沿 x 轴向右平移4π个单位长度。
2017-2018 学年.七中.高一下.第一次月考化学试卷及答案

2.能作为 Cl、Br、I 元素非金属性递变规律的判断依据的是( )
①Cl2、Br2、I2 的熔点
②Cl2、Br2、I2 的氧化性
③HCl、HBr、HI 的热稳定性
④HCl、HBr、HI 的酸性
A.①②③
B.②③
C.②③④
D.①②③④
器 3.下列各组物质中化学键的类型完全相同的是( )
A.NaCl MgCl2 Na2O
2017-2018 学年.七中.高一下.第一次月考.试卷及答案
一、选择题(共 16 小题,每小题 4 分,共 64 分)
1.中国科Lv
的名称为鉝。关于
293 116
Lv
的叙述错误的是
()
A.原子序数 116
B.中子数 177
C.核外电子数 116
D.质 子 数 177
B.H2O
辑 C.Na2S NaOH H2SO4
D.NH4Cl
MgO CO2 NaNO3 NH3
4.下列分子的电子式书写正确的是( )
编 A.氨气
C.氮气
B.四氯化碳 D.二氧化碳
捷PDF 5.下列反应过程中的能量变化与如图一致的是( )
迅A. 2Al + Fe2O3 高温 2Fe + Al2O3 C. C + H2O 高温 CO + H2
B. CaCO3 高温 CaO + CO2 ↑ D. C + CO2 ∆ 2CO
6.关于碱金属元素的说法中正确的是( ) A.ⅠA 族元素都是碱金属元素 B.碱金属单质可将铜从其盐溶液中置换出来 C.金属钾具有强还原性,K+具有强氧化性 D.Cs 常温下与水反应会发生爆炸
7.反应 3A(g) + B(g)=2C(g) + 2D(g) ,在不同条件下,用不同物质表示其反应速率,分别为 ①v(A) = 0.6mol ⋅ L−1 ⋅ min−1 ②v(B) = 0.45mol ⋅ L−1 ⋅ min−1 ③v(C) = 0.02mol ⋅ L−1 ⋅ min−1 ④v(D) = 0.45mol ⋅ L−1 ⋅ min−1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017-2018学年山西省实验中学高一下学期第一次月考数学试题第Ⅰ卷 客观题(36分)一、选择题:本题共12小题,每小题3分,共36分. 1. 已知3cos 25πα⎛⎫+= ⎪⎝⎭,且3,22ππα⎛⎫∈ ⎪⎝⎭,则tan α=( ) A .43 B . 34 C .34- D .34± 2. 点P 从(1,0)出发,沿单位圆221x y +=顺时针方向运动23π弧长到达Q 点,则Q 的坐标为( )A .12⎛- ⎝⎭B .12⎛⎫- ⎪ ⎪⎝⎭C .1,2⎛- ⎝⎭D .12⎛⎫- ⎪ ⎪⎝⎭3. 已知tan 2θ=,则22sin sin cos 2cos θθθθ+-=( )A .43-B . 54C .34-D .454. 在ABC ∆中,已知D 是AB 边上一点,若2AD DB =,CD CA CB λμ=+,则μλ的值为( ) A .1 B .12 C. 2 D .135. 函数2()sin 2cos f x x x =+在区间2,3πθ⎡⎤-⎢⎥⎣⎦上的最大值为1,则θ的值是( ) A . 0 B .3π C. 2π D .2π-6.函数()sin()0,2f x x πωϕωϕ⎛⎫=+><⎪⎝⎭的最小正周期为π,且其图象向左平移6π个单位后得到的函数为奇函数,则函数()f x 的图象( )A .关于点,012π⎛⎫⎪⎝⎭对称 B .关于直线512x π=对称 C. 关于点5,012π⎛⎫⎪⎝⎭对称 D .关于直线12x π=对称7. 已知0ω>,函数()sin 4f x x πω⎛⎫=+⎪⎝⎭在,2ππ⎛⎫⎪⎝⎭单调递减,则ω的取值范围是( ) A . 15,24⎡⎤⎢⎥⎣⎦ B .13,24⎡⎤⎢⎥⎣⎦C.10,2⎛⎤ ⎥⎝⎦D .(]0,28. 右tan 2a =,tan 3b =,tan 5c =,则( )A .a b c <<B . b c a << C. c b a << D .c a b << 9.要得到函数3sin 2y x =的图象,可将函数3cos 24y x π⎛⎫=- ⎪⎝⎭的图象( ) A . 沿x 轴向左平移8π个单位长度 B .沿x 轴向右平移8π个单位长度 C. 沿x 轴向左平移4π个单位长度 D .沿x 轴向右平移4π个单位长度10. 若x 是三角形的最小内角,则函数sin cos sin cos y x x x x =++的值域是( )A .[)1,-+∞B .⎡-⎣ C. (D .12⎛⎤ ⎥⎝⎦11.O 是平面上一定点,A ,B ,C 是平面上不共线的三个点,动点P 满足()OP OA AB AC λ=++,[)0,λ∈+∞,则P 的轨迹一定通过ABC ∆的( )A .外心B .垂心 C. 内心 D .重心 12. 设0a b c >>>,则221121025()a ac c ab a a b ++-++的最小值( )A . 2B . 4 C. .5第Ⅱ卷 主观题(64分)二、填空题:本题共4小题,每小题4分,共16分.13.若a ,b 是两个不共线的向量,若2AB a kb =+,BC a b =+,2CD a b =-,且A 、B 、D 三点共线,则实数k 的值等于 .14. 一扇形的圆心角为120︒,则此扇形的面积与其内切圆的面积之比为 .15.设函数()sin()f x x ωϕ=+,0A >,0ω>,若()f x 在区间,62ππ⎡⎤⎢⎥⎣⎦上单调,且2234f f f πππ⎛⎫⎛⎫⎛⎫== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,则()f x 的最小正周期是 . 16. 若不等式2373x x a a ++-≥-的解集为R ,则实数a 的取值范围是 . 三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17. 求值 (1)设222sin()cos()cos()()(12sin 0)31sin cos sin 22a a a f a a a a a πππππ+--+=+≠⎛⎫⎛⎫+++-+ ⎪ ⎪⎝⎭⎝⎭,求236f π⎛⎫- ⎪⎝⎭的值.(2)已知cos 6a π⎛⎫-=⎪⎝⎭25cos sin 66a a ππ⎛⎫⎛⎫+-- ⎪ ⎪⎝⎭⎝⎭的值. 18.已知函数()sin()(0,0,0)2f x A x h A πωϕωϕ=++>><<的图象如图所示,(1)求()f x 的解析式; (2)求()f x 的对称中心.19.已知函数()12sin 23f x x π⎛⎫=+-⎪⎝⎭,,42x ππ⎡⎤∈⎢⎥⎣⎦, (1)求()f x 的最大值和最小值;(2)若不等式()2f x m -<在,42x ππ⎡⎤∈⎢⎥⎣⎦上恒成立,求实数m 的取值范围. 20. 已知0a >,函数()2sin 226f x a x a b π⎛⎫=-+++ ⎪⎝⎭,当0,2x π⎡⎤∈⎢⎥⎣⎦时,5()1f x -≤≤. (1)求常数a ,b 的值;(2)设()2g x f x π⎛⎫=+ ⎪⎝⎭,且[]lg ()0g x >,求()g x 的单增区间. 21.设全集U R =(1)解关于x 的不等式110()x a a R -+->∈;(2)记A 为(1)中不等式的解集,集合{}2sin 0B x x π==,若()U C A B 恰有3个元素,求a 的取值范围.试卷答案一、选择题1-5: BCDCD 6-10: BADBD 11、12:DB 二、填空题15.56π 16.[]2,5-三、解答题17. 【答案】(1【难度】中【考点】三角函数恒等变形,同角三角函数关系,诱导公式 【解析】(1)222sin()cos()cos()()31sin cos sin 22f a παπαπαππααα+--+=⎛⎫⎛⎫+++-+ ⎪ ⎪⎝⎭⎝⎭22sin cos cos cos 12sin sin sin tan αααααααα+===+2311236tan tan 66f πππ⎛⎫-=== ⎪⎛⎫⎛⎫⎝⎭- ⎪ ⎪⎝⎭⎝⎭.(2)225cos sin cos cos 16666ππππαααα⎛⎫⎛⎫⎛⎫⎛⎫+--=--+--=⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭18.【答案】(1)1()2sin 424f x x π⎛⎫=++⎪⎝⎭(2)对称中心2,0()2k k Z ππ⎛⎫-+∈ ⎪⎝⎭【难度】易【考点】正弦性函数图象、解析式与性质 【解析】(1)由题可得,max min ()()62222f x f x A --===,max min ()()62422f x f x h ++===,24422T ππππω⎡⎤⎛⎫=--⨯==⎪⎢⎥⎝⎭⎣⎦,2142πωπ==,2f π⎛⎫⎪⎝⎭为函数最大值,1+2()222k k Z ππϕπ⨯=+∈,由02πϕ<<得4πϕ=,综上,1()2sin 424f x x π⎛⎫=++⎪⎝⎭.(2)由1()24x k k Z ππ+=∈得对称中心为2,0()2k k Z ππ⎛⎫-+∈ ⎪⎝⎭19.【答案】(1)函数最小值为2,最大值为3 (2)(1,4) 【难度】中【考点】正弦型函数的值域,绝对值不等式 【解析】(1)∵函数()12sin 23f x x π⎛⎫=+-⎪⎝⎭, ∵,42x ππ⎡⎤∈⎢⎥⎣⎦,∴22,363x πππ⎡⎤-∈⎢⎥⎣⎦,1sin 2,132x π⎛⎫⎡⎤-∈ ⎪⎢⎥⎝⎭⎣⎦,∴当236x ππ-=时,函数取得最小值为2,当232x ππ-=时,函数取得最大值为3.(2)若不等式()2f x m -<在,42x ππ⎡⎤∈⎢⎥⎣⎦上恒成立, 即31sin 2232m m x π-+⎛⎫<-<⎪⎝⎭在,42x ππ⎡⎤∈⎢⎥⎣⎦上恒成立, ∴3122m -<,且112m +>,由此求得1m >,或4m <, 故实数m 的取值范围为(1,4). 20. 【答案】(1)2a =,5b =- (2),()6k k k Z πππ⎛⎤+∈ ⎥⎝⎦【难度】中【考点】正弦型函数的图象与性质,诱导公式【解析】(1)∵0,2x π⎡⎤∈⎢⎥⎣⎦,∴72,666x πππ⎡⎤+∈⎢⎥⎣⎦ ∴1sin 2,162x π⎛⎫⎡⎤+∈- ⎪⎢⎥⎝⎭⎣⎦,∴[]2sin 22,6a x a a π⎛⎫-+∈- ⎪⎝⎭, ∴[](),3f x b a b ∈+,又∵5()1f x -≤≤, ∴5b =-,31a b +=,因此2a =,5b =-. (2)由(1)得,()4sin 216f x x π⎛⎫=-+- ⎪⎝⎭. 7()4sin 214sin 21266g x f x x x πππ⎛⎫⎛⎫⎛⎫=+=-+-=+- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,又由[]lg ()0g x >,得()1g x >,∴4sin 2116x π⎛⎫+-> ⎪⎝⎭, ∴1sin 262x π⎛⎫+> ⎪⎝⎭,∴5+222()666k x k k Z πππππ<+<+∈, 其中当222()662k x k k Z πππππ+<+≤+∈时,()g x 单调递增,即()6k x k k Z πππ<≤+∈,∴()g x 的单调增区间为,()6k k k Z πππ⎛⎤+∈ ⎥⎝⎦. 21.【答案】(1)当1a >时,解集是R ;当1a ≤时,解集是{}2x x a x a <>-或 (2)(]1,0- 【难度】中【考点】含参绝对值不等式,集合运算【解析】(1)由110x a -+->得11x a ->-, 当1a >时,解集是R ;当1a ≤时,解集是{}2x x a x a <>-或 (2)当1a >时,U C =∅,不满足条件,当1a ≤时,{}2U C A x a x a =≤≤-,∴2a a -≥,得1a ≤,由2sin 0x π=,得()x k k Z ππ=∈,即()x k k Z =∈,所以B Z =,当()U C A B 恰有3个元素时,a 满足22241a a a a a --≥⎧⎪--<⎨⎪≤⎩成立,解得10a -<≤,即a 的取值范围是(]1,0-.。
