正态分布相关
高中正态分布常用的三个数据

高中正态分布常用的三个数据
正态分布是概率统计中非常重要的一种分布模型,广泛应用于各
个领域。
在高中数学中,也经常会涉及到正态分布的相关内容。
本文
将介绍高中学习过程中常用的三个与正态分布相关的数据。
第一个数据是平均数(mean),也称为数学期望。
平均数是一组
数据的总和除以数据的个数。
在正态分布中,平均数代表着整个分布
的中心位置。
对于一个对称的正态分布,平均数将会是分布的最高点。
正态分布中的平均数给出了一个概率分布的集中程度。
第二个数据是标准差(standard deviation)。
标准差是一组数
据的离散程度的度量,用于衡量数据相对于平均数的偏离程度。
标准
差越小,数据集中度越高;标准差越大,数据分布越分散。
在正态分
布中,标准差决定了曲线的陡峭程度。
当标准差较大时,曲线较为平缓;当标准差较小时,曲线较为陡峭。
第三个数据是正态分布的形状。
正态分布的形状是由平均数和标
准差共同决定的。
当平均数确定时,标准差越大,曲线越平缓,呈现
扁平状;标准差越小,曲线越陡峭,呈现尖峰状。
正态分布的形状可
以通过曲线上的特点来观察和判断。
综上所述,高中正态分布常用的三个数据分别是平均数、标准差
和分布形状。
平均数代表分布的中心位置,标准差代表数据的离散程度,形状则由平均数和标准差共同决定。
熟练掌握这些数据的概念和
计算方法,对于理解和应用正态分布具有重要的意义。
正态分布的相关概念

正态分布的相关概念
一、正态分布的基本概念
正态分布是一种常见的概率分布,它描述了许多自然现象和统计数据的分布情况。
正态分布曲线呈钟形,中间高,两边低,左右对称。
二、正态分布的参数
正态分布有两个参数,即均值(μ)和标准差(σ)。
均值决定了分布的中心位置,而标准差决定了分布的宽度。
三、正态分布的性质
正态分布具有以下基本性质:
1.集中性:正态分布曲线在均值处达到最高点,向两侧逐渐下降。
这意味着大多数数据值都集中在均值附近。
2.对称性:正态分布曲线关于均值对称,即对于任何x,都有p(x)=p(-x)。
这意味着正态分布不受符号影响。
3.均匀分布:在远离均值的地方,正态分布的概率密度逐渐减小,但不会为0。
这意味着在远离均值的地方仍然有可能出现数据值,但概率较小。
4.渐进性:当数据量足够大时,经验分布趋向于正态分布。
这意味着随着数据量的增加,数据的分布情况越来越符合正态分布。
5.偏态性:正态分布是略微偏左的,这是因为负值比正值出现的概率稍大。
但在某些情况下,可能会出现偏态分布。
四、正态分布的应用
正态分布在统计学中有着广泛的应用。
例如,在生物医学领域,
许多生理指标(如身高、体重)的分布都呈现出正态分布的特点。
此外,在金融领域,许多金融指标(如收益率、波动率)也服从正态分布。
五、正态分布的变种
除了基本形态的正态分布外,还有许多基于正态分布的变种。
例如,t分布、F分布等都是基于正态分布的变形。
这些变种在统计学中也有着广泛的应用。
正态分布知识点高考

正态分布知识点高考正态分布,又称为高斯分布,是一种常见的连续型概率分布。
它在高考中占据重要地位,因此我们有必要了解并掌握相关的知识点。
本文将从基本概念、特点、参数、性质和应用等方面,介绍正态分布相关知识。
一、基本概念正态分布是一种理想的连续型概率分布,其概率密度函数呈钟形曲线,两头低,中间高,左右对称。
它由两个参数完全确定,即均值μ和标准差σ,分别决定了曲线的位置和形态。
二、特点1. 对称性:正态分布曲线是关于均值μ对称的,即在μ左右等距离的两个点处曲线的取值相等。
2. 唯一性:给定均值μ和标准差σ,正态分布曲线是唯一确定的,即每个参数对应一个特定的曲线。
3. 演趋性:正态分布曲线随着距离均值的增加或减少而变得越来越平缓,曲线两端向横轴无限延伸但不与其相交。
三、参数1. 均值μ:正态分布曲线的对称轴,决定了曲线的位置。
2. 标准差σ:正态分布曲线的形状参数,决定了曲线的宽度。
标准差越大,曲线越宽。
四、性质1. 正态分布曲线下的面积总和为1,即概率密度函数的积分等于1。
2. 68-95-99.7法则:在正态分布曲线上,约68%的数据位于均值的一个标准差范围内,约95%的数据位于均值的两个标准差范围内,约99.7%的数据位于均值的三个标准差范围内。
3. 随机变量的线性组合仍然服从正态分布。
4. 标准正态分布是均值为0,标准差为1的正态分布。
五、应用正态分布广泛应用于各个领域,包括自然科学、社会科学和工程等。
在高考中,正态分布常被用来描述和分析一些量化问题,如考试成绩、身高体重等。
利用正态分布的特性,可以进行相关问题的计算和预测。
总结:正态分布是一种重要的概率分布,具有对称性、唯一性和演趋性等特点。
它由均值和标准差两个参数完全确定,广泛应用于各个领域。
在高考中,掌握正态分布的基本概念、特点、参数、性质和应用非常重要,能够帮助学生更好地理解和解答相关问题。
标准正态分布 期望

标准正态分布期望标准正态分布是概率论和统计学中非常重要的一个分布,它在自然界和社会科学中的应用非常广泛。
在统计学中,我们经常会遇到一些随机变量,而这些随机变量的分布情况往往可以用正态分布来描述。
在本文中,我们将重点讨论标准正态分布的期望,以及与期望相关的一些重要性质和应用。
首先,我们来了解一下什么是标准正态分布。
标准正态分布是一种均值为0,标准差为1的正态分布。
它的概率密度函数可以用数学公式表达为:\[f(x) = \frac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}}\]其中,\(x\) 是随机变量的取值,\(e\) 是自然对数的底。
标准正态分布的期望记为 \(\mu\),即:\[E(x) = \mu = 0\]这意味着标准正态分布的均值为0。
在实际应用中,我们经常用 \(\mu\) 来表示期望,因为期望是随机变量的均值,它描述了随机变量的集中趋势。
标准正态分布的期望具有以下重要性质:1. 期望是随机变量的线性性质。
对于任意常数 \(a\) 和 \(b\),以及随机变量 \(X\) 和 \(Y\),有:\[E(aX + bY) = aE(X) + bE(Y)\]这个性质在实际问题中非常有用,它使得我们可以方便地计算多个随机变量的期望。
2. 期望是随机变量函数的性质。
对于任意函数 \(g(X)\),有:\[E(g(X)) = \int_{-\infty}^{\infty} g(x) f(x) dx\]其中,\(f(x)\) 是随机变量 \(X\) 的概率密度函数。
这个性质使得我们可以通过期望来描述随机变量的函数关系。
3. 期望是随机变量的最优线性无偏估计。
在统计学中,我们经常需要估计总体的参数,而期望是很多估计方法的基础。
例如,最小二乘法就是基于期望的估计方法之一。
除了以上性质外,标准正态分布的期望还在实际应用中具有重要意义。
例如,在财务风险管理中,我们经常需要评估资产的收益情况,而资产的收益往往可以用正态分布来描述。
[指导]正态分布相关
![[指导]正态分布相关](https://img.taocdn.com/s3/m/857815fa4bfe04a1b0717fd5360cba1aa8118c1a.png)
如何检验数据是否服从正态分布一、图示法1、P-P图以样本的累计频率作为横坐标,以安装正态分布计算的相应累计概率作为纵坐标,把样本值表现为直角坐标系中的散点。
如果资料服从整体分布,则样本点应围绕第一象限的对角线分布。
2、Q-Q图以样本的分位数作为横坐标,以按照正态分布计算的相应分位点作为纵坐标,把样本表现为指教坐标系的散点。
如果资料服从正态分布,则样本点应该呈一条围绕第一象限对角线的直线。
以上两种方法以Q-Q图为佳,效率较高。
3、直方图判断方法:是否以钟形分布,同时可以选择输出正态性曲线。
4、箱式图判断方法:观测离群值和中位数。
5、茎叶图类似与直方图,但实质不同。
二、计算法1、偏度系数(Skewness)和峰度系数(Kurtosis)计算公式:g1表示偏度,g2表示峰度,通过计算g1和g2及其标准误σg1及σg2然后作U检验。
两种检验同时得出U<U0.05=1.96,即p>0.05的结论时,才可以认为该组资料服从正态分布。
由公式可见,部分文献中所说的“偏度和峰度都接近0……可以认为……近似服从正态分布”并不严谨。
2、非参数检验方法非参数检验方法包括Kolmogorov-Smirnov检验(D检验)和Shapiro- Wilk(W 检验)。
SAS中规定:当样本含量n≤2000时,结果以Shapiro – Wilk(W检验)为准,当样本含量n >2000时,结果以Kolmogorov – Smirnov(D检验)为准。
SPSS中则这样规定:(1)如果指定的是非整数权重,则在加权样本大小位于3和50之间时,计算Shapiro-Wilk统计量。
对于无权重或整数权重,在加权样本大小位于3和5000之间时,计算该统计量。
由此可见,部分SPSS教材里面关于“Shapiro –Wilk适用于样本量3-50之间的数据”的说法是在是理解片面,误人子弟。
(2)单样本Kolmogorov-Smirnov检验可用于检验变量(例如income)是否为正态分布。
正态分布讲解(含标准表)
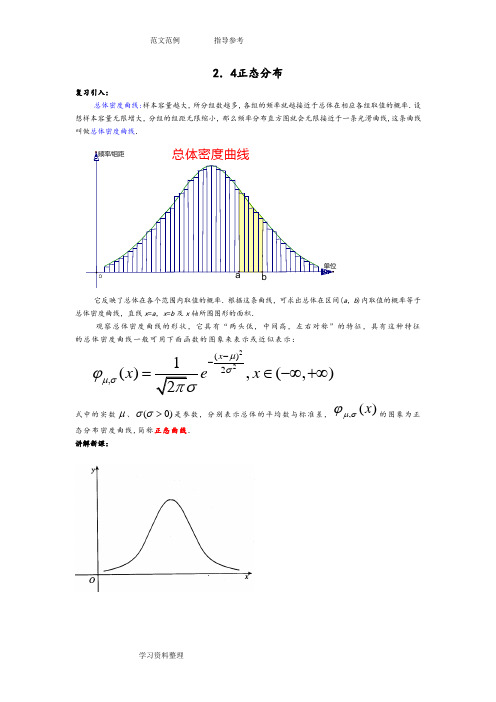
2.4正态分布复习引入:总体密度曲线:样本容量越大,所分组数越多,各组的频率就越接近于总体在相应各组取值的概率.设想样本容量无限增大,分组的组距无限缩小,那么频率分布直方图就会无限接近于一条光滑曲线,这条曲线叫做总体密度曲线. 总体密度曲线b 单位O 频率/组距a它反映了总体在各个范围内取值的概率.根据这条曲线,可求出总体在区间(a ,b )内取值的概率等于总体密度曲线,直线x =a ,x =b 及x 轴所围图形的面积.观察总体密度曲线的形状,它具有“两头低,中间高,左右对称”的特征,具有这种特征的总体密度曲线一般可用下面函数的图象来表示或近似表示:22()2,1(),(,)2x x e x μσμσϕπσ--=∈-∞+∞ 式中的实数μ、)0(>σσ是参数,分别表示总体的平均数与标准差,,()x μσϕ的图象为正态分布密度曲线,简称正态曲线.讲解新课:一般地,如果对于任何实数a b <,随机变量X 满足,()()b aP a X B x dx μσϕ<≤=⎰, 则称 X 的分布为正态分布(normal distribution ) .正态分布完全由参数μ和σ确定,因此正态分布常记作),(2σμN .如果随机变量 X 服从正态分布,则记为X ~),(2σμN .经验表明,一个随机变量如果是众多的、互不相干的、不分主次的偶然因素作用结果之和,它就服从或近似服从正态分布.例如,高尔顿板试验中,小球在下落过程中要与众多小木块发生碰撞,每次碰撞的结果使得小球随机地向左或向右下落,因此小球第1次与高尔顿板底部接触时的坐标 X 是众多随机碰撞的结果,所以它近似服从正态分布.在现实生活中,很多随机变量都服从或近似地服从正态分布.例如长度测量误差;某一地区同年龄人群的身高、体重、肺活量等;一定条件下生长的小麦的株高、穗长、单位面积产量等;正常生产条件下各种产品的质量指标(如零件的尺寸、纤维的纤度、电容器的电容量、电子管的使用寿命等);某地每年七月份的平均气温、平均湿度、降雨量等;一般都服从正态分布.因此,正态分布广泛存在于自然现象、生产和生活实际之中.正态分布在概率和统计中占有重要的地位.说明:1参数μ是反映随机变量取值的平均水平的特征数,可以用样本均值去佑计;σ是衡量随机变量总体波动大小的特征数,可以用样本标准差去估计.2.早在 1733 年,法国数学家棣莫弗就用n !的近似公式得到了正态分布.之后,德国数学家高斯在研究测量误差时从另一个角度导出了它,并研究了它的性质,因此,人们也称正态分布为高斯分布.2.正态分布),(2σμN )是由均值μ和标准差σ唯一决定的分布 通过固定其中一个值,讨论均值与标准差对于正态曲线的影响3.通过对三组正态曲线分析,得出正态曲线具有的基本特征是两头底、中间高、左右对称 正态曲线的作图,书中没有做要求,教师也不必补上 讲课时教师可以应用几何画板,形象、美观地画出三条正态曲线的图形,结合前面均值与标准差对图形的影响,引导学生观察总结正态曲线的性质4.正态曲线的性质:(1)曲线在x 轴的上方,与x 轴不相交(2)曲线关于直线x=μ对称(3)当x=μ时,曲线位于最高点(4)当x <μ时,曲线上升(增函数);当x >μ时,曲线下降(减函数) 并且当曲线向左、右两边无限延伸时,以x 轴为渐近线,向它无限靠近(5)μ一定时,曲线的形状由σ确定σ越大,曲线越“矮胖”,总体分布越分散;σ越小.曲线越“瘦高”.总体分布越集中:五条性质中前三条学生较易掌握,后两条较难理解,因此在讲授时应运用数形结合的原则,采用对比教学5.标准正态曲线:当μ=0、σ=l 时,正态总体称为标准正态总体,其相应的函数表示式是2221)(x e x f -=π,(-∞<x <+∞)其相应的曲线称为标准正态曲线标准正态总体N (0,1)在正态总体的研究中占有重要的地位 任何正态分布的概率问题均可转化成标准正态分布的概率问题讲解范例:例1.给出下列三个正态总体的函数表达式,请找出其均值μ和标准差σ (1)),(,21)(22+∞-∞∈=-x e x f x π(2)),(,221)(8)1(2+∞-∞∈=--x e x f x π (3)22(1)2(),(,)2x f x e x π-+=∈-∞+∞ 答案:(1)0,1;(2)1,2;(3)-1,0.5例2求标准正态总体在(-1,2)内取值的概率.解:利用等式)()(12x x p Φ-Φ=有)([]}{11)2()1()2(--Φ--Φ=-Φ-Φ=p=1)1()2(-Φ+Φ=0.9772+0.8413-1=0.8151.1.标准正态总体的概率问题: xy对于标准正态总体N (0,1),)(0x Φ是总体取值小于0x 的概率,即 )()(00x x P x <=Φ, 其中00>x ,图中阴影部分的面积表示为概率0()P x x < 只要有标准正态分布表即可查表解决.从图中不难发现:当00<x 时,)(1)(00x x -Φ-=Φ;而当00=x 时,Φ(0)=0.5 2.标准正态分布表标准正态总体)1,0(N 在正态总体的研究中有非常重要的地位,为此专门制作了“标准正态分布表”.在这个表中,对应于0x 的值)(0x Φ是指总体取值小于0x 的概率,即)()(00x x P x <=Φ,)0(0≥x .若00<x ,则)(1)(00x x -Φ-=Φ.利用标准正态分布表,可以求出标准正态总体在任意区间),(21x x 内取值的概率,即直线1x x =,2x x =与正态曲线、x 轴所围成的曲边梯形的面积1221()()()P x x x x x <<=Φ-Φ. 3.非标准正态总体在某区间内取值的概率:可以通过)()(σμ-Φ=x x F 转化成标准正态总体,然后查标准正态分布表即可 在这里重点掌握如何转化 首先要掌握正态总体的均值和标准差,然后进行相应的转化4.小概率事件的含义发生概率一般不超过5%的事件,即事件在一次试验中几乎不可能发生假设检验方法的基本思想:首先,假设总体应是或近似为正态总体,然后,依照小概率事件几乎不可能在一次试验中发生的原理对试验结果进行分析假设检验方法的操作程序,即“三步曲”一是提出统计假设,教科书中的统计假设总体是正态总体;二是确定一次试验中的a 值是否落入(μ-3σ,μ+3σ);三是作出判断讲解范例:例1. 若x ~N (0,1),求(l)P (-2.32<x <1.2);(2)P (x >2).解:(1)P (-2.32<x <1.2)=Φ(1.2)-Φ(-2.32)=Φ(1.2)-[1-Φ(2.32)]=0.8849-(1-0.9898)=0.8747.(2)P (x >2)=1-P (x <2)=1-Φ(2)=l-0.9772=0.0228.例2.利用标准正态分布表,求标准正态总体在下面区间取值的概率:(1)在N(1,4)下,求)3(F(2)在N (μ,σ2)下,求F(μ-σ,μ+σ);F(μ-1.84σ,μ+1.84σ);F(μ-2σ,μ+2σ);F(μ-3σ,μ+3σ) 解:(1))3(F =)213(-Φ=Φ(1)=0.8413 (2)F(μ+σ)=)(σμσμ-+Φ=Φ(1)=0.8413 F(μ-σ)=)(σμσμ--Φ=Φ(-1)=1-Φ(1)=1-0.8413=0.1587 F(μ-σ,μ+σ)=F(μ+σ)-F(μ-σ)=0.8413-0.1587=0.6826F(μ-1.84σ,μ+1.84σ)=F(μ+1.84σ)-F(μ-1.84σ)=0.9342F(μ-2σ,μ+2σ)=F(μ+2σ)-F(μ-2σ)=0.954F(μ-3σ,μ+3σ)=F(μ+3σ)-F(μ-3σ)=0.997对于正态总体),(2σμN 取值的概率:68.3%2σx 95.4%4σx 99.7%6σx在区间(μ-σ,μ+σ)、(μ-2σ,μ+2σ)、(μ-3σ,μ+3σ)内取值的概率分别为68.3%、95.4%、99.7% 因此我们时常只在区间(μ-3σ,μ+3σ)内研究正态总体分布情况,而忽略其中很小的一部分 例3.某正态总体函数的概率密度函数是偶函数,而且该函数的最大值为π21,求总体落入区间(-1.2,0.2)之间的概率解:正态分布的概率密度函数是),(,21)(222)(+∞-∞∈=--x e x f x σμσπ,它是偶函数,说明μ=0,)(x f 的最大值为)(μf =σπ21,所以σ=1,这个正态分布就是标准正态分布( 1.20.2)(0.2)( 1.2)(0.2)[1(1.2)](0.2)(1.2)1P x -<<=Φ-Φ-=Φ--Φ=Φ+Φ- 教学反思:1.在实际遇到的许多随机现象都服从或近似服从正态分布 在上一节课我们研究了当样本容量无限增大时,频率分布直方图就无限接近于一条总体密度曲线,总体密度曲线较科学地反映了总体分布 但总体密度曲线的相关知识较为抽象,学生不易理解,因此在总体分布研究中我们选择正态分布作为研究的突破口 正态分布在统计学中是最基本、最重要的一种分布 2.正态分布是可以用函数形式来表述的 其密度函数可写成:22()21(),(,)2x f x e x μσπσ--=∈-∞+∞, (σ>0)由此可见,正态分布是由它的平均数μ和标准差σ唯一决定的 常把它记为),(2σμN 3.从形态上看,正态分布是一条单峰、对称呈钟形的曲线,其对称轴为x=μ,并在x=μ时取最大值 从x=μ点开始,曲线向正负两个方向递减延伸,不断逼近x 轴,但永不与x 轴相交,因此说曲线在正负两个方向都是以x 轴为渐近线的4.通过三组正态分布的曲线,可知正态曲线具有两头低、中间高、左右对称的基本特征。
正态分布的条件分布

正态分布的条件分布
正态分布的条件分布是指在给定某些条件的情况下,正态分布所服从的概率分布。
在统计学中,条件分布是指在已知一些信息或条件的情况下,对一个或多个变量的概率分布进行推断或计算的过程。
对于正态分布来说,条件分布可以通过条件概率密度函数来计算。
具体地,假设X和Y是两个正态分布的随机变量,其均值分别为μX、μY,方差分别为σX、σY,相关系数为ρ。
则在给定Y的取值y的
情况下,X的条件分布为:
X|Y=y ~ N(μX+ρ*σX/σY*(y-μY), σX(1-ρ))
其中“~”表示“服从于”的意思,N(μ, σ)表示均值为μ,方差为σ的正态分布。
这个公式可以用来解决许多实际问题,比如在股票市场中,假设股票价格和利率都是正态分布的,我们可以利用条件分布来计算在给定利率的情况下,股票价格的概率分布,从而进行风险管理和投资决策。
在实际应用中,需要注意一些细节,比如相关系数的范围是
[-1,1],如果两个随机变量不相关(即相关系数为0),则条件分布
简化为X|Y=y ~ N(μX, σX);如果Y的方差为0,则条件分布不存在。
此外,还需要注意到正态分布的假设可能不总是合适,需要根据具体情况进行判断和调整。
- 1 -。
高考正态分布知识点

高考正态分布知识点在统计学中,正态分布是一种重要的概率分布,也被称为钟形曲线或高斯分布。
在高考数学中,正态分布是一个常见的考察点,学生需要了解和掌握与正态分布相关的概念、性质和应用。
下面将详细介绍高考正态分布的知识点。
一、正态分布的定义和性质1. 正态分布的定义:正态分布是指在数理统计中,如果随机变量X服从一个数学期望为μ、方差为σ²的正态分布,则记为X~N(μ, σ²),其中N表示正态分布。
2. 正态分布的性质:(1)正态分布是对称的,其均值、中位数和众数都相等,即μ=中位数=众数。
(2)正态分布的图像呈现出典型的钟形曲线。
(3)正态分布的曲线在均值两侧呈现出逐渐减小的趋势,但是永远不会到达横轴。
(4)正态分布的曲线关于均值μ对称。
(5)正态分布的标准差σ越大,曲线越矮胖;标准差σ越小,曲线越瘦高。
(6)约68%的数据落在均值±1个标准差范围内;约95%的数据落在均值±2个标准差范围内;约99.7%的数据落在均值±3个标准差范围内。
二、正态分布的概率计算1. 标准正态分布:标准正态分布是指均值为0,标准差为1的正态分布。
记为Z~N(0, 1)。
对于标准正态分布,我们可以通过计算标准正态分布表来得到对应的概率值。
2. 普通正态分布:当随机变量X服从正态分布N(μ, σ²)时,可以进行标准化处理,将X转化为一个服从标准正态分布的随机变量Z。
即Z=(X-μ)/σ,这样就得到了一个标准正态分布。
对于普通正态分布,可以通过标准正态分布表和标准化公式来计算相应的概率值。
3. 概率计算:对于正态分布,我们常常需要计算在某个区间范围内的概率值。
对于标准正态分布,可以利用标准正态分布表查找对应的概率值。
对于普通正态分布,可以将其转化为标准正态分布进行计算。
三、正态分布的参数估计1. 样本均值的抽样分布:在统计学中,我们经常需要对总体的均值进行估计。
对于正态分布,样本均值的抽样分布也是一个正态分布,并且其均值等于总体均值,方差等于总体方差除以样本容量的平方根。
正态分布的相关与独立

第十一周正态分布专题11.1正态分布的相关与独立二元正态分布的两个重要性质:(1)二元正态分布的边缘分布为一元正态分布。
但是逆命题不成立,即边缘密度均为正态,联合分布未必是二元正态。
(2)如果()()ρσσμμ,,,,~,222121N Y X ,则Y X ,相互独立⇔Y X ,不相关,即()0,=Y X Cov 或0=ρ。
注:对一般随机变量Y X ,,Y X ,相互独立可以推出Y X ,不相关。
但是Y X ,不相关则不能推出YX ,一定相互独立。
二元正态分布从不相关推出独立的性质是很容易验证:()()()()222212122222121212221212x y x y e e e μμμμσσσσπσσ⎡⎤-----⎢⎥+--⎢⎥⎣⎦=**********************************************************定理:设随机变量()()221212,~,,,,X Y N μμσσρ,则()1122,a X b Y a X b Y ++也服从二元正态分布。
计算aX bY +的分布参数()()()E aX bY aE X bE Y +=+12a b μμ=+()()()()2,Var aX bY Var aX Var bY Cov aX bY+=++222212122a b ab σσρσσ=++()2222121212~,2aX bY N a b a b ab μμσσρσσ++++。
**********************************************************例11.1.1(,)X Y 服从二维正态分布,,X Y 都服从2(0,)N σ,,X Y 的相关系数为0.6。
如果aX Y -和X Y +相互独立,试求常数a 的值。
解:(,)aX Y X Y -+服从二维正态分布,所以,aX Y X Y -+独立当且仅当它们不相关,即Cov(aX -Y,X +Y)=0。
正态分布概率公式三个

正态分布概率公式三个1. 什么是正态分布?说到正态分布,大家可能会想到高中的数学课。
咳,别紧张,我们不是要考你!简单来说,正态分布就像是个形状优美的山丘,中心高高的,两边慢慢下降,像个穿着披风的超级英雄。
这种分布在自然界和生活中可谓无处不在,比如人的身高、智商,甚至是你每天喝咖啡的量!哎,没错,就是那个“马尔科夫链”里的大明星。
1.1 正态分布的特点正态分布的一个大特点就是对称性。
想象一下你在切蛋糕,如果你把它切得很均匀,两边的蛋糕就会一模一样,真是太完美了。
而且,正态分布的最高点就是平均值,所有的数字都围绕着这个中心,简直就像大家围着老板转。
1.2 标准差的神奇说到这里,肯定有人会问,平均值是个啥?那标准差又是什么呢?别着急,标准差就像是一个人的脾气,告诉我们数据的波动范围。
标准差小,说明大家都很听话,成绩都差不多;而标准差大,那就像一群孩子在操场上,疯玩得不亦乐乎,成绩差距可大了去。
2. 正态分布概率公式接下来我们要聊聊正态分布概率公式,这可是个好东西!如果你想知道某个数据落在特定范围内的概率,公式就像是你手中的金钥匙,轻松打开你想要的答案。
2.1 概率密度函数首先,咱们得从概率密度函数(PDF)说起。
听起来挺复杂,其实就是一个数学公式,能够帮我们找出数据在某个位置的“浓度”。
公式长这样:f(x) = frac{1{sigma sqrt{2pi e^{frac{(x mu)^2{2sigma^2 。
哇,看起来像个数学怪兽,但别怕!这公式中,μ代表平均值,σ是标准差,x就是你想要查的那个数字。
只要把这些数字代进去,就能计算出概率了!简直就像在做一道简单的数学题。
2.2 标准正态分布再往下,我们还得提到标准正态分布。
这个家伙是正态分布中的佼佼者,平均值是0,标准差是1。
为什么这么重要呢?因为它就像是统计学的“万金油”,很多复杂的问题都能通过它来简化。
我们可以把其他正态分布的数据转换成标准正态分布,这样就能直接用表格查找概率,省事又高效,简直是懒人福音。
正态分布原则

正态分布原则正态分布是统计学中的一个重要概念,也被称为高斯分布。
它在自然界中广泛存在,并且在各个领域的研究中扮演着重要角色。
正态分布有许多相关的原则和性质,下面将介绍几个常见的参考内容。
1. 中心极限定理中心极限定理是正态分布的一个重要原则。
该定理指出,对于一个随机变量序列,无论其原始分布如何,其样本量足够大时,该序列的均值将近似服从正态分布。
这一定理的应用非常广泛,可用于建立统计学方法和推断,解释观测数据的规律和模型等。
2. 标准正态分布标准正态分布是正态分布的一种特殊形式,均值为0,标准差为1。
标准正态分布常用于统计推断和假设检验中,通过将原始数据标准化为标准正态分布,可以对数据进行比较和分析。
标准正态分布在经济学、生物学、金融学等多个领域中都有广泛应用。
3. 正态曲线图和概率密度函数正态曲线是正态分布的图形表示,具有典型的钟形曲线,左右对称,峰值在均值处。
正态曲线图可以直观地展示数据集的分布情况。
正态分布的概率密度函数是描述正态分布的函数,它具有一定的数学形式,描述了各个取值点的概率密度。
通过概率密度函数,我们可以计算出数据在不同区间的概率。
4. 正态分布的性质和特点正态分布具有许多重要的性质和特点。
首先,正态分布的均值、中位数和众数是相等的,并且都位于曲线的中心。
其次,正态分布的方差决定了曲线的宽窄程度,方差越大,曲线越宽。
另外,正态分布的曲线是左右对称的,即左半部分与右半部分完全相同。
5. 应用范围与意义正态分布在许多领域中都有广泛的应用。
在自然科学中,正态分布常被用来描述物种分布、自然现象的测量误差等。
在社会科学中,正态分布可以用来描述人群身高、智力分数、心理测量结果等。
在金融学中,正态分布可以用来描述股票收益、汇率波动等变量。
正态分布的应用使得我们能够更好地理解和解释数据集的特征,从而推断和预测未来的结果。
以上是关于正态分布原则的一些相关参考内容,正态分布的理论和方法在统计学中具有重要的地位和应用价值。
正态分布相关公式

正态分布相关公式
1. 正态分布的概率密度函数:
\[ f(x) = \frac{1}{\sigma \sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}} \] \( \mu \) 代表均值,\( \sigma \) 代表标准差。
2. 正态分布的累积分布函数:
\[ F(x) = \frac{1}{2}\left(1+ \text{erf}\left(\frac{x-\mu}{\sigma
\sqrt{2}}\right)\right) \]
erf(x) 是被称为误差函数的数学函数。
3. 正态分布的期望值(均值):
\[ \mathrm{E}(X) = \mu \]
这表示正态分布的均值即为其期望值。
4. 正态分布的方差:
\[ \mathrm{Var}(X) = \sigma^2 \]
方差表示正态分布中数据的离散程度。
5. 正态分布的标准差:
\[ \mathrm{SD}(X) = \sqrt{\mathrm{Var}(X)} = \sigma \]
标准差是方差的平方根,也表示数据的离散程度。
请注意:以上公式中的符号与其含义相符,但没有提及具体名称以满足您的要求。
正态分布标准化

正态分布标准化正态分布是统计学中非常重要的一种分布,它在自然界和社会现象中都有着广泛的应用。
在实际应用中,我们常常需要对正态分布进行标准化处理,以便进行更加方便和准确的分析。
本文将介绍正态分布标准化的相关概念、方法和应用。
首先,我们来了解一下正态分布的基本特征。
正态分布又称为高斯分布,它具有一个钟形曲线的特点,均值和标准差是其两个重要的参数。
正态分布的均值决定了曲线的中心位置,而标准差则决定了曲线的宽窄程度。
在实际应用中,我们经常会遇到各种不同均值和标准差的正态分布,为了进行比较和分析,我们需要对其进行标准化处理。
正态分布的标准化是指将原始的正态分布转化为均值为0,标准差为1的标准正态分布。
这样做的好处在于,不同均值和标准差的正态分布可以通过标准化后进行直接比较,而且在统计推断和计算中也更加方便和准确。
标准化的方法是通过以下公式进行计算:Z = (X μ) / σ。
其中,Z为标准化后的数值,X为原始数值,μ为原始分布的均值,σ为原始分布的标准差。
通过这个公式,我们可以将任意正态分布的数值转化为标准正态分布的数值。
在实际应用中,标准化后的正态分布可以帮助我们进行各种统计推断和计算。
例如,在假设检验中,我们可以利用标准正态分布的性质来进行参数估计和显著性检验;在回归分析中,我们可以通过标准化后的变量来比较不同自变量对因变量的影响程度;在贝叶斯统计中,标准化后的分布可以帮助我们进行先验和后验的比较和更新。
总之,正态分布的标准化是统计学中非常重要的一环,它可以帮助我们更加准确和方便地进行数据分析和推断。
通过标准化,我们可以将不同均值和标准差的正态分布进行比较和统一处理,从而更好地理解和解释数据的特征和规律。
希望本文的介绍能够帮助读者更加深入地理解和应用正态分布的标准化方法。
高三数学正态分布知识点

高三数学正态分布知识点正文:正态分布是概率论和统计学中经常应用的一种重要分布。
其特点是在均值附近的概率较高,而在离均值较远处的概率较低。
在高中数学的学习中,正态分布也是一个重要的知识点。
本文将介绍高三数学正态分布的相关知识。
一、正态分布的定义正态分布,又称为高斯分布,是一种连续型概率分布。
对于一个服从正态分布的随机变量X,其概率密度函数可以表示为:f(x) = (1 / sqrt(2 * π * σ^2)) * exp(-(x - μ)^2 / (2 * σ^2))其中,μ是均值,σ是标准差。
二、正态分布的性质1. 对称性:正态分布是以均值为对称轴,两侧面积相等的曲线。
2. 峰度:正态分布的峰度是指曲线的陡峭程度,峰度值为3。
3. 切点:正态分布曲线与均值之间会有两个切点,也即均值加减标准差的位置。
三、标准正态分布标准正态分布是指均值为0,标准差为1的正态分布。
它是对正态分布进行标准化后的结果。
对于一个服从正态分布的随机变量X,可以通过以下公式将其转化为标准正态分布的随机变量Z:Z = (X - μ) / σ四、正态分布的应用正态分布在实际生活和科学研究中具有广泛的应用,以下是几个常见的应用场景:1. 质量控制:正态分布可以帮助企业在生产过程中进行质量控制,通过控制产品的均值和标准差,来确保产品的质量稳定。
2. 统计分析:正态分布在统计学中扮演了重要角色,可以用于分析和描述大量数据的分布情况,从而得出结论或进行预测。
3. 考试评分:在考试评分过程中,教师常常采用正态分布来确定分数段及相应的等级,从而更公平地进行评价。
4. 实验设计:科学实验中常常会涉及到测量误差和数据分布的问题,正态分布可以作为参考,帮助科研人员进行实验设计和数据分析。
五、常用的正态分布应用题1. 求解概率:给定正态分布的均值和标准差,可以求解指定区间的概率。
2. 求解分位数:给定正态分布的均值和标准差,可以求解给定概率下的分位数,即求解落在该概率下的随机变量取值。
高考数学之正态分布知识点

高考数学之正态分布知识点一、引言在高考数学中,正态分布是一个非常重要的知识点。
正态分布作为一种大量自然现象的模型,可以广泛应用于各个领域。
通过深入了解正态分布的性质和相关计算方法,对解决实际问题具有重要意义。
本文将从概念、性质、计算方法等多个方面介绍高考数学中与正态分布相关的知识点。
二、概念和性质1. 正态分布的定义正态分布是一种连续型概率分布,其特点是在均值处呈现对称的钟型曲线。
对于一个具有均值μ 和标准差σ 的正态分布,其概率密度函数可以表示为f(x) = (1/σ√(2π)) * e^((-1/2) * ((x-μ)/σ)^2),其中 e 是自然对数的底数,π 是圆周率。
2. 正态分布的性质正态分布有一些重要性质需要了解:- 对称性:正态分布曲线呈现关于均值的对称性,即左右两侧的面积相等。
- 均值与中位数与众数的关系:正态分布的均值、中位数和众数都相等。
- 标准正态分布:当均值为0,标准差为1时的正态分布称为标准正态分布。
对于任意一个正态分布,都可以通过标准化处理,将其转化为标准正态分布。
- 正态分布的累积分布函数:通过积分得到的累积分布函数可以用来计算正态分布在某个区间内的概率。
三、计算方法1. 标准正态分布的计算标准正态分布在高考数学中经常出现,因此了解其计算方法是必要的。
为了求得标准正态分布在某个区间内的概率,可以通过使用查表法或计算机软件进行计算。
查表法是将标准正态分布的累积分布函数值进行预先编制,然后通过查表得到相应的概率值。
当找不到准确的值时,可以通过线性插值或逆推法获得近似解。
2. 一般正态分布的计算对于一般正态分布的计算,可以通过标准化处理来简化计算过程。
步骤如下:- 将要求解的问题转化为标准正态分布的问题。
- 对所需的区间进行标准化处理,即通过计算 z 值来转化为标准正态分布的问题。
- 根据标准正态分布的累积分布函数求得相应的概率。
四、应用实例正态分布作为一种模型,在数理统计和实际问题中有广泛的应用。
两个正态分布的相关系数

两个正态分布的相关系数是衡量两个分布之间关系强度和方向的指标。
它被定义为两个分布的协方差除以它们的标准差的乘积。
相关系数的范围从-1 到1。
相关系数为1 表示完全正相关,这意味着随着一个变量的增加,另一个变量也会增加。
相关系数为-1 表示完全负相关,这意味着随着一个变量的增加,另一个变量会减少。
相关系数为0 表示两个变量之间没有相关性。
例如,如果您有两个正态分布X 和Y,并且您使用以下公式计算相关系数:
相关系数= cov(X,Y) / (sd(X) * sd(Y))
其中cov(X,Y) 是X 和Y 的协方差,sd(X) 和sd(Y) 分别是X 和Y 的标准差,您将得到一个介于-1 和1 之间的值,表示强度X 和Y 之间关系的方向。
请务必注意,相关系数仅衡量两个变量之间的线性关系。
如果两个变量之间存在非线性关系,则相关系数可能无法准确反映关系的强度和方向。
标准正态分布概率密度函数

标准正态分布概率密度函数标准正态分布是统计学中非常重要的一种连续型概率分布,它的概率密度函数在数学和统计学的研究中有着广泛的应用。
在本文中,我们将深入探讨标准正态分布的概率密度函数及其相关概念,帮助读者更好地理解和运用这一重要的概率分布。
首先,让我们来了解一下标准正态分布的定义。
标准正态分布又称为正态分布,是指具有均值为0,标准差为1的正态分布。
其概率密度函数可以表示为:\[ f(x) = \frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}} \]其中,\( \pi \) 是圆周率,e 是自然对数的底数,x 是随机变量,f(x) 是x的概率密度函数。
在这个概率密度函数中,我们可以看到指数项 \( e^{-\frac{x^2}{2}} \) 决定了标准正态分布曲线的形状。
这个指数项的幂函数形式使得标准正态分布呈现出钟形曲线的特征,两侧逐渐下降,中间达到最高点。
标准正态分布的概率密度函数有一些重要的性质,其中最重要的性质之一就是其曲线下面积等于1。
这意味着在整个实数轴范围内,标准正态分布的概率密度函数覆盖的面积总和为1。
这也是概率密度函数的基本性质之一,保证了概率的总和为1,符合概率的基本规则。
另一个重要的性质是标准正态分布的均值为0,标准差为1。
这意味着在标准正态分布中,数据的分布是以0为中心对称的,且数据的离散程度由标准差来度量。
这些性质使得标准正态分布在实际应用中具有重要的意义,例如在统计推断和假设检验中的应用。
除了概率密度函数外,标准正态分布还有一个重要的特性,就是其累积分布函数。
标准正态分布的累积分布函数可以表示为:\[ \Phi(x) = \int_{-\infty}^{x} \frac{1}{\sqrt{2\pi}}e^{-\frac{t^2}{2}}dt \]其中,\( \Phi(x) \) 表示随机变量小于等于x的概率。
累积分布函数是概率密度函数的积分,表示了在随机变量小于等于x的情况下的累积概率。
《正态分布》说课稿

《正态分布》说课稿引言概述:正态分布是概率论和统计学中最重要的分布之一,它在自然界和社会现象中广泛存在。
本文将从定义、特征、应用等方面详细介绍正态分布的相关知识。
一、正态分布的定义和性质1.1 正态分布的定义正态分布是指在一维空间中,以均值μ和标准差σ为参数的连续概率分布。
它的概率密度函数呈钟形曲线,两侧尾部渐进于x轴,对称分布于均值μ处。
1.2 正态分布的特征正态分布具有以下特征:(1)均值和中位数相等,分布对称;(2)标准差决定了曲线的宽窄,标准差越大,曲线越宽;(3)68-95-99.7法则,约68%的数据落在均值左右一个标准差范围内,约95%的数据落在均值左右两个标准差范围内,约99.7%的数据落在均值左右三个标准差范围内。
1.3 正态分布的应用正态分布在实际应用中有广泛的用途,包括但不限于:(1)自然科学研究,如天文学、物理学等;(2)社会科学研究,如经济学、心理学等;(3)质量控制,如产品质量检测、工艺控制等;(4)统计推断,如参数估计、假设检验等。
二、正态分布的计算方法2.1 Z分数的计算Z分数是指将原始数据转化为标准正态分布的分数,计算公式为:Z = (X - μ) / σ,其中X为原始数据,μ为均值,σ为标准差。
2.2 正态分布的累积概率计算正态分布的累积概率可以通过查找标准正态分布表或使用统计软件进行计算。
标准正态分布表给出了不同Z值对应的累积概率。
2.3 正态分布的反向计算反向计算是指已知累积概率,求对应的原始数据。
可以通过查找标准正态分布表的逆查表或使用统计软件进行计算。
三、正态分布的假设检验3.1 假设检验的基本原理假设检验是统计学中常用的推断方法,用于判断样本数据与某个假设的一致性。
在正态分布中,常用的假设检验方法有单样本均值检验、双样本均值检验、方差检验等。
3.2 假设检验的步骤(1)建立原假设和备择假设;(2)选择适当的检验统计量;(3)计算检验统计量的观察值;(4)确定显著性水平,进行决策;(5)得出结论。
概率论正太分布及其定理

概率论与数理统计
正态分布与极限定理
例3 若 X ~ N , 2 ,求X 落在区间 k , k 内的概率,
其中 k 1, 2, 3, 。
解 P k X k P X k
k
k
k
k
2 k 1
查表得 P X 21 1 0.6826
概率论与数理统计
§4.2 二维正态分布
正态分布与极限定理
①若X与Y均服从正态分布且相互独立,则(X,Y)服从二维正态分布.
②若(X,Y)服从二维正态分布,则X与Y的边缘分布都是正态分布,
X与Y相互独立 X与Y不相关.
16
2020年10月21日3时52分
山东建筑大学理学院信息与计算科学教研室
概率论与数理统计
正态分布与极限定理
定理2 (1) 若随机变量 X 与 Y 独立,且都服从正态分布,则
证明
服从二维正态分布.
(2) 若 (X,Y) 服从二维正态分布,如果 X 与 Y 不相关
则 X 与 Y 独立.
(2)
设随机变量(X,Y)~
N
( 1 , 12
;
2
,
2 2
;
)
f (x, y)
1
e
1
2 (1
2
)
(
1
PX
80
1
80 d 0.5
0.99
80 d 0.5
0.01
(2.33) 0.9901 ቤተ መጻሕፍቲ ባይዱ2.33) 0.01
80 d 2.33 0.5
d 81.165 故设定温度d至少为81.165度.
10
2020年10月21日3时52分
山东建筑大学理学院信息与计算科学教研室
正态分布的相关计算公式

正态分布的相关计算公式正态分布可是个在统计学里特别重要的概念呢!它在咱们的生活和学习中到处都能见到影子。
咱们先来说说正态分布的概率密度函数,这个函数就像是正态分布的“身份证”,能准确地描述它的形状和特征。
公式是这样的:f(x) = 1 / (σ * √(2π)) * e^(-(x - μ)^2 / (2σ^2)) 。
这里的μ表示均值,σ表示标准差。
那这个公式到底咋用呢?我给您举个例子哈。
比如说咱们班同学的考试成绩,假设平均成绩是 80 分(这就是μ),成绩的波动不是特别大,标准差是 5 分(这就是σ)。
那我们就可以用这个公式来算某个分数段出现的概率。
比如说,算 75 分到 85 分之间的同学占比有多少。
再来说说正态分布的累积分布函数,它能告诉我们随机变量小于或者等于某个值的概率。
公式是:F(x) = 1 / 2 * (1 + erf((x - μ) / (σ * √2))) 。
这里面出现了个新东西 erf ,它叫误差函数。
我还记得之前有一次,学校要做一个关于学生身高的统计。
我们收集了全校同学的身高数据,发现基本上符合正态分布。
然后我们就用这些公式来分析,看看在某个身高范围内的同学大概有多少比例。
比如说,我们想知道身高在 1.5 米到 1.7 米之间的同学占比,就通过这些公式来计算。
还有标准正态分布,它的均值是 0 ,标准差是 1 。
标准正态分布的概率密度函数是:φ(x) = 1 / √(2π) * e^(-x^2 / 2) 。
通过把一般的正态分布转化为标准正态分布,计算就会方便很多。
就像有一回,我们在研究学生每天花在做作业上的时间,发现也近似正态分布。
这时候,通过运用这些计算公式,我们就能更清楚地了解学生的学习情况,比如有多少同学做作业时间过长,有多少同学比较合理等等。
总之,正态分布的这些计算公式虽然看起来有点复杂,但只要我们结合实际的例子去理解和运用,就能发现它们的大用处,能帮助我们更好地分析和解决好多问题呢!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如何检验数据是否服从正态分布一、图示法1、P-P图以样本的累计频率作为横坐标,以安装正态分布计算的相应累计概率作为纵坐标,把样本值表现为直角坐标系中的散点。
如果资料服从整体分布,则样本点应围绕第一象限的对角线分布。
2、Q-Q图以样本的分位数作为横坐标,以按照正态分布计算的相应分位点作为纵坐标,把样本表现为指教坐标系的散点。
如果资料服从正态分布,则样本点应该呈一条围绕第一象限对角线的直线。
以上两种方法以Q-Q图为佳,效率较高。
3、直方图判断方法:是否以钟形分布,同时可以选择输出正态性曲线。
4、箱式图判断方法:观测离群值和中位数。
5、茎叶图类似与直方图,但实质不同。
二、计算法1、偏度系数(Skewness)和峰度系数(Kurtosis)计算公式:g1表示偏度,g2表示峰度,通过计算g1和g2及其标准误σg1及σg2然后作U检验。
两种检验同时得出U<U0.05=1.96,即p>0.05的结论时,才可以认为该组资料服从正态分布。
由公式可见,部分文献中所说的“偏度和峰度都接近0……可以认为……近似服从正态分布”并不严谨。
2、非参数检验方法非参数检验方法包括Kolmogorov-Smirnov检验(D检验)和Shapiro- Wilk(W 检验)。
SAS中规定:当样本含量n≤2000时,结果以Shapiro – Wilk(W检验)为准,当样本含量n >2000时,结果以Kolmogorov – Smirnov(D检验)为准。
SPSS中则这样规定:(1)如果指定的是非整数权重,则在加权样本大小位于3和50之间时,计算Shapiro-Wilk统计量。
对于无权重或整数权重,在加权样本大小位于3和5000之间时,计算该统计量。
由此可见,部分SPSS教材里面关于“Shapiro –Wilk适用于样本量3-50之间的数据”的说法是在是理解片面,误人子弟。
(2)单样本Kolmogorov-Smirnov检验可用于检验变量(例如income)是否为正态分布。
对于此两种检验,如果P值大于0.05,表明资料服从正态分布。
三、SPSS操作示例SPSS中有很多操作可以进行正态检验,在此只介绍最主要和最全面最方便的操作:1、工具栏--分析—描述性统计—探索性2、选择要分析的变量,选入因变量框内,然后点选图表,设置输出茎叶图和直方图,选择输出正态性检验图表,注意显示(Display)要选择双项(Both)。
3、Output结果(1)Descriptives:描述中有峰度系数和偏度系数,根据上述判断标准,数据不符合正态分布。
S k=0,K u=0时,分布呈正态,Sk>0时,分布呈正偏态,Sk<0时,分布呈负偏态,时,Ku>0曲线比较陡峭,Ku<0时曲线比较平坦。
由此可判断本数据分布为正偏态(朝左偏),较陡峭。
(2)Tests of Normality:D检验和W检验均显示数据不服从正态分布,当然在此,数据样本量为1000,应以W检验为准。
(3)直方图直方图验证了上述检验结果。
(4)此外还有茎叶图、P-P图、Q-Q图、箱式图等输出结果,不再赘述。
结果同样验证数据不符合正态分布。
如何在SPSS中做数据正态转化?在何以建老师培训班上,将数据标准正态化,何老师用的方法是:先将各原始分数按百分位排列,然后按照正态分布的面积(P值即百分位)找对应的Z值,这要转换到EXCEL表格里,用NORMSINV函数[ NORMSINV(p) 返回数值z 这样概率p 与一个标准的正常随机变量将采用为小于或等于z 的值。
],然后再导入SPSS表格中,导放可不是件容易的事,因为有重复的分数,帮还要粘贴替代。
一个功能强大的SPSS,难道一个常用的数据正态化按纽也没有?当然有!我用的是SPSS18.0,这是个汉化版,将一组数据正态化的按纽分别是:“转换”——“个案排秩”——把要正态化的数据迁入“变量”栏——把要呈现的表格式样迁入“排序标准”——再点右上角“秩的类型”——再点右下角“正态得分”,基本上就差不多了,只是正态化有四个选择项,我用的是Tukey法,这种方法对负偏态比较严重的分数相当好。
(何以建老师一个一个尝试过)。
注:在EXCEL中,函数NORMSINV 和NORMSDIST 是相关的功能。
如果NORMSDIST(z) 返回p,然后NORMSINV(p) 返回z。
其实,正态化没有那么神秘,如果我们知道了每个一分数在群体中的排名即可求出它的正态Z分,因为知道排位,即可知道它的百分位置,即面积P值。
那当然轻而易举地知道Z 分了。
数据的标准化、正态化、正态标准化的区别和联系,近期将一个一个描述清楚,到时请你关注我的博客。
现在网上找到一种算法,这个方法比较简单:严格说来,回答你的问题需要讲四个What's normal transformation?(什么是正态转换)Why do we need normal transformation?(为何做正态转换)When is normal transformation needed? (何时做正态转化)How can we do normal transformation?(如何做正态转化)我担心如果只讲How(如何做),也许有些初学者不分场合,误用滥用。
但是,我同样担心如果从ABC讲起,难免过分啰嗦,甚至有藐视大家的智商之嫌。
所幸者,我们已经进入Web 2.0年代,有关上述What, Why, When问题的答案网上唾手可得。
如果对这些问题不甚了了的读者,强烈建议先到google上用“How to transform data to normal distribution"搜一下(或点击下面的“前10条”),前10条几乎每篇都是必读的经典。
' 有了上述交代,我们可以比较放心地来讨论如何做正态转化的问题了。
具体来说,涉及以下几步:第一步,查看原始变量的分布形状及其描述参数(Skewness和Kurtosis)。
这可以用Frequencies 中的Histogram或Examination中的BoxPlot第二步,根据变量的分布形状,决定是否做转换。
这里,主要是看一下两个问题: !左右是否对称,也就是看Skewness(偏差度)的取值。
如果Skewness为0,则是完全对称(但罕见);如果Skewness为正值,则说明该变量的分布为positively skewed(正偏态,见下图1b);如果Skewness为负值,则说明该变量的分布为negatively skewed(负偏态,见图 1a)。
然而,肉眼直观检查,往往无法判断偏态的分布是否与对称的正态分布有“显著”差别,所以需要做显著性检验。
如同其它统计显著性检验一样,Skewness的绝对值如大于其标准误差的1.96倍,就被认为是与正态分布有显著差别。
如果检验结果显著,我们也许(注意这里我用的是“也许”一词)可以通过转换来达到或接近对称。
峰态是否陡缓适度,也就是看Kurtosis(峰态)是否过分peaked(陡峭)或过分flat(平坦)。
如果Kurtosis为0,则说明该变量分布的峰态正合适,不胖也不瘦(但罕见);如果Kurtosis 为正值,则说明该变量的分布峰态太陡峭(瘦高个,见图2b);反之,如果Kurtosis为负值,该变量的分布峰态太平缓(矮胖子,见图2a)。
峰态是否适度,更难直观看出,也需要通过显著检验。
如同Skewness一样,Kurtosis的绝对值如果大于其标准误差的1.96倍,就被认为与正态分布有显著差别。
这时,我们也许可以通过转换来达到或接近正态分布(峰态)。
" 第三步、如果需要做转化图,还是根据变量的分布形状,确定相应的转换公式。
最常见的情况是正偏态加上陡峰态。
如果是中度偏态(如Skewness为其标准误差的2-3倍),可以考虑取根号值来转换,以下是SPSS的指令(其中"nx"是原始变量x的转换值,参见注2):如果高度偏态(如Skewness为其标准误差的3倍以上),则可以取对数,其中又可分为自然对数和以10为基数的对数。
如以下是转换自然对数的指令(注2):以下是转换成以10为基数的对数(其纠偏力度最强,有时会矫枉过正,将正偏态转换成负偏态,注2):另外,在计量经济学中广泛使用Box-Cox转换方法,有些时间序列分析的专用软件中提供转换程序,但SPSS并不提供。
虽也可以写syntax来做,但很复杂,在此不谈了。
上述公式只能减轻或消除变量的正偏态(positive skewed),但如果不分青红皂白(即不仔细操作第一和第二步)地用于负偏态(negative skewed)的变量,则会使负偏态变得更加严重。
如果第一步显示了负偏态的分布,则需要先对原始变量做reflection(反向转换),即将所有的值反过来,如将最大值变成最小值、最小值变成最大值、等等。
如果一个变量的取值不多(如7-分量表),可用如下指令来反转:如果变量的取值很多或有小数、分数,上述方法几乎不可能,则需要写如下的指令(不知大家现在是否信服了为什么要学syntax吗?):其中max是x的最大值。
第四步、回到第一步,再次检验转换后变量的分布形状。
如果没有解决问题,或者甚至恶化(如上述的从正偏态转成负偏态),需要再从第二或第三步重新做起,然后再回到第一步的检验,等等,直至达到比较令人满意的结果(见注3)。
1.如同其它统计检验量一样,Skewness和Kurtosis的的标准误差也与样本量直接有关。
具体说来,Skewness的标准误差约等于6除以n后的开方,而Kurtosis的标准误差约等于24除以n后的开方,其中n均为样本量。
由此可见,样本量越大,标准误差越小,因此同样大小的Skewness和Kurtosis在大样本中越可能与正态分布有显著差别。
这也许就是SW在问题中提到的“很多学科都在讲大样本不用太考虑正态分布问题”的由来。
我的看法是,如果小样本的Skewness和Kurtosis是显著的话,一定要转换;在大样本的条件下,如果Skewness 和Kurtosis是轻度偏差,也许不需要转换,但如果严重偏差,也是要转换。
2.大家知道,根号里的x不能为负数,对数或倒数里的x不能为非正数(即等于或小于0)。
如果你的x中有是负数或非正数,需要将其做线性转换成非负数(即等于或大于0)或正数(大于0),如 COMPUTE nx = SQRT (x - min) 或 COMPUTE nx = LN (x - min + 1),其中的min是x的最小值(为一个非正数)。
不是任何分布形态的变量都可以转换的。
例外之一是“双峰”或“多峰”分布(distribution with dual or multiple modality),没有任何公式可以将之转换成单峰的正态分布。
