安陆一中2012届高三数学选填题专项训练(八)

合集下载

湖北省安陆一中2012届高三文科数学选填题专项训练16

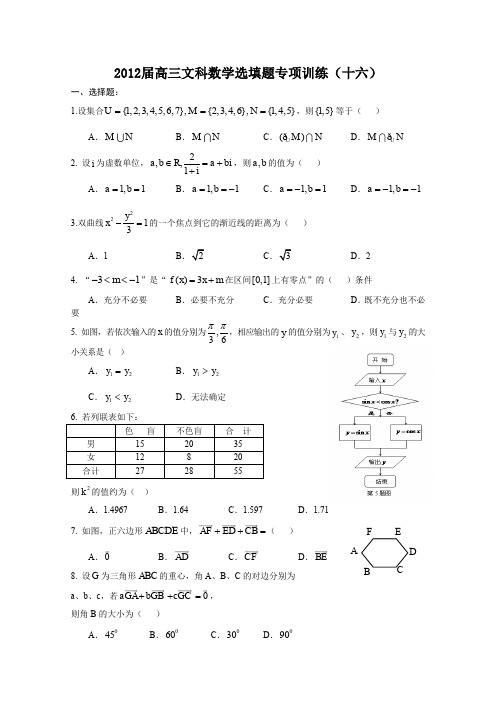
2012届高三文科数学选填题专项训练（十六）一、选择题：1.设集合{1,2,3,4,5,6,7},{2,3,4,6},{1,4,5}U M N ===，则{1,5}等于（）A ．MNB ．M NC ．()U M N ð D ．U MN ð2. 设i 为虚数单位，2,,1a b R a bi i∈=++，则,a b 的值为（） A ．1,1a b ==B ．1,1a b ==-C ．1,1a b =-=D ．1,1a b =-=-3.双曲线2213y x -=的一个焦点到它的渐近线的距离为（） A ．1BCD ．24. “31m -<<-”是“()3f x x m =+在区间[0,1]上有零点”的（）条件A ．充分不必要B ．必要不充分C ．充分必要D ．既不充分也不必要5. 如图，若依次输入的x 的值分别为,36ππ，相应输出的y 的值分别为1y 、2y ，则1y 与2y 的大小关系是（）A ．12y y =B ．12y y >C ．12y y <D ．无法确定则2k 的值约为（）A ．1.4967B ．1.64C ．1.597D ．1.717. 如图，正六边形ABCDE 中，AF ED CB ++=（）A ．B ．ADC ．CFD ．BE8. 设G 为三角形ABC 的重心，角A 、B 、C 的对边分别为 a 、b 、c ，若aGA bGB +cGC +0=，则角B 的大小为（）A ．045B ．060C ．030D ．090A9.体积为（）A．B．4C．D．210.设()y f x=在(,1]-∞上有定义，对于给定的实数k，定义()()kf xf xk⎧=⎨⎩()()f x kf x k≤>，给出函数1()24x xf x+=-，若对于任意(,1]x∈-∞，恒有()()kf x f x=，则（）A．k的最大值为0 B．k的最小值为0C．k的最大值为1 D．k的最小值为1二、填空题：11．已知数列{}n a是公差不为0的等差数列，首项为2，且124111,,a a a成等比数列，则数列{}na的通项公式为．12.命题“2,2390x R x ax∃∈-+<”为假命题，则实数a的取值范围为．13. 已知正数,x y满足211x y+=，若227x y m m+>+恒成立，则实数m的取值范围为.14.设圆C与圆22(2)1x y-+=外切，与直线1x=-相切，则C的圆心轨迹方程为．15．在区间(0,1)上随机取两个数,m n，则关于x的一元二次方程20x m-+=有实根的概率为．16.已知1()sin cosf x x x=+，且21()(),f x f x'=32()(),f x f x'=1()(),n nf x f x-'⋅⋅⋅=⋅⋅⋅侧视图俯视图*(,2)n N n ∈≥，则122012()()()444f f f πππ++⋅⋅⋅+= ．17.若方程lg 5x x =-+在区间(,1)()k k k Z +∈上有解，则满足所有条件的k 的值的和为．2012届高三文科数学选填题专项训练（十六）答题卡二、填空题（共7小题，每题5分，共35分，把答案填在题中横线上）11、 2n a n = ； 12、 ⎡-⎣ ；13、 ()1,8- ；14、 28y x = ； 15、 18；16、 0 ；17、 1- ；。

。湖北省安陆一中2012届高三文科数学选填题专项训练(一)

3bc ， sin C 2 3 sin B ，则
A=( )
A. 300
B.
600
C.
1200
D.
1500
1
9. 已知 an 是首项为 1的等比数列， sn 是 an 的前 n项和，且 9s3 s6 ，则数列 an
前
5项和为 ( )
15
31
31
15
A. 8 或 5 B.
16 或 5 C.
16 D.
8
N* . 设 Tn0 为
数列 { Tn } 的最大项，则 n0 =
题号
1
2
3
4
5
6
7
8
9
10
答案
A
C
C
B
A
D
B
A
C
B
二、填空题（共 5 小题，每题 5 分，共 25 分，把答案填在题中横线上）
1 11 、 _______ 7
____________；
__________ ；
12 、 ____ 3 ______________ ； 13 、 _____ 2
10. 给定函数① y
1
y
x2 ，②
log 1 ( x
2
1) ，③ y
|x
1| ，④ y
2x
1
，其中在区间
（ 0，1
）
上单调递减的函数序号是 ( )
A. ①②
B.
②③
C.
③④
D.
①④
二、填空题
3
cos 2
tan( 2 )
11. 已知为第三象限的角，
5,则 4
.
12．已知向量 a ， b 满足 a 1 ， b 2 ， a 与 b 的夹角为 60°，则 a b

2012年高考数学临考突击专项训练系列：选择 8.pdf

1 知识与技能了解要在一段电路中产生电流，它的两端就有电压知道电压的单位及单位换算，记住干电池及家庭电路电压值知道电压表的用途与符号，知道正确使用电压表的规则，能识别和选择电压表量程，会正确读数2 过程与方法在初步认识电源、电压、电流的过程中，感受推理方法3 情感态度与价值观有认识电压表和正确使用电压表的愿望要在一段电路中产生电流，它的两端就有电压电源是提供电压的装置电压的作用: 使自由电荷定向移动形成电流国际上通常用字母 U 表示电压电压的单位是伏特简称伏符号是 V 常用单位有千伏（kV），毫伏（mV）一节干电池的电压 U＝1.5伏一个铅蓄电池的电压 U＝2伏家庭电路的电压 U＝220伏对人体安全的电压不高于36伏特工业动力电压 U＝380伏发生闪电的云层间电压可达伏特电鳐的模样很怪,扁平身子,头和胸连在一起，浑身光滑无鳞，电鳐凭着自己的“电武器”，能随意放电，在海洋里几乎是无敌的,能产生200伏特以上的电压。

人如果不小心踩着海底的电鳐时，它放出的电足够将一个成年人电倒。

常用电压表电压表的符号是：三个接线柱：一个负接线柱（共用接线柱），两个正接线柱两个量程：0-3V；0-15V 两排刻度值：量程为15Ⅴ时，分度值是0.5Ⅴ；量程为3Ⅴ时，分度值是0.lⅤ V 回顾电流表的使用规则：（1）要_______在电路中；（2）使电流从 __________流入，从________ 流出；（3）________电流表的_______；（4）__________________________________ _________________. 串联 “＋”接线柱 “—”接线柱不能超过量程绝对不允许不经过用电器将电流表直接连在电源的两极上。

校零：检查电压表的指针是否对准零刻度线，如有偏差，进行校正。

并联：电压表必须并联在被测电路两端，使电流从 “＋”接线柱流入电压表，从“－”接线柱流出电压表。

湖北省安陆一中2012届高三数学选填题专题训练(5)

安陆一中2012届高三数学选填题专项训练(五）命题人：李治国审题人：徐友成班级姓名分数一、选择题:本大题共10小题,每小题5分，共50分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1. 复数212m z -=+i i（m R ∈，i 是虚数单位）在复平面上对应的点不可能位于（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限2。

下列说法错误的是（ )A ．自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系;B ．线性回归方程对应的直线错误!＝错误!x ＋错误!至少经过其样本数据点(x 1，y 1),（x 2,y 2）,…，（x n ，y n )中的一个点;C ．在残差图中，残差点分布的带状区域的宽度越狭窄，其模型拟合的精度越高;D ．在回归分析中,2R 为0。

98的模型比2R 为0.80的模型拟合的效果好3. 若1sin()34πα-=，则cos(2)3πα+=( ）A ．78B ．14- C ．14D ．78-4。

已知函数()f x 对应关系如表所示，数列{}na 满足：113,(),n na a f a +==则2011a =（）A ．3B ．2C ．1D ．不确定5。

一个空间几何体的三视图如图所示,则该几何x 12 3 f （x ） 32 1第6题图第10题图体的表面积为（ )A.48B.32817+ C 。

48817+ D 。

806. 函数()y f x =在定义域3(,3)2-内可导,其图象如图所示，记()y f x =的导函数为'()y f x =，则不等式'()0f x ≤的解集为（）A ．31[,][1,2)22- B ．148[1,][,]233-C ．1[,1][2,3)3-D ．3148(,1][,][,3)2233-- 7。

某校在模块考试中约有1000人参加考试，其数学考试成绩2~(90,),N a ξ（0,a >试卷满分150分），统计结果显示数学考试成绩在70分到110分之间的人数约为总人数的35，则此次数学考试成绩不低于110分的学生人数约为（）A ．200B ．300C ．400D ．6008. 把座位编号为1、2、3、4、5、6的六张观看《孔子》的电影票全部分给甲、乙、丙、丁四个人，每人至少一张，至多两张，且分得的票必须是连号，那么不同的分法种数是（ )A ．96B ．144C ．156D ．196 9。

湖北省安陆一中高三数学选填题专项训练(二十一)

2012届高三文科数学选填题专项训练（二十一）一、选择题1.集合{}Z x x x A ∈≤+=,21,{}11,3≤≤-==x x y y B ，则=B A ( ) A ．(]1,∞-B.[]1,1-C.φD.{}1,0,1-2.若z 是复数，且()13=+i z (i 为虚数单位)，则z 的值为 ( ) A ．i +-3B.i --3C.i +3D.i -33.已知甲、乙两名篮球运动员某十场比赛得分的茎叶图如右上图所示，则甲、乙两人在这十场比赛中得分的平均数与方差的大小关系为( )A ．乙甲x x < 22x x S S <<乙甲，乙甲 B. 乙甲x x < 22x x S S <>乙甲，乙甲 C. 乙甲x x >22x x S S >>乙甲，乙甲D. 乙甲x x > 22x x S S ><乙甲，乙甲4. 一个几何体的三视图如右图所示，则该几何体的体积为（）A ．2B ．1C ．23 D ．135．设x ，y 满足36020,3x y x y x y --≤⎧⎪-+≥⎨⎪+≥⎩若目标函数z=ax+y （a>0）的最大值为14，则a=（）A ．1B ．2C ．23D ．5396.等差数列{n a }前n 项和为n s ，满足4020s s =，则下列结论中正确的是（） A ．30s 是n s 中的最大值 B 。

30s 是n s 中的最小值 C ．30s =0D 。

60s =07．已知流程图如右图所示，该程序运行后，为使输出b 的值为16，则循环体的判断框内① 处应填的是（） A. 3 B. 2 C. 4 D. 16 8. 函数22cos ()14y x π=--是（）（）A ．最小正周期为π的奇函数B ．最小正周期为π的偶函数C ．最小正周期为2π的奇函数 D ．最小正周期为2π的偶函数乙甲8 6 4 3 1 5 8 6 3 2 4 5 8 3 49 45 01 3 1 6 7 99.已知双曲线221916x y -=，其右焦点为F ，P 为其上一点，点M 满足MF =1，0=⋅MP MF ，则MP 的最小值为（） A 3B 3 C2 D 210. 已知条件1|:|>x p ,条件2:-<x q ,则p ⌝是q ⌝的（）A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件二、填空题11．已知点(,)P x y 在直线23x y +=上移动，当24xy+取得最小值时，过点(,)P x y 引圆22111()()242x y -++=的切线，则此切线段的长度为12．已知函数()f x 的定义域为[]15-，，部分对应值如右表。

湖北省安陆一中高三数学选填题专项训练(八)

2012届高三文科数学选填题专项训练（八）一、选择题：1、设,,x y R ∈则“2x ≥且2y ≥”是“224x y +≥”的（） A. 充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．即不充分也不必要条件 2、若,a b R ∈，且0ab >，则下列不等式中，恒成立的是（）A.222a b ab +> B.a b +≥ C.11a b +≥D.2b aa b+≥3、在△ABC 中，内角A,B,C 的对边分别是a ,b ,c ，若22a b -=，sin C B =，则A=（）A.30B.60C.120D.1504、函数x x y cos 2sin 2+=在[θπ,3-]上的最小值是1，则θ的最小值为（）A ．0B ．6π C ．3πD ．2π5、已知函数()f x 是奇函数，当0,()(01)xx f x a a a >=>≠时且，且12(log 4)3,f =-则a的值为（）A B ．3C ．9D ．326、已知{}n a 为等差数列，其公差为-2，且7a 是3a 与9a 的等比中项，n S 为{}n a 的前n 项和,*n N ∈,则10S 的值为（）A ．－110B ．－90C ．90D ．110 7、等差数列{}n a 的通项公式是12n a n =-,其前n 项和为n S ，则数列{}nS n的前11项和为（）A. －45B. －50C. －55D. －66 8、某四面体的三视图如图所示，该四面体四个面的面积中，最大的是（）A ．8B ．C ．10D ．9、如图，四棱锥S —ABCD 的底面为正方形，SD ⊥底面ABCD ，则下列结论中不正确．．．的是（） A ．AC ⊥SB ； B ．AB ∥平面SCDC ．A 到平面SBD 的距离等于C 与平面SBD 的距离 D ．AB 与SC 所成的角等于DC 与SA 所成的角10、如果不等式2()0f x ax x c =-->的解集为{|21}x x -<<，那么函数()y f x =-的大致图象是（）二、填空题：11、若函数2[log (3)]y f x =-的定义域为[4,11]，则函数()y f x =的定义域为。

湖北省安陆一中2012届高三数学选填题专题训练(8)

安陆一中2012届高三数学选填题专项训练（八）编号班级姓名出题人：郭斌审题人：徐文婷一、选择题:(本大题共10小题．每小题5分,共50分．)1.已知A 、B 是非空数集,定义{}|,A B x x A B x A B ⊕=∈∉且，若{{}3|,|,xA x yB y y ====则A B ⊕=（） A ．[)03, B ．()3,-∞C ．()()03,,-∞+∞D ．[]03,2。

非零向量错误!与错误!满足错误!·错误!＝0,且错误!·错误!＝－错误!，则△ABC 为（ )A ．等腰非等边三角形B ．等边三角形C ．三边均不相等的三角形D ．直角三角形3。

给出下列命题，其中正确命题的个数是（）①已知,,a b m 都是正数，a m a b m b +>+，则a b <；②1,1,x y a a a a a x y >>>>已知若则; ③“1x ≤，且1y ≤”是“2x y +≤”的充分不必要条件;④命题“x R ∃∈,使得2210x x -+<”的否定是“x R ∃∈，使得2210x x -+≥”。

A ．1B ．2C ．3D ．44。

设l ,m ，n 为三条不同的直线，α为一个平面，下列命题中正确的个数是( )①若l ⊥α，则l 与α相交; ②若m ⊂α,n ⊂α,l ⊥m ，l ⊥n ,则l ⊥α③若l ∥m ,m ∥n ，l ⊥α，则n ⊥α; ④若l ∥m ，m ⊥α，n ⊥α，则l ∥nA ．1B ．2C ．3D ．45. 已知函数f (x ）＝sin 错误!x ，a 等于抛掷一颗骰子得到的点数，则y ＝f (x )在[0，4]上至少有5个零点的概率是( ）A.错误! B 。

错误! C.错误!D.错误!6. 若A 、B 是平面内的两个定点，点P 为该平面内动点，且满足向量错误!与错误!夹角为锐角θ，｜错误!｜｜错误!|＋错误!·错误!＝0，则点P 的轨迹是（）A ．直线(除去与直线AB 的交点) B ．圆(除去与直线AB 的交点)C ．椭圆(除去与直线AB 的交点)D ．抛物线(除去与直线AB 的交点）7. 已知函数6(3)3(7)()(7)x a x x f x a x -⎧--≤⎪=⎨>⎪⎩{}()(),n n a a f n n N *=∈若数列满足且{}n a 是递增数列，那么实数a 的取值范围是 ( ） A 。

湖北省安陆一中2012届高三数学第二次综合试题(文科).pdf

2012届高三数学第二次综合试题（文科）一、选择题(10小题，每小题5分，满分50分) 1. 化简复数得 A. B. C. D. 2. 已知集合，，若，则 A. B. C. 或 D. 或 3. 若曲线在点处的切线方程是，则 A. B. C. D. 4. 已知为不重合的两个平面，直线，那么“”是“”的A. 充要条件B. 必要而不充分条件C. 充分而不必要条件D. 既不充分也不必要条件 5. 将函数的图像向左平移个单位，再向下平移个单位，得到函数的图像，则的解析式为 A. B. C. D. 6. 设是定义在上的周期为的周期函数，如下图表示该函数在区间上的图像，则 A. B. C. D. 7. 某校对高三年级的学生进行体检，现将高三男生的体重（单位：）数据进行整理后分成五组，并绘制频率分布直方图（如上图所示）.根据一般标准，高三男生的体重超过属于偏胖，低于属于偏瘦.已知图中从左到右第一、第三、第四、第五小组的频率分别为，，，，第二小组的频数为，则该校高三年级的男生总数和体重正常的频率分别为 A. B. C. D. 8. 已知流程图如下图所示，该程序运行后，为使输出的值为，则循环体的判断框内① 处应填的是 A. B. C. D. 9. 已知等差数列前项和，则 A. B. C. D. 10. 定义在区间上的函数的图像如下图所示，记以，，为顶点的三角形的面积为，则函数的导函数的图像大致是题号12345678910答案二、填空题(5小题，每小题5分，满分25分) 11. 已知，，则 . 12. 已知均为正数，且，则的最小值为 . 13. 设数列的前项和为，且，则数列的通项公式是 . 14. 设函数的定义在上的偶函数，且是以为周期的周期函数，当时，，则与的大小关系为 . 15. 一个三角形数阵如下： …… 按照以上排列的规律，第行从左向右的第个数为 . 三、解答题（本大题6小题，满分75分），，，向量.（1）若向量与共线，求实数的值；（2）若向量，求实数的取值范围. 17.（12分）某学校共有教职工900人,分成三个批次进行继续教育培训，在三个批次中男、女教职工人数如表所示.已知在全体教职工中随机抽取1名,抽到第二批次中女教职工的概率是0.16 . 第一批次第二批次第三批次女教职工196xy男教职工204156z （1）求的值；（2）现用分层抽样的方法在全体教职工中抽取54名做培训效果的调查, 问应在第三批次中抽取教职工多少名？（3）已知，求第三批次中女教职工比男教职工多的概率.如图，在面体中，平面∥平面，平面，,,∥，且, ．（1）求证：平面平面；（2）求证：∥平面；（3）求三棱锥的体积．的各项均为正数，且前项之和满足，且，，成等比数列.（1）求数列的通项公式；（2）若数列的前项和为，求. 20.（13分）函数．（Ⅰ）若，在处的切线相互垂直，求这两个切线方程（Ⅱ）若单调递增，求的范围．等差数列中，首项，公差，前n项和为，已知数列成等比数列，其中，，．（Ⅰ）求数列，的通项公式；（Ⅱ）令，数列的前n项和为．若存在一个最小正整数M，使得当时，（）恒成立，试求出这个最小正整数M的值．2012届高三数学第二次综合试题（文科）参考答案一、选择题1. D2. D3. A4. C5. B6. A7. D8. B9. A 10. D 二、填空题 11． 12. 13. 14. 15 . 三、解答题 16. （本小题满分12分）解：（I）又（II） 17. （本小题满分12分）解: (1)由,解得. (2)第三批次的人数为, 设应在第三批次中抽取名，则，解得. ∴应在第三批次中抽取12名. （3）设第三批次中女教职工比男教职工多的事件为，第三批次女教职工和男教职工数记为数对，由（2）知，则基本事件总数有：，共9个，而事件包含的基本事件有：共4个， ∴. 解:（1）∵平面∥平面，平面平面, 平面平面 ., ∴为平行四边形，. 平面,平面，平面, ∴平面平面. （2）取的中点为，连接、，则由已知条件易证四边形是平行四边形， ∴，又∵， ∴ ∴四边形是平行四边形，即，又平面故平面. （3）平面∥平面，则F到面ABC的距离为AD. ＝II），公比，所以前项和为 20. （本小题满分13分）解：（I）, ∴ ∵两曲线在处的切线互相垂直 ∴ ∴ ∴ ∴在处的切线方程为，同理，在处的切线方程为 (II) 由得 ∵单调递增 ∴恒成立即令令得，令得 ∴∴的范围为解：（Ⅰ）由，得，解得，，，又在等比数列中，公比，∴，，．（Ⅱ），则，两式相减得：， ∴． ∵， ∴单调递增，∴．又在时单调递增．且，；，；，；，；…．故当时，恒成立，则所求最小正整数M的值为3．第18题图第10题图第8题图第6题图第7题图。

湖北省安陆一中高三数学选填题专项训练(四)

2012届高三文科数学选填题专项训练（四）一、选择题：1．抛物线y ＝4x 2的准线方程为 ( )A ．y ＝－14B ．y ＝18C ．y ＝116D ．y ＝－1162．已知(,1)a x =，(3,2)b x =-,则0a b ⋅<的解集是( ) A ．1(,)2-∞-B ．1(,)2-+∞C ．1(,)2-∞D ．1(,)2+∞3．已知f (x )＝ax 2＋bx 是定义在[a －1,2a ]上的偶函数，那么a ＋b 的值是( )A ．－13 B.13 C.12 D ．－124．已知点(tan ,cos )P αα在第三象限, 则角α的终边在( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限5.过椭圆22156x y +=内的一点P (－1，2)的弦，恰好被P 点平分，则这条弦所在的直线方程为( ) A ．3x －5y ＋13＝0 B ．3x ＋5y+13＝0 C ．5x －3y ＋11＝0 D ．5x ＋3y ＋11＝06．要得到tan 2y x =的图象，则只需将tan(2)6y x π=+的图象( )A ．向左平移6π个单位 B ．向右平移6π个单位 C ．向左平移12π个单位 D ．向右平移12π个单位7．已知{(,)|0}M x y y y ==≠，{(,)|}Nx y y x b ==+，若MN ≠∅，则b ∈( )A ．[-B ．(-C ．(-D ．[-8．已知平面区域D 由以()3,1A 、()2,5B 、()1,3C 为顶点的三角形内部和边界组成.若在区域D 上有无穷多个点()y x ,可使目标函数my x z +=取得最小值，则=m ( )A ． 2-B ．1-C ．1D ．49．在正方体1111ABCD A B C D -中，M 、N 分别为棱11A B 和1BB 的中点，那么异面直线AM 和CN 所成角的余弦值是( )A ．2B ．2C ．25D ．-2510.已知椭圆)0(12222>>=+b a b y a x 与双曲线)0,0(12222>>=-n m ny m x 有相同的焦点)0,(c -和)0,(c ，若c 是a 、m 的等比中项，n 2是2m 2与c 2的等差中项，则椭圆的离心率e = ( ) A ．33 B ．22 C ．41D ．21 二、填空题：11．已知△ABC 中，5tan 12A =-，则cos A = ．12．已知等比数列前3项21，41-，81，则其第8项是．13．某初一年级有500名同学，将他们的身高（单位：cm ）数据绘制成频率分布直方图（如图），若要从身高在[ 120 , 130），（第13题） [130 ，140） , [140 , 150]三组内的学生中，用分层抽样的方法选取30人参加一项活动，则从身高在[130 ，140）内的学生中选取的人数应为．14.若曲线4y x =的一条切线l 与直线480x y +-=垂直，则l 的方程为。

湖北省安陆一中高三数学选填题专题训练(8).doc

安陆一中高三数学选填题专项训练（八）编号班级姓名出题人：郭斌审题人：徐文婷一、选择题：（本大题共10小题．每小题5分，共50分．）1.已知A 、B 是非空数集，定义{}|,A B x x A B x A B ⊕=∈∉且，若{{}3|,|,x A x y B y y ====则A B ⊕=（）A ．[)03,B ．()3,-∞C ．()()03,,-∞+∞D ．[]03, 2. 非零向量AB →与AC →满足⎝ ⎛⎭⎪⎪⎫AB →|AB →|＋AC →|AC →|·BC →＝0，且AB →|AB →|·AC →|AC →|＝－12，则△ABC 为( ) A ．等腰非等边三角形 B ．等边三角形 C ．三边均不相等的三角形 D ．直角三角形3. 给出下列命题，其中正确命题的个数是（）①已知,,a b m 都是正数，a m ab m b +>+，则a b <；②1,1,x y a a a a a x y >>>>已知若则； ③“1x ≤，且1y ≤”是“2x y +≤”的充分不必要条件；④命题“x R ∃∈，使得2210x x -+<”的否定是“x R ∃∈，使得2210x x -+≥”.A ．1B ．2C ．3D ．44. 设l ，m ，n 为三条不同的直线，α为一个平面，下列命题中正确的个数是( )①若l ⊥α，则l 与α相交； ②若m ⊂α，n ⊂α，l ⊥m ，l ⊥n ，则l ⊥α③若l ∥m ，m ∥n ，l ⊥α，则n ⊥α； ④若l ∥m ，m ⊥α，n ⊥α，则l ∥nA ．1B ．2C ．3D ．45. 已知函数f (x )＝sin a π3x ，a 等于抛掷一颗骰子得到的点数，则y ＝f (x )在[0,4]上至少有5个零点的概率是( )A.13B.12C.23D.566. 若A 、B 是平面内的两个定点，点P 为该平面内动点，且满足向量AB →与AP →夹角为锐角θ，|PB →||AB →|＋PA →·AB →＝0，则点P 的轨迹是( )A ．直线(除去与直线AB 的交点) B ．圆(除去与直线AB 的交点)C ．椭圆(除去与直线AB 的交点)D ．抛物线(除去与直线AB 的交点)7. 已知函数6(3)3(7)()(7)x a x x f x ax -⎧--≤⎪=⎨>⎪⎩{}()(),n n a a f n n N *=∈若数列满足且{}n a 是递增数列，那么实数a 的取值范围是（） A . 9[,3)4 B . 9(,3)4C. (2,3)D. (1,3) 8.设x ，y 满足约束条件⎪⎩⎪⎨⎧≥≥≥+-≤--0,002063y x y x y x ，若目标函数z ax by =+（0a >，0b >）的最大值为12，则ab 的取值范围是（）A.(0,)+∞B. 3(0,)2 C. 3[,)2+∞ D. 3(0,]29. 函数⎪⎩⎪⎨⎧≤≤+<≤-+=)380(),sin(2)02(,1πϕωx x x kx y 的图象如下图，则（）A ．6,21,21πϕω===k B ．3,21,21πϕω===k C ．6,2,21πϕω==-=k D ．3,2,2πϕω==-=k 10. 具有性质：f ⎝ ⎛⎭⎪⎫1x ＝－f (x )的函数，我们称为满足“倒负”变换的函数，下列函数：①y ＝x －1x ，②y ＝x ＋1x ，③y ＝⎩⎪⎨⎪⎧ x ，x 0，x＝－1x ，x 中满足“倒负”变换的函数是( )A ．①②B ．②③C ．①③D ．只有①二、填空：本大题共5小题，每小题5分，共25分．11.已知a ，b ，c 为△ABC 的三个内角A ，B ，C 的对边，向量m ＝（1,3-），n ＝（cosA,sinA ）.若n ⊥m ，且acosB+bcosA=csinC ，则角B ＝12.下表给出一个“直角三角形数阵”41 41,21 163,83,43 ……满足每一列的数成等差数列,从第三行起,每一行的数成等比数列,且每一行的公比相等,记第i 行第j 列的数为83(,,),ij a i j i j N a +≥∈则等于13.设,,a b c 为三个非零向量,0,2,2a b c a b c ++==-=，则b c +的最大值是14. 已知P 为椭圆C ：x 225＋y 216＝1上的任意一点，F 为椭圆C 的右焦点，M 的坐标为(1,3)，则|PM |＋|PF |的最小值为________． 15.已知函数2342011()12342011=+-+-+⋅⋅⋅+x x x x f x x ,2342011()12342011=-+-+-⋅⋅⋅-x x x x g x x , 设()(3)(3)=+⋅-F x f x gx , 且函数()F x 的零点均在区间[,](,)a b a b Z ∈内, 则-b a 的最小值为_________。

湖北省安陆一中高三数学选填题专项训练(五)

2012届高三文科数学选填题专项训练（五）一、选择题：1．复数3112i i +等于（） A ．12 B ．12- C ．32i D ．12i 2．设{}n a 是等差数列，则“12a a <”是“数列{}n a 是递增数列”的（）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分与不必要条件3．若0m n <<，则下列结论正确的是（）A ．22m n >B ．11()()22m n <C ．22log log m n >D ．1122log log m n > 4．若抛物线22y px =的焦点与椭圆22162x y +=的右焦点重合，则p 的值等于（） A ．4 B ．2 C ．—4 D ．—25．甲、乙两名运动员，在某项测试中的8次成绩如茎叶图所示，12,x x 分别表示甲、乙两名运动员这项测试成绩的平均数，12,s s 分别表示甲、乙两名运动员这项测试成绩的标准差，则有（）A ．1212,x x s s ><B ．1212,x x s s =<C ．1212,x x s s =>D ．1212,x x s s <>6．在一个袋了中装有分别标注数字1，2，3，4，5的五个小球，这些小球除标注的数字外完全相同，现从中随机取出两个小球，则取出的小球上标注的数字之和为5或7的概率是（）A ．35B ．25C ．310D ．457．若将函数cos 3y x x =-的图象向左平移m （m>0）个单位后，所得图象关于y 轴对称，则实数m 的最小值为（）A ．6πB ．3πC ．23πD ．56π 8．执行如图所示的程序框图，若输出的b 的值为16，则图中判断框内①处应填（）A ．4B ．3C ．2D ．59．已知向量5(1,2),||5,,2a c a c a c ==⋅=若则与的夹角为（）A ．30°B ．60°C ．120°D ．150°10．如果函数()f x 对任意的实数x ，存在常数M ，使得不等式|()|||f x M x ≤恒成立，那么就称函数()f x 为有界泛函数，下面四个函数：①()1f x =； ②2()f x x =；③()(sin cos )f x x x =+；④2()1x f x x x =++ 其中属于有界泛函数的是（）A ．①②B ．①③C ．④D ．③④二、填空题：11．两个志愿者组织共有志愿者2400人，现用分层抽样的方法，从所有志愿者中抽取一个容量为160的样本，已知从甲志愿者组织中抽取的人数为150，那么乙志愿者组织中的人数有。

湖北省安陆一中高三数学选填题专项训练(二十三)

2012届高三文科数学选填题专项训练（二十三）一、选择题1．已知集合{0,},{1,2}M x N ==，若{}2MN =，则MN = （）A ．{0,,1,2}xB ．{}2,1,0,2C ．{}2,1,0D ．不能确定2．已知函数),1lg()(22x x x x f +++=且,)2(a f =则=-)2(f （）A ．4-aB ．a -4C ．a -8D ．8-a 3．命题“对任意直线l ，有平面α与其垂直”的否定（）A ．对任意直线l ，没有平面α与其垂直B ．对任意直线l ，没有平面α与其不垂直C ．存在直线0l ，有平面α与其不垂直D ．存在直线0l ，没有平面α与其垂直4．若函数()(,)y f x a b =的导函数在区间上不是单调函数，则函数()y f x =在区间[,]a b 上的图象可能是（）A ．①③B ．②④C ．②③D ．③④5．已知函数()y f x =的定义域为R ，当0<x 时，()1f x >，且对任意的,x y ∈R ，等式()()()f x f y f x y =+成立．若数列{}n a 满足1(0)a f =，且11()(2)n n f a f a +=--)(*∈N n ，则2011a 的值为（）A ．4021 B ． 4020 C ． 4018 D ．4019 检测次数1 2 3 4 5 6 7 8 检测数据i a （次/分钟）3940424243454647上述数据的统计分析中，一部分计算见如右图所示的程序框图（其中a 是这8个数据的平均数），则输出的的值是（） A ．6 B ．7 C ．8 D ．567．正三棱锥底面边长为a ，侧棱与底面成角为60°，过底面一边作一截面使其与底面成30°的二面角，则此截面的面积为（） A ．34a 2 B ．33a 2C ．13a 2D ．38a 28．投掷两颗骰子，得到其向上的点数分别为m 和n,则复数（m+ni ）（n 一mi ）为实数的概率为（）A ．13B ．14C ．16D ．1129．设,x y 满足约束条件360,20,0,0,x y x y x y --≤⎧⎪-+≥⎨⎪≥≥⎩若目标函数(0,z ax by a b =+＞＞0)的最大值为12，则23a b+的最小值为（） A ．256 B ．83 C ．113 D ． 410．已知2b 是1一a 和1+a 的等比中项，则a +4b 的取值范围是（）A ．⎥⎦⎤ ⎝⎛∞-45，B ．（一∞，45） C ．5-14⎛⎤⎥⎝⎦， D ．（一1，45）二、填空题11．设G 是ABC ∆的重心，且0)sin 35()sin 40()sin 56(=++GC C GB B GA A ，则角B 的大小为________12．设点P 是双曲线22221(,0)x y a b a b-=>>与圆2222x y a b +=+在第一象限的交点F 1，F 2分别是双曲线的左．右焦点，且12||2||PF PF =，则双曲线的离心率为________13．一个人喝了少量酒后，血液中的酒精含量迅速上升到mL mg /3.0，在停止喝酒后，血液中的酒精含量以每小时25%的速度减少，为了保障交通安全，某地根据《道路交通安全法》规定：驾驶员血液中的酒精含量不得超过mL mg /09.0，那么一个喝了少量酒后的驾驶员，至少要经过 ________小时才能开车．（精确到1小时）14．一个几何体的三视图及其尺寸如右图所示，其中正（主）视图是直角三角形，侧（左）视图是半圆，俯视图是等腰三角形，则这个几何体的表面积是 cm 2。

安陆一中高三数学选填题专题训练()

(第7题)安陆一中2012届高三数学选填题专题训练一一、选择题：本大题共10小题，每小题5分，共50分。

（1）已知函数f（x ）＝267,0,100,,x x x x x ++<≥⎧⎪⎨⎪⎩则 f （0)＋f （-1)＝(A) 9 （B ）7110(C) 3 （D ）1110(2) “cos x ＝1”是“sin x ＝0”的(A ）充分而不必要条件 (B ）必要而不充分条件（C ）充分必要条件 (D ）既不充分也不必要条件（3）在等差数列｛a n }中，若a 2＋a 3＝4，a 4＋a 5＝6，则a 9＋a 10＝(A) 9 (B) 10 (C) 11 (D) 12(4）设U 为全集,对集合X ,Y ，“*”，X *Y ＝(X ∩Y )．对X，Z, Y )*Z ＝（A) (X ∪Y ）∩ Z (B) （X ∩Y )∪ Z （C ）（ X ∪ Y ）∩Z (D ）（ X ∩ Y ）∪Z（5）在长方体ABCD －A 1B 1C 1D 1中，AA 1＝AD ＝2AB ．若E ，F分别为线段A 1D 1,CC 1的中点，则直线EF 与平面ABB 1A 1所成角的余弦值为（A ）3（B ）2(C)3(D ）13(6) 设F 是抛物线C 1：y 2＝2px （p的焦点，22221x y ab-=点A 是抛物线与双曲线C 2：（a ＞0,b ＞0）的一条渐近线的一个公共点，且AF ⊥x 轴，则双曲线的离心率为 (A ）2 （ (C)2(D （7）运行后输出的S 的值为(A ） 1 （B ） 12(C ） 14(D ）18(8）下列函数中，在(0,2π)上有零点的函数是(A ） f （x )＝sin x －x （B) f （x ）＝sin x －2πx（C) f （x )＝sin 2x －x (D) f (x ）＝sin 2x －2πx班级姓名分数（9）设,2,,2,x y x y z y x y -≥=<⎧⎨⎩若－2≤x ≤2，－2≤y ≤2，则z 的最小值为(A ）－4 (B)－2 (C ）－1 （D ） 0（10)设2010(12)(1)x x ++＝a 0＋a 1x ＋a 2x 2＋…＋a 10x 10＋29129100(1)b b x b x b x x +++++，则a 9＝(A) 0 (B) 410 （C) 10⋅410 (D) 90⋅410二、填空题: 本大题共5小题，每小题5分，共25分。

湖北省安陆一中高三数学选填题专项训练(二十五)

8. 已知点
P 是双曲线
x2 a2
-
y2 b2
=1
右支上一点
,
F
是双曲线的右焦点，点
M 在直线 x
a2 c
上，若 OP OF OM 且 OP FM 0 , 则双曲线的离心率 e
（）
用心爱心专心
-1-
A． 2
B
．3ห้องสมุดไป่ตู้
C． 2
D
．5
9. 已知棱长为 2 的正方体 ABCD A1B1C1 D1 中， M 为 AB 的中点， P 是平面 ABCD 内的
x2 点（ B 、 A ）可看作同一个“姐妹对” ）．已知函数 f (x) 2
ex
“姐妹点对”的个数为 D． 4 二、填空题
（） A ．1
B
2x ( x (x
．2
0) ，则 f ( x) 的
0)
C
．/3
11 ．若某校高三年级
是
.
8 个班参加合唱比赛的得分如茎叶图所示，则这组数据的中位数
2
12．右图是一个几何体的三视图，根据图中数据，可得
17 、
用心爱心专心
-3-
sin(πｘ) cos(πｘ) 2 1 (
x
5 ) ，则 f（ x）的最小值为
；
x
4
4
16. 关于 x 的不等式 2x2 x 4 的解集为
.
17．如图，线段 AB 长度为 2 ，点 A, B 分别在 x 非负半轴和 y 非负半轴上滑动，以线段 AB 为
一边，在第一象限内作矩形 ABCD ， BC 1，O
A．0
B ．－ 1
C ．1
D ．－ 1 或 0

湖北省安陆一中高三数学培优补差(八)

2012届高三培优补差文科数学（八）一．选择题：本大题共10小题，每小题5分，满分50分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．复数(2)z i i =+的虚部是（）A ． 2B ． -2C ． 2iD ． -2i2．已知全集R,U = 集合{}1,2,3,4,5A =,[)2,B =+∞，则图中阴影部分所表示的集合为（）A ． {0,1,2}B ． {0,1}C ． {1,2}D ． {1}3．设曲线2ax y =在点（1，a ）处的切线与直线062=--y x 平行，则=a （）A ．1B ．12 C ．12- D ．1-4．对某校400名学生的体重（单位：kg ）进行统计，得到如图所示的频率分布直方图，则学生体重在60kg 以上的人数为（）A ． 300B ． 100C ． 60D ． 20 5．下列各式中错误．．的是（） A ． 330.80.7> B ． 0..50..5log 0.4log 0.6> C ． 0.10.10.750.75-< D ． lg1.6lg1.4>6．已知正项组成的等差数列{}n a 的前20项的和为100，那么615a a 的最大值为（） A ． 25B ． 50C ． 100D ．不存在7．如图所示，一个空间几何体的主视图和俯视图都是边长为1的正方形，侧视图是一个直径为1的圆，那么这个几何体的表面积为（）A ．π4B ．π3C ．π2D ．π23（第2题图）（kg ）（第4题图）主视图侧视图俯视图（第7题图）8．实数y x ,满足不等式组20206318x y x y x y -≥⎧⎪+-≥⎨⎪+≤⎩，且()0z ax y a =+>取得最小值的最优解有无穷多个, 则实数a 的取值范围是（）A ． 45-B ． 1C ． 2D ．无法确定 9．已知函数()f x 的部分图象如图所示，则()f x 的解析式可能为（）A ． ()2sin 26x f x π⎛⎫=- ⎪⎝⎭B ．()44f x x π⎛⎫=+ ⎪⎝⎭C ． ()2cos 23x f x π⎛⎫=- ⎪⎝⎭D ． ()2sin 46f x x π⎛⎫=+ ⎪⎝⎭10．已知函数(1)f x +是定义在R 上的奇函数，若对于任意给定的不等实数1x 、2x ，不等式 1212()[()()]0x x f x f x --<恒成立，则不等式(1)0f x -<的解集为（） A ．()1,+∞ B ．(),0-∞ C ．()0,+∞ D ．(),1-∞ 二．填空题：本大题共5小题，每小题5分，满分25分． 11．已知sin π 0()(-1)+1 >0x x f x f x x ≤⎧=⎨⎩，则5()6f 的值为．12．ABC ∆中，如果bc a c b c b a 3))((=-+++，那么A 等于． 13. 已知某算法的流程图如图所示,若将输出的),(y x 值依次记为),(11y x ,),(22y x ， ),,(,n n y x （1）若程序运行中输出的某个数组是(,6)t -，则=t ；（2）程序结束时,共输出),(y x 的组数为． 14．在ABC ∆中，三内角,,A B C 所对边的长分别为,,a b c ，已知60B =︒，不等式2680x x -+-> 的解集为{|}x a x c <<，则b =15．ABCD 与CDEF 是两个全等的正方形，且两个正方形所在平面互相垂直，则DF 与AC 所成角的大小为．三．解答题：本大题共6小题，满分75分，解答应写出文字说明、证明过程或演算步骤．（第13题图）（第9题图）16．已知集合{}2230A x x x =+-<，{}(2)(3)0B x x x =+-<，（1）在区间()3,3-上任取一个实数x ，求“x AB ∈”的概率；（2）设(),a b 为有序实数对，其中a 是从集合A 中任取的一个整数，b 是从集合B 中任取的一个整数，求“a b A B -∈”的概率.17．已知向量()()2sin ,cos m x xπ=--，3cos ,2sin()2n x x π⎛⎫=- ⎪⎭，函数()1f x m n =-⋅．（1）求函数()f x 的解析式；（2）当[]0,x π∈时，求()f x 的单调递增区间；（3）说明()f x 的图象可以由()sin g x x =的图象经过怎样的变换而得到．18. 某商店经销一种洗衣粉，年销售总量为6000包，每包进价为8.2元，销售价为4.3元，全年分若干次进货，每次进货均为x 包，已知每次进货的运输劳务费为5.62元，全部洗衣粉全年保管费为x 5.1元.（1）将该商店经销洗衣粉一年的利润y （元）表示为每次进货量x （包）的函数；（2）为使利润最大，每次应进货多少包？19．如图，AB 为圆O 的直径，点E 、F 在圆O 上，AB ∥EF ，矩形ABCD 所在的平面和圆O 所在的平面互相垂直，且2AB =，1AD EF ==.（1）求证：AF ⊥平面CBF ；（2）设FC 的中点为M ，求证：OM ∥平面DAF ；（3）求三棱锥F CBE -的体积.20. 已知函数()f x xlnx =，（1）求()f x 的最小值；（2）若对所有1x ≥都有()1f x ax ≥-，求实数a 的取值范围. 21．已知一非零向量列{}na 满足：()11,1a =，()()11111,,2n n n n n n n a x y x y x y ----==-+()2n ≥. （1）证明：{}n a 是等比数列；（2）设n θ是1,n n a a -的夹角()2n ≥，n b =21n n θ-，12n n S b b b =+++，求n S ；（3）设n c =2log n n a a ，问数列{}n c 中是否存在最小项？若存在，求出最小值；若不存在，请说明理由.C（第19题图）2012届高三培优补差文科数学（八）答案1．选A ．解析：(2)z i i =+12i =-+，虚部是2.特别提醒：不是2i ．2．选D ．解析：阴影部分的元素x A ∈且x B ∉，即U A B ⋂ð,选项D 符合要求． 3．选A ．解析：由2y ax '=，又点（1，a ）在曲线2ax y =上，依题意得122x k y a ='===，解得1a =．4．选B ．解析：60kg 以频率为0.04050.01050.25⨯+⨯=，故人数为4000.25100⨯=（人）． 5．选C ．解析：构造相应函数，再利用函数的性质解决，对于A ，构造幂函数3y x =，为增函数，故A 是对；对于B 、D ，构造对数函数0.5log y x =为减函数，lg y x =为增函数，B 、D 都正确；对于C ，构造指数函数0.75x y =，为减函数，故C 错．6．选A ．解析：()()1202012020101002a a S a a +==+=，故12010a a +=，615120a a a a =2120252a a +⎛⎫≤= ⎪⎝⎭． 7．选D ．解析：这是一个横放的圆柱体，其底面半径12r =，高1h =，底面面积24S r ππ==底，侧面积2S rh ππ==侧，故322S S S π=+=侧表底． 8．选B ．解析：要使目标函数取得最小值的最优解有无穷多个，令ax +y =0并平移使之与过点C （34,32）（可行域中最左侧的点）的边界重合即可，注意到a >0，只能和AC 重合，∴a =1 9．选C ．解析：由点A 、点C 的横坐标可知4T π=，∴24T ππω==，12ω=，排除B 、D ，又点()0,1在图象上，代入()2sin 26x f x π⎛⎫=-⎪⎝⎭得12sin 6π⎛⎫=- ⎪⎝⎭不成立，排除A ，只有C 合适．说明，本题得出的是最佳选项，由图象无法确定振幅的值．10．选B ．解析：(1)f x +是奇函数，即其的图象关于点(0,0)对称，将(1)f x +向右平移1个单位长度，得()f x ，故()f x 的图象关于点(1,0)对称，由1212()[()()]0x x f x f x --<恒成立，知12120()()0x x f x f x ->⎧⎨-<⎩或12120()()0x x f x f x -<⎧⎨->⎩，()f x 为R 上的减函数；又将(1)0f =，不等式(1)0f x -<即(1)(1)f x f -<，有11x ->，故0x <.11．填12．解析：55111111sin 11666622f f f π⎛⎫⎛⎫⎛⎫⎛⎫=-+=-+=-+=-+= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭． 12填3π．解析：()()a b c b c a +++-()()()223b c a b c a b c a bc +++-=+-=⎡⎤⎡⎤⎣⎦⎣⎦，得222b c a bc +-=，由余弦定理得2221cos 222b c a bc A bc bc +-===，又0A π<<，∴3A π=． 13．填27，1006．解析：（1）按框图，x 是公比为2的等比数列的项，y 是公差为-2的等差数列的项，当6y =-时，为第4项，这时x 是等比数列的第4项，即27t =；（2）n 是公差为2的等差数列的项，当2012n >时，最大的项数为1006，即输出),(y x 共1006组．14． 15．3π．三．解答题：16．（1）由已知{}31A x x =-<<，{}23B x x =-<<，设事件“x A B ∈”的概率为1P ，这是一个几何概型，则13162P ==。

湖北省安陆一中2012届高三文科数学选填题专项训练3

2012届高三文科数学选填题专项训练（三）一、选择题： 1．不等式1x x≥的解集是（） A ．(,1)(0,1)-∞- B ．(](,1)0,1-∞-C ．(,1)[0,1]-∞-D ．(](],10,1-∞-2．已知集合2{,},{1}M m m N ==，若M N φ≠，则M N =（）A ．{-1}B ．1C ．{-1，1}D ．{1，0}3．一支田径队有男运动员44人，女运动员33人，若用分层抽样的方法从该队的全体运动员中抽取一个容量为14的样本，则抽取女运动员的人数为（） A ．6 B ．8 C ．10 D ．12 4．若a ，b 均为正实数，则“1b a<”是“01ab <<”的（） A ．充分而不必要条件 B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件5．已知等差数列{}n a 的前n 项和n S ，且*22232848,n n S S a a n N --++=∈且1n >，则1n a +等于（）A ．212B ．424C ．848D ．10166．已知角α的终边上有一点21(,)(0)4P t t t +>，则tan α的最小值为（）A ．12B ．1CD ．27．在ABC ∆中，角A 、B 、C 的对边分别为a 、b 、c ，且,(0)a b λ==>，45A =︒，则满足条件的三角形个数是（）A ．0B ．1C ．2D ．无数个 8．已知cos sin 1x x +=，则cos2x 等于（） A ．0 B ．1 C ．-1D ．1±9．定义在R 上的奇函数()f x 满足对任意的x 都有(1)(4)f x f x -=-且3(),(0,)2f x x x =∈，则(2012)(2010)f f -等于（）A ．-1B ．0C ．1D ．210．已知实数,s t 满足不等式()(2)0.s t s t -+-≥若14s ≤≤，则ts的取值范围是（）A ．1[,1]4-B ．1,14⎛⎤-⎥⎝⎦C ．1[,1]2-D ．1,12⎛⎤-⎥⎝⎦二、填空题：11.0）之间有下列数据：①3y x =-+；② 2.8y x =-+；③ 2.6y x =-+，其中正确方程的序号是 . 12．与直线1-=x 相切且恒过定点(1,0)的所有圆的圆心方程是 13．若直线1y =与函数3sin 2y x =在区间(0,)2π内有两个交点A 、B ，则线段AB 中点的坐标为。

湖北省安陆一中2012届高三文科数学选填题专项训练20

2012届高三文科数学选填题专项训练（二十）一、选择题 1.已知集合{}20,23x M x N x x x ⎧+⎫=<=≤-⎨⎬-⎩⎭，则集合{}3x x ≥＝（）（A ）M N （B ）MN （C ）()R C MN （D ）()R C M N2.复数11ii+-（i 是虚数单位）的共轭复数的虚部为（）（A ）-1 （B ）0 （C ）1 （D ）2 3.下列选项错误．．的是（）（A ）βα，表示两个不同平面，l 表示直线，“若βα⊥，则βα⊥⊂l l ，”的逆命题为真命题（B ）“2>x ”是“0232>+-x x ”的充分不必要条件（C ）命题p ：存在R x ∈0,使得01020<++x x ，则p ⌝：任意R x ∈,都有012≥++x x （D ）若p 且q 为假命题，则p 、q 均为假命题4.已知{}n a 是等差数列，124a a +=，7828a a +=，则该数列前10项和10S 等于（）（A ）64 （B ）100 （C ）110 （D ）1205.已知函数()2cos(2)6f x x π=+，下面四个结论中正确的是（）（A ）函数()f x 的最小正周期为2π （B ）函数()f x 的图象关于直线6x π=对称（C ）函数()f x 的图象是由2cos2y x =的图象向左平移6π个单位得到（D ）函数6f x π⎛⎫+ ⎪⎝⎭是奇函数6.若12,e e 是夹角为3π的单位向量，且12122,32a e e b e e =+=-+，则a b ∙＝（）（A ）1 （B ）－4 （C ）72- （D ）727.设等比数列{}n a 的公比2q =，前n 项和为n S ，则42Sa =（）(A)2 (B)4 (C)152 (D)1728.函数2()ln f x x x=-的零点所在的大致区间是( ) (A)（1,2） (B)（e ，3） (C)（2，e ） (D)（e ，+∞）9.设实数,x y 满足2025020x y x y y --≤⎧⎪+-≥⎨⎪-≤⎩，则y u x =的取值范围是( )(A)1,23⎡⎤⎢⎥⎣⎦ (B)11,32⎡⎤⎢⎥⎣⎦ (C)1,22⎡⎤⎢⎥⎣⎦ (D)52,2⎡⎤⎢⎥⎣⎦10.一个四棱锥的底面为正方形，其三视图如图所示，则这个四棱锥的体积是( ) A ．1 B ．2 C ．3 D ．4二、填空题11.在ABC ∆中，角,,A B C 的对边分别为,,a b c ，则1cos ,24C AC CB =∙=-且5a b +=，则c 等于12.函数 1sin()26y x π=-的纵坐标不变，将其图象上的各点的横坐标缩短为原来的14，得到的函数记为()()3g x g π=,则； 13.若3sin()25πθ+=，则cos2θ= . 14.已知数列{}n a 对任意的,m n N +∈有m n m n a a a ++=，若119a =,则2011a = . 15.已知{1,0,()1,0,x f x x ≥=-<则不等式)2()2(+⋅++x f x x ≤5的解集是16.给出以下四个结论：①函数21()1x f x x -=+的对称中心是(1,2)-； ②若关于x 的方程10x k x-+=在(0,1)x ∈没有实数根，则k 的取值范围是2k ≥；③在△ABC 中，“cos cos b A a B =”是“△ABC 为等边三角形”的必要不充分条件；④若将函数()sin(2)3f x x π=-的图像向右平移(0)φφ>个单位后变为偶函数，则φ的最小值是12π；其中正确的结论是：17.设抛物线2y =2x 的焦点为F ，过点M 0）的直线与抛物线相交于A ，B 两点，与抛物线的准线相交于C ，BF =2，则∆BCF 与∆ACF 的面积之比BCFACFS S ∆∆= ;2012届高三文科数学选填题专项训练（二十）答题卡一、选择题（每题5分，共10小题共50分）姓名分数二、填空题（共5小题，每题5分，共25分，把答案填在题中横线上）11、__________； 12、______1_______；13、_____725-__________；14、______20119_______； 15、___3,2⎛⎤-∞ ⎥⎝⎦___________；16、_____①③④______； 17、________45______；。

湖北省安陆一中高三数学选填题专题训练(7)

安陆一中2012届高三数学选填题专项训练（七）班级姓名分数一选择题1．等比数列{}n a 的首项为1a , 公比为q , 则 “10a >且1q >” 是 “对于任意正整数n , 都有1n n a a +>” 的（）A ．充分非必要条件B ．必要非充分条件C ．充分且必要条件D ．既非充分也非必要条件 2．要使函数y=x+x k (k>0)在[2，+∞）上有最小值2+2k，则k 的取值范围是（） A ．(4,+∞) B ．[4,+∞) C ．(0,4) D ．(0,4]3．把边长为1的正方形ABCD 沿对角线BD 折起形成三棱锥C ABD -的主视图与俯视图如图所示，则左视图的面积为（）A ．14 B.12 C.16 D.184. 函数2()4f x x x =-+在[,]m n 上的值域是[5,4]-, 则m n +取值所成的集合为（） A ． [0, 6] B ．[-1, 1 ] C ．[ 1, 5 ] D ． [ 1, 7 ] 5．已知||22,||3,,p q p q ==夹角为,4π如图2，若52,AB p q =+3AC p q =-，且D 为BC 中点，则AD 的长度（）A．152 B ．7 D ．86．已知)(x f 是定义域为R 的奇函数，1)4(-=-f ,)(x f 的导函数)('x f 的图象如图所示。

若两正数b a ,满足1)2(<+b a f ，则22++b a 的取值范围是（） A. )2,31( B. )3,21(C. )0,1(-D. )1,(--∞7．已知函数⎰+-t da a t a x)sin (cos 0的图像关于直线x=3π对称，则t 等于（）A ．2B ．－2C ．33D ．33-8．某人每月向银行存入a 元，存期为三年，月利率为r ，且以复利计算（复利：上一期的本金加利息作为下一期的本金），若规定利息所得税为所得总利息的2%，则到期该人应取回的资金金额为（ )A ．r r 1)1(36-+a+0.72aB ．r r r )1()1(37+-+a+0.72aC ．0.98r r 1)1(36-+ a +0.72aD ．0.98rr r )1()1(37+-+a+0.72a9．点P 从点O 出发，按逆时针方向沿周长为l 的图形运动一周，O P 、两点连线的距离y 与点P 走过的路程x 的函数关系如图，那么点P 所走的图形是（）B210．关于x 的二项式(1+2ix)n展开式中各项系数依次为a 0,a 1,a 2,……,a n ,其中i 为虚数单位，则数列{nn a a a 2103||......||||+++}的所有项系数的和为（）A ．23B ．21C ．2D ．3211. 如图，点P 是单位圆上的一个顶点，它从初始位置0P 开始沿单位圆按逆时针方向运动角α（02πα<<）到达点1P ，然后继续沿单位圆逆时针方向运动3π到达点2P ，若点2P 的横坐标为45-，则cos α的值等于 . 12．若10,,a xdx b c ===⎰⎰⎰，则将a ，b ，c 从小到大排列的结果为 .13．数字1,2,3,,9这九个数字填写在如图的9个空格中，要求每一行从左到右依次增大，每列从上到下也依次增大，当数字4固定在中心位置时，则所有填写空格的方法共有14．已知函数ln ()xf x x=,在区间［2，3］上任取一点00,()x f x '使得＞0的概率为 .15．在Rt ABC ∆中斜边AB=1,E 为AB 的中点，CD ⊥AB,则)()(→→→→∙∙∙CE CA CD CA 的最大值为 .安陆一中2012届高三数学选填题专项训练（七）答案ADADA BCDCB 11.10433- 12.c b a << 13.12 14.2-e 15.272。

湖北省安陆一中高三数学选填题专题训练(3).doc

高三上学期数学选填题专项训练（三）班级姓名一．选择题：（本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1．若()f x =，则()f x 的定义域为（） A. (,)1-02 B. (,]1-02 C. (,)1-+∞2D.(,)0+∞ 2.i 为虚数单位，则=⎪⎭⎫ ⎝⎛-+201111i i （）A.i -B.1-C.iD.13．已知幂函数y ＝()f x 的图象经过点1(4,)2，则(2)f ＝（）A ．14B ．22C ． 4D ． 2 4．已知函数()f x 是可导函数，且满足0(1)(1)lim 1x f f x x→--=-，则在曲线()y f x =上的点(1,(1))A f 的切线斜率是（）A ．1-B ．2C ．1D ．2- 5．y=2cos(4π–2x)的单调递减区间是 ( ) (A){x|2k π+π/8≤x ≤2k π+5π/8,k ∈Z} (B) {x|k π–3π/8≤x ≤k π+π/8,k ∈Z}(C){x|k π+π/8≤x ≤k π+5π/8,k ∈Z} (D) {x|2k π–3π/8≤x ≤2k π+π/8,k ∈Z}6.某四面体三视图如图所示，该四面体四个面的面积中最大的是（）A. 8B. C. 10D.7.从1，2，3，4，5中任取2各不同的数，事件A =“取到的2个数之和为偶数”，事件B =“取到的2个数均为偶数”，则P （B ︱A ）=( )A .18 B.14 C .25 D.128．某企业去年销售收入1000万元，年成本为生产成本500万元与年广告成本元两部分．若年利润必须按p %纳税，且年广告费超出年销售收入2%的部分也按p % 纳税，其他不纳税．已知该企业去年共纳税1．则税率p %为（）A ．10%B ．12%C ．25% D．40%9．函数'()y f x =是函数()y f x =的导函数，且函数()y f x =在点00(,())P x f x 处的切线为000:()'()()(),()()()l y g x f x x x f x F x f x g x ==-+=-，如果函数()y f x =在区间[,]a b 上的图象如图所示，且0a x b <<，那么（）A ．00'()0,F x x x ==是()F x 的极大值点B ．0'()F x =00,x x =是()F x 的极小值点C ．00'()0,F x x x ≠=不是()F x 极值点D ．00'()0,F x x x ≠=是()F x 极值点10．若函数()() y f x x R =∈满足(2)()f x f x -=，且[]1,1x ∈-时，()21f x x=-，函数()()()l g 01 0x x g x x x ⎧>⎪=⎨-<⎪⎩，则函数()()()h x f x g x =-在区间[5,6]-内的零点的个数为（）A ．13B ．8C ．9D ．10二．填空题：（本大题共5小题，每小题5分，共25分．）11．设2[0,1]()1(1,]x x f x x e x ∈⎧⎪=⎨-∈⎪⎩（其中e 为自然对数的底数），则0()ef x dx =⎰___________．12．函数)0(2>=x x y 的图象在点),(2k k a a 处的切线与x 轴的交点的横坐标为1+k a ，其中∈k N *，若a 1 = 16，则531a a a ++的值是。