《计算机仿真》试题及答案-工程硕士

合集下载

计算机仿真试题和答案

控制系统计算机辅助设计综合实验指导实验名称：连续与离散系统校正实验，系统可控性与可观性实验，系统的simulink仿真实验陈茜编实验人：苏建聪学号：200830810122班级：08电气工程及其自动化1班信息工程系实验任务书1. 有一个单位负反馈控制系统，如果控制对象的传递函数为设计要求：① 相角裕度≥45°；② 当系统的输入信号是单位斜坡信号时，稳态误差ess ≤0.04。

③ 要求绘制出校正后系统和未校正系统的Bode 图及其闭环系统的单位阶跃响应曲线，并进行对比。

2. 有一个单位负反馈控制系统，如果控制对象的传递函数为：试设计一个串联滞后校正装置。

设计要求：①相角裕度≥45°；② 当系统的输入信号是单位斜坡信号时，稳态误差ess ≤0.04。

③ 要求绘制出校正后系统和未校正系统的Bode 图及其闭环系统的单位阶跃响应曲线，并进行对比。

3. 有一个单位负反馈控制系统，如果控制对象的传递函数为 ()()4+=s s k s G p试设计一个串联超前滞后校正装置，设计要求： ①相角裕度≥45°；② 当系统的输入信号是单位斜坡信号时，稳态误差ess ≤0.04。

③ 要求绘制出校正后系统和未校正系统的Bode 图及其闭环系统的单位阶跃响应曲线，并进行对比。

4. 系统结构图如图所示，其中，采样周期Ts=0.01s ，被控对象()()110+=s s s G ，()s G h 为零阶保持器。

用W 变换法设计一超前校正装置D(z)，使系统相位裕度γ≥50°，校验设计后系统的性能指标。

5. 系统结构图如图所示，其中，采样周期Ts=0.01s ，被控对象1)s(0.2s k )(+=s G ο，()s G h 为零阶保持器。

用对数频率法设计D(z)，使系统开环增益k ≥30(1/s)，截止频率ωc ≥15(1/s),相位裕度γ≥50 °1使 s 11se -1(s)-Tsh T G +≈=，求出未校正系统的开环系统的开环传递函数(s)(s)G G (s)0s =G ,的传递函数模型参数。

计算机仿真技术考试试题(建工)

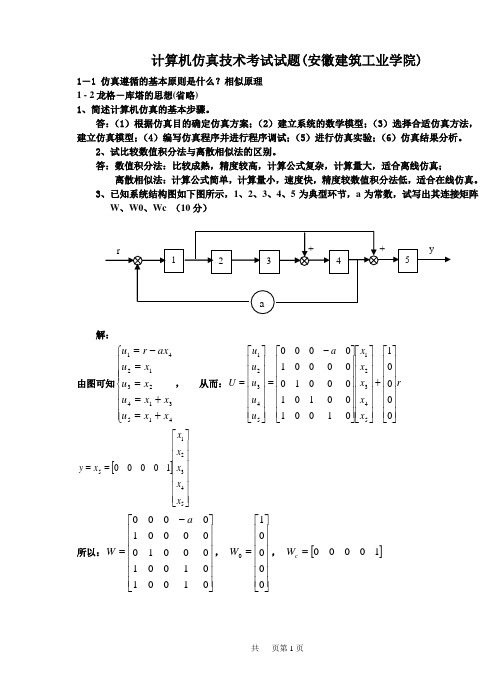
计算机仿真技术考试试题(安徽建筑工业学院)1－1 仿真遵循的基本原则是什么？相似原理 1 - 2龙格－库塔的思想(省略) 1、简述计算机仿真的基本步骤。

答：（1）根据仿真目的确定仿真方案；（2）建立系统的数学模型；（3）选择合适仿真方法，建立仿真模型；（4）编写仿真程序并进行程序调试；（5）进行仿真实验；（6）仿真结果分析。

2、试比较数值积分法与离散相似法的区别。

答：数值积分法：比较成熟，精度较高，计算公式复杂，计算量大，适合离线仿真；离散相似法：计算公式简单，计算量小，速度快，精度较数值积分法低，适合在线仿真。

3、已知系统结构图如下图所示，1、2、3、4、5为典型环节，a 为常数，试写出其连接矩阵W 、W0、Wc （10分）解：由图可知⎪⎪⎪⎩⎪⎪⎪⎨⎧+=+===-=415314231241x x u xx u x u xu ax r u ，从而：r x x x x x a u u u u u U ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=000010100100101000100000100005432154321[]⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡==54321510000x x x x x x y所以：⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-=01001010*******000010000a W ， ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=000010W ， []10000=c W4、已知系统状态空间表达式为[]⎪⎪⎩⎪⎪⎨⎧=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡=Xt y t u X X 01)()(012101 ，⎥⎦⎤⎢⎣⎡=11)0(X ，计算步长1.0=h ，输入信号1=u （0≥t ）试采用欧拉法，四阶龙格－库塔法计算h t =时对应的y 值。

（12分）解：⎥⎦⎤⎢⎣⎡=11)0(X ，⎥⎦⎤⎢⎣⎡=2101A ，⎥⎦⎤⎢⎣⎡=01B ，[]01=C 欧拉法：()()⎥⎦⎤⎢⎣⎡=⋅⎪⎪⎭⎫⎝⎛⋅⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡=++⎥⎦⎤⎢⎣⎡=+=3.12.11.010*********)0()0(11))0(,0()0()(h Bu AX hX f X h X 2.1)()(==h CX h y 四阶龙格－库塔法： ()⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡==3201112101)0(,01X f K ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡+⎪⎪⎭⎫ ⎝⎛⎥⎦⎤⎢⎣⎡⋅+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎪⎭⎫⎝⎛⋅++=4.31.2013221.011210121.0)0(,21.0012K X f K⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡+⎪⎪⎭⎫ ⎝⎛⎥⎦⎤⎢⎣⎡⋅+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎪⎭⎫⎝⎛⋅++=445.3105.2014.31.221.011210121.0)0(,21.0023K X f K()⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡+⎪⎪⎭⎫ ⎝⎛⎥⎦⎤⎢⎣⎡⋅+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⋅++=8995.32105.201445.3105.21.01121011.0)0(,1.0034K X f K()⎥⎦⎤⎢⎣⎡=++++=3432.12103.1226)0()(4321K K K K hX h X 2103.1)()(==h CX h y5、已知系统传递函数)1(2)()()(+==s s s U s Y s G ，试采用双线性变换法求解系统差分方程，计算步长h ＝0.1s （10分）。

《计算机仿真技术》试题(含完整答案)

一、数值计算，编程完成以下各题〔共20分，每题5分〕1、脉冲宽度为d ，周期为T 的矩形脉冲的傅里叶级数如下式描述：)2cos(/)/sin(21[)(1τπππτn T d n T d n T d f n ∑∞=+=当150=n ，41=T d ，2/12/1<<-τ，绘制出函数)(τf 的图形。

解： syms n t;f=((sin(n*pi/4))/(n*pi/4))*cos(2*pi*n*t); s=symsum(f,n,1,150); y=(1+2*s)/4; x=-0.5:0.01:0.5; Y=subs(y,'t',x); plot(x,Y)2、画出函数5505.025.55.15.1cos 5)5(sin )(2x x x x ex x f x +++-=在区间[3,5]的图形，求出该函数在区间[3, 5]中的最小值点m in x 和函数的最小值m in f .解：程序如下 x=3:0.05:5;y=(sin(5*x).^2).*exp(0.05*x.^2)-5*(x.^5).*cos(1.5*x)+1.5*abs(x+5.5)+x.^2.5; mix_where=find(y==min(y)); xmin=x(mix_where); hold on; plot(x,y);plot(xmin,min(y),'go','linewidth',5);str=strcat('(',num2str(xmin),',',num2str(min(y)),')'); text(xmin,min(y),str); Xlabel('x')Ylabel('f(x)')经过运行后得到的图像截图如下：运行后的最小值点m in x =4.6，m in f = -8337.86253、画出函数xe x xf x 5.2cos )(3.02-⋅=-在[1，3]区间的图形，并用编程求解该非线性方程0)(=x f 的一个根，设初始点为20=x .解： x=1:0.02:3; x0=2;y=@(x)(cos(x).^2).*exp(-0.3*x)-2.5*abs(x); fplot(y,[1,3]); Xlabel('x') Ylabel('f(x)')X1=fzero('(cos(x).^2).*exp(-0.3*x)-2.5*abs(x)',x0)运行后求得该方程的一个根为z=0.3256。

2020年秋冬智慧树知道网课《计算机仿真技术》课后章节测试答案

第一章测试1【单选题】(2分)计算机仿真系统的三要素（）A.计算机、模型、系统B.系统、模型、仿真C.计算机、系统、数学公式D.模型、仿真、计算机2【多选题】(2分)系统研究一般有哪些方法（）A.直接描述法B.仿真实验法C.理论解析法D.直接实验法3【单选题】(2分)哪些是以硬件为基础的仿真软件()A.MATHCADB.MAPLEC.MATLABD.Proteus4【判断题】(2分)欠实时仿真，仿真时钟比实际时钟慢。

例如烟火爆炸的仿真分析。

A.错B.对5【多选题】(2分)计算机仿真算法的误差主要有（）A.偶然误差B.截断误差C.舍入误差D.系统误差第二章测试1【单选题】(2分)MATLAB软件中，下面哪个命令是用来显示当前文件夹中文件名字的（）A.whatB.dirC.whoD.whos2【单选题】(2分)下面这些哪个是属于元素群运算（点运算）（）A.x/2B.x+bC.exp(x)D.X*y3【单选题】(2分)哪个是以硬件为基础的仿真软件()A.MAPLEB.MATLABC.ProteusD.MATHCAD4【判断题】(2分)。

计算机仿真技术试题含完整答案

一、数值计算，编程完成以下各题（共20分，每小题5分） 1、脉冲宽度为d ，周期为T 的矩形脉冲的傅里叶级数如下式描述：)2cos(/)/sin(21[)(1τπππτn T d n T d n T d f n ∑∞=+=当150=n ，41=T d ，2/12/1<<-τ，绘制出函数)(τf 的图形。

《计算机仿真技术》试卷A(含答案)

《计算机仿真技术》考试试卷(A卷)班级姓名学号一．填空题。

(每空1分，共20分)1、计算机仿真中系统由_________________、_________________、________________等三个要素组成。

2、常见的系统实验建模法有________________、________________、________________、________________等几种方法。

3、叙述simulink中常见的可变步长的仿真算法有：________________、________________、________________、________________。

(任举四种)4、MA TALB的Comand windows窗口中可以显示workspace中的全部变量的命令是_________________、_________________。

5、计算机仿真算法的算法引起的误差是________________、________________。

6、三维立体绘图中，________________ 是三维曲线绘图命令，________________是三维网格线绘图命令，________________着色表面图绘图命令。

7、符号运算中，泰勒级数计算的函数是________________傅里叶变换的函数________________二．简答题。

(本题5小题，每题8分，共40分)1、计算机仿真的目的和作用2、列举几种计算机仿真软件，并简要介绍一下（要求4种以上）3、matlab主界面主要包括那些窗口，分别有什么样的功能4、局部变量和全局变量之间的区别5、计算机仿真技术中相似性主要包含那几个方面三．编程题 (本题6小题、共40分)根据下面要求，写出程序代码。

1、(5分)设(2E －C -1B)A T =C -1，其中E 是4阶单位矩阵，A T 是4阶矩阵A 的转置。

求矩阵A2、(5分)输入下面的矩阵，求出特征多项式和特征根，并求出特征多项式的微分。

计算机仿真习题3 课后答案

习题3
1、已知系统响应函数为)sin(11)(θ+-=-bt e b
t y bt ，其中21l b -=，)1arctan(2
l
l -=θ，要求用不同的线型或颜色，在同一张图上绘制l 取值为0.2,、0.4、0.6、0.8时，系统在[]18,0∈t 区间内的响应曲线，并要求用2.0=l 和8.0=l 对它们相应的两条曲线进行文字标志。

答：刚开始因为没有考虑到相乘或相除矩阵的维度而总出错，后来理解清楚之后就简单多了。

编写程序如下：
得到结果：
2、用plot
3、mesh 、surf 指令，绘制2222)1()1(1y x y x z ++++-=
三维图（x 、y 范围自定）。

答：用plot3时，我定义]100,0[∈x ，]100,0[∈y ；并分别令22)1(y x a +-=，22)1(y x b ++=。

同时需注意将1变换成与a 、b 同维的矩阵。

得到结果：
在利用mesh、surf绘图时，为了图形美观取]
x，x=y.
[-
∈
100
,
100
程序如下：
得到结果：
3、对向量t进行以下运算可以构成3个坐标的值向量：)
y=，
cos(t
x=，)
sin(t
z=。

利用plot3指令，并选用绿色的实线绘制相应的三维曲线。

t
答：取pi
:0(
:1.0
=。

注意绿色是‘g’。

编写程序如下：
t*
)
10
得到结果：。

计算机仿真与建模考试试题

计算机仿真与建模考试试题一、单项选择题1. 在计算机仿真与建模中，以下哪个软件是用于创建和模拟三维计算机图形的？A. MATLABB. AutoCADC. SolidWorksD. 3ds Max2. 计算机仿真与建模常用的数学建模方法有哪些？A. 微分方程建模B. 蒙特卡洛模拟C. 神经网络模型D. 遗传算法优化3. 下面哪个软件是用于分析流体和气体流动的计算机仿真工具？A. ANSYSB. CATIAC. Pro/ENGINEERD. PTC Creo4. 在计算机仿真中，有哪些常见的物理模型？A. 质点模型B. 弹簧-质点模型C. 流体模型D. 电路模型5. 计算机仿真与建模的主要应用领域是什么？A. 机械工程B. 航空航天C. 生物医学D. 所有以上领域二、简答题1. 什么是计算机仿真与建模？计算机仿真与建模是指使用计算机技术和数学方法对现实世界的问题或系统进行建模和模拟实验的过程。

通过对系统各个组成部分的特性进行数学描述和计算机编程实现，可以模拟真实系统的行为，并进行虚拟实验和预测。

2. 计算机仿真与建模的主要步骤是什么？计算机仿真与建模的主要步骤包括：问题建模与分析、数学建模、软件工具选择与开发、模型验证与调试、模拟实验与结果分析等。

3. 计算机仿真与建模的优势有哪些？计算机仿真与建模具有以下优势：- 可以对复杂系统进行全面、高效的分析和研究，避免了大量实际实验和浪费资源；- 提供了研究系统性能、优化设计和决策支持的基础；- 可以预测系统行为并进行虚拟实验，帮助解决实际问题和提高生产效率；- 提供了客观、可重复的实验环境，方便对结果进行验证和比较。

4. 计算机仿真与建模的应用范围有哪些？计算机仿真与建模广泛应用于工程领域，包括机械工程、电气工程、航空航天、建筑工程等。

此外，它还在生物医学、交通运输、环境科学等领域有重要应用。

三、综合题某工程团队需要设计一种新型的风力发电机，用于发电和供电给一个小型城市。

计算机仿真模拟试题

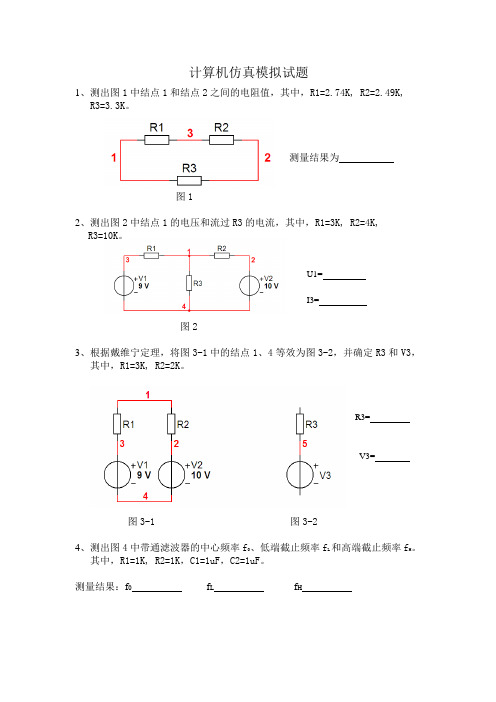
计算机仿真模拟试题1、测出图1中结点1和结点2之间的电阻值，其中，R1=2.74K, R2=2.49K, R3=3.3K 。

测量结果为图12、测出图2中结点1的电压和流过R3的电流，其中，R1=3K, R2=4K, R3=10K 。

U1=I3=图23、根据戴维宁定理，将图3-1中的结点1、4等效为图3-2，并确定R3和V3，其中，R1=3K, R2=2K 。

R3=V3=图3-1 图3-24、测出图4中带通滤波器的中心频率f 0、低端截止频率f L 和高端截止频率f H 。

其中，R1=1K, R2=1K ，C1=1uF ，C2=1uF 。

测量结果：f 0 f L f H图45、测出图5中RLC串联电路的谐振频率f0，其中，R1=20 , L1=1mH，C1=1Uf。

f0 =图56、测出图6中输出端对“地”的电压，其中R1=10K, R2=20K。

U OUT=图67、测出图7中滞回过零比较器的两个滞回比较点（电压），其中R1=10K, R2=430K。

U1 = U2 =图78、测出图8恒流源电路中流过R2的电流，并将它改为200 后从新测量。

I R2= I R2’=图89、如图9所示，A、B为输入端，Y为输出端。

通过仿真实验填写真值表，并将逻辑分析仪上经过调整的波形通过截图并粘贴到“答卷”Word电子文档中。

A B Y0 00 11 01 1图910、如图10所示，将D_FF接成二分频器，将函数发生器按图中的参数设置，并将示波器上经过调整的波形通过截图并粘贴到“答卷”Word电子文档中。

图1011、如图11所示，按图构成一个多谐振荡器，通过仿真实验确定R1的值，将频率尽可能调到1000Hz，并将示波器上经过调整的波形通过截图并粘贴到“答卷”Word电子文档中。

R1=图1112、如图12所示，555电路产生载频信号，V1为低频调制信号，从结点4输出一个调频波，按图构成电路，将V1的偏移量调到6V，用示波器观察（FSK）调频波，并将示波器上经过调整的波形通过截图并粘贴到“答卷”Word电子文档中。

计算机仿真技术试卷B.docx

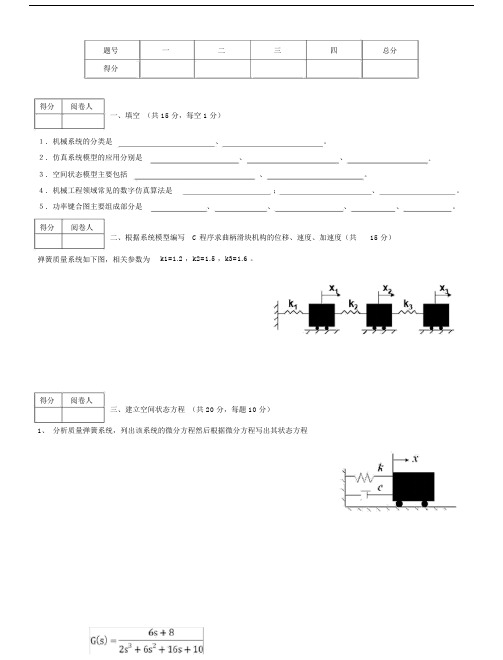
题号一二三四总分得分得分阅卷人一、填空（共 15 分，每空 1 分）１．机械系统的分类是、。

２．仿真系统模型的应用分别是、、。

３．空间状态模型主要包括、。

４．机械工程领域常见的数字仿真算法是；、。

５．功率键合图主要组成部分是、、、、。

得分阅卷人C程序求曲柄滑块机构的位移、速度、加速度（共15 分）二、根据系统模型编写弹簧质量系统如下图，相关参数为k1=1.2 ，k2=1.5 ，k3=1.6 。

得分阅卷人三、建立空间状态方程（共 20 分，每题 10 分）1、分析质量弹簧系统，列出该系统的微分方程然后根据微分方程写出其状态方程2、将传递函数转化为空间状态方程写出计算步骤得分阅卷人四、画出下列系统的功率键合图并写出绘图步骤（共30 分，每题 10 分）１．绘出右图的键合图并写出步骤２.绘出右图小车系统键合图并写出绘图步骤3.一个生长在罐中的细菌的简单模型。

假定细菌的出生率和当前细菌的总数成正比，死亡率和当前的总数的平方成正比，试建立仿真模型，画出键合图。

得分阅卷人五、列出系统的状态方程和simulink 模型（共 20分）列出右图蹦极系统的状态方程并写出其状态方程。

桥梁距地面的距离是h2=50m，人距桥梁的距离是h1=30m。

系统参数为k=20， a1=a2=1，m=70，g=10系统数学模型是22009～2010 学年第二学期《算机仿真技》期卷（ B 卷）⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯装⋯⋯⋯⋯⋯⋯⋯ ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯班姓名学号得分⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯密⋯⋯⋯⋯封⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯第3页共3页。

计算机仿真课后答案

第二章2.1x=[15 22 33 94 85 77 60]x(6)x([1 3 5])x(4:end)x(find(x>70))2.2T=[1 -2 3 -4 2 -3] ;n=length(T);TT=T';for k=n-1:-1:0B(:,n-k)=TT.^k;endBtest=vander(T)2.3A=zeros(2,5);A(:)=-4:5L=abs(A)>3islogical(L)X=A(L)2.4A=[4,15,-45,10,6;56,0,17,-45,0]find(A>=10&A<=20)2.5p1=conv([1,0,2],conv([1,4],[1,1]));p2=[1 0 1 1];[q,r]=deconv(p1,p2);cq='商多项式为'; cr='余多项式为';disp([cq,poly2str(q,'s')]),disp([cr,poly2str(r,'s')])2.6A=[11 12 13;14 15 16;17 18 19];PA=poly(A)PPA=poly2str(PA,'s')第三章3.1n=(-10:10)';y=abs(n);plot(n,y,'r.','MarkerSize',20)axis equalgrid onxlabel('n')3.2x=0:pi/100:2*pi;y=2*exp(-0.5*x).*sin(2*pi*x);plot(x,y),grid on;3.3t=0:pi/50:2*pi;x=8*cos(t);y=4*sqrt(2)*sin(t);z=-4*sqrt(2)*sin(t);plot3(x,y,z,'p');title('Line in 3-D Space');text(0,0,0,'origin');xlabel('X'),ylable('Y'),zlable('Z');grid;3.4theta=0:0.01:2*pi;rho=sin(2*theta).*cos(2*theta); polar(theta,rho,'k');3.5[x,y,z]=sphere(20);z1=z;z1(:,1:4)=NaN;c1=ones(size(z1));surf(3*x,3*y,3*z1,c1);hold onz2=z;c2=2*ones(size(z2));c2(:,1:4)=3*ones(size(c2(:,1:4))); surf(1.5*x,1.5*y,1.5*z2,c2); colormap([0,1,0;0.5,0,0;1,0,0]);grid onhold off第四章4.1for m=100:999m1=fix(m/100);m2=rem(fix(m/10),10);m3=rem(m,10);if m==m1*m1*m1+m2*m2*m2+m3*m3*m3 disp(m)endend4.2function[s,p]=fcircle(r)s=pi*r*r;p=2*pi*r;4.3y=0;n=100;for i=1:ny=y+1/i/i;endy4.4s=0;for i=1:5s=s+factor(i);ends4.5sum=0;i=1;while sum<2000sum=sum+i;i=i+1;end;n=i-24.6function k=jcsum(n)k=0;for i=0:nk=k+2^i;end或function k=jcsum1(n)k=0;i=0;while i<=nk=k+2^i;i=i+1;end第五章5.1A=[2,1,-5,1;1,-5,0,7;0,2,1,-1;1,6,-1,-4];b=[13,-9,6,0]';x=A\b5.2[U,fmin]=fminsearch('fxyz',[0.5,0.5,0.5])function f=fxyz(u)x=u(1);y=u(2);z=u(3);f=x+y.^2./x/4+z.^2./y+2./z;5.3X=linspace(0,2*pi,50);Y=sin(X);P=polyfit(X,Y,3)AX=linspace(0,2*pi,50);Y=sin(X);Y1=polyval(P,X)plot(X,Y,':O',X,Y1,'-*')5.4x=0:2.5:10;h=[0:30:60]';T=[95,14,0,0,0;88,48,32,12,6;67,64,54,48,41];xi=[0:0.5:10];hi=[0:10:60]';temps=interp2(x,h,T,xi,hi,'cubic');mesh(xi,hi,temps);第六章6.1syms xy=finverse(1/tan(x))6.2syms x yf=1/(1+x^2); g=sin(y);fg=compose(f,g)6.3syms xg=(exp(x)+x*sin(x))^(1/2);dg=diff(g)6.4F=int(int('x*exp(-x*y)','x'),'y')6.5syms xF=ztrans(x*exp(-x*10))6.6a=[0 1;-2 -3];syms sinv(s*eye(2)-a);6.7f=solve('a*x^2+b*x+c')6.8f=solve('x+y+z=1','x-y+z=2','2*x-y-z=1')6.9y=dsolve('D2y+2*Dy+2*y=0','y(0)=1','Dy(0)=0') ezplot(y),grid on6.10a=maple('simplify(sin(x)^2+cos(x)^2);')6.11f=maple('laplace(exp(-3*t)*sin(t),t,s);')6.12syms t xF=sin(x*t+2*t);L=laplace(F)第七章7.17.27.37.47.57.67.7第八章8.1（1）num=[5]; den=[1,2,2];sys=tf(num,den)（2）s = tf('s');H = [5/(s^2+2*s+2) ];H.inputdelay =2（3）h=tf([0.5,0],[1,-0.5,0.5],0.1)8.2num=2*[1,0.5];den=[1,0.2,1.01];sys=tf(num,den)[z,p,k]=tf2zp(num,den);zpk(z,p,k)[A,B,C,D]=tf2ss(num,den);ss(A,B,C,D)8.3num=[1,5]; den=[1,6,5,1]; ts=0.1;sysc=tf(num,den);sysd=c2d(sysc,ts,'tustin')8.4r1=1;r2=2;c1=3;c2=4;[A,B,C,D]=linmod('x84');[num,den]=ss2tf(A,B,C,D);sys=tf(num,den)8.5A=[1,1,0;0,1,0;0,0,2];B=[0,0;1,0;0,-2];n=size(A)Tc=ctrb(A,B);if n==rank(Tc)disp('系统完全能控');elsedisp('系统不完全能控');end第九章9.1num=[2,5,1];den=[1,2,3];bode(num,den);grid on ;figure;nyquist(num,den);9.2num=5*[1,5,6];den=[1,6,10,8];step(num,den);grid on ;figure;impulse(num,den);grid on ;9.3kosi=0.7;wn=6;num=wn^2;den=[1,2*kosi*wn,wn^2];step(num,den);grid on ;figure;impulse(num,den);grid on ;9.4den=[1,2,8,12,20,16,16];[rtab,info]=routh(den)a=rtab(:,1)if all(a>0)disp('系统是稳定的');elsedisp('系统是不稳定的');end9.5num=7*[1,5];den=conv([1,0,0],conv([1,10],[1,1]));[gm,pm,wg,wc]=margin(num,den)第十章10.1ng0=[1]; dg0=10000*[1 0 -1.1772];g0=tf(ng0,dg0); %满足开环增益的为校正系统的传递函数s=kw2s(0.7,0.5) %期望的闭环主导极点ngc=rg_lead(ng0,dg0,s);gc=tf(ngc,1)g0c=tf(g0*gc);rlocus(g0,g0c);b1=feedback(g0,1); %未校正系统的闭环传递函数b2=feedback(g0c,1); %校正后系统的闭环传递函数figure,step(b1,'r--',b2,'b'); grid on %绘制校正前后系统的单位阶跃响应曲线10.2KK=20;s1=-2+i*sqrt(6);a=1ng0=[10];dg0=conv([1,0],[1,4]);g0=tf(ng0,dg0);[ngc,dgc,k]=rg_lag(ng0,dg0,KK,s1,a);gc=tf(ngc,dgc)g0c=tf(KK*g0*gc);b1=feedback(k*g0,1);b2=feedback(g0c,1);step(b1,'r--',b2,'b');grid on10.3KK=128;s1=-2+i*2*sqrt(3);a=2ng0=[10];dg0=conv([1,0],conv([1,2],[1,8]));g0=tf(ng0,dg0);[ngc,dgc,k]=rg_lag(ng0,dg0,KK,s1,a);gc=tf(ngc,dgc)g0c=tf(KK*g0*gc);rlocus(g0,g0c);b1=feedback(k*g0,1);b2=feedback(g0c,1);figure,step(b1,'r--',b2,'b');grid on10.4ng0=[1];dg0=conv([1,0,0],[1,5]);g0=tf(ng0,dg0);w=logspace(-3,3);KK=1;Pm=50;[ngc,dgc]=lead4(ng0,dg0,KK,Pm,w);gc=tf(ngc,dgc);g0c=tf(KK*g0*gc);bode(KK*g0,w);hold on,bode(g0c,w);grid on,hold off [gm,pm,wcg,wcp]=margin(g0c)Kg=20*log10(gm)g1=feedback(g0c,1);bode(g1),grid on,[mag,phase,w]=bode(g1);a=find(mag<=0.707*mag(1));wb=w(a(1))max(mag)b=find(mag==max(mag))wr=w(b)10.5KK=40; Pm=50;ng0= KK *[1]; dg0=conv([1,0],conv([1,1],[1,4]));g0=tf(ng0,dg0) ;w=logspace(-2,4);[ngc,dgc]=fg_lead_pm(ng0,dg0,Pm,w)gc=tf(ngc,dgc),g0c=tf(g0*gc);b1=feedback(g0,1); b2=feedback(g0c,1);step(b1,'r--', b2,'b'); grid onfigure, bode(g0,'r--',g0c,'b',w), grid on,[gm,pm,wcg,wcp]=margin(g0c), Km=20*log10(gm)10.6KK=200; bp=0.3; ts=0.7; delta=0.05;ng0=[1];dg0=conv([1,0],conv([0.1,1],conv([0.02 1],conv([0.01,1],[0.005 1]))));g0=tf(ng0,dg0);w=logspace(-4,3);t=[0:0.1:3];[mag,phase]=bode(KK*g0,w);[gm0,pm0,wg0,wc0]=margin(mag,phase,w),gm0=20*log10(gm0)%gm0 = -15.6769%2、确定期望的开环传递函数mr=0.6+2.5*bp;wc=ceil((2+1.5*(mr-1)+2.5*(mr-1)^2)*pi/ts), h=(mr+1)/(mr-1)w1=2*wc/(h+1), w2=h*w1w1=wc/10; w2=25;ng1=[1/w1,1]; dg1=conv([1/w2,1],conv([1,0],[1,0]));g1=tf(ng1,dg1);g=polyval(ng1,j*wc)/polyval(dg1,j*wc); K=abs(1/g); %剪切频率处幅值为1，求K值g1=tf(K*g1)%3、确定反馈环节传递函数h=tf(dg1,ng1); Kh=1/K;h=tf(Kh*h) %期望频率特性的倒特性%4、验算性能指标g2=feedback(KK*g0,h); %校正后，系统的开环传递函数b1=feedback(KK*g0,1); b2=feedback(g2,1);bode(KK*g0,'r--',g2,'b',h,'g',w);grid onfigure,step(b1, 'r--',b2, 'b',t); grid on,[pos,tr,ts,tp]=stepchar(b2,delta)【本文档内容可以自由复制内容或自由编辑修改内容期待你的好评和关注，我们将会做得更好】精选范本,供参考！。

计算机仿真习题及答案

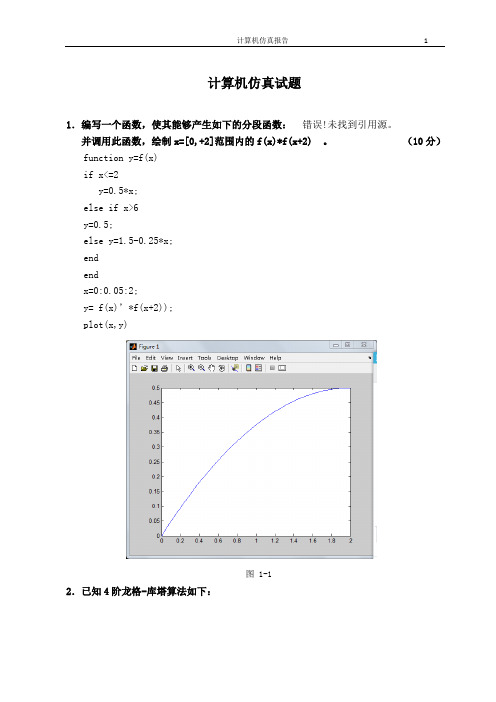
计算机仿真试题1．编写一个函数，使其能够产生如下的分段函数：错误！未找到引用源。

并调用此函数，绘制x=[0,+2]范围内的f(x)*f(x+2) 。

（10分）function y=f(x)if x<=2y=0.5*x;else if x>6y=0.5;else y=1.5-0.25*x;endendx=0:0.05:2;y= f(x)’*f(x+2));plot(x,y)图 1-12．已知4阶龙格-库塔算法如下：试利用该算法求解以下微分方程：（15分）本题可以调用MATLAB函数中龙格-库塔算法函数ode45，首先编写m文件：function dy=func(x,y)dy=-y+1;end再在主窗口调用此文件：[x,y]=ode45('func',[0,5],0)%这里的[0,5]为任取区间，表示方程在此范围的解。

运行结果如下:x =0.00010.00010.00020.00020.00050.00070.00100.00120.00250.00370.00500.00620.01250.01880.02510.0313 0.06270.09410.12550.15690.28190.40690.53190.65690.78190.90691.03191.15691.28191.40691.53191.65691.78191.90692.03192.15692.28192.40692.53192.65692.78192.90693.03193.15693.28193.40693.53193.65693.78193.90694.03194.15694.28194.40694.53194.65694.74274.82854.91425.0000y =0.00010.00010.00020.00020.00050.00070.00100.00120.0025 0.0037 0.0050 0.0062 0.0124 0.0186 0.0248 0.0309 0.0608 0.0898 0.1180 0.1452 0.2457 0.33430.41250.48160.54250.59630.64370.68550.72250.75510.78390.80930.83170.85150.86890.88430.89790.90990.92050.92980.93810.94540.95180.95740.96240.96690.97080.97420.97720.97990.98230.98430.98620.98780.98920.99050.99130.99200.99270.9933为只管起见，我们使用函数命令画出x-y（plot(x,y)）的关系如下图：图1-23．用matlab语言求下列系统的状态方程、传递函数、零极点增益、和部分分式形式的模型参数，并分别写出其相应的数学模型表达式：（15分）（1）G（s）=324327242410355024s s ss s s s+++++++（2）.X=2.25 -5 -1.25 -0.542.25 -4.25 -1.25 -0.2520.25 -0.5 -1.25 -121.25 -1.75 -0.25 -0.75 0X⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥+⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦uy= [0 2 0 2] X解：（1）a)求对应状态方程参数：num=[1 07 24 24]; den=[1 10 35 50 24]; [A,B,C,D]=tf2ss(num,den) 运行结果：A =-10 -35 -50 -241 0 0 00 1 0 00 0 1 0B =1C =1 7 24 24D =故，状态方程为：.X = x+ uY=[1 7 24 24]xb)求对应零极点增益模型参数：num=[1 07 24 24]; den=[1 10 35 50 24]; [Z,P,K]=tf2zp(num,den) 运行结果如下： Z =-2.7306 + 2.8531i -2.7306 - 2.8531i -1.5388P = -4.0000 -3.0000 -2.0000 -1.0000K = 1故变换后的零极点模型为： G(s)=c)求对应部分分式型：num=[1 07 24 24]; den=[1 10 35 50 24]; [R,P,H]=residue(num,den) 运行结果如下： R =4.0000 -6.0000 2.0000 1.0000P =-4.0000 -3.0000 -2.0000 -1.0000H = []故变换后的部分分式模型为：11223644)(+++++-+=s s s s s G（2）由题给条件，知：A=[2.25 -5 -1.25 -0.5; 2.25 -4.25 -1.25 -0.25;0.25 -0.5 -1.25 -1;1.25 -1.75-10 -35 -50 -24 1 0 0 0 0 1 0 0 0 0 1 010 0 0-0.25 -0.75] B=[4;2;2;0] C=[0 2 0 2],D=0 a)求传递函数矩阵： [num,den]=ss2tf(A,B,C,D) 运行结果为： num =0 4.0000 14.0000 22.0000 15.0000 den =1.0000 4.0000 6.2500 5.25002.2500 故，所对应传递函数模型为：25.225.525.641522144)(23423+++++++=s s s s s s s s Gb)求零极点模型：num=[0 4 14 22 15];en=[1 4 6.25 5.25 2.25]; [Z,P,K]=tf2zp(num,den) 运行结果为： Z =-1.0000 + 1.2247i -1.0000 - 1.2247i -1.5000 P =-1.5000 -1.5000 -0.5000 + 0.8660i -0.5000 - 0.8660iK =4.0000故，零极点模型为：)866.05.0()5.1()2247.11)(5.1(4)(2i s s i s s s G ±++±++=c)求对应部分分式模型： [R,P,H]=residue(num,den) 运行结果为： R =4.0000 -0.0000-0.0000 - 2.3094i -0.0000 + 2.3094iP =-1.5000 -1.5000 -0.5000 + 0.8660i -0.5000 - 0.8660iH = []故变换后的部分分式模型为：i s ii s i s s G 866.05.03094.2866.05.03094.25.14)(+++-+-++=4．已知一单位反馈系统开环传递函数为：，试绘制系统Nyquist图，判断闭环系统的稳定性，并求其单位阶跃响应。

《计算机仿真》课程考试试题

《计算机仿真》课程考试试题1. （分）计算下述函数在自变量采样点集{[3,3], 0.01}x ∈-步长为上的值：222(43)/2, -3-1-1, -11(43)/2, 13x x x y x x x x x ⎧---≤<⎪=+≤<⎨⎪-+-≤≤⎩-编写脚本程序，分别创建采样向量x ，计算相应的函数值向量y ，并利用函数绘图函数()绘制曲线。

- 将程序、执行过程及图形结果拷贝至文档打印提交。

（提示： …() …...语句）2. （分）编写函数，返回给定向量中最大元素的下标值。

换言之，()返回的满足()不小于任何()。

要求有合适的帮助信息注解提交测试结果。

（提示：利用 ….循环语句）. （分）按照下图所示画出 0.5sin()3t y t y e -==和, ]3,0[π∈t ，写出绘制程序，并进行适当的标注。

t(deg)m a g n i t u d e sine wave and Ae -αt wave. （分）在环境下完成以下框图所示双通道观测仪系统的建立并进行仿真- 自己自行选定信号源和属性信号发生器双通道合成器示波器信号发生器-自己设定仿真的时间注意事项：、考生须在答卷封面上写明学号、姓名及所在学习中心，并与答题内容装订在一起。

答卷封面见下页（请考生下载打印，并按照此封面样式完成答卷）。

、请考生务必于本学期课程考试时（2013年10月18日至日）将答卷交到当地学习中心，逾期不交者，考试成绩以分计。

年月课程考试答卷课程名称：《计算机仿真》年级：层次：专业：学号：姓名：学习中心：成绩：教师签名：中国传媒大学现代远程教育年月日。

计算机仿真测试题及答案

计算机仿真测试题及答案1. 选择题1.1 下列关于计算机仿真的定义，哪个是正确的？A. 计算机仿真是通过使用计算机来模拟现实世界的过程和现象B. 计算机仿真是通过使用计算机来生成虚拟的3D图像C. 计算机仿真是通过使用计算机来进行数据分析和统计D. 计算机仿真是通过使用计算机进行编程和软件开发答案：A1.2 计算机仿真的主要应用领域是：A. 电影和游戏制作B. 数据分析和统计C. 空气动力学和流体力学D. 软件开发和编程答案：C1.3 以下哪个是计算机仿真的一个重要优点？A. 精确模拟现实世界的过程和现象B. 速度快，可以实时进行模拟C. 不需要消耗大量的计算资源D. 可以替代真实的实验和测试答案：D2. 填空题2.1 计算机仿真可以帮助工程师在设计阶段进行 __________ 和__________。

答案：分析，优化2.2 计算机仿真可以用于预测产品在不同环境条件下的 __________和 __________。

答案：性能，行为2.3 在计算机仿真中，模型是对现实世界中的对象或系统进行的一个 __________ 描述。

答案：数学3. 简答题3.1 请简要解释计算机仿真的工作原理。

答案：计算机仿真的工作原理是基于数学模型和计算机算法。

首先，根据需要模拟的对象或系统的特性，工程师会构建一个数学模型，用来描述该对象或系统的行为。

然后，使用计算机算法对这个数学模型进行求解和模拟。

算法会根据初始条件和输入参数，计算出模拟过程中的各个时间点上的状态和输出结果。

最后，通过可视化等方式，将仿真结果呈现给使用者。

3.2 计算机仿真的主要应用领域有哪些？请举例说明。

答案：计算机仿真的主要应用领域包括航空航天、汽车工程、建筑设计、电子电路设计等。

例如，在航空航天领域，工程师可以使用计算机仿真来模拟飞机或火箭在不同高度、速度和气候条件下的飞行行为，以评估其性能和安全性。

在建筑设计领域，可以使用计算机仿真来模拟建筑物在地震或风暴等自然灾害中的响应，以提前预防和减少损失。

计算机仿真题库

25. 请比较数值积分法与离散相似法的区别。数值积分法比较成熟，精度较高，但计算公式复杂，计算量大，适合离线仿真；而离散相似法计算公式简单，计算量小，速度快，但精度较低，适合在线仿真。 26. 物理仿真以真实系统的物理性质和几何形状相似为基础而其他性质不变来构造系统的物理模型，并在物理模型上进行实验的过程称为物理仿真，也称为实体仿真。其优点在于直观、形象；缺点在于模型改变困难，实验限制较多，投资较大。 27. 虚拟现实虚拟现实是用高科技手段构造出来的一种人工环境，它具有模仿人的视觉、听觉、触觉等感知功能的能力，具有使人可以亲身体验沉浸在这种虚拟环境并与之相互作用的能力。 28. 多媒体仿真将数字、文字、声音、图形、图像和动画等各种媒体有机组合，并与先进的计算机通信和广播电视技术相结合，形成一个可组织、存储、操纵和控制多媒体信息的集成环境和交互系统的仿真技术。 29. 根据系统的动态特性，一般可以将系统做哪些分类？根据系统的动态特性，可以将系统分为：（1）连续系统和离散系统。时间和各个组成部分的变量都具有连续形式的系统称为连续系统；全部或一些组成部分的变量具有离散信号形式的系统称为离散系统。（2）线性或非线性系统。如果微分方程的系数是常数或者仅仅是自变量的函数，则为线性微分方程，其符合叠加性原理，可分为线性定常系统，线性时变系统；非线性系统用非线性微分方程表示，其不符合叠加原理。（3）确定系统和随机系统。确定系统可以用确定的数学模型进行描述，输出和输入变量之间有完全确定的函数关系；随即系统则指系统内部或环境变量发生不确定变动，会影响输出变量。（4）单变量系统和多变量系统。这是对输入输出变量个数而言的。 30. 在连续系统的数字仿真中，仿真算法的选择一般为考虑什么？常用的仿真算法有哪些？在连续系统的数字仿真中，选择仿真算法一般会考虑求解精度、速度、数值稳定性、自启动能力、步长等。常用的仿真方法有：欧拉法、四阶龙格-库塔法、离散相似法等。欧拉法属于自启动算法，适用于线性系统和非线性系统，方法简单，但误差的积累导致求解精度降低。四阶龙格库塔法也属于自启动算法，适用于线性和非线性系统，支持单步长和可变步长，求解速度和精度较高，但仿真时间较长。离散相似法一般用于状态方程，按环节离散相似法可用于非线性系统，按系统离散相似法仅限于线性系统。 31. 什么是实时仿真？什么情况下需要进行实时仿真？它在算法上有什么要求？实时仿真是指仿真模型的时间比例尺等于系统原模型的时间比例尺的一类仿真，对系统进行仿真试验时，如果仿真系统有实物，由于实物和人是按真实时间变化和运动的，因此就需要进行实时仿真。实时仿真要求仿真系统接收实时动态输入，并产生实时动态输出，输入和输出通常为固定采样时间间隔的数列。 32. 什么是数值稳定性问题？如何保证计算中的数值稳定性？所谓的数值稳定性问题，是指在扰动影响下，其计算过程中误差的积累是否受到控制的问题。要保证数值稳定性，应遵循两条原则：（1）保证计算稳定；（2）有一定的计算精度来选择合理的计算步长。

研究生《计算机仿真》考试资料

研究⽣《计算机仿真》考试资料同学们红⾊地⽅、问题重点看我就知道这些…其他知识也要看…只能尽⼒到这⾥加油看楼⼀、填空1、仿真是指⽤模型（物理模型或数学模型）代替实际系统进⾏实验和研究。

2、为使仿真的结果被证实是真实可靠的，也就是结果是可信的，仿真所遵循的基本原则是相似原理：⼏何相似、环境相似和性能相似。

3、按照仿真实验时间标尺τ与实际系统的时间标尺t⽐例来分类，将τ/t=1的仿真称为实时仿真，⽽τ/t≠1的仿真为⾮实时仿真。

⼀般有实物介⼊的半实物仿真属于实时仿真，⽽纯计算机仿真为⾮实时仿真。

4、凡是系统的输⼊量是时间t的连续函数，⽆论其输出量是连续单调函数或是单值或是多值的函数，均称这个系统是连续系统。

⽤微分⽅程表⽰的系统可以是⾮线性或线性系统，⽽对于传递函数表⽰的系统，只适⽤于单输⼊－单输出的线性定常系统，所以表⽰有⼀定的局限性。

5、各种数值积分法的截断误差与积分⽅法的阶次和步长有关。

是由于计算机的字长是有限制的，计算只能限制在有限位数内，因⽽产⽣了舍⼊误差。

6、对于⼀个稳定的微分⽅程，经过转换得到的差分⽅程的计算结果不⼀定是稳定的，不同的数值积分⽅法的计算稳定性也不相同。

7、按环节离散化就是将系统分成若⼲个环节，在每个环节的⼊⼝处加⼀个虚拟的采样开关，并⽴即跟⼀个信号重构过程（加保持器），以便使信号恢复为连续形式，这时系统实际上已成为⼀个采样系统。

当采样周期⾜够⼩时，这个采样系统就近似等价于原连续系统。

⼆、简述系统仿真的特点（8分）1仿真的实验性质仿真基本上是⼀种通过实验来研究系统的综合实验技术，具有⼀般实验的性质。

不论是利⽤仿真技术进⾏系统分析还是设计，都必须通过⼀系统实验来完成。

所建⽴的仿真模型应具有实验的性质，即模型与原型的功能及参数之间应有相似性和对应性2数字仿真与解析法解析法是应⽤数学推导、演绎去求解数学模型的⽅法，⽽数字仿真是通过计算机在数学模型上进⾏⼀系列实验来研究问题的⽅法。

解析法求解问题得出对问题的通解，⽽数字仿真的每⼀次运⾏只能给出在特定条件的数值解（特解）。

第 1.2章习题参考答案

1-1什么是仿真？它的主要优点是什么？它所遵循的基本原则是什么？
答：所谓仿真，就是使用其它相似的系统来模仿真实的需要研究的系统。

计算机仿真是指以数字计算机为主要工具，编写并且运行反映真实系统运行状况的程序。

对计算机输出的信息进行分析和研究，从而对实际系统运行状态和演化规律进行综合评估与预测。

它是非常重要的设计自动控制系统或者评价系统性能和功能的一种技术手段。

仿真的主要优点是：方便快捷、成本低廉、工作效率和计算精度都很高。

它所遵循的基本原则是相似性原理。

1-2你认为计算机仿真的发展方向是什么？
答：向模型更加准确的方向发展，向虚拟现实技术，以及高技术智能化、一体化方向发展。

向更加广阔的时空发展。

1-3计算机数字仿真包括哪些要素？它们的关系如何？
答：计算机仿真的三要素是：系统——研究的对象、模型——系统的抽象、计算机——仿真的工具和手段。

它们的关系是相互依存。

2-1控制算法的步长应该如何选择？
答：控制算法步长的选择应该恰当。

如果步长太小，就会增加迭代次数，增加计算量；如果步长太大，计算误差将显著增加，甚至造成计算结果失真。

2-2通常控制系统的建模有哪几种方法？
答：1）机理建模法；2）实验建模法；3）综合建模法。

2-3用欧拉法求以下系统的输出响应()y t 在0≤t ≤1上，0.1h =时的数值解。

0y
y +=&，(0)0.8y =解：输入以下语句绘制的曲线图
2-4用二阶龙格-库塔法对2-3题求数值解，并且比较两种方法的结果。

解：输入以下语句绘制的曲线图
经过比较两种方法的结果，发现它们几乎没有什么差别。

《计算机仿真技术》试卷B(含答案)

《计算机仿真技术》考试试卷(B 卷)班级姓名学号一．填空题。

(每空1分，共20分)1、计算机仿真技术三要素是_______________、_________________、________________。

2、计算机仿真中模型能够代表系统来进行研究，模型主要有________________、________________、________________、________________等几类模型。

3、叙述simulink 中常见的固定步长的仿真算法有：________________、________________、________________、________________。

(任举四种)4、MATALB 主要相似性主要包含以下几种相似_________________、________________、___________________。

5、Simulink 中主要包含_________________、________________、_______________等几种模块。

6、符号运算中，泰勒级数计算的函数是________________，拉普拉斯变换的函数________________，傅里叶级数的计算函数是________________。

二．简答题。

(本题5小题，每题8分，共40分)1、简述根据信号类型分类，计算机仿真主要包含哪几种类型。

2、简述蒙特卡洛法建模的步骤。

3、m 函数文件和m 文本文件之间的区别。

4、叙述三维立体绘图常用的几个绘图指令及其功能。

5、简述matlab 软件的基本组成三．编程题 (本题6小题、共40分)根据下面要求，只需写出程序代码，不需计算结果和图形。

1、(5分)写出右面的矩阵D ，求出其大于4的元素有几个，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=059123107D并通过变量列出其在矩阵的位置和序号2、(5分)求解下面矩阵A 的行列式和逆矩阵，并利用命令取出系数矩阵的逆矩阵的第二行的数据，以小数点后面两位数值的形式显示出来。

《计算机仿真》试题及答案-工程硕士

计算机仿真试题和答案

计算机仿真技术考试试题(建工)

《计算机仿真技术》试题(含完整答案)

2020年秋冬智慧树知道网课《计算机仿真技术》课后章节测试答案

计算机仿真技术试题含完整答案

《计算机仿真技术》试卷A(含答案)

计算机仿真 习题3 课后答案

计算机仿真与建模考试试题

计算机仿真模拟试题

计算机仿真技术试卷B.docx

计算机仿真课后答案

计算机仿真习题及答案

《计算机仿真》课程考试试题

计算机仿真测试题及答案

计算机仿真题库

研究生《计算机仿真》考试资料

第 1.2章习题参考答案

《计算机仿真技术》试卷B(含答案)

计算机仿真习题3 课后答案