专题10 四边形-2017版[中考15年]深圳市2002-2016年中考数学试题分项解析(解析版)

合集下载

专题10 二次函数与四边形的综合-中考数学函数考点全突破

一、考点分析：二次函数的综合题中在第二三小问比较常考到四边形的问题，这类题目主要考察两种题型：1.四边形的面积最值问题 2.特殊平行四边形的存在性问题，这类包括平行四边形，矩形菱形等。

二、解决此类题目的基本步骤与思路1.四边形面积最值问题的处理方法：核心步骤：对于普通四边形要转化成两个三角形进行研究，然后用求三角形面积最值问题的方法来求解2对于特殊平行四边形问题要先分类，（按照边和对角线进行分类）3.画图，（画出大致的平行四边形的样子，抓住目标点坐标）4. 计算（利用平行四边形的性质以及全等三角形的性质）三、针对于计算的方法选择1.全等三角形抓住对应边对应角的相等2.在利用点坐标进行长度的表示时要利用两点间距离公式3.平行四边形的对应边相等列相关的等式4.利用平行四边形的对角线的交点从而找出四个点坐标之间的关系X A+X C=X B+X D Y A+Y C=Y B+Y D （利用P是中点，以及中点坐标公式）A(x1,y1)、B（x2,y2），那么AB中点坐标就是（,）处理矩形菱形的方法与平行四边形方法类似注意事项：1.简单的直角三角形可以直接利用底乘高进行面积的表示2.复杂的利用“补”的方法构造矩形或者大三角形，整体减去部分的思想 3.利用“割”的方法时，一般选用横割或者竖割，也就是做坐标轴的垂线。

4.利用点坐标表示线段长度时注意要用大的减去小的。

四、二次函数问题中四边形面积最值问题1.如图，已知抛物线213y x bx c =++经过ABC V 的三个顶点，其中点(0,1)A ，点(9,10)B -，//AC x 轴，点P 是直线AC 下方抛物线上的一个动点. (1)求抛物线的解析式;(2)过点P 且与y 轴平行的直线l 与直线AB 、AC 分别交于点E 、F ，当四边形AECP 的面积最大时，求点P 的坐标;【解析】：（1）用待定系数法求出抛物线解析式即可；（2）设点P （m ， m2+2m+1），表示出PE=﹣m2﹣3m ，再用S 四边形AECP=S △AEC+S △APC=AC ×PE ，建立函数关系式，求出最大值即可设点P （m ，m 2+2m+1）∴E（m ，-m+1）∵﹣6＜m＜0∴当m=﹣时，四边形AECP的面积的最大值是此时点P（﹣，﹣）． *网2.抛物线y＝－x2＋6x交x轴正半轴于点A，顶点为M，对称轴MB交x轴于点B，过点C(2，0)作射线CD交MB于点D(D在x轴上方)，OE∥CD交MB于点E，EF∥x轴交CD的延长线于点F，作直线MF.(1)求点A，M的坐标；(2)当BD为何值时，点F恰好落在该抛物线上？(3)当BD＝1时，①求直线MF的表达式，并判断点A是否落在该直线上；②延长OE交FM于点G，取CF中点P，连结PG，△FPG，四边形DEGP，四边形OCDE的面积分别记为S1，S2，S3，则S1∶S2∶S3＝__3∶4∶8__.解：(1)令y＝0，则－x2＋6x＝0，解得x1＝0，x2＝6，∴A(6，0)，∴对称轴是直线x＝3，∴M(3，9)；(3)①当BD＝1时，BE＝3，∴F(5，3)．设MF 的表达式为y ＝kx ＋b ，将M (3，9)，F (5，3)代入，得⎩⎪⎨⎪⎧9＝3k ＋b ，3＝5k ＋b ，解得⎩⎪⎨⎪⎧k ＝－3，b ＝18， ∴y ＝－3x ＋18.∵当x ＝6时，y ＝－3×6＋18＝0， ∴点A 落在直线MF 上； ②∵BD ＝1，BC ＝1， ∴△BDC 为等腰直角三角形， ∴△OBE 为等腰直角三角形，五、二次函数中特殊平行四边形的存在性问题（一）例题演示已知：如图，在平面直角坐标系xOy 中，直线与x 轴、y 轴的交点分别为A 、B ，将∠OBA 对折，使点O 的对应点H 落在直线AB 上，折痕交x 轴于点C ．（1）直接写出点C 的坐标，并求过A 、B 、C 三点的抛物线的解析式；（2）若抛物线的顶点为D，在直线BC上是否存在点P，使得四边形ODAP为平行四边形？若存在，求出点P的坐标；若不存在，说明理由；【解析】：（1）点A的坐标是纵坐标为0，得横坐标为8，所以点A的坐标为（8，0）；点B的坐标是横坐标为0，解得纵坐标为6，所以点B的坐标为（0，6）；由题意得：BC是∠ABO的角平分线，所以OC=CH，BH=OB=6。

广东省深圳市2017年中考数学真题试题(含扫描答案)

深圳市2017年初中毕业生学业考试数学试题解析第Ⅰ卷（共60分）一、选择题1．-2的绝对值是（）A ．-2B ．2C ．12-D ．12 2．图中立体图形的主视图是（）A ．B ．C ．D ．3．随着“一带一路”建设的不断发展，我国已与多个国家建立了经贸合作关系，去年中哈铁路（中国至哈萨克斯坦）运输量达8200000吨，将8200000用科学记数法表示为（）A ．58.210⨯B ．58210⨯C ．68.210⨯D ．78210⨯ 4．观察下列图形，其中既是轴对称又是中心对称图形的是（） A ． B ． C ． D ．5．下列选项中，哪个不可以．．得到12//l l ？（）A ．12∠=∠B ．23∠=∠C ． 35∠=∠D ．34180∠+∠=o6．不等式组32521x x -<⎧⎨-<⎩的解集为（） A ．1x >- B ．3x < C ．1x <-或3x > D ．13x -<<7．一球鞋厂，现打折促销卖出330双球鞋，比上个月多卖10%，设上个月卖出x 双，列出方程（）A ．10%330x =B ．(110%)330x -=C ． 2(110%)330x -=D ．(110%)330x +=8．如图，已知线段AB ，分别以A B 、为圆心，大于12AB 为半径作弧，连接弧的交点得到直线l ，在直线l 上取一点C ，使得25CAB ∠=o ，延长AC 至M ，求BCM ∠的度数为（）A ．40oB ．50oC ． 60oD ．70o9．下列哪一个是假命题（）A ．五边形外角和为360oB ．切线垂直于经过切点的半径C ． (3,2)-关于y 轴的对称点为(3,2)-D ．抛物线242017y x x =-+对称轴为直线2x =10．某共享单车前a 公里1元，超过a 公里的，每公里2元，若要使使用该共享单车50%的人只花1元钱，a 应该要取什么数（）A ．平均数B ．中位数C ．众数D ．方差11．如图，学校环保社成员想测量斜坡CD 旁一棵树AB 的高度，他们先在点C 处测得树顶B 的仰角为60o，然后在坡顶D 测得树顶B 的仰角为30o ，已知斜坡CD 的长度为20m ，DE 的长为10m ，则树AB 的高度是（）mA ．203．30 C ． 303 D ．4012．如图，正方形ABCD 的边长是3，BP CQ =，连接,AQ DP 交于点O ，并分别与边,CD BC 交于点,F E ，连接AE ．下列结论：①AQ DP ⊥；②2OA OE OP =g ；③AOD OECF S S ∆=四边形；④当1BP =时，13tan 16OAE ∠=．其中正确结论的个数是（）A ．1B ．2C ．3D ．4二、填空题13．因式分解：34a a -= ．14．在一个不透明的袋子里，有2个黑球和1个白球，除了颜色外全部相同，任意摸两个球，摸到1黑1白的概率是． 15．阅读理解：引入新数i ，新数i 满足分配律，结合律，交换律，已知21i =-，那么(1)(1)i i +-=g ．16．如图，在Rt ABC ∆中，90ABC ∠=o ，3AB =，4BC =，Rt MPN ∆，90MPN ∠=o ，点P 在AC 上，PM 交AB 于点E ，PN 交BC 于点F ，当2PE PF =时，AP = ．三、解答题17．计算222|2cos45(1)8--+-o18．先化简，再求值：22()224x x x x x x +÷-+-，其中1x =-． 19．深圳市某学校抽样调查，A 类学生骑共享单车，B 类学生坐公交车、私家车等，C 类学生步行，D 类学生（其它），根据调查结果绘制了不完整的统计图．类型频数频率 A30 x B18 0.15 Cm 0.40 D n y（1）学生共__________人，x =__________，y =__________；（2）补全条形统计图；（3）若该校共有2000人，骑共享单车的有___________人．20．一个矩形周长为56厘米，（1）当矩形面积为180平方厘米时，长宽分别为多少？（2）能围成面积为200平方厘米的矩形吗？请说明理由．21．如图一次函数y kx b =+与反比例函数(0)m y x x=>交于(2,4)A 、(,1)B a ，与x 轴，y 轴分别交于点C D 、．（1）直接写出一次函数y kx b =+的表达式和反比例函数(0)m y x x=>的表达式；（2）求证：AD BC =． 22．如图，线段AB 是O e 的直径，弦CD AB ⊥于点H ，点M 是弧CBD 上任意一点，2,4AH CH ==．（1）求O e 的半径r 的长度；（2）求sin CMD ∠；（3）直线BM 交直线CD 于点E ，直线MH 交O e 于点N ，连接BN 交CE 于点F ，求HE HF g 的值．23．如图，抛物线22y ax bx =++经过点(1,0),(4,0)A B -，交y 轴于点C ：（1）求抛物线的解析式（用一般式表示）．（2）点D为y轴右侧抛物线上一点，是否存在点D使23ABC ABDS S∆∆=，若存在请直接给出点D坐标；若不存在请说明理由．（3）将直线BC绕点B顺时针旋转45o，与抛物线交于另一点E，求BE的长．。

(部编版)2020年中考数学试题分项版解析汇编第期专题10四边形含解析6

专题10：四边形一、选择题1.(2017北京第6题)若正多边形的一个内角是150°，则该正多边形的边数是（） A ． 6 B ． 12 C. 16 D ．18 【答案】B. 【解析】试题分析：设多边形的边数为n,则有（n-2）×180°=n ×150°,解得：n=12.故选B. 考点：多边形的内角与外角2. (2017河南第7题)如图，在ABCD 中，对角线AC ，BD 相交于点O ，添加下列条件不能．．判定ABCD 是菱形的只有（）A ．AC BD ⊥B ．AB BC = C.AC BD = D ．12∠=∠ 【答案】C.考点：菱形的判定.3. （2017湖南长沙第10题）如图，菱形ABCD 的对角线BD AC ,的长分别为cm cm 8,6，则这个菱形的周长为（）A ．cm 5B ．cm 10C ．cm 14D ．cm 20 【答案】D 【解析】试题分析：根据菱形的对角线互相垂直，可知OA=3，OB=4，根据勾股定理可知AB=5，所以菱形的周长为4×5=20. 故选：D考点：菱形的性质4. （2017湖南长沙第12题）如图，将正方形ABCD 折叠，使顶点A 与CD 边上的一点H 重合（H 不与端点D C ,重合），折痕交AD 于点E ，交BC 于点F ，边AB 折叠后与边BC 交于点G ，设正方形ABCD 的周长为m ，CHG ∆的周长为n ，则mn的值为（） A ．22 B ．21C ．215-D ．随H 点位置的变化而变化【答案】B 【解析】试题分析：设正方形ABCD 的边长为2a ，正方形的周长为m=8a ，设CM=x ，DE=y ，则DM=2a-x ，EM=2a-y ， ∵∠EMG=90°， ∴∠DME+∠CMG=90°． ∵∠DME+∠DEM=90°， ∴∠DEM=∠CMG ，又∵∠D=∠C=90°△DEM ∽△CMG ， ∴CG CM MGDM DE EM==,即22CG x MG a x y a y ==-- ∴CG=(2)(2)=,x a x x a y CG MG y y--= △CMG 的周长为CM+CG+MG=24ax x y-在Rt △DEM 中，DM 2+DE 2=EM 2即（2a-x ）2+y 2=（2a-y ）2整理得4ax-x 2=4ay∴CM+MG+CG=2444ax x aya y y-===n ．所以12n m = 故选：B ．考点：1、正方形，2、相似三角形的判定与性质，3、勾股定理5. （2017山东临沂第7题）一个多边形的内角和是外角和的2倍，这个多边形是（） A ．四边形 B ．五边形 C ．六边形 D ．八边形【答案】C 【解析】试题分析：根据多边形的外角和为360°，可知其内角和为720°，因此可根据多边形的内角和公式（n-2）·180°=720°，解得n=6，故是六边形. 故选：C考点：多边形的内外角和6. （2017山东临沂第12题）在ABC V 中，点D 是边BC 上的点（与B 、C 两点不重合），过点D 作DE AC ∥，DF AB ∥，分别交AB ，AC 于E 、F 两点，下列说法正确的是（）A ．若AD BC ⊥，则四边形AEDF 是矩形B ．若AD 垂直平分BC ，则四边形AEDF 是矩形 C ．若BD CD =，则四边形AEDF 是菱形 D ．若AD 平分BAC ∠，则四边形AEDF 是菱形【答案】D 【解析】试题分析：根据题意可知：DE AC ∥，DF AB ∥，可得四边形AEDF 是平行四边形. 若AD ⊥BC ，则四边形AEDF 是平行四边形，不一定是矩形；选项A 错误；若AD 垂直平分BC ，则四边形AEDF 是菱形，不一定是矩形；选项B 错误；若BD=CD ，则四边形AEDF 是平行四边形，不一定是菱形；选项C 错误；若AD 平分∠BAC ，则四边形AEDF 是菱形；正确．故选：D考点：特殊平行四边形的判定7. （2017山东青岛第7题）如图，平行四边形ABCD 的对角线AC 与BD 相交于点O ，AE ⊥BC ，垂足为E ，3=AB ，AC ＝2，BD ＝4，则AE 的长为（）A ．23B ．23C ．721 D ．7212 【答案】D考点：1、平行四边形的性质，2、勾股定理，3、面积法求线段长度8. (2017四川泸州第11题)如图，在矩形ABCD 中，点E 是边BC 的中点，AE BD ⊥,垂足为F ，则ta n B D E ∠的值是（）A B ．14 C ．13D【答案】A. 【解析】试题分析：由AD ∥BC 可得△ADF ∽△EBF ，根据相似三角形的性质可得AD AF DFEB EF BF==，因点E 是边BC 的中点且AD=BC,所以AD AF DFEB EF BF===2，设EF=x ，可得AF=2x ，在Rt △ABE 中，由射影定理可得，再由AD AF DFEB EF BF ===2可得，在Rt △DEF 中，tan BDE ∠=4EF DF ==，故选A. 9. （2017江苏苏州第10题）如图，在菱形CD AB 中，60∠A =，D 8A =，F 是AB 的中点．过点F 作F D E ⊥A ，垂足为E ．将F ∆AE 沿点A 到点B 的方向平移，得到F '''∆A E ．设P 、'P 分别是F E 、F ''E 的中点，当点'A 与点B 重合时，四边形CD 'PP 的面积为A ．．．8【答案】A. 【解析】试题分析：作,,DH AB PK AB FL AB ⊥⊥⊥在菱形CD AB 中，60∠A =，D 8A =,F 是AB 的中点4AF EF EL ∴==∴=，P 是F E 的中点，2PK ∴=DH =1PP CD ∴=高为82S ∴==L K H故答案选A.考点：平行四边形的面积，三角函数.10.（2017江苏苏州第7题）如图，在正五边形CDAB E中，连接BE，则∠ABE的度数为A．30 B．36 C.54 D．72【答案】B.【解析】试题分析：∠ABE=3601=3652︒⨯︒故答案选B.考点：多边形的外角，等腰三角形的两底角相等11.（2017浙江台州第10题）如图，矩形EFGH的四个顶点分别在菱形ABCD的四条边上，BE BF=，将,AEH CFG∆∆分别沿,EH FG折叠，当重叠部分为菱形且面积是菱形ABCD面积的116时，则AEEB为（）A．53B．2 C.52D．4【答案】A考点：1、菱形的性质，2、翻折变换（折叠问题）二、填空题1.(2017天津第17题)如图，正方形ABCD 和正方形EFCG 的边长分别为3和1，点G F ,分别在边CD BC ,上，P 为AE 的中点，连接PG ，则PG 的长为 .【解析】试题分析：连结AC,根据正方形的性质可得A 、E 、C 三点共线，连结FG 交AC 于点M ，因正方形ABCD 和正方形EFCG的边长分别为3和1，根据勾股定理可求得,AC=3,即可得AE=2,因P 为AE 的中点，可得,再由正方形的性质可得GM=EM=2,FG 垂直于AC ，在Rt △PGM 中，PM=2 ,由勾股定理即可求得2.(2017福建第15题)两个完全相同的正五边形都有一边在直线l 上，且有一个公共顶点O ，其摆放方式如图所示，则AOB 等于度．【答案】108【解析】∵五边形是正五边形，∴每一个内角都是108°，∴∠OCD=∠ODC=180°-108°=72°，∴∠COD=36°，∴∠AOB=360°-108°-108°-36°=108°.DC3.（2017广东广州第16题）如图9，平面直角坐标系中O 是原点，OABC 的顶点,A C 的坐标分别是()()8,0,3,4，点,D E 把线段OB 三等分，延长,CD CE 分别交,OA AB 于点,F G ，连接FG ，则下列结论：①F 是OA 的中点；②OFD ∆与BEG ∆相似；③四边形DEGF 的面积是203；④OD =；其中正确的结论是．（填写所有正确结论的序号）【答案】①③ 【解析】试题分析：如图，分别过点A 、B 作AN OB ⊥ 于点N ，BM x ⊥ 轴于点M在OABC 中，(80)(34)(114)A C B OB ∴=，，，，，D E 、是线段AB 的三等分点， 12OD BD ∴= ,CB OF ODFBDC ∴∆∆111222OF OD OF BC OA BC BD ∴==∴==， F ∴ 是OA 的中点，故①正确.(34)5C OC OA ∴=≠，，OABC ∴ 不是菱形.,DOF COD EBG ODF COD EBG ∴∠≠∠=∠∠≠∠=∠(40),F CF OC CFO COF ∴=<∴∠>∠，，DFO EBG ∴∠≠∠故OFD ∆ 和BEG ∆ 不相似. 则②错误；由①得，点G 是AB 的中点，FG ∴ 是OAB ∆ 的中位线1,22FG OB FG OB ∴==D E 、是OB 的三等分点，DE ∴=1118416222OAB S OB AN OA BM ∆=⋅=⋅=⨯⨯=解得：1162AN OB=,DF FG ∴ 四边形DEGH 是梯形()551202121223DEGF DE FG h S OB h OB AN -∴==⋅=⋅=四边形则③正确133OD OB == ,故④错误.综上：①③正确.考点：平行四边形和相似三角形的综合运用4.（2017广东广州第11题）如图6，四边形ABCD 中，0//,110AD BC A ∠=，则B ∠=___________.【答案】70° 【解析】试题分析：两直线平行，同旁内角互补，可得：B ∠=180°-110°＝70° 考点：平行线的性质5.（2017山东临沂第18题）在ABCD Y 中，对角线AC ，BD 相交于点O .若4AB =，10BD =，3sin 5BDC ∠=，则ABCD Y 的面积是．【答案】24 【解析】试题分析：作OE ⊥CD 于E ，由平行四边形的性质得出OA=OC ，OB=OD=12BD=5，CD=AB=4，由sin ∠BDC=35，证出AC⊥CD ，OC=3，AC=2OC=6，得出▱ABCD 的面积=CD•AC=24．故答案为：24.考点：1、平行四边形的性质，2、三角函数，3、勾股定理6.（2017山东青岛第13题）如图，在四边形 ABCD 中，∠ABC ＝∠ADC ＝90°，E 为对角线AC 的中点，连接BE 、ED 、BD ，若∠BAD ＝58°，则∠EBD 的度数为__________度．【答案】32 【解析】试题分析：如下图由∠ABC ＝∠ADC ＝90°，E 为对角线AC 的中点，可知A ，B ，C ，D 四点共圆，圆心是E ，直径AC 然后根据圆周角定理由∠BAD ＝58°，得到∠BED ＝116°，然后根据等腰三角形的性质可求得∠EBD=32°. 故答案为：32.考点:1、圆周角性质定理，2、等腰三角形性质7.(2017山东滨州第16题)如图，将矩形ABCD 沿GH 对折，点C 落在Q 处，点D 落在AB 边上的E 处，EQ 与BC 相交于点F ．若AD ＝8，AB ＝6，AE ＝4，则△EBF 周长的大小为___________．ABCDHQGFE【答案】8.【解析】由折叠的性质可得DH=EH ，设AH=x ，则DH=EH=8-x ，在Rt △AEH 中，根据勾股定理可得2224(8)x x +=- ，解得x=3，即可得AH=3，EH=5；根据已知条件易证△AEH ∽△BFE ，根据相似三角形的性质可得AH AE EHBE BF EF==,即3452BF EF ==，解得BF=83 ,EF=103 ,所以△EBF 的周长为2+83+103=8. 8.(2017江苏宿迁第15题)如图，正方形CD AB 的边长为3，点E 在边AB 上，且1BE =．若点P 在对角线D B 上移动，则PA+PE 的最小值是．9.(2017辽宁沈阳第16题)如图，在矩形ABCD 中，53AB BC ==，,将矩形ABCD 绕点B 按顺时针方向旋转得到矩形GBEF ，点A 落在矩形ABCD 的边CD 上，连接CE ，则CE 的长是 .【答案】5. 【解析】试题分析：如图，过点C 作MN ⊥BG ，分别交BG 、EF 于点M 、N ，根据旋转的旋转可得AB=BG=EF=CD=5，AD=GF=3，在Rt △BCG 中，根据勾股定理求得CG=4，再由1122BCGSBC CG BG CM =⋅=⋅,即可求得CM=125,在Rt △BCM 中，根据勾股定理求得95==，根据已知条件和辅助线作法易知四边形BENMW 为矩形，根据矩形的旋转可得BE=MN=3,BM=EN=95,所以CN=MN-CM=3-125=35,在Rt △ECN 中，根据勾股定理求得===.考点：四边形与旋转的综合题.10．（2017江苏苏州第18题）如图，在矩形CD AB 中，将C ∠AB 绕点A 按逆时针方向旋转一定角度后，C B 的对应边C ''B 交CD 边于点G ．连接'BB 、CC '，若D 7A =，CG 4=，G ''AB =B ，则CC '='BB （结果保留根号）．【答案】5. 【解析】试题分析：连接AG,设DG=x,则 G=4+x ''AB =B在'Rt AB G ∆ 中，22492(4)1x x x +=+⇒= ，则5,7AB BC ==''CC BB ∴==考点：旋转的性质，勾股定理 .11. (2017山东菏泽第11题)菱形ABCD 中， 60=∠A ，其周长为cm 24，则菱形的面积为____2cm . 【答案】183. 【解析】试题分析：如图，连接BD ，作DE ⊥AB,已知菱形的周长为cm 24，根据菱形的性质可得AB=6;再由 60=∠A ，即可判定△ABD 是等边三角形；求得DE=33,所以菱形的面积为：6×33=183.12. （2017浙江湖州第13题）已知一个多边形的每一个外角都等于72，则这个多边形的边数是．【答案】5考点：多边形的外角和三、解答题1. (2017北京第20题) 数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线，则所容两长方形面积相等（如图所示）”这一推论，他从这一推论出发，利用“出入相补”原理复原了《海岛算经》九题古证.,（以上材料来源于《古证复原的原理》、《吴文俊与中国数学》和《古代世界数学泰斗刘徽》）请根据上图完成这个推论的证明过程．证明：()ADC ANF FGC NFGD S S S S ∆∆∆=-+矩形，ABC EBMF S S ∆=-矩形（____________+____________）．易知，ADC ABC S S ∆∆=，_____________=______________，______________=_____________．可得NFGD EBMF S S =矩形矩形．【答案】,,,AEF CFM ANF AEF FGC CFM S S S S S ∆∆∆∆∆；；S . 【解析】试题分析：由矩形的对角线的性质，对角线把矩形分成两个面积相等的三角形计算即可. 本题解析：由矩形对角线把矩形分成两个面积相等的两部分可得：(),()ADC ANF FGC ABC AEF FMC NFGD EBMF S S S S S S S S ∆∆∆∆∆=-+=-+矩形矩形 , ∴,,ADC ABC ANF AEF FGC FMC S S S S S S ∆∆∆∆∆∆=== , ∴NFGD EBMF S S =矩形矩形 .考点：矩形的性质，三角形面积计算.2. (2017北京第22题)如图，在四边形ABCD 中，BD 为一条对角线，0//,2,90AD BC AD BC ABD =∠=，E 为AD 的中点，连接BE .（1）求证：四边形BCDE 为菱形；（2）连接AC ，若AC 平分,1BAD BC ∠=，求AC 的长.【答案】（1）证明见解析.（2【解析】试题分析：（1）先证四边形是平行四边形，再证其为菱形；（2）利用等腰三角形的性质，锐角三角函数，即可求解. 本题解析：(1)证明：∵E 为AD 中点，AD=2BC,∴BC=ED, ∵AD ∥BC, ∴四边形ABCD 是平行四边形，∵AD=2BE, ∠ABD=90°,AE=DE ∴BE=ED, ∴四边形ABCD 是菱形.(2)∵AD ∥BC,AC 平分∠BAD ∴∠BAC=∠DAC=∠BCA,∴BA=BC=1, ∵AD=2BC=2，∴sin ∠ADB=12,∠ADB=30°, ∴∠DAC=30°, ∠ADC=60°.在RT △ACD 中，AD=2，CD=1，考点：平行线性质，菱形判定，直角三角形斜边中线定理.3. (2017天津第24题)将一个直角三角形纸片ABO 放置在平面直角坐标系中，点)0,3(A ，点)1,0(B ，点)0,0(O .P 是边AB 上的一点（点P 不与点B A ,重合），沿着OP 折叠该纸片，得点A 的对应点'A . （1）如图①，当点'A 在第一象限，且满足OB B A ⊥'时，求点'A 的坐标；（2）如图②，当P 为AB 中点时，求B A '的长；（3）当030'=∠BPA 时，求点P 的坐标（直接写出结果即可）.【答案】（1）点A ，1）；（2）1；（3）33(,22-或3(,22. 【解析】试题分析：（1）因点)0,3(A ，点)1,0(B ，可得，根据折叠的性质可得△A ’OP ≌△AOP ，由全等三角形的性质可得OA ’,在Rt △A ’OB 中，根据勾股定理求得'A B 的长，即可求得点A 的坐标；（2）在Rt △AOB 中，根据勾股定理求得AB=2，再证△BOP 是等边三角形，从而得∠OPA =120°.在判定四边形OPA ’B 是平行四边形，根据平行四边形的性质即可得B A '的长；试题解析：（1）因点)0,3(A ，点)1,0(B ，∴根据题意，由折叠的性质可得△A ’OP ≌△AOP.∴OA ’由OB B A ⊥'，得∠A ’BO=90°.在Rt △A ’OB 中，'A B =∴点A ，1）.(2) 在Rt △AOB 中，∴2AB ==∵当P 为AB 中点， ∴AP=BP=1,OP=12AB=1. ∴OP=OB=BP,∴△BOP 是等边三角形 ∴∠BOP=∠BPO=60°， ∴∠OPA=180°-∠BPO=120°. 由（1）知，△A ’OP ≌△AOP ， ∴∠OPA’=∠OPA =120°，P ’A=PA=1，又OB=PA ’=1，∴四边形OPA ’B 是平行四边形. ∴A ’B=OP=1.(3)33(22或3(,22. 4. (2017福建第24题)如图，矩形ABCD 中，6,8AB AD ==，,P E 分别是线段AC 、BC 上的点，且四边形PEFD 为矩形．（Ⅰ）若PCD ∆是等腰三角形时，求AP 的长；（Ⅱ）若AP =CF 的长．【答案】（Ⅰ）AP 的长为4或5或145；（Ⅱ）CF=4【解析】试题分析：（Ⅰ）分情况CP=CD 、PD=PC 、DP=DC 讨论即可得；（Ⅱ）连结PF 、DE ，记PF 与DE 的交点为O ，连结OC ，通过证明△ADP ∽△CDF ，从而得34CF CD AP AD == ，由，从而可得 .试题解析：（Ⅰ）在矩形ABCD 中，AB=6，AD=8，∠ADC=90°，∴DC=AB=6，；要使△PCD 是等腰三角形，有如下三种情况：（1）当CP=CD 时，CP=6，∴AP=AC-CP=4 ；（2）当PD=PC 时，∠PDC=∠PCD ，∵∠PCD+∠PAD=∠PDC+∠PDA=90°，∴∠PAD=∠PDA ，∴PD=PA ，∴PA=PC ，∴AP=2AC，即AP=5；（3）当DP=DC 时，过D 作DQ ⊥AC 于Q ，则PQ=CQ ，∵S △ADC =12 AD ·DC=12AC ·DQ ，∴DQ=245AD DC AC =，185=，∴PC=2CQ =365 ,∴AP=AC-PC=145. 综上所述，若△PCD 是等腰三角形，AP 的长为4或5或145；（Ⅱ）连结PF 、DE ，记PF 与DE 的交点为O ，连结OC ，∵四边形ABCD 和PEFD 都是矩形，∴∠ADC=∠PDF=90°，即∠ADP+∠PDC=∠PDC+∠CDF ，∴∠ADP=∠CDF ，∵∠BCD=90°，OE=OD ，∴OC=12 ED ，在矩形PEFD 中，PF=DE ，∴OC=12PF ，∵OP=OF=12PF ，∴OC=OP=OF，∴∠OCF=∠OFC，∠OCP=∠OPC，又∵∠OPC +∠OFC+∠PCF=180°，∴2∠OCP+2∠OCF=180°，∴∠PCF=90°，即∠PCD+∠FCD=90°，在Rt △ADC 中，∠PCD+∠PAD=90°，∴∠PAD=∠FCD ，∴△ADP ∽△CDF ，∴34C F C DA P A D==，，∴CF=4 .5.（2017广东广州第24题）如图13，矩形ABCD的对角线AC，BD相交于点O，COD∆关于CD的对称图形为CED∆．（1）求证：四边形OCED是菱形；（2）连接AE，若6cmAB=，BC=．①求sin EAD∠的值；②若点P为线段AE上一动点（不与点A重合），连接OP，一动点Q从点O出发，以1/cm s的速度沿线段OP匀速运动到点P，再以1.5cm/s的速度沿线段PA匀速运动到点A，到达点A后停止运动．当点Q沿上述路线运动到点A所需要的时间最短时，求AP的长和点Q走完全程所需的时间．【答案】（1）详见解析；（2）①2sin3EAD∠=②32AP=和Q走完全程所需时间为32s【解析】（2）①连接OE ,直线OE分别交AB于点F ,交DC于点G COD∆关于CD的对称图形为CED∆,OE DC DC AB∴⊥,OF AB EF AD∴⊥在矩形ABCD中，G为DC的中点，且O为AC的中点OG∴为CAD∆的中位线OG GE∴==同理可得：F为AB的中点，3OF AF==92AE∴===32sin sin932EAD AEFEAD AEF∠=∠∴∠=∠==②过点P作PM AB⊥交AB于点MQ∴由O运动到P所需的时间为3s由①可得，23AM AP=∴点O以1.5/cm s的速度从P到A所需的时间等于以1/cm s从M运动到A即：11OP PAOP MAt t t OP MA=+=+=+Q∴由O运动到P所需的时间就是OP+MA和最小.如下图，当P运动到1P ,即1PO AB时，所用时间最短.3t OP MA∴=+=在11Rt APM∆中，设112,3AM x AP x==222221111(3)=(2)AP AM PM x x=+∴解得：12x=32AP∴=32AP∴=和Q走完全程所需时间为32s考点：菱形的判定方法；构造直角三角形求三角函数值；确定极值时动点的特殊位置 6. （2017山东青岛第24题）（本小题满分12分）已知：Rt △EFP 和矩形ABCD 如图①摆放（点P 与点B 重合），点F ，B （P ），C 在同一条直线上，AB ＝EF ＝6cm ，BC ＝FP ＝8cm ，∠EFP ＝90°。

2017年深圳市中考数学试卷含答案解析(Word版)

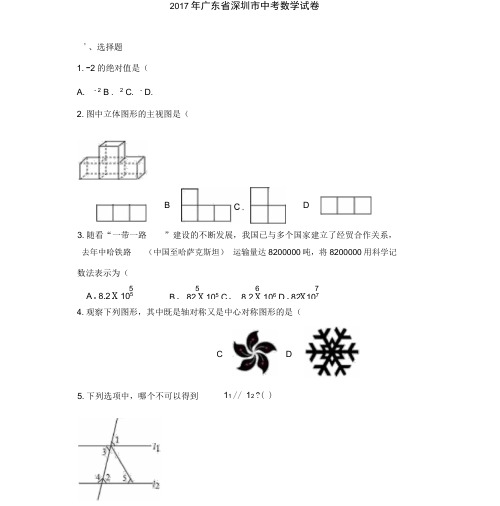
2017年广东省深圳市中考数学试卷'、选择题1.-2的绝对值是（A. - 2 B . 2 C. - D.2.图中立体图形的主视图是（3.随看“一带一路”建设的不断发展，我国已与多个国家建立了经贸合作关系，去年中哈铁路（中国至哈萨克斯坦）运输量达8200000吨，将8200000用科学记数法表示为（5 A . 8.2 X 1055 6 7B . 82 X 105C . 8.2 X 106D . 82X1074.观察下列图形，其中既是轴对称又是中心对称图形的是（5.下列选项中，哪个不可以得到11 // 12?( )B .D. C.D.A. / 1= Z 2B. Z 2= Z 3C .Z 3= Z 5D . Z 3+ Z 4=180 °6.不等式组1Sift MJb... 的解集为7.—球鞋厂，现打折促销卖出330双球鞋，比上个月多卖10%，设上个月卖出x双，列出方程（）A. 10%x=330B.（1 —10%）x=330C. （1 —10%）2x=330 D . （1+10% ）x=3308如图，已知线段AB，分别以A、B为圆心，大于AB为半径作弧，连接弧,dpql的交点得到直线I,在直线I上取一点C,使得/ CAB=25 ° ，延长AC至M，求/ BCM的度数为（）A. 40 °B. 50 ° C . 60 ° D . 70 °9 •下列哪一个是假命题（）A •五边形外角和为360 °B•切线垂直于经过切点的半径C.（3, —2）关于y轴的对称点为（-3, 2）D .抛物线y=x2—4x+2017对称轴为直线x=210 .某共享单车前a公里1元，超过a公里的，每公里2元，若要使使用该共享单车50%的人只花1元钱，a应该要取什么数（）A .平均数B .中位数C .众数D .方差11•如图，学校环保社成员想测量斜坡CD旁一棵树AB的高度，他们先在点CB 60 ° D B 30 °处测得树顶的仰角为，然后在坡顶测得树顶的仰角为，已知斜坡CD的长度为20m，DE的长为10cm，则树AB的高度是（）m .A. 20豳・B. 30C. 30 逐D. 4012 •如图，正方形ABCD的边长是3, BP=CQ，连接AQ , DP交于点O,并分别与边CD , BC交于点F , E,连接AE，下列结论：①AQ丄DP :②OA 2=OE?OP ;③S△ AOD=S四边形OECF;④当BP=1时，tan Z OAE= ，其中正确结论的个数是（）二、填空题313 .因式分解：a - 4a=14 .在一个不透明的袋子里，有2个黑球和1个白球，除了颜色外全部相同，任意摸两个球，摸到1黑1白的概率是15 •阅读理解：引入新数i,新数i满足分配律，结合律，交换律，已知i2=- 1，那么(1+i) ? (1 - i)=16 .如图，在Rt△ ABC 中，Z ABC=90 ° , AB=3 , BC=4 , Rt△ MPN , Z MPN=90点P在AC上，PM交AB于点E, PN交BC于点F，当PE=2PF时，AP=二、解答题17 •计算：一 -2 - 2cos45 ° （- 1）—2+ _ .裨| +诉:18.先化简，再求值：（，其中x= - 1 .19 .深圳市某学校抽样调查，A类学生骑共享单车，B类学生坐公交车、私家车等，C类学生步行，D类学生（其它），根据调查结果绘制了不完整的统计图.类型频数频率A30xB180.15C m0.40D n y20 .一个矩形周长为56厘米.(1) 当矩形面积为180平方厘米时，长宽分别为多少?(2) 能围成面积为200平方米的矩形吗？请说明理由.21 .如图，一次函数y=kx +b与反比例函数y= ' (x>0)交于A (2, 4), B (a, X1), 与x轴，y轴分别交于点C , D.(1)直接写出一次函数y=kx +b的表达式和反比例函数y= (x>0)的表达式;CD丄AB于点H，点M是i上任意一(1 )求。

2024年中考数学二次函数压轴题专题10平行四边形的存在性问题(学生版)

专题10平行四边形的存在性问题_、知识导航考虑到求证平行四边形存在，必先了解平行四边形性质：(1) 对应边平行且相等；(2) 对角线互相平分.这是图形的性质，我们现在需要的是将其性质运用在在坐标系中:(1)对边平行且相等可转化为:x A -x B =x D - x cy A -y B = yD-y c可以理解为点B 移动到点A,点。

移动到点O,移动路径完全相同.(2)对角线互相平分转化为：\ z 乙，、2 一 2可以理解为AC 的中点也是BQ 的中点.D【小结】虽然由两个性质推得的式子并不一样，但其实可以化为统一:X A~X B =X D~ X C -y B = yD-y c + x c = + X by A + % = % + 为x A +x c ^x B +x D2 _ 2 \X A +X C=X B +X D总 + % 二 % + 北 U a + %=% + %、2 — 2当AC 和BQ 为对角线时，结果可简记为：A+C = B + D (各个点对应的横纵坐标相加)以上是对于平行四边形性质的分析，而我们要求证的是平行四边形存在性问题，此处当有一问：若坐标系中的4个点A 、B 、。

、D 满足"A+O8+ZT,则四边形ABCQ 是否一定为平行四边形？反例如下：之所以存在反例是因为“四边形ABCQ 是平行四边形”与“AC 、BD 中点是同一个点”并不是完全等价的转化, 故存在反例.虽有反例，但并不影响运用此结论解题，另外，还需注意对对角线的讨论：(1) 四边形A8CQ 是平行四边形：AC. BQ 一定是对角线.(2) 以A 、B 、。

、。

四个点为顶点是四边形是平行四边形：对角线不确定需要分类讨论.平行四边形存在性问题通常可分为“三定一动”和“两定两动”两大类问题.1.三定一动已知A (1, 2) B (5, 3) C (3, 5),在坐标系内确定点。

使得以A 、B 、。

、。

四个点为顶点的四边形是平行四边形.思路1:利用对角线互相平分，分类讨论：设。

专题10 四边形-2017版[中考15年]上海市2002-2016年中考数学试题分项解析(解析版)

1.（上海市2006年4分）在下列命题中，真命题是【】 A ．两条对角线相等的四边形是矩形； B ．两条对角线互相垂直的四边形是菱形； C ．两条对角线互相平分的四边形是平行四边形； D ．两条对角线互相垂直且相等的四边形是正方形。

【答案】D 。

2.（上海市2007年4分）已知四边形ABCD 中，90A B C ===∠∠∠，如果添加一个条件，即可推出该四边形是正方形，那么这个条件可以是【】 A ．90D =∠B ．AB CD =C ．AD BC =D ．BC CD =【答案】D 。

【考点】正方形的判定。

【分析】由∠A=∠B=∠C=90°可判定为矩形，因此再添加条件：一组邻边相等，即可判定为正方形。

故选D 。

3.（上海市2011年4分）矩形ABCD 中，AB ＝8，BC =，点P 在边AB 上，且BP ＝3AP ，如果圆P 是以点P 为圆心，PD 为半径的圆，那么下列判断正确的是【】．(A) 点B 、C 均在圆P 外； (B) 点B 在圆P 外、点C 在圆P 内； (C) 点B 在圆P 内、点C 在圆P 外； (D) 点B 、C 均在圆P 内．【答案】C。

4.（2013年上海市4分）在梯形ABCD中，AD∥BC，对角线AC和BD交于点O，下列条件中，能判断梯形ABCD是等腰梯形的是【】（A）∠BDC =∠BCD （B）∠ABC =∠DAB （C）∠ADB =∠DAC （D）∠AOB =∠BOC【答案】C。

【考点】等腰梯形的判定，平行的性质，等腰三角形的判定。

【分析】根据等腰梯形的判定，逐一作出判断：A.由∠BDC =∠BCD只能判断△BCD是等腰三角形，而不能判断梯形ABCD是等腰梯形；B.由∠ABC =∠DAB和AD∥BC，可得∠ABC =∠DAB=900，是直角梯形，而不能判断梯形ABCD是等腰梯形；5．（上海市2014年4分）如图，已知AC、BD是菱形ABCD的对角线，那么下列结论一定正确的是（）．(A)△ABD与△ABC的周长相等；(B)△ABD与△ABC的面积相等；(C)菱形的周长等于两条对角线之和的两倍；(D)菱形的面积等于两条对角线之积的两倍．【答案】B.【解析】1.（上海市2002年2分）已知AD是△ABC的角平分线，E、F分别是边AB、AC的中点，连结DE、DF，在不再连结其他线段的前提下，要使四边形AEDF成为菱形，还需添加一个条件，这个条件可以是▲ ．【答案】AB=AC或∠B=∠C或AE=AF。

专题10四边形-2017年中考数学试题分项版解析汇编(解析版)

端点 C , D 重合），折痕交 AD 于点 E ，交 BC 于点 F ，边 AB 折叠后与边 BC 交于点 G ，设正方形 ABCD
的周长为 m ， CHG 的周长为 n ，则 n 的值为（
）
m
2
A．
2
1
B．
2
51
C．
2
D ．随 H 点位置的变化而变化
【答案】 B 【解析】试题分析：设正方形 ABCD 的边长为 2a，正方形的周长为 m=8a，设 CM =x，DE=y，则 DM =2a-x， EM=2a-y， ∵∠ EMG =90°， ∴∠ DME +∠ CMG =90°． ∵∠ DME +∠ DEM =90°， ∴∠ DEM =∠ CMG ，又∵∠ D=∠ C=90°△ DEM ∽△ CMG ，
考点 :1、圆周角性质定理， 2、等腰三角形性质
7.(2017 山东滨州第 16 题 )如图，将矩形 ABCD 沿 GH 对折，点 C 落在 Q 处，点 D 落在 AB 边上的 E 处，EQ
与 BC 相交于点 F ．若 AD＝ 8， AB＝ 6， AE ＝4，则 △EBF 周长的大小为 ___________．
F 沿点到点的方向平移，得到
中点，当点与点重合时，四边形
CD 的面积为
F ．设、分别是 F 、 F 的
A ． 28 3
B ． 24 3
C. 32 3
D ． 32 3 8
【答案】 A. 【解析】
试题分析：作 DH AB, PK AB, FL AB
在菱形 CD 中，
60 ， D 8 , F 是的中点
AF 4， EF 2 3, EL 3
-5-
P 是 F 的中点， PK

中考复习函数专题10 一次函数中的四边形问题(老师版)

专题10 一次函数中的四边形问题知识对接考点一、怎样解一次函数中的四边形问题1、四边形面积常转化为若干个三角形面积之和（或差）．2、画出草图，把要求的图形构建出来，根据面积公式，把直线与坐标轴的交点计算出来，把坐标转化成线段，代入面积公式求解。

3、规则图形（公式法）；不规则图形（切割法）不含参数问题；含参数问题（用参数表示点坐标，转化成线段）注意：坐标的正负、线段的非负性。

求面积时，尽量使底或高中的一者确定下来（通过对图像的观察，确定底和高），然后根据面积公式，建立等式。

专项训练一、单选题1．如图在平面直角坐标系中，直线y kx k =+与x 轴，y 轴分别交于点B 、A ，将线段AB 沿某个方向平移，点A 、B 对应的点M 、N 恰好在直线22y x =-和直线2x =上，则当四边形AMNB 为菱形时N 点坐标为（）A ．()2,1B ．()2,2C ．()2,3D ．()2,4【答案】A 【分析】求出A (0，k )和B (-1，0)，B 的对应点N 的横坐标为2，由此知道往右平移了3个单位，得到A 的对应点M 的横坐标为3，将M 点横坐标代入22y x =-中即可求出M 坐标，进而求解．【详解】解：令y kx k =+中y =0，得到B (-1，0)，令x =0，得到A (0，k )， ∵B 的对应点N 在2x =上，∵N 点横坐标为2，故AB 往右平移了3个单位， ∵M 点横坐标为3，将x =3代入22y x =-中，解得y =4，故M 点的坐标为(3，4)，又四边形AMNB 为菱形， ∵AB ²=AM ²，∵1+k ²=3²+(4-k )²，解得k =3， ∵A (0,3)，即AB 往右平移3个单位，往上平移了1个单位，故N 坐标为(2，1)，故选：A ．【点睛】本题考查了一次函数的平移、菱形的性质等知识点，属于基础题，计算过程中细心即可． 2．如图，在平面直角坐标系中，四边形ABCD 是菱形，//AB x 轴，点B 的坐标为()4,1，60BAD ∠=︒，垂直于x 轴的直线l 从y 轴出发，沿x 轴正方向以每秒1个单位长度的速度向右平移，设直线l 与菱形ABCD 的两边分别交于点M ，N （点N 在点M 的上方），连接OM ，ON ，若OMN 的面积为S ，直线l 的运动时间为t 秒（06t ≤≤），则S 与t 的函数图象大致是（）A ．B ．C ．D ．【答案】C 【分析】当直线l 从A 开始运动，MN 逐渐增大，到经过点MN 达到最大值，此时AM =2,故运动时间为2，此时02t ≤≤; 当直线l 从D 开始运动，MN 保持不变，到经过点B ，此时AB =4，故运动时间为2,此时2<4t ≤;当直线l 从经过B 的位置向右开始运动，MN 开始减小，到经过点C ，MN 为0，此时BG =2，故运动时间为2，此时4<6t ≤三种情形，确定面积S 与t 的函数关系式，根据关系式确定图像即可．【详解】解：由题意知AB =AD =CD =BC =4， ∵∵BAD =60°，∵当直线l 经过点D 时，运动时间为2， ∵C 的横坐标为6，如图1，当02t ≤≤时，//l y 轴,AMN OMN S S S ∆∆∴== ,60,AM t BAD ︒=∠=,MN ∴=21;2S t ∴=⨯=图像是经过原点，开口向_上的- -段抛物线; 如图2，当2<4t ≤时，MN 是定长，4,60,AD BAD ︒=∠=MN ∴=1;2S t =⨯⨯∴图像是经过原点，正比例函数上的一段；2y x =的比例系数2 ∵面积线段的倾斜度要比2y x =的陡；如图3，当4<6t ≤时，4,60,BC CBG ︒=∠=2,C G G B ∴==(4,1),(6,1),C B ∴41,61k b k b +=⎧⎪∴⎨+=⎪⎩解得1k b ⎧=⎪⎨=-⎪⎩∵直线的解析式为1y =+-∵N 坐标为(,1),t M 坐标为(1t +-11MN ∴=-+-=+1(2S t ∴=⨯⨯+;=图像是开口向下的一段抛物线; 故选：C ．【点睛】本题主要考查对动点问题的函数图象，勾股定理，三角形的面积，二次函数的图象，正比例函数的图象，含30度角的直角三角形的性质，菱形的性质等知识点的理解和掌握，能根据这些性质进行计算是解此题的关键，用的数学思想是分类讨论思想．3．如图，在平面直角坐标系中，四边形11112222333,,OA B C A A B C A A B C ，…都是菱形，点123,,A A A …都在x 轴上，点123,,C C C ，…都在直线y x =11212323160,1C OA C A A C A A OA ∠=∠=∠==︒=，则点n C 的横坐标是（）A ．2321n -⨯-B ．2321n -⨯+C ．1321n -⨯-D ．1321n -⨯+【答案】A 【分析】分别过点123,,,...C C C 作x 轴的垂线，交于123,,,...D D D ，再连接112233,,,...C D C D C D，利用勾股定理及根据菱形的边长求得1A 、2A 、3A ⋯的坐标然后分别表示出1C 、2C 、3C ⋯的坐标找出规律进而求得n C 的坐标．【详解】。

(部编版)2020年中考数学试题分项版解析汇编第期专题10四边形含解析0

专题10 四边形一、选择题1.（2017浙江衢州第8题）如图，在直角坐标系中，点A 在函数)0(4>=x xy 的图象上，AB ⊥x 轴于点B ，AB 的垂直平分线与y 轴交于点C ，与函数)0(4>=x xy 的图象交于点D 。

连结AC ，CB ，BD ，DA ，则四边形ACBD 的面积等于（）A. 2B. 32C. 4D. 34 【答案】C ．【解析】试题解析：设A （a ，4a ），可求出D （2a ，2a）， ∵AB ⊥CD ， ∴S 四边形ACBD =12AB•CD=12×2a×4a=4，故选C ．考点：反比例函数系数k 的几何意义.2.（2017浙江衢州第9题）如图，矩形纸片ABCD 中，A B=4，BC=6，将△ABC 沿AC 折叠，使点B 落在点E 处，CE 交AD 于点F ，则DF 的长等于（）A.53 B. 35 C. 37 D. 45 【答案】B ．【解析】试题解析： ∵矩形ABCD 沿对角线AC 对折，使△ABC 落在△ACE 的位置， ∴AE=AB ，∠E=∠B=90°，又∵四边形ABCD 为矩形， ∴AB=CD ， ∴AE=DC ，而∠AFE=∠DFC ， ∵在△AEF 与△CDF 中，AFE CFD E DAE CD ⎧∠=∠⎪∠=∠⎨⎪=⎩， ∴△AEF ≌△CDF （AAS ）， ∴EF=DF ；∵四边形ABCD 为矩形， ∴AD=BC=6，CD=AB=4， ∵Rt △AEF ≌Rt △CDF ， ∴FC=FA ，设FA=x ，则FC=x ，FD=6﹣x ，在Rt △CDF 中，CF 2=CD 2+DF 2，即x 2=42+（6﹣x ）2，解得x=133，则FD=6﹣x=53．故选B ．考点：1.矩形的性质；2.折叠问题.3.（2017山东德州第11题）如图放置的两个正方形，大正方形ABCD 边长为a ，小正方形CEFG 边长为b(a ＞b),M 在边BC 上，且BM=b ，连AM ，MF ，MF 交CG 于点P ，将△ABM 绕点A 旋转至△ADN ，将△MEF 绕点F 旋转至△NGF 。

广东省各市中考数学分类解析专题10：四边形

广东中考数学试题分类解析汇编专题10：四边形一、选择题1. （广东佛山3分）依次连接任意四边形各边的中点，得到一个特殊图形（可认为是一般四边形的性质），则这个图形一定是【】A．平行四边形B．矩形C．菱形D．梯形【答案】 A。

【考点】三角形中位线定理，平行四边形的判定。

【分析】根据题意画出图形，如右图所示：连接AC，∵四边形ABCD各边中点是E、F、G、H，∴HG∥AC，HG=12AC，EF∥AC，EF=12AC。

∴EF=GH，EF∥GH。

∴四边形EFGH是平行四边形。

由于四边形EFGH是平行四边形，它就不可能是梯形；同时由于是任意四边形，所以AC=BD或AC⊥BD不一定成立，从而得不到矩形或菱形的判断。

故选A。

2．（广东广州3分）如图，在等腰梯形ABCD中，BC∥AD，AD=5，DC=4，DE∥AB交BC于点E，且EC=3，则梯形ABCD的周长是【】A．26B．25C．21D．20【答案】C。

【考点】等腰梯形的性质，平行四边形的判定和性质。

【分析】∵BC∥AD，DE∥AB，∴四边形ABED是平行四边形。

∴BE=AD=5。

∵EC=3，∴BC=BE+EC=8。

∵四边形ABCD是等腰梯形，∴AB=DC=4。

∴梯形ABCD的周长为：AB+BC+CD+AD=4+8+4+5=21。

故选C。

3. （广东广州3分）在平面中，下列命题为真命题的是【】A．四边相等的四边形是正方形B．对角线相等的四边形是菱形C．四个角相等的四边形是矩形D．对角线互相垂直的四边形是平行四边形【答案】C。

【考点】命题与定理，正方形的判定，菱形的判定，矩形的判定，平行四边形的判定。

【分析】分析是否为真命题，需要分别分析各题设是否能推出结论，从而利用排除法得出答案，不是真命题的可以举出反例排除：A、四边相等的四边形不一定是正方形，例如菱形，故此选项错误；B、对角线相等的四边形不是菱形，例如矩形，等腰梯形，故此选项错误；C、四个角相等的四边形是矩形，故此选项正确；D、对角线互相垂直的四边形不一定是平行四边形，如铮形（如图），故此选项错误。

专题10四边形(第01期)-2021年中考数学试题分项版解析汇编(广东福建专版)(解析版)

专题10：四边形一、选择题1.（2015•广东深圳，第 12题，3分）如图，已知正方形ABCD 的边长为12，BE=EC ，将正方形边CD 沿DE折叠到DF ，延长EF 交AB 于G ，连接DG ，现在有如下4个结论：①△ADG ≌△FDG ；②GB=2AG ；③△GDE ∽△BEF ；④S ⊿BEF =572。

在以上4个结论中，正确的有（） A 、1 B 、2 C 、3 D 、42.（2015•广东梅州市，第5题，3分）下列命题正确的是（）A ．对角线互相垂直的四边形是菱形B ．一组对边相等，另一组对边平行的四边形是平行四边形C ．对角线相等的四边形是矩形D ．对角线互相垂直平分且相等的四边形是正方形【答案】D.【解析】试题分析：根据矩形、菱形、平行四边形的知识可判断出各选项，从而得出答案．A 、对角线互相垂直的四边形不一定是菱形，故本选项错误；B 、一组对边相等，另一组对边平行的四边形不一定是平行四边形，也可能是等腰梯形，故本选项错误；C 、对角线相等的四边形不一定是矩形，例如等腰梯形，故本选项错误；D 、对角线互相垂直平分且相等的四边形是正方形，故本选项正确．故选:D ．考点：命题与定理．3.（2015•广东广州市，第8题，3分）下列命题中，真命题的个数有（*）①对角线互相平分的四边形是平行四边形②两组对角分别相等的四边形是平行四边形③一组对边平行，另一组对边相等的四边形是平行四边形（A ）3个（B ）2个（C ）1个（D ）0个【答案】B【解析】试题分析：根据平行四边形的判定定理可得：①和②为真命题，根据③可得这个四边形为等腰梯形. 考点：平行四边形的判定.4.（2015•广东汕尾市，第 6题，4分）下列命题正确的是（）A.一组对边相等，另一组对边平行的四边形是平行四边形B.对角线互相垂直的四边形是菱形C.对角线相等的四边形是矩形D.对角线互相垂直平分且相等的四边形是正方形5.（2015•广东汕尾市，第 9题，4分）如图，将矩形纸片ABCD 折叠，使点A 与点C 重合，折痕为EF ，若A B=4，BC=2，那么线段EF 的长为（）A.2 5B. 5C. 455D. 255二、填空题6.（2015•广东茂名，第 14题，3分）如图，将矩形ABCD沿对角线BD折叠，使点C与C′重合．若AB=3，则C′D的长为．【答案】3．【解析】试题分析：在矩形ABCD中，CD=AB，∵矩形ABCD沿对角线BD折叠后点C和点C′重合，∴C′D=CD，∴C′D=AB，∵AB=3，∴C′D=3．故答案为：3．7. （2015•广东佛山，第13题，3分）如图，在Rt△ABC中，AB=BC，∠B=90°，AC=10．四边形BDEF 是△ABC的内接正方形（点D、E、F在三角形的边上）．则此正方形的面积是．8.（2015•广东，第 11题，3分）正五边形的外角和等于（度）.【答案】360【解析】试题分析：任何n边形的外角和都等于360度.考点：多边形的外角和.9.（2015•广东，第 12题，3分）如题12图，菱形ABCD的边长为6，∠ABC=60°，则对角线AC的长是.【答案】6【解析】考点：菱形的性质.10. （2015•广东梅州市，第13题，3分）如图，在□ABCD 中，BE 平分∠ABC ，BC=6，DE=2，则□ABCD 的周长等于．11.（2015•广东梅州市，第14题，3分）如图，将矩形纸片ABCD 折叠，使点A 与点C 重合，折痕为EF ，若AB=4，BC=2，那么线段EF 的长为．【答案】5.【解析】试题分析：如图，AC 交EF 于点O ，由勾股定理先求出AC 的长度，根据折叠的性质可判断出RT △EOC ∽RT △ABC ，从而利用相似三角形的对应边成比例可求出OE ，再由EF=2OE 可得出EF 的长度如图所示，AC 交EF 于点O ，由勾股定理知52 AC ，又∵折叠矩形使C 与A 重合时有EF ⊥AC ，则Rt △AOE ∽Rt △ABC ，∴，∴OE=,故EF=2OE=5．故答案为：5．考点：翻折变换（折叠问题）．12.（2015•广东广州，第 16题，3分）如图，四边形ABCD 中，∠A=90°，AB=33AD=3，点M ，N 分别为线段BC ，AB 上的动点（含端点，但点M 不与点B 重合），点E ，F 分别为DM ，MN 的中点，则EF 长度的最大值为 * .13.（2015•广东汕尾市，第15题，5分）如图，在□ABCD中，BE平分∠ABC，BC = 6，DE = 2 ，则□ABCD 周长等于 .【答案】20【解析】试题分析：由□ABCD可得AD∥BC,AD=BC,因此可得∠AEB=∠CBE，由BC=6，DE=2，可知AE=4，再由BE平分∠ABC，可得∠ABE=∠CBE，因此可知∠AEB=∠ABE，所以AE=AB=4，所以□ABCD的周长为2×（6+4）=20. 考点：平行四边形的性质，角平分线的性质三、解答题：14. （2015•广东，第 21题，7分）如题21图，在边长为6的正方形ABCD中，E是边CD的中点，将△ADE 沿AE对折至△AFE，延长交BC于点G，连接AG.(1)、求证：△ABG≌△AFG； (2)、求BG的长.15.（2015•广东广州，第 18题，9分）如图7，正方形ABCD中，点E、F分别在AD，CD上，且AE=DF，连接BE，AF.求证：BE=AF.【答案】略.【解析】试题分析：根据正方形的性质得出AD=AB，∠D=EAB=90°，然后结合AE=DF得出△ADF和△BAE全等，得到BE=AF.试题解析：∵四边形ABCD是正方形∴AD=AB ∠D=∠EAB=90°在△EAB和△FDA中，AE=DF ∠EAB=∠D AB=AD ∴△EAB≌△FDA ∴BE=AF.考点：正方形的性质、三角形全等.16.（2015•广东广州市，第24题，14分）如图10，四边形OMTN中，OM=ON，TM=TN，我们把这种两组邻边分别相等的四边形叫做筝形.(2)、在筝形ABCD中，已知AB=AD=5，BC=CD，BC>AB，BD，AC为对角线，BD=8.②过点B作BF⊥CD，垂足为F，BF交AC于点E，连接DE.当四边形ABED为菱形时，求点F到AB 的距离.∴∠ABC=∠ADC=90° ∴AC 即为所求圆的直径。

广东省深圳市2017年中考数学真题试题(含扫描答案)

深圳市2017年初中毕业生学业考试数学试题解析第Ⅰ卷（共60分）一、选择题1．-2的绝对值是（）A ．-2B ．2C ．12-D ．12 2．图中立体图形的主视图是（）A ．B ．C ．D ．3．随着“一带一路”建设的不断发展，我国已与多个国家建立了经贸合作关系，去年中哈铁路（中国至哈萨克斯坦）运输量达8200000吨，将8200000用科学记数法表示为（）A ．58.210⨯B ．58210⨯C ．68.210⨯D ．78210⨯ 4．观察下列图形，其中既是轴对称又是中心对称图形的是（） A ． B ． C ． D ．5．下列选项中，哪个不可以．．得到12//l l ？（）A ．12∠=∠B ．23∠=∠C ． 35∠=∠D ．34180∠+∠=o6．不等式组32521x x -<⎧⎨-<⎩的解集为（）A ．1x >-B ．3x <C ．1x <-或3x >D ．13x -<<7．一球鞋厂，现打折促销卖出330双球鞋，比上个月多卖10%，设上个月卖出x 双，列出方程（）A ．10%330x =B ．(110%)330x -=C ． 2(110%)330x -=D ．(110%)330x +=8．如图，已知线段AB ，分别以A B 、为圆心，大于12AB 为半径作弧，连接弧的交点得到直线l ，在直线l 上取一点C ，使得25CAB ∠=o ，延长AC 至M ，求BCM ∠的度数为（）A ．40oB ．50oC ． 60oD ．70o9．下列哪一个是假命题（）A ．五边形外角和为360oB ．切线垂直于经过切点的半径C ． (3,2)-关于y 轴的对称点为(3,2)-D ．抛物线242017y x x =-+对称轴为直线2x =10．某共享单车前a 公里1元，超过a 公里的，每公里2元，若要使使用该共享单车50%的人只花1元钱，a 应该要取什么数（）A ．平均数B ．中位数C ．众数D ．方差11．如图，学校环保社成员想测量斜坡CD 旁一棵树AB 的高度，他们先在点C 处测得树顶B 的仰角为60o，然后在坡顶D 测得树顶B 的仰角为30o ，已知斜坡CD 的长度为20m ，DE 的长为10m ，则树AB 的高度是（）mA ．203．30 C ． 303．4012．如图，正方形ABCD 的边长是3，BP CQ =，连接,AQ DP 交于点O ，并分别与边,CD BC 交于点,F E ，连接AE ．下列结论：①AQ DP ⊥；②2OA OE OP =g ；③AOD OECF S S ∆=四边形；④当1BP =时，13tan 16OAE ∠=．其中正确结论的个数是（）A ．1B ．2C ．3D ．4二、填空题13．因式分解：34a a -= ．14．在一个不透明的袋子里，有2个黑球和1个白球，除了颜色外全部相同，任意摸两个球，摸到1黑1白的概率是． 15．阅读理解：引入新数i ，新数i 满足分配律，结合律，交换律，已知21i =-，那么(1)(1)i i +-=g ．16．如图，在Rt ABC ∆中，90ABC ∠=o ，3AB =，4BC =，Rt MPN ∆，90MPN ∠=o ，点P 在AC 上，PM 交AB 于点E ，PN 交BC 于点F ，当2PE PF =时，AP = ．三、解答题17．计算2|22|2cos45(1)8--+-o18．先化简，再求值：22()224x x x x x x +÷-+-，其中1x =-． 19．深圳市某学校抽样调查，A 类学生骑共享单车，B 类学生坐公交车、私家车等，C 类学生步行，D 类学生（其它），根据调查结果绘制了不完整的统计图．类型频数频率 A30 x B18 0.15 Cm 0.40 D n y（1）学生共__________人，x =__________，y =__________；（2）补全条形统计图；（3）若该校共有2000人，骑共享单车的有___________人．20．一个矩形周长为56厘米，（1）当矩形面积为180平方厘米时，长宽分别为多少？（2）能围成面积为200平方厘米的矩形吗？请说明理由．21．如图一次函数y kx b =+与反比例函数(0)m y x x=>交于(2,4)A 、(,1)B a ，与x 轴，y 轴分别交于点C D 、．（1）直接写出一次函数y kx b =+的表达式和反比例函数(0)m y x x=>的表达式；（2）求证：AD BC =． 22．如图，线段AB 是O e 的直径，弦CD AB ⊥于点H ，点M 是弧CBD 上任意一点，2,4AH CH ==．（1）求O e 的半径r 的长度；（2）求sin CMD ∠；（3）直线BM 交直线CD 于点E ，直线MH 交O e 于点N ，连接BN 交CE 于点F ，求HE HF g 的值．23．如图，抛物线22y ax bx =++经过点(1,0),(4,0)A B -，交y 轴于点C ：（1）求抛物线的解析式（用一般式表示）．（2）点D为y轴右侧抛物线上一点，是否存在点D使23ABC ABDS S∆∆=，若存在请直接给出点D坐标；若不存在请说明理由．（3）将直线BC绕点B顺时针旋转45o，与抛物线交于另一点E，求BE的长．。

专题10 四边形-2017版[中考15年]广州市2002-2016年中考数学试题分项解析(解析版)

2017版[中考15年]广东省2002-2016年中考数学试题分项解析专题10 四边形1. （2002年广东广州2分）如图，若四边形ABCD 是半径为1cm 的⊙O 的内接正方形，则图中四个弓形（即四个阴影部分）的面积和为【】A.()22m 2c π-B.()22m 1c π-C.()2m 2c π-D.()2m 1c π-2. （2003年广东广州3分）如图，在菱形ABCD 中，∠ABC ＝60°．AC ＝4．则BD 的长为【】A.38B.34C.32D.8 【答案】B 。

3.（2009年广东广州3分）如图，在ABCD中，AB=6，AD=9，∠BAD的平分线交BC于点E，4，则ΔCEF的周长为【】交DC的延长线于点F，BG⊥AE，垂足为G，BG=2A.8B.9.5C.10D.5【答案】A。

【考点】平行四边形的判定和性质，勾股定理，等腰三角形的判定和性质，相似三角形的判定和性质。

∴△CEF的周长=CE＋CF＋FE=8。

故选A。

4.（2011年广东广州3分）已知ABCD的周长为32，AB＝4，则BC＝【】A.4B.12C.24D.285. （2012年广东广州3分）如图，在等腰梯形ABCD中，BC∥AD，AD=5，DC=4，DE∥AB交BC于点E，且EC=3，则梯形ABCD的周长是【】A．26B．25C．21D．206. （2012年广东广州3分）在平面中，下列命题为真命题的是【】A．四边相等的四边形是正方形B．对角线相等的四边形是菱形C．四个角相等的四边形是矩形D．对角线互相垂直的四边形是平行四边形故选C。

7.（2013年广东广州3分）如图，四边形ABCD 是梯形，AD ∥BC ，CA 是∠BCD 的平分线，且AB ⊥AC ，AB=4，AD=6 ，则tan B =【】A. B. C.1148.（2015年中考广东广州3分）下列命题中，真命题的个数有【】 ①对角线互相平分的四边形是平行四边形 ②两组对角分别相等的四边形是平行四边形③一组对边平行，另一组对边相等的四边形是平行四边形 A.3个 B.2个 C.1个 D.0个【答案】B考点：平行四边形的判定.1. （2002年广东广州3分）如图，在正方形ABCD 中，AO ⊥BD ，OE 、FG 、HI 都垂直于AD ，EF 、GH 、IJ 都垂直于AO ，若已知AIJ S 1∆=，则ABCD S 正方形= 。

(完整word版)2017深圳中考数学试题及答案解析,推荐文档

2016年广东省深圳市中考数学试卷第一部分选择题（本部分共12小题，每小题3分，共36分。

每小题给出4个选项，其中只有一个选项是正确的）1．下列四个数中，最小的正数是（）A ．—1 B. 0 C. 1 D. 2 2．把下列图形折成一个正方体的盒子，折好后与“中”相对的字是（）A ．祝 B.你 C.顺 D.利 3．下列运算正确的是（）A.8a-a=8B.(-a)4=a 4C.a 3×a 2=a 6D.（a-b ）2=a 2-b 24．下列图形中，是轴对称图形的是（）5．据统计，从2005年到2015年中国累积节能1570000000吨标准煤，1570000000这个数用科学计数法表示为（）A.0.157×1010B.1.57×108C.1.57×109D.15.7×1086．如图，已知a ∥b,直角三角板的直角顶点在直线b 上，若∠1=60°，则下列结论错误的是（）A. ∠2=60°B. ∠3=60°C. ∠4=120°D. ∠5=40° 7．数学老师将全班分成7个小组开展小组合作学习，采用随机抽签法确定一个小组进行展示活动。

则第3小组被抽到的概率是（） A.71 B. 31 C. 211D. 1018．下列命题正确是（）A.一组对边平行，另一组对边相等的四边形是平行四边形B.两边及一角对应相等的两个三角形全等C.16的平方根是4D.一组数据2,0,1,6,6的中位数和众数分别是2和69.施工队要铺设一段全长2000米，的管道，因在中考期间需停工两天，实际每天施工需比原来计划多50米，才能按时完成任务，求原计划每天施工多少米。

设原计划每天施工x 米，则根据题意所列方程正确的是（）A.25020002000=+-x x B.22000502000=-+x x C.25020002000=--x x D.22000502000=--xx10.给出一种运算：对于函数nx y =，规定1-=n nxy 丿。

广东省深圳市2002年中考数学试题分类解析汇编专题10 圆

专题10：圆一、选择题1.（深圳2003年5分）如图，已知四边形ABCD是⊙O的内接四边形，且AB=CD=5，AC=7，BE=3，下列命题错误的是【】A、△AED∽△BECB、∠AEB=90ºC、∠BDA=45ºD、图中全等的三角形共有2对【答案】 D。

【分析】A、根据圆周角定理的推论，可得到：∠ADE=∠BCE，∠DAE=∠CBE∴△AED∽BED，正确；，从而根据等弧所B、由四边形ABCD是⊙O的内接四边形，且AB=CD，有AB CD对圆周角相等的性质，得∠EBC=∠ECB，由等腰三角形等角对等边的性质，得BE=CE，∴BE=CE=3，AB=5，AE=AC－CE=4，根据勾股定理的逆定理，△ABE为直角三角形，即∠AEB=90°，正确；C、AE=DE，∴∠EAD=∠EDA=45°，正确；D、从已知条件不难得到△ABE≌△DCE、△ABC≌△DCB、△ABD≌DCA共3对，错误。

故选D。

2.（深圳2004年3分）已知⊙O1的半径是3，⊙O2的半径是4，O1O2=8，则这两圆的位置关系是【】A、相交B、相切C、内含D、外离【答案】D。

【考点】两圆的位置关系。

【分析】根据两圆的位置关系的判定：外切（两圆圆心距离等于两圆半径之和），内切（两圆圆心距离等于两圆半径之差），相离（两圆圆心距离大于两圆半径之和），相交（两圆圆心距离小于两圆半径之和大于两圆半径之差），内含（两圆圆心距离小于两圆半径之差）。

∵⊙O1的半径是3，⊙O2的半径是4，O1O2=8，则3+4=7＜8，∴两圆外离。

故选D。

3.（深圳2004年3分）如图，⊙O的两弦AB、CD相交于点M，AB=8cm，M是AB的中点，CM：MD=1：4，则CD=【】A 、12cmB 、10cmC 、8cmD 、5cm 【答案】B 。

【考点】相交弦定理。

【分析】根据相交弦定理“圆内两弦相交于圆内一点，各弦被这点所分得的两线段的长的乘积相等”进行计算：∵CM：DM=1：4，∴DM=4CM。

广东省中考数学专题测试四边形课件

16．如图，菱形ABCD的面积为120cm2，正方形 AECF的面积为50cm2，则菱形的边长为 13 cm．
三解答题(一)(本大题3小题，每小题6分，共18分) 17．在四边形ABCD中，∠D=60°，∠B比∠A大 20°，∠C是∠A的2倍，求∠A，∠B，∠C的大小．
解：设∠A=x，则∠B=x+20°，∠C=2x．四边形内角和定理得 x+（x+20°）+2x+60°=360°，解得x=70°． ∴∠A=70°，∠B=90°，∠C=140°．
3．如图，▱ABCD的对角线AC， BD交于点O，已知AD=8，BD=12， AC=6，则△OBC的周长为（B） A．13 B．17 C．20 D．26 4．下列性质中，菱形具有而矩形不一定具有的是（C） A．对角线相等 B．对角线互相平分 C．对角线互相垂直 D．邻边互相垂直
5．如图，矩形ABCD的对角线AC、 BD相交于点O，CE∥BD，DE∥AC，若AC=4，则四边形OCED的周长为（B） A．4 B．8C．10 D．12 6．小敏不慎将一块平行四边形玻璃打碎成如图的
9．如图，在矩形ABCD中（AD＞AB），点E是 BC上一点，且DE=DA，AF⊥DE，垂足为点F，在下列结论中，不一定正确的是（ B） A．△AFD≌△DC B．AF= AD C．AB=AF D．BE=AD﹣DF 10．矩形OABC在平面直角坐标系中的位置如图所示，点B的坐标为（3，4），D是OA的中点，点E在 AB上，当△CDE的周长最小时，点E的坐标为（B）
18．如图，四边形ABCD中，AD∥BC，AE⊥AD 交BD于点E，CF⊥BC交BD于点F，且AE=CF．求证：四边形ABCD是平行四边形．证明：∵AE⊥AD，CF⊥BC， ∴∠EAD=∠FCB=90°， ∵AD∥BC，∴∠ADE=∠CBF，在Rt△AED和Rt△CFB中，

广东省深圳市中考数学试题分类解析专题10 四边形

深圳市2002-2013年中考数学试题分类解析专题10 四边形一、选择题1.（深圳2003年5分）一个等腰梯形的高恰好等于这个梯形的中位线，若分别以这个梯形的上底和下底为直径作圆，则这两个圆的位置关系是【】A 、相离B 、相交C 、外切D 、内切2.（深圳2006年3分）如图，在ABCD 中，AB : AD = 3:2，∠AD B=60°，那么cos Ａ的值等于【】Ａ．36 Ｂ．6Ｃ．36 Ｄ．63.（深圳2008年3分）下列命题中错误．．的是【】Ａ．平行四边形的对边相等Ｂ．两组对边分别相等的四边形是平行四边形Ｃ．矩形的对角线相等Ｄ．对角线相等的四边形是矩形4.（深圳2010年招生3分）如图，正方形ABCD中，E为AB的中点，AF⊥DE于点O，则AO DO等于【】B . 13C . 23D . 12二、填空题1.（深圳2004年3分）在矩形ABCD 中，对角线AC 、BD 相交于点O ，过点O 作OE⊥BC，垂足为E ，连结D E 交AC 于点P ，过P 作PF⊥BC，垂足为F ，则CBCF 的值是 ▲ .2．（深圳2006年3分）如图所示，在四边形ABCD 中，AB=BC=CD=DA ，对角线AC 与BD 相交于点O ．若不增加任何字母与辅助线，要使得四边形ABCD 是正方形，则还需增加的一个条件是 ▲ ．3.（深圳2009年3分）如图，矩形ABCD中，由8个面积均为1的小正方形组成的L型模板如图放置，则矩形ABCD的周长为▲ ．4.（深圳2010年学业3分）如图，在ABCD中，AB＝5，AD＝8，DE平分∠ADC，则BE＝▲ ．5. （2012广东深圳3分）如图，Rt△ABC中，C= 90o，以斜边AB为边向外作正方形 ABDE，且正方形对角线交于点D，连接OC，已知AC=5，OC=62，则另一直角边BC的长为▲ ．三、解答题1.（深圳2002年8分）已知：如图，在口ABCD中，E、F是对角线AC上的两点，且AF=CE。

专题10 四边形-2017版[中考15年]深圳市2002-2016年中考数学试题分项解析(解析版)

专题10 二次函数与四边形的综合-中考数学函数考点全突破

广东省深圳市2017年中考数学真题试题(含扫描答案)

(部编版)2020年中考数学试题分项版解析汇编第期专题10四边形含解析6

2017年深圳市中考数学试卷含答案解析(Word版)

2024年中考数学二次函数压轴题专题10平行四边形的存在性问题(学生版)

专题10 四边形-2017版[中考15年]上海市2002-2016年中考数学试题分项解析(解析版)

专题10四边形-2017年中考数学试题分项版解析汇编(解析版)

中考复习函数专题10 一次函数中的四边形问题(老师版)

(部编版)2020年中考数学试题分项版解析汇编第期专题10四边形含解析0

广东省各市中考数学分类解析 专题10：四边形

专题10四边形(第01期)-2021年中考数学试题分项版解析汇编(广东福建专版)(解析版)

广东省深圳市2017年中考数学真题试题(含扫描答案)

专题10 四边形-2017版[中考15年]广州市2002-2016年中考数学试题分项解析(解析版)

(完整word版)2017深圳中考数学试题及答案解析,推荐文档

广东省深圳市2002年中考数学试题分类解析汇编专题10 圆

广东省中考数学专题测试四边形课件

广东省深圳市中考数学试题分类解析 专题10 四边形

广东省各市中考数学分类解析专题10：四边形

广东省深圳市中考数学试题分类解析专题10 四边形