快速子空间分解

合集下载

2线性子空间与子空间的分解

设欧氏空间 R n 中的基为 1 , 2 , n ，欧氏空间中有两个向量
xii , y j j
i 1 i 1
n
n
计算 , 的内积
( , ) ( xi i , y j j ) xi ( i , j ) y j
i 1 j 1 i 1 j 1
, V ，都有一个实数 ( , ) 与之对应，且满足
(1) ( , ) ( , ) ; (2) ( , ) ( , ) ( , ) ; (3) (k , ) k ( , ) ; (4) ( , ) 0, 当且仅当 0 时 ( , ) 0 . 则称 ( , ) 为与的内积。定义了内积的实线性空间 V 称为内积空间，又称欧几里得空间或 Euclid 空间（简称欧氏空间）
矩阵AT的零空间
N ( A ) { y | A y 0, y R }
T T m
矩阵A的左零空间
例3 矩阵A的四个子空间（续）
n 矩阵A的值域（列空间） R( A) { y | y Ax, x R }
矩阵A的零空间
N ( A) {x | Amn x 0, x Rn }
N(A) ⊥ R(AT)
N(AT) ⊥ R(A)
1 , 2 ,..., m 定理设W是Vn的一个m维子空间，是W的一个基，则这m个向量必定可扩充为 Vn的基.
二、子空间的分解定理如果V1,V2是数域K上线性空间V的两个子空间，那么它们的交V1 ∩V2也是V的子空间；它们的和V1 +V2也是V的子空间。
T T m
矩阵A的行空间 R( AT ) {z | z AT y, y Rm} 矩阵A的左零空间 N ( A ) { y | A y 0, y R } 设矩阵A的秩为r, 即rank(A)=r,则 dim(R(A))=r, dim(N(A))=n-r; dim(R(AT))=r, dim(N(AT))=m-r; dim(N(A)) - dim(N(AT))= n - m.

krylov子空间算法

Krylov 子空间的定义：定义：令N R υ∈，由1m A υυυ-，，，A 所生成的子空间称之为由υ与A 所生成的m 维Krylov 子空间，并记(),m K A v 。

主要思想是为各迭代步递归地造残差向量，即第n 步的残差向量()n r 通过系数矩阵A 的某个多项式与第一个残差向量()0r 相乘得到。

即()()()0n r p A r =。

但要注意，迭代多项式的选取应该使所构造的残差向量在某种内积意义下相互正交，从而保证某种极小性（极小残差性），达到快速收敛的目的。

Krylov 子空间方法具有两个特征：1.极小残差性，以保证收敛速度快。

2.每一迭代的计算量与存储量较少，以保证计算的高效性。

投影方法线性方程组的投影方法方程组Ax b =,A 是n n ⨯的矩阵。

给定初始()0x ,在m 维空间K(右子空间）中寻找x 的近似解()1x 满足残向量()1r b Ax =-与m 维空间L(左子空间）正交，即()1b Ax L -⊥，此条件称为Petrov-Galerkin 条件。

当空间K=L 时，称相应的投影法为正交投影法，否则称为斜交投影法.投影方法的最优性：１. (误差投影)设A 为对称正定矩阵,()0x 为初始近似解,且K=L,则()1x 为采用投影方法得到的新近似解的充要条件是()()()()01min z x Kx z ϕϕ∈+=其中,()()()12,z A x z x z ϕ=--2.(残量投影)设A 为任意方阵,()0x 为初始近似解,且L AK =,则()1x 为采用投影方法得到的新近似解的充要条件是()()()()01min z x Kx z ψψ∈+=其中()()122,z b Az b Az b Az ψ=-=--矩阵特征值的投影方法对于特征值问题Ax x λ=,其中A 是n ×n 的矩阵，斜交投影法是在m 维右子空间K 中寻找i x 和复数i λ满足i i i Ax x L λ-⊥,其中L 为m 维左子空间.当L=K 时，称此投影方法为正交投影法. 误差投影型方法：取L=K 的正交投影法非对称矩阵的FOM 方法（完全正交法）对称矩阵的IOM 方法和DIOM 方法对称矩阵的Lanczos 方法对称正定矩阵的CG 方法残量投影型方法：取L=AK 时的斜交投影法GMERS 方法（广义最小残量法）重启型GMERS 方法、QGMERS 、DGMERSArnoldi 方法标准正交基方法：Arnoldi 方法是求解非对称矩阵的一种正交投影方法。

线性变换不变子空间直和分解定理注

线性变换不变子空间直和分解定理注线性变换不变子空间直和分解定理是线性代数中一个重要的定理，它可以成功地把一个线性变换分解为合理的子空间和线性一致的变换。

它的实际应用非常广泛，从工程设计到算法设计，从数学建模到社会研究，都用到了这个定理。

该定理要求一个n维向量空间V中有一些不变子空间U1, U2, U3, ... Un，且Ui 之间彼此线性独立，满足UiV。

此外，定理要求存在一个n维到n维的线性变换A；映射A：V→V。

下面对该定理具体进行描述。

首先，该定理要求存在n个不变子空间U1, U2, U3, ... Un，且Ui 之间彼此线性独立，满足UiV。

其中，Ui表示一个不变的子空间，V表示一个n维的向量空间，即Ui+Uj = V。

其次，定理还要求存在一个n维到n维的线性变换A；映射A：V →V，即A(v) = Av，其中v∈V，A∈Rn×n。

最后，定理要求存在一组线性变换B1, B2, B3, ... Bn，其中Bi：Vi→Vi，使得对于任意的v∈V，都有A(v) = B1(v) + B2(v) + B3(v)+ ... + Bn(v) +v。

此外，定理还要求不变子空间U1, U2, U3, ... Un 之间要线性独立，即任意线性组合c1U1+c2U2 + c3U3 + ... cnUn = 0，则有ci= 0，i=1,2,3,...n。

最后，定理要求满足二者之后，线性变换A才能成功分解为线性一致的变换B1, B2, B3, ... Bn，即A(v) = B1(v) + B2(v) + B3(v)+ ...+Bn(v) +v，其中v∈V。

综上所述，线性变换不变子空间直和分解定理是一个十分重要且实用的定理，它可以将一个线性变换A：V→V成功分解为以n个不变子空间U1, U2, U3, ...Un线性一致的变换B1, B2, B3, ... Bn来描述，这种把线性变换分解为简单子问题的方法，可以将复杂的问题转换为易于解决的子问题，并大大加快了处理速度并减少了误差，因此，这个定理在工程设计、算法设计、数学建模、社会研究等领域的实际应用就变得十分重要。

线性变换不变子空间直和分解定理注

λ λ ｉｉｉ）第１７卷第４期２０１４年７月高等数学研究ＳＴＵＤＩＥＳＩＮＣＯＬＬＥＧＥＭＡＴＨＥＭＡＴＩＣＳＶｏｌ．１７，Ｎｏ．４Ｊｕｌ．，２０１４ｄｏｉ：１０．３９６９／ｊ．ｉｓｓｎ．１００８－１３９９．２０１４．０４．００８线性变换不变子空间直和分解定理注谭尚旺（中国石油大学（华东）理学院，山东青岛２６６５８０）摘要根据根子空间的定义，确定线性空间关于线性变换不变子空间直和分解定理中子空间和根子空间的关系，并且确定了子空间的维数．关键词不变子空间；维数；根子空间中图分类号Ｏ１５１．２４文献标识码Ａ文章编号１００８－１３９９（２０１４）０４－００２５－０２ＯｎＤｉｒｅｃｔＳｕｍＤｅｃｏｍｐｏｓｉｔｉｏｎＴｈｅｏｒｅｍｆｏｒＩｎｖａｒｉａｎｔＳｕｂｓｐａｃｅｏｆＬｉｎｅａｒＴｒａｎｓｆｏｒｍＴＡＮＳｈａｎｇｗａｎｇ（ＳｃｈｏｏｌｏｆＳｃｉｅｎｃｅ，ＣｈｉｎａＵｎｉｖｅｒｓｉｔｙｏｆＰｅｔｒｏｌｅｕｍ（ＥａｓｔＣｈｉｎａ），Ｑｉｎｇｄａｏ２６６５８０，ＰＲＣ）Ａｂｓｔｒａｃｔ：Ｉｎｔｈｉｓｐａｐｅｒ，ｔｈｅｒｅｌａｔｉｏｎｂｅｔｗｅｅｎｓｕｂｓｐａｃｅｓａｎｄｒｏｏｔ－ｓｕｂｓｐａｃｅｓｉｎｔｈｅｄｉｒｅｃｔｓｕｍｄｅｃｏｍｐｏｓｉｔｉｏｎｔｈｅｏｒｅｍｏｆｉｎｖａｒｉａｎｔｓｕｂｓｐａｃｅｓｏｆａｌｉｎｅａｒｔｒａｎｓｆｏｒｍａｒｅｄｉｓｃｕｓｓｅｄ，ａｎｄｔｈｅｄｉｍｅｎｓｉｏｎｓｏｆｔｈｏｓｅｓｕｂｓｐａｃｅｓａｒｅａｌｓｏｄｅｔｅｒｍｉｎｅｄ．Ｋｅｙｗｏｒｄｓ：ｉｎｖａｒｉａｎｔｓｕｂｓｐａｃｅ，ｄｉｍｅｎｓｉｏｎ，ｒｏｏｔ－ｓｕｂｓｐａｃｅ线性空间、线性变换和矩阵在相似关系下的化Ｗ（ｍ）＝｛：Ｖ，（Ｅ）ｍ０｝．简问题是高等代数的重要内容，其中矩阵在相似关 λ!称Ｗ＝ξξ∈ Ｗ（ｍ） σ－λξ ＝系下的化简问题与线性空间关于线性变换不变子空 λ∪ｍ＝１λ 为线性变换σ 属于特征值λ的根子容易发现，Ｗλ 是的不变子空间．由定义知间的直和分解问题是等价的．空间． σ｛（ｍ）｝!定理１［１］设σ是复数域上ｎ维线性空间Ｖ的Ｗλ ｍ＝１是一个不降的子空间序列，即（１）（２）（３）线性变换，Ｅ是Ｖ上的恒等变换，σ的特征多项式Ｗλ Ｗλ Ｗλ … Ｖ，（２）［２］ｆ（λ）的标准分解式为且存在一个最小正整数ｋ ≤ｎ，使得（１）（ｋ－１）（ｋ）（ｋ＋１）ｆ（λ）＝（λ－λ１）ｒ１（λ－λ２）ｒ２ … （λ－λｓ）ｒｓ，（１）对ｉ＝１，２，…，ｓ，记Ｗλ … Ｗλ Ｗλ ＝Ｗλ＝ …．因此Ｗ＝Ｗ（ｋ）．［２］设是复数域上ｎ维线性空间Ｖ的Ｖｉ＝｛ξ：ξ ∈Ｖ，（σ－λｉＥ）ｒｉξ ＝０｝，则Ｖｉ是σ 的不变子空间并且Ｖ＝Ｖ１Ｖ２ … Ｖｓ．由定理１知，复数域上ｎ维线性空间Ｖ的线性变换在Ｖ的某个基下的矩阵为准对角形，即复矩阵一定相似准对角形．定理２ σ一个线性变换，σ 的特征多项式ｆ（λ）具有标准分解式（１），Ｗλ 是σ 属于特征值λｉ的根子空间．则有ｄｉｍ（Ｗλ ）＝ｒｉ，Ｖ＝Ｗλ１Ｗλ２ … Ｗλｓ．由定理１和定理２，自然会提出如下问题．问题１［１］定理１中子空间Ｖ的维数（即准对问题２对１≤ｉｓ，定理１的子空间Ｖ与定ｉ角形矩阵相应对角块的阶）是多少？理２的子空间Ｗλ ≤ｉ具有什么关系？设σ是复数域上ｎ维线性空间Ｖ的一个线性变对１≤ｉ≤ｓ，尽管文献［２］指出存在一个最小正换，λ 是σ的一个特征值．对ｍ＝１，２，３，…，记整数ｋｉ ≤ｎ，使ＷλＷ（ｋｉ，但仍存在以下问题．ｉ＝λｉ收稿日期：２０１２－０５－０９；修改日期：２０１３－１２－１２作者简介：谭尚旺（１９６４－），男，山东泰安，硕士，教授，从事图论研究．Ｅｍａｉｌ：ｔｓｗａｎｇ＠ｓｉｎａ．ｃｏｍ问题３对１≤ｉ≤ｓ，是否存在ｋｉ的一个更好的上界令Ｉｓ表示ｓ阶的单位矩阵，Ｊ（ａ，ｓ）表示对角元ｉｉ ξ λｉｉｉｉｉｊｊｊｉｉ（）ｉｒ ≤ ｉｉｉｉｉ２６高等数学研究２０１４年７月为ａ的ｓ阶下三角形Ｊｏｒｄａｎ块，并记ｓ－ｔｔＪ（０，ｒｉ）ｍ＝０，而当１≤ ｍ ≤ｒ－１时，有烇烉烋烇烉烋ｉＢｓ，ｔ＝（０，…，０，１，…，１）．对以上３个问题可得如下确切答案．Ｊ（０，ｒｉ）ｍ＝烄００烌．定理３设σ是复数域上ｎ维线性空间Ｖ的一个线性变换，σ 的特征多项式ｆ（λ）具有标准分解烆Ｉｒｉ－ｍ０烎取定正整数２≤ ｍ ≤ｒｉ，令＝（ε１，ε２，…，εｒ）Ｂｒ，ｍ ∈ Ｗλ ，式（１），并且Ｖｉ和Ｗλ 是定理１和定理２中分别定 ξ则有ｉｉｉ义的记号，则有结论（ⅰ）对每个１≤ｉ≤ｓ，都有Ｖｉ＝Ｗλ ，并且（σ－λｉＥ）ｍ＝（σ Ｗλｉ－λｉＥ）ｍξ ＝ｄｉｍ（Ｖｉ）＝ｒｉ．（σ Ｗ－λｉＥ）ｍ（ε１，ε２，…，εｒ）Ｂｒｍ＝，ｉ（ⅱ）对每个１≤ｉ≤ｓ，都有ｋｉ ≤ｒｉ，且ｋｉ＝ｒｉ（ε１，ε２，…，εｒ）Ｊ（０，ｒｉ）ｍＢｒ，ｍ＝０，当且仅当 σ Ｗ在Ｗλ 的某个基下的矩阵是一个（σ－λｉＥ） ξ ＝（σ Ｗｉ－λｉＥ） ξ＝ λｉｉｍ－１ｍ－１λｉＪｏｒｄａｎ块．（ε１，ε２，…，εｒ）Ｊ（０，ｒｉ）ｍ－１Ｂｒ，ｍ＝εｒ．ｉ（ｍ）ｉ（ｍ－１）ｉ（１）证明（ⅰ）由Ｖｉ和Ｗλ 的定义知于是ξ ∈Ｗλｉ且ξ Ｗλｉ．这表明子空间Ｗλ，（２）（ｒ）ＶｉＷλｉ（ｉ＝１，２，…，ｓ）．（３）Ｗλ ，…，Ｗλｉ两两不同，故由ｋｉ ≤ｒｉ及ｋｉ的定义可假设存在一个１≤ｊ≤ｓ，使Ｖｊ ≠Ｗλ ，则存在一个向ｉ知ｋｉ＝ｒｉ．量α ∈Ｗλ且α Ｖｊ．由定理１知Ｖ＝Ｖ１Ｖ２ … Ｖｓ．当ｋｉ＝ｒｉ时，文［２］已证σ Ｗ λｉ（λ－λｉ）ｒｉ，故存在根子空间Ｗ的特征多项式为 ε１，ε２，…，于是存在向量αｌ ∈Ｖｌ（ｌ＝１，２，…，ｓ），使得εｒ，使得σ Ｗλｉ的一个基在该基下的矩阵是Ｊｏｒｄａｎ标准型α ＝α１＋ … ＋αｊ－１＋αｊ＋αｊ＋１＋ … ＋αｓ，ｉλｉＱ＝ｄｉａｇ（Ｊ（λ ｓＪλ ｓＪλ ｓ也即其中ｒｓｉ，１），（ｉ，２），…，（ｉ，ｌ）），ｓｓ．于是（σ－λＥ）ｓ１在该基 α１＋… ＋αｊ－１＋（αｊ－α）＋αｊ＋１＋… ＋αｓ＝０．ｉ ≥ １ ≥ ２ ≥ … ≥ ｌｉ下的矩阵是由式（３），α ∈ Ｗλ 和αｌ ∈Ｖｌ（ｌ＝１，２，…，ｓ）知（Ｑ－λｉＩｒ）ｓ１＝ αｊ－α ∈ Ｗλｊ，ｄｉａｇ（Ｊ（０，ｓＪ０ｓ＝０．４１）ｓ１，…，（，ｌ）ｓ１）（） αｌ ∈ Ｗｌ，ｌ∈ ｛１，２，…，ｓ｝－｛ｊ｝．设σ 在基ε ε ε ε ε Ｊｏｒｄａｎ１，２，…，ｒ，ｒ，…，ｎ下的标准从而由定理２的结论可得ｉｉ＋１αｊ－α ＝０．型为（Ｑ０），其中λ 不是Ｇ的特征值对于正整数于是α＝αｊ ∈Ｖｊ，这与假设α Ｖｊ矛盾．因此，对每个１≤ｉ≤ｓ，总有Ｖｉ＝Ｗλ ，进而从定理２知◇ Ｇｍ ≥ｓ１，任取ξ ∈Ｘｉ．Ｗ（ｍ＋１）λｉ，记ξ 在该基下的坐标为ｄｉｍ（Ｖｉ）＝ｄｉｍ（Ｗλ ）＝ｒｉ．（Ｙ）． σ－λｉ ξ ＝０ｉ（ⅱ）对每个ｉ＝１，２，…，ｓ，由Ｗλ 和Ｖｉ的定义由（（Ｑ－λＩＥ）ｍ＋１知ｍ＋１ｉ以及的结论（ⅰ）知!烄ｉｒｉ）（Ｇ－λｉＩｎ－ｒ） ' Ｘ＝０，Ｗ（ｒ）（ｍ）烆ｍ＋１ｉ烎 λｉ＝Ｖｉ＝Ｗλｉ＝ ∪ Ｗλｉ．知Ｙ＝０ｍ＝１从而（Ｇ－λＩ）ｍ＋１Ｙ０．再由Ｇ λｉＩｎｒ，（ｒ）（ｊ）ｉｎ－ｒｉ＝－－ｉ故对任意正整数ｊ≥ｒｉ，有ＷλｉＷλｉ．另由式（２）故由式（４）得（σ－λｉＥ）ｍξ ＝０，即ξ ∈ Ｗ（ｍ）这表明知Ｗ（ｒ）（ｊ）．因此Ｗ（ｒ）（ｊ）．这表明（ｍｍ λｉ，ｍｍ λｉＷλ λｉ＝ＷλＷ＋１）（）（）（＋１）ｉＷ（１）ｉ（２）ｉｉ（）（ｒｉ＋１） …．λｉＷλｉ，于是结合式（２）得Ｗλｉ＝Ｗλｉ．因 λｉＷλｉ … Ｗλｉ＝Ｗλｉ＝此，由ｋｉ的定义知ｒｉ＝ｋｉ ≤ｓｉ，于是ｓ１＝ｒｉ，从而有因此，由ｋｉ的定义知ｋｉｒｉ．假设σ Ｗ λｉ在Ｗλ 的某ｌ＝１，即σ Ｗ λｉ在某个基下的矩阵是Ｊｏｒｄａｎ块．个基ε１，ε２，…，εｒ下的矩阵是Ｊｏｒｄａｎ块Ｊ（λｉ，ｒｉ），即 σ Ｗλ （ε１，ε２，…，εｒｉ）＝（ε１，ε２，…，εｒｉ）Ｊ（λｉ，ｒｉ）．则对任意的正整数ｍ，有参考文献［１］北京大学数学系几何与代数教研室代数小组．高等代数（σ Ｗ λｉ－λｉＥ）ｍ（ε１，ε２，…，εｒ）＝［Ｍ］．３版．北京：高等教育出版社出版，２００３：（ε１，ε２，…，εｒ）（Ｊ（λｉ，ｒｉ）－λｉＩｒ）ｍ＝３０９－３１１．ｉｉｉｉＹｉ（ε１，ε２，…，εｒ）Ｊ（０，ｒｉ）ｍ，其中当ｍ≥ｒｉ时，有［２］李炯生，查建国．线性代数［Ｍ］．合肥：中国科学技术大学出版社，１９８９：３４６－３５１．。

如何理解空间第一和第二分解定理

文章标题：探索空间第一和第二分解定理的内涵与应用导言在数学领域，我们经常会碰到一些定理和公式，它们看似晦涩难懂，但背后蕴含着深刻的数学内涵和应用意义。

其中，空间第一和第二分解定理就是这样一对经典的定理，它们在线性代数和向量空间理论中有着重要的地位。

通过对这两个定理的深入探讨和理解，我们可以更好地把握向量空间的结构和性质，为进一步的数学研究和应用打下坚实的基础。

第一分解定理的内涵与应用让我们来探讨空间第一分解定理的内涵和应用。

在线性代数中，第一分解定理指出了一个重要的结论：对于任意的向量空间V和其任意子空间W，都存在另一个子空间U，使得V可以分解为W和U的直和。

这个定理对理解向量空间的结构和性质具有重要意义，同时在实际问题的求解中也具有广泛的应用。

举一个具体的例子来说明第一分解定理的应用：假设我们有一个三维向量空间V，其中包含了所有的三维向量，同时我们有一个二维平面子空间W，它包含了V中的所有平面向量。

根据第一分解定理，我们可以找到一个一维直线子空间U，使得V可以表示为W和U的直和。

这个结论在计算机图形学和工程领域有着重要的应用，可以帮助我们更好地理解和处理三维空间中的向量问题。

第二分解定理的内涵与应用接下来，让我们深入探讨空间第二分解定理的内涵和应用。

第二分解定理是第一分解定理的一个重要推论，它指出了对于任意向量空间V和其任意两个子空间W1和W2，存在一个补空间U，使得V可以分解为W1和W2的直和。

这个定理在向量空间的研究和应用中具有重要的地位。

以一个实际问题为例，我们可以考虑一个四维向量空间V，其中包含了所有的四维向量，同时我们有两个三维平面子空间W1和W2，它们分别包含了V中的所有三维平面向量。

通过第二分解定理，我们可以找到一个一维直线子空间U，使得V可以表示为W1和W2的直和。

这个结论在数据压缩和信号处理领域有着广泛的应用，可以帮助我们更好地理解和处理高维向量空间中的问题。

个人观点与理解从我的个人观点来看，空间第一和第二分解定理是线性代数和向量空间理论中非常重要的定理，它们对于理解向量空间的结构和性质具有重要意义。

基于近似零范数的子空间迭代稀疏分解算法

ｒｓｎａｉｎ；ｓｏｔｅ — ｏｍ；ＳｅｅｔｔｏｍｏｈｄｎｒＣＡ（ｐｒｅｃｍｐｎｎｎｌｓｓｓａｓｏｏｅｔａａｙｉ）
对于未知混合系统Ａ和源信号ｓ＝（１ｓ … ）已知观测信号满足＝Ａ＋，盲源分ｓｚ，ｓｌ，
函数的改进算法。在此基础上，用子空间表示的方法确定了满足方程的源信号矢量空间，利以此约束迭代算
法的搜索范围，高算法效率。理论分析和仿真实验表明，于矢量空间迭代的算法收敛速度更快。此外，提基
Ｓｕｐｅｉａｉｅａｌｏｉｍｏｒｓａｒｅｄｏｍｐｉｏｎｂｓｂｓａｃｔｔｖｇｒｔｅｒｈｆｐｓｅｃｏｓｔａｅｄｉｏｒｉｌｍｐｒｅｄｓｏｈ０ｎｒｏｖｍｏｔｅｄＺ一ｏｍｓ
Ｋｅｒｓｖｒｃｍｐｅｅｓａｓｅｏｏｉｏｙｗｏｄ：ｏｅ— ｏｌｔｐｒｅｄｃｍｐｓｔｎ；ｕｄｒｅｅｍｉｅｌｄｓｕｃｓｓｐｒｔｎｕｓａｅｒｐｉｎｅｄｔｒｎｄｂｉｏｒｅｅａａｉ；ｓｂｐｃｅ — ｎｏ
Ｖ０．２Ｎｏ５１１．Ｏａ．２１１ｔ０
基于近似零范数的子空问迭代稀疏分解算法
崔志富，张杭，路威
（解放军理工大学通信工程学院，苏南京２００）江１０７
摘
要：对近似零范数算法单参数代价函数不能协调近似精度与噪声容限的问题，出了基于多参数代价针提

能控能观子空间分解5标准型的能控能观测子空间分解

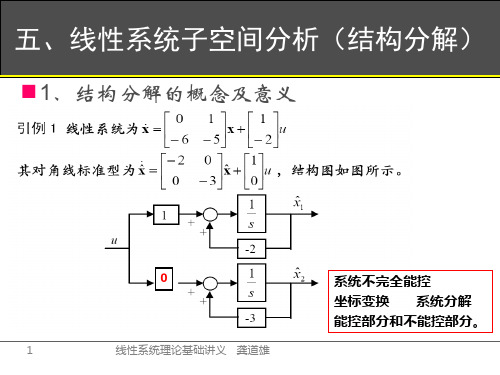
3、能观测子空间分解
25
线性系统理论基础讲义龚道雄
3、能观测子空间分解
26
线性系统理论基础讲义龚道雄
3、能观测子空间分解
27
线性系统理论基础讲义龚道雄
3、能观测子空间分解
28
线性系统理论基础讲义龚道雄
4、能控能观子空间分解
•
Xˆ
Aˆ Xˆ
BˆU
Y CˆXˆ
29
线性系统理论基础讲义龚道雄
P147: 8
61
线性系统理论基础讲义龚道雄
4、能控能观子空间分解
41
线性系统理论基础讲义龚道雄
4、能控能观子空间分解
42
线性系统理论基础讲义龚道雄
4、能控能观子空间分解
43
线性系统理论基础讲义龚道雄
4、能控能观子空间分解
44
线性系统理论基础讲义龚道雄
4、能控能观子空间分解
45
线性系统理论基础讲义龚道雄
4、能控能观子空间分解
35
线性系统理论基础讲义龚道雄
4、能控能观子空间分解
36
线性系统理论基础讲义龚道雄
4、能控能观子空间分解
37
线性系统理论基础讲义龚道雄
4、能控能观子空间分解
38
线性系统理论基础讲义龚道雄
4、能控能观子空间分解
39
线性系统理论基础讲义龚道雄
4、能控能观子空间分解
40
线性系统理论基础讲义龚道雄
线性系统理论基础讲义龚道雄
5、标准型的能控能观测子空间分解
57
线性系统理论基础讲义龚道雄
5、标准型的能控能观测子空间分解
58

任意阵列二维测向的快速子空间算法

ｓａｅｗｉｎｒｆｔｒ（ｔｇｅｅｉｅＭＳＦｌＷ），ｗｅｃｎｇｔｔｅｓｇａｎｏｓｕｓａｅｖｉｉｇｔｅｅｔａｉｎｏｈｏａｉｎｅｍａｒｘａｅｈｉｎｌｄｎｉｅｓｂｐｅ．ａｏｄｎｈｓｉｔｆｔｅｃｖｒｃｔｉａｍｏａ
将ＭＵＳＣ算法推广到三维空间阵列可以对辐射源进行二维高精度测向，由于其需要估计接收数据的协方Ｉ但差矩阵和进行特征分解，而其计算量较大。利用多级维纳滤波器的前向递推获得信号子空间和噪声子空因
维普资讯
第２卷第５期７
弹箭与制导学报
・Ｏ・３５
任意阵列二司锡才，建红唐
（哈尔滨工程大学信息与通信工程学院．尔滨哈摘１００）５０１要：了对空间辐射源进行精确定位．为建立了基于任意阵列对多目标源进行二维ＤＯＡ估计的数学模型。
ｐｒｃｓｌｓｄｎｈｒｅｄｉｅｓｏｎｌｓａｅａｔｎｎａａｒｙＢｕｔｉｏｌｅｓｉａｉｈｅｃａｉｎｃａｒｘｏｆｏｅｖｄｅｉｅｙｂａｅｏｔｅ－ｍｎｉａｐｃｎｅｒａ．ｔｉｎｖｖｓｅｔｍｔｎｇｔｏｖｒａｅｍｔｉｂｓｒｅｄｔｎｄｉｓｅｇｅｄｅｏｍｐｉｉａａａｔｉｎｃｏｓｔｏｎ．ｉｈａｏｒｏｍｐｕａｉｎｌｃｔｓｍｅｃｔｔｏａｏｍｐｅｉｙＵｔｌｉｈｅｏｗａｄｒｃｓｏｎｏｈｅｍｕｌｉｌｘｔ．ｉｚｎｇｔｆｒｒｅｕｒｉｆｔｉｔ—

一种无特征分解的快速子空间DOA算法

一
种无特征分解的快速子空间ＤＯＡ算法
彭巧乐，司锡才，李利
（尔滨工程大学信息与通信工程学院，黑龙江哈尔滨１００）哈５０１
摘要：于子空间正交特性的ＭＵＳＣ算法具有优良的超分辨性能，由于其需要对空间协方差矩阵进行基Ｉ但
ＡｂｔａｔＴｈＵＳＣｌｏｉｈｗｉｕ－ｐｃｒｈｇｎｌｃａａｔｒｔｓｈｓａｘｅｌｎｕｅｅ０ｕｉｎｓｒｃ：ｅＭＩａｇｒｔｍｔｓｂｓａｅｏｔｏｏａｈｒｃｅｉｉａｎｅｃｌｔｓｐ卜ｒｓｌｔｈｓｃｅｏ
ｓａｅｔｒｕｈｔｅｈｇｒｅｏｒｏｈｐｔｌｃｖｒａｃｔｉｒｔｅｉｖｒｅｏｅｔｖｉｈｉｅｄｃｍｐｉｏ．ｐｃｈｏｇｈｉｈｏｄｒｐｗｅｆｔｅｓａｉｏａｉｎｅｍａｒｘｏｈｎｅｓｎＯａｏｄｔｅｅｇｎｅｏｓｔｎａｉ
第３２卷
第４期
系统工程与电子技术
ＳｓｅｓＥｎｉｅｒｎｎｌｃｒｎｃｙｔｍｇｎｅｉｇａｄＥｅｔｏｉｓ
Ｖｏ．２Ｎｏ４１３．
Ａｐｒｌ２０ｉ０１
２１００年４月
文章编号：０１５６（０００６１０１０—０Ｘ２１）４０９－３

子空间的直和与直和分解

子空间的直和与直和分解在线性代数中，我们学习了向量空间的概念和性质。

而向量空间可以由子空间构成，子空间是向量空间中的一个非空集合，满足加法和标量乘法封闭性的子集。

本文将探讨子空间之间的直和和直和分解。

一、子空间的直和在向量空间V中，如果存在子空间U和W，满足两个条件：1.U∩W={0}；2. V是U和W的和集，即任意向量v∈V可以表示为u+w 的形式，其中u∈U，w∈W；那么我们称子空间U和W的直和为子空间V的直和。

直和的概念可以类比于数字的加法。

例如，我们将数字3表示为1+2，其中1和2是3的因子。

同样地，如果向量v可以表示为u+w，其中u和w是v的因子，那么我们可以将向量v看作是子空间U和W 的直和。

二、子空间的直和分解在向量空间V中，如果存在子空间U和W，满足两个条件：1.U∩W={0}；2. 任意向量v∈V，都可以唯一地表示为u+w的形式，其中u∈U，w∈W；那么我们称v关于子空间U和W的直和分解。

直和分解是一种将向量分解为两个子空间的方法。

这种分解在很多算法和数学问题中都有广泛的应用。

例如，对于矩阵的特征值分解和奇异值分解等问题，都可以采用直和分解的方式来求解。

三、子空间的例子与应用1. 平面的直和分解：考虑平面上的向量空间R^2，其中存在两个子空间U和W，分别表示x轴和y轴上的向量。

显然，两个子空间的交集为零向量{0}，任意向量v可以唯一地表示为x轴和y轴上的分量之和。

因此，平面的直和分解是R^2的一种典型示例。

2. 空间的直和分解：类似地，在三维空间R^3中，我们可以将空间分为三个子空间：XY平面、YZ平面和ZX平面。

这三个平面两两相交于一条直线，即它们的交集为零向量{0}。

因此，任意向量v可以唯一地表示为这三个平面上的分量之和。

子空间的直和和直和分解在线性代数的理论和实践中具有重要作用。

它们不仅可以帮助我们理解向量空间的性质和结构，还可以应用于各种数学和工程问题中，例如线性方程组的求解、矩阵分解和数据压缩等。

子空间的直和的充要条件

子空间的直和的充要条件子空间的直和是线性代数中一个重要的概念。

在研究向量空间时，我们常常遇到将一个向量空间分解成若干个子空间的情况，而子空间的直和就是一种特殊的分解方式。

本文将介绍子空间的直和的充要条件。

假设V是一个向量空间，U和W是V的两个子空间。

我们称V是U和W的直和，记作V=U⊕W，如果满足以下两个条件：1. V=U+W：任意向量v∈V都可以写成v=u+w的形式，其中u∈U，w∈W。

2. U∩W={0}：U和W的交集只包含零向量。

我们来证明V=U⊕W的充分性。

假设V=U⊕W，我们需要证明满足上述两个条件。

对于第一个条件，我们可以将任意向量v∈V表示为v=u+w的形式，其中u∈U，w∈W。

由于V=U⊕W，所以v的表示是唯一的。

对于第二个条件，假设存在一个非零向量x∈U∩W。

由于x∈U，所以x也属于V。

那么我们可以找到另外两个向量u'∈U和w'∈W，使得x=u'+w'。

因为x∈W，所以w'∈W；因为x∈U，所以u'∈U。

因此，x=u'+w'既是U和W的一个表示，也是V的一个表示。

但由于v的表示是唯一的，所以u'+w'=u+w。

因此，我们可以得到u-u'=w'-w。

由于u-u'∈U，w'-w∈W，所以u-u'∈U∩W。

但由于U∩W={0}，所以u-u'=0，即u=u'，w=w'。

因此，x=u'+w'=u+w=0。

这与x是一个非零向量矛盾。

因此，U∩W={0}。

接下来，我们来证明V=U⊕W的必要性。

假设V=U⊕W，我们需要证明满足上述两个条件。

对于第一个条件，任意向量v∈V都可以写成v=u+w的形式，其中u∈U，w∈W。

因此，V=U+W。

对于第二个条件，假设存在一个非零向量x∈U∩W。

那么x既属于U 也属于W，所以x可以写成x=0+0的形式。

模态lancos子空间法

模态Lanczos子空间法是一种用于求解线性定常系统特征值和特征向量的数值方法。

这种方法基于Lanczos算法，该算法用于求解实对称正定矩阵的特征向量。

在模态分析中，模态Lanczos子空间法被广泛应用于识别系统的模态。

首先，我们需要了解模态的概念。

在机械工程中，模态分析是用于描述结构振动特性的方法。

这些模态是结构固有的振动模式，反映了结构的动态特性。

通过模态分析，我们可以了解结构的振动行为，并用于设计、分析和优化结构。

模态Lanczos子空间法的应用过程如下：1. 初始化：选择一个合适的初始猜测向量，通常是一个随机向量或由系统响应数据得到的一个初始猜测。

2. 迭代：使用Lanczos算法从当前向量开始，通过一系列矩阵乘积得到一系列向量。

这些向量构成了一个子空间，称为“模态子空间”。

3. 更新：在每次迭代中，根据当前的模态子空间，通过某种方式（如特征分解）得到一个新的向量，并将其作为当前向量的更新。

这个过程一直持续到满足某种停止条件（如达到预设的迭代次数或收敛到预设的精度）。

4. 特征值和特征向量的求解：通过模态子空间法得到的向量就是系统的模态特征向量。

同时，这些向量的模长给出了相应的特征值（即模态频率），从而可以确定系统的模态特性。

这种方法的主要优点是它能够直接得到系统的模态特征向量和频率，而不需要进行复杂的数值积分或拟合。

此外，由于这种方法是基于Lanczos算法的，因此它的计算复杂度相对较低，适用于大规模系统的模态分析。

然而，模态Lanczos子空间法也有其局限性。

首先，它依赖于一个合适的初始猜测向量，如果初始猜测不准确，可能会导致算法陷入局部最优解。

其次，对于某些系统，可能存在多个模态频率接近的情况，这可能导致特征值的精度问题。

最后，这种方法需要大量的计算资源，特别是对于大规模系统，可能需要使用更高效的算法或并行计算技术来加速计算过程。

总之，模态Lanczos子空间法是一种有效的求解线性定常系统特征值和特征向量的方法，适用于大规模系统的模态分析。

希尔伯特正交分解定理

希尔伯特正交分解定理希尔伯特正交分解定理是泛函分析中的一个重要定理，它描述了在一个希尔伯特空间中，任意一个元素都可以唯一地分解为一个子空间的元素与该子空间正交的元素的和。

具体来说，设M是希尔伯特空间H的闭线性子空间，那么对于H中的任意元素f，存在唯一的元素g属于M和唯一的元素h属于M的正交补M⊥，使得f=g+h。

此外，这个分解还具有一些重要的性质，例如f与M中任意元素的内积等于g与M中该元素的内积，以及||f||²=||g||²+||h||²。

希尔伯特正交分解定理在泛函分析和数学物理中都有着广泛的应用。

它提供了一种将一个复杂的问题分解为两个相对简单的问题的方法，从而可以更方便地进行研究。

此外，该定理还具有重要的几何意义，它描述了希尔伯特空间中的元素与子空间之间的正交关系，这种关系在很多领域中都有着重要的应用，例如信号处理、图像处理、优化理论等。

需要注意的是，希尔伯特正交分解定理的前提是子空间M必须是闭的。

如果M不是闭的，那么分解可能就不存在或者不是唯一的。

此外，在实际应用中，还需要注意计算的可行性和数值稳定性等问题。

总之，希尔伯特正交分解定理是泛函分析中的一个重要定理，它为研究希尔伯特空间中的元素与子空间之间的关系提供了一种有效的方法，具有广泛的应用价值。

希尔伯特正交分解定理在多个领域都有广泛的应用。

1.信号处理：在信号处理中，正交分解定理被用来将复杂的信号分解为多个正交的分量，这样可以更方便地分析和处理这些信号。

2.图像压缩：在图像压缩中，正交分解定理也起到了关键的作用。

通过将图像分解为多个正交的分量，可以根据不同的重要性对这些分量进行编码和传输，从而实现图像的有效压缩。

3.最小二乘解：在最小二乘问题中，正交分解定理被用来找到最佳拟合的解。

通过将问题分解为两个正交的部分，可以更容易地找到满足条件的解。

此外，希尔伯特正交分解定理还在线性代数、泛函分析、优化理论等领域中有广泛的应用。

krylov子空间方法

krylov子空间方法一、什么是Krylov子空间方法。

1.1 Krylov子空间方法的基本概念。

Krylov子空间方法啊，那可是数值分析里相当厉害的一个东西。

简单来讲呢，它就是围绕着Krylov子空间来做文章的。

这个Krylov子空间啊，就像是一个特殊的小天地，是由一个向量和一个矩阵通过特定的运算生成的一系列向量张成的空间。

就好比是从一颗种子（初始向量），在一个特定的规则（矩阵运算）下，长出了一片小森林（Krylov子空间）。

这可不是什么故弄玄虚的东西，在很多实际的计算问题里，它可有着大用途。

1.2 它的独特之处。

这方法独特就独特在它能够把一些复杂的线性代数问题转化到这个特殊的子空间里去求解。

这就好比是把一个在大迷宫里找路的难题，转化到一个小迷宫里，一下子就变得相对简单了。

它能够利用这个子空间的一些特性，像什么正交性之类的，就像找到一把特殊的钥匙，去打开那些原本难以解决的数值计算的大门。

二、Krylov子空间方法的应用。

2.1 在求解线性方程组中的应用。

线性方程组是个老大难问题，就像一座大山横在数值计算的道路上。

但是Krylov 子空间方法就像是一群勇敢的登山者。

比如说在处理大型稀疏线性方程组的时候，它可以巧妙地利用Krylov子空间的结构，像走捷径一样快速地找到方程组的解。

这可比那些传统的方法要高效得多，就像骑自行车和开汽车的区别，那速度提升可不是一点半点。

2.2 在矩阵特征值计算中的应用。

矩阵的特征值计算也不是个简单事儿，就像在草丛里找珍珠一样。

Krylov子空间方法呢，就像一个有经验的寻宝者。

它通过在Krylov子空间里构建特殊的矩阵，然后利用这些矩阵的性质来计算原始矩阵的特征值。

这就像是通过一个小模型来推断大物件的特性，真的是很巧妙。

2.3 在其他领域的应用。

这Krylov子空间方法啊，可不仅仅局限于线性代数的小圈子。

在很多工程领域，比如结构力学、电子电路模拟等方面，它都能大展身手。

就像一个万能钥匙，能打开不同领域的数值计算难题这把锁。

高中数学空间分解教案

高中数学空间分解教案
教学目标：
1. 了解空间分解的基本概念和原理。

2. 掌握常见空间分解方法的应用。

3. 能够独立进行空间分解的相关题目解答。

教学重点：
1. 空间分解的基本概念。

2. 常见空间分解方法的应用。

教学难点：
1. 如何灵活运用空间分解方法解决复杂问题。

教学准备：
1. 教案PPT
2. 讲义手册
3. 相关练习题
教学过程：
一、导入：通过一个简单的示例引导学生了解空间分解的概念和重要性。

二、讲解空间分解的基本概念和原理：
1. 定义：空间分解是将一个向量空间分解成若干个互不重叠的子空间的过程。

2. 原理：通过将向量空间划分为基础子空间，可以简化向量的表示和计算。

三、介绍常见的空间分解方法：
1. 直和分解：将向量空间分解为若干个直和的子空间。

2. 正交分解：将向量空间分解为正交的子空间。

3. 特征空间分解：根据矩阵的特征值和特征向量进行空间分解。

四、实际操作：
1. 给学生一些练习题，让他们通过空间分解方法解答。

2. 学生互相讨论，共同解决问题。

五、总结：总结本节课学习的内容，并强调空间分解的重要性和应用。

六、作业布置：布置一些相关练习题，巩固学生的空间分解能力。

七、反馈与检查：下节课开头检查学生的作业情况，并给予及时反馈。

教学延伸：
1. 引导学生深入了解空间分解在数学和工程中的应用。

2. 鼓励学生自主探索更多关于空间分解的知识和技巧。

子空间方法

子空间方法
子空间方法（Subspace methods）是一类矩阵分解方法，主要
用于信号处理和数据分析。

它的基本思想是将原始数据矩阵分解为多个低维子空间的线性组合，以此来提取数据的潜在结构和重要信息。

子空间方法通常包括主成分分析（PCA）、因子分析（FA）、独立成分分析（ICA）等，它们都可以通过矩阵的特征值和特
征向量来实现数据分解和降维。

在实际应用中，子空间方法可以用于信号降噪、图像处理、语音识别、机器学习等领域。

例如，在语音识别中，子空间方法可以将声音信号与噪声信号进行分离，以提高语音识别的准确性。

在机器学习中，子空间方法可以用于特征提取和数据压缩，以降低模型的复杂度和加速训练过程。

有理分式的快速分解方法及其应用

有理分式的快速分解方法及其应用
鲁志波;勒孚龙;张启慧
【期刊名称】《高师理科学刊》
【年(卷),期】2011(031)005
【摘要】根据有理分式的不同结构特点,给出了相应的分解为部分分式的快速算法及其应用,有效解决了这类函数的积分问题.
【总页数】4页(P7-10)
【作者】鲁志波;勒孚龙;张启慧
【作者单位】信息工程大学理学院,河南郑州450001;信息工程大学理学院,河南郑州450001;信息工程大学理学院,河南郑州450001
【正文语种】中文
【中图分类】O13
【相关文献】
1.快速子空间分解方法及其维数的快速估计 [J], 黄磊;吴顺君;张林让;冯大政
2.基于偏微分方程的快速二维经验模态分解方法及其应用 [J], 李翠芸;曹潇男;姬红兵;邹其兵
3.区域分解方法在快速旋转行星流体动力学并行计算中的应用 [J], 冯天厚
4.一种快速特征分解方法及其在高分辨率谱估计中的应用 [J], 王曙光; 何振亚
5.基于局部峰值约束的快速正交匹配追踪地震数据分解方法 [J], 杜泽源;杨森;陶永慧;蔡杰雄;何兵红
因版权原因，仅展示原文概要，查看原文内容请购买。

快速子空间迭代法_迭代Ritz向量法与迭代Lanczos法的比较_宫玉才

a 收稿日期: 2004-08-23; 修订日期: 2004-12-15 基金项目: 高等学校博士学科点专项科研基金资助项目( 20030001112)
22 8
振动工程学报
第 18 卷
力之比, 中间是非平衡节点力与最大惯性力之比[ 3] 。大量算例表明, 在模态误差的意义之下, 收敛过
( 北京大学力学与工程科学系, 北京 100871)
摘要: 以高效的细胞稀疏直接快速解法为核心步骤, 实现了快速的固有振动广义特征值问题解法, 并在相同的允许模态误差的意义下检验了三种常用的大型矩阵特征模态算法—— 子空间迭代法、迭代 R itz 向量法和迭代 L anczo s 法的计算效率。迭代 Rit z 向量法平均最快, 子空间迭代法最慢, 三种解法效率相差不是太大。与 AN SY S 的子空间迭代和 L anczo s 法相比, 本文的子空间迭代比 A N SY S 的效率高很多, L anczo s 法和 A NSY S 的效率差不多。大量较大规模的例题显示, 本文对特征值算法的改进是十分有效的, 算法的健壮性, 通用性都达到了高水平。
谱变换的线性方程组
( K - LM) x = LDLTx = My
( 2)
的解法, 移轴矩阵 K - LM 的 LDLT 三角分解是计算
量最大的。在以变带宽解法为核心步骤的特征值解法
中, 它常常占到特征值问题计算时间的 70% ～90% 。
本文采用了文[ 1] 提出的一个效率非常高的有限元解法——细胞稀疏直接快速解法( 简称细胞解法) 替换变带宽解法, 极大地提高了三角分解的效率。
差( 5) 代替特征值误差作为收敛判据, 来衡量算法
的效率。