工具变量法地Stata命令及实例

合集下载

stata基本命令

stata基本命令+实例+数据+结果--必看，经典2009-08-25 12:29Stata 常用命令save命令FileSave As例1. 表1.为某一降压药临床试验数据，试从键盘输入Stata，并保存为Stata 格式文件。

STATA数据库的维护排序SORT 变量名1 变量名2 ……变量更名rename 原变量名新变量名STATA数据库的维护删除变量或记录drop x1 x2 /* 删除变量x1和x2drop x1-x5 /* 删除数据库中介于x1和x5间的所有变量(包括x1和x5)drop if x<0 /* 删去x1<0的所有记录drop in 10/12 /* 删去第10~12个记录drop if x==. /* 删去x为缺失值的所有记录drop if x==.|y==. /* 删去x或y之一为缺失值的所有记录drop if x==.&y==. /* 删去x和y同时为缺失值的所有记录drop _all /* 删掉数据库中所有变量和数据STATA的变量赋值用generate产生新变量generate 新变量＝表达式generate bh=_n /* 将数据库的内部编号赋给变量bh。

generate group=int((_n-1)/5)+1 /* 按当前数据库的顺序，依次产生5个1，5个2，5个3……。

直到数据库结束。

generate block=mod(_n,6) /* 按当前数据库的顺序，依次产生1,2,3,4,5,0。

generate y=log(x) if x>0 /* 产生新变量y，其值为所有x>0的对数值log(x)，当x<=0时，用缺失值代替。

egen产生新变量set obs 12egen a=seq() /*产生1到N的自然数egen b=seq(),b(3) /*产生一个序列，每个元素重复＃次egen c=seq(),to(4) /*产生多个序列，每个序列从1到＃egen d=seq(),f(4)t(6) /*产生多个序列，每个序列从#1到＃2encode 字符变量名，gen(新数值变量名)作用：将字符型变量转化为数值变量。

工具变量检验stata代码

工具变量检验stata代码
工具变量检验Stata代码包括两个步骤：1)构建多重回归模型，2)对每个变量使用t检验进行检验。

第一步，构建多重回归模型：
• 输入数据：在Stata中输入要分析的数据，可以是.dta 格式的文件，也可以是excel格式的文件。

• 定义回归模型：用命令“regress”定义回归模型，其中包括被解释变量、自变量(工具变量)以及各种控制变量。

• 检验零假设：使用“test”命令检验零假设，即所有工具变量的系数均为零，并将统计量输出。

第二步，使用t检验进行检验：
• 计算t统计量：使用“coefplot”命令计算每个因变量的t统计量，其中可以包括每个变量的估计值，标准误差等。

• 检验零假设：对每个统计量进行t检验，复习允许的显著性水平，并根据结果进行判断。

• 检查模型：如果t统计量显著，则说明工具变量在影响因变量上具有显著的作用，此时可以检查模型的准确性，确保其他因素的合理性。

最后需要注意的是，当模型中包含多个工具变量时，往往需要对多个变量进行检验，因此检验工具变量所需的时间会略有延长。

工具变量法stata代码

工具变量法一、引言在社会科学研究中，研究目的往往是要了解某个因果关系的真实效应。

然而，由于存在内生性问题，观察到的相关性常常无法准确反映因果关系。

工具变量法作为一种常用的因果推断方法，在解决内生性问题上具有重要的作用。

本文将介绍工具变量法的基本原理、实施步骤以及在Stata软件中的具体操作。

二、工具变量法的基本原理工具变量法是通过引入外生性强的工具变量，来解决内生性问题。

内生性问题是指在观察数据中，因变量和解释变量之间存在系统性的关联，其关系与模型设定的相关性不同。

这种关联使得直接通过观察数据进行因果推断变得困难。

工具变量要求关联强，与内生解释变量相关，但与干扰项不相关。

通过工具变量法，我们可以利用工具变量对内生解释变量进行保证，从而得到更准确的因果效应估计。

三、工具变量法的实施步骤3.1 确定内生性问题在应用工具变量法之前，首先需要确定所研究的因果关系是否存在内生性问题。

内生性问题可以通过多种方式产生，比如遗漏变量、测量误差等。

在确定内生性问题后，我们需要找到与内生解释变量相关但与干扰项不相关的工具变量。

3.2 选择合适的工具变量选择合适的工具变量是工具变量法的关键步骤。

一个好的工具变量应该满足一定的条件，比如与内生解释变量的相关性、与干扰因素的无关性、外生性等。

常见的工具变量包括自然实验、随机分配等。

在选择工具变量时，需要结合具体研究对象与背景，寻找符合以上条件的工具变量。

3.3 估计工具变量法模型估计工具变量法模型的关键就是进行两步最小二乘法（Two-stage least squares, 2SLS）估计。

第一步，使用工具变量估计内生解释变量；第二步，将第一步估计得到的内生变量代入原始模型进行估计。

在Stata中，可以使用ivregress命令来估计工具变量法模型。

3.4 检验与解释结果在估计完成后，需要对结果进行检验与解释。

常见的检验方法包括工具变量的合理性检验、过度识别检验等。

在解释结果时，需要注意控制其他可能的干扰因素，确保结果的可信度与可靠性。

stata工具变量法指标

stata工具变量法指标使用Stata工具变量法进行研究引言：在经济学研究中，为了解决内生性问题，研究者常常会使用工具变量法。

Stata是一种流行的统计软件，提供了强大的工具变量法分析功能。

本文将介绍Stata中工具变量法的基本概念、使用方法以及注意事项。

一、什么是工具变量法工具变量法是一种用于解决内生性问题的统计方法。

在经济学研究中，内生性是指自变量与误差项存在相关性，从而导致OLS估计结果的偏误。

工具变量法通过引入一个或多个工具变量来解决内生性问题。

工具变量是与自变量相关但与误差项不相关的变量，可以帮助消除内生性问题。

二、Stata中的工具变量法Stata提供了多种工具变量法的实现方法，包括两阶段最小二乘法（2SLS）、差分工具变量法（DID）和识别方程方法（IVREG）等。

下面以2SLS方法为例，介绍在Stata中如何使用工具变量法进行分析。

1. 数据准备需要准备包含自变量、因变量和工具变量的数据集。

可以使用Stata中的命令导入数据集，或者直接使用已有的数据集。

2. 运行回归模型使用Stata中的命令“regress”来运行普通最小二乘回归模型，得到OLS估计结果。

这一步主要是为了对比工具变量法和OLS方法的差异。

3. 识别方程根据经济理论和实际情况，选择适当的工具变量。

在Stata中，可以使用命令“ivregress”来运行识别方程，得到工具变量的估计结果。

4. 运行工具变量法根据识别方程的结果，使用Stata中的命令“ivregress 2sls”来运行工具变量法。

在命令中指定工具变量和自变量，得到工具变量法的估计结果。

5. 检验工具变量法的有效性使用Stata中的命令“ivregress 2sls”中的选项进行工具变量法的有效性检验，如Hausman检验和Sargan检验。

这些检验可以帮助判断工具变量法是否可靠。

三、使用工具变量法的注意事项在使用Stata进行工具变量法分析时，需要注意以下几点：1. 工具变量的选择：工具变量应该与自变量相关，但与误差项不相关。

stata命令大全(全)

********* 面板数据计量分析与软件实现 *********说明：以下do文件相当一部分内容来自于中山大学连玉君STATA教程，感谢他的贡献。

本人做了一定的修改与筛选。

*----------面板数据模型* 1.静态面板模型：FE 和RE* 2.模型选择：FE vs POLS, RE vs POLS, FE vs RE （pols混合最小二乘估计） * 3.异方差、序列相关和截面相关检验* 4.动态面板模型（DID-GMM,SYS-GMM）* 5.面板随机前沿模型* 6.面板协整分析（FMOLS,DOLS）*** 说明：1-5均用STATA软件实现， 6用GAUSS软件实现。

* 生产效率分析（尤其指TFP）：数据包络分析（DEA）与随机前沿分析（SFA）*** 说明：DEA由DEAP2.1软件实现，SFA由Frontier4.1实现，尤其后者，侧重于比较C-D与Translog生产函数，一步法与两步法的区别。

常应用于地区经济差异、FDI 溢出效应（Spillovers Effect）、工业行业效率状况等。

* 空间计量分析：SLM模型与SEM模型*说明：STATA与Matlab结合使用。

常应用于空间溢出效应（R&D）、财政分权、地方政府公共行为等。

* ---------------------------------* --------一、常用的数据处理与作图-----------* ---------------------------------* 指定面板格式xtset id year （id为截面名称，year为时间名称）xtdes /*数据特征*/xtsum logy h /*数据统计特征*/sum logy h /*数据统计特征*/*添加标签或更改变量名label var h "人力资本"rename h hum*排序sort id year /*是以STATA面板数据格式出现*/sort year id /*是以DEA格式出现*/*删除个别年份或省份drop if year<1992drop if id==2 /*注意用==*/*如何得到连续year或id编号（当完成上述操作时，year或id就不连续，为形成panel 格式，需要用egen命令）egen year_new=group(year)xtset id year_new**保留变量或保留观测值keep inv /*删除变量*/**或keep if year==2000**排序sort id year /*是以STATA面板数据格式出现sort year id /*是以DEA格式出现**长数据和宽数据的转换*长>>>宽数据reshape wide logy,i(id) j(year)*宽>>>长数据reshape logy,i(id) j(year)**追加数据（用于面板数据和时间序列）xtset id year*或者xtdestsappend,add(5) /表示在每个省份再追加5年，用于面板数据/tsset*或者tsdes.tsappend,add(8) /表示追加8年，用于时间序列/*方差分解，比如三个变量Y,X,Z都是面板格式的数据，且满足Y=X+Z，求方差var(Y),协方差Cov(X,Y)和Cov（Z,Y）bysort year:corr Y X Z,cov**生产虚拟变量*生成年份虚拟变量tab year,gen(yr)*生成省份虚拟变量tab id,gen(dum)**生成滞后项和差分项xtset id yeargen ylag=l.y /*产生一阶滞后项)，同样可产生二阶滞后项*/gen ylag2=L2.ygen dy=D.y /*产生差分项*/*求出各省2000年以前的open inv的平均增长率collapse (mean) open inv if year<2000,by(id)变量排序，当变量太多，按规律排列。

stata中工具变量法

stata中工具变量法工具变量法（Instrumental Variable Method）是应用于计量经济学中的一种估计方法，其主要用途是解决回归分析中的内生性（endogeneity）问题。

内生性指的是自变量与误差项之间存在相关性，这种相关性会导致回归分析结果产生偏误和无效性。

在实践中，我们常常会遇到自变量与误差项之间存在内生性的情况。

一个常见的例子是研究教育对收入的影响，如果使用教育水平作为自变量，可能会出现教育水平与遗传因素等不可观测变量的内生性问题。

为了解决这个问题，可以使用工具变量法。

在Stata中，使用工具变量法进行估计有多种方法。

下面我们将介绍其中两种常见的方法。

第一种方法是使用Stata内置的ivregress命令。

该命令提供了一种简单的工具变量法估计的方式。

下面是一个使用ivregress命令进行工具变量法估计的示例：ivregress 2sls y (x = z)其中，y代表因变量，x代表内生自变量，z代表工具变量。

该命令会同时估计两个方程，第一个方程是自变量对因变量的影响，第二个方程是工具变量对内生自变量的影响。

通过估计这两个方程，可以得到调整后的内生自变量的估计值，从而解决内生性问题。

第二种方法是使用Stata的reg命令结合自定义工具变量进行估计。

这种方法相对于使用ivregress命令更加灵活，适用于一些特殊情况。

下面是一个使用reg命令进行工具变量法估计的示例：reg y (x = z)在这个示例中，y代表因变量，x代表内生自变量，z代表工具变量。

通过在reg命令中指定x和z之间的关系，可以实现工具变量法的估计。

需要注意的是，使用reg命令进行工具变量法估计需要确保工具变量满足一些假设条件，比如工具变量与误差项之间不应存在相关性。

总之，Stata中提供了多种方法进行工具变量法的估计。

根据实际问题的需求和假设条件的满足程度，可以选择合适的方法进行估计。

通过使用工具变量法可以有效解决回归分析中的内生性问题，提高估计结果的准确性和有效性。

stata工具变量法案例

stata工具变量法案例Stata工具变量法是一种经济学研究中常用的方法，用于解决内生性问题。

它通过利用某些外生性强的变量作为工具变量，来估计内生变量与因果变量之间的关系。

下面是10个以Stata工具变量法案例为题的内容介绍。

1. 工具变量法的基本原理：介绍工具变量法的基本思想和理论基础，解释为什么需要使用工具变量来解决内生性问题。

2. 数据准备：讲解如何在Stata中导入和准备数据，包括变量的选择和处理，确保数据的质量和可用性。

3. 内生性问题的存在：说明内生性问题在经济学研究中的重要性和普遍存在性，以及内生性问题对实证结果的影响。

4. 工具变量的选择：介绍如何选择合适的工具变量，包括外生性、相关性和可用性等因素的考虑，以及常用的工具变量选择方法。

5. 工具变量法的估计：详细介绍Stata中的工具变量法估计命令，包括IVREG、IVREG2等命令的使用方法和参数解释。

6. 结果解读：解释工具变量法估计结果的含义和解读方法，包括工具变量估计量的一致性和有效性等统计性质。

7. 内生性检验：介绍如何在Stata中进行内生性检验，包括第一阶段回归、Hausman检验等常用的内生性检验方法。

8. IV回归的问题和限制：讨论工具变量法的局限性和可能存在的问题，如工具变量的有效性和外推性等问题。

9. 实证案例分析：以某个具体的经济学研究问题为例，使用Stata 进行实证分析，展示工具变量法的应用过程和结果。

10. 结论和讨论：总结工具变量法的优点和局限性，讨论工具变量法在经济学研究中的应用前景和发展方向。

以上是以Stata工具变量法案例为题的内容介绍，通过对工具变量法的原理、数据准备、工具变量选择、估计方法、结果解读、内生性检验、案例分析等方面的介绍，可以帮助读者更好地理解和应用Stata工具变量法。

stata 截面数据工具变量法

Stata 是一个用于统计数据分析的软件，主要用于经济学、社会科学和生物统计等领域。

在使用 Stata 进行数据分析时，研究人员常常会遇到截面数据和工具变量法的问题。

本文将介绍 Stata 中如何使用截面数据和工具变量法进行分析，并为读者提供使用 Stata 进行数据分析的一般步骤。

1. 什么是截面数据截面数据是指在同一时间或时间点上收集的数据，通常用来描述不同实体（例如人、家庭、公司等）在某一特定时点上的属性和特征。

在经济学中，研究人员经常使用截面数据来分析个体或单位之间的差异，例如收入水平、消费行为、就业情况等。

Stata 软件提供了一系列工具和命令来处理和分析截面数据，包括数据清洗、描述性统计、回归分析等。

2. Stata 中的截面数据分析使用 Stata 进行截面数据分析的一般步骤包括：（1）数据导入：将收集到的截面数据导入到 Stata 软件中。

可以使用Stata 的数据编辑工具或者直接在命令面板中输入相应的命令来进行数据导入。

（2）数据清洗：接下来，对导入的数据进行清洗和处理，包括缺失值处理、异常值检测和处理、变量转换等。

Stata 提供了丰富的数据处理工具和命令，可以帮助研究人员对数据进行清洗和预处理。

（3）描述性统计分析：使用 Stata 中的描述性统计命令对截面数据进行初步分析，包括变量的分布情况、相关性分析等。

这些分析可以帮助研究人员对数据有一个直观的了解，为进一步的分析和建模打下基础。

（4）回归分析：对截面数据进行回归分析是经济学和社会科学研究中常见的分析方法。

Stata 提供了丰富的回归分析命令和工具，可以帮助研究人员进行多元线性回归、逻辑回归、面板数据分析等。

在回归分析中，研究人员可以控制其他影响因素，从而更准确地分析自变量对因变量的影响。

3. 什么是工具变量法工具变量法是一种用于解决内生性（endogeneity）问题的统计方法。

在实际研究中，由于某些原因，自变量和因变量之间存在内生性，并且通常会导致普通最小二乘法（OLS）估计结果的偏误。

stata中工具变量法

stata中工具变量法在Stata 中，工具变量法（Instrumental Variables, IV）是一种处理内生性（endogeneity）问题的方法，通常用于解决因果关系中的回归模型。

内生性问题指的是模型中的某些变量可能与误差项相关，从而导致OLS估计结果的偏误。

工具变量法通过引入一个或多个外生性足够相关但与误差项不相关的变量（称为工具变量）来解决这个问题。

以下是在Stata 中使用工具变量法的一般步骤：1. 确定内生性问题：确定模型中是否存在内生性问题，即某些解释变量与误差项相关。

2. 选择工具变量：选择足够相关但与误差项不相关的工具变量。

这些变量通常被认为是外生的，与误差项独立。

3. 估计工具变量模型：使用Stata 中的`ivregress` 命令估计工具变量模型。

语法如下：```stataivregress 2sls dependent_variable (endogenous_variable = instruments) other_exogenous_variables```其中，`dependent_variable` 是因变量，`endogenous_variable` 是内生变量，`instruments` 是工具变量，`other_exogenous_variables` 是其他外生变量。

例如：```stataivregress 2sls y (x = z) controls```4. 检验工具变量的有效性：使用`ivregress` 命令的`ivendog` 选项来检验工具变量的有效性。

```stataivregress 2sls y (x = z) controls, ivendog(x)```此命令将进行工具变量的内生性检验。

5. 诊断：进行模型诊断，检查模型的合理性和有效性。

2019工具变量法的Stata命令及实例

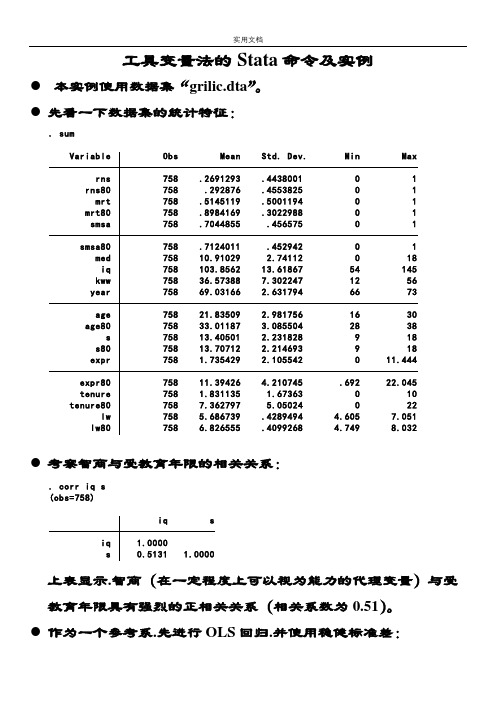
●本实例使用数据集“grilic.dta”。

●先看一下数据集的统计特征：●考察智商与受教育年限的相关关系：上表显示，智商（在一定程度上可以视为能力的代理变量）与受教育年限具有强烈的正相关关系（相关系数为0.51）。

●作为一个参考系，先进行OLS回归，并使用稳健标准差：其中expr, tenure, rns, smsa均为控制变量，而我们主要感兴趣的是变量受教育年限（s）。

回归的结果显示，教育投资的年回报率为10.26%，这个似乎太高了。

可能的原因是，由于遗漏变量“能力”与受教育正相关，故“能力”对工资的贡献也被纳入教育的贡献，因此高估了教育的回报率。

●引入智商iq作为能力的代理变量，再进行OLS回归：虽然教育的投资回报率有所下降，但是依然很高。

●由于用iq作为能力的代理变量有测量误差，故iq是内生变量，考虑使用变量（med（母亲的受教育年限）、kww（在“knowledge of the World of Work”中的成绩）、mrt（婚姻虚拟变量，已婚=1）age（年龄））作为iq的工具变量，进行2SLS回归，并使用稳健的标准差：在此2SLS回归中，教育回报率反而上升到13.73%，而iq对工资的贡献居然为负值。

使用工具变量的前提是工具变量的有效性。

为此，进行过度识别检验，考察是否所有的工具变量均外生，即与扰动项不相关：结果强烈拒绝所有工具变量均外生的原假设。

●考虑仅使用变量（med, kww）作为iq的工具变量，再次进行2SLS回归，同时显示第一阶段的回归结果：上表显示，教育的回报率为6.08%，较为合理，再次进行过度识别检验：接受原假设，认为（med，kww）外生，与扰动项不相关。

●进一步考察有效工具变量的第二个条件，即工具变量与内生变量的相关性。

从第一阶段的回归结果可以看出，工具变量对内生变量具有较好的解释力。

更正式的检验如下：从以上结果可以看出，虽然Shea’s partial R^2不到0.04，但是F统计量为13.40>10。

工具变量法（IV）的Stata操作

⼯具变量法（IV）的Stata操作Stata操作⼯具变量法的难点在于找到⼀个合适的⼯具变量并说明其合理性，Stata操作其实相当简单，只需⼀⾏命令就可以搞定，我们通常使⽤的⼯具变量法的Stata命令主要就是ivregress命令和ivreg2命令。

ivregress命令ivregress命令是Stata⾃带的命令，⽀持两阶段最⼩⼆乘（2SLS）、⼴义矩估计（GMM）和有限信息最⼤似然估计（LIML）三种⼯具变量估计⽅法，我们最常使⽤的是两阶段最⼩⼆乘法（2SLS），因为2SLS最能体现⼯具变量的实质，并且在球形扰动项的情况下，2SLS是最有效率的⼯具变量法。

顾名思义，两阶段最⼩⼆乘法（2SLS）需要做两个回归：（1）第⼀阶段回归：⽤内⽣解释变量对⼯具变量和控制变量回归，得到拟合值。

（2）第⼆阶段回归：⽤被解释变量对第⼀阶段回归的拟合值和控制变量进⾏回归。

如果要使⽤2SLS⽅法，我们只需在ivregress后⾯加上2sls即可，然后将内⽣解释变量lnjinshipop和⼯具变量bprvdist放在⼀个⼩括号中，⽤=号连接。

选项first表⽰报告第⼀阶段回归结果，选项cluster()表⽰使⽤聚类稳健的标准误。

ivregress 2sls lneduyear (lnjinshipop=bprvdist) lnnightlight lncoastdist tri suitability lnpopdensity urbanrates i.provid , first cluster(provid)第⼀阶段回归结果First-stage regressions-----------------------Number of obs = 274No. of clusters = 28F( 7, 239) = 85.27Prob > F = 0.0000R-squared = 0.6487Adj R-squared = 0.5988Root MSE = 0.4442------------------------------------------------------------------------------| Robustlnjinshipop | Coef. Std. Err. t P>|t| [95% Conf. Interval]-------------+----------------------------------------------------------------lnnightlight | .183385 .0682506 2.690.008 .0489354 .3178346lncoastdist | .0350333 .0771580.450.650 -.1169634 .1870299tri | 1.06676 .5637082 1.890.060 -.0437105 2.177231suitability | -.0769726 .0549697 -1.400.163 -.1852596 .0313144lnpopdensity | .196144 .0843727 2.320.021 .0299349 .3623532urbanrates | 3.352916 1.687109 1.990.048 .029414 6.676419|provid |12 | .2051006 .0551604 3.720.000 .096438 .313763213 | -1.890425 .0951146 -19.880.000 -2.077795 -1.703055......64 | -1.301895 .1581021 -8.230.000 -1.613346 -.9904433|bprvdist | -.0846917 .0107859 -7.850.000 -.1059393 -.0634441_cons | 2.126233 .9791046 2.170.031 .1974567 4.05501------------------------------------------------------------------------------从表中可以看出，⼯具变量bprvdist的系数为-0.085，标准误为0.011，在1%的⽔平上显著。

高维回归stata工具变量法命令

高维回归stata工具变量法命令
在高维回归分析中，Stata工具变量法的命令是`ivregress`和`ivreg2`。

其中，`ivregress`是Stata自带的命令，支持两阶段最小二乘（2SLS）、广义矩估计（GMM）和有限信息最大似然估计（LIML）三种工具变量估计方法。

而`ivreg2`是一个更新的命令，支持更多的工具变量估计方法。

使用`ivregress`命令时，需要提供因变量、内生解释变量、工具变量和控制变量。

命令会自动进行两阶段最小二乘回归，第一阶段回归使用内生解释变量对工具变量和控制变量进行回归，得到拟合值，第二阶段回归使用被解释变量对第一阶段回归的拟合值和控制变量进行回归。

如果需要控制固定效应或进行聚类分析，可以使用选择项`absorb`和
`cluster`。

选择项`first`可以报告第一阶段回归的结果。

选择项`endog`可以检验内生解释变量是否为内生变量，即进行内生性检验。

请注意，使用工具变量法需要找到一个合适的工具变量并说明其合理性，这是工具变量法的难点。

另外，由于模型设定错误或数据问题，工具变量法可能无法完全消除内生性问题，因此在使用时需要谨慎。

stata的u型关系工具变量法

stata的u型关系工具变量法Stata的u型关系工具变量法引言：在经济学和社会科学研究中，我们常常面临着因果关系的推断问题。

然而，由于自然实验的不可行性，我们无法直接观察到所有可能的结果。

为了解决这个问题，研究者们常常利用工具变量法来处理内生性问题。

本文将介绍Stata软件中的一种工具变量法——u型关系工具变量法，并讨论其应用和优势。

1. 工具变量法简介工具变量法是一种用来解决内生性问题的统计方法。

在经济学研究中，内生性指的是某个自变量与误差项之间存在相关关系，从而导致回归结果的偏误。

工具变量法的基本思想是利用一个或多个与内生变量高度相关但与误差项无关的变量作为“工具变量”，通过两阶段最小二乘法来估计内生变量的系数。

2. u型关系工具变量法在一些研究中，我们可能遇到自变量与因变量之间存在非线性关系的情况。

此时，传统的线性工具变量法可能无法有效地估计因果效应。

针对这种情况，Stata提供了一种u型关系工具变量法。

u型关系工具变量法的核心思想是引入一个非线性的工具变量来处理u型关系。

具体来说，该方法通过将自变量的平方项作为工具变量，来捕捉自变量与因变量之间的非线性关系。

这种方法可以有效地解决因果效应的非线性估计问题。

3. u型关系工具变量法的应用u型关系工具变量法在实证研究中有着广泛的应用。

以教育经济学为例，研究者常常关注教育水平对收入的影响，并希望探讨该关系是否存在非线性效应。

利用u型关系工具变量法，研究者可以更准确地估计教育水平对收入的因果效应，并得出更精确的结论。

u型关系工具变量法还可以应用于医学研究、环境经济学等领域。

在医学研究中，研究者可能对某种治疗方法对患者健康状况的影响感兴趣。

通过引入自变量的平方项作为工具变量，研究者可以更好地探究治疗方法对健康状况的非线性效应。

4. u型关系工具变量法的优势相比于传统的线性工具变量法，u型关系工具变量法具有以下几个优势：u型关系工具变量法可以更准确地估计因果效应。

STATA常用命令总结(34个含使用示例)

STATA常用命令总结（34个含使用示例）1. sum：计算变量的简要统计信息，如均值、标准差等。

示例：sum variable2. tabulate：生成变量的频数表。

示例：tabulate variable3. describe：显示数据集的基本信息，如变量名和数据类型。

示例：describe dataset4. drop：删除数据集中的变量。

示例：drop variable5. keep：保留数据集中的变量，删除其他变量。

示例：keep variable6. rename：重命名变量。

示例：rename variable newname7. gen：根据已有变量生成新的变量。

示例：gen newvar = expression8. egen：根据已有变量生成新的变量，可以使用更复杂的函数和运算符。

示例：egen newvar = function(variable)9. recode：对变量的取值进行重新编码。

示例：recode variable (oldvalues= newvalues) 10. dropif：根据条件删除观测。

示例：dropif condition11. keepif：根据条件保留观测。

示例：keepif condition12. sort：对数据集按指定变量进行排序。

示例：sort variable13. merge：将两个数据集按照共享变量合并。

示例：merge 1:1 variable using dataset214. reshape：将数据从宽格式转换为长格式或反之。

示例：reshape long var, i(id) j(year)15. regress：进行线性回归分析。

示例：regress dependent_var independent_vars 16. logistic：进行逻辑回归分析。

示例：logistic dependent_var independent_vars 17. probit：进行Probit回归分析。

二阶段工具变量法stata面板数据

二阶段工具变量法stata面板数据二阶段工具变量法是一种常用的计量经济学方法，它可以帮助我们解决内生性问题。

在stata面板数据中，我们可以使用二阶段工具变量法来估计面板数据模型。

一、什么是二阶段工具变量法？二阶段工具变量法是一种解决内生性问题的方法，它需要使用一个或多个外生变量作为工具变量来代替内生变量，从而避免内生性对估计结果的影响。

通常情况下，我们需要通过两个步骤来实现这个目标：第一步是利用工具变量估计内生变量；第二步是将估计得到的内生变量代入面板数据模型中进行估计。

二、如何进行二阶段工具变量法？在stata面板数据中，我们可以使用ivregress命令进行二阶段工具变量法的估计。

该命令的语法格式如下：ivregress 2sls depvar (endogvar = exogvar1 exogvar2 …), instrument(iv1 iv2 …) cluster(clusterid)其中，depvar表示因变量，endogvar表示内生变量，exogvar1 exogvar2 …表示控制变量（即除了内生变量和外生工具变量以外的所有自变量），iv1 i v2 …表示外生工具变量，clusterid表示聚类标识符。

三、如何解读二阶段工具变量法的结果？在stata面板数据中，二阶段工具变量法的结果通常包括以下几个方面：1.第一阶段回归结果：通过ivregress命令估计得到的第一阶段回归结果可以帮助我们判断外生变量是否有效。

如果外生变量与内生变量存在显著相关关系，则说明外生变量是有效的工具变量。

2.第二阶段回归结果：通过ivregress命令估计得到的第二阶段回归结果可以帮助我们判断内生变量对因变量的影响。

如果内生变量系数显著且符号与理论预期一致，则说明内生性问题得到了解决。

3.聚类标准误：在面板数据分析中，由于观测值之间可能存在相关性，因此需要考虑聚类标准误以避免低估标准误。

通过cluster(clusterid)语句可以实现聚类标准误的计算和输出。

工具变量两阶段最小二乘法stata

工具变量两阶段最小二乘法stata工具变量（Instrumental Variables）是一种经济学研究中常用的一种分析工具，它可以解决内生性问题，有效提升研究结果的准确性和可靠性。

然而在实践中，由于实际数据的复杂性和噪声干扰的影响，如何正确地应用工具变量的方法成为了关键问题。

本文将介绍工具变量两阶段最小二乘法，并结合stata软件进行具体操作。

1. 工具变量的原理概述工具变量是一种利用外生性变量替代内生性变量的方法。

在回归分析中，如果变量间存在内生性，即自变量与误差项存在相关性，那么使用传统的最小二乘法得到的估计结果将是偏误的。

这时，可以引入一个外生性变量作为工具变量，通过工具变量的作用将内生性变量与误差项的相关性消除，从而得到准确的估计结果。

2. 工具变量两阶段最小二乘法步骤（1）首先，需要选择一个或多个外生性变量作为工具变量。

这些变量需要满足两个条件：一是与内生变量相关，二是与因变量不相关。

（2）将工具变量与内生变量拟合一个回归方程并得到拟合值（第一阶段回归），将拟合值代入原方程得到新的估计方程。

（3）在新的估计方程中，工具变量被作为自变量进行回归分析，得到最小二乘估计量。

（4）通过判断估计值的显著水平以及其他统计性质，可以检验结果的准确性。

3. STATA软件操作步骤以研究收入对教育的影响为例，演示工具变量两阶段最小二乘法在STATA软件中的操作步骤。

（1）读入数据将所需数据导入STATA软件，例如使用以下命令：use education, clear（2）第一阶段回归运行以下命令进行第一阶段回归，得到工具变量的拟合值。

ivreg income (years = exog)其中“exog”是外生性变量，”income”是因变量，“years”是内生变量。

拟合值可以通过以下命令得到：predict yfit其中“yfit”是自定义的新变量名。

（3）第二阶段回归运行以下命令进行第二阶段回归，得到准确的估计值。

Stata面板数据回归分析中的工具变量法如何选择合适的工具变量

Stata面板数据回归分析中的工具变量法如何选择合适的工具变量工具变量法（Instrumental Variable，简称IV）在面板数据回归分析中被广泛应用。

它通过引入外生变量作为工具变量来解决内生性问题，从而使得回归结果更具可靠性和稳健性。

在Stata软件中，选择合适的工具变量对于IV估计的准确性起着至关重要的作用。

本文将介绍在Stata面板数据回归分析中如何选择合适的工具变量。

一、IV方法简介在介绍IV方法如何选择合适的工具变量之前，先简要介绍一下IV方法的原理和步骤。

IV方法是通过引入工具变量来解决内生性问题，从而得到一致性的估计。

其基本思想是找到一个与内生变量相关但与误差项不相关的变量作为工具变量，从而通过工具变量的外生性来消除内生性引起的估计偏误。

IV方法的具体步骤如下：1. 识别工具变量：首先需要找到一个与内生变量相关但与误差项不相关的变量作为工具变量。

工具变量的选择要满足两个条件：与内生变量有相关性，与误差项无相关性。

2. 检验工具变量：选择好的工具变量需要经过检验，以确保其满足与内生变量相关但与误差项不相关的要求。

常用的检验方法有Hausman检验和Sargan检验。

3. 使用工具变量进行回归：将选定的工具变量引入回归方程中，通过工具变量的外生性来消除内生性引起的估计偏误。

二、选择合适的工具变量在选择合适的工具变量时，需要考虑以下几个因素：1. 相关性：工具变量应该与内生变量有一定的相关性，才能正确地估计内生变量对因变量的影响。

相关性可以通过计算相关系数来衡量，一般要求相关系数大于0.1。

2. 排除性：工具变量与误差项无相关性，即工具变量不能受到其他未观测到的因素的影响。

排除性通常通过进行统计检验来验证，常用的检验方法有Hausman检验和Sargan检验。

3. 弱工具变量：如果工具变量过弱，即相关系数过小，会导致估计结果的方差增大，同时降低估计的准确性和稳健性。

一般来说，工具变量的F统计量应大于10，同时第一阶段回归的R-squared要大于0.1。

工具变量法地Stata命令和实例

工具变量法的Stata命令及实例●本实例使用数据集“grilic.dta”。

●先看一下数据集的统计特征：. sumVariable Obs Mean Std. Dev. Min Maxrns 758 .2691293 .4438001 0 1rns80 758 .292876 .4553825 0 1mrt 758 .5145119 .5001194 0 1mrt80 758 .8984169 .3022988 0 1smsa 758 .7044855 .456575 0 1smsa80 758 .7124011 .452942 0 1med 758 10.91029 2.74112 0 18iq 758 103.8562 13.61867 54 145kww 758 36.57388 7.302247 12 56year 758 69.03166 2.631794 66 73age 758 21.83509 2.981756 16 30age80 758 33.01187 3.085504 28 38s 758 13.40501 2.231828 9 18s80 758 13.70712 2.214693 9 18expr 758 1.735429 2.105542 0 11.444expr80 758 11.39426 4.210745 .692 22.045tenure 758 1.831135 1.67363 0 10tenure80 758 7.362797 5.05024 0 22lw 758 5.686739 .4289494 4.605 7.051lw80 758 6.826555 .4099268 4.749 8.032●考察智商与受教育年限的相关关系：. corr iq s(obs=758)iq siq 1.0000s 0.5131 1.0000上表显示.智商（在一定程度上可以视为能力的代理变量）与受教育年限具有强烈的正相关关系（相关系数为0.51）。

二阶段工具变量法stata面板数据

二阶段工具变量法stata面板数据以二阶段工具变量法stata面板数据为主题，本文将从什么是二阶段工具变量法、如何使用stata面板数据进行分析等角度进行详细介绍。

一、什么是二阶段工具变量法？二阶段工具变量法是一种经济学中常用的方法，用于解决自变量和因变量之间存在内生性的问题。

所谓内生性，是指自变量和因变量之间存在相互影响的关系，不能准确地测量它们之间的关系。

为了解决这个问题，研究者需要引入工具变量，将内生性问题转化为外生性问题。

二阶段工具变量法的基本思路是先通过工具变量来估计内生性自变量的值，然后再将这些估计值代入因变量模型中进行分析。

具体地说，二阶段工具变量法包含两个步骤：第一步是使用工具变量估计内生性自变量的值；第二步是将估计值代入因变量模型中进行分析。

二、如何使用stata面板数据进行分析？stata是一款常用的统计软件，可以用于处理各种数据分析问题。

其中，面板数据分析是stata的一个重要功能。

面板数据是指在时间上和横截面上都有变化的数据，它可以提供更加准确和全面的信息，对于经济学和社会科学研究具有重要意义。

在stata中，进行面板数据分析需要先加载数据文件，然后使用面板数据分析命令进行分析。

具体来说，可以使用xtset命令来定义面板数据的时间和个体标识符，使用xtreg命令来进行面板数据回归分析。

在进行二阶段工具变量法分析时，还需要引入ivreg命令来进行工具变量回归分析。

使用stata进行面板数据分析，可以有效地解决内生性问题，提高数据分析的准确性和可靠性。

三、实例分析为了更好地理解二阶段工具变量法和stata面板数据分析的应用，我们以一个实例进行分析。

假设我们要研究教育对收入的影响，但是由于教育水平与父母收入之间存在内生性问题，无法准确测量教育对收入的影响。

为了解决这个问题，我们可以引入工具变量，例如教育政策的实施时间，作为教育水平的外生性影响因素。

我们需要收集相应的数据，包括个体的收入、教育水平、父母收入等变量信息。

stata工具变量法指标

stata工具变量法指标工具变量法是一种统计方法，用于解决回归模型中存在内生性问题的情况。

内生性是指回归模型中解释变量与误差项之间存在相关性，这会导致估计结果的偏误和不一致性。

为了解决这个问题，工具变量法引入了一个或多个外生性强的变量作为工具变量，用来代替内生解释变量，从而得到一致性的估计结果。

在实践中，我们常用的工具变量有两种类型：显著因子型和随机变动型。

显著因子型的工具变量是指与内生解释变量有相关性，但与误差项无相关性的变量。

例如，假设我们研究教育对收入的影响，如果教育水平存在内生性，我们可以使用家庭背景来作为工具变量。

家庭背景可能与教育有相关性，但与收入的误差项无相关性。

通过使用家庭背景作为工具变量，我们就可以得到一致性的教育对收入的估计结果。

随机变动型的工具变量是指与内生解释变量无相关性，但与误差项有相关性的变量。

例如，假设我们研究医疗保险对健康状态的影响，如果医疗保险存在内生性，我们可以使用个人年龄作为工具变量。

个人年龄可能与医疗保险无关，但与健康状态的误差项有相关性。

通过使用个人年龄作为工具变量，我们就可以得到一致性的医疗保险对健康状态的估计结果。

为了使用工具变量法，我们可以通过两步最小二乘法来进行估计。

首先，我们使用工具变量来估计内生解释变量的预测值，然后将这个预测值作为外生解释变量，在回归模型中进行第二步估计。

这样得到的估计结果就是一致性的。

在Stata中，我们可以使用ivregress命令来估计工具变量回归模型。

该命令需要指定内生解释变量、外生解释变量和工具变量，并可以通过选项来进行一些调整。

例如，我们可以使用下面的语法来进行工具变量回归：ivregress 2sls内生解释变量(外生解释变量=工具变量)其中，2sls表示使用两步最小二乘法进行估计。

除了ivregress命令，Stata中还提供了其他一些用于工具变量法的命令和函数，如ivreg和ivendog。

这些命令和函数可以用于进行一些进一步的分析和检验，如工具变量的有效性检验、工具变量的选择和机理检验等。