2014-2015上学期期末 9 年级试题

合集下载

2014~2015学年度九年级数学上册期末考试

2014~2015学年度九年级数学上册期末考试一、选择题（每小题3分，共45分）１、若已知m 是方程 012=--x x 的一个根，则代数式m m -2的值等于（）Ａ、－１Ｂ、０Ｃ、１Ｄ、２２、下列方程中，是关于x 的一元二次方程的是（）Ａ、)1(2)1(2+=+x x Ｂ、05112=-+xx Ｃ、0)1(2=++-c bx x a Ｄ、1222-=+x x x３、若关于x 的方程0)1(222=+-+k x k x 有实数根，则k 的取值范围是（）21<k A 、 21≤k B 、 21>k Ｃ、 21≥k Ｄ、４、方程0252=+-x x 的两个实数根为1x 和2x ，则21x x +－21x x 的值是（）7-、A 3-、B 7Ｃ、 3Ｄ、５、若关于x 的方程的两个根为11=x ，22=x ，则这个方程是（）0232=-+x x A 、 0232=--x x B 、0322=+-x x Ｃ、 0322=++x x Ｄ、６、用换元法解方程716)1(222=+++x x x x 时，如果设xx y 12+=，那么将原方程化为关于y 的一元二次方程的一般形式是（）06722=+-y y A 、 06722=++y y B 、0672=+-y y Ｃ、 0672=++y y Ｄ、７、若一元二次方程022=--m x x 无实数根，则一次函数1)1(-++=m x m y 图像不经过（）Ａ、第一像限Ｂ、第二像限Ｃ、第三像限Ｄ、第四像限８、某超市一月份的营业额是１００万元，第一季度的营业额共８００万元，如果平均每月的增涨率为x ，那么所列的方程应为（） 800)1(1002=+x A 、 8002100100=⨯+x B 、8003100100=⨯+x Ｃ、 []800)1()1(11002=++++x x Ｄ、９、二次函数322+-=x x y 化为k h x y +-=2)(的形式，的结果是（）4)1(2++=x y A 、 4)1(2+-=x y B 、2)1(2++=x y C 、 2)1(2+-=x y D 、１０、下列四个函数中，y 随x 增大而增大的是（）１１、如图２４－２所示， o 是△ABC 的外接圆，已知∠B=60º,则∠CAO=（）Ａ、１５º Ｂ、３０º Ｃ、４５º Ｄ、６０º １２、如图２４－３所示，⊙o 的外切梯形ABCD 中，若AD ∥BC,则∠DOC=（）Ａ、４５º Ｂ、６０º Ｃ、７０º Ｄ、９０º１３、函数b ax y +=与函数c bx ax y ++=2，在同一平面坐标系里面的图像是（）１４、如图２４－４所示，Ｏ是△ABC 的内心，过点Ｏ作EF ∥AB,与AC,BC 交于E,F,则（）Ａ、EF>AE+BF Ｂ、EF<AE+BF Ｃ、EF=AE+BF Ｄ、EF ≤AE+BF１５、如图２４－５所示，在⊙o 中有拆线ＯＡＢＣ，其中ＯＡ=８,ＡＢ=１２, ∠Ａ=∠Ｂ=60º,则弦ＢＣ的长为（）Ａ、１９Ｂ、１６Ｃ、１８Ｄ、２０二、填空题（每空4分，共28分）１６、方程01)1()1(22=-++-x m x m ，当m 满足时，方程为关于x 的一元二次方程，当m 满足时，方程为一元一次方程。

2014-2015学年九年级上数学期末试卷及答案解析

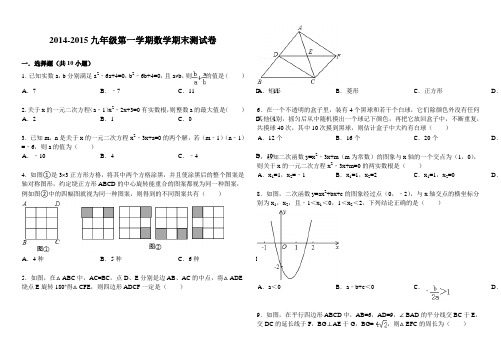
2014-2015九年级第一学期数学期末测试卷一．选择题（共10小题）1．已知实数a ，b 分别满足a 2﹣6a+4=0，b 2﹣6b+4=0，且a ≠b ，则的值是（）23．已知m ，n 是关于x 的一元二次方程x 2﹣3x+a=0的两个解，若（m ﹣1）（n ﹣1）4．如图①是3×3正方形方格，将其中两个方格涂黑，并且使涂黑后的整个图案是轴对称图形，约定绕正方形ABCD 的中心旋转能重合的图案都视为同一种图案，例如图②中的四幅图就视为同一种图案，则得到的不同图案共有（）D ． 7种5．如图，在△ABC 中，AC=BC ，点D 、E 分别是边AB 、AC 的中点，将△ADE 绕点E 旋转180°得△CFE ，则四边形ADCF 一定是（）4个黑球和若干个白球，它们除颜色外没有任何（m 为常数）的图象与x 轴的一个交点为（1，0），8．如图，二次函数y=ax 2+bx+c 的图象经过点（0，﹣2），与x 轴交点的横坐标分别为x 1，x 2，且﹣1＜x 1＜0，1＜x 2＜2，下列结论正确的是（）﹣9．如图，在平行四边形ABCD 中，AB=6，AD=9，∠BAD 的平分线交BC 于E ，交DC 的延长线于F ，BG ⊥AE 于G ，BG=，则△EFC 的周长为（）D．810．如图，在△ABC中，以BC为直径的圆分别交边AC、AB于D、E两点，连接BD、DE．若BD平分∠ABC，则下列结论不一定成立的是（）二．填空题（共8小题）11．如果（2x+2y+1）（2x+2y﹣1）=63，那么x+y的值是_________．12．若，且一元二次方程kx2+ax+b=0有两个实数根，则k的取值范围是_________．13．如图，在平面直角坐标系中，点A，B，C的坐标分别为（1，0），（0，1），（﹣1，0）．一个电动玩具从坐标原点0出发，第一次跳跃到点P1．使得点P1与点O关于点A成中心对称；第二次跳跃到点P2，使得点P2与点P1关于点B成中心对称；第三次跳跃到点P3，使得点P3与点P2关于点C成中心对称；第四次跳跃到点P4，使得点P4与点P3关于点A成中心对称；第五次跳跃到点P5，使得点P5与点P4关于点B成中心对称；…照此规律重复下去，则点P2013的坐标为_________．14．一副扑克牌52张（不含鬼牌），分为黑桃、红心、方块、及梅花4种花色，每种花色各有13张，分别标有字母A、K、Q、J和数字10、9、8、7、6、5、4、3、2．从这副牌中任意抽取一张，则这张牌是标有字母的概率是_________．15．二次函数y=﹣x2+bx+c的图象如图所示，则一次函数y=bx+c的图象不经过第16．如图，以扇形OAB的顶点O为原点，半径OB所在的直线为x轴，建立平面直角坐标系，点B的坐标为（2，0），若抛物线y=x2+k与扇形OAB的边界总有两个公共点，则实数k的取值范围是_________．17．如图，已知抛物线y=x2+bx+c经过点（0，﹣3），请你确定一个b的值，使该抛物线与x轴的一个交点在（1，0）和（3，0）之间．你确定的b的值是_________．18．如图，AB是⊙O的直径，弦CD⊥AB于点G，点F是CD上一点，且满足=，连接AF并延长交⊙O于点E，连接AD、DE，若CF=2，AF=3．给出下列结论：①△ADF∽△AED；②FG=2；③tan∠E=；④S△DEF =4．其中正确的是_________（写出所有正确结论的序号）．三．解答题（共10小题）19．随着铁路客运量的不断增长，重庆火车北站越来越拥挤，为了满足铁路交通的快速发展，该火车站去年开始启动了扩建工程，其中某项工程，甲队单独完成所需时间比乙队单独完成所需时间多5个月，并且两队单独完成所需时间的乘积恰好等于两队单独完成所需时间之和的6倍．（1）求甲、乙两队单独完成这项工程各需几个月？（2）若甲队每月的施工费为100万元，乙队每月的施工费比甲队多50万元．在保证工程质量的前提下，为了缩短工期，拟安排甲、乙两队分工合作完成这项工程，在完成这项工程中，甲队施工时间是乙队施工时间的2倍，那么，甲队最多施工几个月才能使工程款不超过1500万元？（甲、乙两队的施工时间按月取整数）20如图1所示，将一个边长为2的正方形ABCD和一个长为2、宽为1的长方形CEFD拼在一起，构成一个大的长方形ABEF．现将小长方形CEFD绕点C顺时针旋转至CE′F′D′，旋转角为a．（1）当点D′恰好落在EF边上时，求旋转角a的值；（2）如图2，G为BC中点，且0°＜a＜90°，求证：GD′=E′D；（3）小长方形CEFD绕点C顺时针旋转一周的过程中，△DCD′与△CBD′能否全等？若能，直接写出旋转角a的值；若不能说明理由．21．如图，△ABC内接与⊙O，AB是直径，⊙O的切线PC交BA的延长线于点P，OF∥BC交AC于AC点E，交PC于点F，连接AF．（1）判断AF与⊙O的位置关系并说明理由；（2）若⊙O的半径为4，AF=3，求AC的长．22．如图，AD是⊙O的切线，切点为A，AB是⊙O的弦．过点B作BC∥AD，交⊙O 于点C，连接AC，过点C作CD∥AB，交AD于点D．连接AO并延长交BC于点M，交过点C的直线于点P，且∠BCP=∠ACD．（1）判断直线PC与⊙O的位置关系，并说明理由；（2）若AB=9，BC=6．求PC的长．23．如图，对称轴为直线x=﹣1的抛物线y=ax2+bx+c（a≠0）与x轴相交于A、B 两点，其中点A的坐标为（﹣3，0）．（1）求点B的坐标；（2）已知a=1，C为抛物线与y轴的交点．①若点P在抛物线上，且S△POC=4S△BOC．求点P的坐标；②设点Q是线段AC上的动点，作QD⊥x轴交抛物线于点D，求线段QD长度的最大值．24．）为迎接中国森博会，某商家计划从厂家采购A，B两种产品共20件，产品的（1）设A产品的采购数量为x（件），采购单价为y1（元/件），求y1与x的关系式；（2）经商家与厂家协商，采购A产品的数量不少于B产品数量的，且A产品采购单价不低于1200元，求该商家共有几种进货方案；（3）该商家分别以1760元/件和1700元/件的销售单价售出A，B 两种产品，且全部售完，在（2）的条件下，求采购A种产品多少件时总利润最大，并求最大利润．25．如图①，若二次函数y=x2+bx+c的图象与x轴交于A（﹣2，0），B（3，0）两点，点A关于正比例函数y=x的图象的对称点为C．（1）求b、c的值；（2）证明：点C在所求的二次函数的图象上；（3）如图②，过点B作DB⊥x轴交正比例函数y=x的图象于点D，连结AC，交正比例函数y=x的图象于点E，连结AD、CD．如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动，同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动．当其中一个点到达终点时，另一个点随之停止运动，连结PQ、QE、PE．设运动时间为t秒，是否存在某一时刻，使PE平分∠APQ，同时QE平分∠PQC？若存在，求出t的值；若不存在，请说明理由．26．在△ABC中，∠CAB=90°，AD⊥BC于点D，点E为AB的中点，EC与AD交于点G，点F在BC上．（1）如图1，AC：AB=1：2，EF⊥CB，求证：EF=CD．（2）如图2，AC：AB=1：，EF⊥CE，求EF：EG的值．27．如图，在平面直角坐标系xOy中，矩形OABC的边OA、OC分别在y轴和x 轴的正半轴上，且长分别为m、4m（m＞0），D为边AB的中点，一抛物线l经过点A、D及点M（﹣1，﹣1﹣m）．（1）求抛物线l的解析式（用含m的式子表示）；（2）把△OAD沿直线OD折叠后点A落在点A′处，连接OA′并延长与线段BC 的延长线交于点E，若抛物线l与线段CE相交，求实数m的取值范围；（3）在满足（2）的条件下，求出抛物线l顶点P到达最高位置时的坐标．28．如图，直线x=﹣4与x轴交于点E，一开口向上的抛物线过原点交线段OE于点A，交直线x=﹣4于点B，过B且平行于x轴的直线与抛物线交于点C，直线OC交直线AB于D，且AD：BD=1：3．（1）求点A的坐标；（2）若△OBC是等腰三角形，求此抛物线的函数关系式．2014-2015学年九年级[上]数学期末测试卷参考答案与试题解析一．选择题（共10小题）1．（2013•烟台）已知实数a ，b 分别满足a 2﹣6a+4=0，b 2﹣6b+4=0，且a ≠b ，则=此题考查了一元二次方程根与系数的关系，熟练掌握根与系数的关系是解本题的关键． 2．（2013•咸宁）关于x 的一元二次方程（a ﹣1）x 2﹣2x+3=0有实数根，则整数a D ． ﹣1 ，3．（2013•鄂州）已知m ，n 是关于x 的一元二次方程x 2﹣3x+a=0的两个解，若（m的关键．6．（2013•资阳）在一个不透明的盒子里，装有色外没有任何其他区别，÷8．（2013•济南）如图，二次函数y=ax +bx+c 的图象经过点（0，﹣2），与x 轴交点的横坐标分别为x 1，x 2，且﹣1＜x 1＜0，1＜x 2＜2，下列结论正确的是（）﹣＜最小值：＜﹣9．（2013•自贡）如图，在平行四边形ABCD 中，AB=6，AD=9，∠BAD 的平分线交BC 于E ，交DC 的延长线于F ，BG ⊥AE 于G ，BG=，则△EFC 的周长为（），AG=10．（2013•日照）如图，在△ABC 中，以BC 为直径的圆分别交边AC 、AB 于D 、E 两点，连接BD 、DE ．若BD 平分∠ABC ，则下列结论不一定成立的是（） ∴===二．填空题（共8小题） 11．如果（2x+2y+1）（2x+2y ﹣1）=63，那么x+y 的值是 4或﹣4 ．兰州）若，且一元二次方程解：∵，13．（2013•威海）如图，在平面直角坐标系中，点A，B，C的坐标分别为（1，0），（0，1），（﹣1，0）．一个电动玩具从坐标原点0出发，第一次跳跃到点P1．使得点P1与点O关于点A成中心对称；第二次跳跃到点P2，使得点P2与点P1关于点B成中心对称；第三次跳跃到点P3，使得点P3与点P2关于点C成中心对称；第四次跳跃到点P4，使得点P4与点P3关于点A成中心对称；第五次跳跃到点P5，使得点P5与点P4关于点B成中心对称；…照此规律重复下去，则点P2013的坐标为（0，﹣2）．∵=335从这副牌中任意抽取一张，则这张牌是标有字母的概率是=．故答案为：．．15．（2013•营口）二次函数y=﹣x2+bx+c的图象如图所示，则一次函数y=bx+c的图象不经过第四象限．x ＜联立消掉k=时，抛物线与的坐标为（，））时，×y=．17．（2011•湖州）如图，已知抛物线y=x2+bx+c经过点（0，﹣3），请你确定一个b的值，使该抛物线与x轴的一个交点在（1，0）和（3，0）之间．你确定的b的轴的交点的坐标特点是解此题的关=，连接E=．，根据垂径定理可得：，由，E=∴=，∵=，AG=== E=AD=，××=3∴（∴，，；足铁路交通的快速发展，该火车站去年开始启动了扩建工程，其中某项工程，甲队单独完成所需时间比乙队单独完成所需时间多5个月，并且两队单独完成所需时间的乘积恰好等于两队单独完成所需时间之和的6倍．（1）求甲、乙两队单独完成这项工程各需几个月？（2）若甲队每月的施工费为100万元，乙队每月的施工费比甲队多50万元．在保证工程质量的前提下，为了缩短工期，拟安排甲、乙两队分工合作完成这项工程，个月，则乙队施工个月，则乙队施工y≤20．（2013•潍坊）如图1所示，将一个边长为2的正方形ABCD和一个长为2、宽为1的长方形CEFD拼在一起，构成一个大的长方形ABEF．现将小长方形CEFD 绕点C顺时针旋转至CE′F′D′，旋转角为a．（1）当点D′恰好落在EF边上时，求旋转角a的值；（2）如图2，G为BC中点，且0°＜a＜90°，求证：GD′=E′D；，=135﹣垂直于OC ，OB=OC ，利用为公共边，利用SAS ，即可得证；OA=OC 的长，即可确定出AE=CE=AF=AE=AC=2AE=．BC=3，根据等AM=6；r=6r=，则CE=2r=OM=6﹣BE=2OM=然后判断Rt △PCM BM=CM=BC=3=6，r=6﹣r=CE=2r=OM=6=BE=2OM=∠MCP ，∴=，=PC=．求出二次函数的解析式为的方程，解方程），则D 点坐标为（x ，长度的最大值．两点，∴∴××，解得），时，有最大值，且的值，函数关系式即可求＞=11，y=xxy=y=CEQ ，根据y=∴﹣x ，FOB=，∴C 作CK y=x ×，×，﹣y=﹣，当AC===．y=xCD=AD=2，∠AC=∴，即：﹣t=或t=，故舍去）t=本题是二次函数压轴题，考查了二次函数的图象与性质、正比例函数的图象与性质、待定系数法、对称、解直角三角形、相似三角形的判定与性质、解一元二次方程等知识点．试题的难点在于第（3）问，图形中：EQ=BE AE 在△ACD 与△BEF 中，，：B==EQ=AEH==，EH=BE：：DM=OM=x 点坐标，运用待定系数法得到直，解得，m N=N=m ON==m m x ﹣×解得≤，，）﹣当时，m=）=，到达最高位置时的坐标为（，）考点：二次函数综合题．分析：（1）过点D作DF⊥x轴于点根据相似三角形对应边成比例得出=，即AF=1，进而得到点A（2）先由抛物线过原点（（﹣2，0），求出对称轴为直线可知当△OBC是等腰三角形时，可分两种情况讨论：①求出y1的值，将A，设C（2，y2），列出方程，解方程求出抛物线的解析式．∴====362）代入，解得x=36（负值舍去））代入，解得xx x y=x。

2014-2015学年度第一学期九年级期末考试

2014-2015学年度第一学期九年级期末考试化学试卷说明：1．考试时间80分钟，满分共100分2．本试卷分选择题和非选择题两部分，将选择题的正确答案编号填入括号内，非选择题解答写在试卷相应的位置上3．可能用到的相对原子质量： H -1 C- 12 N- 14 O- 16 Mg -24 Ca- 40第Ⅰ卷（选择题共30分）一、选择题（本题包括15小题，每小题2分，共30分。

每题只有一个选项符合题意）1．下列过程中，主要依靠化学变化实现的是：（）2．人们对空气污染程度的关注不断加强，下列气体中可造成空气污染的有（）①NO 2 ②N 2 ③CO ④CO 2 ⑤SO 2 A ．①②③ B ．①③④ C ．①④⑤ D ．①③⑤ 3．下列物质属于纯净物的是（）A ．“天山雪”纯牛奶B ．“飘雪”蒸馏水C ．“纽崔莱”奶粉D ．“无名”啤酒4．下列事实可以用“分子在不断运动”解释的是（）A ．CO 有毒而CO 2无毒B ．温度计中的水银（汞）热胀冷缩C ．花香四溢D ．一滴水有无数个水分子5．下列实验现象描述不正确的是（）A ．红磷在空气中燃烧，产生大量白烟B ．木炭在氧气中燃烧，发出白光C ．细铁丝在氧气中燃烧，火星四射D ．硫在氧气中燃烧，火焰呈淡蓝色 6．下列实验操作中，正确的是（）A ．尝药品的味道B ．用剩的药品放入指定的回收容器中C ．加热试管中的液体时试管口不对着自己可以对着他人D ．量筒可以用作反应器 7．右图是用比例模型来表示物质间发生化学变化的微观示意图。

图中“ ”和“”分别表示两种元素的原子，能用该图示表示的化学反应是（）A ．2H 2+O 点燃 2H 2OB ．CO 2+H 2O===H 2CO 3C ．2CO+O 点燃 2CO 2D ．H 2+Cl 点燃 2HCl8．下列有关二氧化碳性质的实验，无明显现象的是（）////////////////////////////////////////////密封线内不要答题/////////////////////////////9．下列缓慢氧化：①呼吸作用②食物腐败变质③酒和醋的酿造④农家肥的堆积腐烂⑤钢铁生锈⑥日常生活中将鲜豆腐制成臭豆腐，其中对人类或生产不利的是（）A ．②⑤B ．②④C ．①③⑤D ．①⑥10．下列各图所示装置的气密性检查中，漏气的是）B C D 11．美国发明了月球制氧机，它利用聚焦太阳光产生的高温使月球土壤发生化学变化放出氧气。

2014-2015学年人教版九年级上学期期末数学试卷(精选3套,详细解析)

2014-2015学年人教版九年级上学期期末数学试卷考试时间100分钟，试卷满分100分一. 选择题(每小题3分,共30分)1．“ a 是实数，0≥a ”这一事件是（）A ．必然事件B ．不确定事件C ．不可能事件D ．随机事件2. 把△ABC 三边的长度都扩大为原来的3倍，则锐角A 的正弦值（）A ．不变B ．缩小为原来的13C ．扩大为原来的3倍D ．不能确定 3．已知反比例函数xy 1=，下列结论中不正确的是（） A ．图象经过点（－1，－1） B ．图象在第一、三象限C ．当x ＞1 时， 0 ＜y ＜1D ．当 x ＜0 时， y 随着 x 的增大而增大 4．如图，在方格纸中，△ABC 经过变换得到△DEF ，正确的变换是（） A ．把△ABC 绕点C 逆时针方向旋转90°，再向下平移2格 B ．把△ABC 绕点C 顺时针方向旋转90°，再向下平移5格 C ．把△ABC 向下平移4格，再绕点C 逆时针方向旋转180° D ．把△ABC 向下平移5格，再绕点C 顺时针方向旋转180° 5．如果关于x 的一元二次方程22(21)10k x k x -++=有两个不相等的实数根，那么k 的取值范围是（） A ．14k >-B ．14k >-且0k ≠ C ．14k <- D ．14k ≥-且0k ≠ 6．如图，点A 、B 、O 是正方形网格上的三个格点，⊙O 的半径为OA ，点P 是优弧tan 的值是（）A ．1BCD 7．如图，在大小为4×4的正方形网格中与①中三角形相似的是（）A ．②B ． ③C ． ④和③D ． ②和④8．已知抛物线k x a y +-=2)2(（是常数，＞k a a ,0），A （﹣3，y 1）、B （3，y 2）、C （4，y 3）是抛物线上三点，则y 1，y 2，y 3由小到大依序排列为（） A ．y 1＜y 2＜y 3 B ．y 2＜y 1＜y 3 C ．y 2＜y 3＜y 1 D ．y 3＜y 2＜y 1 9．如图，△AOB 是等边三角形，B （2，0），将△AOB 绕O 点逆时针方向旋转90°到△A′OB′位置，则点A′ 的坐标是（）（第4题）（第6题）A ．（﹣1，）B ．（﹣，1）C ．（，﹣1）D ．（1，﹣）10. 已知二次函数c bx ax y ++=2的图象如图所示，那么一次函数c bx y +=和反比例函数xay =在同一平面直角坐标系中的图象大致是（）A ．B ．C ．D ．二．填空题(每小题3分,共24分.) 11. 已知点M )3,21(m -关于原点对称的点在第一象限，那么的取值范围是________. 12. 如图所示，在平行四边形纸片上作随机扎针实验，针头扎在阴影区域内的概率为 13．一种药品经过两次降价，药价从原来每盒 60 元降至现在的 48.6 元，则平均每次降价的百分率是．14. 如图，在平面直角坐标系中，点O为坐标原点，点P 在第一象限，☉P 与x 轴交于O 、A 两点，点A 的坐标为(6,0)，☉P的半径为13，则点P 的坐标为 .15．如图，在△ABC 中，AB=24，AC=18，D 是AC 上一点，AD=12，AB 上取一点E ，A 、D 、E 三点为顶点组成的三角形与△ABC 相似，AE 的长是_____ _. 16．如图，在直角坐标系中，正方形的中心在原点O ，且正方形的一组对边与x 轴平行．点P （a 3，a ）是反比例函数xk y =（k ＞0）的图象上与正方形的一个交点，若图中阴影部分的面积等于9，则k 的值为 .(第16题) 17. 轮船从B 处以每小时50海里的速度沿南偏东30°方向匀速航行，在B 处观测灯塔A 位于南偏东75°方向上，轮船航行半小时到达 C 处，在C 处观测灯塔A 位于北偏东60°方向上，则C 处与灯塔 A 的距离是海里．18. 二次函数y=ax 2+bx+c （a ，b ，c 是常数，a≠0），下列说法：①若b 2﹣4ac=0,则抛物线的顶点一定在x 轴上； ②若a-b+c=0,则抛物线必过点（-1，0）；③若a ＜0，且一元二次方程ax 2+bx+c=0有两根x 1，x 2（x 1＜x 2）,则ax 2+bx+c ＜0的解集为x 1＜x ＜x 2；④若33ca b +=,则方程ax 2+bx+c=0有一根为-3．（第12题）（第14题）（第15题）其中正确的是（把正确的序号都填上）三．解答题(本大题共有5题,满分46分) 19.(每小题6分，共12分)(1)2tan 603sin 30cos 45+--o o o ． (2)解方程：2410x x ++=20.(本题8分) 如图，一次函数y 1=kx+b 的图象与反比例函数2my x=（x ＞0）的图象交于A （1，6），B （a ，2）两点．（1）求一次函数与反比例函数的解析式；（2）直接写出y 1≤y 2时x 的取值范围．21.(本题8分) 小华和小丽两人玩数字游戏，先由小丽心中任意想一个数记为 x ，再由小华猜小丽刚才想的数字，把小华猜的数字记为 y ，且他们想和猜的数字只能在 1、2、3、4这四个数字中．（1）请用树状图或列表法表示出他们想和猜的所有情况；（2）如果他们想和猜的数字相同，则称他们“心灵相通” ．求他们“心灵相通”的概率；（3）如果他们想和猜的数字满足x y 1-≤，则称他们“心有灵犀” ．求他们“心有灵犀”的概率．22. (本题8分) 如图，直线PM 切⊙O 于点M,直线PO 交⊙O 于A 、B 两点，弦AC ∥PM ，连接OM 、BC. 求证：（1）△ABC ∽△POM ；(2)2OA 2=OP·BC.23. (本题10分)某批发市场批发甲、乙两种水果，根据以往经验和市场行情，预计夏季某一段时间内，甲种水果的销售利润甲y (万元)与进货量x(吨)近似满足函数关系x y 3.0=甲；乙种水果的销售利润乙y (万元)与进货量x (吨)近似满足函数关系bx ax y +=2乙(其中0≠a ，a ，b 为常数），且进货量x 为1吨时，销售利润乙y 为1.4万元；进货量x 为2吨时，销售利润乙y 为2.6万元．（1）求乙y (万元)与x (吨)之间的函数关系式．（2）如果市场准备进甲、乙两种水果共10吨，设乙种水果的进货量为t 吨，请你写出这两种水果所获得的销售利润之和W （万元）与t （吨）之间的函数关系式．并求出这两种水果各进多少吨时获得的销售利润之和最大，最大利润是多少？2014—2015学年第一学期九年级数学期末质量检测评分标准11.m0＜ 12.1413.010 14.（3,2） 15.916或16.3 17.25 18.①、②、④三．解答题(本大题共有5题,满分46分)19.(1)21-2⎛⨯⎝…………………………………3分=313+-22…………………………………5分=4………………………………………6分(2)(2)解：2x4x1+=-，2x4x 414++=-+2(x2)3+=…………………………………3分x+2=…………………………………5分12x2,x2==．………………………………………6分20. （1）∵点A（1，6），B（a，2）在y2=的图象上，∴=6，m=6．∴反比例函数的解析式为：y2=，…………………………………3分∴=2，a==3，∵点A（1，6），B（3，2）在函数y1=kx+b的图象上，∴，解这个方程组，得∴一次函数的解析式为y1=-2x+8，反比例函数的解析式为y2=；…………………6分（2）由函数图象可知，当x在A、B之间时一次函数的图象在反比例函数图象的上方，∵点A（1，6），B（3，2），∴1≤x≤3．…………………………………8分（2）根据（1）得所以可能的情况有16中，想和猜的数相同的情况有4种，∴P（心灵相通）=41164=…………………6分（3）根据（1）得所以可能的情况有16中，数字满足|x-y|≤1的情况有10种，∴P（心有灵犀）105168==…………………8分22.（1）证明：∵直线PM切⊙O于点M，∴∠PMO=90°，∵弦AB是直径，∴∠ACB=90°，∴∠ACB=∠PMO，∵AC∥PM，∴∠CAB=∠P，∴△ABC∽△POM；…………………4分（2）∵△ABC∽△POM，∴，又AB=2OA，OA=OM，∴，∴2OA2=OP·BC.…………………8分23．解：（1）由题意，得：解得∴y乙=-0.1x2+1.5x．…………………4分（2）W=y甲+y乙=0.3（10-t）+（-0.1t2+1.5t）∴W=-0.1t2+1.2t+3．W=-0.1（t-6）2+6.6．∴t=6时，W有最大值为6.6．∴10-6=4（吨）．答：甲、乙两种水果的进货量分别为4吨和6吨时，获得的销售利润之和最大，最大利润是6.6万元．…………………10分2014-2015学年人教版九年级上学期期末数学试卷一、选择题（本题共32分，每小题4分）下面各题均有四个选项，其中只有一个是符合题意的．1．已知=，则x的值是（）A．B．C．D．2．已知⊙O的半径是4，OP=3，则点P与⊙O的位置关系是（）A．点P在圆内B．点P在圆上C．点P在圆外D．不能确定3．如图，在Rt△ABC中，∠C=90°，AB=5，BC=4，则sinB的值是（）A．B．C．D．4．如果反比例函数y=在各自象限内，y随x的增大而减小，那么m的取值范围是（）A．m＜0 B．m＞0 C．m＜﹣1 D．m＞﹣15．如图，⊙O是△ABC的外接圆，若∠AOB=100°，则∠ACB的度数是（）A．40° B．50° C．60° D．80°6．一枚质地均匀的正方体骰子，其六个面上分别刻有1、2、3、4、5、6的点数，掷这个骰子一次，则掷得面朝上的点数为奇数的概率是（）A．B．C．D．7．将抛物线y=5x2先向左平移2个单位，再向上平移3个单位后得到新的抛物线，则新抛物线的表达式是（）A．y=5（x+2）2+3 B．y=5（x﹣2）2+3 C．y=5（x﹣2）2﹣3 D．y=5（x+2）2﹣38．如图，等边△ABC边长为2，动点P从点A出发，以每秒1个单位长度的速度，沿A→B→C→A的方向运动，到达点A时停止．设运动时间为x秒，y=PC，则y关于x函数的图象大致为（）A．B．C．D．二、填空题：（本题共16分，每小题4分）9．扇形的半径为9，且圆心角为120°，则它的弧长为．10．三角尺在灯泡O的照射下在墙上形成影子（如图所示）．现测得OA=20cm，OA′=50cm，这个三角尺的周长与它在墙上形成的影子的周长的比是．11．如图，在平面直角坐标系xOy中，抛物线y=ax2+bx+c（a≠0）的对称轴是直线x=，在下列结论中，唯一正确的是．（请将正确的序号填在横线上）①a＜0；②c＜﹣1；③2a+3b=0；④b2﹣4ac＜0；⑤当x=时，y的最小值为．12．如图，在平面直角坐标系xOy中，正方形ABCD顶点A（﹣1，﹣1）、B（﹣3，﹣1）．我们规定“把正方形ABCD先沿x轴翻折，再向右平移2个单位”为一次变换．（1）如果正方形ABCD经过1次这样的变换得到正方形A1B1C1D1，那么B1的坐标是．（2）如果正方形ABCD经过2014次这样的变换得到正方形A2014B2014C2014D2014，那么B2014的坐标是．三、解答题：（本题共30分，每题5分）13．计算：tan30°﹣cos60°×tan45°+sin30°．14．已知抛物线y=x2﹣4x+3．（1）用配方法将y=x2﹣4x+3化成y=a（x﹣h）2+k的形式；（2）求出该抛物线的对称轴和顶点坐标；（3）直接写出当x满足什么条件时，函数y＜0．15．如图，在△ABC中，D是AB上一点，且∠ABC=∠ACD．（1）求证：△ACD∽△ABC；（2）若AD=3，AB=7，求AC的长．16．如图，热气球的探测器显示，从热气球看一栋高楼的顶部B的仰角为45°，看这栋高楼底部C的俯角为60°，热气球与高楼的水平距离AD为20m，求这栋楼的高度．（结果保留根号）17．如图，AB是⊙O的直径，CD是⊙O的一条弦，且CD⊥AB于点E．（1）求证：∠BCO=∠D；（2）若CD=，AE=2，求⊙O的半径．18．如图，一次函数y=kx+2的图象与x轴交于点B，与反比例函数的图象的一个交点为A（2，3）．（1）分别求出反比例函数和一次函数的解析式；（2）过点A作AC⊥x轴，垂足为C，若点P在反比例函数图象上，且△PBC的面积等于18，求P点的坐标．四、解答题：（本题共20分，每题5分）19．如图，在锐角△ABC中，AB=AC，BC=10，sinA=，（1）求tanB的值；（2）求AB的长．20．在平面直角坐标系xOy中，抛物线y=﹣x2+bx+c经过点（﹣3，0）和（1，0）．（1）求抛物线的表达式；（2）在给定的坐标系中，画出此抛物线；（3）设抛物线顶点关于y轴的对称点为A，记抛物线在第二象限之间的部分为图象G．点B是抛物线对称轴上一动点，如果直线AB与图象G有公共点，请结合函数的图象，直接写出点B纵坐标t的取值范围．21．如图，在△ABC，AB=AC，以AB为直径的⊙O分别交AC、BC于点D、E，且BF是⊙O的切线，BF交AC的延长线于F．（1）求证：∠CBF=∠CAB．（2）若AB=5，sin∠CBF=，求BC和BF的长．22．阅读下面材料：小明遇到这样一个问题：如图1，在等边三角形ABC内有一点P，且PA=3，PB=4，PC=5，求∠APB度数．小明发现，利用旋转和全等的知识构造△AP′C，连接PP′，得到两个特殊的三角形，从而将问题解决（如图2）．请回答：图1中∠APB的度数等于，图2中∠PP′C的度数等于．参考小明思考问题的方法，解决问题：如图3，在平面直角坐标系xOy中，点A坐标为（﹣，1），连接AO．如果点B是x轴上的一动点，以AB为边作等边三角形ABC．当C（x，y）在第一象限内时，求y与x之间的函数表达式．五、解答题：（本题共22分，第23题7分，第24题7分，第25题8分）23．已知关于x的方程mx2+（3m+1）x+3=0（m≠0）．（1）求证：方程总有两个实数根；（2）若方程的两个实数根都是整数，求正整数m的值；（3）在（2）的条件下，将关于x的二次函数y=mx2+（3m+1）x+3的图象在x轴下方的部分沿x轴翻折，图象的其余部分保持不变，得到一个新的图象．请结合这个新的图象回答：当直线y=x+b与此图象有两个公共点时，b的取值范围．24．矩形ABCD一条边AD=8，将矩形ABCD折叠，使得点B落在CD边上的点P处．（1）如图1，已知折痕与边BC交于点O，连接AP、OP、OA．①求证：△OCP∽△PDA；②若△OCP与△PDA的面积比为1：4，求边AB的长．（2）如图2，在（1）的条件下，擦去AO和OP，连接BP．动点M在线段AP上（不与点P、A重合），动点N在线段AB的延长线上，且BN=PM，连接MN交PB于点F，作ME⊥BP 于点E．试问动点M、N在移动的过程中，线段EF的长度是否发生变化？若不变，求出线段EF的长度；若变化，说明理由．25．我们规定：函数y=（a、b、k是常数，k≠ab）叫奇特函数．当a=b=0时，奇特函数y=就是反比例函数y=（k是常数，k≠0）．（1）如果某一矩形两边长分别是2和3，当它们分别增加x和y后，得到新矩形的面积为8．求y与x之间的函数表达式，并判断它是否为奇特函数；（2）如图，在平面直角坐标系xOy中，矩形OABC的顶点A、C坐标分别为（6，0）、（0，3），点D是OA中点，连接OB、CD交于E，若奇特函数y=的图象经过点B、E，求该奇特函数的表达式；（3）把反比例函数y=的图象向右平移4个单位，再向上平移个单位就可得到（2）中得到的奇特函数的图象；（4）在（2）的条件下，过线段BE中点M的一条直线l与这个奇特函数图象交于P，Q两点（P在Q右侧），如果以B、E、P、Q为顶点组成的四边形面积为16，请直接写出点P的坐标．2014-2015学年人教版九年级上学期期末数学试卷答案解析参考答案与试题解析一、选择题（本题共32分，每小题4分）下面各题均有四个选项，其中只有一个是符合题意的．1．已知=，则x的值是（）A．B．C．D．考点：比例的性质．专题：计算题．分析：根据内项之积等于外项之积得到2x=15，然后解一次方程即可．解答：解：∵=，∴2x=15，∴x=．故选B．点评：本题是基础题，考查了比例的基本性质，比较简单．2．已知⊙O的半径是4，OP=3，则点P与⊙O的位置关系是（）A．点P在圆内B．点P在圆上C．点P在圆外D．不能确定考点：点与圆的位置关系．分析：点在圆上，则d=r；点在圆外，d＞r；点在圆内，d＜r（d即点到圆心的距离，r即圆的半径）．解答：解：∵OP=3＜4，故点P与⊙O的位置关系是点在圆内．故选A．点评：本题考查了点与圆的位置关系，注意掌握点和圆的位置关系与数量之间的等价关系是解决问题的关键．3．如图，在Rt△ABC中，∠C=90°，AB=5，BC=4，则sinB的值是（）A．B．C．D．考点：锐角三角函数的定义．分析：首先根据勾股定理求得AC的长，然后利用正弦函数的定义即可求解．解答：解：∵在Rt△ABC中，∠C=90°，AB=5，BC=4，∴AC===3，∴sinB==．故选D．点评：本题考查了三角函数的定义，求锐角的三角函数值的方法：利用锐角三角函数的定义，转化成直角三角形的边长的比．4．如果反比例函数y=在各自象限内，y随x的增大而减小，那么m的取值范围是（）A．m＜0 B．m＞0 C．m＜﹣1 D．m＞﹣1考点：反比例函数的性质．分析：如果反比例函数y=在各自象限内，y随x的增大而减小，那么m的取值范围是（）解答：解：∵反比例函数y=的图象在所在象限内，y的值随x值的增大而减小，∴m+1＞0，解得m＞﹣1．故选D．点评：本题考查的是反比例函数的性质，熟知反比例函数的增减性是解答此题的关键．5．如图，⊙O是△ABC的外接圆，若∠AOB=100°，则∠ACB的度数是（）A．40° B．50° C．60° D．80°考点：圆周角定理．分析：已知⊙O是△ABC的外接圆，∠AOB=100°，根据圆周角定理可求得∠ACB的度数．解答：解：∵⊙O是△ABC的外接圆，∠AOB=100°，∴∠ACB=∠AOB=×100°=50°．故选B．点评：本题主要考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角是所对的圆心角的一半．6．一枚质地均匀的正方体骰子，其六个面上分别刻有1、2、3、4、5、6的点数，掷这个骰子一次，则掷得面朝上的点数为奇数的概率是（）A．B．C．D．考点：概率公式．分析：先统计出奇数点的个数，再根据概率公式解答．解答：解：∵正方体骰子共六个面，点数为1，2，3，4，5，6，奇数为1，3，5，∴点数为奇数的概率为：=．故选：C．点评：此题主要考查了概率公式，用到的知识点为：概率=所求情况数与总情况数之比．7．将抛物线y=5x2先向左平移2个单位，再向上平移3个单位后得到新的抛物线，则新抛物线的表达式是（）A．y=5（x+2）2+3 B．y=5（x﹣2）2+3 C．y=5（x﹣2）2﹣3 D．y=5（x+2）2﹣3考点：二次函数图象与几何变换．专题：几何变换．分析：先确定抛物线y=5x2的顶点坐标为（0，0），再利用点平移的规律得到点（0，0）平移后所得对应点的坐标，然后根据顶点式写出平移后的抛物线解析式．解答：解：抛物线y=5x2的顶点坐标为（0，0），把点（0，0）向左平移2个单位，再向上平移3个单位后得到对应点的坐标为（﹣2，3），所以新抛物线的表达式是y=5（x+2）2+3．故选A．点评：本题考查了二次函数图象与几何变换：由于抛物线平移后的形状不变，故a不变，所以求平移后的抛物线解析式通常可利用两种方法：一是求出原抛物线上任意两点平移后的坐标，利用待定系数法求出解析式；二是只考虑平移后的顶点坐标，即可求出解析式．8．如图，等边△ABC边长为2，动点P从点A出发，以每秒1个单位长度的速度，沿A→B→C→A的方向运动，到达点A时停止．设运动时间为x秒，y=PC，则y关于x函数的图象大致为（）A ．B ．C ．D ．考点：动点问题的函数图象．分析：分段讨论，当0≤x ≤2时，作PQ ⊥AC ，根据锐角三角函数和勾股定理求出AQ 、PQ 、CQ 、PC 2；当2＜x ＜4时，PC 在BC 上，是一次函数；当4＜x ≤6时，PC 在AC 上，是一次函数，根据函数关系式分析即可得出结论．解答：解：当0≤x ≤2时，作PQ ⊥AC ，∵AP=x ，∠A=60°∴AQ=，PQ=， ∴CQ=2﹣，∴PC==， ∴PC 2=x 2﹣2x+4=（x ﹣1）2+3；当2＜x ＜4时，PC=4﹣x ，当4＜x ≤6时，PC=2﹣（6﹣x ）=x ﹣4，故选：C ．点评：本题主要考查了动点问题的函数图形，分段讨论，列出每段函数的解析式是解决问题的关键．二、填空题：（本题共16分，每小题4分）9．扇形的半径为9，且圆心角为120°，则它的弧长为 6π ．考点：弧长的计算．分析：直接利用弧长的计算公式计算即可．解答：解：弧长是：=6π．故答案是：6π．点评：本题考查了弧长的计算公式，正确记忆公式是关键．10．三角尺在灯泡O的照射下在墙上形成影子（如图所示）．现测得OA=20cm，OA′=50cm，这个三角尺的周长与它在墙上形成的影子的周长的比是2：5．考点：相似三角形的应用．分析：由题意知三角尺与其影子相似，它们周长的比就等于相似比．解答：解：∵，∴三角尺的周长与它在墙上形成的影子的周长的比是．点评：本题考查相似三角形的性质，相似三角形的周长的比等于相似比．11．如图，在平面直角坐标系xOy中，抛物线y=ax2+bx+c（a≠0）的对称轴是直线x=，在下列结论中，唯一正确的是③⑤．（请将正确的序号填在横线上）①a＜0；②c＜﹣1；③2a+3b=0；④b2﹣4ac＜0；⑤当x=时，y的最小值为．考点：二次函数图象与系数的关系．分析：根据二次函数的图象开口方向即可判断A；由二次函数的图象与y轴的交点位置即可判断B；把x=﹣1代入二次函数的解析式即可判断C；根据二次函数的对称轴即可求出D．解答：解：①∵二次函数的图象开口向上，∴a＞0，故本选项错误；②∵二次函数的图象与y轴的交点在点（0，﹣1）的上方，∴c＞﹣1，故本选项错误；③、∵二次函数的图象的对称轴是直线x=，∴﹣=，﹣3b=2a，2a+3b=0，故本选项正确；④∵二次函数的图象与x轴有两个交点，∴b2﹣4ac＞0，故本选项错误；⑤∵二次函数的图象的对称轴是直线x=，∴﹣=，∴﹣3b=2a，b=﹣a，∴y最小值=a+b+c=a+×（﹣a）+c=；即y的最小值为，故本选项正确；故答案为：③⑤．点评：本题考查了二次函数的图象和系数的关系，题目具有一定的代表性，是一道比较好的题目，注意用了数形结合思想，二次函数的图象开口方向决定a的符号，二次函数的图形与y轴的交点位置决定c的符号，根据二次函数的图象的对称轴是直线x=得出﹣=，把x=代入y=ax2+bx+c（a≠0）得出y=a+b+c等等．12．如图，在平面直角坐标系xOy中，正方形ABCD顶点A（﹣1，﹣1）、B（﹣3，﹣1）．我们规定“把正方形ABCD先沿x轴翻折，再向右平移2个单位”为一次变换．（1）如果正方形ABCD经过1次这样的变换得到正方形A1B1C1D1，那么B1的坐标是（﹣1，1）．（2）如果正方形ABCD经过2014次这样的变换得到正方形A2014B2014C2014D2014，那么B2014的坐标是（4025，﹣1）．考点：规律型：点的坐标．分析：（1）把正方形ABCD先沿x轴翻折，则点B关于x轴对称，得到B点的坐标为：（﹣3，1），再向右平移2个单位”后点B的坐标为：（﹣3+2，1），即B1（﹣1，1）．（2）首先由正方形ABCD，点A、B的坐标分别是（﹣1，﹣1）、（﹣3，﹣1），然后根据题意求得第1次、2次、3次变换后的点B的对应点的坐标，即可得规律：第n次变换后的点B的对应点的为：当n为奇数时为（2n﹣3，1），当n为偶数时为（2n﹣3，﹣1），继而求得把正方形ABCD经过连续2014次这样的变换得到正方形A′B′C′D′，则点B的对应点B′的坐标．解答：解：（1）∵正方形ABCD，点A、B的坐标分别是（﹣1，﹣1）、（﹣3，﹣1），∴根据题意得：第1次变换后的点B的对应点的坐标为（﹣3+2，1），即B1（﹣1，1），（2）第2次变换后的点B的对应点的坐标为：（﹣1+2，﹣1），即（1，﹣1），第3次变换后的点B的对应点的坐标为（1+2，1），即（3，1），第n次变换后的点B的对应点的为：当n为奇数时为（2n﹣3，1），当n为偶数时为（2n﹣3，﹣1），∴把正方形ABCD经过连续2014次这样的变换得到正方形A′B′C′D′，则点B的对应点B′的坐标是：（4025，﹣1）．故答案为：（﹣1，1）；（4025，﹣1）．点评：此题考查了对称与平移的性质．此题难度较大，属于规律性题目，注意得到规律：第n次变换后的点B的对应点的坐标为：当n为奇数时为（2n﹣3，1），当n为偶数时为（2n ﹣3，﹣1）是解此题的关键．三、解答题：（本题共30分，每题5分）13．计算：tan30°﹣cos60°×tan45°+sin30°．考点：特殊角的三角函数值．分析：将tan30°=，cos60°=，tan45°=1，sin30°=分别代入运算，然后合并即可得出答案．解答：解：原式==．点评：本题考查了特殊角的三角函数值，属于基础题，熟练记忆一些特殊角的三角函数值是关键．14．已知抛物线y=x2﹣4x+3．（1）用配方法将y=x2﹣4x+3化成y=a（x﹣h）2+k的形式；（2）求出该抛物线的对称轴和顶点坐标；（3）直接写出当x满足什么条件时，函数y＜0．考点：二次函数的三种形式；二次函数的性质．分析：（1）由于二次项系数是1，所以直接加上一次项系数的一半的平方来凑完全平方式，把一般式转化为顶点式；（2）根据二次函数y=a（x﹣h）2+k的顶点坐标为（h，k），对称轴为x=h求解即可；（3）先求出方程x2﹣4x+3=0的两根，再根据二次函数的性质即可求解．解答：解：（1）y=x2﹣4x+3=（x2﹣4x+4）﹣4+3=（x﹣2）2﹣1；（2）∵y=（x﹣2）2﹣1，∴对称轴为直线x=2，顶点坐标为（2，﹣1）；（3）解方程x2﹣4x+3=0，得x=1或3．∵y=x2﹣4x+3，a=1＞0，∴抛物线开口向上，∴当1＜x＜3时，函数y＜0．点评：本题考查了二次函数解析式的三种形式，二次函数的性质，难度适中．利用配方法将一般式转化为顶点式是解题的关键．15．如图，在△ABC中，D是AB上一点，且∠ABC=∠ACD．（1）求证：△ACD∽△ABC；（2）若AD=3，AB=7，求AC的长．考点：相似三角形的判定与性质．分析：（1）根据两角对应相等，两三角形相似即可证明△ADC∽△ACB；（2）根据相似三角形的对应边成比例得出AC：AB=AD：AC，即AC2=AB•AD，将数值代入计算即可求出AC的长．解答：（1）证明：在△ADC与△ACB中，∵∠ABC=∠ACD，∠A=∠A，∴△ACD∽△ABC；（2）解：∵△ACD∽△ABC，∴AC：AB=AD：AC，∴AC2=AB•AD，∵AD=2，AB=7，∴AC2=7×2=14，∴AC=．点评：本题考查的是相似三角形的判定与性质，用到的知识点为：①如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似（简叙为两角对应相等，两三角形相似）；②相似三角形的对应边成比例．16．如图，热气球的探测器显示，从热气球看一栋高楼的顶部B的仰角为45°，看这栋高楼底部C的俯角为60°，热气球与高楼的水平距离AD为20m，求这栋楼的高度．（结果保留根号）考点：解直角三角形的应用-仰角俯角问题．分析：在Rt△ABD中，求出BD，在Rt△ACD中，求出CD，二者相加即为楼高BC．解答：解：在Rt△ABD中，∠BDA=90°，∠BAD=45°，∴BD=AD=20．在Rt△ACD中，∠ADC=90°，∠CAD=60°，∴CD=AD=20．∴BC=BD+CD=20+20（m）．答：这栋楼高为（20+20）m．点评：本题考查了解直角三角形的应用﹣﹣仰角俯角问题，将原三角形转化为两个直角三角形是解题的关键．17．如图，AB是⊙O的直径，CD是⊙O的一条弦，且CD⊥AB于点E．（1）求证：∠BCO=∠D；（2）若CD=，AE=2，求⊙O的半径．考点：圆周角定理；勾股定理；垂径定理．专题：计算题．分析：（1）由OB=OC，利用等边对等角得到一对角相等，再由同弧所对的圆周角相等得到一对角相等，等量代换即可得证；（2）由弦CD与直径AB垂直，利用垂径定理得到E为CD的中点，求出CE的长，在直角三角形OCE中，设圆的半径OC=r，OE=OA﹣AE，表示出OE，利用勾股定理列出关于r 的方程，求出方程的解即可得到圆的半径r的值．解答：（1）证明：如图．∵OC=OB，∴∠BCO=∠B．∵∠B=∠D，∴∠BCO=∠D；（2）解：∵AB是⊙O的直径，且CD⊥AB于点E，∴CE=CD=×4=2，在Rt△OCE中，OC2=CE2+OE2，设⊙O的半径为r，则OC=r，OE=OA﹣AE=r﹣2，∴r2=（2）2+（r﹣2）2，解得：r=3，∴⊙O的半径为3．点评：此题考查了垂径定理，勾股定理，以及圆周角定理，熟练掌握定理是解本题的关键．18．如图，一次函数y=kx+2的图象与x轴交于点B，与反比例函数的图象的一个交点为A（2，3）．（1）分别求出反比例函数和一次函数的解析式；（2）过点A作AC⊥x轴，垂足为C，若点P在反比例函数图象上，且△PBC的面积等于18，求P点的坐标．考点：反比例函数与一次函数的交点问题；三角形的面积．专题：计算题．分析：（1）先将点A（2，3）代入反比例函数和一次函数y=kx+2，求得m、k的值，（2）可求得点B的坐标，设P（x，y），由S△PBC=18，即可求得x，y的值．解答：解：（1）把A（2，3）代入，∴m=6．∴．（1分）把A（2，3）代入y=kx+2，∴2k+2=3．∴．∴．（2分）（2）令，解得x=﹣4，即B（﹣4，0）．∵AC⊥x轴，∴C（2，0）．∴BC=6．（3分）设P（x，y），∵S△PBC==18，∴y1=6或y2=﹣6．分别代入中，得x1=1或x2=﹣1．∴P1（1，6）或P2（﹣1，﹣6）．（5分）点评：本题考查了一次函数和反比例函数的交点问题，利用待定系数法求解析式是解此题的关键．四、解答题：（本题共20分，每题5分）19．如图，在锐角△ABC中，AB=AC，BC=10，sinA=，（1）求tanB的值；（2）求AB的长．考点：解直角三角形．专题：计算题．分析：（1）过点C作CD⊥AB，垂足为D，设CD=3k，则AB=AC=5k，继而可求出BD=k，从而求出tanB的值；（2）在Rt△BCD中，先求出BC=k=10，求出k的值，继而得出AB的值．解答：解：（1）过点C作CD⊥AB，垂足为D，（1分）在Rt△ACD中，，（1分）设CD=3k，则AB=AC=5k，（1分）∴．（1分）在△BCD中，∵BD=AB﹣AD=5k﹣4k=k．（1分）∴．（1分）（2）在Rt△BCD中，，（1分）∵BC=10，∴．（1分）∴．（1分）∴AB=．（1分）点评：本题考查了解直角三角形的知识，过点C作CD⊥AB，构造直角三角形是关键．20．在平面直角坐标系xOy中，抛物线y=﹣x2+bx+c经过点（﹣3，0）和（1，0）．（1）求抛物线的表达式；（2）在给定的坐标系中，画出此抛物线；（3）设抛物线顶点关于y轴的对称点为A，记抛物线在第二象限之间的部分为图象G．点B是抛物线对称轴上一动点，如果直线AB与图象G有公共点，请结合函数的图象，直接写出点B纵坐标t的取值范围．考点：待定系数法求二次函数解析式；二次函数的图象；二次函数的性质．分析：（1）根据待定系数法即可求得；（2）正确画出图形；（3）通过图象可以看出点B纵坐标t的取值范围．解答：解：（1）∵抛物线y=﹣x2+bx+c经过点（﹣3，0）和（1，0）．∴，解得，∴抛物线的表达式为y=﹣x2﹣2x+3．（2）此抛物线如图所示．（3）2＜t≤4．如图，由图象可知点B纵坐标t的取值范围为2＜t≤4．点评：本题考查了待定系数法求解析式，以及画图的能力和识别图形的能力，要熟练掌握．21．如图，在△ABC，AB=AC，以AB为直径的⊙O分别交AC、BC于点D、E，且BF是⊙O的切线，BF交AC的延长线于F．（1）求证：∠CBF=∠CAB．（2）若AB=5，sin∠CBF=，求BC和BF的长．考点：切线的性质．分析：（1）连接AE，由圆周角定理和等腰三角形的性质，结合切线的性质可证得∠CBF=∠BAE，可证得结论；（2）由（1）结论结合正弦值，在Rt△ABE中可求得BE，可求出BC，过C作CM⊥BF，在Rt△BCM中可求得BM，CM，再利用平行线分线段成比例可求得BF．解答：（1）证明：如图1，连结AE．∵AB是⊙O的直径，∴∠AEB=90°，∴∠BAE=∠BAC．∵BF是⊙O的切线，∴∠CBF=∠BAE，∴∠CBF=∠CAB．（2）解：由（1）可知∠CBF=∠BAE，∴sin∠BAE=sin∠CBF=，在Rt△ABE中，sin∠BAE=，∴=，∴BE=，∴BC=2，如图2，过C作CM⊥BF于点M，则sin∠CBF==，即=，解得CM=2，由勾股定理可求得BM=4，又∵AB∥CM，∴=，。

新人教版2014-2015年九年级上学期期末考试数学试题及答案

新人教版2014－2015年上学期期末考试九年级数学试题（考试时间：120分钟满分：150分）一、选择题（本题共10道题，每小题3分，共30分）1.下列方程中，是一元二次方程的是( )A. 221x x y ++=B. 2110x x+-= C. 20x = D. 2(1)(3)1x x x ++=- 2.下列汽车标志中，既是轴对称又是中心对称图形的是( )3.下列说法中正确的是( )A.不确定事件发生的概率是不确定的B.事件发生的概率可以等于事件不发生的概率C.事件发生的概率不可能等于0D.抛掷一只均匀的骰子两次，朝上一面的点数之和一定大于24.如图45,15中，∠=∠=O CBO CAO ，则AOB ∠的度数是( )A.75 B.30 C.45 D.60 5.掷一枚六面分别标有1到6的均匀骰子，向上一面的点数大于2且小于5的概率为1P ，抛两枚硬币，正面均朝上的概率为2P ，则( )A.12P P <B.12P P >C.12P P =D.不能确定6.在同圆中，下列四个命题:○1圆心角是顶点在圆心的角；○2两个圆心角相等，它们所对的弦也相等；○3两条弦相等，所对的劣弧也相等；○4等弧所对的圆心角相等。

其中真命题有( )A.4个B.3个C.2个D.1个7.抛物线22(1)3y x =---与y 轴交点的纵坐标为( )A.3-B. 4-C.5-D.1-8．用配方法解关于x 的方程20x px q ++=，方程可变形为( ) A.224()24p p q x -+= B.224()24p q p x -+= C.224()24p p q x +-= 第4题D.224()24p p q x --= 9．如图，E 、F 分别是正方形ABCD 的边BC 、CD 上的点，BE=CF ，连接AE 、BF ，将△ABE 绕正方形的中心按逆时针方向旋转到BCF △，旋转角为()0180a a <<，则a =( )A.60 B.90 C.120 D.4510．已知二次函数2y ax bx c =++的图象如图所示，其对称轴为直线1x =-，给出下列结论(1)24b ac >; (2)0abc >; (3)20a b +=; (4)0a b c ++>; (5)420a b c -+<.则正确的结论有( )A. 2个B. 3个C. 4个D. 5个第9题C第16题第17题B二、填空题（本大题共8小题，每小题3分，共24分）11．方程2x =的根是 .12．众所周知，手机的电话号码是由11位数字组成的，某人的手机号码位于中间的数字为5的概率是13．在一幅长为80cm ,宽为50cm 的矩形风景画的四周镶一条相同宽度的金色纸边，制成一幅矩形挂图，如果要使整个挂图的面积是54002cm ，设金色纸边的宽为，那么x 满足的方程是14．如果函数232(3)1k k y k x kx -+=-++是二次函数，那么k 值为15．一个圆锥的侧面展开图是半径为1的半圆，该圆锥的底面半径是16．二次函数2y x bx c =-++的图象如图所示，则一次函数y bx c =+的图象不经过第象限. 17．如图所示，一条公路的转变处是一段圆弧（图中的弧AB ）点O 是这段弧的圆心，C 是AB 上一点，,OC AB ⊥ 垂足为D ，AB=300m ，CD=50m ，则这段弯路的半径是18．观察下列一组数：13579,,,,,27142334⋅⋅⋅它们是按一定规律排列的，那么这一组数的第n 个数是三、解答题（本大题共96分）19．解方程：（10分）(1) 2660x x --=(2) 22760x x -+=20．△ABC 在平面直角坐标系中的位置如图所示（A 、B 、C 三点在格点上），把△ABC 绕原点O 顺时针旋转90，A 、B 、C 旋转后的对应点分别是1A 、1B 、1C(1)画出旋转后的111△ABC ，并直接写出1A、1B 、1C 的坐标； (2)在旋转过程中，求点A 到点1A 所经过的路径的长.（12分）21．某汽车经销商推出A 、B 、C 、D 四种型号的小轿车共1000辆进行展销。

2014-2015年第一学期九年级数学试题答案

2014---2015学年度第一学期期末质量检测九年级数学试题（答案）一、选择题（请把选择题答案填在下列表格中，每题3分，满分36分）二、填空题（本大题共8小题，每小题3分，共24分．） 13.1414. 24π 15. 35︒ 16. 80 17. 10 18. 2 三、解答题19.解： 1）设平均每次下调的百分率为x ，则6000（1-x ）2=4860，解得：x 1=0.1=10%, x 2=1.9(舍).故平均每周下调的百分率为10%.……………………5分（2）方案1优惠：4860×100×（1-0.98）=9720（元）；方案2可优惠：80×100=8000（元）. 故方案1优惠.…………………………9分 20. 解：设小明的身高为x 米，则CD=EF=x 米．在Rt △ACD 中，∠ADC=90°，tan ∠CAD=AD CD ，即tan30°=xAD，AD=3x --2分在Rt △BEF 中，∠BFE=90°，tan ∠EBF=EF BF ，即tan60°=x BF ，BF=x 33 ---4分由题意得DF=2，∴BD=DF-BF=2-x 33，∵AB=AD+BD=4，∴3x+2-x 33=4 --7分即x=3．答：小明的身高为3米．------------------------------------------------------------------------9分21. 解：（1）把A点（1，4）分别代入反比例函数y=，一次函数y=x+b，得k=1×4，1+b═4，解得k=4，b=3，反比例函数的解析式是y=，一次函数解析式是y=x+3；…………4分（每个解析式2分）（2）如图，当x=﹣4时，y=﹣1，B（﹣4，﹣1），当y=0时，x+3=0，x=﹣3，C（﹣3，0）S△AOB=S△AOC+S△BOC==；…………8分（3）∵B（﹣4，﹣1），A（1，4），∴根据图象可知：当x＞1或﹣4＜x＜0时，一次函数值大于反比例函数值．…………12分22.解：（1）∵x%+15%+10%+45%=1，∴x=30；…………1分∵调查的总人数=90÷45%=200（人），…………2分∴B等级人数=200×30%=60（人）；C等级人数=200×10%=20（人），…………4分（求出1个1分）如图：…………5分（2）2500×（10%+30%）=1000（人），所以估计每周课外阅读时间量满足2≤t＜4的人数为1000人；…………7分（3）3人学习组的3个人用甲表示，2人学习组的2个人用乙表示，画树状图为：，共有20种等可能的结果数，其中选出的2人来自不同小组占12种，…………10分所以选出的2人来自不同小组的概率==．…………12分23.（1）证明：∵AB是⊙O的切直径，∴∠ADB=90°，又∵∠BAD=∠BED，∠BED=∠DBC，∴∠BAD=∠DBC，∴∠BAD+∠ABD=∠DBC+∠ABD=90°，∴∠ABC=90°，∴BC是⊙O的切线；…………6分（2）解：∵∠BAD=∠DBC，∠C=∠C，∴△ABC∽△BDC，∴=，即BC2=AC•CD=（AD+CD）•CD=10，∴BC=．…………12分22.………………1分………………6分∴P 点的坐标为（5,2）………………12分………………7分………10分………………11分。

2014-2015第一学期期末物理九年级

2014—2015学年度第一学期期末学业水平测试九年级物理题样注意事项：1. 本试题共6页，满分为70分,考试时间为60分钟。

2.一、选择题（本题包括10个小题，每小题2分，共20分。

每小题只有1 个选项符合题意，把正确选项前面的字母填在选择题答案栏内，选对的得2分，多选、错选或不选均不得分）1．汽车、拖拉机的发动机常用水做冷却剂。

是因为水具有 A ．较小的密度 B ．较大的比热容 C ．较低的凝固点 D ．较高的沸点 2．关于热机，下列说法是正确的是A ．汽油机顶部有喷油嘴，柴油机顶部有火花塞B ．柴油机在吸气冲程中，将柴油和空气的混合气吸入气缸C ．汽油机在做功冲程中，进气门关闭排气门打开D ．汽油机在做功冲程中，是把内能转化为机械能3．如右图所示的电路中，电源电压保持不变，闭合开关S 后 A ．电流表的示数变大 B ．电压表的示数变大C ．电路中的总电阻变大D ．电路消耗的总功率变小 4．学校走廊的灯经常烧坏，更换十分不便，电工师傅为了减少更换灯泡的次数，采用“挑担灯”解决了这个问题，即将“220V 100W”和“220V 60W”的两盏规格不相同的白炽灯串联接入照明电路中，则它们消耗的总功率（灯丝的电阻不受温度影响） A ．等于160w B ．等于60WC ．小于60WD ．大于60W ，小于100W 5．下列物理知识与科学家对应关系中不正确的是 A ．电流的磁效应——奥斯特 B ．I =U /R ——欧姆C ．杠杆平衡原理——阿基米德D ．Q =I 2Rt ——安培6．在去年理化生实验技能测试中，在做测电阻的实验时，小明在连接电路过程中，由于疏忽，把电压表和电流表的位置给颠倒了，其它连接正确无误．这个电路闭合开关后所产生的现象是A ．电压表有读数，电流表的读数几乎为零B ．电压表将被烧坏C ．电流表有读数，电压表的读数几乎为零D ．电流表将被烧坏 7．法国科学家阿尔贝·费尔和德国科学家彼得·格林贝格尔由于发现了巨磁电阻 (GMR)效应，荣获了2007年诺贝尔物理学奖。

2014-2015学年第一学期期末质量检测九年级数学试卷附答案

2014－2015学年第一学期期末质量检测九年级数学试卷（本试卷共三个大题，26个小题，时间90分钟，满分120分）一、精心选一选（本大题共16小题。

1-6题，每题2分；7-16题，每题3分，共42分）每小题给出的4个选项中只有一个符合题意,请将所选选项的字母代号写在题中的括号内. 1. 一元二次方程02=-x x 的解为……………………………………………【】 A.1=x B.0=x C.0,121==x x D.0,121=-=x x 2.在平面直角坐标系中，点M （3，-5）关于原点对称的点的坐标是……………【】 A ．（-3，-5） B ．（3，5） C ．（5，-3） D ．（ -3，5） 3.下列各点中，在函数xy 2-=的图象上的是…………………………………【】 A.（2，1） B.（-2，1） C.（2，-2） D.（1，2）4. 顶点坐标为（－2，3），开口方向和大小与抛物线y ＝x 2相同的解析式为…【】A ．y ＝(x －2)2＋3B ．y ＝(x ＋2)2－3C ．y ＝(x ＋2)2＋3D ．y ＝－(x ＋2)2＋35. 盒子里有3支红色笔芯，2支黑色笔芯，每支笔芯除颜色外均相同．从中任意拿出一支笔芯，则拿出黑色笔芯的概率是………………………………………【】A ．23B ．15C ．25D ． 356. Rt △ABC 中∠C =90°，AC =3cm ，BC =4cm ，则它的外心与顶点C 的距离为……【】 A ．2.4cm B ．2.5cm C ．3cm D ．4cm7.向上发射一枚炮弹，经x 秒后的高度为y 米，且时间与高度关系为y =ax 2+bx .若此炮弹在第6秒与第15秒时的高度相等，则下列几个时刻高度最高的是……【】 A. 第8秒 B.第10秒 C.第12秒 D. 第14秒 8. 如图，⊙O 的直径CD ⊥EF 于G ，若∠EOD =50°,则∠DCF 等于………………【】 A.80° B. 50° C. 40° D. 25°9.如图，为了测量一池塘的宽DE ，在岸边找一点C ，测得CD =30m ，在DC 的延长线上找一点A ，测得AC=5m ，过点A 作AB ∥DE ，交EC 的延长线于B ，测得AB =6m ，则池塘的宽DE 为…………………………………………………………………【】 A.25m B.30m C.36m D.40m10. 已知：如图，PA 切⊙O 于点A ，PB 切⊙O 于点B ，如果∠APB =60°，⊙O 半径是3，则劣弧AB 的长为…………………………………………………………【】 A ．π B ．6π C ．2π D ．3π11.面积为2的直角三角形一直角边长为x ，另一直角边长为y ，则y 与x 的变化规律用图象大致表示为……………………………………………………………【】12.已知反比例函数y ＝xm52 的图象上有A （x 1，y 1）、B （x 2，y 2）两点，当 x 1＜x 2＜0时，y 1＜y 2，则m 的取值范围是………………………………………【】A.m ＜0B.m ＞0C.m ＜52 D.m ＞52 13.如图所示，在一边靠墙（墙足够长）的空地上，修建一个面积为640m 2的矩形临时仓库，仓库一边靠墙，另三边用总长为80 m 的栅栏围成，若设栅栏AB 的长为 xm ，则下列各方程中，符合题意的是………………………………………………【】 A ．21x （80－x ）＝640 B ．21x （80－2x ）＝640 C ．x （80－2x ）＝640 D ． x （80－x ）＝640第8题图第9题图第10题图第13题图第14题图第15题图第16题图14. 如图，若P 为△ABC 的边AB 上一点（AB ＞AC ），则下列条件不一定能保证 △ACP ∽△ABC 的有…………………………………………………………………【】A.∠ACP =∠BB.∠APC =∠ACBC.AC AP AB AC =D.AB ACBC PC = 15.如图，一次函数与反比例函数的图象相交于A 、B 两点，则图中使反比例函数的值小于一次函数的值的x 的取值范围是…………………………………………【】 A.x ＜－1 B.x ＞2 C.－1＜x ＜0或x ＞2 D.x ＜－1或0＜x ＜2 16.如图，量角器的直径与含30°角的直角三角板ABC 的斜边AB 重合，射线CP 从CA 处出发沿顺时针方向以每秒2度的速度旋转，CP 与量角器的半圆弧交于点E ，当第30秒时，点E 在量角器上对应的读数是……………………………………【】 A. 120° B.150° C.75° D. 60°二、细心填一填（本大题共4小题，每小题3分，共12分）把答案直接写在题中的横线上.17. 圆锥的母线长5cm ,底面半径长3cm ,那么它的侧面展开图的面积是 . 18. 如图，△ABC 中，E 、F 分别是AB 、AC 上的两点，且，若△AEF 的面积为3，则四边形EBCF 的面积为 .19. 如图，在平面内将Rt △ABC 绕着直角顶点C 逆时针旋转90°得到Rt △EFC ．若AB =1BC =，则阴影部分的面积为 .20.如图，Rt △ABC 中，∠ACB =90°，∠ABC =60°，BC =4cm ，D 为BC 的中点，若动点E 以1cm /s 的速度从A 点出发，沿着A →B →A 的方向运动，设E 点的运动时间为t 秒（0≤t ＜12），连接DE ，当△BDE 是直角三角形时，t 的值为 .第18题图第19题图第20题图三、专心解一解（本题满分66分）请认真读题，冷静思考.解答题应写出文字说明、解答过程.21. （本题满分9分）已知双曲线xky的图象经过点A （-1，2）. （1）求该反比例函数的解析式.（2）若B （b ，m ）、C （c ，n ）是该双曲线上的两个点，且b ＜c ，判断m ，n 的大小关系.（3）判断关于x 的一元二次方程k x 2+2x -1=0的根的情况.22. （本题满分10分）如图，方格纸中每个小正方形的边长都是单位1，△ABC 在平面直角坐标系中的位置如图所示.（1）将△ABC 绕点B 顺时针方向旋转 90o后得△A 1BC 1，画出△A 1BC 1，并直接写出点C 1的坐标为 . （2）把△ABC 以点C 为位似中心同侧放大，使放大前后对应边长的比为1：2，画作出△A 2B 2C ，并直接写出点B 2的坐标为 .23. （本题满分11分）在一副扑克牌中，拿出黑桃3、黑桃4、黑桃5、黑桃6四张牌，小刚从中随机摸出一张记下牌面上的数字为x，再由小明从剩下的牌中随机摸出一张，记下牌面上的数字为y，组成一对数（x，y）.（1）用列表法或树状图表示出（x，y）的所有可能出现的结果；（2）求小刚、小明各摸一次扑克牌所确定的一对数是方程x+y=9的解的概率.24．（本题满分11分）如图所示，AB 是⊙O 的直径，AD 与⊙O 相切于点A ，DE 与⊙O 相切于点E ,点C 为DE 延长线上一点，且CE =CB .（1）求证：BC 为⊙O 的切线；（2）若AB =4，AD =1，求线段CE 的长.25. （本题满分12分）某商场出售一批进价为3元的小工艺品，在市场营销中发现此工艺品的日销售单价x (单位：元)与日销售量y (单位：个)之间有如下关系：(1) (2)设经营此小工艺品的日销售利润为S元，求出S 与x 之间的函数关系式； (3)物价局规定小商品的利润不得高于进价的200%，请你求出当日销售单价x 定为多少时，才能获得最大日销售利润？最大日销售利润是多少？26. （本题满分13分）如图，抛物线y=ax2＋52x-2与x轴相交于点A(1,0)与点B ，与y轴相交于点C．（1）确定抛物线的解析式；（2）连接AC、BC，△AOC与△COB相似吗？并说明理由.（3）点N在抛物线的对称轴上，在抛物线上是否存在点M，使得以点N、M、A、B为顶点的四边形是平行四边形？若存在，求出对应的点M、N的坐标；若不存在，请说明理由.备用图九年级数学答案一、1.C 2.D 3.B 4.C 5.C 6.B 7.B 8.D 9.C 10. C 11. C 12.D 13.A 14.D 15.D 16.A二、17. π15 18.24 19. 1-π 20. 4或7或9 三、21.解：（1）由题意可知，12-=k ，∴k =-2-----------------2分（2）∵k =-2＜0，∴y 随x 的增大而增大-----------------4分又∵b ＜c ，∴m ＜n-----------------6分（3）△=22-4×(-2)×(-1)=-4＜0 -----------------8分∴关于x 的一元二次方程k x 2+2x -1=0没有实数根-----------------9分22.如图（1）作图 3分 C 1（2，3）2分（2）作图 3分 B 2(1，-2) 2分23.解：(1)分析题意，用树状图表示为：--------------5分所以共有12种等可能的结果，即（3，4）（3,5）（3,6）（4,3）（4,5）（4,6）（5,3）（5,4）（5,6）（6,3）（6,4）（6,5） -----------7分（2）满足所确定的一对数是方程x+y=9的解的结果有4种：（3,6）（4,5）（5,4）（6,3） -----------9分此事件记作A ，则P(A)=31124= -----------11分 24 （1）证明：连接OE,O C …………1分∵DE 与⊙O 相切于点E ∴∠OEC ＝90° -----------3分 ∵OE=OB CB=CE OC=OC∴△CEO ≌△CBO -----------5分 ∴∠OBC=∠OEC ＝90° -----------6分 ∴BC 为⊙O 的切线 -----------7分 (2)过点D 作D F ⊥BC 于F …………………8分设CE=x ∵CE,CB 为⊙O 切线 ∴CB=CE=x ∵DE,DA 为⊙O 切线 ∴DE=DA=1∴DC=x+1………………………………9分 ∵∠DAB=∠ABC ＝∠DFB= 90° ∴四边形ADFB 为矩形 ∴DF=AB=4 BF=AD=1 ∴FC=x-1Rt △CDF 中，(x+1)2-(x-1)2=16 -----------10分 x=4 ∴CE=4 -----------11分25.解：（1）由表中数据规律可知x 与y 的乘积一定，为105×4=420 -----------2分所以函数关系式为xy 420= -----------3分（2）S=（x-3）x420-----------5分=4201260+-x-----------7分 (3)由题意可知：x ≤3+3×200% ∴3≤x ≤9 -----------8分 ∵k=-1260＜0九年级数学试卷共8页，第11页∴S 随x 的增大而增大∴当x=9时，S 的值最大 -----------10分最大值为280 -----------11分∴当日销售单价定为9元时，才能获得最大日销售利润是280元。

人教版2014-2015九年级数学上册期末考试试题含大题答案

2014 ～ 2015学年度九年级数学上学期期末考试（满分:150分考试时间:90分钟）姓名___________ 班级__________ 分数 ________-_____一、选择题（每小题4分，共40分） 1、下列运算正确的是（）A 、325=- B 、428=+ C 、3327= D 、1)21)(21(=-+2.把方程x x 632=+配方得（）A 、12)3(2=-xB 、3)3(2=+xC 、6)3(2=-xD 、6)3(2=+x 2、已知关于x 的一元二次方程(m -2)2x 2+（2m +1）x +1=0有两个实数根，则m 的取值范围是（）（A ）43>m （B ）43≥m （C ）43>m 且2≠m （D ）43≥m 且2≠m3）A B C4、如图，⊿ABC 内接于⊙O ，若∠OAB=28°则∠C 的大小为（）（A ）62° （B ）56° （C ）60° （D ）28°5、随机掷一枚均匀的硬币两次，落地后至少有一次正面朝上的概率是（）（A ）41 （B ）21 （C ）43（D ）1 6、三角形两边长分别是8和6，第三边长是一元二次方程x 2-16x+60=0一个实数根，则该三角形的面积是（）A ．24B ．48C ．24或D ．D7.一个扇形的圆心角为120°,它的面积为3πcm 2,那么这个扇形的半径是 ( )A 、3cm C 、6cm D 、9cm8.一台机器原价60万元，如果每年的折旧率为x ，两年后这台机器的价位应为y 万元，则y 与x 的函数关系表达式为( )A 、260(1)y x =-B 、y=60(1+x)2C 、y = 60（1－x ）D 、y=60－x29知抛物线y=ax 2+bx,当a>0,b<0时,它的图象经过( )A 、一、二、三象限B 、一、二、四象限C 、一、三、四象限D 、一、二、三、四象限10.点B 、C 、E 、F 在同一直线上．现从点C 、E 重合的位置出发，让△ABC 在直线EF 上向右作匀速运动，而△DEF 的位置不动．设两个三角形重合部分的面积为y ，运动的距离为x ．下面表示y 与x 的函数关系式的图象大致是（）二、细心填一填（每小题4分，共20分） 11、已知式子31+-x x有意义，则x 的取值范围是 12、计算20102009)23()23(+-＝13、点P 关于原点对称的点Q 的坐标是（-1，3），则P 的坐标是 14、已知圆锥的底面半径为9cm ，母线长为10cm ，则圆锥的全面积是 cm 215、已知：关于x 的一元二次方程041)(22=++-d x r R x 有两个相等的实数根，其中R 、r 分别是⊙O 1 ⊙O 2的半径，d 为两圆的圆心距，则⊙O 1 与⊙O 2的位置关系是三、解答题16、（8分）计算：)681(2)2124(+--17、（8分）解方程：x2－12x－4＝0(用配方法）18.已知二次函数y＝ax2＋bx＋c的图象经过一次函数y＝－3/2x＋3的图象与x 轴、y轴的交点；且过(1，1)，求这个二次函数解析式，并把它化为y＝a(x－h)2＋k的形式。

2014-2015九年级上册数学期末考试试卷

2014-2015九年级上册数学期末考试试卷一、选择题（每题2分，共24分） 1.下列方程是一元二次方程的是（）A ．12=+y xB ．()32122+=-x x xC ．413=+xx D ．022=-x 2. 一元二次方程032=+x x 的解是（） A ．3-=x B ．3,021-==x x C ．3,021==x x D ．3=x 3. 下列平面图形中，既是轴对称图形，又是中心对称图形的是（）4.抛物线3)2(2+-=x y 的顶点坐标是（）A ．（2，3）B ．（－2，3）C ．（2，－3）D ．（－2，－3）5.把抛物线2x y -=向左平移1个单位，再向上平移3个单位，得到抛物线的解析式为（）A 、2(1)3y x =--+B 、2(1)3y x =-+ C 、2(1)3y x =-++ D 、2(1)3y x =++ 6.正方形绕着它的中心旋转，要想与原来的图形重合，至少要旋转( ) A. 3600 B. 2000 C. 1800 D. 900 7. 若关于x 的方程kx 2-8x+5=0有实数根，则k 的取值范围是( )A. k ≤564B. k ≥-516C. k ≥516D. k ≤5168. 在半径为1的圆中，长为2的弦所对的劣孤为( )A. πB.2 π C. 4π D. 6π9.⊙O 的半径为6，⊙O 的一条弦AB 长为43，以4为半径的同心圆与AB 的关系是( )A. 相离B. 相切C. 相交D.不能10.将5个白球，4个红球，3个黑球放入一个不透明的袋子里，从中摸出10个13题图C 1B 1C BA16题图DC BA球，恰好白球、红球、黑球都摸到，这事件( )A. 可能发生B. 不可能发生C. 很可能发生D. 必然发生11. 在⊙O 中，⊙O 的半径为5cm ，圆心O 到弦AB 的距离为3cm ，则弦AB 的长为( )A. 4cmB. 6cmC. 34cmD. 8cm12.如图1，半径为5的⊙P 与y 轴相交于M （0,-3）, N （0,-11）两点，则P 到原点O 的距离OP 的长为A. 6B. 7C. 58D. 8如图1二、填空题（每题2分，共20分）13. 如图，△ABC 以点A 为旋转中心，按逆时针方向旋转60°得到的△A B 1B 是三角形14. 二次函数2365y x x =--+的图象的顶点坐标是15.把一元二次方程(x －3)2＝4化为一般形式为：___________，二次项系数为：________，一次项系数为：________，常数项为：________.16.如图，等腰△ABC 绕点A 旋转到△ACD 的位置。

2014～2015学年上学期期末考试九年级英语试卷附答案

2014～2015学年上学期期末考试九年级英语试卷一、听力理解（20小题，每小题1分，共20分）第一节听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳答案，并将其标号填入题前括号内。

每段对话读两遍。

1．Where is Alicc now?A. At home. B,At the supermarket. C.At school.2.Who has got longer hair?A. Sam.B.Tom.C.Tina.3. How is the weather today?A. Windy.B.Rainy.C.Sunny.4．What would the woman like to eat?A. The beef noodles,B.The mutton noodles.C．The tomato noodles.5. When did the woman become an art teacher?A. In 2004.B.In 2006.C.In 2008.第二节听下面几段对话或独白。

每段对话或独白后有几个小题，从题中所给的A、B、C三个选项中选出最佳答案，并将其标号填入题前括号内。

每段对话或独白读两遍。

听下面一段对话。

回答第6至第7两个小题。

6. What are they going to do together?A. Play tennis.B.Watch movies.C.Have violin lessons.7. What time will they meet?A. At 5:30.B.At 6:30.C.At 7:30.听下面一段对话，回答第8至第9两个小题。

8. What did Megan see in the omce?A.A bee.B.A mouse.C.A bird.9. Where did they see it in the office?A. On a chair.B.On a desk.C.Under a desk.听下面一段独白，回答第10至第12三个小题。

2014-2015九年级数学上册期末考试试题(人教版_含答案)

(第7题图）B 2014-2015九年级数学上册期末考试试题姓名----一、选择题（30分）1、下列方程中一定是关于x 的一元二次方程是（）A )1(2)1(32+=+x x Ｂ、02112=-+x xＣ02=++c bx ax Ｄ、0)7(2=+-x x x2、将函数231yx =-+）。

A.(231y x=-+ B.(231y x =-++C.23yx =-23y x =-3，如图中∠BOD 的度数是（）A ．55°B ．110°C ．125°D ．150°4，如果关于x 的方程（m ﹣3）﹣x+3=0是关于x 的一元二次方程，那么m 的值为（）A 、在同圆或等圆中，相等的圆心角所对的狐相等。

B 、平分弦的直径垂直于弦。

C 、长度相等的两条狐相等。

D 、圆是轴对称图形，任何一条直径都是它的对称轴。

7、如图，将△ABC 绕点C 旋转60°得到△C B A '',已知AC=6,BC=4,则线段AB 扫过的图形的面积为( )A 、32πB 、310π C 、6π D 、38π。

8，如图2，有6张写有数字的卡片，它们的背面都相同，现将它们,背面朝上（如图2），从中任意一张是数字3的概率是（） A.61 B 、31 C 、21 D 、329，若⊙O 所在平面内一点P 到⊙O 上的点的最大距离为a ，最小距离为b （a>b ），则此圆的半径为（）A ．2b a + B ．2ba - C ．22ba b a -+或D ．b a b a -+或图210，已知二次函数c bx ax y ++=2的图象过点A （1，2），B （3，2），C （5，7）．若点M （－2，y 1）， N （－1，y 2），K （8，y 3）也在二次函数c bx ax y ++=2的图象上，则下列结论正确的是( ) A ．y 1＜y 2＜y 3B ．y 2＜y 1＜y 3C ．y 3＜y 1＜y 2D ．y 1＜y 3＜y 2二、填空题（24分）11，一元二次方程12)3)(31(2+=-+x x x 化为一般形式为。

2014~2015学年度第一学期期末考试九年级数学试卷答案

2014——2015学年度第一学期期末测试九年级数学参考答案一、选择题：本大题共10小题,每小题3分,共30分．在每小题给出的四个选项中,恰有一项是符合题目要求的，请将正确选项的代号填入题后括号内．1．D 2．B 3．Ｃ 4．A 5．B 6．C 7．D 8．A 9．B 10．C二、填空题:本大题共8小题，每小题3分，共24分．请把最后结果填在题中横线上． 11．0。

6 12．25 13．24 14．52 15．277 16．（9，0) 17．－1＜x ＜3 18．②④三、解答题：本大题共10小题，共96分．解答时应写出文字说明、证明过程或演算步骤． 19．(本小题满分8分）每图4分解:由表可以看出，随机地摸取一个小球然后放回，再随机地摸出一个小球,可能出现的结果有16个,它们出现的可能性相等．…………4分（1）满足两次取的小球的标号相同的结果有4个，所以P (1)=164=41．……6分 (2）满足两次取的小球的标号的和等于4的结果有3个，所以P （2）=163．…8分21．(本小题满分9分)(1）8π (3分）（2)(3分）（3)③（3分）22．（本小题满分8分)证明：连接OC ．………………………………………………1分∵OA =OC ,∴∠OAC =∠OCA ．………………………2分∵CD 切⊙O 于点C ，∴OC ⊥CD ．……………………3分∵AD ⊥CD ,∴∠ADC =∠OCD =90°，即∠ADC ＋∠OCD =180°，∴AD ∥OC ,……………………………………………5分∴∠DAC =∠OCA =∠OAC ，……………………………7分∴AC 平分∠DAB ．……………………………………8分一二1 2 3 4 1 （1，1) （2,1) （3,1) (4，1) 2 （1,2）（2，2) （3,2）（4,2） 3 （1，3）（2，3) (3，3）（4，3）4 (1，4) （2，4） (3，4）（4，4) A ＢＣＤＯ．（第22题图）．O A B C解:设所围成圆锥的底面半径和高分别为r 和h ．∵扇形半径为3㎝，圆心角为120°， ∴12032180r ππ⋅⋅=,……………………………………………………………………4分 ∴r =1,……………………………………………………………………………………6分∴h ==8分24．(本小题满分10分)解:（1）令y =0,得2230x x --=，………………………………………………………1分解得x 1=3，x 2=－1，………………………………………………………………3分 ∴抛物线与x 轴交点坐标为(3，0)和(－1，0）．……………………………4分（2）令x =0，得y =－3，∴抛物线与y 轴交点坐标为（0，－3),…………………………………………5分 ∴将此抛物线向上平移3个单位后可以经过原点．……………………………7分平移后抛物线解析式为22y x x =-．………………………………………10分25．（本小题满分9分）(1）证明：∵DE ∥BC ，EF ∥AB ，∴∠AED =∠ECF ，∠A =∠FEC ，……………2分∴△ADE ∽△EFC ．………………………………………………………………4分（2）解:∵△ADE ∽△EFC , ∴AD DE EF FC=．…………………………5分 ∵AD =4,DE =5,EF =2, ∴FC =52．……………………………………6分 ∵DE ∥BC ，EF ∥AB ，∴四边形DEFB 是平行四边形，∴BF =DE =5,……8分∴BC =BF + FC =5+52=152．………………………………………………………9分26．(本小题满分10分）（1)证明:∵四边形ABCD 是正方形，∴∠A =∠B =90°，∴∠DEA +∠ADE =90°．…1分∵EF ⊥DE ，∴∠DEF =90°，∴∠DEA +∠FEB =90°，……………………………2分 ∴∠ADE =∠FEB ，……………………………………………………………………4分 ∴△ADE ∽△BEF ．……………………………………………………………………5分(2）解:∵正方形的边长为4，AE =x ，∴BE =4－x ．∵△ADE ∽△BEF ， ∴DA AE EB BF =，……………………………………………7分 ∴44x x y =-， ∴2(4)144x x y x x -==-+，…………………………………10分解：(1)由题意得1060x y -=．…………………………………………………………3分 (2)由题意得1200040101)200)(1060()200(2++-=+-=+=x x x x x y z ．6分（3）由题意得)1060(201200040101202x x x y z w --++-=-= 10800421012++-=x x ．…………………………………………9分当每个房间的定价2102=-=a b x (元）时，w 有最大值，最大值是15210．………12分28．（本小题满分14分）解：（1）∵点A 坐标为（0，3)，∴OA =3．∵矩形ABCO 面积为12，∴AB =4，……2分∴抛物线的对称轴为直线x =2．…………………………………………………4分（2)∵∠ADM =∠DOM ，∠AMD =∠DMO ,∴△ADM ∽△DOM , ∴MOMD MD AM =，∴MO AM MD ⋅=2．设MO=x ，则MA= x －3． ∴)3(4-=x x ，∴41=x ，12-=x ，∴MO=4，∴D 点坐标为（2,4）．…6分设抛物线的解析式为4)2(2+-=x a y ．将点A （0，3）代入得443+=a ,∴41-=a ， ∴抛物线的解析式为4)2(412+--=x y ．……………………………8分（3）∵⊙P 在y 轴上截得线段长为2，OA =3， ∴P 点纵坐标为2或4．……9分在4)2(412+--=x y 中，令y=2或4得 4)2(4122+--=x 或4)2(4142+--=x ,………………………………11分解得2221+=x ,2222-=x ,23=x ,∴P 点坐标为（222+，2）、(222-，2）或（2，4)．………………14分。

2014-2015学年度九年级数学(上)期末质量检测试题

2014-2015学年度（上）期末数学九年级质量检测试题（满分：120分；时间 90分钟）一、选择题（每小题3分，共30分）1、已知135＝a b ，则b a ba ＋－的值是（）A 、32B 、23C 、49D 、942、关于x 的一元二次方程22(1)10a x x a --+-=的一个根是0，则a 的值为（） A 、1或-1. B 、-1 C 、1 D 、123、已知x －1x =3，则4－12x 2+32x 的值为（） A 、1 B 、32 C 、52 D 、724、如图，在平面直角坐标系中，点A 的坐标为（0，3），△OAB 沿x 轴向右平移后得到△O ′A ′B ′，点A 的对应点A ′在直线y=34x 上，则点B 与其对应点B ′间的距离为（） A 、94B 、3C 、4D 、55、如图是三个大小不等的正方体拼成的几何体，其中两个较小正方体的棱长之和等于大正方体的棱长．该几何体的主视图、俯视图和左视图的面积分别是S 1，S 2，S 3，则S 1，S 2，S 3的大小关系是（） A 、S 1＞S 2＞S 3 B 、 S 3＞S 2＞S 1C 、S 2＞S 3＞S 1D 、S 1＞S 3＞S 26、如图，在平面直角坐标系中,点A 1,A 2在x 轴上，点B 1,B 2在y 轴上，其坐标分别为A 1(1，0),A 2(2,0),B 1(0,1)，B 2(0,2)，分别以 A 1，A 2，B 1，B 2其中的任意两点与点O 为顶点作三角形，所作三角形是等腰三角形的概率是（）A 、34B 、13C 、23D 、127、在同一时刻，身高1.6m 的小强的影长是1.2m ，旗杆的影长是15m ，则旗杆高为（A 、16mB 、18mC 、20mD 、22m8、如图，边长为6的大正方形中有两个小正方形，若两个小正方形的面积分别为S 1，S 2则S 1+S2的值为（）A 、16 B 、17 C 、18 D 、199、如图，△ABC 中，AC 的垂直平分线分别交AC 、AB 与点D 、F,BE ⊥DF 交DF 的延长线于点E ，已知∠A=30°，BC=2，AF=BF,则四边形BCDE 的面积是（）A 、32B 、33C 、4D 、34第4题图第5题图10、已知函数y=kx+b的图象如图所示，则一元二次方程x2+x+k－1=0根的存在情况是（）A、没有实数根B、有两个相等的实数根C、有两个不相等的实数根D、无法确定二、填空题（每小题3分，共24分）11、如图,点D，E分别在AB，AC上且∠ABC=∠AED，若DE=4cm，AE=5cm， BC=8cm，则AB的长为 .12、关于x的方程ax2－(3a+1)x+2(a+1)=0有两个不相等的实根x1、x2，且有x1+x2－x1·x2=1－a,则a= .13、如图，四边形OABC是矩形，ADEF是正方形，点A、D在x轴的正半轴上，点C在y轴的正半轴上，点F在AB上，点B、E在反比例函数y=的图象上，OA=1，OC=6，则正方形ADEF的边长为．14、一水塘里有鲤鱼、鲫鱼、鲢鱼共10000尾，一渔民通过多次捕捞试验后发现，鲤鱼、鲫鱼出现的频率是31%和42%，则这个水塘里大约有鲢鱼 _____尾.15、在平面直角坐标系中，已知A（6,3），B（6,0）两点，以坐标原点为位似中心，位似比为3∶1，把线段AB缩小后得到线段A′B′，则A′B′的长度为 .16、如图，点E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点，当四边形ABCD的边至少满足条件时，四边形EFGH是菱形.17、在锐角三角形ABC中，已知∠A，∠B满足2sin2A⎛-⎝⎭＋tan B|＝0，则∠C＝______.18、已知矩形ABCD中，AB=1，在BC上取一点E，沿AE将△ABE向上折叠，使B点落在AD上的F点．若四边形EFDC与矩形ABCD相似，则AD= .三、解答题（本题共八小题，共66分）19、(本题6分)作出如下图所示的三种视图.G第16题图E第18题图第19题第13题图20、(本题6分)已知()()0622222=-+-+b ab a ,求：22b a +的值。

2014-2015学年九年级上学期期末考试试卷

秘密★启用前2014－2015学年九年级上学期期末模拟考试数学试卷第Ⅰ卷选择题（共40分）一、选择题（每小题4分，共40分）1、函数y ＝x 2－2x ＋3的图象的顶点坐标是A ．(1，－4)B ．(－1，2)C ．(1，2)D ．(0，3) 2、下列方程中，一元二次方程共①3x 2＋x ＝20； ②x 2＋y 2＝5； ③412=-x x； ④x 2＝1； ⑤．0332=+-xx A ．5个 B ．4个 C ．3个 D ．2个3．下列图形中，既是轴对称图形，又是中心对称图形的是ABC D 4．下列事件中是必然事件的是A ．从一个装有蓝．白两色球的缸里摸出一个球，摸出的球是白球B ．小丹的自行车轮胎被钉子扎坏C ．小红期末考试数学成绩一定得满分D ．将油滴入水中，油会浮在水面上5．若关于x 的一元二次方程3x 2＋k ＝0有实数根，则A ．k 0>B ．k 0<C ．k 0≥D ．k 0≤6．一扇形的半径为24cm ，若此扇形围成的圆锥的底面半径为10cm ，那么这个扇形的面积是A ．120πcm 2B ．240πcm 2C ．260πcm 2D ．480πcm 2 7．如图，⊙P 内含于⊙O ，⊙O 的弦AB 切⊙P 于点C ，且AB ∥OP ，若阴影部分的面积为9π，则弦AB 的长为 A ．3 B ．4 C ．2 D ．38．下列说法中，①平分弦的直径垂直于弦；②直角所对的弦是直径；③相等的弦所对的弧相等；④等弧所对的弦相等；⑤圆周角等于圆心角的一半；⑥x 2－5x ＋7＝0两根之和为5。

其中正确命题的个数为A ．0个B ．1个C ．2个D ．3个 9．小军从所给的二次函数图象中观察得出了下面的信息：①a ＜0；②c ＝0；③函数的最小值是∠3；④当x ＜0时y ＞0；⑤当0＜x 1＜x 2＜2时y 1＞y 2。

你认为其中正确的个数为A .2个B .3个C .4个D .5个10．如图，在△ABC 中，AB ＝10，AC ＝8，BC ＝6，经过点C 且与边AB 相切的动圆与CA 、CB 分别相交于点P ．Q ，则线段PQ 长度的最小值是A ．4.8B ．4.75C ．5D ．24第Ⅱ卷非选择题（共110分）二、填空题（共5个小题，每小题4分，共20分）11．已知关于x 的方程x 2＋3x ＋k 2＝0的一个根是－1，则k ＝．12．当实验次数很大时，同一事件发生的频率稳定在相应的附近，所以我们可以通过多次实验，用同一事件发生的来估计这事件发生的概率．（填“频率”或“概率”） 13．已知点A (2a ＋3b ，－2)和B (0，3a ＋2b )关于原点对称，则a ＋b ＝．14．把抛物线y ＝2(x －1)2＋3的图象先向左平移3个单位长度后再向下平移4个单长度得到的新抛物线A CBOPAB QPC的解析式为．15．用两个全等的含30°角的直角三角形制作如图①所示的两种卡片，两种卡片中扇形的半径均为1，且扇形所在圆的圆心分别为长直角边的中点和30°角的顶点，按先A 后B 的顺序交替摆放A 、B 两张卡片得到图②所示的图案，若摆放这个图案共用两种卡片8张，则这个图案中阴影部分的面积之和为；若摆放这个图案共用两种卡片(2n ＋1)张（n 为正整数），则这个图中阴影部分的面积之和为．（结果保留π）三、解答题（共2个题，每题8分，共16分） 16．解下列一元二次方程：（1）(x －2)2 ＝2x －4 （2）2x 2 －4x －1＝017．已知二次函数y ＝2x 2＋bx ＋c 的图象经过A (0，1)、B (－2，1)两点。

新人教版2014—2015学年第一学期九年级数学期末试卷

密班级姓名考号密封线内不得答题2014—2015学年第一学期期末试卷九年级数学一、选择题(每小题3分,共30分)1.(2013·呼和浩特中考)观察下列图形,既是轴对称图形又是中心对称图形的有( )A.1个B.2个C.3个D.4个 2.一个正多边形的每个外角都等于30°,那么这个正多边形的中心角为( ) A.15° B.30° C.45° D.60°3.要得到y=-2(x+2)2-3的图象,需将抛物线y=-2x 2作如下平移( ) A.向右平移2个单位,再向上平移3个单位 B.向右平移2个单位,再向下平移3个单位 C.向左平移2个单位,再向上平移3个单位 D.向左平移2个单位,再向下平移3个单位4.一个不透明的袋子中有3个红球和2个黄球,这些球除颜色外完全相同.从袋子中随机摸出1个球, 这个球是黄球的概率为( )A.错误！未找到引用源。

B.错误！未找到引用源。

C.错误！未找到引用源。

D.错误！未找到引用源。

5.某药品经过两次降价,每瓶零售价由168元降为108元,已知两次降价的百分率相同,设每次降价的百分率为x,根据题意列方程得( )A.168(1+x)2=108B.168(1-x)2=108C.168(1-2x)=108D.168(1-x 2)=1086.(2013·呼和浩特中考)在同一平面直角坐标系中,函数y=mx+m 和函数y=-mx 2+2x+2(m 是常数,且m ≠0) 的图象可能是( )7.(2013·呼和浩特中考)已知α,β是关于x 的一元二次方程x 2+(2m+3)x+m 2=0的两个不相等的实数根, 且满足错误！未找到引用源。

+错误！未找到引用源。

=-1,则m 的值是( ) A.3 B.1 C.3或-1 D.-3或18.在学校组织的实践活动中,小新同学用纸板制作了一个圆锥模型,它的底面半径为1,高为2错误！未找到引用源。

2014-2015第一学期新人教版九年级数学上期末试题[1]

2014-2015新人教版九年级数学上期末试题、细心选一选。

（每小题 3分，共42分）1 •下列各图中，是中心对称图形的是（）B. 三角形任意两边之和大于第三边。

C. 在一个装着白球和黑球的袋中摸球，摸出红球。

D. 某种彩票中奖率是 1%买这种彩票100张一定会中奖。

3.已知O O 的半径是5cm,圆心O 到直线L 的距离是3cm,则直线L 与O O 的位置关系是（）。

A.相交B.相切C .相离D.以上答案都不是4•教练对小明推铅球的录像进行技术分析，发现铅球行进高度 y （m ）与水平距离x （ m ）之间的关系为（x - 4〕'"十3，由此可知铅球推出的距离是（）A . 10mB . 3mC . 4mD . 2m 或 10m5•如果一个扇形的弧长是 -n,半径是6,那么此扇形的圆心角为（）。

3A. 40° B . 45° C . 60° D . 80°6.抛物线y=x 2的图象向左平移2个单位，再向下平移1个单位，则所得抛物线的解析式为（）2 2 2 2A.y=x +4x+3B.y=x +4x+5C.y=x — 4x+3D.y=x — 4x — 5A. 29.若关于 x 的一元2. A. 下列事件中是必然事件的为打开电视，正在播放《新闻联播》节目。

头A7.下列二次函数中，图象以直线 x=2为对称轴、且经过点（0, 1）的是(x 2)2 (x+2 )2 1 (x 2)2y (x+2)23&已知x1是方程ax0的一个根, 则方程的另一个根为（）。

2x m 0有两个不相等的实数根，则m的取值范围是.次方程( )11CBDm )A 80°D E=70° 90°CB85DBG） 8 16 4 CABD151515213 ☆A B)1 1 1 1 CBD824A. 60A.m (1) 3x 2 6x 50 m 1m 1A16(2) (2x3)2 25 、用心填一填（每小题4分，共16分）15.抛物线y x 2 x 4与y 轴的交点坐标 _______________________216•已知（m 2）x 3x 10是关于x 的一元二次方程，则m 的取值范围是第10题图形是（）14•在一个不透明的袋子里，有 2个白球和2个红球，它们只有颜色上的区别, 从袋子里随机摸出一个球记下颜色放回，再随机地摸出一个球，则两次都摸到白球的概率为（ 17•在一个不透明的口袋中，有若干个红球和白球，它们除颜色外都相同, 个球，摸到红球的概率 0.75，若白球有3个，则红球有 _______________________________________________________________ 个。