第2章一元线性回归分析

合集下载

计量经济学【一元线性回归模型——回归分析概述】

四、随机误差项的涵义
随机误差项是在模型设定中省略下来而又集体的
影响着被解释变量 Y 的全部变量的替代物。涵义如
下： 1、在解释变量中被忽略的因素的影响； 2、变量观测值观测误差的影响； 3、模型关系的设定误差的影响； 4、其它随机因素的影响。设定随机误差项的主要原因： 1、理论的含糊性； 2、数据的欠缺； 3、节省的原则。
➢ 例如：
二、总体回归函数（方程）PRF Population regression function
由于变量间统计相关关系的随机性(非确定性)，回归分析关心的是根据解释变量的已知或给定值，考察被解释变量的总体均值，即当解释变量取某个确定值时，与之统计相关的被解释变量所有可能出现的对应值的平均值。
样本回归函数的随机形式：
其中为(样本)残差(Residual)，可看成是随机误差项的的具体估计值。由于引入随机项，称为样本回归模型。
总体回归线与样本回归线的基本关系
例2.1：一个假想的社区是由60户家庭组成的总体，要
研究该社区每月家庭消费支出Y 与每月家庭可支配收入 X 的关系；即知道了家庭的每月收入，预测该社区家庭
每月消费支出的 (总体) 平均水平。为达到此目的，将该 60户家庭划分为组内收入差不多的10组，以分析每一收入组的家庭消费支出。
表2.1 某社区家庭每月收入与消费支出调查统计表
回归分析是研究因果相关，也就是有因果关系的相关关系；既然回归分析是研究变量之间的因果关系，因此回归分析对变量的处理方法存在不对称性，也就是说，回归分析将变量区分为被解释变量和解释变量，其中被解释变量是“结果”，解释变量是“原因”，并且回归分析方法认为作为“原因”的解释变量属于非随机变量，作为“结果”的被解释变量为随机变量；也就是说，作为“原因”的解释变量取确定值时，作为“结果”的被解释变量取值是随机的。

一元线性回归分析

C=α+βy + µ
其中， µ是随机误差项。是随机误差项。其中，是随机误差项根据该方程，的值，根据该方程，每给定一个收入 y 的值，消并不是唯一确定的，费C并不是唯一确定的，而是有许多值，并不是唯一确定的而是有许多值，他们的概率分布与µ的概率分布相同的概率分布相同。他们的概率分布与的概率分布相同。线性回归模型的特征：线性回归模型的特征：有随机误差项！有随机误差项！
21
说
明
一、严格地说，只有通过了线性关系的检验，才严格地说，只有通过了线性关系的检验，能进行回归参数显著性的检验。能进行回归参数显著性的检验。有些教科书在介绍回归参数的检验时没有考虑线性关系的检验，这是不正确的。性关系的检验，这是不正确的。因为当变量之间的关系没有通过线性检验时，的关系没有通过线性检验时，进行回归参数显著性的检验是没有意义的。性的检验是没有意义的。在一元线性回归分析中，二、在一元线性回归分析中，即只有一个解释变量时，这两种检验是统一的。量时，这两种检验是统一的。但在多元回归分析这两种检验的意义是不同的。中，这两种检验的意义是不同的。为了说明该问题，为了说明该问题，我们在本章中依然把两种检验分开论述。分开论述。
13
为了达到上述目的，为了达到上述目的，我们直观上会采用以下准则：用以下准则：选择这样的SRF，使得：选择这样的，使得：
残差和∑ ε i = ∑ ( yi − yi )尽可能小！ ˆ
但这个直观上的准则是否是一个很好的准则呢？我们通过以下图示说明：的准则呢？我们通过以下图示说明：
14
12
ˆx i + ε i yi = α + β ˆ ˆ 即：y i = y i + ε i ˆ ∴ ε i = yi − yi

计量经济学第2章一元线性回归模型

15
~ ~ • 因为 2是β2的线性无偏估计，因此根据线性性， 2 ~ 可以写成下列形式： 2 CiYi
• 其中αi是线性组合的系数，为确定性的数值。则有
E ( 2 ) E[ Ci ( 1 2 X i ui )]
E[ 1 Ci 2 Ci X i Ci ui ]
6
ˆ ˆ X )2 ] ˆ , ˆ ) [ (Yi Q( 1 2 i 1 2 ˆ ˆ X 2 Yi 1 2 i ˆ ˆ 1 1 2 ˆ ˆ ˆ ˆ [ ( Y X ) ] 1 2 i Q( 1 , 2 ) i ˆ ˆ X X 2 Yi 1 2 i i ˆ ˆ 2 2
16
~
i
i
• 因此 ~ 2 CiYi 1 Ci 2 Ci X i Ci ui 2 Ci ui
• 再计算方差Var( ) 2 ，得 ~ ~ ~ 2 ~ Var ( 2 ) E[ 2 E ( 2 )] E ( 2 2 ) 2
C E (ui )
2 i 2 i
i
~
i
i
i
i
E ( 2 Ci ui 2 ) 2 E ( Ci ui ) 2
i
2 u
C
i
2 i
i
~ ˆ)的大小，可以对上述表达式做一 • 为了比较Var( ) 和 Var( 2 2
些处理： ~ 2 2 2 2 Var ( 2 ) u C ( C b b ) i u i i i
8
• 2.几个常用的结果
• （1） • （2） • （3） • （4）

计量经济学课件4

以上5个假设也称为线性回归模型的经典假设，满足该假设的线性回归模型称为经典线性回归模型。而前4个假设称为高斯-马尔可夫假设，这些假设能保证估计
方法G有i*良好的统计性质。
2.3 一元线性回归模型的参数估计 2.3.1普通最小二乘法
由（2.3.2）、（2.3.3）式得：
（2.3.4）
（2.3.5）
这样我们就定义了变量x和y之间的一个简单线性回归模型，也称为两变量或一元线性回归模型。其线性的含义表示无论变量x的取值如何，它的任何一单位变化都对变量y产生相同的影响。
2.2 一元线性回归模型的基本假设 2.2.1对回归模型设定的假设
假设1：回归模型是正确设定的。模型的正确设定主要包括两方面的内容：（1）模型选择了正确的变量；（2）模型选择了正确的函数形式。计量经济模型应用于现实经济问题时，因果关系必须有经济理论为其依据，函数关系也必须要有可靠的依据。模型选择了正确的变量指既没有遗漏重要的相关变量，也没有多选无关变量且有经济理论支持该因果关系。当假设1满足时，称模型没有设定偏误，否则模型存在设定偏误。假设1‘：线性回归模型回归模型对变量不一定是线性的，但对参数是线性的。在计量经济学里说到的线性回归都是指关于参数是线性的。要注意的是回归模型的估计原理不依赖于y和x的定义，但系数的解释依赖于它们的定义。
xi(yi y ) (xi x )xi
x(y i x(xi
y) x)
(xi x )(yi y ) (xi x )2
2.3 一元线性回归模型的参数估计 2.3.2最小二乘估计量的统计性质
(1)线性性
这里指 ˆ0和 ˆ1分别是 y1, y2 , , yn 的线性函数。
令 ki
(xi x ) ，代入上式得

第二章一元线性回归

n ei 0 i 1 n xe 0 i i i 1
经整理后,得正规方程组
n n ˆ ˆ n ( x ) 0 i 1 yi i 1 i 1 n n n ( x ) ˆ ( x 2 ) ˆ xy i 0 i 1 i i i 1 i 1 i 1
y ˆ i 0 1xi ˆi 之间残差的平方和最小。使观测值 y i 和拟合值 y
ei y i y ˆi
n
称为yi的残差
ˆ , ˆ ) ˆ ˆ x )2 Q( ( y i 0 1i 0 1
i 1
min ( yi 0 1 xi ) 2
i
xi x
2 ( x x ) i i 1 n
yi
2 .3 最小二乘估计的性质
二、无偏性
ˆ ) E ( 1
i 1 n
n
xi x
2 ( x x ) j j 1 n
其中用到
E ( yi )
( x x) 0 (xi x) xi (xi x)2
二、用统计软件计算
1．例2.1 用Excel软件计算
什么是P 值?(P-value)
• P 值即显著性概率值，Significence Probability Value
•
是当原假设为真时所得到的样本观察结果或更极端情况出现的概率。
P值与t值： P t t值 P值

•
它是用此样本拒绝原假设所犯弃真错误的真实概率，被称为观察到的(或实测的)显著性水平。P值也可以理解为在零假设正确的情况下，利用观测数据得到与零假设相一致的结果的概率。
2 .1 一元线性回归模型

第二章经典单方程计量经济学模型：一元线性回归模型

第二章经典单方程计量经济学模型：一元线性回归模型一、内容提要本章介绍了回归分析的大体思想与大体方式。

第一，本章从整体回归模型与整体回归函数、样本回归模型与样本回归函数这两组概念开始，成立了回归分析的大体思想。

整体回归函数是对整体变量间关系的定量表述，由整体回归模型在假设干大体假设下取得，但它只是成立在理论之上，在现实中只能先从整体中抽取一个样本，取得样本回归函数，并用它对整体回归函数做出统计推断。

本章的一个重点是如何获取线性的样本回归函数，要紧涉及到一般最小二乘法（OLS）的学习与把握。

同时，也介绍了极大似然估量法（ML）和矩估量法（MM）。

本章的另一个重点是对样本回归函数可否代表整体回归函数进行统计推断，即进行所谓的统计查验。

统计查验包括两个方面，一是先查验样本回归函数与样本点的“拟合优度”，第二是查验样本回归函数与整体回归函数的“接近”程度。

后者又包括两个层次：第一，查验说明变量对被说明变量是不是存在着显著的线性阻碍关系，通过变量的t查验完成；第二，查验回归函数与整体回归函数的“接近”程度，通过参数估量值的“区间查验”完成。

本章还有三方面的内容不容轻忽。

其一，假设干大体假设。

样本回归函数参数的估量和对参数估量量的统计性质的分析和所进行的统计推断都是成立在这些大体假设之上的。

其二，参数估量量统计性质的分析，包括小样本性质与大样本性质，尤其是无偏性、有效性与一致性组成了对样本估量量好坏的最要紧的衡量准那么。

Goss-markov定理说明OLS估量量是最正确线性无偏估量量。

其三，运用样本回归函数进行预测，包括被说明变量条件均值与个值的预测，和预测置信区间的计算及其转变特点。

二、典型例题分析例一、令kids表示一名妇女生育小孩的数量，educ表示该妇女同意过教育的年数。

生育率对教育年数的简单回归模型为β+μβkids=educ+1（1）随机扰动项μ包括什么样的因素？它们可能与教育水平相关吗？（2）上述简单回归分析能够揭露教育对生育率在其他条件不变下的阻碍吗？请说明。

计量经济学第二篇一元线性回归模型

第二章一元线性回归模型2.1 一元线性回归模型的基本假定有一元线性回归模型（统计模型）如下， y t = β0 + β1 x t + u t上式表示变量y t 和x t 之间的真实关系。

其中y t 称被解释变量（因变量），x t 称解释变量（自变量），u t 称随机误差项，β0称常数项，β1称回归系数（通常未知）。

上模型可以分为两部分。

（1）回归函数部分，E(y t ) = β0 + β1 x t ,（2）随机部分，u t 。

图2.1 真实的回归直线这种模型可以赋予各种实际意义，居民收入与支出的关系；商品价格与供给量的关系；企业产量与库存的关系；身高与体重的关系等。

以收入与支出的关系为例。

假设固定对一个家庭进行观察，随着收入水平的不同，与支出呈线性函数关系。

但实际上数据来自各个家庭，来自同一收入水平的家庭，受其他条件的影响，如家庭子女的多少、消费习惯等等，其出也不尽相同。

所以由数据得到的散点图不在一条直线上（不呈函数关系），而是散在直线周围，服从统计关系。

“线性”一词在这里有两重含义。

它一方面指被解释变量Y 与解释变量X 之间为线性关系，即另一方面也指被解释变量与参数0β、1β之间的线性关系，即。

1ty x β∂=∂，221ty β∂=∂0 ，1ty β∂=∂，2200ty β∂=∂2.1.2 随机误差项的性质随机误差项u t 中可能包括家庭人口数不同，消费习惯不同，不同地域的消费指数不同，不同家庭的外来收入不同等因素。

所以在经济问题上“控制其他因素不变”是不可能的。

随机误差项u t 正是计量模型与其它模型的区别所在，也是其优势所在，今后咱们的很多内容，都是围绕随机误差项u t 进行了。

回归模型的随机误差项中一般包括如下几项内容：（1）非重要解释变量的省略，（2）数学模型形式欠妥，（3）测量误差等，（4）随机误差（自然灾害、经济危机、人的偶然行为等）。

2.1.3 一元线性回归模型的基本假定通常线性回归函数E(y t ) = β0 + β1 x t 是观察不到的，利用样本得到的只是对E(y t ) =β0 + β1 x t 的估计，即对β0和β1的估计。

第二章一元线性回归模型知识点

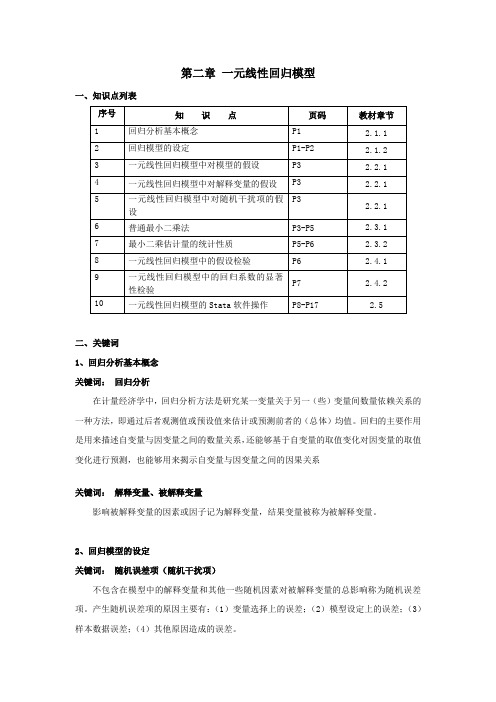
第二章一元线性回归模型一、知识点列表二、关键词1、回归分析基本概念关键词：回归分析在计量经济学中，回归分析方法是研究某一变量关于另一（些）变量间数量依赖关系的一种方法，即通过后者观测值或预设值来估计或预测前者的（总体）均值。

回归的主要作用是用来描述自变量与因变量之间的数量关系，还能够基于自变量的取值变化对因变量的取值变化进行预测，也能够用来揭示自变量与因变量之间的因果关系关键词：解释变量、被解释变量影响被解释变量的因素或因子记为解释变量，结果变量被称为被解释变量。

2、回归模型的设定关键词：随机误差项（随机干扰项）不包含在模型中的解释变量和其他一些随机因素对被解释变量的总影响称为随机误差项。

产生随机误差项的原因主要有：（1）变量选择上的误差；（2）模型设定上的误差；（3）样本数据误差；（4）其他原因造成的误差。

关键词：残差项（residual ）通过样本数据对回归模型中参数估计后，得到样本回归模型。

通过样本回归模型计算得到的样本估计值与样本实际值之差，称为残差项。

也可以认为残差项是随机误差项的估计值。

3、一元线性回归模型中对随机干扰项的假设关键词：线性回归模型经典假设线性回归模型经典假设有5个，分别为：（1）回归模型的正确设立；（2）解释变量是确定性变量，并能够从样本中重复抽样取得；（3）解释变量的抽取随着样本容量的无限增加，其样本方差趋于非零有限常数；（4）给定被解释变量，随机误差项具有零均值，同方差和无序列相关性。

（5）随机误差项服从零均值、同方差的正态分布。

前四个假设也称为高斯马尔科夫假设。

4、最小二乘估计量的统计性质关键词：普通最小二乘法（Ordinary Least Squares ，OLS ）普通最小二乘法是通过构造合适的样本回归函数，从而使得样本回归线上的点与真实的样本观测值点的“总体误差”最小，即：被解释变量的估计值与实际观测值之差的平方和最小。

ββ==---∑∑∑nn n222i i 01ii=111ˆˆmin =min ()=min ()i i i i u y y y x关键词：无偏性由于未知参数的估计量是一个随机变量，对于不同的样本有不同的估计量。

第2章一元线性回归模型

第二章
一元线性回归模型
回归分析是计量经济学的基础内容！
本章介绍一元线性回归模型，最小二乘估计方法及其性质，参数估计的假设检验、预测等。
浙江财经大学倪伟才
1
本章主要内容
2 .1 一元线性回归模型
2 .2 参数β0、β1的估计
2 .3 最小二乘估计的性质
2 .4 回归方程的显著性检验 2 .5 残差分析 2 .6 回归系数的区间估计
浙江财经大学倪伟才 10
回归的术语
y的各种名称：因变量(dependent variable)或被解释变量 (explained variable)或回归子(regressand)或内生(endogenous)； X的各种名称：自变量(independent variable)或解释变量 (explanatory variable)或回归元(regressor)或外生(exogenous) U的各种名称：随机误差项或随机扰动项(stochastic error term, random disturbance term ): 表示其它因素的影响，是不可观测的随机误差！
浙江财经大学倪伟才
9
2.1一元线性回归模型
由于两个变量y, x具有明显的线性关系，故考虑直线方程y=0+1x（函数表达的是确定性关系，有缺陷！） y=0+1x+u, 其中u表示除x外，影响y的其它一切因素。将y与x之间的关系用两部分来描述： a. 一部分0+1x ，由x的变化引起y变化； b.另一部分u ，除x外的其它一切因素引起y变化。参数(parameters) 0 , 1 ; 0 称为回归常数(截距)（intercept, constant）， 1称为回归斜率(slope)

第二章一元线性回归模型1

第二章一元线性回归模型计量经济学在对经济现象建立经济计量模型时，大量地运用了回归分析这一统计技术，本章和下一章将通过一元线性回归模型、多元线性回归模型来介绍回归分析的基本思想。

第一节回归分析的几个基本问题回归分析是经济计量学的主要工具，下面我们将要讨论这一工具的性质。

一、回归分析的性质（一）回归释义回归一词最先由F •加尔顿（Francis Galt on ）提出。

加尔顿发现，虽然有一个趋势，父母高，儿女也高：父母矮，儿女也矮，但给定父母的身高，儿女辈的平均身高却趋向于或者“回归” 到全体人口的平均身高。

或者说，尽管父母双亲都异常高或异常矮，而儿女的身高则有走向人口总体平均身高的趋势（普遍回归规律）。

加尔顿的这一结论被他的朋友K •皮尔逊（Karl pearson）证实。

皮尔逊收集了一些家庭出身1000多名成员的身高记录，发现对于一个父亲高的群体，儿辈的平均身高低于他们父辈的身高，而对于一个父亲矮的群体，儿辈的平均身高则高于其父辈的身高。

这样就把高的和矮的儿辈一同“回归”到所有男子的平均身高，用加尔顿的话说，这是“回归到中等” 。

回归分析是用来研究一个变量（被解释变量Explained variable或因变量Dependent variable 与另一个或多个变量（解释变量Explanatory variable或自变量Independent variable之间的关系。

其用意在于通过后者（在重复抽样中）的已知或设定值去估计或预测前者的（总体）均值。

下面通过几个简单的例子，介绍一下回归的基本概念。

例子1.加尔顿的普遍回归规律。

加尔顿的兴趣在于发现为什么人口的身高分布有一种稳定性,我们关心的是，在给定父辈身高的条件下找出儿辈平均身高的变化。

也就是一旦知道了父辈的身高，怎样预测儿辈的平均身高。

为了弄清楚这一点，用图 1.1 表示如下图 1.1 对应于给定父亲身高的儿子身高的假想分布图 1.1 展示了对应于设定的父亲身高, 儿子在一个假想人口总体中的身高分布, 我们不难发现,对应于任一给定的父亲身高, 相对应都有着儿子身高的一个分布范围，同时随着父亲身高的增加，儿子的平均身高也增加，为了清楚起见，在1.1散点图中勾画了一条通过这些散点的直线，以表明儿子的平均身高是怎样随着父亲的身高增加而增加的。

第二章一元线性回归模型

0 1
∂Q ˆ ˆ = −2∑ (Yi − β 0 − β1 X i ) = 0 ∂β ˆ0 ˆ ˆ ∂Q = −2∑ (Y − β − β X )X = 0 i 0 1 i i ˆ ∂β1
化简得：化简得：
ˆ ˆ ∑ (Yi − β 0 − β1 X i ) = 0 ˆ ˆ ∑ (Yi − β 0 − β1 X i )X i = 0
2.总体回归方程（线）或回归函数总体回归方程（总体回归方程即对（）式两端取数学期望：即对（2.8）式两端取数学期望：
E y i）= β 0 + β 1 x i （
（2.9）
（2.9）为总体回归方程。由于随机项的影响，所）为总体回归方程。由于随机项的影响，有的点（）一般不在一条直线上；有的点（x,y）一般不在一条直线上；但所有的点（x,Ey）在一条直线上。总体回归线描述了与y ）在一条直线上。总体回归线描述了x与之间近似的线性关系。之间近似的线性关系。
Yi = β X i + ui
需要估计，这个模型只有一个参数需要估计，其最小二乘估计量的表达式为：小二乘估计量的表达式为：
∑XY ˆ β= ∑X
i i 2 i
例2.2.1：在上述家庭可支配收入-消费支出例中，对：在上述家庭可支配收入-消费支出例中，于所抽出的一组样本数据，于所抽出的一组样本数据，参数估计的计算可通过下面的表2.2.1进行。进行。的表进行
二、一元线性回归模型上述模型中，为线性的，上述模型中，若f(Xi)为线性的，这时的模型为线性的一元线性回归模型：即为一元线性回归模型：
yi = β 0 + β1 xi + ui 其中：yi为被解释变量，xi为解释变量，ui为随机误差项，β 0、β1为回归系数。

计量经济学第二章一元线性回归模型

计量经济学第二章一元线性回归模型第二章一元线性回归模型第一节一元线性回归模型及其古典假定第二节参数估计第三节最小二乘估计量的统计特性第四节统计显著性检验第五节预测与控制第一节回归模型的一般描述（1）确定性关系或函数关系：变量之间有唯一确定性的函数关系。

其一般表现形式为：一、回归模型的一般形式变量间的关系经济变量之间的关系，大体可分为两类：（2.1)（2）统计关系或相关关系：变量之间为非确定性依赖关系。

其一般表现形式为：(2.2)例如：函数关系：圆面积S =统计依赖关系/统计相关关系：若x和y之间确有因果关系，则称(2.2)为总体回归模型，x(一个或几个）为自变量（或解释变量或外生变量），y为因变量（或被解释变量或内生变量），u为随机项，是没有包含在模型中的自变量和其他一些随机因素对y的总影响。

一般说来，随机项来自以下几个方面：1、变量的省略。

由于人们认识的局限不能穷尽所有的影响因素或由于受时间、费用、数据质量等制约而没有引入模型之中的对被解释变量有一定影响的自变量。

2、统计误差。

数据搜集中由于计量、计算、记录等导致的登记误差；或由样本信息推断总体信息时产生的代表性误差。

3、模型的设定误差。

如在模型构造时，非线性关系用线性模型描述了；复杂关系用简单模型描述了；此非线性关系用彼非线性模型描述了等等。

4、随机误差。

被解释变量还受一些不可控制的众多的、细小的偶然因素的影响。

若相互依赖的变量间没有因果关系，则称其有相关关系。

对变量间统计关系的分析主要是通过相关分析、方差分析或回归分析(regression analysis)来完成的。

他们各有特点、职责和分析范围。

相关分析和方差分析本身虽然可以独立的进行某些方面的数量分析，但在大多数情况下，则是和回归分析结合在一起，进行综合分析，作为回归分析方法的补充。

回归分析(regression analysis)是研究一个变量关于另一个（些）变量的具体依赖关系的计算方法和理论。

第二章一元线性回归模型

__
__
2
/n
★样本相关系数r是总体相关系数的一致估计
相关系数有以下特点：
• • • • 相关系数的取值在-1与1之间。（2）当r=0时，线性无关。（3）若r＞0 ，正相关，若r＜0 ，负相关。（4）当0＜|r|＜1时，存在一定的线性相关关系，越接近于1，相关程度越高。 • （5）当|r|=1时，表明x与y完全线性相关（线性函数），若r=1，称x与y完全正相关；若r=-1，称x与y完全负相关。 • 多个变量之间的线性相关程度，可用复相关系数和偏相关系数去度量。
●假定解释变量X在重复抽样中取固定值。但与扰动项u是不相关的。(从变量X角度看是外生的)
注意: 解释变量非随机在自然科学的实验研究中相对
Yi 1 2 X i ui
●假定解释变量X是非随机的，或者虽然X是随机的，
容易满足，经济领域中变量的观测是被动不可控的， X非随机的假定并不一定都满足。
E( y xi ) 0 1xi
11
• 可以看出,虽然每个家庭的消费支出存在差异,但平均来说，家庭消费支出是随家庭可支配收入的递增而递增的。当x取各种值时, y的条件均值的轨迹接近一条直线,该直线称为y对x的回归直线。（回归曲线）。 • 把y的条件均值表示为x的某种函数，可写为：
E( y xi ) 0 1xi
Var ( y xi ) 2
Cov( yi , y j ) 0
y | xi ~ N (0 1xi , )
2
22
第三节参数估计
• 一、样本回归方程
• 对于
yi 0 1 xi ui
• 在满足古典假定下，两边求条件均值，得到总体回归函数：

第2章一元线性回归模型

布图上的点接近于一条曲线时，称为非线性相关。简单相关按
符号又可分为正相关（见图2.3.4 ）、负相关（见图2.3.8 ）和零相关（见图2.3.6 ）。两个变量趋于在同一个方向变化时，即同
增或同减，称为变量之间存在正相关；当两个变量趋于在相反
方向变化时，即当一个变量增加，另一个变量减少时，称为变量之间存在负相关；当两个变量的变化相互没有关系时，称为
4、普通最小二乘法
为什么要使用OLS？（1）OLS的应用相对简便；（2）以最小化残差平方和为目标在理论很合理；（3）OLS估计量有很多有用的性质。 1）估计的回归线通过Y和X的均值。下列等式总是
ˆ ˆX 严格成立的：设下，可以证明，OLS是 “最优”的估计方法。
2.2.2 最小二乘估计量的性质
一个用于考察总体的估计量，可从如下几个方面考察其
优劣性：（1）线性。即它是否是另一个随机变量的线性函数；
（2）无偏性。即它的均值或期望是否等于总体的真实值；
（3）有效性。即它是否在所有的线性无偏估计量中具有最小方差；（4）渐近无偏性。即样本容量趋于无穷大时，它的均值序列趋于总体的真值；（5）一致性。即样本容量趋于无穷大时，它是否依概率收敛于总体的真值；
1．总变差的分解
ˆ b ˆX ˆ b Yt的估计值位于估计的回归线 Y t 0 1 t 上，Y围绕其均值的变异 (Y Y )可被分解为两部分：
ˆ Y ) (1) (Y t
ˆ) (2) (Yt Y t
样本回归函数：
3．相关系数检验
（1）变量相关的定义和分类
相关：指两个或两个以上变量间相互关系的程度或强度。
2 2 ˆ e ( Y Y ) i i OLS 最小化 i i 1 i 1

第二章一元线性回归分析基础

加，消费增加，但消费的增长低于收入的增长，即消
费对收入的弹性小于1。它的数学表述为
Y X
0
Y X
1,
Y X
Y X
其中Y为消费额，X为收入。
该线性方程描述了消费与收入之间的确定关系，即给定一个收入值，可以根据方程得到一个唯一确定的消费值。但实际上消费与收入间的关系不是准确实现的。
原因：入随机误差项，将变量之间的关系用一个线性随机方程来描述，用随机数学的方法来估计方程中的参数，这就是线性回归模型的特征，也就是线性计量经济学模型的特征。
二、一元线性回归模型
单方程线性回归模型的一般形式为
Yi 1 2 X2i 3 X3i k Xki ui ,i 1,2, ,n 其中Y为被解释变量，X 2 ,X 3 , ,X n 为解释变量。
化。
如果误差项的方差不同，那么与其对应的观测值Yi的可靠程度也不相同。这会使参数的检验和利用模型进行预测复杂化。而满足同方差假设，将使检验和预测简化。
假设3 表示不同的误差项之间互相独立，同时，不同的被解释变量在统计上也是互相独立的。即
Cov(Yi, Yj)= E(Yi－E(Yi)) (Yj－E(Yj))= E(uiuj)=0， i≠j 假假设设4，自通动常满X足i为，确即定性变量，即非随机变量，此时，该
也可以用显函数形式表示为 Y f ( X1,X 2 , ,X n )
其中最简单的形式为一元线性函数关系。
例如当某种商品单价P固定不变，其销售收入y与销售的商品数量x之间的关系为一元线性关系，即y = Px
如果用x，y构成的直角坐标图来表示，上式所表示的函数关系为一条经过坐标原点的直线，所有可能的点都在这条直线上。
Cov(ui, Xi)= E(ui－E(ui)) (Xi－E(Xi))=0，i=1,2, ……,n 假设5 随机误差项服从零均值，同方差的正态分布。即

第二节一元线性回归分析

第二节一元线性回归分析本节主要内容：回归是分析变量之间关系类型的方法，按照变量之间的关系，回归分析分为：线性回归分析和非线性回归分析。

本节研究的是线性回归，即如何通过统计模型反映两个变量之间的线性依存关系.回归分析的主要内容:1.从样本数据出发，确定变量之间的数学关系式；2.估计回归模型参数；3.对确定的关系式进行各种统计检验,并从影响某一特定变量的诸多变量中找出影响显著的变量。

一、一元线性回归模型:一元线性模型是指两个变量x、y之间的直线因果关系。

理论回归模型:理论回归模型中的参数是未知的,但是在观察中我们通常用样本观察值估计参数值，通常用分别表示的估计值，即称回归估计模型：回归估计模型：二、模型参数估计：用最小二乘法估计：【例3】实测某地四周岁至十一岁女孩的七个年龄组的平均身高（单位：厘米）如下表所示某地女孩身高的实测数据建立身高与年龄的线性回归方程。

根据上面公式求出b0=80。

84，b1=4。

68。

三．回归系数的含义（2）回归方程中的两个回归系数，其中b0为回归直线的启动值，在相关图上变现为x=0时，纵轴上的一个点,称为y截距；b1是回归直线的斜率，它是自变量(x）每变动一个单位量时，因变量（y）的平均变化量。

（3）回归系数b1的取值有正负号。

如果b1为正值，则表示两个变量为正相关关系,如果b1为负值，则表示两个变量为负相关关系。

[例题·判断题］回归系数b的符号与相关系数r的符号，可以相同也可以不同.（ )答案：错误解析：回归系数b的符号与相关系数r的符号是相同的=a+bx，b<0，则x与y之间的相关系数（ )［例题·判断题]在回归直线yca。

r=0 b.r=1 c。

0<r〈1 d.—1<r〈0答案:d解析：b〈0,则x与y之间的相关系数为负即—1〈r〈0［例题·单选题］回归系数和相关系数的符号是一致的，其符号均可用来判断现象( ）a。

线性相关还是非线性相关 b.正相关还是负相关c。

第02章-一元线性回归模型

四、拟合优度的度量
• 基本概念：
拟合优度衡量的是样本回归线对样本观测值的拟合程度。样本观测值距回归线越近，拟合优度越高，x对y的解释程度越强。
• 样本观测值、拟合值、样本均值之间的关系
ˆ ˆ ( yt − y ) = ( yt − yt ) + ( yt − y )
?相关分析适用于无明确因果关系的变量之间的关系判断常使用的工具是相关系数相关系数对称的看待两个变量相关系数仅判断变量间是否存在线性相关相关系数判断的是统计依赖关系?如果两个变量之间存在因果关系则需要建立回归模型采用回归分析的方法判断变量之间的因果性效应一元线性回归模型的建立?在回归模型中往往假定解释变量是因被解释变量是果而分析的目标则是确定解释变量对被解释变量的因果性效应的具体数值
5. 一元线性回归模型的假定条件 • 用样本估计总体回归函数，总会存在偏差（样本不是总体，而且模型存在随机干扰项），为了保证估计结果具有良好的性质，通常要对模型中的变量、模型形式以及随机误差项提出一些假定条件 • 对模型形式和变量的假定
–假定解释变量x是非随机的，或者虽然是随机的，但与随机误差项u不相关 –假定变量和模型无设定误差
第2章一元线性回归模型
一、模型的建立及其假定条件二、普通最小二乘估计（OLS）三、OLS估计量的统计性质四、拟合优度的度量五、回归参数的显著性检验与置信区间六、一元线性回归模型的预测
一、模型的建立及其假定条件
1. 经济变量之间的关系 • 计量经济分析研究经济变量之间的关系及其变化规律。 • 两变量之间可能存在的关系：
ˆ ˆ ˆ yt = β 0 + β1 xt
• 样本回归函数（SRF）表示在图形中即为样本回归线 • 需要注意：

第二章：一元线性回归模型理论与方法(第二部分)

最小二乘法的数学原理
• 纵向距离是Y的实际值与拟合值之差，差异大拟合不好，差异小拟合好，所以又称为拟合误差或残差。 • 将所有纵向距离平方后相加，即得误差平方和，“最好”直线就是使误差平方和最小的直线。 • 于是可以运用求极值的原理，将求最好拟合直线问题转换为求误差平方和最小。
普通最小二乘法（OLS）
这三个准则也称作估计量的小样本性质。
拥有这类性质的估计量称为最佳线性无偏估计量（best liner unbiased estimator, BLUE）。
高斯—马尔可夫定理(Gauss-Markov theorem)
在给定经典线性回归的假定下，最小二乘估计量是具有最小方差的线性无偏估计量。
ˆ , ˆ 的均 2、无偏性，即以X的所有样本值为条件，估计量 0 1 0与1 。值（期望）等于总体回归参数真值
ˆ X i2 Yi X i Yi X i 0 nX i2 (X i ) 2 ˆ nYi X i Yi X i 1 2 2 n X ( X ) i i
对数似然函数极大化的一阶条件
结构参数的 ML估计量
最大似然法与普通最小二乘法讨论

已知一组样本观测值（Yi，Xi）(i=1,2, …,n)，要求样本回归函数尽可能好地拟合这组值，即样本回归线上的点Y ˆi 与真实观测点Yi的“总体” 误差尽可能地小。在技术处理上我们一般采用 “最小二乘法”。

最小二乘原则：由于估计值和实测值之差可正可负，简单求和可能将很大的误差抵消掉，因此，只有平方和才能反映二者在总体上的接近程度。
n 1
证残差与 Yˆ 的样本协方差为0，即证： i
eiYˆ i
0
ห้องสมุดไป่ตู้

第2章一元线性回归分析

计量经济学【一元线性回归模型——回归分析概述】

一元线性回归分析

计量经济学第2章 一元线性回归模型

计量经济学课件4

第二章 一元线性回归

第二章经典单方程计量经济学模型：一元线性回归模型

计量经济学第二篇一元线性回归模型

第二章 一元线性回归模型 知识点

第2章一元线性回归模型

第二章一元线性回归模型1

第二章 一元线性回归模型

计量经济学 第二章 一元线性回归模型

第二章 一元线性回归模型

第2章一元线性回归模型

第二章 一元线性回归分析基础

第二节一元线性回归分析

第02章-一元线性回归模型

第二章：一元线性回归模型理论与方法(第二部分)

计量经济学第2章一元线性回归模型

第二章一元线性回归

第二章一元线性回归模型知识点

第二章一元线性回归模型

计量经济学第二章一元线性回归模型

第二章一元线性回归模型

第二章一元线性回归分析基础