IIR数字滤波器的优化设计和DSP实现
实验二IR数字滤波器设计与实现

实验二IIR数字滤波器设计与实现一.实验目的.1. 学会调用DSPM程序设计IIR数字滤波器,并给出H(z)的具体表达式。
2. 学会将滤波器“系数”与滤波汇编程序结合,编译、链接、装入DSP试验箱电路板内存,并装入DSP芯片运行,完成对模拟信号的采样进行滤波。
3. 通过改变信号源信号频率,观察滤波后信号的衰减情况与信号频率的关系,体会滤波器的工作原理。
二.实验原理1.调用DSP试验箱配套的Matlab源程序DSPM,通过自己给定IIR数字滤波器关键参数(f p,f st,f s, N,A p,A s等)由计算机系统完成IIR数字滤波器H(z)函数系数的计算,并给出(b0,b1,…b M,a1,…a N)。
2.通过将(b0,b1,…b M,a1,…a;f s, N )与滤波器汇编程序结合,并编译、链接、装入DSP试验箱电路板内存,并装入DSP芯片运行实现对信号的滤波,这一系列过程均在DSPM程序管理下自动进行。
3.滤波效果的检验,可通过改变信号源频率、观察输出信号在示波器屏上衰减情况来完成。
三.实验任务1.进一步熟悉DSP实验箱电路各模块的功能。
2.能独立完成实验一所提的软件安装过程。
3.设计一个IIR数字滤波器,要求Fs=64kHz,fp=3000Hz,N=3,调用DSPM完成设计,记录相关参数,并给出H(z)的具体表达式。
4.调用DSP.exe程序,实现对信号的滤波。
5.记录信号开始衰减的频率及信号衰减为0.7、0.5、0.1各处相应的信号频率。
6.信号分别选为三角波,正弦波,方波,调整信号频率,观察记录输出信号波形及输入信号频率及示波器通带截止频率的关系。
四.试验设备及准备1.所用设备:DSP试验箱,微机,示波器。
2.连线微机------------ DSP实验箱(COM口)示波器:CH1---------信号源CH2---------D/A输出(TPD05)DSP实验箱电路板:A/D:PA01-------TP501(信号源)PA02-------GN DP A03-------TP902(DSP串口1收数据)1)PA04-------TP911(FSR1)PA05-------TP913(BCLKD/A:PD01------TP905(DX0)PD02-------TP908(BCLK0)PD03-------TP907(FS0)五.试验数据分析1.画所设计的IIR滤波器的幅频特性曲线。
用DSP实现IIR滤波器

前
MPY @B2,A LTD @x1
;计算前向通道,x2*B2→A ;x1送T寄存器,x1移至x2单元
向 MAC @B1,A ;x2*B2+x1*B1→A
运 LTD @x0
;x0送T寄存器,x0移至x1单元
算
MAC @B0,A STH A,@x0
;x2*B2+x1*B1+x0*B0→A ;暂存y(n)=x2*B2+x1*B1+x0*B0→x0单元
X x(n-2)
Y y(n-2)
B B2
A A2
x(n-1) AR4 y(n-1)
AR2 x(n)
y(n) AR5
B1 AR3 A1
B0
(未用)
15
例5-32 编写直接形式二阶IIR滤波器的源程序。
.title “IIR3.asm” ;给汇编程序取名
.mmregs
;说明存储器映象寄存器
.def start ;定义标号start的起始位置
.text
start: SSBX FRCT ;指明进行小数乘法
STM #x,AR1 ;传送初始数据x(n-2),x(n-1)
RPT #1
;重复二次下条指令
MVPD #table,*AR1+ ;x(n-2)=0,x(n-1)=0
STM #Y,AR1 ;传送初始数据y(n-2),y(n-1)
RPT #1
是有限长序列。而IIR滤波器的脉冲传递在Z平面上有
极点存在,ai≠0,其单位冲激响应是无限长序列。 2
特点
IIR滤波器与FIR滤波器的一个重要区别是,IIR滤 波器可以用较少的阶数获得很高的选择特性,所用的 存储单元少,运算次数少,具有经济、高效的特点。 但是,在有限精度的运算中,可能出现不稳定现象。 而且,选择性越好,相位的非线性越严重,不像FIR 滤波器可以得到严格的线性相位。
IIR滤波器的DSP实现

IIR滤波器的DSP实现IIR滤波器(Infinite Impulse Response Filter)是一种数字滤波器,其输出跟输入信号有无穷多个时刻的关联,因此称为无限冲激响应滤波器。
与之相对的是有限冲激响应滤波器(FIR Filter)。
以一阶IIR低通滤波器为例,其差分方程可以表示为:y[n]=b0*x[n]+b1*x[n-1]-a1*y[n-1]其中,y[n]表示输出信号,x[n]表示输入信号,b0、b1、a1是滤波器的系数。
在DSP实现中,我们可以按照如下的步骤进行操作:1.初始化滤波器的系数:根据滤波器的设计需求,计算出b0、b1、a1的值。
2.初始化输入输出缓冲区:分配内存空间来存储输入信号x[n]和输出信号y[n]。
3.计算滤波器输出:按照差分方程的形式,遍历输入信号的每个采样点,并根据当前和过去的输入信号和输出信号值,计算当前输出信号的值。
4.更新输入输出缓冲区:将当前输出信号的值保存在输出缓冲区中,并更新输入缓冲区的值,将当前输入信号的值保存在输入缓冲区中。
5.重复步骤3和4,直到处理完所有输入信号的采样点。
6.释放内存空间:在处理完所有输入信号后,释放之前分配的内存空间。
需要注意的是,在实际的DSP实现中,由于数字信号的存储和处理是以离散的方式进行的,可能会遇到一些数值精度和计算精度的问题。
因此,在设计和实现IIR滤波器时,需要进行适当的处理和优化,以减小误差和提高性能。
此外,IIR滤波器还有其他的实现方法,如级联形式(Cascade Form)、直接形式转置(Direct Form II)等。
这些实现方法在性能、计算复杂度和资源消耗等方面可能存在差异,选择合适的实现方法需要综合考虑实际应用需求和性能要求。
总之,IIR滤波器的DSP实现是一项复杂的任务,需要深入理解滤波器的原理和算法,并结合具体应用需求进行实现和优化。
通过合理的设计和实现,可以有效地应用IIR滤波器来处理数字信号,满足各种信号处理应用的需求。
实验四IIR数字滤波器的设计数字信号处理DSP

实验四IIR数字滤波器的设计数字信号处理DSP
IIR数字滤波器是一种基于无限脉冲响应(Infinite Impulse Response)的数字滤波器。
相比于FIR(有限脉冲响应)滤波器,IIR滤
波器具有更低的复杂度和更快的响应速度,但可能会引入一定的稳定性问题。
设计IIR数字滤波器的一般步骤如下:
1.确定滤波器的规格:包括截止频率、通带增益、阻带衰减等参数。
这些参数将直接影响到滤波器的设计和性能。
2.选择滤波器结构:常见的IIR滤波器结构包括直接型I和II结构、级联型结构、并行型结构等。
选择适当的结构取决于滤波器的性能要求和
计算复杂度。
3. 选择滤波器的类型:根据滤波器的设计规格,可以选择巴特沃斯(Butterworth)、切比雪夫(Chebyshev)、椭圆(Elliptic)等不同类
型的IIR滤波器。
4.滤波器设计:根据所选择的滤波器类型和规格,设计滤波器的传递
函数。
可以借助MATLAB等工具进行数值计算和优化。
5.模拟滤波器转为数字滤波器:将设计好的IIR滤波器转换为数字滤
波器。
可以使用双线性变换等方法来实现。
6.实现滤波器:根据转换后的数字滤波器的差分方程,编写相应的代
码来实现滤波器功能。
7.评估滤波器性能:对设计好的IIR数字滤波器进行性能评估,包括
幅频响应、相频响应、群延迟等指标。
8.优化滤波器性能:根据实际情况,对滤波器的设计参数进行优化,以获得更好的性能。
以上是设计IIR数字滤波器的一般步骤,具体的设计方法和过程还需要根据实际情况进行调整。
基于MATLAB的IIR数字滤波器的设计与DSP实现开题报告

《基于MATLAB的IIR数字滤波器的设计与DSP实现》开题报告一、课题的目的和意义1、研究目的我选择了《基于MATLAB的IIR滤波器的设计》这个课题作为毕业设计其主要目的是通过此次课程设计进一步学习和巩固数字信号处理和DSP及其相关知识,并学会利用所学的知识技能,在设计过程中能综合运用所学知识内容,进一步熟悉和掌握MATLAB和DSP的使用方法;对IIR滤波器的原理及其实现有较深的了解;为即将进入社会参加工作打下坚实的基础;掌握收集资料、消化资料和综合资料的能力等等。
2、研究意义随着信息时代和数字世界的到来,数字信号处理已成为今一门极其重要的学科和技术领域。
数字信号处理在通信、语音、图像、自动控制、雷达、军事、航空航天、医疗和家用电器等众多领域得到了广泛的应用。
在数字信号处理应用中,数字滤波器十分重要并已获得广泛应用。
随着电子工业的发展,对滤波器的性能要求越来越高,功能也越来越多,并且要求它们向集成方向发展。
我国滤波器研制和生产与上述要求相差甚远,为缩短这个差距,电子工程和科技人员负有重大的历史责任。
从事电子通信业而不能熟练操作使用MATLAB电子线路设计软件,在工作和学习中将是寸步难行的。
在数学、电子、金融等行业,使用MATLAB等计算机软件对产品进行设计、仿真在很早以前就已经成为了一种趋势,这类软件的问世也极大地提高了设计人员在通信、电子等行业的产品设计质量与效率。
二、文献综述数字滤波器是具有一定传输选择特性的数字信号处理装置,其输入、输出均为数字信号,实质上是一个由有限精度算法实现的线性时不变离散系统。
它的基本工作原理是利用离散系统特性对系统输入信号进行加工和变换,改变输入序列的频谱或信号波形,让有用频率的信号分量通过,抑制无用的信号分量输出。
数字滤波器和模拟滤波器有着相同的滤波概念,根据其频率响应特性可分为低通、高通、带通、带阻等类型,与模拟滤波器相比,数字滤波器除了具有数字信号处理的固有优点外,还有滤波精度高(与系统字长有关)、稳定性好(仅运行在0与1两个电平状态)、灵活性强等优点。
基于DSP的IIR滤波器的设计

基于DSP的IIR滤波器的设计IIR滤波器是一种数字信号处理(DSP)中常用的滤波器,其设计基于离散时间传递函数。
IIR滤波器的设计可以通过不同的方法实现,包括模拟滤波器的转换方法、频率变换方法以及优化方法。
在本文中,我们将讨论基于DSP的IIR滤波器的设计。
IIR滤波器的设计通常包括以下几个步骤:确定滤波器的要求、选择滤波器类型、确定滤波器的阶数、计算滤波器系数、实现滤波器。
首先,确定滤波器的要求是设计IIR滤波器的第一步。
这包括确定滤波器的通带和阻带的频率范围,以及通带和阻带的衰减要求。
这些要求将决定滤波器的类型和阶数。
其次,选择滤波器类型是设计中的第二步。
常见的IIR滤波器类型包括低通滤波器、高通滤波器、带通滤波器和带阻滤波器。
滤波器类型将决定滤波器的架构和系数。
确定滤波器的阶数是设计中的第三步。
滤波器的阶数表示滤波器的复杂程度和能力。
阶数越高,滤波器的频率响应越陡峭,但计算和实现的复杂度也会相应增加。
一般来说,较低阶数的滤波器可以满足大多数应用的要求。
计算滤波器系数是设计中的第四步。
滤波器的系数决定了滤波器的频率响应。
常见的计算方法包括巴特沃斯方法、切比雪夫方法和椭圆方法。
这些方法将根据滤波器的类型、阶数和要求的频率响应计算出滤波器的系数。
最后,实现滤波器是设计中的最后一步。
实现滤波器可以通过直接计算、级联计算或者时域转换等方法。
其中,级联计算是最常用的方法,可以将滤波器的高阶拆分为多个低阶滤波器,以降低计算的消耗。
总结起来,基于DSP的IIR滤波器的设计是一个相对复杂的过程,需要确定滤波器的要求、选择滤波器类型、确定滤波器的阶数、计算滤波器系数,并最终实现滤波器。
这些步骤需要根据具体的应用场景和信号要求进行调整和优化,以获得满意的滤波效果。
IIR数字滤波器的优化设计和DSP实现

II R 数字滤波器的优化设计和D SP 实现张晓光,徐 钊(中国矿业大学信电学院,江苏省徐州市221008)摘 要:首先叙述了直接Ⅱ型II R (无限冲击响应)数字滤波器能够克服使用定点DSP 实现II R 数字滤波器时引起的输入数据的溢出问题;然后利用MAT LAB 软件生成滤波器的输入数据和系数,进行相应的数据压缩处理,并生成仿真波形;最后给出了用DSP 语言实现直接Ⅱ型结构II R 数字滤波器的完整程序、仿真结果,同时对仿真结果进行了分析、比较。
关键词:II R 数字滤波器;MAT LAB;定点DSP中图分类号:T N911.72收稿日期:2005208209;修回日期:2005210210。
0 引 言数字滤波在DSP (数字信号处理)中占有重要地位。
数字滤波器按实现的网络结构或者从单位脉冲响应,分为II R (无限脉冲响应)和F I R (有限脉冲响应)滤波器。
如果II R 滤波器和F I R 滤波器具有相同的性能,那么通常II R 滤波器可以用较低的阶数获得高的选择性,执行速度更快,所用的存储单元更少,所以既经济又高效。
一般说来,从使用要求上来看,在对象为要求不敏感的场合,如语音通信等,选用II R 滤波器较为合适,这样可以充分发挥其经济、高效的特点。
使用定点DSP 实现II R 滤波器是不容易的,II R 滤波器的反馈回路容易引起计算溢出。
一般采用定标输入数据克服溢出问题,但定标的结果使输出信号幅度降低。
为克服输出信号电平低的问题,一般在硬件上人为地多加一个运算放大器,以自举输出信号电平。
本文介绍一种II R 滤波器的优化设计方法,即借助组合两节II R 滤波器输入计算,克服输入数据溢出问题,从而可删除末级运算放大器。
1 II R 滤波器的设计一个高阶的II R 滤波器可以简化成几个二阶滤波器级联。
高阶II R 滤波器的传递函数可表示为:H (z )=H 1(z )H 2(z )…H n (z )(1)式中:n 为滤波器的阶数。
(完整版)基于MATLAB的IIR数字滤波器的设计与DSP实现毕业论文

1 绪论 (1)1.1课题分析 (1)1.2数字滤波器在国内外发展概况 (1)1.3MATLAB简介 (3)1.4数字信号处理(DSP)器简介 (5)1.5DSP芯片开发工具 (6)2 IIR数字滤波器设计的方案选择及原理分析 (12)2.1总体方案比较 (12)2.2IIR滤波器的基本原理 (13)2.3IIR数字滤波器的设计方法 (16)3 IIR滤波器的MATLAB设计与仿真 (21)3.1FDAT OOL界面设计 (21)3.2程序设计 (25)3.3IIR数字滤波器的仿真 (27)4 IIR滤波器在DSP上的实现 (40)4.1IIR数字滤波器在DSP上的实现步骤和条件 (40)4.2IIR数字滤波器在TMS320VC5416DSP上的实现过程 (40)5 总结 (45)参考文献 (46)致谢 (47)附录一:XP-IIR-AD.C (47)附录二:XP-IIR-AD.CMD (59)1绪论1.1 课题分析在现代通信系统中,由于信号中经常混有各种复杂成分,所以很多信号的处理和分析都是基于滤波器而进行的。
但是,传统数字滤波器的设计使用繁琐的公式计算,改变参数后需要重新计算,从而在设计滤波器尤其是高阶滤波器时工作量很大。
利用MATLAB信号处理箱(Signal Processing Toolbox)可以快速有效地实现数字滤波器的设计与仿真。
本课题正是利用MATLAB软件进行IIR数字滤波器的设计并进行仿真,这使得滤波器的设计更加快速和有效。
21 世纪是信息科学与技术的世纪, 其中, 数字信号处理技术(DSP) 已经成为当今一门极其重要的学科。
数字信号处理(DSP) 在通信, 语音, 图像, 自动控制, 雷达, 军事, 航空航天, 医疗和家用电器等很多领域已经得到广泛的应用。
[10]近年来,在数字信号处理领域具有绝对优势的DSP技术得到了迅速发展,不仅应用于通信、计算机领域,还逐渐渗透到其他科学研究领域。
基于MATLAB的IIR数字滤波器设计与DSP实现

基于MATLAB的IIR数字滤波器设计与DSP实现[摘要]对IIR数字滤波器进行研究,站在全面的角度来分析,对函数设计与计算方案的形成进行相应的探讨,找到相关的技术支持手段;通过对IIR数字过滤器中的信号处理技术,将MATLAB常用设计函数手段与DSP进行完善连接,同时,本文也将该技术实施中的参考手段与技术标准呈现了出来,以供参考。
[Abstract]To study the IIR digital filter,stand in the overall point of view to analyze the formation of the function,design and calculation programs were discussed,to find the relevant technical support;the signal processing technology of IIR digital filter in common use of MATLAB,the design method and the DSP function to improve connection,at the same time,this paper will also reference means and technical standards in the implementation of the technology were presented,for reference.[关键词]MATLAB;IIR数字滤波器;DSP[Keyword]MATLAB;IIR digital filter;DSP首先,对近年来的数字技术的发展来看,DSP技术已经作为直接性的科技领军技术产品来带动数字融合手段的发展了,在数字滤波器的带动下,它得以得到全面快速的发展;其次,结构简单的IIR数字过滤器得到了完善发展,其运算速度更快、占用空间更小,实现了DSP的质的突破与进步。
FIR_IIR滤波器设计与DSP实现

南京航空航天大学研究生DSP公共实验实验报告学生学号:学生姓名:实验地点:2015年6月一、实验目的1、掌握数字滤波器的设计过程2、了解FIR/IIR 的原理和特性3、熟悉设计FIR/IIR 数字滤波器的原理和方法二、实验内容1、通过MATLAB 设计确定FIR/IIR 滤波器系数2、DSP 初始化3、A/D 采样4、FIR/IIR 运算,观察滤波前后的波形变化三、实验背景知识1、FIR 基础理论FIR 数字滤波器是一种非递归系统,其冲激响应h(n)是有限长序列,其差分方程表达式为:11y(n)(i)x(n i)N i h -==-∑N 为FIR 滤波器阶数。
在数字信号处理应用中往往需要设计线性相位的滤波器,FIR 滤波器在保证幅度特性满足技术要求的同时,很容易做到严格的线性相位特性。
为了是滤波器满足线性相位条件,要求其单位脉冲响应h(n)为实序列,且满足偶对称或奇对称条件,即h(n)=h(N-1-n)或h(n)=-h(N-1-n)。
这样,当N 为偶数时,偶对称线性相位FIR 滤波器的差分方程表达式为/211(n)(i)(x(n i)x(N 1n i))N i y h -==-+---∑由此可见,FIR 滤波器不断的对输入样本x(n)延时后,再做乘法累加计算,将滤波器结果y(n)输出。
因此,FIR 实际上是一种乘法累加运算。
而对于线性相位FIR 而言,利用线性相位FIR 滤波器系数的对称性,可以采用结构精简的FIR 结构将乘法器数目减少一半。
2、IIR 基础理论IIR 数字滤波器是一种离散时间系统,其系统函数为11(z)1m i ii Nii i b z H a z -=-==-∑∑ 假设M ≤N ,当M >N 时,系统函数可以看作一个IIR 的子系统和一个(M-N)的FIR 子系统的级联。
IIR 数字滤波器的设计实际上是求解滤波器的系数a i 和b i ,它是数学上的一种逼近问题,即在规定意义上(通常采用最小均方误差准则)去逼近系统的特性。
IIR数字滤波器设计与实现

IIR数字滤波器设计与实现摘要IIR数字滤波器可以用较少的阶数获得较高的传输特性,所用的存储单元少,运算次数少,计算量小、效率高,在工程应用中发挥着十分重要的作用。
本文针对机电伺服领域中对线位移反馈的较高要求,提出了一套基于MATLAB 仿真分析的采用数字信号处理器(DSP)的数字滤波器的设计方法,并对滤波器对频率特性的影响进行了分析。
分析及试验证明,IIR数字滤波器在不影响伺服机构频率特性的情况下可以对机构抖动起到明显的抑制效果。
关键词无限冲击响应数字滤波器;带通滤波器;数字信号处理器;MATLAB前言在机电伺服领域中,由于较高的位置精度要求,因此在线位移反馈回路中的任何噪声干扰都会对影响伺服系统位置闭环的精度。
同时为满足较强动态特性,系统往往具有较高的开环增益,在这种情况下,噪声干扰特别是一些高频噪声干扰会被系统放大从而降低的系统的稳定裕度,严重时会使系统产生抖动。
随着数字控制器的发展,采用基于数字信号处理器(DSP)的数字滤波器可以有效解决这一难题。
数字滤波器在工程应用中发挥着十分重要的作用,并以得到成熟应用。
相比于传统的通过硬件电路实现的滤波器,数字滤波器具有运算精度高、运行可靠性高、应用灵活、便于集成等优点。
常用的数字滤波器有有限冲击响应(FIR)滤波器和无限冲击响应(IIR)滤波器,其中IIR数字滤波器因为结构简单、占用存储空间少、运算速度快、较高的计算精度及能够用较低的迭代阶数实现较好选频特性等特點,本文首先介绍在MATLAB环境下进行IIR滤波器滤波参数的计算及选取,然后结合基于DSP的IIR数字滤波器的具体实现,并通过试验验证IIR滤波器在高精度、动态特性的机电伺服领域中十分显著的滤波效果。
1 数字IIR滤波器的模型介绍IIR数字滤波器可以用较少的阶数获得较高的传输特性,所用的存储单元少,运算次数少,计算量小、效率高。
但以相位的非线性为代价,选择性越好,则相位非线性越严重。
从结构上,IIR滤波器必须采用递归结构来配置极点,并保证极点位置在单位院内。
IIR数字滤波器的DSP实现

湖南科技大学信息与电气工程学院《课程设计报告》题目:IIR数字滤波器的DSP实现专业: _________ 电子信息工程________班级: ____________ 电子二班_________姓名: ______________ 高二奎_________学号:1104030205 _______指导教师: ___________ 尹艳群_________2015年1 月8 日信息与电气工程学院课程设计任务书2014—2015学年第一学期专业:电子信息工程班级: 电子二班学号:1104030205姓名:高二奎课程设计名称:DSP 原理及应用设计题目:IIR 数字滤波器的DSP实现完成期限:自2015 年1月丄日至2015 年1月_8_日共1周设计依据、要求及主要内容(可另加附页):1、设计目的:通过课程设计,使学生综合运用DSP技术课程和其他有关先修课程的理论和生产实际知识去分析和解决具体问题的能力得到提高,并使其所学知识得到进一步巩固、深化和发展。
通过课程设计初步培养学生对工程设计的独立工作能力,学习设计的一般方法。
通过课程设计树立正确的设计思想,提高学生分析问题、解决问题的能力。
通过课程设计训练学生的设计基本技能,如计算、绘图、查阅设计资料和手册,熟悉标准与规范等。
2、要求:1 •熟悉DSP处理器及其结构性能,掌握DSP芯片配套开发工具的使用方法。
2 •按要求设计出硬件电路。
3 •画出硬件连接原理图,并对硬件工作原理进行说明。
4 •给出软件流程图及编写程序,每一条指令的后面附上相应的注释。
5.进行软、硬件调试,检查是否达到相关的功能。
6•写出调试方法。
7.设计报告结尾附上心得体会。
3、主要内容:熟悉5410DSP的MCBSP的使用,了解AD50的结构,掌握AD50 各寄存器的意义及其设置,掌握AD50与DSP的接口,AD50的通讯格式及AD50 的DA实验。
指导教师(签字):__________________批准日期:年月日目录一、摘要 (3)二、数字滤波器介绍和IIR数字滤波器的理论分析 (3)2.1数字滤波器介绍 (3)2.2 IIR 滤波器的设计方法及原理4三、DSP软件的简单介绍 (6)3.1DSP系统的特点 (6)3.2DSP系统的设计流程 (7)3.3DSP系统的开发工具CCS (7)四、TMS320C540的介绍 (9)五、基于DSP的IIR程序设计及软件调试 (11)5.1IIR 程序设计115.2 软件调试结果13六、总结和心得15七、参考文献、摘要随着计算机和信息技术的飞速发展,数字信号处理已经成为高速实时处理的一项关键技术,广泛应用在语音识别、智能检测、工业控制等各个领域。
IIR滤波器的DSP实现

1.输入波形: ①时域波形:
②频域波形:
2.输出波形: ①时域波形:
②频域波形:
八、心得体会
在课堂上我们做过 FIR 滤波器的设计,于是在课程大作业时,我想到了改变滤波器即将 FIR 改为 IIR 滤波器来完成我的大作业。正好这段时间在复习数字信号处理这门课,在加上做这个大作业,可 谓将理论与实际相结合,更完全的理解了滤波器的原理与应用,收获很大。
设计 IIR 滤波器的基础是设计模拟滤波器的原型,这些原型滤波器主要有: ①巴特沃兹(Butterworth)滤波器,其幅度响应在通带内具有最平特性; ②切比雪夫(Chebyshev)滤波器,在通带内具有等波纹特性,且阶数小于巴特沃兹滤波器. ③椭圆(Elliptic)滤波器,在通带内具有等波纹特性,且阶数最小. 将模拟滤波器转换为数字滤波器常用的方法是双线性变换,其作用是完成从 s 平面到 z 平面的一 个映射.其关系为: 双线性变换的基本性质如下: ①s 平面上的轴映射到 z 平面的单位圆上; ②s 平面的左半平面映射到 z 平面的单位圆内; ③s 平面的右半平面映射到 z 平面的单位圆外. 考虑到 s 平面上的虚轴映射为 z 平面的单位圆,令,它代表一个可变的模拟频率.其 z 平面上相应的 数字频率为,即,将以上两式代入 2.1 式得: 对上式求解得: 模拟频率和相应的数字频率之间的映射关系如图 4 所示:
由于这种结构所使用的延迟单元最少(只有 2 个),得到了广泛地应用,因此称之为标准型 IIR 滤波器.
图 3 标准型二阶 IIR 滤波器
二、IIR 滤波器的设计
IIR 滤波器的设计可以利用模拟滤波器原型,借鉴成熟的模拟滤波器的设计结果进行双线性变换, 将模拟滤波器变换成满足预定指标的数字滤波器,即根据模拟设计理论设计出满足要求的传递函数 H(s),然后将 H(s)变换成数字滤波器的传递函数 H(z).
IIR数字低通滤波器设计及DSP实现

IIR 数字低通滤波器的设计及DSP 实现一、设计要求设计一个通带截止频率为5KHz 的数字低通滤波器,其中采样频率为100KHz ,其它设计参数自拟。
并利用DSP 编程实现对输入为1.5KHz 、10KHz 、20KHz 的合成波形的滤波。
二、设计过程1. 设计目标根据所给的设计要求,确定设计目标如下:在通带截止频率5KHz 处的衰减不大于3dB ,在阻带截止频率10KHz 处的衰减不小于30dB ,A/D 采样频率为100KHz 。
用双线性变换法进行设计,巴特沃斯型低通滤波器。
2. 模拟参数转化为数字参数通带截止频率p ω=p FsΩ=0.1π,阻带截止频率s ω=sFsΩ=0.2π。
通带最大衰减为p α=3dB ,阻带最小衰减为s α=30dB ,同时根据巴特沃斯滤波器的“通带最平幅度”特性可以定出通带最大衰减在p ω处,而阻带最小衰减在s ω处。
3.利用MATLAB 获取滤波器的参数 (1)MATLAB 程序如下: clear;close;Fs=100000; Ap=3;As=30;Wp=2*Fs*tan(pi/20);Ws=2*Fs*tan(pi/10);%预畸变处理 [n,Wn]=buttord(Wp,Ws,Ap,As,'s'); [b,a]=butter(n,Wn,'s');%离散化处理[bn,an]=bilinear(b,a,Fs) %没有加分号,方便获取参数 [H1,W]=freqz(bn,an);plot(W*50/pi,20*log10(abs(H1)/max(H1)));grid; xlabel('频率(KHz )');ylabel('幅度(dB )');(2)得到参数如下: bn =1.0e-003 *0.0678 0.3388 0.6776 0.6776 0.3388 0.0678 an =1.0000 -3.9564 6.3496 -5.15512.1137 -0.3497(3)得到差分方程为:012345()()(1)(2)(3)(4)(5)y n b x n b x n b x n b x n b x n b x n =+-+-+-+-+-12345((1)(2)(3)(4)(5))a y n a y n a y n a y n a y n --+-+-+-+-(4)得到的滤波器的幅频特性图如图1:频率(KHz )幅度(d B )图1(5)对幅频特性图局部放大以查看其是否满足设计的要求频率(KHz )幅度(d B )频率(KHz )幅度(d B )图2 (5KHz 处放大图) 图3 (10KHz 处放大图) 从以上两张图中可以读出所设计的滤波器在10KHz 处恰好满足衰减30dB ,而在5KHz 处的衰减为2.45dB ,小于3dB ,有富裕产生,满足要求。
华航 IIR数字滤波器dsp编程实现

实验三 IIR数字滤波器一、实验目的本实验学习数字滤波器的DSP实现原理和C54X编程技巧。
进一步熟悉使用CCS调试程序的方法。
二、实验要求1.用MATLAB设计满足要求的IIR滤波器;2.用C语言编写产生滤波器输入信号的文件;3. IIR数字滤波器的汇编源程序的编写;4. IIR滤波器链接命令文件的编写;5. 在CCS中观察输入、输出信号的波形及频谱。
三、实验内容本实验要求设计一个采样频率Fs为16000Hz,输入信号频率为4000Hz和6500Hz的合成信号,通过设计的带通滤波器将6500Hz信号滤掉,余下4000Hz信号。
要求设计一个三阶的切比雪夫Ⅰ型带通数字滤波器,其采样频率Fs =16KHZ,其通频带3.2KHz<f<4.8KHz,内损耗不大于1dB;f<2.4KHz和f>5.6KHz为阻带,其衰减大于20dB。
四、实验步骤1. IIR滤波器的设计在MATLAB中设计IIR滤波器,程序为:wp=[3.2,4.8];ws=[2.4,5.6];rp=1;rs=20[n,wn]=cheb1ord(wp/8,ws/8,rp,rs)[b,a]=cheby1(n,rp,wn)在设计IIR滤波器时,会出现一个或一个以上系数≥1的情况,为了用Q15定点小数格式表示系数,可以用大数去除所有的系数。
为避免在累加过程中出现≥1情况,将系数进一步缩小,为此,在MATLAB中:B=round(b/6*2^15);A=round(a/6*2^15);2.产生滤波器输入信号的文件在使用CCS的Simulator进行滤波器特性的测试时,需要输入时间信号x(n)。
以下是一个产生输入信号的C语言程序,文件名为iirinput.c#include <stdio.h>#include <math.h>void main(){int i;double f[256];FILE *fp;if((fp=fopen("iirin.inc","wt"))==NULL){printf("can't open file! \n");return;}fprintf(fp,"INPUT: .sect %cINPUT %c\n",'"','"');for(i=0;i<=255;i++){f[i]=sin(2*3.14159*i*4000/16000)+sin(2*3.14159*i*6500/16000);fprintf(fp," .word %1d\n",(long)(f[i]*32768/2)); }fclose(fp);}该程序将产生名为iirin.inc的输入信号程序。
基于DSP的IIR数字滤波器的设计与实现

DSP 上 实 现 。
解 决 此 问 题 的 有 效 方 法 是 把 高 阶 IIR 数 字 滤 波 器 简
化成几个 2 阶滤波器来设计, 即采用级联结构。因此系
统函数为:
H(z)=H1(z)H2(z)… Hn(z)
(3)
上 述 7 阶 IIR 数 字 滤 波 器 采 用 级 联 的 结 构 后 变 成 4
! 1 - ak z- k
(2)
器 , 其 中 IIR 数 字 滤 波 器 因 具 有 结 构 简 单 、占 用 存 储 空 间
k=0
少 、运 算 速 度 快 、较 高 的 计 算 精 度 和 能 够 用 较 低 的 阶 数 的 IIR 数 字 波 滤 器 来 说 , 设 计 的 任 务 就 是 寻 求 一 种 因 果
程序流 程如 图 2。采用 间接 寻址 指向数 据存 储 单 元 , 主 要 指 令 为 加 法 、乘 法 和 循 环 实 现 , 这 些 都 可 以 通 过 MAC 等 指 令 直 接 实 现 。 需 注 意 的 是 要 对 乘 法 运 算 结 果 进行溢出保护。另外, 因为主程序框架采用 C 结构, 而 算法由汇编语言实现, 所以要注意不同环境下寻址方式 的 区 别 , 当 从 C 环 境 进 入 直 接 寻 址 时 , 要 先 确 定 DP 值 , 以 免 带 来 不 确 定 的 计 算 结 果 。数 据 采 集 时 要 先 通 过 DSP 的 DMA 功 能 将 输 入 数 据 保 存 在 外 部 SRAM 中 , 采 样 结 束 后 再 将 要 滤 波 的 数 据 通 过 DMA 载 入 内 部 RAM 中 , 从 而 提 高 处 理 速 度 。 考 虑 到 IIR 数 字 滤 波 器 的 运 算 特 点 , 某一时刻的输入数据参加一次运算后不再参与下次运 算, 只有各级滤波器输出结果需要参与多次运算, 因此 滤波结果和输入数据可以共用同一存储地址, 从而节省 存储空间。
IIR滤波器的DSP实现
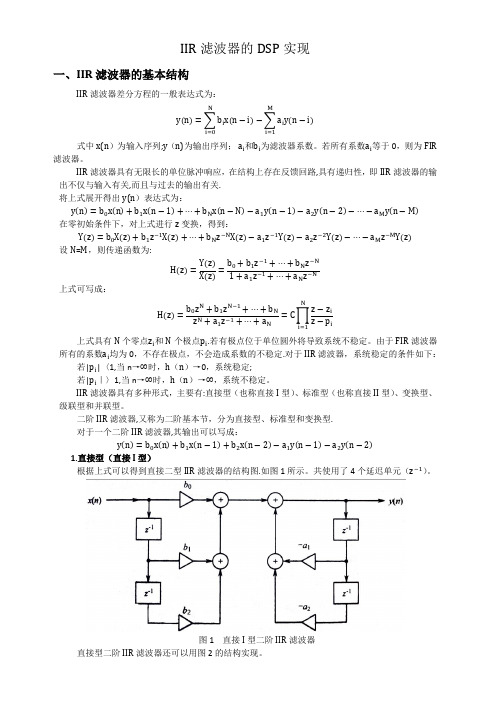
IIR滤波器的DSP实现一、IIR滤波器的基本结构IIR滤波器差分方程的一般表达式为:y(n)=∑b i x(n−i)Ni=0−∑a i y(n−i) Mi=1式中x(n)为输入序列;y(n)为输出序列; a i和b i为滤波器系数。
若所有系数a i等于0,则为FIR 滤波器。
IIR滤波器具有无限长的单位脉冲响应,在结构上存在反馈回路,具有递归性,即IIR滤波器的输出不仅与输入有关,而且与过去的输出有关.将上式展开得出y(n)表达式为:y(n)=b0x(n)+b1x(n−1)+⋯+b N x(n−N)−a1y(n−1)−a2y(n−2)−⋯−a M y(n−M)在零初始条件下,对上式进行z变换,得到:Y(z)=b0X(z)+b1z−1X(z)+⋯+b N z−N X(z)−a1z−1Y(z)−a2z−2Y(z)−⋯−a M z−M Y(z)设N=M,则传递函数为:H(z)=Y(z)X(z)=b0+b1z−1+⋯+b N z−N1+a1z−1+⋯+a N z−N上式可写成:H(z)=b0z N+b1z N−1+⋯+b Nz N+a1z−1+⋯+a N=C∏z−z iz−p iNi=1上式具有N个零点z i和N个极点p i.若有极点位于单位圆外将导致系统不稳定。
由于FIR滤波器所有的系数a i均为0,不存在极点,不会造成系数的不稳定.对于IIR滤波器,系统稳定的条件如下:若|p i|〈1,当n→∞时,h(n)→0,系统稳定;若|p i|〉1,当n→∞时,h(n)→∞,系统不稳定。
IIR滤波器具有多种形式,主要有:直接型(也称直接I型)、标准型(也称直接II型)、变换型、级联型和并联型。
二阶IIR滤波器,又称为二阶基本节,分为直接型、标准型和变换型.对于一个二阶IIR滤波器,其输出可以写成:y(n)=b0x(n)+b1x(n−1)+b2x(n−2)−a1y(n−1)−a2y(n−2)1.直接型(直接I型)根据上式可以得到直接二型IIR滤波器的结构图.如图1所示。
基于MATLAB的IIR数字滤波器的设计及DSP实现12

基于MATLAB的IIR数字滤波器的设计及DSP实现12————————————————————————————————作者:————————————————————————————————日期:基于MATLAB的IIR数字滤波器的设计(MATLAB在通信中的应用—-———课程论文)论文作者:王紫艳专业:通信工程专业10—-04班学号:311009020405指导老师:候艳芳基于MATLAB的IIR数字滤波器的设计摘要:在现代通信系统中,由于信号中经常会混有各种复杂成分,很多信号分析都是基于滤波器而进行的,而数字滤波器是通过数值运算实现滤波的,具有处理精确度高、稳定、灵活、不存在阻抗匹配问题,可以实现模拟滤波器无法实现的特殊滤功能。
数字滤波器根据其冲激响应函数的时域特性,可以分为两类:无限长冲激响应(IIR)数字滤波器和有限长冲激响应(FIR)数字滤波器。
传统的数字滤波器设计使用繁琐的公式计算,尤其是设计高阶滤波器时工作量很大。
利用MATLAB数字信号处理(DSP)工具箱(signal processing toolbox)可以快速有效的实现数字滤波器的设计与仿真。
MATLAB软件的频谱分析和滤波器的分析设计功能很强,从而使数字信号处理变得十分简单。
本文比较了设计IIR数字滤波器的两种方法,介绍了利用双线性变换法设计IIR滤波器的原理、步骤,并在MATLAB下进行了仿真。
关键字:MATLAB IIR 数字滤波器 DSP一引言随着数字时代的到来,数字信号处理技术在电子产品中得到越来越广泛的应用,竞争的激烈也促使是数字信号处理技术的不断发展。
而数字滤波在数字信号处理过程中占有举足轻重的低位,数字滤波的优劣直接关系到数字信号处理的好坏,常用的数字滤波器有FIR数字滤波器和IIR数字滤波器,其中IIR数字滤波器具有结构简单,运算速度快,占用存储空少,较高的计算精度和较低的阶数实现,较好的选频特性等优点,等到广泛的应用。
通用DSP实现IIR滤波器实验报告

六.实验内容
1).Fs=20kHz
①低通:Wn=0.3 频率 50 2.1K 2.4K 2.5K 2.6K 2.8K 2.9K 3K /Hz 幅度 195 170 150 140 130 120 96 86 /mV
3.2K 3.4K 3.7K 4.1 K
68 54 38 25
②高通:Wn=0.2
频 50 1.4 1.6 1.8 2K 2.1 2.3 2.5 2.7 2.8 3K 4K 6K
3)实际滤波带宽与理论带宽的误差计算 Fs=20kHz
①.低通:Wn=0.3 实际:
理论:
误差:
②.高通:Wn=0.2 实际:
理论:
误差:
Fs=27.9kHz ①.低通:Wn=0.3 实际:
理论:
误差:
②.高通:Wn=0.2 实际: 理论:
误差:
4)比较相同 Ωn,不同采样频率下实际所得同种滤波器的带宽,与采样频率 之间的关系。
五.实验步骤:
1、按实验连接图检查连线是否正确,然后依次打开信号源﹑示波器﹑ 实验装置的电源开关。
2、将信号源的频率调至 50HZ,Vpp 调至 500mv,按试验箱上的提示选择
1(fs=20KHz),再选择 2(iir),然后选择 1(低通:ωn=0.3)。 3、观察示波器上的输出信号。将信号源的频率从 50Hz 逐渐提高,观察示波
Magnitude Response
1
0.5
0 0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000 Hertz
0
-100
-200
-300
-400 0
1000 2000 3000 4000 5000 6000 7000 8000 9000 10000 Hertz
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
II R 数字滤波器的优化设计和D SP 实现张晓光,徐 钊(中国矿业大学信电学院,江苏省徐州市221008)摘 要:首先叙述了直接Ⅱ型II R (无限冲击响应)数字滤波器能够克服使用定点DSP 实现II R 数字滤波器时引起的输入数据的溢出问题;然后利用MAT LAB 软件生成滤波器的输入数据和系数,进行相应的数据压缩处理,并生成仿真波形;最后给出了用DSP 语言实现直接Ⅱ型结构II R 数字滤波器的完整程序、仿真结果,同时对仿真结果进行了分析、比较。
关键词:II R 数字滤波器;MAT LAB;定点DSP中图分类号:T N911.72收稿日期:2005208209;修回日期:2005210210。
0 引 言数字滤波在DSP (数字信号处理)中占有重要地位。
数字滤波器按实现的网络结构或者从单位脉冲响应,分为II R (无限脉冲响应)和F I R (有限脉冲响应)滤波器。
如果II R 滤波器和F I R 滤波器具有相同的性能,那么通常II R 滤波器可以用较低的阶数获得高的选择性,执行速度更快,所用的存储单元更少,所以既经济又高效。
一般说来,从使用要求上来看,在对象为要求不敏感的场合,如语音通信等,选用II R 滤波器较为合适,这样可以充分发挥其经济、高效的特点。
使用定点DSP 实现II R 滤波器是不容易的,II R 滤波器的反馈回路容易引起计算溢出。
一般采用定标输入数据克服溢出问题,但定标的结果使输出信号幅度降低。
为克服输出信号电平低的问题,一般在硬件上人为地多加一个运算放大器,以自举输出信号电平。
本文介绍一种II R 滤波器的优化设计方法,即借助组合两节II R 滤波器输入计算,克服输入数据溢出问题,从而可删除末级运算放大器。
1 II R 滤波器的设计一个高阶的II R 滤波器可以简化成几个二阶滤波器级联。
高阶II R 滤波器的传递函数可表示为:H (z )=H 1(z )H 2(z )…H n (z )(1)式中:n 为滤波器的阶数。
式(1)可以转化为若干个二阶II R 滤波器级联,每个二阶II R 滤波器的传递函数可以表示成:H k (z )=1+b 1k z -1+b 2k z-11-a 1k z-1-a 2k z-1 k =1,2, (2)式中:H k (z )为二阶II R 滤波器(见图1)的传递函数。
图1 直接Ⅰ型二阶II R 滤波器该II R 滤波器提供输入和输出序列分离的延迟缓冲器,属于直接Ⅰ型。
从该滤波器得到的输出为:y (n )=a 11y (n -1)+a 12y (n -2)+ b 11x (n -1)+b 12x (n -2)(3) 二阶II R 滤波器是两个级联的部分:零点和极点。
因为II R 滤波器是线性系统,所以两部分可以交换,交换之后,由于延迟线的输出是相同的,所以可从滤波器结构中消除一对延迟线。
这样得到图2,它可以使用较少的延迟单元,这种滤波器属于直接Ⅱ型结构,也是一种典型、规范的结构。
使用定点DSP 来实现II R 滤波器时,数据溢出是由于32比特的体系结构限制造成的。
滤波器的增益是从极点部分得到的,如果该增益增加,会产生输出数据溢出,也就是这个数据值会突破CP U32比特范围。
在滤波应用中,只有输入数非常小,输出才能不溢出。
图2 二阶II R 滤波器典型结构如果我们使用直接Ⅰ型的II R 滤波器结构来编码,那么将出现两个问题:为了避免输出溢出,要浪费・73・第32卷第3期2006年3月 电子工程师 E LECTRON I C E NGI N EER Vol.32No .3 M ar .2006时间调解输入值;系统需要附加硬件,即末级增加运算放大器以恢复输出信号电平。
相反,使用直接Ⅱ型II R 滤波器能够解决这些问题。
当使用直接Ⅰ型II R 滤波器(见图1),在正向通道中计算零点,然后在反馈通路计算极点,由于零点的运算,中间结果m (n )非常小;在图2中,由于极点运算,中间结果d (n )比m (n )值大,输出数据y (n )能够借助传送中间值d (n )得到,因此能得到合适的电平。
所以使用直接Ⅱ型II R 滤波器能消除溢出问题。
多级二阶II R 滤波器级联的高阶II R 滤波器结构图如图3所示,每一个二阶II R 滤波器都采用直接Ⅱ型。
延迟器的数量借助于组合当前级的二阶II R 滤波器极点(a 11,a 12)和下一级的二阶II R 滤波器零点(b 11,b 12)。
级联部分的软件使用重复的块结构,附加的软件来自第一部分零点(b 11,b 12)计算和最后一部分的极点(a n 1,a n 2)计算。
输出数据y (n )处在正常电平,因此这种形式删除了原始II R 滤波器的运算放大器。
图3 典型高阶II R 滤波器结构2 II R 滤波器的D SP 实现下面以一具体例子为参照,进行具体设计说明。
已知一信号为x (t )=sin (2π×450t ),由于某种原因,信号被两个频率分别为200Hz 和220Hz 的噪声污染,设取样频率为1kHz,要求设计一个II R 高通滤波器对输入信号进行滤波。
2.1 系统框图II R 滤波器的DSP 实现框图如图4所示。
图4 II R 滤波器的D SP 实现框图2.2 应用M AT LAB 得到滤波器的输入数据和系数首先应用MAT LAB 编程生成频率为450Hz 的有用信号和频率分别为200Hz 、220Hz 的噪声,并进行FFT 频谱分析,见图5。
然后根据要求,利用MAT LAB 软件中的滤波器设计工具箱fda 设计相应的高通滤波器,设计指标为:R p =1dB ,R s =60d B ,f p =0.4kHz,f s =0.3kHz,F =1kHz,见图6。
最后用所设计的滤波器对输入信号进行滤波处理,其频谱见图5。
图5 M AT LAB 软件实现的滤波前后的信号频谱图6 M AT LAB 软件实现的II R 滤波器频谱 a )输入信号处理:将MAT LAB 中产生的256点x (n )进行一定比例的压缩,使所有数据处于-1~1之间,然后采用Q15格式进行数据格式转换,使转换后的数据处于-32768~32768之间,作为.data 段的输入数据存储在数据存储区。
b )将以上所设计的滤波器系数进行类似输入数据的压扩变换,引入到汇编语言程序中。
在此例中,经过MAT LAB 程序设计得到满足技术要求的滤波器系数如下:b =10-3[0.0464 -0.2782 0.6956 -0.9274 0.6956 -0.2782 0.0464]a =1.0000 4.8694 10.3807 12.33678.5969 3.3268 0.5586] 千万注意不能原封不动把MAT LAB 生成的系数拿过来直接用,其中最大的数据12.3367超出了-1~1的范围,不能直接进行Q15格式转换,要先对数据进行压扩变换。
因为a,b 中有大于1的数。
为将所有数据压缩至-1~1之间,所有系数a,b 同除以一个大数c (c >|max [h (n )]|)。
2.3 D SP 汇编语言实现II R 滤波器前面已经分析,二阶II R 滤波器可以化成如图2所示的直接Ⅱ型结构,其优点是在运算过程中先衰减后增益,系统的动态范围和鲁棒性都要好一些。
编程时,将变量和系数都存放在DARAM 中,并采・83・・信号处理与显示技术・电子工程师2006年3月用循环缓冲区方式寻址;程序算法主要实现部分如下:filter_start: ST M #K_C I R,BK //设置循环缓冲区长度 ST M #1,AR0 ST M #inputdata,OR I GI N ST M #bufferdatax,I N P UT ST M #bufferdatay,F I L TER ST M #filterdata,OUTP UT //初始化 RPT #K_A -1 //a1,a2的个数 MVDD 3OR I GI N +,3I N P UT +0% //初始化前K_A 个Y值 ST M #bufferdatax,I N P UT //设置初始化滤波数据 RPT #K_A -1 MVDD 3I N P UT +0%,3F I L TER +0% //初始化K_A 个Y值 ST M #bufferdatay,F I L TER //滤波 ST M #K_DAT A_SI ZE -3-1,BRC //前K_A 个X 值直接通过 RPT B filter_end -1 MVDD 3OR I GI N +,3I N P UT RPT #K_B -1-1 //b1,b2,b3的个数 MAR 3I N P UT -0% //调整输入到相应位置 MPY 3I N P UT +0%,#b3,B //B =b33x (i ) LD B,A MPY 3I N P UT +0%,#b2,B //B =b23x (i +1) ADD B,A MPY 3I N P UT +0%,#b1,B //B =b13x (i +2) ADD B,A //y (x +2)=A MPY 3F I L TER +0%,#a2,B //B =y (i )3a2 ADD B,A //A =A +B MPY 3F I L TER +0%,#a1,B //B =y (i +1)3a1 ADD B,A //y (i +2)=A +B STH A,3F I L TER STH A,3OUTP UT + RPT #K_A -1-1 MAR 3F I L TER -0% //调整滤波器到相应位置filter_end: NOP RET2.4 滤波结果分析图7(a )、(b )分别为II R 高通滤波器的输入、输出信号的频谱图,滤波器性能要求为:f p =400Hz,f s =300Hz,F =1kHz,R p =1d B ,R s =60d B 。
由于采用归一化频率,可看出在坐标ω的0.2,0.45附近共有3个频率分量,根据模拟频率和数字频率间的对应关系:f =ωF ,可知3个频率分量分别为f 1=200Hz ,f 2=220Hz,f 3=450Hz,对比输入、输出信号频谱图,可以看出处在滤波器阻带内的200Hz 、220Hz 的低频分量被滤除,剩下了通带内450Hz 的高频分量,可见滤波性能很好。
图7 汇编语言实现的滤波前后的信号频谱3 结束语本文介绍了基于DSP 实现的数字滤波器,该滤波器实时滤波效果比较理想,并且可以随时调整滤波器参数,具有比较高的实用价值。
参 考 文 献[1]戴明桢,周建江.T M S320C54XDSP 结构、原理及应用[M ].北京:北京航空航天大学出版社,2001.[2]丁玉美,高西全.数字信号处理[M ].第2版.西安:西安电子科技大学出版社,2000.[3]张雄伟,陈 亮,徐光辉.集成开发与应用实例[M ].北京:电子工业出版社,2002.Opti m i zed Desi gn of II R D i git al Filter and Its Reali zati on with DSPZHANG X i a o 2guang,XU Zhao(Chinese University of M ine &Technol ogy,Xuzhou 221008,China )Abstract:Firstly,this paper describes why direct 222type filter can overcome the overfl o w of input data when we design II R filter with fixed 2point DSP .Secondly,the paper sho ws how t o generate the input data and coefficients by MAT LAB ,then t o comp ress the data and t o generate the si m ulati on wave f or m.Finally,the comp lete p r ogra m ,si m ulati on wave f or m of direct 222type II R filter are p resented using DSP .A t the sa me ti m e,the si m ulati on wave f or m based on DSP is analyzed in detail and compared with that fr om MAT LAB.Keywords:II R digital filter;MAT LAB;fixed 2point DSP・93・第32卷第3期张晓光,等:II R 数字滤波器的优化设计和DSP 实现・信号处理与显示技术・。
