2009年广州民校联考数学试题
广州2008、2009、2010小升初民校联合考试数学试卷及答案

⼴州2008、2009、2010⼩升初民校联合考试数学试卷及答案2008年⼴州市⼗六所民办初中新⽣⼊学检测题答案⼀、填空题1、57002、6:7 ;6/7;3、964、a-b+c5、6;2106、9/207、4 8、35670 9、55 10、120⼆、判断题×√√×三、选择题1、④2、③3、①4、④四、计算题1、(1)50 (2)1/8 (3)1/72、(1)7.8 (2)4/253、(1)20.5 (2)130五、应⽤题1、(1)12×1/5 ;120×(1/3+1/5);120×(1/2-1/5)(2)48×4+48×2/3×42、荔枝25棵,龙眼15棵3、800本4、8厘⽶5、162⼈2009年⼗六所民校新⽣⼊学检测题数学参考答案⼀、填空题。
1.80202000,8020.2;2.14,2104.1445.3136 25006.6407.208.499.1507.210.36⼆、判断题。
1.√ 2 X 3X 4√5√三、选择题。
1.B 2.C 3.D 4.C 5.C四、计算题。
1.0.76 1000 10/9 10080/9 25/64 1/12 3/2 5.925 122.X= 8/19 X= 123.(1)51.25 (2)21 (3)300/301 (4)3/14五、应⽤题1.(200—5.5—38 ×4)÷50 =0.852.(1—1/6)÷(1/60 +1/40)=203.设铅锤的⾼为X,则1/3 ×5 ×5 X×3.14 =10×10×2 ×3.14 X =24 4.设两地相距X千⽶210 -1/5 X =2/5 X X =3505.0.16 ×500 ÷(0.5 ×0.5)=320(块)6.设这批零件共有X个,则120 +(X -120)×2/5 =1/2 X X=720 7.(97—67)÷(86 .49 -85 .74)=40 8.设花坛的半径为X,则3.14 X +2X =10.28X= 2 |1/2 ×3.14 ×4 =6.28附加题1。
2009年广州市普通高中毕业班综合测试(一)数学(理科)

2009年广州市普通高中毕业班综合测试(一)数 学(理 科) 2009.3一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.函数()x x f 2sin =的最小正周期为 A .πB.π2C. π3D. π42.已知z =i (1+i )(i 为虚数单位),则复数z 在复平面上所对应的点位于 A .第一象限 B .第二象限 C .第三象限 D .第四象限3.某商场在国庆黄金周的促销活动中,对10月2号9时至14时 的销售额进行统计,其频率分布直方图如图1所示.已知9时 至10时的销售额为2.5万元,则11时至12时的销售额为 A . 6万元 B . 8万元C . 10万元D .12万元4.已知过()a A ,1-、()8,a B 两点的直线与直线012=+-y x 平行,则a 的值为A. 10-B. 17C. 5D. 25.阅读图2的程序框图(框图中的赋值符号“=”也可以写成“←”或“:=”),若输出的S 的值等于16,那么在程序框图中的判断框内应填写的条件是A .5>i ? B. 6>i ?C. 7>i ?D. 8>i ?6.已知p :关于x 的不等式022>-+a ax x 的解集是R ,q :01<<-a ,则p 是q 的A .充分非必要条件B .必要非充分条件C .充分必要条件D .既非充分又非必要条件7.在()nn nx a x a x a x a a x +⋅⋅⋅++++=-3322101中,若0252=+-n a a ,则自然数n 的值是A .7B .8C .9D .108.在区间[]1,0上任意取两个实数,则函数在区间[]1,1-上有且仅 一个零点的概率为 A .81 B .41C .43D .87二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分.(一)必做题(9~12题)9. 若()22log 2=+a ,则=a 3 . 10.若⎰ax 0d x =1, 则实数a 的值是 .11.一个几何体的三视图及其尺寸(单位:cm )如图3所示, 则该几何体的侧面积为 cm 2.12.已知数列{}n a 的前n 项和为n S ,对任意∈n N *都有3132-=n n a S , 且91<<k S (∈k N *),则1a 的值为 ,k 的值为 .(二)选做题(13~15题,考生只能从中选做两题) 13.(坐标系与参数方程选做题)在极坐标系中,直线24sin =⎪⎭⎫⎝⎛+πθρ被圆4=ρ截得的弦长为__ .14.(几何证明选讲选做题)已知PA 是圆O (O 为圆心)的切线,切点为A ,PO 交圆O 于C B , 两点,︒=∠=30,3PAB AC ,则线段PB 的长为 .15.(不等式选讲选做题)已知∈c b a ,,R ,且432,2222=++=++c b a c b a ,则实数a 的取值范围为_____________.三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)已知△ABC 的内角C B A ,,所对的边分别为,,,c b a 且53cos ,2==B a . (1)若4=b , 求A sin 的值;(2) 若△ABC 的面积,4=∆ABC S 求c b ,的值.b a ,()b ax x x f -+=321甲、乙两名同学参加一项射击游戏,两人约定,其中任何一人每射击一次,击中目标得2分,未击中目标得0分. 若甲、乙两名同学射击的命中率分别为53和p , 且甲、乙两人各射击一次所得分数之和为2的概率为209.假设甲、乙两人射击互不影响. (1)求p 的值;(2)记甲、乙两人各射击一次所得分数之和为ξ,求ξ的分布列和数学期望.18. (本小题满分14分)如图4, 在三棱锥ABC P -中,⊥PA 平面ABC ,AC AB ⊥,F E D ,,分别是棱PC PB PA ,,的中点,连接EF DF DE ,,.(1) 求证: 平面//DEF 平面ABC ;(2) 若2==BC PA , 当三棱锥ABC P -的体积最大时, 求二面角D EF A --的平面角的余弦值.图419.(本小题满分12分)某车间有50名工人,要完成150件产品的生产任务,每件产品由3个A 型零件和1个B 型零件配套组成.每个工人每小时能加工5个A 型零件或者3个B 型零件,现在把这些工人分成两组同时工作(分组后人数不再进行调整),每组加工同一种型号的零件.设加工A 型零件的工人人数为x 名(∈x N *). (1)设完成A 型零件加工所需时间为()x f 小时,写出()x f 的解析式; (2)为了在最短时间内完成全部生产任务,x 应取何值?20.(本小题满分14分)已知动圆C 过点()0,2-A ,且与圆()642:22=+-y x M 相内切.(1)求动圆C 的圆心的轨迹方程;(2)设直线:l y kx m =+(其中,)k m Z ∈与(1)中所求轨迹交于不同两点B ,D ,与双曲线112422=-y x 交于不同两点,E F ,问是否存在直线l ,使得向量DF BE +=0,若存在,指出这样的直线有多少条?若不存在,请说明理由.已知数列{}n a 的相邻两项1,+n n a a 是关于x 的方程022=+-n n b x x ∈n (N )*的两根,且.(1) 求数列{}n a 和{}n b 的通项公式;(2) 设n S 是数列{}n a 的前n 项和, 问是否存在常数λ,使得0>-n n S b λ对任意∈n N *都成立,若存在,求出λ的取值范围; 若不存在, 请说明理由.2009年广州市普通高中毕业班综合测试(一)数学(理科)试题参考答案及评分标准一、选择题:本大题主要考查基本知识和基本运算.共8小题,每小题5分,满分40分.二、填空题:本大题主要考查基本知识和基本运算.本大题共7小题,每小题5分,满分30分.其中13~15是选做题,考生只能选做两题. 第12题第一个空2分,第二个空3分.9.9 10.2 11.80 12.-1;4 13.34 14.1 15. ⎥⎦⎤⎢⎣⎡2,112三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)(本小题主要考查正弦定理、余弦定理、同角三角函数的基本关系等基础知识,考查运算求解能力) 解: (1)∵053cos >=B , 且π<<B 0, ∴ 54cos 1sin 2=-=B B . 由正弦定理得B b A a sin sin =. ∴524542sin sin =⨯==b B a A . (2)∵,4sin 21==∆B ac S ABC ∴454221=⨯⨯⨯c . ∴ .由余弦定理得B ac c a b cos 2222-+=,∴175352252cos 22222=⨯⨯⨯-+=-+=B ac c a b . 17.(本小题满分14分)(本小题主要考查概率、随机变量的分布列及其数学期望等基础知识,考查运算求解能力)11=a 5=cFEDCBAP 解:(1)记“甲射击一次,击中目标”为事件A ,“乙射击一次,击中目标”为事件B ,“甲射击一次,未击中目标”为事件A ,“乙射击一次,未击中目标”为事件B , 则()()52,53==A P A P ,()()p B P p B P -==1,. 依题意得()209531153=⎪⎭⎫ ⎝⎛-+-p p , 解得43=p . 故p 的值为43. (2)ξ的取值分别为,4,2,0.()()()()10141520=⨯=⋅===B P A P B A P P ξ, ()2092==ξP , ()()()()20943534=⨯=⋅===B P A P AB P P ξ, ξ∴的分布列为∴E .1027209420921010=⨯+⨯+⨯=ξ 18.(本小题满分14分)(本小题主要考查空间中线面的位置关系、空间的角、几何体体积等基础知识,考查空间想象能力、推理论证能力和运算求解能力) (1) 证明: ∵E D ,分别是棱PB PA ,的中点,∴DE 是△PAB 的中位线.∴AB DE //. ∵⊄DE 平面⊂AB ABC ,平面,ABC∴//DE 平面ABC . 同理可证 //DF 平面ABC .∵⊂=DE D DF DE , 平面DEF ,⊂DF 平面DEF ,∴平面DEF // 平面ABC .(2) 求三棱锥ABC P -的体积的最大值, 给出如下两种解法:解法1: 由已知⊥PA 平面ABC , AB AC ⊥,2==BC PA ∴4222==+BC AC AB .∴三棱锥ABC P -的体积为ABC S PA V ∆⨯⨯=31AC AB PA ⨯⨯⨯⨯=2131 AC AB ⨯⨯⨯=261 23122AC AB +⨯≤ 2312BC ⨯= 32=.GFED CBAP 当且仅当AC AB =时等号成立,V 取得最大值,其值为32, 此时AC AB =2=.解法2:设x AB =,在R t △ABC 中,2224x AB BC AC -=-=()20<<x .∴三棱锥ABC P -的体积为ABC S PA V ∆⨯⨯=31 AC AB PA ⨯⨯⨯⨯=2131 2431x x -=42431x x -= ()423122+--=x . ∵40,202<<<<x x , ∴ 当22=x ,即2=x 时,V 取得最大值,其值为32,此时2==AC AB .求二面角D EF A --的平面角的余弦值, 给出如下两种解法: 解法1:作EF DG ⊥,垂足为G , 连接AG . ∵ ⊥PA 平面ABC ,平面//ABC 平面DEF ,∴ ⊥PA 平面DEF . ∵ ⊂EF 平面DEF , ∴ ⊥PA EF . ∵ D PA DG = , ∴ ⊥EF 平面PAG .∵⊂AG 平面PAG ,∴⊥EF AG . ∴ AGD ∠是二面角D EF A --的平面角.在R t △EDF 中,121,2221=====BC EF AB DF DE , ∴21=DG . 在R t △ADG 中,2541122=+=+=DG AD AG ,552521cos ===∠AG DG AGD . ∴二面角D EF A --的平面角的余弦值为55. 解法2:分别以AP AC AB ,,所在直线为x 轴, y 轴, z 轴, 建立如图的空间直角坐标系xyz A -,则()()⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫⎝⎛1,22,0,1,0,22,1,0,0,0,0,0F E D A .∴⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛=0,22,22,1,0,22. 设n ()z y x ,,=为平面AEF 的法向量,∴⎪⎩⎪⎨⎧=⋅=⋅.0,0n AE n 即⎪⎪⎩⎪⎪⎨⎧=+-=+.02222,022y x z x 令2=x , 则1,2-==z y .∴n ()1,2,2-=为平面AEF 的一个法向量. ∵平面DEF 的一个法向量为()100-=,,,∴()()()5511221222=⨯-++==n cos . ∴二面角D EF A --的平面角的余弦值为55. 19.(本小题满分12分)(本小题主要考查函数最值、不等式、导数及其应用等基础知识,考查分类与整合的数学思想方法,以及运算求解能力和应用意识)解:(1)生产150件产品,需加工A 型零件450个,则完成A 型零件加工所需时间()x f ∈==x xx (905450N *,且)491≤≤x . (2)生产150件产品,需加工B 型零件150个,则完成B 型零件加工所需时间()x g ()∈-=-=x xx (5050503150N *,且)491≤≤x .设完成全部生产任务所需时间为()x h 小时,则()x h 为()x f 与()x g 的较大者. 令()()x g x f ≥,即x x -≥505090,解得71321≤≤x . 所以,当321≤≤x 时,()()x g x f >;当4933≤≤x 时,()()x g x f <.故()()()⎪⎩⎪⎨⎧≤≤∈-≤≤∈=4933,,5050321,,90**x N x xx N x x x h .当321≤≤x 时,()0902'<-=xx h ,故()x h 在[]32,1上单调递减, 则()x h 在[]32,1上的最小值为()1645329032==h (小时); 当4933≤≤x 时,()()050502'>-=x x h ,故()x h 在[]49,33上单调递增,则()x h 在[]49,33上的最小值为()175033505033=-=h (小时);()()3233h h > ,∴()x h 在[]49,1上的最小值为()32h .32=∴x .答:为了在最短时间内完成生产任务,x 应取32.20.(本小题满分14分)(本小题主要考查圆、椭圆、直线等基础知识和数学探究,考查数形结合、分类与整合的数学思想方法,以及推理论证能力、运算求解能力和创新意识) 解:(1)圆()642:22=+-y x M , 圆心M 的坐标为()0,2,半径8=R .∵R AM <=4,∴点()0,2-A 在圆M 内. 设动圆C 的半径为r ,圆心为C ,依题意得CA r =,且r R CM -=, 即AM CA CM >=+8. ∴圆心C 的轨迹是中心在原点,以M A ,两点为焦点,长轴长为8的椭圆,设其方程为()012222>>=+b a by a x , 则2,4==c a .∴12222=-=c a b . ∴所求动圆C 的圆心的轨迹方程为1121622=+y x . (2)由⎪⎩⎪⎨⎧=++=.11216,22y x m kx y 消去y 化简整理得:()0484843222=-+++m kmx x k . 设11(,)B x y ,22(,)D x y ,则122834kmx x k+=-+. △1()()()04844348222>-+-=m k km . ①由⎪⎩⎪⎨⎧=-+=.1124,22y x m kx y 消去y 化简整理得:()01223222=----m kmx x k . 设()()4433,,,y x F y x E ,则24332kkmx x -=+,△2()()()012342222>+-+-=m k km . ②∵DF BE +=0,∴4231()()0x x x x -+-=,即1234x x x x +=+,∴2232438kkmk km -=+-. ∴02=km 或2231434k k -=+-.解得0k =或0m =.当0k =时,由①、②得 3232<<-m ,∵∈m Z ,∴m 的值为2,3-- 1-,0,13,2,;当0m =,由①、②得 33<<-k ,∵∈k Z ,∴1,0,1-=k .∴满足条件的直线共有9条. 21.(本小题满分14分)(本小题主要考查数列的通项公式、数列前n 项和、不等式等基础知识,考查化归与转化、分类与整合、特殊与一般的数学思想方法,以及推理论证能力、运算求解能力和抽象概括能力) 解: (1) ∵1,+n n a a 是关于x 的方程022=+-n n b x x ∈n (N )*的两根,∴⎩⎨⎧==+++.,211n n n n n n a a b a a 求数列{}n a 的通项公式, 给出如下四种解法:解法1: 由n n n a a 21=++,得⎪⎭⎫⎝⎛⨯--=⨯-++n n n n a a 23123111, 故数列⎭⎬⎫⎩⎨⎧⨯-n n a 231是首项为31321=-a ,公比为1-的等比数列.∴()1131231--⨯=⨯-n n n a , 即()[]nn n a 1231--=. 解法2: 由n n n a a 21=++,两边同除以()11+-n , 得()()()nnnn n a a 21111--=---++,令()nnn a c 1-=, 则()nn n c c 21--=-+.故()()()123121--++-+-+=n n n c c c c c c c c()()()()13222221-----------=n ()()[]()2121211----⋅---=-n()[]1231--=n ()2≥n .且1111-=-=a c 也适合上式, ∴()nna 1-()[]1231--=n , 即()[]n n n a 1231--=. 解法3: 由n n n a a 21=++,得1212+++=+n n n a a , 两式相减得n n n n n a a 22212=-=-++. 当n 为正奇数时,()()()235131--++-+-+=n n n a a a a a a a a25322221-+++++=n 41412121-⎪⎪⎭⎫ ⎝⎛-+=-n 312+=n ()3≥n . 且11=a 也适合上式. 当n 为正偶数时,()()()246242--++-+-+=n n n a a a a a a a a264222221-+++++=n 41414122-⎪⎪⎭⎫ ⎝⎛-+=-n312-=n ()4≥n . 且12112=-=a a 也适合上式. ∴ 当∈n N *时,n a ()[]nn 1231--=.解法4:由nn n a a 21=++,11=a ,得122-=a ()()()1231212122-=---+-=, ()()()123121211222332223+=----=+-=-=a a . 猜想n a ()[]nn 1231--=.下面用数学归纳法证明猜想正确. ① 当1=n 时,易知猜想成立;② 假设当k n =∈k (N *)时,猜想成立,即()[]kk k a 1231--=, 由k k k a a 21=++,得()[]()[]1111231123122+++--=---=-=k k k k k k k k a a ,故当1+=k n 时,猜想也成立. 由①、②得,对任意∈n N *,n a ()[]nn 1231--=.∴()[]()[]111121291+++--⨯--==n n n n n n n a a b ()[]1229112---=+nn . (2)n n a a a a S ++++= 321 ()()()()[]{}nn 111222231232-++-+--++++=()⎥⎦⎤⎢⎣⎡----=+21122311nn .要使0>-n n S b λ对任意∈n N *都成立,即()[]1229112---+n n ()02112231>⎥⎦⎤⎢⎣⎡-----+nn λ(*)对任意∈n N *都成立.① 当n 为正奇数时, 由(*)式得[]1229112-++n n ()01231>--+n λ, 即()()1212911+-+n n ()01231>--+n λ,∵0121>-+n , ∴()1231+<n λ对任意正奇数n 都成立.当且仅当1=n 时, ()1231+n有最小值1.∴1<λ.② 当n 为正偶数时, 由(*)式得[]1229112--+n n ()02231>--+n λ, 即()()1212911-++nn ()01232>--n λ, ∵012>-n,∴()12611+<+n λ对任意正偶数n 都成立.当且仅当2=n 时, ()12611++n 有最小值23.∴<λ23.综上所述, 存在常数λ,使得0>-n n S b λ对任意∈n N *都成立, λ的取值范围是()1,∞-.。
2009年高考试题——广东卷(数学理)扫描版

绝密★启用前试卷类型:B 2009年普通高等学校招生全国统一考试(广东卷)数学(理科)本试卷共4页,21小题,满分150分,,考试用时120分钟。
注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。
用2B铅笔将试卷类型(B)填涂在答题卡相应位置上。
将条形码横贴•在答题卡右上角“条形码粘贴处”。
2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题冃指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液°不按以上要求作答的答案无效。
4.作答选做题时,请先用2B铅笔玻涂选做题的题号对应的信息点,再作答° 漏涂、错涂、多涂的,答案无效。
5.考生必须保持答题卡的整洁。
考试结束后,将试卷和答题卡一并交回°参考公式:锥体的体积公式V =寺se其中S是镣体的底面积,人是锥体的高•一、选择题:本大题共8小题,每小题5分,满分4()分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知全集V = R,集合M <2| 和艸二\x\x =2^-1,A = 1,2,…}的关系的韦恩(Venn)图如图1所示,则阴影部分所示的集合的元索共有A. 3个B. 2个C. 1个D.无穷多个2.设< 是复数,a(z)表示满足列=1的最小正整数n,则对虚数单位:,«(*) =A. 8B. 6C. 4D. 23.若函数y = f(x)是函数y = a\a > 0,且a H 1)的反函数,其图像经过点(舟,a),则心)=A. log2x B・log护 D. x24.已知等比数列{叫I满足a w > 0,n = 1,2,…,且佝•如-s = 2"(〃N 3),则当n > 1时,1叫2如 + + …+=22 D. 5 -l)2二、填空题:本大题共7小题,琴生作答6小题,毎小题5分,满分30分.(-)必做题(9 ~ 12题)9. 随机抽取某产品“件,测得其长度分别为5卫2 ,…,J 则图3所示的程序框图输岀的$ = ________ ,$表示的样本的数字特征是 _______________ .(注:框图中的赋值符号“=”也可以写成“―”或“:=")10. 若平面向S.a.b 满足|a +, = l t a+b 平行于兀轴,b = (2,・1),则 a = _________ . 已知椭圆G 的中心在坐标原点,长仙在*轴上, 离心率为专•,且G上一点到G 的两个焦点的飯 结束] 2 图3离之和为12,则椭圆G 的方程为. ________________ . 5. 给定下列四个命题:① 若•个平面内的两条宜线与另一个平面都平行,那么这两个平血相互平行;② 若一个平面经过另个平面的垂线,那么这两个平面相互垂宜;③ 垂直尸同一直线的两条直线相互平行;④ 若两个平面垂直,那么一个平瓯内与它们的交线不垂直的直线与另一个平面也不垂宜. 具中,为真命题的是A.①和② 出②和③ C.③和④ D.②和④6. —质点受到平而上的三个力巴,码,码(单位:牛顿)的作用而处于平衡状态.已知F.,F 2 成60°角,冃许,F 2的大小分别为2和4,则P 3的大小为A. 6B. 2C. 2/5 •D. 2/7 7- 2010年广州亚运会组委会要从小张、小赵、小李、小罗、小王五名志愿者中选派四人分别 从事翻译、导游、礼仪、司机四项不同工作,若其中小张和小赵只能从事前两项匸作,其余 三人均能从事这四项工作,则不同的选派方案共有A. 36 种B. 12 种 C ・ 18 种 • D. 48 种8- 已知甲、乙两车由同-起点同时出发,并沿同一路线(假定为直线)行驶.甲车、乙车的速 度曲线分别为卩甲和"乙(如图2所示).那么对于图中给定的%和妇,卜'列判断中一定【E 确的是A.在柿时刻,甲年在乙车前面v(l) B. “时刻后,甲车在乙车后面 ■$=0, i-1 否▼C.在®时刻,两车的位置相冋\ r D・5时刻后■乙车在甲车前面kill图212. 已知离散型随机变量X 的分布列如右表•若EX = 0,(-)选做题(13 ~ 15题,考生只能从中选做两題)13. (坐标系与参数方程选做题)若直线= 1 为参数)与直线1/ = 2 + 竝・ ly = I - 2$.($为参数)垂宜,则% = _________ .14. (不等式选讲选做题)不等式 > 1的实数解为 _______ .15. (几何证明选讲选做题)如图4,点A 』,C 是圆0上的点,且AB = 49 AACB =45。
2009广东省普通高中数学水平测试真题及答案
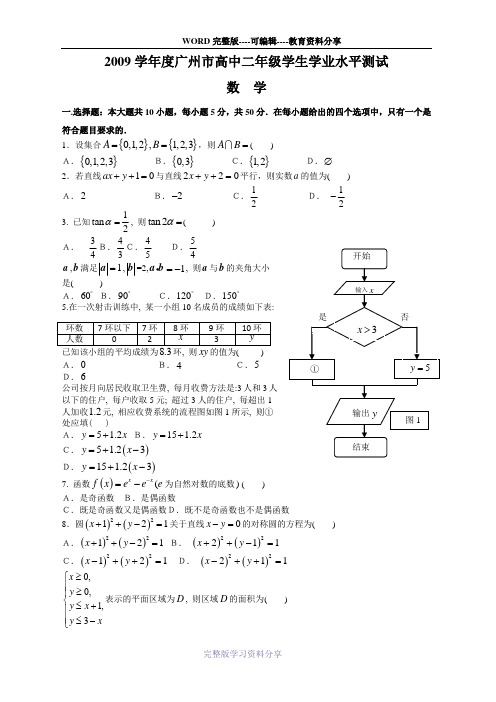
2009学年度广州市高中二年级学生学业水平测试数 学一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一个是符合题目要求的.1.设集合{}{}0,1,2,1,2,3A B ==,则AB =( )A.{}0,1,2,3 B.{}0,3 C.{}1,2 D.∅ 2.若直线10ax y ++=与直线220x y ++=平行,则实数a 的值为( ) A.2 B.2- C.12 D. 12- 3. 已知1tan 2α=, 则tan 2α=( ) A. 34B.43C.45 D.54a ,b 满足1=a ,b =2,a b 1=-, 则a 与b 的夹角大小是( )A.60︒ B.90︒ C.120︒ D.150︒5.在一次射击训练中, 某一小组10名成员的成绩如下表:A.0 B.4 C.5 D.6公司按月向居民收取卫生费, 每月收费方法是:3人和3人以下的住户, 每户收取5元; 超过3人的住户, 每超出1人加收1.2元, 相应收费系统的流程图如图1所示, 则①处应填( )A.5 1.2y x =+ B.15 1.2y x =+ C.()5 1.23y x =+- D.()15 1.23y x =+-7. 函数()(xxf x e e e -=-为自然对数的底数)( )A.是奇函数 B.是偶函数C.既是奇函数又是偶函数D.既不是奇函数也不是偶函数8.圆()()22121x y ++-=关于直线0x y -=的对称圆的方程为( ) A.()()22121x y ++-= B. ()()22211x y ++-= C.()()22121x y -++= D. ()()22211x y -++=0,0,1,3x y y x y x≥⎧⎪≥⎪⎨≤+⎪⎪≤-⎩表示的平面区域为D , 则区域D 的面积为( )A.1 B.32 C.52 D.7210. 某班运动队由足球运动员18人、篮球运动员12人、乒乓球运动员6人组成,现从这些运动员中抽取1个容量为n 的样本,若分别采用系统抽样和分层抽样,则都不用剔除个体;当样本容量为1n +个时,若采用系统抽样,则需要剔除1个个体,那么样本容量n 为( ) A.5 B.6 C.12 D.18 二.填空题:本大题共4小题,每小题5分,满分20分. 11. 已知等差数列{}n a 的首项为1,公差为2,则通项公式n a =.12. 在△ABC 中,角A 、B 、C 所对的边分别为a 、b 、c ,已知11,2,sin 3a b A ===,则sin B 的值为. 13. 一个几何体的三视图如图2所示,那么这个几何体的表.面积..为. 14.已知0,0a b >>,且三点()()()1,1,,0,0,A B a C b 共线,则a b +的最小值为.三.解答题:本大题共6小题,共80分.解答应写出文字说明、演算步骤和推证过程.15.(本小题满分12分) 已知函数()sin ,f x x x =∈R. (1) 求函数()f x 的最小正周期和最大值;(2) 若θ为第一象限的角, 且满足()35f θ=, 求4f πθ⎛⎫- ⎪⎝⎭的值.16.(本小题满分12分)有四条线段,其长度分别为2,3,5,7.(1)从这四条线段中任意取出两条,求所取出的两条线段的长度之和大于7的概率; (2)从这四条线段中任意取出三条,求所取出的三条线段能构成三角形的概率.17.(本小题满分14分)在长方体1111D C B A ABCD -中,11==AA AD ,截面11D ABC 为正方形. (1)求长方体1111D C B A ABCD -的体积; (2)求证:⊥D A 1平面11D ABC .18.(本小题满分14分) 已知a ∈R , 函数()()11,0,11,0.x f x xa x x ⎧->⎪=⎨⎪-+≤⎩(1) 求()1f 的值;(2) 证明: 函数()f x 在()0,+∞上单调递增; (3) 求函数()f x 的零点.19.(本小题满分14分)已知圆M 经过三点()()()2,2,2,4,3,3A B C ,从圆M 外一点(),P a b 向该圆引切线PT ,T 为切点,且PT PO =(O 为坐标原点). (1) 求圆M 的方程;(2)试判断点P 是否总在某一定直线上,若是,求出该直线方程;若不是,请说明理由.2242224222俯视图侧视图正视图图220.(本小题满分14分)已知二次函数()()20f x x tx t =+>在区间[]1,0-上的最小值为1-.(1)求t 的值;(2)记n S 为数列{}n a 的前n 项和, 且11,a =0(n a n >∈N *),点)12n a +在函数()f x 的图象上, 求n S 的表达式.2009年度上学期广州市高中二年级学生学业水平测试数学试题参考答案及评分标准5分,满分50分.5分,满分20分.11. 21n - 12.313. 11π 14. 4 三、解答题15. 本小题主要考查三角函数和三角恒等变换等基本知识.满分12分. 解: (1)∵函数()sin ,f x x x =∈R,∴函数()f x 的最小正周期为2π, 最大值为1.……4分 (2)∵()35f θ=, ∴3sin 5θ=. ……6分∵θ为第一象限角,∴4cos 5θ==.……8分 ∴4f πθ⎛⎫-⎪⎝⎭sin 4πθ⎛⎫=- ⎪⎝⎭sin coscos sin44ππθθ=-……10分3455=-⨯=.……12分 16. 本小题主要考查古典概型等基本知识.满分12分. 解:(1)从这四条线段中任意取出两条,共有6种不同的取法:()()()()()()2,3,2,5,2,7,3,5,3,7,5,7, (2)分其中两条线段的长度之和大于7的共有4种取法:()()()()2,7,3,5,3,7,5,7, (4)分∴所取出的两条线段的长度之和大于7的概率为4263P ==. ……6分(2)从这四条线段中任意取出三条,共有3种不同的取法:()()()()2,3,5,2,3,7,2,5,7,3,5,7……8分其中能构成三角形的只有1种取法()3,5,7,……10分∴所取出的三条线段能构成三角形的概率为14P =. ……12分答:(1)所取出的两条线段的长度之和大于7的概率为23; (2)所取出的三条线段能构成三角形的概率14. 17. 本小题主要考查空间线面位置关系,几何体体积等基本知识,考查空间想象能力和推理论证能力.满分14分.(1) 解: 在直角三角形11D AA 中,11=AA ,111==AD D A , ∴2211211=+=D A AA AD . ……2分∵截面11D ABC 为正方形, ∴21==AD AB . ……4分∴长方体1111D C B A ABCD -的体积V =21211=⨯⨯=⋅AA S ABCD . ……6分(2)证法一:∵1111D C B A ABCD -为长方体, ∴⊥AB 平面D D AA 11. ∵⊂D A 1平面D D AA 11, ∴D A AB 1⊥.……8分 ∵1AA AD =,∴四边形D D AA 11为正方形. ……10分∴D A AD 11⊥. ……12分 ∵⊂=AB A AD AB ,1 平面11D ABC ,1AD ⊂平面11D ABC ,∴⊥D A 1平面11D ABC . ……14分 证法二:∵1111D C B A ABCD -为长方体, ∴⊥AB 平面D D AA 11.∵⊂AB 平面11D ABC ,∴平面11D ABC ⊥平面D D AA 11.……8分 ∵1AA AD =,∴四边形D D AA 11为正方形. ……10分 ∴D A AD 11⊥. ……12分 ∵平面11D ABC 平面D D AA 111AD =,1A D ⊂平面D D AA 11,∴⊥D A 1平面11D ABC . ……14分18.本小题主要考查函数的性质、函数的零点等基本知识,考查运算求解能力和推理论证能力.满分14分.(1)解: 当0x >时, ()11f x x=-, ∴()11101f =-=. ……2分(2)证明:在()0,+∞上任取两个实数12,x x ,且12x x <, ……3分则()()12121111f x f x x x ⎛⎫⎛⎫-=--- ⎪ ⎪⎝⎭⎝⎭……4分1212x xx x -=. ……5分∵120x x <<,∴12120,0x x x x -<>. ∴12120x x x x -<, 即()()120f x f x -<. ∴()()12f x f x <. ……7分∴函数()f x 在()0,+∞上单调递增. ……8分(3)(ⅰ)当0x >时, 令()0f x =, 即110x-=, 解得10x =>. ∴1x =是函数()f x 的一个零点. ……9分 (ⅱ)当0x ≤时, 令()0f x =, 即()110a x -+=.(※)① 当1a >时, 由(※)得101x a=<-, ∴11x a=-是函数()f x 的一个零点; ……11分② 当1a =时, 方程(※)无解; ③ 当1a <时, 由(※)得101x a=>-,(不合题意,舍去). ……13分 综上所述, 当1a >时,函数()f x 的零点是1和11a-; 当1a ≤时,函数()f x 的零点是1.……14分19.本小题主要考查直线和圆等基本知识,考查运算求解能力和抽象概括能力.满分14分. (1)解法一:设圆M 的方程为220x y Dx Ey F ++++=, ……1分∵圆M 经过三点()()()2,2,2,4,3,3A B C ,∴22222222220,24240,33330.D E F D E F D E F ⎧++++=⎪++++=⎨⎪++++=⎩……4分 解得4,6,12.D E F =-⎧⎪=-⎨⎪=⎩……7分∴圆M 的方程为()()22231x y -+-=. ……8分 解法二:设圆M 的方程为()()222x a y b r -+-=()0r >, ……1分∵圆M 经过三点()()()2,2,2,4,3,3A B C ,∴()()()()()()22222222222,24,33.a b r a b r a b r ⎧-+-=⎪⎪-+-=⎨⎪-+-=⎪⎩……4分 解得2,3,1.a b r =⎧⎪=⎨⎪=⎩……7分∴圆M 的方程为()()22231x y -+-=. ……8分 解法三:∵()()2,2,2,4A B ,∴线段AB 的垂直平分线方程为3y =, ……2分∵()()2,2,3,3A C ,∴线段AC 的垂直平分线方程为5522y x ⎛⎫-=-- ⎪⎝⎭即50x y +-=, ……4分由3,50.y x y =⎧⎨+-=⎩解得圆心M 的坐标为()2,3.……6分故圆M 的半径1r AM ===.∴圆M 的方程为()()22231x y -+-=. ……8分解法四:∵2AB ==,AC ==BC == ……2分∴2224AC BC AB +==.∴△ABC 是直角三角形. ……4分∵圆M 经过,,A B C 三点,∴圆M 是Rt △ACB 的外接圆. ……6分 ∴圆M 的圆心M 的坐标为AB 的中点()2,3,半径112r AB ==. ∴圆M 的方程为()()22231x y -+-=. ……8分 (2)连接PM ,则PT ==, ……10分∵PO =PT PO =,∴=……12分化简得2360a b +-=.∴点P 总在定直线2360x y +-=上. ……14分20.本小题主要考查函数、数列等基本知识,考查运算求解能力和推理论证能力.满分14分.解:(1)()2f x x tx =+=2224t t x ⎛⎫+- ⎪⎝⎭. ……1分① 若102t -≤-<,即02t <≤,则当2tx =-时,()f x 取得最小值24t -,依题意得24t -1=-,解得2t =或2t =-(舍去). ……3分② 若12t-<-即2t >,则当1x =-时,()f x 取得最小值1t -, 依题意得1t -1=-,解得2t =(不合舍去). ……5分综合①、②得2t =. ……6分(2)由(1)得()22f x x x =+,∵点)12n a +在函数()f x 的图象上,∴2122n a +=+.∴())122n n S S +-=, ……8分即()()()()22-+=+.∵0n a >,∴0n S >+0>.∴2=2,即3=2. ……10分)131=.∴数列}112=,公比为3的等比数列. ……12分1123n -=⨯. ∴()21231n n S -=⨯-. ……14分。
2009年广州市普通高中毕业班综合测试(二)数学(文科)

数学(文科)试题A 参考答案及评分标准 第 1 页 共 13 页试卷类型:A2009年广州市普通高中毕业班综合测试(二)数 学(文科)2009.4 本试卷共4页,21小题, 满分150分。
考试用时120分钟。
注意事项:1.答卷前,考生务必用2B 铅笔在“考生号”处填涂考生号,用黑色字迹钢笔或签字笔将自己所在的市、县/区、学校,以及自己的姓名和考生号、试室号、座位号填写在答题卡上。
用2B 铅笔将试卷类型(A )填涂在答题卡相应位置上。
2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4.作答选做题时,请先用2B 铅笔填涂选做题的题号(或题组号)对应的信息点,再作答。
漏涂、错涂、多涂的,答案无效。
5.考生必须保持答题卡的整洁。
考试结束后,将试卷和答题卡一并交回。
参考公式:锥体的体积公式Sh V 31=, 其中S 是锥体的底面积,h 是锥体的高. 球的表面积公式24SR π=,其中R 为球的半径.一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知全集{}1,2,3,4,5,6,7,8U =,集合{}1,2,3A =,{}2,3,4,5B =,则() U A B = ðA .{}6,7,8B .{}1,4,5,6,7,8C .{}2,3D .{}1,2,3,4,52.如果复数()()22356i m m m m -+-+是纯虚数,则实数m 的值为A .0B .2C .0或3D .2或33.已知函数()()()40,40.x x x f x x x x +<⎧⎪=⎨-≥⎪⎩,, 则函数()f x 的零点个数为A .1B .2C .3D .44.命题“x ∃∈R ,2210x x -+<”的否定是数学(文科)试题A 参考答案及评分标准图1 俯视图 图2A .x ∃∈R ,221x x -+≥0 B .x ∃∈R ,2210x x -+> C .x ∀∈R ,221x x -+≥0D .x ∀∈R ,2210x x -+<5.在空间直角坐标系中,以点()4 1 9A ,,,()101 6B -,,,() 4 3C x ,,为顶点的ABC ∆是以BC 为底边的等腰三角形,则实数x 的值为 A .2- B .2 C .6 D .2或6 6.如图1视图与俯视图,同一位置上叠放的小正方体的个数,则这个几何体的正(主)视图是A .B.C.D.7.曲线3y x =在点()1 1,处的切线与x 轴及直线1x =所围成的三角形的面积为A .112 B .16 C .13 D .128.已知圆229x y +=与圆224410x y x y +-+-=关于直线l 对称,则直线l 的方程为A .4410x y -+=B .0x y -=C .0x y +=D .20x y --=9.在长为1的线段上任取两点,则这两点之间的距离小于12的概率为 A .14 B .12 C .34 D .7810.在平面内有n (*,n n N ∈≥)3条直线,其中任何两条不平行,任何三条不过同一点,若这n条直线把平面分成()f n 个平面区域,则()6f 等于 A .18B .22C .24D .32二、填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分. (一)必做题(11~13题) 11.阅读如图2所示的程序框图,若输入x 的值为2,则输出y 的值为 .12.在某项才艺竞赛中,有9位评委,主办单位规定计算 参赛者比赛成绩的规则如下:剔除评委中的一个最高分和一个最低分后,再计算其他7位评委的平均分作为此参赛者的比赛成绩.现有一位参赛者所获9位评数学(文科)试题A 参考答案及评分标准 第 3 页委一个最高分为86分、一个最低分为45分,若未剔除最高分与最低分时9位评委的平均分为76分,则这位参赛者的比赛成绩为 分.13.在ABC ∆中,已知tan 3tan A B =,则)tan A B - 的最大值为 ,此时角A 的大小为 . (二)选做题(14~15题,考生只能从中选做一题) 14.(几何证明选讲选做题)如图3所示,在四边形ABCD 中,EF BC ,FG AD ,则EF FGBC AD+的值为 . 15.(坐标系与参数方程选做题) 直线()24,13x t t y t =-+⎧⎨=--⎩为参数被圆25c o s ,15s i n x y θθ=+⎧⎨=+⎩(θ为参数)所截得的弦长为 .三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)已知向量2cos, 12x ⎛⎫= ⎪⎝⎭m ,sin 12x ⎛⎫= ⎪⎝⎭,n ()x ∈R ,设函数()1f x =- m n . (1)求函数()f x 的值域;(2)已知锐角ABC ∆的三个内角分别为A B C ,,,若()513f A =,()35f B =,求()f A B + 的值.17.(本小题满分12分)已知实数a ,{}2 1 1 2b ∈--,,,.(1)求直线 y a x b =+不经过...第四象限的概率; (2)求直线 y a x b =+与圆221x y +=有公共点的概率.18.(本小题满分14分)在长方体1111ABCD A BC D -中,2AB BC ==,过1A 、1C 、B 三点的平面截去长方体的一个角后,得到如图4所示的几何体111ABCD AC D -,且这个几何体的体积为403. (1)证明:直线1A B 平面11CDD C ; (2)求棱1A A 的长;图3数学(文科)试题A 参考答案及评分标准 第 4 页 共 13 页(3)求经过11A C B D 、、、四点的球的表面积.19.(本小题满分14分)已知椭圆C :22221x y a b+=()0a b >>的离心率12为,且经过点P31 2⎛⎫⎪⎝⎭,. (1)求椭圆C 的方程;(2)设F 是椭圆C 的左焦点,判断以PF 为直径的圆与以椭圆长轴为直径的圆的位置关系,并说明理由.20.(本小题满分14分)已知等比数列{}n a 的前n 项和为n S ,若m a ,2m a +,1m a +()*m ∈N 成等差数列,试判断m S ,2m S +,1m S +是否成等差数列,并证明你的结论.21.(本小题满分14分)已知函数()2a f x x x=+,()ln g x x x =+,其中0a >.(1)若1x =是函数()()()h x f x g x =+的极值点,求实数a 的值;(2)若对任意的[]12,1x x e ∈,(e 为自然对数的底数)都有()1f x ≥()2g x 成立,求实数a 的取值范围.2009年广州市普通高中毕业班综合测试(二)数学(文科)试题参考答案及评分标准说明:1.参考答案与评分标准指出了每道题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可根据试题主要考查的知识点和能力比照评分标准给以相应的分数.2.对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数.4.只给整数分数,选择题和填空题不给中间分.一、选择题:本大题考查基本知识和基本运算.共10小题,每小题5分,满分50分.二、填空题:本大题共5小题,每小题5分,满分20分.其中14~15题是选做题,考生只能选做一题,两题全答的,只计算前一题得分.第13题第1个空3分,第2个空2分.数学(文科)试题A参考答案及评分标准第5 页共13 页数学(文科)试题A 参考答案及评分标准 第 6 页 共 13 页11.0 12.79 133π14.1 15.6 三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题主要考查三角函数性质和三角函数的基本关系等知识,考查化归与转化的数学思想方法,以及运算求解能力)解:(1)()12cos 1sin 1122x x f x ⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭,,m n 2c o s s i n 11s i n 22x xx =+-=. ∵x ∈R ,∴函数()f x 的值域为[]1 1-,.(2)∵()513f A =,()35f B =, ∴5sin 13A =,3sin 5B =.∵,A B 都是锐角,∴12cos 13A ==,4cos 5B ==. ∴()()sin f A B A B +=+sin cos cos sin A B A B =+541231351355665=⨯+⨯=.∴()f A B +的值为5665.17.(本小题主要考查古典概型等基础知识,考查化归和转化、分类与整合的数学思想方法,数学(文科)试题A 参考答案及评分标准 第 7 页 共 13 页以及简单的推理论证能力)解:由于实数对(),a b 的所有取值为:()22--,,()21--,,()2 1-,,()2 2-,,()12--,,()11--,,()1 1-,,()1 2-,,()12-,,()11-,,()1 1,,()1 2,,()22-,,()21-,,()2 1,,()2 2,,共16种. 设“直线 y a x b =+不经过第四象限”为事件A ,“直线y ax b =+与圆221x y +=有公共点”为事件B . (1)若直线 y a x b =+不经过第四象限,则必须满足0,0.a b ⎧⎨⎩≥ ≥ 即满足条件的实数对()a b ,有()1 1,,()1 2,,()2 1,,()2 2,,共4种. ∴()41164P A ==. 故直线 y a x b =+不经过第四象限的概率为14. (2)若直线y ax b =+与圆221x y +=有公共点,≤1,即2b ≤21a +.若2a =-,则21 1 2b =--,,,符合要求,此时实数对(a b ,)有4种不同取值; 若1a =-,则1 1b =-,符合要求,此时实数对(a b ,)有2种不同取值; 若1a =,则1 1b =-,符合要求,此时实数对(a b ,)有2种不同取值; 若2a =,则21 1 2b =--,,,符合要求,此时实数对(a b ,)有4种不同取值. ∴满足条件的实数对()a b ,共有12种不同取值. ∴()123164P B ==. 故直线y ax b =+与圆221x y +=有公共点的概率为34.18.(本小题主要考查空间线面关系、几何体的表面积与体积等知识,考查数形结合的数学思数学(文科)试题A 参考答案及评分标准 第 8 页 共 13 页想方法,以及空间想象能力、运算求解能力) (1)证法1:如图,连结1D C , ∵1111ABCD A BC D -是长方体, ∴11A D BC 且11A D BC =.∴四边形11A BCD 是平行四边形. ∴11A B D C .∵1A B ⊄平面11CDD C ,1D C ⊂平面11CDD C ,∴1A B 平面11CDD C . 证法2:∵1111ABCD A BC D -是长方体, ∴平面1A AB 平面11CDD C .∵1A B ⊂平面1A AB ,1A B ⊄平面11CDD C ,∴1A B 平面11CDD C . (2)解:设1A A h =,∵几何体111ABCD AC D -的体积为403, ∴1111111111403ABCD A C D ABCD A B C D B A B C V V V ---=-=,即11114033ABCD A B C S h S h ∆⨯-⨯⨯=,即11402222323h h ⨯⨯-⨯⨯⨯⨯=,解得4h =.∴1A A 的长为4.(3)如图,连结1D B ,设1D B 的中点为O ,连11OA OC OD ,,, ∵1111ABCD A BC D -是长方体,∴11A D ⊥平面1A AB . ∵1A B ⊂平面1A AB ,∴11A D ⊥1A B .∴1112OA D B =.同理1112OD OC D B ==. ∴11OA OD OC OB ===.∴经过1A ,1C ,B ,D 四点的球的球心为点O . ∵2222222111124224D B A D A A AB =++=++=. ∴()2221144242D B S OB D B ππππ⎛⎫=⨯=⨯=⨯= ⎪⎝⎭球.数学(文科)试题A 参考答案及评分标准 第 9 页 共 13 页故经过1A ,1C ,B ,D 四点的球的表面积为24π.19.(本小题主要考查椭圆、圆的方程和圆与圆的位置关系等基础知识,考查数形结合思想,以及运算求解能力)解:(1)∵椭圆22221x y a b+=(0)a b >>的离心率为12,且经过点P31 2⎛⎫⎪⎝⎭,,∴221,219 1.4a a b =⎪⎨⎪+=⎪⎩ 即2222340,191.4a b a b⎧-=⎪⎨+=⎪⎩解得224,3.a b ⎧=⎪⎨=⎪⎩ ∴椭圆C 的方程为22143x y +=. (2)∵24a =,23b =,∴1c ==.∴椭圆C 的左焦点坐标为( 1 0-,.以椭圆C 的长轴为直径的圆的方程为224x y +=,圆心坐标是()0 0,,半径为2.以PF 为直径的圆的方程为22325416x y ⎛⎫+-= ⎪⎝⎭,圆心坐标是30 4⎛⎫ ⎪⎝⎭,,半径为54.35= 244-,故以PF 为直径的圆与以椭圆长轴为直径的圆内切.20.(本小题主要考查等差数列、等比数列的通项公式与前n 项求和公式等知识,考查化归与转化、分类与整合的数学思想方法,以及推理论证能力和运算求解能力) 解:设等比数列{}n a 的首项为1a ,公比为q ()10,0a q ≠≠,若m a ,2m a +,1m a +成等差数列,数学(文科)试题A 参考答案及评分标准 第 10 页 共 13 页则22m a +=m a +1m a +.∴111112m m m a q a q a q +-=+.∵10a ≠,0q ≠,∴2210q q --=. 解得1q =或12q =-. 当1q =时,∵1m S ma =,()111m S m a +=+,()212m S m a +=+, ∴212m m m S S S ++≠+.∴当1q =时,m S ,2m S +,1m S +不成等差数列.当12q =-时,m S ,2m S +,1m S +成等差数列.下面给出两种证明方法. 证法1:∵()()()1211222m m m m m m m m m S S S S S a S a a ++++++-=++-++ 122m m a a ++=-- 112m m a a q ++=-- 11122m m a a ++⎛⎫=--- ⎪⎝⎭0=, ∴212m m m S S S ++=+. ∴当12q =-时,m S ,2m S +,1m S +成等差数列.证法2:∵212211212412113212m m m a S a +++⎡⎤⎛⎫--⎢⎥ ⎪⎡⎤⎝⎭⎢⎥⎛⎫⎣⎦==--⎢⎥ ⎪⎝⎭⎢⎥⎣⎦+,数学(文科)试题A 参考答案及评分标准 第 11 页 共 13 页 又1111111111222112113221122m m m m m m a a S S a +++⎡⎤⎡⎤⎛⎫⎛⎫----⎢⎥⎢⎥ ⎪ ⎪⎡⎤⎝⎭⎝⎭⎢⎥⎢⎥⎛⎫⎛⎫⎣⎦⎣⎦+=+=----⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦++ 221211242322m m a ++⎡⎤⎛⎫⎛⎫=--+-⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦2141132m a +⎡⎤⎛⎫=--⎢⎥ ⎪⎝⎭⎢⎥⎣⎦, ∴212m m m S S S ++=+.∴当12q =-时,m S ,2m S +,1m S +成等差数列.21.(本小题主要考查函数的性质、函数与导数等知识,考查化归与转化、分类与整合的数学思想方法,以及抽象概括能力、推理论证能力和运算求解能力) (1)解法1:∵()22ln a h x x x x=++,其定义域为()0,+∞, ∴()2212a h x x x'=-+. ∵1x =是函数()h x 的极值点,∴()10h '=,即230a -=, ∵0a >,∴a =经检验,当a =x =1是函数()h x 的极值点,∴a =解法2:∵()22ln a h x x x x=++,其定义域为()0,+∞, ∴()2212a h x x x'=-+. 令()0h x '=,即22120a x x-+=,整理得,2220x x a +-=. ∵2180a ∆=+>,∴()0h x '=的两个实根114x -=(舍去),214x -+=,数学(文科)试题A 参考答案及评分标准 第 12 页 共 13 页 当x 变化时,()h x ,()h x '的变化情况如下表:1=,即23a =, ∵0a >,∴a =(2)解:对任意的[]12,1x x e ∈,都有()1f x ≥()2g x 成立等价于对任意的[]12,1x x e ∈, 都有()min f x ⎡⎤⎣⎦≥()max g x ⎡⎤⎣⎦.当[]1 x e ∈,时,()110g x x'=+>. ∴函数()ln g x x x =+在[]1e ,上是增函数. ∴()()max 1g x g e e ==+⎡⎤⎣⎦.∵()()()2221x a x a a f x x x+-'=-=,且[]1x e ∈,,0a >, ①当01a <<且[]1x e ,∈时,()()()20x a x a f x x +-'=>, ∴函数()2a f x x x=+在[]1e ,上是增函数. ∴()()2min 11f x f a ==+⎡⎤⎣⎦.由21a +≥1e +,得a又01a <<,∴a 不合题意. ②当1≤a ≤e 时,若1≤x a <,则()()()20x a x a f x x +-'=<,若a x <≤e ,则()()()20x a x a f x x +-'=>. ∴函数()2a f x x x =+在[)1a ,上是减函数,在(]a e ,上是增函数.数学(文科)试题A 参考答案及评分标准 第 13 页 共 13 页 ∴()()min 2f x f a a ==⎡⎤⎣⎦.由2a ≥1e +,得a ≥12e +, 又1≤a ≤e ,∴12e +≤a ≤e . ③当a e >且[]1x e ,∈时,()()()20x a x a f x x +-'=<, ∴函数()2a f x x x=+在[]1e ,上是减函数. ∴()()2min a f x f e e e==+⎡⎤⎣⎦. 由2a e e+≥1e +,得a又a e >,∴a e >.综上所述,a 的取值范围为1,2e +⎡⎫+∞⎪⎢⎣⎭.。
2009年广东高考数学理科卷带详解

2009年普通高等学校招生全国统一考试(广东卷)数学(理科)一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知全集U R =,集合{}212M x x =--和{}21,1,2N x x k k ==-=的关系的韦恩(V enn )图如图所示,则阴影部分所示的集合的元素共有 ( )第1题图A. 3个B. 2个C. 1个D. 无穷多个 【测量目标】集合的表示方法(描述法),集合的并集.【考查方式】给出2个集合,通过并集运算求出集合的元素共有几个. 【难易程度】容易 【参考答案】B【试题解析】由{}212M x x =--得{|13}M x x =-,{1,3,5,}N =则{1,3}M N =,有2个,选B.2.设z 是复数,()a z 表示满足1nz =的最小正整数n ,则对虚数单位i ,()i a = ( ) A. 8 B. 6 C. 4 D. 2 【测量目标】复数的基本概念.【考查方式】给出相关信息,求解出满足i 1n=最小正整数n 【难易程度】容易 【参考答案】C【试题解析】()i i 1na ==,则最小正整数n 为4,选C.3.若函数()y f x =是函数(0,xy aa =>且)1a ≠的反函数,其图象经过点),,a a 则()f x = ( )A.2log xB. 12log x C.12x D. 2x 【测量目标】反函数.【考查方式】给出反函数的原函数的方程和其图象经过点(),a a ,求解出反函数的方程.【难易程度】容易 【参考答案】B【试题解析】()log ,a f x x =代入(),,a a 解得1,2a =所以()12log ,f x x =选B.4.已知等比数列{}n a 满足0,1,2,n a n >=且()252523,n n a a n -=则当1n 时,2123221log log log n a a a -+++= ( )A.()21n n -B. ()21n + C. 2n D.()21n - 【测量目标】已知递推关系求通项.【考查方式】给出相关信息,先求出通项n a ,再利用对数函数化简,求解. 【难易程度】中等 【参考答案】C【试题解析】由()252523nn a a n -=得222,0,n nn a a =>(步骤1) 则2,nn a = ()22123221log log log 1321,n a a a n n -+++=+++-=选C.(步骤2)5.给定下列四个命题:①若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行; ②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直; ③垂直于同一直线的两条直线相互平行;④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直. 其中,为真命题的是( )A. ①和②B. ②和③C. ③和④D. ②和④ 【测量目标】平行与垂直关系的综合问题.【考查方式】给出4个命题,通过直线与直线、面,面与面之间的位置关系判断其真假. 【难易程度】容易【参考答案】D【试题解析】显然 ①和③是假命题,故否定A,B,C,选D.6.一质点受到平面上的三个力123,,F F F (单位:牛顿)的作用而处于平衡状态.已知12,F F 成60角,且12,F F 的大小分别为2和4,则3F 的大小为 ( )A. 6B. 2C. 25D. 27【测量目标】余弦定理.【考查方式】给出物理学相关信息,通过余弦定理求解. 【难易程度】容易 【参考答案】D【试题解析】()222312122cos 1806028,F F F F F =+--=所以327F =,选D.7.2010年广州亚运会组委会要从小张、小赵、小李、小罗、小王五名志愿者中选派四人分别从事翻译、导游、礼仪、司机四项不同工作,若其中小张和小赵只能从事前两项工作,其余三人均能从事这四项工作,则不同的选派方案共有 ( )A. 36种B. 12种C. 18种D. 48种 【测量目标】排列组合及其应用..【考查方式】给出相关信息,考查了排列组合的公式. 【难易程度】中等 【参考答案】A【试题解析】分两类:若小张或小赵入选,则有选法113223C C A 24,=若小张、小赵都入选,则有选法2223A A 12,=共有选法36种,选A.8.已知甲、乙两车由同一起点同时出发,并沿同一路线(假定为直线)行驶.甲车、乙车的速度曲线分别为v 甲和v 乙(如图所示).那么对于图中给定的0t 和1t ,下列判断中一定正确的是 ( )第8题图A.在1t 时刻,甲车在乙车前面B.1t 时刻后,甲车在乙车后面C.在0t 时刻,两车的位置相同D.0t 时刻后,乙车在甲车前面 【测量目标】函数图象的应用. 【考查方式】给出相关图象,再求解. 【难易程度】中等 【参考答案】A【试题解析】由图象可知,曲线v 甲比v 乙在0100t t ~、~与x 轴所围成图形面积大,则在01t t 、时刻,甲车均在乙车前面,选A.二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分. (一)必做题(9 ~ 12题)9.随机抽取某产品n 件,测得其长度分别为12,,,,n a a a 则如图所示的程序框图输出的s = ,s 表示的样本的数字特征是 .(注:框图中的赋值符号“=”也可以写成“←”“:=”)第9题图【测量目标】循环结构的程序框图.【考查方式】给出算法流程图,阅读框图,运行程序,得出结果. 【难易程度】容易 【参考答案】12na a a n+++ 平均数【试题解析】第一次当i =1时,1;s a =第二次当i =2时,12;2a a s +=最后输出12+;na a a s n++=s =平均数.10.若平面向量,a b 满足1,+=+a b a b 平行于x 轴,()2,1,=-b 则=a .【测量目标】向量的坐标运算.【考查方式】考查向量的基本概念及向量的坐标运算. 【难易程度】中等【参考答案】()1,1-或()3,1-【试题解析】设(,)x y =a ,则(2,1)x y +=+-a b ,依题意,得⎪⎩⎪⎨⎧=-=-++011)1()2(22y y x ,(步骤1)解得⎩⎨⎧=-=11y x 或⎩⎨⎧=-=13y x ,所以(1,1)=-a 或(3,1)=-a .(步骤2) 11.已知椭圆G 的中心在坐标原点,长轴在x 轴上,离心率为32,且G 上一点到G 的两个焦点的距离之和为12,则椭圆G 的方程为 . 【测量目标】椭圆的标准方程.【考查方式】给出相关信息,通过离心率公式,长短轴间的关系,求解出标准方程. 【难易程度】中等【参考答案】221369x y += 【试题解析】3,212,6,3,2e a a b ====则所求椭圆方程为22 1.369x y += 12.已知离散型随机变量X 的分布列如右表.若0,1,EX DX ==则a = ,b = .第12题图【测量目标】离散型随机变量的分布列.【考查方式】给出离散型随机变量的分布列,通过公式求解. 【难易程度】中等 【参考答案】51,124【试题解析】由题知2221111,0,1121,12612a b c a c a c ++=-++=⨯+⨯+⨯= 解得51,124a b ==. (二)选做题(13 ~ 15题,考生只能从中选做两题) 13.(坐标系与参数方程选做题)若直线112,:2,x t l y kt =-⎧⎨=+⎩(t 为参数)与直线2,:12,x s l y s =⎧⎨=-⎩(s 为参数)垂直,则k = . 【测量目标】坐标系与参数方程.【考查方式】给出两条直线的参数方程,且两条直线垂直,求解. 【难易程度】较难 【参考答案】1-【试题解析】直线112,:2,x t l y kt =-⎧⎨=+⎩(t 为参数)化为普通方程是)1(22--=-x ky ,该直线的斜率为2k-,(步骤1)直线2,:12,x s l y s =⎧⎨=-⎩(s 为参数)化为普通方程是12+-=x y ,该直线的斜率为2-,(步骤2)则由两直线垂直的充要条件,得()212k ⎛⎫--=- ⎪⎝⎭, 1.k =-(步骤3) 14.(不等式选讲选做题)不等式112x x ++的实数解为 .【测量目标】解一元二次不等式【考查方式】给出不等式方程,先求定义域,再把它换成整数不等式求解. 【难易程度】中等 【参考答案】{x |32x-且2-≠x }【试题解析】112xx++1220x xx⎧++⎪⇔⎨+≠⎪⎩22(1)(2)2x xx⎧++⇔⎨≠-⎩2302xx+⎧⇔⎨≠-⎩解得32x-且2-≠x.所以原不等式的解集为{x|32x-且2-≠x}. 15.(几何证明选讲选做题)如图,点,,A B C是圆O上的点,且4,45AB ACB=∠=,则圆O的面积等于.第15题图【测量目标】几何证明选讲.【考查方式】给出圆上线段长,角度大小,求解圆的面积.【难易程度】容易【参考答案】8π【试题解析】解法一:连结,,OA OB则902,AOB ACB∠==∠(步骤1)所以AOB△为等腰直角三角形,又4AB=,(步骤2)所以,圆O的半径22R=O的面积等于22ππ(22)8πR=⨯=(步骤3)解法二:设圆O的半径为R,在ABC△中,由正弦定理,得42sin45R=,解得22R=(步骤1)所以,圆O的面积等于22ππ(22)8πR=⨯=.(步骤2)三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.16.(本小题满分12分)已知向量(sin,2)θ=-a与(1,cos)θ=b互相垂直,其中π(0,)2θ∈.(1)求sinθ和cosθ的值;(2)若10πsin()102θϕϕ-=<<,求cosϕ的值.【测量目标】余弦定理.【考查方式】利用两向量垂直公式、诱导公式、余弦定理求解.【难易程度】中等【试题解析】(1)∵向量()sin,2θ=-a与()1cosθ,b=互相垂直,∴ sin 2cos 0θθ=-=a b ,即θθcos 2sin =①,(步骤1)又 1cos sin 22=+θθ ② ① 代入②,整理,得51cos 2=θ,(步骤2) 由π0,2θ⎛⎫∈ ⎪⎝⎭,可知0cos >θ, ∴55cos =θ,(步骤3)代入①得552sin =θ. 故55cos =θ, 552sin =θ.(步骤4)(2)ππππ0,0,,2222ϕθθϕ<<<<∴-<-<(步骤5)则()()2310cos 1sin ,10θϕθϕ-=--=(步骤6)()()()2cos cos cos cos sin sin .2ϕθθϕθθϕθθϕ∴=--=-+-=⎡⎤⎣⎦(步骤7) 17.(本小题满分12分)根据空气质量指数API (为整数)的不同,可将空气质量分级如下表:API0~50 51~100 101~150 151~200 201~250 251~300 >300 级别 I II 1III2III1IV2IVV状况 优 良轻微污染 轻度污染 中度污染 中度重污染 重度污染xy67 xy68xy69xy70xy71对某城市一年(365天)的空气质量进行监测,获得的API 数据按照区间[0,50],(50,100],(100,150],(150,200],(200,250],(250,300]进行分组,得到频率分布直方图如图所示. (1)求直方图中x 的值;(2)计算一年中空气质量分别为良和轻微污染的天数;(3)求该城市某一周至少有2天的空气质量为良或轻微污染的概率. (结果用分数表示.已知77578125,2128,==32738123,18253651825182591259125++++=365735=⨯)第17题图 【测量目标】频率分布直方图.【考查方式】给出直方图,阅读,从图中找到相关信息,利用公式定理求解. 【难易程度】中等【试题解析】(1)因为,在频率分布直方图中,各个小矩形的面积之和等于1,依题意,得327385011825365182518259125x ⎛⎫+++++=⎪⎝⎭(步骤1)又 9125123912581825318257365218253=++++ 所以 182501199125123501=-=x .(步骤2) (2)一年中空气质量为良的天数为 1195018250119365=⨯⨯(天);(步骤3) 一年中空气质量为轻微污染的天数为 100503652365=⨯⨯(天);(步骤4) (3)由(2)可知,在一年之中空气质量为良或轻微污染的天数共有119+100=219(天) 所以,在一年之中的任何一天空气质量为良或轻微污染的概率是21933655P ==,(步骤5) 设一周中的空气质量为良或轻微污染的天数为ξ,则ξ~B (7,53) 7733()C 155kkk P k ξ-⎛⎫⎛⎫==- ⎪⎪⎝⎭⎝⎭,(k =0,1,2,…,7)(步骤6)设“该城市某一周至少有2天的空气质量为良或轻微污染”为事件A ,则)1()0(1)(=-=-=ξξP P A P =-1070733C 155⎛⎫⎛⎫- ⎪⎪⎝⎭⎝⎭161733C 155⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭=6752537521⎪⎭⎫ ⎝⎛⨯⨯-⎪⎭⎫⎝⎛-=78125766537812513441281522121767=+-=⨯+-.(步骤7) 18.(本小题满分14分)如图,已知正方体1111ABCD A B C D -的棱长为2,点E 是正方形11BCC B 的中心,点F G 、分别是棱111,C D AA 的中点.设点1,1E G 分别是点,E G 在平面11DCC D 内的正投影.(1)求以E 为顶点,以四边形FGAE 在平面11DCC D 内的正投影为底面边界的棱锥的体积;(2)证明:直线1FG ⊥平面1FEE ; (3)求异面直线11E G EA 与所成角的正弦值.第18题图【测量目标】锥的体积、空间直角坐标系.【考查方式】考查了锥的体积、线面垂直的判定、异面直线所成的角,建立空间直角坐标系求解【难易程度】较难【试题解析】(1)依题得所求为四棱锥11FG DE E -的体积,其底面11FG DE 面积为111111Rt Rt E FG DG E DE FG S S S =+△△四边形221212221=⨯⨯+⨯⨯=,(步骤1) 又⊥1EE 面11FG DE ,11=EE ,∴111111233E DE FG DE FG V S EE -==四边形.(步骤2)(2)以D 为坐标原点,DA 、DC 、1DD 所在直线分别作x 轴,y 轴,z 轴,得)1,2,0(1E ,)1,0,0(1G ,又因为)1,0,2(G ,)2,1,0(F ,)1,2,1(E ,则)1,1,0(1--=FG ,)1,1,1(-=FE ,)1,1,0(1-=FE ,(步骤3) ∴10(1)10FG FE =+-+=,110(1)10FG FE =+-+=, 即FE FG ⊥1,11FE FG ⊥,(步骤4) 又1FE FE F =,∴⊥1FG 平面1FEE .(步骤5)第18(2)题图(3))0,2,0(11-=G E ,)1,2,1(--=EA , 则111111cos ,6E G EA E G EA E G EA<>==(步骤6) 设异面直线11E G EA 与所成角为θ,则33321sin =-=θ.(步骤7)19.(本小题满分14分)已知曲线2:C y x =与直线:20l x y -+=交于两点(,)A A A x y 和(,)B B B x y ,且A B x x <.记曲线C 在点A 和点B 之间那一段L 与线段AB 所围成的平面区域(含边界)为D .设点(,)P s t 是L 上的任一点,且点P 与点A 和点B 均不重合.(1)若点Q 是线段AB 的中点,试求线段PQ 的中点M 的轨迹方程;(2)若曲线22251:24025G x ax y y a -+-++=与D 有公共点,试求a 的最小值. 【测量目标】直线与抛物线的位置关系,圆锥曲线中的探索性问题. 【考查方式】给出了抛物线方程与直线方程,利用公式、定理求解. 【难易程度】较难【试题解析】曲线C 与直线l 的联立方程组⎩⎨⎧=+-=022y x x y ,得⎩⎨⎧=-=1111y x ,⎩⎨⎧==4222y x ,(步骤1)又A B x x <,所以点,A B 的坐标分别为)4,2(),1,1(B A -(步骤2) ∵点Q 是线段AB 的中点∴点Q 的坐标为⎪⎭⎫⎝⎛25,21Q (步骤3)∵点(,)P s t 是L 上的任一点,且点P 与点A 和点B 均不重合.∴2s t = ,即),(2s s P ,且21<<-s (步骤4) 设线段PQ 的中点为(),M x y ,则点M 的轨迹的参数方程为⎪⎪⎪⎩⎪⎪⎪⎨⎧+=+=2252212s y s x (s 为参数,且21<<-s );消去s 整理,得454122+⎪⎭⎫ ⎝⎛-=x y ,且⎪⎭⎫ ⎝⎛<<-4541x所以,线段PQ 的中点M 的轨迹方程是454122+⎪⎭⎫ ⎝⎛-=x y ,⎪⎭⎫ ⎝⎛<<-4541x ;(步骤5)(2)曲线22251:24025G x ax y y a -+-++=可化为()()222572⎪⎭⎫ ⎝⎛=-+-y a x , 它是以(),2G a 为圆心,以57为半径的圆,(步骤6)设直线:20l x y -+=与y 轴相交于点E ,则E 点的坐标为()0,2E ; 自点A 做直线:20l x y -+=的垂线,交直线2y =于点F ,在Rt △EAF 中,45,AEF ∠=2=AE ,所以2=AF ,∵257<, ∴当0<a 且圆G 与直线l 相切时,圆心G 必定在线段FE 上,且切点必定在线段AE 上,(步骤7) 于是,此时的a 的值就是所求的最小值. 当圆G 与直线:20l x y -+=相切时 571122=++-a , 解得527-=a ,或者527=a (舍去) 所以,使曲线G 与平面区域D 有公共点的a 的最小值是527-.(步骤8)第19(2)题图20.(本小题满分14分)已知二次函数()y g x =的导函数的图象与直线2y x =平行,且()y g x =在1x =-处取得极小值1(0)m m -≠.设()()g x f x x=. (1)若曲线()y f x =上的点P 到点()0,2Q 2,求m 的值; (2)()k k ∈R 如何取值时,函数()y f x kx =-存在零点,并求出零点.【测量目标】函数零点的应用.【考查方式】利用导数求函数的极值、两点间距离公式、函数零点的判断等求解. 【难易程度】较难【试题解析】设二次函数()y g x =的解析式为)0()(2≠++=a c bx ax x g则它的导函数为)0(2)(≠+='a b ax x g ,(步骤1)∵函数)0(2)(≠+='a b ax x g 的图象与直线x y 2=平行, ∴22a = ,解得1a =,所以c bx x x g ++=2)(,b x x g +='2)((步骤2)∵()y g x =在1x =-处取得极小值1(0)m m -≠∴⎩⎨⎧-=-=-'1)1(0)1(m g g ,即⎩⎨⎧-=+-=+-1102m c b b ,解得⎩⎨⎧==mc b 2.所以m x x x g ++=2)(2,()()g x f x x ==2++xm x (0≠x )(步骤3)(1)设点P ⎪⎭⎫⎝⎛++2,x m x x (0≠x ,0≠m )为曲线()y f x =上的任意一点则点P 到点(0,2)Q 的距离为m x m x x m x x PQ 2222222++=⎪⎭⎫ ⎝⎛++=(步骤4)22m当且仅当222m x =时,等号成立,此时min PQ =m m 222+(步骤5)又已知点P 到点(0,2)Q 2222=+m m两边平方整理, 得12=+m m当0>m 时,12=+m m ,解得12-=m当0<m 时,12=+-m m ,解得12--=m 所以m 的值为12-或者12--;(步骤6)(2)函数令kx x f x h -=)()(=2)1(2++-=-++xmx k kx x m x (0≠x )令0)(=x h ,即02)1(=++-xmx k (0≠x ),整理,得02)1(2=++-m x x k (0≠x ),①(步骤7)函数kx x f x h -=)()(存在零点,等价于方程①有非零实数根,由0≠m 可知,方程①不可能有零根,当1k =时,方程①变为02=+m x ,解得02≠=mx ,方程①有唯一实数根, 此时, 函数kx x f x h -=)()(存在唯一的零点2mx =;(步骤8)当1k ≠时,方程①根的判别式为)1(44k m --=∆,0≠m令)1(44k m --=∆=0,解得mk 11-=,方程①有两个相等的实数根m x x -==21,(步骤9)此时,函数kx x f x h -=)()(存在唯一的零点m x -=; 令44(1)0m k ∆=-->,得()11m k -<,当0m >时,解得mk 11->,当0m <时,解得mk 11-<, 以上两种情况下,方程①都有两个不相等的实数根kk m x ---+-=1)1(111,k k m x -----=1)1(112此时, 函数kx x f x h -=)()(存在两个零点k k m x ---+-=1)1(111,kk m x -----=1)1(112(步骤10)综上所述,函数()y f x kx =-存在零点的情况可概括为当1k =时,函数kx x f x h -=)()(存在唯一的零点2mx =;当mk 11-=时,函数kx x f x h -=)()(存在唯一的零点m x -=; 当0m >且m k 11->,或者0m <且mk 11-<时,函数kx x f x h -=)()(存在两个零点 k k m x ---+-=1)1(111,kk m x -----=1)1(112.(步骤11)21.(本小题满分14分)已知曲线22:20(1,2,)n C x nx y n -+==,从点(1,0)P -向曲线n C 引斜率为(0)n n k k >的切线n l ,切点为(,)n n n P x y .(1)求数列{}{}n n x y 与的通项公式;(2)证明:13521n n nxx x x x y -<< 【测量目标】数列的实际应用,间接证明.【考查方式】利用圆锥曲线性质求通项公式,放缩法等求解. 【难易程度】较难【试题解析】曲线22:20(1,2,)n C x nx y n -+==可化为222)(n y n x =+-,所以,它表示以)0,(n C n 为圆心,以n 为半径的圆, 切线n l 的方程为)1(+=x k y n ,联立⎩⎨⎧=+-+=02)1(22y nx x x k y n ,消去y 整理,得 0)22()1(2222=+-++n n n k x n k x k ,①(步骤1)222222)12(44)1(4)22(n n n n k n n k k n k +-=+--=∆,0>n k 令0=∆,解得1222+=n n k n, 12+=n n k n (步骤2)此时,方程①化为012)2122()121(2222=++-++++n n x n n n x n n整理,得[]0)1(2=-+n x n ,解得1+=n n x x ,(步骤3) 所以121)11(12++=+++=n n n n n n ny n∴数列}{n x 的通项公式为1+=n nx x数列}{n y 的通项公式为121++=n n ny n .(步骤4)(2)证明:∵121111111+=+++-=+-n n n n n x x n n ,212n n -=<=135211352113521246235721n n n x x x x n n ---∴=⨯⨯⨯⨯<⨯⨯⨯⨯+ =121+n =nn x x +-11(步骤5)∵121+=n y x nn=n n x x +-11,又因为π043<< 令x y x n n =,则π04x <<, 要证明n n n n y x y x sin 2<,只需证明当π04x <<时,x x sin 2<恒成立即可. (步骤6)设函数x x x f sin 2)(-=,π04x <<则x x f cos 21)(-=',π04x <<(步骤7)∵在区间π0,4⎛⎫⎪⎝⎭上x x f cos 21)(-='为增函数,∴当π04x <<时,π()1104f x x '=<=,(步骤8)∴x x x f sin 2)(-=在区间π0,4⎛⎫⎪⎝⎭上为单调递减函数,∴ x x x f sin 2)(-=0)0(=<f 对于一切π04x <<恒成立,(步骤9)∴x x sin 2<,即n n x x +-11=n n nny x y x sin 2< 综上,得13521n n nxx x x x y -<<(步骤10)。
2009年广州市数字试题(理科)

2009年广州市普通高中毕业班综合测试(二)数 学(理科)一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.如果复数()()22356i m m m m -+-+是纯虚数,则实数m 的值为 A .0 B .2 C .0或3 D .2或32.已知函数()()()4040.x x x f x x x x ⎧+<⎪=⎨-⎪⎩≥,,, 则函数()f x 的零点个数为A .1B .2C .3D .43.已知全集U =R ,集合{3A x =≤}7x <,{}27100B x x x =-+<,则() AB R =ðA .()(),35,-∞+∞B .()[),35,-∞+∞C .(][),35,-∞+∞D .(](),35,-∞+∞4.命题“x ∃∈R ,2210x x -+<”的否定是 A .x ∃∈R ,221x x -+≥0 B .x ∃∈R ,2210x x -+> C .x ∀∈R ,221x x -+≥0D .x ∀∈R ,2210x x -+<5.已知点()1,0A ,直线l :24y x =-,点R 是直线l 上的一点,若RA AP =,则点P 的轨迹方程为 A .2y x =- B .2y x = C .28y x =- D .24y x =+6.函数()cos f x x x =的导函数()f x '在区间[],ππ-上的图像大致是A. B. C. D.7.现有4种不同颜色要对如图1所示的四个部分进行着色,要求有公共边界的两块不能用同一种颜色,则不同的着色方法共有 A .24种 B .30种C .36种D .48种8.设直线l 与球O 有且只有一个公共点P ,从直线l 出发的两个半平面α、β截球O 的两个截面圆的半径分别为1,二面角l αβ--的平面角为150,则球O 的表面积为 A .4πB .16πC .28πD .112π图12图2 二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分. (一)必做题(9~12题)9.在空间直角坐标系中,以点()4 1 9A ,,,()101 6B -,,,() 4 3C x ,,为顶点的ABC ∆是以BC 为斜边的等腰直角三角形,则实数x 的值为 .10.在某项才艺竞赛中,有9位评委,主办单位规定计算参赛者比赛成绩的规则如下:剔除评委中的一个最高分和一个最低分后,再计算其他7位评委的平均分作为此参赛者的比赛成绩.现有一位参赛者所获9位评委一个最高分为86分、一个最低分为45分,若未剔除最高分与最低分时9位评委的平均分为76分,则这位参赛者的比赛成绩为 分.11.阅读如图2所示的程序框图,若输出y 的值为0, 则输入x 的值为 .12.在平面内有n (*,n n N ∈≥)3条直线,其中任何两条不平行,任何三条不过同一点,若这n 条直线把平面分成()f n 个平面区域,则()5f 的值是 ,()f n 的表达式是 .(二)选做题(13~15题,考生只能从中选做两题) 13.(几何证明选讲选做题)如图3所示,在四边形ABCD 中,EF BC ,FGAD ,则EF FGBC AD+的值为 .14.(不等式选讲选做题) 函数()f x =12x x -++的最小值为 .15.(坐标系与参数方程选做题)直线()24,13x t t y t=-+⎧⎨=--⎩为参数被圆25c o s ,15s i n x y θθ=+⎧⎨=+⎩(θ为参数)所截得的弦长为 .图3数学(理科)试题参考答案及评分标准 第 3 页 共 12 页三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题满分12分)已知向量2cos 12x ⎛⎫= ⎪⎝⎭,m ,sin 12x ⎛⎫= ⎪⎝⎭,n ()x ∈R ,设函数()1f x =-m n . (1)求函数()f x 的值域;(2) 已知锐角ABC ∆的三个内角分别为A ,B ,C ,若()513f A =,()35f B =,求()f C 的值.17.(本小题满分12分)在长方体1111ABCD A B C D -中,2AB BC ==,过1A 、1C 、B 三点的平面截去长方体的一个角后,得到如图4所示的几何体111ABCD AC D -(1)求棱1A A 的长;(2)在线段1BC 上是否存在点P ,使直线1A P 与1C D 垂直,如果存在,求线段1A P 的长,如果不存在,请说明理由.18.(本小题满分14分)已知等比数列{}n a 的前n 项和为n S ,若m a ,2m a +,1m a +()*m ∈N 成等差数列,试判断m S ,2m S +,1m S +是否成等差数列,并证明你的结论.19.(本小题满分14分)一个口袋中装有2个白球和n 个红球(n ≥2且*n ∈N ),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖. (1)试用含n 的代数式表示一次摸球中奖的概率p ; (2)若3n =,求三次摸球恰有一次中奖的概率;(3)记三次摸球恰有一次中奖的概率为()f p ,当n 为何值时,()f p 最大?420.(本小题满分14分)已知函数()2a f x x x=+,()ln g x x x =+,其中0a >.(1)若1x =是函数()()()h x f x g x =+的极值点,求实数a 的值;(2)若对任意的[]12,1x x e ∈,(e 为自然对数的底数)都有()1f x ≥()2g x 成立,求实数a 的取值范围.21.(本小题满分14分)已知双曲线C :22221x y a b-=00(,)a b >>,左、右焦点分别为1F 、2F ,在双曲线C 上有一点M ,使12MF MF ⊥,且12MF F ∆的面积为1. (1)求双曲线C 的方程;(2)过点()3,1P 的动直线l 与双曲线C 的左、右两支分别相交于两点A 、B ,在线段AB 上取异于A 、B 的点Q ,满足AP QB AQ PB =.证明:点Q 总在某定直线上.数学(理科)试题参考答案及评分标准 第 5 页 共 12 页2009年广州市普通高中毕业班综合测试(二)数学(理科)试题参考答案及评分标准一、选择题:本大题考查基本知识和基本运算.共8小题,每小题5分,满分40分.二、填空题:本大题共7小题,每小题5分,满分30分.其中13~15题是选做题,考生只能选做二题,三题全答的,只计算前二题得分.第12题第1个空3分,第2个空2分.9.2 10.79 11.0 或 2 12.16,222n n ++13.1 14.3 15.6三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.16.(本小题主要考查三角函数性质和三角函数的基本关系等知识,考查化归与转化的数学思想方法,以及运算求解能力)解:(1)()12cos 1sin 1122x x f x ⎛⎫⎛⎫=-=-⎪ ⎪⎝⎭⎝⎭,,m n2cos sin 11sin 22x xx =+-=.∵x ∈R ,∴函数()f x 的值域为[]1 1-,.(2)∵()513f A =,()35f B =,∴5sin 13A =,3sin 5B =. ∵,A B 都为锐角,∴12cos 13A ==,4cos 5B ==.∴()()()sin sin sin f C C A B A B π==-+=+⎡⎤⎣⎦sin cos cos sin A B A B =+541235613513565=⨯+⨯=. ∴()f C 的值为5665.17.(本小题主要考查空间线面关系、几何体的表面积与体积等基本知识,考查数形结合的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力) 解:(1)设1A A h =,∵几何体111ABCD AC D -的体积为403, ∴1111111111403ABCD A C D ABCD A B C D B A B C V V V ---=-=, 即11114033ABCD A B C S h S h ∆⨯-⨯⨯=,6A即11402222323h h ⨯⨯-⨯⨯⨯⨯=,解得4h =. ∴1A A 的长为4. (2)在线段1BC 上存在点P ,使直线1A P 与1C D 垂直. 以下给出两种证明方法:方法1:过点1D 作1C D 的垂线交1C C 于点Q ,过点Q 作PQ BC交1BC 于点P .∵11C D D Q ⊥,111C D A D ⊥,1111D Q A D D =,∴1C D ⊥平面11A D Q .∵1AQ ⊂平面11A D Q ,∴11C D AQ ⊥. ∵1C D PQ ⊥,∴1C D ⊥平面1A PQ . ∵1A P ⊂平面1A PQ ,∴11C D A P ⊥. 在矩形11CDD C 中,∵11Rt D C Q∆∽1Rt C CD ∆,∴1111C QD C CD C C =,即1224C Q =,∴11C Q =. ∵1C PQ ∆∽1C BC ∆,∴1111C P C Q C B C C =14=,∴1C P =.在11APC ∆中,∵11AC =1111112cos A C A C P C B ∠==由余弦定理,得1A P =2==. ∴在线段1BC 上存在点P ,使直线1A P 与1C D 垂直,且线段1A P 的长为2. 方法2:以点D 为坐标原点,分别以DA ,DC ,1DD 所在的直线为x 轴,y 轴,z 轴建立如图的空间直角坐标系,由已知条件与(1)可知,()10,2,4C ,()12,0,4A ,()0,0,0D , 假设在线段1BC 上存在点()P x y z ,,(0≤x ≤2,2y =,0≤z ≤)4 使直线1A P 与1C D 垂直,过点P 作PQ BC ⊥交BC 于点Q .由BPQ ∆∽1BC C ∆,得1PQ BQC C BC=, ∴124422BQ xPQ C C x BC-=⨯=⨯=-. ∴42z x =-. ∴()12 2 2A P x x =--,,,()10 2 4C D =--,,. ∵11A P C D ⊥,∴110A P C D =,即()()2 2 20 2 40x x ----=,,,,,∴12x =.数学(理科)试题参考答案及评分标准 第 7 页 共 12 页此时点P 的坐标为1 2 32⎛⎫ ⎪⎝⎭,,,在线段1BC 上. ∵13 2 12A P ⎛⎫=-- ⎪⎝⎭,,,∴12A P ⎛=-= . ∴在线段1BC 上存在点P ,使直线1A P与1C D 垂直,且线段1A P 的长为2. 18.(本小题主要考查等差数列、等比数列的通项公式与前n 项和公式等基础知识,考查化归与转化、分类与整合的数学思想方法,以及推理论证能力和运算求解能力)解:设等比数列{}n a 的首项为1a ,公比为q ()10,0a q ≠≠, 若m a ,2m a +,1m a +成等差数列, 则22m a +=m a +1m a +. ∴111112m m m a qa q a q +-=+.∵10a ≠,0q ≠,∴2210q q --=. 解得1q =或12q =-. 当1q =时,∵1m S ma =,()111m S m a +=+,()212m S m a +=+,∴212m m m S S S ++≠+.∴当1q =时,m S ,2m S +,1m S +不成等差数列.当12q =-时,m S ,2m S +,1m S +成等差数列.下面给出两种证明方法. 证法1:∵()()()1211222m m m m m m m m m S S S S S a S a a ++++++-=++-++122m m a a ++=-- 112m m a a q ++=-- 11122m m a a ++⎛⎫=--- ⎪⎝⎭0=, ∴212m m m S S S ++=+.∴当12q =-时,m S ,2m S +,1m S +成等差数列. 证法2:∵212211212412113212m m m a S a +++⎡⎤⎛⎫--⎢⎥ ⎪⎡⎤⎝⎭⎢⎥⎛⎫⎣⎦==--⎢⎥ ⎪⎝⎭⎢⎥⎣⎦+,又1111111111222112113221122m m m m m m a a S S a +++⎡⎤⎡⎤⎛⎫⎛⎫----⎢⎥⎢⎥ ⎪ ⎪⎡⎤⎝⎭⎝⎭⎢⎥⎢⎥⎛⎫⎛⎫⎣⎦⎣⎦+=+=----⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦++ 221211242322m m a ++⎡⎤⎛⎫⎛⎫=-⨯-+⨯-⎢⎥ ⎪⎪⎝⎭⎝⎭⎢⎥⎣⎦2141132m a +⎡⎤⎛⎫=--⎢⎥ ⎪⎝⎭⎢⎥⎣⎦, ∴212m m m S S S ++=+.∴当12q =-时,m S ,2m S +,1m S +成等差数列.19.(本小题主要考查等可能事件、互斥事件和独立重复试验等基础知识,考查化归与转化的数学思想方8法,以及推理论证能力和运算求解能力)解:(1)∵一次摸球从2n +个球中任选两个,有22C n +种选法,任何一个球被选出都是等可能的,其中两球颜色相同有222C C n +种选法,∴一次摸球中奖的概率2222222C C 2C 32n n n n p n n ++-+==++. (2)若3n =,则一次摸球中奖的概率25p =, 三次摸球是独立重复试验,三次摸球恰有一次中奖的概率是123354(1)C (1)125P p p =⋅⋅-=. (3)设一次摸球中奖的概率为p ,则三次摸球恰有一次中奖的概率为()()213233(1)C 1363f p P p p p p p ==⋅⋅-=-+,01p <<,∵()()()291233131f p p p p p '=-+=--,∴()f p 在10 3⎛⎫ ⎪⎝⎭,上为增函数,在1 13⎛⎫ ⎪⎝⎭,上为减函数.∴当13p =时,()f p 取得最大值. ∵2221323n n p n n -+==++(n ≥)*2,n ∈N 且, 解得2n =.故当2n =时,三次摸球恰有一次中奖的概率最大.20.(本小题主要考查函数的性质、函数与导数等知识,考查化归与转化、分类与整合的数学思想方法,以及抽象概括能力、推理论证能力和运算求解能力)(1)解法1:∵()22ln a h x x x x=++,其定义域为()0 +∞,, ∴()2212a h x x x'=-+.∵1x =是函数()h x 的极值点,∴()10h '=,即230a -=.∵0a >,∴a =经检验当a =1x =是函数()h x 的极值点,∴a =解法2:∵()22ln a h x x x x =++,其定义域为()0+∞,, ∴()2212a h x x x'=-+.令()0h x '=,即22120a x x-+=,整理,得2220x x a +-=.∵2180a ∆=+>,∴()0h x '=的两个实根1x =(舍去),2x =当x 变化时,()h x ,()h x '的变化情况如下表:1=,即23a=,∵0a>,∴a=(2)解:对任意的[]12,1x x e∈,都有()1f x≥()2g x成立等价于对任意的[]12,1x x e∈,都有()mi nf x⎡⎤⎣⎦≥()maxg x⎡⎤⎣⎦.当x∈[1,e]时,()110g xx'=+>.∴函数()lng x x x=+在[]1e,上是增函数.∴()()max1g x g e e==+⎡⎤⎣⎦.∵()()()2221x a x aaf xx x+-'=-=,且[]1,x e∈,0a>.①当01a<<且x∈[1,e]时,()()()2x a x af xx+-'=>,∴函数()2af x xx=+在[1,e]上是增函数,∴()()2min11f x f a==+⎡⎤⎣⎦.由21a+≥1e+,得a又01a<<,∴a不合题意.②当1≤a≤e时,若1≤x<a,则()()()2x a x af xx+-'=<,若a<x≤e,则()()()2x a x af xx+-'=>.∴函数()2af x xx=+在[)1,a上是减函数,在(]a e,上是增函数.∴()()min2f x f a a==⎡⎤⎣⎦.由2a≥1e+,得a≥12e+,又1≤a≤e,∴12e+≤a≤e.③当a e>且x∈[1,e]时,()()()2x a x af xx+-'=<,∴函数()2af x xx=+在[]1e,上是减函数.∴()()2minaf x f e ee==+⎡⎤⎣⎦.数学(理科)试题参考答案及评分标准第9 页共12 页10由2a e e+≥1e +,得a,又a e >,∴a e >.综上所述,a 的取值范围为1,2e +⎡⎫+∞⎪⎢⎣⎭.21.(本小题主要考查双曲线、解方程和直线与圆锥曲线的位置关系等知识,考查化归与转化、数形结合的数学思想方法,以及抽象概括能力、推理论证能力和运算求解能力)(1)解:∵双曲线22221x y a b -=()0,0a b >>,∴3a =.即223a b =. ① ∵12MF MF ⊥,且12MF F ∆的面积为1.∴1212112MF F S MF MF ∆==,即122MF MF =.∵122MF MF a -=,∴222112224MF MF MF MF a -+=.∴221244F F a -=.∴()222444a b a +-=,∴21b =. ② 将②代入①,得23a =.∴双曲线C 的方程为2213x y -=. (2)解法1:设点Q A B ,,的坐标分别为(x y ,),(11x y ,),(22x y ,),且1x <2x <3,又设直线l 的倾斜角为θ2πθ⎛⎫≠ ⎪⎝⎭,分别过点P Q A B ,,,作x 轴的垂线,垂足分别为1111P Q A B ,,,, 则 1113cos cos A P x AP θθ-==,112cos cos PB x PB θθ-3== ,112cos cos Q B x x QB θθ-==,111-cos cos AQ x x AQ θθ==, ∵AP QB AQ PB =,∴(3-1x )(2x x -)=123x x x --()(),即[]1212126()3()2x x x x x x x -+=+-. ③ 设直线l 的方程为1(3)y k x -=-, ④将④代入223x y -=1中整理,得 (1-3222)6133(13)10k x k k x k ⎡⎤----+=⎣⎦().依题意1x ,2x 是上述方程的两个根,且2130k -≠,数学(理科)试题参考答案及评分标准 第 11 页 共 12 页∴()()1222122613133131.13k k x x k k x x k -⎧+=⎪-⎪⎨⎡⎤-+⎪⎣⎦=-⎪-⎩, ⑤将⑤代入③整理,得2(3)x k x -=-. ⑥ 由④、⑥消去k 得21x y -=-,这就是点Q 所在的直线方程. ∴点Q (x y ,)总在定直线 10x y --=上.解法2:设点Q ,A B ,的坐标分别为,(x )y ,11,()x y ,22(,)x y ,且1x <2x <3, ∵AP QB AQ PB =,∴AP AQ PB QB=-,即112233x x x x x x --=---, 即[]1212126()3()2x x x x x x x -+=+-.以下同解法1.解法3:设点Q A B ,,的坐标分别为1122() () ()x y x y x y ,,,,,, 由题设知 AP PB AQ QB ,,,均不为零,记AP AQ PB QBλ==. ∵过点P 的直线l 与双曲线C 的左、右两支相交于两点A ,B ,∴0λ>且1λ≠.∵A P B Q ,,,四点共线, ∴ AP PB AQ QB λλ=-=,. 即()()()()112211223,13,1,,,.x y x y x x y y x x y y λλ--=---⎧⎪⎨--=--⎪⎩∴1212311x x x x x λλλλ-⎧=⎪⎪-⎨+⎪=⎪+⎩③ 由③消去λ,得[]1212126()3()2x x x x x x x -+=+-. 以下同解法1.解法4:设点Q A B ,,的坐标分别为1122() () ()x y x y x y ,,,,,, 由题设知 AP PB AQ QB ,,,均不为零,记AP PB AQ QBλ==. ∵过点P 的直线l 与双曲线C 的左、右两支分别相交于两点A B 、, ∴0λ>且1λ≠. ∵A P B Q ,,,四点共线, 设12 PA AQ PB BQ λλ==,,则120λλ+=.12 即()()()()11111222223,1,,3,1,.x y x x y y x y x x y y λλ--=--⎧⎪⎨--=--⎪⎩ ∴111111311.1x x y y λλλλ+⎧=⎪+⎪⎨+⎪=⎪+⎩, 2222223,11.1x x y y λλλλ+⎧=⎪+⎪⎨+⎪=⎪+⎩∵点11()A x y ,,22()B x y ,在双曲线C 上, ∴22313311i i i i x y λλλλ⎛⎫⎛⎫++-= ⎪ ⎪++⎝⎭⎝⎭,其中1 2i =,. ∴12λλ,是方程22313311x y λλλλ++⎛⎫⎛⎫-= ⎪ ⎪++⎝⎭⎝⎭的两个根. 即12 λλ,是方程()()222336130x y x y λλ--+--+=的两个根. ∵120λλ+=,且22330x y --≠, ∴()122261033x y x y λλ--+=-=--,即10x y --=. ∴点()Q x y ,总在定直线10x y --=上.。
2009年广东省广州市普通高中毕业班综合测试(二)数 学(文科)-推荐下载

则 EF FG 的值为
.
BC AD
15.(坐标系与参数方程选做题)
直线
x y
2 1
4t, 3t
t为参数被圆
x y
2 5cos 1 5sin
,
(
为参数)所截得的弦长为
.
图 3
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
A. x R , x2 2x 1≥0
B. x R , x2 2x 1 0
C. x R , x2 2x 1≥0
D. x R , x2 2x 1 0
5.在空间直角坐标系中,以点 A4,1,9, B 10,,1 6, C x,4,3为顶点的 ABC 是以 BC 为底边
Sm2 , Sm1 是否成等差数列,并证明你的结论.
21.(本小题满分14分)
已知函数 f x x a2 , g x x ln x ,其中 a 0 .
x
(1)若 x 1 是函数 h x f x g x的极值点,求实数 a 的值; (2)若对任意的 x1, x2 1,e( e 为自然对数的底数)都有 f x1 ≥ g x2 成立,求实数 a 的取
本试卷共 4 页,21 小题, 满分 150 分。 考试用时 120 分钟。 注意事项:
1.答卷前,考生务必用 2B 铅笔在“考生号”处填涂考生号,用黑色字迹钢笔或签字笔将自己所在 的市、县/区、学校,以及自己的姓名和考生号、试室号、座位号填写在答题卡上。用 2B 铅笔将 试卷类型(A)填涂在答题卡相应位置上。
2009 年广东省广州市普通高中毕业班综合测试(二)
数 学(文科) 2009.4
2009年广东理数B

2009年普通高等学校招生全国统一考试(广东卷)数学(理科)本试卷共4页,21小题,满分150分。
考试用时120分钟。
注意事项:1 •答卷前,考生务必用黑色字迹的钢笔或签宇笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。
用2B 铅笔将试卷类型(B )填涂在答题卡相应位置上。
将条形码横贴在答题卡右上角“条形码粘贴处”。
2 •选择题每小题选出答案后,用 2B 铅笔把答题卡上对应题目选项的答案信息 点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。
答案不能答在试卷 上。
3 •非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案; 不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4 •作答选做题时,请先用 2B 铅笔填涂选做题的题组号对应的信息点,再作答。
漏涂、错涂、多涂的,答案无效。
5 •考生必须保持答题卡的整洁。
考试结束后,将试卷和答题卡一并交回。
1参考公式:锥体的体积公式 V sh ,其中S 是锥体的底面积,h 是锥体的高3一、选择题:本大题共 8小题,每小题5分,满分40分.在每小题给出的四个选项中,只 有一项是符合题目要求的.1•巳知全集U =R ,集合M 二{x -2乞x-1乞2}和N 二{xx =2k-1,k =1,2川(}的关系 的韦恩(V enn )图如图1所示,则阴影部分所示的集合的元素共有 A. 3个 E.2个 C.1个D.无穷个2•设z 是复数,a (z )表示满足z n =1的最小正整数n ,则对虚数单拦I |1位 i , a (i )= A.8E.6 C.4 D.23•若函数y=f (x )是函数y 二a x (a • 0,且a = 1)的反函数,其图像经过点 G a,a ),则f(x)=4 .巳知等比数列{a n }满足a n 0, n=1,2川,且a5 a 2n _^ = 22n (n_3),则当n_1时,Iog 2a 1 Iog 2a 3 川 log 2a 2n_1 =A. log 2 xB. log 1 x2C. D.x 2A. n(2 n-1)B. (n 1)2 c. n2D. (n-1)2数学(理科)试题8第1页(共4页)5 .给定下列四个命题:①若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;③垂直于同一直线的两条直线相互平行;④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直. 其中,为真命题的是A.①和② E.②和③ C..③和④ D.②和④6.一质点受到平面上的三个力F|, F2, F3(单位:牛顿)的作用而处于平衡状态. 已知F1, F2成60°角,且F2的大小分别为2和4,则F3的大小为A.6B.2C. 2.5D. 2.17.2010年广州亚运会组委会要从小张、小赵、小李、小罗、小王五名志愿者中选派四人分别从事翻译、导游、礼仪、司机四项不同工作,若其中小张和小赵只能从事前两项工作,其余三人均能从事这四项工作,则不同的选派方案共有A. 36 种B. 12 种C. 18 种D. 48 种&已知甲、乙两车由同一起点同时出发,并沿同一路线〈假定为直线)行驶.甲车、乙车的速度曲线分别为V甲和V乙(如图2所示).那么对于图中给定的 ^和屯,下列判断中一定正确的是A. 在t1时刻,甲车在乙车前面B. 匕时刻后,甲车在乙车后面C. 在t°时刻,两车的位置相同D. t0时刻后,乙车在甲车前面二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分.(一)必做题(9〜12题)9 .随机抽取某产品n件,测得其长度分别为a1,a2^l,a n,则图3所示的程序框图输出的S ,表示的样本的数字特征是_______ .(注:框图中的赋值符号“=”也可以写成=”)1 0 .若平面向量a,b满足a b =1 , a b平行于x轴,b =(2,- 1)则a = ____1*13一罷11.巳知椭圆G的中心在坐标原点,长轴在x轴上,离心率为,2垂直,则k =15.(几何证明选讲选做题)如图AB = 4,. ACB 二450,则圆O 的面积等于三、解答题:本大题共 6小题,满分80分.解答须写出文字说明、证 明过程和演算步骤, 16.(本小题满分12分)已知向量a =(sin ’-2)与b=(1,cosv )互相垂直,其中- (0/ )2 °(1) 求 sin 二禾口 cos 二的值;■"10(2)若 sin( v - ) — ,0 ,求 cos 「的值.10 217. (本小题满分12分)根据空气质量指数 API (为整数)的不同,可将空气质量分级如下表 :对某城市一年(365天)的空气质量进行监测,获得API 数据按照区间[0,50],(50,100],(100,150],(150,200],(200,250],(250,300]进行分组,得到频率分布直 方图如图5API 0 50 51 ~ 100 101 2 150 151 - 200 201 - 250 251 - 300> 300级别 InHIi1112V狀况优良轻微污染 轻度污染 中度污染 中度重污染 重度污染©©(1)求直方图中x 的值;(2 )计算一年屮空气质量分别为良和轻微污染的天数;(3 )求该城市某一周至少有 2天的空气质量为良或轻微污染的概率 (结果用分数表示.已知且G 上一点到G 的两个焦点的距离之和为 12,则椭圆G 的方程为 数学(理科)试题 B 第2页(共4页)EX =0 ,12•已知离散型随机变量 X 的分布列如右表•若DX =1,则 a , b.(二)选做题(13 ~ 15题,考生只能从中选做两题)11: 「x =1 _2ty ;kt (t 为参数)与直线1x = s,J y=1—2s. (s 为参数)X -1 0 1 2 Pab1C1214.(不等式选讲选做题)不等式匕1 > 1的实数解为x 2)若直线4,点A, B,C 是圆O 上的点,7 7 3 2 7 3 8 1235 =78125,2 =128,亠亠亠亠,365 =73 5)1825 365 1825 1825 9125 9125数学〈理科)试题B第3页(共4页)18. (本小题满分14分)如图6,已知正方体ABCD -ABGU的棱长为2,点E是正方形BCC1B1的中心,点F、DCC1D1内的正投影.G分别是棱C1D1, AA,的中点.设点E1,G1分别是点E、G在平面(1)求以E为顶点,以四边形FGAE在平面DCC1D1内的正投影为底面边界的棱锥的体积;(2)证明:直线FG _平面FEE1;(3)求异面直线E1G1与EA所成角的正统值19. (本小题满分14分)2已知曲线C : y = x与直线丨:x -y • 2 = 0交于两点A(x A, y A)和B(x B, y B),且x A:::x B.记曲线C 在点A和点B之间那一段L与线段AB所围成的平面区域(含边界)为D .设点P(s, t)是L上的任一点,且点P与点A和点B均不重合.(1)若点Q是线段AB的中点,试求线段PQ的中点M的轨迹方程;2 2 2 51(2)若曲线G :x2-2ax y-4y a20与点D有公共点,试求a的最小值.2520. (本小题满分14分)已知二次函数y =g(x)的导函数的图像与直线y=2x平行,且y = g(x)在x - -1处取得极小值m -1(m =0).设f (x) = g(x).x(1)若曲线y=f(x)上的点P到点Q(0,2)的距离的最小值为..2,求m的值;(2)k(k • R)如何取值时,函数y = f (x) -kx存在零点,并求出零点.21 .(本小题满分14分)已知曲线G:x2 -2nx • y2 =0(n=1,2,ll|).从点P(-1,0)向曲线G引斜率为心(心0)的切线I n,切点为R(X n, Y n).(1)求数列{xj与{y n}的通项公式;数学(理科)试题E 第4页(共4页)Whe n you are old and grey and full ofsleep,And no ddi ng by the fire, take dow n this book,And slowly read, and dream of the soft lookYour eyes had once, and of their shadows deep;How many loved your mome nts of glad grace,And loved your beauty with love false or true,But one man loved the pilgrim soul in you,And loved the sorrows of your cha nging face;And bending dow n beside the glow ing bars,Murmur, a little sadly, how love fledAnd paced upon the mountains overheadAnd hid his face amid a crowd of stars.The furthest dista nee in the worldIs not betwee n life and deathBut whe n I sta nd in front of you(2)证明:[_ x一x^X1X3m -二 T%Yet you don't know thatI love you.The furthest distance in the worldIs not when I stand in front of youYet you can't see my loveBut when undoubtedly knowing the love from both Yet cannot be together.The furthest distance in the worldIs not being apart while being in loveBut when I plainly cannot resist the yearningYet pretending you have never been in my heart. The furthest distance in the worldIs not struggling against the tidesBut using one's indifferent heartTo dig an uncrossable riverFor the one who loves you.。
广州中考

广州市2009年初中毕业生学业考试数 学第一部分选择题(共30分)一、选择题(本大题共10小题,每小题3分,满分30分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1. 将图1所示的图案通过平移后可以得到的图案是( )2. 如图2,AB ∥CD ,直线l 分别与AB 、CD 相交,若∠1=130°,则∠2=( )(A )40°(B )50° (C )130° (D )140° 3. 实数a 、b 在数轴上的位置如图3所示,则a 与b 的大小关系是( )(A )b a < (B )b a = (C )b a > (D )无法确定4. 二次函数2)1(2+-=x y 的最小值是( ) (A )2 (B )1 (C )-1 (D )-25. 图4是广州市某一天内的气温变化图,根据图4,下列说法中错误..的是( ) (A )这一天中最高气温是24℃(B )这一天中最高气温与最低气温的差为16℃ (C )这一天中2时至14时之间的气温在逐渐升高 (D )这一天中只有14时至24时之间的气温在逐渐降低 6. 下列运算正确的是( )(A )222)(n m n m -=- (B ))0(122≠=-m mm (C )422)(mn n m =⋅ (D )642)(m m =7. 下列函数中,自变量x 的取值范围是x ≥3的是( ) (A )31-=x y (B )31-=x y (C )3-=x y (D )3-=x y8. 只用下列正多边形地砖中的一种,能够铺满地面的是( ) (A )正十边形 (B )正八边形(C )正六边形 (D )正五边形9. 已知圆锥的底面半径为5cm ,侧面积为65πcm 2,设圆锥的母线与高的夹角为θ(如图5)所示),则sin θ的值为( ) (A )125 (B )135 (C )1310 (D )1312 10. 如图6,在ABCD 中,AB=6,AD=9,∠BAD 的平分线交BC 于点E ,交DC 的延长线于点F ,BG ⊥AE ,垂足为G ,BG=24,则ΔCEF 的周长为( )(A )8 (B )9.5 (C )10 (D )11.5第二部分 非选择题(共120分)二、填空题(本大题共6小题,每小题3分,满分18分) 11. 已知函数xy 2=,当x =1时,y 的值是________ 12. 在某校举行的艺术节的文艺演出比赛中,九位评委给其中一个表演节目现场打出的分数如下:9.3,8.9,9.3,9.1,8.9,8.8,9.3,9.5,9.3,则这组数据的众数是________ 13. 绝对值是6的数是________14. 已知命题“如果一个平行四边形的两条对角线互相垂直,那么这个平行四边形是菱形”,写出它的逆命题:________________________________15. 如图7-①,图7-②,图7-③,图7-④,…,是用围棋棋子按照某种规律摆成的一行“广”字,按照这种规律,第5个“广”字中的棋子个数是________,第n 个“广”字中的棋子个数是________16. 如图8是由一些相同长方体的积木块搭成的几何体的三视图,则此几何体共由________块长方体的积木搭成三、解答题(本大题共9小题,满分102分。
2009年广东省广州市普通高中毕业班综合测试(二)数 学(文科)-推荐下载

2.如果复数 m2 3m m2 5m 6 i 是纯虚数,则实数 m 的值为
A.0
B.2
C.0 或 3
D.2 或 3
3.已知函数
f
x
x x
x x
4,x 4,x
0, 0.
则函数 f x的零点个数为
A.1
B.2
C.3
D.4
4.命题“ x R , x2 2x 1 0 ”的否定是
y2 b2
1 a
b 0的离心率为 1
2
40 3
.
(2)设 F 是椭圆 C 的左焦点,判断以 PF 为直径的圆与以椭圆长轴为直径的圆的位置关系,并说明
理由.
20.(本小题满分14分)
已知等比数列an的前 n 项和为 Sn ,若 am , am2 , am1 m N* 成等差数列,试判断 Sm ,
本试卷共 4 页,21 小题, 满分 150 分。 考试用时 120 分钟。 注意事项:
1.答卷前,考生务必用 2B 铅笔在“考生号”处填涂考生号,用黑色字迹钢笔或签字笔将自己所在 的市、县/区、学校,以及自己的姓名和考生号、试室号、座位号填写在答题卡上。用 2B 铅笔将 试卷类型(A)填涂在答题卡相应位置上。
A. x R , x2 2x 1≥0
B. x R , x2 2x 1 0
C. x R , x2 2x 1≥0
D. x R , x2 2x 1 0
5.在空间直角坐标系中,以点 A4,1,9, B 10,,1 6, C x,4,3为顶点的 ABC 是以 BC 为底边
2.选择题每小题选出答案后,用 2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动, 用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
2009年广州市普通高中毕业班综合测试(文科)(二)

图1俯视图 试卷类型:A2009年广州市普通高中毕业班综合测试(二)数 学(文科)2009.4 本试卷共4页,21小题, 满分150分。
考试用时120分钟。
注意事项:1.答卷前,考生务必用2B 铅笔在“考生号”处填涂考生号,用黑色字迹钢笔或签字笔将自己所在的市、县/区、学校,以及自己的姓名和考生号、试室号、座位号填写在答题卡上。
用2B 铅笔将试卷类型(A )填涂在答题卡相应位置上。
2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4.作答选做题时,请先用2B 铅笔填涂选做题的题号(或题组号)对应的信息点,再作答。
漏涂、错涂、多涂的,答案无效。
5.考生必须保持答题卡的整洁。
考试结束后,将试卷和答题卡一并交回。
参考公式:锥体的体积公式Sh V 31=, 其中S 是锥体的底面积,h 是锥体的高. 球的表面积公式24SR π=,其中R 为球的半径.一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知全集{}1,2,3,4,5,6,7,8U =,集合{}1,2,3A =,{}2,3,4,5B =,则() U A B =ðA .{}6,7,8B .{}1,4,5,6,7,8C .{}2,3D .{}1,2,3,4,52.如果复数()()22356i m m m m -+-+是纯虚数,则实数m 的值为A .0B .2C .0或3D .2或33.已知函数()()()40,40.x x x f x x x x +<⎧⎪=⎨-≥⎪⎩,, 则函数()f x 的零点个数为A .1B .2C .3D .44.命题“x ∃∈R ,2210x x -+<”的否定是A .x ∃∈R ,221x x -+≥0B .x ∃∈R ,2210x x -+> C .x ∀∈R ,221x x -+≥0D .x ∀∈R ,2210x x -+<5.在空间直角坐标系中,以点()4 1 9A ,,,()101 6B -,,,() 4 3C x ,,为顶点的ABC ∆是以BC 为底边的等腰三角形,则实数x 的值为 A .2- B .2 C .6 D .2或6 6.如图1视图与俯视图,同一位置上叠放的小正方体的个数,则这个几何体的正(主)图2视图是A .B.C.D.7.曲线3y x =在点()1 1,处的切线与x 轴及直线1x =所围成的三角形的面积为A .112 B .16 C .13 D .128.已知圆229x y +=与圆224410x y x y +-+-=关于直线l 对称,则直线l 的方程为A .4410x y -+=B .0x y -=C .0x y +=D .20x y --=9.在长为1的线段上任取两点,则这两点之间的距离小于12的概率为 A .14 B .12 C .34 D .7810.在平面内有n (*,n n N ∈≥)3条直线,其中任何两条不平行,任何三条不过同一点,若这n条直线把平面分成()f n 个平面区域,则()6f 等于 A .18B .22C .24D .32二、填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分. (一)必做题(11~13题) 11.阅读如图2所示的程序框图,若输入x 的值为2,则输出y 的值为 .12.在某项才艺竞赛中,有9位评委,主办单位规定计算 参赛者比赛成绩的规则如下:剔除评委中的一个最高分和一个最低分后,再计算其他7位评委的平均分作为此参赛者的比赛成绩.现有一位参赛者所获9位评委一个最高分为86分、一个最低分为45分,若未剔除最高分与最低分时9位评委的平均分为76分,则这位参赛者的比赛成绩为分.13.在ABC ∆中,已知tan 3tan A B =,则()t a n A B - 的最大值为 ,此时角A 的大小为 .(二)选做题(14~15题,考生只能从中选做一题) 14.(几何证明选讲选做题)如图3所示,在四边形ABCD 中,EFBC ,FG AD ,则EF FGBC AD+的值为 . 15.(坐标系与参数方程选做题) 直线()24,13x t t y t=-+⎧⎨=--⎩为参数被圆25c o s ,15s i n xy θθ=+⎧⎨=+⎩(θ为参数)所截得的弦长为.三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.图316.(本小题满分12分)已知向量2cos, 12x ⎛⎫= ⎪⎝⎭m ,sin 12x ⎛⎫= ⎪⎝⎭,n ()x ∈R ,设函数()1f x =-m n . (1)求函数()f x 的值域;(2)已知锐角ABC ∆的三个内角分别为A B C ,,,若()513f A =,()35f B =,求()f A B + 的值.17.(本小题满分12分)已知实数a ,{}2 1 1 2b ∈--,,,.(1)求直线 y a x b =+不经过...第四象限的概率; (2)求直线 y a x b =+与圆221x y +=有公共点的概率.18.(本小题满分14分)在长方体1111ABCD A BC D -中,2AB BC ==,过1A 、1C 、 B 三点的平面截去长方体的一个角后,得到如图4所示的几何体111ABCD AC D -,且这个几何体的体积为403. (1)证明:直线1A B 平面11CDD C ;(2)求棱1A A 的长;(3)求经过11A C B D 、、、四点的球的表面积.19.(本小题满分14分)已知椭圆C :22221x y a b+=()0a b >>的离心率12为,且经过点P 31 2⎛⎫ ⎪⎝⎭,. (1)求椭圆C 的方程;(2)设F 是椭圆C 的左焦点,判断以PF 为直径的圆与以椭圆长轴为直径的圆的位置关系,并说明理由.20.(本小题满分14分)已知等比数列{}n a 的前n 项和为n S ,若m a ,2m a +,1m a +()*m ∈N 成等差数列,试判断m S ,2m S +,1m S +是否成等差数列,并证明你的结论.21.(本小题满分14分)已知函数()2a f x x x=+,()ln g x x x =+,其中0a >.(1)若1x =是函数()()()h x f x g x =+的极值点,求实数a 的值;(2)若对任意的[]12,1x x e ∈,(e 为自然对数的底数)都有()1f x ≥()2g x 成立,求实数a 的取值范围.2009年广州市普通高中毕业班综合测试(二)数学(文科)试题参考答案及评分标准说明:1.参考答案与评分标准指出了每道题要考查的主要知识和能力,并给出了一种或几种解法供参考,如果考生的解法与参考答案不同,可根据试题主要考查的知识点和能力比照评分标准给以相应的分数.2.对解答题中的计算题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的得分,但所给分数不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.3.解答右端所注分数,表示考生正确做到这一步应得的累加分数. 4.只给整数分数,选择题和填空题不给中间分.一、选择题:本大题考查基本知识和基本运算.共10小题,每小题5分,满分50分.二、填空题:本大题共5小题,每小题5分,满分20分.其中14~15题是选做题,考生只能选做一题,两题全答的,只计算前一题得分.第13题第1个空3分,第2个空2分. 11.0 12.79 13.3,3π14.1 15.6 三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 16.(本小题主要考查三角函数性质和三角函数的基本关系等知识,考查化归与转化的数学思想方法,以及运算求解能力)解:(1)()12cos 1sin 1122x x f x ⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭,,m n 2c o s s i n 11s i n 22x xx =+-=.∵x ∈R ,∴函数()f x 的值域为[]1 1-,.(2)∵()513f A =,()35f B =, ∴5sin 13A =,3sin 5B =.∵,A B 都是锐角, ∴12cos 13A ==,4cos 5B ==. ∴()()sin f A B A B +=+sin cos cos sin A B A B =+541231351355665=⨯+⨯=.∴()f A B +的值为5665.17.(本小题主要考查古典概型等基础知识,考查化归和转化、分类与整合的数学思想方法,以及简单的推理论证能力)解:由于实数对(),a b 的所有取值为:()22--,,()21--,,()2 1-,,()2 2-,,()12--,,()11--,,()1 1-,,()1 2-,,()12-,,()11-,,()1 1,,()1 2,,()22-,,()21-,,()2 1,,()2 2,,共16种. 设“直线 y a x b =+不经过第四象限”为事件A ,“直线y ax b =+与圆221x y +=有公共点”为事件B .(1)若直线 y a x b =+不经过第四象限,则必须满足0,0.a b ⎧⎨⎩≥ ≥ 即满足条件的实数对()a b ,有()1 1,,()1 2,,()2 1,,()2 2,,共4种.∴()41164P A ==. 故直线 y a x b =+不经过第四象限的概率为14. (2)若直线y ax b =+与圆221x y +=有公共点,≤1,即2b ≤21a +.若2a =-,则21 1 2b =--,,,符合要求,此时实数对(a b ,)有4种不同取值; 若1a =-,则1 1b =-,符合要求,此时实数对(a b ,)有2种不同取值; 若1a =,则1 1b =-,符合要求,此时实数对(a b ,)有2种不同取值; 若2a =,则21 1 2b =--,,,符合要求,此时实数对(a b ,)有4种不同取值. ∴满足条件的实数对()a b ,共有12种不同取值. ∴()123164P B ==. 故直线y ax b =+与圆221x y +=有公共点的概率为34.18.(本小题主要考查空间线面关系、几何体的表面积与体积等知识,考查数形结合的数学思想方法,以及空间想象能力、运算求解能力) (1)证法1:如图,连结1D C , ∵1111ABCD A BC D -是长方体, ∴11A D BC 且11A D BC =. ∴四边形11A BCD 是平行四边形.∴11A B D C .∵1A B ⊄平面11CDD C ,1D C ⊂平面11CDD C ,∴1A B平面11CDD C .证法2:∵1111ABCD A BC D -是长方体, ∴平面1A AB 平面11CDD C .∵1A B ⊂平面1A AB ,1A B ⊄平面11CDD C ,∴1A B平面11CDD C .(2)解:设1A A h =,∵几何体111ABCD AC D -的体积为403, ∴1111111111403ABCD A C D ABCD A B C D B A B C V V V ---=-=,即11114033ABCD A B C S h S h ∆⨯-⨯⨯=,即11402222323h h ⨯⨯-⨯⨯⨯⨯=,解得4h =.∴1A A 的长为4.(3)如图,连结1D B ,设1D B 的中点为O ,连11OA OC OD ,,, ∵1111ABCD A BC D -是长方体,∴11A D ⊥平面1A AB . ∵1A B ⊂平面1A AB ,∴11A D ⊥1A B .∴1112OA D B =.同理1112OD OC D B ==. ∴11OA OD OC OB ===.∴经过1A ,1C ,B ,D 四点的球的球心为点O . ∵2222222111124224D B A D A A AB =++=++=.∴()2221144242D B S OB D B ππππ⎛⎫=⨯=⨯=⨯= ⎪⎝⎭球.故经过1A ,1C ,B ,D 四点的球的表面积为24π.19.(本小题主要考查椭圆、圆的方程和圆与圆的位置关系等基础知识,考查数形结合思想,以及运算求解能力)解:(1)∵椭圆22221x y a b+=(0)a b >>的离心率为12,且经过点P31 2⎛⎫⎪⎝⎭,,∴221,219 1.4a b =⎨⎪+=⎪⎩ 即2222340,191.4a b a b⎧-=⎪⎨+=⎪⎩解得224,3.a b ⎧=⎪⎨=⎪⎩ ∴椭圆C 的方程为22143x y +=.(2)∵24a =,23b =,∴1c ==. ∴椭圆C 的左焦点坐标为( 1 0-,.以椭圆C 的长轴为直径的圆的方程为224x y +=,圆心坐标是()0 0,,半径为2.以PF 为直径的圆的方程为22325416x y ⎛⎫+-= ⎪,圆心坐标是30 4⎛⎫ ⎪⎝⎭,,半径为54.35= 244-,故以PF 为直径的圆与以椭圆长轴为直径的圆内切.20.(本小题主要考查等差数列、等比数列的通项公式与前n 项求和公式等知识,考查化归与转化、分类与整合的数学思想方法,以及推理论证能力和运算求解能力) 解:设等比数列{}n a 的首项为1a ,公比为q ()10,0a q ≠≠,若m a ,2m a +,1m a +成等差数列, 则22m a +=m a +1m a +. ∴111112m m m a q a q a q +-=+.∵10a ≠,0q ≠,∴2210q q --=. 解得1q =或12q =-. 当1q =时,∵1m S ma =,()111m S m a +=+,()212m S m a +=+, ∴212m m m S S S ++≠+.∴当1q =时,m S ,2m S +,1m S +不成等差数列.当12q =-时,m S ,2m S +,1m S +成等差数列.下面给出两种证明方法. 证法1:∵()()()1211222m m m m m m m m m S S S S S a S a a ++++++-=++-++ 122m m a a ++=-- 112m m a a q ++=-- 11122m m a a ++⎛⎫=---⎪⎝⎭0=, ∴212m m m S S S ++=+. ∴当12q =-时,m S ,2m S +,1m S +成等差数列.证法2:∵212211212412113212m m m a S a +++⎡⎤⎛⎫--⎢⎥ ⎪⎡⎤⎝⎭⎢⎥⎛⎫⎣⎦==--⎢⎥ ⎪⎝⎭⎢⎥⎣⎦+, 又1111111111222112113221122m m m m m m a a S S a +++⎡⎤⎡⎤⎛⎫⎛⎫----⎢⎥⎢⎥ ⎪ ⎪⎡⎤⎝⎭⎝⎭⎢⎥⎢⎥⎛⎫⎛⎫⎣⎦⎣⎦+=+=----⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦++ 221211242322m m a ++⎡⎤⎛⎫⎛⎫=--+-⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦2141132m a +⎡⎤⎛⎫=--⎢⎥ ⎪⎝⎭⎢⎥⎣⎦, ∴212m m m S S S ++=+. ∴当12q =-时,m S ,2m S +,1m S +成等差数列.21.(本小题主要考查函数的性质、函数与导数等知识,考查化归与转化、分类与整合的数学思想方法,以及抽象概括能力、推理论证能力和运算求解能力)(1)解法1:∵()22ln a h x x x x=++,其定义域为()0,+∞, ∴()2212a h x x x'=-+.∵1x =是函数()h x 的极值点,∴()10h '=,即230a -=,∵0a >,∴a =经检验,当a =x =1是函数()h x 的极值点,∴a =解法2:∵()22ln a h x x x x=++,其定义域为()0,+∞, ∴()2212a h x x x'=-+.令()0h x '=,即22120a x x-+=,整理得,2220x x a +-=.∵2180a ∆=+>,∴()0h x '=的两个实根114x -=(舍去),214x -+=,当x 变化时,()h x ,()h x '的变化情况如下表:1=,即23a =,∵0a >,∴a =(2)解:对任意的[]12,1x x e ∈,都有()1f x ≥()2g x 成立等价于对任意的[]12,1x x e ∈, 都有()min f x ⎡⎤⎣⎦≥()max g x ⎡⎤⎣⎦.当[]1 x e ∈,时,()110g x x'=+>. ∴函数()ln g x x x =+在[]1e ,上是增函数.∴()()max 1g x g e e ==+⎡⎤⎣⎦.∵()()()2221x a x a a f x x x+-'=-=,且[]1x e ∈,,0a >, ①当01a <<且[]1x e ,∈时,()()()20x a x a f x x +-'=>,∴函数()2a f x x x=+在[]1e ,上是增函数.∴()()2min11f x f a ==+⎡⎤⎣⎦.由21a +≥1e +,得a又01a <<,∴a 不合题意. ②当1≤a ≤e 时, 若1≤x a <,则()()()20x a x a f x x +-'=<,若a x <≤e ,则()()()20x a x a f x x +-'=>. ∴函数()2a f x x x=+在[)1a ,上是减函数,在(]a e ,上是增函数.∴()()min 2f x f a a ==⎡⎤⎣⎦.由2a ≥1e +,得a ≥12e +, 又1≤a ≤e ,∴12e +≤a ≤e .数学(文科)试题A 参考答案及评分标准 第 11 页 共 11 页 ③当a e >且[]1x e ,∈时,()()()20x a x a f x x+-'=<, ∴函数()2a f x x x =+在[]1e ,上是减函数.∴()()2min a f x f e e e ==+⎡⎤⎣⎦. 由2a e e +≥1e +,得a又a e >,∴a e >.综上所述,a 的取值范围为1,2e +⎡⎫+∞⎪⎢⎣⎭.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2009年广州16所民办中学联考试题(数学)
一、填空题(2×10分)
1、一个8位数,最高位是8,百万位是最小的数,十万位和千位是最小的质数,其他
各位数都是0,这个数写作(),改写成以“万”作单位的数是()万。
2、A = 2×3×7,B = 2×5×7 A和B的最大公约数是(),最小公倍数是()。
3、在一道减法算式中,被减数、减数、差三个数的和为200,差与减的比数为3:2,
那么差是()。
4、有甲、乙两堆煤,从甲中取出12吨放到乙中,两堆煤重量相等;从乙中取出12
吨放到甲中,甲是乙的两倍。
甲、乙两堆煤共重()吨。
5、一种树的成活率为98%,如果植3200棵树则成活()棵,要重活2450棵,需
要种()棵。
6、在比例尺为1:8000000的地图上,广州-鹰潭距离为8cm。
实际距离为()
千米。
7、一件衣服降价50元后,售200元,降幅()%。
8、合唱队里有男生21人,比女生少1/4,合唱队共有()人。
9、一个圆柱形水池,低面直径8m,高为直径的3/4,若在水池内壁涂水泥,每平方米
用水泥5千克,共需要()千克。
10、一个正方形的边长增加2cm,面积增加20c㎡,扩大后正方形面积为()c
㎡。
二、判断题(1×5分)
1、在同一圆中,周长与半径成正比例。
2、锐角三角形的两个锐角之和一定小于90°。
3、25g糖溶入100g水中,糖占糖水的25%。
4、如a×4/5=b÷4/5,a、b均﹥0为自然数,那么a﹥b。
5、32:40化简后得4/5,与其比值相等。
三、选择题(1×5分)
1、一个三角形,三个内角度数的比为2:5:3,则此三角形为()
A.锐角三角形
B.直角三角形
C.锐角三角形
D.无法确定
2、圆柱体底面半径扩大到原来的2倍,则体积()
A.扩大8倍
B.扩大2倍
C.扩大4倍
D.不变
3、80×☆+5与80×(☆+5)相差()
A.75
B.5
C.400
D.395
4、一批水泥,用去4/9,剩下的是用去的()
A. 5/9
B. 4/5
C. 5/4
D. 10/9
5、在一个正方形里画一个最大的圆,圆的面积是正方形面积的()。
A. 1/2
B. 3/4
C. ∏/4
D. ∏
四、计算题(30分)
1、直接写得数(0.5×10)
0.36 + 0.4 = 12.5 × 32 × 2.5 =
1 ÷ 0.9 = 8 × (1
2 + 0.5) =
9-
1 5+0.8= 6+6-+=
2、求未知数(2.5×2)
(1)3x-x=
(2)
3、计算尽量用简便方法(5×4)
(1)32.5+3.6×2.5÷0.48
(2)22-×
(3)299÷(299+)
(4)[-(+)]×
应用题(5x8分)
1、实验小学买了4副乒乓球拍和50个乒乓球,付出200元,找回5.5元,每副拍38元,每个球几元?
2、开凿一条隧道,甲队单独干要60天完成,乙队单独干要40天完成。
两队同时从两侧对凿,当两队还距整个洞长的1/6时,已工作了多少天?
3、在一个底面半径是10cm的圆柱形水桶中装水,水中放一个底面半径是5cm的圆锥形铅锤,铅锤全部淹没,取出铅锤后桶面水面下降2cm,求铅锤的高。
4、一辆汽车从甲地向乙地行使,行了一段距离后,距离乙地还有210千米,接着又行了全程距离的20%,此时已行驶的距离与未行使的距离比为3:2,求甲乙两地的距离。
5、用地板砖铺教室地面,若用面积为0.16㎡的正方形地砖需要500块,如果改用边长0.5m 的正方形地砖,则需要多少块?
6、一批零件,先加工120个,又加工余下的2/5,这是已加工的零件个数与未加工的零件个数相等,这批零件共多少个?
7、小明统计班里的数学成绩,平均分数为85.74,后来发现一个同学原来的分数为97,统计时误统计为67。
重新统计后平均分数为86.49,此班共有多少个学生?
8、一个半圆形花坛,周长为10.28米,面积为多少平方米?
数学附加题
某中学计划建设一个400m跑道的运动场(如下图所示),聘请你任工程师,问:(1)若直道长100m,则弯道弧长半径r为多少m?(2)共8个跑道,每条宽1.2m,操场最外圈长多少m?(3)若操场中心铺绿草,跑道铺塑胶,则各需绿草、塑胶多少㎡?(4)若绿草50元/㎡,塑胶350元/㎡,学校现有200万元,可以开工吗?为什么?
2011年广州小升初考辅资料
一、真题系列
1.《广州民校联考06—09年试题汇编》
注:广州民校06—09年四年考试试题及答案汇编成册
2.《省实附属天河中学07—09年试题汇编》
注:广东省实验中学07—09年考试试题汇编及详细答案
3.《中大附中09—10年初一入学测评参考练习》
注:中大附中09、10年初一入学测评参考资料,内含部分历年考试试题。
4.《广州名校小升初真题汇编》
注:包括中大附中、16中、七中、番禺华附、番禺执信等名校近年小升初招生试题。
二、考辅系列
1.《广州小升初知识大集结》
注:本资料包括语数英三科,汇集小学阶段课本、读本中的知识精华,搜罗课内外常用必备的相关资料,使广大小升初考生在较短的复习、应考时间内,对重难知识点掌握得更加牢固,理解得更加透彻。
推出时间:2010年8月30日
2.《广州小升初高频考点解析》
注:本资料包括语数英三科,从近年来广州小升初考试试题中,总结提炼出常考点、易考点、必考点,这些都是考试重点,重点中的得分点。
推出时间:2010年10月15日
3.《广州民校联考全真模拟卷》、《中大附中初一招生全真模拟卷》、《省实天河中学招一招生全真模拟卷》
注:本资料包括语数英三科,全真模拟联考、各单考民校和公校择校考试卷,预测性强,实战模拟。
推出时间:2011年1月1日
5.《广州小升初考前30天押题模考卷》
注:本资料包括语数英三科,以模考形式惠及考生,实战演练。
推出时间:2011年5月10日
以上资料以实际推出时间为准,敬请关注!
联系电话:020-8776 8616
2009年十六所民校新生入学检测题
数学参考答案
一、填空题。
1.80202000,8020.2;
2.14,210
3.60
4.144
5.3136 2500
6.640
7.20
8.49
9.1507.2
10.36
二、判断题。
1.√ 2 X 3X 4√5√
三、选择题。
1.B 2.C 3.D 4.C 5.C
四、计算题。
1.0.76 1000 10/9 100
80/9 25/64 1/12 3/2 5.925 12
2.X= 8/19 X= 12
3.(1)51.25 (2)21 (3)300/301 (4)3/14
五、应用题
1.(200—5.5—38 ×4)÷50 =0.85
2.(1—1/6)÷(1/60 +1/40)=20
3.设铅锤的高为X,则
1/3 ×5 ×5 X×3.14 =10×10×2 ×3.14 X =24
4.设两地相距X千米
210 -1/5 X =2/5 X X =350
5.0.16 ×500 ÷(0.5 ×0.5)=320(块)
6.设这批零件共有X个,则
120 +(X -120)×2/5 =1/2 X X=720 7.(97—67)÷(86 .49 -85 .74)=40
8.设花坛的半径为X,则
3.14 X +2X =10.28
X= 2 1/2 ×3.14 ×4 =6.28。
