高三数学一轮复习 第六章 数列
数学课标通用(理科)一轮复习配套教师用书:第六章 数列 数列的概念与简单表示

必考部分第六章数列§6.1 数列的概念与简单表示考纲展示► 1.了解数列的概念和几种简单的表示方法(列表、图象、通项公式).2.了解数列是自变量为正整数的一类特殊函数.考点1 由数列的前几项求数列的通项公式1.数列的概念(1)数列的定义:按照________排列的一列数称为数列,数列中的每一个数叫做这个数列的________.(2)数列与函数的关系:从函数观点看,数列可以看成以正整数集N*(或它的有限子集)为________的函数a n=f(n).当自变量按照从小到大的顺序依次取值时所对应的一列函数值.(3)数列有三种表示法,它们分别是________、________和________.答案:(1)一定顺序项(2)定义域(3)列表法图象法通项公式法2.数列的分类答案:有限无限><3.数列的两种常用的表示方法(1)通项公式:如果数列{a n}的第n项a n与________之间的关系可以用一个式子________来表示,那么这个公式叫做这个数列的通项公式.(2)递推公式:如果已知数列{a n}的第1项(或前几项),且从第二项(或某一项)开始的任一项a n与它的前一项a n-1(或前几项)间的关系可以用一个公式来表示,那么这个公式就叫做这个数列的递推公式.答案:(1)序号n a n=f(n)4.已知数列{a n}的前n项和S n,则a n=错误!答案:S1S n-S n-1(1)[教材习题改编]已知数列{a n}的前四项分别为1,0,1,0,给出下列各式:①a n=错误!;②a n=错误!;③a n=sin2错误!;④a n=错误!;⑤a n=错误!⑥a n=错误!+(n-1)(n-2).其中可以作为数列{a n}的通项公式的有________.(写出所有正确结论的序号)答案:①③④(2)[教材习题改编]已知{a n}满足a n=错误!+1(n≥2), a7=错误!,则a5=__________.答案:错误!解析:由递推公式,得a 7=-1a 6+1,a 6=错误!+1,则a 5=错误!。
2023版高考数学一轮总复习6-1数列的概念及表示课件

3.结合相应函数的图象直观判断.
例3
(1)已知数列{an}满足an=
(3 an5
a)n 2, , n 6,
n
6,
且{an}是递增数列,则实数a
2)an=
SS1n(n
1), Sn1 (n
2).
考法一 利用Sn与an的关系求通项公式 1.已知Sn求an的步骤: 1)先利用a1=S1求出a1. 2)用n-1替换Sn中的n得到一个新的关系,利用an=Sn-Sn-1(n≥2)便可求出当n ≥2时an的表达式. 3)对n=1时的结果进行检验,看是否符合n≥2时an的表达式,若符合,则数列 的通项公式合写;若不符合,则应该分n=1与n≥2两段来写.
=n+3× (n 1) n = (3n 1)n ,
2
2
∴a10=
(3
1021)来自10=145.故选B.
答案 B
考法三 数列的单调性和最大(小)项 1.用作差比较法,根据an+1-an的符号判断数列{an}是递增数列、递减数列 或常数列.
2.用作商比较法,根据 an1 (an>0或an<0)与1的大小关系进行判断.
2.数列的性质
递增数列 递减数列 常数列 摆动数列
周期数列
∀n∈N*,an+1>an ∀n∈N*,an+1<an ∀n∈N*,an+1=an 从第2项起,有些项大于它的前一项,有些项小于 它的前一项的数列 ∀n∈N*,存在正整数k,使得an+k=an
3.数列的通项公式和递推公式 1)通项公式:如果数列{an}的第n项an与序号n之间的关系可以用一个式子 an=f(n)来表示,那么这个式子叫做这个数列的通项公式. 2)递推公式:如果已知数列{an}的第一项(或前几项),且从第二项(或某一 项)开始,任何一项an与它的前一项an-1(n≥2)(或前几项)间的关系可以用一 个式子来表示,那么这个式子叫做数列{an}的递推公式. 4.数列{an}的前n项和及其与通项公式的关系 1)Sn=a1+a2+…+an.
湘教版高考总复习一轮数学精品课件 第六章 数列 第一节 数列的概念与简单表示法

1,公比为 6 的等比数列,则 Sn=6n-1,于是当 n≥2
时,an=Sn-Sn-1=6n-1-6n-2=5×6n-2,且 a1=1 不适合上式,因此数列{an}的通项公式
1, = 1,
为 an=
故选 C.
-2
5 × 6 , ≥ 2.
引申探究(变条件)在本例中,若其他条件不变,将“an+1=5Sn(n≥1)”改为
以运用累加法an=(an-an-1)+(an-1-an-2)+(an-2-an-3)+…+(a2-a1)+a1(n≥2),并验
证a1,求出数列{an}的通项公式.
考向2累乘法
题组(1)(2023·江苏宿迁高三月考)已知数列{an}满足
1
+1
a1= ,an+1= an(n∈N+),则
4
4
an=
.
(2)(2023·福建泉州高三期中)已知数列{an}的前n项和为Sn,且满足
Sn=(n+1)2an-3,则{an}的通项公式为
答案
(1)
4
6
(2)an=
(+1)(+2)
.
解析 (1)由
因此当
又
1
+1
+1
a1=4,an+1= 4 an,得
2
n≥2 时,an=a1·
1
1
.
答案 (1)A (2)an=
-1, = 1,
2·3-2 , ≥ 2
解析 (1)当n≥2时,由a1+2a2+3a3+…+nan=(n-1)·2n+1,可得
数列的概念及简单表示法(高三一轮复习)

所以数列
S 2
n
是首项为S
2 1
=a
2 1
=1,公差为1的等差数列,所以S
2 n
=n,所以Sn=
n
(n∈N*).
数学 N 必备知识 自主学习 关键能力 互动探究
— 20 —
命题点2 由数列的递推公式求通项公式
考向1 累加法
例2
设数列
a
n
满足a1=1,且an+1-an=1(n∈N*),则数列
1 3
an+1,所以a2=3S1=3×
16 3
=16.当n≥2时,有an=Sn-Sn-1
=13an+1-13an,即an+1=4an.
所以从第二项起,数列an为首项为16,公比为4的等比数列,所以an= 4n(n≥2).
经检验,an=4n对n=1不成立,
所以an=136,n=1, 4n,n≥2.
数学 N 必备知识 自主学习 关键能力 互动探究
,所以a2=
4 2-a1
=
4 2-4
=-2,a3=
4 2-a2
=
4 2+2
=1,a4=
4 2-a3
=
4 2-1
=4,…,所以数列
a
n
是以3为周期的周期数列,又2
022=
673×3+3,所以a2 022=a673×3+3=1.
数学 N 必备知识 自主学习 关键能力 互动探究
— 12 —
4.(易错题)若数列
— 7—
4.数列的表示法 数列有三种表示法,它们分别是 8 列表法 、图象法和 9 解析法 .
数学 N 必备知识 自主学习 关键能力 互动探究
— 8—
常用结论► (1)数列是按一定“次序”排列的一列数,一个数列不仅与构成它的“数”有 关,还与这些“数”的排列顺序有关. (2)项与项数的概念:数列的项是指数列中某一确定的数,而项数是指数列的项 对应的位置序号. (3)若数列{an}的前n项和为Sn,则数列{an}的通项公式为an=SS1n,-nS=n-11,,n≥2.
高考数学一轮复习 第六章 数列6

高考数学一轮复习 第六章 数列6.2 等差数列考试要求 1.理解等差数列的概念.2.掌握等差数列的通项公式与前n 项和公式.3.能在具体的问题情境中识别数列的等差关系,并能用有关知识解决相应的问题.4.了解等差数列与一次函数、二次函数的关系.知识梳理1.等差数列的有关概念 (1)等差数列的定义一般地,如果一个数列从第2项起,每一项与它的前一项的差都等于同一个常数,那么这个数列就叫做等差数列,这个常数叫做等差数列的公差,通常用字母d 表示,定义表达式为a n -a n -1=d (常数)(n ≥2,n ∈N *). (2)等差中项若三个数a ,A ,b 成等差数列,则A 叫做a 与b 的等差中项,且有A =a +b2.2.等差数列的有关公式 (1)通项公式:a n =a 1+(n -1)d . (2)前n 项和公式:S n =na 1+nn -12d 或S n =na 1+a n2. 3.等差数列的常用性质(1)通项公式的推广:a n =a m +(n -m )d (n ,m ∈N *).(2)若{a n }为等差数列,且k +l =m +n (k ,l ,m ,n ∈N *),则a k +a l =a m +a n .(3)若{a n }是等差数列,公差为d ,则a k ,a k +m ,a k +2m ,…(k ,m ∈N *)是公差为md 的等差数列. (4)数列S m ,S 2m -S m ,S 3m -S 2m ,…也是等差数列.(5)S 2n -1=(2n -1)a n .(6)等差数列{a n }的前n 项和为S n ,⎩⎨⎧⎭⎬⎫S n n 为等差数列.常用结论1.已知数列{a n }的通项公式是a n =pn +q (其中p ,q 为常数),则数列{a n }一定是等差数列,且公差为p .2.在等差数列{a n }中,a 1>0,d <0,则S n 存在最大值;若a 1<0,d >0,则S n 存在最小值. 3.等差数列{a n }的单调性:当d >0时,{a n }是递增数列;当d <0时,{a n }是递减数列;当d =0时,{a n }是常数列.4.数列{a n }是等差数列⇔S n =An 2+Bn (A ,B 为常数).这里公差d =2A . 思考辨析判断下列结论是否正确(请在括号中打“√”或“×”) (1)等差数列{a n }的单调性是由公差d 决定的.( √ )(2)若一个数列每一项与它的前一项的差都是常数,则这个数列是等差数列.( × ) (3)数列{a n }为等差数列的充要条件是对任意n ∈N *,都有2a n +1=a n +a n +2.( √ )(4)已知数列{a n }的通项公式是a n =pn +q (其中p ,q 为常数),则数列{a n }一定是等差数列.( √ ) 教材改编题1.已知等差数列{a n }中,a 2=3,前5项和S 5=10,则数列{a n }的公差为( ) A .-1 B .-52C .-2D .-4答案 A解析 设等差数列{a n }的公差为d , ∵S 5=5a 3=10, ∴a 3=a 2+d =2, 又∵a 2=3,∴d =-1.2.在等差数列{a n }中,若a 3+a 4+a 5+a 6+a 7=450,则a 5=________. 答案 903.已知{a n }是等差数列,其前n 项和为S n ,若a 3=2,且S 6=30,则S 9=________. 答案 126解析 由已知可得⎩⎪⎨⎪⎧a 1+2d =2,2a 1+5d =10,解得⎩⎪⎨⎪⎧a 1=-10,d =6.∴S 9=9a 1+9×82d =-90+36×6=126.题型一 等差数列基本量的运算例1 (1)(2022·包头模拟)已知等差数列{a n }中,S n 为其前n 项和,S 4=24,S 9=99,则a 7等于( )A .13B .14C .15D .16 答案 C解析 ∵⎩⎪⎨⎪⎧ S 4=24,S 9=99,∴⎩⎪⎨⎪⎧4a 1+6d =24,9a 1+36d =99,解得⎩⎪⎨⎪⎧a 1=3,d =2.则a 7=a 1+6d =15.(2)记S n 为等差数列{a n }的前n 项和.已知S 4=0,a 5=5,则下列结论正确的有________.(填序号) ①a 2+a 3=0; ②a n =2n -5; ③S n =n (n -4); ④d =-2.答案 ①②③解析 S 4=4×a 1+a 42=0,∴a 1+a 4=a 2+a 3=0,①正确; a 5=a 1+4d =5, (*) a 1+a 4=a 1+a 1+3d =0,(**)联立(*)(**)得⎩⎪⎨⎪⎧d =2,a 1=-3,∴a n =-3+(n -1)×2=2n -5, ②正确,④错误;S n =-3n +n n -12×2=n 2-4n ,③正确.教师备选1.已知等差数列{a n }的前n 项和为S n ,若a 3=5,S 4=24,则a 9等于( ) A .-5 B .-7 C .-9 D .-11答案 B解析 ∵a 3=5,S 4=24, ∴a 1+2d =5,4a 1+6d =24, 解得a 1=9,d =-2, ∴a n =11-2n , ∴a 9=11-2×9=-7.2.已知{a n }是公差不为零的等差数列,且a 1+a 10=a 9,则a 1+a 2+…+a 9a 10=________.答案278解析 ∵a 1+a 10=a 9,∴a 1+a 1+9d =a 1+8d ,即a 1=-d , ∴a 1+a 2+…+a 9=S 9=9a 1+9×82d =27d , a 10=a 1+9d =8d ,∴a 1+a 2+…+a 9a 10=278.思维升华 (1)等差数列的通项公式及前n 项和公式共涉及五个量a 1,n ,d ,a n ,S n ,知道其中三个就能求出另外两个(简称“知三求二”).(2)确定等差数列的关键是求出两个最基本的量,即首项a 1和公差d .跟踪训练1 (1)记S n 为等差数列{a n }的前n 项和.若a 3+a 6=24,S 6=48,则下列选项正确的是( ) A .a 1=-2 B .a 1=2 C .d =3 D .d =-3答案 A解析 因为⎩⎪⎨⎪⎧a 3+a 6=2a 1+7d =24,S 6=6a 1+15d =48,所以⎩⎪⎨⎪⎧a 1=-2,d =4.(2)(2020·全国Ⅱ)记S n 为等差数列{a n }的前n 项和.若a 1=-2,a 2+a 6=2,则S 10=______. 答案 25解析 设等差数列{a n }的公差为d , 则a 2+a 6=2a 1+6d =2. 因为a 1=-2,所以d =1. 所以S 10=10×(-2)+10×92×1=25.题型二 等差数列的判定与证明例2 (2021·全国甲卷)已知数列{a n }的各项均为正数,记S n 为{a n }的前n 项和,从下面①②③中选取两个作为条件,证明另外一个成立.①数列{a n }是等差数列;②数列{S n }是等差数列;③a 2=3a 1. 注:若选择不同的组合分别解答,则按第一个解答计分. 解 ①③⇒②.已知{a n }是等差数列,a 2=3a 1. 设数列{a n }的公差为d ,则a 2=3a 1=a 1+d ,得d =2a 1, 所以S n =na 1+nn -12d =n 2a 1. 因为数列{a n }的各项均为正数, 所以S n =n a 1,所以S n +1-S n =(n +1)a 1-n a 1=a 1(常数),所以数列{S n }是等差数列. ①②⇒③.已知{a n }是等差数列,{S n }是等差数列. 设数列{a n }的公差为d , 则S n =na 1+nn -12d =12n 2d +⎝⎛⎭⎫a 1-d 2n . 因为数列{S n }是等差数列,所以数列{S n }的通项公式是关于n 的一次函数,则a 1-d2=0,即d =2a 1,所以a 2=a 1+d =3a 1. ②③⇒①.已知数列{S n }是等差数列,a 2=3a 1, 所以S 1=a 1,S 2=a 1+a 2=4a 1. 设数列{S n }的公差为d ,d >0,则S 2-S 1=4a 1-a 1=d ,得a 1=d 2, 所以S n =S 1+(n -1)d =nd , 所以S n =n 2d 2,所以a n =S n -S n -1=n 2d 2-(n -1)2d 2=2d 2n -d 2(n ≥2),是关于n 的一次函数,且a 1=d 2满足上式,所以数列{a n }是等差数列. 高考改编已知数列{a n }中,a 1=1,前n 项和为S n ,且满足nS n +1-(n +1)S n -32n 2-32n =0,证明:数列⎩⎨⎧⎭⎬⎫S n n 是等差数列,并求{a n }的通项公式.解 因为nS n +1-(n +1)S n -32n 2-32n =0,所以nS n +1-(n +1)S n =32n (n +1),所以S n +1n +1-S n n =32,S 11=a 1=1,所以数列⎩⎨⎧⎭⎬⎫S n n 是以1为首项,32为公差的等差数列,S n n =32n -12, 所以S n =32n 2-12n ,当n ≥2时, a n =S n -S n -1 =32n 2-12n -⎣⎡⎦⎤32n -12-12n -1 =3n -2,当n =1时,上式也成立, 所以a n =3n -2. 教师备选(2022·烟台模拟)已知在数列{a n }中,a 1=1,a n =2a n -1+1(n ≥2,n ∈N *),记b n =log 2(a n +1). (1)判断{b n }是否为等差数列,并说明理由; (2)求数列{a n }的通项公式. 解 (1){b n }是等差数列,理由如下: b 1=log 2(a 1+1)=log 22=1,当n ≥2时,b n -b n -1=log 2(a n +1)-log 2(a n -1+1) =log 2a n +1a n -1+1=log 22a n -1+2a n -1+1=1,∴{b n }是以1为首项,1为公差的等差数列. (2)由(1)知,b n =1+(n -1)×1=n ,∴a n +1=2n b=2n , ∴a n =2n -1.思维升华 判断数列{a n }是等差数列的常用方法 (1)定义法:对任意n ∈N *,a n +1-a n 是同一常数.(2)等差中项法:对任意n ≥2,n ∈N *,满足2a n =a n +1+a n -1. (3)通项公式法:对任意n ∈N *,都满足a n =pn +q (p ,q 为常数). (4)前n 项和公式法:对任意n ∈N *,都满足S n =An 2+Bn (A ,B 为常数). 跟踪训练2 已知数列{a n }满足a 1=1,且na n +1-(n +1)a n =2n 2+2n . (1)求a 2,a 3;(2)证明数列⎩⎨⎧⎭⎬⎫a n n 是等差数列,并求{a n }的通项公式.解 (1)由题意可得a 2-2a 1=4, 则a 2=2a 1+4, 又a 1=1,所以a 2=6.由2a 3-3a 2=12,得2a 3=12+3a 2, 所以a 3=15.(2)由已知得na n +1-n +1a nn n +1=2,即a n +1n +1-a nn=2, 所以数列⎩⎨⎧⎭⎬⎫a n n 是首项为a 11=1,公差为d =2的等差数列,则a nn =1+2(n -1)=2n -1, 所以a n =2n 2-n . 题型三 等差数列的性质 命题点1 等差数列项的性质例3 (1)已知数列{a n }满足2a n =a n -1+a n +1(n ≥2),a 2+a 4+a 6=12,a 1+a 3+a 5=9,则a 3+a 4等于( ) A .6 B .7 C .8 D .9答案 B解析 因为2a n =a n -1+a n +1, 所以{a n }是等差数列,由等差数列性质可得a 2+a 4+a 6=3a 4=12, a 1+a 3+a 5=3a 3=9, 所以a 3+a 4=3+4=7.(2)(2022·崇左模拟)已知等差数列{a n }的前n 项和为S n ,且a 3+a 4+a 5+a 6+a 7=150,则S 9等于( ) A .225 B .250 C .270 D .300 答案 C解析 等差数列{a n }的前n 项和为S n , 且a 3+a 4+a 5+a 6+a 7=150, ∴a 3+a 4+a 5+a 6+a 7=5a 5=150, 解得a 5=30,∴S 9=92(a 1+a 9)=9a 5=270.命题点2 等差数列前n 项和的性质例4 (1)已知等差数列{a n }的前n 项和为S n ,若S 10=10,S 20=60,则S 40等于( ) A .110 B .150 C .210 D .280答案 D解析 因为等差数列{a n }的前n 项和为S n ,所以S 10,S 20-S 10,S 30-S 20,S 40-S 30也成等差数列. 故(S 30-S 20)+S 10=2(S 20-S 10), 所以S 30=150.又因为(S 20-S 10)+(S 40-S 30)=2(S 30-S 20), 所以S 40=280.(2)等差数列{a n },{b n }的前n 项和分别为S n ,T n ,若对任意正整数n 都有S n T n =2n -13n -2,则a 11b 6+b 10+a 5b 7+b 9的值为________. 答案2943解析a 11b 6+b 10+a 5b 7+b 9=a 11+a 52b 8=2a 82b 8=a 8b 8,∴a 8b 8=S 2×8-1T 2×8-1=S 15T 15=2×15-13×15-2=2943. 延伸探究 将本例(2)部分条件改为若a 2+a 8b 4+b 6=57,则S 9T 9=________.答案 57解析a 2+a 8b 4+b 6=2a 52b 5=a 5b 5=57, ∴S 9T 9=9a 1+a 929b 1+b 92=9a 59b 5=a 5b 5=57. 教师备选1.若等差数列{a n }的前15项和S 15=30,则2a 5-a 6-a 10+a 14等于( ) A .2 B .3 C .4 D .5解析 ∵S 15=30,∴152(a 1+a 15)=30,∴a 1+a 15=4, ∴2a 8=4,∴a 8=2.∴2a 5-a 6-a 10+a 14=a 4+a 6-a 6-a 10+a 14=a 4-a 10+a 14=a 10+a 8-a 10=a 8=2.2.已知S n 是等差数列{a n }的前n 项和,若a 1=-2 020,S 2 0202 020-S 2 0142 014=6,则S 2 023等于( )A .2 023B .-2 023C .4 046D .-4 046答案 C解析 ∵⎩⎨⎧⎭⎬⎫S n n 为等差数列,设公差为d ′,则S 2 0202 020-S 2 0142 014=6d ′=6,∴d ′=1, 首项为S 11=-2 020,∴S 2 0232 023=-2 020+(2 023-1)×1=2, ∴S 2 023=2 023×2=4 046.思维升华 (1)项的性质:在等差数列{a n }中,若m +n =p +q (m ,n ,p ,q ∈N *),则a m +a n =a p +a q .(2)和的性质:在等差数列{a n }中,S n 为其前n 项和,则 ①S 2n =n (a 1+a 2n )=…=n (a n +a n +1). ②S 2n -1=(2n -1)a n .③依次k 项和成等差数列,即S k ,S 2k -S k ,S 3k -S 2k ,…成等差数列.跟踪训练3 (1)(2021·北京){a n }和{b n }是两个等差数列,其中a k b k (1≤k ≤5)为常值,若a 1=288,a 5=96,b 1=192,则b 3等于( ) A .64 B .128 C .256 D .512解析 由已知条件可得a 1b 1=a 5b 5,则b 5=a 5b 1a 1=96×192288=64,因此,b 3=b 1+b 52=192+642=128.(2)(2022·吕梁模拟)已知S n 为等差数列{a n }的前n 项和,满足a 3=3a 1,a 2=3a 1-1,则数列⎩⎨⎧⎭⎬⎫S n n 的前10项和为( ) A.552 B .55C.652 D .65答案 C解析 设等差数列{a n }的公差为d ,则⎩⎪⎨⎪⎧a 1+2d =3a 1,a 1+d =3a 1-1,所以a 1=1,d =1, 所以S n =n +n n -12=nn +12, 所以S n n =n +12,所以S n +1n +1-S n n=n +1+12-n +12=12,所以⎩⎨⎧⎭⎬⎫S n n 是以1为首项,12为公差的等差数列,数列⎩⎨⎧⎭⎬⎫S n n 的前10项和T 10=10+10×10-12×12=652.课时精练1.(2022·信阳模拟)在等差数列{a n }中,若a 3+a 9=30,a 4=11,则{a n }的公差为( ) A .-2 B .2 C .-3 D .3 答案 B解析 设公差为d ,因为a 3+a 9=2a 6=30, 所以a 6=15,从而d =a 6-a 46-4=2.2.(2022·莆田模拟)已知等差数列{a n }满足a 3+a 6+a 8+a 11=12,则2a 9-a 11的值为( ) A .-3 B .3 C .-12 D .12 答案 B解析 由等差中项的性质可得, a 3+a 6+a 8+a 11=4a 7=12, 解得a 7=3, ∵a 7+a 11=2a 9, ∴2a 9-a 11=a 7=3.3.(2022·铁岭模拟)中国古代数学名著《张邱建算经》中有如下问题:今有十等人,每等一人,宫赐金以等次差降之(等差数列),上三人先入,得金四斤,持出;下四人后入,得金三斤,持出;中间三人未到者,亦依等次更给.则第一等人(得金最多者)得金斤数是( ) A.3726 B.3727 C.5239 D.5639答案 A解析 由题设知在等差数列{a n }中, a 1+a 2+a 3=4,a 7+a 8+a 9+a 10=3. 所以3a 1+3d =4,4a 1+30d =3, 解得a 1=3726.4.(2022·山东省实验中学模拟)已知等差数列{a n }的项数为奇数,其中所有奇数项之和为319,所有偶数项之和为290,则该数列的中间项为( ) A .28 B .29 C .30 D .31答案 B解析 设等差数列{a n }共有2n +1项, 则S 奇=a 1+a 3+a 5+…+a 2n +1, S 偶=a 2+a 4+a 6+…+a 2n , 该数列的中间项为a n +1,又S 奇-S 偶=a 1+(a 3-a 2)+(a 5-a 4)+…+(a 2n +1-a 2n )=a 1+d +d +…+d =a 1+nd =a n +1, 所以a n +1=S 奇-S 偶=319-290=29.5.等差数列{a n }的公差为d ,前n 项和为S n ,当首项a 1和d 变化时,a 3+a 8+a 13是一个定值,则下列各数也为定值的是( ) A .a 11 B .a 12 C .S 15 D .S 16 答案 C解析 由等差中项的性质可得a 3+a 8+a 13=3a 8为定值,则a 8为定值, S 15=15()a 1+a 152=15a 8为定值,但S 16=16()a 1+a 162=8()a 8+a 9不是定值.6.在等差数列{a n }中,若a 10a 9<-1,且它的前n 项和S n 有最大值,则使S n >0成立的正整数n的最大值是( )A .15B .16C .17D .14 答案 C解析 ∵等差数列{a n }的前n 项和有最大值, ∴等差数列{a n }为递减数列, 又a 10a 9<-1,∴a 9>0,a 10<0, 且a 9+a 10<0, 又S 18=18a 1+a 182=9(a 9+a 10)<0,S 17=17a 1+a 172=17a 9>0,∴使S n >0成立的正整数n 的最大值是17.7.(2019·北京)设等差数列{a n }的前n 项和为S n .若a 2=-3,S 5=-10,则a 5=________. 答案 0解析 设等差数列{a n }的公差为d ,∵⎩⎪⎨⎪⎧a 2=-3,S 5=-10, 即⎩⎪⎨⎪⎧a 1+d =-3,5a 1+10d =-10, ∴⎩⎪⎨⎪⎧a 1=-4,d =1,∴a 5=a 1+4d =0. 8.(2022·新乡模拟)一百零八塔,位于宁夏吴忠青铜峡市,是始建于西夏时期的喇嘛式实心塔群,是中国现存最大且排列最整齐的喇嘛塔群之一.一百零八塔,因塔群的塔数而得名,塔群随山势凿石分阶而建,由下而上逐层增高,依山势自上而下各层的塔数分别为1,3,3,5,5,7,…,该数列从第5项开始成等差数列,则该塔群最下面三层的塔数之和为________.答案 51解析 设该数列为{a n },依题意可知,a 5,a 6,…成等差数列,且公差为2,a 5=5, 设塔群共有n 层,则1+3+3+5+5(n -4)+n -4n -52×2=108,解得n =12(n =-8舍去).故最下面三层的塔数之和为a 10+a 11+a 12=3a 11=3×(5+2×6)=51.9.(2021·全国乙卷)记S n 为数列{a n }的前n 项和,b n 为数列{S n }的前n 项积,已知2S n +1b n =2.(1)证明:数列{b n }是等差数列; (2)求{a n }的通项公式.(1)证明 因为b n 是数列{S n }的前n 项积, 所以n ≥2时,S n =b nb n -1,代入2S n +1b n =2可得,2b n -1b n +1b n =2,整理可得2b n -1+1=2b n , 即b n -b n -1=12(n ≥2).又2S 1+1b 1=3b 1=2,所以b 1=32, 故{b n }是以32为首项,12为公差的等差数列.(2)解 由(1)可知,b n =n +22,则2S n +2n +2=2,所以S n =n +2n +1, 当n =1时,a 1=S 1=32,当n ≥2时,a n =S n -S n -1=n +2n +1-n +1n =-1nn +1. 故a n=⎩⎨⎧32,n =1,-1nn +1,n ≥2.10.在数列{a n }中,a 1=8,a 4=2,且满足a n +2-2a n +1+a n =0(n ∈N *). (1)求数列{a n }的通项公式;(2)设T n =|a 1|+|a 2|+…+|a n |,求T n . 解 (1)∵a n +2-2a n +1+a n =0, ∴a n +2-a n +1=a n +1-a n ,∴数列{a n }是等差数列,设其公差为d , ∵a 1=8,a 4=2, ∴d =a 4-a 14-1=-2,∴a n =a 1+(n -1)d =10-2n ,n ∈N *.(2)设数列{a n }的前n 项和为S n ,则由(1)可得, S n =8n +nn -12×(-2)=9n -n 2,n ∈N *. 由(1)知a n =10-2n ,令a n =0,得n =5, ∴当n >5时,a n <0, 则T n =|a 1|+|a 2|+…+|a n |=a 1+a 2+…+a 5-(a 6+a 7+…+a n ) =S 5-(S n -S 5)=2S 5-S n=2×(9×5-25)-(9n -n 2)=n 2-9n +40; 当n ≤5时,a n ≥0, 则T n =|a 1|+|a 2|+…+|a n | =a 1+a 2+…+a n =9n -n 2,∴T n =⎩⎪⎨⎪⎧9n -n 2,n ≤5,n ∈N *,n 2-9n +40,n ≥6,n ∈N *.11.设等差数列{a n }的前n 项和为S n ,若S m -1=-2,S m =0,S m +1=3,则m 等于( ) A .3 B .4 C .5 D .6 答案 C解析 ∵数列{a n }为等差数列,且前n 项和为S n ,∴数列⎩⎨⎧⎭⎬⎫S n n 也为等差数列.∴S m -1m -1+S m +1m +1=2S mm , 即-2m -1+3m +1=0, 解得m =5,经检验为原方程的解.12.(2022·济宁模拟)设等差数列{a n }的前n 项和是S n ,已知S 14>0,S 15<0,则下列选项不正确的是( ) A .a 1>0,d <0 B .a 7+a 8>0C .S 6与S 7均为S n 的最大值D .a 8<0 答案 C解析 因为S 14>0, 所以S 14=14×a 1+a 142=7(a 1+a 14)=7(a 7+a 8)>0, 即a 7+a 8>0, 因为S 15<0,所以S 15=15×a 1+a 152=15a 8<0,所以a 8<0,所以a 7>0,所以等差数列{a n }的前7项为正数,从第8项开始为负数, 则a 1>0,d <0,S 7为S n 的最大值.13.(2020·新高考全国Ⅰ)将数列{2n -1}与{3n -2}的公共项从小到大排列得到数列{a n },则{a n }的前n 项和为________.答案 3n 2-2n解析 方法一 (观察归纳法)数列{2n -1}的各项为1,3,5,7,9,11,13,…; 数列{3n -2}的各项为1,4,7,10,13,….观察归纳可知,两个数列的公共项为1,7,13,…,是首项为1,公差为6的等差数列, 则a n =1+6(n -1)=6n -5. 故前n 项和为S n =na 1+a n 2=n1+6n -52=3n 2-2n .方法二 (引入参变量法)令b n =2n -1,c m =3m -2,b n =c m ,则2n -1=3m -2,即3m =2n +1,m 必为奇数. 令m =2t -1,则n =3t -2(t =1,2,3,…). a t =b 3t -2=c 2t -1=6t -5,即a n =6n -5. 以下同方法一.14.(2022·东莞东方明珠学校模拟)已知等差数列{a n }的首项a 1=1,公差为d ,前n 项和为S n .若S n ≤S 8恒成立,则公差d 的取值范围是__________. 答案 ⎣⎡⎦⎤-17,-18 解析 根据等差数列{a n }的前n 项和S n 满足S n ≤S 8恒成立, 可知a 8≥0且a 9≤0, 所以1+7d ≥0且1+8d ≤0, 解得-17≤d ≤-18.15.定义向量列a 1,a 2,a 3,…,a n 从第二项开始,每一项与它的前一项的差都等于同一个常向量(即坐标都是常数的向量),即a n =a n -1+d (n ≥2,且n ∈N *),其中d 为常向量,则称这个向量列{a n }为等差向量列.这个常向量叫做等差向量列的公差向量,且向量列{a n }的前n 项和S n =a 1+a 2+…+a n .已知等差向量列{a n }满足a 1=(1,1),a 2+a 4=(6,10),则向量列{a n }的前n 项和S n =____________________. 答案⎝⎛⎭⎫n +n 22,n 2解析 因为向量线性运算的坐标运算,是向量的横坐标、纵坐标分别进行对应的线性运算,则等差数列的性质在等差向量列里面也适用,由等差数列的等差中项的性质知2a 3=a 2+a 4=(6,10),解得a 3=(3,5),则等差向量列{a n }的公差向量为d =a 3-a 12=3,5-1,12=3-1,5-12=2,42=(1,2), 由等差数列的通项公式可得等差向量列{a n }的通项公式为a n =a 1+(n -1)d =(1,1)+(n -1)(1,2)=(1,1)+(n -1,2n -2) =(1+n -1,1+2n -2)=(n ,2n -1),由等差数列的前n 项和公式,可得等差向量列{a n }的前n 项和S n =na 1+a n2=n [1,1+n ,2n -1]2=n1+n ,2n2=n +n 2,2n 22=⎝⎛⎭⎫n +n 22,n 2.16.在等差数列{a n }中,a 3+a 4=4,a 5+a 7=6. (1)求{a n }的通项公式;(2)设{b n }=[a n ],求数列{b n }的前10项和,其中[x ]表示不超过x 的最大整数,如[0.9]=0,[2.6]=2.解 (1)设数列{a n }的公差为d ,由题意得2a 1+5d =4,a 1+5d =3,解得a 1=1,d =25,所以{a n }的通项公式为a n =2n +35.(2)由(1)知,b n =⎣⎡⎦⎤2n +35,当n =1,2,3时,1≤2n +35<2,b n =1; 当n =4,5时,2<2n +35<3,b n =2; 当n =6,7,8时,3≤2n +35<4,b n =3; 当n =9,10时,4<2n +35<5,b n =4. 所以数列{b n }的前10项和为1×3+2×2+3×3+4×2=24.。
高三理科数学一轮总复习第六章 数列
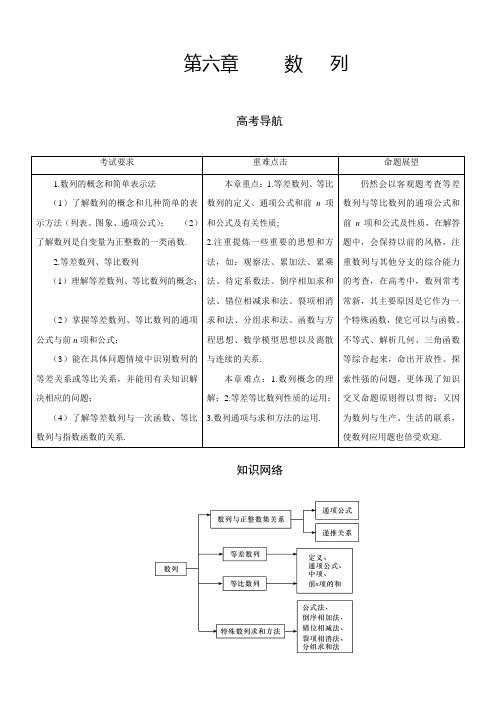
第六章数列高考导航知识网络6.1 数列的概念与简单表示法典例精析题型一 归纳、猜想法求数列通项【例1】根据下列数列的前几项,分别写出它们的一个通项公式: (1)7,77,777,7 777,… (2)23,-415,635,-863,… (3)1,3,3,5,5,7,7,9,9,…【解析】(1)将数列变形为79·(10-1),79(102-1),79(103-1),…,79(10n -1),故a n =79(10n -1).(2)分开观察,正负号由(-1)n+1确定,分子是偶数2n ,分母是1×3,3×5,5×7, …,(2n -1)(2n +1),故数列的通项公式可写成a n =(-1)n+1)12)(12(2+-n n n.(3)将已知数列变为1+0,2+1,3+0,4+1,5+0,6+1,7+0,8+1,9+0,….故数列的通项公式为a n =n +2)1(1n-+.【点拨】联想与转换是由已知认识未知的两种有效的思维方法,观察归纳是由特殊到一般的有效手段,本例的求解关键是通过分析、比较、联想、归纳、转换获得项与项序数的一般规律,从而求得通项.【变式训练1】如下表定义函数f (x ):对于数列{a n },a 1=4,a n =f (n -1 2 008 ) A.1B.2C.3D.4【解析】a 1=4,a 2=1,a 3=5,a 4=2,a 5=4,…,可得a n +4=a n . 所以a 2 008=a 4=2,故选B.题型二 应用a n =⎪⎩⎪⎨⎧≥-=-)2(),1(11n S S n S n n求数列通项【例2】已知数列{a n }的前n 项和S n ,分别求其通项公式: (1)S n =3n -2; (2)S n =18(a n +2)2 (a n >0).【解析】(1)当n =1时,a 1=S 1=31-2=1,当n ≥2时,a n =S n -S n -1=(3n -2)-(3n -1-2)=2×3n -1,又a 1=1不适合上式,故a n =⎪⎩⎪⎨⎧≥⨯=-)2(32),1(11n n n(2)当n =1时,a 1=S 1=18(a 1+2)2,解得a 1=2,当n ≥2时,a n =S n -S n -1=18(a n +2)2-18(a n -1+2)2,所以(a n -2)2-(a n -1+2)2=0,所以(a n +a n -1)(a n -a n -1-4)=0, 又a n >0,所以a n -a n -1=4, 可知{a n }为等差数列,公差为4,所以a n =a 1+(n -1)d =2+(n -1)·4=4n -2, a 1=2也适合上式,故a n =4n -2.【点拨】本例的关键是应用a n =⎪⎩⎪⎨⎧≥-=-)2(),1(11n S S n S n n求数列的通项,特别要注意验证a 1的值是否满足“n ≥2”的一般性通项公式.【变式训练2】已知a 1=1,a n =n (a n +1-a n )(n ∈N *),则数列{a n }的通项公式是( ) A.2n -1B.(n +1n)n -1C.n 2D.n【解析】由a n =n (a n +1-a n )⇒a n +1a n =n +1n. 所以a n =a n a n -1×a n -1a n -2×…×a 2a 1=n n -1×n -1n -2×…×32×21=n ,故选D.题型三 利用递推关系求数列的通项【例3】已知在数列{a n }中a 1=1,求满足下列条件的数列的通项公式: (1)a n +1=a n 1+2a n ;(2)a n +1=2a n +2n +1.【解析】(1)因为对于一切n ∈N *,a n ≠0,因此由a n +1=a n 1+2a n 得1a n +1=1a n +2,即1a n +1-1a n=2.所以{1a n }是等差数列,1a n =1a 1+(n -1)·2=2n -1,即a n =12n -1.(2)根据已知条件得a n +12n +1=a n 2n +1,即a n +12n +1-a n2n =1.所以数列{a n 2n }是等差数列,a n 2n =12+(n -1)=2n -12,即a n =(2n -1)·2n -1.【点拨】通项公式及递推关系是给出数列的常用方法,尤其是后者,可以通过进一步的计算,将其进行转化,构造新数列求通项,进而可以求得所求数列的通项公式.【变式训练3】设{a n }是首项为1的正项数列,且(n +1)·a 2n +1-na 2n +a n +1a n =0(n =1,2,3,…),求a n .【解析】因为数列{a n }是首项为1的正项数列, 所以a n a n +1≠0,所以(n +1)a n +1a n -na n a n +1+1=0,令a n +1a n=t ,所以(n +1)t 2+t -n =0, 所以[(n +1)t -n ](t +1)=0,得t =n n +1或t =-1(舍去),即a n +1a n =nn +1.所以a 2a 1·a 3a 2·a 4a 3·a 5a 4·…·a n a n -1=12·23·34·45·…·n -1n ,所以a n =1n .总结提高1.给出数列的前几项求通项时,常用特征分析法与化归法,所求通项不唯一.2.由S n 求a n 时,要分n =1和n ≥2两种情况.3.给出S n 与a n 的递推关系,要求a n ,常用思路是:一是利用S n -S n -1=a n (n ≥2)转化为a n 的递推关系,再求其通项公式;二是转化为S n 的递推关系,先求出S n 与n 之间的关系,再求a n .6.2 等差数列典例精析题型一 等差数列的判定与基本运算 【例1】已知数列{a n }前n 项和S n =n 2-9n .(1)求证:{a n }为等差数列;(2)记数列{|a n |}的前n 项和为T n ,求 T n 的表达式. 【解析】(1)证明:n =1时,a 1=S 1=-8,当n ≥2时,a n =S n -S n -1=n 2-9n -[(n -1)2-9(n -1)]=2n -10, 当n =1时,也适合该式,所以a n =2n -10 (n ∈N *). 当n ≥2时,a n -a n -1=2,所以{a n }为等差数列. (2)因为n ≤5时,a n ≤0,n ≥6时,a n >0. 所以当n ≤5时,T n =-S n =9n -n 2,当n ≥6时,T n =||a 1+||a 2+…+||a 5+||a 6+…+||a n =-a 1-a 2-…-a 5+a 6+a 7+…+a n =S n -2S 5=n 2-9n -2×(-20)=n 2-9n +40,所以,【点拨】根据定义法判断数列为等差数列,灵活运用求和公式.【变式训练1】已知等差数列{a n }的前n 项和为S n ,且S 21=42,若记b n =1391122a a a --,则数列{b n }( )A.是等差数列,但不是等比数列B.是等比数列,但不是等差数列C.既是等差数列,又是等比数列D.既不是等差数列,又不是等比数列【解析】本题考查了两类常见数列,特别是等差数列的性质.根据条件找出等差数列{a n }的首项与公差之间的关系从而确定数列{b n }的通项是解决问题的突破口.{a n }是等差数列,则S 21=21a 1+21×202d =42.所以a 1+10d =2,即a 11=2.所以b n =1391122a a a--=22-(2a 11)=20=1,即数列{b n }是非0常数列,既是等差数列又是等比数列.答案为C.题型二 公式的应用【例2】设等差数列{a n }的前n 项和为S n ,已知a 3=12,S 12>0,S 13<0. (1)求公差d 的取值范围;(2)指出S 1,S 2,…,S 12中哪一个值最大,并说明理由. 【解析】(1)依题意,有S 12=12a 1+12×(12-1)d 2>0,S 13=13a 1+13×(13-1)d2<0,即⎩⎨⎧<+>+②① 06 011211d a d a由a 3=12,得a 1=12-2d .③将③分别代入①②式,得⎩⎨⎧<+>+03,0724d d所以-247<d <-3.(2)方法一:由d <0可知a 1>a 2>a 3>…>a 12>a 13,因此,若在1≤n ≤12中存在自然数n ,使得a n >0,a n +1<0, 则S n 就是S 1,S 2,…,S 12中的最大值. 由于S 12=6(a 6+a 7)>0,S 13=13a 7<0, 即a 6+a 7>0,a 7<0,因此a 6>0,a 7<0, 故在S 1,S 2,…,S 12中,S 6的值最大.方法二:由d <0可知a 1>a 2>a 3>…>a 12>a 13,因此,若在1≤n ≤12中存在自然数n ,使得a n >0,a n +1<0, 则S n 就是S 1,S 2,…,S 12中的最大值.故在S 1,S 2,…,S 12中,S 6的值最大.【变式训练2】在等差数列{a n }中,公差d >0,a 2 008,a 2 009是方程x 2-3x -5=0的两个根,S n 是数列{a n }的前n 项的和,那么满足条件S n <0的最大自然数n = .【解析】由题意知⎩⎨⎧<-=>=+,05,030092008 2009 2008 2a a a a 又因为公差d >0,所以a 2 008<0,a 2 009>0. 当n =4 015时,S 4 015=a 1+a 4 0152×4 015=a 2 008×4 015<0;当n =4 016时,S 4 016=a 1+a 4 0162×4 016=a 2 008+a 2 0092×4 016>0.所以满足条件S n <0的最大自然数n =4 015.题型三 性质的应用【例3】某地区2010年9月份曾发生流感,据统计,9月1日该地区流感病毒的新感染者有40人,此后,每天的新感染者人数比前一天增加40人;但从9月11日起,该地区医疗部门采取措施,使该种病毒的传播得到控制,每天的新感染者人数比前一天减少10人.(1)分别求出该地区在9月10日和9月11日这两天的流感病毒的新感染者人数; (2)该地区9月份(共30天)该病毒新感染者共有多少人?【解析】(1)由题意知,该地区9月份前10天流感病毒的新感染者的人数构成一个首项为40,公差为40的等差数列.所以9月10日的新感染者人数为40+(10-1)×40=400(人). 所以9月11日的新感染者人数为400-10=390(人).(2)9月份前10天的新感染者人数和为S 10=10(40+400)2=2 200(人),9月份后20天流感病毒的新感染者的人数,构成一个首项为390,公差为-10的等差数列. 所以后20天新感染者的人数和为T 20=20×390+20(20-1)2×(-10)=5 900(人).所以该地区9月份流感病毒的新感染者共有2 200+5 900=8 100(人).【变式训练3】设等差数列{a n }的前n 项和为S n ,若S 4≥10,S 5≤15,则a 4的最大值为 .【解析】因为等差数列{a n }的前n 项和为S n ,且S 4≥10,S 5≤15,所以5+3d 2≤a 4≤3+d ,即5+3d ≤6+2d ,所以d ≤1,所以a 4≤3+d ≤3+1=4,故a 4的最大值为4.总结提高1.在熟练应用基本公式的同时,还要会用变通的公式,如在等差数列中,a m =a n +(m -n )d .2.在五个量a 1、d 、n 、a n 、S n 中,知其中的三个量可求出其余两个量,要求选用公式要恰当,即善于减少运算量,达到快速、准确的目的.3.已知三个或四个数成等差数列这类问题,要善于设元,目的仍在于减少运算量,如三个数成等差数列时,除了设a ,a +d ,a +2d 外,还可设a -d ,a ,a +d ;四个数成等差数列时,可设为a -3m ,a -m ,a +m ,a +3m .4.在求解数列问题时,要注意函数思想、方程思想、消元及整体消元的方法的应用.6.3 等比数列典例精析题型一 等比数列的基本运算与判定【例1】数列{a n }的前n 项和记为S n ,已知a 1=1,a n +1=n +2n S n(n =1,2,3,…).求证: (1)数列{S nn}是等比数列;(2)S n +1=4a n .【解析】(1)因为a n +1=S n +1-S n ,a n +1=n +2n S n ,所以(n +2)S n =n (S n +1-S n ).整理得nS n +1=2(n +1)S n ,所以S n +1n +1=2·S nn ,故{S nn }是以2为公比的等比数列.(2)由(1)知S n +1n +1=4·S n -1n -1=4a nn +1(n ≥2),于是S n +1=4(n +1)·S n -1n -1=4a n (n ≥2).又a 2=3S 1=3,故S 2=a 1+a 2=4.因此对于任意正整数n ≥1,都有S n +1=4a n .【点拨】①运用等比数列的基本公式,将已知条件转化为关于等比数列的特征量a 1、q 的方程是求解等比数列问题的常用方法之一,同时应注意在使用等比数列前n 项和公式时,应充分讨论公比q 是否等于1;②应用定义判断数列是否是等比数列是最直接,最有依据的方法,也是通法,若判断一个数列是等比数列可用a n +1a n=q (常数)恒成立,也可用a 2n +1 =a n ·a n +2 恒成立,若判定一个数列不是等比数列则只需举出反例即可,也可以用反证法.【变式训练1】等比数列{a n }中,a 1=317,q =-12.记f (n )=a 1a 2…a n ,则当f (n )最大时,n 的值为( )A.7B.8C.9D.10【解析】a n =317×(-12)n -1,易知a 9=317×1256>1,a 10<0,0<a 11<1.又a 1a 2…a 9>0,故f (9)=a 1a 2…a 9的值最大,此时n =9.故选C.题型二 性质运用【例2】在等比数列{a n }中,a 1+a 6=33,a 3a 4=32,a n >a n +1(n ∈N *). (1)求a n ;(2)若T n =lg a 1+lg a 2+…+lg a n ,求T n .【解析】(1)由等比数列的性质可知a 1a 6=a 3a 4=32, 又a 1+a 6=33,a 1>a 6,解得a 1=32,a 6=1, 所以a 6a 1=132,即q 5=132,所以q =12,所以a n =32·(12)n -1=26-n .(2)由等比数列的性质可知,{lg a n }是等差数列, 因为lg a n =lg 26-n =(6-n )lg 2,lg a 1=5lg 2,所以T n =(lg a 1+lg a n )n 2=n (11-n )2lg 2.【点拨】历年高考对性质考查较多,主要是利用“等积性”,题目“小而巧”且背景不断更新,要熟练掌握.【变式训练2】在等差数列{a n }中,若a 15=0,则有等式a 1+a 2+…+a n =a 1+a 2+…+a 29-n (n <29,n ∈N *)成立,类比上述性质,相应地在等比数列{b n }中,若b 19=1,能得到什么等式?【解析】由题设可知,如果a m =0,在等差数列中有a 1+a 2+…+a n =a 1+a 2+…+a 2m -1-n (n <2m -1,n ∈N *)成立, 我们知道,如果m +n =p +q ,则a m +a n =a p +a q , 而对于等比数列{b n },则有若m +n =p +q ,则a m a n =a p a q , 所以可以得出结论:若b m =1,则有b 1b 2…b n =b 1b 2…b 2m -1-n (n <2m -1,n ∈N *)成立. 在本题中则有b 1b 2…b n =b 1b 2…b 37-n (n <37,n ∈N *). 题型三 综合运用【例3】设数列{a n }的前n 项和为S n ,其中a n ≠0,a 1为常数,且-a 1,S n ,a n +1成等差数列. (1)求{a n }的通项公式;(2)设b n =1-S n ,问是否存在a 1,使数列{b n }为等比数列?若存在,则求出a 1的值;若不存在,说明理由.【解析】(1)由题意可得2S n =a n +1-a 1.所以当n ≥2时,有⎩⎨⎧-=-=-+11,1122a a S a a S n n n n两式相减得a n +1=3a n (n ≥2). 又a 2=2S 1+a 1=3a 1,a n ≠0,所以{a n }是以首项为a 1,公比为q =3的等比数列. 所以a n =a 1·3n -1.(2)因为S n =a 1(1-q n )1-q =-12a 1+12a 1·3n ,所以b n =1-S n =1+12a 1-12a 1·3n .要使{b n }为等比数列,当且仅当1+12a 1=0,即a 1=-2,此时b n =3n .所以{b n }是首项为3,公比为q =3的等比数列. 所以{b n }能为等比数列,此时a 1=-2.【变式训练3】已知命题:若{a n }为等差数列,且a m =a ,a n =b (m <n ,m 、n ∈N *),则a m +n =bn -amn -m .现在已知数列{b n }(b n >0,n ∈N *)为等比数列,且b m =a ,b n =b (m <n ,m ,n ∈N *),类比上述结论得b m +n = .【解析】n -m b na m.总结提高1.方程思想,即等比数列{a n }中五个量a 1,n ,q ,a n ,S n ,一般可“知三求二”,通过求和与通项两公式列方程组求解.2.对于已知数列{a n }递推公式a n 与S n 的混合关系式,利用公式a n =S n -S n -1(n ≥2),再引入辅助数列,转化为等比数列问题求解.3.分类讨论思想:当a 1>0,q >1或a 1<0,0<q <1时,等比数列{a n }为递增数列;当a 1>0,0<q <1或a 1<0,q >1时,{a n }为递减数列;q <0时,{a n }为摆动数列;q =1时,{a n }为常数列.6.4 数列求和典例精析题型一 错位相减法求和【例1】求和:S n =1a +2a 2+3a 3+…+nan .【解析】(1)a =1时,S n =1+2+3+…+n =n (n +1)2.(2)a ≠1时,因为a ≠0, S n =1a +2a 2+3a 3+…+nan ,①1a S n =1a 2+2a 3+…+n -1a n +n an +1.② 由①-②得(1-1a )S n =1a +1a 2+…+1a n -n a n +1=1a (1-1a n )1-1a-n a n +1, 所以S n =a (a n -1)-n (a -1)a n (a -1)2. 综上所述,S n =⎪⎪⎩⎪⎪⎨⎧≠----=+).1()1()1()1(),1(2)1(2a a a a n a a a n n n n 【点拨】(1)若数列{a n }是等差数列,{b n }是等比数列,则求数列{a n ·b n }的前n 项和时,可采用错位相减法;(2)当等比数列公比为字母时,应对字母是否为1进行讨论;(3)当将S n 与qS n 相减合并同类项时,注意错位及未合并项的正负号.【变式训练1】数列{2n -32n -3}的前n 项和为( ) A.4-2n -12n -1 B.4+2n -72n -2 C.8-2n +12n -3 D.6-3n +22n -1 【解析】取n =1,2n -32n -3=-4.故选C. 题型二 分组并项求和法【例2】求和S n =1+(1+12)+(1+12+14)+…+(1+12+14+…+12n -1). 【解析】和式中第k 项为a k =1+12+14+…+12k -1=1-(12)k 1-12=2(1-12k ). 所以S n =2[(1-12)+(1-122)+…+(1-12n )] =])111([2个n +⋯++-(12+122+…+12n )] =2[n -12(1-12n )1-12]=2[n -(1-12n )]=2n -2+12n -1. 【变式训练2】数列1, 1+2, 1+2+22,1+2+22+23,…,1+2+22+…+2n -1,…的前n 项和为( ) A.2n -1B.n ·2n -nC.2n +1-nD.2n +1-n -2 【解析】a n =1+2+22+…+2n -1=2n -1,S n =(21-1)+(22-1)+…+(2n -1)=2n +1-n -2.故选D.题型三 裂项相消法求和【例3】数列{a n }满足a 1=8,a 4=2,且a n +2-2a n +1+a n =0 (n ∈N *).(1)求数列{a n }的通项公式;(2)设b n =1n (14-a n )(n ∈N *),T n =b 1+b 2+…+b n (n ∈N *),若对任意非零自然数n ,T n >m 32恒成立,求m 的最大整数值.【解析】(1)由a n +2-2a n +1+a n =0,得a n +2-a n +1=a n +1-a n ,从而可知数列{a n }为等差数列,设其公差为d ,则d =a 4-a 14-1=-2, 所以a n =8+(n -1)×(-2)=10-2n .(2)b n =1n (14-a n )=12n (n +2)=14(1n -1n +2), 所以T n =b 1+b 2+…+b n =14[(11-13)+(12-14)+…+(1n -1n +2)] =14(1+12-1n +1-1n +2)=38-14(n +1)-14(n +2)>m 32, 上式对一切n ∈N *恒成立.所以m <12-8n +1-8n +2对一切n ∈N *恒成立. 对n ∈N *,(12-8n +1-8n +2)min =12-81+1-81+2=163, 所以m <163,故m 的最大整数值为5. 【点拨】(1)若数列{a n }的通项能转化为f (n +1)-f (n )的形式,常采用裂项相消法求和.(2)使用裂项相消法求和时,要注意正负项相消时,消去了哪些项,保留了哪些项.【变式训练3】已知数列{a n },{b n }的前n 项和为A n ,B n ,记c n =a n B n +b n A n -a n b n (n ∈N *),则数列{c n }的前10项和为( )A.A 10+B 10B.A 10+B 102C.A 10B 10D.A 10B 10【解析】n =1,c 1=A 1B 1;n ≥2,c n =A n B n -A n -1B n -1,即可推出{c n }的前10项和为A 10B 10,故选C. 总结提高1.常用的基本求和法均对应数列通项的特殊结构特征,分析数列通项公式的特征联想相应的求和方法既是根本,也是关键.2.数列求和实质就是求数列{S n }的通项公式,它几乎涵盖了数列中所有的思想策略、方法和技巧,对学生的知识和思维有很高的要求,应充分重视并系统训练.6.5 数列的综合应用典例精析题型一 函数与数列的综合问题【例1】已知f (x )=log a x (a >0且a ≠1),设f (a 1),f (a 2),…,f (a n )(n ∈N *)是首项为4,公差为2的等差数列.(1)设a 是常数,求证:{a n }成等比数列;(2)若b n =a n f (a n ),{b n }的前n 项和是S n ,当a =2时,求S n .【解析】(1)f (a n )=4+(n -1)×2=2n +2,即log a a n =2n +2,所以a n =a 2n +2, 所以a n a n -1=a 2n +2a2n =a 2(n ≥2)为定值,所以{a n }为等比数列. (2)b n =a n f (a n )=a 2n +2log a a 2n +2=(2n +2)a 2n +2, 当a =2时,b n =(2n +2) ·(2)2n +2=(n +1) ·2n +2, S n =2·23+3·24+4·25+…+(n +1) ·2n +2, 2S n =2·24+3·25+…+n ·2n +2+(n +1)·2n +3, 两式相减得-S n =2·23+24+25+…+2n +2-(n +1)·2n +3=16+24(1-2n -1)1-2-(n +1)·2n +3, 所以S n =n ·2n +3. 【点拨】本例是数列与函数综合的基本题型之一,特征是以函数为载体构建数列的递推关系,通过由函数的解析式获知数列的通项公式,从而问题得到求解.【变式训练1】设函数f (x )=x m +ax 的导函数f ′(x )=2x +1,则数列{1f (n )}(n ∈N *)的前n 项和是( ) A.n n +1 B.n +2n +1C.n n +1D.n +1n 【解析】由f ′(x )=mx m -1+a =2x +1得m =2,a =1.所以f (x )=x 2+x ,则1f (n )=1n (n +1)=1n -1n +1.所以S n =1-12+12-13+13-14+…+1n -1n +1=1-1n +1=n n +1.故选C. 题型二 数列模型实际应用问题【例2】某县位于沙漠地带,人与自然长期进行着顽强的斗争,到2009年底全县的绿化率已达30%,从2010年开始,每年将出现这样的局面:原有沙漠面积的16%将被绿化,与此同时,由于各种原因,原有绿化面积的4%又被沙化.(1)设全县面积为1,2009年底绿化面积为a 1=310,经过n 年绿化面积为a n +1,求证:a n +1=45a n +425; (2)至少需要多少年(取整数)的努力,才能使全县的绿化率达到60%?【解析】(1)证明:由已知可得a n 确定后,a n +1可表示为a n +1=a n (1-4%)+(1-a n )16%,即a n +1=80%a n +16%=45a n +425. (2)由a n +1=45a n +425有,a n +1-45=45(a n -45), 又a 1-45=-12≠0,所以a n +1-45=-12·(45)n ,即a n +1=45-12·(45)n , 若a n +1≥35,则有45-12·(45)n ≥35,即(45)n -1≤12,(n -1)lg 45≤-lg 2, (n -1)(2lg 2-lg 5)≤-lg 2,即(n -1)(3lg 2-1)≤-lg 2,所以n ≥1+lg 21-3lg 2>4,n ∈N *, 所以n 取最小整数为5,故至少需要经过5年的努力,才能使全县的绿化率达到60%.【点拨】解决此类问题的关键是如何把实际问题转化为数学问题,通过反复读题,列出有关信息,转化为数列的有关问题.【变式训练2】规定一机器狗每秒钟只能前进或后退一步,现程序设计师让机器狗以“前进3步,然后再后退2步”的规律进行移动.如果将此机器狗放在数轴的原点,面向正方向,以1步的距离为1单位长移动,令P (n )表示第n 秒时机器狗所在的位置坐标,且P (0)=0,则下列结论中错误的是( )A.P (2 006)=402B.P (2 007)=403C.P (2 008)=404D.P (2 009)=405【解析】考查数列的应用.构造数列{P n },由题知P (0)=0,P (5)=1,P (10)=2,P (15)=3.所以P (2 005)=401,P (2 006)=401+1=402,P (2 007)=401+1+1=403,P (2 008)=401+3=404,P (2 009)=404-1=403.故D 错.题型三 数列中的探索性问题【例3】{a n },{b n }为两个数列,点M (1,2),A n (2,a n ),B n (n -1n ,2n)为直角坐标平面上的点. (1)对n ∈N *,若点M ,A n ,B n 在同一直线上,求数列{a n }的通项公式;(2)若数列{b n }满足log 2C n =a 1b 1+a 2b 2+…+a n b n a 1+a 2+…+a n,其中{C n }是第三项为8,公比为4的等比数列,求证:点列(1,b 1),(2,b 2),…,(n ,b n )在同一直线上,并求此直线方程.【解析】(1)由a n -22-1=2n -2n -1n-1,得a n =2n . (2)由已知有C n =22n -3,由log 2C n 的表达式可知: 2(b 1+2b 2+…+nb n )=n (n +1)(2n -3),①所以2[b 1+2b 2+…+(n -1)b n -1]=(n -1)n (2n -5).②①-②得b n =3n -4,所以{b n }为等差数列.故点列(1,b 1),(2,b 2),…,(n ,b n )共线,直线方程为y =3x -4.【变式训练3】已知等差数列{a n }的首项a 1及公差d 都是整数,前n 项和为S n (n ∈N *).若a 1>1,a 4>3,S3≤9,则通项公式a n=.【解析】本题考查二元一次不等式的整数解以及等差数列的通项公式.由a1>1,a4>3,S3≤9得令x=a1,y=d得在平面直角坐标系中画出可行域如图所示.符合要求的整数点只有(2,1),即a1=2,d=1.所以a n=2+n -1=n+1.故答案填n+1.总结提高1.数列模型应用问题的求解策略(1)认真审题,准确理解题意;(2)依据问题情境,构造等差、等比数列,然后应用通项公式、前n项和公式以及性质求解,或通过探索、归纳构造递推数列求解;(3)验证、反思结果与实际是否相符.2.数列综合问题的求解策略(1)数列与函数综合问题或应用数学思想解决数列问题,或以函数为载体构造数列,应用数列的知识求解;(2)数列的几何型综合问题,探究几何性质和规律特征建立数列的递推关系式,然后求解问题.。
2022届高考数学大一轮总复习第六章 数 列:第六章 6

§6.4 数列求和1.求数列的前n 项和的方法 (1)公式法①等差数列的前n 项和公式 S n =n (a 1+a n )2=na 1+n (n -1)2d .②等比数列的前n 项和公式 (Ⅰ)当q =1时,S n =na 1;(Ⅱ)当q ≠1时,S n =a 1(1-q n )1-q =a 1-a n q1-q .(2)分组转化法把数列的每一项分成两项或几项,使其转化为几个等差、等比数列,再求解. (3)裂项相消法把数列的通项拆成两项之差求和,正负相消剩下首尾若干项. (4)倒序相加法把数列分别正着写和倒着写再相加,即等差数列求和公式的推导过程的推广. (5)错位相减法主要用于一个等差数列与一个等比数列对应项相乘所得的数列的求和,即等比数列求和公式的推导过程的推广. (6)并项求和法一个数列的前n 项和中,可两两结合求解,则称之为并项求和.形如a n =(-1)n f (n )类型,可采用两项合并求解.例如,S n =1002-992+982-972+…+22-12=(100+99)+(98+97)+…+(2+1)=5 050. 2.常见的裂项公式 (1)1n (n +1)=1n -1n +1; (2)1(2n -1)(2n +1)=12⎝⎛⎭⎫12n -1-12n +1;(3)1n +n +1=n +1-n .【思考辨析】判断下面结论是否正确(请在括号中打“√”或“×”)(1)如果数列{a n }为等比数列,且公比不等于1,则其前n 项和S n =a 1-a n +11-q .( √ )(2)当n ≥2时,1n 2-1=12(1n -1-1n +1).( √ )(3)求S n =a +2a 2+3a 3+…+na n 之和时只要把上式等号两边同时乘以a 即可根据错位相减法求得.( × )(4)数列{12n +2n -1}的前n 项和为n 2+12n .( × )(5)若数列a 1,a 2-a 1,…,a n -a n -1是首项为1,公比为3的等比数列,则数列{a n }的通项公式是a n =3n -12.( √ )(6)推导等差数列求和公式的方法叫做倒序求和法,利用此法可求得sin 21°+sin 22°+sin 23°+…+sin 288°+sin 289°=44.5.( √ )1.已知等差数列{a n }的前n 项和为S n ,a 5=5,S 5=15,则数列⎩⎨⎧⎭⎬⎫1a n a n +1的前100项和为( )A.100101B.99101C.99100D.101100 答案 A解析 利用裂项相消法求和. 设等差数列{a n }的首项为a 1,公差为d . ∵a 5=5,S 5=15,∴⎩⎪⎨⎪⎧a 1+4d =5,5a 1+5×(5-1)2d =15,∴⎩⎪⎨⎪⎧a 1=1,d =1, ∴a n =a 1+(n -1)d =n . ∴1a n a n +1=1n (n +1)=1n -1n +1, ∴数列⎩⎨⎧⎭⎬⎫1a n a n +1的前100项和为1-12+12-13+…+1100-1101=1-1101=100101.2.数列{a n }的通项公式为a n =(-1)n -1·(4n -3),则它的前100项之和S 100等于( ) A .200 B .-200 C .400 D .-400 答案 B解析 S 100=(4×1-3)-(4×2-3)+(4×3-3)-…-(4×100-3)=4×[(1-2)+(3-4)+…+(99-100)]=4×(-50)=-200.3.(2014·广东)若等比数列{a n }的各项均为正数,且a 10a 11+a 9a 12=2e 5,则ln a 1+ln a 2+…+ln a 20=________ 答案 50解析 因为a 10a 11+a 9a 12=2a 10a 11=2e 5, 所以a 10a 11=e 5.所以ln a 1+ln a 2+…+ln a 20=ln(a 1a 2…a 20)=ln [(a 1a 20)·(a 2a 19)·…·(a 10a 11)]=ln(a 10a 11)10=10ln(a 10a 11)=10ln e 5=50ln e =50. 4.3·2-1+4·2-2+5·2-3+…+(n +2)·2-n =________. 答案 4-n +42n解析 设S =3×12+4×122+5×123+…+(n +2)×12n ,则12S =3×122+4×123+5×124+…+(n +2)×12n +1. 两式相减得12S =3×12+(122+123+…+12n )-n +22n +1.∴S =3+(12+122+…+12n -1)-n +22n=3+12[1-(12)n -1]1-12-n +22n =4-n +42n .题型一 分组转化法求和例1 已知数列{a n }的通项公式是a n =2·3n -1+(-1)n (ln 2-ln 3)+(-1)n n ln 3,求其前n 项和S n .解 S n =2(1+3+…+3n -1)+[-1+1-1+…+(-1)n ]·(ln 2-ln 3)+[-1+2-3+…+(-1)n n ]ln 3,所以当n 为偶数时,S n =2×1-3n 1-3+n 2ln 3=3n +n2ln 3-1;当n 为奇数时,S n =2×1-3n 1-3-(ln 2-ln 3)+(n -12-n )ln 3=3n -n -12ln 3-ln 2-1.综上所述,S n=⎩⎨⎧3n+n2ln 3-1,n 为偶数,3n-n -12ln 3-ln 2-1,n 为奇数.思维升华 某些数列的求和是将数列分解转化为若干个可求和的新数列的和或差,从而求得原数列的和,这就要通过对数列通项结构特点进行分析研究,将数列的通项合理分解转化.特别注意在含有字母的数列中对字母的讨论.(1)数列{a n }中,a n +1+(-1)n a n =2n -1,则数列{a n }前12项和等于( )A .76B .78C .80D .82(2)已知数列{a n }的前n 项是3+2-1,6+4-1,9+8-1,12+16-1,…,则数列{a n }的通项公式a n =________,其前n 项和S n =________. 答案 (1)B (2)3n -1+2n12n (3n +1)+2n +1-2 解析 (1)由已知a n +1+(-1)n a n =2n -1,① 得a n +2+(-1)n +1a n +1=2n +1,②由①②得a n +2+a n =(-1)n ·(2n -1)+(2n +1), 取n =1,5,9及n =2,6,10, 结果相加可得S 12=a 1+a 2+a 3+a 4+…+a 11+a 12=78. (2)由已知得数列{a n }的通项公式为 a n =3n +2n -1=3n -1+2n , ∴S n =a 1+a 2+…+a n=(2+5+…+3n -1)+(2+22+…+2n ) =n (2+3n -1)2+2(1-2n )1-2=12n (3n +1)+2n +1-2. 题型二 错位相减法求和例2 已知等差数列{a n }的前3项和为6,前8项和为-4. (1)求数列{a n }的通项公式;(2)设b n =(4-a n )q n -1(q ≠0,n ∈N *),求数列{b n }的前n 项和S n . 思维点拨 (1)列方程组求{a n }的首项、公差,然后写出通项a n . (2)q =1时,b n 为等差数列,直接求和;q ≠1时,用错位相减法求和. 解 (1)设等差数列{a n }的公差为d .由已知得⎩⎪⎨⎪⎧ 3a 1+3d =6,8a 1+28d =-4,解得⎩⎪⎨⎪⎧a 1=3,d =-1.故a n =3+(n -1)·(-1)=4-n . (2)由(1)得,b n =n ·q n -1,于是 S n =1·q 0+2·q 1+3·q 2+…+n ·q n -1. 若q ≠1,将上式两边同乘以q 有 qS n =1·q 1+2·q 2+…+(n -1)·q n -1+n ·q n .两式相减得到(q -1)S n =nq n -1-q 1-q 2-…-q n -1 =nq n-q n -1q -1=nq n +1-(n +1)q n +1q -1.于是,S n =nq n +1-(n +1)q n +1(q -1)2.若q =1,则S n =1+2+3+…+n =n (n +1)2.所以S n=⎩⎪⎨⎪⎧n (n +1)2,q =1,nq n +1-(n +1)q n +1(q -1)2,q ≠1.思维升华 (1)错位相减法是求解由等差数列{b n }和等比数列{c n }对应项之积组成的数列{a n },即a n =b n ×c n 的前n 项和的方法.这种方法运算量较大,要重视解题过程的训练. (2)注意错位相减法中等比数列求和公式的应用范围.已知首项为12的等比数列{a n }是递减数列,其前n 项和为S n ,且S 1+a 1,S 2+a 2,S 3+a 3成等差数列. (1)求数列{a n }的通项公式;(2)若b n =a n ·log 2a n ,数列{b n }的前n 项和为T n ,求满足不等式T n +2n +2≥116的最大n 值.解 (1)设等比数列{a n }的公比为q ,由题意知a 1=12,又∵S 1+a 1,S 2+a 2,S 3+a 3成等差数列, ∴2(S 2+a 2)=S 1+a 1+S 3+a 3, 变形得S 2-S 1+2a 2=a 1+S 3-S 2+a 3, 即得3a 2=a 1+2a 3,∴32q =12+q 2,解得q =1或q =12, 又由{a n }为递减数列,于是q =12,∴a n =a 1q n -1=(12)n .(2)由于b n =a n log 2a n =-n ·(12)n ,∴T n =-[1·12+2·(12)2+…+(n -1)·(12)n -1+n ·(12)n ],于是12T n =-[1·(12)2+…+(n -1)·(12)n +n ·(12)n +1],两式相减得:12T n =-[12+(12)2+…+(12)n -n ·(12)n +1]=-12·[1-(12)n ]1-12+n ·(12)n +1,∴T n =(n +2)·(12)n -2.∴T n +2n +2=(12)n ≥116,解得n ≤4, ∴n 的最大值为4. 题型三 裂项相消法求和例3 (2014·山东)已知等差数列{a n }的公差为2,前n 项和为S n ,且S 1,S 2,S 4成等比数列. (1)求数列{a n }的通项公式; (2)令b n =(-1)n-14na n a n +1,求数列{b n }的前n 项和T n . 解 (1)因为S 1=a 1,S 2=2a 1+2×12×2=2a 1+2,S 4=4a 1+4×32×2=4a 1+12,由题意得(2a 1+2)2=a 1(4a 1+12),解得a 1=1, 所以a n =2n -1. (2)b n =(-1)n-14n a n a n +1=(-1)n -14n (2n -1)(2n +1)=(-1)n -1(12n -1+12n +1). 当n 为偶数时,T n =(1+13)-(13+15)+…+(12n -3+12n -1)-(12n -1+12n +1)=1-12n +1=2n2n +1.当n 为奇数时,T n =(1+13)-(13+15)+…-(12n -3+12n -1)+(12n -1+12n +1)=1+12n +1=2n +22n +1.所以T n=⎩⎪⎨⎪⎧2n +22n +1,n 为奇数,2n2n +1,n 为偶数.(或T n =2n +1+(-1)n -12n +1)思维升华 利用裂项相消法求和时,应注意抵消后并不一定只剩下第一项和最后一项,也有可能前面剩两项,后面也剩两项,再就是将通项公式裂项后,有时候需要调整前面的系数,使裂开的两项之差和系数之积与原通项公式相等.在数列{a n }中,a 1=1,当n ≥2时,其前n 项和S n 满足S 2n =a n⎝⎛⎭⎫S n -12. (1)求S n 的表达式;(2)设b n =S n2n +1,求{b n }的前n 项和T n .解 (1)∵S 2n =a n ⎝⎛⎭⎫S n -12, a n =S n -S n -1 (n ≥2), ∴S 2n =(S n -S n -1)⎝⎛⎭⎫S n -12, 即2S n -1S n =S n -1-S n ,① 由题意得S n -1·S n ≠0,①式两边同除以S n -1·S n ,得1S n -1S n -1=2,∴数列⎩⎨⎧⎭⎬⎫1S n 是首项为1S 1=1a 1=1,公差为2的等差数列.∴1S n =1+2(n -1)=2n -1,∴S n =12n -1. (2)∵b n =S n 2n +1=1(2n -1)(2n +1)=12⎝⎛⎭⎫12n -1-12n +1, ∴T n =b 1+b 2+…+b n =12[(1-13)+(13-15)+…+(12n -1-12n +1)]=12⎝⎛⎭⎫1-12n +1=n2n +1.四审结构定方案典例:(12分)已知数列{a n }的前n 项和S n =-12n 2+kn (其中k ∈N *),且S n 的最大值为8.(1)确定常数k ,并求a n ;(2)求数列⎩⎨⎧⎭⎬⎫9-2a n 2n 的前n 项和T n .审题路线图S n =-12n 2+kn 及S n 最大值为8S n 是n 的函数n =k 时(S n )max =S k =8(根据S n 的结构特征确定k 值)k =4,S n =-12n 2+4n利用a n 、S n 的关系a n =92-n化简数列{}9-2a n 2n9-2a n 2n =n2n -1根据数列的结构特征,确定求和方法:错位相减法T n =1+22+322+…+n -12n -2+n 2n -1①①式两边同乘以22T n =2+2+32+…+n -12n -3+n2n -2②错位相减T n =2+1+12+…+12n -2-n2n -1=4-n +22n -1.规范解答解 (1)当n =k ∈N *时,S n =-12n 2+kn 取得最大值,即8=S k =-12k 2+k 2=12k 2,故k 2=16,k =4.当n =1时,a 1=S 1=-12+4=72,[3分]当n ≥2时,a n =S n -S n -1=92-n .[6分]当n =1时,上式也成立,综上,a n =92-n .(2)因为9-2a n 2n =n2n -1,所以T n =1+22+322+…+n -12n -2+n2n -1,① [7分]所以2T n =2+2+32+…+n -12n -3+n2n -2 ②②-①得:2T n -T n =2+1+12+…+12n -2-n2n -1=4-12n -2-n2n -1=4-n +22n -1.[11分]故T n =4-n +22n -1.[12分]温馨提醒 (1)根据数列前n 项和的结构特征和最值确定k 和S n ,求出a n 后再根据{9-2a n2n }的结构特征确定利用错位相减法求T n .在审题时,要审题目中数式的结构特征判定解题方案; (2)利用S n 求a n 时不要忽视n =1的情况;错位相减时不要漏项或算错项数. (3)可以通过n =1,2时的特殊情况对结论进行验证.方法与技巧非等差、等比数列的一般数列求和,主要有两种思想:(1)转化的思想,即将一般数列设法转化为等差或等比数列,这一思想方法往往通过通项分解或错位相消来完成;(2)不能转化为等差或等比的特殊数列,往往通过裂项相消法、错位相减法、倒序相加法等来求和. 失误与防范1.直接应用公式求和时,要注意公式的应用范围,如当等比数列公比为参数(字母)时,应对其公比是否为1进行讨论.2.在应用错位相减法时,注意观察未合并项的正负号;结论中形如a n ,a n +1的式子应进行合并.3.在应用裂项相消法时,要注意消项的规律具有对称性,即前剩多少项则后剩多少项.A 组 专项基础训练 (时间:45分钟)1.数列112,314,518,7116,…,(2n -1)+12n ,…的前n 项和S n 的值等于( )A .n 2+1-12nB .2n 2-n +1-12nC .n 2+1-12n -1D .n 2-n +1-12n答案 A解析 该数列的通项公式为a n =(2n -1)+12n ,则S n =[1+3+5+…+(2n -1)]+(12+122+…+12n )=n 2+1-12n .2.已知函数f (n )=n 2cos n π,且a n =f (n )+f (n +1),则a 1+a 2+a 3+…+a 100等于( ) A .0 B .-100 C .100 D .10 200 答案 B解析 f (n )=n 2cos n π=⎩⎪⎨⎪⎧-n 2(n 为奇数)n 2(n 为偶数)=(-1)n ·n 2, 由a n =f (n )+f (n +1) =(-1)n ·n 2+(-1)n +1·(n +1)2 =(-1)n [n 2-(n +1)2] =(-1)n +1·(2n +1), 得a 1+a 2+a 3+…+a 100=3+(-5)+7+(-9)+…+199+(-201) =50×(-2)=-100.3.数列a 1+2,…,a k +2k ,…,a 10+20共有十项,且其和为240,则a 1+…+a k +…+a 10的值为( )A .31B .120C .130D .185 答案 C解析 a 1+…+a k +…+a 10 =240-(2+…+2k +…+20) =240-(2+20)×102=240-110=130.4.已知数列{a n }的前n 项和S n =n 2-6n ,则{|a n |}的前n 项和T n 等于( ) A .6n -n 2B .n 2-6n +18C.⎩⎪⎨⎪⎧6n -n 2(1≤n ≤3),n 2-6n +18(n >3) D.⎩⎪⎨⎪⎧6n -n 2(1≤n ≤3),n 2-6n (n >3) 答案 C解析 ∵由S n =n 2-6n 得{a n }是等差数列,且首项为-5,公差为2.∴a n =-5+(n -1)×2=2n -7,∴n ≤3时,a n <0,n >3时,a n >0,∴T n =⎩⎪⎨⎪⎧6n -n 2(1≤n ≤3),n 2-6n +18(n >3). 5.数列a n =1n (n +1),其前n 项之和为910,则在平面直角坐标系中,直线(n +1)x +y +n =0在y 轴上的截距为( )A .-10B .-9C .10D .9答案 B解析 数列的前n 项和为11×2+12×3+…+1n (n +1)=1-1n +1=n n +1=910, ∴n =9,∴直线方程为10x +y +9=0.令x =0,得y =-9,∴在y 轴上的截距为-9.6.数列{a n }满足a n +a n +1=12(n ∈N *),且a 1=1,S n 是数列{a n }的前n 项和,则S 21=________. 答案 6解析 由a n +a n +1=12=a n +1+a n +2, ∴a n +2=a n ,则a 1=a 3=a 5=…=a 21,a 2=a 4=a 6=…=a 20,∴S 21=a 1+(a 2+a 3)+(a 4+a 5)+…+(a 20+a 21)=1+10×12=6. 7.已知数列{a n }满足a n +a n +1=(-1)n +12(n ∈N *),a 1=-12,S n是数列{a n }的前n 项和,则S 2 013=________.答案 -1 0072解析 由题意知,a 1=-12,a 2=1,a 3=-32,a 4=2,a 5=-52,a 6=3,…, 所以数列{a n }的奇数项构成了首项为-12, 公差为-1的等差数列,偶数项构成了首项为1,公差为1的等差数列,通过分组求和可得S 2 013=[(-12)×1 007+1 007×1 0062×(-1)]+(1×1 006+1 006×1 0052×1)=-1 0072. 8.设f (x )=4x 4x +2,若S =f (12 015)+f (22 015)+…+f (2 0142 015),则S =________. 答案 1 007解析 ∵f (x )=4x 4x +2,∴f (1-x )=41-x 41-x +2=22+4x, ∴f (x )+f (1-x )=4x 4x +2+22+4x=1. S =f (12 015)+f (22 015)+…+f (2 0142 015),① S =f (2 0142 015)+f (2 0132 015)+…+f (12 015),② ①+②得,2S =[f (12 015)+f (2 0142 015)]+[f (22 015)+f (2 0132 015)]+…+[f (2 0142 015)+f (12 015)]=2 014, ∴S =2 0142=1 007. 9.已知数列{a n }是首项为a 1=14,公比为q =14的等比数列,设b n +2=143log n a (n ∈N *),数列{c n }满足c n =a n ·b n .(1)求数列{b n }的通项公式;(2)求数列{c n }的前n 项和S n .解 (1)由题意,知a n =(14)n (n ∈N *), 又b n =143log 2n a ,故b n =3n -2(n ∈N *).(2)由(1),知a n =(14)n ,b n =3n -2(n ∈N *), 所以c n =(3n -2)×(14)n (n ∈N *). 所以S n =1×14+4×(14)2+7×(14)3+…+(3n -5)×(14)n -1+(3n -2)×(14)n , 于是14S n =1×(14)2+4×(14)3+7×(14)4+…+(3n -5)×(14)n +(3n -2)×(14)n +1. 两式相减,得34S n =14+3[(14)2+(14)3+…+(14)n ]-(3n -2)×(14)n +1=12-(3n +2)×(14)n +1. 所以S n =23-3n +23×(14)n (n ∈N *). 10.(2013·江西)正项数列{a n }的前n 项和S n 满足:S 2n -(n 2+n -1)S n-(n 2+n )=0. (1)求数列{a n }的通项公式a n ;(2)令b n =n +1(n +2)2a 2n,数列{b n }的前n 项和为T n ,证明:对于任意的n ∈N *,都有T n <564. (1)解 由S 2n -(n 2+n -1)S n -(n 2+n )=0,得[S n -(n 2+n )](S n +1)=0,由于{a n }是正项数列,所以S n +1>0.所以S n =n 2+n (n ∈N *).n ≥2时,a n =S n -S n -1=2n ,n =1时,a 1=S 1=2适合上式.∴a n =2n (n ∈N *).(2)证明 由a n =2n (n ∈N *)得b n =n +1(n +2)2a 2n =n +14n 2(n +2)2 =116⎣⎡⎦⎤1n 2-1(n +2)2 T n =116⎣⎡⎝⎛⎭⎫1-132+⎝⎛⎭⎫122-142+⎝⎛⎭⎫132-152+… ⎦⎤+⎝⎛⎭⎫1(n -1)2-1(n +1)2+⎝⎛⎭⎫1n 2-1(n +2)2 =116⎣⎡⎦⎤1+122-1(n +1)2-1(n +2)2<116⎝⎛⎭⎫1+122=564(n ∈N *). 即对于任意的n ∈N *,都有T n <564. B 组 专项能力提升(时间:30分钟)11.已知数列2 008,2 009,1,-2 008,-2 009,…,这个数列的特点是从第二项起,每一项都等于它的前后两项之和,则这个数列的前2 014项之和S 2 014等于( )A .2 008B .2 010C .1D .0答案 B解析 由已知得a n =a n -1+a n +1(n ≥2),∴a n +1=a n -a n -1.故数列的前8项依次为2 008,2 009,1,-2 008,-2 009,-1,2 008,2 009.由此可知数列为周期数列,周期为6,且S 6=0.∵2 014=6×335+4,∴S 2 014=S 4=2 008+2 009+1+(-2 008)=2 010.12.1-4+9-16+…+(-1)n +1n 2等于( )A.n (n +1)2 B .-n (n +1)2C .(-1)n+1n (n +1)2 D .以上答案均不对答案 C 解析 当n 为偶数时,1-4+9-16+…+(-1)n +1n 2=-3-7-…-(2n -1)=-n 2(3+2n -1)2=-n (n +1)2; 当n 为奇数时,1-4+9-16+…+(-1)n +1n 2=-3-7-…-[2(n -1)-1]+n 2=-n -12[3+2(n -1)-1]2+n 2 =n (n +1)2, 综上可得,原式=(-1)n +1n (n +1)2. 13.(2013·湖南)设S n 为数列{a n }的前n 项和,S n =(-1)n a n -12n ,n ∈N *,则: (1)a 3=________;(2)S 1+S 2+…+S 100=________.答案 (1)-116 (2)13⎝⎛⎭⎫12100-1 解析 ∵a n =S n -S n -1=(-1)n a n -12n -(-1)n -1a n -1+12n -1(n ≥2), ∴a n =(-1)n a n -(-1)n -1a n -1+12n (n ≥2). 当n 为偶数时,a n -1=-12n , 当n 为奇数时,2a n +a n -1=12n , ∴当n =4时,a 3=-124=-116. 根据以上{a n }的关系式及递推式可求.a 1=-122,a 3=-124,a 5=-126,a 7=-128, a 2=122,a 4=124,a 6=126,a 8=128. ∴a 2-a 1=12,a 4-a 3=123,a 6-a 5=125,…,∴S 1+S 2+…+S 100=(a 2-a 1)+(a 4-a 3)+…+(a 100-a 99)-⎝⎛⎭⎫12+122+123+…+12100 =⎝⎛⎭⎫12+123+…+1299-⎝⎛⎭⎫12+122+…+12100 =13⎝⎛⎭⎫12100-1. 14.已知数列{a n }的前n 项和S n ,满足:S n =2a n -2n (n ∈N *).(1)求数列{a n }的通项a n ;(2)若数列{b n }满足b n =log 2(a n +2),T n 为数列{b n a n +2}的前n 项和,求证:T n ≥12. (1)解 当n ∈N *时,S n =2a n -2n ,则当n ≥2时,S n -1=2a n -1-2(n -1),两式相减得a n =2a n -2a n -1-2,即a n =2a n -1+2,∴a n +2=2(a n -1+2),∴a n +2a n -1+2=2, 当n =1时,S 1=2a 1-2,则a 1=2,∴{a n +2}是以a 1+2=4为首项,2为公比的等比数列,∴a n +2=4·2n -1,∴a n =2n +1-2;(2)证明 b n =log 2(a n +2)=log 22n +1=n +1,∴b n a n +2=n +12n +1,则T n =222+323+…+n +12n +1, 12T n =223+324+…+n 2n +1+n +12n +2, 两式相减得12T n =222+123+124+…+12n +1-n +12n +2 =14+14(1-12n )1-12-n +12n +2 =14+12-12n +1-n +12n +2=34-n +32n +2, ∴T n =32-n +32n +1, 当n ≥2时,T n -T n -1=-n +32n +1+n +22n =n +12n +1>0, ∴{T n }为递增数列,∴T n ≥T 1=12. 15.直线l n :y =x -2n 与圆C n :x 2+y 2=2a n +n 交于不同的两点A n ,B n ,n ∈N *.数列{a n }满足:a 1=1,a n +1=14|A n B n |2.(1)求数列{a n }的通项公式;(2)若b n =⎩⎪⎨⎪⎧2n -1(n 为奇数),a n (n 为偶数),求数列{b n }的前n 项和T n . 解 (1)由题意,知圆C n 的圆心到直线l n 的距离d n =n , 半径r n =2a n +n ,所以a n +1=(12|A n B n |)2=r 2n -d 2n =(2a n +n )-n =2a n . 又a 1=1,所以a n =2n -1.(2)当n 为偶数时,T n =(b 1+b 3+…+b n -1)+(b 2+b 4+…+b n ) =[1+5+…+(2n -3)]+(2+23+…+2n -1) =n (n -1)2+2(1-2n )1-4=n 2-n 2+23(2n -1). 当n 为奇数时,n +1为偶数,T n +1=(n +1)2-(n +1)2+23(2n +1-1) =n 2+n 2+23(2n +1-1). 而T n +1=T n +b n +1=T n +2n ,所以T n =n 2+n 2+13(2n -2). 所以T n =⎩⎨⎧n 2-n 2+23(2n -1)(n 为偶数),n 2+n 2+13(2n -2)(n 为奇数).。
高三数学第一轮复习——数列(知识点很全)

高三数学第一轮复习——数列一、知识梳理数列概念1.数列的定义:按照一定顺序排列的一列数称为数列,数列中的每个数称为该数列的项.2.通项公式:如果数列{}n a 的第n 项与序号之间可以用一个式子表示,那么这个公式叫做这个数列的通项公式,即)(n f a n=.3.递推公式:如果已知数列{}n a 的第一项(或前几项),且任何一项n a 与它的前一项1-n a (或前几项)间的关系可以用一个式子来表示,即)(1-=n n a f a 或),(21--=n n n a a f a ,那么这个式子叫做数列{}n a 的递推公式. 如数列{}n a 中,12,11+==n n a a a ,其中12+=n n a a 是数列{}n a 的递推公式.4.数列的前n 项和与通项的公式①n n a a a S +++= 21; ②⎩⎨⎧≥-==-)2()1(11n S S n S a n nn .5. 数列的表示方法:解析法、图像法、列举法、递推法.6. 数列的分类:有穷数列,无穷数列;递增数列,递减数列,摆动数列,常数数列;有界数列,无界数列.①递增数列:对于任何+∈N n ,均有n n a a >+1.②递减数列:对于任何+∈N n ,均有n n a a <+1.③摆动数列:例如: .,1,1,1,1,1 --- ④常数数列:例如:6,6,6,6,……. ⑤有界数列:存在正数M 使+∈≤N n M a n ,.⑥无界数列:对于任何正数M ,总有项n a 使得M a n >.等差数列1.等差数列的概念如果一个数列从第二项起,每一项与它前一项的差等于同一个常数d ,这个数列叫做等差数列,常数d 称为等差数列的公差.2.通项公式与前n 项和公式⑴通项公式d n a a n)1(1-+=,1a 为首项,d为公差.⑵前n 项和公式2)(1n n a a n S +=或d n n na S n )1(211-+=.3.等差中项如果b A a ,,成等差数列,那么A 叫做a 与b 的等差中项.即:A 是a 与b 的等差中项⇔b a A +=2⇔a ,A ,b 成等差数列.4.等差数列的判定方法 ⑴定义法:d a a n n =-+1(+∈N n ,d是常数)⇔{}n a 是等差数列;⑵中项法:212+++=n n n a a a (+∈N n )⇔{}n a 是等差数列.5.等差数列的常用性质⑴数列{}n a 是等差数列,则数列{}p a n +、{}n pa (p 是常数)都是等差数列;⑵在等差数列{}n a 中,等距离取出若干项也构成一个等差数列,即 ,,,,32k n k n k n n a a a a +++为等差数列,公差为kd .⑶d m n a a m n)(-+=;b an a n +=(a ,b 是常数);bn an S n +=2(a ,b 是常数,0≠a )⑷若),,,(+∈+=+N q p n m q p nm ,则q p n m a a a a +=+;⑸若等差数列{}n a 的前n 项和n S ,则⎭⎬⎫⎩⎨⎧n S n 是等差数列;⑹当项数为)(2+∈N n n ,则nn a a S S nd S S 1,+==-奇偶奇偶;当项数为)(12+∈-N n n ,则nn S S a S S n 1,-==-奇偶偶奇. 等比数列1.等比数列的概念如果一个数列从第二项起,每一项与它前一项的比等于同一个常数)0(≠q q ,这个数列叫做等比数列,常数q 称为等比数列的公比.2.通项公式与前n 项和公式⑴通项公式:11-=n nq a a ,1a 为首项,q 为公比 .⑵前n 项和公式:①当1=q时,1na S n =②当1≠q 时,qqa a q q a S n n n --=--=11)1(11. 3.等比中项如果b G a ,,成等比数列,那么G 叫做a 与b 的等比中项. 即:G 是a 与b 的等差中项⇔a ,A ,b 成等差数列⇒b a G ⋅=2.4.等比数列的判定方法 ⑴定义法:q a a nn =+1(+∈N n ,0≠q 是常数)⇔{}n a 是等比数列; ⑵中项法:221++⋅=n n n a a a (+∈N n )且0≠n a ⇔{}n a 是等比数列.5.等比数列的常用性质⑴数列{}n a 是等比数列,则数列{}n pa 、{}n pa (0≠q 是常数)都是等比数列;⑵在等比数列{}n a 中,等距离取出若干项也构成一个等比数列,即 ,,,,32k n k n k n n a a a a +++为等比数列,公比为kq .⑶),(+-∈⋅=N m n q a a m n m n⑷若),,,(+∈+=+N q p n m q p n m ,则q p n m a a a a ⋅=⋅;⑸若等比数列{}n a 的前n 项和n S ,则k S 、k k S S -2、k k S S 23-、k k S S 34-是等比数列.二、典型例题A 、求值类的计算题(多关于等差等比数列)1)根据基本量求解(方程的思想)1、已知n S 为等差数列{}n a 的前n 项和,63,6,994=-==n S a a ,求n ;2、等差数列{}n a 中,410a =且3610a a a ,,成等比数列,求数列{}n a 前20项的和20S .3、设{}n a 是公比为正数的等比数列,若16,151==a a ,求数列{}n a 前7项的和.4、已知四个实数,前三个数成等差数列,后三个数成等比数列,首末两数之和为37,中间两数之和为36,求这四个数.2)根据数列的性质求解(整体思想)1、已知n S 为等差数列{}n a 的前n 项和,1006=a ,则=11S ;2、设n S 、n T 分别是等差数列{}n a 、{}n a 的前n 项和,327++=n n T S n n ,则=55b a. 3、设n S 是等差数列{}n a 的前n 项和,若==5935,95S Sa a 则( ) 4、等差数列{}n a ,{}nb 的前n 项和分别为n S ,n T ,若231n n S nT n =+,则n na b =( )5、已知n S 为等差数列{}n a 的前n 项和,)(,m n n S m S m n ≠==,则=+n m S .6、在正项等比数列{}n a 中,153537225a a a a a a ++=,则35a a +=_______。
高中数学高考2022届高考数学一轮复习(新高考版) 第6章 高考专题突破三 高考中的数列问题

(1)求a4的值;
解 因为 4Sn+2+5Sn=8Sn+1+Sn-1,a1=1,a2=32,a3=54,
当n=2时,4S4+5S2=8S3+S1,
即 4×1+32+54+a4+5×1+32=8×1+32+45+1,
解得 a4=78.
(2)证明:an+1-12an为等比数列.
证明 由4Sn+2+5Sn=8Sn+1+Sn-1(n≥2), 得4Sn+2-4Sn+1+Sn-Sn-1=4Sn+1-4Sn(n≥2), 即4an+2+an=4an+1(n≥2). 当 n=1 时,有 4a3+a1=4×54+1=6=4a2,∴4an+2+an=4an+1, ∴aan+n+2-1-2112aan+n 1=44aan+n+2-1-22aan+n 1=4an4+a1-n+a1-n-22aan n+1=222aann++11--aann=12, ∴数列an+1-12an是以 a2-12a1=1 为首项,12为公比的等比数列.
4.错位相减法 如果一个数列的各项是由一个等差数列和一个等比数列的对应项之积构 成的,那么这个数列的前n项和即可用此法来求,如等比数列的前n项和 公式就是用此法推导的.
题型突破 核心探究
TIXINGTUPO HEXINTANJIU
题型一 数列与数学文化
自主演练
1.(多选)(2020·山东曲阜一中月考)在《增删算法统宗》中有这样一则故事:
2.我国古代数学名著《算法统宗》中说:“九百九十六斤棉,赠分八子
做盘缠.次第每人多十七,要将第八数来言.务要分明依次第,孝和休惹
外人传.”意为:“996斤棉花,分别赠送给8个子女做旅费,从第1个孩
Байду номын сангаас
子开始,以后每人依次多17斤,直到第8个孩子为止.分配时一定要按照
高考总复习一轮数学精品课件 第六章 数列 第三节 等比数列

解得
1 = 5√2-5.
(2)由题意,a2=2a1+2,即a1q=2a1+2,①
a3=2(a1+a2)+2,即a1q2=2(a1+a1q)+2,②
联立①②可得a1=2,q=3,则a4=a1q3=54.故选C.
考点二
等比数列的判断与证明
典例突破
例2.已知数列{an}中,a1=1,它的前n项和Sn满足2Sn+an+1=2n+1-1.
则a6+a8=(a1+a3)q5=1×q5=-32,
所以q5=-32,
10 + 12
故
5 + 7
=
( 5 + 7 ) 5
=q5=-32.
5 + 7
(2)方法一:设等比数列{an}的公比为q,则由a2a4a5=a3a6,a9a10=-8,
1 = 1,
1 ·1 3 ·1 4 = 1 2 ·1 5 ,
)
D.2
答案 A
解析由已知 a3=S3-S2=2,公比
4
q=
3
=
4
=2,所以
2
3
a1= 2
=
2
22
=
1
.
2
3.(2023全国甲,理5)设等比数列{an}的各项均为正数,前n项和为Sn,若
a1=1,S5=5S3-4,则S4=(
15A. 8) Nhomakorabea65
B. 8
C.15
D.30
答案 C
解析设等比数列{an}的公比为q,易知q>0,且q≠1.
得
可得 5
8
高考总复习一轮数学精品课件 第六章 数列 第二节 等差数列

考点二
等差数列的判断与证明
典例突破
例2.已知各项均为正数的数列{an}的前n项和为Sn,a1=2,且对任意
n∈N*,anSn+1-an+1Sn=2an+1-2an恒成立.
+ 2
(1)求证:数列{ }是等差数列;
(2)求数列{an}的通项公式;
(3)若不等式λan>n-5对任意的正整数n恒成立,求实数λ的取值范围.
(1)证明 因为anSn+1-an+1Sn=2an+1-2an,
所以an(Sn+1+2)=an+1(Sn+2).又数列{an}各项均为正数,即anan+1>0,所以
+1 +2
+2
−
=0,
+1
所以数列
+2
是等差数列.
(2)解 由(1)知数列
+2
是首项为 2,公差为 0
答案 C
解析由等差数列{an}知,a2+a2 023=a1+a2 024=6,
所以S2 024= 2 024(1 + 2 024 ) =1 012×6=6 072.
2
)
3.记Sn为等差数列{an}的前n项和.若2S3=3S2+6,则公差d=
答案 2
解析设等差数列的公差为d.
由题意得2(3a1+3d)=3(2a1+d)+6,即3d=6,解得d=2.
第六章
第二节 等差数列
内
容
索
引
01
强基础 增分策略
02
北师版高考数学一轮总复习课后习题 第六章 数列 课时规范练26

课时规范练26《素养分级练》P365基础巩固组1.(河南平顶山高三月考)已知数列{a n }的前n 项和为S n ,且S n =2n +1,则a 10=( ) A.512 B.1 025 C.256 D.1 024答案:A解析:由数列{a n }的前n 项和为S n ,且S n =2n +1,得a 10=S 10-S 9=(210+1)-(29+1)=512.故选A.2.(广东佛山高三月考)已知数列{a n }满足a 1=1,a n+1=a n 4a n +1(n ∈N *),则满足a n >137的n 的最大取值为( )A.7B.8C.9D.10答案:C解析:因为a 1=1,a n+1=a n4a n +1,所以1a n+1=4+1a n,即1a n+1−1a n=4.又1a 1=1,所以数列1a n是以1为首项,4为公差的等差数列,于是1a n=1+4(n-1)=4n-3,所以a n =14n -3.由a n >137,即14n -3>137,即0<4n-3<37,解得34<n<10.因为n 为正整数,所以n 的最大取值为9.故选C.3.(山东东营高三月考)在数列{a n }中,a 1=2,a n =1-1a n -1(n≥2),则a 2 022等于( ) A.-12B.12C.-1D.2答案:C解析:由a 1=2,a n =1-1a n -1(n≥2),可得a 2=1-1a 1=12,a 3=1-1a 2=-1,a 4=1-1a 3=2,a 5=1-1a 4=12,故数列{a n }为周期为3的周期数列,而=3×674,故a=a 3=-1.故选C.4.(浙江温州高三模拟)已知数列{a n }为递增数列,前n 项和S n =n 2+n+λ,则实数λ的取值范围是 ( )A.(-∞,2]B.(-∞,2)C.(-∞,0]D.(-∞,0)答案:B解析:当n≥2时,a n =S n -S n-1=n 2+n+λ-[(n-1)2+(n-1)+λ]=2n,可知当n≥2时,{a n }是递增数列,因此要使{a n }为递增数列只需满足a 2>a 1,即4>2+λ⇒λ<2.故选B.5.(山东济南高三模拟)在数列{a n }中,a 1=5,a 2=9,若数列{a n +n 2}是等差数列,则{a n }的最大项的值为( ) A.9B.11C.454D.12答案:B解析:令b n =a n +n 2,∵a 1=5,a 2=9,∴b 2=a 2+4=13,b 1=a 1+1=6,∴数列{a n +n 2}的公差为13-6=7,则a n +n 2=6+7(n-1)=7n-1,∴a n =-n 2+7n-1=-n-722+454.又n ∈N *,∴当n=3或4时,a n 取最大值-14+454=11.故选B.6.(多选)(福建宁德高三模拟)已知数列{a n }满足a 1=1,a n -a n+1=na n a n+1,则下列说法正确的有 ( )A.数列1a n为等差数列B.a 3=14C.a n =2n 2-n+2D.数列{a n }的最大项的值为1 答案:BCD解析:a n -a n+1=na n a n+1,等式两边同除以a n a n+1,得1a n+1−1a n=n,因此数列1a n不是等差数列,故A 错误;又1a 2−1a 1=1,1a 3−1a 2=2,…,1a n −1a n -1=n-1,n≥2,累加可得1a 2−1a 1+1a 3−1a 2+…+1a n−1a n -1=1+2+…+n -1,即1a n−1a 1=(n -1)n 2,又a 1=1,所以1a n=(n -1)n2+1,于是a n =2n 2-n+2,n≥2,又a 1=1也满足上式,故a n =2n 2-n+2,所以a 3=14,故B,C 正确;由于n 2-n+2=n-122+74,而n ∈N *,所以数列{a n }为递减数列,其最大项为a 1=1,故D 正确.故选BCD.7.已知数列{a n }的前n 项和为S n ,且满足S n +a n =4,则S 4= .答案:154解析:当n=1时,有2a 1=4,可得a 1=2.当n≥2时,由S n +a n =4可得S n-1+a n-1=4,两式作差得2a n -a n-1=0,所以a na n -1=12,即数列{a n }是以2为首项,12为公比的等比数列,因此S 4=2×[1-(12) 4]1-12=154.8.(湖南师大附中高三期中)已知在数列{a n }中,a 1=2,a 1+a22+a 33+…+an n=a n+1-2,则a n = .答案:2n解析:a 1+a22+a33+…+an n=a n+1-2,当n≥2时,a 1+a22+a33+…+a n -1n -1=a n -2,则a n n=a n+1-a n ,即a n+1n+1=a n n.当n=1时,a 1=a 2-2,得a 2=4,a 22=a 11满足上式.所以a n+1n+1=a n n,因此数列a nn是常数列,即a n n=a 11=2,所以a n =2n.9.(山东潍坊高三模拟)数列{a n }满足a n+1=5a n +3×5n+1,且a 1=6,则数列{a n }的通项公式为 . 答案:a n =3n-95·5n解析:因为a n+1=5a n +3×5n+1,所以a n+15n+1=a n 5n+3,即a n+15n+1−a n 5n=3,所以a n 5n是等差数列,而a 15=65,所以a n5n=65+3(n-1)=3n-95,所以a n =3n-95·5n .综合提升组10.已知等差数列{a n},其前n项和为S n,若a1=13,S5=45,则nS n的最大值为( )A.400B.405C.410D.415答案:B解析:设等差数列{a n}的公差为d,则S5=5a1+5×42d=5a1+10d=45,解得d=-2,所以S n=na1+n(n-1)d2=13n-n(n-1)=14n-n2,则nS n=14n2-n3.令b n=14n2-n3,则b n+1-b n=[14(n+1)2-(n+1)3]-(14n2-n3)=-3n2+25n+13,所以当n≤8时,b n+1-b n>0,即b1<b2<…<b9;当n≥9时,b n+1-b n<0,即b9>b10>…,所以数列{b n}中的最大项为b9=14×92-93=405.故选B.11.(安徽蚌埠高三期中)已知数列{a n}的首项a1=2,且满足a n+1=a n+12n(n∈N*).若对于任意的正整数n,存在M使得a n<M恒成立,则M的最小值是.答案:3解析:由已知得a n+1-a n=12n,∴当n=1时,a2-a1=121,当n=2时,a3-a2=122,当n=3时,a4-a3=123,……,当n=n-1时,an-a n-1=12n-1(n≥2),以上各式相加得a n-a1=121+122+123+…+12n-1=12×[1-(12)n-1]1-12=1-12n-1,n≥2.又a1=2,∴a n=3-12n-1,n≥2,又a1=2也符合上式,故a n=3-12n-1.∵12n-1>0,∴an<3.若对于任意的正整数n,存在M使得a n<M恒成立,则有M≥3,故M的最小值是3.创新应用组12.(湖南长沙高三期中)数列{a n}的前n项的和S n满足S n+1+S n=n(n∈N*),则下列选项正确的是( )A.数列{a n+1+a n}是常数列,则{a n}是递增数列B.若a1<13C.若a1=-1,则S2 022=1 013D.若a1=1,则{a n}的最小项的值为-1答案:D解析:当n=1时,S2+S1=2a1+a2=1,当n≥2时,S n+S n-1=n-1,则a n+1+a n=1,而a1+a2=1不一定成立,故{a n+1+a n}不一定是常数列,故A错误;由a n+1+a n=a n+a n-1=…=a3+a2=1,得a n+1=a n-1=a n-3=…且a n=a n-2=a n-4=…,即{a n}不是单调数列,故B错误;若a1=-1,则a2=3,a3=-2,故当n≥2时,{a n}的偶数项的值为3,奇数项的值为-2,而S=a1+(a2+a3)+(a4+a5)+…+(a+a)+a=-1+1010+3=1012,故C错误;若a1=1,则a2=-1,a3=2,故当n≥2时,{a n}的偶数项的值为-1,奇数项的值为2,故{a n}的最小项的值为-1,故D正确.故选D.13.(辽宁锦州高三月考)已知数列{a n }是首项为a,公差为1的等差数列,数列{b n }满足b n =1+a n a n,若对任意的n ∈N *,都有b n ≥b 8成立,则实数a 的取值范围是 . 答案:(-8,-7)解析:因为对任意的n ∈N *,都有b n ≥b 8成立,且b n =1+a n a n=1+1a n,所以1a n≥1a 8.又数列{a n }的公差为1,所以数列{a n }为递增数列,所以{a 8<0,a 9>0,即{a +7<0,a +8>0,解得-8<a<-7,即实数a 的取值范围是(-8,-7).。
高考数学一轮总复习教学课件第六章 数 列第1节 数列的概念

[针对训练] 数列 0,,,,…的一个通项公式为(
-
*
(n∈N )
C.a =
√
-
n
*
*
B.an=+(n∈N )
A.an=+(n∈N )
(-)
-
)
*
D.an=
+
(n∈N )
解析:注意到分子0,2,4,6都是偶数,对照选项排除即可.故选C.
考点二
[针对训练] 已知Sn=2n+3,则an=
, = ,
- , ≥
解析:当n=1时,a1=5;
当n≥2时,
an=Sn-Sn-1=2n+3-(2n-1+3)=2n-1,
当n=1时,21-1=1≠a
, = ,
1,所以an=
- , ≥ .
.
考点三
由数列的递推关系求通项
角度一
数列,则实数k的取值范围为(
A.(3,+∞)
B.(2,+∞)
C.(1,+∞)
D.(0,+∞)
√
)
+
,若数列{an}为递减
解析:(1)因为 an+1-an=
*
++ + --
+
-
=
--
任意 n∈N ,an+1-an=
+
<0,
所以k>3-3n对任意n∈N*恒成立,
3.若数列{an}满足a1=2,an+1=
A.2
C.-
√
B.-3
+
解析:因为 a1=2,an+1=
2025版高考数学一轮总复习第6章数列第4讲数列求和课件

裂项相消法——多维探究 角度 1 形如 bn=ana1n+1({an}为等差数列)型
求和: (1)Sn=1+1+1 2+1+12+3+…+1+2+1…+n; (2)Sn=1×1 3+2×1 4+…+nn1+2; (3)Sn=1×1 3+3×1 5+…+2n-112n+1.
[解析] (1)∵an=nn2+1=21n-n+1 1, ∴ Sn = a1 + a2 + … + an = 2 1-12+12-13 21-n+1 1=n2+n1.
3.(选修 2P56T11 改编)已知数列{an}的通项公式为 an=nsin n3π,则 a1
+a2+a3+…+a2 021=( D )
A.1 011 3
B.-52 3
C.52 3
D.-1 011 3
[解析] 因为 f(n)=sin n3π的周期为 T=2ππ=6,所以 a6k-5+a6k-4+ 3
a6k-3+a6k-2+a6k-1+a6k=(6k-5)× 23+(6k-4)× 23+(6k-3)×0+(6k-
2)×-
23+(6k-1)×-
23+6k×0=-3
3,然后求和即可.因为 f(n)=
sin n3π的周期为 T=2ππ=6,a6k-5+a6k-4+a6k-3+a6k-2+a6k-1+a6k=(6k- 3
(3)求Sn=a+2a2+3a3+…+nan时只要把上式等号两边同时乘以a即 可根据错位相减法求得.( × )
(4)当 n≥2 时,n2-1 1=12n-1 1-n+1 1.( √ ) (5)求数列21n+2n+3的前 n 项和可用分组求和.( √ )
[解析] (1)因为数列{an}为等比数列,且公比不等于 1.则其前 n 项和 为 Sn=a111--qqn=a11--aq1qn=a11--aqn+1.
高三数学一轮复习 第六章《数列》63精品课件

二、分类讨论思想 当 q=1 时,{an}的前 n 项和 Sn=na1;当 q≠1 时,{an} a11-qn a1-anq 的前 n 项和 Sn= = .等比数列的前 n 项和公式 1-q 1-q 涉及对公比 q 的分类讨论,此处是常考易错点.
三、解题技巧 1.等比数列的设项技巧 a a (1)对于连续奇数项的等比数列,通常可设为…,q2,q, a,aq,aq2,…; (2)对于连续偶数项且公比为正的等比数列,通常可设 a a 为…,q3,q,aq,aq3,….
an (2){an}{bn}均为等比数列⇒{an· bn}、b 是等比数列. n
am m-n (3){an}为等比数列,则 a = q n
.
(4)若 m、 n、 p、 q∈N*且 m+n=p+q, 则 am· an=ap· aq. 特别地,a1an=a2an-1=a3an-2=…
(5)等间隔的 k 项和(或积)仍成等比数列. 例如:{an}是等比数列,则 ①a1, a3, a5, …, a2n-1; ②a1+a2, a2+a3, a3+a4, …; ③a1a2,a2a3,a3a4,…;④a1+a2,a3+a4,a5+a6……均 成等比数列. (6)an2=an-k· an+k (1≤k<n,n、k∈N*).
1 1 3 解析:a4=a1 2 = a1, 8
15 S4 S4= = a1,∴ =15. 1 8 a4 1-2 答案:15
1 a11-24
• (理)(09·全国Ⅱ)设等比数列{an}的前n项和为Sn.若a1=1, S6=4S3,则a4=________.
解析:设等比数列的公比为 q. 当 q=1 时,由 S6=4S3 得,6a1=4×3a1⇒a1=0(舍). a11-q6 a11-q3 当 q≠1 时,由 S6=4S3⇒ =4· ⇒ 1-q 1-q • 答案: 3 3 1+q =4⇒q3=3⇒a4=a1q3=3.
高考总复习一轮数学精品课件 第6章 数列 素能培优(九) 数列中的构造问题

n
2
1
1
所以{2 }是以 2 = 2为首项,1 为公差的等差数列.
1
1
所以 = +n-1=n- ,所以 an=(2n-1)2n-1.
2
2
2
[对点训练2]已知数列{an}满足a1=2,a2=8,an+2=4an+1-3an,则数列{an}的通项
an=3n-1
公式为_______________.
例1(2024·江西景德镇一中检测)已知在数列{an}中,a1=1,an+1=4an-6,
则a2 023=( C )
A.-42 023+2
B.-42 023-2
C.-42 022+2
D.-42 022-2
解析 由an+1=4an-6,得an+1-2=4(an-2),而a1-2=-1,
因此数列{an-2}是首项为-1,公比为4的等比数列,则an-2=-1×4n-1,
-3n=2n+2-3n-4,故
1-2
D 正确.
本 课 结 束
探究三 形如
an+1= +型
例 5 已知数列{an}Βιβλιοθήκη 首项4an=
__________.
1+4
4
4
a1=5,an+1=3 +1,n∈N*,则数列{an}的通项公式为
4
4
解析 因为 an+1=3 +1,a1=5 ≠0,所以 an≠0,
1
3
1
1
1
1
1 1
两边同时取倒数得 = 4 + 4 ,所以 -1=4 − 4 = 4 ( -1).
高考总复习一轮数学精品课件 第6章 数列 课时规范练45 裂项相消法

+1
1
2+1- 2-1
1
则 bn= 2-1+ 2+1=( 2-1+ 2+1)( 2+1- 2-1) = 2 ( 2 + 1 − 2-1),
1
1
所以 Tn=2 ( 3 − 1 + 5 − 3+…+ 2 + 1 − 2-1)=2 ( 2 + 1-1).
2+3
2+3
1
1
课时规范练45
裂项相消法
1.(2024·山东聊城模拟)记 Sn 是公差不为 0 的等差数列{an}的前 n 项和,若
a4=12 ,S4=3S2.
(1)求{an}的通项公式;
1
(2)设 b1=2,(bn+bn+1)Sn=2,求数列{bn}的前 2n+1 项的和 T2n+1.
1 2 3 4 5 6
解 (1)设等差数列{an}的公差为 d(d≠0),易知 a1≠0,
(1)求{an}的通项公式;
(2)设
1
bn=
,数列{bn}的前
+1
n 项和为 Tn,若
2
Tm= ,求
25
m 的值.
解 (1)设{an}的公差为 d,因为 S5=45,
5( 1 + 5 )
S5= 2 =5a3=45,解得
所以
a3=9.又 a2=7,所以 d=a3-a2=2.
所以 an=a2+(n-2)d=7+2(n-2)=2n+3.
2, = 1,
3.已知数列{an}的通项公式为 an=
等差数列{bn}是递增数列,且满
高考总复习一轮数学精品课件 第6章 数列 素能培优(十一) 数列中的增项、减项问题

若第100项来自{bn},则应有m+2×1-1+2×2-1+…+2m-1≥100,
整理可得,m2+m-100≥0.
当m=9时,92+9-100=-10<0,不满足,
当m=10时,102+10-100=10>0,故m=10.
所以数列{cn}中含有10项数列{an}中的项,含有90项数列{bn}中的项.
ak,ak+1之间插入2k-1项,从而构成一个新数列{cn},求数列{cn}的前100项的
和.
解 (1)Sn+1=2Sn+n+3,当n≥2时,Sn=2Sn-1+n+2,两式相减得an+1=2an+1.
又因为a1+a2=2a1+4,所以a2=7=2a1+1,满足上式.
所以an+1+1=2(an+1).又a1+1=4,
6Sn=2 +3an-4 ,且an>0.
(1)求数列{an}的通项公式an;
(2)数列{bn}依次为a1,3,a2,32,33,a3,34,35,36,a4,37,38,39,310,…,规律是在ak和
ak+1中间插入k(k∈N*)项,所有插入的项构成以3为首项,3为公比的等比数
列,求数列{bn}的前100项的和.
(1)证明数列{an+1}是等比数列,并求数列{an}的通项公式;
(2)若数列{bn}中去掉数列{an}的项后余下的项按原顺序组成数列{cn},求
c1+c2+…+c50的值.
解 (1)因为n,an,Sn成等差数列,所以Sn+n=2an,①
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章 数列 2009年高考题一、选择题1.(2009年广东卷文)已知等比数列}{n a 的公比为正数,且3a ·9a =225a ,2a =1,则1a = A.21 B. 22 C. 2 D.2 2.(2009安徽卷文)已知为等差数列,,则等于A. -1B. 1C. 3D.73.(2009江西卷文)公差不为零的等差数列{}n a 的前n 项和为n S .若4a 是37a a 与的等比中项, 832S =,则10S 等于A. 18B. 24C. 60D. 904.(2009湖南卷文)设n S 是等差数列{}n a 的前n 项和,已知23a =,611a =,则7S 等于( )A .13B .35C .49D . 63 5.(2009福建卷理)等差数列{}n a 的前n 项和为n S ,且3S =6,1a =4, 则公差d 等于 A .1 B53C.- 2 D 3 6.(2009辽宁卷文)已知{}n a 为等差数列,且7a -24a =-1, 3a =0,则公差d = A.-2 B.-12 C.12D.2 7.(2009四川卷文)等差数列{n a }的公差不为零,首项1a =1,2a 是1a 和5a 的等比中项,则数列的前10项之和是A. 90B. 100C. 145D. 1908.(2009宁夏海南卷文)等差数列{}n a 的前n 项和为n S ,已知2110m m m a a a -++-=,2138m S -=,则m =A.38B.20C.10D.99..(2009重庆卷文)设{}n a 是公差不为0的等差数列,12a =且136,,a a a 成等比数列,则{}n a 的前n 项和n S =( )A .2744n n + B .2533n n + C .2324n n+ D .2n n +二、填空题10.(2009全国卷Ⅰ理) 设等差数列{}n a 的前n 项和为n S ,若972S =,则249a a a ++= 11.(2009浙江理)设等比数列{}n a 的公比12q =,前n 项和为n S ,则44Sa = . 12.(2009北京文)若数列{}n a 满足:111,2()n n a a a n N *+==∈,则5a = ;前8项的和8S = .(用数字作答)13.(2009全国卷Ⅱ文)设等比数列{n a }的前n 项和为n s 。
若3614,1s s a ==,则4a = 15.(2009辽宁卷理)等差数列{}n a 的前n 项和为n S ,且53655,S S -=则4a = 三、解答题16.(2009浙江文)设n S 为数列{}n a 的前n 项和,2n S kn n =+,*n N ∈,其中k 是常数. (I ) 求1a 及n a ;(II )若对于任意的*m N ∈,m a ,2m a ,4m a 成等比数列,求k 的值.17.(2009北京文)设数列{}n a 的通项公式为(,0)n a pn q n N P *=+∈>. 数列{}n b 定义如下:对于正整数m ,m b 是使得不等式n a m ≥成立的所有n 中的最小值. (Ⅰ)若11,23p q ==-,求3b ; (Ⅱ)若2,1p q ==-,求数列{}m b 的前2m 项和公式;(Ⅲ)是否存在p 和q ,使得32()m b m m N *=+∈?如果存在,求p 和q 的取值范围;如果不存在,请说明理由.18.(2009山东卷文)等比数列{n a }的前n 项和为n S , 已知对任意的n N +∈ ,点(,)n n S ,均在函数(0x y b r b =+>且1,,b b r ≠均为常数)的图像上. (1)求r 的值; (11)当b=2时,记 1()4n nn b n N a ++=∈ 求数列{}n b 的前n 项和n T19.(2009全国卷Ⅱ文)已知等差数列{n a }中,0,166473=+-=a a a a 求{n a }前n 项和n s .20.(2009安徽卷文)已知数列{} 的前n 项和,数列{}的前n项和(Ⅰ)求数列{}与{}的通项公式;(Ⅱ)设,证明:当且仅当n ≥3时,<21.(2009江西卷文)数列{}n a 的通项222(cos sin )33n n n a n ππ=-,其前n 项和为n S . (1) 求n S ; (2) 3,4nn nS b n =⋅求数列{n b }的前n 项和n T .22. (2009天津卷文)已知等差数列}{n a 的公差d 不为0,设121-+++=n n n q a q a a S*1121,0,)1(N n q q a q a a T n n n n ∈≠-++-=--(Ⅰ)若15,1,131===S a q ,求数列}{n a 的通项公式; (Ⅱ)若3211,,,S S S d a 且=成等比数列,求q 的值。
(Ⅲ)若*2222,1)1(2)1(1,1N n qq dq T q S q q n n n ∈--=+--±≠)证明(23. (2009全国卷Ⅱ理)设数列{}n a 的前n 项和为,n S 已知11,a =142n n S a +=+ (I )设12n n n b a a +=-,证明数列{}n b 是等比数列(II )求数列{}n a 的通项公式。
24. (2009辽宁卷文)等比数列{n a }的前n 项和为n s ,已知1S ,3S ,2S 成等差数列 (1)求{n a }的公比q ;(2)求1a -3a =3,求n s26.(2009湖北卷文)已知{a n }是一个公差大于0的等差数列, 且满足a 3a 6=55, a 2+a 7=16. (Ⅰ)求数列{a n }的通项公式:(Ⅱ)若数列{a n }和数列{b n }满足等式:a n ==)(2...222n 33221为正整数n b b b b n +++,求数列{b n }的前n 项和S n1222(21)426,2621n n n n S +++--=-=--即27. (2009福建卷文)等比数列{}n a 中,已知142,16a a == (I )求数列{}n a 的通项公式;(Ⅱ)若35,a a 分别为等差数列{}n b 的第3项和第5项,试求数列{}n b 的通项公式及前n 项和n S 。
2(161228)6222n n n S n n -+-==-28(2009重庆卷文)(本小题满分12分,(Ⅰ)问3分,(Ⅱ)问4分,(Ⅲ)问5分) 已知112211,4,4,,n n n n n na a a a a ab n N a *+++===+=∈. (Ⅰ)求123,,b b b 的值;(Ⅱ)设1,n n n n c b b S +=为数列{}n c 的前n 项和,求证:17n S n ≥; (Ⅲ)求证:22116417n n n b b --< .2005——2008年高考题一、选择题1.(2008天津)若等差数列{}n a 的前5项和525S =,且23a =,则7a =( ) A.12 B.13 C.14 D.152.(2008陕西)已知{}n a 是等差数列,124a a +=,7828a a +=,则该数列前10项和10S 等于( )A .64B .100C .110D .120 3.(2008广东)记等差数列{}n a 的前n 项和为n S ,若112a =,420S =,则6S =( ) A .16 B .24C .36D .484.(2008浙江)已知{}n a 是等比数列,41252==a a ,,则13221++++n n a a a a a a =( ) A.16(n--41) B.6(n--21)C.332(n --41) D.332(n--21) 5.(2008四川)已知等比数列()n a 中21a =,则其前3项的和3S 的取值范围是() A.(],1-∞- B.()(),01,-∞+∞ C.[)3,+∞ D.(][),13,-∞-+∞6.(2008福建)设{a n }是公比为正数的等比数列,若n 1=7,a 5=16,则数列{a n }前7项的和为( ) A.63B.64C.127D.1287.(2007重庆)在等比数列{a n }中,a 2=8,a 5=64,,则公比q 为( ) A .2 B .3 C .4 D .88.(2007安徽)等差数列{}n a 的前n 项和为x S 若=则432,3,1S a a ==( ) A .12 B .10 C .8 D .69.(2007辽宁)设等差数列{}n a 的前n 项和为n S ,若39S =,636S =,则789a a a ++=( )A .63B .45C .36D .27 10.(2007湖南) 在等比数列{}n a (n ∈N *)中,若11a =,418a =,则该数列的前10项和为( ) A .4122-B .2122-C .10122-D .11122-11.(2007湖北)已知两个等差数列{}n a 和{}n b 的前n 项和分别为A n和n B ,且7453n n A n B n +=+,则使得n na b 为整数的正整数n 的个数是( ) A .2 B .3 C .4 D .512.(2007宁夏)已知a b c d ,,,成等比数列,且曲线223y x x =-+的顶点是()b c ,,则ad 等于( )A .3B .2C .1D .2-13.(2007四川)等差数列{a n }中,a 1=1,a 3+a 5=14,其前n 项和S n =100,则n =( ) A .9 B .10 C .11 D .1214.(2006湖北)若互不相等的实数 成等差数列, 成等比数列,且310a b c ++=,则a =A .4B .2C .-2D .-415.(2005福建)已知等差数列}{n a 中,12497,1,16a a a a 则==+的值是 ( ) A .15B .30C .31D .6416.(2005江苏卷)在各项都为正数的等比数列{a n }中,首项a 1=3 ,前三项和为21,则a 3+ a 4+ a 5=( )A .33 B. 72 C. 84 D .189 二、填空题17.(2008四川)设等差数列{}n a 的前n 项和为n S ,若4510,15S S ≥≤,则4a 的最大值为______.18.(2008重庆)设S n =是等差数列{a n }的前n 项和,a 12=-8,S 9=-9,则S 16= . 19.(2007全国I) 等比数列{}n a 的前n 项和为n S ,已知1S ,22S ,33S 成等差数列,则{}n a 的公比为 .20.(2007江西)已知等差数列{}n a 的前n 项和为n S ,若1221S =,则25811a a a a +++=.21.(2007北京)若数列{}n a 的前n 项和210(123)n S n n n =-= ,,,,则此数列的通项公式为;数列{}n na 中数值最小的项是第项.22.(2006湖南)数列{}n a 满足:1.2,111===+n a a a n n ,2,3….则=+++n a a a 21 .第六章 数列 2009年高考题一、选择题1.(2009广东卷理)已知等比数列{}n a 满足0,1,2,n a n >= ,且25252(3)n n a a n -⋅=≥,,,a b c ,,c a b则当1n ≥时,2123221log log log n a a a -+++=A. (21)n n -B. 2(1)n +C. 2n D. 2(1)n - 2.(2009辽宁卷理)设等比数列{ n a }的前n 项和为n S ,若 63S S =3 ,则 69SS =A. 2B.73 C. 83D.3 3.(2009宁夏海南卷理)等比数列{}n a 的前n 项和为n s ,且41a ,22a ,3a 成等差数列。
