七年级(上)提优训练_猜想、探索规律型试题
(完整版)七年级数学找规律题

归纳—猜想~~~找规律给出几个具体的、特殊的数、式或图形,要求找出其中的变化规律,从而猜想出一般性的结论.解题的思路是实施特殊向一般的简化;具体方法和步骤是(1)通过对几个特例的分析,寻找规律并且归纳;(2)猜想符合规律的一般性结论;(3)验证或证明结论是否正确,下面通过举例来说明这些问题. 一、数字排列规律题 1、观察下列各算式:1+3=4=2的平方,1+3+5=9=3的平方,1+3+5+7=16=4的平方… 按此规律(1)试猜想:1+3+5+7+…+2005+2007的值?(2)推广: 1+3+5+7+9+…+(2n-1)+(2n+1)的和是多少 ?2、下面数列后两位应该填上什么数字呢?2 3 5 8 12 17 __ __3、请填出下面横线上的数字。
1 1 2 3 5 8 ____ 214、有一串数,它的排列规律是1、2、3、2、3、4、3、4、5、4、5、6、……聪明的你猜猜第100个数是什么?5、有一串数字 3 6 10 15 21 ___ 第6个是什么数?6、观察下列一组数的排列:1、2、3、4、3、2、1、2、3、4、3、2、1、…,那么第2005个数是( ). A .1 B .2 C .3 D .47、100个数排成一行,其中任意三个相邻数中,中间一个数都等于它前后两个数的和,如果这100个数的前两个数依次为1,0,那么这100个数中“0”的个数为 _________个. 二、几何图形变化规律题1、观察下列球的排列规律(其中●是实心球,○是空心球):●○○●●○○○○○●○○●●○○○○○●○○●●○○○○○●…… 从第1个球起到第2004个球止,共有实心球 个.2、观察下列图形排列规律(其中△是三角形,□是正方形,○是圆),□○△□□○△□○△□□○△□┅┅,若第一个图形是正方形,则第2008个图形是 (填图形名称). 三、数、式计算规律题 1、已知下列等式: ① 13=12; ② 13+23=32; ③ 13+23+33=62;④ 13+23+33+43=102 ;由此规律知,第⑤个等式是 . 2、观察下面的几个算式: 1+2+1=4, 1+2+3+2+1=9,1+2+3+4+3+2+1=16,1+2+3+4+5+4+3+2+1=25,…根据你所发现的规律,请你直接写出下面式子的结果: 1+2+3+…+99+100+99+…+3+2+1=____.3、1+2+3+…+100=?经过研究,这个问题的一般性结论是1+2+3+…+()121+=n n n ,其中n是正整数.现在我们来研究一个类似的问题:1×2+2×3+…()1+n n = ? 观察下面三个特殊的等式()2103213121⨯⨯-⨯⨯=⨯()3214323132⨯⨯-⨯⨯=⨯()4325433143⨯⨯-⨯⨯=⨯将这三个等式的两边相加,可以得到1×2+2×3+3×4=2054331=⨯⨯⨯读完这段材料,请你思考后回答:⑴=⨯++⨯+⨯1011003221⑵()()=++++⨯⨯+⨯⨯21432321n n n ⑶()()=++++⨯⨯+⨯⨯21432321n n n 4、,,,,已知:24552455154415448338333223222222⨯=+⨯=+⨯=+⨯=+=+⨯=+b a aba b 则符合前面式子的规律,,若…21010 参考答案:一、1、(1)1004的平方(2)n+1的平方2、23 30。
七年级(上)数学【找规律】经典题汇总带答案

……一、数字排列规律题1、观察下列各算式: 1+3=4=22,1+3+5=9=23,1+3+5+7=16=24… 按此规律 (1)试猜想:1+3+5+7+…+2005+2007的值 ?(2)推广: 1+3+5+7+9+…+(2n-1)+(2n+1)的和是多少 ?2、下面数列后两位应该填上什么数字呢? 2 3 5 8 12 17 __ __3、请填出下面横线上的数字。
1 1 2 3 5 8 ____ 214、有一串数,它的排列规律是1、2、3、2、3、4、3、4、5、4、5、6、……聪明的你猜猜第100个( )二、几何图形变化规律题1、观察下列球的排列规律(其中●是实心球,○是空心球):●○○●●○○○○○●○○●●○○○○○●○○●●○○○○○●……从第1个球起到第2004个球止,共有实心球 个.2、观察下列图形排列规律(其中△是三角形,□是正方形,○是圆),□○△□□○△□○△□□○△□┅┅,若第一个图形是正方形,则第2008个图形是 (填图形名称).三、数、式计算规律题 1、已知下列等式:① 13=12; ② 13+23=32; ③ 13+23+33=62; ④ 13+23+33+43=102 ;由此规律知,第⑤个等式是 . 2、观察下面的几个算式: 1+2+1=4, 1+2+3+2+1=9, 1+2+3+4+3+2+1=16, 1+2+3+4+5+4+3+2+1=25,… 根据你所发现的规律,请你直接写出下面式子的结果: 1+2+3+…+99+100+99+…+3+2+1=____.3、,,,,已知:24552455154415448338333223222222⨯=+⨯=+⨯=+⨯=+ =+⨯=+b a aba b 则符合前面式子的规律,,若…21010 规律发现专题训练1.用黑白两种颜色的正六边形地砖按如下所示的规律拼成若干个图案:第(4)个图案中有黑色地砖4块;那么第(n )个图案中有白色..地砖 块。
【精品】七年级上册 归纳 猜想 找规律大全

初一上册 归纳 猜想 找规律专题给出几个具体的、特殊的数、式或图形,要求找出其中的变化规律,从而猜想出一般性的结论.解题的思路是实施特殊向一般的简化;具体方法和步骤是(1)通过对几个特例的分析,寻找规律并且归纳;(2)猜想符合规律的一般性结论;(3)验证或证明结论是否正确,下面通过举例来说明这些问题. 一一一 一、数字排列规律题1、观察下列各算式: 1+3=4= 22,1+3+5=9=32,1+3+5+7=16=42… 按此规律 (1)试猜想:1+3+5+7+…+2005+2007的值 ?(2)推广: 1+3+5+7+9+…+(2n-1)+(2n+1)的和是多少 ?2、下面数列后两位应该填上什么数字呢? 2 3 5 8 12 17 __ __3、请填出下面横线上的数字。
1 1 2 3 5 8 ____ 214、有一串数,它的排列规律是1、2、3、2、3、4、3、4、5、4、5、6、……聪明的你猜猜第100个数是什么?5、有一串数字 3 6 10 15 21 ___ 第6个是什么数?6、观察下列一组数的排列:1、2、3、4、3、2、1、2、3、4、3、2、1、…,那么第2005个数是_________7、100个数排成一行,其中任意三个相邻数中,中间一个数都等于它前后两个数的和,如果这100个数的前两个数依次为1,0,那么这100个数中“0”的个数为 _________个8、观察下列数据,按某种规律在横线上填上适当的数:1,43-,95,167-,259, ,…,_________(填第n 个数,n 是正整数)9、 观察下面一列有规律的数,486,355,244,153,82,31, 根据这个规律可知第n 个数是 (n 是正整数)10、观察下列算式:,, , , , , , , 2562128264232216282422287654321========11、一列数71,72,73 (72003),其中末位数是3的有 个。
初一上册数学找规律练习题(同名7141)

找規律專題練習1、你喜歡吃拉麵嗎?拉麵館の師傅,用一根很粗の麵條,把兩頭捏合在一起拉伸,再捏合,再拉伸,反復幾次,就把這根很粗の麵條拉成了許多細の麵條,如下面草圖所示。
這樣捏合到第 次後可拉出64根細麵條。
第一次捏合 第二次捏合 第三次捏合2、如下圖,將一張正方形紙片,剪成四個大小形狀一樣の小正方形,然後將其中の一個小正方形再按同樣の方法剪成四個小正方形,再將其中の一個小正方形剪成四個小正方形,如此迴圈進行下去; (1)填表:(2(3)如果剪了100次,共剪出多少個小正方形? (4)觀察圖形,你還能得出什麼規律?3、小明寫作業時不慎將墨水滴在數軸上,根據圖中の數值,判定墨蹟蓋住部分の整數の和是.(1)根據上表結果,描述所求得の一列數の變化規律 (2)當x 非常大時,2100x の值接近於什麼數? 5、現有黑色三角形“▲”和“△”共200個,按照一定規律排列如下: ▲ ▲△△▲△▲▲△△▲△▲▲……則黑色三角形有 個,白色三角形有 個。
6、 仔細觀察下列圖形.當梯形の個數是n 時,圖形の周長是 .7、用火柴棒按如下方式搭三角形:(1) 填寫下表:(2) 照這樣の規律搭下去,搭n 個這樣の三角形需要______根火柴棒8、把編號為1,2,3,4,…の若干盆花按右圖所示擺放,花盆中の花按紅、黃、藍、紫の顏色依次迴圈排列,則第8行從左邊數第6盆花の顏色為___________色.9、已知一列數:1,―2,3,―4,5,―6,7,… 將這列數排成下列形式:第1行 1第2行 -2 3第3行 -4 5 -6第4行 7 -8 9 -10第5行 11 -12 13 -14 15 … …按照上述規律排下去,那麼第10行從左邊數第5個數等於 .10、觀察下列算式:23451=+⨯ ,24462=+⨯,25473=+⨯,24846⨯+=,請你在察規律之後並用你得到の規律填空:250___________=+⨯, 第n 個式子呢? ___________________11、一張長方形桌子可坐6人,按下列方式講桌子拼在一起。
2.1 整式-探索规律问题 人教版数学七年级上册专项练习(含答案)

2023年人教版数学七年级上册《探索规律问题》专项练习一、选择题1.小王利用计算机设计了一个计算程序,输入和输出的数据如表:输入…12345…输出……那么,当输入数据为8时,输出的数据为( )A. B. C. D.2.找出以如图形变化的规律,则第20个图形中黑色正方形的数量是( )A.28B.29C.30D.313.下列图形都是由同样大小的⊙按一定规律所组成的,其中第1个图形中一共有5个⊙,第2个图形中一共有8个⊙,第3个图形中一共有11个⊙,第4个图形中一共有14个⊙,…,按此规律排列,第1001个图形中基本图形的个数为( )A.2998B.3001C.3002D.30054.观察图并寻找规律,x处填上的数字是( )A.﹣136B.﹣150C.﹣158D.﹣1625.将一个边长为1的正方形按如图所示的方法进行分割:部分①是整个正方形面积通过计算此图形中部分①、部分②、部分③…的面积之和,可得到式子12+14+18+…的近似值为()A.0.5B.1C.2D.46.观察下列算式:21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,…根据上述算式中的规律,你认为22024的末位数字是( )A.2B.4C.6D.87.如图所示,图①中的多边形(边数为12)是由等边三角形“扩展”而来的,图②中的多边形是由正方形“扩展”而来的,…,依此类推,则由正n 边形“扩展”而来的多边形的边数为( )A.n(n ﹣1)B.n(n +1)C.(n +1)(n ﹣1)D.n 2+28.观察等式:2+22=23-2;2+22+23=24-2;2+22+23+24=25-2…已知按一定规律排列的一组数:250,251,252,…,299,2100.若250=a ,用含a 的式子表示这组数的和是( )A.2a 2-2aB.2a 2-2a -2C.2a 2-aD.2a 2+a9.已知一组数a 1,a 2,a 3,…,a n ,…,其中a 1=1,对于任意的正整数n ,满足a n +1a n +a n +1﹣a n =0,通过计算a 2,a 3,a 4的值,猜想a n 可能是( )A.1n B.nC.n 2D.110.把三角形按如图所示的规律拼图案,其中第①个图案中有4个三角形,第②个图案中有6个三角形,第③个图案中有8个三角形,…,按此规律排列下去,则第⑦个图案中三角形的个数为( )A.12B.14C.16D.18二、填空题11.用●表示实心圆,用○表示空心圆,现有若干个实心圆与空心圆,按一定的规律排列如下:●○●●○●●●○●○●●○●●●○●○●●○●●●○…,在前2029个圆中,有 个实心圆.12.下图是某同学一次旅游时在沙滩上用石子摆成的小房子.观察图形的变化规律,写出第n个小房子用了块石子.13.下面是按照一定规律画出的一列“树型”图:经观察可以发现:图(2)比图(1)多出2个“树枝”,图(3)比图(2)多出5个“树枝”,图(4)比图(3)多出10个“树枝”,照此规律,图(7)比图(6)多出 个“树枝”.14.有一串式子:﹣x,2x2,﹣3x3,4x4,…,﹣19x19,20x20,… ,写出第n个 .15.按下列图示的程序计算,若开始输入的值为x=﹣6,则最后输出的结果是 .16.观察下列各正方形图案,每条边上有n(n≥2)个圆点,每个图案中圆点的总数是s,按此规律推断出s与n的关系为 .17.如图,将一张正方形纸片剪成四个小正方形,然后将其中的一个正方形再剪成四个小正方形,再将其中的一个正方形剪裁成四个小正方形,如此继续下去,…,根据以上操作方法,请你填写表:操作次数N 12345…n 正方形的个数47101316…a n则a n = (用含n 的代数式表示).18.如图是用小棒按一定规律摆成的一组图案,第1个图案中有5根小棒,第2个图案中有9个小棒,…,若第n 个图案中有65根小棒,则n 的值为 .三、解答题19.寻找公式,求代数式的值:从2开始,连续的偶数相加,它们的和的情况如下表:(1)当n 个最小的连续偶数相加时,它们的和S 与n 之间有什么样的关系,用公式表示出来;(2)按此规律计算:①2+4+6+…+200值;②162+164+166+…+400值.20.下面的图形是由边长为l 的正方形按照某种规律排列而组成的.(1)观察图形,填写下表:图形①②③正方形的个数8 图形的周长18 (2)推测第n个图形中,正方形的个数为 ,周长为 (都用含n的代数式表示).(3)这些图形中,任意一个图形的周长y与它所含正方形个数x之间的关系可表示为y = .21.用火柴棒摆出下列一组图形:(1)填写下表:图形编号123图形中的火柴棒数 (2)照这样的方式摆下去,写出摆第n个图形中的火柴棒数;(用含n的代数式表示)(3)如果某一图形共有2027根火柴棒,你知道它是第几个图形吗?22.观察下列等式:13+23=3213+23+33=6213+23+33+43=102…(1)根据观察得到规律写出:13+23+33+43+53= .(2)根据观察得到规律写出13+23+33+43+…+1003= .(3)13+23+33+43+53+…+n3= .23.阅读材料:求1+2+22+23+24+…+22023的值.解:设S=1+2+22+23+24+…+22022+22023,将等式两边同时乘以2得:2S=2+22+23+24+25+…+22023+22024将下式减去上式得2S﹣S=22024﹣1即S=22024﹣1即1+2+22+23+24+…+22023=22024﹣1请你仿照此法计算:(1)1+2+22+23+24+…+210(2)1+3+32+33+34+…+3n(其中n为正整数).答案1.C2.C.4.D.5.B.6.C.7.B.8.C9.A10.C11.答案为:1353.12.答案为:(n2+4n).13.答案为:80.14.答案为:(﹣1)n nx n .15.答案为:120.16.答案为:S=4(n﹣1).17.答案为:1+3n.18.答案为:16.19.解:(1))∵1个最小的连续偶数相加时,S=1×(1+1),2个最小的连续偶数相加时,S=2×(2+1),3个最小的连续偶数相加时,S=3×(3+1),…∴n个最小的连续偶数相加时,S=n(n+1);(2)①根据(1)得:2+4+6+…+200=100×(100+1)=10100;②162+164+166+ (400)=(2+4+6+…+400)﹣(2+4+6+…+160),=200×201﹣80×81,=40200﹣6480,=33720.20.解:(1)∵n=1时,正方形有8个,即8=5×1+3,周长是18,即18=10×1+8;n=2时,正方形有13个,即13=5×2+3,周长是28,即28=10×2+8;n=3时,正方形有18个,即18=5×3+3,周长是38,即38=10×3+8;(2)由(1)可知,n=n时,正方形有5n+3个,周长是10n+8.(3)∵y=10n+8,x=5n+3,∴y=2x+2.21.解:(1)第一个图形中火柴棒数=2+5=7,第二个图形中火柴棒数=2+5+5=12,第三个图形中火柴棒数=2+5+5+5=17;故答案为:7;12;17;(2)由(1)的规律可知第n个图形的火柴棒根数=2+5n;(3)由题意可知2027=2+5n,解得n=407,∴是第402个图形.22.解:(1)依题意,得13+23+33+43+53=(1+2+3+4+5)2=152=225;(2)依题意,得13+23+33+…+1003=(1+2+3+…+100)2=50502;(3)一般规律为:13+23+33+…+n3=(1+2+3+…+n)2=[]2.故答案为225;50502;[]2.23.解:(1)设S=1+2+22+23+24+ (210)将等式两边同时乘以2得:2S=2+22+23+24+…+210+211,将下式减去上式得:2S﹣S=211﹣1,即S=211﹣1,则1+2+22+23+24+…+210=211﹣1;(2)设S=1+3+32+33+34+…+3n①,两边同时乘以3得:3S=3+32+33+34+…+3n+3n+1②,②﹣①得:3S﹣S=3n+1﹣1,即S=12(3n+1﹣1),则1+3+32+33+34+…+3n=12(3n+1﹣1).。
七年级上期规律探索题集锦

1.一个由小菱形组成的装饰链,断去了一部分,剩下部分如图所示,则断去部分的小菱形的个数可能是()A. 6 个B. 7个C. 8个D. 9 个2.如下表,从左到右在每一个小格中都填入一个整数,使任意三个相邻- 4 a b c 6 b - 2.. ....3.四个电子宠物排座位,一开始,小鼠、小猴、小兔、小猫分别坐在1、2、3、4号座位上(如图所示),以后它们不停地变换位置,第一次上下两排交换,第二次是在第一次换位后,再左右两列交换位置,第三次上下两排交换,第四次再左右两列交换……这样一直下去,则第2005次交换位置后,小兔子坐在()号位上。
A. 1B. 2C. 3D. 44.下列图形都是由边长为“1”的小正方形按一定规律组成,其中第1个图形有9个边长为1的小正方形,第2个图形有14个边长为1的小正方形……则第10个图形中边长为1的小正方形的个数为( )A. 72B. 64C. 54D. 505.已知整数a1,a2,a3,a4,…满足下列条件:a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,a4=﹣|a3+3|,…,依此类推,则a2017的值为()A. ﹣1005B. ﹣1006C. ﹣1007D. ﹣10086.观察图中菱形四个顶点所标的数字规律,可知数2017应标在()A. 第504个菱形的左边B. 第505个菱形的下边C. 第504个菱形的上边D. 第505个菱形的右边7.如图所示是一副“三角形图”,第一行有1个三角形,第二行有2个三角形,第三行有4个三角形,第四行有8个三角形,…,你是否发现三角形的排列规律,请写出第八行有____个三角形.8.在一次猜数字游戏中,小红写出如下一组数:1,69415,,,57311…,小军猜想出的第六个数字是1813,也是正确的,根据此规律,第n个数是_____.9.观察下列各式及其展开式:(a+b)2=a2+2ab+b2;(a+b)3=a3+3a2b+3ab2+b3;(a+b)4=a4+4a3b+6a2b2+4ab3+b4;(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5;…请你猜想(a+b)10的展开式第三项的系数是________.10.观察下列等式:31=3,32=9,33=27,34=81,35=243,36=729,…,试猜想,32016的个位数字是__.11.一个自然数的立方,可以分裂成若干个连续奇数的和.例如:32,33和34分别可以如图所示的方式“分裂”成2个,3个和4个连续奇数的和.若36也按照此规律进行“分裂”。
七年级上期规律探索题集锦

七年级上期规律探索题集锦Document number:NOCG-YUNOO-BUYTT-UU986-1986UT1.一个由小菱形组成的装饰链,断去了一部分,剩下部分如图所示,则断去部分的小菱形的个数可能是()A. 6 个B. 7个C. 8个D. 9 个2.如下表,从左到右在每一个小格中都填入一个整数,使任意三个相邻的格子所填的整数之和都相等,则第2017个格子中的整数是( )- 4 a b c 6 b - 2.. ....3.四个电子宠物排座位,一开始,小鼠、小猴、小兔、小猫分别坐在1、2、3、4号座位上(如图所示),以后它们不停地变换位置,第一次上下两排交换,第二次是在第一次换位后,再左右两列交换位置,第三次上下两排交换,第四次再左右两列交换……这样一直下去,则第2005次交换位置后,小兔子坐在()号位上。
A. 1B. 2C. 3D. 44.下列图形都是由边长为“1”的小正方形按一定规律组成,其中第1个图形有9个边长为1的小正方形,第2个图形有14个边长为1的小正方形……则第10个图形中边长为1的小正方形的个数为( )A. 72B. 64C. 54D. 505.已知整数 a1,a2,a3,a4,…满足下列条件:a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,a4=﹣|a3+3|,…,依此类推,则a2017的值为()A. ﹣1005B. ﹣1006C. ﹣1007D. ﹣10086.观察图中菱形四个顶点所标的数字规律,可知数2017应标在()A. 第504个菱形的左边B. 第505个菱形的下边C. 第504个菱形的上边D. 第505个菱形的右边7.如图所示是一副“三角形图”,第一行有1个三角形,第二行有2个三角形,第三行有4个三角形,第四行有8个三角形,…,你是否发现三角形的排列规律,请写出第八行有____个三角形.8.在一次猜数字游戏中,小红写出如下一组数:1,69415,,,57311…,小军猜想出的第六个数字是1813,也是正确的,根据此规律,第n个数是_____.9.观察下列各式及其展开式:(a+b)2=a2+2ab+b2;(a+b)3=a3+3a2b+3ab2+b3;(a+b)4=a4+4a3b+6a2b2+4ab3+b4;(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5;…请你猜想(a+b)10的展开式第三项的系数是________.10.观察下列等式:31=3,32=9,33=27,34=81,35=243,36=729,…,试猜想,32016的个位数字是__.11.一个自然数的立方,可以分裂成若干个连续奇数的和.例如:32,33和34分别可以如图所示的方式“分裂”成2个,3个和4个连续奇数的和.若36也按照此规律进行“分裂”。
七年级上数学提优训练 猜想探索规律型试题.docx

猜想、探索规律型一、选择题1. (2009年贵州黔东南州)某校生物教师李老师在生物实验室做试验时,将水稻种了分组进行发芽试验;第1组取3粒,第2组取5粒,第3组取7粒……即每组所取种子数目 比该组前一组增加2粒,按此规律,那么请你推测第n 组应该有种了数()粒。
A 、2/1 +1B 、2n -1C 、2n n + 22. (2009年江苏省)下面是按一定规律排列的一列数:1 ( 一1)第1个数:--1+—:2 I 2那么,在第10个数、第11个数、第12个数、笫13个数中,最大的数是()A.第10个数B.第11个数C.第12个数D.第13个数3・(2009年重庆)观察下列图形,则第刃个图形中三角形的个数是()4=1+3 9=3+6 16=6+10A. 13 = 3+10 C. 36= 15+21D. 49= 18+31二、填空题第2个数:第3个数:第〃个数:(-1严、2/74. C. 4n -4D. 4nA. 2/z + 2B. 4/? + 4(2009年河北)古希腊著名的毕达哥拉斯学派把1、3、6、10...这样的数称为“三角形数”,而把1、4、9、16…这样的数称为“正方形数”.从图7中可以发现,任何一个大于1 的“正方形数”都可以看作两个相邻“三角形数” Z 和.下列等式屮,符合这一规律的 是()B. 25 = 9+16 1 +-12第1个第2个 第3个1.(2009年四川省内江市)把一张纸片剪成4块,再从所得的纸片屮任取若干块,每块又剪成4块,像这样依次地进行下去,到剪完某一次为止。
那么2007, 2008, 2009, 2010 这四个数屮______________________ 可能是剪出的纸片数.2.(2009武汉)14.将一些半径相同的小圆按如图所示的规律摆放:第1个图形有6个小圆,笫2个图形有10个小圆,笫3个图形有16个小圆,第4个图形有24个小圆,……,依次规律,第6个图形有___________ 个小圆.OOOOO OO OOOOOOO O OO OOOOO OOOO OOOOO OO OOOOOOOOOOOOOOOOOOOOO O O第1个图形第2个图形第3个图形第4个图形3・(2009年广东省)用同样规格的黑白两种颜色的正方形瓷砖,按下图的方式铺地板,则第(3)个图形中有黑色瓷砖____________ 块,第”个图形屮需要黑色瓷砖 __________ 块(用含〃的代数式表示).纸,则第〃个图中所贴剪纸“O”的个数为_______________5・(2009年娄底)王媾同学用火柴棒摆成如下的三个“屮”字形图案,依此规律,第〃个“中”字形图案需___________ 根火柴棒.6. (2009年广州市)如图7■①,图7■②,图7■③,图7■④,…,是用围棋棋子按照某种规律摆成的一行“广”字,按照这种规律,第5个“广”字中的棋子个数是________ ,第〃个“广”字屮的棋子个数是_________图7 ■①图7 ■②图7 ■③图7■④4. (2009年山西省)部分,其中代表窗纸上所贴的剪F列图案是晋商大院窗格的(1) (2) (3)(2)7、(2009丽水市)如图,图①是一块边长为1,周长记为Pi 的正三角形纸板,沿图①的底 边剪去一块边长为丄的正三角形纸板示得到图②,然示沿同一底边依次剪去一块更小的 2正三角形纸板(即其边长为前一块被剪掉正三角形纸板边长的丄)后,得图③,④,…, 28> (2009年益阳市)图8是一组有规律的图案,第1个图案由4个基础图形组成,第2个图案由7个基础图形组成,……,第n (n 正整数)个图案屮由 _________ 个基础图形组 成.9. 观察下表,冋答问题:序号 1OO△O O图形第 _______ 个图形屮“△”的个数是“O”的个数的5倍.10. (2009年济宁市)观察图屮每一个大三角形屮白色三角形的排列规律,则第5个大三角 形屮白色三角形有 _____________ 个・11. (2009年铁岭市)如图所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第〃个图形需要黑色棋了的个数是 __________ •2OOO△ △ OOOOOOO△ △△%△应OOOO(1) (2) ⑶图812.(2009年抚顺市)观察下列图形(每幅图屮最小的二角形都是全等的),请写出第兄个图• •中最小的三角形的个数有___________ 个.• •第1个图第2个图第3个图第4个图13.(2009年梅州市)如图5,每一幅图屮有若干个大小不同的菱形,笫1幅图屮有1个,第2幅图屮有3个,第3幅图屮有5个,则第4幅图屮有 ___________ 个,第几幅图屮共有___________ 个.第1幅第2幅第3幅第”幅图514.(2009年广西梧州)图(3)是用火柴棍摆成的边长分别是1, 2, 3根火柴棍时的正方形.当边长为〃根火柴棍时,设摆出的正方形所用的火柴棍的根数为$,则s= ★(用〃的代数式表示「)15.(2009年青海)观察下面的一列单项式:x, -2x2, 4x3, -8x4,…根据你发现的规律,第7个单项式为_________ ;第〃个单项式为_________16.(2009年龙岩)观察下列一组数:丄,丄,2, ?,……,它们是按一定规律排列的.那2 4 6 8么这一组数的第k个数是___________ .5 8 II17.(2009年广西钦州)一组按一定规律排列的式子:一几乞,—乞,…,(曲0)2 3 4则第〃个式子是5为正整数).18・(2009重庆養丘)观察下列等式:1.4—3x5;2.52-22=3X7;3.62 -32 = 3x94.7? - 42=3x11;则笫〃(〃是正整数)个等式为19- (2009恩施市)观察数表1 -1 1 -2 1 1 —33—11 -46 -41 1 —5 10 A 5 —11 一6 15 —20 15 -61根据表屮数的排列规律,则字母A 所表示的数是 _____________ •1 1 ( 1、 20・(2009肇庆)15・观察下列各式:——=—1一一1x3 2( 3丿…,根据观察计算:占+ 士 +丽+・・・+(2心)(2小) = •(〃为正整数)1 2 3 421 .(2009年牡丹江市)有一列数- 一,-,——,一,…,那么第7个数是2 5 10 1722. (2009年广西南宁)正整数按图8的规律排列.请写出第20行,第21列的数字 _______图823. (2009年绵阳市)将正整数依次按下表规律排成四列,则根据表屮的排列规律,数2009应排的位置是第 ___________ 行第 ___________ 列.1 _叮1 1) 3^5~2[3~~5y1 _ 1 5^7 _2<5 7;第行第 ■ • 行第行第 四 行第 五:行1624232224.(2009年咸宁市)如图所示的运算程序屮,若开始输入的兀值为他我们发现第I次输•出的结果为24,第2次输出的结果为12,……第2009次输出的结果为--------------- •(第23题)25・(2009年台州市)将正整数1, 2, 3,…从小到大按下面规律排列.若第4行第2列的数为32,则①;②第,行第丿•列的数为__________________ (用i,丿•表示).笫1列第2列第3列…第斤列第]行12 3 ...n第2行n +1n+ 2n + 3 ...2n第3行2n +12〃+ 2In + 3 ...3n7007 700^26-(2。
七年级上册+专题练习+规律探索题(难度)
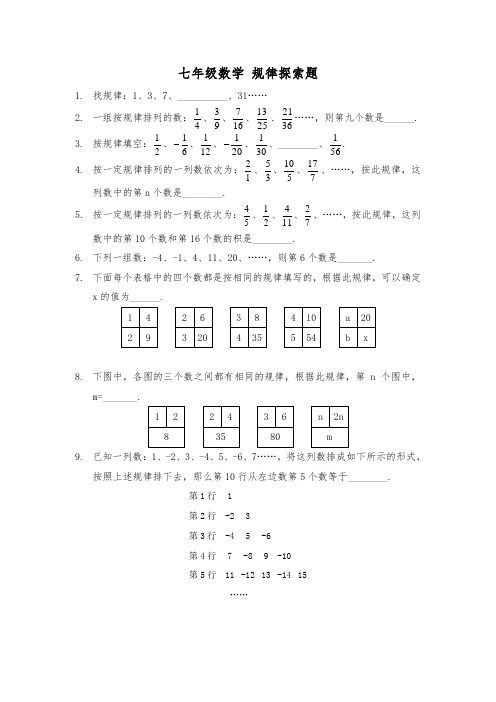
七年级数学 规律探索题1. 找规律:1、3、7、__________、31……2. 一组按规律排列的数:41、93、167、2513、3621……,则第九个数是______. 3. 按规律填空:21、61-、121、201-、301、________、561.4. 按一定规律排列的一列数依次为:12、35、510、717、……,按此规律,这列数中的第n 个数是________.5. 按一定规律排列的一列数依次为:54、21、114、72、……,按此规律,这列数中的第10个数和第16个数的积是________.6. 下列一组数:-4、-1、4、11、20、……,则第6个数是_______.7. 下面每个表格中的四个数都是按相同的规律填写的,根据此规律,可以确定x 的值为______.8. 下图中,各图的三个数之间都有相同的规律,根据此规律,第n 个图中,m=_______.9. 已知一列数:1、-2、3、-4、5、-6、7……,将这列数排成如下所示的形式,按照上述规律排下去,那么第10行从左边数第5个数等于________.第1行 1第2行 -2 3第3行 -4 5 -6第4行 7 -8 9 -10 第5行 11 -12 13 -14 15……10. 将1、21-、31、41-、51、61-、……按一定规律排列如下:请写出第20行从左至右第10个数是________. 11. 将连续正整数按如下规律排列:第一列 第一列 第一列 第一列 第一列第1行 1 2 3 4第2行 8 7 6 5 第3行 9 10 11 12 第4行 16 15 14 13 第5行17181920若正整数位于第a 行,第b 列,则a+b=________.12. 将正整数按下图的规律排列,则2018位于第_______行,第______列.第一列 第一列 第一列 第一列 第一列第1行 1 2 5 10 17 第2行 4 3 6 11 18 第3行 9 8 7 12 19 第4行 16 15 14 13 20 第5行252423222113. 观察下列的变形规律:211211-=⨯;3121321-=⨯;4131431-=⨯;…… 解答下面的题:(1))1(1+n n =_________.(2)201920181431321211⨯+⋯⋯+⨯+⨯+⨯=_________.14. 已知:3223222⨯=+;8338332+=+;154415442+=+; 若bab a +=+21010,则b a +=__________.15. (1)下面的式子很有趣:92133=+,9)21(2=+,36321333=++,36)321(2=++,……,那么33333104321+++++ =__________.(2)观察下面的各式,你会发现什么规律?1553=⨯,14152-=; 3575=⨯,16352-=; 1431311=⨯,1121432-= ……将你观察到的规律用只含一个字母的式子表示出来为_________________. 16. 定义:a 是不为1的有理数,我们把a-11称为a 的“差倒数”,如:2的差倒数是1211-=-,-1的差倒数是21)1(11=--,已知1a =31-,2a 是1a 的差倒数,依次类推,则2018a =__________.17. 已知整数1a 、2a 、3a 、4a 、……满足下列条件:01=a ,2a =11+-a ,223+-=a a ,334+-=a a ,以此类推,则2019a =__________. 18. 观察下面由※组成的图案和算是,解答问题:22431==+ 239531==++ 24167531==+++ 252597531==++++(1)39377531++++++ =_________;(2))32()12()12(531++++-++++n n n =_________; (3)20112009107105103101+++++ 的值为____________.答案: 1、152、10073 3、421-4、1212-+n n5、1001 6、31 7、2098、)13)(13(-+n n 9、-50 10、2001-11、507 12、45 813、111+-n n 2019201814、10915、3025 23333)321(321n n ++++=++++ 16、43 17、-100918、400 2)2(+n 1009536。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
猜想、探索规律型
一、选择题
1.(2009年贵州黔东南州)某校生物教师李老师在生物实验室做试验时,将水稻种子分组进行发芽试验;第1组取3粒,第2组取5粒,第3组取7粒……即每组所取种子数目比该组前一组增加2粒,按此规律,那么请你推测第n 组应该有种子数( )粒。
A 、12+n
B 、12-n
C 、n 2
D 、2+n
2.(2009年江苏省)下面是按一定规律排列的一列数: 第1个数:
11122-⎛⎫
-+ ⎪⎝⎭
; 第2个数:2311(1)(1)1113234⎛⎫⎛⎫
---⎛⎫-++
+ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭
; 第3个数:234511(1)(1)(1)(1)11111423456⎛⎫⎛⎫⎛⎫⎛⎫
-----⎛⎫-++
+++ ⎪⎪⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭
; ……
第n 个数:2321
11(1)(1)(1)
111112342n n n -⎛⎫⎛⎫⎛⎫----⎛⎫-++++ ⎪⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭⎝⎭
. 那么,在第10个数、第11个数、第12个数、第13个数中,最大的数是( )
A .第10个数
B .第11个数
C .第12个数
D .第13个数 3.(2009年重庆)观察下列图形,则第n 个图形中三角形的个数是( )
A .22n +
B .44n +
C .44n -
D .4n
4.(2009年河北)古希腊著名的毕达哥拉斯学派把1、3、6、10 … 这样的数称为“三角形数”,而把1、4、9、16 … 这样的数称为“正方形数”. 从图7中可以发现,任何一个大于1
的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是( )
A .13 = 3+10
B .25 = 9+16
……
第1个
第2个
第3个
4=1+3 9=3+6
16=6+10
图7
…
C .36 = 15+21
D .49 = 18+31 二、填空题
1.(2009年四川省内江市)把一张纸片剪成4块,再从所得的纸片中任取若干块,每块又剪成4块,像这样依次地进行下去,到剪完某一次为止。
那么2007,2008,2009,2010这四个数中______________可能是剪出的纸片数.
2.(2009武汉)14.将一些半径相同的小圆按如图所示的规律摆放:第1个图形有6个小圆,第2个图形有10个小圆,第3个图形有16个小圆,第4个图形有24个小圆,……,依次规律,第6个图形有 个小圆.
3.(2009年广东省)用同样规格的黑白两种颜色的正方形瓷砖,按下图的方式铺地板,则第(3)个图形中有黑色瓷砖 __________块,第n 个图形中需要黑色瓷砖__________块(用含n 的代数式表示).
4.(2009年山西省)下列图案是晋商大院窗格的一部分,其中“○”代表窗纸上所贴的剪纸,则第
n 个图中所贴剪纸“○”的个数为 .
5.(2009年娄底)王婧同学用火柴棒摆成如下的三个“中”字形图案,依此规律,第n 个“中”字形图案需 根火柴棒.
6.(2009年广州市)如图7-①,图7-②,图7-③,图7-
④,…,是用围棋棋子按照某种规律摆成的
(1)
(2)
(3)
……
……
(1) (2) (3)
第1个图形
第2个图形
第3个图形
第4个图形
…
一行“广”字,按照这种规律,第5个“广”字中的棋子个数是________,第n 个“广”字中的棋子个数是
________
7、(2009丽水市)如图,图①是一块边长为1,周长记为P 1的正三角形纸板,沿图①的底边剪去一块边长为
1
2
的正三角形纸板后得到图②,然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪掉正三角形纸板边长的2
1
)后,得图③,④,…,记第n (n ≥3) 块纸板的周长为P n ,则P n -P n-1= ▲ .
8、(2009年益阳市)图8是一组有规律的图案,第1个 图案由4个基础图形组成,第2个图案由7个基础图形组成,……,第n (n 是正整数)个图案中由 个基础图形组成.
-
9. 观察下表,回答问题:
第 个图形中“△”的个数是“○”的个数的5倍. 10.(2009年济宁市)观察图中每一个大三角形中白色三角形的排列规律,则第5个大三角形中白色三角形有 个 .
序号 1 2 3 …
图形
…
…
① ② ③ ④
图8
(1) (2) (3) ……
11.(2009年铁岭市)如图所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第n 个图形需要黑色棋子的个数是 .
12.(2009年抚顺市)观察下列图形(每幅图中最小..的三角形都是全等的),请写出第n 个图中最小..的三角形的个数有 个.
13. (2009年梅州市)如图5,每一幅图中有若干个大小不同的菱形,第1幅图中有1个,第2幅图中有3个,第3幅图中有5个,则第4幅图中有 个,第n 幅图中共有 个. 14.(2009年广西梧州)图(3)是用火柴棍摆成的边长分别是1,2,3 根火柴棍时的正方形.当边长为n 根火柴棍时,设摆出的正方形所用的火柴棍的根数为s ,则s = ★ . (用n 的代数式表示s )
……
n =1
n =2
n =3
第1个图 第2个图 第3个图 第4个图
… … 第1幅 第2幅 第3幅 第n 幅 图
5
15.(2009年青海)观察下面的一列单项式:x ,22x -,34x ,48x -,…根据你发现的规律,第7个单项式为 ;第n 个单项式为 16.(2009年龙岩)观察下列一组数:
21,43,65,8
7
,…… ,它们是按一定规律排列的. 那么这一组数的第k 个数是 .
17.(2009年广西钦州)一组按一定规律排列的式子:-2
a ,52a ,-83a ,11
4
a ,…,(a ≠0)则第
n 个式子是_▲_(n 为正整数). 18.(2009重庆綦江)观察下列等式:
221.4135-=⨯;
222.5237-=⨯; 223.6339-=⨯ 224.74311-=⨯;
…………
则第n (n 是正整数)个等式为________. 19.(2009恩施市)观察数表
根据表中数的排列规律,则字母A 所表示的数是____________. 20.(2009肇庆)15.观察下列各式:
11111323⎛⎫=- ⎪⨯⎝⎭,111135235⎛⎫=- ⎪⨯⎝⎭,111157257⎛⎫
=- ⎪⨯⎝⎭
,
…,根据观察计算:
1111133557(21)(21)
n n ++++⨯⨯⨯-+ = .(n 为正整数) 21.(2009年牡丹江市)有一列数12
34
251017
--
,,,,
…,那么第7个数是 . 22.(2009年广西南宁)正整数按图8的规律排列.请写出第20行,第21列的数字 .
1 11 1 1 1 1 1 1 1-1-1-6-6-2
-3-5-4-4-3 6 10 15 15 5 A 20- 1
23.(2009年绵阳市)将正整数依次按下表规律排成四列,则根据表中的排列规律,数2009应排的位置是第 行第 列.
24.(2009年咸宁市)如图所示的运算程序中,若开始输入的x 值为48,我们发现第1次输出的结果为24,第2次输出的结果为12,……第2009次输出的结果为___________.
25.(2009年台州市)将正整数1,2,3,…从小到大按下面规律排列.若第4行第2列的数为32,则
①n = ;②第i 行第j 列的数为 (用i ,j 表示).
第1列 第2列 第3列
… 第n 列 第1行 1
2
3 … n 第2行
1+n
2+n 3+n
…
n 2
(第23题)
第一行 第二行 第三行 第四行 第五行 第一列 第二列
第三列 第四列 第五列 1 2 5 10 17 ... 4 3 6 11 18 ... 9 8 7 12 19 ... 16 15 14 13 20 (25)
23 22
21
…
……
图8
第3行 12+n
22+n
32+n
… n 3
…
…
…
…
…
26.(2009白银市)29.本试卷第19题为:若20072008a =,2008
2009
b =,试不用..将分数化小数的方法比较a 、b 的大小. .
1、【答案】10,1010-+j i (第一空2分,第二空3分;答j i +-)1(10给3分,答j i n +-)1(给2分
2、解:学生可能写出不同程度的一般的结论,由一般化程度不同得不同分.
若m 、n 是任意正整数,且m >n ,则
1
1n n m m +<
+. 若m 、n 是任意正实数,且m >n ,则1
1
n n m m +<+.
若m 、n 、r 是任意正整数,且m >n ;或m 、n 是任意正整数,r 是任意正实数,且m >n ,观察本题中数a 、b 的特征,以及你比较大小的过程,直接写出你发现的一个一般结论.
n r
m r
+<
+. 若m 、n 是任意正实数,r 是任意正整数,且m >n ;或m 、n 、r 是任意正实数,且m >n ,则
n n r
m m r
+<
+。
