灰色理论与预测
灰色理论关联度与预测,数学建模必备知识,很实用哦

X m {xm ( jm )} | jm 1, 2,..., nm} 比较序列
灰色关联分析3
设x0(k)为X0(为参考序列)的第k个数;xi(k) 为Xi(比较序列)的第k个数;
则比较序列Xi对参考序列X0的灰色关联度为:
(X0 ,
Xi )
1 n
n k 1
r(x0 (k),
度,根据经验,当ρ=0.5时,关联度大于0.6便 满意了。
回总目录 回本章目录
(3)后验差检验 a.计算原始序列标准差:
X 0 i X 0 2
S1
n 1
回总目录 回本章目录
b. 计算绝对误差序列的标准差:
0 i 0 2
S2
X 0 t ,
3
X 0 t ,...,
n
X 0 t
t1
t 1
t 1
t 1
目录
基本概念 灰色关联分析 灰色预测模型
灰色关联分析1
基本特征
建立的模型属于非函数形式的序列模型 计算方便易行 对样本数量多寡没有严格要求 不要求序列数据必须符合正态分布 不会产生与定性分析大相径庭的结论
n 1
c. 计算方差比:
C S2 S1
回总目录 回本章目录
d. 计算小误差概率:
P P 0i 0 0.6745S1
令: 则:
ei 0i 0 , S0 0.6745S1 P Pei S0
P >0.95 >0.80 >0.70 ≤0.70
灰色关联分析3
灰色关联度的数学模型
X 0 {x0 ( j0 )} | j0 1, 2,..., n0} X1 {x1( j1)} | j1 1, 2,..., n1} X 2 {x2 ( j2 )} | j2 1, 2,..., n2}
灰色系统理论在市场预测中的应用

灰色系统理论在市场预测中的应用绪论市场预测一直是商业决策的重要组成部分。
在过去,市场预测更多依靠主观经验、历史趋势和数据分析等方法。
但是随着大数据、人工智能和数学方法的发展,灰色系统理论开始在市场预测中得到应用。
灰色系统理论是20世纪80年代由我国学者建立的一种数学模型和分析方法,因其高效可靠性以及能够有效处理不规则数据而在市场预测、经济决策等领域得到广泛应用。
一、灰色系统理论的概念灰色系统理论是从一个灰色系统的角度出发,在统计学的基础上发现系统规律,揭示系统内部关系的一种理论。
与其他数学方法相比,灰色系统理论更加强调系统的分析与描述,以此更好地理解和解决现实问题。
灰色系统理论通常基于少量的数据样本建立灰色模型,然后利用该模型进行预测。
与其他模型不同的是,灰色系统理论不需要数据服从一定的分布,可以利用少量的样本数据进行分析。
二、灰色系统理论可以有效地应用于市场预测,尤其是预测不稳定、非线性、不规则的情况。
市场中存在许多因素导致的波动,灰色系统理论通过建立灰色模型,可以更好地把握市场的变化趋势,从而为商业决策提供可靠的依据。
在市场营销中,灰色系统理论在目标市场、销售策略和产品定价等方面得到了广泛应用。
一个关键性质是灰色系统理论在市场预测中对样本数据量的要求相对较低,而在实际应用中可以通过大量数据的自动化集成快速获得准确的预测结果,因此受到越来越多的关注和借鉴。
三、灰色系统理论的实践案例1. 物流配送中心的配送效率评估,基于灰色系统理论对仓储数据和大量的交通数据进行分析,确定最佳的时间和路线,大大提升了物流配送效率。
2. 汽车市场的销售预测,利用灰色模型对市场数据和销售趋势进行预测,为企业提供了更精准的决策依据。
3. 大型游戏的用户活跃度预测,通过对用户行为数据的灰色分析,得出用户活跃度的预测结果,并据此制定广告、营销策略。
四、灰色系统理论的优势和局限性灰色系统理论与其他数学方法相比,具有明显的优势:1. 数据要求相对较低:灰色系统理论适用于不规则、少量的数据样本。
灰色理论预测模型
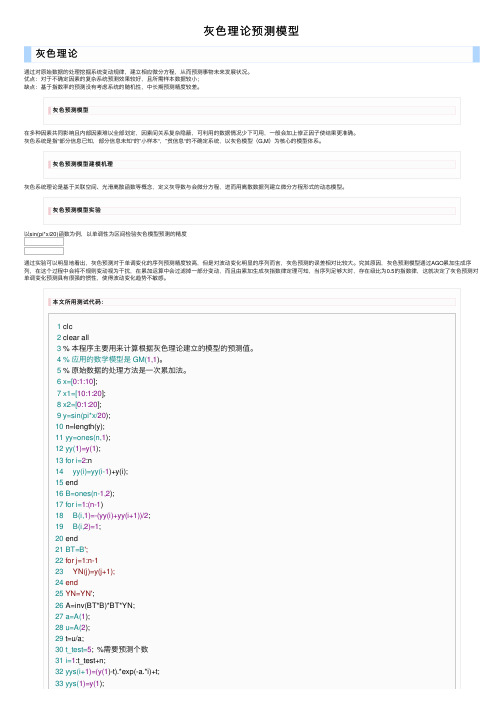
灰⾊理论预测模型灰⾊理论通过对原始数据的处理挖掘系统变动规律,建⽴相应微分⽅程,从⽽预测事物未来发展状况。
优点:对于不确定因素的复杂系统预测效果较好,且所需样本数据较⼩;缺点:基于指数率的预测没有考虑系统的随机性,中长期预测精度较差。
灰⾊预测模型在多种因素共同影响且内部因素难以全部划定,因素间关系复杂隐蔽,可利⽤的数据情况少下可⽤,⼀般会加上修正因⼦使结果更准确。
灰⾊系统是指“部分信息已知,部分信息未知“的”⼩样本“,”贫信息“的不确定系统,以灰⾊模型(G,M)为核⼼的模型体系。
灰⾊预测模型建模机理灰⾊系统理论是基于关联空间、光滑离散函数等概念,定义灰导数与会微分⽅程,进⽽⽤离散数据列建⽴微分⽅程形式的动态模型。
灰⾊预测模型实验以sin(pi*x/20)函数为例,以单调性为区间检验灰⾊模型预测的精度通过实验可以明显地看出,灰⾊预测对于单调变化的序列预测精度较⾼,但是对波动变化明显的序列⽽⾔,灰⾊预测的误差相对⽐较⼤。
究其原因,灰⾊预测模型通过AGO累加⽣成序列,在这个过程中会将不规则变动视为⼲扰,在累加运算中会过滤掉⼀部分变动,⽽且由累加⽣成灰指数律定理可知,当序列⾜够⼤时,存在级⽐为0.5的指数律,这就决定了灰⾊预测对单调变化预测具有很强的惯性,使得波动变化趋势不敏感。
本⽂所⽤测试代码:1 clc2 clear all3 % 本程序主要⽤来计算根据灰⾊理论建⽴的模型的预测值。
4 % 应⽤的数学模型是 GM(1,1)。
5 % 原始数据的处理⽅法是⼀次累加法。
6 x=[0:1:10];7 x1=[10:1:20];8 x2=[0:1:20];9 y=sin(pi*x/20);10 n=length(y);11 yy=ones(n,1);12 yy(1)=y(1);13 for i=2:n14 yy(i)=yy(i-1)+y(i);15 end16 B=ones(n-1,2);17 for i=1:(n-1)18 B(i,1)=-(yy(i)+yy(i+1))/2;19 B(i,2)=1;20 end21 BT=B';22 for j=1:n-123 YN(j)=y(j+1);24 end25 YN=YN';26 A=inv(BT*B)*BT*YN;27 a=A(1);28 u=A(2);29 t=u/a;30 t_test=5; %需要预测个数31 i=1:t_test+n;32 yys(i+1)=(y(1)-t).*exp(-a.*i)+t;33 yys(1)=y(1);34 for j=n+t_test:-1:235 ys(j)=yys(j)-yys(j-1);36 end37 x=1:n;38 xs=2:n+t_test;39 yn=ys(2:n+t_test);40 det=0;41 for i=2:n42 det=det+abs(yn(i)-y(i));43 end44 det=det/(n-1);4546 subplot(2,2,1),plot(x,y,'^r-',xs,yn,'b-o'),title('单调递增' ),legend('实测值','预测值');47 disp(['百分绝对误差为:',num2str(det),'%']);48 disp(['预测值为: ',num2str(ys(n+1:n+t_test))]);495051 %递减52 y1=sin(pi*x1/20);53 n1=length(y1);54 yy1=ones(n1,1);55 yy1(1)=y1(1);56 for i=2:n157 yy1(i)=yy1(i-1)+y1(i);58 end59 B1=ones(n1-1,2);60 for i=1:(n1-1)61 B1(i,1)=-(yy1(i)+yy1(i+1))/2;62 B1(i,2)=1;63 end64 BT1=B1';65 for j=1:n1-166 YN1(j)=y1(j+1);67 end68 YN1=YN1';69 A1=inv(BT1*B1)*BT1*YN1;70 a1=A1(1);71 u1=A1(2);72 t1=u1/a1;73 t_test1=5; %需要预测个数74 i=1:t_test1+n1;75 yys1(i+1)=(y1(1)-t1).*exp(-a1.*i)+t1;76 yys1(1)=y1(1);77 for j=n1+t_test1:-1:278 ys1(j)=yys1(j)-yys1(j-1);79 end80 x21=1:n1;81 xs1=2:n1+t_test1;82 yn1=ys1(2:n1+t_test1);83 det1=0;84 for i=2:n185 det1=det1+abs(yn1(i)-y1(i));86 end87 det1=det1/(n1-1);8889 subplot(2,2,2),plot(x1,y1,'^r-',xs1,yn1,'b-o'),title('单调递增' ),legend('实测值','预测值');90 disp(['百分绝对误差为:',num2str(det1),'%']);91 disp(['预测值为: ',num2str(ys1(n1+1:n1+t_test1))]);9293 %整个区间93 %整个区间94 y2=sin(pi*x2/20);95 n2=length(y2);96 yy2=ones(n2,1);97 yy2(1)=y2(1);98 for i=2:n299 yy2(i)=yy2(i-1)+y2(i);100 end101 B2=ones(n2-1,2);102 for i=1:(n2-1)103 B2(i,1)=-(yy2(i)+yy2(i+1))/2;104 B2(i,2)=1;105 end106 BT2=B2';107 for j=1:n2-1108 YN2(j)=y2(j+1);109 end110 YN2=YN2';111 A2=inv(BT2*B2)*BT2*YN2;112 a2=A2(1);113 u2=A2(2);114 t2=u2/a2;115 t_test2=5; %需要预测个数116 i=1:t_test2+n2;117 yys2(i+1)=(y2(1)-t2).*exp(-a2.*i)+t2;118 yys2(1)=y2(1);119 for j=n2+t_test2:-1:2120 ys2(j)=yys2(j)-yys2(j-1);121 end122 x22=1:n2;123 xs2=2:n2+t_test2;124 yn2=ys2(2:n2+t_test2);125 det2=0;126 for i=2:n2127 det2=det2+abs(yn2(i)-y2(i));128 end129 det2=det2/(n2-1);130131 subplot(2,1,2),plot(x2,y2,'^r-',xs2,yn2,'b-o'),title('全区间' ),legend('实测值','预测值'); 132 disp(['百分绝对误差为:',num2str(det2),'%']);133 disp(['预测值为: ',num2str(ys2(n2+1:n2+t_test2))]);。
常用预测模型

常用预测模型(一) 灰色预测模型1. 灰色系统理论灰色系统理论认为对既含有已知信息又含有未知或非确定信息的系统进行预测,就是对在一定方位内变化的、与时间有关的灰色过程的预测。
尽管过程中所显示的现象是随机的、杂乱无章的,但毕竟是有序的、有界的,因此这一数据集合具备潜在的规律,灰色预测就是利用这种规律建立灰色模型对灰色系统进行预测。
灰色预测通过鉴别系统因素之间发展趋势的相异程度,即进行关联分析,并对原始数据进行生成处理,来寻找系统变动的规律,生成有较强规律性的数据序列,然后建立相应的微分方程模型,从而预测事物未来发展趋势状况。
灰色预测法用等时距观测到的反映预测对象特征的一系列数量值构造灰色预测模型,预测未来某一时刻的特征量,或达到某一特征量的时间。
2.灰色预测理论模型数学形式在通过灰色理论建立预测模型时,常需要先进行累加或累减后计算数据列间的关联度,再建立最终的预测模型。
如原始数据列为: ()()()()()()()()(){}n X X X X X 00000,...3,2,1=;通过累加后变为: ()()()()()()()()(){}n X X X X X 11111,...3,2,1=;那么进行m 次累加后有:()()()()∑=−=ki m m i X k X 11关联度:是分析系统中各因素关联程度的方法,在计算关联度之前需先计算关联系数。
设:()()()()()()()(){}n X X X k X 0000ˆ,...,2ˆ,1ˆˆ=,()()()()()()()(){}n X X X k X 0000,...,2,1= ()()()()()()()()()()()()()()()()k X k X k X k X k X k X k X k X00000000ˆmax max ˆˆmax max ˆmin min −+−−+−ρρ 则关联系数定义为:式中:()()()()k X k X00ˆ−为第k 个点()0X 和()0ˆX 的绝对误差;()()()()k X k X 00ˆmin min −为两级最小差; ()()()()k X k X00ˆmax max −为两级最大差;ρ称为分辨率,0<ρ<1,一般取ρ=0.5;对单位不一,初值不同的序列,在计算相关系数前应首先进行初始化,即将该序列所有数据分别除以第一个数据。
灰色预测理论-定义

什么是灰色预测法?灰色预测是就灰色系统所做的预测。
所谓灰色系统是介于白色系统和黑箱系统之间的过渡系统,其具体的含义是:如果某一系统的全部信息已知为白色系统,全部信息未知为黑箱系统,部分信息已知,部分信息未知,那么这一系统就是灰色系统。
一般地说,社会系统、经济系统、生态系统都是灰色系统。
例如物价系统,导致物价上涨的因素很多,但已知的却不多,因此对物价这一灰色系统的预测可以用灰色预测方法。
灰色系统理论认为对既含有已知信息又含有未知或非确定信息的系统进行预测,就是对在一定方位内变化的、与时间有关的灰色过程的预测。
尽管过程中所显示的现象是随机的、杂乱无章的,但毕竟是有序的、有界的,因此这一数据集合具备潜在的规律,灰色预测就是利用这种规律建立灰色模型对灰色系统进行预测。
灰色预测通过鉴别系统因素之间发展趋势的相异程度,即进行关联分析,并对原始数据进行生成处理来寻找系统变动的规律,生成有较强规律性的数据序列,然后建立相应的微分方程模型,从而预测事物未来发展趋势的状况。
其用等时距观测到的反应预测对象特征的一系列数量值构造灰色预测模型,预测未来某一时刻的特征量,或达到某一特征量的时间。
简言之,灰色预测模型是通过少量的、不完全的信息,建立灰色微分预测模型,对事物发展规律作出模糊性的长期描述(模糊预测领域中理论、方法较为完善的预测学分支)。
灰色系统的概念是由邓聚龙教授于1982年提出的,它描述部分信急己知,部分未知介于黑白系统之间的系统。
GM(1,1)模型是灰色理论中较常用的预测方法,它以定性分析为先导,定量与定性结合,对离散序列建立微分方程以及白化方程,一般要经历思想开发、因素分析、量化、动态化、优化五个步骤。
灰色系统通过对原始数据的整理来寻求其变化规律,这是一种就数据寻找数据的现实规律的途径,称为灰色序列的生成。
生成数通过对原始数据的整理寻找数的规律,分为三类:a、累加生成:通过数列间各时刻数据的依个累加得到新的数据与数列。
第七章灰色预测

• 部分信尽知可信息能息发的挥作现用有。已
已知,部分
信息未知
• 灰色系统
•白
• 信息完 全已知
• 白色系 统
13
2020年7月23日星期四 greytheory@
灰色预测第一篇论文
邓聚龙,灰色动态模型(GM)及在粮食长期预测中的应用[J], 大自然探索,1984年第3期,37-43.
2 灰色预测基 本思想
3 累加生成建 模思想
4 五步建模思 想
24
2020年7月23日星期四 greytheory@
➢灰色预测模型是通过数据处理来分析和对待随机量,也就是通过数据到数据 的”映射”,时间序列到时间序列的”映射”来处理和发现规律, 称之为灰色 序列生成;
➢累加生成是一种有• 效邓的的聚优弱龙化化数.信累据息加序处生列理随成机问的性题灰的[指J方].数法华.律中—工灰学色院控学制报系,19统87.
• 建立系统模型,一般要经历思想开发、因素分析、量化、动态化、 优化五个步骤,故称为五步建模。
语言模型 网络模型 量化模型 动态模型
优化模型
开发思想,形 成概念,通过 定性分析、研 究,明确研究 的方向、目标 、途径、措施 ,并将结果用 准确简练的语 言加以表达。
对语言模型 中的因素及 各因素之间 的关系进行 剖析,找出 影响事物发 展的前因、 后果,并将 这种因果关 系用框图表 示。
• 公理2 解的非唯一性原理
•
信息不完全、不确定的解是非唯一的。该原理是灰色
系统理论解决实际问题所遵循的基本法则。
• 公理3 最少信息原理
•
灰色系统理论的特点是充分利用已占有的“最少信
息”。
10
2020年7月23日星期四 greytheory@
灰色预测理论详解

xN(0) (1), xN(0) (2),...,xN(0) (n)
为Z1相(1) 关为因X1素(1)序的列紧。邻X生i(成1) 为序列X i(,0) 的则1称-AGO序列 i 1,2,...,,N
N
x (0) 1
(k
)
az1(1)
(k )
bi xi (1) (k )
i2
为GM(1,N)灰色微分方程。
灰色预测
灰色预测是对既含有已知信息又含有不确定信息 的系统进行预测,就是对在一定范围内变化的、 与时间有关的灰色过程进行预测。
通过对原始数据的生成处理来和灰色模型的建立, 挖掘、发现、掌握寻求系统变动的规律。生成数 据序列有较强的规律性,可以用它来建立相应的 微分方程模型,从而预测事物未来的发展趋势和 未来状态,对系统的未来状态做出科学的定量分 析。
x (1)(k 1) (x(1) (1) b )eak b
还原到原始数据
a
a
x (0)(k 1) x(1) (k 1) x(k)
DGM(1,1)模型
X(1() 1) 1
B
X(1() 1)
1
X(1() n
-
1 )1
GM(1,1)和DGM(1,1)的关系
灰色生成:建立灰色模型之前,需要对原始时间序列按照 某种要求进行预处理,得到有规律的时间序列数据—生成 列。即对原始数据的生成就是企图从杂乱无章的现象中去 发现内在规律.
常用的灰色系统生成方式有: 累加生成,累减生成,均值生 成,级比生成等,下面对这几种生成做简单介绍:
1.累加生成 通过数列间时刻各数据的依个累加以得到新的数据与数 列,累加所得的新数列叫做累加生成数列。
灰色系统理论的应用

灰色系统理论的应用灰色系统理论是一种基于不完全信息、缺乏数据和知识的系统分析方法。
它是由我国著名学者李兴钢教授于上世纪80年代提出的,是一种集数学、统计、经济、管理、环境等多学科为一体的理论体系。
在实际应用中,灰色系统理论可以通过对已有数据的预处理、模型建立、模型检验、模型应用等步骤来解决实际问题。
一、灰色系统理论的优点相比较于其他的统计与预测方法,灰色系统理论的特点主要有以下几个:1. 灰色系统理论可以通过对有限或者不确定的历史数据进行分析,得到一些有用的信息。
2. 灰色系统理论适合处理小样本、非稳态、非线性等情况下的系统分析。
3. 灰色系统理论可以得出相对较为精确但是不需过多历史数据的预测结果,这对于预测风险较高的领域非常有用。
二、灰色系统理论应用的具体场景灰色系统理论在很多领域得到了广泛应用,以下是一些典型的应用场景:1. 企业管理在企业的生产经营中,灰色系统理论可以通过对生产数据、销售数据、库存数据等进行分析,帮助企业管理人员制定合理的生产计划、销售策略和库存控制策略。
同时,灰色系统理论也能较为准确地预测某种商品的需求情况,有助于企业制定产销计划并减少存货积压。
2. 金融风险控制在金融领域,灰色系统理论可以用于控制风险,规避可能出现的金融波动和风险事件。
它可以通过大量的历史数据,去发现其中蕴含的信息和规律,并将其运用到风险控制中。
3. 能源管理对于电力、煤炭、石油等能源行业,灰色系统理论可以用于分析煤炭储量、电力供需情况、石油开采效果等问题。
同时还可以对得到了地下水位与地温的数据,预测天然气的渗透性、储量与分布规律。
4. 医疗领域在医疗领域,灰色系统理论可以用于预测疾病的流行趋势、治疗效果和疾病的概率。
同时,它也可以用于分析不同治疗方式造成的费用差异,并为医疗机构提供合理的方案。
三、灰色系统理论的应用案例以下是几个具体的应用案例:1. 预测手机销售某通讯公司通过调查与分析了解到,在某一段时间内销售的手机数量与之前销售的时间和数量有关系。
灰色预测模型原理

灰色预测模型原理灰色预测模型(Grey Prediction Model)是一种基于灰色系统理论和数学建模方法的预测模型。
灰色系统理论是我国学者黄金云教授于1982年提出的一种系统理论,它是研究非确定性和不完备信息系统的一种新方法,可用于研究多变量、小样本和非线性系统。
灰色预测模型主要基于灰色数学建模方法,通过对已知的部分序列数据进行建模和预测,来推测未知的序列数据趋势。
它适用于研究数据量小、信息不完备、非线性关系复杂的系统。
下面将简要介绍灰色预测模型的原理、模型建立过程以及一些应用案例。
1. 灰色预测模型的原理灰色预测模型的核心思想是通过对已知数据进行灰色关联度的度量,从而建立出合适的数学模型,进行未来数据的预测。
其基本原理可以概括为以下五个步骤:(1)建立灰色微分方程:根据原始数据的特点,确定合适的灰色微分方程,通常使用一阶或高阶灰色微分方程。
(2)求解灰色微分方程:根据所选择的灰色微分方程,求解其参数,得到模型的特征参数。
(3)模型检验:检验所建立的灰色预测模型的拟合程度和误差是否符合要求。
(4)进行灰色关联度分析:根据已知数据的变化规律,计算各个因素的灰色关联度,确定相关因素的重要性。
(5)进行预测:利用建立好的灰色预测模型,对未来的数据进行预测和分析,得出预测值。
2. 模型建立过程灰色预测模型的建立过程中,通常包括以下几个步骤:(1)数据的建立与处理:对原始数据进行筛选、预处理和归一化处理,以满足模型的要求。
(2)建立灰色微分方程:从已知数据中提取主要特征,并根据数据的特点选择合适的灰色微分方程。
(3)求解灰色微分方程:根据所选的灰色微分方程,通过累加生成序列、求解参数等方法,得到模型的特征参数。
(4)模型的检验:根据已知数据的拟合程度和误差范围,评估所建立的灰色预测模型的准确性和可靠性。
(5)模型的应用与预测:利用已建立的模型进行未来数据的预测和分析,得出预测结果。
3. 应用案例灰色预测模型在实际应用中具有广泛的应用范围,以下是一些常见的应用案例:(1)经济领域:用于对经济指标、市场需求、价格变动等进行预测,为经济决策提供参考。
灰色预测模型理论及其应用

灰色预测模型理论及其应用Document number【980KGB-6898YT-769T8CB-246UT-18GG08】灰色预测模型理论及其应用灰色系统理论认为对既含有已知信息又含有未知或非确定信息的系统进行预测,就是对在一定方位内变化的、与时间有关的灰色过程的预测. 尽管过程中所显示的现象是随机的、杂乱无章的,但毕竟是有序的、有界的,因此这一数据集合具备潜在的规律,灰色预测就是利用这种规律建立灰色模型对灰色系统进行预测.灰色预测模型只需要较少的观测数据即可,这和时间序列分析,多元回归分析等需要较多数据的统计模型不一样. 因此,对于只有少量观测数据的项目来说,灰色预测是一种有用的工具.本文主要围绕灰色预测GM(1,1)模型及其应用进行展开。
一、灰色系统及灰色预测的概念灰色系统灰色系统产生于控制理论的研究中。
若一个系统的内部特征是完全已知的,即系统的信息是充足完全的,我们称之为白色系统。
若一个系统的内部信息是一无所知,一团漆黑,只能从它同外部的联系来观测研究,这种系统便是黑色系统。
灰色系统介于二者之间,灰色系统的一部分信息是已知的,一部分是未知的。
区别白色和灰色系统的重要标志是系统各因素间是否有确定的关系。
特点:灰色系统理论以“部分信息已知、部分信息未知”的“小样本”、“贫信息”不确定型系统的研究对象。
灰色预测灰色系统分析方法是通过鉴别系统因素之间发展趋势的相似或相异程度,即进行关联度分析,并通过对原始数据的生成处理来寻求系统变动的规律。
生成数据序列有较强的规律性,可以用它来建立相应的微分方程模型,从而预测事物未来的发展趋势和未来状态。
灰色预测是用灰色模型GM(1,1)来进行定量分析的,通常分为以下几类:(1) 灰色时间序列预测。
用等时距观测到的反映预测对象特征的一系列数量(如产量、销量、人口数量、存款数量、利率等)构造灰色预测模型,预测未来某一时刻的特征量,或者达到某特征量的时间。
(2) 畸变预测(灾变预测)。
灰色预测模型的研究及其应用

灰色预测模型的研究及其应用
灰色预测模型(Grey System Prediction Model)是指在不能得到完
全的定性分析或定量关系的基础上,根据历史数据观察研究发展趋势的一
种统计学的预测模型。
灰色预测模型由灰色系统理论的预测和模糊系统理
论的分析组成,灰色理论是一种动态系统理论,它可以把一般现象用数学
模型很好地表示出来,从而模拟现象并预测它们的未来发展趋势。
目前,
灰色系统理论已经广泛地应用于经济学、管理学、决策学、社会学等领域,用以对复杂系统的研究和预测。
例如,可以应用灰色预测模型来预测某一
地区的经济发展情况;可以应用灰色预测模型来预测一种货币的发行情况;可以应用灰色预测模型来预测某一社会团体的发展趋势;还可以应用灰色
预测模型来预测某一股票市场的发展趋势等。
灰色预测模型的研究和应用
越来越广泛,已经成为现代管理学领域的一种热门研究话题。
基于灰色理论的物流配送风险分析与预测

基于灰色理论的物流配送风险分析与预测近年来,随着网络购物的普及以及电商平台的快速发展,物流配送行业迎来了巨大的发展机遇。
然而,在快速发展的同时,物流配送行业也面临着越来越多的风险。
因此,对物流配送风险的分析和预测显得尤为重要。
本文将基于灰色理论,对物流配送风险进行分析和预测。
一、灰色理论简介灰色理论是20世纪80年代初由中国科学家葛红伟教授提出的。
它是一种基于不确定信息处理的理论,适用于样本数据量较小或信息不完整的情况。
灰色理论的核心概念是灰色系统模型。
灰色系统模型是由灰色关联度、灰色预测和灰色模态分析三部分组成的。
其中,灰色关联度是灰色理论的基础,它是指研究两个或多个灰度数列之间的联系程度。
灰度数列是指由少量数据组成的数列,其信息量不足,难以进行传统的统计分析。
通过灰色关联度分析,可以确定出数据之间的关系。
而灰色预测则是基于灰色关联度分析的结果进行的预测,它可以在数据不充分的情况下进行较为准确的预测。
最后,灰色模态分析则是对灰度数列进行分解和重构,以便更全面地了解数据的内在结构和变化规律。
二、物流配送风险的分类物流配送风险是指在物流配送过程中可能出现的各种潜在风险。
根据风险的性质和来源,可以将物流配送风险分为以下几类:1. 自然风险自然风险是指在物流配送过程中受到自然因素的影响而出现的各种风险。
例如,自然灾害、气候变化、地质灾害等都可能导致物流配送过程中的延误、货物损失等问题。
2. 技术风险技术风险是指在物流配送过程中受到技术因素的影响而出现的各种风险。
例如,货物跟踪系统故障、交通工具故障、通信系统故障等都可能导致物流配送过程中的延误、货物损失等问题。
3. 人为风险人为风险是指在物流配送过程中受到人为因素的影响而出现的各种风险。
例如,作业操作不当、未按规定程序操作、人员不当等都可能导致物流配送过程中的延误、货物损失等问题。
三、物流配送风险分析与预测为了有效地减少物流配送风险,可以基于灰色理论对物流配送风险进行分析和预测。
关于“灰色预测模型”讲解

集成学习可以通过组合多个基模型的预测结果来提高整体 预测性能。可以将灰色预测模型作为基模型之一,与其他 预测方法一起构建集成学习模型。
与模糊逻辑融合
模糊逻辑能够处理不确定性和模糊性问题,可以与灰色预 测模型相结合,提高模型在处理不确定信息时的预测性能 。
THANKS
感谢观看
灰色差分方程
灰色预测模型的核心是建立灰色差分方程,通过对原始数据序列进行累加或累减 生成,构造出具有指数规律的数据序列,进而建立相应的微分方程进行求解。
适用范围及优势
适用范围
小样本建模
适应性强
预测精度高
灰色预测模型适用于数据量较 少、信息不完全、具有不确定 性和动态性的系统。它可以在 数据序列较短、波动较大、趋 势不明显的情况下,进行有效 的预测和分析。
04
灰色预测模型检验与评 估
残差检验法
01
02
03
残差计算
通过比较实际值与预测值 之间的差异,计算残差序 列。
残差分析
对残差序列进行统计分析 ,包括计算均值、方差等 指标,以评估模型的预测 精度。
残差图
绘制实际值与预测值的散 点图,以及残差序列的折 线图,直观展示模型的拟 合效果。
后验差检验法
金融市场分析
灰色预测模型可以用于分析金融市场的波动性和 趋势,帮助投资者做出更明智的投资决策。
3
物价水平预测
利用灰色预测模型可以对物价水平进行短期和长 期预测,为政府制定物价调控政策提供依据。
社会领域应用案例
人口数量预测
通过收集历史人口数据,利用灰色预测模型可以对未来人 口数量进行预测,为政府制定人口政策提供参考。
关于“灰色预测模型 ”讲解
灰色预测法

灰色预测法1.介绍灰色预测就是灰色系统所做的预测,灰色系统理论是我国著名学者邓聚龙教授创立的一种兼具软硬科学特性的新理论。
灰色系统的具体含义就是:部分信息已知,部分信息未知的某一系统。
一般地说,社会系统、经济系统、生态系统都是灰色系统。
例如物价系统,导致物价上涨的因素有很多,但已知的却不多,因此对物价这一灰色系统的预测可以用灰色预测方法。
2.适用问题灰色系统理论认为对既含有已知信息又含有未知或非确定信息的系统进行预测,就是对在一定方位内变化的、与时间有关的灰色过程的预测。
比如说人口预测、气象预报、初霜预测、灾变预测(如地震时间的预测)、数列预测(如对消费物价指数的预测)。
灰色预测模型所需要的数据量比较少,预测比较准确,精确度比较高。
样本分布不需要有规律性,计算简便,检验方便。
灰色GM(1,1) 模型是指运用曲线拟合和灰色系统理论进行预测的方法,对历史数据有很强的依赖性,没有考虑各个因素之间的联系,所以误差偏大,只适合做中长期的预测,不适合长期预测。
3.数学方法核心步骤3.1数据的检验与处理首先,为了确保建模方法的可行性,需要对抑制数据作必要的检验处理,设参考数据为(0)(0)(0)(0)((1),(2),...,())x x x x n =,计算数列的级比(0)(0)(1)().2,3,...,()x k k k n x k λ-== 如果所有的级比()k λ 都在可容覆盖2212(,)n n e e -++ 内,则数列(0)x 可以作为模型GM(1,1)的数据进行灰色预测,否则,需要对(0)x 做必要地变换处理,使其落入可容覆盖内,即取适当的c ,做平移变换 (0)(0)()(),1,2,...,y k x k c k n =+=则是数列(0)(0)(0)(0)()((1),(2),...,())y k y y y n =的级比(0)(0)(1)(),2,3,...,()y y k k X k n y k λ-=∈= 3.2 建立模型按照下面的办法建立模型GM (1,1)(1) 由上面的叙述知道参考数据列为(0)(0)(0)(0)((1),(2),...,())x x x x n =,对其做一次累加(AGO )生成数列(1)x(1)(1)(1)(1)(1)(1)(0)(1)(0)((1),(2),...,())((1),(1)(2),...,(1)())x x x x n x x x x n x n ==+-+其中(1)(0)1()()(1,2,...,)k i x k x i k n ===∑ 。
灰色理论的名词解释

灰色理论的名词解释灰色理论是一种基于少量可用数据的预测和决策模型推理分析方法。
它由中国科学家陈纳言在20世纪80年代初提出,并在实际应用中得到广泛使用。
灰色理论可以应用于不完全、不精确以及缺乏相关性的数据,通过建立灰色模型实现对未知事物或系统行为的预测。
1. 灰色系统灰色理论的核心思想是"灰色系统",它指的是具有未知、模糊、不完整或难以测量的特征的系统。
相对于传统的黑白系统,灰色系统是介于黑与白之间的灰色区域,即信息不完备的状态。
2. 灰色关联度灰色关联度是灰色理论中的关键指标,用于度量两个灰色序列之间的相关性。
通过计算灰色关联度可以判断两个序列是否存在相关性,并进一步分析序列之间的关联程度。
灰色关联度的计算包括数据的正规化和关联度的计算两个步骤。
3. 灰色模型灰色模型是灰色理论的基础工具,用于建立未知事物或系统行为的预测模型。
灰色模型包括GM(1,1)模型和GM(2,1)模型等不同类型,通过对已知数据序列进行处理,得到系统的特性参数,然后利用这些参数进行预测或决策。
4. 灰色预测灰色预测是灰色理论的应用之一,它通过对已有的数据序列进行分析和处理,预测未来序列的趋势和规律。
与传统的统计分析方法相比,灰色预测更适用于数据量少、关系复杂以及存在不确定性的问题。
5. 灰色决策灰色决策是灰色理论的另一重要应用领域,它主要用于多目标决策问题中。
通过灰色决策方法,我们可以在多个因素或目标之间进行权衡和选择,找到最优解或较好的决策方案。
6. 灰色系统工程灰色系统工程是灰色理论领域的一个重要研究方向,它将灰色理论与系统工程相结合,旨在寻找更好的工程解决方案。
通过运用灰色系统工程方法,我们可以解决那些特征不完备、难以测量或缺乏实际数据的问题。
总结:灰色理论作为一种基于少量可用数据的推理分析方法,提供了一种有效的工具用于预测和决策。
通过灰色模型的建立和灰色关联度的计算,我们可以对未知事物或系统行为进行预测和分析。
灰色系统理论及其应用

灰色系统理论及其应用一、灰色系统理论概述灰色系统理论,是一种研究不确定性问题的方法。
它起源于20世纪80年代,由中国学者邓聚龙教授提出。
灰色系统理论认为,现实世界中的许多问题并非非黑即白,而是介于黑白之间的灰色地带。
这种理论为我们处理复杂、模糊、不确定性问题提供了一种新的视角。
灰色系统理论的核心思想是通过对部分已知信息的挖掘和加工,实现对整个系统行为的合理预测和控制。
它将系统分为白色系统、黑色系统和灰色系统。
白色系统是指信息完全已知的系统,黑色系统是指信息完全未知的系统,而灰色系统则是介于两者之间的系统,部分信息已知,部分信息未知。
二、灰色系统理论的基本原理1. 灰灰是灰色系统理论的基础,它通过对原始数据进行处理,具有规律性的序列。
常见的灰方法有累加(AGO)、累减(IGO)和均值等。
2. 灰关联分析灰关联分析是灰色系统理论的重要方法,用于分析系统中各因素之间的关联程度。
通过对系统各因素发展变化的相似度进行比较,揭示系统内部因素之间的联系。
3. 灰预测灰预测是灰色系统理论在实际应用中的重要手段,它通过对部分已知信息的挖掘,建立灰色模型,对系统未来发展趋势进行预测。
三、灰色系统理论的应用领域1. 经济管理灰色系统理论在经济学和管理学领域具有广泛的应用,如企业竞争力分析、市场预测、投资决策等。
通过灰关联分析,可以找出影响企业发展的关键因素,为企业制定发展战略提供依据。
2. 工程技术在工程技术领域,灰色系统理论可用于设备故障预测、质量控制、能源消耗分析等。
例如,通过对设备运行数据的分析,建立灰色预测模型,提前发现潜在故障,确保设备安全运行。
3. 社会科学4. 生态环境在生态环境领域,灰色系统理论可以用于水资源评价、环境污染预测、生态平衡分析等。
通过对生态环境数据的挖掘,有助于我们更好地了解和把握生态环境的发展态势。
四、灰色系统理论的优势与局限性优势:1. 对小样本数据的适用性:灰色系统理论不需要大量数据即可进行建模和分析,这对于样本量有限的情况尤其有价值。
灰色预测理论与应用

n
k
k 1
0
称为
X
0
k
与 Xˆ k 的关联度
灰色模型 GM
1、GM(1,1)模型的建立
( n )) 有n个观察值,通 设时间序列 过累加生成新序列 x (1 ) ( x (1 ) (1), x (1 ) ( 2 ), , x (1 ) ( n )) 则GM(1,1)模型相应的微分方程为: x (1), x ( 2 ), , x
令x
(0)
为 原 始 序 列 ,x
(1 )
(0)
[x
(1 )
(0)
(1), x
(1 )
(0)
( 2 ), , x
(1 )
(0)
( n )],
记生成数为x x
(1 )
,x
(1 )
[x
(1), x
( 2 ), , x
( n )], 如 果
与x
(0)
之间满足如下关系 :
x
(1 )
(k )
k
x
(0)
( i ); k 1, 2 , , n
( 2 1)
i1
则 称 为 一 次 累 加 生 成 , 记 为 1 A G O ( A ccu m u la tin g G en era tio n O p era to r )
r次 累 加 生 成 有 下 述 关 系 :
x
(r )
(0)
[x [x
(r)
( k 1)] ( k 1)] (2 5)
(2)
(r )
(1 )
(r )
(1 )
(r)
2016数模选修——灰色预测与灰色关联度分析

解之得,即80%转化为7.
19
4.逐个计算每个被评价对象指标序列(比较 序列)与参考序列对应元素的绝对差值 即 x0 (k ) xi (k ) ( k 1,, m i 1,, n )n 为被评 价对象的个数). 5.确定 min min x0 (k ) xi (k )
i 1 k 1 n m
i k i k
i (k )
x0 ( k ) xi ( k ) maxmax x0 ( k ) xi ( k )
i k
( 12 5)
k 1,, m
式中为分辨系数,在(0,1)内取值,若 越小, 关联系数间差异越大,区分能力越强。通常 取0.5
21
如果{ x0 ( k )}为最优值数据列, i( k )越大,越好; 如果{ x0 ( k )}为最劣值数据列, i( k )越大,越不好。
x0 (1) , x0 2 , , x0 m X0
T
16
3.对指标数据进行无量纲化
无量纲化后的数据序列形成如下矩阵:
x0 1 x0 2 X 0 , X1 , , X n x0 m x1 2 x1 m x1 1 xn 1 xn 2 xn m
28
存在的问题及解决方法
29
《灰色预测与决策模型研究》 党耀国 刘思峰等著 科学出版社 本书中提及了一些其它的灰色关联度,如绝对 关联度,相对关联度等 等,并且针对各自的适 用范围进行了讨论。
所以如果是在数学建模的过程中,我们可以根 据实际的需要,确定我们的关联度的计算公式。
30
生成数
31
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
⑥要素间的关系是相对的、多重的 ⑦要素分析,系统行为研究,不应该停留在一种关系上,而应 该考虑其发展变化,即动态变化。 ⑧为了将控制理论中卓有成效的方法、成果推广到社会、经济 等系统,模型应控制化。 ⑨要通过模型了解系统的基本控制性能,如是否可控,变化过 程是否可以观测。 ⑩应从模型获得尽可能多的信息,特别是发展变化的信息。 ⑾建立模型要为使用先进的实验科学手段,使用自然科学方法 研究社会、经济等系统提供基础,特别要为电子计算机对抽象 系统进行数字仿真模拟提供条件。
二、灰色系统的研究内容 灰色系统的分析,建模,预测,决策,控制等多个内容。 (一)系统分析 现有系统分析的量化方法,大都是数理统计方法,如:回归 分析,主成分分析,方差分析. 不足: 1要求大样本 2要求样本有较大的分布规律. 3计算工作量大. 3计算工作量大. 4可能出现量化的结果与定性分析的结果不符. 4可能出现量化的结果与定性分析的结果不符. 说明回归分析有较大的局限性,特别是对我国的经济分析局 限性就更大. 灰色系统理论提出了一种新的分析方法,称为系统的关联度 分析方法.这是根据因素之间发展态势的相似或相异程度,来衡 量因素间关联程度的方法。
灰色系统解决了这个一向认为不能解决的连续微分方程的建模问题. 灰色系统解决了这个一向认为不能解决的连续微分方程的建模问题.为什 么灰色系统理论能解决这个问题呢?其重点是灰色系统有一种新观点, 么灰色系统理论能解决这个问题呢?其重点是灰色系统有一种新观点,即 1.任何随机过程都是在一定幅值范围,一定时区内变化的灰色量,我们称随 1.任何随机过程都是在一定幅值范围,一定时区内变化的灰色量, 机过程为灰色过程。 2.在处理手法上,灰色过程是通过原始数据的整理来寻找数的规律的,叫数 2.在处理手法上,灰色过程是通过原始数据的整理来寻找数的规律的, 的生成, 的生成,这就是一种就数找数的现实规律的途径。 概率统计的随机过程,则是按统计规律,按先验规律来处理问题,作这种处理, 概率统计的随机过程,则是按统计规律,按先验规律来处理问题,作这种处理, 要求数据越多越好(大样本).事实上, 要求数据越多越好(大样本).事实上,即使有了大样本也不一定能够找到统计规 律,即使有统计规律也不一定典型,而非典型的过程(如非平稳,非高斯分布,非白 即使有统计规律也不一定典型,而非典型的过程(如非平稳,非高斯分布, 噪音等) 噪音等)是难处理的。 而灰色过程则无此限制.事实上, 而灰色过程则无此限制.事实上,将许多原始数据累加处理后便出现了明 显的指数规律.为什么能做到这一点呢? 显的指数规律.为什么能做到这一点呢? 灰色系统认为:尽管客观系统表象复杂,数据离散, 灰色系统认为:尽管客观系统表象复杂,数据离散,但它们总是有整体功能 的,总是有序的.因此,它必然潜藏着某种内在规律.关键在于要用适当方式去挖 总是有序的.因此,它必然潜藏着某种内在规律. 掘它, 掘它,然后利用它。
由于关联度的分析方法是按发展趋势作分析,因此对样本 量的多少没有过分要求,也不需要典型的分布规律,计算量小, 且不致出现关联度的量化结果与定性分析不一至的现象。 关联度分析的应用情况:农业经济,水利,材料科学,宏 观经济等.对抽象系统,社会现象等进行关联度分析,首先要 找准数据序列,而用什么数据才能反映系统的行为特征,是首 先要研究的.用某种数据来间接地表征系统行为,称为找映射 量.即找系统行为的映射量。 如:1. 如:1.法国人口学家曾统计和研究过中国的宋朝,元朝, 明朝,清朝的人口.这些人口数字都不是直接统计的,而是根 据中国食盐的销售量折算得到的。(食盐作为人口的映射量是 恰当的)。 2.照相行业的收入反映社会精神面貌的变化。
◆年平均降水量大于某个阈值(可容许值)便是涝灾 ◆年平均降水量小于某个阈值是旱灾 ◆年产量大于某个指定值,是丰年 ◆年产量小于某个指定值,是欠年 ◆环境中某种物质含量超出某个阈值,是污染 ◆人体中某个参数(如体温、血压、血中成分)超出一定范围就发生病变 ◆银行存款超出某个值是经济跃变 灾变预测的特点是:对异常值出现的时间进行预测。预测的任务不是 确定异常值的大小(因为异常值的大小是指定的灰数),而是确定异常值 出现的时间。灾变预测建模所用数据已不是行为特征量本身,而是异常行 为特征值发生的时间,这是对时间来说不是等间距的,或者说建模数据的 序列,是按序号给出的时间间隔。 ③季节灾变预测 若行为特征量异常值的出现,或者某种事件的发生是在一年中个特定 时区,则这种预测称为季节灾变预测。 ◆云南春雨是在春天出现 ◆临西早霜是在秋末冬初的9、10、11月出现 ◆洪水是在汛期出现 季节灾变预测,是一种特定时区内的灾变预测。其特点是:灾变一般 仅仅发生在一年的某个特定时段。
生成数
1
x(1)(1)
3
x(1)(2)
4 . 5 7. 5
x(1)(3) x(1)(4)
8 7 6 5 4 3 2 1 0 1 2 3 4
无规律的原始数据生成后,得到较规律的数据,即无 摆动的递增规律数据。 在建立系统各要素的关联模型时,灰色理论是五步建 立的,分别是: 语言模型 网络模型 量化模型 动态量化模型 优化模型 五步建立模型的思路与模型的特点如下:
1.定性分析是建立模型的前提 2.定量模型是定性分析的具体化,规格化,关系化, 数量化 3.定性与定量紧密结合 4.明确系统潜在的显露的因素,弄清要素间的因果关 系,是系统研究的基本任务,建模的基础 5.要素间的关系: 事理系统中,是“前因、后果”关系 技术系统中,是“输入、输出”关系 经济系统中,是“投入、投出”关系
3.5 3 2.5 2 1.5 1 0.5 0 1 2 3 4
无规律,其发展态势是摆动的。 如果将原始数据作累加生成,已将K个累加生成数为x(1)(k), 并且 X(1)(1)= X(0)(1)=1 X(1)(2)= X(0)(1)+ X(0)(2)=1+2=3 X(1)(3)= X(0(1)+ X(0)(2)+ X(0)(3)=1+2+1.5=4.5 X(1)(4)= X(0)(1)+ X(0)(2)+ X(0)(3)+ X(0)(4)=7.5 序号 1 2 3 4
2.灰色系统的应用情况 例1.1983年,邓聚龙接受了我国粮食发展决策中的一个课 题,即粮食发展预测与粮食发展的长期规划.建立GM(1, 1)模型,预测1983-2000年粮食产量,1983年 预测值与统计值误差仅为4‰ 预测值与统计值误差仅为4‰。 例2.对湖北省2000年宏观经济的发展趋势进行预测,提出 自己的结论和建议,受到湖北省科协的奖励。 例3.河南省人民胜利渠利用灰色系统理论制定最佳灌溉方案, 使全流区农田得到大丰收。
④拓扑预测(亦称波形预测、整体预测)
拓扑预测是对一段时间内行为特征数据波形的预测。拓 扑预测在不同的场合有不同的意义。 对水利方面年径流量曲线来说,拓扑预测意味着在对未来 某段时间内总径流量的预测。 对气象方面年平均降水量曲线来说,拓扑预测是对某几年 总降水量的预测。 对生产系统来说,拓扑预测可以是对几年内生产总产值、 总产量的预测。 而从本质来看,拓扑预测则是对一个变化不规则的行为 数据数列的整体发展进行预测。
(三)灰色预测
预测方法有300种,通常用回归分析 预测方法有300种,通常用回归分析 法、德尔菲法、趋势外推法、最小方差预测 法、马尔克夫预测法、模型法、指数平滑 法、残差辨识方法等。 三种类型:回归— 三种类型:回归—马尔可夫称统计型 灰色预测与模型法属连续型 指数平滑与残差辨识则属递推型 灰色系统模型的预测,称灰色预测。 灰色预测可分为五类:
3.用学生人数来反映教育的发达程度,用大专以上文化程度 的人数来反映教育水平的高低。 以上这些是各种社会现象的一些可能的映射量.当有了系统 行为的数据列(即各时刻的数据)后,根据关联度计算公式便可 算出关联程度。 关联度不仅是一种系统分析方法,而且进一步可拓广为关联 空间.这将为离散数学的分析学奠定基础。 (二)系统模型的建立 微分方程模型的不足:微分方程中的系统数据的出现是输入 输出的导数,他们一般是不能量测得到的;实际上,由于导数信 号难获得,所以解不存在。
⑿建立模型常用的数据:科学实验数据、统计数据、经验数据、 生产数据(实验室化验分析)、决策数据。前三种数据有较大 局限性;生产数据较易获得,包涵难以用语言文字描述的全部 因素,有丰实的内涵。 ⒀建模的目的不仅仅是为了认识世界,更重要的是为了改造世 界。 ⒁五步建模的基本任务,是沟通社会科学与自然科学,使社会 科学研究做到数学化、计算机化、自然科学化。 ⒂五步建模的灰色建模思路(如下图说明),用原始数据 x ( 0 ) ˆ(1) ˆ(1) ,经生成得到 x (1) ,对 x(1) 按GM建模,得模型计算值 x ,将 x (1) (1) (1) (1) 与 x 进行比较,得到残差 ∆ x ,用残差对模型GM作修正。残差 ∆ x = x ∆ ˆ(1) ,∆x (1) ⇒ min,通过; x (1) ⇒ max,修正GM。 x ⒃所建立的模型是多要素的、关联的、整体的,决定系统发展 态势,不是某个因素,而是所有因素协调发强的规律, 由于生成数据列有了较强的规律,有可能对变化过程做较 长时间的描述,因此,有可能建立微分方程.建立微分方程模型, 长时间的描述,因此,有可能建立微分方程.建立微分方程模型, 还要利用到灰色理论的其他成果, 关联空间的知识, 还要利用到灰色理论的其他成果,如:关联空间的知识,离散函 数的收敛,根据,离散函数的光滑度,灰导数,灰微分方程, 数的收敛,根据,离散函数的光滑度,灰导数,灰微分方程,平蛇等 概念。 以例说明灰色过程如何通过生成数来寻找规律 例:记x(0)(1) ,x(0)(2) ,x(0)(3), x(0)(4)其值如下: (4)其值如下: 序号 数据 1 1 x(0)(1) 2 2 x(0)(2) 3 1. 5 x(0)(3) 4 3 x(0)(4)
①数列预测
对系统行为特征值大小的发展变化进行预测,称为系 统行为数据列的变化预测,简称数列预测。例如 ◆粮食产量的预测 ◆商品销售量发展变化的预测 ◆年平均降水量发展变化的预测 ◆人口的预测 ◆货运量的预测 ◆外贸额发展变化的预测 这种预测的特点是:对行为特征量等时距地观测。 预测的任务是:了解这些行为特征量在下一个时刻有多 大。 ②灾变预测 对系统行为特征量超出某个阈值(界限值)的异常值 将在何时出现的预测称为灾变预测。所以说,灾变预测 即对异常值出现时刻的预测。由于异常值往往会使人们 的生活、生态环境、农业生产等的正常活动带来异常结 果,造成灾害,所以也称为这种预测为灾变预测。如
