常微分方程与动力系统第二章课后题参考答案

合集下载

第四版微分几何第二章课后习题答案

x a cos a sin 0
y b sin b cos 0
zt
0 0 ，即 x bcos + y asin
1
－ab=0
此方程与 t 无关，对于的每一确定的值，确定唯一一个切平面，而
对应一条直母线，说明沿每一条直母线，此曲面只有一个切平面
。
的每一数值
3
5．证明曲面 r
a { u,v,
} 的切平面和三个坐标平面所构成的四面体的体积是常
( Edu v Fdv u)
2
2
E u ds
( Fdu v Gdv
2
2
G v ds
2
2
v ) ，即 ( Edu Fdv )
E
2
( Fdu Gdv ) 。
G
展开并化简得 E(EG- F 2 ) du 2 =G(EG-F 2 ) dv 2 , 而 EG-F 2 >0，消去 EG-F 2 得坐标曲线
的二等分角线的微分方程为 Edu 2 =Gdv 2 .
第二章曲面论 §1 曲面的概念
1. 求正螺面 r ={ u cos v ,u sin v , bv } 的坐标曲线 . 解 u- 曲线为 r ={u cos v 0 ,u sin v 0 ,bv 0 }= ｛0,0 ，bv 0 ｝＋u { cos v 0 , sin v 0 ,0} ，为曲线的直母线； v- 曲线为 r ={ u 0 cos v , u 0 sin v ,bv } 为圆柱螺线．２．证明双曲抛物面 r ＝｛ a（ u+v）, b （u-v ）,2uv ｝的坐标曲线就是它的直母线。证 u- 曲线为 r ={ a（u+v 0 ）, b（u- v 0 ）,2u v 0 }={ a v 0 , bv 0 ,0}+ u{a,b,2 v 0 } 表示过点 { a v 0 , b v 0 ,0} 以 {a,b,2 v0 } 为方向向量的直线 ; v- 曲线为 r =｛ a（ u 0 +v）, b（ u 0 -v ）,2 u 0 v｝=｛a u 0 , b u 0 ,0 ｝+v{a,-b,2 u 0 } 表示过点 (a u 0 , b u 0 ,0) 以 {a,-b,2 u 0 } 为方向向量的直线。 3．求球面 r ={ a cos sin , a cos sin , a sin } 上任意点的切平面和法线方程。

大学物理课后习题答案第02章

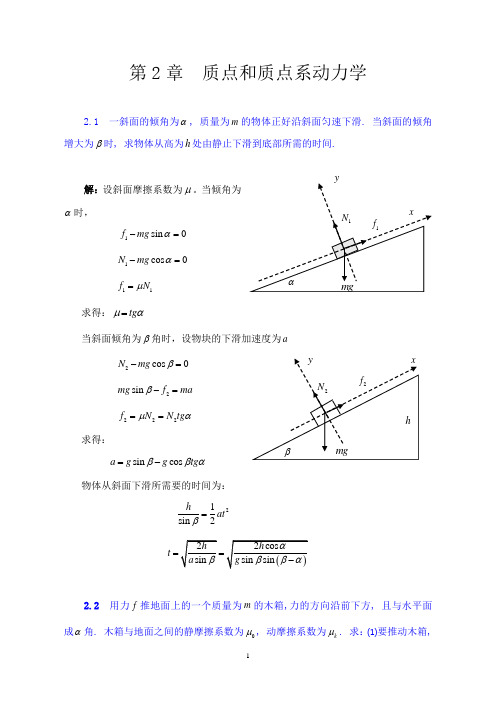
第2章质点和质点系动力学2.1 一斜面的倾角为α, 质量为m 的物体正好沿斜面匀速下滑. 当斜面的倾角增大为β时, 求物体从高为h 处由静止下滑到底部所需的时间.解：设斜面摩擦系数为μ。

当倾角为α时，1sin 0f mg α-=1cos 0N mg α-= 11f N μ= 求得：tg μα=当斜面倾角为β角时，设物块的下滑加速度为a2cos 0N mg β-= 2sin mg f ma β-= 222f N N tg μα==求得：sin cos a g g tg ββα=- 物体从斜面下滑所需要的时间为：21sin 2h at β=t ==2.2 用力f 推地面上的一个质量为m 的木箱,力的方向沿前下方, 且与水平面成α角. 木箱与地面之间的静摩擦系数为0μ, 动摩擦系数为k μ. 求：⑴要推动木箱,f 最小为多少？使木箱作匀速运动, f 为多少？⑵证明当α大于某值时, 无论f 为何值都不能推动木箱, 并求α值.解：⑴当f 的水平分力克服最大静摩擦力时，木箱可以运动，即 ()0cos sin f mg f αμα≥+ 00cos sin mgf μαμα≥-0min 0cos sin mgf μαμα=-使木箱做匀速运动，则()cos sin k f mg f αμα=+ cos sin k k mgf μαμα=-⑵由能推动木箱的条件: ()0cos sin f mg f αμα≥+ 00cos sin f f mg αμαμ-≥若0cos sin 0f f αμα-<时,上式不可能成立,即不可能推动木箱的条件为: 01tg αμ>， 01arctgαμ>2.3 质量为5000kg 的直升飞机吊起1500kg 的物体, 以0.6m/s 2的加速度上升, 求：（1）空气作用在螺旋桨上的升力为多少. （2）吊绳中的张力为多少.解：（1）对飞机物体整体进行受力分析，得()()f M m g M m a -+=+()()4650010.2 6.8910f M m g a N =++=⨯=⨯ （2）对物体m 进行受力分析，得T mg ma -=()4150010.6 1.5910T m g a N =+=⨯=⨯2.4质量为m 汽车以速率0v 高速行驶, 受到2kv f -=的阻力作用, k 为常数.当汽车关闭发动机后, 求：（1）速率v 随时间的变化关系. （2）路程x 随时间的变化关系. （3）证明速率v 与路程x 之间的函数关系为x mke v v -=0．（4）若020/v m s =, 经过15s 后, 速率降为10/t v m s =, 则k 为多少？解：由题意， 2dvmkv dt =- 两边积分 020v tv dv k dt v m =-⎰⎰011kt v v m ⎛⎫-=- ⎪⎝⎭即 00001v mv v k m kv t v t m ==+⎛⎫+ ⎪⎝⎭（2）由上式两边积分 0000xtmv dx dt m kv t =+⎰⎰即 0ln m kv t m x k m +⎛⎫=⎪⎝⎭（3）由（1）中得 00mv kv t m v =-，代入（2）中的结果，得 00ln ln mv m m v m m v x k m k v ⎛⎫+- ⎪⎛⎫== ⎪ ⎪⎝⎭⎪⎝⎭即 0k x mv v e-=（4）020/v m s =,15t s =,10/t v m s =代入00mv v m kv t=+，求得300m k =2.5质量为m 的质点以初速度0v 竖直上抛, 设质点在运动中受到的空气阻力与质点的速率成正比, 比例系数为0>k ．试求：（1）质点运动的速度随时间的变化规律. （2）质点上升的最大高度.解：（1） dvm mg kv dt=--mdvdt mg kv=-+1()kd kv mg dt mg kv m+=-+两边积分 001()vtv k d kv mg dt mg kv m +=-+⎰⎰0lnkv mg kt kv mg m+=-+即 k mg e k mg v v t m k-⎪⎭⎫ ⎝⎛+=-0 （2）由（1）中方程得 dv dv dy dv mg kv mm mv dt dy dt dy--=== ()mg kv mg mvdv m dy dv mg kv k mg kv+--==-++两边积分 00(1)yv v m mgdy dv k mg kv=--+⎰⎰ ()2020ln m m g mg kvy v v k k mg kv +=-++当0v =时，有 20max02ln mg kv m m g y v k k mg ⎛⎫+=- ⎪⎝⎭2.6自动枪以每分钟发射120发子弹的速率连续发射. 每发子弹的质量为7.9g , 出口速率为735/m s . 求射击时枪托对肩部的平均压力.解：设肩部所受的平均作用力为F ，由动量定理得 Ft mv =∑即 31207.91073511.660mv F N t-⨯⨯⨯==≈∑2.7 质点在x 轴上受x 方向的变力F 的作用．F 随时间的变化关系为：在刚开始的0.1s 内均匀由0增至20N ，又在随后的0.2s 内保持不变，再经过0.1s 从20N 均匀地减少到0. 求：（1）力随时间变化的t F -图. （2）这段时间内力的冲量和力的平均值. （3）如果质点的质量为3kg , 初始速度为1/m s , 运动方向与力的方向相同. 当力变为零时, 质点速度为多少？解：（1）由题意得（2）由上图得11200.1200.2200.1622I N s =⨯⨯+⨯+⨯⨯=⋅0.5200.1200.20.5200.1150.4I F N t ⨯⨯+⨯+⨯⨯=== （3）由动量定理得 0t I mv mv =-0.10.30.4即 06313/3t I mv v m s m ++⨯===2.8子弹脱离枪口的速度为300/m s , 在枪管内子弹受力为5400410/3F t =-⨯（SI ）, 设子弹到枪口时受力变为零. 求：（1）子弹在枪管中的运行的时间. （2）该力冲量的大小. （3）子弹的质量.解：（1）由541040003tF ⨯=-=得3310t s -=⨯ （2）35310004104000.63tt I Fdt dt N s -⨯⎛⎫⨯==-=⋅ ⎪⎝⎭⎰⎰（3）由0I Ft mv ==-得 30.6210300I m kg v -===⨯2.9 自由电子在沿x 轴的振荡电场()0cos E t ωϕ=+E i中运动, 其中0E , ω,ϕ为常数. 设电子电量为e -, 质量为m , 初始条件为：0=t 时, 00v =v i, 00x =r i . 略去重力和阻力的作用, 求电子的运动方程.解：由()0cos F eE t ωϕ=-+得 0tvv Fdt mdv =⎰⎰解得()000sin sin eE eEv v t m m ϕωϕωω=+-+ 两边同乘dt 积分，()000sin sin eE eE dx v t dt m m ϕωϕωω⎛⎫=+-+ ⎪⎝⎭两边积分，()ϕωωϕωϕω++⎪⎭⎫⎝⎛++⎪⎭⎫ ⎝⎛-=t m eE t m eE v m eE x x cos sin cos 20002002.10 质量为m 的物体与一劲度系数为k 的弹簧连接, 物体可以在水平桌面上运动, 摩擦系数为μ. 当用一个不变的水平力拉物体, 物体从平衡位置开始运动. 求物体到达最远时, 系统的势能和物体在运动中的最大动能.解：分析物体水平受力，物体受外力、弹性力以及摩擦力，如图所示物体到达最远时，速度为0。

第二章课后习题答案

第二章牛顿定律2 -1 如图(a)所示,质量为m 的物体用平行于斜面的细线联结置于光滑的斜面上,若斜面向左方作加速运动,当物体刚脱离斜面时,它的加速度的大小为( )(A) g sin θ (B) g cos θ (C) g tan θ (D) g cot θ分析与解当物体离开斜面瞬间,斜面对物体的支持力消失为零,物体在绳子拉力F Ｔ (其方向仍可认为平行于斜面)和重力作用下产生平行水平面向左的加速度a ,如图(b)所示,由其可解得合外力为mg cot θ,故选(D)．求解的关键是正确分析物体刚离开斜面瞬间的物体受力情况和状态特征． 2 -2 用水平力F N 把一个物体压着靠在粗糙的竖直墙面上保持静止．当F N 逐渐增大时,物体所受的静摩擦力F f 的大小( )(A) 不为零,但保持不变(B) 随F N 成正比地增大(C) 开始随F N 增大,达到某一最大值后,就保持不变(D) 无法确定分析与解与滑动摩擦力不同的是,静摩擦力可在零与最大值μF N 范围内取值．当F N 增加时,静摩擦力可取的最大值成正比增加,但具体大小则取决于被作用物体的运动状态．由题意知,物体一直保持静止状态,故静摩擦力与重力大小相等,方向相反,并保持不变,故选(A)．2 -3 一段路面水平的公路,转弯处轨道半径为R ,汽车轮胎与路面间的摩擦因数为μ,要使汽车不至于发生侧向打滑,汽车在该处的行驶速率( )(A) 不得小于gR μ (B) 必须等于gR μ(C) 不得大于gR μ (D) 还应由汽车的质量m 决定分析与解由题意知,汽车应在水平面内作匀速率圆周运动,为保证汽车转弯时不侧向打滑,所需向心力只能由路面与轮胎间的静摩擦力提供,能够提供的最大向心力应为μF N ．由此可算得汽车转弯的最大速率应为v ＝μRg ．因此只要汽车转弯时的实际速率不大于此值,均能保证不侧向打滑．应选(C)．2 -4 一物体沿固定圆弧形光滑轨道由静止下滑,在下滑过程中,则( )(A) 它的加速度方向永远指向圆心,其速率保持不变(B) 它受到的轨道的作用力的大小不断增加(C) 它受到的合外力大小变化,方向永远指向圆心(D) 它受到的合外力大小不变,其速率不断增加分析与解由图可知,物体在下滑过程中受到大小和方向不变的重力以及时刻指向圆轨道中心的轨道支持力F N 作用,其合外力方向并非指向圆心,其大小和方向均与物体所在位置有关．重力的切向分量(m g cos θ) 使物体的速率将会不断增加(由机械能守恒亦可判断),则物体作圆周运动的向心力(又称法向力)将不断增大,由轨道法向方向上的动力学方程Rm θmg F N 2sin v =-可判断,随θ 角的不断增大过程,轨道支持力F N 也将不断增大,由此可见应选(B)．2 -5 图(a)示系统置于以a ＝1/4 g 的加速度上升的升降机内,A 、B 两物体质量相同均为m ,A 所在的桌面是水平的,绳子和定滑轮质量均不计,若忽略滑轮轴上和桌面上的摩擦,并不计空气阻力,则绳中张力为( )(A) 58 mg (B) 12 mg (C) mg (D) 2mg分析与解本题可考虑对A 、B 两物体加上惯性力后,以电梯这个非惯性参考系进行求解．此时A、B 两物体受力情况如图(b)所示,图中a′为A、B 两物体相对电梯的加速度,m a′为惯性力．对A、B 两物体应用牛顿第二定律,可解得FＴ＝5/8 mg．故选(A)．讨论对于习题2 -5 这种类型的物理问题,往往从非惯性参考系(本题为电梯)观察到的运动图像较为明确,但由于牛顿定律只适用于惯性参考系,故从非惯性参考系求解力学问题时,必须对物体加上一个虚拟的惯性力．如以地面为惯性参考系求解,则两物体的加速度a A和a B均应对地而言,本题中a A和a B的大小与方向均不相同．其中aA 应斜向上．对a A、a B、a和a′之间还要用到相对运动规律,求解过程较繁．有兴趣的读者不妨自己尝试一下．2 -6图示一斜面,倾角为α,底边AB 长为l＝2.1 m,质量为m的物体从题2 -6 图斜面顶端由静止开始向下滑动,斜面的摩擦因数为μ＝．试问,当α为何值时,物体在斜面上下滑的时间最短其数值为多少分析动力学问题一般分为两类：(1) 已知物体受力求其运动情况；(2) 已知物体的运动情况来分析其所受的力．当然,在一个具体题目中,这两类问题并无截然的界限,且都是以加速度作为中介,把动力学方程和运动学规律联系起来．本题关键在列出动力学和运动学方程后,解出倾角与时间的函数关系α＝f (t ),然后运用对t 求极值的方法即可得出数值来．解取沿斜面为坐标轴Ox ,原点O 位于斜面顶点,则由牛顿第二定律有ma αmg μαmg =-cos sin (1)又物体在斜面上作匀变速直线运动,故有()22cos sin 2121cos t αμαg at αl -== 则 ()αμααg l t cos sin cos 2-= (2) 为使下滑的时间最短,可令0d d =αt ,由式(2)有 ()()0sin cos cos cos sin sin =-+--αμαααμαα则可得 μα12tan -=,o 49=α 此时 ()s 99.0cos sin cos 2=-=αμααg l t2 -7工地上有一吊车,将甲、乙两块混凝土预制板吊起送至高空．甲块质量为m1＝×102 kg,乙块质量为m2＝×102 kg．设吊车、框架和钢丝绳的质量不计．试求下述两种情况下,钢丝绳所受的张力以及乙块对甲块的作用力：(1) 两物块以10.0 m·ｓ-2的加速度上升；(2) 两物块以1.0 m·ｓ-2的加速度上升．从本题的结果,你能体会到起吊重物时必须缓慢加速的道理吗分析预制板、吊车框架、钢丝等可视为一组物体．处理动力学问题通常采用“隔离体”的方法,分析物体所受的各种作用力,在所选定的惯性系中列出它们各自的动力学方程．根据连接体中物体的多少可列出相应数目的方程式．结合各物体之间的相互作用和联系,可解决物体的运动或相互作用力．解按题意,可分别取吊车(含甲、乙)和乙作为隔离体,画示力图,并取竖直向上为Oy轴正方向(如图所示)．当框架以加速度a 上升时,有FＴ -(m1 ＋m2 )g ＝(m1＋m2 )a (1)F N2 - m2 g ＝m2 a (2)解上述方程,得FＴ＝(m1＋m2 )(g ＋a) (3)F N2＝m2 (g ＋a) (4)(1) 当整个装置以加速度a＝10 m·ｓ-2上升时,由式(3)可得绳所受张力的值为FＴ＝×103 N乙对甲的作用力为F′N2＝-F N2＝-m2 (g ＋a)＝×103 N(2) 当整个装置以加速度a＝1 m·ｓ-2上升时,得绳张力的值为F Ｔ＝ ×103 N此时,乙对甲的作用力则为F′N2 ＝ ×103 N由上述计算可见,在起吊相同重量的物体时,由于起吊加速度不同,绳中所受张力也不同,加速度大,绳中张力也大．因此,起吊重物时必须缓慢加速,以确保起吊过程的安全．2 -8 如图(a)所示,已知两物体A 、B 的质量均为m ＝3.0kg 物体A 以加速度a ＝1.0 m·ｓ-2运动,求物体B 与桌面间的摩擦力．(滑轮与连接绳的质量不计)分析该题为连接体问题,同样可用隔离体法求解．分析时应注意到绳中张力大小处处相等是有条件的,即必须在绳的质量和伸长可忽略、滑轮与绳之间的摩擦不计的前提下成立．同时也要注意到张力方向是不同的．解分别对物体和滑轮作受力分析［图(b)］．由牛顿定律分别对物体A 、B 及滑轮列动力学方程,有 m A g -F Ｔ＝m A a (1)F ′Ｔ1 -F ｆ＝m B a ′ (2)F ′Ｔ -2F Ｔ1 ＝0 (3)考虑到m A ＝m B ＝m , F Ｔ＝F′Ｔ , F Ｔ1 ＝F ′Ｔ1 ,a ′＝2a ,可联立解得物体与桌面的摩擦力()N a m m mg F 2724f .=+-=讨论动力学问题的一般解题步骤可分为：(1) 分析题意,确定研究对象,分析受力,选定坐标；(2) 根据物理的定理和定律列出原始方程组；(3) 解方程组,得出文字结果；(4) 核对量纲,再代入数据,计算出结果来．2 -9质量为m′的长平板A 以速度v′在光滑平面上作直线运动,现将质量为m 的木块B 轻轻平稳地放在长平板上,板与木块之间的动摩擦因数为μ,求木块在长平板上滑行多远才能与板取得共同速度分析当木块B 平稳地轻轻放至运动着的平板A 上时,木块的初速度可视为零,由于它与平板之间速度的差异而存在滑动摩擦力,该力将改变它们的运动状态．根据牛顿定律可得到它们各自相对地面的加速度．换以平板为参考系来分析,此时,木块以初速度-v′(与平板运动速率大小相等、方向相反)作匀减速运动,其加速度为相对加速度,按运动学公式即可解得．该题也可应用第三章所讲述的系统的动能定理来解．将平板与木块作为系统,该系统的动能由平板原有的动能变为木块和平板一起运动的动能,而它们的共同速度可根据动量定理求得．又因为系统内只有摩擦力作功,根据系统的动能定理,摩擦力的功应等于系统动能的增量．木块相对平板移动的距离即可求出．解1 以地面为参考系,在摩擦力F ｆ＝μmg 的作用下,根据牛顿定律分别对木块、平板列出动力学方程F ｆ＝μmg ＝ma 1F ′ｆ＝-F ｆ＝m ′a 2a 1 和a 2 分别是木块和木板相对地面参考系的加速度．若以木板为参考系,木块相对平板的加速度a ＝a 1 ＋a 2 ,木块相对平板以初速度- v ′作匀减速运动直至最终停止．由运动学规律有- v ′2＝2as由上述各式可得木块相对于平板所移动的距离为 ()m m g μm s +'''=22v 解2 以木块和平板为系统,它们之间一对摩擦力作的总功为W ＝F ｆ (s ＋l ) -F ｆl ＝μmgs式中l 为平板相对地面移动的距离．由于系统在水平方向上不受外力,当木块放至平板上时,根据动量守恒定律,有m ′v ′＝(m ′＋m ) v ″由系统的动能定理,有()222121v v ''+'-''=m m m mgs μ 由上述各式可得()m m g μm s +'''=22v 2 -10 如图(a)所示,在一只半径为R 的半球形碗内,有一粒质量为m的小钢球,当小球以角速度ω在水平面内沿碗内壁作匀速圆周运动时,它距碗底有多高分析维持钢球在水平面内作匀角速度转动时,必须使钢球受到一与向心加速度相对应的力(向心力),而该力是由碗内壁对球的支持力F N 的分力来提供的,由于支持力F N 始终垂直于碗内壁,所以支持力的大小和方向是随ω而变的．取图示Oxy 坐标,列出动力学方程,即可求解钢球距碗底的高度．解取钢球为隔离体,其受力分析如图(b)所示．在图示坐标中列动力学方程θωmR ma θF n N sin sin 2== (1)mg θF N =cos (2) 且有 ()Rh R θ-=cos (3) 由上述各式可解得钢球距碗底的高度为2ωg R h -= 可见,h 随ω的变化而变化． 2 -11 火车转弯时需要较大的向心力,如果两条铁轨都在同一水平面内(内轨、外轨等高),这个向心力只能由外轨提供,也就是说外轨会受到车轮对它很大的向外侧压力,这是很危险的．因此,对应于火车的速率及转弯处的曲率半径,必须使外轨适当地高出内轨,称为外轨超高．现有一质量为m 的火车,以速率v 沿半径为R 的圆弧轨道转弯,已知路面倾角为θ,试求：(1) 在此条件下,火车速率v 0 为多大时,才能使车轮对铁轨内外轨的侧压力均为零(2) 如果火车的速率v ≠v 0 ,则车轮对铁轨的侧压力为多少分析如题所述,外轨超高的目的欲使火车转弯的所需向心力仅由轨道支持力的水平分量F N sin θ 提供(式中θ 角为路面倾角)．从而不会对内外轨产生挤压．与其对应的是火车转弯时必须以规定的速率v 0行驶．当火车行驶速率v ≠v 0 时,则会产生两种情况：如图所示,如v ＞v 0 时,外轨将会对车轮产生斜向内的侧压力F 1 ,以补偿原向心力的不足,如v ＜v 0时,则内轨对车轮产生斜向外的侧压力F 2 ,以抵消多余的向心力,无论哪种情况火车都将对外轨或内轨产生挤压．由此可知,铁路部门为什么会在每个铁轨的转弯处规定时速,从而确保行车安全．解 (1) 以火车为研究对象,建立如图所示坐标系．据分析,由牛顿定律有Rm θF N 2sin v = (1) 0cos =-mg θF N (2)解(1)(2)两式可得火车转弯时规定速率为θgR tan 0=v(2) 当v ＞v 0 时,根据分析有R m θF θF N 21cos sin v =+ (3) 0sin cos 1=--mg θF θF N (4)解(3)(4)两式,可得外轨侧压力为⎪⎪⎭⎫ ⎝⎛-=θg θR F sin cos m 21v 当v ＜v 0 时,根据分析有RθF θF N 22m cos sin v =- (5) 0sin cos 2=-+mg θF θF N (6)解(5)(6)两式,可得内轨侧压力为⎪⎪⎭⎫ ⎝⎛-=θR θg m F cos sin 22v 2 -12 一杂技演员在圆筒形建筑物内表演飞车走壁．设演员和摩托车的总质量为m ,圆筒半径为R ,演员骑摩托车在直壁上以速率v 作匀速圆周螺旋运动,每绕一周上升距离为h ,如图所示．求壁对演员和摩托车的作用力．分析杂技演员(连同摩托车)的运动可以看成一个水平面内的匀速率圆周运动和一个竖直向上匀速直线运动的叠加．其旋转一周所形成的旋线轨迹展开后,相当于如图(b)所示的斜面．把演员的运动速度分解为图示的v 1 和v 2 两个分量,显然v 1是竖直向上作匀速直线运动的分速度,而v 2则是绕圆筒壁作水平圆周运动的分速度,其中向心力由筒壁对演员的支持力F N 的水平分量F N2 提供,而竖直分量F N1 则与重力相平衡．如图(c)所示,其中φ角为摩托车与筒壁所夹角．运用牛顿定律即可求得筒壁支持力的大小和方向解设杂技演员连同摩托车整体为研究对象,据(b)(c)两图应有01=-mg F N (1)Rm F N 22v = (2) ()222π2π2cos h R Rθ+==v v v (3)2221N N N F F F += (4)以式(3)代入式(2),得222222222222π4π4π4π4h R Rm h R R R m F N +=+=v v (5) 将式(1)和式(5)代入式(4),可求出圆筒壁对杂技演员的作用力(即支承力)大小为22222222221π4π4⎪⎪⎭⎫ ⎝⎛++=+=h R R g m F F F N N N v 与壁的夹角φ为()g h R R F F N N 2222212π4π4arctan arctan +==v 讨论表演飞车走壁时,演员必须控制好运动速度,行车路线以及摩托车的方位,以确保三者之间满足解题用到的各个力学规律．2 -13 一质点沿x 轴运动,其受力如图所示,设t ＝0 时,v 0＝5m·ｓ-1 ,x 0＝2 m,质点质量m ＝1kg,试求该质点7ｓ末的速度和位置坐标．分析首先应由题图求得两个时间段的F (t )函数,进而求得相应的加速度函数,运用积分方法求解题目所问,积分时应注意积分上下限的取值应与两时间段相应的时刻相对应．解由题图得()⎩⎨⎧<<-<<=7s t 5s,5355s t 0 ,2t t t F 由牛顿定律可得两时间段质点的加速度分别为5s t 0 ,2<<=t a7s t 5s ,535<<-=t a对0 ＜t ＜5ｓ时间段,由t a d d v =得 ⎰⎰=tt a 0d d 0v v v 积分后得 25t +=v 再由tx d d =v 得 ⎰⎰=t t x 0d d 0v x x 积分后得33152t t x ++= 将t ＝5ｓ代入,得v 5＝30 m·ｓ-1 和x 5 ＝68.7 m对5ｓ＜t ＜7ｓ时间段,用同样方法有⎰⎰=t t a s 52d d 0v v v得 t t t 5.825.2352--=v再由⎰⎰=tx x t x s 55d d v 得 x ＝＋将t ＝7ｓ代入分别得v 7＝40 m·ｓ-1 和 x 7 ＝142 m2 -14 一质量为10 kg 的质点在力F 的作用下沿x 轴作直线运动,已知F ＝120t ＋40,式中F 的单位为N,t 的单位的ｓ．在t ＝0 时,质点位于x ＝5.0 m 处,其速度v 0＝6.0 m·ｓ-1 ．求质点在任意时刻的速度和位置．分析这是在变力作用下的动力学问题．由于力是时间的函数,而加速度a ＝d v /d t ,这时,动力学方程就成为速度对时间的一阶微分方程,解此微分方程可得质点的速度v (t )；由速度的定义v ＝d x /d t ,用积分的方法可求出质点的位置．解因加速度a ＝d v /d t ,在直线运动中,根据牛顿运动定律有tm t d d 40120v =+ 依据质点运动的初始条件,即t 0 ＝0 时v 0 ＝6.0 m·ｓ-1 ,运用分离变量法对上式积分,得()⎰⎰+=tt t 0d 0.40.12d 0v v v v ＝++又因v ＝d x /d t ,并由质点运动的初始条件：t 0 ＝0 时x 0 ＝5.0 m,对上式分离变量后积分,有()⎰⎰++=t x x t t t x 020d 0.60.40.6d x ＝++ +2 -15 轻型飞机连同驾驶员总质量为 ×103 kg ．飞机以55.0 m·ｓ-1的速率在水平跑道上着陆后,驾驶员开始制动,若阻力与时间成正比,比例系数α＝ ×102 N·ｓ-1 ,空气对飞机升力不计,求：(1) 10ｓ后飞机的速率；(2) 飞机着陆后10ｓ内滑行的距离．分析飞机连同驾驶员在水平跑道上运动可视为质点作直线运动．其水平方向所受制动力F 为变力,且是时间的函数．在求速率和距离时,可根据动力学方程和运动学规律,采用分离变量法求解．解以地面飞机滑行方向为坐标正方向,由牛顿运动定律及初始条件,有t αt m ma F -===d d v ⎰⎰-=t t m t α0d d 0v v v得 202t m α-=v v 因此,飞机着陆10ｓ后的速率为v ＝30 m·ｓ-1又 ⎰⎰⎪⎭⎫ ⎝⎛-=t xx t t m αx 0200d 2d v 故飞机着陆后10ｓ内所滑行的距离m 4676300=-=-=t mαt x x s v 2 -16 质量为m 的跳水运动员,从10.0 m 高台上由静止跳下落入水中．高台距水面距离为h ．把跳水运动员视为质点,并略去空气阻力．运动员入水后垂直下沉,水对其阻力为bv 2,其中b 为一常量．若以水面上一点为坐标原点O ,竖直向下为Oy 轴,求：(1) 运动员在水中的速率v 与y 的函数关系；(2) 如b /m ＝0.40m -1 ,跳水运动员在水中下沉多少距离才能使其速率v 减少到落水速率v 0 的1 /10 (假定跳水运动员在水中的浮力与所受的重力大小恰好相等)分析该题可以分为两个过程,入水前是自由落体运动,入水后,物体受重力P 、浮力F 和水的阻力F ｆ的作用,其合力是一变力,因此,物体作变加速运动．虽然物体的受力分析比较简单,但是,由于变力是速度的函数(在有些问题中变力是时间、位置的函数),对这类问题列出动力学方程并不复杂,但要从它计算出物体运动的位置和速度就比较困难了．通常需要采用积分的方法去解所列出的微分方程．这也成了解题过程中的难点．在解方程的过程中,特别需要注意到积分变量的统一和初始条件的确定．解 (1) 运动员入水前可视为自由落体运动,故入水时的速度为gh 20=v运动员入水后,由牛顿定律得P -F ｆ -F ＝ma由题意P ＝F 、F ｆ＝bv 2,而a ＝d v /d t ＝v (d v /d y ),代入上式后得 -bv 2＝ mv (d v /d y )考虑到初始条件y 0 ＝0 时, gh 20=v ,对上式积分,有 ⎰⎰=⎪⎭⎫ ⎝⎛-v v v v 0d d 0t y b m m by m by e gh e //02--==v v(2) 将已知条件b/m ＝0.4 m -1,v ＝代入上式,则得 m 76.5ln 0=-=v v b m y *2 -17 直升飞机的螺旋桨由两个对称的叶片组成．每一叶片的质量m ＝136 kg,长l ＝3.66 m ．求当它的转速n ＝320 r/min 时,两个叶片根部的张力．(设叶片是宽度一定、厚度均匀的薄片)分析螺旋桨旋转时,叶片上各点的加速度不同,在其各部分两侧的张力也不同；由于叶片的质量是连续分布的,在求叶片根部的张力时,可选取叶片上一小段,分析其受力,列出动力学方程,然后采用积分的方法求解．解设叶片根部为原点O ,沿叶片背离原点O 的方向为正向,距原点O 为r 处的长为d r 一小段叶片,其两侧对它的拉力分别为F Ｔ(r)与F Ｔ(r ＋d r )．叶片转动时,该小段叶片作圆周运动,由牛顿定律有()()r r ωlm r r F r F F T T T d d d 2=+-= 由于r ＝l 时外侧F Ｔ＝0,所以有 ()r r lωm F lr tr F T T d d 2⎰⎰= ()()()22222222r l l mn πr l l ωm r F T --=--= 上式中取r ＝0,即得叶片根部的张力F Ｔ0 ＝ ×105 N负号表示张力方向与坐标方向相反．2 -18 一质量为m 的小球最初位于如图(a)所示的A 点,然后沿半径为r 的光滑圆轨道ADCB 下滑．试求小球到达点C 时的角速度和对圆轨道的作用力．分析该题可由牛顿第二定律求解．在取自然坐标的情况下,沿圆弧方向的加速度就是切向加速度a ｔ,与其相对应的外力F ｔ是重力的切向分量mg sin α,而与法向加速度a n 相对应的外力是支持力F N 和重力的法向分量mg cos α．由此,可分别列出切向和法向的动力学方程F ｔ＝m d v/d t 和F n ＝ma n ．由于小球在滑动过程中加速度不是恒定的,因此,需应用积分求解,为使运算简便,可转换积分变量．倡该题也能应用以小球、圆弧与地球为系统的机械能守恒定律求解小球的速度和角速度,方法比较简便．但它不能直接给出小球与圆弧表面之间的作用力．解小球在运动过程中受到重力P 和圆轨道对它的支持力F N ．取图(b)所示的自然坐标系,由牛顿定律得tm αmg F t d d sin v =-= (1) Rm m αmg F F N n 2cos v =-= (2) 由t αr t s d d d d ==v ,得vαr t d d =,代入式(1),并根据小球从点A 运动到点C 的始末条件,进行积分,有()⎰⎰-=αααrg o 090d sin d vv v v得 αrg cos 2=v则小球在点C 的角速度为 r αg rω/cos 2==v 由式(2)得 αmg αmg rm m F N cos 3cos 2=+=v 由此可得小球对圆轨道的作用力为αmg F F N Ncos 3-=-=' 负号表示F ′N 与e n 反向．2 -19 光滑的水平桌面上放置一半径为R 的固定圆环,物体紧贴环的内侧作圆周运动,其摩擦因数为μ,开始时物体的速率为v 0 ,求：(1) t 时刻物体的速率；(2) 当物体速率从v 0减少到12 v 0时,物体所经历的时间及经过的路程．分析运动学与动力学之间的联系是以加速度为桥梁的,因而,可先分析动力学问题．物体在作圆周运动的过程中,促使其运动状态发生变化的是圆环内侧对物体的支持力F N 和环与物体之间的摩擦力F ｆ ,而摩擦力大小与正压力F N ′成正比,且F N 与F N ′又是作用力与反作用力,这样,就可通过它们把切向和法向两个加速度联系起来了,从而可用运动学的积分关系式求解速率和路程．解 (1) 设物体质量为m ,取图中所示的自然坐标,按牛顿定律,有Rm ma F n N 2v ==tma F t d d f v -=-= 由分析中可知,摩擦力的大小F ｆ＝μF N ,由上述各式可得tR μd d 2v v -= 取初始条件t ＝0 时v ＝v 0 ,并对上式进行积分,有⎰⎰-=v v v v 020d d μR t t tμR R 00v v v += (2) 当物体的速率从v 0 减少到1/2v 0时,由上式可得所需的时间为v μR t =' 物体在这段时间内所经过的路程 ⎰⎰''+==t t t tμR R t s 0000d d v v v 2ln μR s = 2 -20 质量为45.0 kg 的物体,由地面以初速60.0 m·ｓ-1 竖直向上发射,物体受到空气的阻力为F r ＝kv,且k ＝ N/( m·ｓ-1)．(1) 求物体发射到最大高度所需的时间．(2) 最大高度为多少分析物体在发射过程中,同时受到重力和空气阻力的作用,其合力是速率v 的一次函数,动力学方程是速率的一阶微分方程,求解时,只需采用分离变量的数学方法即可．但是,在求解高度时,则必须将时间变量通过速度定义式转换为位置变量后求解,并注意到物体上升至最大高度时,速率应为零．解 (1) 物体在空中受重力mg 和空气阻力F r ＝kv 作用而减速．由牛顿定律得 t m k mg d d v v =-- (1)根据始末条件对上式积分,有⎰⎰+-=v v vv v 0d d 0k mg m t t s 11.61ln 0≈⎪⎪⎭⎫ ⎝⎛+=mg k k m t v (2) 利用yv t d d d d v v =的关系代入式(1),可得 ym k mg d d v v v =-- 分离变量后积分⎰⎰+-=000d d v vv v k mg m y y故 m 1831ln 00≈⎥⎦⎤⎢⎣⎡-⎪⎪⎭⎫ ⎝⎛+-=v v mg k k mg k m y 讨论如不考虑空气阻力,则物体向上作匀减速运动．由公式g t 0v =和gy 220v =分别算得t ≈ｓ和y≈184 m,均比实际值略大一些． 2 -21 一物体自地球表面以速率v 0 竖直上抛．假定空气对物体阻力的值为F r ＝kmv 2,其中m 为物体的质量,k 为常量．试求：(1) 该物体能上升的高度；(2)物体返回地面时速度的值．(设重力加速度为常量．)分析由于空气对物体的阻力始终与物体运动的方向相反,因此,物体在上抛过程中所受重力P 和阻力F r 的方向相同；而下落过程中,所受重力P 和阻力F r 的方向则相反．又因阻力是变力,在解动力学方程时,需用积分的方法．解分别对物体上抛、下落时作受力分析,以地面为原点,竖直向上为y 轴(如图所示)．(1) 物体在上抛过程中,根据牛顿定律有ym t mkm mg d d d d 2v v v v ==-- 依据初始条件对上式积分,有 ⎰⎰+-=0200d d v vv v k g y y ⎪⎪⎭⎫ ⎝⎛++-=202ln 21v v k g k g k y 物体到达最高处时, v ＝0,故有⎪⎪⎭⎫ ⎝⎛+==g k g k y h 20max ln 21v (2) 物体下落过程中,有yv m km mg d d 2v v =+-对上式积分,有⎰⎰--=0200d d v v v v k g y y则 2/1201-⎪⎪⎭⎫ ⎝⎛+=g k v v v2 -22 质量为m 的摩托车,在恒定的牵引力F 的作用下工作,它所受的阻力与其速率的平方成正比,它能达到的最大速率是v m ．试计算从静止加速到v m /2所需的时间以及所走过的路程．分析该题依然是运用动力学方程求解变力作用下的速度和位置的问题,求解方法与前两题相似,只是在解题过程中必须设法求出阻力系数k ．由于阻力F r ＝kv 2,且F r 又与恒力F 的方向相反；故当阻力随速度增加至与恒力大小相等时,加速度为零,此时速度达到最大．因此,根据速度最大值可求出阻力系数来．但在求摩托车所走路程时,需对变量作变换．解设摩托车沿x 轴正方向运动,在牵引力F 和阻力F r 同时作用下,由牛顿定律有 tm k F d d 2v v =- (1) 当加速度a ＝d v /d t ＝0 时,摩托车的速率最大,因此可得k ＝F/v m 2 (2)由式(1)和式(2)可得t m F m d d 122v v v =⎪⎪⎭⎫ ⎝⎛- (3) 根据始末条件对式(3)积分,有⎰⎰-⎪⎪⎭⎫ ⎝⎛-=m m tF m t v v v v 2101220d 1d则 3ln 2F m t m v =又因式(3)中xm t m d d d d v v v =,再利用始末条件对式(3)积分,有⎰⎰-⎪⎪⎭⎫ ⎝⎛-=m m xF m x v v v v 2101220d 1d则 F m F m x m m 22144.034ln 2v v ≈= *2 -23 飞机降落时,以v 0 的水平速度着落后自由滑行,滑行期间飞机受到的空气阻力F 1＝-k 1 v 2 ,升力F 2＝k 2 v 2 ,其中v 为飞机的滑行速度,两个系数之比k 1/ k 2 称为飞机的升阻比．实验表明,物体在流体中运动时,所受阻力与速度的关系与多种因素有关,如速度大小、流体性质、物体形状等．在速度较小或流体密度较小时有F ∝v ,而在速度较大或流体密度较大的有F ∝v 2 ,需要精确计算时则应由实验测定．本题中由于飞机速率较大,故取F ∝v 2 作为计算依据．设飞机与跑道间的滑动摩擦因数为μ,试求飞机从触地到静止所滑行的距离．以上计算实际上已成为飞机跑道长度设计的依据之一．分析如图所示,飞机触地后滑行期间受到5 个力作用,其中F 1为空气阻力, F 2 为空气升力, F 3 为跑道作用于飞机的摩擦力,很显然飞机是在合外力为变力的情况下作减速运动,列出牛顿第二定律方程后,用运动学第二类问题的相关规律解题．由于作用于飞机的合外力为速度v 的函数,所求的又是飞机滑行距离x ,因此比较简便方法是直接对牛顿第二定律方程中的积分变量d t 进行代换,将d t 用vx d 代替,得到一个有关v 和x 的微分方程,分离变量后再作积分．解取飞机滑行方向为x 的正方向,着陆点为坐标原点,如图所示,根据牛顿第二定律有tm k F N d d 21v v =- (1)。

常微分方程第二章

m
6：x
dy x− y =e dx 解：变量分离， e dy = e dx 两边积分得： e =e +c 11.
2 dy = ( x + y) dx y x y x
变量分离得：2
1 +1
12．解
令x + y = t，则变量分离
t2 dt = dx，两边积分t − arctgt = x + c，代回变量 t 2 +1 x + y − arctg ( x + y) = x + c dy 2 x − y − 1 = dx x − 2 y + 1
2
ww
w.
e
y x
解：变量分离，得
9 : x (ln x − ln y )dy − ydx = 0 y y 解：方程可变为： − ln • dy − dx = 0 x x y 1 ln u 令u = , 则有： dx = − d ln u x x 1 + ln u y 代回原变量得：cy = 1 + ln 。 x dy x− y 10： = e dx 解：变量分离 e dy = e dx 两边积分 e = e + c
w.
0
19. 已知 f(x) ∫ f ( x)dt = 1, x ≠ 0, 试求函数f ( x)的一般表达式 .
x
1 y = − 2 y' 1 y 解：设 f(x)=y, 则原方程化为 ∫ f (x)dt = 两边求导得 y 0 − y3 = dy 1 1 1 1 ; ; ; ; ; ; ; ; ; ; dx = − 3 ; ; ; ; ; ; ; ; ; ; ; ; 两边积分得x + c = ; ; ; ; ; 所以y = ± 2 dx 2y y dy 2x + c 1 代入

常微分方程课后习题答案.doc

习题2.1 1．dxdy =2xy,并满足初始条件：x=0,y=1的特解。

解：ydy =2xdx 两边积分有：ln|y|=x 2+cy=e 2x +e c =cex 2另外y=0也是原方程的解，c=0时，y=0原方程的通解为y= cex 2,x=0 y=1时 c=1 特解为y= e 2x .2. y 2dx+(x+1)dy=0 并求满足初始条件：x=0,y=1的特解。

解：y 2dx=-(x+1)dy2ydy dy=-11+x dx两边积分: -y1=-ln|x+1|+ln|c| y=|)1(|ln 1+x c另外y=0,x=-1也是原方程的解 x=0,y=1时 c=e 特解：y=|)1(|ln 1+x c3．dxdy =yx xy y321++解：原方程为：dx dy =yy 21+31xx +yy 21+dy=31xx +dx两边积分：x(1+x 2)(1+y 2)=cx 24. (1+x)ydx+(1-y)xdy=0 解：原方程为：yy -1dy=-xx 1+dx两边积分：ln|xy|+x-y=c另外 x=0,y=0也是原方程的解。

5．（y+x ）dy+(x-y)dx=0 解：原方程为：dxdy =-yx y x +-令xy =u 则dx dy =u+x dxdu 代入有：-112++uu du=x1dxln(u 2+1)x=c-2arctgu 即 ln(y 2+x 2)=c-2arctg 2xy .6. xdxdy -y+22y x -=0解：原方程为：dx dy =xy +x x ||-2)(1xy -则令xy =u dxdy =u+ xdxdu211u- du=sgnx x1dxarcsinxy =sgnx ln|x|+c7. tgydx-ctgxdy=0 解:原方程为：tgydy =ctgxdx两边积分：ln|siny|=-ln|cosx|-ln|c| siny=xc cos 1=xc cos 另外y=0也是原方程的解，而c=0时，y=0.所以原方程的通解为sinycosx=c. 8dxdy +yexy 32+=0解：原方程为：dxdy =yey2e x 32 ex3-3e2y-=c.9.x(lnx-lny)dy-ydx=0 解：原方程为：dx dy =xy lnx y令xy =u ,则dxdy =u+ xdxduu+ xdxdu =ulnuln(lnu-1)=-ln|cx| 1+lnxy =cy.10.dxdy =e y x -解：原方程为：dxdy =e x e y -e y =ce x11dxdy =(x+y)2解：令x+y=u,则dxdy =dxdu -1dxdu -1=u 2211u+du=dxarctgu=x+c arctg(x+y)=x+c12.dxdy =2)(1y x +解：令x+y=u,则dxdy =dxdu -1dxdu -1=21uu-arctgu=x+c y-arctg(x+y)=c. 13.dxdy =1212+-+-y x y x解: 原方程为：（x-2y+1）dy=(2x-y+1)dx xdy+ydx-(2y-1)dy-(2x+1)dx=0 dxy-d(y 2-y)-dx 2+x=c xy-y 2+y-x 2-x=c14: dxdy =25--+-y x y x解：原方程为：（x-y-2）dy=(x-y+5)dx xdy+ydx-(y+2)dy-(x+5)dx=0 dxy-d(21y 2+2y)-d(21x 2+5x)=0y 2+4y+x 2+10x-2xy=c. 15:dxdy =(x+1) 2+(4y+1) 2+8xy 1+解：原方程为：dx dy=（x+4y ）2+3 令x+4y=u 则dxdy=41dxdu -4141dx du -41=u 2+3dxdu =4 u 2+13u=23tg(6x+c)-1tg(6x+c)=32(x+4y+1).16:证明方程y x dxdy =f(xy),经变换xy=u 可化为变量分离方程，并由此求下列方程：1） y(1+x 2y 2)dx=xdy2） y x dxdy =2222x -2 y x 2y+证明：令xy=u,则x dxdy +y=dxdu则dxdy =x 1dxdu -2xu ，有：u x dxdu =f(u)+1)1)((1+u f u du=x1dx所以原方程可化为变量分离方程。

常微分方程第2章习题答案

习题２-4１．求解下列微分方程：（１）yx xy y --='22；解：令ux y =，则原方程化为uu u dx du x --=+212，即x dxdu u u =--122，积分得：c x u u u +=--+-ln 1ln 2111ln2 还原变量并化简得：3)()(y x c x y +=-（２）4252--+-='y x x y y ；解：由⎩⎨⎧=--=+-042052y x x y 得 ⎩⎨⎧-==21y x令2,1+=-=y v x u ，则有vu u v du dv --=22，由第一题的结果知此方程解为3)()(v u c u v +=-，还原变量并化简得：.)1(33++=+-y x c x y（３）14212-+++='y x y x y ；解：令y x v 2+=，则1212121-++=+=v v dx dy dx dv ，即1214-+=v v dx dv ，此方程为变量分离方程，分离变量并积分得：c x v v +=+-14ln 8321，还原变量并化简得：c y x x y =++--184ln 348．（４）xy y x y -='33．解：①当0≠y 时，方程两边同时乘以32--y ,则233222--+-='-xy x y y ，令2-=y z ，则322x xz dxdz-=, 此方程为一阶线性方程，由公式得：122++=x ce z x还原变量得：122)1(2-++=x ce y x . ②0=y 也是方程的解．2. 利用适当的变换，求解下列方程：（１）)cos(y x y -='；解：令y x u -=，则u dx dy dx du cos 11-=-=， ①当1cos ≠u 时，有dx udu =-cos 1，即 dx u du=2sin 22，两边积分得：c x uctg +=221还原变量化简得：2sin 2sin 22cos yx c y x x y x -+-=-． ②当1cos =u 时，即πk x y 2+=)(Z k ∈也是方程的解．（２）0)()3(22=+++dv uv u du v uv ；解：方程两边同时乘以u 则原方程化为：0)()3(2322=+++dv v u u du uv v u ，即 0)()3(2232=+++vdv u du uv dv u vdu u 此方程为全微分方程，则原方程的解为：c v u v u =+22321．（３）)2(2)3(222yx y x dx dy y x -=++；解：原方程即为324222222++-=y x x y xdx ydy ，令u y v x ==22,，则324++-=v u vu dv du ,由⎩⎨⎧=++=-03024v u v u 得⎩⎨⎧-=-=21v u ，令⎩⎨⎧+=+=21v n u m ，则有n m n m dn dm +-=24令z n m=，则zn m =， 124+-=+=z z z n dn dz dn dm ，则有1)2)(1(+--=z z z n dn dz ，此方程为变量分离方程，分离变量并积分得：n c zz ln 2)1(ln32+=--，还原变量并化简得：322222)32()1(-+-=+-y x c y x .（４）yy y x xxy x dx dy 8237323223-+-+=．解：原方程即为823732222222-+-+=y x y x xdx ydy ，令22,x v y u ==,则823732-+-+=u v u v dv du ，由⎩⎨⎧=++=-+08230732u v u v ⎩⎨⎧==⇒21v u ，令⎩⎨⎧-=-=21v n u m ，则m n m n dn dm 2332++=，令z n m=，可将方程化为变量分离形方程， n dn dz zz =-+)2223(2，两边积分得：c n z z z +=---+ln 1ln 2111ln 432，还原变量并化简得：)3()1(22522-+=--y x c y x ．3. 求解下列微分方程：（１）．2241xy y --='；解：令xy z =，则原方程可化为：)41(12-+-=z z x dx dz ， ①当21≠z 时，即21≠xy 时方程为x dxdz z =--2)21(1 ，此方程为变量分离方程，两边积分得：c x z +=-ln 211还原变量并化简得：cxx x x y ++=ln 121； ②当21=z 时，xy 21=是方程的特解．（２）．1222++='xy y x y x ；解：原方程即为：221x x y y y ++='，令xy z =，则2)1(1+=z xdx dz ，此方程为变量分离方程，分离变量积分得：c x z +=+-ln 11，还原变量并化简得：cxx x x y +--=ln 11． 4. 试把二阶微分方程0)()(=+'+''y x q y x p y 化为一个黎卡提方程．解：令⎰=udxe y ，则⎰='udxue y ，+⎰=''udxe u y 2⎰'udxe u ，代入原方程可得：=+'+''y x q y x p y )()(+⎰udxe u 2⎰'udxe u ＋)()(x q ue x p udx+⎰⎰udxe ＝０，即有：0)()(2=++'+x q u x p u u ，此方程为一个黎卡提方程．5. 求一曲线，使得过这一曲线上任一点的切线与该点向径的夹角等于45．解：设此曲线为)(x y y =，由题意得：1451==+-tg xy dx dy x y dx dy ，化简得：y x y x dx dy -+=，此方程为齐次方程，解之得：c y x x y arctg =+-)ln(2122．6. 探照灯的反光镜（旋转面）应具有何种形状，才能使点光源发射的光束反射成平行线束？解：取点光源所在处为坐标原点，而x 轴平行于光的反射方向，建立三维坐标系．设所求曲面由曲线⎩⎨⎧==0)(z x f y 绕x 轴旋转而成,则求反射镜面问题归结为求 xy 平面上的曲线y=f(x)的问题．由题意及光的反射定律，可得到函数)(x f y =所应满足的微分方程式：22yx x ydx dy ++=，此方程为齐次方程，解之得：)2(2x c c y +=，（其中c 为任意正常数）．)2(2x c c y +=就是所求的平面曲线，它是抛物线，因此反射镜面的形状为旋转抛物面)2(22x c c z y +=+．习题２-5１．求解下列微分方程：（１）．0)()23(2232=++++dy y x dx y xy y x ；解：方程两边同乘xe33，则)33()369(233323323=++++dy y e dx y e dy x e xydx e ydx x e x x x x x ，此方程为全微分方程，即 c y e y x e x x =+33233．（２）．0)2(2=-+-dy e xy ydx y ；解：方程两边同乘y e y 21，则 0)12(22=-+dy yxe dx e y y即01)2(22=-+dy ydy xe dx e yy 此方程为全微分方程，即有 c y xe y =-ln 2 ．（３）．0)3()63(2=+++dy xyy x dx y x ；解：方程两边同乘 xy ，则0)3()63(232=+++dy y x dx x y x即 0)36()3(232=+++dy y xdx dy x ydx x 此方程为全微分方程，即有c x y y x =++2333 ．（４）．22()0ydx x y x dy -++=; 解：方程两边同乘221y x +，则 022=-+-dy yx xdyydx ，此方程为全微分方程，即 c y yxarctg=- （5）．0)1(2223=-+dy y x dx xy ；解：方程两边同乘21y ，则0)1(222=-+dy y x xydx ，此方程为全微分方程，即c y x y=+21. （6）．0)1(=-+xd y dx xy y ；解：方程两边同乘21y ，则0)1(2=-+dy y xdx y xdx ，此方程为全微分方程，即c x y x =+221. （7）0)(2223=-+dy xy x dx y ；解：方程两边同乘y x 21，则 02)2(22=+-dy y dy x y dx x y ，此方程为全微分方程，即 c y xy =+-ln 22（8）．0)c o s2(=++dy y y ctgy e dx e xx解：方程两边同乘y sin ，则02sin )cos sin (=++ydy yc ydy e ydx e x x ，此方程为全微分方程，即 11cos cos 2sin 224xe y y y y c -+=. 2. 证明方程（5.1）有形如)),((y x φμμ=的积分因子的充要条件是)),((y x f yP P x Q Q xQy P φ=∂∂-∂∂∂∂-∂∂，并写出这个积分因子。

马知恩周义仓编常微分方程定性与稳定性方法部分习题参考解答

马知恩周义仓编常微分⽅程定性与稳定性⽅法部分习题参考解答第⼀章基本定理1设有 $$\bex \frac{\rd \bbx}{\rd t}=\bbf(t,\bbx),\quad \bbx(t_0)=\bbx^0,\quad (t_0,\bbx^0)\in \bbR\times \bbR^n. \eex$$试证: 若 $\bbf\in C^1(G)$, 则在 $(t_0,\bbx^0)$ 的领域内, 此 Cauchy 问题的解存在惟⼀.证明: 由 $f\in C^1(G)$ 蕴含 $f\in C(G)$ 且在 $G$ 内适合 Lipschitz 条件知有结论.2试讨论下列⽅程解的存在区间:(1) $\dps{\frac{\rd y}{\rd x}=\frac{1}{x^2+y^2}}$;(2) $\dps{\frac{\rd y}{\rd x}=y(y-1)}$.解答:(1) 由 $\dps{\frac{\rd x}{\rd y}=x^2+y^2}$ 的解的存在区间有限知 $y$ 有界, ⽽由解的延拓定理, 原⽅程解的存在区间为 $\bbR$.(2) 直接求解有 $\dps{y=\frac{1}{1-\frac{y_0-1}{y_0}e^x}}$, ⽽a.当 $0\leq y_0\leq 1$ 时, 原⽅程解的存在区间为 $\bbR$;b.当 $y_0<0$ 时, 原⽅程解的存在区间为 $\dps{\sex{\ln\frac{y_0}{y_0-1},\infty}}$;c.当 $y_0>1$ 时, 原⽅程解的存在区间为 $\dps{\sex{-\infty,\ln\frac{y_0}{y_0-1}}}$.3 设有⼀阶微分⽅程式 $$\bex \frac{\rd x}{\rd t}=(t-x)e^{tx^2}. \eex$$ 试证: 过任⼀点 $(t_0,x_0)\in\bbR^2$ 的右⾏解的存在区间均为 $[t_0,+\infty)$.证明: 由 $$\bex \frac{\rd x}{\rd t}=(t-x)e^{tx^2}=\left\{\ba{ll} <0,&x>t,\\ >0,&x<t \ea\right. \eex$$ 知解在 $\sed{x>t}$ 内递减,在 $\sed{x<t}$ 内递增. 当 $x_0>t_0$ 时, 在 $$\bex \sed{(t,x);t\in\bbR, t_0<x<x_0} \eex$$ 内应⽤解的延伸定理知解定与$\sed{x=t}$ 相交, 之后解递增, 在 $$\bex \sed{(t,x);t\in\bbR,x<t} \eex$$ 内应⽤延伸定理及⽐较定理即知结论.4设有⼀阶⽅程 $\dps{\frac{\rd x}{\rd t}=f(x)}$, 若 $f\in C(-\infty,+\infty)$, 且当 $x\neq 0$ 时有 $xf(x)<0$. 求证过 $\forall\(t_0,x_0)\in\bbR^2$, Cauchy 问题的右⾏解均在 $[t_0,+\infty)$ 上存在, 且 $\dps{\lim_{t\to+\infty}x(t)=0}$.证明: 由题意, $$\bex f(x)\left\{\ba{ll} >0,&x<0,\\ <0,&x>0. \ea\right. \eex$$ ⽽由 $f$ 的连续性, $f(0)=0$. 于是当 $x_0=0$ 时,由解的唯⼀性知 $x=0$. 当 $x_0>0$ 时, 在 $$\bex \sed{(t,x);t\in\bbR,0<x<x_0} \eex$$ 内应⽤延伸定理及惟⼀性定理知 $x(t)$ 递减趋于 $0$. 当 $x_0<0$ 时, 在 $$\bex \sed{(t,x);t\in\bbR,x_0<x<0} \eex$$ 内应⽤延伸定理及惟⼀性定理知 $x(t)$ 递增趋于 $0$.5若 $\bbf(t,\bbx)$ 在全空间 $\bbR\times\bbR^n$ 上连续且对 $\bbx$ 满⾜局部 Lipschitz 条件且 $$\bex \sen{\bbf(t,\bbx)}\leq L(r),\quad r=\sqrt{\sum_{i=1}^n x_i^2},\quad \bbx=(x_1,\cdots,x_n)^T, \eex$$ 其中 $L(r)>0, r>0$, 且 $$\bee\label{1.5:1}\int_a^{+\infty}\frac{\rd r}{L(r)}=+\infty,\quad a>0. \eee$$ 试证: 对 $\forall\ (t_0,\bbx^0)\in\bbR\times\bbR^n$, Cauchy 问题的解均可对 $t$ ⽆限延拓.证明: 由解的延伸定理, 仅须证明在任何有限区间 $-\infty<\alpha<t<\beta<+\infty$ 上, $\bbx(t)$ 有界. 为此, 令 $y(t)=\sen{\bbx(t)}$,则 $$\beex \bea \frac{\rd y(t)}{\rd t}&=2\bbx(t)\cdot\frac{\rd \bbx(t)}{\rd t} =2\bbx(t)\cdot \bbf(t,\bbx(t)),\\\sev{\frac{\rd y(t)}{\rd t}} &\leq 2\sqrt{y(t)}\cdot L\sex{\sqrt{y(t)}},\\ \frac{\rd \sqrt{y(t)}}{L\sex{\sqrt{y(t)}}}&\leq \rd t,\\ \int_\alpha^\beta \frac{\rd \sqrt{y(t)}}{L\sex{\sqrt{y(t)}}} &\leq \int_\alpha^\beta \rd t=\beta-\alpha. \eea \eeex$$ 这与\eqref{1.5:1} ⽭盾 (事实上, 当 $\alpha,\beta\gg 1$, $|\alpha-\beta|\ll 1$ 时, 不等式右端可任意⼩, ⽽不等式左端有积分发散知可⼤于某⼀正常数).6设有微分⽅程 $$\bex \frac{\rd \bbx}{\rd t}=\bbf(t,\bbx), \eex$$ $\bbf\in C(G\subset \bbR\times\bbR^n)$, 试证: 若对$\forall\ (t_0,\bbx^0)\in G$, Cauchy 问题的解都存在唯⼀, 则解必对初值连续依赖.证明: 参考[家⾥蹲⼤学数学杂志第134期, 常微分⽅程习题集, 第1600页].7 试在定理 1.1 的假设下, 利⽤ Gronwall 引理直接证明解对初始时刻 $t_0$ 的连续依赖性.证明: 参考定理 1.7 的证明.8 设有⼀阶 Cauchy 问题 $$\bex \frac{\rd y}{\rd x}=x^2+(y+1)^2,\quad y(0)=0. \eex$$ 试利⽤⽐较定理证明, 若设解的右⾏饱和区间为 $[0,\beta)$, 则 $\dps{\frac{\pi}{4}\leq \beta\leq 1}$.证明: 仅须注意到当 $0\leq x\leq 1$ 时, $$\bex (y+1)^2\leq x^2+(y+1)^2\leq 1+(y+1)^2. \eex$$ 再利⽤⽐较定理即知结论.第⼆章动⼒系统的基本知识1试证明: $\Omega_P=\vno$ 的充要条件是 $L_P^+$ 趋于⽆穷.证明: $\ra$ ⽤反证法. 若 $L_P^+$ 不趋于⽆穷, 则 $$\bex \exists\ M>0, t_n\nearrow +\infty,\st \sen{\mbox{ $\varphi$}(P,t_n)}\leq M. \eex$$ 由 Weierstrass 定理, $$\bex \exists\ \sed{t_n'}\subset \sed{t_n},\st \mbox{ $\varphi$}(P,t_n)\to Q,\eex$$ ⽽ $Q\in \Omega_P$, 这是⼀个⽭盾. $\la$ 亦⽤反证法. 若 $\Omega_P\neq \vno$, ⽽设 $Q\in \Omega_P$, 则 $$\bex\exists\ t_n\nearrow+\infty,\st \mbox{ $\varphi$}(P,t_n)\to Q. \eex$$ 这与 $L_P^+$ 趋于⽆穷⽭盾.2试证明: 若 $\Omega_P$ 仅含惟⼀奇点 $P^*$, 则当 $t\to+\infty$ 时必有 $L_P^+$ 趋向于 $P^*$.证明: ⽤反证法. 设 $$\bee\label{2.2:1} \exists\ \ve_0>0,\ t_n\nearrow+\infty, \st \sen{\mbox{ $\varphi$}(P,t_n)-P^*}\geq\ve_0. \eee$$ 则(1)若 $\sed{t_n}$ 有有界的⼦列, 则适当抽取⼦列 $\sed{t_n'}$ 后有 $$\bex \mbox{ $\varphi$}(P,t_n')\to Q. \eex$$ 于是 $Q\in\Omega_P=\sed{P^*}$. 这与 \eqref{2.2:1} ⽭盾.(2)若 $\sed{t_n}$ ⽆有界的⼦列, 则 $\dps{\lim_{n\to\infty}\mbox{ $\varphi$}(P,t_n)=\infty}$, ⽽ $\infty\in\Omega_P=\sed{P^*}$, ⼜是⼀个⽭盾.3试证明: 若 $\Omega_P$ 有界且 $\Omega_P$ ⾮闭轨, 则 $\forall\ R\in \Omega_P$, $\Omega_R$ 与 $A_R$ 必均为奇点.证明: ⽤反证法证明 $\Omega_R$ 为奇点集, $A_R$ 为奇点集类似可证. 设 $\Omega_R$ 含有常点. 由 $R\in \Omega_P$ 及$\Omega_P$ 为不变集知 $L_R\subset \Omega_Q$. 于是按引理 2.3, $L_R$ 为闭轨线, $L_R=\Omega_R\subset \Omega_P$. 这与 $\Omega_P$ ⾮闭轨⽭盾.4试证明: ⼀系统的圈闭奇点的集合是⼀闭集.证明: 全体奇点的集合为 $$\bex \sed{\bbx^*\in G; \bbf(\bbx^*)=\mbox{ $0$}}. \eex$$ 由 $\bbf$ 的连续性即知结论.5 若 $L_P^+$ 有界且 $\Omega_P$ 仅由奇点构成, 能否断定 $\Omega_P$ 仅含⼀个奇点?解答: 不能断定. 仅能说 $\Omega_P$ 为由奇点构成的连通闭集或闭轨线.6 设 $O(0,0)$ 是⼀平⾯⾃治系统的惟⼀奇点, 且是稳定的, 全平⾯没有闭轨线. 试证: (1) 此系统的任⼀轨线必负向⽆界; (2) 任⼀有界的正半轨闭进⼊奇点 $O$.证明:(1) ⽤反证法. 若有⼀轨线负向有界, 则在定理 2.8 中, 由全平⾯没有闭轨线知 (3),(4) 不成⽴; 由 $O$ 为惟⼀奇点知 (1),(2),(5) 不成⽴. 这是⼀个⽭盾.(2) 对有界正半轨⽽⾔, 定理 2.8 中仅有 (1),(2),(5) 可能成⽴. 若 (1),(2) 成⽴, 则结论已证; ⽽由全平⾯没有闭轨线知 (5) 不成⽴.第三章稳定性理论1 讨论⽅程 $$\bee\label{3.1:1} \sedd{\ba{ll}\frac{\rd x_1}{\rd t}=x_2,\\ \frac{\rd x_2}{\rd t}=-a^2\sin x_1\ea} \eee$$ 零解的稳定性.解答: 选取 $$\bex V(\bbx)=\frac{x_2^2}{2}+a^2(1-\cos x_1), \eex$$ 则 $V$ 在原点的⼀邻域内是正定的, 且沿 \eqref{3.1:1} 的轨线有 $$\bex \dot V(\bbx)=V_{x_1}x_1'+V_{x_2}x_2'=0. \eex$$ 由此, 零解是稳定的, 但不是渐近稳定的.2 证明⽅程 $\dps{\frac{\rd x}{\rd t}=-x+x^2}$ 的零解是指数渐近稳定的, 但不是全局渐近稳定的.证明: 解该微分⽅程有: $$\bex \ba{ccc} -\frac{1}{x^2}\frac{\rd x}{\rd t}=\frac{1}{x}-1,&\frac{\rd y}{\rd t}=y-1\\sex{y=\frac{1}{x}},&\frac{\rd z}{\rd t}=-e^{-t}\ \sex{z=e^{-t}y},\\ z=e^{-t}+C,&y=Ce^t+1,&x=\frac{1}{1+Ce^t}. \ea \eex$$由此, 原微分⽅程的解为 $$\bex x=0,\mbox{ 或 }x(t)=\frac{1}{1+Ce^t}. \eex$$ 取初值 $(t_0,x_0),\ x_0\neq 0$, 有 $$\bexx(t,t_0,x_0)=\frac{x_0}{1+e^{t-t_0}(1-x_0)}. \eex$$ 故当 $|x_0|<1$ 时, $$\bex |x(t,t_0,x_0)|\leq \sev{\frac{1}{x_0}-1}e^{-(t-t_0)}. \eex$$ 这说明零解是指数渐近稳定的. 但由于从 $(t_0,1)$ 出发的解 $x(t,t_0,1)=1$ 不趋于零解, ⽽零解不是全局渐近稳定的.3 在相空间 $\bbR^n$ 中给出 $\dps{\frac{\rd \bbx}{\rd t}=\bbf(t,\bbx),\ \bbf(t,0)=0}$ 的零解稳定、渐近稳定、不稳定的⼏何解释.解答: 零解是稳定的 $\lra\ \forall\ \ve>0,\ \exists\ \delta>0,\ \forall\ P\in B_\delta,\ L_P^+\subset B_\ve$; 零解是渐进稳定的$\lra\ \exists\ U\ni O,\ \forall\ P\in U,\ L_P^+\to 0$; 零解是不稳定的 $\lra\ \exists\ \ve_0>0,\ \exists\ P_n\to0, \stL_{P_n}^+\bs B_\ve\neq \vno$.4判断下列系统零解的稳定性:(1) $\dps{\sedd{\ba{ll} \frac{\rd x_1}{\rd t}=mx_2+\alpha x_1(x_1^2+x_2^2),\\ \frac{\rd x_2}{\rd t}=-mx_1+\alphax_2(x_1^2+x_2^2); \ea}}$;(2) $\dps{\frac{\rd^2x}{\rd t^2}+\sex{\frac{\rd x}{\rd t}}^3+f(x)=0,}$ 其中 $xf(x)>0\ (x\neq 0), f(0)=0$;(3) $\dps{\frac{\rd^2x}{\rd t^2}-\sex{\frac{\rd x}{\rd t}}^2sgn\sex{\frac{\rd x}{\rd t}}+x=0}$.解答:(1) 取 $$\bex V=x_1^2+x_2^2, \eex$$ 则 $V$ 正定, 且沿微分⽅程的轨线有 $$\bex \dot V=2\alpha(x_1^2+x_2^2)\sedd{\ba{lll} \mbox{正定},&\alpha>0,\\ 0,&\alpha=0,\\ \mbox{负定},&\alpha<0. \ea} \eex$$ 于是当 $\alpha>0$ 时, 由定理 3.3, 零解是不稳定的; 当 $\alpha=0$ 时, 由定理 3.1, 定理是稳定的; 当 $\alpha<0$ 时, 由定理 3.1, 零解是渐近稳定的.(2) 令 $\dps{x_1=x,x_2=\frac{\rd x}{\rd t}}$, 则 $$\bex \frac{\rd x_1}{\rd t}=x_2,\quad \frac{\rd x_2}{\rd t}=-x_2^3-f(x_1). \eex$$ 取 $$\bex V=\frac{x_2^2}{2}+\int_0^{x_1}f(t)\rd t, \eex$$ 则 $V$ 正定, 且沿微分⽅程的轨线有 $\dot V=-x_2^4\leq 0.$再 $$\bex \sed{\bbx;\dot V(\bbx)=0}=\sed{0}, \eex$$ 我们据定理 3.2 知零解是渐近稳定的.(3) 令 $\dps{x_1=x,x_2=\frac{\rd x}{\rd t}}$, 则 $$\bex \frac{\rd x_1}{\rd t}=x_2,\quad \frac{\rd x_2}{\rd t}=x_2^2sgn(x_2)-x_1. \eex$$ 取 $$\bex V=\frac{x_1^2+x_2^2}{2}, \eex$$ 则 $V$ 正定, 且沿微分⽅程的轨线有 $\dot V=x_2^2|x_2|$是正定的. 我们据定理 3.3 知零解是不稳定的.5 若存在有⽆穷⼩上界的正定函数 $V(t,\bbx)$, 它沿着 $$\bex (3.3.1)\quad \frac{\rd\bbx}{\rd t}=\bbf(t,\bbx),\quad \bbf(t,0)=0 \eex$$ 解曲线的全导数 $\dot V(t,\bbx)$ 负定, 证明 (3.3.1) 的零解是渐近稳定的.证明: 仅须注意到存在正定函数 $W(x)$, $W_1(x)$ 使得 $$\bex W(\bbx)\leq V(t,\bbx)\leq W_1(\bbx). \eex$$ ⽽可仿照定理 3.1 的证明.6 讨论 $\dps{\frac{\rd x}{\rd t}=\frac{g'(t)}{g(t)}x}$ 零解的稳定性, 其中 $\dps{g(t)=\sum_{n=1}^\infty \frac{1}{1+n^4(t-n)^2}}$. 能否得到零解渐近稳定的结果? 为什么?解答: 直接求解有 $$\bex x(t)=\frac{x_0}{g(t_0)}{g(t)}, \eex$$ ⽽由 $$\bex |x(t)|\leq\frac{|x_0|}{g(t_0)}\sez{2+\sum_{n\neq [t],[t]+1}\frac{1}{1+n^4(t-n)^2}} \leq \frac{|x_0|}{g(t_0)}\sez{2+\sum_{n=1}^\infty\frac{1}{n^4}} \eex$$ 知零解是稳定的; 由$$\bex |x(k)|=\frac{|x_0|}{g(t_0)}\sez{1+\sum_{n\neq k}\frac{1}{n^4(k-n)^2}}\geq \frac{|x_0|}{g(t_0)} \eex$$ 知零解不是渐近稳定的.7证明 $\dps{\frac{\rd x}{\rd t}=-\frac{x}{t+1}}$ 的零解是渐近稳定的, 但不存在有⽆穷⼩上界的正定函数 $V(t,x)$, 使得 $\dotV(t,x)$ 负定 (该习题表明习题 5 中渐近稳定性定理中的条件不是必要的).证明: 直接求解有 $$\bex x(t)=\frac{x_0}{1+t}. \eex$$ ⽽零解是渐近稳定的.。

高等数学上册第六版课后习题详细图文答案第二章

高等数学上册第六版课后习题详细答案第二章习题2-11. 设物体绕定轴旋转, 在时间间隔[0, t ]内转过的角度为θ, 从而转角θ是t 的函数: θ=θ(t ). 如果旋转是匀速的, 那么称tθω=为该物体旋转的角速度, 如果旋转是非匀速的, 应怎样确定该物体在时刻t 0的角速度？解在时间间隔[t 0, t 0+∆t ]内的平均角速度ω为tt t t t ∆-∆+=∆∆=)()(00θθθω, 故t 0时刻的角速度为)()()(l i m l i m l i m 000000t tt t t t t t t θθθθωω'=∆-∆+=∆∆==→∆→∆→∆. 2. 当物体的温度高于周围介质的温度时, 物体就不断冷却, 若物体的温度T 与时间t 的函数关系为T =T (t ), 应怎样确定该物体在时刻t 的冷却速度？解物体在时间间隔[t 0, t 0+∆t ]内, 温度的改变量为∆T =T (t +∆t )-T (t ),平均冷却速度为tt T t t T t T ∆-∆+=∆∆)()(, 故物体在时刻t 的冷却速度为)()()(lim lim 00t T tt T t t T t T t t '=∆-∆+=∆∆→∆→∆. 3. 设某工厂生产x 单位产品所花费的成本是f (x )元, 此函数f (x )称为成本函数, 成本函数f (x )的导数f '(x )在经济学中称为边际成本. 试说明边际成本f '(x )的实际意义.解 f (x +∆x )-f (x )表示当产量由x 改变到x +∆x 时成本的改变量.xx f x x f ∆-∆+)()(表示当产量由x 改变到x +∆x 时单位产量的成本. xx f x x f x f x ∆-∆+='→∆)()(lim )(0表示当产量为x 时单位产量的成本. 4. 设f (x )=10x 2, 试按定义, 求f '(-1).解 xx x f x f f x x ∆--∆+-=∆--∆+-=-'→∆→∆2200)1(10)1(10lim )1()1(lim)1( 20)2(lim 102lim 10020-=∆+-=∆∆+∆-=→∆→∆x x x x x x . 5. 证明(cos x )'=-sin x .解 xx x x x x ∆-∆+='→∆cos )cos(lim )(cos 0xx x x x ∆∆∆+-=→∆2s i n )2s i n (2lim 0 x x x x x x s i n ]22s i n )2s i n ([lim 0-=∆∆∆+-=→∆. 6. 下列各题中均假定f '(x 0)存在, 按照导数定义观察下列极限, 指出A 表示什么:(1)A xx f x x f x =∆-∆-→∆)()(lim000; 解 xx f x x f A x ∆-∆-=→∆)()(lim 000 )()()(lim 0000x f xx f x x f x '-=∆--∆--=→∆-. (2)A xx f x =→)(lim 0, 其中f (0)=0, 且f '(0)存在; 解 )0()0()0(lim )(lim 00f xf x f x x f A x x '=-+==→→. (3)A hh x f h x f h =--+→)()(lim 000. 解 hh x f h x f A h )()(lim 000--+=→ hx f h x f x f h x f h )]()([)]()([lim 00000----+=→ h x f h x f h x f h x f h h )()(lim )()(lim 000000----+=→→ =f '(x 0)-[-f '(x 0)]=2f '(x 0).7. 求下列函数的导数:(1)y =x 4;(2)32x y =;(3)y =x 1. 6;(4)xy 1=; (5)21xy =; (6)53x x y =;(7)5322x x x y =; 解 (1)y '=(x 4)'=4x 4-1=4x 3 .(2)3113232323232)()(--=='='='x x x x y . (3)y '=(x 1. 6)'=1.6x 1. 6-1=1.6x 0. 6.(4)23121212121)()1(-----=-='='='x x x x y . (5)3222)()1(---='='='x x x y . (6)511151651653516516)()(x x x x x y =='='='-. (7)651616153226161)()(--=='='='x x x x x x y . 8. 已知物体的运动规律为s =t 3(m). 求这物体在t =2秒(s )时的速度. 解v =(s )'=3t 2, v |t =2=12(米/秒).9. 如果f (x )为偶函数, 且f (0)存在, 证明f (0)=0.证明当f (x )为偶函数时, f (-x )=f (x ), 所以)0(0)0()(l i m 0)0()(l i m 0)0()(l i m )0(000f x f x f x f x f x f x f f x x x '-=-----=---=--='→-→→, 从而有2f '(0)=0, 即f '(0)=0.10. 求曲线y =sin x 在具有下列横坐标的各点处切线的斜率: π32=x , x =π. 解因为y '=cos x , 所以斜率分别为2132c o s 1-==πk , 1cos 2-==πk . 11. 求曲线y =cos x 上点)21 ,3(π处的切线方程和法线方程式. 解y '=-sin x , 233sin 3-=-='=ππx y , 故在点)21 ,3(π处, 切线方程为)3(2321π--=-x y , 法线方程为)3(3221π--=-x y . 12. 求曲线y =e x 在点(0,1)处的切线方程.解y '=e x , y '|x =0=1, 故在(0, 1)处的切线方程为y -1=1⋅(x -0), 即y =x +1.13. 在抛物线y =x 2上取横坐标为x 1=1及x 2=3的两点, 作过这两点的割线, 问该抛物线上哪一点的切线平行于这条割线？解 y '=2x , 割线斜率为421913)1()3(=-=--=y y k . 令2x =4, 得x =2. 因此抛物线y =x 2上点(2, 4)处的切线平行于这条割线.14. 讨论下列函数在x =0处的连续性与可导性:(1)y =|sin x |;(2)⎪⎩⎪⎨⎧=≠=000 1sin 2x x x x y . 解 (1)因为y (0)=0, 0)sin (lim |sin |lim lim 000=-==---→→→x x y x x x , 0sin lim |sin |lim lim 000===+++→→→x x y x x x , 所以函数在x =0处连续.又因为1s i n l i m 0|0s i n ||s i n |l i m 0)0()(l i m )0(000-=-=--=--='---→→→-xx x x x y x y y x x x , 1s i n lim 0|0sin ||sin |lim 0)0()(lim )0(000==--=--='+++→→→+xx x x x y x y y x x x , 而y '-(0)≠y '+(0), 所以函数在x =0处不可导.解因为01sin lim )(lim 200==→→xx x y x x , 又y (0)=0, 所以函数在x =0处连续. 又因为01s i n l i m 01s i n l i m 0)0()(l i m 0200==-=--→→→xx x x x x y x y x x x , 所以函数在点x =0处可导, 且y '(0)=0.15. 设函数⎩⎨⎧>+≤=1 1 )(2x b ax x x x f 为了使函数f (x )在x =1处连续且可导, a , b 应取什么值？解因为1lim )(lim 211==--→→x x f x x , b a b ax x f x x +=+=++→→)(lim )(lim 11, f (1)=a +b , 所以要使函数在x =1处连续, 必须a +b =1 .又因为当a +b =1时211l i m )1(21=--='-→-x x f x ,a x x a xb a x a x b ax f x x x =--=--++-=--+='+++→→→+1)1(lim 11)1(lim 11lim )1(111, 所以要使函数在x =1处可导, 必须a =2, 此时b =-1.16. 已知⎩⎨⎧<-≥=00 )(2x x x x x f 求f +'(0)及f -'(0), 又f '(0)是否存在？解因为f -'(0)=10lim )0()(lim 00-=--=---→→xx x f x f x x , f +'(0)=00lim )0()(lim 200=-=-++→→xx x f x f x x , 而f -'(0)≠f +'(0), 所以f '(0)不存在. 17. 已知f (x )=⎩⎨⎧≥<0 0 sin x x x x , 求f '(x ) . 解当x <0时, f (x )=sin x , f '(x )=cos x ;当x >0时, f (x )=x , f '(x )=1;因为 f -'(0)=10sin lim )0()(lim 00=-=---→→xx x f x f x x , f +'(0)=10lim )0()(lim 00=-=-++→→xx x f x f x x , 所以f '(0)=1, 从而 f '(x )=⎩⎨⎧≥<0 10 cos x x x . 18. 证明: 双曲线xy =a 2上任一点处的切线与两坐标轴构成的三角形的面积都等于2a 2 .解由xy =a 2得x a y 2=, 22x a y k -='=. 设(x 0, y 0)为曲线上任一点, 则过该点的切线方程为)(02020x x x a y y --=-. 令y =0, 并注意x 0y 0=a 2, 解得0022002x x a x y x =+=, 为切线在x 轴上的距. 令x =0, 并注意x 0y 0=a 2, 解得00022y y x a y =+=, 为切线在y 轴上的距. 此切线与二坐标轴构成的三角形的面积为200002||2|2||2|21a y x y x S ===.习题 2-21. 推导余切函数及余割函数的导数公式:(cot x )'=-csc 2x ; (csc x )'=-csc x cot x .解 xx x x x x x x 2sin cos cos sin sin )sin cos ()(cot ⋅-⋅-='=' x xx x x 22222c s c s i n 1s i n c o s s i n -=-=+-=. x x xx x x c o t c s c s i n c os )s i n 1()(c s c 2⋅-=-='='. 2. 求下列函数的导数:(1)1227445+-+=xx x y ; (2) y =5x 3-2x +3e x ;(3) y =2tan x +sec x -1;(4) y =sin x ⋅cos x ;(5) y =x 2ln x ;(6) y =3e x cos x ;(7)xx y ln =; (8)3ln 2+=xe y x ; (9) y =x 2ln x cos x ;(10)tt s cos 1sin 1++=; 解 (1))12274()12274(14545'+-+='+-+='---x x x xx x y 2562562282022820x x x x x x +--=+--=---. (2) y '=(5x 3-2x +3e x )'=15x 2-2x ln2+3e x .(3) y '=(2tan x +sec x -1)'=2sec 2x +sec x ⋅tan x =sec x (2sec x +tan x ).(4) y '=(sin x ⋅cos x )'=(sin x )'⋅cos x +sin x ⋅(cos x )'=cos x ⋅cos x +sin x ⋅(-sin x )=cos 2x .(5) y '=(x 2ln x )'=2x ⋅ln x +x 2⋅x1=x (2ln x +1) . (6) y '=(3e x cos x )'=3e x ⋅cos x +3e x ⋅(-sin x )=3e x (cos x -sin x ).(7)22ln 1ln 1)ln (x x x x x x x x y -=-⋅='='. (8)3422)2(2)3ln (x x e x x e x e x e y x x x x -=⋅-⋅='+='. (9) y '=(x 2ln x cos x )'=2x ⋅ln x cos x +x 2⋅x1⋅cos x +x 2 ln x ⋅(-sin x )2x ln x cos x +x cos x -x 2 ln x sin x .(10)22)cos 1(cos sin 1)cos 1()sin )(sin 1()cos 1(cos )cos 1sin 1(t t t t t t t t tt s +++=+-+-+='++='.3. 求下列函数在给定点处的导数:(1) y =sin x -cos x , 求6π='x y 和4π='x y .(2)θθθρcos 21sin +=,求4πθθρ=d d .(3)553)(2x x x f +-=, 求f '(0)和f '(2) . 解 (1)y '=cos x +sin x ,21321236s i n 6c o s 6+=+=+='=πππx y , 222224s i n 4c o s 4=+=+='=πππx y . (2)θθθθθθθρcos sin 21sin 21cos sin +=-+=d d , )21(4222422214c o s 44s i n 214πππππθρπθ+=⋅+⋅=+==d d . (3)x x x f 52)5(3)(2+-=', 253)0(='f , 1517)2(='f . 4. 以初速v 0竖直上抛的物体, 其上升高度s 与时间t 的关系是2021gt t v s -=. 求:(1)该物体的速度v (t );(2)该物体达到最高点的时刻.解 (1)v (t )=s '(t )=v 0-gt .(2)令v (t )=0, 即v 0-gt =0, 得gv t 0=, 这就是物体达到最高点的时刻. 5. 求曲线y =2sin x +x 2上横坐标为x =0的点处的切线方程和法线方程. 解因为y '=2cos x +2x , y '|x =0=2, 又当x =0时, y =0, 所以所求的切线方程为 y =2x ,所求的法线方程为x y 21-=, 即x +2y =0. 6. 求下列函数的导数:(1) y =(2x +5)4(2) y =cos(4-3x );(3)23x e y -=;(4) y =ln(1+x 2);(5) y =sin 2x ;(6)22x a y -=;(7) y =tan(x 2);(8) y =arctan(e x );(9) y =(arcsin x )2;(10) y =lncos x .解 (1) y '=4(2x +5)4-1⋅(2x +5)'=4(2x +5)3⋅2=8(2x +5)3.(2) y '=-sin(4-3x )⋅(4-3x )'=-sin(4-3x )⋅(-3)=3sin(4-3x ).(3)22233236)6()3(x x x xe x e x e y ----=-⋅='-⋅='.(4)222212211)1(11xxx x x x y +=⋅+='+⋅+='. (5) y '=2sin x ⋅(sin x )'=2sin x ⋅cos x =sin 2x .(6))()(21])[(221122122'-⋅-='-='-x a x a x a y 222122)2()(21x a x x x a --=-⋅-=-. (7) y '=sec 2(x 2)⋅(x 2)'=2x sec 2(x 2).(8)xx x x e e e e y 221)()(11+='⋅+='. (9) y '21arcsin 2)(arcsin arcsin 2xx x x -='⋅=. (10)x x xx x y tan )sin (cos 1)(cos cos 1-=-='⋅='. 7. 求下列函数的导数:(1) y =arcsin(1-2x );(2)211x y -=; (3)x e y x3cos 2-=;(4)xy 1arccos =; (5)xx y ln 1ln 1+-=; (6)xx y 2sin =; (7)x y arcsin =;(8))ln(22x a x y ++=;(9) y =ln(sec x +tan x );(10) y =ln(csc x -cot x ).解 (1)2221)21(12)21()21(11x x x x x y --=---='-⋅--='. (2))1()1(21])1[(21212212'-⋅--='-='---x x x y 222321)1()2()1(21xx x x x --=-⋅--=-. (3))3)(3sin (3cos )2()3(cos 3cos )(2222'-+'-='+'='----x x e x x e x e x e y x xx x )3s i n 63(c o s 213s i n 33c o s 21222x x e x e x e x xx +-=--=---. (4)1||)1()1(11)1()1(1122222-=---='--='x x x x xx x y . (5)22)ln 1(2)ln 1(1)ln 1()ln 1(1x x x x x x x y +-=+--+-='. (6)222sin 2cos 212sin 22cos x x xx x x xx y -=⋅-⋅⋅='. (7)2222121)(11)()(11x x x x x x y -=⋅-='⋅-='.(8)])(211[1)(12222222222'+++⋅++='++⋅++='x a x a x a x x a x x a x y 2222221)]2(211[1x a x x a x a x +=++⋅++=. (9) x xx x x x x x x x y sec tan sec sec tan sec )tan (sec tan sec 12=++='+⋅+='. (10) x xx x x x x x x x y csc cot csc csc cot csc )cot (csc cot csc 12=-+-='-⋅-='.8. 求下列函数的导数:(1)2)2(arcsin x y =; (2)2tan ln x y =; (3)x y 2ln 1+=;(4)x e y arctan =;(5)y =sin n x cos nx ;(6)11arctan -+=x x y ; (7)xx y arccos arcsin =; (8) y =ln[ln(ln x )] ;(9)xx x x y -++--+1111; (10)xx y +-=11arcsin . 解 (1)'⋅=')2(arcsin )2(arcsin 2x x y )2()2(11)2(a r c s i n 22'⋅-⋅=x x x21)2(11)2(a r c s i n 22⋅-⋅=x x . 242a r c s i n 2x x -= (2))2(2sec 2tan 1)2(tan 2tan 12'⋅⋅='⋅='x x x x xy x x x c s c 212s e c 2t a n 12=⋅⋅=. (3))ln 1(ln 121ln 1222'+⋅+=+='x xx y )(l n ln 2ln 1212'⋅⋅+=x x x x x x1ln 2ln 1212⋅⋅+= xx x 2ln 1ln +=. (4))(arctan arctan '⋅='x e y x )()(112arctan '⋅+⋅=x x e x)1(221)(11a r c t a n 2a r c t a n x x e x x e x x +=⋅+⋅=. (5) y '=n sin n -1x ⋅(sin x )'⋅cos nx +sin n x ⋅(-sin nx )⋅(nx )'=n sin n -1x ⋅cos x ⋅cos nx +sin n x ⋅(-sin nx )⋅n=n sin n -1x ⋅(cos x ⋅cos nx -sin x ⋅sin nx )= n sin n -1x cos(n +1)x .(6)222211)1()1()1()11(11)11()11(11x x x x x x x x x x y +-=-+--⋅-++='-+⋅-++='. (7)222)(arccos arcsin 11arccos 11x x x x x y -+-=' 22)(a r c c o s a r c s i n a r c c o s 11x x x x +⋅-=22)(a r c c o s 12x x -=π. (8))(ln ln 1)ln(ln 1])[ln(ln )ln(ln 1'⋅⋅='⋅='x xx x x y )l n (l n ln 11ln 1)ln(ln 1x x x x x x ⋅=⋅⋅=.(9)2)11()121121)(11()11)(121121(x x x x x x x x xx y -++--+--+--++-++=' 22111x x -+-=. (10)2)1()1()1(1111)11(1111x x x xx x x x x y +--+-⋅+--='+-⋅+--=' )1(2)1(1x x x -+-=. 9. 设函数f (x )和g (x )可导, 且f 2(x )+g 2(x )≠0, 试求函数)()(22x g x f y +=的导数.解 ])()([)()(212222'+⋅+='x g x f x g x f y )]()(2)()(2[)()(2122x g x g x f x f x g x f '+'⋅+= )()()()()()(22x g x f x g x g x f x f +'+'=. 10. 设f (x )可导, 求下列函数y 的导数dx dy : (1) y =f (x 2);(2) y =f (sin 2x )+f (cos 2x ).解 (1) y '=f '(x 2)⋅(x 2)'= f '(x 2)⋅2x =2x ⋅f '(x 2).(2) y '=f '(sin 2x )⋅(sin 2x )'+f '(cos 2x )⋅(cos 2x )'= f '(sin 2x )⋅2sin x ⋅cos x +f '(cos 2x )⋅2cos x ⋅(-sin x )=sin 2x [f '(sin 2x )- f '(cos 2x )].11. 求下列函数的导数:(1) y =ch(sh x );(2) y =sh x ⋅e ch x ;(3) y =th(ln x );(4) y =sh 3x +ch 2x ;(5) y =th(1-x 2);(6) y =arch(x 2+1);(7) y =arch(e 2x );(8) y =arctan(th x );(9)xx y 2ch 21ch ln +=; (10))11(ch 2+-=x x y 解 (1) y '=sh(sh x )⋅(sh x )'=sh(sh x )⋅ch x .(2) y '=ch x ⋅e ch x +sh x ⋅e ch x ⋅sh x =e ch x (ch x +sh 2x ) .(3))(ln ch 1)(ln )(ln ch 122x x x x y ⋅='⋅='. (4) y '=3sh 2x ⋅ch x +2ch x ⋅sh x =sh x ⋅ch x ⋅(3sh x +2) .(5))1(ch 2)1()1(ch 122222x x x x y --=-⋅-='. (6)222)1()1(112422++='+⋅++='x x x x x y . (7)12)(1)(142222-='⋅-='x x x x e ee e y . (8)xxx x x x x y 222222ch 1ch sh 11ch 1th 11)th ()th (11⋅+=⋅+='⋅+=' xx x 222sh 211sh ch 1+=+=. (9))ch (ch 21)ch (ch 124'⋅-'⋅='x xx x y x x xx x sh ch 2ch 21ch sh 4⋅⋅-= xx x x x x x x 323ch sh ch sh ch sh ch sh -⋅=-= x xx x x x 33332th ch sh ch )1ch (sh ==-⋅=. (10)'+-⋅+-⋅+-='+-⋅+-=')11()11(sh )11(ch 2])11(ch [)11(ch 2x x x x x x x x x x y )112(sh )1(2)1()1()1()112(sh 22+-⋅+=+--+⋅+-⋅=x x x x x x x x . 12. 求下列函数的导数:(1) y =e -x (x 2-2x +3);(2) y =sin 2x ⋅sin(x 2);(3)2)2(arctan x y =; (4)n xx y ln=;(5)t t t t ee e e y --+-=; (6)xy 1cos ln =; (7)x e y 1sin 2-=;(8)x x y +=;(9) 242arcsin x x x y -+=; (10)212arcsin tty +=. 解 (1) y '=-e -x (x 2-2x +3)+e -x (2x -2)=e -x (-x 2+4x -5).(2) y '=2sin x ⋅cos x ⋅sin(x 2)+sin 2x ⋅cos(x 2)⋅2x=sin2x ⋅sin(x 2)+2x ⋅sin 2x ⋅cos(x 2).(3)2arctan 44214112arctan 222x x xx y +=⋅+⋅='. (4)121ln 1ln 1+--=⋅-⋅='n n n n x x n x nx x x xy . (5)2222)1(4)())(())((+=+---++='-----t t t t t t t t t t t t e e e e e e e e e e e e y . (6)x x x x x x x y 1tan 1)1()1sin (1sec )1(cos 1sec 22=-⋅-⋅='⋅='. (7))1(1cos )1sin 2()1sin (21sin 21sin 22x x x e xe y x x -⋅⋅-⋅='-⋅='-- x e x x1s i n 222s i n 1-⋅⋅=. (8))211(21)(21x xx x x x x y +⋅+='+⋅+=' xx x x +⋅+=412. (9)2arcsin )2(421214112arcsin 22x x x x x x y =-⋅-+⋅-⋅+='.(10)22222222)1()2(2)1(2)12(11)12()12(11t t t t tt t t t t y +⋅-+⋅⋅+-='+⋅+-=' )1(|1|)1(2)1()1(2)1(1222222222t t t t t t t +--=+-⋅-+=.习题 2-31. 求函数的二阶导数:(1) y =2x 2+ln x ;(2) y =e 2x -1;(3) y =x cos x ;(4) y =e -t sin t ;(5)22x a y -=;(6) y =ln(1-x 2)(7) y =tan x ;(8)113+=x y ; (9) y =(1+x 2)arctan x ;(10)xe y x =; (11)2x xe y =;(12))1ln(2x x y ++=.解 (1)x x y 14+=', 14x y -=''. (2) y '=e 2x -1 ⋅2=2e 2x -1, y ''=2e 2x -1 ⋅2=4e 2x -1.(3) y =x cos x ; y '=cos x -x sin x ,y ''=-sin x -sin x -x cos x =-2sin x -x cos x .(4) y '=-e -t sin t +e -t cos t =e -t (cos t -sin t )y ''=-e -t (cos t -sin t )+e -t (-sin t -cos t )=-2e -t cos t .(5)222222)(21xa x x a x a y --='-⋅-=', 22222222222)(xa x a a x a x a x x x a y ---=---⋅---=''.(6) 22212)1(11xxx x y --='-⋅-=', 22)1()1(2)1()2(2)1(2x x x x x x y -+-=--⋅---=''. (7) y '=sec 2 x ,y ''=2sec x ⋅(sec x )'=2sec x ⋅sec x ⋅tan x =2sec 2x ⋅tan x .(8)232233)1(3)1()1(+-=+'+-='x x x x y , 333433223)1()12(6)1(3)1(23)1(6+-=+⋅+⋅-+⋅-=''x x x x x x x x x y . (9)1arctan 211)1(arctan 222+=+⋅++='x x xx x x y , 212a r c t a n 2xxx y ++=''. (10)22)1(1xx e x e x e y x x x -=⋅-⋅=', 3242)22(2)1(])1([x x x e x x x e x e x e y x x x x +-=⋅--⋅+-=''. (11))21()2(2222x e x e x e y x x x +=⋅⋅+=',)23(24)21(222222x xe x e x x e y x x x +=⋅++⋅⋅=''.(12)2222211)1221(11)1(11x x x x x x x x x y +=++⋅++='++⋅++=', xx x x x x x x y ++-=+⋅+-='⋅+⋅+-=''1)1()12211)1(1122222. 2. 设f (x )=(x +10)6, f '''(2)=?解f '(x )=6(x +10)5, f ''(x )=30(x +10)4, f '''(x )=120(x +10)3,f '''(2)=120(2+10)3=207360.3. 若f ''(x )存在, 求下列函数y 的二阶导数22dxy d : (1) y =f (x 2);(2) y =ln[f (x )] .解 (1)y '= f '(x 2)⋅(x 2)'=2xf '(x 2),y ''=2f '(x 2)+2x ⋅2xf ''(x 2)=2f '(x 2)+4x 2f ''(x 2).(2))()(1x f x f y '=',2)]([)()()()(x f x f x f x f x f y ''-''=''22)]([)]([)()(x f x f x f x f '-''=. 4. 试从y dy dx '=1导出: (1)322)(y y dy x d '''-=; (2)5233)()(3y y y y dy x d '''''-''=. 解 (1)()()()3222)(1)(11y y y y y dy dx y dx d y dy d dy dx dy d dy xd '''-='⋅'''-=⋅'='==. (2)(())(())dy dx y y dx d y y dy d dy x d ⋅'''-='''-=3333 223)()(31)()(3)(y y y y y y y y y y y ''''-''=⋅'''⋅''-''''-=.5. 已知物体的运动规律为s =A sin ωt (A 、ω是常数), 求物体运动的加速度, 并验证:0222=+s dts d ω. 解 t A dtds ωωcos =, t A dts d ωωsin 222-=. 22dt s d 就是物体运动的加速度. 0s i n s i n 22222=+-=+t A t A s dts d ωωωωω. 6. 验证函数y =C 1e λx +C 2e -λx (λ,C 1, C 2是常数)满足关系式:y ''-λ2y =0 .解 y '=C 1λe λx -C 2λe -λx ,y ''=C 1λ2e λx +C 2λ2e -λx .y ''-λ2y =(C 1λ2e λx +C 2λ2e -λx )-λ2(C 1e λx +C 2e -λx )=(C 1λ2e λx +C 2λ2e -λx )-(C 1λ2e λx +C 2λ2e -λx )=0 .7. 验证函数y =e x sin x 满足关系式:y ''-2y '+2y =0 .解 y '=e x sin x +e x cos x =e x (sin x +cos x ),y ''=e x (sin x +cos x )+e x (cos x -sin x )=2e x cos x .y ''-2y '+2y =2e x cos x -2e x (sin x +cos x )+2e x sin x=2e x cos x -2e x sin x -2e x cos x +2e x sin x =0 . 8. 求下列函数的n 阶导数的一般表达式:(1) y =x n +a 1x n -1+a 2x n -2+ ⋅ ⋅ ⋅ +a n -1x +a n (a 1, a 2, ⋅ ⋅ ⋅, a n 都是常数);(2) y =sin 2x ;(3) y =x ln x ;(4) y =xe x .解 (1) y '=nx n -1+(n -1)a 1x n -2+(n -2)a 2x n -3+ ⋅ ⋅ ⋅ +a n -1, y ''=n (n -1)x n -2+(n -1)(n -2)a 1x n -3+(n -2)(n -3)a 2x n -4+ ⋅ ⋅ ⋅ +a n -2, ⋅ ⋅ ⋅,y (n )=n (n -1)(n -2)⋅ ⋅ ⋅2⋅1x 0=n ! .(2) y '=2sin x cos x =sin2x ,)22s i n (22c o s 2π+==''x x y , )222s i n (2)22c o s (222ππ⋅+=+='''x x y , )232s i n (2)222c o s (233)4(ππ⋅+=⋅+=x x y , ⋅ ⋅ ⋅,]2)1(2s i n [21)(π⋅-+=-n x y n n . (3) 1ln +='x y ,11-==''x xy , y '''=(-1)x -2,y (4)=(-1)(-2)x -3,⋅ ⋅ ⋅,y (n )=(-1)(-2)(-3)⋅ ⋅ ⋅(-n +2)x -n +1112)!2()1()!2()1(-----=--=n n n n x n x n . (4) y '=e x +xe x ,y ''=e x +e x +xe x =2e x +xe x ,y '''=2e x +e x +xe x =3e x +xe x ,⋅ ⋅ ⋅,y (n )=ne x +xe x =e x (n +x ) .9. 求下列函数所指定的阶的导数:(1) y =e x cos x , 求y (4) ;(2) y =x sh x , 求y (100) ;(3) y =x 2sin 2x , 求y (50) .解 (1)令u =e x , v =cos x , 有u '=u ''=u '''=u (4)=e x ;v '=-sin x , v ''=-cos x , v '''=sin x , v (4)=cos x ,所以 y (4)=u (4)⋅v +4u '''⋅v '+6u ''⋅v ''+4u '⋅v '''+u ⋅v (4)=e x [cos x +4(-sin x )+6(-cos x )+4sin x +cos x ]=-4e x cos x .(2)令u =x , v =sh x , 则有u '=1, u ''=0;v '=ch x , v ''=sh x , ⋅ ⋅ ⋅ , v (99)=ch x , v (100)=sh x ,所以)100()99(99100)98(98100)98(2100)99(1100)100()100( v u v u C v u C v u C v u C v u y ⋅+⋅'+⋅''⋅⋅⋅+''⋅+'⋅+⋅==100ch x +x sh x .(3)令u =x 2 , v =sin 2x , 则有u '=2x , u ''=2, u '''=0;x x v 2s i n 2)2482sin(24848)48(=⋅+=π, v (49)=249cos 2x , v (50)=-250sin 2x ,所以 )50()49(4950)48(4850)48(250)49(1150)50()50( v u v u C v u C v u C v u C v u y ⋅+⋅'+⋅''⋅⋅⋅+''⋅+'⋅+⋅=)50()49(4950)48(4850v u v u C v u C ⋅+⋅'+⋅''=)2s i n 2(2c o s 22502sin 22249505024928x x x x x -⋅+⋅⋅+⋅⋅⋅= )2s i n 212252c o s 502sin (2250x x x x x ++-=.习题2-41. 求由下列方程所确定的隐函数y 的导数dxdy : (1) y 2-2x y +9=0;(2) x 3+y 3-3axy =0;(3) xy =e x +y ;(4) y =1-xe y .解 (1)方程两边求导数得2y y '-2y -2x y ' =0 ,于是 (y -x )y '=y ,xy y y -='. (2)方程两边求导数得3x 2+3y 2y '-2ay -3axy '=0,于是 (y 2-ax )y '=ay -x 2 ,axy x ay y --='22. (3)方程两边求导数得y +xy '=e x +y (1+y '),于是 (x -e x +y )y '=e x +y -y ,yx y x e x y e y ++--='. (4)方程两边求导数得y '=-e y -xe y y ',于是 (1+xe y )y '=-e y ,y y xeey +-='1. 2. 求曲线323232a y x =+在点)42 ,42(a a 处的切线方程和法线方程. 解方程两边求导数得 032323131='+--y y x , 于是 3131---='y x y , 在点)42 ,42(a a 处y '=-1. 所求切线方程为)42(42a x a y --=-, 即a y x 22=+. 所求法线方程为)42(42a x a y -=-, 即x -y =0. 3. 求由下列方程所确定的隐函数y 的二阶导数22dx y d : (1) x 2-y 2=1;(2) b 2x 2+a 2y 2=a 2b 2;(3) y =tan(x +y );(4) y =1+xe y .解 (1)方程两边求导数得2x -2yy '=0,y '=yx , 3322221)(y y x y y y xx y y y x y y x y -=-=-='-='=''. (2)方程两边求导数得2b 2x +2a 2yy '=0,yx a b y ⋅-='22, 22222222)(y y x a b x y a by y x y a by ⋅--⋅-='-⋅-='' 32432222222ya b y a x b y a a b -=+⋅-=. (3)方程两边求导数得y '=sec 2(x +y )⋅(1+y '),1)(c o s 1)(s e c 1)(s e c 222-+=+-+='y x y x y x y 222211)(s i n )(c o s )(s i n y y x y x y x --=+-+++=, 52233)1(2)11(22yy y y y y y +-=--='=''. (4)方程两边求导数得y '=e y +xe y y ',ye y e xe e y y y y y -=--=-='2)1(11, 3222)2()3()2()3()2()()2(y y e y y y e y y e y y e y y y y y --=-'-=-'---'=''. 4. 用对数求导法求下列函数的导数:(1) x xx y )1(+=;(2)55225+-=x x y ;(3)54)1()3(2+-+=x x x y ; (4)x e x x y -=1sin .解 (1)两边取对数得ln y =x ln|x |-x ln|1+x |，两边求导得xx x x x x y y +⋅-+-⋅+='11)1l n (1ln 1, 于是 ]111[l n )1(xx x x x y x ++++='. (2)两边取对数得)2l n (251|5|ln 51ln 2+--=x x y , 两边求导得22251515112+⋅--⋅='x x x y y , 于是 ]225151[25512552+⋅--=+-='x x x x x y . (3)两边取对数得)1l n (5)3l n (4)2l n (21ln +--++=x x x y , 两边求导得1534)2(211+---+='x x x y y , 于是 ]1534)2(21[)1()3(254+--+++-+='x x x x x x y (4)两边取对数得)1l n (41s i n ln 21ln 21ln x e x x y -++=, 两边求导得)1(4c o t 21211x e e x x y y --+=', 于是 ])1(4c o t 2121[1s i n x x xe e x x e x x y --+-=' ]1c o t 22[1s i n 41-++-=x x x e e x x e x x . 5. 求下列参数方程所确定的函数的导数dxdy : (1) ⎩⎨⎧==22bt y at x ; (2) ⎩⎨⎧=-=θθθθcos )sin 1(y x .解 (1)t ab at bt x y dx dy t t 23232==''=. (2)θθθθθθθθcos sin 1sin cos ---=''=x y dx dy . 6. 已知⎩⎨⎧==.cos ,sin t e y t e x t t 求当3π=t 时dx dy 的值. 解 tt t t t e t e t e t e x y dx dy t t t t t t cos sin sin cos cos sin sin cos +-=+-=''=, 当3π=t 时, 23313123212321-=+-=+-=dx dy . 7. 写出下列曲线在所给参数值相应的点处的切线方程和法线方程:(1) ⎩⎨⎧==t y t x 2cos sin , 在4π=t 处; (2) ⎪⎩⎪⎨⎧+=+=2221313taty t atx , 在t =2处.解 (1)tt x y dx dy t t cos 2sin 2-=''=. 当4π=t 时, 222224cos )42sin(2-=-=⋅-=ππdx dy , 220=x , 00=y , 所求切线方程为)22(22--=x y , 即0222=-+y x ; 所求法线方程为)22(221---=x y , 即0142=--y x . (2)222222)1(6)1(23)1(6t at t t at t at y t +=+⋅-+=', 222222)1(33)1(23)1(3t at a t t at t a x t +-=+⋅-+=', 2212336ttat a atx y dx dy t t -=-=''=. 当t =2时, 3421222-=-⋅=dx dy , a x 560=, a y 5120=, 所求切线方程为)56(34512a x a y --=-, 即4x +3y -12a =0; 所求法线方程为)56(43512a x a y -=-, 即3x -4y +6a =0. 8. 求下列参数方程所确定的函数的二阶导数22dxy d : (1) ⎪⎩⎪⎨⎧-==.122t y t x ;(2) ⎩⎨⎧==t b y t a x sin cos ; (3) ⎩⎨⎧==-t t ey e x 23; (4) ⎩⎨⎧-==)()()(t f t tf y t f x t t , 设f ''(t )存在且不为零. 解 (1) t x y dx dy t t 1-=''=, 322211)(t t t x y dx y d t t x =='''=. (2) t ab t a t b x y dx dy t t cot sin cos -=-=''=, ta b t a t a b x y dx y d t t x 32222sin sin csc )(-=-='''=. (3) t t t t t e e e x y dx dy 23232-=-=''=-, t t t t x e e e x y dx y d 322943232)(=-⋅-=''=. (4) t t f t f t f t t f x y dx dy t t ='''-''+'=''=)()()()(, )(1)(22t f x y dx y d t t x ''='''=. 9. 求下列参数方程所确定的函数的三阶导数33dxy d : (1)⎩⎨⎧-=-=321t t y t x ; (2)⎩⎨⎧-=+=t t y t x arctan )1ln(2. 解(1)tt t t t dx dy 231)1()(223--='-'-=, )31(412)231(3222t t t t t dx y d +-=-'--=,)1(832)31(4125333t t t t t dx y d +-=-'+-=. (2)t tt t t t t dx dy 2112111])1[ln()arctan (22=++-='+'-=, t t t t t dxy d 4112)21(2222+=+'=, 3422338112)41(t t tt t t dx y d -=+'+=. 10. 落在平静水面上的石头, 产生同心波纹, 若最外一圈波半径的增大率总是6m/s , 问在2秒末扰动水面面积的增大率为多少？解设波的半径为r , 对应圆面积为S , 则S =πr 2, 两边同时对t 求导得 S t '=2πrr '.当t =2时, r =6⋅2=12, r 't =6,故S t '|t =2=2⋅12⋅6π=144π (米2/秒).11. 注水入深8m 上顶直径8m 的正圆锥形容器中, 其速率为4m 2/min . 当水深为5m 时, 其表面上升的速度为多少？解水深为h 时, 水面半径为h r 21=, 水面面积为π241h S =, 水的体积为3212413131h h h hS V ππ=⋅==, dt dh h dt dV ⋅⋅=2312π, dtdV h dt dh ⋅=24π. 已知h =5(m)，4=dtdV (m 3/min), 因此 πππ2516425442=⋅=⋅=dt dV h dt dh (m/min).12. 溶液自深18cm 直径12cm 的正圆锥形漏斗中漏入一直径为10cm 的圆柱形筒中, 开始时漏斗中盛满了溶液, 已知当溶液在漏斗中深为12cm 时, 其表面下降的速率为1cm/min . 问此时圆柱形筒中溶液表面上升的速率为多少？解设在t 时刻漏斗在的水深为y , 圆柱形筒中水深为h . 于是有h y r 22253118631=-⋅⋅ππ. 由186y r =, 得3y r =, 代入上式得 h y y 2225)3(3118631=-⋅⋅ππ, 即 h y 233253118631=-⋅⋅π. 两边对t 求导得h y y t '='-222531. 当y =12时, y 't =-1代入上式得64.025165)1(1231222≈=-⋅⋅-='t h (cm/min)..2-71. 已知y =x 3-x , 计算在x =2处当∆x 分别等于1, 0.1, 0.01时的∆y 及dy . 解 ∆y |x =2, ∆x =1=[(2+1)3-(2+1)]-(23-2)=18,dy |x =2, ∆x =1=(3x 2-1)∆x |x =2, ∆x =1=11;∆y |x =2, ∆x =0.1=[(2+0.1)3-(2+0.1)]-(23-2)=1.161,dy |x =2, ∆x =0.1=(3x 2-1)∆x |x =2, ∆x =0.1=1.1;∆y |x =2, ∆x =0.01=[(2+0.01)3-(2+0.01)]-(23-2)=0.110601,dy |x =2, ∆x =0.01=(3x 2-1)∆x |x =2, ∆x =0.01=0.11.2. 设函数y =f (x )的图形如图所示, 试在图(a )、(b )、(c )、(d )中分别标出在点x 0的dy 、∆y 及∆y -d y 并说明其正负.解 (a )∆y >0, dy >0, ∆y -dy >0.(b )∆y >0, dy >0, ∆y -dy <0.(c )∆y <0, dy <0, ∆y -dy <0.(d )∆y <0, dy <0, ∆y -dy >0.3. 求下列函数的微分:(1)x xy 21+=; (2) y =x sin 2x ;(3)12+=x xy ;(4) y =ln 2(1-x );(5) y =x 2e 2x ;(6) y =e -x cos(3-x );(7)21arcsin x y -=;(8) y =tan 2(1+2x 2);(9)2211arctan x x y +-=; (10) s =A sin(ωt +ϕ) (A , ω, ϕ是常数) .解 (1)因为xx y 112+-=', 所以dx x x dy )11(2+-=. (2)因为y '=sin2x +2x cos2x , 所以dy =(sin2x +2x cos2x )dx .(3)因为1)1(111122222++=++⋅-+='x x x x x x y , 所以dx x x dy 1)1(122++=. (4)dx x x dx x x dx x dx y dy )1ln(12])1(1)1ln(2[])1([ln 2--=--⋅-='-='=. (5)dy =y 'dx =(x 2e 2x )'dx =(2xe 2x +2x 2e 2x )dx =2x (1+x )e 2x .(6) dy =y 'dx =[e -x cos(3-x )]dx =[-e -x cos(3-x )+e -x sin(3-x )]dx=e -x [sin(3-x )-cos(3-x )]dx .(7)dx xx x dx x x dx x dx y dy 22221||)12()1(11)1(arcsin --=--⋅--='-='=. (8) dy =d tan 2(1+2x 2)=2tan(1+2x 2)d tan(1+2x 2)=2tan(1+2x 2)⋅sec 2(1+2x 2)d (1+2x 2)=2tan(1+2x 2)⋅sec 2(1+2x 2)⋅4xdx=8x ⋅tan(1+2x 2)⋅sec 2(1+2x 2)dx .(9))11()11(1111arctan 2222222x x d x x x x d dy +-+-+=+-= dx x x dx x x x x x x x 4222222214)1()1(2)1(2)11(11+-=+--+-⋅+-+=.(10) dy =d [A sin(ω t +ϕ)]=A cos(ω t +ϕ)d (ωt +ϕ)=A ω cos(ωt +ϕ)dx .4. 将适当的函数填入下列括号内, 使等式成立:(1) d ( )=2dx ;(2) d ( )=3xdx ;(3) d ( )=cos tdt ;(4) d ( )=sin ωxdx ;(5) d ( )dx x 11+=; (6) d ( )=e -2x dx ;(7) d ( )dx x1=; (8) d ( )=sec 23xdx .解 (1) d ( 2x +C )=2dx .(2) d (C x +223)=3xdx . (3) d ( sin t +C )=cos tdt .(4) d (C x +-ωωcos 1)=sin ωxdx . (5) d ( ln(1+x )+C )dx x 11+=. (6) d (C e x +--221)=e -2x dx . (7) d (C x +2)dx x1=. (8) d (C x +3tan 31)=sec 23xdx .5. 如图所示的电缆B O A的长为s , 跨度为2l , 电缆的最低点O 与杆顶连线AB 的距离为f , 则电缆长可按下面公式计算:)321(222lf l s +=, 当f 变化了∆f 时, 电缆长的变化约为多少？解 f f l df lf l dS S ∆='+=≈∆38)321(222. 6. 设扇形的圆心角α=60︒, 半径R =100cm(如图), 如果R 不变, α 减少30', 问扇形面积大约改变了多少？又如果α 不变, R 增加1cm , 问扇形面积大约改变了多少？解 (1)扇形面积221R S α=, αααα∆='=≈∆2221)21(R d R dS S . 将α=60︒3π=, R =100, 36003πα-='-=∆ 代入上式得 63.43)360(100212-≈-⋅⋅≈∆πS (cm 2). (2) R R dR R dS S R ∆='=≈∆αα)21(2. 将α=60︒3π=, R =100, ∆R =1代入上式得 72.10411003≈⋅⋅≈∆πS (cm 2). 7. 计算下列三角函数值的近似值:(1) cos29︒;(2) tan136︒.解 (1)已知f (x +∆x )≈f (x )+f '(x )∆x , 当f (x )=cos x 时, 有cos(x +∆x )≈cos x -sin x ⋅∆x , 所以cos29︒=87467.01802123)180(6sin 6cos )1806cos(≈⋅+=-⋅-≈-ππππππ. (2)已知f (x +∆x )≈f (x )+f '(x )∆x , 当f (x )=tan x 时, 有tan(x +∆x )≈tan x +sec 2x ⋅∆x , 所以。

常微分方程2.2习题参考解答

习题2.2求下列方程的解1．dxdy =x y sin +解：y=e ⎰dx (⎰x sin e ⎰-dx c dx +)=e x [-21e x -(x x cos sin +)+c]=c e x -21(x x cos sin +)是原方程的解。

2．dt dx +3x=e t2解：原方程可化为：dt dx =-3x+e t 2所以：x=e ⎰-dt 3(⎰e t 2e -⎰-dt 3c dt +)=e t 3-(51e t 5+c)=c e t 3-+51e t 2是原方程的解。

3．dt ds =-s t cos +21t 2sin 解：s=e ⎰-tdt cos (t 2sin 21⎰e dt dt ⎰3c +)=e t sin -(⎰+c dt te t t sin cos sin )=e t sin -(c e te t t +-sin sin sin )=1sin sin -+-t ce t 是原方程的解。

4．dx dy nx x e y n x =-，n 为常数.解：原方程可化为：dx dy nx x e y nx +=)(c dx e x e e y dx x n n x x n +⎰⎰=⎰-)(c e x x n +=是原方程的解.5．dx dy +1212--y x x =0解：原方程可化为：dx dy =-1212+-y x x ⎰=-dx x x e y 212(c dx e x x+⎰-221))21(ln 2+=x e )(1ln 2⎰+--c dx ex x =)1(12x ce x +是原方程的解.6．dx dy 234xy x x +=解：dx dy 234xy x x +==23y x +x y 令x y u =则uxy =dx dy =u dx du x +因此：dx du x u +=2u x 21udx du =dxdu u =2c x u +=331c x x u +=-33（*）将x y u =带入（*）中得：3433cx x y =-是原方程的解.3332()21()227.(1)12(1)12(),()(1)1(1)(())1(1)dx P x dx x P x dx dy y x dx x dy y x dx x P x Q x x x e e x e Q x dx c x +--=++=+++==++⎰⎰==+⎰⎰++⎰⎰P(x)dx 232解：方程的通解为： y=e =(x+1)(*(x+1)dx+c) =(x+1)((x+23221(1)()211,()(())dy y x c dy y dx x y dx x y dy y yQ y y ye yQ y dy c -+++==+=⎰⎰==⎰⎰+⎰⎰2243P(y)dy P(y)dy P(y)dy 1)dx+c)=(x+1) 即：2y=c(x+1)+(x+1)为方程的通解。

常微分方程课后答案

3.设连续函数f (x)在区间(−∞, +∞)上有界，证明：方程
dy dx
−
y
=
f (x)
在区间(−∞, +∞)上有且仅有一个有界解。试求出这个有界解，并进而证明：当f (x)还是一个以ω为周期
的周期函数时，这个解也是一个以ω为周期的周期函数。
证明：设|f (x)| ≤ M ，方程两边乘以因子e−x，得到通解为y = ex(C + f (s)e−s ds)，其中C为任意常
dy dx
=
y x+y
3
.
3
解： (1)方程两边同时乘以因子e−x，由此得到方程的通解为
y
=
C ex
−
sin
x
+ 2
cos x
其中C为任意常数；
R
(2)方程两边同时乘以因子e−
1 1−x2
dx，由此得到方程的通解为
y=
1 1
+ −
x x
(C
+
π 2
)
其中C为任意常数；再由初始条件可得C
=
1
−
π 2
ex y
)
=
0;
(11)
2x sin y
+
y3ex
+
(x2
cos y
+
3y2ex
)
dy dx
=
0;
(12)
y2 2
− 2yex
+ (y
−
ex)
dy dx
=
0;
(13)
1
+
(1
+
xy)exy
+

(完整版)理论力学课后答案第二章

解册究対繼*晦矍*曲：/」平衛ii 殳宦廉，交廉”的钓痕力耳欝珊谊寸c 乃向如I 用 b 陌示.収啪杯爺Cy*血平胡那论鬥式⑴* (?)峡立・解紂佔2…已暂 F 兰5 am N .棗与撑祎自虫不计匚求 BC'ffK 内力及铁员的反力。

解该系统曼力如图(訂，三力匸交于艰0・苴封訥的力三角膠如图冷人祥得屉二5OOON 』仏二疔000 W2-2在铰链A 、B 处有力F i , F 2作用，如图所示。

该机 F i 与F 2的关系。

2-3铰链4杆机构CABD 的CD 边固定, 构在图示位置平衡，不计杆自重。

求力 30T >◎60°检(b)B解⑴柠点掐坐WAS 力如囲归所示"H3平祈刖论咼节点瓦腿标歴覺力如国所小*血丫轉理论得2S -F^ ccs 30fr -f ； cosW ）0 =0^=-^=—^— = 1.553^F 、: - 0.644已扣两伦备車P A ^P L •处于T册状态,杆電不比求I ）若片=丹=巴角e -?2）若 P A - 300 B = 0血=?ffi 八5两轮受力分别如图示■对A 辂育SX = 0* F 刚 cEjedO* — F\g oos$ = 0SY 二 0a F sx tin60T - F 屈 sinfl - P A = tj对 B 轮育 SX ■ 0, Fn ooa? - F,\&8^3(/ = 0 IV = 0. F rw sinff 下 F 斶 anJO* - P n =(1) 四牛封程嬴立求AL 爾＜3-30*(2) 把拧-0\F A - 300 M 代入方社，联立解筹P fl = 100 N2-5如图2-10所示，刚架上作用力F 。

试分别计算力F解 M A (F) = -FbcoseM s [F) - -Fb cos0 + FosinB二F(osiii0-bcos0)2-6已知梁AB 上作用1力偶，力偶矩为M ，梁长为I ，梁重不计。

信号与系统第2章答案

0 t 1时,
( 2).1 t 2时,
h(t ) h(t 1) h(t 2) h(t ) h(t 1) 1
h(t ) 1 h(t 1) 1 (t 1) 2 t (3).2 t 3时, h(t ) h(t 1) h(t 2) 1
解: (a) 特征方程为 λ2+3λ+2=0 得 λ1=-2， λ2=-1。
(f). (D2+2D+2)y(t)=Dx(t)
则 h(t)= (c1eλ1 t+ c2eλ2t)u(t)=( c1e- 2 t+ c2e-t)u(t) h`(t)= (c1+ c2)δ(t)+(-2c1e- 2 t-c2e-t)u(t) h``(t)= (c1+ c2)δ`(t)+(-2c1-c2) δ(t)+ (4c1e- 2 t+c2e-t)u(t)

E 4
e
3 ( t T ) 8
]u (t T )
e
u (t T )
2.22 某LTI系统的输入信号x(t)和其零状态响应yx(t)的波形如图P2.22所示。(a)求该系囊统的冲激响应 h(t),(b)用积分器，加法器和延时器(T=1s)构成该系统。解: (a)
0
x(t ) (t ) (t 1) (t 2) t, 0 t 1 y x (t ) 1, 1 t 3 4 t , 3 t 4 x(t ) h(t ) (t ) (t 1) (t 2) h(t ) y x (t ) t, 0 t 1 h(t ) h(t 1) h(t 2) 1, 1 t 3 4 t , 3 t 4

常微分方程与动力系统第二章课后题参考答案

常微分方程与动力系统第二章习题参考答案 1.证明：因为()t Φ是线性齐次系统（LH ）的一个基本解矩阵，由定理2.5知()t Φ在区间J 上满足矩阵微分系统()M LH ,即.()()()t A t t Φ=Φ，.1()()()A t t t -=ΦΦ所以由()A t 确定的线性齐次系统（LH ）必唯一。

2.证明：因为()t ϕ，()t ψ分别是.()x A t x=和.()T x A t x =-的解，所以111()()()nk k k nnk k k a d t A t t dt a ϕϕϕϕ==⎛⎫ ⎪ ⎪== ⎪ ⎪⎪ ⎪⎝⎭∑∑ ，11211111122222*121()()()nn k k k n n kn kn n n nnk a a a a a a a d t A t t dta a a a ψψψψψψ==⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪ ⎪⎪ ⎪=-ψ=-=- ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭ ⎪⎝⎭∑∑ 因而1111112211(,)(,)(,),,nnk k k k k k nnkn k k nk k n n k a a d d d dt dt dt a a ψϕϕψψϕϕψϕψψϕψϕψϕ====⎡⎤⎛⎫⎡⎤⎛⎫⎛⎫⎛⎫⎢⎥ ⎪-⎢⎥ ⎪⎪ ⎪⎢⎥ ⎪⎢⎥ ⎪ ⎪ ⎪⎢⎥=+= ⎪+⎢⎥ ⎪ ⎪ ⎪⎢⎥ ⎪-⎢⎥ ⎪⎪ ⎪⎢⎥⎪⎝⎭⎢⎥⎝⎭⎝⎭ ⎪⎣⎦⎢⎥⎝⎭⎣⎦∑∑∑∑ 11111111()0nnn n nnnnn n nnm m m m i ij j i ij j i mk k km k mk k km m m m m i j i j k k k k a a a a a a ϕψψϕϕψϕψϕψϕψ============-=+=-=-=∑∑∑∑∑∑∑∑∑∑∑∑所以(),()()()1nt t t t k kk ϕψϕψ≡≡∑=常数。

3.证明：设)t Φ(为系统.()x A t x=的一个基本解矩阵，则由定理2.11知[]1()Tt -Φ是系统.()Tx At x =-的基本解矩阵，由定理2.4知系统.()x A t x=满足初始条件00()x t x =的特解为100()))t t t x ϕ-=Φ(Φ(，[)0,0,t t ∈+∞由题可知)t Φ(与[]1()Tt -Φ在[)0,+∞上有界，从而由定理2.24知110()0k k t ∃=>和220()0k k t =>使得10120(),(),T t k t t t k t t -⎧Φ≤≤<+∞⎪⎨Φ≤≤<+∞⎪⎩,利用常数变易法公式（2.32），可知式.()()y A t y B t y=+的初始条件为00()y t y =的解满足1()()()()()()tt y t t t s B s y s ds ϕ-=+ΦΦ⎰因为1111()()(Ttttt---ΦΦ≤Φ所以12120()()(),tt y t k kx k k B s y s≤+≥⎰，利用格朗瓦尔不等式有12()120().tt k k B s dsy t k k x e⎰≤记12()12tt k k B s dsC k k e ⎰=设0()B t dt M +∞=<+∞⎰则()()tt B s ds B t dt M+∞≤=⎰⎰有1212k k MCk k e≤从而00(),y t C x t t ≤≥所以系统.()()y A t y B t y =+的一切解都在[)0,+∞上有界。

微积分课后题答案第二章习题详解

.
（2）因为，而且，
所以，由夹逼定理得
4. 利用单调有界数列收敛准则证明下列数列的极限存在.
(1) xn=，n=1,2,…；
(2) x1=,xn+1＝,n=1,2,….
证：（1）略。
（2）因为，不妨设，则
故有对于任意正整数n，有，即数列有上界，
又，而,，
所以即，
即数列是单调递增数列。
综上所述，数列是单调递增有上界的数列，故其极限存在。
由数列极限的定义得.
2. 试利用不等式说明：若xn=a,则∣xn∣=|a|.考察数列xn=(-1)n，说明上述结论反之不成立.
证：
而
于是，
即
由数列极限的定义得
考察数列，知不存在，而，，
所以前面所证结论反之不成立。
3. 利用夹逼定理证明：
(1) =0；(2) =0.
证：（1）因为
而且，，
所以由夹逼定理，得
即a=1.
6※.设f(x)= ，讨论f(x)的连续性.
解:
所以, f(x)在上连续,x=0为跳跃间断点.
7. 求下列极限：
(1) ；(2) ；
(3) ln(x-1);(4) arcsin；
(5) (lnx)x.
解:
习题2-8
1. 证明方程x5-x4-x2-3x=1至少有一个介于1和2之间的根.
证: 令,则在[1,2]上连续,
习题2-2
1※. 证明：f(x)=a的充要条件是f(x)在x0处的左、右极限均存在且都等于a.
证：先证充分性：即证若，则.
由及知：
,当时，有，
当时，有。
取，则当或时，有，
而或就是，
于是，当时，有，
所以.

周义仓编常微分方程习题答案

1.(1) (x, y) y' = y + xtgα x − ytgα
答案 1.1
(2) (x
−
y y'
2
)
+(y
−
xy' )2
=
l2
(3) xy' + y = 0
(4) ( y − xy' )(x − y ) = 2a2 (5) y − xy' = x2 y'
提示：过点 (x,
y) 的切线的横截距和纵截距分别为
不妨假设 x1 是使得 h(x) = 0 的最靠近的点，则 φ (x1 ) = ψ (x1 ) ，且
h' (x1 ) ≤ 0 h' (x1 ) = F (x1,ψ (x1 )) − f (x1,φ (x1 )) > 0 ，矛盾，所以当 x > x0 时 h(x) 必
然大于零。
2
2
因此对任意常数 c y = c 2 + cx + 2c + 1是方程的解，在 C ≤ − 1 时满足 2
把 y = − x(x + 4) 带入方程中易得： y = − x(x + 4) 也是方程的解。
4
4
3.
1) y= x 2 ，2)y= e5x ，3)y=x2/2，4)y=2，5)y=ex，6) y = x
返回目录
1 我们还是在以原点为中心的矩形 R={(x,y)| x ≤ 1, y ≤ 1 }内画方程的向量场和积分曲线：
程序如下：DEtools[phaseportrait] ([diff(y(x),x)=x/y],y(x),x= -1..1, [[y(-1)=1],[y(-1)=0],[y(-1)= -1]], dirgrid=[33,33], Arrows=LINE, Axes=NORMAL);#其余三个只需把初值和函数还一下即可

常微分方程第二章练习与答案

1 / 16习题２-１判断下列方程是否为恰当方程,并且对恰当方程求解：１．0)12()13(2=++-dy x dx x解：13),(2-=x y x P , 12),(+=x y x Q ,则0=∂∂y P ,2=∂∂xQ, 所以 x Q y P ∂∂≠∂∂ 即原方程不是恰当方程．２．0)2()2(=+++dy y x dx y x 解：,2),(y x y x P +=,2),(y x y x Q -=则,2=∂∂y P ,2=∂∂xQ所以x Q y P ∂∂=∂∂,即原方程为恰当方程则,0)22(=-++ydy xdy ydx xdx两边积分得：.22222C y xy x =-+ 3．0)()(=+++dy cy bx dx by ax 〔a,b 和c 为常数〕．解：,),(by ax y x P +=,),(cy bx y x Q +=则,b y P =∂∂,b xQ =∂∂ 所以x Q y P ∂∂=∂∂,即原方程为恰当方程则,0=+++cydy bxdy bydx axdx两边积分得：.2222C cy bxy ax =++ 4．)0(0)()(≠=-+-b dy cy bx dx by ax解：,),(by ax y x P -=,),(cy bx y x Q -=则,b y P -=∂∂,b xQ=∂∂ 因为 0≠b , 所以x Q y P ∂∂≠∂∂,即原方程不为恰当方程５．0sin 2cos )1(2=++udt t udu t解：,cos )1(),(2u t u t P +=u t u t Q sin 2),(=则,cos 2u t t P =∂∂,cos 2u t xQ=∂∂ 所以x Q y P ∂∂=∂∂,即原方程为恰当方程则,0cos )sin 2cos (2=++udu udt t udu t2 / 16两边积分得：.sin )1(2C u t =+ ６．0)2()2(2=++++dy xy e dx y e ye xxx解： xy e y x Q y e ye y x P xxx2),(,2,(2+=++=,则,2y e y P x +=∂∂,2y e xQx +=∂∂ 所以x Q y P ∂∂=∂∂,即原方程为恰当方程则,0])2()[(22=++++dy xy e dx y ye dx e xxx两边积分得：.)2(2C xy e y x=++７．0)2(ln )(2=-++dy y x dx x xy解：,2ln ),(),(2y x y x Q x xy y x P -=+=则,1x y P =∂∂,1x x Q =∂∂ 所以xQy P ∂∂=∂∂,即原方程为恰当方程则02)ln (2=-++ydy dx x xdy dx x y两边积分得：23ln 3y x y x -+.C = ８．),(0)(22为常数和c b a cxydy dx by ax =++解：,),(,),(22cxy y x Q by ax y x P =+=则,2by y P =∂∂,cy xQ =∂∂ 所以当x Q y P ∂∂=∂∂,即 c b =2时, 原方程为恰当方程则0)(22=++cxydy dx by dx ax两边积分得：233bxy ax +.C = 而当c b ≠2时原方程不是恰当方程．９．01222=-+-dt ts s ds t s 解：,),(,12),(22ts s s t Q t s s t P -=-= 则,212t s t P -=∂∂,212tss Q -=∂∂ 所以x Q y P ∂∂=∂∂, 即原方程为恰当方程,两边积分得：C ts s =-2．3 / 1610．,0)()(2222=+++dy y x yf dx y x xf 其中)(⋅f 是连续的可微函数．解：),(),(),(),(2222y x yf y x Q y x xf y x P +=+=则,2f xy y P '=∂∂,2f xy xQ '=∂∂ 所以x Q y P ∂∂=∂∂, 即原方程为恰当方程,两边积分得：22()f xy dx C +=⎰,即原方程的解为C y x F =+)(22<其中F 为f 的原积分>．习题２-2. 1. 求解下列微分方程,并指出这些方程在平面上的有意义的区域:：〔１〕yx dx dy 2= 解：原方程即为：dx x ydy 2= 两边积分得：0,2332≠=-y C x y ．〔２〕)1(32x y x dx dy += 解：原方程即为：dx xx ydy 321+=4 / 16两边积分得：1,0,1ln 2332-≠≠=+-x y C x y ．〔３〕0sin 2=+x y dxdy解：当0≠y 时原方程为：0sin 2=+xdx y dy两边积分得：0)cos (1=++y x c ．又y=0也是方程的解,包含在通解中,则方程的通解为0)cos (1=++y x c ．〔４〕221xy y x dx dy +++=；解：原方程即为：2(1)1dyx dx y =++ 两边积分得：c x x arctgy ++=22, 即 )2(2c x x tg y ++=．〔５〕2)2cos (cos y x dxdy= 解：①当02cos ≠y 时原方程即为：dx x y dy 22)(cos )2(cos = 两边积分得：2222sin 2tg y x x c --=． ②y 2cos =0,即42ππ+=k y 也是方程的解. 〔N k ∈〕〔６〕21y dxdyx-= 解：①当1±≠y 时原方程即为：xdx y dy =-21 两边积分得：c x y =-ln arcsin ． ②1±=y 也是方程的解.〔７〕．yxe y e x dx dy +-=- 解．原方程即为：dx ex dy e y xy)()(--=+5 / 16两边积分得：c e x e y x y++=+-2222, 原方程的解为：c ee x y xy=-+--)(222.2. 解下列微分方程的初值问题．〔１〕,03cos 2sin =+ydy xdx 3)2(ππ=y ；解：两边积分得：c yx =+-33sin 22cos , 即c x y =-2cos 33sin 2因为 3)2(ππ=y , 所以 3=c .所以原方程满足初值问题的解为：32cos 33sin 2=-x y ．〔２〕．0=+-dy ye xdx x, 1)0(=y ；解：原方程即为：0=+ydy dx xe x,两边积分得：c dy y dx e x x=+-2)1(2, 因为1)0(=y , 所以21-=c , 所以原方程满足初值问题的解为：01)1(22=++-dy y dx e x x．〔３〕．r d dr=θ, 2)0(=r ；解：原方程即为：θd rdr=,两边积分得：c r =-θln ,因为2)0(=r , 所以2ln =c ,所以原方程满足初值问题的解为：2ln ln =-θr 即θe r 2=．〔４〕．,1ln 2yx dx dy+=0)1(=y ; 解：原方程即为：dx x dy y ln )1(2=+,两边积分得：3ln 3y y x x x c ++-=, 因为0)1(=y , 所以1=c ,所以原方程满足初值为：3ln 13y y x x x ++-=6 / 16〔５〕．321xy dxdyx=+, 1)0(=y ；解：原方程即为：dx xx y dy 231+=, 两边积分得：c x y ++=--22121, 因为1)0(=y , 所以23-=c ,所以原方程满足初值问题的解为：311222=++yx ．１．解下列微分方程,并作出相应积分曲线的简图．〔１〕．x dxdycos = 解：两边积分得：c x y +=sin ．积分曲线的简图如下：〔２〕．ay dxdy=, 〔常数0≠a 〕；解：①当0≠y 时,原方程即为：dx ay dy = 积分得：c x y a +=ln 1, 即 )0(>=c cey ax②0=y 也是方程的解．积分曲线的简图如下：7 / 16〔３〕．21y dxdy-=；解：①当1±≠y 时,原方程即为：dx y dy =-)1(2 积分得：c x yy+=-+211ln ,即 1122+-=x x ce ce y ．②1±=y 也是方程的解．积分曲线的简图如下：〔４〕．n y dx dy =, )2,1,31(=n ；解：①当0≠y 时, ⅰ〕2,31=n 时,原方程即为 dx y dy n =,积分得：c y n x n=-+-111．8 / 16ⅱ〕1=n 时,原方程即为dx ydy= 积分得：c x y +=ln ,即 )0(>=c ce y x．②0=y 也是方程的解．积分曲线的简图如下：4. 跟踪：设某A 从xoy 平面上的原点出发,沿x 轴正方向前进；同时某9 / 16B 从点开始跟踪A,即B 与A 永远保持等距b ．试求B 的光滑运动轨迹．解：设B 的运动轨迹为)(x y y =,由题意与导数的几何意义,则有22yb ydx dy --=,所以求B 的运动轨迹即是求此微分方程满足b y =)0(的解．解之得：222222ln21y b y b b y b b b x ----++=． 5. 设微分方程)(y f dxdy=〔2.27〕,其中f<y> 在a y =的某邻域〔例如,区间ε<-a y 〕内连续,而且a y y f =⇔=0)(,则在直线a y =上的每一点,方程〔2.27〕的解局部唯一,当且仅当瑕积分∞=⎰±εa ay f dy)(〔发散〕．证明：〔⇒〕首先经过域1R ：,+∞<<∞-x a y a <≤-ε 和域2R ：,+∞<<∞-x ε+≤<a y a内任一点〔00,y x 〕恰有方程〔2.13〕的一条积分曲线, 它由下式确定00)(x x y f dyyy-=⎰. 〔*〕这些积分曲线彼此不相交. 其次,域1R 〔2R 〕内的所有积分曲线c x y f dy +=⎰)(都可由其中一条,比如0)(c x y f dy+=⎰ 沿着 x 轴的方向平移而得到。

《常微分方程》东师大第二版习题答案

2 2
dy y y = 2( ) − ( ) 2 dx x x y du 令 u = ，有 u + x = 2u − u 2 x dx
积分，得 ln
整理为 (
1 1 dx − )du = u u −1 x
(u ≠ 0,1)
u = ln c1 x u −1
即u =
c1 x c1 x − 1
代回变量，得通解 x( y − x) = cy, (4) xy ′ − y = x tan
6
积分，得
1+ ω = cξ 4 (1 − ω ) 5
2 2 5 2 2
代回原变量，得原方程的通解为 ( x − y − 1) = c( x + y − 3)
4 1.4 习题 1.
1 解下列方程. (1)
dy + 2 xy = 4 x dx
2 dy ̃ = Ce − x . + 2 xy = 0 的通解为 y dx
−2
− x = −e − 2 e x y 为所求的解。 y
4．求解方程 x 1 − y dx + y 1 − x dy = 0 解： x = ±1 ( −1 ≤ y ≤ 1), y = ±1 ( −1 ≤ x ≤ 1) 为特解，当 x ≠ ±1, y ≠ ±1 时，
2
2
x
1− x
2
dx +
y
1− y2
ln sin y cos x = c1 ,
积分，得 ln sin y = − ln cos x + c1 , 即 sin y cos x = ± e
c1
= c, c ≠ 0
2．求下列方程满足给定初值条件的解： (1)
dy = y ( y − 1), y (0) = 1 dx y = 1 为特解，当 y ≠ 0, y −1 = x + c1 , y y ≠ 1 时， (

大学物理参编教材习题详解——第二章习题解答

习题二答案2.1 质量为16kg 的质点在XOY 平面内运动，受一恒力作用，力的分量为6x f N =,7y f N =- ，当0t =时，0x y ==，12x v m s --⋅，0y v =。

求当2t s =时质点的位矢和速度。

解：283166-⋅===sm m f a x x 2167-⋅-==s m mf a y y(1)⎰⎰--⋅-=⨯-=+=⋅-=⨯+-=+=20101200872167452832s m dt a v v s m dt a v v y y y x x x于是质点在2s 时的速度18745-⋅--=s m ji v(2)m t a t a t v y x j i j i j i r 874134)167(21)4832122(21)21(220--=⨯-+⨯⨯+⨯-=++=2.2 质量为0.25kg 的质点受力()F ti N =的作用，0t =时该质点以2()v j m s =的速度通过坐标原点，则该质点任意时刻的位置矢量是（A ）222()t i j m +（B ）2(23)2()t i tj m + （C ）433423()t i t j m +（D ）条件不足不能确定答案：B2.3 用一种钳子夹住一块质量M=50kg 的混凝土砌块起吊（如图示）。

已知钳子与砌块接触处的最大静摩擦系数4.0=μ。

如果（1）钳子匀速上升，（2）钳子以0.2m/s 2的加速度上升，（3）钳子在沿水平方向以4m/s 的速度行驶时，上端悬挂点突然停止运动（设悬挂点到砌块重心之间的距离4l m =），为使砌块不从钳子口滑出，至少必须对砌块施加多大正压力？解：（1）水平方向21N N =，竖直方向Mg f f =+21，又,,2211N f N f μμ==N Mg N N 5.6124.028.950221=⨯⨯===∴μ（2）水平方向21N N =，竖直方向Ma Mg f f =-+21，N a g M N N 6254.02)2.08.9(502)(21=⨯+⨯=+==∴μ（3）物体以s m v /4=的速率，在半径为l 的圆周上运动，水平方向21N N =，竖直方向l v M Mg f f 221=-+，N l v g M N N 5.8624.02)448.9(502)(2221=⨯+⨯=+==∴μ2.4 一滑轮两边分别挂着A 和B 两物体，它们的质量分别为m A =20kg,m B =10kg ，今用力F 将滑轮提起（如图示），当F 分别等于（1）98N ，（2）196N ，（3）392N ，（4）784N 时，求物体A 和B 的加速度以及两边绳中的张力（滑轮的质量与摩擦不计）。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

4.解：设以矩阵cos sin ()sin cos t te tt t e tt ϕ⎛⎫-= ⎪⎝⎭为基本解矩阵的线性齐次系统为.1112.2122()()()()x a t x a t y y a t x a t y ⎧=+⎪⎨⎪=+⎩则.11122122()()a a t t a a ϕϕ⎛⎫=⎪⎝⎭即11122122cos sin cos cos sin sin sin cos sin cos t t ttt t e t e t a a t e t t t a a e t t e t e t ⎛--⎛⎫-⎛⎫⎫= ⎪ ⎪⎪ -+⎭⎝⎭⎝⎭⎝得1112111221222122cos sin cos sin cos sin cos sin cos cos sin sin sin cos t t t t tt t te t e t a e t a e t t a t a t e t e t a e t a e t t a t a t ⎧-=+⎪-=-+⎪⎨+=+⎪⎪-=-+⎩整理得11121112212122cos sin cos sin cos sin cos sin cos cos sin sin sin cos t t a t a t t a t a t t t a t t t a t a t -=+⎧⎪=-⎪⎨+=+⎪⎪=-⎩解得1221121222cos sin 1cos 1sin cos sin a t t a t a t t a t=-⎧⎪=⎪⎨=+⎪⎪=⎩所以齐次系统.2.2cos (cos sin 1)(1sin cos )sin x x t t t yy t t x y t⎧=+-⎪⎨⎪=++⎩即为所求。

5.（1）解：由.cos x x t =，分离变量得c o s dx tdtx=解得s i n1t x C e=由.sin sin sin 1ttty xeC ee--==得.1y C =，解得12y C t C =+故原方程组得通解为sin 112t x C e y C t C ⎧=⎨=+⎩（1C ，2C 为不为零的常数）（2）解：由第一个分离变量得dx dt xt=解得1x C t =。

由.1xy t=+得.11y C=+解得122y t C t C t x C =++=++故原方程组得通解为12x C ty t x C =⎧⎨=++⎩6. (1)解：原方程组化为dx y dt tdy x dtt ⎧=-⎪⎪⎨⎪=-⎪⎩可化简为()1()()1()d x y x y dt td x y x y dt t +⎧=-+⎪⎪⎨-⎪=-⎪⎩由初等积分法得12C x y t x y C t ⎧+=⎪⎨⎪-=⎩ （Ⅰ）又知初值(1)2(1)0x y =⎧⎨=⎩代入（Ⅰ）得1222C C =⎧⎨=⎩，所以22x y tx y t ⎧+=⎪⎨⎪-=⎩解得11x t tx t t ⎧=+⎪⎪⎨⎪=-⎪⎩（2）解：①+②得()d x y x ydt+=+解得1tx y C e+=（1C 为常数）③令x u t=则dx du u tdt dt=+代入①得21du u t u dt++=，即131dudtu t =--两边积分得01l n 31l n 3u t C -=-+（0C 为常数），整理得123(31)C u t-=（02C Ce=）代回原变量得1233(1)C x t t -= ④。

将初值1(1)31(1)3x y ⎧=⎪⎪⎨⎪=-⎪⎩代入③，④得12311(11)11133C C e ⎧-=⎪⎪⎨⎪-=⎪⎩得1200C C =⎧⎨=⎩得解33t x ty ⎧=⎪⎪⎨⎪=-⎪⎩7．证明：令1()))t t s C ϕ=Φ(Φ(（C 为常值向量）2())t t s C ϕ=Φ(+，那么1()))d t d t s CdtdtϕΦ(=Φ(，2())().d t d t s d t s C dtdt dt ϕΦ(++=。

因为)t Φ(是)()dX t X t dt(=A 的解，所以由以上两式得11()())()d t t s C t dt ϕϕ=A ΦΦ(=A ，22())()d t A t s C A t dtϕϕ=Φ(+=。

又因为(0)X I=,所以有1(0))sC ϕ=Φ(，2(0))s Cϕ=Φ(。

所以根据解的惟一性定理可知，)))t s Ct s CΦ(+=Φ(Φ(，因而有())t s ΦΦ())t s =Φ(Φ(。

令s t=-，代入上式得(0)))t t E Φ=Φ(Φ(-=,因而1))t t -Φ(=Φ(-。

8.证明：此方程的满足初始条件0(0)x x =的初值问题可等价于积分方程0()()()tt X t x A s x s ds=+⎰对上述方程，应用毕卡逐次逼近法，只需考虑00()X x x E==,0()X t E=，10()()()()ttt t X t E A s X s ds E A s ds=+=+⎰⎰，2211()()()()()(())()(())(())()(())2t t t t tt tt t t t t t t t t t X t E A s X s ds E A s ds A t A s ds d E A s ds A s ds d A s d E A s ds A s ds τττττ=+=++=++=++!⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰22332111()()()()()(())()(())()(())(())223t t t t t t t t t t t t t t X t E A s X s ds E A s ds A A s ds d A A s ds d E A s ds A s ds A s ds ττττττττ=+=+++=+++!!!⎰⎰⎰⎰⎰⎰⎰⎰⎰由归纳法易知211()()(())(())2t ttnn t t t X t E A s ds A s ds A s ds n =+++!!⎰⎰⎰显然0()l i m ()e xp (())tnt t X t X t A s d s →+∞==⎰，可得原方程的通解为0exp(())tt A s ds c⎰，其中c 为任意的常值列向量。

9. (1)解：矩阵A 的特征值为3，-2，对应于1λ=3的特征向量12x Xx ⎛⎫= ⎪⎝⎭满足代数方程组11200()005x E A x λ⎛⎫⎛⎫-== ⎪ ⎪⎝⎭⎝⎭，所以10x ⎛⎫= ⎪⎝⎭是1λ=3的一个特征向量。

同理22λ=-对应的特征向量为01y ⎛⎫= ⎪⎝⎭，1001P ⎛⎫= ⎪⎝⎭故331220000Ae e e P P e e ---⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭（2）A 的特征方程为11E A λλλ-==-，解之，得特征根为iλ=±。

对应于1iλ=的特征向量12x X x ⎛⎫= ⎪⎝⎭满足代数方程组1121()01x i E A i x λ⎛⎫⎛⎫-== ⎪⎪-⎝⎭⎝⎭所以1X i ⎛⎫= ⎪⎝⎭是1i λ=对应的一个特征向量。

同样可得2i λ=-对应的一个特征向量为1Y i ⎛⎫= ⎪-⎝⎭。

由A 的特征值的特征向量组成的矩阵11P i i ⎛⎫=⎪-⎝⎭，其逆矩阵*11112211222i i P P i i P i -⎛⎫-⎪--⎛⎫=== ⎪ ⎪--⎝⎭⎪ ⎪⎝⎭，所以1111()()011cos1sin 12222221111sin 1cos10()()222222i ii i i i iAi iii i i i i i e e ie ie e e e e i i i i e ie ie ie ie e e -------⎛⎫⎛⎫⎛⎫--+-- ⎪ ⎪ ⎪⎛⎫⎛⎫⎛⎫⎛⎫==== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪---⎝⎭⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭（3）解：有：2102S SI A S --⎛⎫-= ⎪-⎝⎭从而*2111()2(2)()()102SI A S S SI A SI A S -⎛⎫ ⎪--- ⎪-==-⎪⎪-⎝⎭于是22112()0Ae e e SI A e --⎫⎛⎡⎤=ζ-=⎪ ⎣⎦⎪⎝⎭（4）解：有24()12S SI A S +⎛⎫-=⎪--⎝⎭，从而*221224()()2()1S SI A S S SI A S SI A S ---⎛⎫ ⎪--== ⎪+- ⎪⎪⎝⎭于是1114()13Ae SI A ----⎛⎫⎡⎤=ζ-= ⎪⎣⎦⎝⎭10.（1）解：103103120023011011A B ⎛⎫⎛⎫⎪ ⎪=-→= ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭,矩阵A 经过初等变换变为矩阵B ，则矩阵A 与矩阵B 有相同的特征值。

常微分方程与动力系统第二章课后题参考答案

第四版微分几何第二章课后习题答案

大学物理课后习题答案第02章

第二章课后习题答案

常微分方程第二章

常微分方程课后习题答案.doc

常微分方程第2章习题答案

马知恩周义仓编常微分方程定性与稳定性方法部分习题参考解答

高等数学上册第六版课后习题详细图文答案第二章

最新2.第二章习题答案-1-教学讲义ppt

常微分方程2.2习题参考解答

常微分方程课后答案

(完整版)理论力学课后答案第二章

信号与系统第2章答案

常微分方程与动力系统第二章课后题参考答案

微积分课后题答案第二章习题详解

周义仓编常微分方程习题答案

常微分方程第二章练习与答案

《常微分方程》东师大第二版习题答案

大学物理参编教材习题详解——第二章 习题解答

大学物理参编教材习题详解——第二章习题解答