四边形难题攻略
中考数学四边形求解题技巧

中考数学四边形求解题技巧中考数学中,四边形是一个非常重要的知识点,也是考试中常出现的题型之一。
四边形题目涉及到求解角度、边长、面积等方面的知识,掌握一些解题技巧能够有效提高解题速度和准确性。
下面我将介绍一些中考数学四边形求解题的技巧。
1. 利用图形性质分析题目在解决四边形问题时,首先要观察给出的图形,分析各个角的大小关系以及边长的关系。
根据图形的特点,我们可以推导出一些性质,这些性质可以帮助我们解决问题。
例如,互补角的性质:如果两个角的和等于90度,则它们是互补角。
利用这个性质,我们可以求解出两个互补角中的一个。
2. 利用角的性质在解四边形题时,经常需要求解各个角的大小。
对于平行四边形和矩形来说,对角线之间的夹角都是相等的;对于菱形来说,它的所有内角都是直角;对于等腰梯形来说,它的两个底角是相等的。
利用这些角的特点,我们可以通过已知条件求解出其他角的大小。
同时,还需要掌握计算角度的方法,如180度减去一个角的度数可以求出另一个角的度数。
3. 利用截线性质在解四边形问题时,有时会用到线段的截线性质。
截线性质是指当一条直线截断两条平行线时,所得截线与平行线之间的对应角是相等的。
利用这个性质,我们可以推导出两条平行线之间的一些角的大小关系,然后通过已知条件求解其他角的大小。
4. 利用边长的性质在解决四边形问题时,有时需要求解各个边的长度。
根据已知条件和图形的特点,我们可以列方程,然后求解出未知边长。
例如,如果题目已知一个矩形的长和宽之比为3:2,并且矩形的周长为40,我们可以设矩形的长为3x,宽为2x,列出方程3x + 2x + 3x + 2x = 40,然后解方程求解出x 的值,进而求解出长和宽的值。
5. 利用面积的性质在解决四边形问题时,有时需要求解图形的面积。
对于矩形、正方形、菱形来说,我们可以利用边长或对角线的性质求解出面积。
例如,对于矩形来说,我们可以用长和宽的乘积求解出面积;对于菱形来说,我们可以用对角线的乘积除以2求解出面积。
专题02 特殊平行四边形中的四种最值问题(解析版)-2024年常考压轴题攻略(9年级上册人教版)
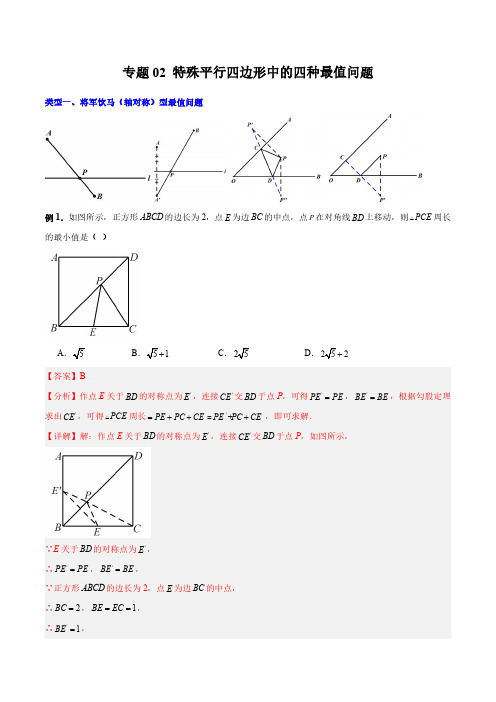
专题02特殊平行四边形中的四种最值问题类型一、将军饮马(轴对称)型最值问题A .5B .【答案】B 【分析】作点E 关于BD 的对称点为∵E 关于BD 的对称点为'E ,∴'PE PE =,'BE BE =,∵正方形ABCD 的边长为2,点A.0B.3【答案】C【分析】要使四边形APQE的周长最小,由于在BC边上确定点P、Q的位置,可在与BC交于一点即为Q点,过A点作后过G点作BC的平行线交DC的延长线于长度.∵四边形ABCD 是矩形,∴8BC AD ==,90D Ð=°,∠QCE =90°,∵2PQ =,∴6DF AD AF =-=,∵点F 点关于BC 的对称点G ,∴FG AD⊥∴90DFG ∠=︒∴四边形FGHD 是矩形,∴GH =DF =6,∠H =90°,∵点E 是CD 中点,∴CE =2,∴EH =2+4=6,∴∠GEH =45°,∴∠CEQ =45°,设BP =x ,则CQ =BC ﹣BP ﹣PQ =8﹣x ﹣2=6﹣x ,在△CQE 中,∵∠QCE =90°,∠CEQ =45°,∴CQ =EC ,∴6﹣x =2,解得x =4.故选:C .【点睛】本题考查了矩形的性质,轴对称﹣最短路线问题的应用,题目具有一定的代表性,是一道难度较大的题目,对学生提出了较高的要求.例3.如图,在矩形ABCD 中,26AB AD ==,,O 为对角线AC 的中点,点P 在AD 边上,且2AP =,点Q【答案】210【分析】①连接PO并延长交BC 明四边形APHB是矩形可得AB②过点O作关于BC的对称点PQ OQ+的最小值为PO'的长度,延长∵GO AD'⊥,点O是AC的中点,∴132AG AD==,【点睛】本题考查矩形的性质、全等三角形的判定与性质、勾股定理及轴对称识是解题的关键.【变式训练1】如图,正方形ABCD的周长为24,P为对角线AC上的一个动点,E是CD的中点,则PE PD+的最小值为()A .35B .32C .6D .5【答案】A 【详解】解:如图,连接BE ,设BE 与AC 交于点P',∵四边形ABCD 是正方形,∴点B 与D 关于AC 对称,∴P'D =P'B ,∴P'D +P'E =P'B +P'E =BE 最小.即P 在AC 与BE 的交点上时,PD +PE 最小,即为BE 的长度.∵正方形ABCD 的周长为24,∴直角△CBE 中,∠BCE =90°,BC =6,CE =12CD =3,∴226335BE =+=故选A.【变式训练2】如图,在矩形ABCD 中,AB =2,AD =3,动点P 满足S △PBC =14S 矩形ABCD ,则点P 到B ,C 两点距离之和PB +PC 的最小值为()A 10B 13C 15D .3【答案】B 【详解】解:设△PBC 中BC 边上的高是h .∵S △PBC =14S 矩形ABCD .∴12BC •h =14AB •AD ,∴h =12AB =1,∴动点P 在与BC 平行且与BC 的距离是1的直线l 上,如图,作B 关于直线l 的对称点E ,连接CE ,则CE 的长就是所求的最短距离.在Rt △BCE 中,∵BC =3,BE =BA =2,∴CE 2213+AB BC 即PB +PC 13故选:B .【变式训练3】如图,在正方形ABCD 中,4AB =,AC 与BD 交于点O ,N 是AO 的中点,点M 在BC 边上,且3BM =,P 为对角线BD 上一点,则PM PN -的最大值为_____________.【答案】1【分析】作N 关于BD 的对称点E ,连接PE ,ME ,过点M 作MQ ⊥AC ,垂足为Q ,可判定当点P ,E ,M 三点共线时,PM -PE 的值最大,为ME 的长,求出CE ,CQ ,得到EQ ,利用垂直平分线的性质得到EM =CM =1即可.【详解】解:如图:作N 关于BD 的对称点E ,连接PE ,ME ,过点M 作MQ ⊥AC ,垂足为Q ,∴PN =PE ,则PM -PN =PM -PE ,【答案】13【分析】连接CF、AF+=+,故当EF MN EF AF类型二、翻折型最值问题例1.如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN 沿MN所在直线翻折得到△A'MN,连接A'C,则A'C长度的最小值是()【变式训练1】如图,在矩形ABCD 中,3AB =,4=AD ,E 在AB 上,1BE =,F 是线段BC 上的动点,将EBF △沿EF 所在的直线折叠得到'EB F △,连接'B D ,则'B D 的最小值是()A .6B .4C .2D .1-【答案】D 【详解】解:如图,'B 的运动轨迹是以E 为圆心,以BE 的长为半径的圆.所以,当'B 点落在DE 上时,'B D 取得最小值.根据折叠的性质,△EBF ≌△EB’F ,∴E 'B ⊥'B F ,∴E 'B =EB ,∵1BE =∴E 'B =1,∵3AB =,4=AD ,∴AE =3-1=2,∴DE =D 'B =.故选:D .【变式训练2】如图,在正方形ABCD 中,AB =6,E 是CD 边上的中点,F 是线段BC 上的动点,将△ECF 沿EF 所在的直线折叠得到EC F '△,连接AC ',则的最小值是AC '_______.【答案】3【详解】解:∵四边形ABCD 是正方形,∴6CD AB AD ===,∵E 是CD 边上的中点,∴132EC CD ==∵△ECF 沿EF 所在的直线折叠得到EC F '△,∴3EC EC '==,∴当点A ,C ',E 三点共线时,AC '最小,如图,在Rt ADE △中,由勾股定理得:AE ==3AE EC '-=-,∴AC '的最小值为3.类型三、旋转型最值问题【答案】353-【分析】过点M 作MP CD ⊥,垂足为P ,连接CM ,根据正方形的性质求出CE ,证明EDC DMP △≌△股定理求出CM ,根据CN MN CM +≥即可求出CN 【详解】解:过点M 作MP CD ⊥,垂足为P ,连接由旋转可得:DE DM =,3EF MN ==,90EDM ∠=例2.如图,长方形ABCD 中,6AB =,8BC =,E 为BC 上一点,且2BE =,F 为AB 边上的一个动点,连接EF ,将EF 绕着点E 顺时针旋转30°到EG 的位置,连接FG 和CG ,则CG 的最小值为______.【答案】2+【详解】解:如图,将线段BE 绕点E 顺时针旋转30°得到线段ET ,连接GT ,过E 作EJ CG ⊥,垂足为J ,∵四边形ABCD 是矩形,∴AB =CD =6,∠B =∠BCD =90°,∵∠BET =∠FEG =30°,∴∠BEF =∠TEG ,在△EBF 和△TEG 中,EB ET BEF TEG EF EG =⎧⎪∠=∠⎨⎪=⎩,∴△EBF ≌△ETG (SAS ),∴∠B =∠ETG =90°,∴点G 的在射线TG 上运动,∴当CG ⊥TG 时,CG 的值最小,∵∠EJG =∠ETG =∠JGT =90°,∴四边形ETGJ 是矩形,∴∠JET =90°,GJ =TE =BE =2,∵∠BET =30°,∴∠JEC =180°-∠JET -∠BET =60°,∵8BC =,∴226,3,3EC BC BE EJ CJ EC EJ =-===-=,∴CG =CJ +GJ =332+.∴CG 的最小值为332+.故答案为:332.【变式训练1】如图,已知正方形ABCD 的边长为a ,点E 是AB 边上一动点,连接ED ,将ED 绕点E 顺时针旋转90︒到EF ,连接DF ,CF ,则当DF CF +之和取最小值时,DCF 的周长为______.(用含a 的代数式表示)【答案】()51a +【分析】连接BF ,过点F 作FG AB ⊥交AB 延长线于点G ,先证明AED GFE △≌△,即可得到点F 在CBG ∠的角平分线上运动,作点C 关于BF 的对称点C ',当点D ,F ,C 三点共线时,DF CF DC +='最小,根据勾股定理求出DC DF CF '=+的最小值为35,即可求出此时DCF 的周长为353+.将ED绕点E顺时针旋转90︒到EF,=,∴⊥,EF DEEF DEDEA FEG DEA ADE∴∠+∠=∠+∠=︒,90∴∠=∠,ADE FEG又90,∠=∠=︒DAE FGE(1)试猜想线段BG 和AE 的数量关系,并证明你得到的结论;(2)将正方形DEFG 绕点D 逆时针方向旋转一定角度后(旋转角度大于过观察或测量等方法判断(1)中的结论是否仍然成立?如果成立,请予以证明;如果不成立,请说明理由;(3)若2BC DE ==,在(2)的旋转过程中,①当AE 为最大值时,则AF =___________.ABC 是等腰直角三角形,AD BC ∴⊥,BD CD =,90ADB ADC ∴∠=∠=︒.四边形DEFG 是正方形,DE DG ∴=.在BDG 和ADE V 中,BD AD BDG ADE GD ED =⎧⎪∠=∠⎨⎪=⎩,(SAS)ADE BDG ∴△≌△,BG AE ∴=;(2)(1)中的结论仍然成立,BG AE =,BG AE ⊥.理由如下:如图②,连接AD ,延长EA 交BG 于K ,交DG 于O .在Rt BAC 中,D 为斜边BC 中点,AD BD ∴=,AD BC ⊥,90ADG GDB ∴∠+∠=︒.四边形EFGD 为正方形,DE DG ∴=,且90GDE ∠=︒,90ADG ADE ∴∠+∠=︒,BDG ADE ∴∠=∠.在BDG 和ADE V 中,BD AD BDG ADE GD ED =⎧⎪∠=∠⎨⎪=⎩,(SAS)BDG ADE ∴△≌△,BG AE ∴=,BGD AED ∠=∠,2,==BC DEBG∴=+=.213AE∴=.3在Rt AEF中,由勾股定理,得222=+=+3AF AE EF中,如图②中,在BDGBG∴-≤≤+,2112∴的最小值为1,此时如图④中,AE在Rt AEF中,2=AF EF【点睛】本题属于四边形综合题,考查了旋转的性质的运用,等腰直角三角形的性质的运用,勾股定理的运用,全等三角形的判定及性质的运用,正方形的性质的运用,解答时证明三角形全等是关键.类型四、PA+KPB型最值问题3A.27B.23【答案】C【分析】连接AC与EF相交于∵四边形ABCD是菱形,∠=∠,∴OAE OCFA.3B.22【答案】D【分析】连接AF,利用三角形中位线定理,可知四边形ABCD是菱形,∴==,AB BC23,H分别为AE,EF的中点,GGH∴是AEF△的中位线,【答案】51-【分析】连接BD交EF的中点,求出OB的长,得到AH AM MH>=-–51直线l平分正方形∴O是BD的中点,四边形ABCD是正方形,∴==,BD AB24【答案】26【分析】利用轴对称的性质作出如图的辅助线,在【详解】解:延长DC '''∴E F G H E '''、、、、在同一直线上时,四边形EFCH 作E K AB '⊥交AB 延长于点K ,则23EK BE CD A E AB CD '''=++=+=,E K BC '=+在△ABH中,∠AHB=90°,∠ABH过点D作DE∥AC交BC延长线于点E,作点C【点睛】本题考查了对称的性质,勾股定理,等边三角形的判定和性质,最值问题,直角三角形的性质,多边形的面积,知识点较多,难度较大,解题的关键是作出辅助线,得出当且仅当B,D,F三点共线时,BD+CD取得最小值.。
四边形最值问题解题技巧

四边形最值问题解题技巧介绍四边形是几何图形中最常见的形状之一。
对于给定的四边形,我们常常需要解决最值问题,即找出四边形的最大或最小值。
本文将介绍一些解决四边形最值问题的技巧和方法。
一、四边形的基本概念在开始讨论解题技巧之前,我们首先需要了解一些关于四边形的基本概念。
一个四边形由四条线段组成,相邻的两个线段之间有一个角。
四边形的内角和为360度。
常见的四边形类型包括矩形、正方形、平行四边形、菱形等。
二、解决四边形最值问题的一般步骤解决四边形最值问题的一般步骤可以分为以下几步:1. 确定四边形的类型根据给定的条件,确定四边形的类型。
不同类型的四边形具有不同的属性和特点,需要根据具体的情况选择相应的解题技巧。
2. 利用基本几何性质寻找约束条件根据四边形的性质和已知条件,寻找约束条件。
这些约束条件将帮助我们确定四边形的其他属性,从而解决最值问题。
3. 应用数学方法求解最值根据已知条件,利用数学方法求解四边形的最值。
这些方法可能包括求导、代数运算、三角函数等。
4. 检验结果求解完最值问题后,需要检验结果是否合理。
检验过程包括验证数学计算的正确性和对结果的合理性进行分析。
三、解决不同类型四边形最值问题的技巧下面将介绍一些常见的四边形类型及其对应的最值问题解题技巧。
1. 矩形和正方形矩形和正方形是最常见的四边形类型。
对于矩形和正方形的最值问题,常用的解题技巧包括:(1)对角线长度最值问题对角线长度最值问题是指在给定矩形或正方形的周长不变的情况下,找出对角线长度的最大或最小值。
解决该问题的技巧是使用两个对角线的长度表示矩形或正方形的面积,并应用数学方法求解。
(2)面积最值问题面积最值问题是指在给定矩形或正方形的周长不变的情况下,找出面积的最大或最小值。
解决该问题的技巧是使用两个相等的邻边的长度表示矩形或正方形的面积,并应用数学方法求解。
2. 平行四边形和菱形平行四边形和菱形也是常见的四边形类型。
对于平行四边形和菱形的最值问题,常用的解题技巧包括:(1)对角线长度最值问题对角线长度最值问题是指在给定平行四边形或菱形的周长不变的情况下,找出对角线长度的最大或最小值。
揭开高中数学中的四边形问题的解题方法

揭开高中数学中的四边形问题的解题方法数学中的四边形问题是高中阶段的数学课程中一个非常重要的内容。
四边形作为几何图形的一种,具有丰富的特性和性质,解题方法也有多种。
本文将揭开高中数学中四边形问题的解题方法,帮助同学们更好地理解和应用于实际问题中。
一、四边形的基本概念在开始讨论解题方法之前,我们首先要了解四边形的基本概念。
四边形是一个有四条边和四个顶点的几何图形,根据边的长短和角的大小,可以分为不同的类型,如矩形、正方形、菱形等。
掌握四边形的基本概念是理解解题方法的前提。
二、四边形的性质与定理在解题过程中,我们需要运用四边形的性质与定理,来帮助分析和解决问题。
以下是高中数学中常用的四边形性质与定理:1. 任意四边形的内角和等于360度。
2. 矩形的对角线相等且垂直。
3. 正方形是特殊的矩形,其四条边相等且对角线相等垂直。
4. 菱形是四边形的特殊情况,其四条边相等且对角线相等垂直。
5. 平行四边形的对边平行且相等。
6. 对角线平分平行四边形的内角。
7. 特殊的平行四边形——矩形、正方形的对边相等。
掌握这些四边形的性质与定理,可以在解题过程中运用它们来推导出正确的结论,简化解题步骤。
三、解题方法示例为了更好地理解解题方法,我们来看几个具体的例子。
例一:已知矩形ABCD,AB=4cm,BC=5cm,求矩形的面积。
解:矩形的面积可以通过边长求解,即S=AB×BC=4cm×5cm=20cm²。
例二:已知平行四边形ABCD,其中AD=10cm,BC=8cm,AC的垂直线段为AE,垂直线段BF与AC交于点F,求BF的长度。
解:根据平行四边形的性质,我们知道对边平行且相等,因此AE=BC=8cm。
由垂直线段的性质可知,四边形ACBF是个矩形,所以BF=AC=10cm。
例三:已知正方形ABCD,其中AD=6cm,点E是BC边上的一点,且BE=3cm,连接AE,求△ABE的面积。
解:根据正方形的性质,我们知道对角线相等且垂直,所以AC=BD=6cm,并且AE=CE=BE=3cm。
四边形动点问题解题技巧

四边形动点问题解题技巧
四边形动点问题是指在四边形中,指定一个或多个点 (动点) 的运动方式及方向,求其余点 (定点) 在发展过程中的坐标及对应数量关系的问题。
解决四边形动点问题需要掌握以下技巧:
1. 分析题意:认真阅读题干,了解动点的运动方式、方向及限制条件,提取关键信息,确定解题方向。
2. 建立坐标系:通常是在平面直角坐标系中解决这个问题,需要将动点的位置转化为坐标,以便于应用代数方法解决问题。
3. 建立等量关系:通过分析题目中的限制条件和运动方式,建立动点和定点的等量关系,通常可以用行程问题、角度问题等来表示。
4. 列方程解题:根据等量关系,列出代数方程,求解未知数的值,然后根据题意进行画图、分析、总结。
5. 分类讨论:对于存在角度限制或速度限制等问题的题目,需要进行分类讨论,以确保解答的正确性。
6. 注意细节:在解决问题的过程中,需要注意细节,如动点的速度、方向、持续时间等因素,以免出现不必要的错误。
综上所述,解决四边形动点问题需要有清晰的思路和扎实的数学知识基础,需要善于发现问题的本质,善于运用代数方法解决问题,同时需要注意细节和分类讨论。
四边形求解技巧

四边形求解技巧四边形是一个具有四条边的几何图形,常见的四边形有矩形、正方形、菱形和梯形等。
在解题过程中,我们可以运用一些技巧来简化问题和提高解题效率。
以下是一些常见的四边形求解技巧。
1. 利用四边形的对称性:在有关对称性的问题中,我们可以利用四边形的对称性来简化计算。
例如,在矩形和正方形中,对角线相等,对边平行且相等。
在菱形中,对角线相等,对边平行且相等。
如果一个四边形具有对称轴,我们可以根据对称性质来推导出其他边和角的关系,从而简化问题。
2. 利用四边形的角的性质:根据四边形内角和为360度的性质,我们可以得到以下推论:- 矩形和正方形中,对角线是相等的;- 矩形和菱形中,相对的角是相等的;- 矩形、菱形和正方形中,对边相等。
3. 利用四边形的边的性质:根据四边形的边的性质,我们可以得到以下推论:- 正方形中,所有边相等;- 矩形中,对边相等;- 菱形中,对边相等。
4. 利用四边形的对角线:对于矩形和正方形,对角线相等,我们可以利用对角线的性质来简化计算。
例如,在矩形中,如果对角线相交于点M,则M是对角线的中点。
5. 利用四边形的相似性:如果两个四边形具有相似性质,即对应的角相等,对应的边成比例,我们可以利用相似性质来求解问题。
例如,在相似的矩形中,我们可以利用比例关系来确定相应的长度。
6. 利用平行线性质:如果在四边形中,有两组对边分别平行,我们可以利用平行线性质来简化计算。
例如,在梯形中,底边平行且相等,我们可以利用平行线的性质来推导出其他边和角的关系。
7. 利用垂直线性质:如果在四边形中,有两组对边相互垂直,我们可以利用垂直线性质来简化计算。
例如,在矩形中,对边相互垂直,我们可以利用垂直线的性质来推导出其他边和角的关系。
8. 利用外接圆和内切圆:四边形可以内接于一个圆或外接于一个圆。
如果我们能找到这个圆,我们可以利用圆的性质来求解问题。
对于矩形和正方形,外接圆和内切圆的圆心是相等的。
9. 利用面积公式:根据四边形的性质,我们可以计算四边形的面积。
专题03 特殊平行四边形中的三种几何动点问题(原卷版)-2024年常考压轴题攻略(9年级上册人教版)

专题03特殊平行四边形中的三种几何动点问题类型一、面积问题例.如图,在四边形ABCD 中,AB CD ∥,90BCD ∠= ,10cm AB AD ==,=8cm BC .点P 从点A 出发,以每秒3cm 的速度沿折线ABC 方向运动,点Q 从点D 出发,以每秒2cm 的速度沿线段DC 方向向点C 运动.已知动点P ,Q 同时发,当点Q 运动到点C 时,P ,Q 运动停止,设运动时间为t .(1)直接写出CD 的长(cm );(2)当四边形PBQD 为平行四边形时,直接写出四边形PBQD 的周长(cm );(3)在点P 、点Q 的运动过程中,是否存在某一时刻,使得BPQ V 的面积为215cm ?若存在,请求出所有满足条件的t 的值;若不存在,请说明理由.【变式训练1】如图,在四边形ABCD 中,,90,120,12cm,15cm AD BC A B ADC AD BC ∠=∠=︒∠=︒==∥,点P 自点A 沿折线AD DC -以1cm/s 的速度运动,点Q 自点C 沿向CB BA -以1cm/s 的速度运动.点P ,Q 同时出发,其中一个点到达终点,另一个点也停止运动.设运动时间为(s)t .(1)当P 在AD 边上,点Q 在BC 边上时,如图1.①用含t 的代数式表示:DP =___________,BQ =___________;②若四边形APQB 是平行四边形,求t 的值?(2)求BPQ V 的面积S 与运动时间t 之间的数量关系式,并写出t 的取值范围.【变式训练2】如图,在矩形ABCD 中,AB =12,BC =18,点P 从点A 出发,以每秒2个单位长度的速度沿类型二、几何图形存在性问题长的速度向点A 匀速运动,同时点E 从点A 出发沿AB 方向以每秒1个单位长的速度向点B 匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D E ,运动的时间是t 秒()0t >.过点D 作DF BC ⊥于点F ,连接DE ,EF .(1)求AB AC ,的长;(2)求证:AE DF =;(3)当t 为何值时,DEF 为直角三角形?请说明理由.例2.如图,已知正方形ABCD 的边长为4cm ,动点P 从点B 出发,以2cm /s 的速度沿B C D →→方向向点D 运动,动点Q 从点A 出发,以1cm /s 的速度沿A B →方向向点B 运动,若P 、Q 两点同时出发运动时间为s t .(1)连接PD 、PQ 、DQ ,求当t 为何值时,PQD △的面积为27cm ?(2)当点P 在BC 上运动时,是否存在这样的t 使得PQD △是以PD 为一腰的等腰三角形?若存在,请求出符合条件的t 的值;若不存在,请说明理由.例3.如图,在四边形ABCD 中,AD ∥BC ,∠B =90°,AB =8cm ,AD =12cm ,BC =18cm ,点P 从点A 出发以1cm/s 的速度向点D 运动;点Q 从点C 同时出发,以2cm/s 的速度向点B 运动,当点Q 到达点B 时,(1)填空:AB =;菱形ABCD 的面积S =;菱形的高h =.(2)若点M 的速度为每秒1个单位,点N 的速度为每秒a 个单位(其中52a <),当4t =时在平面内存在点得以A ,M ,N ,E 为顶点的四边形为菱形,请求出所有满足条件的a 的值.类型三、直线位置关系问题例1.如图,在Rt ABC △中,90ABC ∠=︒,5AC =,4BC =,点D 是边AB 的中点,动点P 从点A 出发(1)直接写出AB的长.(2)当点Q落在AB边上时,用含t的代数式表示(1)分别求BD和BE的长度;(2)连接PQ,当95t=时,判断PQ与AD是否垂直,并说明理由;(3)试判断是否存在t的值,使得以P,Q,C,DC 点以1cm /s 的速度运动,动点Q 从点B 开始沿BA 向A 点以3cm /s 的速度运动,P ,Q 分别从点D ,B 同时出发,当其中一点到达终点时,另一点也随之停止运动,运动的时间为t 秒.(1)t 为何值时,四边形DPQA 为矩形?(2)t 为何值时,四边形PQBC 为平行四边形?2.如图,在ABC 中,6cm AC =,=8cm BC ,点O 以每秒1cm 的速度由点A 向点C 运动(不与点C 重合),过点O 作直线MN BC ∥,BCA ∠的外角平分线CF 于点F ,ACB ∠的平分线CE 于点.E 设运动时间为t 秒.发现:(1)在点O 的运动过程中,OE 与OF 的关系是______,请写出理由.(2)当=2t 时,=EF ______cm .探究:当=t ______时,四边形AECF 是矩形,并证明你的结论.拓展:若点O 在运动过程中,能使四边形AECF 是正方形,试写出线段AB 的长度.(直接写出结论即可)3.已知正方形ABCD 中,8AB BC CD DA ====,90A B C D ∠=∠=∠=∠=︒.动点P 以每秒2个单位速度从点B 出发沿线段BC 方向运动,动点Q 同时以每秒8个单位速度从B 点出发沿正方形的边(1)当运动时间为秒时,点P与点Q相遇;∥时,求线段DQ的长度;(2)当BQ PD全等时,求t的值.(3)连接PA,当PAB和QAD(1)CB的长为______.(2)用含t的代数式表示线段QB的长.(3)连接PQ,=;(1)求证:PE DQ(1)=a______cm,b=______cm;(2)t为何值时,EP把四边形BCDE的周长平分?(1)当2t =时,BP =___________cm ;(2)当t 为何值时,连接,,CP DP CDP △是等腰三角形;(3)Q 为AD 边上的点,且6DQ =,P 与Q 不重合,当t 为何值时,以长方形的两个顶点及点P 为顶点的三角形与DCQ 全等.。
四边形面积最值问题解题技巧

四边形面积最值问题解题技巧
解决四边形面积最值问题,可以使用以下技巧:
1. 首先,计算四边形的面积公式。
对于一般的四边形,可以使用海龙公式或狄利克雷公式来计算面积。
如果是特殊的四边形(如矩形、平行四边形等),则可以使用其特定的面积公式。
2. 确定四边形的类型。
不同类型的四边形有不同的性质和限制条件,因此需要根据具体情况采用不同的方法求解。
3. 利用不等式技巧。
对于某些特定的四边形类型,可以运用不等式技巧来求解其最大或最小面积。
例如,对于一个长方形,可以利用不等式“算术平均数大于等于几何平均数”来证明其最大面积出现在正方形时。
4. 画图分析。
通过画图来理解和分析四边形的性质和限制条件,可以更加直观地找到最大或最小面积。
同时,画图也可以帮助我们发现一些规律和特点,为解决问题提供思路和启示。
总之,在解决四边形面积最值问题时,需要结合具体情况选择合适的方法和技巧,充分利用已知条件和性质来求解。
同时,需要多加练习,不断提高自己的数学水平和解题能力。
四边形类题型解题技巧-

四边形类题型解题技巧四边形是几何知识中非常重要一块内容,因其“变化多端”更是成为中高考数学考试一个热门考点。
如其中特殊四边形--平行四边形具有对边平行且相等、对角相等、对角线互相平分等性质,它们在计算、证明中都有广泛的应用,如求角的度数、求线段的长、求周长、求第三边的取值范围、综合计算题、探索题等等问题.典型例题1:解题反思:本题考查了平行四边形的判定和性质,全等三角形的判定和性质,熟练掌握平行四边形的判定定理是解题的关键。
辅助线是解决四边形一个重要知识点,如构造三角形中位线。
实现线段或角的转移,从而迅速找到解题突破口,往往会使得某些看似无法解决的几何题化难为易,迎刃而解。
解题反思:本题考查了三角形的中位线平行于第三边并且等于第三边的一半,熟记定理是解题的关键,难点在于作辅助线构造出全等三角形和平行四边形.除了中位线,在一些四边形问题解决过程中,出现这样解法:顺次连结四边形四条边的中点所得的四边形叫中点四边形。
这个中点四边形有许多重要性质,在中考试题中也屡见不鲜,中点四边形的四个结论如下:任意四边形的中点四边形是平行四边形、对角线相等的四边形的中点四边形是菱形、对角线垂直的四边形的中点四边形是矩形、对角线相等且垂直的四边形的中点四边形是正方形。
因为四边形的两条对角线垂直,所以这个四边形的中点四边形是矩形,又因为这个四边形的。
两条对角线相等,所以这个四边形的中点四边形是菱形。
既是矩形又是菱形的图形就是正方形。
近几年随着新课改不断的深入,中考题更加考查学生思维能力,如出现一些图形折叠、翻转等问题。
这类问题的实践性强,要利用图形变化过程中利前后线段、角的对应相等关系,构造一些特殊三角形等知识来求解。
解题反思:考查了几何变换综合题,涉及的知识点有:等腰直角三角形的性质,等量代换,旋转的性质,全等三角形的判定和性质,平行四边形的判定和性质,综合性较强,难度中等.四边形中另一种特殊图形--梯形,也是热门考点。
中考动点四边形问题解题思路及要点

动点四边形问题解题思路及要点动点四边形问题题型特点分析:四个顶点中,有三个是定点;或者有两个是定点,两个是动点。
解题的突破口:根据确定的点的位置,判断出另外两个顶点的位置。
①如果是三定+一动,我们可以取任意两个定点所在的线段,当做四边形的边或者对角线来进行讨论。
当这个线段是边时,另外一个定点和动点所在的线段一定是它的对边,根据特殊四边形对边平行且相等的性质,可以得出另外一个定点和动点之间的距离。
因为只确定定点和动点的距离,不确定定点和动点左右或上下位置,此时要分两种情况讨论。
然后再把两个定点所在的线段当对角线,利用平行四边形对角线互相平分的性质,另外一个定点和动点的中点,一定经过对角线的中点。
②如果是两定+两动,基本思路也是把两个定点所在的线段当做边或对角线进行讨论。
区别在于,另外两个点都是动点讨论的情况会更多。
如果把两个定点所在的线段当做边,另外两个动点所在的是边时,不仅要确保对边平行且相等,而且另外两个动点的位置还要互相交换,此时一共有四种不同的情况;当两个动点所在的线段是对角线时,这两个动点交换位置会存在两种情况。
③当题中的定点或者动点处在特殊的位置时,讨论的情况会相应的减少。
比如,四个点所在的两个线段互相平行,那此时只需要确保对边相等即可。
若题中明确指出,其中两个点所在的线段为边时,就不需要把它当对角线进行讨论。
④在确定具体的点的坐标时,我们可以利用平行四边形对边平行且相等、对角线互相平分的性质,直接计算动点坐标、也可以列方程解方程求出动点坐标;也可以根据特殊四边形平移的方式,求出平移之后的对应的点的坐标。
⑤在解决正方形的存在性问题时,要把正方形问题转化为等腰直角三角形的问题;解决矩形的存在型问题时,要把矩形问题转化为直角三角形的问题。
这两种类型题中都存在直角三角形,那么在解题方法上有共同点:第一种可以用一线三垂直来求点坐标;可以利用直角三角相似来求点坐标;若题中存在特殊角,也可以用特殊角三角函数值求动点坐标;可以用同角三角函数值列方程;也可以利用斜率成绩为负一求点坐标;还可以利用直角三角形勾股定理来列方程解方程,但这种情况计算量比较大,必须是动点有一个坐标已经确定时或横纵坐标之间的关系非常确定时,可列方程,具体列方程时,直接用勾股定理避免出现开方。
初二数学四边形的折叠问题技巧

初二数学:四边形的折叠问题技巧四边形是几何学中重要的图形之一,它具有丰富的性质和应用。
在数学学习中,我们常常会遇到与四边形相关的问题。
其中一个有趣且常见的问题就是四边形的折叠问题。
本文将介绍四边形折叠问题的基本概念和解题技巧,帮助初中生更好地理解和解决这类问题。
什么是四边形的折叠问题?四边形的折叠问题是指给定一个四边形,在保持边长不变的情况下,把它折叠成二维平面上的一个点或一条线段。
常见的四边形包括正方形、长方形、平行四边形和梯形等。
这类问题常常涉及如何折叠和旋转四边形,并要求计算折叠后的形状、面积、体积等数值。
基本概念在解决四边形的折叠问题之前,先了解一些基本概念是很有帮助的。
1.边长:四边形的每条边的长度,通常用a、b、c和d表示。
2.对角线:连接四边形的两个非相邻顶点的线段,通常用e和f表示。
3.高度:以顶点为基点,垂直于底边或顶边的线段的长度,通常用h表示。
4.面积:四边形所围成的区域的大小,通常用S表示。
折叠技巧解决四边形折叠问题的关键在于理解形状的变化和如何利用对称性质。
下面将介绍常见四边形的折叠技巧。
正方形折叠技巧正方形是最简单的四边形之一,它的所有边长相等,对角线相等且互相垂直。
当折叠一个正方形时,我们可以沿着对角线折叠,从而使正方形折叠成一个边长等于对角线长度的等边三角形。
长方形折叠技巧长方形是另一种常见的四边形,它拥有两组相等的边长,且相邻边互相垂直。
当折叠一个长方形时,我们可以沿着较短的一组边折叠,从而使长方形折叠成一个等腰直角三角形。
平行四边形折叠技巧平行四边形具有两对平行边,对角线互相交叉,但长度不相等。
当折叠一个平行四边形时,我们可以选择沿着任意一条对角线折叠。
如果选择沿着短对角线折叠,平行四边形会折叠成一个与原平行四边形等面积的直角梯形;如果选择沿着长对角线折叠,平行四边形会折叠成一个与原平行四边形相等的直角三角形。
梯形折叠技巧梯形的特点是两边平行,而另外两边不平行。
四边形最值问题解题技巧

四边形最值问题解题技巧
1.确定四边形属性:确定四边形属性很重要,四边形属性指的是四边
形的特定性质,例如是否是矩形或平行四边形等。
根据属性分析,可以推
断出四边形其他性质,例如角度、边长等。
2.利用角度性质:四边形的角度性质非常重要,利用它可以得到很多
信息。
例如,矩形四个角度都是90度,对角线相等,平行四边形对角线
交点的角度相等等。
3.应用相似三角形:当四边形有相似三角形时,可以用相似三角形的
性质来解题。
例如,平行四边形的对角线交点分割成的四个三角形都是相
似的三角形,利用相似三角形的比例可以得到四边形的一些边长。
4.利用面积公式:四边形的面积公式有很多,其中最常用的是矩形和
平行四边形的面积公式。
利用面积公式可以得到四边形的面积,此时需要
注意单位统一。
5.利用勾股定理:当四边形是矩形或正方形时,可以利用勾股定理解题。
例如,矩形的对角线是勾股定理中的斜边,可以利用勾股定理求出其
长度。
6.利用平面几何知识:除了以上方法,还可以利用平面几何知识解题,例如平行线之间的夹角相等、对顶角相等等。
利用这些知识可以得到四边
形的一些性质。
解四边形最值问题

解四边形最值问题问题描述给定一个四边形,其中两条边与坐标轴平行,另外两条边与坐标轴不平行。
我们需要找到这个四边形内所有点的最大和最小的 x坐标和 y 坐标。
解决方案我们可以将四边形分为两个三角形,一个三角形的两条边与坐标轴平行,另外一个三角形的两条边与坐标轴不平行。
然后,我们可以分别找到每个三角形内所有点的最大和最小的 x 坐标和 y 坐标。
对于与坐标轴平行的三角形,我们可以通过比较顶点的坐标来找到最大和最小的 x 坐标和 y 坐标。
对于与坐标轴不平行的三角形,我们可以通过找到两条边的交点,然后再通过比较交点和顶点的坐标来找到最大和最小的 x 坐标和 y 坐标。
最后,我们将两个三角形内所有点的最大和最小的 x 坐标和 y 坐标进行比较,得到四边形内所有点的最大和最小的 x 坐标和 y 坐标。
示例假设我们有一个四边形,其中两条边与坐标轴平行,坐标分别为 (0, 0)、(0, 4)、(2, 3)、(2, 1)。
我们可以将这个四边形分为两个三角形:(0, 0)、(0, 4)、(2, 3) 以及 (0, 0)、(2, 3)、(2, 1)。
通过比较顶点的坐标,我们可以找到第一个三角形内所有点的最大和最小的 x 坐标和 y 坐标为 (0, 4) 和 (0, 0);通过找到两条边的交点,我们可以找到第二个三角形内所有点的最大和最小的 x 坐标和 y 坐标为 (2, 3) 和 (0, 0)。
最后,我们比较两个三角形内所有点的最大和最小的 x坐标和 y 坐标,得到四边形内所有点的最大和最小的 x 坐标和 y 坐标为 (2, 4) 和 (0, 0)。
总结通过将四边形分为两个三角形,并比较顶点坐标和交点坐标,我们可以找到四边形内所有点的最大和最小的 x 坐标和 y 坐标。
这个方法简单且无需考虑法律问题,非常适合解决四边形最值问题。
专题19 四边形综合题破解策略(含答案)

专题19 四边形综合题破解策略一、递进式——实际上就是将一个复杂问题加了个台阶例1如图4-19-1,在四边形ABCD 中,AD//BC ,∠ABC=90°.点E 是DC 的中点,过点作DC 的垂线交AB 于点P ,交CB 的延长线于点M.点F 在线段ME 上,且满足CF=AD ,MF=MA(1)若∠MFC=120°,求证:AM=2MB ; (2)求证:∠MPB=90°-21∠FCM.【提示】先看第(1)题,从待证结论看:由于∠ABM=90°,要证明AM=2MB ,很显然需要证明∠MAB=30°;从条件看,由于ME 垂直平分CD ,可考虑连接MD ,得到MD=MC ,接着证明△DAMQ△CFM.即可证得∠DAM=120°,从而获证。
再看第(2)题,如果不考虑第(1)问的结论,直接证明第(2)题,这题确实不容易证明,要证明“∠MPB = 90*-号∠FCM”,由于∠MPB=90°-∠PMB,而∠PMB=号∠DM C ,联想到第(1)题证明了“△DAM 经△CFM”,∠FCM=∠ADM,最后根据AD/BC 可把由已知推得的结论和证明需要的条件对接起来,完成本题的证明.【解答】【技巧点评】现在的中考试卷,大多数综合题的设置都是递进式,在证明的过程中,当证明后面的问题比较困难的时候,尝试着从前面已经证得的结论入手,寻找解决问题的途径。
跟踪训练1.如图4-19-2,四边形ABCD是边长为2的菱形,∠BAD=60°,对角线AC与BD交于点 O,过点O的直线EF交AD于点E,交BC于点F.(1)求证:△AOE≌△COF;(2)若∠EOD=30°,求CE的长.二、图形与几何例2如图4-19-3①,已知正方形ABCD中,E为对角线BD上一点,过E点作EF BD交BC于F,连接DF,G为DF中点,连接EG,CG.(1)求证:EG=CG;(2)将图①中△BEF绕B点逆时针旋转45°,如图4-19-3②所示,取DF中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;(3)将图①中△BEF绕B点旋转任意角度,如图4-19-3③所示,再连接相应的线段,问(1)中的结论是否仍然成立?通过观察你还能得出什么结论?(均不要求证明)【提示】对于第(1)小题,可利用直角三角形斜边上的中线等于斜边的一半,证得EG和CG都等于DF的对于第(2)题,辅助线作法有以下几种。
四边形角格点问题解题技巧详解与方法详解

四边形角格点问题解题技巧详解与方法详解嘿,咱今儿就来唠唠四边形角格点问题!这可是个有趣又有点头疼的玩意儿呢。
你想想啊,四边形就像个四四方方的小天地,可这角格点问题就像是在这个小天地里藏了不少小秘密,等着我们去揭开。
比如说,遇到一个四边形,它的角上有点特别的情况,那咱就得好好琢磨琢磨了。
咱得先观察观察,看看这些角之间有啥关系,是不是有啥规律可循。
这就好比你找宝藏,得先留意周围的线索呀!然后呢,咱可以试着画画辅助线。
这辅助线可神奇了,就像给你打开了一扇通往解题新世界的门。
它能把那些看似杂乱无章的角啊边啊给联系起来,让你一下子豁然开朗。
再来说说具体的解题技巧。
咱可以从一些特殊的角度入手,比如直角啦、平角啦。
你想想,这些特殊的角就像是一把钥匙,说不定就能打开解题的大门呢!还有啊,利用三角形的内角和定理也是个好办法。
把四边形分割成几个三角形,那问题不就变得简单多了嘛。
还有哦,有时候咱得学会换个角度看问题。
就像你走路,有时候直走不通,那咱就绕个弯呗。
解题也是一样,别死磕一个方法,多试试几种,说不定就柳暗花明又一村了呢。
咱举个例子哈,有个四边形,它的几个角都怪怪的。
这时候咱就可以根据已知条件,慢慢分析,一步一步来。
就像走迷宫,只要方向对了,总能走出去的。
哎呀,这四边形角格点问题啊,真的是需要我们细心加耐心。
可别嫌麻烦,当你解开一道难题的时候,那成就感,啧啧,别提多棒了!总之呢,面对四边形角格点问题,咱不能怕,得鼓起勇气去挑战。
多观察,多思考,多尝试不同的方法。
就像那句话说的,办法总比困难多嘛!相信自己,咱一定能把这些难题都拿下!这就是我给大家分享的四边形角格点问题解题技巧和方法,大家可得好好记住哦!。
初中数学四边形求解题技巧

初中数学四边形求解题技巧初中数学中关于四边形的求解题目有很多,下面我将介绍一些常见的求解四边形题目的技巧和方法。
一、平行四边形的性质和求解平行四边形是指具有两组对边平行的四边形。
在求解平行四边形的问题中,我们可以利用以下性质和方法:1. 对角线等分性质:平行四边形的两条对角线互相等分。
应用技巧:利用对角线等分性质,可方便地求解平行四边形的各边长。
2. 交错角性质:平行四边形的两组对边交错相等。
应用技巧:根据交错角性质,可求解平行四边形的角度。
3. 逆用:若两组对边都平行,则是平行四边形。
应用技巧:当题目给出两组对边都平行时,可直接判定为平行四边形。
二、矩形和正方形的性质和求解矩形是指具有四个直角的四边形,而正方形是一种特殊的矩形,它具有四个相等的边和四个直角。
在求解矩形和正方形的问题中,我们可以利用以下性质和方法:1. 特殊对角线性质:矩形和正方形的对角线相等。
应用技巧:利用特殊对角线性质,可方便地求解矩形和正方形的对角线长度。
2. 邻边和对角线关系:矩形的邻边和对角线之间存在特定的关系。
应用技巧:根据邻边和对角线的关系,可求解矩形的边长和对角线长度。
3. 邻边与对角线之间的关系:正方形的邻边和对角线之间存在特定的关系。
应用技巧:根据邻边和对角线的关系,可求解正方形的边长和对角线长度。
三、菱形的性质和求解菱形是指具有四个相等边的四边形,它具有一些特殊的性质。
在求解菱形的问题中,我们可以利用以下性质和方法:1. 对角线垂直性质:菱形的对角线相互垂直。
应用技巧:利用对角线垂直性质,可方便地求解菱形的对角线长度。
2. 对角线和邻边的关系:菱形的对角线和邻边之间存在特定的关系。
应用技巧:根据对角线和邻边的关系,可求解菱形的边长和对角线长度。
四、梯形的性质和求解梯形是指具有一对平行边的四边形。
在求解梯形的问题中,我们可以利用以下性质和方法:1. 对角线平分性质:梯形的对角线互相平分。
应用技巧:利用对角线平分性质,可方便地求解梯形的对角线长度。
理解高中数学中的四边形问题的解题技巧

理解高中数学中的四边形问题的解题技巧高中数学中的四边形问题是一类常见的数学问题,它涉及到对四边形的特性和性质进行分析、计算和解答。
在解题过程中,我们可以运用一些技巧来帮助我们更好地理解及解决这类问题。
本文将介绍一些理解高中数学中的四边形问题的解题技巧。
1. 理解四边形的基本概念在解答四边形问题前,首先应确保对四边形的基本概念有清晰的理解。
四边形是一个有四条边和四个角的图形。
常见的四边形包括矩形、正方形、平行四边形、菱形等。
对于每种四边形,其独特的性质和特点需要被熟知。
2. 关注四边形的已知条件在解决四边形问题时,需要仔细审题并注意已知条件。
已知条件提供了相关的信息,可以帮助我们推断和确定未知的问题。
例如,已知一个四边形的两对边平行,那么可以推断出它是一个平行四边形。
3. 运用四边形的性质四边形有很多性质和定理,熟悉并运用这些性质能够在解题中起到重要的作用。
一些常见的四边形性质包括:(1) 矩形的对边相等且相邻边垂直;(2) 正方形是矩形的特例,具有矩形的所有性质;(3) 平行四边形的对边平行且相等;(4) 菱形的对角线相等且垂直;(5) 梯形的一对相邻边平行。
通过运用这些性质,可以简化解题过程,并帮助我们快速得出结论。
4. 运用四边形的面积计算公式解决四边形问题时,有时需要计算四边形的面积。
不同类型的四边形有不同的面积计算公式。
例如,矩形的面积可以通过长度乘宽得到,而三角形的面积可以通过底边乘以高的一半得到。
熟悉这些计算公式可以帮助我们更快速地解答问题,并验证答案的正确性。
5. 运用四边形的相似性质相似性质在解决四边形问题中也是常被运用的。
如果两个四边形相似,它们对应的角度相等,对应的边长成比例。
通过利用这种相似性质,我们可以快速得到未知长度、角度等的值。
6. 综合运用解题技巧在解决四边形问题时,常常需要综合运用多个解题技巧。
通过将已知条件和四边形的性质结合,我们可以建立数学模型并解答问题。
总结起来,理解高中数学中的四边形问题的解题技巧包括:理解四边形的基本概念、关注四边形的已知条件、运用四边形的性质、计算四边形的面积、运用四边形的相似性质以及综合运用不同的解题技巧。
解谜四边形高中数学四边形问题的解题方法

解谜四边形高中数学四边形问题的解题方法四边形是高中数学中一个常见的图形,包含矩形、正方形、平行四边形、菱形等等。
在解谜四边形问题时,我们面临着寻找其性质、判断其类型、求解其特定值等难题。
本文将介绍一些解谜四边形问题的解题方法,帮助读者更好地理解与应用数学知识。
一、性质分析法首先,我们可以通过分析四边形的性质来解答问题。
以矩形为例,我们知道矩形的四个内角均为90度,且具有两对相等的对边。
因此,如果一道题目给定了四边形的某些性质,我们可以利用这些已知条件进行推理和求解。
通过分析四边形的性质,我们可以有针对性地应用相关定理和公式进行计算。
二、相似性质法相似性质法是解答四边形问题常用的方法之一。
通过找出两个或多个四边形之间的相似性质,我们可以推导出一些重要的结论。
例如,当两个三角形的对应角相等,对应边成比例时,我们可以得出这两个三角形相似的结论。
同样地,当两个四边形的对应角相等,对应边成比例时,我们也可以得出这两个四边形相似的结论。
利用相似性质,我们可以解答关于四边形比例、面积比等问题。
三、变形法变形法是另一种解答四边形问题的重要方法。
在解谜过程中,问题可能需要我们进行变形操作,使得问题更易于解决。
例如,在某道题目中,我们需要求解一个平行四边形的面积,但只给出了其对角线的长度。
这时,我们可以利用平行四边形的性质将其变形为两个相等的三角形,然后分别计算每个三角形的面积,最后相加得到平行四边形的面积。
通过巧妙地进行四边形的变形操作,我们能够更快、更准确地解答问题。
四、向量法在解答某些特殊四边形问题时,向量法是一种有效的解题方法。
通过引入向量的概念,我们可以借助向量的性质来解答四边形问题。
例如,在解答平行四边形的面积问题时,我们可以利用向量的加法和数量积来推导出平行四边形的面积公式。
在利用向量解答四边形问题时,注意要符合向量的加法和数量积的运算规则,从而得到正确的解答结果。
通过以上所述的方法,我们可以更好地解答高中数学中的四边形问题。
2023年初中数学奥林匹克竞赛解题方法大全配版四边形的趣味问题

第十章四边形旳趣味问题第一节四边形旳分类与鉴定【知识点拨】1.四边形旳性质: 四边形旳内角和等于3600。
2、四边形旳旳分类: (1)对边平行;(2)对边不平行。
本节研究是对边不平行旳四边形。
没用措施是转化为三角形进行研究。
【赛题精选】例2.如图: 求∠A+∠B+∠C+∠D+∠E+∠F旳度数。
(1999年重庆市竞赛题)【阐明】探索存在型问题是指在一定条件下, 判断与否存在某个结论。
解答此类问题, 先假设结论存在, 从假设出发, 根据题设条件及有关性质进行推理论证, 若推出矛盾, 则不定假设, 若推出合理旳成果, 则阐明假设对旳。
这种措施叫“假设法”。
【阐明】对于四边形, 作对角是常用旳辅助线!【针对训练】第二节平行四边形旳问题【知识点拨】1.平行四边形性质: 对边平行且相等、对角相等、邻角互补、对角线互相平分。
2.矩形性质: 矩形除具有平行四边形旳性质外, 还具有对角线相等、四个角是直角。
3、菱形性质:除具有平行四边形旳性质外, 尚有四条边相等、对角线互相垂直、且每一条对角线平分一组对角。
4、平行四边形问题旳处理措施:(1)转化为三角形问题来处理;(2)常用平行四边形旳性质来处理。
【赛题精选】例2.凸四边形ABCD中, AB∥CD, 且AB+BC=CD+AD求证: ABCD是平行四边形。
(1990年芜湖市竞赛题)例3.平面上有三个正△ABD.△ACE、△BCF, 两两共有一种顶点。
求证: CD与EF互相平分。
(1990年芜湖市竞赛题)例4.在Rt△ABC中, ∠ACB=900, CD⊥AB于D, AE平分∠BAC, 交CD于K, 交BC 于E、, F是BE上一点, 且BF=CE。
求证: FK∥AB。
(大连市第八届“育英杯”竞赛题)例6.矩形ABCD中, AB=20cm, BC=10cm, 若在AC.AB上各取一点M、N, 使BM+MN旳值最小, 求这个最小值。
(1998年北京市竞赛题)例7、设P为等腰三角形ABC斜边AB上任意一点, PE⊥AC于点E, PF⊥BC于点F, PG⊥EF于G, 延长GP并在其延长线上取一点D, 使得PD=PC。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、如图1―4―15,矩形ABCD中,E在AD上,且EF⊥EC,EF=EC,DE=2,矩形的周长为16,则AE 的长是()
A.3 B.4 C.5 D.7
2、如图1―4―2l,在边长为a的菱形ABCD中,∠DAB=60°,E是异于A、D两点的动点,F是CD上的动点,满足A E+CF=a,说明:不论E、F怎样移动,三角形BEF总是正三角形.
3、如图1-4-38,等腰梯形ABCD中,AD∥B C,AB =CD,∠DBC=45○,翻折梯形使点B重合于点D,
折痕分别交边AB、BC于点F、E,若AD=2,BC=8,求BE的长.
4、如图l-4-45,求∠A+∠B+∠C+∠D+∠E+∠F+∠G的和.
5、如图1-4-53,矩形ABCD中,AC与BD交于O点,BE⊥AC于E,CF⊥BD于F.求证:BE=CF.
6、如图1-4-57,顺次连结圆内接矩形各边的中点,得到菱形ABCD,若BD=10,DF=4,则菱形ABCD
的边长为()
(C)6 (D)9
7、如图1-4-59,是根据四边形的不稳定性制作的边长均为15㎝的可活动菱形衣架.若墙上钉子间的距离AB=BC=15㎝,则∠1=_____度
8、小明家用瓷砖装修卫生间,还有一块墙角面未完工(如图1-4-61甲所示),他想在现有的六块瓷砖余料中(如图1-4-61乙所示)挑选2块或3块余料进行铺设,请你帮小明设计两种不同的铺设方案(在下面图丙、图丁中画出铺设示意图,并标出所选用每块余料的编号)
9、已知:如图l-4-23,以△ABC的三边长为边在BC的同一侧分别作三个等边三角形,即△ABD、△ACF、△BCE,请回答下列问题:
(1)四边形ADEF是什么四边形?
(2)当△ABC满足什么条件时,四边形ADEF是
矩形?
10、在一次数学兴趣小组活动中,组长将两条等宽的长纸条倾斜地重叠着,并问同学,重叠部分是一个什
么样的四边形?同学说:这是一个平行四边形.乙同学说:这是一个菱形.
请问:你同意谁的看法.要解决此题,需建构数学模型,将实际问题转化成数学问题来解决,即已知:如图1-4-24,四边形ABCD中,AB∥CD,AD∥BC,边CD与边BC上的高相等,试判断四边形ABCD 的形状.
11、如图1-4-62,正方形ABCD的边长为1 cm,AC是对角线,AE平分∠BAC,EF⊥AC.(1)求证:BE
=CF.(2)求BE的长.
12、如图1-4-65,在四边形ABCD中,对角线AC、BD相交于点O,已知∠ADC=∠BCD,AD=BC,
C
13、从等腰三角形底边上任意一点分别作两腰的平行线,与两腰所围成的平行四边形的周长等于三角形的
( )
A .两腰长的和
B .周长的一半
C .周长
D .一腰长与底边长的和
14、如图,在梯形ABCD 中,AD BC ∥,AB AC ⊥,45B ∠=
,AD =
BC =求DC 的长.
15、如图,在平行四边形ABCD 中,E 为BC 的中点,连接AE 并延长交DC 的延长线于点F .
(1)求证:CF AB =;
(2)当BC 与AF 满足什么数量关系时,
四边形ABFC 是矩形,并说明理由.
16、在梯形ABCD 中,AB∥CD,0
90A ∠=,AB=2,BC=3,CD=1,E 是AD 中点,试判断EC 与EB 的位置关系,并写出推理过程。
17、如图l -4-80,已知正方形ABCD 的对角线AC 、BD 相交于点O ,E 是AC 上一点,过点A 作AG
⊥EB ,垂足为G ,AG 交BD 于F ,则OE=OF . (1)请证明0E=OF
(2)解答(1)题后,某同学产生了如下猜测:对上述命题,若点E 在AC 的延长线上,AG ⊥EB ,AG 交 EB 的延长线于 G ,AG 的延长线交DB 的延长线于点F ,其他条件不变,则仍有OE=OF .问:猜测所得结论是否成立?若成立,请给出证明;若不成立,请说明理由.
F
E
D
C
B A
A B
C
D
18、.延长正方形ABCD 的一边BC 至E ,使CE =AC ,连结AE 交CD 于F ,则∠AFC 的度数是( ) A 、112.5° B 、120° C 、122.5° D 、135°
19、.如图△ABC 与△CDE 都是等边三角形,点E 、F 分别在AC 、BC 上,且EF∥AB
(1)求证:四边形EFCD 是菱形; (2)设CD =4,求D 、F 两点间的距离.
20、如图,已知在菱形ABCD 中,E 、F 分别是BC 、CD 上的点,•且CE=CF . (1)求证:△ABE ≌△ADF ;
(2)过点C 作CG ∥EA 交AF 于H ,交AD 于G ,若∠BAE=25°,∠BCD=130°,求∠AHG 的度数.
21、已知梯形ABCD 中,AD ∥BC ,AD=2,BC=4,对角线AC=5,BD=3,•试求此梯形的面积.
A D F
E C B
22、如图l-4-70,一张矩形纸片,要折叠出一个最大的正方形,小明把矩形的一个角沿折痕AE翻折上去,使AB和AD边上的AF重合,则四边形ABEF就是一个最大的正方形,他的判断方法是__一组邻边相等的矩形是正方形______-。
