华东师大版数学八年级上幂的运算和整式的乘法专题训练含答案

合集下载

八年级数学上册第12章整式的乘除幂的运算练习题新版华东师大版(含答案)

八年级数学上册：12.1 幂的运算一、选择题(每题4分,共28分)1.计算(a2)4的结果是（)A.2a4B.4a2C.a8D.a62.计算(-2a3)2的结果是（)A.-4a5B.4a5C.-4a6D.4a63.计算(-x)2·x3的结果是（)A.x5B.-x5C.x6D.-x64.计算下列代数式,结果为x5的是（)A.x2+x3B.x·x5C.x6-xD.2x5-x55.x4m+2可以写成（)A.x4m÷x2B.(x2m+1)2C.(x·x4m)2D.x4m+x26.下列计算不正确的是（)A.=x6y2B.(x-y)3÷(y-x)2=x-yC.x2·x4=x6D.(-x2)3=-x57.若3x=2,3y=5,则32x-y的值是（)A.-1B.C.20D.二、填空题(每题5分,共30分)8.计算(-a)2·(-a)3的结果为.9.一个长方体的长、宽、高分别为a2,a,a3,则这个长方体的体积是.10.计算:(a7÷a)÷(a4÷a2)=.11.若m-n=2,则10m÷10n=.12.计算:(-3)2020×=.13.若2a=m,2b=m2,则a,b之间的数量关系是.三、解答题(共42分)14.(10分)计算:(1)(-2x2)2+x3·x-x5÷x;(2)(104)2÷(102)3×(103)2.15.(8分)已知m,n都是正整数,且x m÷x n=x6,x m·x n=x10,求m,n的值.16.(10分)已知10a=2,10b=3,求:(1)102a×103b的值;(2)102a-3b的值.17.(14分)(1)填空:因为(23)2=,(22)3=,所以(23)2=(22)3.因为(32)3=,(33)2=,所以.因为[(-4)3]4=,[(-4)4]3=,所以.…(2)由上面的计算,你能发现什么?请用字母表示出你发现的规律:.(3)请用上面的规律解答下面的问题:若2x=m,求8x的值.答案1.C[解析] 根据“幂的乘方,底数不变,指数相乘”的运算法则计算即可.(a2)4=a2×4=a8.故选C.2.D[解析] 原式=4a6.故选D.3.A[解析] 根据积的乘方法则、同底数幂的乘法运算法则,计算后直接选取答案.(-x)2·x3=x 2·x3=x2+3=x5.故选A.4.D[解析] x2与x3不是同类项,不能合并同类项,故A不合题意;x·x5=x6,故B不合题意;x6与x不是同类项,不能合并同类项,故C不合题意;2x5-x5=x5,故D符合题意.故选D.5.B6.D[解析] 这是一道综合运用幂的乘方与积的乘方、同底数幂的乘法和除法的选择题.可根据幂的乘方与积的乘方、同底数幂的乘法和除法运算法则逐一计算作出判断.A项,=x6y2,正确;B项,(x-y)3÷(y-x)2=x-y,正确;C项,x2·x4=x6,正确;D项,(-x2)3=-x6,不正确.故选D.7.D[解析] 因为3x=2,3y=5,所以32x-y=32x÷3y=(3x)2÷3y=22÷5=.故选D.8.-a5[解析] (-a)2·(-a)3=(-a)5=-a5.故答案为-a5.9.a610.a4[解析] (a7÷a)÷(a4÷a2)=a6÷a2=a4.11.100[解析] 10m÷10n=10m-n=102=100.12.-13.b=2a [解析] 因为2a=m,2b=m2,所以2b=(2a)2=22a,所以b=2a.故答案为b=2a.14.解:(1)原式=4x4+x4-x4=4x4.(2)(104)2÷(102)3×(103)2=108÷106×106=108-6+6=108.15.解:由已知,得x m-n=x6,x m+n=x10,于是解得即m,n的值分别为8,2.16.解:(1)102a×103b=(10a)2×(10b)3=4×27=108.(2)102a-3b=102a÷103b=(10a)2÷(10b)3=4÷27=.17.解:(1)26263636(32)3=(33)2 412412[(-4)3]4=[(-4)4]3(2)(a m)n=(a n)m(m,n为正整数)(3)因为2x=m,所以8x=(23)x=(2x)3=m3.。

部编数学八年级上册专题07幂的运算与整式的乘法之七大题型(解析版)含答案

专题07 幂的运算与整式的乘法之七大题型判断幂的运算、整式运算正确例题：（2023上·福建厦门·八年级校考期末）下列运算结果正确的是（）A ．326a a a ×=B ．()32628a a =C ．()211a a a +=+D ．()32a a a a+¸=【答案】B【分析】根据同底数幂乘法、积的乘方、幂的乘方以及整式的乘除运算法则进行判断即可．【详解】解：A 、33522a a a a +×==，故此选项计算错误，不符合题意；B 、()32628a a =，故此选项计算正确，符合题意；C 、()21a a a a +=+，故此选项计算错误，不符合题意；D 、()321a a a a +¸=+，故此选项计算错误，不符合题意；故选：B ．【点睛】本题考查了幂的相关运算以及整式的乘除运算法则，熟练掌握相关运算法则是解本题的关键．【变式训练】1．（2023下·四川达州·七年级校考期末）下列计算正确的是（）A ．5552x x x ×= B ．325a a a +=C ．2383()a b a b =D ．4222()()bc bc b c -¸-=【答案】D【分析】分别运用同底数幂的乘法，合并同类项法则，幂的乘方和同底数幂的除法运算即可．【详解】解：A 、5510x x x ×=，所以此选项错误；幂的运算【点睛】本题主要考查了积的乘方，解题的关键是熟练掌握积的乘方运算法则，准确计算．【变式训练】整式的四则混合运算【变式训练】【变式训练】多项式乘多项式【变式训练】1．（2023下·广东揭阳·七年级统考期末）先化简再求值：()()()()222213123x x x x x x -++---，其中3x =．【答案】3238133,45x x x -+-，【分析】根据单项式乘多项式，多项式乘多项式法则运算，再合并同类项，最后代入求值即可．【详解】解：()22(2)21(31)(23)x x x x x x -++---()32322226923x x x x x x x =-++---+32322226923x x x x x x x =-++-++-3238133x x x =-+-，当3x =时，原式3233831333=´-´+´-32789393=´-´+-45=．多项式乘多项式与图形面积【答案】2252a ab b --平方米，【分析】长方形的面积等于：方形面积﹣中间部分面积，化简出结果后，把【详解】解：(3S a =阴影2252a ab b --=（平方米），当6a =，4b =时，原式53664216=´-´-´1802432=--124=（平方米）．【点睛】本题主要考查多项式乘多项式，解答的关键是对相应的运算法则的掌握．【变式训练】1．（2023上·江西上饶·八年级校联考期末）如图，某小区有一块长为()23a b +米，宽为()2a b -米的长方形地块，管理部门规划了4块边长均为b 米的正方形空地用于栽种梅、兰、竹、菊，剩余地块将铺设草坪．(1)用含a ，b 的代数式表示铺设的草坪的面积．（结果化为最简形式）(2)若105a b ==，，预计每平方米铺设草坪的费用为30元，请预计铺设草坪所需要的费用．【答案】(1)()22447a ab b +-平方米(2)12750元【分析】（1）用长方形面积减去4个正方形面积即可得到答案；（2）根据（1）所求代入105a b ==，求出草坪的面积，进而求出对应的费用即可．【详解】（1）解：()()22324a b a b b +--22246234a ab ab b b =+---()22447a ab b =+-平方米，∴铺设的草坪的面积为()22445a ab b +-平方米；（2）解：当105a b ==，时，2222445410410575425a ab b +-=´+´´-´=平方米，∴铺设草坪所需要的费用为4253012750´=元．【点睛】本题主要考查了多项式乘法在几何图形中的应用，代数式求值，熟练掌握多项式乘以多项式的计算法则是解题的关键．2．（2023下·陕西榆林·七年级统考期末）如图，在某高铁站广场前有一块长为2a b +，宽为a b +的长方形空地，计划在中间留两个长方形喷泉池（图中阴影部分），两个长方形喷泉池及周边留有宽度为b 的人行通道．(1)求该长方形空地的面积；（用代数式表示）(2)求这两个长方形喷泉池的总面积；（用代数式表示）(3)当200a =，100b =时，求这两个长方形喷泉池的总面积．【答案】(1)2223a ab b ++；(2)22242a ab b -+；(3)20000．【分析】（1）根据长方形的面积列式并计算即可；（2）根据“长为2a b +，宽为a b +的长方形空地，两个长方形喷泉池及周边留有宽度为b 的人行通道”列式计算即可；（3）把200a =，100b =代入（2）中得到结果计算即可．【详解】（1）解：()()22223a b a b a ab b ++=++，答：该长方形空地的面积为2223a ab b ++．（2）()()223a b b a b b +-+-()()22a b a b =--22242a ab b =-+．答：这两个长方形喷泉池的总面积为22242a ab b -+．（3）当200a =，100b =时，这两个长方形喷泉池的总面积为222202220042001002041020002a ab b =´-´´+´-+=．即这两个长方形喷泉池的总面积为20000．【点睛】此题考查了列代数式、多项式乘法的应用、代数式的值等知识，根据题意正确列出代数式是解题的关键．多项式乘积中的规律性问题例题：（2023上·重庆永川·八年级统考期末）根据多项式乘法法则可得：()2222a b a ab b +=++；【答案】10【分析】根据“杨辉三角形”，计算出()5a b +，即可确定字母部分为【详解】解：根据“杨辉三角形”，可知()55a a b =+∴字母部分为32a b 的项的系数为10，【变式训练】1．（2023下·甘肃酒泉·七年级统考期末）观察下列各式()()2111x x x -+=-()()23111x x x x -++=-()()324111x x x x x -+++=-……(1)根据以上规律，则()()6543211x x x x x x x -++++++=______(2)若()1511x M x -×=-，则M =______(3)能否由此归纳出一般性规律：()()111n n x x x x --++++=L ______(4)由（3）直接写出结果：()()54322343a b a a b a b a b ab b -+++++=______(5)根据（3）求：3534222221+++++L 的结果．【答案】(1)71x -(2)()1413121x x x x +++++L(3)11n x +-(4)66a b -(5)3621-【分析】（1）根据题目中给出的式子总结规律，得出答案即可；（2）根据题目中给出的规律得出()()14131213111x x x x x x -+++++=-L ，即可得出答案；（3）根据规律得出结果即可；（4）由()()11a b a b -=---，根据题目中给出的规律得出结果即可；（4）用题目中提供的规律进行计算即可．【详解】（1）解：根据以上规律，可得()()654327111x x x x x x x x -++++++=-，故答案为：71x -；（2）解：根据以上规律，可得：若()1511x M x -×=-，则()1413121M x x x x =+++++L ，故答案为：()1413121x x x x +++++L ；（3）解：由所给算式可得规律为：()()11111n n n x x x x x -+-++++=-L ，故答案为：11n x +-；（4）解：∵()()11a b a b -=---，∴原式()()()5432234511a a b a b a a b b ab b =--++++-ëû+éù()()()()543223455432234511a a b a b a b ab b a a b a b a b b a b a b +++++-++++-+=-()()6611a b =---66a b =-；故答案为：66a b -；（5）解：根据以上规律可得：2343512222+++++L ()()353422122221=-+++++L 3621=-．【点睛】本题主要考查了规律探究，解题的关键是根据题干得出一般规律()()11111n n n x x x x x -+-++++=-L ．一、单选题②()()23111x x x x -++=-；③()()324111x x x x x -+++=-；……【归纳】由此可得：()()121111n n n n x x x x x x --+-+++++=-L ；【应用】请运用上面的结论，计算：2023202220212222221++++++=K （）A ．202321-B ．202421-C ．20242D ．202521-【答案】B【分析】根据所给规律求解即可．【详解】解：∵()()121111n n n n x x x x x x --+-+++++=-L ，∴()()202320222021220242122222121-×++++++=-K ，∴2023202220212202422222121++++++=-K ．故选：B ．【点睛】本题考查了多形式与多项式的乘法的规律问题，灵活运用规律求解是解答本题的关键．二、填空题【答案】5a b =/5b a=【分析】设左上角阴影部分的长为示阴影部分面积之差，可得x 变化，【详解】设左上角阴影部分的长为则右下角阴影部分的长为x a +三、解答题11．（2023下·江苏扬州·七年级统考期末）计算：(1)()()3642a a a a -×+×-(2)()()3x y x y -+【答案】(1)77a -(2)2223x xy y --【分析】（1）先计算积的乘方，再计算单项式乘单项式，最后合并同类项即可；（2）利用多项式乘多项式法则计算．【详解】（1）解：()()3642a a a a -×+×-()3468a a a a =-×+×778a a =-+77a =-；（2）解：()()3x y x y -+ 2233x xy xy y =+--2223x xy y =--．【点睛】本题考查积的乘方、单项式乘单项式、多项式乘多项式等知识点，解题的关键是熟练掌握各项运算法则并正确计算．12．（2023下·山西晋中·七年级统考期末）计算：(1)()322324a b ab a ×¸(2)()()253x x +-．【答案】(1)422a b (2)2215x x --【分析】（1）先算幂的乘方和积的乘方，再计算单项式的乘除法；∵化简后不含2x 项和常数项，∴20a -=且120b -=，解得：212a b ==，．【点睛】本题考查了整式的混合运算一化简求值，绝对值和偶次方的非负性，平方差公式，准确熟练地进行计算是解题的关键．14．（2023下·山东烟台·六年级统考期末）已知()()43229323316A x x x x B x x =¸=-+--，．(1)求A 和B ；(2)若y 满足y B A -=，请用含x 的代数式表示y ；(3)在（2）的条件下，当10y =时，求()2225416x x y +--的值．【答案】(1)22932936A x xB x x =--=+-，(2)2188y x =-(3)25【分析】（1）利用多项式除以单项式法则得到A ，利用单项式乘以多项式法则即可得到B ；（2）把（1）中求得的A 和B 代入y A B =+即可得到答案；（3）把10y =代入（2）中关系式得218810x -=求得21x =，再整体代入即可得到答案．【详解】（1）解：()43222932932A x x x x x x =¸=----，，()23316936B x x x x =+-=+-；（2）由y B A -=，得到222932936188y A B x x x x x =+=--++-=-；（3）把10y =代入（2）中关系式得218810x -=，解得21x =．原式()2514110165361625=´+´--=+-=．【点睛】此题考查了整式的乘法和除法，代数式的求值，熟练掌握多项式除以单项式法则、单项式乘以多项式法则、整体代入是解题的关键．15．（2023下·辽宁沈阳·七年级统考期末）甲、乙两个长方形，其边长如图所示（0m >），其面积分别为1S ，2S ．(1)用含m 的代数式表示：1S =______，2S =______；（结果化为最简形式）(2)用“＜”、“＞”或“=”填空：1S ______2S ；(3)若一个正方形的周长等于甲、乙两个长方形的周长之和，设该正方形的面积为3S ，试探究：3S 与()122S S +的差是否为定值？若为定值，请求出该值；如果不是，请说明理由．【答案】(1)265m m ++，268m m ++；(2)<(3)是，10【分析】（1）利用长方形的面积公式进行求解即可；（2）利用求差法可比较两个式子大小；（3）先求出正方形的边长，得到大正方形面积，再结合（1）列出相应的式子，进行运算即可．【详解】（1）解：()()215165S m m m m =++=++；()()224268S m m m m =++=++；（2）∵2212(65)(68)30S S m m m m -=++-++=-<，∴12S S <故答案为：<；（3）解：大正方形的边长为：2(1524)426m m m m m +++++++¸=+，大正方形面积为：223(26)42436S m m m =+=++，()222122 2(6568)42426S S m m m m m m +=+++++=++，()223122(42436)(42426)10S S S m m m m -+=++-++=．答：3S 与()122S S +的差为定值，值为10．【点睛】本题考查了多项式乘多项式，整式的加减，长方形和正方形的面积，熟练掌握运算法则是解题的关键．16．（2023下·黑龙江哈尔滨·六年级统考期末）阅读材料：我们知道，()424213x x x x x -+=-+=，类似地，我们把()a b +看成一个整体，则()()()()()()424213a b a b a b a b a b +-+++=-++=+．“整体思想”是中学教学解题中的一种重要的思想方法，它在多项式的化简与求值中应用极为广泛，尝试应用整体思想解决下列问题：(1)把()2a b -看成一个整体，合并()()()222265a b a b a b ---+-；(2)已知222x y -=-，求261215x y --的值；(3)已知21a b -=-，25b c -=，10c d -=-，求()()()22a c b d b c -+---的值．【答案】(1)()2a b -(2)27-(3)6-【分析】（1）把()2a b -提出了进行计算即可得；（2）()22612156215x y x y --=--，把222x y -=-代入进行计算即可得；（3）()()()()()()2222a c b d b c a b b c c d -+---=-+-+-，把21a b -=-，25b c -=，10c d -=-代入进行计算即可得．【详解】（1）解：()()()()()()22222265265a b a b a b a b a b ---+-=-+-=-．（2）解：()22612156215x y x y --=--，把222x y -=-代入得，原式()621527=´--=-．（3）解：()()()()()()222222a c b d b c a c b d b c a b b c c d -+---=-+--+=-+-+-把21a b -=-，25b c -=，10c d -=-代入得，原式()15106=-++-=-．【点睛】本题考查了多项式的变形和整体代入的思想，解题的关键是理解题意，掌握这些知识点．。

华师大版初中数学八年级上册《12.1 幂的运算》同步练习卷(含答案解析

华师大新版八年级上学期《12.1 幂的运算》同步练习卷一．选择题（共36小题）1．计算：（﹣a）2•a4的结果是（）A．a8B．﹣a6C．﹣a8D．a62．若a•24=28，则a等于（）A．2B．4C．16D．183．若x，y为正整数，且2x•22y=29，则x，y的值有（）A．1对B．2对C．3对D．4对4．如果a2n﹣1a n+5=a16，那么n的值为（）A．3B．4C．5D．65．计算（﹣a）3（﹣a）2的结果是（）A．﹣a5B．a5C．﹣a6D．a66．已知x m=2，x n=8，则x m+n=（）A．4B．8C．16D．647．计算：a x•a2=（）A．a x+2B．a2x C．2a x D．a4x8．下列计算中正确的是（）A．a3•a3=2a3B．a3•a3=a3C．a3•a3=a6D．a3•a3=2a6 9．计算（﹣a）2•a3的结果正确的是（）A．﹣a6B．a6C．﹣a5D．a510．下列运算正确的是（）A．a2•a3=a6B．a3+a3=a6C．a•a3=a4D．（﹣a2）3=a6 11．下列运算正确的是（）A．a3×a=a4B．（﹣a4）=a4C．a2+a3=a5D．（a2）3=a5 12．下列运算正确的是（）A．a2•a3=a6B．C．D．（﹣2a2b）3=﹣8a6b313．计算的结果是（）A．B．C．D．14．计算（﹣x2y）3的结果是（）A．﹣x6y3B．x6y3C．﹣x5y3=3D．x2y3 15．下列计算正确的是（）A．a2+a2=a4B．a2•a4=a8C．（a3）2=a6D．（2a）3=2a3 16．下列运算正确的是（）A．||=B．（2x3）2=4x5C．x2+x2=x4D．x2•x3=x5 17．下列计算正确的是（）A．2a+3b=5ab B．（a2）3=a5C．（2a）2=4a D．a4•a3=a7 18．下列计算正确的是（）A．b3•b3=2b3B．（ab2）3=ab6C．（a5）2=a10D．y3+y3=y6 19．计算（）2017•（﹣1.5）2018的结果是（）A．B．C．D．20．如果（a2b3）n=a4b m，那么m，n的值分别是（）A．m=3，n=2B．m=6，n=2C．m=5，n=2D．m=3，n=1 21．下列运算中，计算结果正确的是（）A．a2•a3=a6B．（a2）3=a5C．a3+a3=2a3D．（a2b）2=a2b222．下列计算正确的是（）A．a3•a4=a12B．（2a）2=2a2C．（a3）2=a9D．（﹣2×102）3=﹣8×106 23．计算（2）3正确的结果是（）A．B．C．D．24．计算（﹣1）2018×（﹣）2018的结果为（）A．1B．﹣1C．0D．199725．下列计算中，错误的是（）A．m n•m2n+1=m3n+1B．（﹣a n﹣1）2=a2n﹣2C．（a2b）n=a2n b n D．（﹣3x2）3=﹣9x626．下列运算正确的是（）A．﹣22÷（﹣2）2=1B．（﹣a）3=﹣a3C．（﹣2b2）2=﹣4b4D．（xy2）3=xy627．下面是芳芳同学计算（a•a2）3的过程：解：（a•a2）3=a3•（a2）3…①=a3•a6…②=a9…③则步骤①②③依据的运算性质分别是（）A．积的乘方，幂的乘方，同底数幂的乘法B．幂的乘方，积的乘方，同底数幂的乘法C．同底数幂的乘法，幂的乘方，积的乘方D．幂的乘方，同底数幂的乘法，积的乘方28．已知：2m=a，2n=b，则22m+3n用a、b可以表示为（）A．6ab B．a2+b3C．2a+3b D．a2b329．已知2x+5y﹣3=0，则4x•32y的值为（）A．4B．8C．32D．12830．下列计算：①a2n•a n=a3n；②22•33=65；③32÷32=1；④a3÷a2=5a；⑤（﹣a）2•（﹣a）3=a5．其中正确的式子有（）A．4个B．3个C．2个D．1个31．下列算式中，结果等于x5的是（）A．x10÷x2B．x2+x3C．x2•x3D．（x2）332．已知3a=5，3b=4，则32a﹣b等于（）A．6B．C．100D．33．已知2a=3，8b=4，23a﹣3b+1的值为（）A．25B．﹣2C．﹣1D．34．下列计算正确的是（）A．a2•a3=a6B．（a2）3=a5C．（a2b）2=a2b2D．a3÷a2=a35．计算26×（22）3÷24的结果是（）A．23B．27C．28D．29 36．若a=，b=，则下列结论正确的是（）A．a＜b B．a=b C．a＞b D．ab=1二．填空题（共4小题）37．已知x a=3，x b=4，则x a+b=．38．已知（a n b m+4）3=a9b6，则m n=39．已知m、n是整数，x m=9，x n=，那么x m﹣n=40．计算：﹣（﹣2）6÷（﹣2）3=．华师大新版八年级上学期《12.1 幂的运算》同步练习卷参考答案与试题解析一．选择题（共36小题）1．计算：（﹣a）2•a4的结果是（）A．a8B．﹣a6C．﹣a8D．a6【分析】直接利用同底数幂的乘法运算法则计算得出答案．【解答】解：（﹣a）2•a4=a6．故选：D．【点评】此题主要考查了同底数幂的乘法运算，正确掌握运算法则是解题关键．2．若a•24=28，则a等于（）A．2B．4C．16D．18【分析】直接利用同底数幂的乘法运算法则计算得出答案．【解答】解：∵a•24=28，∴a=28÷24=24=16．故选：C．【点评】此题主要考查了同底数幂的乘法运算，正确掌握运算法则是解题关键．3．若x，y为正整数，且2x•22y=29，则x，y的值有（）A．1对B．2对C．3对D．4对【分析】根据同底数幂的运算即可求出答案．【解答】解：∵2x•22y=29，∴2x+2y=29，∴x+2y=9，∵x，y为正整数，∴9﹣2y＞0，∴y＜，∴y=1，2，3，4故x，y的值有4对，故选：D．【点评】本题考查同底数幂的运算，解题的关键是熟练运用同底数幂的运算法则，本题属于基础题型．4．如果a2n﹣1a n+5=a16，那么n的值为（）A．3B．4C．5D．6【分析】根据同底数幂的乘法法则：同底数幂相乘，底数不变，指数相加，可得出关于n的方程，解出即可．【解答】解：∵a2n﹣1a n+5=a16，∴a2n﹣1+n+5=a16，即a3n+4=a16，则3n+4=16，解得n=4，故选：B．【点评】本题考查了同底数幂的乘法，属于基础题，解答本题的关键掌握同底数幂的运算法则．5．计算（﹣a）3（﹣a）2的结果是（）A．﹣a5B．a5C．﹣a6D．a6【分析】根据同底数幂的运算即可求出答案．【解答】解：原式=﹣a3•a2=﹣a5，故选：A．【点评】本题考查同底数幂的运算，解题的关键是熟练运用同底数幂的运算法则，本题属于基础题型．6．已知x m=2，x n=8，则x m+n=（）A．4B．8C．16D．64【分析】同底数幂相乘，底数不变，指数相加．依据同底数幂的乘法法则进行计算即可．【解答】解：∵x m=2，x n=8，∴x m+n=x m•x n=2×8=16，故选：C．【点评】本题主要考查了同底数幂的乘法法则，解决问题的关键是逆用同底数幂的乘法法则．7．计算：a x•a2=（）A．a x+2B．a2x C．2a x D．a4x【分析】根据同底数幂的乘法法则求出即可．【解答】解：a x•a2=a x+2，故选：A．【点评】本题考查了同底数幂的乘法，能正确根据法则进行计算是解此题的关键．8．下列计算中正确的是（）A．a3•a3=2a3B．a3•a3=a3C．a3•a3=a6D．a3•a3=2a6【分析】先根据同底数幂的乘法分别求出每个式子的值，再判断即可．【解答】解：A、结果是a6，故本选项不符合题意；B、结果是a6，故本选项不符合题意；C、结果是a6，故本选项符合题意；D、结果是a6，故本选项不符合题意；故选：C．【点评】本题考查了同底数幂的乘法，能正确根据法则求出每个式子的值是解此题的关键．9．计算（﹣a）2•a3的结果正确的是（）A．﹣a6B．a6C．﹣a5D．a5【分析】直接利用积的乘方运算法则以及结合同底数幂的乘法运算法则计算得出答案．【解答】解：（﹣a）2•a3=a2•a3=a5．故选：D．【点评】此题主要考查了同底数幂的乘法运算，正确掌握运算法则是解题关键．10．下列运算正确的是（）A．a2•a3=a6B．a3+a3=a6C．a•a3=a4D．（﹣a2）3=a6【分析】直接利用合并同类项法则以及积的乘方运算法则分别化简得出答案．【解答】解：A、a2•a3=a5，故此选项错误；B、a3+a3=2a3，故此选项错误；C、a•a3=a4，正确；D、（﹣a2）3=﹣a6，故此选项错误．故选：C．【点评】此题主要考查了合并同类项法则以及积的乘方运算，正确掌握相关运算法则是解题关键．11．下列运算正确的是（）A．a3×a=a4B．（﹣a4）=a4C．a2+a3=a5D．（a2）3=a5【分析】直接利用幂的乘方运算法则以及同底数幂的乘法运算法则化简得出答案．【解答】解：A、a3×a=a4，正确；B、（﹣a4）=﹣a4，故此选项错误；C、a2+a3，无法计算，故此选项错误；D、（a2）3=a6，故此选项错误；故选：A．【点评】此题主要考查了幂的乘方运算以及同底数幂的乘法运算，正确掌握相关运算法则是解题关键．12．下列运算正确的是（）A．a2•a3=a6B．C．D．（﹣2a2b）3=﹣8a6b3【分析】直接利用整式的乘法运算法则以及积的乘方运算法则、有理数的乘除运算法则分别判断得出答案．【解答】解：A、a2•a3=a5，故此选项错误；B、=2，故此选项错误；C、﹣4÷5×（）=﹣，故此选项错误；D、（﹣2a2b）3=﹣8a6b3，正确．故选：D．【点评】此题主要考查了整式的乘法运算以及积的乘方运算、有理数的乘除运算，正确掌握相关运算法则是解题关键．13．计算的结果是（）A．B．C．D．【分析】运用同底数幂的乘法法则以及积的乘方法则，即可得到计算结果．【解答】解：=••=•=1×=．故选：A．【点评】本题主要考查了同底数幂的乘法法则以及积的乘方法则，解决问题的关键是逆用积的乘方法则．14．计算（﹣x2y）3的结果是（）A．﹣x6y3B．x6y3C．﹣x5y3=3D．x2y3【分析】直接利用积的乘方运算法则计算得出答案．【解答】解：（﹣x2y）3=﹣x6y3．故选：A．【点评】此题主要考查了积的乘方运算，正确掌握运算法则是解题关键．15．下列计算正确的是（）A．a2+a2=a4B．a2•a4=a8C．（a3）2=a6D．（2a）3=2a3【分析】依据同底数幂的乘法、幂的乘方、合并同类项法则即可判断．【解答】解：A、a2+a2=2a2，错误；B、a2•a4=a6，错误；C、（a3）2=a6，正确；D、（2a）3=8a3，错误；故选：C．【点评】此题考查幂的乘方与积的乘方，关键是依据同底数幂的乘法、幂的乘方、合并同类项法则解答．16．下列运算正确的是（）A．||=B．（2x3）2=4x5C．x2+x2=x4D．x2•x3=x5【分析】根据合并同类项法则、单项式乘法、幂的乘方、绝对值的运算方法，利用排除法求解．【解答】解：A、，错误；B、（2x3）2=4x6，错误；C、x2+x2=2x2，错误；D、x2•x3=x5，正确；故选：D．【点评】本题主要考查了合并同类项法则、单项式乘法、幂的乘方、绝对值，熟练掌握运算法则是解题的关键．17．下列计算正确的是（）A．2a+3b=5ab B．（a2）3=a5C．（2a）2=4a D．a4•a3=a7【分析】直接利用合并同类项法则以及积的乘方运算法则和同底数幂的乘法运算法则分别计算得出答案．【解答】解：A、2a+3b，无法计算，故此选项错误；B、（a2）3=a6，故此选项错误；C、（2a）2=4a2，故此选项错误；D、a4•a3=a7，正确；故选：D．【点评】此题主要考查了合并同类项以及积的乘方运算和同底数幂的乘法运算，正确掌握相关运算法则是解题关键．18．下列计算正确的是（）A．b3•b3=2b3B．（ab2）3=ab6C．（a5）2=a10D．y3+y3=y6【分析】直接利用合并同类项法则以及幂的乘方运算法则和积的乘方运算法则分别计算得出答案．【解答】解：A、b3•b3=b6，故此选项错误；B、（ab2）3=a3b6，故此选项错误；C、（a5）2=a10，正确；D、y3+y3=2y3，故此选项错误；故选：C．【点评】此题主要考查了合并同类项以及幂的乘方运算和积的乘方运算，正确掌握相关运算法则是解题关键．19．计算（）2017•（﹣1.5）2018的结果是（）A．B．C．D．【分析】直接利用积的乘方运算法则将原式变形进而得出答案．【解答】解：（）2017•（﹣1.5）2018=[×（﹣1.5）]2017×（﹣）=．故选：B．【点评】此题主要考查了积的乘方运算，正确将原式变形是解题关键．20．如果（a2b3）n=a4b m，那么m，n的值分别是（）A．m=3，n=2B．m=6，n=2C．m=5，n=2D．m=3，n=1【分析】根据幂的乘方与积的乘方得出a2n b3n=a4b m，据此可得关于m，n的方程，解之可得．【解答】解：∵（a2b3）n=a4b m，∴a2n b3n=a4b m，则2n=4且3n=m，解得：n=2，m=6，故选：B．【点评】本题主要考查幂的乘方与积的乘方，解题的关键是根据幂的乘方与积的乘方的运算法则得出关于m，n的方程．21．下列运算中，计算结果正确的是（）A．a2•a3=a6B．（a2）3=a5C．a3+a3=2a3D．（a2b）2=a2b2【分析】直接利用同底数幂的乘法运算法则以及幂的乘方运算法则分别计算得出答案．【解答】解：A、a2•a3=a5，故此选项错误；B、（a2）3=a6，故此选项错误；C、a3+a3=2a3，正确；D、（a2b）2=a4b2，故此选项错误；故选：C．【点评】此题主要考查了同底数幂的乘法运算以及幂的乘方运算，正确掌握相关运算法则是解题关键．22．下列计算正确的是（）A．a3•a4=a12B．（2a）2=2a2C．（a3）2=a9D．（﹣2×102）3=﹣8×106【分析】根据整式的运算法则即可求出答案．【解答】解：（A）原式=a7，故A错误；（B）原式=4a2，故B错误；（C）原式=a6，故C错误；故选：D．【点评】本题考查整式的运算，解题的关键是熟练运用整式的运算法则，本题属于基础题型．23．计算（2）3正确的结果是（）A．B．C．D．【分析】根据幂的乘方（a m）n=a mn（m，n为正整数），即可解答．【解答】解：，故选：A．【点评】本题考查了幂的乘方，解决本题的关键是熟记幂的乘方的法则．24．计算（﹣1）2018×（﹣）2018的结果为（）A．1B．﹣1C．0D．1997【分析】直接利用积的乘方运算法则计算得出答案．【解答】解：（﹣1）2018×（﹣）2018=[（﹣1）×（﹣）]2018=1．故选：A．【点评】此题主要考查了积的乘方运算，正确将原式变形是解题关键．25．下列计算中，错误的是（）A．m n•m2n+1=m3n+1B．（﹣a n﹣1）2=a2n﹣2C．（a2b）n=a2n b n D．（﹣3x2）3=﹣9x6【分析】直接利用同底数幂的乘法运算法则以及积的乘方运算法则计算得出答案．【解答】解：A、m n•m2n+1=m3n+1，正确，不合题意；B、（﹣a n﹣1）2=a2n﹣2，正确，不合题意；C、（a2b）n=a2n b n，正确，不合题意；D、（﹣3x2）3=﹣27x6，故此选项错误，符合题意．故选：D．【点评】此题主要考查了同底数幂的乘法运算以及积的乘方运算，正确掌握相关运算法则是解题关键．26．下列运算正确的是（）A．﹣22÷（﹣2）2=1B．（﹣a）3=﹣a3C．（﹣2b2）2=﹣4b4D．（xy2）3=xy6【分析】直接利用积的乘方运算法则以及有理数的除法运算法则计算得出答案．【解答】解：A、﹣22÷（﹣2）2=﹣4÷4=﹣1，故此选项错误；B、（﹣a）3=﹣a3，正确；C、（﹣2b2）2=4b4，故此选项错误；D、（xy2）3=x3y6，故此选项错误；故选：B．【点评】此题主要考查了积的乘方运算以及有理数的除法运算，正确掌握相关运算法则是解题关键．27．下面是芳芳同学计算（a•a2）3的过程：解：（a•a2）3=a3•（a2）3…①=a3•a6…②=a9…③则步骤①②③依据的运算性质分别是（）A．积的乘方，幂的乘方，同底数幂的乘法B．幂的乘方，积的乘方，同底数幂的乘法C．同底数幂的乘法，幂的乘方，积的乘方D．幂的乘方，同底数幂的乘法，积的乘方【分析】直接利用幂的乘方运算法则以及同底数幂的乘法运算法则分别计算得出答案．【解答】解：（a•a2）3=a3•（a2）3…①=a3•a6…②=a9…③则步骤①②③依据的运算性质分别是积的乘方，幂的乘方，同底数幂的乘法．故选：A．【点评】此题主要考查了幂的乘方运算以及同底数幂的乘法运算，正确掌握相关运算法则是解题关键．28．已知：2m=a，2n=b，则22m+3n用a、b可以表示为（）A．6ab B．a2+b3C．2a+3b D．a2b3【分析】直接利用幂的乘方运算法则以及同底数幂的乘法运算法则计算得出答案．【解答】解：∵2m=a，2n=b，∴22m+3n=（2m）2×（2n）3=a2b3，故选：D．【点评】此题主要考查了幂的乘方运算以及同底数幂的乘法运算，正确掌握相关运算法则是解题关键．29．已知2x+5y﹣3=0，则4x•32y的值为（）A．4B．8C．32D．128【分析】根据幂的乘方进行解答即可．【解答】解：由2x+5y﹣3=0可得：2x+5y=3，所以4x•32y=22x+5y=23=8，故选：B．【点评】此题考查幂的乘方，关键是根据幂的乘方法则解答．30．下列计算：①a2n•a n=a3n；②22•33=65；③32÷32=1；④a3÷a2=5a；⑤（﹣a）2•（﹣a）3=a5．其中正确的式子有（）A．4个B．3个C．2个D．1个【分析】直接利用同底数幂的乘除运算法则计算得出答案．【解答】解：①a2n•a n=a3n，正确；②22•33=4×27=108，故此选项错误；③32÷32=1，正确；④a3÷a2=a，故此选项错误；⑤（﹣a）2•（﹣a）3=﹣a5，故此选项错误．故选：C．【点评】此题主要考查了用同底数幂的乘除运算，正确掌握相关运算法则是解题关键．31．下列算式中，结果等于x5的是（）A．x10÷x2B．x2+x3C．x2•x3D．（x2）3【分析】根据同底数幂的乘法、除法和幂的乘方和合并同类项解答即可．【解答】解：A、x10÷x2=x8，错误；B、x2+x3=x2+x3，错误；C、x2•x3=x5，正确；D、（x2）3=x6，错误；故选：C．【点评】此题考查同底数幂的除法，关键是根据同底数幂的乘法、除法和幂的乘方和合并同类项解答．32．已知3a=5，3b=4，则32a﹣b等于（）A．6B．C．100D．【分析】根据同底数幂的运算法则即可求出答案．【解答】解：∵3a=5，3b=4，∴32a﹣b=（3a）2÷3b=52÷4=故选：B．【点评】本题考查同底数幂的运算，解题的关键是熟练运用同底数幂的运算法则，本题属于基础题型33．已知2a=3，8b=4，23a﹣3b+1的值为（）A．25B．﹣2C．﹣1D．【分析】直接利用同底数幂的乘除运算法则将原式变形计算得出答案．【解答】解：∵2a=3，8b=4，∴23a﹣3b+1=（2a）3÷（8b）×2=33÷4×2=．故选：D．【点评】此题主要考查了同底数幂的乘除运算，正确掌握相关运算法则是解题关键．34．下列计算正确的是（）A．a2•a3=a6B．（a2）3=a5C．（a2b）2=a2b2D．a3÷a2=a【分析】根据同底数幂的乘法法则对A进行判断；根据同低数幂的乘方对B进行判断；根据幂的乘方与积的乘方对C进行判断；根据同底数幂的除法法则对D进行判断．【解答】解：a2•a3=a2+3=a5，（a2）3=a6，（a2b）2=a4b2，a3÷a2=a．故选：D．【点评】本题考查了同底数幂的除法：底数不变，指数相减，即a m÷a n=a m﹣n（a ≠0，m，n是正整数，m＞n）．也考查了同底数幂的乘法和幂的乘方．35．计算26×（22）3÷24的结果是（）A．23B．27C．28D．29【分析】根据同底数幂的除法和乘法计算即可．【解答】解：26×（22）3÷24=26×26÷24=28，故选：C．【点评】此题考查同底数幂的除法和乘法，关键是根据同底数幂的除法和乘法的法则计算．36．若a=，b=，则下列结论正确的是（）A．a＜b B．a=b C．a＞b D．ab=1【分析】直接利用同底数幂的乘除运算法则将原式变形进而得出答案．【解答】解：∵a===，b=，∴a=b．故选：B．【点评】此题主要考查了同底数幂的乘除运算，正确将原式变形是解题关键．二．填空题（共4小题）37．已知x a=3，x b=4，则x a+b=12．【分析】直接利用同底数幂的乘法运算法则计算得出答案．【解答】解：∵x a=3，x b=4，∴x a+b=x a×x b=12．故答案为：12．【点评】此题主要考查了同底数幂的乘法运算，正确掌握相关运算法则是解题关键．38．已知（a n b m+4）3=a9b6，则m n=﹣8【分析】先根据积的乘方进行计算，根据已知得出3n=9，3m+12=6，求出m、n，再代入求出即可．【解答】解：（a n b m+4）3=a3n b3m+12，∵（a n b m+4）3=a9b6，∴3n=9，3m+12=6，解得：n=3，m=﹣2，∴m n=（﹣2）3=﹣8，故答案为：﹣8．【点评】本题考查了求代数式的值和幂的乘方与积的乘方，能得出关于m、n的方程是解此题的关键．39．已知m、n是整数，x m=9，x n=，那么x m﹣n=27【分析】逆用同底数幂的除法化为x m﹣n=x m÷x n即可求解．【解答】解：∵x m=9，x n=，∴x m﹣n=x m÷x n=9÷=27，故答案为：27．【点评】本题考查了同底数幂的除法，解题的关键是牢记法则，难度不大．40．计算：﹣（﹣2）6÷（﹣2）3=8．【分析】直接利用同底数幂的运算性质进行计算即可．【解答】解：﹣（﹣2）6÷（﹣2）3=﹣（﹣2）6﹣3=﹣（﹣2）3=8，故答案为：8．【点评】本题考查了同底数幂的除法的运算，解题的关键是注意算式的符号．。

华师大版八年级数学上册《整式的乘除》单元试卷检测练习及答案解析

华师大版八年级数学上册《整式的乘除》单元试卷检测练习及答案解析一、选择题1、下列运算正确的是（）A．(a3)2＝a6B．2a＋3a＝5a2C．a8÷a4＝a2D．a2·a3＝a62、若、、是正整数，则=（）A．B．C．D．3、若，，则等于（）A．B．C．2 D．4、计算的结果是（）A．B．C．D．5、若，，则代数式的值等于（）A．B．C．D．26、若(x2+px+q)(x2+7)的计算结果中，不含x2项，则q的值是（）A．0 B．7 C．-7 D．±77、已知x+y=-5，x-y=2，则x2-y2=（）A．. B．C．D．8、如果是一个完全平方式，那么的值是（）．A．B．C．D．9、计算（36x6-16x2）÷4x2的结果为（）A．9x3﹣4x2B．9x4+4 C．9x3+4x D．9x4﹣4 10、某同学粗心大意，因式分解时，把等式x4－■＝(x2＋4)(x＋2)(x－▲)中的两个数字弄污了，则式子中的■，▲对应的一组数字可以是( )A．8，1 B．16，2C．24，3 D．64，8二、填空题11、分解因式：3a3-3a=______．12、已知x a=3，x b=4，则x3a﹣2b的值是_____．13、计算：=_______．14、若的结果中不含x的一次项，则=________.15、已知x﹣y=4，则代数式x2﹣2xy+y2﹣25的值为_____．16、已知一个三角形的面积为8x3y2－4x2y3，一条边长为8x2y2，则这条边上的高为___________.17、计算：（﹣a）2÷（﹣a）= ，0.252007×（﹣4）2008= ．18、已知，则=______．19、计算的结果是_______．20、若=7，则___________．三、计算题21、计算：（1）（2）（3）（4）22、因式分解：⑴⑵⑶⑷四、解答题23、一个三角形的底边长为，高为，该三角形面积为S，试用含的代数式表示S，并求当时，S的值．24、先化简，再求值：，其中x =-1，y =.25、计算：（1）已知a＋b＝－3，ab＝5，求多项式4a2b＋4ab2－4a－4b的值；（2）已知x2-3x-1=0,求代数式3-3 x2+9x的值？26、已知（x2+px+8）与（x2﹣3x+q）的乘积中不含x3和x2项，求p、q的值．27、阅读：将代数式转化为的形式，（期中为常数），则其中．（1）仿照此法将代数式化为的形式，并指出的值．（2）若代数式可化为的形式，求的值．参考答案1、A2、C3、A4、B5、B6、C7、D8、D9、D10、B11、3a(a+1)(a-1)12、13、214、-815、-916、2x－y17、﹣a，﹣4．18、-219、.20、±321、（1）1；（2）；（3）；（4）2．22、⑴==⑵==⑶===4⑷=== 23、．24、原式==025、（1）-48；（2）026、p=3，q=1．27、①；②答案详细解析【解析】1、分析：结合选项分别进行幂的乘方、合并同类项、同底数幂的乘除法等运算，然后选择计算正确选项即可．详解：A、(a3)2＝a6，原式计算正确，故本选项正确；B、2a+3a=5a，原式计算错误，故本选项错误；C、a8÷a4＝a4，原式计算错误，故本选项错误；D、a2·a3＝a5，原式计算错误，故本选项错误.故选A.点睛：本题考查了幂的乘方乘方，合并同类项，同底数幂的乘除法. 熟练掌握它们的计算法则是计算正确的关键.2、分析：首先根据同底数幂的乘法将括号里面的进行计算，然后根据积的乘方计算法则得出答案．详解：原式=，故选C．点睛：本题主要考查的是同底数幂的乘法以及幂的乘方计算，属于基础题型．解决这个问题的关键就是明确幂的计算法则．3、分析：先把23m﹣2n化为（2m）3÷（2n）2，再求解．详解：∵2m=3，2n=5，∴23m﹣2n=（2m）3÷（2n）2=27÷25=．故选A．点睛：本题主要考查了同底数幂的除法及幂的乘方与积的乘方，解题的关键是把23m﹣2n化为（2m）3÷（2n）2．4、试题解析：故选B.5、∵，,∴（x-1）（y+1）=xy+x-y-1=.故选B.6、(x2+px+q)(x2+7)=x4+7x2+px3+7px+qx2+7q=x4+px3+(7+q)x2+7px+7q，因为计算结果中不含x2项，所以7+q=0，所以q=-7；故选C.7、本题考查平方差公式进行因式分解,因为x2－y2=（x＋y）（x－y）,将x＋y=－5,x－y=2,代入得: －5×2=－10,因此,正确选项是D.8、∵形如的式子叫完全平方式，而，∴若是完全平方式，则，∴，故选D.9、多项式除以单项式，先把这个多项式的每一项分别除以单项式，再把所得的商相加．所以（36x6-16x2）÷4x2= 9x4﹣4考点：整式的除法．10、由（x2+4）（x+2）（x-▲）得出▲=2，则（x2+4）（x+2）（x-2）=（x2+4）（x2-4）=x4-16，则■=16．故选B．【点睛】此题考查了学生用平方差公式分解因式的掌握情况，灵活性比较强．11、分析：提取公因式法和公式法相结合进行因式分解即可.详解：原式故答案为：点睛：考查因数分解，提取公因式法和公式法相结合进行因式分解.注意分解一定要彻底.12、分析：直接利用同底数幂的除法运算法则计算得出答案．详解：∵x a=3，x b=4，∴x3a﹣2b=（x a）3÷（x b）2=33÷42=．故答案为：．点睛：本题主要考查了同底数幂的乘除运算，正确将原式变形是解题的关键．13、分析：先把改写成2100=，然后逆用积的乘方公式(ab)m=a m·b m,即a m·b m=(ab)m解答.详解：====2.点睛：本题考查了偶次幂的性质和积的乘方运算，解答本题的关键是逆用乘方运算公式.14、试题解析：结果中不含的一次项.故答案为：15、解： x2﹣2xy+y2﹣25=（x﹣y）2﹣25 =42﹣25=﹣9，故答案为：﹣9．16、∵三角形的面积为8x3y2－4x2y3，一条边长为8x2y2，∴这条边上的高为2(8x3y2－4x2y3) ÷8x2y2=16x3y2÷8x2y2－8x2y3÷8x2y2=2x－y，故答案为：2x－y.17、试题分析：根据同底数幂的除法底数不变指数相减，可得答案；根据同底数幂的乘法底数不变指数相加，可得积的乘方，根据积的乘方，可得答案．解：（﹣a）2÷（﹣a）=﹣a，0.252007×（﹣4）2008=[0.25×（﹣4）]2007×（﹣4）=﹣4，故答案为：﹣a，﹣4．18、本题利用拆常数项凑完全平方的方法进行求解,,可变形为:,即,根据非负数的非负性可得:解得: :,所以19、原式===12017=-.故答案为-.点睛：积的乘方公式：(ab)n=a n b n（n为正整数）的逆运算：a n b n = (ab)n（n为正整数）也成立.20、（x+）2=x2+2+=7+2=9，x+=±3.故答案为±3.点睛：（1）（x+）2=x2+2+；（x－）2=x2－2+.21、试题分析：（1）原式=；（2）原式=；（3）原式=；（4）原式=．考点：整式的混合运算．22、试题解析：点睛：因式分解：把一个多项式分解成几个整式的积的形式.因式分解的主要方法：提公因式法，公式法，十字相乘法，分组分解法.23、分析：利用三角形的面积公式得到三角形的面积S=（4a+2）（2a-1），然后利用平方差公式计算可得用含a的代数式表示S；再将a=2代入计算即可求解．详解：，当时，．点睛：本题考查了多项式乘多项式，平方差公式的知识，解决此类问题的关键是牢记平方差公式.24、分析：首先根据乘法公式将括号去掉，然后进行合并同类项，最后根据多项式除以单项式的法则得出答案，将x和y的值代入化简后的式子进行计算得出答案．详解：原式===，将x =，y =代入上式，原式=0．点睛：本题主要考查的是多项式的乘法和除法的计算法则，属于基础题型．在解决这个问题的时候，公式的应用是非常关键的．25、分析：(1)、首先进行分组分解，然后提取公因式，最后利用整体代入的思想进行求解；(2)、首先提取公因式－3，然后整体代入进行求解．详解：(1)、解：原式 ="4" ab（a＋b）-4（a＋b）="（4" ab-4）（a＋b）=4（ab-1）（a ＋b）当a＋b＝－3，ab＝5时，原式=4×（5－1）×（－3）=4×4×（－3）=－48(2)、原式=－3（x2－3x－1），当x2-3x-1="0，" 原式=-3×0=0．点睛：本题主要考查的是利用因式分解进行简便计算，属于基础题型．解决这个问题的关键就是将所求的代数式进行因式分解．26、试题分析：根据整式的乘法，化简完成后，根据不含项的系数为0求解即可.试题解析：∵（x2+px+8）（x2﹣3x+q）=x4﹣3x3+qx2+px3﹣3px2+pqx+8x2﹣24x+8q=x4+（p﹣3）x3+（q﹣3p+8）x2+（pq﹣24）x+8q．∵乘积中不含x2与x3项，∴p﹣3=0，q﹣3p+8=0，∴p=3，q=1．27、试题分析：根据完全平方公式的结构，按照要求即可得出答案．试题解析：①则②则．。

华东师大版八年级数学上册《12.2整式的乘法》同步练习题(附答案)

华东师大版八年级数学上册《12.2整式的乘法》同步练习题（附答案）一、单选题1．计算(−2m)3×(−m2)的结果是（）A．8m6B．−8m6C．8m5D．−8m52．下列运算正确的是（）A．a(a−1)=a2−a B．3a(a−b)=3a2−ab C．−3(a+b)=−3a+3bD．a(−a+2b)=−a2−2ab3．若(3x+2)(x+p)=mx2+nx−2，则下列结论正确的是（）A．m=6B．n=1C．p=−2D．mnp=34．如果多项式(x+a)与多项式(1−x)的乘积中不含x的一次项，那么a的值为（）A．0B．1C．−1D．25．已知a2+a+5=0，代数式(a2+5)(a+1)的值是（）A．4B．−5C．5D．−46．若长方形的一边长为3m+n，另一边比它长m−n(m>n)，则这个长方形的面积是（）A．12m2+4mn B．12m2−4mn C．3m2−2mn−n2D．3m2+2mn−n27．小华和小军两人共同计算一道整式乘法题：(3x+a)(2x+b)，由于小华抄错了a的符号、得到的结果为6x2−17x+12；由于小军漏抄了第二个多项式中x的系数，得到的结果为3x2−5x−12，则（）A．a=4,b=−3B．a=−4,b=3C．a=4,b=3D．a=−4,b=−38．通过计算比较图中图①，图②中阴影部分的面积，可以验证的计算式子是（）A．a(b−x)=ab−aB．b(a−x)=ab−bxC．(a−x)(b−x)=ab−ax−bxD．(a−x)(b−x)=ab−ax−bx+x2二、填空题9．计算：−3ab×4a2b3=．10．计算：(x2+2x+3)(2x−5)=．11．已知a2−3a+1=0，则代数式(a+1)(2a−8)的值为．12．已知x+y=3,xy=1，则(x−2)(y−2)=．13．如果(x−3)(x−2)−(x+9)(x−1)=2，那么x的值是．14．如图，有一块长为8am，宽为4am的长方形土地，规划部门计划在中间长方形部分修建一个喷泉广场，将其余部分都留出宽为2m的绿化带，则绿化带的面积为m2（请用含a的式子表示）．15．根据(x−1)(x+1)=x2−1，(x−1)(x2+x+1)=x3−1，(x−1)(x3+x2+x+1)=x4−1，(x−1)(x4+x3+x2+x+1)=x5−1的规律，则可以得出22023+22022+22021+...+23+22+2+1的末位数字是．16．如图所示的正方形和长方形卡片若干张，拼成一个长为(a+3b)、宽为(a+b)的矩形，需要B类卡片张．三、解答题17．计算：(1)(3×103)2×(2×104)3×(4×102)2；(2)(59x3y)⋅(−3xy2)3⋅(12x)2；(3)10a⋅(−35ab)−4a2⋅(−12b)+8ab⋅(−34a).18．计算：(1)(x+2y)(x−2y)；(2)(−2x+3)(−3x+5)；(3)(a−b)(a2+ab+b2)；(4)(1−x+y)(x+y)．19．先化简，再求值：(3a+2b)(2a−3b)−(a−3b)(2a−b)，其中a=−12，b=1.20．解不等式：3(x+1)(x−2)≤(3x−1)(x+4)．21．设M=123456789×123456786，N=123456788×123456787，试比较M与N的大小．22．观察算式，解答下列问题：第1个式子：13×17=221=1×2×100+21第2个式子：23×27=621=2×3×100+21第3个式子：33×37=1221=(1)观察算式规律，补全第3个式子；(2)写出第n个式子，并利用所学知识证明你的结论；(3)利用发现的规律，直接写出第11个式子：．23．如图，一个长方形运动场被分隔成A，B，A，B，C，C共6个区，A区是边长为am的正方形，B区是边长为bm的正方形．(1)列式表示每个C区长方形场地的周长，并将式子化简；（用含a、b的代数式表示）(2)列式表示整个长方形运动场的周长，并将式子化简；（用含a、b的代数式表示）(3)如果a=30，b=10，求整个长方形运动场的面积．参考答案：题号 1 2 3 4 5 6 7 8答案 C A D B C A A D1．解：(−2m)3×(−m2)=(−8m3)×(−m2)=8m5故选：C2．A3．D4．解：由题意知，(x+a)(1−x)=−x2+(1−a)x+a∵多项式(x+a)与多项式(1−x)的乘积中不含x的一次项∵1−a=0解得a=1故选：B．5．解：∵a2+a+5=0∵a2+5=−a，−a2−a=5∵(a2+5)(a+1)=−a(a+1)=−a2−a=5故选C．6．解：由题意得，长方形的另一边长为：3m+n+m−n=4m所以长方形的面积为：4m⋅(3m+n)=12m2+4mn，故A正确．故选：A．7．解：∵小华抄错了a的符号，得到的结果为6x2−17x+12∴(3x−a)(2x+b)=6x2−17x+12∴3b−2a=−17①，同理小军漏抄了第二个多项式中x的系数，得到的结果为3x2−5x−12，∴(3x+ a)(x+b)=3x2−5x−12∴a+3b=−5②联立①②可得{3b−2a=−17 a+3b=−5解得{a=4b=−3故选A．8．解：图1中的阴影部分的面积为(a−x)(b−x)图2中的阴影部分的面积为ab−ax−bx+x2∵(a−x)(b−x)=ab−ax−bx+x2．故选：D．9．解：原式=−12a3b4；故答案：−12a3b4.10．解：(x2+2x+3)(2x−5)=2x3−5x2+4x2−10x+6x−15 =2x3−x2−4x−15．故答案为：2x3−x2−4x−15．11．解：∵a2−3a+1=0∵a2−3a=−1∵(a+1)(2a−8)=2a2−6a−8=2(a2−3a)−8=−2−8=−10．故答案为：−10．12．解：∵x+y=3,xy=1∵(x−2)(y−2)=xy−2x−2y+4=xy−2(x+y)+4=1−2×3+4=−1．故答案为：−1．13．解：(x−3)(x−2)−(x+9)(x−1)=x2−2x−3x+6−(x2−x+9x−9)=−13x+15∴−13x+15=2解得x=1故答案为：1．14．解：根据题意，如图所示：∴绿化带的面积为8a×4a−(8a−4)(4a−2)=32a2−(32a2−16a−16a+8)=32a2−32a2+16a+16a−8=32a−8故答案为：(32a−8)．15．解：第1个等式为(x−1)(x+1)=x2−1第2个等式为(x−1)(x2+x+1)=x3−1第3个等式为(x−1)(x3+x2+x+1)=x4−1第4个等式为(x−1)(x4+x3+x2+x+1)=x5−1……第n个等式为(x−1)(x n+x n−1+x n−2+⋯+x+1)=x n+1−1∵22023+22022+22021+...+23+22+2+1=(2−1)(22023+22022+22021+...+23+22+2+1)=22024−1∵21=2，22=4，23=8，24=16，25=32，26=64，27=128，28=256……∵2n的末位数是以2、4、8、6每四个一个循环又2024÷4=506∵22024−1即22023+22022+22021+...+23+22+2+1的末位数为5故答案为：5．16．解：长为(a+3b)、宽为(a+b)的矩形面积为长为(a+3b)(a+b)=a2+4ab+3b2 A图形面积为a2B图形面积为abC图形面积为b2则可知需要A类卡片1张，B类卡片4张，C类卡片3张．故答案为：4．17．解：（1）原式=(9×106)×(8×1012)×(16×104)=1152×1022=1.152×1025.（2）原式=59x3y⋅(−27x3y6)⋅14x2=−154x8y7.（3）原式=−6a2b+2a2b−6a2b=−10a2b.18．解：（1）(x+2y)(x−2y)=x⋅x−x⋅2y+2y⋅x−2y⋅2y=x2−2xy+2yx−4y2=x2−4y2．（2）(−2x+3)(−3x+5)=−2x×(−3x)−2x×5−3×3x+3×5=6x2−10x−9x+15=6x2−19x+15．（3）(a−b)(a2+ab+b2)=a⋅a2+a⋅ab+a⋅b2+(−b)⋅a2+(−b)⋅ab+(−b)⋅b2 =a3+a2b+ab2−a2b−ab2−b3=a3−b3．（4）(1−x+y)(x+y)=x+y−x2−xy+xy+y2=x+y−x2+y2．19．解：原式=6a2−9ab+4ab−6b2−2a2+ab+6ab−3b2=4a2+2ab−9b2.当a=−12，b=1时原式=4×(−12)2+2×(−12)×1−9×12=1+(−1)−9=−9.20．解：3(x+1)(x−2)≤(3x−1)(x+4)3x2−3x−6≤3x2+11x−4−14x≤2x≥−17．21．解：设a=123456788则M=(a+1)(a−2)=a2−a−2，N=a(a−1)=a2−a∴M−N=a2−a−2−(a2−a)=−2<0∴M<N．22．（1）解：∵第1个式子：13×17=221=1×2×100+21；第2个式子：23×27=621=2×3×100+21；∴第3个式子：33×37=1221=3×4×100+21；故答案为：3×4×100+21；（2）解：由（1）可得(10n+3)(10n+7))=100n2+100n+21=100n(n+1)+21证明：(10n+3)(10n+7)=100n2+70n+30n+21=100n2+100n+21=100n(n+1)+21；（3）解：由（2）规律(10n+3)(10n+7)=100n(n+1)+21当n=11时113×117=100×11×12+21=13221．23．（1）解：A区是边长为am的正方形，B区是边长为bm的正方形∵C区长方形场地的长为：(a+2b)m，宽为：(a−b)m∵右上方C区长方形场地的周长为：[(a+2b)+(a−b)]×2=4a+2b(m)左下角C区长方形场地的周长为：[(a+2b)+(a−b)]×2=4a+2b(m)．（2）解：由（1）可知，C区长方形场地的长为：(a+2b)m，宽为(a−b)m∵整个长方形运动场的长为：(a+2b)+a=2a+2b(m)，宽为：(a−b)+a=2a−b(m)∵整个长方形运动场的周长为：(2a+2b+2a−b)×2=8a+2b(m)．（3）解：整个长方形运动场的长为：2a+2b(m)，宽为：2a−b(m)∵整个长方形运动场的面积为：(2a+2b)×(2a−b)=4a2+2ab−2b2当a=30，b=10时，原式=4×302+2×30×10−2×102=4000(m)∵整个长方形运动场的面积为4000m．。

华师大八年级数学上第13章整式的乘除单元复习(含答案)

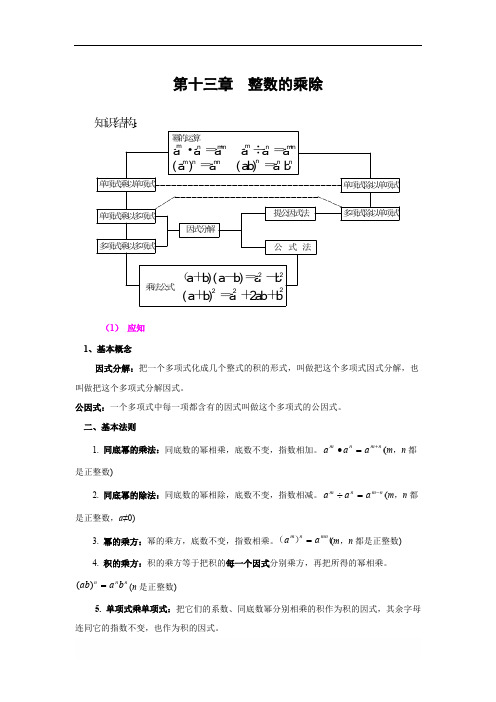
第十三章整数的乘除知识结构：单项式乘以单项式单项式乘以多项式多项式乘以多项式因式分解冪的运算a ·a ＝a a ÷a ＝amn m +n m n m +n (a )＝a (a b )＝a b m m n n n n n 多项式除以单项式提公因式法公式法（a ＋b )(a －b )＝a －b 22(a ＋b )＝a ＋2a b ＋b222乘法公式单项式除以单项式（1）应知1、基本概念因式分解：把一个多项式化成几个整式的积的形式，叫做把这个多项式因式分解，也叫做把这个多项式分解因式。

公因式：一个多项式中每一项都含有的因式叫做这个多项式的公因式。

二、基本法则1. 同底冪的乘法：同底数的幂相乘，底数不变，指数相加。

m ，n 都,(都是正整数n m a a a n m n m +=∙是正整数)2. 同底冪的除法：同底数的幂相除，底数不变，指数相减。

m ，n 都0,,(≠=÷-a n m a a a n m n m 都是正整数是正整数，a ≠0)3. 冪的乘方：幂的乘方，底数不变，指数相乘。

(m ，n 都是正整数),(都是正整数）（n m a a mn n m =4. 积的乘方：积的乘方等于把积的每一个因式分别乘方，再把所得的幂相乘。

(n 是正整数)()(都是正整数n b a ab n n n =5. 单项式乘单项式：把它们的系数、同底数幂分别相乘的积作为积的因式，其余字母连同它的指数不变，也作为积的因式。

6. 单项式乘多项式：用单项式乘以多项式的每一项，再把所得的积相加。

7. 多项式乘多项式：先用一个多项式的每一项乘以另一个多项式的每一项，再把所得的积相加。

8. 单项式除以单项式：把系数、同底数幂分别相除作为商的因式，对于只在被除式里含有的字母，则连同它的指数作为商的一个因式。

9. 多项式除以单项式：先把多项式的每一项除以单项式，再把所得的商相加。

【注意】（1）单项式乘单项式的结果仍然是单项式。

2019—2020年最新华东师大版八年级数学上册《整式的乘除》综合测评及答案解析.docx

第12章整式的乘除综合测评一、选择题（每小题3分，共24分）1. 计算-a2·a3，正确的结果是（）A. -a6B. -a5C. a6D. a52. 下列各式从左到右的变形中，属于因式分解的是（）A. x（2a＋1）＝2ax＋xB. x2－2x＋4＝（x－2）2Ｃ. m2－n2＝（m－n）（m＋n）Ｄ. x2－36＋9x＝（x＋6）（x－6）＋9x3. 如果□×（-3ab）=9a2b，则□内应填的式子是（）A. 3abB. -3abC. 3aD. -3a4. 若x+y=6，x2-y2=24，则y-x的值为（）A. 14B. -14C. -4D. 45. 分解因式（x－2）2－16的结果是（）A. （x－2）（x＋6）B. （x＋14）（x－18）Ｃ. （x＋2）（x－6）Ｄ. （x－14）（x＋18）6. 已知A=-4x2，B是多项式，在计算B+A时，小马虎同学把B+A看成了B·A，结果得32x5-16x4，则B+A为（）A. -8x3+4x2B. -8x3+8x2C. -8x3D. 8x37. 若a=240，b=332，c=424，则下列关系式正确的是（）A. a>b>cB. b>c>aC. c>a>bD. c>b>a8. 如图1，已知长方形的长为a，宽为b，周长为14，面积为10，则a2b＋ab2－ab的值为（）A. 70B. 60 Ｃ. 130 Ｄ. 140二、填空题（每小题4分，共32分）9. 已知a6·a4÷（ax）2=a2，则x-1= .10. 一个正方形的边长为（a+1）cm，如果它的边长增加1 cm，则面积增加cm2.11. 若x是最大的负整数，y是最小的正整数，则（-8x3y2+4x2y3）÷（-2xy）2的值为 .12. 请写出一个三项式，使它能先“提公因式”，再“运用公式”来分解因式.你编写的三项式是：，分解因式的结果是13. 若（x-2）（2x+1）=ax2+bx-2，则a= ，b= .14. 给出下列算式：32－12＝8＝8×1，52－32＝16＝8×2，72－52＝24＝8×3，92－72＝32＝8×4，……观察上面的算式，那么第n个算式可表示为 .15. 若（mx2-nx+2）·（-2x2）-4x3的结果中不含x4项和x3项，则m= ，n= .16. 若两个有理数和的平方等于64，差的平方等于16，则这两个数的积为 .三、解答题（共64分）17. （8分）已知1平方千米的土地上，1年内从太阳得到的能量相当于燃烧1.3×108千克煤所产生的能量，求2×104平方千米的土地上，10年内从太阳得到的能量相当于燃烧多少千克煤所产生的能量.18. （每小题5分，共10分）把下列多项式分解因式：（1）6（m－n）3－12（m－n）2；（2）（p－q）2－（16p－16q）＋64.19. （每小题6分，共12分）先化简，再求值：（1）（x-3）2+（x-2）（-2-x），其中x=-1.（2）3（a＋1）2－（a＋1）（2a－1），其中a＝1.20. （10分）王明将一条长20分米的镀金彩带剪成两段，恰好可以用来镶两张大小不同的正方形壁画的边（不计接头处）.已知两张壁画的面积相差20分米2，问：这条彩带剪成的两段分别是多长？21. （12分）在对某二次三项式进行因式分解时，甲同学因看错了一次项系数而将其分解为2（x－1）（x－9）；乙同学看错了常数项，将其分解为2（x－2）（x－4），请你写出正确的二次三项式，并将其因式分解.22. （12分）图2是一个长为2a，宽为2b的长方形纸片，沿图中虚线用剪刀把它剪成4个相同的小长方形，然后用这4个小长方形纸片拼成图3所示的正方形.（1）请你仔细观察图3，并用两种不同的方法表示大正方形的面积；（2）由（1）你能得出什么结论？（3）根据（2）的结论，解决如下问题：已知a+b=10，a-b=8，求ab的值.第12章整式的乘除综合测评一、1. B 2. C 3. Ｄ 4. C 5. C 6. C 7. B 8. B二、9. 3 10. （2a＋3）11. 312. 答案不唯一，如ax2＋2ax＋a a（x＋1）213. 2 －314. （2n＋1）2－（2n－1）2＝8n 15. 0 2 16. 12三、17. 解：1.3×108×2×104×10＝2.6×1013（千克）.所以2×104平方千米的土地上，10年内从太阳得到的能量相当于燃烧2.6×1013千克煤所产生的能量.18. （1）6（ｍ－n）2（ｍ－n－2）；（2）（ｐ－ｑ－8）2.19. 解：（1）（x-3）2+（x-2）（-2-x）＝x2－6x＋9＋4－x2＝－6x＋13.当x＝－1时，原式＝－6×（－1）＋13＝6＋13＝19.（2）3（a＋1）2－（a＋1）（2a－1）＝（a＋1）［3（a＋1）－2a＋1］＝（a＋1）（a＋4）. 当a＝1时，原式＝（1＋1）×（1＋4）＝2×5＝10.20. 解：设大正方形的边长为x分米，小正方形的边长为y分米.由题意，得x2－y2＝20，即（x－y）（x＋y）＝20.又4（x＋y）＝20，所以x＋y＝5.所以x－y＝4.联立得x y5x y 4.⎧⎨⎩＋＝，－＝解得9,21.2xy⎧=⎪⎪⎨⎪=⎪⎩所以剪成的两段长分别为4x＝18分米，4y＝2分米.21. 解：2（x－1）（x－9）＝2x2－20x＋18，2（x－2）（x－4）＝2x2－12x＋16.因为甲同学看错了一次项系数，乙同学看错了常数项，所以正确的二次三项式为2x2－12x ＋18.将其因式分解可得2x2－12x＋18＝2（x－3）2.22. 解：（1）S大正方形＝（a＋b）2，S大正方形＝（a－b）2＋4ab.（2）（a＋b）2＝（a－b）2＋4ab.（3）当a＋b＝10，a－b＝8时，102＝82＋4ab，即4ab＝102－82＝100－64＝36，所以ab＝9.。

华师大版八年级上数学-整式的乘除单元测试(附答案)

华师大版八年级上数学-整式的乘除单元测试(附答案)华师大版八年级上学期“整式的乘除”单元测试一、填空题：（每空3分，共36分）1．计算：._______53=⋅a a 2．计算：._____)2(23=-a3．计算：._______2142=÷-a b a 4．计算：._________________)12(2=-x5．计算：.___________________)3)(2(=+-x x6．因式分解：.______________252=-x x7．因式分解：.__________42=-x8．因式分解：.___________________442=+-x x9．计算：._______)1098.5()109.1(2427≈⨯÷⨯（保留三个有效数字）10．有三个连续的自然数，中间一个是x ，则它们的积是____________。

11．若多项式442++kx x 恰好是另一个多项式的平方，则k=___________。

12．一块边长为a 米的正方形广场，扩建后的正方形边长比原来长2米，问扩建后的广场面积增大了______________平方米。

二、选择题：（每小题4分，共24分）13．下列运算中正确的是（）A ．43x x x =+B ．43x x x =⋅C ．532)(x x =D ．236x x x =÷（3）22)5()5(y x y x +-- （4）)(]12)1)(1[(22ab b a ab ab -÷+--+20．（8分）化简求值：x y x x y x y x y x 2)]2(2)2)(2()2[(2÷--+-+-。

其中 6,5-==y x 。

21．（8分）已知1,5==+xy y x ，求：① 22y x + ； ② 2)(y x - 。

22．分解因式（各小题6分，共24分）（1）223242ab b a a +- （2）44y x -（3）22125)(5m y x -+ （4）)34(3422y xy x ++23．（8分）有一块直径为2a + b 的圆形木板，挖去直径分别为2a 和 b 的两个圆，问剩下的木板的面积是多少？24．（8分）说明对于任意正整数n ，式子n （n +5）－（n －3）（n +2）的值都能被6整除。

2018秋八年级数学上册第12章整式的乘除 12.1 幂的运算 12.1.2 幂的乘方习题 (新版)华东师大版

10. (1)设 n 为正整数，且 x2n＝7，求(x3n)2－4·(x2)2n 的值；
(2)若 x3m ＝4，y3n＝5，求(x2m )3＋(yn)3－x2m ·yn·x4m ·y2n 的值．
解：(1)147； (2)－59.
(1)已知a＝355，b＝444，c＝533，试比较a、b、c 的大小；
A．a12＝( )3
B．a12＝( )4
C．a12＝( )2
D．a12＝( )6
3. 已知 a＝－34，b＝(－3)4，c＝(23)4，d＝(22)6，则
下列对 a，b，c，d 四者关系的判断，正确的是( C )
A．a＝b，c＝d B．a＝b，c≠d
C．a≠b，c＝d
D．a≠b，c≠d
4. (1)(a7)3＝ a21 ； (2)[－(－2)2]3＝－64 ； (3)(－an＋1)2·(a2)n＋1＝ a4n＋4 ； (4)(x3)2·x5＝ x11 ．
(2)比较大小：①16100与8140； ②2100与375.
解：(1)a＝355＝35×11＝(35)11＝24311， b＝444＝44×11＝(44)11＝25611， c＝533＝53×11＝(53)11＝12511， ∵125＜243＜256，∴c＜a＜b. (2)①中：16100＝(24)100＝2400，8140＝(23)140＝2420. ∵2400<2420，∴16100＜8140. ②中：∵2100＝(24)25＝1625，375＝(33)25＝2725，而 16＜27，∴1625＜2725，即2100＜375.
2b)9.
4. 若 3×9m ×27m ＝321，则 m 的值为( B )
A．3
B．4
C．5

华师大版八年级数学上册第12章整式的乘除整合【新版】

专训一：整体思想在整式乘除运算中的应用名师点金：解决某些数学问题时，把一组数或一个式子看作一个整体进行处理，不仅可以简化解题过程，而且还能拓宽思路，培养创新意识，体现了数学中的一种重要思想——整体思想．这一思想在整式的乘法运算中体现明显，在解题中应用较多，要引起重视．幂的运算中的整体思想1．已知2x ＋5y －3＝0，求4x ·32y 的值．乘法公式运算中的整体思想类型1 化繁为简整体代入2．已知a ＝38x －20，b ＝38x －18，c ＝38x －16，求式子a 2＋b 2＋c 2－ab －ac －bc 的值．类型2 变形后整体代入3．已知x ＋y ＝4，xy ＝1，求式子(x 2＋1)(y 2＋1)的值．4．已知a －b ＝b －c ＝35，a 2＋b 2＋c 2＝1，求ab ＋bc ＋ca 的值．5．已知a2＋a－1＝0，求a3＋2a2＋2 016的值．6．已知(2 016－a)(2 014－a)＝2 015，求(2 016－a)2＋(2 014－a)2的值．多项式乘法运算中的整体思想类型1大数中的换元7．若M＝123 456 789×123 456 786，N＝123 456 788×123 456 787，试比较M与N的大小．类型2多项式中的换元8．计算：(a1＋a2＋…＋a n－1)(a2＋a3＋…＋a n－1＋a n)－(a2＋a3＋…＋a n－1)(a1＋a2＋…＋a n)(n≥3，且n为正整数)．专训二：因式分解的七种常见用途名师点金：因式分解是整式恒等变形中的一种重要变形，它与整式的乘法是两个互逆的过程，是代数恒等变形的重要手段，在有理数计算、式子的化简求值、几何等方面起着重要作用．用于简便计算1．计算：2 0162－4 034×2 016＋2 0172.2．计算：⎝ ⎛⎭⎪⎫1－122⎝ ⎛⎭⎪⎫1－132⎝ ⎛⎭⎪⎫1－142·…·(1－1102)·(1－1112)．用于化简求值3．已知2x －3＝0，求式子x(x 2－x)＋x 2(5－x)－9的值．用于判断整除4．随便写出一个十位数字与个位数字不相等的两位数，把它的十位数字与个位数字对调得到另一个两位数，并用较大的两位数减去较小的两位数，所得的差一定能被9整除吗？为什么？用于判断三角形的形状5．已知a，b，c是△ABC的三边长，且满足a2＋b2＋c2－ab－bc－ac＝0，试判断△ABC的形状．用于比较大小6．已知A＝a＋2，B＝a2＋a－7，其中a＞2，比较A与B的大小．用于解方程(组)7．已知大正方形的周长比小正方形的周长大96 cm，大正方形的面积比小正方形的面积大960 cm2，请你分别求出这两个正方形的边长．用于探究规律8．观察下列各式：12＋(1×2)2＋22＝9＝32，22＋(2×3)2＋32＝49＝72，32＋(3×4)2＋42＝169＝132，….你发现了什么规律？请用含有n(n为正整数)的等式表示出来，并说明理由．专训三：整式的乘除中的几种热门考点名师点金：本章的主要内容有幂的运算，整式的乘除法，乘法公式，以及利用提公因式法和公式法分解因式等，在考试中，常常与数的运算、式子的化简求值、几何等知识综合在一起考查．中考中一般以基础题为主．幂的运算1．(2015·临沂)下列计算正确的是()A．a2＋a2＝2a4B．(－a2b)3＝－a6b3C．a2·a3＝a6D．a8÷a2＝a42．计算：(1)(－a2b)2＝________；(2)42 016×(－0.25)2 017＝________．3．已知：3x＋5y＝8，求8x·32y的值．整式的乘除运算4．下列计算结果是x2－6x＋5的是()A．(x－2)(x－3) B．(x－6)(x＋1)C．(x－1)(x－5) D．(x＋6)(x－1)5．若(－2x2)(3x2－ax－6)－3x3＋x2的结果中不含x的三次项，则a＝________．6．小明在进行两个多项式的乘法运算时，不小心把乘(x－2y)错抄成除以(x －2y)，结果得到3x，则第一个多项式是什么？正确的结果应该是什么？7．先化简，再求值：2(2x－1)(2x＋1)－5x(－x＋3y)＋4x(－4x－52y)，其中x＝－1，y＝2.乘法公式的运用8．下列计算正确的是()A．(－x－y)(x＋y)＝x2－y2B．(x－y)2＝x2－y2C．(x＋3y)(x－3y)＝x2－3y2D．(－x＋y)2＝x2－2xy＋y29．运用乘法公式计算：(1)(m－2n＋3)(m＋2n－3)；(2)(a－3b＋2)2.10．(2014·绍兴)先化简，再求值：a(a －3b)＋(a ＋b)2－a(a －b)，其中a ＝1，b ＝－12.11．已知x ＋y ＝3，xy ＝－7，求下列各式的值：(1)x 2＋y 2； (2)x 2－xy ＋y 2； (3)(x －y)2.利用提公因式法和公式法分解因式12．将下列各式分解因式：(1)2a 3b 2c ＋4ab 3c －abc ；(2)x 2＋4x ＋4；(3)(2a ＋b)(2a －b)＋b(4a ＋2b)；(4)x2(x－y)＋(y－x)；(5)3ax2－6axy＋3ay2.整式乘除的应用13．已知(x＋y)2＝5，(x－y)2＝3，求3xy－1的值．14．已知n是整数，试说明(2n＋1)2－1能被8整除．(第15题)15．(2014·青海)如图，长和宽分别为a ，b 的长方形，它的周长为15，面积为10，则a 2b ＋ab 2的值为________．16．△ABC 的三边长分别是a ，b ，c ，且a ＋2ab ＝c ＋2bc ，请判断△ABC 是等边三角形、等腰三角形还是直角三角形？并说明理由．17．一天，小明在纸上写了一个算式：4x 2＋8x ＋11，并对小刚说：“无论x 取何值，这个式子的值都是正值，不信你试一试！”小刚动笔演算许多次，结果正如小明所说．小刚很困惑，你能运用所学的知识说明一下其中的道理吗？数学思想方法的应用a ．转化思想18．若2x ＝3，4y ＝5，则2x －2y 的值是( )A .35B ．－2C .355D .65b ．整体思想19．若m ＋n ＝3，则2m 2＋4mn ＋2n 2－6的值为( )A ．12B ．6C ．3D ．0c ．换元思想20．计算：2 0153－2 014×2 015×2 016.答案专训一1．解：4x ·32y ＝(22)x ·(25)y ＝22x ·25y ＝22x ＋5y .因为2x ＋5y －3＝0，所以2x ＋5y ＝3，所以原式＝23＝8.点拨：本题运用了整体思想和转化思想．2．解：由a ＝38x －20，b ＝38x －18，c ＝38x －16，可得a －b ＝－2，b －c ＝－2，c －a ＝4.从而a 2＋b 2＋c 2－ab －ac －bc ＝12[(a －b)2＋(b －c)2＋(c －a)2]＝12×[(－2)2＋(－2)2＋42]＝12×24＝12.3．解：(x 2＋1)(y 2＋1)＝x 2y 2＋x 2＋y 2＋1＝(xy)2＋(x ＋y)2－2xy ＋1.把x ＋y ＝4，xy ＝1整体代入，原式＝12＋42－2×1＋1＝16.4．解：由a －b ＝b －c ＝35，可以得到a －c ＝65.由(a －b)2＋(b －c)2＋(a －c)2＝2(a 2＋b 2＋c 2)－2(ab ＋bc ＋ca)，得到ab ＋bc ＋ca ＝(a 2＋b 2＋c 2)－12[(a －b)2＋(b－c)2＋(a －c)2]．将a 2＋b 2＋c 2，a －b ，b －c 及a －c 的值整体代入，可得ab ＋bc＋ca ＝1－12×[(35)2＋⎝ ⎛⎭⎪⎫352＋⎝ ⎛⎭⎪⎫652]＝1－12×5425＝－225. 5．解：因为a 2＋a －1＝0①，所以将等式两边都乘a ，可得a 3＋a 2－a ＝0②.将①②相加，得a 3＋2a 2－1＝0，即a 3＋2a 2＝1.所以a 3＋2a 2＋2 016＝1＋2 016＝2 017.6．解：(2 016－a)2＋(2 014－a)2＝[(2 016－a)－(2 014－a)]2＋2(2 016－a)(2 014－a)＝22＋2×2 015＝4＋4 030＝4 034.点拨：本题运用乘法公式的变形x 2＋y 2＝(x －y)2＋2xy ，结合整体思想求解，使计算简便．7．解：设123 456 788＝a ，则123 456 789＝a ＋1，123 456 786＝a －2，123 456 787＝a －1.从而M ＝(a ＋1)(a －2)＝a 2－a －2，N ＝a(a －1)＝a 2－a.所以M －N ＝(a 2－a －2)－(a 2－a)＝－2＜0，所以M ＜N.8．解：设a 2＋a 3＋…＋a n －1＝M ，则原式＝(a 1＋M)(M ＋a n )－M(a 1＋M ＋a n )＝a 1M ＋a 1a n ＋M 2＋a n M －a 1M －M 2－a n M ＝a 1a n .点拨：本题如果按正常展开的方式来运算显然是很复杂的．这一类带“…”的题中，往往蕴藏着重要的技巧，而发现技巧的关键是观察．因此，在解决这类问题时，不要忙于解答，而要冷静观察，寻找解决问题的突破口．比如此题，在观察时能发现a 2＋a 3＋…＋a n －1这个式子在每一个因式中都存在．因此，可以考虑将这个式子作为一个整体，设为M ，问题就简化了，体现了整体思想的运用．专训二1．解：2 0162－4 034×2 016＋2 0172＝2 0162－2×2 016×2 017＋2 0172＝(2 016－2 017)2＝1.2．解：原式＝⎝ ⎛⎭⎪⎫1＋12⎝ ⎛⎭⎪⎫1－12(1＋13)⎝ ⎛⎭⎪⎫1－13(1＋14)⎝ ⎛⎭⎪⎫1－14·…·(1＋110)(1－110)(1＋111)(1－111)＝32×12×43×23×54×34×…×1110×910×1211×1011＝12×1211＝611.3．解：原式＝x 3－x 2＋5x 2－x 3－9＝4x 2－9＝(2x ＋3)(2x －3)．当2x －3＝0时，(2x ＋3)(2x －3)＝0.4．解：所得的差一定能被9整除．理由：设该两位数个位上的数字是b ，十位上的数字是a ，且a ≠b ，则这个两位数是10a ＋b.将十位数字与个位数字对调后的数是10b ＋a ，则这两个两位数中，较大的数减较小的数的差是|10a ＋b －(10b ＋a)|＝9|a －b|，所以所得的差一定能被9整除．5．解：∵a 2＋b 2＋c 2－ab －bc －ac ＝0，∴2a 2＋2b 2＋2c 2－2ab －2bc －2ac ＝0.即a 2－2ab ＋b 2＋b 2－2bc ＋c 2＋a 2－2ac ＋c 2＝0.∴(a －b)2＋(b －c)2＋(a －c)2＝0.又∵(a －b)2≥0，(b －c)2≥0，(a －c)2≥0，∴a －b ＝0，b －c ＝0，a －c ＝0，即a ＝b ＝c ，∴△ABC 为等边三角形．6．解：B －A ＝a 2＋a －7－a －2＝a 2－9＝(a ＋3)(a －3)．因为a ＞2，所以a ＋3＞0，从而当2＜a ＜3时，a －3＜0，所以A ＞B ；当a ＝3时，a －3＝0，所以A ＝B ；当a ＞3时，a －3＞0，所以A ＜B.7．解：设大正方形和小正方形的边长分别为x cm ，y cm ，根据题意，得⎩⎨⎧4x －4y ＝96，①x 2－y 2＝960.②由①得x －y ＝24，③由②得(x ＋y)(x －y)＝960，④把③代入④得x ＋y ＝40.⑤由③⑤得方程组⎩⎨⎧x －y ＝24，x ＋y ＝40，解得⎩⎨⎧x ＝32，y ＝8.答：大正方形的边长为32 cm ，小正方形的边长为8 cm .点拨：根据目前我们所学的知识，还无法解方程组⎩⎨⎧4x －4y ＝96，x 2－y 2＝960，但是我们可以利用因式分解，把这个问题转化为解关于x ，y 的二元一次方程组的问题．8．解：规律：n 2＋[n(n ＋1)]2＋(n ＋1)2＝(n 2＋n ＋1)2.理由如下：n 2＋[n(n ＋1)]2＋(n ＋1)2＝[n(n ＋1)]2＋2n 2＋2n ＋1＝[n(n ＋1)]2＋2n(n ＋1)＋1＝[n(n ＋1)＋1]2＝(n 2＋n ＋1)2.专训三1．B2．(1)a 4b 2 (2)－0.253．解：8x ·32y ＝23x ·25y ＝23x ＋5y ＝28＝256.4．C 5.326．解：第一个多项式是3x(x －2y)＝3x 2－6xy.正确的结果是(3x 2－6xy)(x －2y)＝3x 3－12x 2y ＋12xy 2.7．解：原式＝2(4x 2－1)＋5x 2－15xy －16x 2－10xy＝8x 2－2＋5x 2－15xy －16x 2－10xy＝－3x 2－25xy －2.当x ＝－1，y ＝2时，原式＝－3×(－1)2－25×(－1)×2－2＝45.8．D9．解：(1)原式＝[m －(2n －3)][m ＋(2n －3)]＝m 2－(2n －3)2＝m 2－(4n 2－12n ＋9)＝m 2－4n 2＋12n －9.(2)原式＝[(a －3b)＋2]2＝(a －3b)2＋4(a －3b)＋4＝a 2－6ab ＋9b 2＋4a －12b ＋4.10．解：原式＝a 2－3ab ＋a 2＋2ab ＋b 2－a 2＋ab ＝a 2＋b 2.当a＝1，b＝－12时，原式＝12＋⎝⎛⎭⎪⎫－122＝54.11．解：(1)x2＋y2＝x2＋2xy＋y2－2xy＝(x＋y)2－2xy＝32－2×(－7)＝23.(2)x2－xy＋y2＝x2＋2xy＋y2－3xy＝(x＋y)2－3xy＝32－3×(－7)＝30.(3)(x－y)2＝x2－2xy＋y2＝x2＋2xy＋y2－4xy＝(x＋y)2－4xy＝32－4×(－7)＝37.12．解：(1)原式＝abc(2a2b＋4b2－1)．(2)原式＝(x＋2)2.(3)原式＝(2a＋b)(2a－b)＋2b(2a＋b)＝(2a＋b)(2a－b＋2b)＝(2a＋b)2.(4)原式＝x2(x－y)－(x－y)＝(x－y)(x2－1)＝(x－y)(x＋1)(x－1)．(5)原式＝3a(x2－2xy＋y2)＝3a(x－y)2.13．解：由(x＋y)2＝5，(x－y)2＝3，可得x2＋2xy＋y2＝5①，x2－2xy＋y2＝3②.①－②得4xy＝2，∴xy＝1 2.∴3xy－1＝3×12－1＝12.14．解：(2n＋1)2－1＝[(2n＋1)＋1][(2n＋1)－1]＝2(n＋1)·2n＝4n·(n＋1)．因为n是整数，所以n与n＋1是两个连续的整数，而两个连续的整数中必有一个偶数，所以n·(n＋1)能被2整除，所以4n·(n＋1)能被8整除．故(2n＋1)2－1能被8整除．点拨：要说明(2n＋1)2－1能被8整除，只要将此式因式分解，说明各因式的积能被8整除即可．15．7516．解：△ABC是等腰三角形．理由如下：∵a＋2ab＝c＋2bc，∴(a－c)＋2b(a－c)＝0，∴(a－c)(1＋2b)＝0.∵1＋2b＞0，∴a＝c.∴△ABC为等腰三角形．17．解：∵4x2＋8x＋11＝4(x2＋2x＋1)＋7＝4(x＋1)2＋7，且(x＋1)2≥0，∴4(x ＋1)2＋7≥7.即无论x取何值，4x2＋8x＋11的值都是正值．18．A19.A20．解：设2 015＝a，则原式＝a3－(a－1)·a·(a＋1) ＝a3－a(a2－1)＝a3－a3＋a＝a＝2 015.。

2020华师大版八年级数学上册期末复习《整式的乘除》(含答案)

29.（1）如图是用 4 个全等的长方形拼成的一个“回形”正方形，图中阴影部分面积用 2 种方
法表示可得一个等式，这个等式为
．
（2）若(4x﹣y)2=9，(4x+y)2=169，求 xy 的值．
30.中国古贤常说万物皆自然，而古希腊学者说万物皆数.同学们还记得我们最初接触的数就是 “自然数”吧!在数的学习过程中，我们会对其中一些具有某种特性的自然数进行研究，我们研究了奇数、偶数、质数、合数等.现在我们来研究另一种特珠的自然数—“n 喜数”. 定义：对于一个两位自然数，如果它的个位和十位上的数字均不为零，且它正好等于其个位和十位上的数字的和的 n 倍(n 为正整数)，我们就说这个自然数是一个“n 喜数”. 例如：24 就是一个“4 喜数”，因为 24=4×(2+4)； 25 就不是一个“n 喜数”因为 25≠n(2+5). (1)判断 44 和 72 是否是“n 喜数”？请说明理由； (2)试讨论是否存在“7 喜数”若存在请写出来，若不存在请说明理由.
23.原式=(x-y)(2a-3b)
24.原式=3(x+y)(x-y) 25.原式=(5x+4y)(5x-4y)； 26.原式=(5x+2y)2； 27.解：小新的说法正确.
∵(2x-y)(2x＋y)＋(2x-y)(y-4x)＋2y(y-3x) =4x2-y2-8x2＋6xy-y2＋2y2-6xy=-4x2， ∴小新的说法正确. 28.解：由题意可得，方案二：a2+ab+(a+b)b=a2+ab+ab+b2=a2+2ab+b2=(a+b)2，
华师大版八年级数学上册期末复习《整式的乘除》
一、选择题

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

华东师大版八年级上册第12章整式的乘除
专题训练幂的运算和整式的乘法
1．计算(－a)3·(a2)3·(－a)2的结果正确的是( )
A．a11B．－a11C．－a10D．a13
2．下列计算正确的是( )
A．x2(m＋1)÷x m＋1＝x2B．(xy)8÷(xy)4＝(xy)2
C．x10÷(x7÷x2)＝x5D．x4n÷x2n·x2n＝1
3．已知(x＋a)(x＋b)＝x2－13x＋36，则ab的值是( )
A．36 B．13 C．－13 D．－36
4．若(ax＋2y)(x－y)展开式中，不含xy项，则a的值为( )
A．－2 B．0 C．1 D．2
5．若x＋y＝1，xy＝－2，则(2－x)(2－y)的值为( )
A．－2 B．0 C．2 D．4
6．若(x＋a)(x＋b)＝x2＋px＋q，且p＞0，q＜0，那么a、b必须满足的条件是( ) A．a、b都是正数B．a、b异号，且正数的绝对值较大
C．a、b都是负数D．a、b异号，且负数的绝对值较大
7．一个长方体的长、宽、高分别是3x－4、2x－1和x，则它的体积是( ) A．6x3－5x2＋4x B．6x3－11x2＋4x
C．6x3－4x2D．6x3－4x2＋x＋4
8．观察下列多项式的乘法计算：
(1)(x＋3)(x＋4)＝x2＋7x＋12；(2)(x＋3)(x－4)＝x2－x－12；(3)(x－3)(x＋4)＝x2＋x－12；(4)(x－3)(x－4)＝x2－7x＋12
根据你发现的规律，若(x＋p)(x＋q)＝x2－8x＋15，则p＋q的值为( ) A．－8 B．－2 C．2 D．8
9．如图，甲、乙、丙、丁四位同学给出了四种表示该长方形面积的多项式：①(2a＋b)(m＋n)；②2a(m＋n)＋b(m＋n)；③m(2a＋b)＋n(2a＋b)；④2am＋2an ＋bm＋bn，
你认为其中正确的有( )
A．①②B．③④C．①②③D．①②③④
10．计算：
(1)(－3ab2c3)2＝________；
(2)a3b2·(－ab3)3＝________；
(3)(－x3y2)(7xy2－9x2y)＝_______________.
11．若3m＝81，3n＝9，则m＋n＝________. 12．若a5·(a m)3＝a4m，则m＝________.
13．若x2＋kx－15＝(x＋3)(x＋b)，则k＝________.
14．计算：
(1)(a2)3·a3－(3a3)3＋(5a7)·a2；
(2)(－4x2y)·(－x2y2)·(1
2y)
3
(3)(－3ab)(2a2b＋ab－1)；
(4)(m－2
3)(m＋
1
6)；
(5)(－1
3xy)
2·[xy(x－y)＋x(xy－y2)]；
15．若多项式x2＋ax＋8和多项式x2－3x＋b相乘的积中不含x3项且含x项的系数是－3，求a和b的值．
16．如图，长为10 cm，宽为6 cm的长方形，在4个角剪去4个边长为x cm的小正方形，按折痕做一个有底无盖的长方体盒子，求盒子的体积．
17．化简求值：(3x＋2y)(4x－5y)－11(x＋y)(x－y)＋5xy，其中x＝31
2，y＝－2
1
2.
18．解方程：(2x＋5)(3x－1)＋(2x＋3)(1－3x)＝28. 19．已知x2－8x－3＝0，求(x－1)(x－3)(x－5)(x－7)的值．
答案
1. B
2. C
3. A
4. D
5. B
6. B
7. B
8. A
9. D
10. （1）9a 2b 4c 6
（2）－a 6b 11
（3）－7x 4y 4＋9x 5y 3
11. 6
12. 5
13. －2
14. （1）原式＝－21a 9
（2）原式＝(－4x 2y)·(－x 2y 2)(18y 3)＝12x 4y 6
（3）原式＝(－4x 2y)·(－x 2y 2)(18y 3)＝12x 4y 6
（3）原式＝－6a 3b 2－3a 2b 2＋3ab
（4）原式＝m 2＋(－23m ＋16m)＋(－23)×16＝m 2－12m －19
（5）原式＝19x 2y 2(2x 2y －2xy 2)＝29x 4y 3－29x 3y 4
15. ∵(x 2＋ax ＋8)(x 2－3x ＋b)＝x 4＋(－3＋a)x 3＋(b －3a ＋8)x 2－(－ab ＋24)x ＋8b ，又∵不含x 3项且含x 项的系数是－3，
∴⎩⎨⎧a －3＝0－ab ＋24＝3，解得⎩⎨⎧a ＝3b ＝7
16. (4x 3－32x 2＋60x) cm 3
17. 原式＝x 2－2xy ＋y 2＝36
18. (2x ＋5)(3x －1)＋(2x ＋3)(1－3x)＝28，6x 2＋13x －5－6x 2－9x ＋2x ＋3＝28，
整理得：6x＝30，解得：x＝5
19. ∵x2－8x－3＝0，∴x2－8x＝3，(x－1)(x－3)(x－5)(x－7)＝(x2－8x＋7)(x2－8x＋15)，把x2－8x＝3
代入得：原式＝(3＋7)(3＋15)＝180。