实验三RSA算法代码的实现
RSA的C语言算法实现

三、程序运行结果及相关说明 主函数实现求 N 的欧拉数、由公钥求解私钥、加密解密选择以及相应的密文明文输出。 子函数 candp 实现加密解密时的求幂取余运算, fun 实现 e 与 t 的互素判断,已验证 e 是否 符合要求。程序主体参考了网上的相关 RSA 算法程序,我对其中 e 的合法性判断、主函数 实现的顺序以及相关提示信息做了补充与修改并加上了注释, 这样程序可读性更强, 运行时 更容易操作,思路也更加严密。 当 P=43, q=59 时,对 13不互素,提示需重新输入,输入 13 后,便可以进行正确操作。 由于 int 型变量为十六位,因此 n 最大只能小于 65536,此程序只是对 RSA 算法的入门,无 法实现达到安全要求的数据位数。
//公钥 e 与 t 的互素判断
x=y; y=t%y; } if(x == 1) return 0; else return 1; }
//x 与 y 互素时返回 0 //x 与 y 不互素时返回 1
void main() { int p,q,e,d,m,n,t,c,r; printf("请输入两个素数 p,q: "); scanf("%d%d",&p,&q); n=p*q; printf("计算得 n 为 %3d\n",n); t=(p-1)*(q-1); //求 n 的欧拉数 printf("计算得 t 为 %3d\n",t); printf("请输入公钥 e: "); scanf("%d",&e); if(e<1||e>t||fun(e,t)) { printf("e 不合要求,请重新输入: "); //e<1 或 e>t 或 e 与 t 不互素时,重新输入 scanf("%d",&e); } d=1; while(((e*d)%t)!=1) d++; //由公钥 e 求出私钥 d printf("经计算 d 为 %d\n",d); printf("加密请输入 1\n"); //加密或解密选择 printf("解密请输入 2\n"); scanf("%d",&r); switch(r) { case 1: printf("请输入明文 m: "); //输入要加密的明文数字 scanf("%d",&m); c=candp(m,e,n); printf("密文为 %d\n",c);break; case 2: printf("请输入密文 c: "); //输入要解密的密文数字 scanf("%d",&c); m=candp(c,d,n); printf("明文为 %d\n",m);break; } }
RSA加密算法(C语言实现)

RSA加密算法(C语言实现)RSA(Rivest-Shamir-Adleman)算法是一种非对称加密算法,它是目前应用最广泛的加密算法之一、RSA算法基于两个大素数之间的乘积很难分解的特性,并使用公钥和私钥进行加密和解密。
在C语言中实现RSA算法需要进行以下步骤:1.生成大素数p和q:选择两个大素数p和q,它们需要满足p≠q。
这样选取p和q是为了使得计算n=p*q变得困难,保护私钥。
2.计算n:计算n=p*q,n即为公钥和私钥的参数之一3.计算欧拉函数φ(n):计算欧拉函数φ(n)=(p-1)*(q-1)。
4.选择e:选择一个与φ(n)互质且小于φ(n)的整数e作为加密指数,e即为公钥的参数。
5. 计算d:计算d = e^(-1) mod φ(n),d即为私钥的参数。
可以使用扩展欧几里得算法来计算d。
6. 加密:将明文M转换为整数m,加密后的密文C = m^e mod n。
7. 解密:解密密文C得到明文M = C^d mod n。
以下是C语言实现RSA加密算法的代码示例:```c#include <stdio.h>int gcd(int a, int b)if(b == 0)}return gcd(b, a % b);int extendedGcd(int a, int b, int *x, int *y) if(a == 0)*x=0;*y=1;return b;}int x1, y1;int gcd = extendedGcd(b % a, a, &x1, &y1);*x=y1-(b/a)*x1;*y=x1;return gcd;int modInverse(int a, int m)int x, y;int gcd = extendedGcd(a, m, &x, &y);if(gcd != 1)printf("Inverse doesn't exist\n");}return (x % m + m) % m;int powerMod(int x, unsigned int y, int m) if (y == 0)return 1;}int p = powerMod(x, y/2, m) % m;p=(p*p)%m;return (y%2 == 0) ? p : (x*p) % m;int maiint p, q, n, phiN, e, d;//选择两个大素数p和qp=31;q=17;//计算n和φ(n)n=p*q;phiN = (p - 1) * (q - 1);//选择加密指数ee=7;//计算解密指数dd = modInverse(e, phiN);int plaintext = 88;int ciphertext = powerMod(plaintext, e, n);int decryptedtext = powerMod(ciphertext, d, n);printf("Plaintext: %d\n", plaintext);printf("Ciphertext: %d\n", ciphertext);printf("Decryptedtext: %d\n", decryptedtext);return 0;```在上面的代码中,我们使用了几个辅助函数来实现扩展欧几里得算法、计算模反元素和快速幂算法。
C语言实现RSA算法

C语言实现RSA算法RSA算法是一种非对称加密算法,用于在网络通信中进行数据加密和解密。
下面我将给出C语言中RSA算法的实现。
首先,我们需要生成RSA密钥对,包括公钥和私钥。
以下是生成RSA 密钥对的C代码实现:```c#include <stdio.h>#include <stdlib.h>#include <math.h>//定义最大素数范围//定义RSA密钥结构体typedef structunsigned long long e; // 公钥指数unsigned long long d; // 私钥指数unsigned long long n; // 模数} RSAKey;//判断一个数是否为素数int isPrime(unsigned long long num)//小于等于1的数不是素数if (num <= 1) return 0;//判断是否存在因子for (unsigned long long i = 2; i <= sqrt(num); i++)if (num % i == 0)return 0;}}return 1;//生成一个指定范围内的随机素数unsigned long long generateRandomPrime(unsigned long long min, unsigned long long max)unsigned long long num;donum = rand( % (max - min + 1) + min;} while (!isPrime(num));return num;//求最大公约数unsigned long long gcd(unsigned long long a, unsigned long long b)unsigned long long temp;while (b != 0)temp = a % b;a=b;b = temp;}return a;//求模反元素unsigned long long modReverse(unsigned long long a, unsigned long long b)unsigned long long m0 = b, t, q;unsigned long long x0 = 0, x1 = 1;if (b == 1) return 0;while (a > 1)q=a/b;t=b;b=a%b;a=t;t=x0;x0=x1-q*x0;x1=t;}if (x1 < 0) x1 += m0;return x1;//生成RSA密钥对RSAKey generateRSAKeys(unsigned long long p, unsigned long long q)RSAKey keys;//计算模数keys.n = p * q;//计算欧拉函数值unsigned long long phi = (p - 1) * (q - 1);//选择公钥指数ekeys.e = generateRandomPrime(2, phi - 1);//计算私钥指数dkeys.d = modReverse(keys.e, phi);return keys;int mai//设置随机种子//生成两个不同的随机素数unsigned long long p = generateRandomPrime(2,MAX_PRIME_NUMBER);unsigned long long q = generateRandomPrime(2,MAX_PRIME_NUMBER);RSAKey keys = generateRSAKeys(p, q);printf("公钥指数e: %llu\n", keys.e);printf("私钥指数d: %llu\n", keys.d);printf("模数n: %llu\n", keys.n);return 0;```运行上述代码,即可生成RSA密钥对。
RSA算法和实现及实例

RSA算法和实现及实例<一>基础RSA算法非常简单,概述如下:找两素数p和q取n=p*q取t=(p-1)*(q-1)取任何一个数e,要求满足e<t并且e与t互素(就是最大公因数为1)取d*e%t==1这样最终得到三个数:n d e设消息为数M (M <n)设c=(M**d)%n就得到了加密后的消息c设m=(c**e)%n则m == M,从而完成对c的解密。
注:**表示次方,上面两式中的d和e可以互换。
在对称加密中:n d两个数构成公钥,可以告诉别人;n e两个数构成私钥,e自己保留,不让任何人知道。
给别人发送的信息使用e加密,只要别人能用d解开就证明信息是由你发送的,构成了签名机制。
别人给你发送信息时使用d加密,这样只有拥有e的你能够对其解密。
rsa的安全性在于对于一个大数n,没有有效的方法能够将其分解从而在已知n d的情况下无法获得e;同样在已知n e的情况下无法求得d。
或者说,rsa的安全性在于对于一个大数n,没有有效的办法将其分解成p和q。
<二>实践接下来我们来一个实践,看看实际的操作:找两个素数:p=47q=59这样n=p*q=2773t=(p-1)*(q-1)=2668取e=63,满足e<t并且e和t互素用perl简单穷举可以获得满主e*d%t ==1的数d:C:\Temp>perl -e "foreach $i (1..9999){ print($i),last if$i*63%2668==1 }"847即d=847最终我们获得关键的n=2773d=847e=63取消息M=244我们看看加密:c=M**d%n = 244**847%2773用perl的大数计算来算一下:C:\Temp>perl -Mbigint -e "print 244**847%2773"465即用d对M加密后获得加密信息c=465解密:我们可以用e来对加密后的c进行解密,还原M:m=c**e%n=465**63%2773 :C:\Temp>perl -Mbigint -e "print 465**63%2773"244即用e对c解密后获得m=244 , 该值和原始信息M相等。
实验三RSA算法代码的实现

实验三RSA算法代码的实现RSA算法是一种非对称加密算法,主要用于数据的加密和解密。
在本实验中,我们将实现RSA算法的加密和解密部分,并编写测试代码来验证算法的正确性。
首先,我们需要实现RSA算法的关键步骤之一,生成公钥和私钥。
以下代码展示了如何生成公钥和私钥:```pythonimport randomdef generate_keypair(p, q):n=p*qphi = (p - 1) * (q - 1)e = random.randrange(1, phi)while gcd(e, phi) != 1:e = random.randrange(1, phi)d = mod_inverse(e, phi)return ((e, n), (d, n))```在这段代码中,我们首先选择两个大素数p和q,并计算出n和phi。
然后,我们选择一个在1到phi之间互质的整数e作为公钥的指数。
最后,我们使用扩展欧几里得算法找到d,使得e * d与phi模相等,从而形成私钥。
返回的结果是一个元组,包含公钥和私钥。
接下来,我们实现RSA算法的加密过程。
以下代码展示了如何实现RSA加密:```pythondef encrypt(public_key, message):e, n = public_keyencrypted_message = [pow(ord(c), e, n) for c in message]return encrypted_message```在这段代码中,我们首先从公钥中提取出指数e和模数n。
然后,我们将明文逐字符进行加密,使用公式c=(m^e)%n计算密文。
最后,返回一个列表,包含所有加密后的字符。
最后,我们实现RSA算法的解密过程。
以下代码展示了如何实现RSA 解密:```pythondef decrypt(private_key, encrypted_message):d, n = private_keydecrypted_message = [chr(pow(c, d, n)) for c inencrypted_message]return ''.join(decrypted_message)```在这段代码中,我们首先从私钥中提取出指数d和模数n。
实验3_RSA加解密算法

实验3:RSA加密、解密算法实验一、实验目的掌握数论的重要概念和算法(模逆算法、大整数幂的模运算)。
掌握RSA算法。
二、RSA算法原理:1.生成密钥参数①任取两个比较大的素数p,q②计算整数n,n=p*q③计算欧拉函数φ(n)=(p-1)*(q-1)④计算一个较小的正整数w,w应该满足条件gcd(w,φ(n))=1⑤计算一个正整数 d,d应该满足条件w d≡1 (mod φ(n))注:参数(w,n)用于加密,参数(d,n)用于解密2. 加密算法假设需要加密的明文是整数m,加密后的密文是c3.解密算法三、实验任务【实验任务一】(必做)小素数RSA算法①.从键盘输入两个素数p,q,并输出参数n,φ(n),w,d②.从键盘输入明文数据m,计算出密文数据c,输出c③.根据计算机出的密文数据c,计算出明文数据m,输出m④从键盘输入明文字符串mStr,例如"I love you",或者"我爱你"都可以,计算出密文数据cStr,输出cStr⑤解密计算,根据密文数据cStr,计算出明文数据mStr【实验任务二】(可选)大素数RSA算法①给定一个比较整数下限xmin(比如要求xmin>100000),xmin可以大于现有的整数表示范围,因此要求用大整数表示。
②自动计算选取两个大于xmin的大素数p,q,并输出p,q③从键盘输入明文字符串mStr,例如"I love you",或者"我爱你"都可以,计算出密文数据cStr,输出cStr④解密计算,根据密文数据cStr,计算出明文数据mStr。
RSA算法分析和实现
六、教师评语
签名:
日期:
成绩
这个定理说明a经过编码为b在经过解码为C时,a==c mod n(n=pq)
但我们在做编码解码时,限制0<= a < n, 0 <= c < n,
所以这就是说a等於c,所以这个过程确实能做到编码解码的功能。
四、实验结果与数据处理
五、总结
通过对RSA公钥密码体制进行了分析与研究,了解了怎样的密码体制才能充分发挥RSA的安全作用。分析了RSA加密解密的安全性,以及如何选取RSA密钥长度的问题。同时我们考虑到在实际的应用过程中,在满足安全性前提下应当降低计算的复杂度,提高信息加、解密的速度。便于降低成本,利于推广应用等因素,目前国内外对RSA算法实现的研究大多是在运算速度很高的计算机上,在硬件上也主要采用串行处理,为了提高速度,安全性就必然很差,相反,为提高安全强度,则运算处理速度又会降低。在RSA算法中,最基本的算法主要包括模加、模乘、模逆和模幂运算。大数运算很费时间,尤其是大整数的模逆和模幂运算。为了得到较快的加/解密速度,本程序进行了深层次的优化,主要采用移位的方法,大大提高了RSA算法实际应用的运算速度和执行效率。
《应用密码学》实验报告
实验序号:03实验项目名称:RSA密码技术
学 号
姓 名
专业、班
实验地点
指导教师
实验时间
一、实验目的及要求
实验目的:
1.深入理解RSA原理,特别是大数分解难题的原理
2.明确选择RSA的参数p、q、e、d的条件,以及明文分段的条件
3.掌握求逆元素和求高次幂的计算方法
(完整版)RSA算法实验报告

RSA算法的实现实验原理算法原理RSA公开密钥密码体制。
所谓的公开密钥密码体制就是使用不同的加密密钥与解密密钥,是一种“由已知加密密钥推导出解密密钥在计算上是不可行的”密码体制。
RSA算法是一种非对称密码算法,所谓非对称,就是指该算法需要一对密钥,使用其中一个加密,则需要用另一个才能解密。
RSA的算法涉及三个参数,n、e1、e2。
其中,n是两个大质数p、q的积,n的二进制表示时所占用的位数,就是所谓的密钥长度。
e1和e2是一对相关的值,e1可以任意取,但要求e1与(p-1)*(q-1)互质;再选择e2,要求(e2*e1)mod((p-1)*(q-1))=1。
(n,e1),(n,e2)就是密钥对。
其中(n,e1)为公钥,(n,e2)为私钥。
RSA加解密的算法完全相同,设A为明文,B为密文,则:A=B^e2 mod n;B=A^e1 mod n;(公钥加密体制中,一般用公钥加密,私钥解密)e1和e2可以互换使用,即:A=B^e1 mod n;B=A^e2 mod n;密钥生成首先要使用概率算法来验证随机产生的大的整数是否质数,这样的算法比较快而且可以消除掉大多数非质数。
假如有一个数通过了这个测试的话,那么要使用一个精确的测试来保证它的确是一个质数。
密钥分配和其它加密过程一样,对RSA来说分配公钥的过程是非常重要的。
分配公钥的过程必须能够抵挡一个从中取代的攻击。
假设Eve交给Bob一个公钥,并使Bob相信这是Alice的公钥,并且她可以截下Alice和Bob之间的信息传递,那么她可以将她自己的公钥传给Bob,Bob以为这是Alice的公钥。
步骤如下(这里设B为是实现着)(1)B寻找出两个大素数p和q。
(2)B计算出n=p*q和ϕ(n)=)(p-1)*(q-1)。
(3)B选择一个随机数e(0<e<ϕ(n)),满足(e,ϕ(n))=1 (即e与欧拉函数互素ϕ(n))。
(4)B使用欧几里得算法计算e的模余ϕ(n)的乘法逆元素d。
rsa算法实验报告

rsa算法实验报告RSA算法实验报告引言RSA算法是一种非对称加密算法,广泛应用于信息安全领域。
本实验旨在通过实际操作,深入了解RSA算法的原理和应用。
一、RSA算法原理RSA算法是基于大数因子分解的数论问题,其基本原理如下:1. 选择两个大素数p和q,并计算n=p*q。
2. 计算欧拉函数φ(n)=(p-1)*(q-1)。
3. 选择一个小于φ(n)且与φ(n)互质的整数e,作为公钥。
4. 计算e关于φ(n)的模反元素d,作为私钥。
5. 公钥为(n, e),私钥为(n, d)。
6. 加密过程:将明文m通过公钥进行加密,得到密文c=(m^e) mod n。
7. 解密过程:将密文c通过私钥进行解密,得到明文m=(c^d) mod n。
二、实验步骤1. 选择两个大素数p和q,并计算n=p*q。
2. 计算欧拉函数φ(n)=(p-1)*(q-1)。
3. 选择一个小于φ(n)且与φ(n)互质的整数e,作为公钥。
4. 计算e关于φ(n)的模反元素d,作为私钥。
5. 生成公钥(n, e)和私钥(n, d)。
6. 输入明文m。
7. 加密过程:计算密文c=(m^e) mod n。
8. 解密过程:计算明文m=(c^d) mod n。
9. 输出解密后的明文m。
三、实验结果本次实验选择了p=61,q=53作为素数,计算得到n=3233,φ(n)=3120。
选择e=17作为公钥,计算得到d=2753作为私钥。
输入明文m=1234,经过加密过程得到密文c=855。
再经过解密过程,得到解密后的明文m=1234。
四、实验分析通过本次实验,我们可以看到RSA算法具有较高的安全性和可靠性。
由于大素数因子分解问题的难解性,即使知道公钥(n, e)和密文c,也很难推导出私钥d 和明文m。
这使得RSA算法成为一种重要的加密算法。
然而,RSA算法的加解密过程涉及大数的运算,速度较慢,特别是对于较长的密钥长度。
因此,在实际应用中,需要权衡安全性和效率,选择合适的密钥长度。
(完整word版)RSA算法的实现实验报告

RSA算法的实现一、实验目的1. 熟悉公钥密码体制;2.掌握产生密钥对的程序设计方法;3.掌握产生加密/解密的程序设计方法。
二、实验内容和要求1.进行RSA加密/解密算法的设计;2.对RSA程序进行编译和调试;3.使用编写的程序进行加密和解密。
三、实验环境运行Windows操作系统的PC机,可以利用具有VC++语言环境;如果所运用的语言是JAVA,那么也可以利用JAVA语言环境来实现RSA算法的加密和解密。
四、实验步骤1.采用C++语言进行本次实验的编写,实验的代码如下:#include <stdio.h>#include<conio.h>int candp(int a,int b,int c){ int r=1;b=b+1;while(b!=1){r=r*a;r=r%c;b--;}printf("%d\n",r);return r;}void main(){int p,q,e,d,m,n,t,c,r;char s;printf("please input the p,q: ");scanf("%d%d",&p,&q);n=p*q;printf("the n is %3d\n",n);t=(p-1)*(q-1);printf("the t is %3d\n",t);printf("please input the e: ");scanf("%d",&e);if(e<1||e>t){printf("e is error,please input again: ");scanf("%d",&e);}d=1;while(((e*d)%t)!=1) d++;printf("then caculate out that the d is %d\n",d);printf("the cipher please input 1\n");printf("the plain please input 2\n");scanf("%d",&r);switch(r){case 1: printf("input the m: "); /*输入要加密的明文数字*/ scanf("%d",&m);c=candp(m,e,n);printf("the cipher is %d\n",c);break;case 2: printf("input the c: "); /*输入要解密的密文数字*/ scanf("%d",&c);m=candp(c,d,n);printf("the cipher is %d\n",m);break;}getch();}2、代码的思想:首先随意输入两个素数p和q,然后利用算法计算出p*q 即n,再算出(p-1)*(q-1)即t,并且同时输出计算的结果n和t,接下来输入e,经过算法可以计算出d,由此可以知道RSA算法的公钥和私钥;接下来可以有两个选择:一选择输入明文,有明文经过算法可以计算出密文;二输入密文,有密文经过算法可以计算出明文。
RSA的加解密C#实现
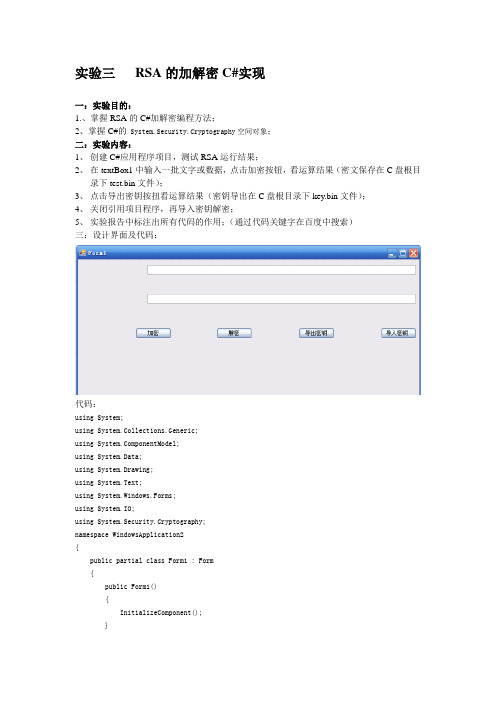
实验三RSA的加解密C#实现一:实验目的:1.、掌握RSA的C#加解密编程方法;2、掌握C#的 System.Security.Cryptography空间对象;二:实验内容:1、创建C#应用程序项目,测试RSA运行结果;2、在textBox1中输入一批文字或数据,点击加密按钮,看运算结果(密文保存在C盘根目录下test.bin文件);3、点击导出密钥按扭看运算结果(密钥导出在C盘根目录下key.bin文件);4、关闭引用项目程序,再导入密钥解密;5、实验报告中标注出所有代码的作用;(通过代码关键字在百度中搜索)三:设计界面及代码:代码:using System;using System.Collections.Generic;using ponentModel;using System.Data;using System.Drawing;using System.Text;using System.Windows.Forms;using System.IO;using System.Security.Cryptography;namespace WindowsApplication2{public partial class Form1 : Form{public Form1(){InitializeComponent();}private void textBox2_TextChanged(object sender, EventArgs e){}private void Form1_Load(object sender, EventArgs e){}RSACryptoServiceProvider crypt = new RSACryptoServiceProvider();private void button1_Click(object sender, EventArgs e){System.Text.UTF8Encoding enc = new System.Text.UTF8Encoding(); byte[] bytes = enc.GetBytes(textBox1.Text);bytes = crypt.Encrypt(bytes, false);FileStream fs = new FileStream("c:\\test.bin", FileMode.Create); fs.Write(bytes, 0, bytes.Length);fs.Flush();fs.Close();textBox2.Text = BitConverter.ToString(bytes);}private void button2_Click(object sender, EventArgs e){FileStream fs = new FileStream("c:\\test.bin", FileMode.Open); byte[] bytes = new byte[fs.Length];fs.Read(bytes, 0, bytes.Length);fs.Close();bytes = crypt.Decrypt(bytes, false);System.Text.UTF8Encoding enc = new System.Text.UTF8Encoding(); textBox2.Text = enc.GetString(bytes);}private void button3_Click(object sender, EventArgs e){string key = crypt.ToXmlString(true);FileStream fs = new FileStream("c:\\key.bin", FileMode.Create); System.Text.UTF8Encoding enc = new System.Text.UTF8Encoding(); byte[] bytes = enc.GetBytes(key);fs.Write(bytes, 0, bytes.Length);fs.Flush();fs.Close();}private void button4_Click(object sender, EventArgs e){FileStream fs = new FileStream("c:\\key.bin", FileMode.Open);System.Text.UTF8Encoding enc = new System.Text.UTF8Encoding(); byte[] bytes = new byte[fs.Length];fs.Read(bytes, 0, (int)fs.Length);string op = enc.GetString(bytes); crypt.FromXmlString(op);fs.Close();}}}四:运行结果为:。
rsa加密算法c语言编程实验的步骤和内容

rsa加密算法c语言编程实验的步骤和内容## 1. RSA加密算法简介RSA加密算法是一种非对称加密算法,由三位数学家Rivest、Shamir和Adleman于1977年提出,是目前最广泛使用的公钥加密算法之一。
RSA算法的安全性基于大数分解的困难性,即将一个大的合数分解成其质数因子的乘积。
## 2. RSA加密算法的基本原理RSA加密算法基于公钥和私钥的概念,其中公钥用于加密数据,私钥用于解密数据。
具体的加密和解密过程如下:### 2.1 密钥生成过程- 选择两个大素数p和q,计算其乘积n = p * q。
- 计算欧拉函数值φ(n) = (p-1) * (q-1)。
- 选择一个整数e,使得1 < e < φ(n)且e与φ(n)互质。
- 计算e对于φ(n)的模反元素d,即满足(e * d) mod φ(n) = 1。
- 公钥为(n, e),私钥为(n, d)。
### 2.2 加密过程- 将明文M转化为整数m,满足0 <= m < n。
- 加密后的密文C = m^e mod n。
### 2.3 解密过程- 将密文C转化为整数c,满足0 <= c < n。
- 解密后的明文M = c^d mod n。
## 3. RSA加密算法的C语言实现步骤为了实现RSA加密算法的C语言程序,我们需要按照以下步骤进行:### 3.1 定义必要的数据结构和函数我们需要定义一个结构体来存储公钥和私钥的信息,包括n、e和d。
同时,我们还需要定义一些函数来实现加密和解密的过程,包括计算模幂、计算最大公约数等。
### 3.2 生成密钥对根据密钥生成过程,我们需要实现一个函数来生成公钥和私钥。
在这个函数中,我们需要选择两个大素数p和q,并计算n、φ(n)、e 和d的值,并将其存储在定义的结构体中。
### 3.3 实现加密函数实现加密函数,输入明文M和公钥(n, e),输出密文C。
在这个函数中,我们需要将明文转化为整数m,并通过计算模幂的方法得到加密后的密文。
rsa算法c语言实现,(完整版)RSA算法C语言代码

rsa算法c语⾔实现,(完整版)RSA算法C语⾔代码《(完整版)RSA算法C语⾔代码》由会员分享,可在线阅读,更多相关《(完整版)RSA算法C语⾔代码(5页珍藏版)》请在⼈⼈⽂库⽹上搜索。
1、include #include #include #include #include char s100,*c; int n,e,d,i,C,j,k=0,len; int str100,b30; unsigned gcd(unsigned a, unsigned b ) if(a%b=0) return b; else return gcd(b,a%b); void Egcd(int a, int b,int y=0; return ; if(ab) Egcd(a,b%a,x,y); x=(int) (b*y+1)/a; else Egcd(a%b,b,x,y); y=(int)(a*x-1)。
2、/b; void RSA() int p,q,N,Y; printf(请输⼊素数p和q:); scanf(%d %d, n=p*q; N=(p-1)*(q-1); 初始化随机数 产⽣随机整数e, e与N互质 /printf(n=%d N=%dn,n,N); srand( (unsigned)time( NULL ) );/ while(1) / e=rand()%N; / printf(e=%dn,e); if(e=0) continue;if(gcd(N,e)=1) break; /printf(e=%dn,e); Egcd(e,N,d,Y); / printf(d=%d Y=%dn,d,。
3、Y); printf( 公钥 PU=e=%d,n=%dn,e,n); printf( 私钥 PR=d=%d,n=%dn,d,n); void encrypt() /加密函数 len=strlen(s);/hgprintf(len=%dn,len); for(i=0;ilen;i+) /去掉 s100 中的空格 if(si122) bk=i; k+; for(j=i;jlen-1;j+) sj=sj+1; len-; slen=0; /结束符printf( 密⽂是: ); for(i=0;ilen;i+) C=1; /printf(shiji=%dn,si-97); for(int j=0;。
RSA算法和实现及实例

RSA算法和实现及实例一、RSA算法原理1.密钥生成首先,选择两个不相等的素数p和q,并计算它们的乘积n。
然后计算n的欧拉函数φ(n)=(p-1)(q-1)。
选择一个与φ(n)互质的数e,这个数即为公钥e。
然后选择一个数d,使得(d * e)mod φ(n) = 1,即d是e的模φ(n)的乘法逆元,d即为私钥。
2.加密解密加密时,将明文M进行加密,得到密文C = M^e mod n。
解密时,用私钥d对密文C进行解密,得到明文M = C^d mod n。
二、RSA算法实现实现RSA算法需要以下几个步骤:1.选择两个大素数p和q,计算乘积n=p*q。
2.计算n的欧拉函数φ(n)=(p-1)(q-1)。
3.选择一个与φ(n)互质的正整数e,计算其模φ(n)的乘法逆元d。
4.所得到的公钥为(e,n),私钥为(d,n)。
5. 加密时,将明文M通过公钥加密得到密文C = M^e mod n。
6. 解密时,用私钥对密文C进行解密得到明文M = C^d mod n。
三、RSA算法实例假设选择的两个素数p=13,q=17,计算乘积n=p*q=221计算n的欧拉函数φ(n)=(p-1)(q-1)=12*16=192选择一个与φ(n)互质的正整数e=5计算e的模φ(n)的乘法逆元d=77所以所得到的公钥为(e,n)=(5,221),私钥为(d,n)=(77,221)。
加密时,假设明文M = 8,利用公钥进行加密:C = M^e mod n =8^5 mod 221 = 40。
解密时,利用私钥进行解密:M = C^d mod n = 40^77 mod 221 = 8所以加密后的密文为40,解密后恢复得到原始明文为8总结:本文详细介绍了RSA算法的原理、实现方法以及一个实例。
RSA算法是一种非对称加密算法,通过选择两个大素数和计算乘积、欧拉函数、乘法逆元等步骤,实现了安全可靠的加密和解密过程。
通过加密后的密文可以通过相应的私钥解密得到原始明文,确保数据的安全性。
rsa算法加解密代码的编写

rsa算法加解密代码的编写一、引言RSA算法是一种非对称加密算法,广泛应用于数据加密和数字签名等领域。
本文将介绍如何使用Python语言编写RSA算法的加解密代码,包括密钥生成、加密和解密操作。
二、算法原理RSA算法基于大数分解的困难性,通过使用公钥和私钥来实现加密和解密操作。
公钥用于加密数据,私钥用于解密数据。
在加密和解密过程中,使用了模幂运算和异或运算等基本运算。
三、代码实现以下是一个简单的RSA算法加解密代码示例,使用Python语言实现:```pythonimportrandom#生成RSA密钥对defgenerate_keypair(bits):#生成公钥和私钥public_key=e=65537#常用的公钥指数,需要是质数private_key=d=random.randrange(bits)#返回公钥和私钥returnpublic_key,private_key#加密函数defencrypt(data,public_key):#将数据转换为二进制字符串bin_data=str(data).encode('hex')#计算加密结果encrypted=pow(bin_data,public_key,10**n)%10**mreturnencrypted.hex()#解密函数defdecrypt(encrypted_data,private_key):#将加密结果转换为二进制字符串bin_encrypted=encrypted_data.decode('hex')#计算解密结果decrypted=pow(bin_encrypted,d,10**n)%10**mreturnint(decrypted)```代码说明:*`generate_keypair`函数用于生成RSA密钥对,其中`bits`参数指定密钥长度,常见的有1024位和2048位。
*`encrypt`函数用于对数据进行加密,其中`data`是要加密的数据,`public_key`是公钥。
rsa数字签名算法代码

rsa数字签名算法代码下面是使用Python编写的RSA数字签名算法的代码示例:```pythonimport hashlibimport rsa# 生成RSA密钥对(公钥和私钥)public_key, private_key = rsa.newkeys(1024)# 要签名的数据data = b"Hello, World!"# 使用SHA-256对数据进行哈希hash = hashlib.sha256(data).digest()# 使用私钥对哈希值进行签名signature = rsa.sign(hash, private_key, "SHA-256")# 使用公钥验证签名is_valid = rsa.verify(hash, signature, public_key)print("Signature valid: ", is_valid)```请确保你已经安装了python-rsa库,可以使用以下命令进行安装:```pip install rsa```以上代码中,首先使用rsa.newkeys(1024)生成了1024位的RSA密钥对,其中公钥保存在public_key变量中,私钥保存在private_key变量中。
然后,定义了要签名的数据data,并使用hashlib.sha256对其进行哈希运算,得到哈希值hash。
接下来,使用私钥private_key对哈希值进行签名,生成了数字签名signature。
最后,使用公钥public_key对哈希值和签名进行验证,并将验证结果保存在is_valid变量中,输出验证结果。
请注意,这只是RSA数字签名算法的简单示例。
在实际应用中,你还需要使用安全的哈希算法,例如SHA-256,生成哈希值,并考虑到安全性和性能方面的因素进行相应的优化。
RSA算法实验代码

RSA算法实验代码#include<stdio.h>#define MAX_NUM 63001#define MAX_PRIME 251//! 返回代码#define OK 100#define ERROR_NOEACHPRIME 101#define ERROR_NOPUBLICKEY 102#define ERROR_GENERROR 103unsigned int MakePrivatedKeye( unsigned int uiP, unsigned int uiQ );unsigned int GetPrivateKeye( unsigned int iWhich );unsigned int MakePairkey( unsigned int uiP, unsigned int uiQ, unsigned int uiD ); unsigned int GetPairKey( unsigned int &d, unsigned int &e );int rsa_encrypt( int n, int e, int mw,int p,int q);int rsa_decrypt( int n, int d, int cw, int p,int q);void outputkey();//!保存私钥d集合struct pKeyset{unsigned int set[ MAX_NUM ];unsigned int size;}pset;//! 保存公、私钥对struct pPairkey{unsigned int d;unsigned int e;unsigned int n;}pairkey;// 名称:isPrime// 功能:判断两个数是否互质// 参数:m: 数a; n: 数b// 返回:m、n互质返回true; 否则返回falsebool isPrime( unsigned int m, unsigned int n ){unsigned int i=0;bool Flag = true;if( m<2 || n<2 )return false;unsigned int tem = ( m > n ) ? n : m;for( i=2; i<=tem && Flag; i++ ){bool mFlag = true;bool nFlag = true;if( m % i == 0 )mFlag = false;if( n % i == 0 )nFlag = false;if( !mFlag && !nFlag )Flag = false;}if( Flag )return true;elsereturn false;}// 名称:MakePrivatedKeye// 功能:由素数P、Q生成公钥e// 参数:uiP: 素数P; uiQ: 素数Q// 返回:私钥dunsigned int MakePrivatedKeye( unsigned int uiP, unsigned int uiQ ) {unsigned int i=0;//! 得到所有与z互质的数( 私钥d的集合 )unsigned int z = ( uiP -1 ) * ( uiQ -1 );pset.size = 0;for( i=0; i<z; i++ ){if( isPrime( i, z ) ){pset.set[ pset.size++ ] = i;}}return pset.size;}// 名称:MakePairKey// 功能:生成RSA公、私钥对// 参数:uiP: 素数P; uiQ: 素数Q; uiD: 私钥d// 返回:错误代码unsigned int MakePairkey( unsigned int uiP, unsigned int uiQ, unsigned int uiD ) {bool bFlag = true;unsigned int i = 0, d;unsigned int z = ( uiP-1 ) * ( uiQ-1 );unsigned int e = pset.set[uiD];if( !isPrime( z, e ) )return ERROR_NOEACHPRIME;for( i=2; i<z; i++ ){if( (i*e)%z == 1 ){d = i;bFlag = false;}}if( bFlag )return ERROR_NOPUBLICKEY;if( (d*e)%z != 1 )ERROR_GENERROR;pairkey.d = d;pairkey.e = e;pairkey.n = uiP * uiQ;return OK;}// 名称:GetPairKey// 功能:对外提供接口,获得公、私钥对// 参数:uiP: 素数P; uiQ: 素数Q; uiD: 私钥d// 返回:unsigned int GetPairKey( unsigned int &d, unsigned int &e ) {d = pairkey.d;e = pairkey.e;return pairkey.n;}// 名称:GetPrivateKeye// 功能:对外提供接口,由用户选择ID得以私钥d// 参数:iWhich: 用户选择公钥e的ID// 返回:私钥d值unsigned int GetPrivateKeye( unsigned int iWhich ){if( pset.size >= iWhich )return pset.set[ iWhich ];elsereturn 0;}// 名称:rsa_encrypt// 功能:RSA加密运算// 参数:d: 公钥n; e: 私钥e; mw: 加密明文; cw: 密文输出// 返回:无int rsa_encrypt( int d, int e,int mw, int p,int q){int i, j=0,cw;int temInt ;temInt = mw;i=p*q;/**/for( j=1; j<e; j++ )temInt = temInt * mw ;temInt = temInt % i;cw= temInt;return cw;}// 名称:rsa_decrypt// 功能:RSA解密运算// 参数:d: 公钥n; d: 私钥d; cw: 密文; cLength: 密文长度; mw: 明文输出// 返回:无int rsa_decrypt( int d, int e, int cw, int p,int q ){int i, j=-1,mw;int temInt = 0;i=p*q;mw= 0;temInt = cw;//printf("temInt %d\n",temInt);//printf("d %d;e %d\n; mW %d;p %d;q %d",d,e,cw,p,q);if( d != 0 ){for( j=1; j<d; j++ )temInt = temInt * cw ;//printf("temInt1 %d\n",temInt);temInt=temInt% i;//printf("temInt2 %d\n",temInt);mw = temInt;//printf("mw %d\n",mw);return mw;}void outputkey(){printf("PublicKey(e,n): (%d,%d)\n",pairkey.e,pairkey.n);printf("PrivateKey(d,n): (%d,%d)\n",pairkey.d,pairkey.n);}//! 程序主函数int main( ){int mingwen ,miwen=0,miwen1,mw;unsigned int p , q , d , n , e;//two prime p & q, public key(n, e) , private key(n , d) printf("输入p:");scanf("%d",&p);printf("输入q:");scanf("%d",&q);while(isPrime(p,q)!=1){printf("输入的数不是质数,请重新输入\n");printf("p:");scanf("%d",&p);printf("q:");scanf("%d",&q);}n=MakePrivatedKeye(p, q);printf("产生的私钥的长度为%d\n",n);printf("输入小于私钥长度的数:\n");scanf("%d",&d);MakePairkey(p, q, d );outputkey();printf("请输入明文:\n");scanf("%d",&mingwen);miwen=rsa_encrypt( pairkey.d , pairkey.e,mingwen,p,q);printf("加密后的密文为:\n");printf("%d\n",miwen);printf("请输入密文:\n");scanf("%d",&miwen1);mw=rsa_decrypt( pairkey.d , pairkey.e,miwen1,p,q); printf("解密后的明文为:\n");printf("%d\n",mw);return 0;}。
实验三RSA算法代码的实现

//选取两个素数p=563,q=823 double n=0,fn=0,p=563,q=823,d=0; n=p*q;fn=(q-1)*(p-1);
for(double e=2;e<fn;e+=3) {
if(Euclid(e,fn)==1) break;
} //选e使得与fn的最大公因数为1 d=extenEuclid(e,fn);//求d=e^-1 mod fn
for(int k=0,n=0;k<2*strlen(cypher);k+=4) {
c[n]=m[k]*1000+m[k+1]*100+m[k+2]*10+m[k+3];//两个字母 一组,例如AB为0102
n++; } for(;c[n-1]<1000;)//最后一个数填充零,不过此例可要可不要
transfer(cypher,c);//明文字母变数字的过程,输出结果将I LOVE......变 为090012152205....
for(int k1=0;c[k1]!='\0';k1++) cout<<c[k1]<<" ";//将4位数字整理成有效的十进制数并再次输
实验3 非对称密码算法RSA

实验3 非对称密码算法RSA一、实验目的通过实际编程了解非对称密码算法RSA的加密和解密过程,加深对非对称密码算法的认识。
二、实验原理对称密码算法要求通信双方通过交换密钥实现使用同一个密钥,这在密钥的管理、发布和安全性方面存在很多问题,而非对称密码算法解决了这个问题。
加密密钥和解密密钥是不同的,其中加密密钥是可以公开的,解密密钥是要求保密的,并且不能用其中的一个推导出另一个。
它的安全性是建立在“大数分解和素性检测”这个数论难题的基础上,即将两个大素数相乘在计算上容易实现,而将该乘积分解为两个大素数因子的计算量相当大。
虽然它的安全性还未能得到理论证明,但经过30年的密码分析和攻击,迄今仍然被实践证明是安全的。
三、实验环境运行Windows或者Linux操作系统的PC机,具有gcc(Linux)、VC(Windows)等C语言编译环境。
四、实验内容和步骤1、为了加深对RSA算法的了解,根据已知参数:2qp,手工=M=11,3=,计算公私钥,并对明文进行加密,然后对密文进行解密。
2、编写RSA程序,实现对数字和字符进行加密,了解RSA算法原理。
其中p、q不要求为大素数,实现基本功能流程即可。
参考:/*扩展欧几里德算法例如,求5关于模14的乘法逆元:14=5*2+45=4+1说明5与14互素,存在5关于14的乘法逆元。
1=5-4=5-(14-5*2)=5*3-14因此,5关于模14的乘法逆元为3。
Extended Euclid (d,f) //算法求d关于模f的乘法逆元d-1 ,即d* d-1 modf = 11 。
(X1,X2,X3) := (1,0,f);(Y1,Y2,Y3) := (0,1,d)2。
if (Y3=0) then return d-1 = null //无逆元3。
if (Y3=1) then return d-1 = Y2 //Y2为逆元4。
Q := X3 div Y3 //整除5。
RSA算法python实现

RSA算法python实现RSA算法是⼀种⾮对称加密算法,是现在⼴泛使⽤的公钥加密算法,主要应⽤是加密信息和数字签名。
详情请看维基:算法基本思路:1.公钥与私钥的⽣成:(1)随机挑选两个⼤质数 p 和 q,构造N = p*q;(2)计算欧拉函数φ(N) = (p-1) * (q-1);(3)随机挑选e,使得gcd(e, φ(N)) = 1,即 e 与φ(N) 互素;(4)计算d,使得 e*d ≡ 1 (mod φ(N)),即d 是e 的乘法逆元。
此时,公钥为(e, N),私钥为(d, N),公钥公开,私钥⾃⼰保管。
2.加密信息:(1)待加密信息(明⽂)为 M,M < N;(因为要做模运算,若M⼤于N,则后⾯的运算不会成⽴,因此当信息⽐N要⼤时,应该分块加密)(2)密⽂C = M e mod N(3)解密C d mod N = (M e)d mod N = M d*e mod N ;要理解为什么能解密?要⽤到欧拉定理(其实是费马⼩定理的推⼴)aφ(n)≡ 1 (mod n),再推⼴:aφ(n)*k≡ 1 (mod n),得:aφ(n)*k+1≡ a (mod n)注意到 e*d ≡ 1 mod φ(N),即:e*d = 1 + k*φ(N)。
因此,M d*e mod N = M1 + k*φ(N) mod N = M简单来说,别⼈⽤我的公钥加密信息发给我,然后我⽤私钥解密。
3.数字签名:(1)密⽂C = M d mod N(2)解密M = C e mod N = (M d)e mod N = M d*e mod N = M ;(原理同上)简单来说,我⽤⾃⼰的密钥加密签名,别⼈⽤我的公钥解密可以看到这是我的签名。
注意,这个不具有隐私性,即任何⼈都可以解密此签名。
算法的安全性:基于⼤整数N难以分解出p和q,构造φ(N);或由N直接构造φ(N)同样难。
算法的实现:1.快速幂取模;2.素性测试;3.扩展欧⼏⾥得求乘法逆元和最⼤公约数;实现代码:import randomdef fastExpMod(b, e, m):"""e = e0*(2^0) + e1*(2^1) + e2*(2^2) + ... + en * (2^n)b^e = b^(e0*(2^0) + e1*(2^1) + e2*(2^2) + ... + en * (2^n))= b^(e0*(2^0)) * b^(e1*(2^1)) * b^(e2*(2^2)) * ... * b^(en*(2^n))b^e mod m = ((b^(e0*(2^0)) mod m) * (b^(e1*(2^1)) mod m) * (b^(e2*(2^2)) mod m) * ... * (b^(en*(2^n)) mod m) mod m"""result = 1while e != 0:if (e&1) == 1:# ei = 1, then mulresult = (result * b) % me >>= 1# b, b^2, b^4, b^8, ... , b^(2^n)b = (b*b) % mreturn resultdef primeTest(n):q = n - 1k = 0#Find k, q, satisfied 2^k * q = n - 1while q % 2 == 0:k += 1;q /= 2a = random.randint(2, n-2);#If a^q mod n= 1, n maybe is a prime numberif fastExpMod(a, q, n) == 1:return"inconclusive"#If there exists j satisfy a ^ ((2 ^ j) * q) mod n == n-1, n maybe is a prime number for j in range(0, k):if fastExpMod(a, (2**j)*q, n) == n - 1:return"inconclusive"#a is not a prime numberreturn"composite"def findPrime(halfkeyLength):while True:#Select a random number nn = random.randint(0, 1<<halfkeyLength)if n % 2 != 0:found = True#If n satisfy primeTest 10 times, then n should be a prime numberfor i in range(0, 10):if primeTest(n) == "composite":found = Falsebreakif found:return ndef extendedGCD(a, b):#a*xi + b*yi = riif b == 0:return (1, 0, a)#a*x1 + b*y1 = ax1 = 1y1 = 0#a*x2 + b*y2 = bx2 = 0y2 = 1while b != 0:q = a / b#ri = r(i-2) % r(i-1)r = a % ba = bb = r#xi = x(i-2) - q*x(i-1)x = x1 - q*x2x1 = x2x2 = x#yi = y(i-2) - q*y(i-1)y = y1 - q*y2y1 = y2y2 = yreturn(x1, y1, a)def selectE(fn, halfkeyLength):while True:#e and fn are relatively primee = random.randint(0, 1<<halfkeyLength)(x, y, r) = extendedGCD(e, fn)if r == 1:return edef computeD(fn, e):(x, y, r) = extendedGCD(fn, e)#y maybe < 0, so convert itif y < 0:return fn + yreturn ydef keyGeneration(keyLength):#generate public key and private keyp = findPrime(keyLength/2)q = findPrime(keyLength/2)n = p * qfn = (p-1) * (q-1)e = selectE(fn, keyLength/2)d = computeD(fn, e)return (n, e, d)def encryption(M, e, n):#RSA C = M^e mod nreturn fastExpMod(M, e, n)def decryption(C, d, n):#RSA M = C^d mod nreturn fastExpMod(C, d, n)#Unit Testing(n, e, d) = keyGeneration(1024)#AES keyLength = 256X = random.randint(0, 1<<256)C = encryption(X, e, n)M = decryption(C, d, n) print"PlainText:", X print"Encryption of plainText:", C print"Decryption of cipherText:", M print"The algorithm is correct:", X == M Python。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验三 RSA 算法代码实现
代码实现结果:
四、实验要求 1、在RSA算法中,求解私钥d可以采用扩展欧几里得算法和线性代入 法两种方法,但这两种方法的计算效率很低(即计算d要花费很多时间, 特别是数次乘积运算占用了大量计算时间,使得RSA时间复杂度增加) ,请你通过网络或自己设计一种及一种以上更为高效的求解d的方法, 并写出详细计算过程。 2、用VC调试实验步骤给出的RSA加解密程序,结合原理分析程序中 密钥是如何产生的?如何加密的?如何解密的?并在程序中给于解 释。 3、你还能采用别的方法自主设计RSA公钥密码算法吗?如果能请列
for(int i=b.size()-1;i>=0;i--) {
c*=2; d=(d*d)-int((d*d)/n)*n; if(b[i]==1) {
c+=1; d=(d*a)-int((d*a)/n)*n; } } return d; }
void transfer(char cypher[],double c[])//字母变数字的过程 {
transfer(cypher,c);//明文字母变数字的过程,输出结果将I LOVE......变 为090012152205....
for(int k1=0;c[k1]!='\0';k1++) cout<<c[k1]<<" ";//将4位数字整理成有效的十进制数并再次输
出,目的在于后面加密计算,例如“I ”的数字0900整理后为900,“LO” 的数字1215整理后为1215“ L”0020整理为20
c[n-1]*=10; }
void main() {
double c[100]={0};//存放密文 double a[100]={0};//存放加解密中间变量 double b[100]={0};//存放明文 char cypher[]="I LOVE THE PEOPLE'S REPUBLIC OF CHINA";// 明文字符 //对“我爱中华人民共和国”加解密
using namespace std;
int Euclid(int a, int n)//n>a,求n和a的最大公因数为1 {
int x,y,r;
x=n;y=a; for (int i=0;;) {
if(y==0) return x;//a=0
if(y==1) return y;//a=1
r=x%y;//a≠0,1,r=n%a x=y; y=r; } }
cout<<b[j]<<" "; } cout<<endl;
}
cout<<endl<<"密码和密钥 e d and n:"; cout<<e<<" "<<d<<" "<<n<<endl; //加密过程
cout<<endl<<"加密:"; for(int i=0;c[i]!='\0';i++) {
a[i]=quickindex1(c[i],e,n);//实现c=E(m)=m^e mod n的运算,例如 第一个加密为900^5 mod 563*823=389807
//选取两个素数p=563,q=823 double n=0,fn=0,p=563,q=823,d=0; n=p*q;fn=(q-1)*(p-1);
for(double e=2;e<fn;e+=3) {
if(Euclid(e,fn)==1) break;
} //选e使得与fn的最大公因数为1 d=extenEuclid(e,fn);//求d=e^-1 mod fn
double extenEuclid(double a,double n)//利用扩展的Euclid计算a^-1 mod n 的乘法逆元 {
double x1=1,x2=0,x3=n,y1=0,y2=1,y3=a,Q; double t1,t2,t3; for(int i=0;;) {
if(y3==0) {
else b.push_back(0);
j*=2; }//将n-1表示成二进制形式 for(int k=0;k<b.size();k++)
cout<<b[k]; cout<<endl;
int d=1,x=0; for(int ii=b.size()-1;ii>=0;ii--) {
x=d; d=(d*d)%n; if(d==1&&x!=1&&x!=n-1)
bool Rabin(int a,int n)//Miler-Rabin素性测试算法对一个给定的大数进 行测试 {
vector<int> b;//判断一个变量b是否是素数 unsigned int N=n-1; for(int i=0,j=1;;i++) {
if(j>N) break;
if((N>>i)&(unsigned int)1) b.push_back(1);
int m[100]={0};
for(int i=0,j=0;cypher[j]!='\0';i+=2) {
if(cypher[j]==' ') {
m[i]=0;m[i+1]=0; }//空格变为00 else {
m[i]=cypher[j]-64;//A的ASCII码为65,65-64=1 if(m[i]<10) {
vector<int> b; unsigned double N=m;//公钥m=e for(int ii=0,j=1;;ii++) {
if(j>N) break;
if((N>>ii)&(unsigned double)1) b.push_back(1);
else b.push_back(0);
j*=2; }//将m表示成二进制形式 double c=0,d=1;
cout<<a[i]<<" ";//输出密文信息 }
cout<<endl<<"解密:";
/\0';j++) {
b[j]=quickindex1(a[j],d,n);//实现m=D(c)= c^d mod n,例如第一 个解密为389807^92393 mod 563*823=900
return x3; cout<<"no reverse"<<endl;//a=0,无乘法逆元 } if(y3==1) return y2;//a=1,a%n=1 Q=int(x3/y3);//Q=[n/a] t1=x1-Q*y1;//t1=x1=1 t2=x2-Q*y2;//t2=Q t3=x3-Q*y3;//t3=n-Qa,相当于d原理中的1=de-xfn x1=y1;x2=y2;x3=y3; y1=t1;y2=t2;y3=t3;//返回d的结果 } }
出相关代码。 【参考答案】 1. 在RSA算法中,求解私钥d可以采用以下方法:
① 扩展欧几里得算法(模幂乘法运算) ① 线性代入法(模幂乘法运算) ① 平方-乘法:按平方计算模指数运算 ① 一种二进制查表方幂模快速计算方法:该方法根据指数二
进制形式结构进行分组计算,记忆典型操作数,通过查表法 大量减少了乘法次数。 ① 采用分解计算和内联汇编方法加速RSA算法的执行 ① 设计规划密钥空间 2. 【代码分析】 #include<iostream> #include<vector> #include<string>
for(int k=0,n=0;k<2*strlen(cypher);k+=4) {
c[n]=m[k]*1000+m[k+1]*100+m[k+2]*10+m[k+3];//两个字母 一组,例如AB为0102
n++; } for(;c[n-1]<1000;)//最后一个数填充零,不过此例可要可不要
return false; if(b[ii]==1)
d=(d*a)%n; }//b为素数
if(d!=1) return false;//不为素数
return true; }
double quickindex1(double a,double m, double n)//实现a^m mod n 的运 算 {
