参考解答-2009-2010第一学期并行程序设计期末考试卷
【中国海洋大学】2009并行算法与编程期末考试并行B卷

海洋地球科学学院《并行算法与编程》课程试题(B卷) 共3页第1页共3 页第2 页四、请写出下列程序的执行结果(假设共启动了2个进程)(15分)#include<stdio.h>#include<math.h>#include<mpi.h>#include <stdlib.h>void main(int argc,char *argv[]){int myid, n, m, i, count, ext, bufsize;const int N=128;double outbuf[N], inbuf[N], *buf;MPI_Status stat;MPI_Init(&argc,&argv);MPI_Comm_rank(MPI_COMM_WORLD,&myid);MPI_Pack_size(N,MPI_DOUBLE,MPI_COMM_WORLD,&ext);printf("ext=%d overhead=%d\n",ext,MPI_BSEND_OVERHEAD);bufsize=ext+MPI_BSEND_OVERHEAD;buf=(double *)malloc(bufsize);printf("buffersize=%d\n",bufsize);MPI_Buffer_attach(buf,bufsize);for (m=1; m<8; m++){n=(int) pow(2,m);if (myid == 0){for(i=0; i<N; i++)outbuf[i]=0;MPI_Bsend(outbuf,n,MPI_DOUBLE,1,0,MPI_COMM_WORLD);MPI_Recv(inbuf,n,MPI_DOUBLE,1,1,MPI_COMM_WORLD,&stat);MPI_Get_count(&stat,MPI_DOUBLE,&count);printf("Porcessor 0 received %d numbers\n",count);}else {for(i=0; i<N; i++)outbuf[i]=1;MPI_Bsend(outbuf,n,MPI_DOUBLE,0,1,MPI_COMM_WORLD);MPI_Recv(inbuf,n,MPI_DOUBLE,0,0,MPI_COMM_WORLD,&stat);MPI_Get_count(&stat,MPI_DOUBLE,&count);printf("Porcessor 1 received %d numbers\n",count);}}MPI_Buffer_detach(buf,&bufsize);free(buf);MPI_Finalize();}五、请说明下列MPI函数能够实现什么功能(每小题3分,共24分)1、MPI_WAITSOME2、MPI_GET_VERSION3、MPI_RECV4、MPI_COMM_SIZE5、MPI_GET_COUNT6、MPI_IPROBE7、MPI_SSEND_INIT 8、MPI_START六、编程题(26分)编写一个完整的MPI并行程序,求 值。
2009-2010软工期末试题_a卷_附答案
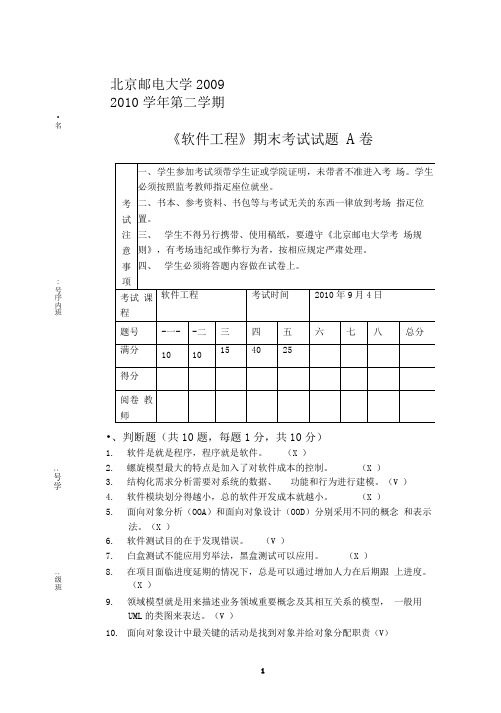
北京邮电大学2009 2010学年第二学期•、判断题(共10题,每题1分,共10分)1. 软件是就是程序,程序就是软件。
(X )2. 螺旋模型最大的特点是加入了对软件成本的控制。
(X )3. 结构化需求分析需要对系统的数据、 功能和行为进行建模。
(V )4. 软件模块划分得越小,总的软件开发成本就越小。
(X )5. 面向对象分析(OOA )和面向对象设计(OOD )分别采用不同的概念 和表示法。
(X )6. 软件测试目的在于发现错误。
(V )7. 白盒测试不能应用穷举法,黑盒测试可以应用。
(X )8. 在项目面临进度延期的情况下,总是可以通过增加人力在后期跟 上进度。
(X ) 9. 领域模型就是用来描述业务领域重要概念及其相互关系的模型, 一般用UML 的类图来表达。
(V )10. 面向对象设计中最关键的活动是找到对象并给对象分配职责(V )•名姓《软件工程》期末考试试题 A 卷:号序内班:号学:级班A. 改正性维护 C. 完善性维护B. 适应性维护 D. 预防性维护、单项选择题(共 10 题,每题 1 分,共 10 分)1、下面关于软件生命周期模型的描述正确的是( C )A •软件生命周期是指从软件需求分析到上线运行的全过程B •原型方法只能用于软件的需求分析阶段C. 按照瀑布模型开发系统时,必须完成需求分析才能开始系统设计D. 增量模型又叫做迭代模型2、 下面哪一个不是数据词典的构成之一( C )。
A. 数据流词条描述B. 数据文件词条描述C. 数据流层次词条描述D. 加工逻辑词条描述3、 为了提高模块的独立性,模块最好是(B )A. 逻辑内聚B. 功能内聚C. 过程内聚D. 信息内聚4、OOA 所要完成的工作不包括(D )A.建立用例模型B.建立领域模型C.建立操作契约D.定义完善的类的属性和操作 位的标准建模语言。
6、 结构化程序设计采用的三种基本控制结构是( D ) A. 顺序、分支、选择 B. 选择、循环、重复 C. 输入、变换、输出 D. 顺序、选择、重复 7、 下面哪一个不属于 UML 中的图( D )。
2009-2010年计算机统考考研真题解析os

2009-2010年计算机统考考研真题解析os2009年计算机统考真题解析(含答案)一、单项选择题,每小题 2 分,共 80 分。
23.单处理机系统中,可并行的是I 进程与进程 II 处理机与设备 III 处理机与通道 IV 设备与设备A.I、II 和 III B. I、II 和 IV C. I、III 和 IV D. II、III 和 IV24.下列进程调度算法中,综合考虑进程等待时间和执行时间的是A.时间片轮转调度算法B.短进程优先调度算法C.先来先服务调度算法 D.高响应比优先调度算法25.某计算机系统中有 8 台打印机,有 K 个进程竞争使用,每个进程最多需要 3 台打印机。
该系统可能会发生死锁的 K 的最小值是A.2 B.3 C.4 D.526.分区分配内存管理方式的主要保护措施是A.界地址保护 B.程序代码保护 C.数据保护 D.栈保护27.一个分段存储管理系统中,地址长度为32 位,其中段号占8 位,则最大段长是A.28 字节 B.216 字节 C.224 字节 D.232 字节28.下列文件物理结构中,适合随机访问且易于文件扩展的是A.连续结构B.索引结构C.链式结构且磁盘块定长D.链式结构且磁盘块变长29.假设磁头当前位于第 105 道,正在向磁道序号增加的方向移动。
现有一个磁道访问请求序列为 35,4 5,12,68,110,180,170,195,采用 SCAN 调度(电梯调度)算法得到的磁道访问序列是A.110,170,180,195,68,45,35,12B.110,68,45,35,12,170,180,195C.110,170,180,195,12,35,45,68D.12,35,45,68,110,170,180,19530.文件系统中,文件访问控制信息存储的合理位置是A.文件控制块 B.文件分配表 C.用户口令表 D.系统注册表31.设文件F1 的当前引用计数值为1,先建立F1 的符号链接(软链接)文件F2,再建立F1 的硬链接文件F3,然后删除F1。
2009-2010学年北京市丰台区九年级(上)期末数学试卷

2009-2010学年北京市丰台区九年级(上)期末数学试卷一、选择题(共8小题,每小题4分,满分32分)1.(4分)若=,则的值是( )A.B.C.﹣D.2.(4分)一个不透明的布袋里装有3个红球、2个白球,每个球除颜色外其它均相同,搅拌均匀后从中任意摸出一个球,则摸出的球是红球的概率是( )A.B.C.D.3.(4分)在Rt△ABC中,∠C=90°,AB=4,BC=1,则cosA的值是( )A.B.C.D.44.(4分)将抛物线y=2x2向下平移1个单位,得到的抛物线是( )A.y=2(x+1)2B.y=2(x﹣1)2C.y=2x2+1D.y=2x2﹣1 5.(4分)已知△ABC∽△DEF,相似比为3:1,且△ABC的周长为18,则△DEF的周长为( )A.2B.3C.6D.546.(4分)若反比例函数y=的图象在其每个象限内,y随x的增大而减小,则k的值可以为( )A.﹣1B.3C.0D.﹣37.(4分)如图,AB是⊙O的弦,OD⊥AB于D交⊙O于E,则下列说法错误的是( )A.AD=BD B.∠ACB=∠AOE C.D.OD=DE8.(4分)如图,A,B,C,D为⊙O的四等分点,动点P从圆心O出发,沿O﹣C﹣D﹣O路线作匀速运动,设运动时间为t(s).∠APB=y(°),则下列图象中表示y与t之间函数关系最恰当的是( )A.B.C.D.二、填空题(共4小题,每小题4分,满分16分)9.(4分)如果反比例函数的图象过点(2,﹣3),那么k= .10.(4分)若扇形的半径为6cm,圆心角的度数为90°,则扇形的面积为 cm2.11.(4分)如图,D,E两点分别在△ABC的边AB,AC上,DE,BC不平行,若使△ADE∽△ABC,需要添加的条件是 (写出一个即可).12.(4分)如图所示,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠AED的正切值等于 .三、解答题(共13小题,满分72分)13.(5分)计算:tan45°﹣2cos30°+sin60°14.(5分)已知:二次函数的表达式为y=﹣4x2+8x(1)写出这个函数图象的对称轴和顶点坐标;(2)求图象与x轴的交点坐标;(3)若点A(﹣1,y1)、B(,y2)都在该函数图象上,试比较y1与y2的大小.15.(4分)已知:如图,在△ABC中,DE∥BC,EF∥AB,试判断成立吗?并说明理由.16.(5分)已知:如图,在⊙O中,弦MN=16,半径OA⊥MN,垂足为点B,AB=4,求⊙O半径的长.17.(5分)已知:如图,在平面直角坐标系xOy中,直线AB分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,tan∠ABO=,OB=4,OE=2.(1)求该反比例函数的解析式;(2)求直线AB的解析式.18.(5分)在学校田径运动会4×100米接力比赛时,用抽签的方法安排跑道,九年级(1)、(2)、(3)三个班恰好分在一组,求九年级(1)、(2)班恰好依次排在第一、第二道的概率.19.(5分)2008年初,我国南方部分省区发生了雪灾,造成通讯受阴.如图,现有某处山坡上一座发射塔被冰雪从C处压折,塔尖恰好落在坡面上的点B 处,在B处测得点C的仰角为38°,塔基A的俯角为21°,又测得斜坡上点A到点B的坡面距离AB为15米,求折断前发射塔的高.(精确到0.1米)20.(5分)如图,已知抛物线C1:y=a(x+2)2﹣5的顶点为P,与x轴相交于A、B两点(点A在点B的左侧),点B的横坐标是1;(1)求a的值;(2)如图,抛物线C2与抛物线C1关于x轴对称,将抛物线C2向右平移,平移后的抛物线记为C3,抛物线C3的顶点为M,当点P、M关于点O成中心对称时,求抛物线C3的解析式.21.(6分)已知:如图,等腰△ABC中,AB=BC,AE⊥BC于点E,EF⊥AB于点F,若CE=1,,求EF的长.22.(5分)某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y 与x之间的函数表达式;(不要求写自变量的取值范围)(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?23.(7分)如图,已知:在⊙O中,直径AB=4,点E是OA上任意一点,过E 作弦CD⊥AB,点F是上一点,连接AF交CE于H,连接AC、CF、BD、OD.(1)求证:△ACH∽△AFC;(2)猜想:AH•AF与AE•AB的数量关系,并说明你的猜想;(3)探究:当点E位于何处时,S△AEC:S△BOD=1:4,并加以说明.24.(8分)下表给出了代数式x2+bx+c与x的一些对应值:x…﹣101234…X2+bx+c…3﹣13…(1)根据表格中的数据,确定b、c的值,并填齐表格中空白处的对应值;(2)代数式x2+bx+c是否有最小值?如果有,求出最小值;如果没有,请说明理由;(3)设y=x2+bx+c的图象与x轴的交点为A、B两点(A点在B点左侧),与y 轴交于点C,P点为线段AB上一动点,过P点作PE∥AC交BC于E,连接PC,当△PEC的面积最大时,求P点的坐标.25.(7分)在平面直角坐标系中,以点A(﹣3,0)为圆心,半径为5的圆与x 轴相交于点B,C(点B在点C的左边),与y轴相交于点D,M(点D在点M的下方).(1)求以直线x=﹣3为对称轴,且经过点C,D的抛物线的解析式;(2)若点P是该抛物线对称轴上的一个动点,求PC+PD的取值范围;(3)若E为这个抛物线对称轴上的点,则在抛物线上是否存在这样的点F,使得以点B,C,E,F为顶点的四边形是平行四边形?若存在,求出点F的坐标;若不存在,说明理由.2009-2010学年北京市丰台区九年级(上)期末数学试卷参考答案与试题解析一、选择题(共8小题,每小题4分,满分32分)1.(4分)若=,则的值是( )A.B.C.﹣D.【分析】若=,则可以设a=2k,则b=3k.将其代入分式求解.【解答】解:∵=,∴设a=2k,则b=3k.∴===﹣,故选:C.【点评】已知几个量的比值时,常用的解法是:设一个未知数,把题目中的几个量用所设的未知数表示出来,实现消元.2.(4分)一个不透明的布袋里装有3个红球、2个白球,每个球除颜色外其它均相同,搅拌均匀后从中任意摸出一个球,则摸出的球是红球的概率是( )A.B.C.D.【分析】让红球的个数除以球的总数即为摸到红球的概率.【解答】解:3个红球、2个白球一共是5个,搅拌均匀后从中任意摸出一个球,则摸出的球是红球的概率是.故选:D.【点评】用到的知识点为:概率=所求情况数与总情况数之比.3.(4分)在Rt△ABC中,∠C=90°,AB=4,BC=1,则cosA的值是( )A.B.C.D.4【分析】依据勾股定理求出AC的长,根据三角函数的定义就可以解决.【解答】解:在Rt△ABC中,∠C=90°,AB=4,BC=1,由勾股定理可知AC=,则cosA==.故选:A.【点评】本题考查锐角三角函数的定义:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.4.(4分)将抛物线y=2x2向下平移1个单位,得到的抛物线是( )A.y=2(x+1)2B.y=2(x﹣1)2C.y=2x2+1D.y=2x2﹣1【分析】按照“左加右减,上加下减”的规律.【解答】解:将抛物线y=2x2向下平移1个单位抛物线变为y=2x2﹣1.故选D.【点评】考查了抛物线的平移以及抛物线解析式的变化规律:左加右减,上加下减.5.(4分)已知△ABC∽△DEF,相似比为3:1,且△ABC的周长为18,则△DEF的周长为( )A.2B.3C.6D.54【分析】因为△ABC∽△DEF,相似比为3:1,根据相似三角形周长比等于相似比,即可求出周长.【解答】解:∵△ABC∽△DEF,相似比为3:1∴△ABC的周长:△DEF的周长=3:1∵△ABC的周长为18∴△DEF的周长为6.故选:C.【点评】本题考查对相似三角形性质的理解.(1)相似三角形周长的比等于相似比;(2)相似三角形面积的比等于相似比的平方;(3)相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比.6.(4分)若反比例函数y=的图象在其每个象限内,y随x的增大而减小,则k的值可以为( )A.﹣1B.3C.0D.﹣3【分析】根据题意列出不等式确定k的范围,再找出符合范围的选项.【解答】解:根据题意k﹣1>0,则k>1.故选:B.【点评】本题考查了反比例函数图象的性质:①、当k>0时,图象分别位于第一、三象限;当k<0时,图象分别位于第二、四象限.②、当k>0时,在同一个象限内,y随x的增大而减小;当k<0时,在同一个象限,y随x的增大而增大.7.(4分)如图,AB是⊙O的弦,OD⊥AB于D交⊙O于E,则下列说法错误的是( )A.AD=BD B.∠ACB=∠AOE C.D.OD=DE【分析】由垂径定理和圆周角定理可证,AD=BD,AD=BD,,而点D不一定是OE的中点,故D错误.【解答】解:∵OD⊥AB∴由垂径定理知,点D是AB的中点,有AD=BD,,∴△AOB是等腰三角形,OD是∠AOB的平分线,有∠AOE=∠AOB,由圆周角定理知,∠C=∠AOB,∴∠ACB=∠AOE,故A、B、C正确,D中点D不一定是OE的中点,故错误.故选:D.【点评】本题利用了垂径定理,等腰三角形的性质和圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.8.(4分)如图,A,B,C,D为⊙O的四等分点,动点P从圆心O出发,沿O﹣C﹣D﹣O路线作匀速运动,设运动时间为t(s).∠APB=y(°),则下列图象中表示y与t之间函数关系最恰当的是( )A.B.C.D.【分析】本题考查动点函数图象的问题.【解答】解:当动点P在OC上运动时,∠APB逐渐减小;当P在上运动时,∠APB不变;当P在DO上运动时,∠APB逐渐增大.故选:C.【点评】本题主要考查学生对圆周角、圆内的角及函数图象认识的问题.要能根据几何图形和图形上的数据分析得出所对应的函数的类型和所需要的条件,结合实际意义画出正确的图象.二、填空题(共4小题,每小题4分,满分16分)9.(4分)如果反比例函数的图象过点(2,﹣3),那么k= ﹣6 .【分析】先设y=,再把已知点的坐标代入可求出k值,即得到反比例函数的解析式.【解答】解:将点(2,﹣3)代入解析式可得k=﹣6.故答案为:﹣6.【点评】本题比较简单,考查的是用待定系数法求反比例函数的比例系数,是中学阶段的重点内容.10.(4分)若扇形的半径为6cm,圆心角的度数为90°,则扇形的面积为 9π cm2.【分析】根据扇形的面积S=,把相应值代入求值即可.【解答】解:扇形的面积==9πcm2,故答案为9π.【点评】本题主要考查扇形的面积公式.11.(4分)如图,D,E两点分别在△ABC的边AB,AC上,DE,BC不平行,若使△ADE∽△ABC,需要添加的条件是 ∠ADE=∠C (写出一个即可).【分析】由图可得,两三角形已有一组角对应相等,再加一组角对应相等即可.【解答】解:由图可得,∠DAE=∠CAB,要使△ADE∽△ABC,根据两角对应相等,两三角形相似,可添加条件:∠ADE=∠C或∠AED=∠ABC;根据两边对应成比例且夹角相等,两三角形相似,可添加条件:AB:AC=AE:AD.【点评】相似三角形的判定:(1)两角对应相等,两三角形相似;(2)两边对应成比例且夹角相等,两三角形相似;(3)三边对应成比例,两三角形相似;(4)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.12.(4分)如图所示,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠AED的正切值等于 .【分析】在Rt△ABC中,易知∠ABC的正切值为;根据圆周角定理可得,∠AED=∠ABC,由此可求出∠AED的正切值.【解答】解:在Rt△ABC中,AC=1,AB=2;∴tan∠ABC==;∵∠AED=∠ABC,∴tan∠AED=tan∠ABC=.故答案为:.【点评】本题主要考查圆周角定理及锐角三角函数的概念:在直角三角形中,正弦等于对比斜;余弦等于邻比斜;正切等于对比邻.三、解答题(共13小题,满分72分)13.(5分)计算:tan45°﹣2cos30°+sin60°【分析】根据特殊角的三角函数值,分别把30°、45°、60°角的三角函数值代入原式计算即可.【解答】解:tan45°﹣2cos30°+sin60°,=1﹣2×+,=.【点评】解答此题要熟悉三角函数的特殊值以及有理数的混合运算法则,难度不大.【相关链接】特殊角三角函数值:sin30°=,cos30°=,tan30°=,cot30°=;sin45°=,cos45°=,tan45°=1,cot45°=1;sin60°=,cos60°=,tan60°=,cot60°=.14.(5分)已知:二次函数的表达式为y=﹣4x2+8x(1)写出这个函数图象的对称轴和顶点坐标;(2)求图象与x轴的交点坐标;(3)若点A(﹣1,y1)、B(,y2)都在该函数图象上,试比较y1与y2的大小.【分析】(1)用配方法把抛物线的一般式转化为顶点式,可求顶点坐标及对称轴;(2)令y=0,求x的值,可确定抛物线与x轴的交点坐标;(3)抛物线的对称轴是x=1,抛物线开口向下,比较可知,已知两点都在对称轴左边,y随x的增大而增大,由此可比较大小.【解答】解:(1)∵y=﹣4(x﹣1)2+4,∴对称轴为x=1,顶点坐标为(1,4);(2)令y=0,﹣4x2+8x=0,∴x1=0,x2=2、∴抛物线与x轴交点坐标为(0,0),(2,0);(3)∵a=﹣4<0,∴抛物线开口向下,在对称轴x=1左侧,y随x增大而增大,∵,∴y2>y1.【点评】抛物线的顶点式适合与确定抛物线的开口方向,顶点坐标,对称轴,最大(小)值,增减性等;抛物线的交点式适合于确定函数值y>0,y=0,y<0.15.(4分)已知:如图,在△ABC中,DE∥BC,EF∥AB,试判断成立吗?并说明理由.【分析】首先由DE∥BC,得,根据EF∥AB,得,根据等式的传递性即可证明结论.【解答】解:成立.理由如下:∵DE∥BC,∴.∵EF∥AB,∴.∴.【点评】此题主要是运用了平行线分线段成比例定理.16.(5分)已知:如图,在⊙O中,弦MN=16,半径OA⊥MN,垂足为点B,AB=4,求⊙O半径的长.【分析】根据垂径定理,易求得MB的长;连接OM,在Rt△OMB中,可用半径表示出OB的长,再根据勾股定理求出⊙O的半径.【解答】解:∵半径OA⊥弦MN于点B,MN=16,∴MB=MN=8;(1分)连接OM,(2分)设半径为R,∵AB=4,∴OB=OA﹣AB=R﹣4;(3分)在Rt△OMB中,∠OBM=90°,∴OM2﹣OB2=MB2即R2﹣(R﹣4)2=82,(4分)∴R=10;(5分)∴⊙O的半径长为10.【点评】此题主要考查的是垂径定理及勾股定理的应用.17.(5分)已知:如图,在平面直角坐标系xOy中,直线AB分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,tan∠ABO=,OB=4,OE=2.(1)求该反比例函数的解析式;(2)求直线AB的解析式.【分析】(1)根据已知条件求出c点坐标,用待定系数法求出反比例的函数解析式;(2)根据已知条件求出A,B两点的坐标,用待定系数法求出一次函数的解析式.【解答】解:(1)∵OB=4,OE=2,∴BE=2+4=6.∵CE⊥x轴于点E.tan∠ABO=.∴CE=3.(1分)∴点C的坐标为C(﹣2,3).(2分)设反比例函数的解析式为y=,(m≠0)将点C的坐标代入,得3=.(3分)∴m=﹣6.(4分)∴该反比例函数的解析式为y=﹣.(5分)(2)∵OB=4,∴B(4,0).(6分)∵tan∠ABO=,∴OA=2,∴A(0,2).设直线AB的解析式为y=kx+b(k≠0),将点A、B的坐标分别代入,得.(8分)解得.(9分)∴直线AB的解析式为y=﹣x+2.(10分).【点评】本题是一次函数与反比例函数的综合题.主要考查待定系数法求函数解析式.求A、B、C点的坐标需用正切定义或相似三角形的性质,起点稍高,部分学生感觉较难.18.(5分)在学校田径运动会4×100米接力比赛时,用抽签的方法安排跑道,九年级(1)、(2)、(3)三个班恰好分在一组,求九年级(1)、(2)班恰好依次排在第一、第二道的概率.【分析】列举出所有情况,看(1)、(2)班恰好依次排在第一、第二道的情况占总情况的多少即可.【解答】解:列举所有可能发生的结果:∵所有可能出现的结果有6个,且每个结果发生的可能性相等,其中(1)、(2)班恰好依次排在第一、第二道的结果只有1个,∴P(1、2班恰好依次排在第一、二道)=.【点评】如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A 出现m种结果,那么事件A的概率P(A)=.注意本题是不放回实验.19.(5分)2008年初,我国南方部分省区发生了雪灾,造成通讯受阴.如图,现有某处山坡上一座发射塔被冰雪从C处压折,塔尖恰好落在坡面上的点B 处,在B处测得点C的仰角为38°,塔基A的俯角为21°,又测得斜坡上点A到点B的坡面距离AB为15米,求折断前发射塔的高.(精确到0.1米)【分析】首先分析图形,据题意构造直角三角形;本题涉及到两个直角三角形,应利用其公共边构造三角关系,进而可求出答案.【解答】解:作BD⊥AC于D.在Rt△ADB中,sin∠ABD=.∴AD=AB•sin∠ABD=15×sin21°≈5.38米.(3分)∵cos∠ABD=.∴BD=AB•cos∠ABD=15×cos21°≈14.00米.(5分)在Rt△BDC中,tan∠CBD=.∴CD=BD•tan∠CBD≈14.00×tan38°≈10.94米.(8分)∵cos∠CBD=.∴BC=≈≈17.77米(10分)∴AD+CD+BC≈5.38+10.94+17.77=34.09≈34.1米(11分)答:折断前发射塔的高约为34.1米.(12分)注意:按以下方法进行近似计算视为正确,请相应评分.①若到最后再进行近似计算结果为:AD+CD+BC=34.1;②若解题过程中所有三角函数值均先精确到0.01,则近似计算的结果为:AD+CD+BC≈5.40+10.88+17.66=33.94≈33.9.【点评】本题要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.20.(5分)如图,已知抛物线C1:y=a(x+2)2﹣5的顶点为P,与x轴相交于A、B两点(点A在点B的左侧),点B的横坐标是1;(1)求a的值;(2)如图,抛物线C2与抛物线C1关于x轴对称,将抛物线C2向右平移,平移后的抛物线记为C3,抛物线C3的顶点为M,当点P、M关于点O成中心对称时,求抛物线C3的解析式.【分析】(1)将B点坐标代入抛物线C1的解析式中,即可求得待定系数a的值.(2)在抛物线平移过程中,抛物线的开口大小没有发现变化,变化的只是抛物线的位置和开口方向,所以C3的二次项系数与C1的互为相反数,而C3的顶点M与C1的顶点P关于原点对称,P点坐标易求得,即可得到M点坐标,从而求出抛物线C3的解析式.【解答】解:(1)∵点B是抛物线与x轴的交点,横坐标是1,∴点B的坐标为(1,0),∴当x=1时,0=a(1+2)2﹣5,∴.(2)设抛物线C3解析式为y=a′(x﹣h)2+k,∵抛物线C2与C1关于x轴对称,且C3为C2向右平移得到,∴,∵点P、M关于点O对称,且点P的坐标为(﹣2,﹣5),∴点M的坐标为(2,5),∴抛物线C3的解析式为y=﹣(x﹣2)2+5=﹣x2+x+.【点评】此题主要考查的是二次函数解析式的确定、二次函数图象的几何变化以及系数与函数图象的关系,需要熟练掌握.21.(6分)已知:如图,等腰△ABC中,AB=BC,AE⊥BC于点E,EF⊥AB于点F,若CE=1,,求EF的长.【分析】Rt△ABE中,EF⊥AB,易得∠AEF=∠B,即cos∠B=,由此可求得BE、AB的比例关系,即BE、BC的比例关系,根据EC=BC﹣BE,即可求出BE、AE的长;然后根据∠AEF的余弦值,即可在Rt△AEF中,求出EF的长.【解答】解:∵AE⊥BC,∴∠AEF+∠1=90°;∵EF⊥AB,∴∠1+∠B=90°;∴∠B=∠AEF;(1分)∴∵在Rt△ABE中,∠AEB=90°∴;(2分)设BE=4k,AB=5k,∵BC=AB,∴EC=BC﹣BE=BA﹣BE=k;∵EC=1,∴k=1;(3分)∴BE=4,AB=5;∴AE=3;(4分)在Rt△AEF中,∠AFE=90°,∵,(5分)∴.(6分)【点评】此题主要考查了直角三角形的性质、等腰三角形的性质、锐角三角函数的应用等知识.22.(5分)某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y 与x之间的函数表达式;(不要求写自变量的取值范围)(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?【分析】(1)根据题意易求y与x之间的函数表达式.(2)已知函数解析式,设y=4800可从实际得x的值.(3)利用x=﹣求出x的值,然后可求出y的最大值.【解答】解:(1)根据题意,得y=(2400﹣2000﹣x)(8+4×),即y=﹣x2+24x+3200;(2)由题意,得﹣x2+24x+3200=4800.整理,得x2﹣300x+20000=0.解这个方程,得x1=100,x2=200.要使百姓得到实惠,取x=200元.∴每台冰箱应降价200元;(3)对于y=﹣x2+24x+3200=﹣(x﹣150)2+5000,当x=150时,y最大值=5000(元).所以,每台冰箱的售价降价150元时,商场的利润最大,最大利润是5000元.【点评】求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法,常用的是后两种方法.借助二次函数解决实际问题.23.(7分)如图,已知:在⊙O中,直径AB=4,点E是OA上任意一点,过E 作弦CD⊥AB,点F是上一点,连接AF交CE于H,连接AC、CF、BD、OD.(1)求证:△ACH∽△AFC;(2)猜想:AH•AF与AE•AB的数量关系,并说明你的猜想;(3)探究:当点E位于何处时,S△AEC:S△BOD=1:4,并加以说明.【分析】(1)根据垂径定理得到弧AC=弧AD,再根据圆周角定理的推论得到∠F=∠ACH,根据两个角对应相等证明两个三角形相似;(2)连接BF,构造直角三角形,把要探索的四条线段放到两个三角形中,根据相似三角形的判定和性质证明;(3)根据三角形的面积公式,得到两个三角形的面积比即为AE:OB,进一步转化为AE:AO的比,再根据半径的长求得OE的长.【解答】(1)证明:∵直径AB⊥CD,∴,∴∠F=∠ACH,又∠CAF=∠FAC,∴△ACH∽△AFC.(2)解:AH•AF=AE•AB.证明:连接FB,∵AB是直径,∴∠AFB=∠AEH=90°,又∠EAH=∠FAB,∴Rt△AEH∽Rt△AFB,∴,∴AH•AF=AE•AB.(3)解:当时,S△AEC:S△BOD=1:4.理由:∵直径AB⊥CD,∴CE=ED,∵S△AEC=AE•EC,S△BOD=OB•ED,∴===,∵⊙O的半径为2,∴,∴8﹣4OE=2,∴OE=.即当点E距离点O 时S△AEC:S△BOD=1:4.【点评】能够综合运用垂径定理和圆周角定理的推论得到有关的角相等.掌握相似三角形的判定和性质.24.(8分)下表给出了代数式x2+bx+c与x的一些对应值:x…﹣101234…X2+bx+c…3﹣13…(1)根据表格中的数据,确定b、c的值,并填齐表格中空白处的对应值;(2)代数式x2+bx+c是否有最小值?如果有,求出最小值;如果没有,请说明理由;(3)设y=x2+bx+c的图象与x轴的交点为A、B两点(A点在B点左侧),与y 轴交于点C,P点为线段AB上一动点,过P点作PE∥AC交BC于E,连接PC,当△PEC的面积最大时,求P点的坐标.【分析】(1)根据图表中已知的三组数据,用待定系数法即可求出b、c的值;进而可由抛物线的解析式填齐空白处的对应值;(2)根据(1)所得函数的解析式,可用配方法或公式法求出其最小值;(3)由于△PEC的面积无法直接得出,所以要转化为其他图形面积的和差来解;可设出P点的坐标,过E作EM⊥x轴于M,易证得△BPE∽△BAC,那么它们的对应高等于相似比,由此可求出EM的表达式;那么△PEC的面积可由△ABC、△BPE、△APC的面积差求得,也就得到了关于△PEC的面积与P点横坐标的函数关系式,根据函数的性质即可求出S的最大值及对应的P 点坐标.【解答】解:(1)由题意知:解得b=﹣4(1分)x…﹣101234…X2+bx+c…830﹣103…(2)∵x2﹣4x+3=(x﹣2)2﹣1≥﹣1∴x2﹣4x+3有最小值,最小值为﹣1;(3分)(3)由(1)可知,点A、B的坐标分别为(1,0),(3,0)、设点P的坐标为(x,0),过点E作EM⊥x轴于点M,∵PE∥AC,∴△EPB∽△CAB∵EM、CO分别为△EPB与△CAB边上的高,∴(4分)∵CO=3,AB=2,PB=3﹣x,∴(5分)∴S△PEC=S△PBC﹣S△PBE=PB•CO﹣PB•EM(6分)==(7分)∴当x=2时,S有最大值;∴当点P的坐标为(2,0)时,△PEC的面积最大.(8分)【点评】此题主要考查了用待定系数法求二次函数解析式、相似三角形的判定和性质、图形面积的求法及二次函数的应用等,综合性较强,难度偏大.25.(7分)在平面直角坐标系中,以点A(﹣3,0)为圆心,半径为5的圆与x 轴相交于点B,C(点B在点C的左边),与y轴相交于点D,M(点D在点M的下方).(1)求以直线x=﹣3为对称轴,且经过点C,D的抛物线的解析式;(2)若点P是该抛物线对称轴上的一个动点,求PC+PD的取值范围;(3)若E为这个抛物线对称轴上的点,则在抛物线上是否存在这样的点F,使得以点B,C,E,F为顶点的四边形是平行四边形?若存在,求出点F的坐标;若不存在,说明理由.【分析】(1)根据圆的对称性,圆心的坐标和圆的半径可得出B点的坐标为(﹣8,0),C点的坐标为(2,0),M点的坐标为(0,4),D点的坐标为(0,﹣4).已知抛物线过C,D两点,且对称轴为x=﹣3,可用顶点式二次函数通式来设出抛物线的解析式,然后将C、D两点的坐标代入抛物线中即可得出过C、D两点的二次函数的解析式.(2)由于P是动点,因此PC+PD的最大值可以视作为无穷大;那么求PC+PD 最小值时,关键是找出P点的位置,由于B、C关于抛物线的对称轴对称,因此连接BC,直线BC与抛物线对称轴的交点就是PC+PD最小时P点的位置.那么此时PC+PD=BD,可在直角三角形BOD中用勾股定理求出BD的长,即可得出PC+PD的取值范围.(3)本题要分两种情况进行讨论:①当平行四边形以BC为边时,可在x轴上方找出两个符合条件的点,由于EF平行且相等于BC,那么可根据BC的长和抛物线的对称轴得出此时F点的横坐标,然后代入抛物线的解析式中即可求出F点的坐标.②平行四边形以BC为对角线,可在x轴下方找出一个符合条件的点且此时F点正好是抛物线的顶点.【解答】解:(1)设以直线x=﹣3为对称轴的抛物线的解析式为y=a(x+3)2+k,由已知得点C、D的坐标分别为C(2,0)、D(0,﹣4),分别代入解析式中,得,解得,∴y=(x+3)2﹣为所求;(2)(图1)∴点C(2,0)关于直线x=﹣3的对称点为B(﹣8,0),∴使PC+PD值最小的P点是BD与直线x=﹣3的交点.∴PC+PD的最小值即线段BD的长.在Rt△BOD中,由勾股定理得BD=4,∴PC+PD的最小值是4∵点P是对称轴上的动点,∴PC+PD无最大值.∴PC+PD的取值范围是PC+PD≥4.(3)存在.①(图2)当BC为所求平行四边形的一边时.点F在抛物线上,且使四边形BCFE或四边形BCEF为平行四边形,则有BC∥EF 且BC=EF,设点E(﹣3,t),过点E作直线EF∥BC与抛物线交于点F(m,t).由BC=EF,得EF=1O.∴F1(7,t),F2(﹣13,t).又当m=7时,t=∴F1(7,),F2(﹣13,);②(图3)当BC为所求平行四边形的对角线时.由平行四边形的性质可知,点F即为抛物线的顶点(﹣3,)∴存在三个符合条件得F点,分别为F1(7,),F2(﹣13,),F3(﹣3,).【点评】本题着重考查了待定系数法求二次函数解析式、平行四边形的判定和性质等重要知识点,综合性强,考查学生分类讨论,数形结合的数学思想方法.。
高等数学大一期末试卷(B)及答案

中国传媒大学2009—2010学年第 一 学期期末考试试卷(B 卷)及参考解答与评分标准考试科目: 高等数学A (上) 考试班级: 2009级工科各班 考试方式: 闭卷命题教师:.本大题共3小题,每小题3分,总计9分 ) 1、0)(0='x f 是可导函数)(x f 在0x 点处取得极值的 必要 条件. 2、设)20()1tan(cos ln π<<⎩⎨⎧+==t e y t x t,确定函数)(x y y =,则=dxdy)1(sec cot 2t t e t e +-. 3、=++⎰522x x dx C x ++21arctan 21。
填在题末的括号中.本大题共3小题,每小题3分,总计 9分)1、,则,若设0)(lim 134)(2=++-+=∞→x f b ax x x x f x )44()()44()()44()()44).((,.; ,.; ,.; ,)可表示为,的值,用数组(,----D C B A b a b a答( B )2、下列结论正确的是( ))(A 初等函数必存在原函数;)(B 每个不定积分都可以表示为初等函数; )(C 初等函数的原函数必定是初等函数; )(D C B A ,,都不对。
答( D )3、若⎰-=x e xe dt tf dxd 0)(,则=)(x fxx e D e C x B x A 2222)( )()( )(----- 答( A )2小题,每小题5分,总计10分 )1、求极限0lim →x xxx 3sin arcsin -。
解:0lim →x =-x x x 3sin arcsin 0lim →x 3arcsin x xx - (3分)lim→=x 311122=--x x 0lim →x ()()xx x62121232---61-=。
(5分)2、2tanln x y =,求dx dy . 解: 2sec 212tan 12xx y ⋅⋅=' (3分)x x x x csc sin 12cos2sin 21==⋅=。
2009年上学期《C语言程序设计》期末试卷(A)参考答案

华东师范大学期末试卷(A)2008 —2009学年第二学期课程名称:C语言程序设计学生姓名:学号:______________专业:年级/班级 2007级课程性质:专业必修一二三四五六总分阅卷人签名(请将所有答案写在答题纸上)一、填空题(每空1分,共10分)1. 设x和y均为int型变量,且x=2,y=3,则表达式1.0+x/y的值为1.0。
2. 有如下输入语句:scanf(“a=%d,b=%d,c=%d”,&a,&b,&c);为使变量a的值为1,b的值为3,c的值为2,从键盘输入数据的正确形式应是a=1,b=3,c=2 。
3. 变量y满足以下两条件中的任意一个:①能被4整除,但不能被100整除;②能被400整除。
请用逻辑表达式表示所给条件:___(y%4==0&&y%100!=0)||(y%400==0)_ __4. 在内存中存储“A”要占用 2 个字节,存储‘A’要占用 1 个字节。
5. C语言编译系统在判断一个量是否为“真”时,以0代表“假”,以非0代表“真”。
6. 结构化程序设计方法规定程序或程序段的结构有三种:顺序结构、选择结构和循环结构。
7. 设有“int x=1;”,则“x>0 ? 2*x+1 : 0”表达式的值是___3_______。
8. C语言的表达式与语句的区别在于 C语言的语句是以分号结束的,而表达式是没有分号的。
二、选择题(每小题1分,共20分)1. 以下关于C程序执行叙述正确的是( A )A)程序的执行总是从main函数开始,在main函数结束B)程序的执行总是从程序的第一个函数开始,在main函数结束C)程序的执行总是从main函数开始,在程序的最后一个函数中结束D)程序的执行总是从程序的第一个函数开始,在程序的最后一个函数中结束2. 下列叙述中错误的是( D )A)计算机不能直接执行用C语言编写的源程序B)C程序经C编译程序编译后,生成后缀为.obj的文件是一个二进制文件C)后缀为.obj的文件,经连接程序生成后缀为.exe的文件是一个二进制文件D)后缀为.obj和.exe的二进制文件都可以直接运行3. 设有定义:int k=0;,以下选项的四个表达式中与其他三个表达式的值不相同的是( A )A)k++ B) k+=1 C) ++k D) k+14. 若用数组名作为函数调用时的实参,则实际上传递给形参的是(A)。
2009-2010学年第一学期线性代数A期末试卷A卷及参考答案

2.(6 分)设 n 阶方阵 A 满足 A2 + 9 A + 7 E = 0, ,求证 A − 2 E 可逆且求其逆.
⎛ 0 1 0 ⎞ ⎛ 1 0 0 ⎞ ⎛ 1 −4 3 ⎞ ⎜ ⎟ ⎜ ⎟ ⎜ ⎟ 3、 (8 分)解矩阵方程 ⎜ 1 0 0 ⎟ X ⎜ 0 0 1 ⎟ = ⎜ 2 0 −1 ⎟ . ⎜ 0 0 1 ⎟ ⎜ 0 1 0 ⎟ ⎜ 1 −2 0 ⎟ ⎝ ⎠ ⎝ ⎠ ⎝ ⎠
浙江科技学院 2009-2010 学年第一学期线性代数A考试试卷A卷 一、填空题(每小题 4 分,共 20 分)
1. 已知 4 阶行列式 D 的第二行元素分别为 1、2、3、4,与它们对应的余子式依次 为 4、 −3 、2、 −1 ,则 D =__________ . 2. 设 A 是三阶方阵, A* 是其伴随矩阵, | A |=
第 3 页
⎛1 0 0 ⎞ ⎛ 1 2 1⎞ ⎜ ⎟ ⎟ −1 5.(8 分)解: A= (α 1 , α 2 , α 3 )= ⎜ 1 2 3 ⎟ , B= ( β1 , β 2 , β 3 )= ⎜ ⎜- 1 1 3 ⎟, P = A B , ⎜1 3 4 ⎟ ⎜ 0 1 - 1⎟ ⎝ ⎠ ⎝ ⎠ 2 1 ⎞ ⎛ 1 ⎜ ⎟ 由 ( A, B ) ⎯⎯ →( E , A B ), 求得P = A B = ⎜ 5 1 −14 ⎟ ⎜ −4 −1 10 ⎟ ⎝ ⎠
第 4 页
⎛ 1 0 5 ⎜ ⎜ 令 P = ( p1 , p2 , p3 ) = ⎜ −2 0 5 ⎜ 1 ⎜ 0 ⎝ 2 ⎞ 5⎟ 1 ⎟ ,则 P 为正交矩阵, 5⎟ ⎟ 0 ⎟ ⎠
从而 x = Py 为正交变换,使 f = − y12 + 2 y2 2 + 4 y32 四、证明题(6 分) 证:设 k1α1 + k 2α 2 + k3α 3 + k 4 (α 5 − α 4 ) = 0, 由 R(I)=R(II)=3, 得 α 4 可由 α 1 ,α 2 ,α 3 惟一线性表示, 设为 α 4 = l1α1 + l2α 2 + l3α 3 , 代入得 (k1 − l1 k 4 )α 1 + (k 2 − l 2 k 4 )α 2 + (k 3 − l3 k 4 )α 3 + k 4α 5 = 0, 因为 α1 , α 2 , α 3 , α 5 线性无关, 所以 k1 − l1 k 4 = k 2 − l 2 k 4 = k 3 − l 3 k 4 = k 4 = 0, 从而 k1 = k 2 = k 3 = k 4 = 0 ,得证。
2009-2010学年第一学期期末试题

2009-2010学年第一学期期末试题1.UML图不包括( D )(A)用例图(B)类图(C)状态图(D)流程图2.Rational Rose的代码生成功能可以针对不同类型的目标语言生成相应的代码,Rational Rose企业版默认支持的目标语言不包括( D )(A)Java (B)CORBA (C)Visual Basic (D)C# 3.在类图中,下面哪个符号表示继承关系( C4.在类图中,“ #”表示的可见性是( B )(A)Public (B)Protected (C)Private (D)Package 5.消息的组成不包括( C )(A)接口(B)活动(C)发送者(D)接收者6.下面哪个视图属于UML语言的交互图( D )(A)行为图(B)状态图(C)实现图(D)顺序图7.UML语言包含几大类图形( B )(A)3 (B)5 (C)7 (D)98.OMT方法是由下面哪位科学家提出的( B )(A)Booch (B)Rumbaugh (C)Coad (D)Jacobson9.类之间的关系不包括( D )(A)依赖关系(B)泛化关系(C)实现关系(D)分解关系10.在UML中,协作图的组成不包括( C )(A)对象(B)消息(C)发送者(D)链11.下面哪个符号代表包图( A )12.下列对状态图描述不正确的是( C )(A)状态图通过建立类对象的生命周期模型来描述对象随时间变化的动态行为(B)状态图适用于描述状态和动作的顺序,不仅可以展现一个对象拥有的状态,还可与说明事件如何随着时间的推移来影响这些状态(C)状态图的主要目的是描述对象创建和撤销的过程中资源的不同状态,有利于开发人员提高开发效率(B)(A) (C) (D)(B)(A) (D)(D)状态图描述了一个实体基于事件反应的动态行为,显示了该实体如何根据当前所处状态对不同的事件作出反应13.在UML的顺序图中,通常由左向右分层排列各个对象,正确的排列方法是( A)(A)执行者角色控制类用户接口业务层后台数据库(B)执行者角色用户接口控制类业务层后台数据库(C)执行者角色控制类用户接口后台数据库业务层(D)执行者角色用户接口业务层控制类后台数据库14.多对象是UML哪个视图中的概念( C )(A)类图(B)状态图(C)协作图(D)组件图15.构件图的组成不包括( C )(A)接口(B)构件(C)发送者(D)依赖关系16.在UML中,接口有几种表达方式( A )(A)2 (B)4 (C)6 (D)817.部署图的组成不包括( C )(A)处理器(B)设备(C)构件(D)连接18.下面哪个UML视图是描述一个对象的生命周期的( B )(A)类图(B)状态图(C)协作图(D)顺序19.顺序图由类角色,生命线,激活期和(B)组成(A)关系(B)消息(C)用例(D)实体20.UML中关联的多重度是指( B)(A)一个类有多个方法被另一个类调用(B)一个类的实类能够与另一个类的多个实类相关联(C)一个类的某个方法被另一个类调用的次数(D)两个类所具有的相同的方法和属性二填空1. 面向对象程序的基本特征是:抽象、封装、继承和多态。
七年级上学情阶段检测试卷--数学

2009—2010学年度第一学期期末学情阶段检测七年级数学试题(考试时间:120分钟;满分:130分)三四五合计合计人复核人题号一二17 18 19 20 21 22 23得分真情提示:亲爱的同学,欢迎你参加本次考试,祝你答题成功!1.请将密封线内的项目填写清楚.2.本试题共有23道题.其中1—8题为选择题,请将所选答案的标号填写在第8题后面给出表格的相应位置上;9—16题为填空题,请将做出的答案填写在第16题后面给出表格的相应位置上;17—23题请在试题给出的本题位置上做答.3.本试题采用等级制(A.B.C.D)评价.得分阅卷人一、选择题(本题满分24分,共有8道小题,每小题3分)下列每小题都给出标号为A、B、C、D的四个结论,其中只有一个是正确的.每小题选对得分;不选、选错或选出的标号超过一个的不得分.请将1—8各小题所选答案的标号填写在第8小题后面表格的相应位置上.1.下列图形中,含有曲面的是()①②③④A.①②B.①③C.②③D.②④2.下列四个数中,其相反数是负分数的是()A .-7B .-17C .5D .153.下列各题合并同类项,结果正确的是( )A .1349ab ab -=B .222527a b a b a b --=- C .2221257a a a -+= D .336235x x x +=4.如图,下列说法错误的是( )A .∠DAE 也可以表示为∠AB .∠1也可以表示为∠ABC C .∠BCE 也可以表示为∠CD .∠ABD 是一个平角5.下列方程中,是一元一次方程的是( )A .0y =B .32x y -=C .225x x +=-D .110x-= 6.如果每人都节约1分钱,那么全国13亿人将节约的总钱数是( )A .71.310⨯元B .71310⨯元C .81.310⨯元D .91.310⨯元7.“掷一枚均匀的骰子,3点朝上”这一事件是( )A .必然事件B .不可能事件C .不确定事件D .无法确定8.某种商品的进价为a 元,商场按进价提高50%后标价,当销售旺季过后,又以7折(即按标价的70%)的价格开展促销活动,这时这种商品的销售单价为( )A .a 元B .0.7a 元C .0.98a 元D .1.05a 元请将1—8各小题所选答案的标号填写在下表的相应位置上:二、填空题(本题满分24分,共有8道小题,每小题3分) 请将 9—16各小题的答案填写在第16小题后面表格的相应位置上.9.一个几何体由若干小正方体搭成,它的主视图、左视图和俯视图题 号 1 2 3 4 5 6 7 8 答 案得 分 阅卷人A B DC E110.计算:2521(1)()35-+-⨯-得 . 11.如果代数式2423x x -+的值为11,那么代数式227x x --的值等于 . 12.已知:如图,线段AB =10cm , 点O 是线段AB 的中点,线段BC =3cm , 则线段OC = cm.13.在一次捐款活动中,七年级(3)班50名同学人 人拿出自己的零花钱,有捐5元、10元、20元的,还有捐 50元和100元的.下面的统计图反映了不同捐款数的人数 比例,那么该班同学平均每人捐款 元.14.一个袋子中已有红球5个,再放入 个白球,摇匀后,摸到白球的可能 性大(填入一个你认为合适的数即可).15.若32x +与314x --互为相反数,则x 的值为 .16.有一列数123,,,,,n a a a a ⋅⋅⋅从第二个数开始,每一个数都等于1与它前面那个数的倒数的差,若1513a =,则2009a = . 请将9—16各小题的答案填写在下表的相应位置上:题 号 9101112答 案题 号 13 14 15 16 答 案ABCO 50元 6%20元 12% 10元 20%5元60%100元 2%三、作图题(本题满分6分)用直尺、圆规作图,不写作法,但要保留作图痕迹.17.已知:线段a,b 求作:线段AB ,使AB =a +b解:结论:四、解答题(本题满分66分,共有5道小题) 18.(本小题满分18分) (1)计算: 221143(2)(1)(1)33-+⨯-⨯-÷-解:(2)化简:22233(2)(46)4x y x x y +--- 解: 得 分 阅卷人得 分 阅卷人ab(3)解方程:11(1)1(2)25x x -=-+ 解:19.(本小题满分8分) 如图是一个可以自由转动的转盘,自由转动这个转盘四次后得到4个数字,分别填在各个空格内(顺序自定),组成一个数.(1)你认为有可能得到的最小的数是多少?(2)利用这个转盘,可能得到的最大的四位数是多少? 可能得到的最小的四位数是多少?它们出现的可能性谁大?解:(1) (2)20.(本小题满分12分) 如图是某月的日历:(1)设由6个数形成的阴影方框中,最大的数为x ,这6个数的和为y ,请你用含x 的代数式 表示y ;(2)现想框出6个数的和为111,你能办得到吗?若能,请求出这六个数,若不能,请说明理由.解:(1) 得 分 阅卷人得 分 阅卷人(2)21.(本小题满分12分)某公司用A 、B 、C 三台机器加工生产同一种产品.公司统计部对2009年第三季度的生产情况进行了统计,并绘制了如下统计图,图①是三台机器的产量统计图,图②是三台机器产量的比例分布图(图中有部分信息未给出).得 分 阅卷人比例分布图产量统计图 500400 300 200 100 0产量/件A15%B 25%C图① 图②根据统计图提供的信息,请你解决下列问题: (1)图②中的各个扇形分别代表了什么? (2)计算图②中各个扇形的圆心角的度数;(3)写出B 机器的生产产量,并分别求出A 机器、C 机器的产量. 解:(1) (2) (3)22.(本小题满分16分) 如图,请你根据图形,求解下列问题:(1)在∠EOA ,∠EOC ,∠EOB ,∠EOD 中,哪些角是锐角?哪些角是直角?哪些角是钝角? 哪些角是平角?并用“<”把它们连接起来;(2)∠BOD 是哪两个角的和?(3)写出∠EOD ,∠EOC ,∠DOC ,∠EOA 中 某些角之间的两个等量关系;(4)如果∠EOD =∠COB ,试判断OB 与OD 的位置关系,并用符号表示. 得 分 阅卷人ABCDEO(2)(3)(4)五、附加题(本题满分10分)23.阅读材料,解决问题:由31=3,32=9,33=27,34=81,35=243,36=729,37=2187,38=6561,……,不难发现3的正整数幂的个位数字以3、9、7、1为一个周期循环出现,由此可以得到:因为3100=34×25,所以3100的个位数字与34的个位数字相同,应为1;因为32009=34×502+1,所以32009的个位数字与31的个位数字相同,应为3.(1)请你仿照材料,分析求出299的个位数字及999的个位数字;(2)请探索出22010+32010+92010的个位数字;201020102010解:(1)(2)(3)真情提示:亲爱的同学,请认真检查,不要漏题哟!2009—2010学年度第一学期期末学情阶段检测七年级数学试题参考答案及评分标准一、选择题(本题满分24分,共有8道小题,每小题3分)1、C2、D3、B4、C5、A6、A7、C8、D 二、填空题(本题满分24分,共有8道小题,每小题3分)9、 510、1715-11、-3 12、213、12.4 14、 6(答案不唯一) 15、7 16、85- 三、作图题(本题满分6分)17.略 (作图正确5分,结论1分). 四、解答题(本题满分66分,共有5道小题) 18. (1)10-(6分) (2)21122x y -+(6分) (3)117x =(6分) 19. 解:(1)0000 (2分)(2)7777(2分), 1000(2分), 它们出现的可能性一样大.(2分)20. 解:(1)设最大的数为x ,则其余的五个数分别为:1,2,7,8,9x x x x x -----……………………………………………………………2分∴ (1)(2)(7)(8)(9)627y x x x x x x x =+-+-+-+-+-=- …………………6分 (2)设最大的数为x ,由题意得:627111x -=解得:23x =,∴122x -=,221x -=,716x -=,815x -=,914x -=答:能办到,这六个数分别是23,22,21,16,15,14. ………………………………12分 21.解:(1)图②中扇形A 表示A 机器第三季度的产量占总产量的百分比扇形B 表示B 机器第三季度的产量占总产量的百分比扇形C 表示C 机器第三季度的产量占总产量的百分比………………………3分 (2) 扇形A 的圆心角度数为:15%×360°=54° 扇形B 的圆心角度数为:25%×360°=90°扇形C 的圆心角度数为:(1-15%-25%)×360°=216°……………………6分(3)B机器的产量为200件…………………………………………………………8分A机器的产量为:200÷25%×15%=120(件)……………………………………10分C机器的产量为:800×60%=480(件) …………………………………12分22.解:(1)∠EOD是锐角,∠EOC是直角,∠EOB是钝角,∠EOA是平角……………4分∠EOD<∠EOC<∠EOB<∠EOA ……………………………………………6分(2)∠BOD=∠BOC+∠COD …………………………………………………………8分(3)∠EOC=∠EOD+∠DOC∠EOA=2∠EOC(答案不唯一,只要正确写出两个即可)………………………14分(4)如果∠EOD=∠BOC那么OB与OD垂直,即OB⊥OD …………………………………………………16分五、附加题(本题满分10分)23.解: (1)由21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,……,不难发现2的正整数幂的个位数字以2、4、8、6为一个周期循环出现,由此可以得到:因为299=24×24+3,所以299的个位数字与23的个位数字相同,应为8.………………2分由91=9,92=81,93=729,94=6561,……,不难发现9的正整数幂的个位数字以9、1为一个周期循环出现,由此可以得到:因为999=92×49+1,所以999的个位数字与91的个位数字相同,应为9.………………4分(2) 因为22010=24×502+2,所以22010的个位数字与22的个位数字相同,应为4;因为32010=34×502+2,所以32010的个位数字与32的个位数字相同,应为9;因为92010=92×1005,所以92009的个位数字与92的个位数字相同,应为1.∴4+9+1=14∴22010+32010+92010的个位数字为4 ………………………………………………………8分(3) 92010-22010-32010的个位数字为8 ………………………………………………………10分。
0Uecoka2009-2010计算机基础考试试卷(附答案)

秋风清,秋月明,落叶聚还散,寒鸦栖复惊。
2009-2010计算机基础考试试卷(附答案)业(本科)学生使用1、在ENIAC诞生后的短短的50多年中,计算机所采用的基本电子元件已经经历了四个发展阶段,通常称为计算机发展的4个时代,按发展先后依次为 B 。
A、晶体管、电子管、中小规模集成电路、大规模和超大规模集成电路。
B、电子管、晶体管、中小规模集成电路、大规模和超大规模集成电路。
C、中小规模集成电路、电子管、晶体管、大规模和超大规模集成电路。
D、大规模和超大规模集成电路、电子管、晶体管、中小规模集成电路。
2、冯·诺依曼“程序存储”的设想首次在 C计算机上得到了体现。
A、ENIACB、PCC、EDVACD、大型3、爱德华·罗伯茨1971年发明了第一台微机 C 。
A、Apple ⅡB、IBM PC/PCC、牛郎星D、织女星4、指令的数量与类型是由 A 决定的。
A、CPUB、DRAMC、SRAMD、BIOS5、主板性能的高低主要由 C 芯片决定。
A、CPUB、南桥C、北桥D、内存6、微机硬件的主要技术指标有:性能、功能、B 、兼容性等技术参数。
A、安全性B、可靠性C、实用性D、经济性7、配置在计算机硬件上的第一层软件是 B 。
A、语言处理程序B、操作系统C、工具软件D、数据库管理系统8、在Windows XP中复制当前屏幕图像到剪贴板的键名为 B 。
A、Alt+SpaceB、PrintScreen(Prtsc)C、Alt+ PrintScreen(Prtsc)D、F19、Windows XP任务栏不能完成的工作是D 。
A、显示改变系统日期和时间B、启动应用程序C、多个程序和任务之间的切换D、桌面上图标的排列10、大写字母锁定键的标志是 A 。
A、Caps LockB、Num LockC、Scroll LockD、Pause11、回收站是在 D 中开辟的一块存放已删除文件或文件夹的空间。
2009-2010年计算机统考真题解析

单项选择题
1.为解决计算机与打印机之间速度不匹配的问题,通常设置一个打印数据缓冲区,主机将要输出的数据 依次写入该缓冲区,而打印机则依次从该缓冲区中取出数据。该缓冲区的逻辑结构应该是______。 A.栈 B.队列 C.树 D.图 【解答】B。考察栈和队列的特点。 C 和 D 直接排除,缓冲区的特点需要先进先出,若用栈,则先进入缓冲区的数据则要排队到最后才 能打印,不符题意,所以只有队列符合题意。 2.设栈 S 和队列 Q 的初始状态均为空,元素 abcdefg 依次进入栈 S。若每个元素出栈后立即进入队列 Q,且 7 个元素出队的顺序是 bdcfeag,则栈 S 的容量至少是______。 A.1 B .2 C .3 D.4 【解答】C。考察栈的最大深度。 时刻注意栈的特点是先进后出。下面是出入栈的详细过程: 序号 1 2 3 4 5 6 7
60 K 8 30 片,采用字和位同时扩展方式。 4K 4
王道论坛 — 予人玫瑰 手留余香
。
B. 指令和数据的寻址方式 D. 指令和数据所在的存储单元
- 3 -
通常完成一条指令可分为取指阶段和执行阶段。在取指阶段通过访问存储器可将指令取出;在执行 阶段通过访问存储器可以将操作数取出。这样,虽然指令和数据都是以二进制代码形式存放在存储器中, 但 CPU 可以判断在取指阶段访问存储器取出的二进制代码是指令; 在执行阶段访存取出的二进制代码是 数据。 12.一个 C 语言程序在一台 32 位机器上运行。程序中定义了三个变量 xyz,其中 x 和 z 是 int 型,y 为 short 型。当 x=127,y=-9 时,执行赋值语句 z=x+y 后,xyz 的值分别是 A. X=0000007FH,y=FFF9H,z=00000076H B. X=0000007FH,y=FFF9H,z=FFFF0076H C. X=0000007FH,y=FFF7H,z=FFFF0076H D. X=0000007FH,y=FFF7H,z=00000076H 【解答】D。考察符号位的扩展。 结合题干及选项可知,int 为 32 位,short 为 16 位;又 C 语言的数据在内存中为补码形式,故 x、y 的机器数写为 0000007F 、FFFFH; 执行 z=x+y 时,由于 x 是 int 型,y 为 short 型,故需将 y 的类型强制转换为 int,在机器中通过符号 位扩展实现,由于 y 的符号位为 1,故在 y 的前面添加 16 个 1,即可将 y 强制转换为 int 型,其十六进制 形式为 FFFFFFF7H; 然后执行加法, 即 0000007FH+FFFFFFF7H=00000076H, 其中最高位的进位 1 自然丢弃。 故选 D。 13.浮点数加减运算过程一般包括对阶、尾数运算、规格化、舍入和判溢出等步骤。设浮点数的阶码和 尾数均采用补码表示, 且位数分别为 5 位和 7 位 (均含 2 位符号位) 。 若有两个数 X=27 ×29/32, Y=25×5/8, 则用浮点加法计算 X+Y 的最终结果是 A.00111 1100010 C.01000 0010001 【解答】D。考察浮点加法。 根据题意,X 可记为 00,111;00,11101(分号前为阶码,分号后为尾数),Y 可记为 00,101; 00,10100; 首先对阶,X、Y 阶码相减,即 00,111-00,101=00,111+11,0111=00,010,可知 X 的阶码比 Y 的价码大 2,根据小阶向大阶看齐的原则,将 Y 的阶码加 2,尾数右移 2 位,可得 Y 为 00,111;00, 00101; 尾数相加,即 00,11101+00,00101=01,00010,尾数相加结果符号位为 01,故需进行右规; 规格化,将尾数右移 1 位,阶码加 1,得 X+Y 为 01,000;00,1000,阶码符号位为 01,说明发 生溢出,故选 D。 14.某计算机的 Cache 共有16块,采用2路组相联映射方式(即每组2块) 。每个主存块大小32字节,按 字节编址。主存129号单元所在主存块应装入到的 Cache 组号是 。 A.0 B.2 C.4 D.6 【解答】C。考察 Cache 与主存之间的映射方式。 由于 Cache 共有16块,采用2路组相联,因此共有8组,0,1,2,...,7。并且主存的某一字块按模 8映像到 Cache 某组的任一字块中,即主存的第0,8,16...字块可以映像到 Cache 第0组2个字块的任一 字块中,而129号单元是位于第4块主存块中,因此将映射到 Cache 第4组2个字块的任一字块中。 注意:由于在计算机系统结构中和计算机组成原理的某些教材中介绍的组相联跟此处的组相联并不相同, 导致部分考生理解错题目。考生应以真题为准,以后再出现类似题目,应以此种解答为标准。 15.某计算机主存容量为64KB,其中 ROM 区为4KB,其余为 RAM 区,按字节编址。现要用2K×8位的
高等数学-期末考试题-A3

西安交通大学城市学院2009-2010学年上学期高等数学期末考试模拟试题(文科)姓名班级学号成绩考试时间:120分钟满分:100分命题人:高兵龙说明:1、考生必须在规定时间内完成该试卷;2、必须使用黑色签字笔作答;3、考生必须按时交卷。
4、(7分)设)(x y y =由⎩⎨⎧=+-=52arctan 2te ty y t x 所确定,求dx dy,并求出0=t 处曲线的切线方程.解:5、(8分)已知曲线nx x f =)(,求:(1)曲线在点(1,1)处的切线方程; (2)设该切线与x 轴的交点为)0,(n ξ,试计算).(lim n n f ξ∞→解:四、(6分)证明当10<<x 时,xxe x-+<112 证明:五、(8分)已知函数)(x f 在]2008,0[上连续,在)2008,0(内可导,且0)2008(=f ,求证:在)2008,0(内至少存在一点c ,使cc f c f )()('-=成立. 证明:六、(8分)设某厂生产某种商品的固定成本为200(百元),每生产一个单位产品,成本增加5(百元),已知需求函数q =100—2p (其中p 为价格,q 为产量),问产量多少时利润最大?并求最大利润. 解:七、(10分)求函数21xy x x =+-的单调区间、极值、凸性区间、拐点及渐近线,并作出函数的图形。
解:西安交通大学城市学院2009-2010学年上学期高等数学期末考试模拟试题(文科)参考答案一、选择题(共6小题,每小题3分,共18分)二、填空题(共6小题,每小题3分,共18分)1. 92. !)2(n n-3. 1 4.22e 5.C xxx +-sin 2cos 6. 4-三、计算题(共5小题,共32分) 1.(5分) 解:2. 解:⎰+-dx e e x x 11⎰⎰+-+=dx e dx e ex x x1111分 ⎰⎰--+-+=dx ee dx e e xxx x 11 3分 ⎰⎰--+++++=)1(11)1(11xx x x e d ee d e 4分 C e e x x ++++=-)1ln()1ln( 5分3. 解:点连续在点可导,故在1)(1)(==x x f x x f 1分)1(lim lim 21)1(21++=∴-+→-→bx ax ex x x 0=+b a 即 3分1)1(lim )1()1(21-++-='-→++x b a e f x x 又 21)1(2lim 11lim 1)1(21=--=--=++→-→x x x e x x x 5分 1)1()1(lim )1(21-++-++='-→-x b a bx ax f xa x axax x bx ax x x =--=-+=--→→1lim 1lim 2121 6分 2,2-==∴b a 7分4.解:对522=+-te ty y 两边对t 求导0222=+--t e dtdyty y dt dy 222--=ty y e dt dy t 3分22)1)((\22-+-==ty t y e dt dx dt dy dx dy t 5分 2,0,23,0====y x dx dy t 时 切线方程:223+=x y 7分5.解:(1)1)(-='n nx x f ,n f k ='=)1( 2分切线方程 )1(--=n nx y 4分(2)令0=y 得n n x 1-=故nn n 1-=ξ 6分 )(lim n n f ξ∞→nn n n ⎪⎭⎫ ⎝⎛-=∞→1lim )1(11lim -⋅-∞→⎪⎭⎫⎝⎛-=n n n 1-=e 8分四、 证明:)1()1()(2x e x x f x+--=令 1分 则 1)21()(2--='xex x f 3分04)(2<-=''x xe x f内单调减少在所以)1,0()(x f ' 4分 单调减少从而,故又)(,0)(0)0(x f x f f <'=' 5分 即,故又,0)0()(0)0(=<=f x f fxxe x -+<112 6分五、证明:令 )()(x xf x F =, 1分则)(x F 在]2008,0[上连续,在)2008,0(内可导, 3分 且0)2008()0(==F F ,由罗尔定理得 5分至少存在一点c ,使0)('=c F ,即0)()('=+c f c c f ,也即cc f c f )()('-= 得证。
【中国海洋大学】2010并行算法与编程期末考试B卷

{Байду номын сангаас
MPI_Recv(buf,256,…,MPI_ANY_SOURCE,MPI_ANY_TAG,comm,&status);
switch (status.MPI_TAG)
{
case MSG_EXIT: nslave--; break;
case MSG_PRINT_UNORDERED:
sprintf(buf,"Hello from slave %d,ordered print\n", rank );
MPI_Send(buf,strlen(buf)+1,…,0,MSG_PRINT_ORDERED,comm);
sprintf(buf,"Goodbye from slave %d, ordered print\n",rank); MPI_Send(buf,strlen(buf)+1,…,0,MSG_PRINT_ORDERED,comm);
}
void master_io(void)
{
int nslave,size,rank;
MPI_Starus status;
MPI_Comm comm;
comm=MPI_COMM_WORLD;
MPI_Comm_rank(comm,&rank);
MPI_Comm_size(comm,&size);
nslave=size-1; /*size为总的进程个数*/
sprintf(buf,"I'm exiting (%d),unordered print\n",rank );
MPI_Send(buf,strlen(buf)+1,…,0,MSG_PRINT_UNORDERED,comm);
【中国海洋大学】2010并行算法与编程期末考试A卷

海洋地球科学学院《并行算法与编程》课程试题(A卷) 共3页第1页共3页第2 页共3页第3 页else{MPI_Recv(&m,1,MPI_FLOAT,0,myid,MPI_COMM_WORLD,&status);m=m*myid;MPI_Send(&m,1,MPI_FLOAT,0,myid,MPI_COMM_WORLD);}}三、请写出下列程序的运行结果(假设零进程读入的数为12.3,共启动了5个进程)(10分)#include “mpi.h”#include <stdio.h>main(int agrc,char **argv){int rank,num_processes,i,j,k;float a;MPI_Status status;MPI_Init(&argc,&argv);MPI_Comm_rank(&rank,MPI_COMM_WORLD);MPI_Comm_size(&num_processes,MPI_COMM_WORLD);if(rank==0) scanf(“%f”,&a);if(rank>0){MPI_Recv(&a,1,MPI_FLOAT,rank-1,rank-1,MPI_COMM_WORLD,status);a=a*(i+1.0);}if(rank<num_processes-1){MPI_Send(&a,1,MPI_FLOAT,rank+1,rank,MPI_COMM_WORLD);}printf(“myid=%d, value=%f\n”,myid,a);MPI_Finalize();}四、请说明下列MPI函数能够实现什么功能(每小题2分,共24分)1、MPI_GET_PROCESSOR_NAME;2、 MPI_SENDRECV;3、MPI_BCAST;4、MPI_BUFFER_ATTACH;5、 MPI_SSEND;6、MPI_IRECV;7、MPI_WAIT;8、MPI_IPROBE9、MPI_GATHER; 10、MPI_BARRIER11、MPI_REDUCE; 12、MPI_COMM_RANK。
2009级期末上机考试试题 (B1卷)

2009-2010年度《高级语言程序设计》
第一学期期末上机考试试题(B1卷)
(请注意:在每道题的程序第一行加一行注释行,注明:学号、姓名、专业、试卷类型:B、题号。
每道题存储为一个独立的Cpp文件,使用题号和卷号命名,例如:B1_1.cpp,并建立一个文件夹存储这些文件,文件夹使用学号命名。
)
1.已知公元N年9月1日是星期五,请使用for或while循环的方式计算出N+1年2月份的日历。
并采用循环的方式将之打印到屏幕上。
(请考虑闰年问题)
输入:第N年的年份
输出:第N+1年的2月份日历(采用类似Windows下的月份日历显示方式排版)
2.任意输入n个实数(10<=n<=100),首先按照从大到小的顺序排列,然后计算这n个数的平均值,并按顺序将该值插入到序列的之中。
例如:序列为(1,4,2,5,6,3,10,7,8,9),平均值为5.5,插入后的序列为(10,9,8,7,6,5.5,5,4,3,2,1)。
输入:不少于10的n个实数
输出:平均值和从大到小排列的n+1实数序列
3.利用质因数分解法求解任意两个正整数m和n的质数公约因子和。
例如m=60,n=24时,首先求得m=60=2*2*3*5,n=2*2*2*3,则其共有的质因数是两个2和一个3,得到所求质数公约因子和为2+3=5。
输入:两个正整数
输出:每个输入正整数的分解因子序列,和质数公约因子和计算式。
并行计算试题及答案

计算机学院研究生《并行计算》课程考试试题(2010级研究生,2011.1)1.(12分)定义图中节点u 和v 之间的距离为从u 到v 最短路径的长度。
已知一个d 维的超立方体,1)指定其中的一个源节点s ,问有多少个节点与s 的距离为i ,其中0≤i ≤d 。
证明你的结论。
2)证明如果在一个超立方体中节点u 与节点v 的距离为i ,则存在i !条从u 到v 的长度为i 的路径。
1)有id C 个节点与s 的距离为i 。
证明:由超立方体的性质知:一个d 维的超立方体的每个节点都可由d 位二进制来表示,则与某个节点的距离为i 的节点必定在这d 位二进制中有i 位与之不同,那么随机从d 位中选择i 位就有id C 种选择方式,即与s 的距离为i 得节点就有id C 个。
2)证明:由1)所述可知:节点u 与节点v 的距离为i 则分别表示u 、v 节点的二进制位数中有i 位是不同的。
设节点u 表示为:121D .........j j i j i d D D D D D +-+,节点v 表示为:''121D .........j j i j i dD D D D D +-+,则现在就是要求得从121D .........j j i j i d D D D D D +-+变换到''121D .........j j i j i d D D D D D +-+ 的途径有多少种。
那么利用组合理论知识可知共有*(1)*(2)*...*2*1i i i --即!i 中途径。
所以存在i !条从u 到v 的长度为i 的路径。
2.(18分)6个并行程序的执行时间,用I-VI 表示,在1-8个处理器上执行了测试。
下表表示了各程序达到的加速比。
对其中的每个程序,选出最适合描述其在16个处理器上性能的陈述。
a ) 在16个处理器上的加速比至少比8个处理器上的加速比高出40%。
b ) 由于程序中的串行程序比例很大,在16个处理器上的加速比不会比8个处理器上的加速比高出40%。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
使用 private 子句和 critical 部分并行化的程序
//OpenMP PI Program:
中国科学技术大学
2009-2010 学年第一学期考试试卷
考试科目: 并行程序设计 学生所在系:___________
参考解答
得分:____ ______
姓名:____ _
_____ 学号:_____ ______
一、给出用基本的 MPI_Send 和 MPI_Recv 函数实现 MPI_Allgather 函数功能的伪代码。 这三个函数的调用格式如下:(20 分)
static long num_steps = 100000;
double step;
#define NUM_THREADS 2
void main ()
{
int i;
double x, pi, sum[NUM_THREADS];
step = 1.0/(double) num_steps;
omp_set_num_threads(NUM_THREADS)
}
二、以下是一个用 C 语言描述的计算 的串行程序。(30 分)
static long num_steps = 100000;
double step;
void main ()
{
int i; double x, pi, sum = 0.0;
step = 1.0/(double) num_steps;
for (i=1;i<= num_steps; i++){
omp_set_num_threads(NUM_THREADS)
#pragma omp parallel
{
double x;
int id;
id = omp_get_thread_num();
for (i=id, sum[id]=0.0;i< num_steps; i=i+NUM_THREADS){
x = (i+0.5)*step;
//private clause and a critical section
#include <omp.h>
static long num_steps = 100000;
double step;
#define NUM_THREADS 2
void main ()
{
int i;
double x, sum, pi=0.0;
#pragma omp parallel
{
double x;
int id;
2009-2010 学年第一学期 《并行程序设计》期末考试
第 1 页(共 1 页)
id = omp_get_thraead_num(); sum[id] = 0; #pragma omp for for (i=0;i< num_steps; i++){
x = (i-0.5)*step;
sum = sum + 4.0/(1.0+x*x);
}
pi = step * sum;
}
请给出四种不同的 OpenMP 程序实现来并行计算 。
参考解答:
使用并行域并行化的程序ຫໍສະໝຸດ //OpenMP PI Program:
//Parallel Region example (SPMD Program)
#include <omp.h>
static long num_steps = 100000;
double step;
#define NUM_THREADS 2
void main ()
{
int i;
double x, pi, sum[NUM_THREADS];
step = 1.0/(double) num_steps;
x = (i+0.5)*step;
sum += 4.0/(1.0+x*x);
}
#pragma omp critical
pi += sum
}
}
使用并行归约得出的并行程序
//OpenMP PI Program : //Parallel for with a reduction #include <omp.h> static long num_steps = 100000;
step = 1.0/(double) num_steps;
omp_set_num_threads(NUM_THREADS)
#pragma omp parallel private (x, sum)
{
id = omp_get_thread_num();
for (i=id,sum=0.0;i< num_steps;i=i+NUM_THREADS){
(1) MPI_Send(buf, count, datatype, dest, tag, comm) (2) MPI_Recv(buf, count, datatype, source, tag, comm, status) (3) MPI_Allgather(sendbuf, sendcount, sendtype, recvbuf, recvcount,
sum[id] += 4.0/(1.0+x*x);
}
}
for(i=0, pi=0.0;i<NUM_THREADS;i++)pi += sum[i] * step;
}
使用共享任务结构并行化的程序
//OpenMP PI Program:
//Work sharing construct
#include <omp.h>
recvtype, comm)
参考解答:
for( i=0; i<GroupSize; i++ ){ MPI_Send(sendbuf, sendcount, sendtype, i, myrank, MPI_COMM_WORLD);
} for( i=0; i<GroupSize; i++ ){
MPI_Recv(recvbuf+i*recvcount, recvcount, recvtype, i, i, MPI_COMM_WORLD,status);
double step;
#define NUM_THREADS 2
void main ()
{
int i;
double x, pi, sum = 0.0;
