09宣武初三一模
北京宣武区2009中考一模及答案

北京市宣武区2008-2009学年度第二学期一模质量检测九 年 级 化 学 2009.5考生须 知 1. 本试卷共8 页。
全卷共四道大题,35道小题。
2. 本试卷满分80分,考试时间100分钟。
3. 试卷答案一律填写在答题卡上,在试卷上作答无效。
选择题的答案用2B 铅笔规范填涂;其它题一律用黑色签字笔规范书写。
4. 在试卷、答题卡的密封线内准确填写学校、班级、姓名和学号。
5. 考试结束后,将试卷和答题卡一并交回。
6. 本试卷化学方程式中的“=”和“ ”含义相同。
可能用到的相对原子质量H 1 C 12 N 14 O 16 S 32 Ca 40 Cu 64 Zn 65 部分碱和盐的溶解性表(20 ℃)Ba 2+ Ca 2+ Mg 2+ Ag + OH - 溶 微 不CO 32-不不微不Cl –溶 溶 溶 不 一、选择题(每小题只有一个选项符合题意。
共25个小题,每小题1分,共25分。
) 1.地壳中含量最多的金属元素是A .铝元素B .硅元素C .氧元素D .铁元素 2.为解决登山人员的呼吸困难,需提供的物质是A .氮气B .二氧化碳C .氧气D .水3.“84消毒液”的主要成分是次氯酸钠(NaClO )的水溶液。
“84消毒液”属于A .氧化物B .单质C .化合物D .混合物 4.“金银铜铁锡”俗称五金。
在这五种金属中,金属活动性最弱的是A .铁B .金C .银D .铜 5.下列粒子不能..直接构成物质的是 A .电子 B .分子 C .离子 D .原子6.在缺氮的情况下,植物的生长发育迟缓或停滞。
这时应施用的化肥是 A .KCl B .NH 4Cl C .K 2CO 3 D .Ca(H 2PO 4 )2 7.下列物质的变化属于化学性质的是A .红磷可以点燃B .浓盐酸的挥发C .氢氧化钠的潮解D .石蜡的熔化8.右图为简易的净水装置示意图,关于此装置的作用说法正确的是 A . 能杀菌消毒 B .能得到纯净水C .能除去可溶性杂质D .能除去固体杂质 9.下列实验操作不正确...的是A .稀释浓硫酸B .氯化钠溶解C .取用氢氧化钠固体D .取粉末状固体药品阳离子阴离子10.下列清洗方法中,利用乳化原理的是A.用洗涤剂清洗餐具B.用汽油清洗油污C.用自来水洗蔬菜D.用水冲洗试管内残留的氯化钠固体11.下列各图能说明分子间的间隔变小的是A.炒菜闻到香味B.湿衣服晾干C.酚酞遇氨水变红D.压缩空气12.二氧化碳由碳、氧两种元素组成,这两种元素的本质区别是A.质子数不同B.中子数不同C.电子数不同D.最外层电子数不同13.下列有关木炭、一氧化碳、酒精的说法不正确...的是A. 都是含碳的物质 B.燃烧时都有蓝色火焰C.完全燃烧都有二氧化碳气体生成 D.燃烧时都放出大量热14.每种植物都有适宜自己生长的酸碱性环境。
2009年北京市宣武区数学一模(含答案)
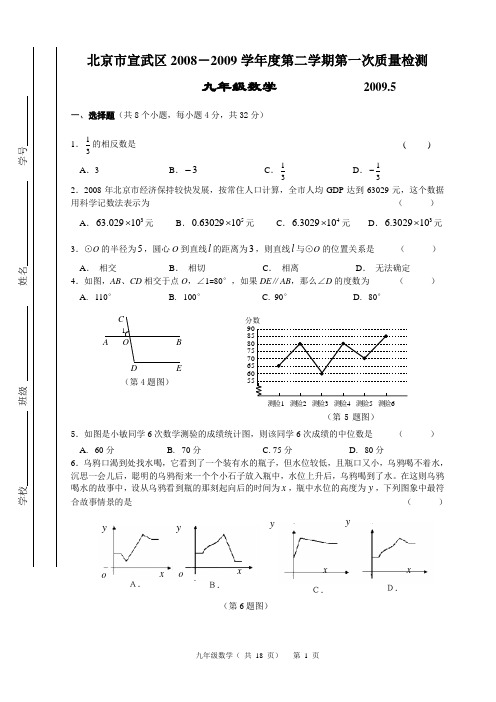
北京市宣武区2008-2009学年度第二学期第一次质量检测九年级数学 2009.5一、选择题(共8个小题,每小题4分,共32分)1.31的相反数是 ( )A .3B .3-C .31D .31-2.2008年北京市经济保持较快发展,按常住人口计算,全市人均GDP 达到63029元,这个数据用科学记数法表示为 ( ) A .363.02910⨯元B .50.6302910⨯元C .46.302910⨯元D .36.302910⨯元3.⊙O 的半径为5,圆心O 到直线l 的距离为3,则直线l 与⊙O 的位置关系是 ( ) A . 相交 B . 相切 C . 相离 D . 无法确定4.如图,AB 、CD 相交于点O ,∠1=80°,如果DE ∥AB ,那么∠D 的度数为 ( ) A . 110° B . 100° C . 90° D . 80°5.如图是小敏同学6次数学测验的成绩统计图,则该同学6次成绩的中位数是 ( ) A . 60分 B . 70分 C .75分 D . 80分6.乌鸦口渴到处找水喝,它看到了一个装有水的瓶子,但水位较低,且瓶口又小,乌鸦喝不着水,沉思一会儿后,聪明的乌鸦衔来一个个小石子放入瓶中,水位上升后,乌鸦喝到了水。
在这则乌鸦喝水的故事中,设从乌鸦看到瓶的那刻起向后的时间为x ,瓶中水位的高度为y ,下列图象中最符合故事情景的是 ( )(第6题图)分数 测验1 测验2 测验3 测验4 测验5 测验6(第5题图)A B CO E1D(第4题图)A. B. C. D. x o o x x x y y y y7.如图是某几何体的三视图及相关数据,则判断正确的是 ( ) A . 222a b c += B .b c > C . 2224a b c += D .a c >(第7题图)8.任何一个正整数n 都可以进行这样的分解:q p n ⨯=(q p 、是正整数,且q p ≤),如果p q ⨯在n 的所有这种分解中两因数之差的绝对值最小,我们就称p q ⨯是n 的最佳分解,并规定:()pF n q=.例如18可以分解成118⨯、29⨯或36⨯,这时就有31(18)62F ==.给出下列关于()F n 的说法:(1)1(2)2F =;(2)3(24)8F =;(3)(27)3F =;(4)若n 是一个完全平方数,则()1F n =.其中正确说法的个数是 ( )A.1 B.2 C.3 D.4二、填空题(共4个小题,每小题4分,共16分) 9. 某商场为了解本商场服务质量,随机调查了来本商场的200名顾客,调查的结果如图所示,根据图中给出的信息,这200名顾客中对该商场的服务质量表示不满意...的有_________名.10.将抛物线2x y =的图象向右平移3个单位,则平移后的抛物线的解析式为 __ _ ___.11. 已知关于x 的一元二次方程 ()21210k x x ++-= 有两个不相等的实数根 ,则k 的取值范围是 ___ ___.12.如图,在梯形ABCD 中,AB ∥DC ,AB ⊥BC ,AB =2cm ,CD =4cm .以BC 上一点O 为圆心的圆经过A 、D 两点,且∠AOD =90°,则圆心O 到弦AD 的距离是 cm .(第12题图)BA COD :很满意 :满意 :基本满意 :不满意三、解答题(共5个小题,共25分) 13.(本小题满分5分)计算:()︒+--⎪⎭⎫⎝⎛---60sin 233121.14.(本小题满分5分)解不等式组:212(1) 1.x xx -⎧⎨+-⎩≤≥15. (本小题满分5分)如图,在ABCD 中E 是AD 的中点,BE 的延长线与CD 的延长线相交于点F .(1) 求证:△ABE ≌△DFE ;(2) 连结BD 、AF ,请判断四边形ABDF(第15题图)16. (本小题满分5分)如图,一次函数y kx b =+的图象与反比例函数my x=的图象交()3,1(2)A B n -、,于两点,直线AB 分别交x 轴、y 轴于D C 、两点. (1)求上述反比例函数和一次函数的解析式;(2)求ADCD的值.17. (本小题满分5分)先化简,再求值:22212221x x x x x x --+--+÷x ,其中x =23.四、解答题(共2个小题,共10分) 18.(本小题满分5分)小明在复习数学知识时,针对“求一元二次方程的解”,整理了以下的几种方法,请你将有关内容补充完整:例题:求一元二次方程210x x --=的两个解.解法一:选择合适的一种方法(公式法、配方法、分解因式法)求解. 解方程:210x x --=.解法二:利用二次函数图象与坐标轴的交点求解. 如图1所示,把方程210x x --=的解看成是二次函数y = 的图象与x 轴交点的 x 横坐标,即12,x x 就是方程的解.(第18题图1)解法三:利用两个函数图象的交点求解.(1)把方程210x x --=的解看成是一个二次函数y = 的图象与一个一次函数y = 的图象交点的横坐标;(2)画出这两个函数的图象,用12,x x 在x 轴上标出方程的解.(第18题图2)1x 2x y12 3 -11 o23 -1 -219.(本小题满分5分)如图,在梯形ABCD 中,AD ∥BC ,AC ⊥AB ,AD CD =,cosB =135,26BC =. 求(1)cos DAC ∠的值;(2)线段AD 的长.(第19题图)五、解答题(本题满分6分)20.在物理实验中,当电流在一定时间段内正常通过电子元件 时,每个电子元件的状态有两种可能:通电或断开,并且这两种状态的可能性相等.(第20题图1) (第20题图2) (第20题图3) (1) 如图1,当只有1个电子元件时,P 、Q 之间电流通过的概率是 ___________; (2) 如图2,当有2个电子元件a 、b 并联时,请你用树状图(或列表法)表示图中P 、Q 之间电流能否通过的所有可能情况,并求出P 、Q 之间电流通过的概率; (3) 如图3,当有3个电子元件并联时,P 、Q 之间电流通过的概率是__________. CB AD六、解答题(共2个小题,共9分)21.(本小题满分5分)列方程(组)或不等式(组)解应用题:B两种商品,销售完后共获利6万元,其进价和售价如下表:某商场用36万元购进A(1)该商场购进A、B两种商品各多少件;(2)商场第二次以原进价购进A、B两种商品.购进B种商品的件数不变,而购进A种商品的件数是第一次的2倍,A种商品按原售价出售,而B种商品打折销售.若两种商品销售完毕,要使第二次经营活动获利不少于81600元,B种商品最低售价为每件多少元?22.(本小题满分4分)如图,⊙O的直径AB=6cm,点P是AB延长线上的动点,过点P作⊙O的切线,切点为C, 的平分线交AC于点M,你认为∠CMP的大小是否发生变化?若变化,连结AC.若CPA请说明理由;若不变,求出∠CMP的度数.(第22题图)23.如图, 已知等边三角形ABC 中,点D 、E 、F 分别为边AB 、AC 、BC 的中点,M 为直线BC上一动点,△DMN 为等边三角形(点M 的位置改变时, △DMN 也随之整体移动).(1)如图1,当点M 在点B 左侧时,请你连结EN ,并判断EN 与MF 有怎样的数量关系?点F 是否在直线NE 上?请写出结论,并说明理由; (2)如图2,当点M 在BC 上时,其它条件不变,(1)的结论中EN 与MF 的数量关系是否仍然成立? 若成立,请利用图2证明;若不成立,请说明理由;(3)如图3,若点M 在点C 右侧时,请你判断(1)的结论中EN 与MF 的数量关系是否仍然成立? 若成立,请直接写出结论;若不成立,请说明理由.(第23题图1) (第23题图2) (第23题图3)M24.对于三个数a b c 、、,{},,M a b c 表示,,a b c 这三个数的平均数,{}min ,,a b c 表示a b c 、、这三个数中最小的数,如:{}12341,2,333M -++-==,{}min 1,2,31-=-; {}1211,2,33a a M a -+++-==,{}()()1min 1,2,11a a a a ≤-⎧⎪-=⎨->-⎪⎩.解决下列问题:(1)填空:{}min sin30,cos45,tan30︒︒︒= ;若{}min 2,22,422x x +-=,则x 的取值范围是 ;(2)①若{}{}2,1,2min 2,1,2M x x x x +=+,那么x = ;②根据①,你发现结论“若{}{},,min ,,M a b c a b c =,那么 ”(填,,a b c 大小关系);③运用②,填空:若{}{}22,2,2min 22,2,2M x y x y x y x y x y x y +++-=+++-,则x y += ;(3)在同一直角坐标系中作出函数1y x =+,()21y x =-,2y x =-的图象(不需列表,描点),通过图象,得出(){}2min 1,1,2x x x +--最大值为 .(第24题图)25.如图,矩形OABC 的边OC 、OA 分别与x 轴、y 轴重合,点B 的坐标是)1,3(,点D 是AB边上一个动点(与点A 不重合),沿OD 将△OAD 翻折,点A 落在点P 处. (1)若点P 在一次函数21y x =-的图象上,求点P 的坐标;(2)若点P 在抛物线2y ax =图象上,并满足△PCB 是等腰三角形,求该抛物线解析式; (3)当线段OD 与PC 所在直线垂直时,在PC 所在直线上作出一点M ,使DM+BM 最小,并求出这个最小值.y xOPDCBAABCOxy ABCOxy(第25题图) (第25题备用图1) (第25题备用图2)北京市宣武区2008-2009学年度第二学期第一次质量检测九年级数学参考答案及评分参考2009.5 一、选择题(共8个小题,每小题4分,共32分)二、填空题(共4个小题,每小题4分,共16分)三、解答题(共5个小题,共25分)13.(本小题满分5分)解:()0160sin23312+--⎪⎭⎫⎝⎛---=1322-⨯………………………………………………………………………4分=2-.…………………………………………………………………………………5分14.(本小题满分5)解:解不等式xx≤-12,得1x≤,……………………………………………………………2分不等式1)1(2-≥+x,得32x-≥.…………………………………………………………4分所以原不等式组的解集为312x-≤≤…………………………………………………………5分15.(本小题满分5分)证明:(1) ∵四边形ABCD是平行四边形,∴AB∥CF,∴∠1=∠2,∠3=∠4.∵E是AD的中点,∴AE=DE,∴△ABE≌△DFE.…………………………2分(2) 四边形ABDF是平行四边形.………………………3分∵△ABE≌△DFE,(第15题答图)∴AB=DF.又∵AB∥CF,∴四边形ABDF是平行四边形.……………………………………………………5分16.(本小题满分5分)解:(1)把3x=-,1y=代入myx=,得:3m=-.∴反比例函数的解析式为3y x=-. (1)把2x =,y n =代入3y x =-得32n =-. 把3x =-,1y =;2x =,32y =-分别代入y kx b =+得31322k b k b -+=⎧⎪⎨+=-⎪⎩, (第16题答图)解得1212k b ⎧=-⎪⎪⎨⎪=-⎪⎩,∴一次函数的解析式为1122y x =--.………………………… 3分(2)过点A 作AE x ⊥轴于点E .A 点的纵坐标为1,1AE ∴=. 由一次函数的解析式为1122y x =--得C 点的坐标为102⎛⎫- ⎪⎝⎭,, 12OC ∴=. 在Rt OCD △和Rt EAD △中,Rt COD AED ∠=∠=∠,CDO ADE ∠=∠, ∴Rt Rt OCD EAD △∽△. 2AD AE CD CO∴==. ……………………………………………………………………… 5分17.(本小题满分5分)解: 22212221x x xx x x --+--+÷x =2(1)(1)(2)1(1)2x x x x x x x+--+⋅-- ……………………………………………………………… 2分=111x x ++- …………………………………………………………………………3分 =21xx - ………………………………………………………………………… 4分 当23x =时, 原式=2234213⨯=-- . ……………………………………………………………………5分 四、解答题(共2个小题,共10分) 18.(本小题满分5分)(1)解:∵1,1,1a b c ==-=-, ∴245b ac -=.∴x =. ∴原方程的解是1x=12+,2x=12. ………………………………………………2分 (2)21x x --. …………………………………………………………………………………… 1分 (3)2x 与1x +或21x -与x 等. ………………………………………………………………… 1分正确画出函数图象给1分.19.(本小题满分5分)解:(1)在Rt △ABC 中,90BAC ∠= ,cos B =513AB BC =. ∵BC =26,∴AB =10.∴AC24=.∵AD //BC ,∴∠DAC =∠ACB . ∴cos ∠DAC = cos ∠ACB =1213AC BC =; ……………………………………… 2分 (2)过点D 作DE ⊥AC ,垂足为E . ∵AD =DC , AE =EC =1122AC =. 在Rt △ADE 中,cos ∠DAE =1213AE AD =, (第19题答图) ∴AD =13. …………………………………………………………5分五、解答题(本题满分6分)20.解:(1)0.5. ……………………………………………………………… 2分 (2)用树状图表示是:断开通电断开断开通电A B CD EFMN PP 、Q 之间电流通过的概率是43. ……………………………………………………………… 4分 (3)87. …………………………………………………………………………………………6分 六、解答题(共2个小题,共9分) 21.(本小题满分5分) 解:(1)设购进A 种商品x 件,B 种商品y 件.根据题意,得12001000360000,(13801200)(12001000)60000.x y x y +=⎧⎨-+-=⎩化简,得651800,9103000.x y x y +=⎧⎨+=⎩解之,得200,120.x y =⎧⎨=⎩答:该商场购进A 、B 两种商品分别为200件和120件. ……………………………… 3分(2)由于A 商品购进400件,获利为(1380-1200)×400 = 72000(元).从而B 商品售完获利应不少于81600-72000 = 9600(元). 设B 商品每件售价为x 元,则120(x -1000)≥9600. 解之,得x ≥1080.所以,B 种商品最低售价为每件1080元. ………………………………………… 5分 22.(本小题满分4分)解:∠CMP 的大小不发生变化. ……………………………………………………………………1分 连结OC ,PC 是⊙O 的切线,∴∠OCP=Rt ∠.∵PM 是∠CP A 的平分线, ∴∠APC =2∠APM .∵OA =OC ,∴∠A =∠ACO ,∴∠COP=∠A+∠ACO=2∠A . (第22题答图) 在Rt △OCP 中,∠OCP=90°, ∴∠COP+∠OPC=90°, ∴2∠A+2∠APM=90°, ∴∠CMP=∠A+∠APM=45°. …………………………………………………………… 4分 即∠CMP 的大小不发生变化.七、解答题(本题满分7分)23.解:(1)判断: EN=MF ,点F 在直线NE 上.证明:如答图1,连结DE 、DF 、EF . ∵△ABC 是等边三角形, ∴AB=AC=BC . 又∵D 、E 、F 是三边的中点, ∴DE 、DF 、EF 为△ABC 的中位线.FEDCBAM N∴DE=DF=EF ,∴∠FDE=∠DFE =60°. ∵△DMN 是等边三角形, ∴∠MDN =60°,DM=DN . ∴∠FDE +∠NDF=∠MDN+∠NDF , ∴∠MDF=∠NDE .在△DMF 和△DNE 中,DF=DE ,∠MDF=∠NDE , DM=DN , (第23题答图1) ∴△DMF ≌△DNE . ∴MF=NE . 设EN 与BC 交点为P ,连结NF .由△ABC 是等边三角形且D 、F 分别是AB 、BC 的中点可得△DBF 是等边三角形, ∴∠MDN=∠BDF =60°,∴∠MDN -∠BDN =∠BDF -∠BDN ,即∠MDB=∠NDF. 在△DMB 和△DNF 中,DM=DN ,∠MDB=∠NDF ,DB=DF , ∴△DMB ≌△DNF . ∴∠DBM=∠DFN . ∵∠ABC =60°, ∴∠DBM =120°,∴∠NFD =120°. (第23题答图2) ∴∠NFD+∠DFE =120°+60°=180°.∴N 、F 、E 三点共线,∴F 与P 重合,F 在直线NE 上.……………………………………4分 (2)成立。
电子版 宣武初三练习2009

北京市宣武区2009—2010学年度初三练习四、单项填空(共15分,每小题1分)从下列各题所给的A、B、C、D四个选项中,选择可以填入空白处的最佳选项。
21.It isn’t cell phone. I left it at home.A. mineB. meC. ID. my22.—When did Hong Kong return to our motherland.'?—1997.A. OnB. InC. AtD. For23.—is your new teacher?—The one standing with a dictionary in his hand.A.WhoB.WhatC.WhereD.Which24. —Listen, what’s the noise?—My fatherr the programme of the World Cup.A. watchesB. has watchedC. is watchingD. will watch25. Li Ming has the key to our class, and he often comes to school .A. earlyB. earliestC. much earlierD. earlier26.—Lucy, what about going camping if it tomorrow?—Sounds great!A. didn’t rainB. hasn’t rain edC. won’t rainD. doesn’t rain27.—What was the weather like in Guangxi Province this spring?—There very little rain.A. hasB. haveC. isD. was28.—It’s very important to save water.—I agree with you. I hope ________ can realize that.A. somebodyB. nobodyC. everybodyD. anybody29. The teachers ask us not _________ in class.A. to sleepB. sleepC. sleepingD. sleeps30.—How long Mr. Li you English, Daming?—For three years.A. does; teachB. did; teachC. has; taughtD. are; teaching31. The students _________ their homework when the teacher came into theclassroom.A. doB. will doC. didD. were doing32.The players kept on training it rained heavily.A. sinceB. thoughC. becauseD. for33. —May I copy your homework?—Sorry, you .A. may notB. n eedn’tC. mustn’tD. w on’t34.The workers are building a school. I hope it before August this year.A. finishesB. will finishC. is finishedD. will be finished35. — Do you know ? I’m going to see him.— Sorry, I don’t know.A. where he livesB. where does he liveC. where did he liveD. where he lived五、完形填空(共12分,每小题1分)阅读下面的短文,掌握其大意,然后从短文后各题所给的A、B、C、D 四个选项中,选择最佳选项。
—度北京市宣武区九年级数学第二学期第一次质量检测试卷

2008—2009学年度北京市宣武区九年级数学第二学期第一次质量检测试卷一、选择题(共8个小题,每小题4分,共32分) 1.31的相反数是 ( )A. 3B. -3C.31 D. -31 2. 2008年北京市经济保持较快发展,按常住人口计算,全市人均GDP 达到63029元,这个数据用科学记数法表示为 ( )A. 310029.63⨯元B. 51063029.0⨯元C. 4103029.6⨯元D. 3103029.6⨯元 3. ⊙O 的半径为5,圆心O 到直线l 的距离为3,则直线l 与⊙O 的位置关系是 ( ) A. 相交 B. 相切 C. 相离 D. 无法确定 4. 如图,AB 、CD 相交于点O ,∠1=80°,如果DE ∥AB ,那么∠D 的度数为 ( )A. 110°B. 100°C. 90°D. 80° 5. 如图是小敏同学6次数学测验的成绩统计图,则该同学6次成绩的中位数是 ( )A. 60分B. 70分C. 75分D. 80分6. 乌鸦口渴到处找水喝,它看到了一个装有水的瓶子,但水位较低,且瓶口又小,乌鸦喝不着水,沉思一会儿后,聪明的乌鸦衔来一个个小石子放入瓶中,水位上升后,乌鸦喝到了水. 在这则乌鸦喝水的故事中,设从乌鸦看到瓶的那刻起向后的时间为x ,瓶中水位的高度为y ,下列图象中最符合故事情景的是 ( )7. 如图是某几何体的三视图及相关数据,则判断正确的是 ( ) A. 222c b a =+ B. c b > C. 222c b a 4=+ D. c a >8. 任何一个正整数n 都可以进行这样的分解:n=p ×q (p 、q 是正整数,且p ≤q ),如果p ×q 在n 的所有这种分解中两因数之差的绝对值最小,我们就称p ×q 是n 的最佳分解,并规定:.q p )n (F = 例如18可以分解成1×18、2×9或3×6,这时就有F (18)=2163=. 给出下列关于F (n )的说法:(1)21)2(F =;(2)83)24(F =;(3)3)27(F =;(4)若n 是一个完全平方数,则F (n )=1. 其中正确说法的个数是 ( )A. 1B. 2C. 3D. 4二、填空题(共4个小题,每小题4分,共16分)9. 某商场为了解本商场服务质量,随机调查了来本商场的200名顾客,调查的结果如图所示,根据图中给出的信息,这200名顾客中对该商场的服务质量表示不满意...的有 名.10. 将抛物线y=x 2的图象向右平移3个单位,则平移后的抛物线的解析式为 .11. 已知关于x 的一元二次方程01x 2x )1k (2=-++有两个不相等的实数根,则k 的取值范围是 .12. 如图,在梯形ABCD 中,AB ∥DC ,AB ⊥BC ,AB=2cm ,CD=4cm. 以BC 上一点O 为圆心的圆经过A 、D 两点,且∠AOD=90°,则圆心O 到弦AD 的距离是 cm.三、解答题(共5个小题,共25分) 13. (本小题满分5分)计算:.60sin 2|3|)31()2(10︒+----- 14. (本小题满分5分)解不等式组:⎩⎨⎧-≥+≤-.1)1x (2,x 1x 215. (本小题满分5分)如图,在平行四边形ABCD 中,点E 是AD 的中点,BE 的延长线与CD 的延长线相交于点F.(1)求证:△ABE ≌△DFE ;(2)连结BD 、AF ,请判断四边形ABDF 的形状,并证明你的结论.16. (本小题满分5分)如图,一次函数y=kx+b 的图象与反比例函数xmy =的图象交于A (-3,1)、B (2,n )两点,直线AB 分别交x 轴、y 轴于D 、C 两点.(1)求上述反比例函数和一次函数的解析式;(2)求CDAD的值.17. (本小题满分5分)先化简,再求值:x 2x x 2x 1x 2x 1x 222÷--++--,其中.32x =四、解答题(共2个小题,共10分) 18. (本小题满分5分)小明在复习数学知识时,针对“求一元二次方程的解”,整理了以下的几种方法,请你将有关内容补充完整:例题:求一元二次方程01x x 2=--的两个解.解法一:选择合适的一种方法(公式法、配方法、分解因式法)求解,解方程:.01x x 2=--解法二:利用二次函数图象与坐标轴的交点求解. 如图1所示,把方程01x x 2=--的解看成是二次函数y= 的图象与x 轴交点的横坐标,即x 1,x 2就是方程的解.解法三:利用两个函数图象的交点求解.(1)把方程01x x 2=--的解看成是一个二次函数y= 的图象与一个一次函数y= 的图象交点的横坐标;(2)画出这两个函数的图象,用x 1,x 2在x 轴上标出方程的解.19. (本小题满分5分)如图,在梯形ABCD 中,AD ∥BC ,AC ⊥AB ,AD=CD ,cosB=135,BC=26. 求(1)cos ∠DAC 的值;(2)线段AD 的长.五、解答题(本题满分6分)20. 在物理实验中,当电流在一定时间段内正常通过电子元件 时,每个电子元件的状态有两种可能:通电或断开,并且这两种状态的可能性相等.(1)如图1,当只有1个电子元件时,P 、Q 之间电流通过的概率是 ;(2)如图2,当有2个电子元件a 、b 并联时,请你用树状图(或列表法)表示图中P 、Q 之间电流能否通过的所有可能情况,并求出P 、Q 之间电流通过的概率;(3)如图3,当有3个电子元件并联时,P 、Q 之间电流通过的概率是 .六、解答题(共2个小题,共9分)21. (本小题满分5分)列方程(组)或不等式(组)解应用题:(注:获利=售价-进价)(1)该商场购进A、B两种商品各多少件;(2)商场第二次以原进价购进A、B两种商品. 购进B种商品的件数不变,而购进A 种商品的件数是第一次的2倍,A种商品按原售价出售,而B种商品打折销售. 若两种商品销售完毕,要使第二次经营活动获利不少于81600元,B种商品最低售价为每件多少元?22. (本小题满分4分)如图,⊙O的直径AB=6cm,点P是AB延长线上的动点,过点P作⊙O的切线,切点为C,连结AC若∠CPA的平分线交AC于点M,你认为∠CMP的大小是否发生变化?若变化,请说明理由;若不变,求出∠CMP的度数.七、解答题(本题满分7分)23. 如图,已知等边三角形ABC中,点D、E、F分别为边AB、AC、BC的中点,M为直线BC上一动点,△DMN为等边三角形(点M的位置改变时,△DMN也随之整体移动).(1)如图1,当点M在点B左侧时,请你连结EN,并判断EN与MF有怎样的数量关系?点F是否在直线NE上?请写出结论,并说明理由;(2)如图2,当点M在BC上时,其它条件不变,(1)的结论中EN与MF的数量关系是否仍然成立?若成立,请利用图2证明;若不成立,请说明理由;(3)如图3,当点M 在点C 右侧时,请你判断(1)的结论中EN 与MF 的数量关系是否仍然成立?若成立,请直接写出结论;若不成立,请说明理由.八、解答题(本题满分7分)24. 对于三个数a 、b 、c ,M{a ,b ,c}表示这三个数的平均数,min{a ,b ,c}表示a 、b 、c 这三个数中最小的数,如:1}3,2,1min{,343321}3,2,1{M -=-=++-=-; ⎩⎨⎧->--≤=-+=++-=-).1a (1),1a (a }a ,2,1min{,31a 3a 21}a ,2,1{M 解决下列问题:(1)填空:min{sin30°,cos45°,tan30°}= ;若}x 24,2x 2,2min{-+=2,则x 的取值范围是 ;(2)①若M{2,x+1,2x}=min{2,x+1,2x},那么x = ;②根据①,你发现结论“若M{a ,b ,c}=min{a ,b ,c},那么 ”(填a ,b ,c 大小关系);③运用②,填空:若}y x 2,y 2x ,2y x 2min{}y x 2,y 2x ,2y x 2{M -+++=-+++,则 =+y x ;(3)在同一直角坐标系中作出函数x 2y ,)1x (y ,1x y 2-=-=+=的图象(不需列表,描点),通过图象,得出}x 2,)1x (,1x min{2--+最大值为 .九、解答题(本题满分8分)25. 如图,矩形OABC 的边OC 、OA 分别与x 轴、y 轴重合,点B 的坐标是(3,1),点D是AB边上一个动点(与点A不重合),沿OD将△OAD翻折后,点A落在点P处.(1)若点P在一次函数y=2x-1的图象上,求点P的坐标;(2)若点P在抛物线y=ax2图象上,并满足△PCB是等腰三角形,求该抛物线解析式;(3)当线段OD与PC所在直线垂直时,在PC所在直线上作出一点M,使DM+BM 最小,并求出这个最小值.【参考答案】一、选择题(共8个小题,每小题4分,共32分) 1. D 2. C 3. A 4. B 5. C 6. D 7. A 8. B 二、填空题(共4个小题,每小题4分,共16分) 9. 14 10. 2)3x (y -= 11. 1k 2k -≠->且 12. 10三、解答题(共5个小题,共25分) 13. (本小题满分5分)解:︒+-----60sin 2|3|)31()2(10232331⨯+--= 4分 2-=.5分 14. (本小题满分5分)解:解不等式.1x ,x 1x 2≤≤-得 2分解不等式.23x ,1)1x (2-≥-≥+得 4分所以原不等式组的解集为.1x 23≤≤- 5分15. (本小题满分5分)证明:(1)∵四边形ABCD 是平行四边形,∴AB ∥CF ,∴∠1=∠2,∠3=∠4.∵E 是AD 的中点,∴AE=DE , ∴△ABE ≌△DFE 2分(2)四边形ABDF 是平行四边形. 3分 ∵△ABE ≌△DFE ,∴AB=DF. 又∵AB ∥CF ,∴四边形ABDF 是平行四边形. 5分 16. (本小题满分5分)解:(1)把3x -=,y=1代入xmy =,得.3m -= ∴反比例函数的解析式为.x3y -=1分把x=2,y=n 代入x 3y -=得.23n -= 把23y ,2x ;1y ,3x -===-=分别代入b kx y +=得⎪⎩⎪⎨⎧-=+=+-,23b k 2,1b k 3解得⎪⎪⎩⎪⎪⎨⎧-=-=.21b ,21k ∴一次函数的解析式为.21x 21y --=3分(2)过点A 作AE ⊥x 轴于点E.∵A 点的纵坐标为1,∴AE=1. 由一次函数的解析式21x 21y --=得点C 的坐标为(21,0-), .21OC =∴在Rt △OCD 和Rt △EAD 中,∠COD=∠AED=90°,∠CDO=∠ADE , ∴Rt △OCD ∽Rt △EAD ,.2COAECD AD ==∴5分17. (本小题满分5分)解:x 2x x2x 1x 2x 1x 222÷--++-- x 12x )2x (x )1x ()1x )(1x (2⋅--+--+=2分11x 1x +-+=3分.1x x2-=4分当32x =时,原式.4132322-=-⨯= 5分四、解答题(共2个小题,共10分) 18. (本小题满分5分)(1)解:.5ac 4b ,1c ,1b ,1a 2=-∴-=-==.251x ±=∴ ∴原方程的解是.251x ,251x 21-=+=2分(2).1x x 2-- 3分 (3)1x 1x x 22-+或与与x 等. 4分正确画出函数图象给1分. 19. (本小题满分5分)解:(1)在Rt △ABC 中,∠BAC=90°,.135BC AB B cos ==.10AB ,26BC =∴=.241026AB BC AC 2222=-=-=∴ .ACB DAC ,BC //AD ∠=∠∴∴cos ∠DAC =cos ∠ACB =.13122624BC AC ==2分(2)过点D 作DE ⊥AC ,垂足为E..12AC 21EC AE ,DC AD ===∴=在Rt △ADE 中,cos ∠DAE =1312AD AE =,∴AD=13. 5分 五、解答题(本题满分6分) 20. 解:(1)0.52分(2)用树状图表示是:或用列表法表示是:P 、Q 之间电流通过的概率是.43 4分(3).876分六、解答题(共2个小题,共9分) 21. (本小题满分5分)解:(1)设购进A 种商品x 件,B 种商品y 件.根据题意,得⎩⎨⎧=-+-=+.60000y )10001200(x )12001380(,360000y 1000x 1200解得⎩⎨⎧==.120y ,200x答:该商场购进A 、B 两种商品分别为200件和120件. 3分(2)由于A 种商品购进400件,获利为 (1380-1200)×400=72000(元).从而B 种商品售完获利应不少于81600-72000=9600(元). 设B 种商品每件售价为x 元,则120(x -1000)≥9600. 解得x ≥1080.答:B 种商品最低售价为每件1080元. 5分 22. (本小题满分4分)解:∠CMP 的大小不发生变化. 1分 连结OC.∵PC 是⊙O 的切线, ∴∠OCP=90°.∵PM 是∠CPA 的平分线, ∴∠APC=2∠APM.∵OA=OC. ∴∠A=∠ACO , ∴∠COP=∠A+∠ACO=2∠A. 在Rt △OCP 中,∠OCP=90°, ∴∠COP+∠OPC=90°, ∴2∠A+2∠APM =90°,∴∠CMP=∠A+∠APM=45°. 故∠CMP 的大小不发生变化. 4分 七、解答题(本题满分7分)23. 解:(1)判断:EN=MF ,点F 在直线NE 上. 证明:如答图1,连结DE 、DF 、EF.∵△ABC是等边三角形,∴AB=AC=BC.又∵D、E、F是三边的中点,∴DE、DF、EF为△ABC的中位线.∴DE=DF=EF. ∴∠FDE=∠DFE=60°.∵△DMN是等边三角形,∴∠MDN=60°,DM=DN.∴∠FDE+∠NDF=∠MDN+∠NDF,∴∠MDF=∠NDE.在△DMF和△DNE中,DF=DE,∠MDF=∠NDE,DM=DN,∴△DMF≌△DNE. ∴MF=NE.设EN与BC交点为P,连结NF.由△ABC是等边三角形且D、F分别是AB、BC的中点可得△DBF是等边三角形,∴∠MDN=∠BDF=60°,∴∠MDN-∠BDN=∠BDF-∠BDN,即∠MDB=∠NDF.在△DMB和△DNF中,DM=DN,∠MDB=∠NDF,DB=DF,∴△DMB≌△DNF. ∴∠DBM=∠DFN.∵∠ABC=60°.∴∠DBM=120°,∴∠NFD=120°.∴∠NFD+∠DFE=120°+60°=180°.∴N、F、E三点共线,∴F与P重合,F在直线NE上. 4分(2)成立.证明:如答图2,连结DE、DF、EF.∵△ABC是等边三角形,∴AB=AC=BC.又∵D,E,F是三边的中点,∴DE,DF,EF为△ABC的中位线.∴DE=DF=EF. ∠FDE=60°.又∠MDF+∠FDN=60°.∠NDE+∠FDN=60°,∴∠MDF=∠NDE.在△DMF和△DNE中,DF=DE,∠MDF=∠NDE,DM=DN,∴△DMF≌△DNE. ∴MF=NE. ……6分(3)MF=NE仍成立. ………………………7分八、解答题(本题满分7分) 24. 解:(1)1x 0,21≤≤; 2分 (2)①1,②a=b=c ,③-4;5分 (3)图象如图所示,}x 2,)1x (,1x min{2--+最大值为1.7分九、解答题(本题满分8分) 25. 解:(1)∵B (3,1), ∴BC=OA=OP=1,OC=3.∵点P 在一次函数y=2x -1的图象上, ∴设P (x ,2x -1).如答图1,过P 作PH ⊥x 轴于H.在Rt △OPH 中,PH=2x -1,OH=x. OP=1,.1)1x 2(x 22=-+∴解得:0x ,54x 21==(不合题意,舍去).).5,5(P ∴2分(2)解法1:连结PB 、PC. ①若PB=PC ,则P 在BC 中垂线21y =上. ∴设P (21,x ). 如答图2,过P 作PH ⊥x 轴于H.在Rt △OPH 中,1OP ,x OH ,21PH ===, .141x 2=+∴ 解得:23x ,23x 21-==(不合题意,舍去). )21,23(P ∴,43a 21⨯=∴, 解得:.x 32y .32a 2=∴=②若BP=BC ,则BP=1.连结OB. ∵OP=1, ∴OP+PB=2. 在Rt △OBC 中,∠OCB=90°,.213OB =+=∴OP+PB=OB ;∴O 、P 、B 三点共线,P 为线段OB 中点. 又B )1,3(,)21,23(P ∴, 43a 21⨯=∴, 解得:.32a =.x 3y 2=∴ ③若CP=CB ,则CP=1。
北京市宣武区2009-2010学年度第二学期第一次质量检测

第3题图第5题图延庆县2011年毕业考试试卷 初 三 数 学考生须知1.本试卷共6页,共五道大题,25道小题,满分120分。
考试时间120分钟。
2.在试卷和答题卡上认真填写学校名称、姓名和准考证号。
3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效。
4.在答题卡上,选择题、作图题用2B 铅笔作答,其他试题用黑色签字笔作答。
5.考试结束,请将本试卷、答题卡和草稿纸一并交回。
第Ⅰ卷 (选择题 32分)一、选择题:(共8个小题,每小题4分, 共32分)在下列每小题给出的四个选项中,只有一个是符合题目要求的,请在答题纸上将所选项涂黑。
1.2-的绝对值是A .2B .2-C .21D .21-2.十一五期间,延庆县加大生态建设和环境保护力度,完成了京津风沙源治理、康庄风沙危害区治理、S2线和110国道绿色通道等绿化美化工程.全年实现造林31000亩,将31000用科学记数法表示为A .5101.3⨯ B .4101.3⨯C .31031⨯D .51031.0⨯3.一个几何体的三视图如图所示, 这个几何体是 A .圆锥 B .圆柱 C .球 D .三棱柱4.2010年4月份,某市一周空气质量报告中某项污染指数的数据是:31323034313531,,,,,,,这组数据的平均数与中位数分别是A .3231,B .3132,C .3131,D .3432, 5.如图是一张矩形纸片ABCD ,cm 10AD =,若将纸片沿DE 折叠, 使DC 落在DA 上,点C 的对应点为点F ,若cm BE 6=, 则DC 的长是A .cm 4B .cm 6C .cm 8D .cm 10 6.因式分解:32a ab -,结果正确的是F EDBA CA OPCB第11题图第8题图A .)(22a b a -B .2)(a b a -C .))((a b a b a -+D .))((b a b a a +-7.一个袋子中装有2个黑球3个白球,这些球除颜色外,形状、大小、质地等完全相同,在看不到球的条件下,随机地从这个袋子中摸出一个球,摸到白球的概率A .31B . 21C .51D . 538. 如图:已知P 是线段AB 上的动点(P 不与B A ,重合),分别以AP 、PB 为边在线段AB 的同侧作等边AEP ∆和等 边PFB ∆,连结EF ,设EF 的中点为G ;点D C 、在线段AB 上且BD AC =,当点P 从点C 运动到点D 时,设点G 到直线AB 的距离为y ,则能表示y 与P 点移动的时间x 之间函数关系的大致图象是第Ⅱ卷 (非选择题 88分)二、填空题(共4个小题,每小题4分,共16分) 9. 函数2y x =-中自变量x 的取值范围是 .10. 已知:a x x y +-=42的顶点纵坐标为b ,那么b a -的值是 . 11.如图,⊙O 是等边三角形ABC 的外接圆,点P 在劣弧AB 上,ABP ∠22=,则BCP ∠的度数为_____________.12.如图,图①是一块边长为1,周长记为1P 的正三角形纸板,沿图①的底边剪去一块边长为12的正三角形纸板后得到图②,然后沿同一底边依次剪去一块更小的正三角形纸板(即其边长为前一块被剪掉正三角形纸板边长的21)后,得图③,④,…,记第)3(≥n n 块纸板的周长为n P ,则=-34P P ;1--n n P P = .A .B .C .D .ABC DPEFGOEDCBA第12题图 第15题图第17题图…21世纪教育网三、解答题(共6个小题,每小题5分,共30分)13.计算:计算: 021( 3.14)2cos30()123π---︒++14.解不等式组: )1(42121+<-≤-x x x 并写出不等式组的整数解.15.如图,AE AB =,AC AD =,E A C B A D ∠=∠, DE BC ,交于点O . 求证:AED ABC ∠=∠.16.已知02=++b a ,求b a ba a ---1222的值. 17. 如图,M 点是正比例函数kx y =和反比例函数x my =的图象的一个交点.(1)求这两个函数的解析式;(2)在反比例函数x my =的图象上取一点P ,过点P 做A P 垂直于x 轴,垂足为A ,点Q 是直线MO 上一点,QB 垂直于y 轴,垂足为B ,直线MO 上是否存在这样的点Q ,使得O B Q ∆的面积是OPA ∆的面积的2倍?如果存在,请求出 点Q 的坐标,如果不存在,请说明理由;18.列方程或方程组解应用题:2011年4月10日,以“休闲延庆踏青赏花”为主题的第十届延庆杏花节开幕,(1)2000年“杏花节”期间旅游收入为1.01万元,2005年“杏花节”期间旅游收入为35.2万元,求“杏花节”期间,2005年的旅游收入比2000年增加了几倍? (结果精确到整数) (2)“杏花节”期间,2009年旅游收入与2010年的旅游收入的总和是153.99万元,且2010年的旅游收入是2009年的3倍少0.25万元,问2010年“杏花节”期间的旅游收入是否突6 ADCBA 第19题图破了百万元大关?四、解答题(共4个小题,第19,20小题各5分,第21题6分,第22题4分,共20分,)19. 已知如图:直角梯形ABCD 中,BC AD //,90=∠BAD ,26CD ==BC ,1312sin =C ,求:梯形ABCD 的面积;20.如图,ABC ∆是等腰三角形,AC AB =,以AC 为 直径的⊙O 与BC 交于点D ,AB DE ⊥,垂足为E ,ED 的延长线与AC 的延长线交于点F .(1)求证:DE 是⊙O 的切线;(2)若⊙O 的半径为2,1=BE ,求A cos 的值.21.“知识改变命运,科技繁荣祖国”.我市中小学每年都要举办一届科技运动会.下图为我市某校2010年参加科技运动会航模比赛(包括空模、海模、车模、建模四个类别)的参赛人数统计图:(1)该校参加车模、建模比赛的人数分别是 人和 人; (2)该校参加航模比赛的总人数是 人, 并把条形统计图补充完整;(3)从全市中小学参加航模比赛选手中随机抽取80人,其中有32人获奖. 今年我市中小学参加航模比赛人数共有2485人,请你估算今年参加航模比赛的获奖人数约是多少人?22.阅读下列材料:根据所给的图形解答下列问题:(1)如图1,ABC ∆中,AC AB =,90=∠BAC ,空模 建模车模 海模2525某校2010年航模比赛 参赛人数扇形统计图 某校2010年航模比赛 参赛人数条形统计图 ABFCDE O第20题图参赛人数(单位:人) 参赛类别 02 空模 684 海模 车模 建模 6 4 6第22题图1第22题图3 D C B A 第22题图2 CBAD BC AD 于⊥,把ABD ∆绕点A 旋转,并拼接成一个正方形,请你在图1中完成这个作图;(2)如图2,ABC ∆中,AC AB =,90=∠BAC ,请你设计一种与(1)不同方法,将这个三角形拆分并拼接成一个与其面积相等的正方形,画出利用这个三角形得 到的正方形;(3)设计一种方法把图3中的矩形ABCD 拆分并拼接为一个与其面积相等的正方形, 请你依据此矩形画出正方形.五、解答题(共3个小题, 23小题7分,24小题8分,25小题7分,共22分)23.已知:关于x 的一元二次方程012)1(22=+++-m x m x (1)求证:方程有两个实数根;(2)设0<m ,且方程的两个实数根分别为21,x x (其中21x x <),若y 是关于m 的函数,且y =1216x x -,求这个函数的解析式; (3)在(2)的条件下,利用函数图象求关于m 的方程02=-+m y 的解.24. 如图1,已知矩形ABCD 的顶点A 与点O 重合,AD 、AB 分别在x 轴、y 轴上,2=AD ,3=AB ;抛物线c bx x y ++-=2经过坐标原点O 和x 轴上另一点)0,4(E(1)当x 取何值时,该抛物线的最大值是多少?(2)将矩形ABCD 以每秒1个单位长度的速度从图1所示的位置沿x 轴的正方向匀速平行移动,同时一动点P 也以相同的速度从点A 出发向B 匀速移动.设它们运动的时间为t 秒(30≤≤t ),直线AB 与该抛物线的交点为N (如图2所示).第24题图1 第24题图2① 当411=t 时,判断点P 是否在直线ME 上,并说明理由;② 以D C N 、、、P 为顶点的多边形面积是否可能为5,若有可能,求出此时N 点的坐标;若无可能,请说明理由.25. 在Rt ABC △中,902BAC AB AC ∠===,,点D 在BC 所在的直线上运动,作45ADE ∠=(A D E ,,按逆时针方向).21世纪教育网(1)如图1,若点D 在线段BC 上运动,DE 交AC 于E. ①求证:ABD DCE △∽△;②当ADE △是等腰三角形时,求AE 的长.(2)①如图2,若点D 在BC 的延长线上运动,DE 的反向延长线与AC 的延长线相交于点E ',是否存在点D ,使ADE '△是等腰三角形?若存在,写出所有点D 的位置;若不存在,请简要说明理由;②如图3,若点D 在BC 的反向延长线上运动,是否存在点D ,使ADE △是等腰三角形?若存在,写出所有点D 的位置;若不存在,请简要说明理由.4545CDB A EE 'CABDE第25题图2第25题图345ABDCE第25题图1OEDCBA延庆县2010—2011毕业考试参考答案 初三数学一、选择题(每小题4分,共32分)1. A2.B3. A4. B5. A6. C7.D 8 .D二、填空题(每小题4分,共16分)9. 2≥x 10.4 11.38 12. 81,121-⎪⎭⎫ ⎝⎛n三、解答题(共6个小题,每小题5分,共30分)13.计算:021( 3.14)2cos30()123π---︒++=3292321++⨯-=32931++- =310+14.解不等式组: )1(42121+<-≤-x x x解:由不等式①,得到 x ≤3 ………………1分 由不等式②,得到 x>-2 ………………2分 所以这个不等式组的解集是3x 2-≤< ……………… 3分 将这个解集在数轴上略 ……………… 4分 所以这个不等式组的整数解集是-1,0 1,2,3 ………………5分15. 证明: ∵EAC BAD ∠=∠∴DAC EAC DAC BAD ∠+∠=∠+∠即: EAD BAC ∠=∠在EAD BAC ∆∆和 AE AB =EAD BAC ∠=∠ AC AD = ∴EAD BAC ∆≅∆………………4分………………5分①②………………1分 ………………4分 ………………5分∴AED ABC ∠=∠16. b a ba a ---1222 =))(())((2b a b a b a b a b a a -++--+ =))(()(2b a b a b a a -++- =))((b a b a ba -+- =b a +1∵02=++b a ∴2-=+b a∴原式=21-17. (1)由图可知,M 点的坐标为(-1,2)M 点是正比例函数kx y =和反比例函数x m y =的图象的一个交点 ∴x y 2-=,x y 2-= (2) ∵点P 在反比例函数x y 2-=的图象上,且2-=p x∴1=p y设)2,(a a Q - 由题意可知:O PAO BQ S S ∆∆=2………………1分………………3分………………2分………………4分………………5分………………1分………………2分………………3分3分∴12212221-⨯=-a a∴22=a ∴2±=a∴点Q 的坐标(22,2-)或(22,2-)21世纪教育网18. 解:(1)(35.2-1.01)÷1.01≈34答:2005年的成交金额比2000年约增加了34倍 …………………1分(2)设2010年成交金额为x 万元,则2009年成交金额为(3x -0.25)万元 30.25153.99x x +-=解得:x=38.56∴30.25115.43x -=>100∴2010年“杏花节”期间的旅游收入突破了百亿元大关.……………5分19.解:过点D 做E BC DE 于点⊥,CD=26在DCE Rt ∆中,26DECD DE 1312sin ===C∴DE=24∴由勾股定理得:CE=10 ∴BE=CD-CE=16∵90=∠BAD ,E BC DE 于点⊥∴DE//BC ∵BC AD //∴四边形ABED 是平行四边形 ∴AD=BE=16∴5042DEBC AD S ABCD =+=)(20. 证明:(1)连结AD ,OD ∵AC 是直径………………4分 ………………5分………………2分 ………………4分 ………………1分………………2分………………3分………………4分………………5分 ………………1分∴BC AD ⊥ ∵AB=AC∴D 是BC 的中点 ∵O 是AC 的中点∴AB //OD ∵AB DE ⊥ ∴DE OD ⊥ ∴DE 是⊙O 的切线 (2)由(1)可知,AE OD //∴AE OD FAFO =∴BE AB OD AC FC OC FC -=++ ∴14242-=++FC FC∴FC=2∴AF=621世纪教育网∴21cos ==AF AE A21.(1) 4 , 6 ……………………………(每空1分,共2分) (2) 24 , 120… ………………………………(每空1分,共2分) (图略) ………………………………………5分 (3)32÷80=0.4……………………1分 0.4×2485=994答:今年参加航模比赛的获奖人数约是994人.………………………………6分22.图略五、解答题23.解:(1)∵12),1(2,1+=+-==m c m b a2224)12(14)]1(2[4mm m ac b =+⨯⨯-+-=-=∆∴ ………………2分………………3分………………4分 ………………5分 ………………1分x x y 42+-= ∵无论m 取何值时,都有02≥m∴方程有两个实数根(2)方程的两个实数根分别为21,x x ∴m m m m a ac b b x x ±+=±+=-±-==)1(22)1(224221∵0<m ,21x x <21世纪教育网∴1,1221=+=x m x∴y =m m m x x 32612161612-=-=--=- (3)关于m 的方程02=-+m y 的解是1,3-==m m24.解:(1)因抛物线c bx x y ++-=2经过坐标原点O (0,0)和点E (4,0) 故可得c=0,b=4所以抛物线的解析式为 ………………………1分由4)2(422+--=+-=x x x y 得当x=2时,该抛物线的最大值是4. …………………………………………2分(2)① 点P 不在直线ME 上.已知M 点的坐标为(2,4),E 点的坐标为(4,0),设直线ME 的关系式为y=kx+b.于是得⎩⎨⎧=+=+4204b k b k ,解得⎩⎨⎧=-=82b k所以直线ME 的关系式为y=-2x+8. …………………………………………3分 由已知条件易得,当411=t 时,OA=AP=411,)411,411(P …………………4分∵ P 点的坐标不满足直线ME 的关系式y=-2x+8. 21世纪教育网∴ 当411=t 时,点P 不在直线ME 上. ……………………………………5分②以P 、N 、C 、D 为顶点的多边形面积可能为5∵ 点A 在x 轴的非负半轴上,且N 在抛物线上,………………2分 ………………3分 ………………5分 ………………7分∴ OA=AP=t.∴ 点P ,N 的坐标分别为(t,t)、(t,-t 2+4t)∴ AN=-t 2+4t (0≤t ≤3) ,∴ AN-AP=(-t 2+4 t)- t=-t 2+3 t=t(3-t)≥0 ,∴ PN=-t 2+3 t ……………………………6分(ⅰ)当PN=0,即t=0或t=3时,以点P ,N ,C ,D 为顶点的多边形是三角形,此三角形的高为AD ,∴ S=21DC ·AD=21×3×2=3.(ⅱ)当PN ≠0时,以点P ,N ,C ,D 为顶点的多边形是四边形∵ PN ∥CD ,AD ⊥CD ,∴ S=21(CD+PN)·AD=21[3+(-t 2+3 t)]×2=-t 2+3 t+3当-t 2+3 t+3=5时,解得t=1、2而1、2都在0≤t ≤3范围内,故以P 、N 、C 、D 为顶点的多边形面积为5综上所述,当t=1、2时,以点P ,N ,C ,D 为顶点的多边形面积为5,…………………………………………………7分当t=1时,此时N 点的坐标(1,3)当t=2时,此时N 点的坐标(2,4)………………………………………8分25. ①证明:在Rt ABC △中,∵902BAC AB AC ∠===,∴∠B=∠C=45°又 ∠ADE=45°∴∠ADB+∠EBC=∠EBC+∠DEC=135°∴∠ADB=∠DEC∴ ABD DCE △∽△② 当ADE △是等腰三角形时,分以下三种情况讨论第一种情况:DE=AE∵DE=AE∴∠ADE=∠DAE=45°∴ ∠AED=90°, 此时,E 为AC 的中点, ∴AE=12AC=1.第二种情况:AD=AE (D 与B 重合)AE=2第三种情况 :AD=AE如果AD=DE ,由于ABD DCE △∽△, ………………2分………………1分 ………………3分∴ △ABD ≌△DCE,∴BD=CE,AB=DC,设BD=CE=x在Rt ABC △中,∵902BAC AB AC ∠===,,∴ BC=22, DC=22-x ∴22-x =2 ,解得,x =22-2 ,∴ AE= 4 -22综上所述:AE 的值是1,2, 4 -22(2)①存在。
2008-2009学年北京宣武区第二学期九年级第一次质量检测

2008-2009学年度北京市宣武区第二学期九年级第一次质量检测数学试卷一、选择题(共8个小题,每小题4分,共32分)1.31的相反数是 ( ) A .3 B .3- C .31 D .31- 2.2008年北京市经济保持较快发展,按常住人口计算,全市人均GDP 达到63029元,这个数据用科学记数法表示为 ( )A .363.02910⨯元B .50.6302910⨯元C .46.302910⨯元D .36.302910⨯元3.⊙O 的半径为5,圆心O 到直线l 的距离为3,则直线l 与⊙O 的位置关系是 ( )A .相交B . 相切C . 相离D .无法确定4.如图,AB 、CD 相交于点O ,∠1=80°,如果DE ∥AB ,那么∠D 的度数为 ( )A .110°B .100°C .90°D .80°5.如图是小敏同学6次数学测验的成绩统计图,则该同学6次成绩的中位数是 ( )A .60分B .70分C .75分D .80分6.乌鸦口渴到处找水喝,它看到了一个装有水的瓶子,但水位较低,且瓶口又小,乌鸦喝不着水,沉思一会儿后,聪明的乌鸦衔来一个个小石子放入瓶中,水位上升后,乌鸦喝到了水。
在这则乌鸦喝水的故事中,设从乌鸦看到瓶的那刻起向后的时间为x ,瓶中水位的高度为y ,下列图象中最符合故事情景的是 ( )7.如图是某几何体的三视图及相关数据,则判断正确的是 ( )A .222a b c +=B .b c >C .2224a b c +=D .a c >8.任何一个正整数n 都可以进行这样的分解:q p n ⨯=(q p 、是正整数,且q p ≤),如果p q ⨯在n 的所有这种分解中两因数之差的绝对值最小,我们就称p q ⨯是n 的最佳分解,并规定:()p F n q =.例如18可以分解成118⨯、29⨯或36⨯,这时就有31(18)62F ==.给出下列关于()F n 的说法:(1)1(2)2F =;(2)3(24)8F =;(3)(27)3F =;(4)若n 是一个完全平方数,则()1F n =.其中正确说法的个数是( ) A .1 B .2 C .3 D .4二、填空题(共4个小题,每小题4分,共16分)9.某商场为了解本商场服务质量,随机调查了来本商场的200名顾客,调查的结果如图所示,根据图中给出的信息,这200名顾客中对该商场的服务质量表示不满意...的有_________名.10.将抛物线2x y =的图象向右平移3个单位,则平移后的抛物线的解析式为 __ _.11.已知关于x 的一元二次方程 ()21210k x x ++-= 有两个不相等的实数根 ,则k 的取值范围是 ___ ___.12.如图,在梯形ABCD 中,AB ∥DC ,AB ⊥BC ,AB =2cm ,CD =4cm .以BC上一点O为圆心的圆经过A 、D 两点,且∠AOD =90°,则圆心O 到弦AD 的距离是 cm .三、解答题(共5个小题,共25分)13.(本小题满分5分)计算:()︒+--⎪⎭⎫ ⎝⎛---60sin 2331210. 14.(本小题满分5分)解不等式组:212(1) 1.x x x -⎧⎨+-⎩≤≥ 15.(本小题满分5分)如图,在ABCD 中,点E 是AD 的中点,BE 的延长线与CD 的延长线相交于点F .(1)求证:△ABE ≌△DFE ;(2)连结BD 、AF ,请判断四边形ABDF 的形状,并证明你的结论.16.(本小题满分5分)如图,一次函数y kx b =+的图象与反比例函数m y x=的图象交()3,1(2)A B n -、,于两点,直线AB 分别交x 轴、y 轴于D C 、两点.(1)求上述反比例函数和一次函数的解析式;(2)求AD CD 的值.17.(本小题满分5分)先化简,再求值:22212221x x x x x x --+--+÷x ,其中x =23. 四、解答题(共2个小题,共10分)18.(本小题满分5分)小明在复习数学知识时,针对“求一元二次方程的解”,整理了以下的几种方法,请你将有关内容补充完整:例题:求一元二次方程210x x --=的两个解.解法一:选择合适的一种方法(公式法、配方法、分解因式法)求解.解方程:210x x --=.解法二:利用二次函数图象与坐标轴的交点求解.如图1所示,把方程210x x --=的解看成是二次函数y = 的图象与x 轴交点的x 横坐标,即12,x x 就是方程的解.解法三:利用两个函数图象的交点求解.(1)把方程210x x --=的解看成是一个二次函数y = 的图象与一个一次函数y = 的图象交点的横坐标;(2)画出这两个函数的图象,用12,x x 在x 轴上标出方程的解.19.(本小题满分5分)如图,在梯形ABCD 中,AD ∥BC ,AC ⊥AB ,AD CD =,cosB =135,26BC =. 求(1)cos DAC ∠的值;(2)线段AD 的长.五、解答题(本题满分6分)20.在物理实验中,当电流在一定时间段内正常通过电子元件时,每个电子元件的状态有两种可能:通电或断开,并且这两种状态的可能性相等.(1) 如图1,当只有1个电子元件时,P 、Q 之间电流通过的概率是 ___________;(2) 如图2,当有2个电子元件a 、b 并联时,请你用树状图(或列表法)表示图中P 、Q 之间电流能否通过的所有可能情况,并求出P 、Q 之间电流通过的概率;(3) 如图3,当有3个电子元件并联时,P 、Q 之间电流通过的概率是__________.六、解答题(共2个小题,共9分)21.(本小题满分5分)列方程(组)或不等式(组)解应用题:某商场用36万元购进A 、B 两种商品,销售完后共获利6万元,其进价和售价如下表:A B进价(元/件)1200 1000售价(元/件)1380 1200(注:获利= 售价—进价)(1)该商场购进A、B两种商品各多少件;(2)商场第二次以原进价购进A、B两种商品.购进B种商品的件数不变,而购进A种商品的件数是第一次的2倍,A种商品按原售价出售,而B种商品打折销售.若两种商品销售完毕,要使第二次经营活动获利不少于81600元,B种商品最低售价为每件多少元?22.(本小题满分4分)如图,⊙O的直径AB=6cm,点P是AB延长线上的动点,过点P作⊙O的切线,切的平分线交AC于点M,你认为∠CMP的大小是否发点为C,连结AC.若CPA生变化?若变化,请说明理由;若不变,求出∠CMP的度数.七、解答题(本题满分7分)23.如图,已知等边三角形ABC中,点D、E、F分别为边AB、AC、BC的中点,M为直线BC上一动点,△DMN为等边三角形(点M的位置改变时,△DMN也随之整体移动).(1)如图1,当点M在点B左侧时,请你连结EN,并判断EN与MF有怎样的数量关系?点F是否在直线NE上?请写出结论,并说明理由;(2)如图2,当点M在BC上时,其它条件不变,(1)的结论中EN与MF的数量关系是否仍然成立? 若成立,请利用图2证明;若不成立,请说明理由;(3)如图3,若点M在点C右侧时,请你判断(1)的结论中EN与MF的数量关系是否仍然成立? 若成立,请直接写出结论;若不成立,请说明理由.八、解答题(本题满分7分)24.对于三个数a b c 、、,{},,M a b c 表示,,a b c 这三个数的平均数,{}min ,,a b c 表示a b c 、、这三个数中最小的数,如:{}12341,2,333M -++-==,{}min 1,2,31-=-;{}1211,2,33a a M a -+++-==,{}()()1min 1,2,11a a a a ≤-⎧⎪-=⎨->-⎪⎩. 解决下列问题:(1)填空:{}min sin30,cos45,tan30︒︒︒= ;若{}min 2,22,422x x +-=,则x 的取值范围是 ;(2)①若{}{}2,1,2min 2,1,2M x x x x +=+,那么x = ;②根据①,你发现结论“若{}{},,min ,,M a b c a b c =,那么 ”(填,,a b c 大小关系); ③运用②,填空:若{}{}22,2,2min 22,2,2M x y x y x y x y x y x y +++-=+++-,则x y += ;(3)在同一直角坐标系中作出函数1y x =+,()21y x =-,2y x =-的图象(不需列表,描点),通过图象,得出(){}2min 1,1,2x x x +--最大值为 .九、解答题(本题满分8分)25.如图,矩形OABC 的边OC 、OA 分别与x 轴、y 轴重合,点B 的坐标是)1,3(,点D是AB 边上一个动点(与点A 不重合),沿OD 将△OAD 翻折,点A 落在点P 处.(1)若点P 在一次函数21y x =-的图象上,求点P 的坐标;(2)若点P 在抛物线2y ax =图象上,并满足△PCB 是等腰三角形,求该抛物线解析式;(3)当线段OD 与PC 所在直线垂直时,在PC 所在直线上作出一点M ,使DM+BM 最小,并求出这个最小值.。
初三 中考 试题 汇编09宣武区一模语文试卷分析.doc

09年宣武区一模语文试卷分析一、选择题1.考查字音的识别【点评】字音范围在1000个中考必考词语中,主要是针对平时易混淆的字音进行辨析,如“着落、逮住、星宿”2、字形的辨析与识记【点评】字形范围在1000个中考必考词语中,主要是针对音同意不同的易错字进行考查,如“漠不关心”、“涣散”、“今非昔比”、这些都是应该重点注意的词语。
3.成语、俗语的理解与运用【点评】本题主要是考查成语和俗语的理解与运用,两个成语两个俗语,在不增加总题量的情况下增加了题的难度,建议这种试题采用排除法完成。
4、考查句意的连贯性【点评】本题主要是考查前后照应,相对而言,难度不大,只要认真审题,弄清前后关系就不会出问题。
建议此类题型特别是偏难试题采用排除法。
降低难度。
5、文学常识考查【点评】范围是《中考说明》中的考查篇目,主要涉及到是作家、作品、朝代的考查;难度不大,建议此类型的试题采用排除法。
二、填空、简答6、默写【点评】包括直接默写和理解性默写两类。
范围是十九篇必考篇目,一般直接默写题难度不大,主要是考查学生对易错字的把握。
理解性默写相对比较难,需要学生综合考虑性定性的要求,一般情况下是对名句的理解。
7、名著的赏析《西游记》【点评】此题的考查内容比较简单,但是考查形式稍有变化,但依然是对主要人物性格特点的分析,要求学生用词的准确、贴切,难度较小。
三、综合性学习8.信息提取【点评】两则材料一则文字信息,一则图表信息,关于现实生活中的实际问题,比较贴近学生生活。
在一定的限定性条件下概括信息,学生不能全面分析、概括图表信息,属于易失分的试题。
9.文字表述,根据图表中出现的信息,结合实际谈主观感受,并且有一定的内容和字数限制。
【点评】此题注重的是语言的表达,难度不大,只要表达流畅、符合要求,就没问题。
另外学生审题也应该仔细。
10.文字表述【点评】本题主要是考查学生文字表述能力,语言的组织和运用能力。
针对特定社会现象并且结合材料,表达自己的观点,这一点对学生来说并不困难,难的是语言成型后是否完整流畅甚至是有文采。
北京市宣武区九年级数学中考一模试题(word版)

北京市宣武区2009-2010学年度第二学期第一次质量检测 九年级数学 2010.5第Ⅰ卷 (选择题 共32分)一、选择题(本题共有8个小题,每小题4分,共32分)在下列各题的四个备选答案中,只有一个是正确的。
1. 5-的绝对值是 A. 5 B. 5- C. 51-D. 51 2. 据《法制晚报》报道2010年北京市即将参加中考的考生共有约10300人. 这里数字10300用科学记数法表示为 A. 41003.1⨯ B. 51003.1⨯ C. 31003.1⨯ D. 5103.10⨯ 3. 某物体的展开图如图所示,它的左视图为4.不等式93≥-x 的解集为A. 3-≥xB. 6-≥xC. 3-≤xD. 6-≤x5.如图,点A 、B 、C 都在⊙O 上,且点C 在弦AB 所对的优弧上, 若72AOB ∠=︒,则ACB ∠ 的度数是 A .18° B .30° C .36° D .72°6. 某次器乐比赛共有11名选手参加且他们的得分都互不相同.现在知道这次比赛按选手得分由高到低的顺序设置了6个获奖名额.若已知某位选手参加这次比赛的得分,要判断他能否获奖,则在下列描述选手比赛成绩的统计量中,只需知道A .方差B .平均数C .众数D .中位数O C B A 第5题图A .B .C .D .7. 若4=-n m ,则22242n mn m +-的值为 A.32 B.22 C. 12 D. 08. 如图,正方形ABCD 的边长为2, 将长为2的线段QF 的两端放在正 方形相邻的两边上同时滑动.如果点Q 从点A 出发,沿图中所示方向按A D CB A →→→→滑动到点A 为止,同时点F 从点B 出发,沿 图中所示方向按B A DC B →→→→滑动到点B 为止,那么在这个过程中,线段QF 的中点M 所经过的路线围成的图形的面积为 A. 2 B. 4-π C.π D.1π-第Ⅱ卷 (非选择题 共88分)二、填空题(本题共有4个小题,每小题4分,共16分) 9.分解因式:=-23ab a ______ .10.如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=28o ,那么∠2的度数是 __.11.从2-,1-,0,1,2这五个数中任取一个数,作为关于x 的一元二次方程0=中的k 值,则所得的方程中有两个不相等的实数根的概率是 .12.如图,在第一象限内作与x 轴的夹角为030的射线OC ,在射线 OC 上取一点A ,过点A 作x AH ⊥轴于点H .在抛物线)0(2>=x x y 上取一点P ,在y 轴上取一点Q ,使得以P ,O ,Q 为顶点的三角形与△AOH 全等,则符合条件的点A 的坐标是 .Q三、解答题(本题共有6个小题,每小题5分,共30分)13.计算:()001201030cos 4112+⋅⎪⎭⎫ ⎝⎛---.14.用配方法解一元二次方程:0142=--x x .15.先化简,再求值: 11a b a b ⎛⎫-⎪-+⎝⎭÷222b a ab b -+,其中21+=a ,21-=b .16.已知:如图,ABCD 是正方形.G 是 BC 上的一点,AG DE ⊥于E ,AG BF ⊥于F .(1)求证:△ABF ≌△DAE ; (2)求证:FB EF AF +=.17.已知:如图,直线b kx y +=与反比例函数,k y x=(x <0)的图象相交于点A 、点B ,与x 轴交于点C ,其中点A 的坐标为(-2,4),点B 的横坐标为-4.(1)试确定反比例函数的关系式; (2)求△AOC 的面积. 第18.请在所给网格中按下列要求操作:⑴ 请在网格中建立平面直角坐标系, 使A 点坐标为(0,2),B 点坐标为(-2,0);⑵ 在(1)的条件下,在x 轴上画点C ,使△ABC 为等腰三角形,请画出所有符 合条件的点C ,并直接写出相应的C 点坐标.A DE F C GB四、应用题(本题6分)19.为了防控甲型H1N1流感,某校积极进行校园的环境消毒,为此购买了甲、乙两种消毒(1)求每瓶甲种消毒液和每瓶乙种消毒液各多少元?(2)销售员提示,现在买乙种消毒液有优惠,具体方法是:如果买乙种消毒液超过30瓶,那么超出部分可以享受8折优惠.学校现决定从甲、乙两种消毒液中买其中一种消毒液,数量为100瓶,请你帮助学校判断一下买哪种消毒液比较省钱,并说明理由.五、解答题(本题共有2个小题,共11分,其中第20题5分,第21题6分) 20.已知:如图,在△ABC 中,AD 是BC 上的高,tan cos B DAC =∠. (1)求证:AC=BD ;(2)当12sin 13C =,BC =12时,求AD 的长.CBA21.已知:如图,⊙O 是△ABC 的外接圆,AB 为⊙O 直径, 且PA ⊥AB 于点A ,PO ⊥AC 于点M . (1)求证:PC 是⊙O 的切线;(2)当OM =2,B cos =42时,求PC 的长.六、解答题(本题4分)22. 某校为了解九年级学生体育测试情况,以九年级(1)班学生的体育测试成绩为样本,按A B C D ,,,四个等级进行统计,并将统计结果绘制成如下的统计图.(说明:A 级:90分~100分;B 级:75分~89分;C 级:60分~74分;D 级:60分以下) 请你结合图中所给信息解答下列问题: (1)请把条形统计图补充完整;(2)样本中D 级的学生人数占全班学生人数的百分比是 ; (3)扇形统计图中A 级所在的扇形的圆心角度数是 ;(4)若该校九年级有500名学生,请你用此样本估计体育测试中A 级和B 级的学生人数约为 人.B 46%C 24%D A20%等级5Bx七、解答题(本题共3个小题,每小题7分,共21分)23.已知:MAN ∠,AC 平分MAN ∠. ⑴在图1中,若MAN ∠=120°,ABC ∠=ADC ∠=90°, AB +AD AC .(填写“>”,“<”,“=”)⑵在图2中,若MAN ∠=120°,ABC ∠+ADC ∠=180°,则⑴中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由. ⑶在图3中: ①若MAN ∠=60°,ABC ∠+ADC ∠=180°,判断AB +AD 与AC 的数量关系,并说明理由; ②若MAN ∠=α(0°<α<180°),ABC ∠+ADC ∠=180°,则AB +AD =____AC (用含α的三角函数表示,直接写出结果,不必证明)24.已知:将函数y =的图象向上平移2个单位,得到一个新的函数的图像. (1)求这个新的函数的解析式;(2)若平移前后的这两个函数图象分别与y 轴交于O 、A 两点,与直线x =C 、B 两点.试判断以A 、B 、C 、O 四点为顶点的四边形形状,并说明理由;(3)若⑵中的四边形(不包括边界)始终覆盖着二次函数22+-=bx x y 的图象的一部分,求满足条件的实数b 的取值范围.N M C D BA M N DB A CNMA B DC25.已知:如图,在直角坐标系中,已知点0P 的坐标为(10),,将线段0OP 按逆时针方向旋转45,再将其长度伸长为0OP 的2倍,得到线段1OP ;又将线段1OP 按逆时针方向旋转45,长度伸长为1OP 的2倍,得到线段2OP ;如此下去,得到线段3OP ,4OP ,,n OP (n 为正整数)(1)求点6P 的坐标; (2)求56POP △的面积;(3)我们规定:把点()n n n P x y ,(0123n =,,,,)的横坐标n x 、纵坐标n y 都取绝对值后得到的新坐标()n n x y ,称之为点 n P 的“绝对坐标”.根据图中点n P 的分布规律,请你猜想点n P的“绝对坐标”,并写出来.P北京市宣武区2009-2010学年度第二学期第一次质量检测九年级数学参考答案及评分标准 2010.5审核人:陈亮 校对:张浩一、选择题(本题共有8个小题,每小题4分,共32分)在下列各题的四个备选答案中,只二、填空题(本题共有4个小题,每小题4分,共16分)三、解答题(本题共有6个小题,每小题5分,共30分)13.计算:()001)2010(30cos 4112+⋅⎪⎭⎫⎝⎛---.解:原式=123432+⨯- -----------------------------------------------------------4分 =1. -------------------------------------------------------------------------------------5分 14.用配方法解一元二次方程: 0142=--x x . 解:原方程化为 142=-x x .配方,得 41442+=+-x x .即 5)2(2=-x , ∴ 52±=x . --------------------------------------------------4分∴ 原方程的解为521+=x ,522-=x . ----------------------------------------5分 15.解:原式=bb a b a b a b a b a 2)())(()()(-⋅+---+=ba b a +-)(2. . ---------------------------------------------------------------------------4分当21+=a ,21-=b 时,原式=222222=⨯. --------------------------5分 16.证明:(1)∵ ABCD 是正方形, ∴ 090=∠BAD . ∴ 090=∠+∠DAE BAF .∵ AG DE ⊥于E , ∴ 090=∠+∠ADE DAE . ∴ ADE BAF ∠=∠.∵ AG DE ⊥于E ,AG BF ⊥于F , ∴ 090=∠=∠DEA AFB .∵ 在正方形ABCD 中,AD AB =, ∴ △ABF ≌△DAE .------------------------4分 (2)证明:∵ △ABF ≌△DAE , ∴ AE BF =.∵ EF AE AF +=, ∴ EF BF AF +=. -------------------------------------------5分 17.解:(1)∵ 反比例函数xk y '=(x <0)的图象相交于点A (-2,4),∴ 8-=k . ∴ 所求的反比例函数的解析式为 xy 8-=.-----------------------------2分 (2)∵ 反比例函数xy 8-=(x <0)的图象相交于点B ,且点B 的横坐标为-4,∴ 点B 的纵坐标为2,即点B 的坐标为)2,4(-. ∵ 直线b kx y +=过点A )4,2(-、点B )2,4(-,∴ ⎩⎨⎧=+-=+-24,42b k b k 解得⎩⎨⎧==6,1b k .∴ b kx y +=的解析式为6+=x y .此时,点C 的坐标为)0,6(-. ∴ △AOC 的面积为S =124621=⨯⨯. ---------5分 18.解:⑴在网格中建立平面直角坐标系如图所示. ----------------------------------------------------2分 ⑵满足条件的点有4个: C 1:(2,0);C 2:(222-,0)C 3:(0,0);C 4:(222--,0). -----------------------------------------------------5分四、应用题(本题6分)19.解:(1)设甲种消毒液每瓶售价x 元,乙种消毒液每瓶售价y 元. 依题意得:⎩⎨⎧=+=+6903080,6606040y x y x解得⎩⎨⎧==.7,6y x 答:甲、乙两种消毒液每瓶各6元和8元.-----------------------------------------------------4分(2)买甲种消毒液所需费用为6×100=600 (元); 买乙种消毒液所需费用为7×30+7×0.86×(100-30)=602 (元). 因为,602>600, 所以,买甲种消毒液省钱.答:学校应买甲种消毒液.----------------------------------------------------------------- --------6分 五、解答题(本题共有2个小题,共11分,其中第20题5分,第21题6分) 20.解:(1)∵AD 是BC 上的高,∴AD ⊥BC .∴∠ADB =90°,∠ADC =90°. 在Rt △ABD 和Rt △ADC 中,∵tan B =AD BD ,cos DAC ∠=ADAC. 又已知tan cos B DAC =∠,∴ AD BD =AD AC.∴ AC=BD . -----------------------------------------------------------------3分(2)在Rt △ADC 中, 12sin 13C =,故可设AD =12k ,AC =13k .∴ CD k .∵CD BD BC +=,又BD AC =,∴ k k k BC 18513=+=. 由已知BC=12, ∴ 18k=12. ∴ k=23. ∴ AD =12k=1223⨯=8. ------------------------------------------------------------------------5分21. 解:(1)如图,连接OC .∵PA ⊥AB , ∴ ∠PAO=90°. ∵AO=CO ,PO ⊥AC 于点M ,∴∠AOP=∠COP . 又∵PO=PO , ∴△PAO ≌△PCO . ∴∠PCO=∠PAO=90°,PA=PC ,∴PC 是⊙O 的切线.------------------------3分(2)方法一:∵ PO ⊥AC 于点M , ∴ M 为AC 中点. 又∵ O 是AB 中点, ∴ MO ∥BC , ∴ ∠MOA=∠B , ∴ cos ∠MOA=cos ∠B=42. ∵ PO ⊥AC 于点M , ∴ 在Rt △AMO 中,AO=MOA MO ∠cos =422=4.∵ cos ∠POA =42, ∴ 在Rt △PAO 中,PO=POA AO∠cos =424=82.∴ PA=22AO PO -=47, ∴PC=PA=47.-------------------------------------------6分 方法二:同方法一,求出AO=4. ∵ cos ∠POA =42, ∴ tan ∠POA=7.∴ PA=AO· tan ∠POA=47. ∴ PC=PA=47.------------------------------------------- 6分 六、解答题(本题4分) 22. 解:(1)如图;------------------------------------------------------------------------------------------------1分 (2) 10%;------------------------------------------------------------------------------------ -----------2分 (3)72度;------------------------------------------------------------------------------------------------3分B5(4)330.--------------------------------------------------------------------------------------------------4分七、解答题(本题共3个小题,每小题7分,共21分) 23.解:(1) AB +AD = AC .--------------------------------------------------------------------------1分 (2) 仍然成立.证明:如图2过C 作CE ⊥AM 于E ,CF ⊥AN 于F , 则∠CEA=∠CFA=90°. ∵ AC 平分∠MAN ,∠MAN=120°, ∴ ∠MAC=∠NAC=60°.又∵ AC=AC , ∴ △AEC ≌△AFC ,∴ AE=AF ,CE=CF . ∵ 在Rt △CEA 中,∠EAC=60°, ∴ ∠ECA=30°, ∴ AC=2AE . ∴ AE+AF=2AE=AC . ∴ ED+DA+AF=AC . ∵ ∠ABC +∠AD C =180°,∠CDE+∠ADC=180°, ∴ ∠CDE=∠CBF .又∵ CE=CF ,∠CED=∠CFB , ∴ △CED ≌△CFB . ∴ ED=FB , ∴ FB+DA+AF=AC .∴ AB+AD=AC .----------------------------------------- 4分(3)①AB+AD=3AC .证明:如图3,方法同(2)可证△AGC ≌△AHC . ∴AG=AH . ∵∠MAN=60°, ∴∠GAC=∠HAC=30°. ∴AG=AH=23AC .∴AG+AH=3AC . ∴GD+DA+AH=3AC . 方法同(2)可证△GDC ≌△HBC . ∴GD=HB , ∴ HB+DA+AH=3AC .∴AD+AB=3AC .-------------------------------------------------------------------------------------6分②AB +AD =2cos2α·AC .-------------------------------------------------------------------7分24.解:⑴2y x =+. ----------------------------------------------------------------------------------------1分⑵答:四边形AOCB 为菱形.由题意可得AB//CO ,BC//AO ,AO=2.∴四边形AOCB 为平行四边形易得A(0,2),B (.由勾股定理可得AB=2, ∴AB= AO ∴平行四边形AOCB 为菱形.----------------------3分AAOCB⑶二次函数22122y x bx b =-++化为顶点式为:21()2y x b =-+.∴ 抛物线顶点在直线12y =上移动.假设四边形的边界可以覆盖到二次函数,则B 点和A 点分别是二次函数与四边形接触的边界点,将B (,代入二次函数,解得b =,b =,舍去). 将A (0,2),代入二次函数,解得2b =,b =(不合题意,舍去). 所以实数b的取值范围:b <<.-------------------------------------------------------7分25.解:(1)根据旋转规律,点6P 落在y 轴的负半轴,而点n P 到坐标原点的距离始终等于前一个点到原点距离的2倍,故其坐标为66(02)P ,,即6(064)P ,.------------------------------------------1分 (2)由已知可得,01121n n P OP POP P OP -△∽△∽∽△,设111()P x y ,,则12sin 452y ==011122P OP S ∴=⨯=△, 又6132OP OP =. 560123210241P OP P OP S S ⎛⎫∴== ⎪⎝⎭△△.561024P OP S ==△.--------------------------------4分 (3)由题意知,0OP 旋转8次之后回到x 轴正半轴,在这8次中,点n P 分别落在坐标象限的平分线上或x 轴或y 轴上,但各点绝对坐标的横、纵坐标均为非负数,因此,点n P 的坐标可分三类情况:A OCB令旋转次数为n .①当8n k =或84n k =+时(其中k 为自然数),点n P 落在x 轴上,此时,点n P 的绝对坐标为(20)n,; ②当81n k =+或83n k =+或85n k =+或87n k =+时(其中k 为自然数),点n P 落在各象限的平分线上,此时,点n P的绝对坐标为222n n ⎛⎫⎪ ⎪⎝⎭2,2,即(2n n --. ③当82n k =+或86n k =+时(其中k 为自然数),点n P 落在y 轴上,此时,点n P 的绝对坐标为(02)n,.--------------------------------------------------------------------7分。
宣武语文试题(word版)

北京市宣武区2009——2010学年度第二学期第一次质量检测九年级语文一、各题均有四个选项,其中只有一个符合题意,选出答案后在答题卡上用铅笔把对应题目的选项字母涂黑涂满。
(共10分,每小题2分)( )1.下列词语中加点字读音完全正确的是A. 庇.护(bì)机械.(xiè)斤斤计较.(jiǎo)B. 倔.强(juè)解剖.(pōu)毛遂.自荐(suí)C. 订.正(dìng)字帖.(tiē)追本溯.源(sù)D. 惩.罚(chéng)脖颈.(gěng)高屋建瓴.(líng)( )2.下列词语书写完全正确的是A. 淳朴粘贴谈笑风生B. 必竟恻隐语重心长C. 赔偿邮戳一愁莫展D. 斟酌云霄因地制宜( )3.下列句中划线词语使用不当的是A. 花点时间掌握学习方法,可以大大提高学习效率,磨刀不误砍柴工嘛。
B. 行百里者半九十,最后进入决赛的选手更要认真对待,不可掉以轻心。
C. 有些人取得一点成绩,眼里就没有别人了,真实一叶障目,不见泰山。
D.到什么山上唱什么歌,我们说话做事要依情况变化而采取不同方式。
( )4.结合语境,填入横线处最恰当的一项是自1999年起,我国普通高校开始实行扩招。
大幅度的扩招,因此出现了高校学生质量滑坡的现象。
A.给就业带来了巨大压力B.让更多学生有了上学机会C.使入学的门槛骤然降低D.缓解了学生和家长的压力( )5.下列诗词名句的作者均为同一朝代的是①塞下秋来风景异②不畏浮云遮望眼③乱花渐欲迷人眼④沉舟侧畔千帆过⑤直挂云帆济沧海A.①②③B.③④⑤C.①③⑤D.②④⑤二、填空(共8分)6.将原文默写在答题卡的相应序号后(5分)酒文化是中华文化的组成部分,古诗文中的“酒”不胜枚举。
“①?把酒问青天”是苏东坡中秋佳节的遐想;“把酒临风,②”是迁客骚人登楼远观的喜悦:“今日听君歌一曲,③”是刘禹锡以酒振奋精神;“浊酒一杯家万里,④”是范仲淹以酒排遣患乡之苦;虽是“金樽清酒斗十千,⑤”,酒仙李白却是“停杯投箸不能食”。
2009中考各区一模试题

二类卷(51—44) 46—39
三类卷(43—36) 38—31
四类卷(35—0) 30—0
书写(5 分)
总分
阅卷人
六、作文
题目:
100
200
300
宣武区 2008—2009 学年度第一次质量检测 初三语文试卷(第Ⅱ卷) 第 1 页 (共 2 页)
400 500
600 700
宣武区 2008—2009 学年度第一次质量检测 初三语文试卷(第Ⅱ卷) 第 2 页 (共 2 页)
北京市宣武区 2008—2009 学年度第一次质量检测
初三语文试卷答题卡(第Ⅱ卷)
2009.5
注意 1.答题前务必将学校、班级、姓名、考试编号等信息填写在密封线内的规定位置。 事项 2.在对应答题区域内作答,未在对应的答题区域内作答或超出答题区域均不给分。
项目 等级
内容、表达(55 分)
2008—2009 学年度第一次质量检测 初三语文试卷(第Ⅱ卷) 第 3 页 (共 2 页)
09宣武语文一模答题卡(第2卷)

初三语文试卷答题卡(第Ⅱ卷)
2009.5
注意 事项
1. 答题前务必将学校、班级、姓名、考试编号等信息填写在密封线内的规定位置。 2. 在对应答题区域内作答,未在对应的答题区域内作答或超出答题区域均不给分。
项目 等级 一类卷( 60— 52)
二类卷( 51— 44) 三类卷( 43— 36) 四类卷( 35— 0)
初三语文试卷(第Ⅱ卷)
第 2 页 (共 2 页)
宣武区 2008— 2009 学年度第一次质量检测
初三语文试卷(第Ⅱ卷)
第 3 页 (共 2 页)
内容、表达(பைடு நூலகம்55 分)
55—47 46—39 38—31 30— 0
书写( 5 分)
总分
阅卷人
六、作文
题目:
100
200
300
宣武区 2008— 2009 学年度第一次质量检测
初三语文试卷(第Ⅱ卷)
第 1 页 (共 2 页)
400 500
600
700
宣武区 2008— 2009 学年度第一次质量检测
宣武区2009-2010学年度初三年级四套试卷命题设计
期末
会考(含补考)
一模
二模
时间
2009.1
150分钟
2010.4
120分钟
2010.5
150分钟
2010.6
150分钟
总分值
120分
80分
120分
120分
总体难度
中
易
难
中
考试范围
九年级上
会考说明
中考说明
中考说明
字
题型:字音单独考查;字形可在词中考,可在句中考,可与字义结合考。
词
内容:成语,多义词,近义词,关联词,俗语。
句
病句
段
题型:排列语序,段中填句。
修辞
比喻、拟人、夸张、排比、对偶、反复、反问、设问。
文学常识
题型:归类,表述有误。
默写
记忆背诵、理解背诵、运用背诵三种试题在每次考试中都要有。
《渔家傲》《江城子》《破阵子》
会考说明和中考说明的共同部分
中考说明
中考说明
名著
《水浒传》《西游记》《朝花夕拾》
记叙文阅读
写人、记事、写景、状物四类记叙文最好都有涉及。
说明文阅读
注意结构梳理。
议论文阅读
注意思路和逻辑思维。
作文
体现对自我对世界的认识。鼓励创造性的自由表达。
题型:全命题、半命题为主,话题、材料为辅。
说明:
1.每类考查内容中的各类题型尽量在四套试卷中有所体现,每套试题的侧重点有所不同。
2.每套试题的总题量均不多于21道。
综合性学习
体现语文学科与其他学科、书本学习与实践运用的综合。(会考无此题)
文言文阅读
北京市宣武区中考英语一模试题及答案

北京市宣武区2009-2010学年度英语第二学期第一次质量检测九年级英语参考答案及评分标准2010. 5一、听对话,选择与对话内容相符的图片。
(共4分,每小题1分)1.A 3. C 4. B二、听对话和独白,根据对话和独白的内容,选择正确答案。
(共12分,每小题1分)5.C三、听对话,记录关键信息。
(共8分,每小题2分)17. Tom 18. birthday 19. (at)1:00 pm/13:00 20. go to the park四、单项填空(共15分,每小题1分)21. A五、完形填空(共12分,每小题1分)六、阅读下面的四篇短文,根据短文内容,从短文后各题所给的A、B、C、D四个选项中,选择最佳选项。
(共26分,每小题2分)七、阅读下面短文,根据短文内容,从短文后的选项中选出适当的选项补全短文,并将选项的答案写在答题卡上。
(共8分,每小题2分)八、阅读短文,根据其内容回答问题。
(共10分,每小题2分)65. Yes. / Yes, it is.66. When they are in good health.67. The color green.68. It means fast happy music.69. Meanings of different colours.九、完成句子(共10分,每小题2分)70. late for71. tells us not to read73. She will go on/keep training hard74. can not only help students(to)know about America as much as possible but also improvetheir English十、文段表达(15分)75. One possible version:Dear Tony,I have received your e-mail recently. I can understand you. You should tell him it’swrong to cheat because it’s bad for him. If he forms a habit of copying others’ answers, he will not work hard at his lessons. What’s more, it’s not honest to do that.What should you do? You’d better help him to study English hard. For example, you can ask him to listen to the teacher carefully in class. After class, you should make him use his head to do exercises. If he really needs help, you can help him. I’m sure, with your help, he will get rid of his bad habit and make progress soon.I hope these will help you!Yours,Li Ming书面表达评分标准:第一档:(15-13分)完全符合题目要求,内容完整、丰富,思想健康、积极向上。
北京市宣武区第二学期九年级第一次质量检测.doc

北京市宣武区第二学期九年级第一次质量检测姓名:_____________ 年级:____________ 学号:______________一、作文(共1题) 1. 题目:(l )我们(2)你们(3)他们(4)她们要求:(l )从以上题目中选择一个抄写在答题卡上,作为你的题目。
(2)自选文体(诗歌除外)。
(3)字数在600字以上。
(4)作文中不要出现所在学校的校名或师生姓名。
【答案】 略难度:中等 知识点:命题作文 二、现代文阅读(共3题)1. 阅读《拔苗助长,事与愿违》,完成第1—2题。
拔苗助长,事与愿违崔宇①教育并不是越早越好,而是越合适越好。
可是很多家长固执地相信,抢跑是在为孩子争分夺秒。
②自然界万物都按照生长规律自然生长,适当施加外力可以促其生长,倘若施用外力不当,就很容易出现倒退甚至枯萎现象。
教育孩子也是一样的道理。
卡尔就是这样一个被毁的天才。
少年卡尔在父亲的强迫下,每一分钟都要学习,一切与学业无关的兴趣爱好都被父亲隔在门外。
最初,这样的教育取得了成就,卡尔8岁学习大学数学,11岁大学毕业。
教授们预言卡尔会成为一名世界顶尖级数学家。
父亲更是一心想使他早日成名。
然而不久,卡尔对数学再也提不起兴趣,再也不想动脑筋,再也不想思考问题。
最后,曾经的天才做了办事员,远远偏离了他父亲的培养轨道。
③教育抢跑的不利影响不容忽视。
抢跑将扼杀孩子的兴趣和智慧。
孩子有强烈的求知欲、好奇心,这对其成才是极为重要的。
居里夫人说:“好奇心是学者的第一美德。
”如果家长只有望子成龙之心,但不讲究教子成才之术,结果只能事与愿违。
④徐悲鸿的父亲徐达章是一名画师,当幼小的徐悲鸿要求学画时,父亲温和地拒绝了:“要想成为一个画家,先要好好读书。
”两年后,9岁的他才如愿以偿,开始从父习画,终成一代大师。
对孩子的培养应该遵循教育规律和人的身心发展规律,以这个规律为依据,先了解孩子的现有的身心发展水平和所学知识水平,再谋求合适的教育内容和有效的教育方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北京市宣武区2008-2009学年度第二学期一模质量检测九 年 级 化 学 2009.5考生须 知 1. 本试卷共8 页。
全卷共四道大题,35道小题。
2. 本试卷满分80分,考试时间100分钟。
3. 试卷答案一律填写在答题卡上,在试卷上作答无效。
选择题的答案用2B 铅笔规范填涂;其它题一律用黑色签字笔规范书写。
4. 在试卷、答题卡的密封线内准确填写学校、班级、姓名和学号。
5. 考试结束后,将试卷和答题卡一并交回。
6. 本试卷化学方程式中的“=”和“ ”含义相同。
可能用到的相对原子质量H 1 C 12 N 14 O 16 S 32 Ca 40 Cu 64 Zn 65 部分碱和盐的溶解性表(20 ℃)Ba 2+ Ca 2+ Mg 2+ Ag + OH - 溶 微 不 CO 32- 不 不 微 不 Cl –溶溶溶不一、选择题(每小题只有一个选项符合题意。
共25个小题,每小题1分,共25分。
) 1.地壳中含量最多的金属元素是A .铝元素B .硅元素C .氧元素D .铁元素 2.为解决登山人员的呼吸困难,需提供的物质是A .氮气B .二氧化碳C .氧气D .水 3.“84消毒液”的主要成分是次氯酸钠(NaClO )的水溶液。
“84消毒液”属于A .氧化物B .单质C .化合物D .混合物 4.“金银铜铁锡”俗称五金。
在这五种金属中,金属活动性最弱的是A .铁B .金C .银D .铜 5.下列粒子不能..直接构成物质的是 A .电子 B .分子 C .离子 D .原子6.在缺氮的情况下,植物的生长发育迟缓或停滞。
这时应施用的化肥是 A .KCl B .NH 4Cl C .K 2CO 3 D .Ca(H 2PO 4 )2 7.下列物质的变化属于化学性质的是A .红磷可以点燃B .浓盐酸的挥发C .氢氧化钠的潮解D .石蜡的熔化8.右图为简易的净水装置示意图,关于此装置的作用说法正确的是 A . 能杀菌消毒 B .能得到纯净水C .能除去可溶性杂质D .能除去固体杂质 9.下列实验操作不正确...的是A .稀释浓硫酸B .氯化钠溶解C .取用氢氧化钠固体D .取粉末状固体药品阳离子阴离子10.下列清洗方法中,利用乳化原理的是A.用洗涤剂清洗餐具B.用汽油清洗油污C.用自来水洗蔬菜D.用水冲洗试管内残留的氯化钠固体11.下列各图能说明分子间的间隔变小的是A.炒菜闻到香味B.湿衣服晾干C.酚酞遇氨水变红D.压缩空气12.二氧化碳由碳、氧两种元素组成,这两种元素的本质区别是A.质子数不同B.中子数不同C.电子数不同D.最外层电子数不同13.下列有关木炭、一氧化碳、酒精的说法不正确...的是A. 都是含碳的物质 B.燃烧时都有蓝色火焰C.完全燃烧都有二氧化碳气体生成 D.燃烧时都放出大量热14.每种植物都有适宜自己生长的酸碱性环境。
下表为四种作物适宜生长的pH范围:作物水稻茶树玉米马铃薯pH 6.0~7.0 5.0~5.5 7.0~8.0 4.8~5.5取某地土壤浸出的液体,加入石蕊溶液后溶液显红色,该土壤最不适宜...种植的作物是 A.水稻 B.茶树 C.玉米 D.马铃薯15.下列变化与空气成分无关..的是A.久置的双氧水变轻 B.生石灰在空气中变质C.氢氧化钠密闭保存 D.浓硫酸敞口放置质量增加16.下列做法正确的是A. 人体补钙可多吃动物的肝脏B. 皮肤上沾有较浓的碱液用大量的水冲洗即可C. 场馆附近的绿化采用微灌或滴灌智能控制技术D. 为防止水产品腐烂可将水产品浸泡在甲醛溶液中17.下列现象不能..用质量守恒定律解释的是A.蜡烛燃烧逐渐变短B.干冰在升华时,吸收周围空气的热量C.铝条燃烧后生成物的质量比铝条的质量大D.纸燃烧变为灰烬,灰烬的质量比纸的质量小18.雄伟壮观的国家大剧院主体建筑表面使用的是钛合金板,将钛(Ti)放在海水中数年后取出仍光亮如初。
下列关于钛及其化合物的说法正确的是A.钛酸亚铁(FeTiO3)属于氧化物B.二氧化钛(TiO2)中含有氧分子C.钛单质具有较强的抗腐蚀性D.Ti可以表示钛元素,也可以表示1个钛分子,还可以表示钛单质19.下列关于金属的叙述正确的是A.常温下金属单质都是固体B.铜的活动性比铁弱,可以用铁容器盛放硫酸铜溶液C.铁的化学性质比较活泼,可以在空气中燃烧D.铝不易被腐蚀,是因为铝的表面能形成一层致密的氧化膜20.下列物质的用途利用了中和反应原理的是①用稀硫酸除铁锈②用氯化钠配制生理盐水③用生石灰作食品干燥剂④用氨水涂抹蚊虫叮咬(蚁酸)处进行止痒⑤用氢氧化钠溶液处理石油产品中残留的硫酸A.③④B.②④C.②⑤D.④⑤21.右图为某有机物的分子模型(化学式:C6H6O),该有机物的稀溶液具有杀菌防腐的功能。
下列说法不正确...的是A.该有机物可用于消毒防腐B.该有机物共由13个原子构成C.该有机物中氢元素的质量分数最小D.该有机物分子中碳、氢原子的个数比为1:122.甲、乙两个排污口排放了H2SO4、KNO3、MgCl2和NaOH四种物质,它们各含其中的两种。
依据卷首给出的“部分碱和盐的溶解性表”,判断下列关于污水的分析正确的是A.H2SO4和KNO3一定来自同一排污口B.H2SO4和MgCl2一定来自同一排污口C.MgCl2和KNO3一定来自同一排污口D.H2SO4和NaOH一定来自同一排污口23.下列表达式表示的是氟利昂(CF2Cl2)对臭氧层的破坏历程(已知:氟气和氯气均为双原子分子),关于这个历程描述正确的是A.②发生了置换反应B.在化学反应前后微粒的个数都不变C.在化学反应中,分子可分、原子不能分D.臭氧与氧气的转化过程属于物理变化24.向装有30 g稀硫酸的小烧杯中,逐滴加入5 %的氢氧化钡溶液至过量,小烧杯中有关量的变化如下图(反应方程式H2SO4 + B a(O H)2= BaSO4↓+ 2H2O)。
其中不正确...的是25.A、B、C三种物质各20 g,它们化合时只能生成40 g的新物质D。
再增加5 g A,反应停止时只有B剩余。
下列说法正确的是A.反应中B和C的质量比是5:4 B.第一次反应后,B剩余质量为4 gC.反应中D和C的质量比是5:2 D.第二次反应后,D的质量为65 g二、填空题(本题包括5个小题,共30分) 26.(共4分)日常饮食中蕴含着丰富的化学知识。
(1)北方人常说“好吃不过饺子”。
制作三鲜馅饺子的原料主要有面粉、油、韭菜、肉类、虾仁、盐和鸡蛋等。
①食用盐的品种丰富,有碘盐、硒盐、锌盐等。
这些盐中含的“碘、硒、锌”是指 (填“元素”或“单质”)。
②上述原料除虾仁、肉类外,还可以提供蛋白质的是 。
③韭菜富含的营养素是 。
(2)雪碧是一种碳酸饮料,加热滴有雪碧的石蕊溶液,溶液的颜色由红色变成紫色,用化学方程式说明上述变化的原因 。
27.(共9分)燃料在社会发展过程中起着重要的作用。
(1)下列燃料的变化属于物理变化的是 。
A .酒精的挥发B .煤的燃烧C . 石油气的液化(2)酒精作为燃料的一种在其它领域中也有着广泛应用,如:通过酒精检测仪显示的颜色变化,交警可快速测出司机是否酒后驾车。
反应原理:2CrO 3(红色)+3C 2H 5OH +3H 2SO 4==Cr 2(SO 4)3(绿色)+3CH 3CHO +6X ,X 的化学式为_________。
(3)氢气被誉为“最清洁的燃料”,请用化学方程式解释“美名”得来的原因 。
(4)家庭燃气热水器上常标注“燃气热水器切勿安装于密闭浴室或通风不良处”,解释标注此标识的原因 。
(5)京城悄然出现“纸火锅”(如右图)。
“纸火锅”是用纸代替金属材料做容器来盛放汤料,当酒精燃烧时纸不会被点燃。
关于此现象,下列解释不合理...的是 (填序号)。
A.空气不充足,纸不会燃烧B.纸被水淋湿,纸的着火点降低C.水蒸发时吸收热量,温度达不到纸的着火点D.酒精燃烧时产生热量少,温度达不到纸的着火点 (6)下表列出的是每克气体....燃料完全燃烧时放出的热量及氢元素的质量分数。
燃料名称 甲烷 乙烷 丙烷 乙烯 乙炔 化学式 CH 4 C 2H 6 C 3H 8 C 2H 4 C 2H 2 热量(×104 J/g ) 5.56 5.20 5.05 5.04 5.00 氢元素的质量分数(%)25.020.018.214.37.7根据上述数据分析,最好选用的气体燃料是 ;选用它的原因是 ; 。
28.(共4分)下列数据是四种固体物质在20℃时的溶解度。
(1)20℃时,分别向盛有100 g 水的四个烧杯中加入34.0 g 上述四种物质,充分溶解后,一定能得到饱和溶液的是 (填化学式)。
(2)质量分数为25%的氯化钠溶液,其溶质与溶剂的质量比为 。
(3)甲图烧杯A 中是20℃时硝酸钾的饱和溶液,乙图是硝酸钾溶液的溶解度曲线,a 、 b 分别表示硝酸钾的两种状态。
下列做法能实现a 转化为b 的是(填字母)。
A .向烧杯B 中加一定量的浓硫酸 B .向烧杯A 中加一定量的水 C .向烧杯B 中加一定量的硝酸铵固体 D .向烧杯B 中加一定量的氯化钠固体 E .向烧杯B 中加一定量的氧化钙固体物质名称 氯化铵 硝酸钾 氯化钾 氯化钠化学式NH 4Cl KNO 3 K Cl NaCl 溶解度(g )37.2 31.6 34.0 36.029.(共7分)自然界中人与动物的生存都离不开氧气。
(1)核潜艇舱室中氧气的来源主要靠电解水制得(原理如图)。
①正极收集的气体是 ,②A 试管和B 试管中收集到的气体的 体积比约等于___________,③水是由 组成的。
(2)过氧化钠(Na 2O 2)可作为宇航员供氧剂。
它与人体呼出的二氧化碳气体反应生成氧气和另一种能用于造纸、纺织等生产的物质,这种物质的俗名为 。
(3)亚氯酸钠(NaClO 2)不仅可以制得氧气,还可用于漂白杀菌,其中氯元素的化合价为 。
(4)过氧化钙(CaO 2)用于鱼池供氧剂,同时有熟石灰生成。
①写出过氧化钙与水反应的化学方程式 。
②现将7.2 g 过氧化钙放入36.0 g 水中,使之充分反应,所得混合物中氧元素的质量分数 (结果保留一位小数)。
30.(共6分)A ~G 是初中化学常见的七种物质。
“ ”表示两端的物质能发生化学反应;“”表示物质间存在转化关系。
(部分生成物和反应条件已略去)(1)若A 、D 两物质的相对分子质量比为11:7,A 、C 、D 均含有一种相同元素, E 、F 、G 间的反应均在常温下进行,B 与G 的反应属于化合反应。
则B 的化学式 ; G E 的反应条件是 ;写出下列反应的化学方程式:①D+ E ②B+G(2)若A 与 F 、C与D、E与G它们两两之间属于同一类物质,B 为另一类物质。
