图解球体表面积和体积正确计算方法及计算公式
球体的体积与表面积计算

球体的体积与表面积计算球体作为一种几何体,其体积与表面积的计算是解决很多相关问题的基础。
本文将详细介绍如何计算球体的体积与表面积,并给出相关的数学公式和实例。
一、球体的体积计算球体的体积表示球体所包围的三维空间的容积大小。
下面我们将介绍球体体积计算的数学公式。
设球的半径为r,则球体的体积V可以通过下面的公式计算得出:V = (4/3)πr³其中,π是一个常数,近似值为3.14159。
例如,当半径r=5时,可以通过代入数值计算球体的体积:V = (4/3)π(5³) = (4/3)π125 ≈ 523.6所以,半径为5的球体的体积约为523.6。
需要注意的是,球体的半径必须为正数,否则体积计算将无意义。
二、球体的表面积计算球体的表面积表示球体外部所覆盖的面积大小。
下面我们将介绍球体表面积计算的数学公式。
与体积计算类似,球的半径为r时,球体的表面积S可以通过下面的公式计算得出:S = 4πr²依然以半径r=5为例,可以通过代入数值计算球体的表面积:S = 4π(5²) = 4π25 ≈ 314.16所以,半径为5的球体的表面积约为314.16。
同样地,球体的半径必须为正数,否则表面积计算将无意义。
总结:本文介绍了如何计算球体的体积与表面积。
球体的体积由半径决定,通过(V = (4/3)πr³)公式求得;球体的表面积同样由半径决定,通过(S =4πr²)公式求得。
这些计算公式可以帮助我们解决与球体相关的数学和物理问题,例如容器的容积、球形物体的设计等。
需要注意的是,对于球体的计算,我们需要确保半径为正数,以保证计算的准确性。
另外,利用计算机软件和计算器可以更方便地完成这些计算,减少人工计算出错的可能性。
通过了解球体的体积与表面积的计算方法,我们可以更好地理解球体的属性,并将其应用于实际问题中,进一步拓宽我们的数学知识和解决问题的能力。
球体的表面积和体积计算

球体的表面积和体积计算球体是一种简单而常见的几何图形,它具有很多独特的性质和特点。
在数学和物理学中,计算球体的表面积和体积是一个基本而重要的问题。
在本文中,我们将介绍如何准确计算球体的表面积和体积。
一、球体的表面积计算公式要计算球体的表面积,我们可以使用以下公式:S = 4πr²其中,S表示球体的表面积,π是圆周率(约为3.14159),r是球体的半径。
这个公式的推导过程较为复杂,我们可以简单解释一下。
我们可以将球体看作由无数微小的面元组成,每个面元都是一个微小的圆形。
球体的表面积就是这些微小圆形的面积之和。
而每个微小圆形的半径都等于球体的半径r,因此我们可以将每个微小圆形的面积表示为πr²。
最后,将所有的微小圆形面积之和即得到了球体的表面积。
二、球体的体积计算公式要计算球体的体积,我们可以使用以下公式:V = (4/3)πr³其中,V表示球体的体积,π是圆周率,r是球体的半径。
这个公式的推导也较为复杂,我们可以简单解释一下。
我们可以将球体看作无数个微小的圆柱体叠加而成。
每个微小圆柱体的体积可以表示为πr²h,其中h是圆柱体的高度,也就是球体半径r对应的微小圆柱体的高度。
由于球体是各向同性的,每个微小圆柱体的高度都等于r。
因此,我们将微小圆柱体的体积表示为πr²r,即πr³。
最后将所有微小圆柱体的体积之和即得到了球体的体积。
三、实例应用假设我们需要计算一个半径为5cm的球体的表面积和体积。
根据上述公式,我们可以按照以下步骤进行计算:1. 计算表面积:S = 4πr²= 4 × 3.14159 × 5²≈ 314.159 cm²2. 计算体积:V = (4/3)πr³= (4/3) × 3.14159 × 5³≈ 523.599 cm³因此,半径为5cm的球体的表面积约为314.159 cm²,体积约为523.599 cm³。
球体体积和表面积的公式

球体体积和表面积的公式球体是一种几何体,具有独特的性质和特征。
在数学中,对于球体的体积和表面积有着严格的计算公式。
本文将对球体的体积和表面积进行介绍,并详细解释其计算公式。
一、球体的体积公式球体的体积是指球体所占据的空间大小。
我们可以通过计算球体的体积来了解其大小和容量。
球体的体积公式如下:V = (4/3)πr³其中,V表示球体的体积,π是一个数学常数,约等于3.14159,r 表示球体的半径。
通过这个公式,我们可以方便地计算出球体的体积。
例如,如果一个球体的半径r为5厘米,则可以使用上述公式计算出其体积V为(4/3)π(5³) ≈ 523.6立方厘米。
二、球体的表面积公式球体的表面积是指球体外部的总面积。
我们可以通过计算球体的表面积来了解其外部曲面的大小和形状。
球体的表面积公式如下:A = 4πr²其中,A表示球体的表面积,π是一个数学常数,约等于 3.14159,r表示球体的半径。
通过这个公式,我们可以方便地计算出球体的表面积。
例如,如果一个球体的半径r为5厘米,则可以使用上述公式计算出其表面积A为4π(5²) ≈ 314.16平方厘米。
三、球体的体积和表面积的关系通过球体的体积公式和表面积公式,我们可以看出,球体的体积和表面积之间存在一定的关系。
具体而言,当半径r固定时,球体的体积和表面积是不同的。
体积与r³成正比,而表面积与r²成正比。
这意味着,当半径增大时,球体的体积和表面积都会增大;当半径减小时,球体的体积和表面积都会减小。
这一关系可以通过计算公式得到验证。
四、应用举例球体的体积和表面积公式在实际生活中有着广泛的应用。
以下是一些具体的举例:1. 建筑领域:在建筑设计中,设计师需要计算球形穹顶的体积和表面积,以确保其结构的稳定性和合理性。
2. 化学实验:在化学实验中,需要计算球形试剂瓶中所装液体的体积,以便准确调配实验药液。
球的表面积与体积求法

球的表面积与体积求法简介球是一种常见的几何体,具有许多独特的性质。
在几何学中,球的表面积和体积是求解球体特征的重要指标。
本文将介绍如何计算球的表面积和体积,并提供求解公式和示例。
球的表面积球的表面积是指球体外部各点构成的集合的总面积。
求解球的表面积需要知道球的半径。
下面将介绍两种常用的方法来计算球的表面积。
方法一:使用球的半径如果已知球的半径r,可以使用以下公式来计算球的表面积S:S = 4πr^2其中,π约等于3.14159。
根据该公式,表面积与半径的平方成正比,表明球体的表面积随半径的增加而增加。
这个公式非常简单,适用于一般情况下的表面积计算。
方法二:使用球的直径另一种常用的方法是使用球的直径D计算表面积。
直径是连接球体两个相对点的线段的长度,等于半径的两倍。
因此,球的直径D等于2r。
在这种情况下,球的表面积计算公式为:S = πD^2这个公式可以通过将半径r的两倍代入第一种方法中的公式来得到。
无论使用半径还是直径,只要参数给定正确,都可以得到正确的表面积结果。
球的体积球的体积是指球体内部的三维空间容量大小,也是球内放满液体的容积。
求解球的体积同样需要知道球的半径。
下面将介绍球的体积计算方法。
方法:使用半径我们可以使用以下公式来计算球的体积V:V = (4/3)πr^3根据该公式,体积与半径的立方成正比,说明球体的体积相对于半径的增长要更快。
这是由于球的体积是三维空间的量度,增加半径会带来更多的体积空间。
示例下面是一个计算球的表面积和体积的示例:假设球的半径为5cm。
1.计算表面积:根据方法一,使用半径计算,可以得到:S = 4πr^2≈ 4 * 3.14159 * 5^2≈ 314.159 cm^2根据方法二,使用直径计算,可得:D = 2r = 2 * 5 = 10 cmS = πD^2≈ 3.14159 * 10^2≈ 314.159 cm^22.计算体积:根据方法一,使用半径计算,可得:V = (4/3)πr^3≈ (4/3) * 3.14159 * 5^3≈ 523.599 cm^3可以看到,不论使用哪种方法,计算结果都接近。
初数数学公式如何计算球体的体积和表面积

初数数学公式如何计算球体的体积和表面积球体是一种常见的几何形体,其体积和表面积计算是初等数学里的基础知识。
在初数学中,我们可以通过特定的公式来计算球体的体积和表面积。
一、球体体积的计算公式球体的体积是指球体所包含的三维空间的容积。
假设球体的半径为r,则球体体积的计算公式为V = (4/3)πr³。
其中,V表示球体的体积,π表示圆周率,取近似值3.14159。
例如,如果给定一个半径为5的球体,那么根据公式,可以计算出它的体积为:V = (4/3) × 3.14159 × 5³ = 523.59875。
所以,这个球体的体积约为523.59875立方单位(如立方厘米、立方米等)。
二、球体表面积的计算公式球体的表面积是指球体外表面的总面积。
同样假设球体的半径为r,则球体表面积的计算公式为A = 4πr²。
其中,A表示球体的表面积,π表示圆周率,取近似值3.14159。
以同样的例子,如果给定一个半径为5的球体,那么根据公式,可以计算出它的表面积为:A = 4 × 3.14159 × 5² = 314.159。
所以,这个球体的表面积约为314.159平方单位(如平方厘米、平方米等)。
三、实际应用举例球体的计算公式在实际生活中有广泛的应用。
以下是一些常见的实际应用举例:1. 建筑设计:在建筑设计过程中,工程师需要计算建筑物的圆顶或球形部分的体积和表面积,以便做出合理的设计和规划。
2. 水池容量:当我们想要知道一个圆形或球形水池的容量时,可以利用球体的体积公式进行计算,以便安排合适的供水量或估算储水能力。
3. 行星研究:天文学家可以通过测量行星的半径,使用球体的体积公式来计算其体积,从而更全面地了解行星的特征和组成。
4. 球体物体的购买和制造:当我们购买一个球体物体时,例如定制的篮球、足球等,可以根据球体的表面积公式来估算其需要的材料数量和成本。
球的体积公式和表面积公式

球的体积公式和表面积公式
球的表面积公式:球的表面积=4πr^2,r为球半径;球的体积计算公式:V球=(4/3)πr^3,r为球半径。
1、球体表面积是指球面所围成的几何体的面积,它包括球面和球面所围成的空间用周长公式计算球的表面积。
而求球的体积只需一个条件,那就是球的半径,两个球的半径比的立方等于这两个球的体积比。
2、球体的性质用一个平面去截一个球,截面是圆。
球的截面有以下性质:球心和截面圆心的连线垂直于截面。
球心到截面的距离d与球的半径R及截面的半径r有下面的关系:r^2=R^2-d^2。
3、空间中到定点的距离等于定长的所有点组成的图形叫做球,球体是一个连续曲面的立体图形,由球面围成的几何体称为球体。
球体表面积和体积公式

球体表面积和体积公式球体是一个非常常见的几何形状,它具有许多独特的性质和特征。
在这篇文章中,我们将重点介绍球体的表面积和体积公式,以及它们的应用。
一、球体的表面积公式球体的表面积是指球体外部所有点的集合所形成的曲面的总面积。
球体表面积的计算公式如下:S = 4πr^2其中,S表示球体的表面积,π是一个数学常数,约等于3.14159,r是球体的半径。
这个公式的推导可以通过将球体划分为无数个微小的表面元素,并对每个表面元素的面积进行累加得到。
然而,在这里我们不会对公式的推导过程进行详细讲解。
二、球体的体积公式球体的体积是指球体内部所有点的集合所形成的空间的总体积。
球体体积的计算公式如下:V = (4/3)πr^3其中,V表示球体的体积,π是一个数学常数,约等于3.14159,r 是球体的半径。
这个公式的推导可以通过将球体划分为无数个微小的体积元素,并对每个体积元素的体积进行累加得到。
同样,在这里我们不会对公式的推导过程进行详细讲解。
三、球体表面积和体积的应用球体的表面积和体积公式在许多领域都有着广泛的应用。
1. 建筑工程:在建筑设计中,球体的表面积公式可以用于计算建筑物的外墙面积,从而确定建筑材料的使用量。
而球体的体积公式则可以用于计算建筑物内部空间的容积,从而确定建筑物的可使用面积。
2. 包装设计:在包装设计中,球体的表面积公式可以用于计算圆形容器的外表面积,从而确定包装纸的大小。
而球体的体积公式则可以用于计算圆形容器的容积,从而确定包装物的容量。
3. 天文学:在天文学中,球体的表面积公式可以用于计算恒星的表面积,从而确定恒星的辐射能力。
而球体的体积公式则可以用于计算行星的体积,从而确定行星的质量。
4. 地理学:在地理学中,球体的表面积公式可以用于计算地球的表面积,从而确定地球的大小。
而球体的体积公式则可以用于计算地球的体积,从而确定地球的体积。
除了上述应用领域,球体的表面积和体积公式还可以在数学、物理、化学等学科中找到许多其他的应用。
球形计算公式图文解析

球形计算公式图文解析球体是一种常见的几何体,具有许多重要的性质和应用。
在数学和物理学中,我们经常需要计算球体的表面积、体积和其他相关参数。
本文将通过图文解析的方式,详细介绍球形的计算公式及其推导过程,帮助读者更好地理解球体的性质和应用。
1. 球体的基本性质。
在开始介绍球体的计算公式之前,我们先来回顾一下球体的基本性质。
球体是一个三维几何体,其表面由无数个等距的点组成,这些点到球心的距离都相等。
球体的表面积和体积是球体的重要参数,它们可以通过数学公式来计算。
2. 球体的表面积计算公式。
球体的表面积是指球体表面的总面积,可以通过数学公式来计算。
假设球体的半径为r,则球体的表面积S可以通过以下公式计算:S = 4πr^2。
其中,π是一个数学常数,约为3.14159。
通过这个公式,我们可以很容易地计算出球体的表面积。
例如,当球体的半径为5时,其表面积为4π5^2=100π。
3. 球体的体积计算公式。
球体的体积是指球体内部的总体积,同样可以通过数学公式来计算。
球体的体积V可以通过以下公式计算:V = (4/3)πr^3。
通过这个公式,我们可以很容易地计算出球体的体积。
例如,当球体的半径为5时,其体积为(4/3)π5^3=500π/3。
4. 球体的其他相关参数。
除了表面积和体积之外,球体还有许多其他相关的参数,比如球冠的表面积和体积、球扇的表面积和体积等。
这些参数的计算公式可以通过对球体进行切割和积分来推导得到,但由于篇幅有限,本文将不再详细介绍。
5. 球体计算公式的应用。
球体的计算公式在数学和物理学中有着广泛的应用。
在数学中,我们可以通过球体的表面积和体积来解决各种几何问题,比如球体的包装问题、球体的最优设计问题等。
在物理学中,球体的计算公式可以帮助我们计算物体的密度、质量等重要参数,从而更好地理解物体的性质和运动规律。
6. 总结。
通过本文的介绍,我们详细了解了球体的计算公式及其应用。
球体的表面积和体积是球体的重要参数,可以通过数学公式来计算。
球的体积与表面积公式

球的体积与表面积公式球体是一种三维几何体,其特点是每一点到中心点的距离都相等。
计算球的体积和表面积是在数学和几何学中的基本问题。
本文将介绍球的体积和表面积的计算公式,并且通过实例演示如何应用这些公式进行计算。
一、球的体积公式球体的体积是指球内部所占据的空间大小,用于描述球体的容积。
球的体积公式如下:V = (4/3)πr³其中,V表示球的体积,π是一个数学常数,近似值为3.14159,r 表示球的半径。
例如,如果已知一个球的半径为5单位长度,我们可以使用体积公式计算该球的体积。
V = (4/3)π(5)³≈ 523.6因此,该球的体积近似为523.6个单位体积。
二、球的表面积公式球体的表面积是指球的外部曲面的总面积,用于描述球的大小。
球的表面积公式如下:A = 4πr²其中,A表示球的表面积,π是一个数学常数,近似值为3.14159,r表示球的半径。
举个例子,如果已知一个球的半径为5单位长度,我们可以使用表面积公式计算该球的表面积。
A = 4π(5)²≈ 314.159因此,该球的表面积近似为314.159个单位面积。
三、应用实例为了更好地理解球的体积和表面积公式的应用,我们举个具体的实例。
假设有一个网球,其半径为3.5单位长度,我们可以通过体积公式计算该网球的体积。
V = (4/3)π(3.5)³≈ 179.592因此,该网球的体积近似为179.592个单位体积。
同时,我们可以通过表面积公式计算该网球的表面积。
A = 4π(3.5)²≈ 153.937因此,该网球的表面积近似为153.937个单位面积。
这个实例向我们展示了如何使用球的体积和表面积公式进行计算。
通过掌握这些公式,我们可以方便地计算不同半径的球体的体积和表面积,为实际问题解决提供了数学工具和便利。
总结:本文介绍了球的体积和表面积的公式,并通过实例演示了如何应用这些公式进行计算。
计算球体的体积和表面积

计算球体的体积和表面积球体是一种特殊的几何体,它具有无限多个对称轴,表面上的每一点到球心的距离都相等。
在数学中,计算球体的体积和表面积是一个常见的问题,也是中学数学中的重要内容之一。
本文将为大家介绍如何计算球体的体积和表面积,并通过实例进行说明。
一、计算球体的体积球体的体积是指球体所占据的空间大小。
我们可以通过数学公式来计算球体的体积。
球体的体积公式为:V = (4/3)πr³其中,V表示球体的体积,π为圆周率,r为球体的半径。
例如,如果一个球体的半径为5cm,那么它的体积可以通过以下计算得到:V = (4/3)π(5)³ ≈ 523.6 cm³所以,这个球体的体积约为523.6 cm³。
二、计算球体的表面积球体的表面积是指球体外部的总面积。
同样,我们可以通过数学公式来计算球体的表面积。
球体的表面积公式为:A = 4πr²其中,A表示球体的表面积,π为圆周率,r为球体的半径。
例如,如果一个球体的半径为5cm,那么它的表面积可以通过以下计算得到:A = 4π(5)² ≈ 314.16 cm²所以,这个球体的表面积约为314.16 cm²。
三、实际应用举例计算球体的体积和表面积在实际生活中有很多应用。
例如,我们可以利用这些计算来解决以下问题:1. 设计水池容量:如果我们要设计一个球形水池,我们需要计算出水池的体积,以确定所需的材料和容量。
通过计算球体的体积,我们可以准确地确定水池的容量。
2. 体积比较:当我们需要比较两个球体的体积大小时,我们可以通过计算它们的体积来进行比较。
这对于选择合适的容器或者比较不同大小的球体非常有帮助。
3. 表面积计算:在某些情况下,我们需要计算球体的表面积,例如涂料的用量计算、球形物体的包装设计等。
通过计算球体的表面积,我们可以准确地估计所需的材料用量。
总结:计算球体的体积和表面积是中学数学中的重要内容,也是实际生活中的常见问题。
球体表面积和体积的公式

球体表面积和体积的公式一、球体表面积公式。
1. 公式内容。
- 球体的表面积公式为S = 4π r^2,其中S表示球体的表面积,r表示球的半径,π是圆周率,通常取3.14。
2. 公式推导(高中阶段了解)- 可以通过对球体进行无限分割,将球体表面分割成无数个小的曲面三角形。
利用极限的思想,当分割得足够细时,这些小曲面三角形的面积之和就近似等于球体的表面积。
- 从数学分析的角度,利用球坐标变换等高等数学方法可以严格推导出这个公式。
3. 应用示例。
- 例:已知一个球的半径r = 5厘米,求这个球的表面积。
- 解:根据球体表面积公式S = 4π r^2,将r = 5代入公式,可得S=4×3.14×5^2=4×3.14×25 = 314(平方厘米)。
二、球体体积公式。
1. 公式内容。
- 球体的体积公式为V=(4)/(3)π r^3,其中V表示球体的体积,r表示球的半径,π是圆周率,通常取3.14。
2. 公式推导(高中阶段了解)- 可以使用祖暅原理(等积原理)来推导球体体积公式。
将一个半球体与一个底面半径和高都等于球半径r的圆柱体挖去一个底面半径和高都为r的圆锥体进行对比,利用祖暅原理可知它们的体积相等,从而推导出球体体积公式。
- 从高等数学角度,也可以通过三重积分等方法进行推导。
3. 应用示例。
- 例:已知球的半径r = 3厘米,求这个球的体积。
- 解:根据球体体积公式V = (4)/(3)π r^3,将r = 3代入公式,可得V=(4)/(3)×3.14×3^3=(4)/(3)×3.14×27 = 113.04(立方厘米)。
球体的表面积和体积的公式

球体的表面积和体积的公式
一、球体的表面积公式。
1. 公式内容。
- 设球的半径为r,球的表面积公式为S = 4π r^2。
2. 公式推导(简单理解)
- 可以把球的表面想象成由很多个小的三角形组成。
当把这些小三角形分得足够小的时候,它们的面积之和就近似等于球的表面积。
- 通过复杂的数学积分等方法可以严格证明得到S = 4π r^2这个公式。
3. 应用示例。
- 例:已知一个球的半径r = 3,求其表面积。
- 解:根据公式S = 4π r^2,将r = 3代入可得S=4π×3^2=4π×9 = 36π。
二、球体的体积公式。
1. 公式内容。
- 设球的半径为r,球的体积公式为V=(4)/(3)π r^3。
2. 公式推导(简单理解)
- 可以使用积分的方法推导。
从球的截面来看,随着高度的变化,截面圆的面积是一个关于高度的函数,对这个函数在球的直径范围内进行积分就可以得到球的体积公式。
- 也可以通过祖暅原理(等幂等积定理),将球与其他已知体积公式的几何体(如圆柱、圆锥等)进行比较推导得出。
3. 应用示例。
- 例:已知球的半径r = 2,求其体积。
- 解:根据公式V=(4)/(3)π r^3,将r = 2代入可得V=(4)/(3)π×2^3=(4)/(3)π×8=(32)/(3)π。
球体体积和表面积计算公式

球体体积和表面积计算公式球体是一个非常常见的几何形状,它具有一些特殊的性质。
在本文中,我们将讨论球体的体积和表面积的计算公式,并对其进行解释和推导。
让我们来看看球体的体积计算公式。
球体的体积是指球体所占据的空间。
为了计算球体的体积,我们需要知道球体的半径。
球体的半径是指从球心到球体表面上的任意一点的距离。
球体的体积计算公式如下:V = (4/3)πr³其中,V表示球体的体积,π是一个常数,近似取值为3.14159,r 表示球体的半径。
接下来,让我们来看看球体的表面积计算公式。
球体的表面积是指球体表面的总面积。
为了计算球体的表面积,同样需要知道球体的半径。
球体的表面积计算公式如下:A = 4πr²其中,A表示球体的表面积,π是一个常数,近似取值为3.14159,r表示球体的半径。
下面,我们将对这两个公式进行推导和解释。
首先,让我们从球体的体积公式开始推导。
球体可以看作是无限多个无穷小的圆柱叠加而成。
每个圆柱的体积可以表示为:Vc = πr²h,其中,r是圆柱的底面半径,h是圆柱的高度。
当我们将无限多个无穷小的圆柱叠加在一起时,高度h将趋近于0,而底面半径r将趋近于球体的半径r。
因此,我们可以得到球体的体积公式:V = lim(ΔVc) = lim(πr²h) = πr²lim(h) = πr²(0) = 0但是,我们知道球体是有体积的,因此上述推导是不正确的。
事实上,球体的体积公式应该是使用积分来表示。
通过对圆柱体积的连续求和,我们可以得到球体的体积公式:V = ∫(0 to R)πr²dh = π∫(0 to R)r²dh = πr²h∣∣∣(0 to R) = πr²R其中,R是球体的半径。
这个公式是通过使用积分来考虑球体的无穷小高度h,从而得到球体的体积。
接下来,让我们来看看球体的表面积公式的推导。
图解球体表面积和体积正确计算方法及计算公式
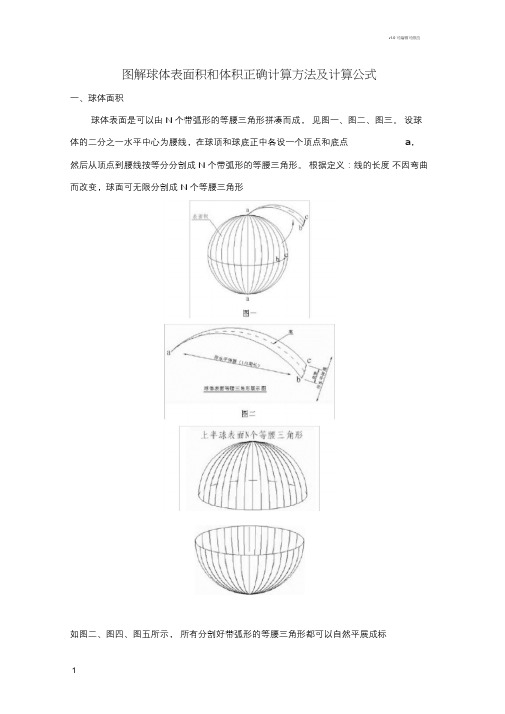
图解球体表面积和体积正确计算方法及计算公式一、球体面积球体表面是可以由N 个带弧形的等腰三角形拼凑而成,见图一、图二、图三。
设球体的二分之一水平中心为腰线,在球顶和球底正中各设一个顶点和底点a,然后从顶点到腰线按等分分割成N 个带弧形的等腰三角形。
根据定义:线的长度不因弯曲而改变,球面可无限分割成N 个等腰三角形如图二、图四、图五所示,所有分割好带弧形的等腰三角形都可以自然平展成标准的等腰三角形,亦可将等腰三角形拼凑成方形在理解上述图例球体表面和等腰三角形的关系后,我们可以对球体表面积的计算有比较清晰的判断。
即,球体表面可以分割成N 个相等的等腰三角形,等腰三角形亦可拼凑成方形,由此推导出球体面积可以用矩形公式计算。
即S = 长×宽,如果我们设球体1/4 之一的周长为宽,设球体的周长为长,则球体表面积公式为:S=1/4 周长×周长(见图六)例1 :已知球体直径是1 个单位,求球体表面积(用上述最新推导公式S=1/4周长×周长)S =(÷ 4)× = ㎡二、球体体积设以球心作一条垂线或水平中心线,然后以垂线或水平中心向外将球体按等分无限分割成N 个半圆楔形体。
见图七、图八。
球体分割完成后,将半圆楔形体镜像排列成圆柱体,见图九、图十从图七、图八、图九、图十看,球体从中心按等分分割成半圆楔形体后可以排列堆砌成圆柱体,根据计算得出定义:与球体同直径同体积的圆柱体的柱高正好是球体周长的1/4 。
则球体体积公式为:V =πR平方×周长的1/4 或:V = D(直径的三次方)×例2:已知球体直径是1 个单位,求球体体积(用上述最新推导公式)V = πR平方×周长的1/4= ××三、公知公式在球体面积、体积计算中出现的错误1、球体面积如何检验球体面积计算的正确,最好的方法就是用计算结果制成N 个等腰三角形的薄膜反贴球体表面。
球体表面积与体积的计算方法

计算方法及步骤
解释:V代表球体体积,r 代表球体半径,π是圆周率
公式:V = 4/3 * π * r^3
步骤:首先确定球体半径, 然后代入公式计算球体体积
注意事项:计算时要注意单 位和精度要求
实例演示
计算公式:V = 4/3 * π * r^3
实例1:半径为3 厘米的球体,体 积为113.1立方厘 米
天文学:天文学 家利用球体表面 积与体积的计算 方法来研究星球 的形状和大小, 以及星球之间的 距离和相对位置。
物理学:在物理 学中,球体表面 积与体积的计算 方法常用于研究 物体的运动规律, 如地球绕太阳转
动的轨道等。
医学:在医学领 域,球体表面积 与体积的计算方 法可用于药物研 发和人体组织结 构的模拟,如药 物在体内的分布
实例2:半径为5 厘米的球体,体 积为523.6立方厘 米
实例3:半径为8 厘米的球体,体 积为1001.9立方 厘米
03
球体表面积与体积的应用
在几何学中的应用
球体表面积公式:4πr²,其中r为 球半径
球体体积公式:4/3πr³,其中r为 球半径
球体表面积与体积在几何学中常 用于计算球体的表面积和体积, 以及解决与球体相关的几何问题
单击此处添加副标题
球体表面积与体积的计算
方法
汇报人:XX
目录
01 02 03
球体表面积的计算 球体体积的计算
球体表面积与体积的应用
01
球体表面积的计算
球体表面积的公式
球体表面积计算 公式:4πr²
公式推导:由球 体表面积的定义 和几何性质推导 得出
适用范围:适用 于计算球体的表 面积
注意事项:在计 算时需要注意半 径r的取值范围
图解球体表面积和体积正确计算方法及计算公式
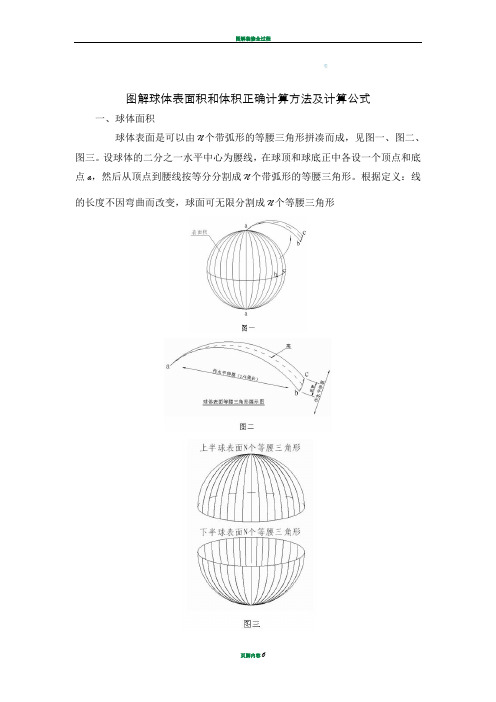
图解球体表面积和体积正确计算方法及计算公式一、球体面积球体表面是可以由N个带弧形的等腰三角形拼凑而成,见图一、图二、图三。
设球体的二分之一水平中心为腰线,在球顶和球底正中各设一个顶点和底点a,然后从顶点到腰线按等分分割成N个带弧形的等腰三角形。
根据定义:线的长度不因弯曲而改变,球面可无限分割成N个等腰三角形如图二、图四、图五所示,所有分割好带弧形的等腰三角形都可以自然平展成标准的等腰三角形,亦可将等腰三角形拼凑成方形。
在理解上述图例球体表面和等腰三角形的关系后,我们可以对球体表面积的计算有比较清晰的判断。
即,球体表面可以分割成N个相等的等腰三角形,等腰三角形亦可拼凑成方形,由此推导出球体面积可以用矩形公式计算。
即S = 长×宽,如果我们设球体1/4之一的周长为宽,设球体的周长为长,则球体表面积公式为:S=1/4周长×周长(见图六)例1:已知球体直径是1个单位,求球体表面积(用上述最新推导公式 S=1/4周长×周长)S =(3.14159÷4)×3.14159 = 2.4674㎡二、球体体积设以球心作一条垂线或水平中心线,然后以垂线或水平中心向外将球体按等分无限分割成N个半圆楔形体。
见图七、图八。
球体分割完成后,将半圆楔形体镜像排列成圆柱体,见图九、图十。
从图七、图八、图九、图十看,球体从中心按等分分割成半圆楔形体后可以排列堆砌成圆柱体,根据计算得出定义:与球体同直径同体积的圆柱体的柱高正好是球体周长的1/4。
则球体体积公式为:V =πR平方×周长的1/4或:V = D(直径的三次方)×0.616849233例2:已知球体直径是1个单位,求球体体积(用上述最新推导公式)V =πR平方×周长的1/4= 3.14159×0.25×0.7853975= 0.616849233三、公知公式在球体面积、体积计算中出现的错误1、球体面积如何检验球体面积计算的正确,最好的方法就是用计算结果制成N个等腰三角形的薄膜反贴球体表面。
球体与圆锥的计算

球体与圆锥的计算球体和圆锥是几何学中两种常见的几何体,在数学和物理等领域有广泛的应用。
本文将介绍球体和圆锥的计算方法,包括计算体积、表面积和其他相关参数的公式和步骤。
一、球体的计算1. 球体的体积计算公式:球体的体积V可以通过以下公式进行计算:V = (4/3) * π * r^3其中,V表示体积,π是一个常数,约等于3.14159,r表示球体的半径。
2. 球体的表面积计算公式:球体的表面积A可以通过以下公式进行计算:A = 4 * π * r^2其中,A表示表面积,π是一个常数,约等于3.14159,r表示球体的半径。
二、圆锥的计算1. 圆锥的体积计算公式:圆锥的体积V可以通过以下公式进行计算:V = (1/3) * π * r^2 * h其中,V表示体积,π是一个常数,约等于3.14159,r表示圆锥的底面半径,h表示圆锥的高。
2. 圆锥的侧面积计算公式:圆锥的侧面积S可以通过以下公式进行计算:S = π * r * l其中,S表示侧面积,π是一个常数,约等于3.14159,r表示圆锥的底面半径,l表示圆锥的斜高。
圆锥的斜高可以通过勾股定理计算:l = √(r^2 + h^2)其中,r表示圆锥的底面半径,h表示圆锥的高。
3. 圆锥的全面积计算公式:圆锥的全面积A可以通过以下公式进行计算:A = π * r * (r + l)其中,A表示全面积,π是一个常数,约等于3.14159,r表示圆锥的底面半径,l表示圆锥的斜高。
三、应用示例1. 示例一:计算一个半径为3cm的球体的体积和表面积。
根据球体的计算公式,可以得到:V = (4/3) * π * 3^3 ≈ 113.097 cm^3A = 4 * π * 3^2 ≈ 113.097 cm^2因此,该球体的体积约为113.097 cm^3,表面积约为113.097 cm^2。
2. 示例二:计算一个底面半径为5cm,高为8cm的圆锥的体积、侧面积和全面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图解球体表面积和体积正确计算方法及计算公式
一、球体面积
球体表面是可以由N个带弧形的等腰三角形拼凑而成,见图一、图二、图三。
设球体的二分之一水平中心为腰线,在球顶和球底正中各设一个顶点和底点a,然后从顶点到腰线按等分分割成N个带弧形的等腰三角形。
根据定义:线的长度不因弯曲而改变,球面可无限分割成N个等腰三角形
如图二、图四、图五所示,所有分割好带弧形的等腰三角形都可以自然平展成标准的等腰三角形,亦可将等腰三角形拼凑成方形。
在理解上述图例球体表面和等腰三角形的关系后,我们可以对球体表面积的计算有比较清晰的判断。
即,球体表面可以分割成N个相等的等腰三角形,等腰三角形亦可拼凑成方形,由此推导出球体面积可以用矩形公式计算。
即S = 长×宽,如果我们设球体1/4之一的周长为宽,设球体的周长为长,则球体表面积公式为:S=1/4周长×周长(见图六)
例1:已知球体直径是1个单位,求球体表面积(用上述最新推导公式S=1/4周长×周长)
S =(3.14159÷4)×3.14159 = 2.4674㎡
二、球体体积
设以球心作一条垂线或水平中心线,然后以垂线或水平中心向外将球体按等分无限分割成N个半圆楔形体。
见图七、图八。
?
球体分割完成后,将半圆楔形体镜像排列成圆柱体,见图九、图十。
从图七、图八、图九、图十看,球体从中心按等分分割成半圆楔形体后可以排列堆砌成圆柱体,根据计算得出定义:与球体同直径同体积的圆柱体的柱高正好是
球体周长的1/4。
则球体体积公式为:V =πR平方×周长的1/4
例2:已知球体直径是1个单位,求球体体积(用上述最新推导公式)
V =πR平方×周长的1/4
= 3.14159×0.25×0.7853975
三、公知公式在球体面积、体积计算中出现的错误
1、球体面积
如何检验球体面积计算的正确,最好的方法就是用计算结果制成N个等腰三角形的薄膜反贴球体表面。
如薄膜能完整不剩的覆盖球体表面则公式应用和计算正确,如薄膜有剩余或薄膜未能完全覆盖球体表面则公式应用和计算不正确,见图十一。
图十一是用新公式和公知公式分别计算球体直径同是一个单位半球面积的结果对比,新公式计算结果反贴复原后正好能覆盖直径是一个单位半球的球体面积。
计算过程:?
S =(1.570795×0.7853975)= 1.2336㎡
公知公式计算结果反贴复原后剩余有0.337㎡的面积。
计算过程:?
S = 1×3.14159÷2 = 1.570795㎡
2、球体体积
如何检验球体体积计算的正确,最好的方法就是用溢水法进行检验。
根据公知的容积单位:每立方米的水为1000升,每立方厘米的水为1毫升。
因此我们可以将同直径的球体分别用两种不同的公式计算,将计算结果再与用溢水法实际测量的结果进行对比。
在大量的实验中我们的确发现了公知公式的问题,下表是实验中两种公式计算结果与实际测量的数据对比(球体体积):
上表数据对比清楚的表明,用量筒实际测量的结果与新公式计算的结果最为接近,可以证明球体体积新公式是正确可靠的。
