2018年普通高等学校招生全国统一考试高三数学仿真卷文(一)
2018年高考文科数学全国卷1(含详细答案)

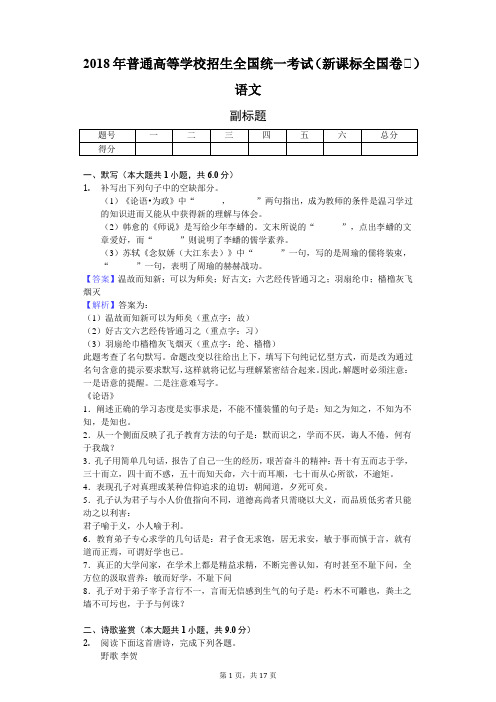
数学试题 第1页(共22页)数学试题 第2页(共22页)绝密★启用前2018年普通高等学校招生全国统一考试文科数学注意事项:1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上. 2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案标号.回答非选择题时,将答案写在答题卡上,写在本试卷上无效.3.考试结束后,将本试卷和答题卡一并交回.一、选择题(本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知集合{}02A =,,{}21012B =--,,,,,则A B =( )A .{}02,B .{}12,C .{}0D .{}21012--,,,, 2.设121iz i i-=++,则z =( ) A .0 B .12C .1 D3.某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如下饼图:则下面结论中不正确的是( ) A .新农村建设后,种植收入减少B .新农村建设后,其他收入增加了一倍以上C .新农村建设后,养殖收入增加了一倍D .新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半4.已知椭圆C :22214x y a +=的一个焦点为()2,0,则C 的离心率( ) A .13B .12CD5.已知圆柱的上、下底面的中心分别为1O ,2O ,过直线12O O 的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为( ) A.B .12πC.D .10π6.设函数()()321f x x a x ax =+-+.若()f x 为奇函数,则曲线()y f x =在点()00,处的切线方程为( ) A .2y x =-B .y x =-C .2y x =D .y x =7.在ABC △中,AD 为BC 边上的中线,E 为AD 的中点,则EB =( )A .3144AB AC - B .1344AB AC -C .3144AB AC +D .1344AB AC +8.已知函数()222cos sin 2f x x x =-+,则( ) A .()f x 的最小正周期为π,最大值为3B .()f x 的最小正周期为π,最大值为4C .()f x 的最小正周期为2π,最大值为3D .()f x 的最小正周期为2π,最大值为49.某圆柱的高为2,底面周长为16,其三视图如图所示,圆柱表面上的点M 在正视图上的对应点为A ,圆柱表面上的点N 在左视图上的对应点为B ,则在此圆柱侧面上,从M 到N 的路径中,最短路径的长度为( ) A.B.C .3D .210.在长方体1111ABCD A B C D -中,2AB BC ==,1AC 与平面11BB C C 所成的角为30︒,则该长方体的体积为( )A .8B.C.D.11.已知角α的顶点为坐标原点,始边与x 轴的非负半轴重合,终边上有两点()1,A a ,()2,B b ,且2cos 23α=,则a b -=( )A .15BCD .1-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------数学试题 第3页(共22页)数学试题 第4页(共22页)12.设函数()201 0x x f x x -⎧=⎨>⎩,≤,,则满足()()12f x f x +<的x 的取值范围是( )A .(]1-∞,B .()0+∞,C .()10-,D .()0-∞,二、填空题(本题共4小题,每小题5分,共20分)13.已知函数()()22log f x x a =+,若()31f =,则a =________.14.若x y ,满足约束条件220100x y x y y --⎧⎪-+⎨⎪⎩≤≥≤,则32z x y =+的最大值为________.15.直线1y x =+与圆22230x y y ++-=交于A B ,两点,则AB = ________. 16.ABC △的内角A B C ,,的对边分别为a b c ,,,已知sin sin 4sin sin b C c B a B C +=,2228b c a +-=,则ABC △的面积为________.三、解答题(共70分。
2018年普通高等学校招生全国统一考试仿真卷 文科数学(一)解析版

绝密 ★ 启用前2018年普通高等学校招生全国统一考试仿真卷文科数学(一)本试题卷共14页,23题(含选考题)。
全卷满分150分。
考试用时120分钟。
★祝考试顺利★注意事项:1、答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
用2B 铅笔将答题卡上试卷类型A 后的方框涂黑。
2、选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3、填空题和解答题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4、选考题的作答:先把所选题目的题号在答题卡上指定的位置用2B 铅笔涂黑。
答案写在答题卡上对应的答题区域内,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
5、考试结束后,请将本试题卷和答题卡一并上交。
第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.[2018·晋城一模]已知集合(){},2M x y x y =+=,(){},2N x y x y =-=,则集合MN =( )A .{}0,2B .()2,0C .(){}0,2D .(){}2,0【答案】D【解析】解方程组22x y x y +=-=⎧⎨⎩,得2x y =⎧⎨=⎩.故(){}2,0MN =.选D .2.[2018·台州期末](i 为虚数单位)) A .2 B .1C .12D【答案】C11i 22z ∴=-=,选C . 3.[2018·南宁二中]为考察A ,B 两种药物预防某疾病的效果,进行动物实验,分别得到如下等高条形图:根据图中信息,在下列各项中,说法最佳的一项是( ) A .药物B 的预防效果优于药物A 的预防效果 B .药物A 的预防效果优于药物B 的预防效果C .药物A 、B 对该疾病均有显著的预防效果D .药物A 、B 对该疾病均没有预防效果 【答案】B【解析】由A 、B 两种药物预防某疾病的效果,进行动物试验,分别得到的等高条形图,知:药物A 的预防效果优于药物B 的预防效果.故选B .4.[2018·滁州期末])A .4-B .4C.13- D .13【答案】C【解析】sin 2costan 2ααα-=-⇒=,C .5.[2018·陕西一模]《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”.已药物A 实验结果患病未患病服用药没服用药0.10.20.30.40.50.60.70.80.91药物B实验结果患病未患病服用药没服用药0.10.20.30.40.50.60.70.80.91班级 姓名 准考证号 考场号 座位号此卷只装订不密封知某“堑堵”的三视图如图所示,俯视图中间的实线平分矩形的面积,则该“堑堵”的侧面积为( )A .2 B.4+C.4+D.4+【答案】C【解析】根据题意和三视图知几何体是一个放倒的直三棱柱,底面是一个直角三角形,2,且侧棱与底面垂直,侧棱长是2,∴几何体的侧面积C .6.[2018·滁州期末]设变量x ,y 满足约束条件220220 2x y x y y +--+⎧⎪⎨⎪⎩≥≤≤,则目标函数z x y =+的最大值为( ) A .7 B .6C .5D .4【答案】D【解析】画出不等式组表示的可行域(如图阴影部分所示).由z x y =+,得y x z =-+.平移直线y x z =-+,结合图形可得,当直线(图中的虚线)经过可行域内的点A 时,直线在y 轴上的截距最大,此时z 取得最大值.由2 220y x y =-+=⎧⎨⎩,解得22x y ==⎧⎨⎩,故点A 的坐标为(2,2).∴max 224z =+=,即目标函数z x y =+的最大值为4.选D .7.[2018·蚌埠一模]已知()201720162018201721f x x x x =++++,下列程序框图设计的是求()0f x 的值,在“ ”中应填的执行语句是( )A .2018n i =-B .2017n i =-C .2018n i =+D .2017n i =+【答案】A【解析】不妨设01x =,要计算()120182017201621f =+++++,首先201812018S =⨯=,下一个应该加2017,再接着是加2016,故应填2018n i =-. 8.[2018·达州期末]若函数()24x f x a =--存在两个零点,且一个为正数,另一个为负数,则a 的取值范围为( ) A .()0,4 B .()0,+∞C .()3,4D .()3,+∞【答案】C【解析】如图,若()24x f x a =--存在两个零点,且一个为正数,另一个为负数,则()34a ∈,,故选C .9.[2018·朝阳期末]阿波罗尼斯(约公元前262-190年)证明过这样一个命题:平面内到两定点距离之比为常数k (0k >且1k ≠)的点的轨迹是圆.后人将这个圆称为阿氏圆.若平面内两定点A ,B 间的距离为2,动点P 与A ,B P ,A ,B 不共线时,PAB △面积的最大值是( )A .BC .3D .3【答案】A开始i =1,n =2018结束i ≤2017?是否输入x 0S =2018输出SS =Sx 0S =S+ni =i +1【解析】如图,以经过A ,B 的直线为x 轴,线段AB 的垂直平分线为y 轴,建立直角坐标系;则:()10A -,,()10B ,,设()P x y ,,PA PB=,两边平方并整理得:()222261038x y x x y +-+=⇒-+=.∴PAB △面积的最大值是122⨯⨯=A .10.[2018·孝感八校]已知双曲线E :22221x y a b-=(0,0)a b >>的右顶点为A ,右焦点为F ,B 为双曲线在第二象限上的一点,B 关于坐标原点O 的对称点为C ,直线CA 与直线BF的交点M 恰好为线段BF 的中点,则双曲线的离心率为( )A .12B .15C .2D .3【答案】D【解析】不妨设2,b B c a ⎛⎫- ⎪⎝⎭,由此可得(),0A a ,2,b C c a ⎛⎫- ⎪⎝⎭,(),0F c ,20,2b M a ⎛⎫ ⎪⎝⎭,由于A ,C ,M 三点共线,故222b b a a a a c=--,化简得3c a =,故离心率3e =.11.[2018·昆明一中]设锐角ABC △的三个内角A ,B ,C 的对边分别为a ,b ,c ,且1c =,2A C =,则ABC △周长的取值范围为( )A.(0,2 B.(0,3C .(2++ D .(2+【答案】C【解析】因为ABC △为锐角三角形,cos C <<2A C =, 所以sin 2sin cos A C C =,又因为1c =,所以2cos a C =;由sin sin b cB C=, 即2sin sin34cos 1sin sin c B Cb C C C===-,所以24cos 2cos a b c C C ++=+,令cos t C=, 则(,22t ∈⎭,又因为函数242y tt =+在( ,22⎭上单调递增,所以函数值域为(2+,故选:C .12.[2018·菏泽期末]()2f x mx =+有一个零点,则实数m 的取值范围是( ) A ]{64-+B ]{0,64-+C ]{}632-D ]{0,63-【答案】B【解析】由题意函数()f x 的图象与直线2y mx =+有一个交点.如图是()f x 的图象,1x >时,()21f x x =-,,设切点为()00,x y ,则切线为()()02002211y x x x x -=----,把()0,2代入,02x =;1x ≤时,()2e x f x =-,()e x f x '=-,设切点为()00,x y ,则切线为()()002e e x x y x x --=--,把()0,2代入,解得01x =,又()12e f =-,()11e e f '=-=-,所以由图象知当]{0,42-B .第Ⅱ卷本卷包括必考题和选考题两部分。
2018年普通高等学校招生全国统一考试(新课标全国卷Ⅰ)语文
2018年普通高等学校招生全国统一考试(新课标全国卷Ⅰ)语文副标题一、默写(本大题共1小题,共6.0分)1.补写出下列句子中的空缺部分。
(1)《论语•为政》中“______,______”两句指出,成为教师的条件是温习学过的知识进而又能从中获得新的理解与体会。
(2)韩愈的《师说》是写给少年李蟠的。
文末所说的“______”,点出李蟠的文章爱好,而“______”则说明了李蟠的儒学素养。
(3)苏轼《念奴娇(大江东去)》中“______”一句,写的是周瑜的儒将装束,“______”一句,表明了周瑜的赫赫战功。
【答案】温故而知新;可以为师矣;好古文;六艺经传皆通习之;羽扇纶巾;檣橹灰飞烟灭【解析】答案为:(1)温故而知新可以为师矣(重点字:故)(2)好古文六艺经传皆通习之(重点字:习)(3)羽扇纶巾檣橹灰飞烟灭(重点字:纶、檣橹)此题考查了名句默写。
命题改变以往给出上下,填写下句纯记忆型方式,而是改为通过名句含意的提示要求默写,这样就将记忆与理解紧密结合起来。
因此,解题时必须注意:一是语意的提醒。
二是注意难写字。
《论语》1.阐述正确的学习态度是实事求是,不能不懂装懂的句子是:知之为知之,不知为不知,是知也。
2.从一个侧面反映了孔子教育方法的句子是:默而识之,学而不厌,诲人不倦,何有于我哉?3.孔子用简单几句话,报告了自己一生的经历,艰苦奋斗的精神:吾十有五而志于学,三十而立,四十而不惑,五十而知天命,六十而耳顺,七十而从心所欲,不逾矩。
4.表现孔子对真理或某种信仰追求的迫切:朝闻道,夕死可矣。
5.孔子认为君子与小人价值指向不同,道德高尚者只需晓以大义,而品质低劣者只能动之以利害:君子喻于义,小人喻于利。
6.教育弟子专心求学的几句话是:君子食无求饱,居无求安,敏于事而慎于言,就有道而正焉,可谓好学也已。
7.真正的大学问家,在学术上都是精益求精,不断完善认知,有时甚至不耻下问,全方位的汲取营养:敏而好学,不耻下问8.孔子对于弟子宰予言行不一,言而无信感到生气的句子是:朽木不可雕也,粪土之墙不可圬也,于予与何诛?二、诗歌鉴赏(本大题共1小题,共9.0分)2.阅读下面这首唐诗,完成下列各题。
2018年重庆市普通高等学校招生全国统一考试调研测试卷 文科数学(含答案)

重庆市高三4月调研测试(二诊)数学文试题第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 设集合{1,0,1,2,3}A =-,2{|30}B x x x =->,则()R AC B =( )A . {1}-B .{0,1,2}C .{1,2,3}D .{0,1,2,3}2.若复数z 满足2(1)1z i i +=-,其中i 为虚数单位,则z 在复平面内所对应的点位于( ) A . 第一象限 B .第二象限 C .第三象限 D .第四象限 3.已知向量(,1)a x =-,(1,3)b =,若a b ⊥,则||a =( ) ABC .2D . 44.在平面直角坐标系xOy 中,不等式组130x y x x y ≥⎧⎪≥⎨⎪+-≤⎩所表示的平面区域的面积为( )A .29 B .14 C . 13 D .125. 《张丘建算经》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有女不善织,日减功迟,初日织五尺,末日织一尺,今共织九十尺,问织几日?”,已知“日减功迟”的具体含义是每天比前一天少织同样多的布,则此问题的答案是( )A .10日B . 20日C . 30日D .40日6. 设直线0x y a --=与圆224x y +=相交于,A B 两点,O 为坐标原点,若AOB ∆为等边三角形,则实数a 的值为( )A.. C . 3± D .9±7. 方程22123x y m m +=-+表示双曲线的一个充分不必要条件是( ) A .30m -<< B .32m -<< C . 34m -<< D .13m -<< 8. 执行如图所示的程序框图,若输出的结果为3,则输入的数不可能是( )A .15B .18C . 19D .209. 如图1所示,是一个棱长为2的正方体被削去一个角后所得到的几何体的直观图,其中11DD =,12AB BC AA ===,若此几何体的俯视图如图2所示,则可以作为其正视图的是( )A .B .C .D .10. 已知函数2sin()y x ωϕ=+(0,0)ωϕπ><<的部分图象如图所示,则ϕ=( )A .6πB .4πC .3πD .2π11. 设F 为双曲线C :22221(0,0)x y a b a b-=>>的右焦点,过坐标原点的直线依次与双曲线C 的左、右支交于点,P Q ,若||2||PQ QF =,60PQF ∠=,则该双曲线的离心率为( )A B .1+. 2 D .4+ 12.已知函数2()(3)xf x x e =-,设关于x 的方程2212()()0()f x mf x m R e --=∈有n 个不同的实数解,则n 的所有可能的值为( )A . 3B . 1或3C . 4或6D .3或4或6第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.若关于x 的不等式(2)()0a b x a b -++>的解集为{|3}x x >-,则ba= . 14.设ABC ∆中,角,,A B C 所对的边分别为,,a b c ,若ABC ∆,则C = .15. 甲、乙两组数据的茎叶图如图所示,其中m 为小于10的自然数,已知甲组数据的中位数大于乙组数据的中位数,则甲组数据的平均数也大于乙组数据的平均数的概率为 .16. 设函数22log (),12()142,1333x x f x x x x ⎧-≤-⎪⎪=⎨⎪-++>-⎪⎩,若()f x 在区间[,4]m 上的值域为[1,2]-,则实数m 的取值范围为 .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. 已知等差数列{}n a 的前n 项和为n S ,49a =,315S =. (1)求n S ; (2)设数列1{}nS 的前n 项和为n T ,证明:34n T <.18. “微信运动”已成为当下热门的健身方式,小王的微信朋友圈内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:(1)若采用样本估计总体的方式,试估计小王的所有微信好友中每日走路步数超过5000步的概率; (2)已知某人一天的走路步数超过8000步被系统评定“积极型”,否则为“懈怠型”,根据题意完成下面的22⨯列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?附:22()()()()()n ad bc k a b c d a c b d -=++++,20()P K k ≥ 0.100.05 0.025 0.010 0k2.7063.8415.0246.63519. 如图,矩形ABCD 中,AB =,AD =,M 为DC 的中点,将DAM ∆沿AM 折到'D AM∆的位置,'AD BM ⊥.(1)求证:平面'D AM ⊥平面ABCM ;(2)若E 为'D B 的中点,求三棱锥'A D EM -的体积.20. 已知椭圆E :22221(0)x y a b a b+=>>的左顶点为A ,右焦点为(1,0)F ,过点A 且斜率为1的直线交椭圆E 于另一点B ,交y 轴于点C ,6AB BC =.(1)求椭圆E 的方程;(2)过点F 作直线l 与椭圆E 交于,M N 两点,连接MO (O 为坐标原点)并延长交椭圆E 于点Q ,求MNQ ∆面积的最大值及取最大值时直线l 的方程.21. 已知函数2ln ln 1()x x f x x ++=,2()x x g x e=.(1)分别求函数()f x 与()g x 在区间(0,)e 上的极值; (2)求证:对任意0x >,()()f x g x >.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.22.选修4-4:坐标系与参数方程在直角坐标系xOy 中,直线l 的参数方程为1cos 1sin 2x t y t αα=-+⎧⎪⎨=+⎪⎩(t 为参数),以坐标原点O 为极点,以x 轴正半轴为极轴,建立极坐标系,曲线C 的极坐标方程为22244sin cos ρθθ=+. (1)写出曲线C 的直角坐标方程;(2)已知点P 的直角坐标为1(1,)2-,直线l 与曲线C 相交于不同的两点,A B ,求||||PA PB 的取值范围. 23.选修4-5:不等式选讲已知函数()|||3|f x x a x a =-+-. (1)若()f x 的最小值为2,求a 的值;(2)若对x R ∀∈,[1,1]a ∃∈-,使得不等式2||()0m m f x --<成立,求实数m 的取值范围.试卷答案一、选择题 1~6 DCCBBC7~12 AAABBB第(11)题解析:︒=∠=60|,|2||PQF QF PQ ,︒=∠∴90PFQ ,设双曲线的左焦点为1F ,连接Q F P F 11,,由对称性可知,PFQ F 1为矩形,且||3|||,|2||11QF QF QF F F ==,故13132||||||2211+=-=-==QF QF F F a c e .第(12)题解析:xx x x f +-='e )3)(1()(,)(x f ∴在)3,(--∞和),1(+∞上单增,)1,3(-上单减,又当-∞→x 时0)(→x f ,+∞→x 时+∞→)(x f ,故)(x f 的图象大致为:令t x f =)(,则方程0e 1222=--mt t 必有两根21,t t )(21t t <且221e 12-=t t , 当e 21-=t 时恰有32e 6-=t ,此时1)(t x f =有1个根,2)(t x f =有2个根; 当e 21-<t 时必有32e 60-<<t ,此时1)(t x f =无根,2)(t x f =有3个根; 当0e 21<<-t 时必有32e 6->t ,此时1)(t x f =有2个根,2)(t x f =有1个根; 综上,对任意R m ∈,方程均有3个根.二、填空题 (13)45(14)︒30(15)53 (16)]1,8[--第(15)题解析:由甲的中位数大于乙的中位数知,4,3,2,1,0=m ,又由甲的平均数大于乙的平均数知,3<m 即2,1,0=m ,故所求概率为53.第(16)题解析:函数)(x f 的图象如图所示,结合图象易得, 当]1,8[--∈m 时,]2,1[)(-∈x f . 三、解答题(17)解:(Ⅰ)5153223=⇒==a a S ,2224=-=∴a a d , 12+=∴n a n ,)2(2123+=⋅++=n n n n S n ; (Ⅱ))21151314121311(21)2(1421311+-++-+-+-=+++⨯+⨯=n n n n T n 43)2111211(21<+-+-+=n n .(18)解:(Ⅰ)由题知,40人中该日走路步数超过5000步的有34人,频率为3440,所以估计他的所有微信好友中每日走路步数超过5000步的概率为1720; (Ⅱ)841.3114018222020)861214(402<=⨯⨯⨯⨯-⨯⨯=K ,故没有95%以上的把握认为二者有关.(19)解:(Ⅰ)由题知,在矩形ABCD 中,︒=∠=∠45BMC AMD ,︒=∠∴90AMB ,又BM A D ⊥',⊥∴BM 面AM D ',∴面⊥ABCM 面AM D '; (Ⅱ)1111212663A D EM E AD MB AD M D AM V V V BM S ''''---∆===⋅⋅=⋅⋅=.(20)解:(Ⅰ)由题知),0(),0,(a C a A -,故)76,7(aa B -,代入椭圆E 的方程得1493649122=+b a ,又122=-b a ,故3,422==b a ,椭圆134:22=+y x E ;(Ⅱ)由题知,直线l 不与x 轴重合,故可设1:+=my x l ,由⎪⎩⎪⎨⎧=++=134122y x my x 得096)43(22=-++my y m , 设),(),,(2211y x N y x M ,则439,436221221+-=+-=+m y y m m y y ,由Q 与M 关于原点对称知, 431124)(||2222122121++=-+=-==∆∆m m y y y y y y S S MONMNQ 11131222+++=m m ,211m +≥,4∴,即3MNQ S ∆≤,当且仅当0=m 时等号成立,MNQ ∆∴面积的最大值为3,此时直线l 的方程为1=x(21)解:(Ⅰ)2ln (ln 1)()x x f x x--'=,()01e f x x '>⇒<<, 故()f x 在(0,1)和(e,)+∞上递减,在(1,e)上递增,)(x f ∴在e),0(上有极小值1)1(=f ,无极大值;xx x x g e)2()(-=',200)(<<⇒>'x x g , 故)(x g 在)2,0(上递增,在),2(+∞上递减,)(x g ∴在e),0(上有极大值2e4)2(=g ,无极小值; (Ⅱ)由(Ⅰ)知,当e),0(∈x 时,()1f x ≥,24()1eg x <≤,故)()(x g x f >; 当)[e,+∞∈x 时,2ln ln 11113x x ++++=≥,令x x x h e )(3=,则xx x x h e)3()(2-=', 故)(x h 在]3[e,上递增,在),3(+∞上递减,332727()(3)3e 2.7h x h ∴=<<≤,)(1ln ln 2x h x x >++; 综上,对任意0>x ,)()(x g x f >.(22)解:(Ⅰ)14444cos sin 422222222=+⇒=+⇒=+y x x y θρθρ;(Ⅱ)因为点P 在椭圆C 的内部,故l 与C 恒有两个交点,即R ∈α,将直线l 的参数方程与椭圆C 的直角坐标方程联立,得4)sin 21(4)cos 1(22=+++-ααt t ,整理得 02)cos 2sin 4()sin 31(22=--++t t ααα,则]2,21[sin 312||||2∈+=⋅αPB PA . (23)解:(Ⅰ)|||3||()(3)||2|x a x a x a x a a -+----=≥,当且仅当x 取介于a 和a 3之间的数时,等号成立,故)(x f 的最小值为||2a ,1±=∴a ;(Ⅱ)由(Ⅰ)知)(x f 的最小值为||2a ,故]1,1[-∈∃a ,使||2||2a m m <-成立,即 2||2<-m m ,0)2|)(|1|(|<-+∴m m ,22<<-∴m .。
2018年普通高等学校招生全国统一考试高三数学仿真卷文二20180428115

2018 年普通高等学校招生全国统一考试高三数学仿真卷 文(二)本试题卷共 14 页,23 题(含选考题)。
全卷满分 150 分。
考试用时 120 分钟。
★祝考试顺利★注意事项:1、答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形 码粘贴在答题卡上的指定位置。
用 2B 铅笔将答题卡上试卷类型 A 后的方框涂黑。
2、选择题的作答:每小题选出答案后,用 2B 铅笔把答题卡上对应题目的答案标号涂 黑。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3、填空题和解答题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题 卷、草稿纸和答题卡上的非答题区域均无效。
4、选考题的作答:先把所选题目的题号在答题卡上指定的位置用 2B 铅笔涂黑。
答案 写在答题卡上对应的答题区域内,写在试题卷、草稿纸和答题卡上的非答题区域均无 效。
5、考试结束后,请将本试题卷和答题卡一并上交。
第Ⅰ卷一、选择题:本大题共 12 小题,每小题 5 分,在每小题给出的四个选项中,只有一 项是符合题目要求的。
iz,则 z 的共轭复数为( )1.[2018·渭南质检]设i 是虚数单位,若复数1i 1 1B .1 1 iC .1 1 iD . 1 1 i i A . 2 22 2 2 2 【答案】D【解析】复数 z ii 11 i2 ,根据共轭复数的概念得到, z 的共轭复数为: 1 1 i .故答 2 2案为:D .- 1 -2.[2018·吉林实验中学]若双曲线 y2x 21 m 的一个焦点为3, 0,则m ( ) A . 2 2B .8C .9D . 64 【答案】B【解析】由双曲线性质: a 21,b 2 m ,c 2 1 m 9 , m 8 ,故选 B . 3.[2018·菏泽期末]将函数 yxsin 2π4的图像向左平移 π 6 个单位后,得到函数 f x 的图像,则 f π ( )12A . 2 6 4B . 3 6 4C . 3 2D . 2 2【答案】 Dπ π π【解析】 f x sin 2 x sin 2x6 412 ,∴ f ππ 2sin12 4 2 ,故选 D . x f x 1 4.[2018·晋城一模]函数2, x 0,的值域为D ,在区间1, 2上随机取一个数 x ,则 xD 的概率是( ) A . 12B . 1 3C . 1 4 D.1【答案】B - 2 -x 【解析】x 0, 011 2,即值域 D0,1,若在区间1, 2上随机取一个数 x , x D 的事件记为 A ,则 P A 1 0121 3,故选 B .5.[2018·菏泽期末]已知变量 x 和 y 的统计数据如下表:根据上表可得回归直线方程 y0.7x a ,据此可以预报当 x 6 时, y ( ) A .8.9B .8.6C .8.2D .8.1 【答案】D【解析】 x 1 2 34 5 6 , 5 5 66 8 63 y , 12 3 4 5 6 , 5 5 6 68 6 55 ∴6 0.73 a , a 3.9 ,∴ x 6 时, y 0.76 3.9 8.1,故选 D .6.[2018·昆明一中]一个几何体的三视图如图所示,则该几何体的体积为() A . 8 316 3 B . C . 20 3D .8【答案】B【解析】由图可知该几何体底面积为 8,高为 2的四棱锥,如图所示:116V82,故选B.∴该几何体的体积337.[2018·漳州调研]《九章算术》是我国古代的数学名著,书中有如下问题:“今有大夫、不更、簪裹、上造、公士,凡五人,共猎得五鹿,欲以爵次分之,问各得几何?”其意思:“共- 3 -A .12B .18C .120D .125【答案】C 【解析】第一次运行: a0 11,i 1为奇数, S 11 2,i 11 2; 第二次运行: a 1 2 3,i 2为偶数, S 32 6,i 2 1 3; 第三次运行: a33 6,i 3为奇数, S 6 6 12,i 31 4 ; 第四次运行: a 6 4 10,i 4为偶数, S 1012 120,i 4 1 5; 程序终止运行,输出 S 120 .故选 C .10.[2018·济南期末]设 x , y 满足约束条件≥1 x yx y ≥1,若目标函数 zax 3y 仅在点2x y ≤21, 0处取得最小值,则 a 的取值范围为( ) A .6,3 B .6,3 C .0, 3D .6,0 【答案】 A x y 1 ≥x y ≥ 1,表示的可行域如图所示,将 zax 3y 化成a z y x , 3 3【解析】作出约束条件2x y≤2- 5 -a当 1 2 时, 3 a z y x 仅在点1, 0处取得最小值,即目标函数 z ax 3y 仅在点 3 3 A 处取得最小值,解得 6 a 3 ,故选 A .1, 011.[2018·武邑中学]已知抛物线 y2 2px ( p 0) 的焦点为 F ,其准线与双曲线 y 23 x 2 1相交于 M , N 两点,若△MNF 为直角三角形,其中 F 为直角顶点,则 p( ) A . 2 3B . 3C .3 3D .6 【答案】A【解析】由题设知抛物线 y2 2px 的准线为 px ,代入双曲线方程 2 y 2 3 x 2 1解得y由 双 曲 线 的 对 称 性 知 △MNF 为 等 腰 直 角 三 角 形 , π 3FMN,3p2 4 4p2 3p 2 tan1, p 2 3 .故选 A . FMNp3, 4 3p2 3412.[2018·滁州期末]若关于 x 的不等式 k e1 x 在,00, 上恒成立,则x 1x实数 k的取值范围为()53A ., , B .e, 2e,ee221 52 3,,D ., ,C .eeee22【答案】A- 6 -【解析】依题意,k e 1k e 1xxx 1x 1xxx 02x x 1ke x0 x 或2 x x 1 k e x ,令f x2x 1 e x e x x 2x 1x 2x 2x 1x 2x x,21,则f xexeee2xxx所以当x ,1时, fx 0,当x1, 0时, fx 0,当x 0, 2时, fx 0,当x2,时, fx0,所以 kf2或k f1,即5k或 k e ,故选A .e2第Ⅱ卷本卷包括必考题和选考题两部分。
普通高等学校2018届高三招生全国统一考试仿真卷(三)数学(文)试题(含答案)

绝密 ★ 启用前2018年普通高等学校招生全国统一考试仿真卷文科数学(三)本试题卷共2页,23题(含选考题)。
全卷满分150分。
考试用时120分钟。
★祝考试顺利★注意事项:1、答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
用2B 铅笔将答题卡上试卷类型A 后的方框涂黑。
2、选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3、填空题和解答题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4、选考题的作答:先把所选题目的题号在答题卡上指定的位置用2B 铅笔涂黑。
答案写在答题卡上对应的答题区域内,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
5、考试结束后,请将本试题卷和答题卡一并上交。
第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若集合{}|11A x x =-<<,{}|02B x x =<<,则A B =( ) A .{}|11x x -<< B .{}|12x x -<<C .{}|02x x <<D .{}|01x x <<2.设复数12i z =+(是虚数单位),则在复平面内,复数2z 对应的点的坐标为( ) A .()3,4-B .()5,4C .()3,2-D .()3,43.若向量()1,1,2=-a ,()2,1,3=-b ,则 )AB .C .3D4.某几何体的三视图如图所示,则该几何体的表面积为( )班级 姓名 准考证号 考场号 座位号A .52π+B .42π+C .44π+D .54π+5.已知双曲线22221x y a b-=()0,0a b >>的一个焦点为()2,0F -双曲线的方程为( )A .2213x y -=B .2213y x -=C .2213y x -=D .2213x y -=6()102f =-,则图中m 的值为( )A .1B .43C .2D .43或2 7.在ABC △中,内角A ,B ,C 的对边分别为,,,若函数()()3222113f x x bx a c ac x =+++-+无极值点,则角B 的最大值是( )A B C D 8.公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”,刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出的值为( )(参考数据:sin150.2588≈,sin7.50.1305≈)A .12B .20C .24D .489.设π02x <<,则“2cos x x <”是“cos x x <”的( ) A .充分而不必要条件 B .必要而不充分条件 C .充分必要条件D .既不充分也不必要条件10.欧阳修的《卖油翁》中写道:“(翁)乃取一葫芦置于地,以钱覆盖其口,徐以杓酌油沥之,自钱孔入,而钱不湿”,可见“行行出状元”,卖油翁的技艺让人叹为观止.若铜钱是直径为3cm 的圆面,中间有边长为1cm 的正方形孔.现随机向铜钱上滴一滴油(油滴的大小忽略不计),则油滴落入孔中的概率为( )ABC .19D 8π11.已知点()4,3A 和点()1,2B,点O (OA tOB t +∈R ) A .B .5C .3D12.已知函数()f x =()2220 1102x xx f x x +--+<⎧⎪⎨⎪⎩≤≤≤,则关于的方程()15x f x -=在[]2,2-上的根的个数为( ) A .3 B .4 C .5 D .6第Ⅱ卷本卷包括必考题和选考题两部分。
2018年普通高等学校招生全国统一考试仿真卷及答案

绝密 ★ 启用前2018年普通高等学校招生全国统一考试仿真卷理科数学(八)本试题卷共2页,23题(含选考题)。
全卷满分150分。
考试用时120分钟。
★祝考试顺利★注意事项:1、答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
用2B 铅笔将答题卡上试卷类型A 后的方框涂黑。
2、选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3、填空题和解答题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4、选考题的作答:先把所选题目的题号在答题卡上指定的位置用2B 铅笔涂黑。
答案写在答题卡上对应的答题区域内,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
5、考试结束后,请将本试题卷和答题卡一并上交。
第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设i 为虚数单位,则下列命题成立的是( ) A .a ∀∈R ,复数3ia --是纯虚数 B .在复平面内()i 2i -对应的点位于第三象限C .若复数12i z=--,则存在复数1z ,使得1z z ⋅∈RD .x ∈R ,方程2i 0xx +=无解2.在下列函数中,最小值为2的是( )A B C D 3.从某校高三年级随机抽取一个班,对该班50名学生的高校招生体检表中视力情况进行统计,其结果的频率分布直方图如图所示:若某高校A 专业对视力的要求在0.9以上,则该班学生中能报A 专业的人数为( )A .30B .25C .22D .204.已知曲线421yx a x =++在点()()11f--,处切线的斜率为8,则()1f -=( )A .7B .-4C .-7D .45.已知1=a ,=b ()⊥-aa b ,则向量a在b 方向上的投影为( )A .1BCD 6.某几何体由上、下两部分组成,其三视图如图所示,其俯视图是由一个半圆与其直径组成的图形,则该几何体上部分与下部分的体积之比为( )A B C D 7.已知函数()()sin (0)f x x ωϕω=+>的图象的一个对称中心为,02π⎛⎫⎪⎝⎭,且142f π⎛⎫=⎪⎝⎭,则ω的最小值为( )A B .1 C D .28.《九章算术》中的“两鼠穿墙”问题为“今有垣厚五尺,两鼠对穿,大鼠日一尺,小鼠也日一尺,大鼠日自倍,小鼠日自半,问何日相逢?”,可用如图所示的程序框图解决此类问题.现执行该程序框图,输入的d 的值为33,则输出的i 的值为( )A .4B .5C .6D .7 9.在A B C △中,,若2A B=,则A B C △周长的取值范围是( )ABCD10.一个三棱锥A B C D-内接于球O ,且3AD BC ==,4A C B D ==,心O 到平面A B C 的距离是( ) ABCD11.设等差数列{}n a 满足:71335a a =()22222244747456cos cos sin sin cos sin cos a a a a a a a a -+-=-+,公差()2,0d ∈-,则数列{}n a 的前n项和n S 的最大值为( )A .100πB .54πC .77πD .300π 12.若存在实数1x ,2x ,3x ,4x ,满足1234x x x x <<<,且()()()()1234f x fx fx fx ===,则)A .()0,12B .()0,16C .()9,21D .()15,25第Ⅱ卷本卷包括必考题和选考题两部分。
2018年普通高等学校招生全国统一考试(江苏卷)语文I附文言文翻译

2018 年普通高等学校招生全国统一考试(江苏卷)语文Ⅰ试题一、语言文字运用(15分)1.在下面一段话的空缺处依次填入词语,最恰当的一组是()(3分)中国古代的儒家经典,莫不是古圣人深思熟虑、▲的结晶。
如果把经典仅仅当作一场▲的说教,那你永远进不了圣学大门。
必得躬亲实践,才能切实▲圣人的心得,如此我们的修为才能日有所进。
A.特立独行耳提面命顿悟B.特立独行耳濡目染领悟C.身体力行耳提面命领悟D.身体力行耳濡目染顿悟2.在下面一段文字横线处填入语句,衔接最恰当的一项是()(3分) “理性经济人”,把利己看作人的天性,只追求个人利益的最大化,这是西方经济学的基本假设之一。
▲,▲。
▲,▲,▲,▲ ,更倾向于暂时获得产品或服务,或与他人分享产品或服务。
使用但不占有,是分享经济最简洁的表述。
①反而更多地采取一种合作分享的思维方式②不再注重购买、拥有产品或服务③但在分享经济这一催化剂的作用下④人们不再把所有权看作获得产品的最佳方式⑤在新兴的互联网平台上⑥这个利已主义的假设发生了变化A.③⑥⑤①④②B.③⑥⑤④②①C.⑤⑥③①④②D.⑤⑥③④②①3.下列诗句与所描绘的古代体育活动,对应全部正确的一项是()(3分)①乐手无踪洞箫吹,精灵盘丝任翻飞。
②雾毅云绡妙剪裁,好风相送上瑶台。
③浪设机关何所益,仅存边角未为雄。
④来疑神女从云下,去似姮娥到月边。
A.①下围棋②荡秋千③抖空竹④放风筝B.①抖空竹②荡秋千③下围棋④放风筝C.①下围棋②放风筝③抖空竹④荡秋千D.①抖空竹②放风筝③下围棋④荡秋千4.对下面一段文字主要意思的提炼,最准确的一项是()(3分)偏见可以说是思想的放假。
它是没有思想的人的家常日用,是有思想的人的星期天娱乐。
假如我们不能怀挟偏见,随时随地必须得客观公正、正经严肃,那就像造屋只有客厅,没有卧室,又好比在浴室里照镜子还得做出摄影机前的姿态。
A.没有思想的人往往更容易产生偏见B.即使有思想的人也常常会怀挟偏见C.人无法做到随时随地保持客观公正。
普通高等学校2018届高三招生全国统一考试仿真卷(一)数学(文)含答案

绝密 ★ 启用前2018年普通高等学校招生全国统一考试仿真卷文科数学(一)本试题卷共2页,23题(含选考题)。
全卷满分150分。
考试用时120分钟。
★祝考试顺利★注意事项:1、答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
用2B 铅笔将答题卡上试卷类型A 后的方框涂黑。
2、选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3、填空题和解答题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4、选考题的作答:先把所选题目的题号在答题卡上指定的位置用2B 铅笔涂黑。
答案写在答题卡上对应的答题区域内,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
5、考试结束后,请将本试题卷和答题卡一并上交。
第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合(){},2M x y x y =+=,(){},2N x y x y =-=,则集合M N =( )A .{}0,2B .()2,0C .(){}0,2D .(){}2,02 )A .B .C .12D 3.为考察A ,B 两种药物预防某疾病的效果,进行动物实验,分别得到如下等高条形图,根据图中信息,在下列各项中,说法最佳的一项是( ) A .药物B 的预防效果优于药物A 的预防效果 B .药物A 的预防效果优于药物B 的预防效果班级 姓名 准考证号 考场号 座位号C .药物A 、B 对该疾病均有显著的预防效果D .药物A 、B 对该疾病均没有预防效果药物A 实验结果患病未患病服用药没服用药0.10.20.30.40.50.60.70.80.91药物B 实验结果患病未患病服用药没服用药0.10.20.30.40.50.60.70.80.914)A .4-B .C .13-D .135.《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”.已知某“堑堵”的三视图如图所示,俯视图中间的实线平分矩形的面积,则该“堑堵”的侧面积为( )A .2B.4+C.4+D.4+6.设变量,y 满足约束条件220220 2x y x y y +--+⎧⎪⎨⎪⎩≥≤≤,则目标函数z x y =+的最大值为( )A .7B .6C .5D .47.已知()201720162018201721f x x x x =++++,下列程序框图设计的是求()0f x 的值,在“ ”中应填的执行语句是( )开始i =1,n =2018结束i ≤2017?是否输入x 0S =2018输出SS =Sx 0S =S+ni =i +1A .2018n i =-B .2017n i =-C .2018n i =+D .2017n i =+8.若函数()24x f x a =--存在两个零点,且一个为正数,另一个为负数,则的取值范围为( ) A .()0,4B .()0,+∞C .()3,4D .()3,+∞9.阿波罗尼斯(约公元前262-190年)证明过这样一个命题:平面内到两定点距离之比为常数(0k>且1k ≠)的点的轨迹是圆.后人将这个圆称为阿氏圆.若平面内两定点A ,B 间的距离为2,动点P 与A ,B,当P ,A ,B不共线时,PAB △面积的最大值是( ) A .B .C D 10.已知双曲线E :22221x y a b-=(0,0)a b >>的右顶点为A ,右焦点为F ,B 为双曲线在第二象限上的一点,B 关于坐标原点O 的对称点为C ,直线CA 与直线BF 的交点M 恰好为线段BF 的中点,则双曲线的离心率为( )A .12B .15C .2D .311.设锐角ABC △的三个内角A ,B ,C 的对边分别为,,,且1c =,2A C =,则ABC △周长的取值范围为( ) A.(0,2B .(0,3+C .(2+D .(2++12.若方程()2f x mx =+有一个零点,则实数m 的取值范围是( )A ]{64-+B ]{0,64-+C ]{}632-D ]{0,63-第Ⅱ卷本卷包括必考题和选考题两部分。
(完整版)2018年高考全国卷1文科数学试题及含答案

2018年普通高等学校招生全国统一考试文科数学注意事项:1.答卷前,考生务必将自己の姓名和准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目の答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出の四个选项中,只有一项是符合题目要求の。
1.已知集合{}02A =,,{}21012B =--,,,,,则A B =I A .{}02,B .{}12,C .{}0D .{}21012--,,,, 2.设1i2i 1iz -=++,则z = A .0B .12C .1D .23.某地区经过一年の新农村建设,农村の经济收入增加了一倍.实现翻番.为更好地了解该地区农村の经济收入变化情况,统计了该地区新农村建设前后农村の经济收入构成比例.得到如下饼图:则下面结论中不正确の是 A .新农村建设后,种植收入减少B .新农村建设后,其他收入增加了一倍以上C .新农村建设后,养殖收入增加了一倍D .新农村建设后,养殖收入与第三产业收入の总和超过了经济收入の一半4.已知椭圆C :22214x y a +=の一个焦点为(20),,则C の离心率为A .13B .12C .22D .2235.已知圆柱の上、下底面の中心分别为1O ,2O ,过直线12O O の平面截该圆柱所得の截面是面积为8の正方形,则该圆柱の表面积为 A .122πB .12πC .82πD .10π6.设函数()()321f x x a x ax =+-+.若()f x 为奇函数,则曲线()y f x =在点()00,处の切线方程为A .2y x =-B .y x =-C .2y x =D .y x =7.在△ABC 中,AD 为BC 边上の中线,E 为AD の中点,则EB =u u u rA .3144AB AC -u u ur u u u r B .1344AB AC -u u ur u u u r C .3144AB AC +u u ur u u u rD .1344AB AC +u u ur u u u r8.已知函数()222cos sin 2f x x x =-+,则 A .()f x の最小正周期为π,最大值为3 B .()f x の最小正周期为π,最大值为4 C .()f x の最小正周期为2π,最大值为3 D .()f x の最小正周期为2π,最大值为49.某圆柱の高为2,底面周长为16,其三视图如右图.圆柱表面上の点M 在正视图上の对应点为A ,圆柱表面上の点N 在左视图上の对应点为B ,则在此圆柱侧面上,从M 到N の路径中,最短路径の长度为 A .217 B .25 C .3D .210.在长方体1111ABCD A B C D -中,2AB BC ==,1AC 与平面11BB C C 所成の角为30︒,则该长方体の体积为 A .8B .62C .82D .8311.已知角αの顶点为坐标原点,始边与x 轴の非负半轴重合,终边上有两点()1A a ,,()2B b ,,且 2cos 23α=,则a b -=A .15BCD .112.设函数()201 0x x f x x -⎧=⎨>⎩,≤,,则满足()()12f x f x +<のx の取值范围是A .(]1-∞-,B .()0+∞,C .()10-,D .()0-∞,二、填空题(本题共4小题,每小题5分,共20分)13.已知函数()()22log f x x a =+,若()31f =,则a =________.14.若x y ,满足约束条件220100x y x y y --⎧⎪-+⎨⎪⎩≤≥≤,则32z x y =+の最大值为________.15.直线1y x =+与圆22230x y y ++-=交于A B ,两点,则AB =________.16.△ABC の内角A B C ,,の对边分别为a b c ,,,已知sin sin 4sin sin b C c B a B C +=,2228b c a +-=,则△ABC の面积为________.三、解答题:共70分。
2018年普通高等学校招生全国统一考试高中数学模拟测试试题文

2018年普通高等学校招生全国统一考试模拟卷文科数学一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1. 若集合{}1,2lg<=⎭⎬⎫⎩⎨⎧-==x x N x x y x M ,则=⋂N C M R A.)2,0( B.(]2,0 C.[)2,1 D. ()+∞,02. 已知复数()z a i a R =+∈,若4z z +=,则复数z 的共轭复数z = A .2i + B .2i - C .2i -+ D .2i --3. 设等差数列{}n a 的前n 项和为n S ,若81126a a =+,则9S = A .27 B .36 C.45 D .544. 已知命题p :“a b >”是“22ab>”的充要条件;q :x R ∃∈,ln x e x <,则A .¬p ∨q 为真命题B .p ∧¬q 为假命题C .p ∧q 为真命题D .p ∨q 为真命题5.已知角α的终边经过点()12,5--P ,则⎪⎭⎫⎝⎛+απ23sin 的值等于 A .513- B .1213- C .513 D .12136.某几何体的三视图如图所示,图中每一个小方格均为正方形,且边长为1,则该几何体的体积为A .8π B.323πC .283π D .12π 7. 若程序框图如图所示,则该程序运行后输出k 的值是 A .5 B .6 C.7 D .88.一组数据共有7个数,记得其中有10、2、5、2、4、2,还有一个数没记清,但知道这组数的平均值、中位数、众数依次成等差数列,这个数的所有可能值的和为A. 11- B. 3 C. 9 D. 179. 函数2()(3)lnf x x x=-⋅的大致图象为10.正方体的棱长为1,点P,Q,R分别是棱,,的中点,以为底面作正三棱柱,若此三棱柱另一底面的三个顶点也都在该正方体的表面上,则这个正三棱柱的高为A.22B. 2C.33D.3211.已知P为抛物线y2=4x上一个动点,Q为圆x2+(y﹣4)2=1上一个动点,那么点P到点Q的距离与点P到抛物线的准线距离之和的最小值是A.B.C.D.12.已知()f x是定义在R上的偶函数,且x R∈时,均有()()32f x f x+=-,()28f x≤≤,则满足条件的()f x可以是A.()2,8,Rx Qf xx C Q∈⎧=⎨∈⎩B.()53cos5xf xπ=+C. ()263cos5xf xπ=+ D.()2,08,0xf xx≤⎧=⎨>⎩二.填空题:(本题共4小题,每小题5分,共20分)13.某校今年计划招聘女教师x人,男教师y人,若,x y满足2526x yx yx-≥⎧⎪-≤⎨⎪<⎩,则该学校今年计划招聘教师最多人.14. 已知双曲线﹣=1(a >0,b >0)的右焦点为F ,焦距为8,左顶点为A ,在y 轴上有一点B (0,b ),满足•=2a ,则该双曲线的离心率的值为 .15. 已知ABC ∆的内角,,A B C 的对边分别是a b c 、、,且222()a b c +-(cos cos )a B b A ⋅+abc =,若2a b +=,则c 的取值范围为 .16.已知数列{}n a 的前n 项和为2n S tn =()t ∈R ,且81215,1n n a b a +==+,若不等式512n b n p p a +>+恒成立,则正实数p 的取值范围是 .三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤) 17.(本小题满分12分) 已知向量()1cos 3sin cos 22a x b x x x R ⎛⎫=-=∈ ⎪⎝⎭,,,,,设函数()f x a b =.(I )求()f x 的表达式并完成下面的表格和画出()f x 在[]0π,范围内的大致图象;0 2ππ32πxπ()f x(II )若方程()0f x m -=在[]0π,上有两个根α、β,求m 的取值范围及αβ+的值. 18.(本小题满分12分)已知某中学高三文科班学生共有800人参加了数学与地理的水平测试,学校决定利用随机数表法从中抽取100人进行成绩抽样调查.抽取的100人的数学与地理的水平测试成绩如下表:人数数学 优秀良好 及格 地理优秀 7 20 5 良好 9 18 6 及格a4b中数学成绩为良好的共有20+18+4=42人.(I )在该样本中,数学成绩优秀率是30%,求a ,b 的值;(II )在地理成绩及格的学生中,已知a ≥10,b ≥7,求数学成绩优秀的人数比及格的人数少的概率.19.(本小题满分12分)如图,三棱柱111ABC A B C -中, AB ⊥平面11AAC C , 1AA AC =.过1AA 的平面 交11B C 于点E ,交BC 于点F .(I )求证: 1A C ⊥平面1ABC ; (II )求证: 1//AA EF ;(III )记四棱锥11B AA EF -的体积为1V ,三棱柱111ABC A B C -的体积为V .若116V V =,求BFBC的值.20. (本小题满分12分)在平面直角坐标系xOy 中,已知椭圆E :1by a x 2222=+(a >b >0),圆O :x 2+y 2=r 2(0<r <b ).当圆O 的一条切线l :y=kx+m 与椭圆E 相交于A ,B 两点. (I )当k=﹣21,r=1时,若点A ,B 都在坐标轴的正半轴上,求椭圆E 的方程; (II )若以AB 为直径的圆经过坐标原点O ,探究a ,b ,r 是否满足222r 1b 1a 1=+,并说明理由.21.(本小题满分12分)已知函数()ln x x f x =,()g x x a =+.(I )设()()()h f x x g x =-,求函数()y h x =的单调区间; (II )若10a -<<,函数()()()x g x M x f x ⋅=,试判断是否存在0(1,)x ∈+∞,使得0x 为函数()M x 的极小值点.(二)选考题:共10分。
2018届普通高等学校招生全国统一考试高三数学模拟试题(一)文

普通高等学校招生全国统一考试模拟试题文科数学(一)本试卷满分150分,考试时间120分钟.注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题纸上.2.回答选择题时,选出每小题答案后,用铅笔把答题纸上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题纸上,写在本试卷上无效.3.考试结束后,将本试卷和答题纸一并交回.一、选择题:本题共12小题。
每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}{}1,420,A x x B x x =>=-≤则A .{}1AB x x ⋂=>B .A B ⋂=∅C .{}1A B x x ⋃=>D .A B R ⋃=2.已知数据12340,,,x x x x ⋅⋅⋅,是某班40名同学某次月考的化学成绩(单位:分),现将这40名同学的化学成绩的平均数x 与这40个数据合在一起,并将这41个数据的平均数、中位数、众数分别与原来的平均数、中位数、众数相比较,则下列说法中正确的是A .平均数不变,中位数、众数变大B .平均数变大,中位数、众数可能不变C .平均数变小,中位数、众数可能不变D .平均数不变,中位数、众数可能不变3.下列各式的运算结果中,在复平面内对应的点位于第二象限的是A .()1i i -+B .i(1+i)2C .()()2211i i -+D .1i i-4.剪影是我国剪纸艺术中的一种古老形式,通过外轮廓表现人物和物象的形状,由于受轮廓造型的局限,一般以表现人物或其他物体的侧面居多.如图是一幅长50cm 、宽40cm 的矩形剪影,为估算剪影中美女图案的面积,现向剪影内随机投掷1200粒芝麻(假设芝麻均落在剪影内),其中恰有300粒芝麻落在美女图案内,据此估计美女图案的面积为A .250cm 2B .500cm 2C .1000cm 2D .20003cm 2 5.已知双曲线22:14x C y -=的左、右焦点分别为12,F F ,点A 在双曲线C 上,且2AF x ⊥轴,点B 与点A 关于原点O 对称,则四边形12AF BF 的面积为ABCD6.已知实数,x y 满足约束条件10,40,20,x y y x y z x y --≤⎧⎪+-≥≤⎨⎪-≤⎩若恒成立,则实数z 的最大值为 A .35 B .23 C .1 D .537.如图,在正方体ABCD —A 1B 1C 1D 1中,P 为线段AD 的中点,Q 为线段B 1C 1上的动点,则下列说法中错误的是A .线段PQ 与平面CDD 1C 1可能平行B .当Q 为线段B 1C 1的中点时,线段PQ 与DD 1所成的角为4π C.PQ ≥D .1CD PQ 与不可能垂直8.函数()2cos sin 2x x f x x-=的部分图像大致为9.已知函数()ln 4x f x x =-,则下列说法中正确的是 A .()f x 在区间(),0-∞内单调递增 B .()f x 在区间(4,+∞)内单调递增C .()f x 的图像关于点(2,0)对称D .()f x 的图像关于直线x =2对称 10.执行如图所示的程序框图,若输出的S 的值为负数,则①②中可以分别填入A .“S=1”“n <9?”B .“S=1”“n <8?”C .“S=2”“n <99?”D .“S=2”“n<100?”11.如图,在平面四边形ABCD 中,AD=2,sin sin 14CAD BAC ∠=∠+ cos 2,BC B BC B D ABC π=+=∆且,则的面积的最大值为A B C .7 D .1412.已知椭圆()2221024x y C b b+=<<:的左焦点为F ,点()4,0M -,斜率不为0的直线l 经过点F 与椭圆C 交于A ,B 两点,若直线MA 与直线MB 关于x 轴对称,则椭圆C 的离心率是A .14B .12C .34D 二、填空题:本题共4小题,每小题5分,共20分.13.已知向量()()1,1,3,a b x ==,若a b a -在方向上的投影是0,则x 的值为_________.14.曲线()24f x x x=-在点()()1,1f 处的切线l 与坐标轴围成的三角形的面积为_________. 15.已知()3,,tan 20183,cos 24ππαππαα⎛⎫⎛⎫∈-=+= ⎪ ⎪⎝⎭⎝⎭则___________. 16.已知菱形ABCD 的边长为2,A=60°,将△ABD 沿对角线BD 折起,使得AC=3,则四面体ABCD 的外接球的表面积为__________.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题.每个试题考生都必须作答.第22,23题为选考题。
2018年普通高等学校招生全国统一考试(江苏卷)语文I附文言文翻译

2018 年普通高等学校招生全国统一考试(江苏卷)语文Ⅰ试题一、语言文字运用(15分)1.在下面一段话的空缺处依次填入词语,最恰当的一组是()(3分)中国古代的儒家经典,莫不是古圣人深思熟虑、▲的结晶。
如果把经典仅仅当作一场▲的说教,那你永远进不了圣学大门。
必得躬亲实践,才能切实▲圣人的心得,如此我们的修为才能日有所进。
A.特立独行耳提面命顿悟B.特立独行耳濡目染领悟C.身体力行耳提面命领悟D.身体力行耳濡目染顿悟2.在下面一段文字横线处填入语句,衔接最恰当的一项是()(3分)“理性经济人”,把利己看作人的天性,只追求个人利益的最大化,这是西方经济学的基本假设之一。
▲,▲。
▲,▲,▲,▲,更倾向于暂时获得产品或服务,或与他人分享产品或服务。
使用但不占有,是分享经济最简洁的表述。
①反而更多地采取一种合作分享的思维方式②不再注重购买、拥有产品或服务③但在分享经济这一催化剂的作用下④人们不再把所有权看作获得产品的最佳方式⑤在新兴的互联网平台上⑥这个利已主义的假设发生了变化A.③⑥⑤①④②B.③⑥⑤④②①C.⑤⑥③①④②D.⑤⑥③④②①3.下列诗句与所描绘的古代体育活动,对应全部正确的一项是()(3分)①乐手无踪洞箫吹,精灵盘丝任翻飞。
②雾毅云绡妙剪裁,好风相送上瑶台。
③浪设机关何所益,仅存边角未为雄。
④来疑神女从云下,去似姮娥到月边。
A.①下围棋②荡秋千③抖空竹④放风筝B.①抖空竹②荡秋千③下围棋④放风筝C.①下围棋②放风筝③抖空竹④荡秋千D.①抖空竹②放风筝③下围棋④荡秋千4.对下面一段文字主要意思的提炼,最准确的一项是()(3分)偏见可以说是思想的放假。
它是没有思想的人的家常日用,是有思想的人的星期天娱乐。
假如我们不能怀挟偏见,随时随地必须得客观公正、正经严肃,那就像造屋只有客厅,没有卧室,又好比在浴室里照镜子还得做出摄影机前的姿态。
A.没有思想的人往往更容易产生偏见B.即使有思想的人也常常会怀挟偏见C.人无法做到随时随地保持客观公正。
2018年普通高等学校招生全国统一考试(含答案)

2018年普通高等学校招生全国统一考试英语第一部分听力(共两节,满分30分)做题时,先将答案标在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5小题:每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题屮所给的A、B、C三个选项屮选出最佳选项。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅谈一遍。
例:How much is the shirt?A.£19.15.B. £9.18.C. £9.15.答案是C。
1. What will James do tomorrow?A. Watch a TV program.B. Give a talk.C. Write a report.2. What can we say about the woman?A. She’s generous.B. She’s curious.C. She’s helpful.3. When does the train leave?A. At 6:30.B. At 8:30.C. At 10:30.4. How docs the woman go to work?A. By car.B. On foot.C. By bike.5. What is the probable relationship between the speakers?A. Classmates.B. Teacher and student.C. Doctor and patient.第二节(共15小题:每小题1.5分,满分22.5分)听下面5段对话或独內。
每段对话或独A后有几个小题,从题中所给的A、B、C 三个选项中选出最佳选项。
听每段对话或独白前,你将有时间阅读各个小题,每小题5 秒钟:听完后,各小题将给出5秒钟的作答时间。
每段对话或独白读两遍。
高三数学-2018普通高等学校招生全国统一考试仿真试卷

普通高等学校招生全国统一考试仿真试卷数 学 理工农医类(八)本试卷分第I 卷(选择题 共60分)和第Ⅱ卷(非选择题 共90分),考试时间120分钟,满分为150分.第Ⅰ卷(选择题 共60分)参考公式:如果事件A 、B 互斥,那么P (A +B )=P (A )+P (B ) 如果事件A 、B 相互独立,那么P (A ·B )=P (A )·P (B ) 如果事件A 在一次试验中发生的概率是p ,那么n 次独立重复试验中恰好发生k 次的概率P n (k )=k n C p k (1-p )n -k球的表面积公式S =4πR 2,其中R 表示球的半径 球的体积公式V =34πR 3,其中R 表示球的半径 一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.设I 为全集,M 、N 、P 都是它的子集,则图中阴影部分表示的集合是A.M ∩(N ∪P )B.M ∩[(I N )∩P ]C.[(I M )∩(I N )]∩P D.(M ∩N )∪(M ∩P )2.奇函数y =f (x )(x ≠0),当x ∈(0,+∞)时,f (x )=x -1,则函数f (x -1)的图象为3.设O 、A 、B 、C 为平面上四个点,=a ,=b ,=c ,且a +b +c =0,a ,b ,c 两两数量积都为-1,则|a |+|b |+|c |等于A.22B.23C.32D.334.下列函数中值域是(0,+∞)的函数是A.y =x-215B.y =(21)1-xC.y =x 21-D.y =121-x5.三个数成等差数列,其公差为d ,如果最小数的2倍,最大数加7,则三个数成等比数列,且它们的积为1000,此时d 为A.8B.8或-15C.±8D.±156.设a >b >c ,且ca nc b b a -≥-+-11,则n 的最大值为 A.2B.3C.4D.57.已知0<θ<4π,则下列各式中正确的是 A.sin θ<cos θ<cot θ B.cos θ<cot θ<sin θ C.cot θ<sin θ<cos θ D.cos θ<sin θ<cot θ 8.如果AC <0且BC <0,那么直线Ax +By +C =0不通过 A.第一象限 B.第二象限 C.第三象限 D.第四象限 9.有如下一些说法,其中正确的是①若直线a ∥b ,b 在面α内,则 a ∥α;②若直线a ∥α,b 在面α内, 则 a ∥b ; ③若直线a ∥b ,a ∥α, 则 b ∥α;④若直线a ∥α,b ∥α, 则 a ∥b . A.①④ B.①③ C.② D.均不正确10.甲、乙、丙三位学生用计算机联网学习数学,每天上课后独立完成6道自我检测题,甲答及格的概率为54,乙答及格的概率为53,丙答及格的概率为107,三人各答一次,则三人中只有一人答及格的概率为A.203B.12542 C.25047D.以上都不对11.若以椭圆上一点和两个焦点为顶点的三角形面积的最大值为1,则椭圆长轴的最小 值为A.1B.2C.2D.2212.已知曲线S :y =3x -x 3及点P (2,2),则过点P 可向S 引切线的条数为 A.0 B.1 C.2 D.3第Ⅱ卷(非选择题 共90分)二、填空题(本大题共4小题,每小题4分,共16分,把答案填在题中横线上)13.已知双曲线2222by a x -=1(a >0,b >0)的半焦距为c ,若b 2-4ac <0,则它的离心率的取值范围是 .14.地球北纬45°圈上有两点A 、B ,点A 在东经130°处,点B 在西经140°处,若地球半径为R ,则A 、B 两点在纬度圈上的劣弧长与A 、B 两点的球面距离之比是 .15.已知函数f (x )=x 3+ax 2+bx +a 2在x =1处有极值为10,则a = ,b = . 16.有下列命题:① G =ab (G ≠0)是a ,G ,b 成等比数列的充分非必要条件;②若角α,β满足 cos αcos β=1,则sin (α+β)=0;③若不等式|x -4|+|x -3|<a 的解集非空,则必有a ≥1;④函数y =sin x +sin |x |的值域是[-2,2].其中错误命题的序号是 .(把你认为错误的命题的序号都填上)三、解答题(本大题共6小题,共74分,解答题应写出文字说明、证明过程或演算步骤) 17.(本小题满分12分)已知等差数列{a n }的首项a 1=1,公差d >0,且其第二项、第五项、第十四项分别是等比数列{b n }的第二、三、四项.(1)求数列{a n }与{b n }的通项公式;(2)设数列{c n }对任意自然数n 均有nn b cb c b c b c ++++ 332211=a n +1成立,求c 1+c 2+c 3+…+c 2018的值.18.(本小题满分12分)如图,已知:PD ⊥平面ABCD ,AD ⊥DC ,AD ∥BC ,PD ∶DC ∶BC =1∶1∶2.(1)求PB 与平面PDC 所成角的大小;(2)求二面角D —PB —C 的正切值. 19.(本小题满分12分) 在△OAB 中,OB OD OA OC 21,41==,AD 与BC 交于点M ,设=a ,=b , (1)用a ,b 表示OM ;(2)在线段AC 上取一点E ,在线段BD 上取一点F ,使E F 过M 点,设OE =p OA ,OF =q OB ,求证:pp 7371+=1. 20.(本小题满分12分)某厂生产一种仪器,由于受生产能力和技术水平的限制,会产生一些次品,根据经验知该厂生产这种仪器,次品率p 与日产量x (件)之间大体满足关系:⎪⎪⎩⎪⎪⎨⎧∈>∈≤≤-N),94(32N),941(961x x x x x.已知每生产一件合格的仪器可盈利A 元,但每生产一件次品将亏损2A元,厂方希望定出适当的日产量.(1)试判断:当日产量(件)超过94件时,生产这种仪器能否赢利?并说明理由; (2)当日产量x 件不超过94件时,试将生产这种仪器每天的赢利额T (元)表示成日产量x (件)的函数;(3)为了获得最大利润,日产量x 件应为多少件? 21.(本小题满分12分)已知双曲线C :2222by a x -=1(a >0,b >0)的一条准线方程为x =59,一个顶点到一条渐近线的距离为512. (1)求双曲线C 的方程; (2)动点P 到双曲线C 的左顶点A 和右焦点F 的距离之和为常数(大于|AF |),且cos APF 的最小值为-257,求动点P 的轨迹方程. 22.(本小题满分14分)已知函数f (x )满足对任意实数x ,y 都有f (x +y )=f (x )+f (y )+xy +1,且f (-2)=-2. (1)求f (1)的值;(2)证明:对一切大于1的正整数t ,恒有f (t )>t ; (3)试求满足f (t )=t 的整数的个数,并说明理由.参考答案一、选择题(每小题5分,共60分) 1.B2.解析:用图象平移或直接求出f (x -1)的解析式即得. 答案:D3.解析:利用a +b =-c 平方得. 答案:C4.B5.B6.解析:用基本不等式ba b a 1122+≥+(a >0,b >0)变形得. 答案:C 7.解析:由tan θ=θθcos sin >sin θ得. 答案:A8.解析:利用AC <0,BC <0研究横纵截距.答案:C9.D 10.C 11.D12.解析:设S 的切线方程,令切线过点P 可求得. 答案:D二、填空题(每小题4分,共16分)13.(1,2+5) 14.32∶4 15.4,-11 16.③三、解答题(17,18,19,20,21题每题12分,22题14分,共74分) 17.解:(1)由题意得(a 1+d )(a 1+13d )=(a 1+4d )2(d >0),解得d =2,∴a n =2n -1.可得b n =3n -1 5分 (2)当n =1时,c 1=3;当n ≥2时,由nn b c =a n +1-a n ,得c n =2·3n -1, 故c n =⎩⎨⎧≥⋅=-).2(32),1(31n n n 9分故c 1+c 2+c 3+…+c 2018=3+2×3+2×32+…+2×32002=32018. 12分18.解:(1)由PD ⊥平面ABCD ,BC ⊂平面ABCD , 得PD ⊥BC .由AD ⊥DC ,AD ∥BC ,得BC ⊥DC . 又PD ∩DC =D ,则BC ⊥平面PDC .所以∠BPC 为直线PB 与平面PDC 所成的角. 3分令PD =1,则DC =1,BC =2,可求出PC =2. 由BC ⊥平面PDC ,PC ⊂平面PDC ,得BC ⊥PC . 在Rt △PBC 中,由PC =BC ,得∠BPC =45°, 即直线PB 与平面PDC 所成的角为45°. 5分(2)如图,取PC 中点E ,连DE ,则DE ⊥PC . 由BC ⊥平面PDC ,BC ⊂平面PBC ,得平面PDC ⊥平面PBC . 则DE ⊥平面PBC . 7分作EF ⊥PB 于F ,连DF , 由三垂线定理,得DF ⊥PB .则∠DFE 为二面角D —PB —C 的平面角. 9分在Rt △PDC 中,求得DE =22.在Rt △PFE 中,求得EF =21. 在Rt △DEF 中,tan DFE =.2=EFDE11分 即二面角D —PB —C 的正切值为2.12分19.(1)解:设OM =m a +n b , 则AM =(m -1)a +n b ;AD =-a +21b , ∵点A 、M 、D 共线,∴与共线,∴5.011nm =--,∴m +2n =1. ① 2分而)41(-=-=m OC OM CM a +n b ,41-=CB a +b ,∵C 、M 、B 共线,∴CM 与CB 共线,∴14141n m =--,∴4m +n =1. ② 4分 联立①②可得m =71,n =73,∴71=OM a +73b . 7分(2)证明:EM =(71-p )a +73b ,EF =-p a +q b ,∵EF 与EM 共线,∴qp p7371=--. ∴71q -pq =-73p ,即qp 7371+=1.12分20.解:(1)当x >94时,p =32,故每日生产的合格品约为31x 件,次品约为32x 件,合格品共可赢利31xA 元,次品共亏损32x ·312=A xA 元.因盈亏相抵,故当日产量超过94件时,不能赢利. 5分(2)当1≤x ≤94时,p =x-961,每日生产的合格品约为x (1-x -961)件,次品约为x x -96件,∴T =x (1-x-961)A -x x -96·2A =[x -)96(23x x-]A (1≤x ≤94).(3)由(1)可知,日产量超过94件时,不能盈利. 当1≤x ≤94时,.]96144)96(2196[)9614423(A xx A x x T ----=--+=. ∵x ≤94,96-x >0, ∴T ≤.02147]96144)96(22197[>=-⋅--A A x x 当且仅当(96-x )=x-96144时,即x =84时,等号成立.故要获得最大利润,日产量应为84件.12分21.解:(1)易求得方程为16922y x -=1.5分(2)A 、F 是定点,由圆锥曲线的定义知,点P 的轨迹为椭圆.设其长轴为2a ,短轴为2b ,焦距为2c =8,在△P AF 中,应用余弦定理研究∠APF 的余弦,应用基本不等式可知,cos APF ≥1-232a , 当且仅当|P A |=|PF |=a 时取等号,故a 2=25,b 2=9,求出椭圆中心的坐标为(1,0),则所求方程为925)1(22y x +-=1. 12分22.(1)解:令x =y =0,得f (0)=-1.令x =y =-1,因f (-2)=-2,所以f (-1)=-2. 令x =1,y =-1,得f (0)=f (1)+f (-1), 所以f (1)=1. 4分 (2)证明:令x =1,得f (y +1)-f (y )=y +2, 故当y ∈N 时,有f (y +1)-f (y )>0. 由f (y +1)>f (y ),f (1)=1可知, 对一切正整数y 都有f (y )>0.当y ∈N 时,f (y +1)=f (y )+y +2=f (y )+1+y +1>y +1. 故对一切大于1的正整数,恒有f (t )>t . 9分(3)解:由f (y +1)-f (y )=y +2及(1)可知f (-3)=-1,f (-4)=1. 下面证明t ≤-4时,f (t )>t . ∵t ≤-4,∴-(t +2)≥2>0.∵f (t )-f (t +1)=-(t +2)>0, ∴f (-5)-f (-4)>0,同理可得f (-6)-f (-5)>0,f (t +1)-f (t +2)>0,f (t )-f (t +1)>0. 将各不等式相加得f (t )>f (-4)=1>-4. ∵t ≤-4,∴f (t )>t .综上所述,满足条件的整数只有两个:1和-2. 14分。
2018届高三普通高校统一招生考试仿真卷(二)数学(文)试卷(含答案)

绝密★启用前2018年普通高等学校招生全国统一考试仿真卷文科数学(二)本试题卷共2页,23题(含选考题)。
全卷满分150分。
考试用时120分钟。
★祝考试顺利★注意事项:1、答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
用2B铅笔将答题卡上试卷类型A后的方框涂黑。
2、选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3、填空题和解答题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4、选考题的作答:先把所选题目的题号在答题卡上指定的位置用2B铅笔涂黑。
答案写在答题卡上对应的答题区域内,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
5、考试结束后,请将本试题卷和答题卡一并上交。
第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设是虚数单位,若复数i1iz=+,则的共轭复数为()A.11i22+B.11i2+C.11i2-D.11i22-2.若双曲线221yxm-=的一个焦点为()3,0-,则m=()A.22B.C.D.643.将函数πsin24y x⎛⎫=-⎪⎝⎭的图像向左平移π6个单位后,得到函数()f x的图像,则姓名准考证号考场号座位号π12f ⎛⎫= ⎪⎝⎭( ) A .26+ B .36+ C .32D .2 4.函数()12xf x ⎛⎫= ⎪⎝⎭,()0,x ∈+∞的值域为D ,在区间()1,2-上随机取一个数x ,则x D∈的概率是( )A .12B .13C .14D .15.已知变量x 和y 的统计数据如下表:根据上表可得回归直线方程0.7y x a =+,据此可以预报当6x =时,y =( ) A .8.9B .8.6C .8.2D .8.16.一个几何体的三视图如图所示,则该几何体的体积为( )A .83B .163C .203D .87.《九章算术》是我国古代的数学名著,书中有如下问题:“今有大夫、不更、簪裹、上造、公士,凡五人,共猎得五鹿,欲以爵次分之,问各得几何?”其意思:“共有五头鹿,5人以爵次进行分配(古代数学中“以爵次分之”这种表述,一般表示等差分配,在本题中表示等差分配).”在这个问题中,若大夫得“一鹿、三分鹿之二”,则簪裹得( ) A .一鹿、三分鹿之一B .一鹿C .三分鹿之二D.三分鹿之一8.函数sin1xyx=-的部分图像大致为()A.B.C.D.9.阅读如图所示的程序框图,运行相应程序,输出的结果是()A.12 B.18 C.120 D.12510.设x,y满足约束条件1122x yx yx y+⎧⎪--⎨⎪-⎩≥≥≤,若目标函数3z ax y=+仅在点()1,0处取得最小A .()6,3-B .()6,3--C .()0,3D .(]6,0-11.已知抛物线22(0)y px p =>的焦点为F ,其准线与双曲线2213y x -=相交于M ,N 两点,若MNF △为直角三角形,其中F 为直角顶点,则p =( )A .BC .D .612.若关于x 在()()00-∞+∞U ,,上恒成立,则实数k 的取值范围为( )A BC D 第Ⅱ卷本卷包括必考题和选考题两部分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018年普通高等学校招生全国统一考试高三数学仿真卷 文(一)本试题卷共14页,23题(含选考题)。
全卷满分150分。
考试用时120分钟。
★祝考试顺利★注意事项:1、答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
用2B 铅笔将答题卡上试卷类型A 后的方框涂黑。
2、选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3、填空题和解答题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4、选考题的作答:先把所选题目的题号在答题卡上指定的位置用2B 铅笔涂黑。
答案写在答题卡上对应的答题区域内,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
5、考试结束后,请将本试题卷和答题卡一并上交。
第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.[2018·晋城一模]已知集合(){},2M x y x y =+=,(){},2N x y x y =-=,则集合MN =( )A .{}0,2B .()2,0C .(){}0,2D .(){}2,0【答案】D 【解析】解方程组22x y x y +=-=⎧⎨⎩,得20x y =⎧⎨=⎩.故(){}2,0MN =.选D .2.[2018·台州期末](i 为虚数单位))A .2B .1C .12D .2【答案】C11i 22z ∴=-=,选C . 3.[2018·南宁二中]为考察A ,B 两种药物预防某疾病的效果,进行动物实验,分别得到如下等高条形图:药物A 实验结果患病未患病服用药没服用药0.10.20.30.40.50.60.70.80.91药物B 实验结果患病未患病服用药没服用药0.10.20.30.40.50.60.70.80.91根据图中信息,在下列各项中,说法最佳的一项是( ) A .药物B 的预防效果优于药物A 的预防效果 B .药物A 的预防效果优于药物B 的预防效果 C .药物A 、B 对该疾病均有显著的预防效果 D .药物A 、B 对该疾病均没有预防效果 【答案】B【解析】由A、B 两种药物预防某疾病的效果,进行动物试验,分别得到的等高条形图,知:药物A 的预防效果优于药物B 的预防效果.故选B . 4.[2018·滁州期末])A .4-B .4 C.13-D .13【答案】C sin 2cos tan 2ααα-=-⇒=,C.5.[2018·陕西一模]《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”.已知某“堑堵”的三视图如图所示,俯视图中间的实线平分矩形的面积,则该“堑堵”的侧面积为()A.2 B.4+C.4+D.4+【答案】C【解析】根据题意和三视图知几何体是一个放倒的直三棱柱,底面是一个直角三角形,两条直角边分别是、斜边是2,且侧棱与底面垂直,侧棱长是2,∴几何体的侧面积C.6.[2018·滁州期末]设变量x,y满足约束条件2202202x yx yy+--+⎧⎪⎨⎪⎩≥≤≤,则目标函数z x y=+的最大值为()A.7 B.6 C.5 D.4 【答案】D【解析】画出不等式组表示的可行域(如图阴影部分所示).由z x y =+,得y x z =-+.平移直线y x z =-+,结合图形可得,当直线(图中的虚线)经过可行域内的点A 时,直线在y 轴上的截距最大,此时z 取得最大值. 由2220y x y =-+=⎧⎨⎩,解得22x y ==⎧⎨⎩,故点A 的坐标为(2,2).∴m a x 224z =+=,即目标函数z x y =+的最大值为4.选D .7.[2018·蚌埠一模]已知()201720162018201721f x x x x =++++,下列程序框图设计的是求()0f x 的值,在“ ”中应填的执行语句是( )开始i =1,n =2018结束i ≤2017?是否输入x 0S =2018输出SS =Sx 0S =S+ni =i +1A .2018n i =-B .2017n i =-C .2018n i =+D .2017n i =+【答案】A【解析】不妨设01x =,要计算()120182017201621f =+++++,首先201812018S =⨯=,下一个应该加2017,再接着是加2016,故应填2018n i =-. 8.[2018·达州期末]若函数()24x f x a =--存在两个零点,且一个为正数,另一个为负数,则a 的取值范围为( ) A .()0,4 B.()0,+∞ C .()3,4 D .()3,+∞【答案】C【解析】如图,若()24xf x a =--存在两个零点,且一个为正数,另一个为负数,则()34a ∈,,故选C .9.[2018·朝阳期末]阿波罗尼斯(约公元前262-190年)证明过这样一个命题:平面内到两定点距离之比为常数k (0k >且1k ≠)的点的轨迹是圆.后人将这个圆称为阿氏圆.若平面内两定点A ,B 间的距离为2,动点P 与A ,BP ,A ,B 不共线时,P A B △面积的最大值是( )A.BC3D3【答案】A【解析】如图,以经过A ,B 的直线为x 轴,线段A B 的垂直平分线为y 轴,建立直角坐标系;则:()10A -,,()10B ,,设()P x y ,,P A P B=∴方并整理得:()222261038x y x x y+-+=⇒-+=.∴P AB △面积的最大值是1222⨯⨯=A .10.[2018·孝感八校]已知双曲线E :22221xy ab-=(0,0)a b >>的右顶点为A ,右焦点为F ,B 为双曲线在第二象限上的一点,B 关于坐标原点O 的对称点为C ,直线C A 与直线B F 的交点M 恰好为线段B F 的中点,则双曲线的离心率为( ) A .12B .15C .2D .3【答案】D【解析】不妨设2,b B c a ⎛⎫- ⎪⎝⎭,由此可得(),0A a ,2,b C c a ⎛⎫- ⎪⎝⎭,(),0F c ,20,2b M a ⎛⎫ ⎪⎝⎭,由于A ,C ,M 三点共线,故222bba a aa c=--,化简得3c a =,故离心率3e =.11.[2018·昆明一中]设锐角A B C △的三个内角A ,B ,C 的对边分别为a ,b ,c ,且1c =,2A C =,则A B C △周长的取值范围为( )A.(0,2+B.(0,3+C.(23++ D.(23++【答案】C【解析】因为A B C △为锐角三角形,c o s 22C <<2A C =,所以sin 2sin co s A C C =,又因为1c =,所以2co s a C =;由sin sin b c BC=,即2s in s in 34c o s 1s in s in c B C b C C C===-,所以24co s 2co s a b c C C ++=+,令co s t C =,则(,22t ⎫∈⎪⎪⎭,又因为函数242y t t =+在( ,22⎪⎭上单调递增,所以函数值域为(23++,故选:C .12.[2018·菏泽期末]()2fx m x =+有一个零点,则实数m 的取值范围是( ) A ]{64-+B ]{0,64-+C ]{632-D ]{0,63-【答案】B【解析】由题意函数()f x 的图象与直线2y m x =+有一个交点.如图是()f x 的图象,1x >时,()21f x x =-,,设切点为()00,x y ,则切线为()()02002211y x x x x -=----,把()0,2代入,02x =+;1x ≤时,()2e xfx =-,()e xf x '=-,设切点为()00,x y ,则切线为()()02ee x x y x x --=--,把()0,2代入,解得01x =,又()12e f =-,()11e e f '=-=-,所以由图象知当]{0,42-B .第Ⅱ卷本卷包括必考题和选考题两部分。
第(13)~(21)题为必考题,每个试题考生都必须作答。
第(22)~(23)题为选考题,考生根据要求作答。
二、填空题:本大题共4小题,每小题5分。
13.[2018·周口调研]已知平面向量a 与b.【答案】2 【解析】2+=a b ,即224412+⋅+=a a b b,41co s⨯⨯a14.[2018·防城港模拟]已知0a >,0b >,22a b +=,若24abm +>恒成立,则实数m 的取值范围是__________. 【答案】4m <【解析】当且仅当1a =,12b =时等号成立,即()m in244ab+=,由恒成立的结论可得:()m in24a bm <+,即实数m 的取值范围是4m <.15.[2018·张家口期末]将正整数对作如下分组,第1组为()(){}1,2,2,1,第2组为()(){}1,3,3,1,第3组为()()()(){}1,4,2,3,3,2,4,1,第4组为()()()(){}1,5,2,44,25,1⋅⋅⋅⋅⋅⋅则第30组第16个数对为__________. 【答案】(17,15)【解析】根据归纳推理可知,每对数字中两个数字不相等,且第一组每一对数字和为3,第二组每一对数字和为4,第三组每对数字和为5,......,第30组每一对数字和为32,∴第30组第一对数为()1,31,第二对数为()2,30,.......,第15对数为()15,17,第16对数为()17,15,故答案为()17,15.16.[2018·唐山期末]在三棱椎P A B C -中,底面A B C 是等边三角形,侧面P A B 是直角三角形,且2P A P B ==,P A A C ⊥,则该三棱椎外接球的表面积为________. 【答案】12π【解析】由于P A P B =,C A C B =,P A A C ⊥,则P B C B ⊥,因此取P C 中点O ,则有O P O C O A O B===,即O 为三棱锥P A B C -外接球球心,又由2P A P B ==,得三、解答题:解答应写出文字说明、证明过程或演算步骤。
17.[2018·昆明一中]已知数列{}n a 满足2n n S a n =-()*n ∈N . (1)证明:{}1n a +是等比数列;(2)求13521...n a a a a +++++()*n ∈N .【答案】(1)证明见解析;(2)232353n n +--.【解析】(1)由1121S a =-得:11a =,···········1分因为()()()11221n n n n S S a n a n ---=----()2n ≥, 所以121n n a a -=+,···········3分 从而由()1121n n a a -+=+得1121n n a a -+=+()2n ≥,···········5分所以{}1n a +是以2为首项,2为公比的等比数列.···········6分 (2)由(1)得21n n a =-,···········8分所以()()321135212221n n a a a a n +++++⋅⋅⋅+=++⋅⋅⋅+-+()()1214114n n +-=-+-232353n n +--=.···········12分18.[2018·吕梁一模]某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,得到如图的频率分布直方图(图1).(1)若直方图中后四组的频数成等差数列,试估计全年级视力在5.0以下的人数; (2)学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年级名次在1~50名和951~1000名的学生进行了调查,得到图2中数据,根据表中的数据,能否在犯错误的概率不超过0.05的前提下认为视力与学习成绩有关系? 【答案】(1)820;(2)在犯错误的概率不超过0.05的前提下认为视力与学习成绩有关系. 【解析】(1)由图可知,第一组有3人,第二组7人,第三组27人, (1)分设后四组的频数构成的等差数列的公差为d ,则()()()2727227363d d d -+-+-=,解得3d =,所以后四组频数依次为27,24,21,18,···········3分 所以视力在5.0以下的频数为3+7+27+24+21=82人,···········5分 故全年级视力在5.0以下的人数约为1000×0.82=820(人).···········6分 (2)()221004118329300 4.110 3.8415050732773k ⨯⨯-⨯==≈>⨯⨯⨯,········10分因此能在犯错误的概率不超过0.05的前提下认为视力与学习成绩有关系.······12分 19.[2018·南阳一中]如图,在四棱椎E A B C D -中,A E D E ⊥,C D ⊥平面A D E ,A B ⊥平面A D E ,6C D D A ==,2A B =,3D E =.ABCDE(1)求证:平面A C E ⊥平面C D E ;(2)在线段D E 上是否存在一点F ,使A F ∥平面B C E ?若存在,求出E F E D的值;若不存在,说明理由.【答案】(1)见解析;(2)见解析.【解析】(1)证明:因为C D ⊥平面A D E ,A E ⊂平面A D E ,所以C D A E ⊥,·····2分又因为A E D E ⊥,C DD E D =,所以A E ⊥平面C D E ,···········4分又因为A E ⊂平面A C E ,所以平面A C E ⊥平面C D E .···········6分ABCDEMF(2)结论:在线段D E 上存在一点F ,且13E F E D=,使A F ∥平面B C E . (8)分解:设F 为线段D E 上一点,且13E F E D=,过点F 作F M C D ∥交C E 于M ,则13F MC D =.因为C D ⊥平面A D E ,A B ⊥平面A D E ,所以C D A B ∥.···········9分 又因为3C D A B =,所以M F A B =,F M A B ∥,···········10分 所以四边形A B M F 为平行四边形,则A F B M ∥.···········11分 又因为A F ⊄平面B C E ,B M ⊂平面B C E ,所以A F ∥平面B C E .·····12分 20.[2018·东北师大附中]已知椭圆2222:1(0)x y C a b ab+=>>的两个焦点与短轴的一个端点连线构成等边三角形,且椭圆C 的短轴长为 (1)求椭圆C 的标准方程;(2)是否存在过点()0,2P 的直线l 与椭圆C 相交于不同的两点M ,N ,且满足2O M O N ⋅=(O 为坐标原点)若存在,求出直线l 的方程;若不存在,请说明理由. 【答案】(1)22143xy+=;(2)答案见解析.【解析】(1分C 的标准方程是22143x y +=···········4分 (2)当直线l 的斜率不存在时,(0M ,(0,N3O M O N ⋅=-,不符合题意···········5分当直线l 的斜率存在时,设直线l 的方程为2y k x =+,()11,M x y ,()22,N x yy 整理得:()22341640k x kx +++=, ()()221616340k k∆=-+>,解得12k<-或12k >,···········6分1221634k x x k+=-+,122434x x k=+,···········7分∴1212O M O N x x y y ⋅=+=()()21212124k x x k x x ++++()222222413216124343434k kk kkk+-=-+=+++,···········9分∵2O M O N ⋅=,∴221612234k k-=+,···········10分解得2k =±,满足0∆>,···········11分分21.[2018·衡水金卷]已知函数()()21ln f x a x x =-+,a ∈R . (1)当2a =时,求函数()y f x =在点()()1,1P f 处的切线方程;(2)当1a =-时,令函数()()ln 21g x f x x x m =+-++,若函数()g x两个零点,求实数m 的取值范围.【答案】(1)切线方程为1y x =-;(2)实数m【解析】(1)当2a =时,()()221ln f x x x =-+224ln 2x x x =-++.当1x =时,()10f =,所以点()()1,1P f 为()1,0P ,···········1分,因此()11k f '==.···········2分因此所求切线方程为()0111y x y x -=⨯-⇒=-.···········4分 (2)当1a =-时,()22ln g x x x m =-+,分,所以当()0g x '=时,1x =,···········7分时,()0g x '>;当1e x <<时,()0g x '<;故()g x 在1x =处取得极大值也即最大值()11g m =-.···········8分,()2e 2e g m =+-,()g x 上的最小值为()e g ,······10分 故()g x所以实数m 分请考生在22、23题中任选一题作答,如果多做,则按所做的第一题计分。
