图像相似度计算方法
曲线相似度算法范文

曲线相似度算法范文曲线相似度算法是用于比较两条曲线之间的相似程度的算法。
在许多应用场景中,我们需要判断两条曲线是否相似,比如在数据挖掘中用于模式识别和分类,或者在图像处理中用于图像匹配和图像识别。
本文将介绍几种常见的曲线相似度算法。
1.欧几里德距离算法:欧几里德距离是最简单的一种相似度算法,它衡量的是两条曲线之间的几何距离。
通过计算两条曲线上对应点的坐标之差的平方和再开方,可以得到两条曲线之间的欧几里德距离。
欧几里德距离越小,则表示两条曲线越相似。
2.动态时间规整算法(DTW):DTW算法是一种基于时间序列相似度比较的算法,它可以衡量两条曲线之间在时间上的扭曲程度。
DTW算法首先将两条曲线上的所有点两两配对,然后计算每对点之间的距离。
通过动态规划的方法,可以找到一条最佳匹配路径,使得整条曲线之间的距离最小化。
DTW算法可以有效地处理两条曲线之间的时间偏移和长度不一致的情况。
3.弦图相似度算法:弦图相似度算法是一种基于形状特征的相似度算法,它主要用于比较两条曲线的形状相似程度。
弦图相似度算法首先将两条曲线上的点按照等分弦长的方式进行采样,然后计算每对采样点之间的距离。
通过计算两条曲线上所有点之间的距离,可以得到每条曲线的弦图。
最后,通过比较两个弦图的相似度指标,可以得到两条曲线的相似度。
4.小波变换相似度算法:小波变换相似度算法是一种基于频率特征的相似度算法,它主要用于比较两条曲线的频率分布情况。
小波变换相似度算法通过对两条曲线进行小波变换,得到每个频率段上的能量分布。
通过比较两个频率分布的相似度指标,可以得到两条曲线的相似度。
以上介绍的是常见的几种曲线相似度算法,不同的算法适用于不同的应用场景。
在实际应用中,我们可以根据具体需求选择合适的算法进行曲线相似度比较。
同时,也可以根据需要将多个算法进行组合,以得到更准确的相似度评估结果。
图像检索中类似度度量公式:各种距离(1)

图像检索中类似度度量公式:各种距离(1)基于内容的图像检索(Content-Based Image Retrieval)是指通过对图像视觉特征和上下⽂联系的分析,提取出图像的内容特征作为图像索引来得到所需的图像。
相似度度量⽅法在基于内容的图像检索中须要通过计算查询和候选图像之间在视觉特征上的相似度匹配。
因此须要定义⼀个合适的视觉特征相似度度量⽅法对图像检索的效果⽆疑是⼀个⾮常⼤的影响。
提取的视觉特征⼤都能够表⽰成向量的形式,其实,经常使⽤的相似度度量⽅法都是向量空间模型。
也就是把视觉特征看作是向量空间中的点,通过计算两个点之间的接近程度来衡量图像特征间的相似度。
经常使⽤的度量⽅法:街区距离、欧式距离、⽆穷范数、直⽅图相交、⼆次式距离、马⽒距离、EMD距离等等。
⾸先介绍下经常使⽤的距离:1. 欧⽒距离(EuclideanDistance)欧⽒距离是最易于理解的⼀种距离计算⽅法,源⾃欧⽒空间中两点间的距离公式。
(1)⼆维平⾯上两点a(x1,y1)与b(x2,y2)间的欧⽒距离:(2)三维空间两点a(x1,y1,z1)与b(x2,y2,z2)间的欧⽒距离:(3)两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的欧⽒距离: 也能够⽤表⽰成向量运算的形式:(4)Matlab计算欧⽒距离Matlab计算距离主要使⽤pdist函数。
若X是⼀个M×N的矩阵,则pdist(X)将X矩阵M⾏的每⼀⾏作为⼀个N维向量。
然后计算这M个向量两两间的距离。
样例:计算向量(0,0)、(1,0)、(0,2)两两间的欧式距离:<span style="font-size:18px;">X= [0 0 ; 1 0 ; 0 2]D= pdist(X,'euclidean')结果:D=1.00002.0000 2.2361</span><span style="font-size:18px; font-family: Arial; background-color: rgb(255, 255, 255);"> </span>2. 曼哈顿距离(ManhattanDistance)从名字就能够猜出这样的距离的计算⽅法了。
人脸识别算法 欧氏距离 余弦相似度

人脸识别算法欧氏距离余弦相似度一、人脸识别算法的基本原理人脸识别算法是一种利用人脸特征信息进行身份识别的技术。
它主要通过采集图像或视频中的人脸信息,然后提取特征并对比库中已存在的人脸信息,最终确定身份的一种技术手段。
在人脸识别算法中,欧氏距离和余弦相似度是两种常用的相似度计算方法。
在我们深入讨论这两种方法之前,我们需要先了解一下它们的基本原理。
欧氏距离是一种用于度量向量之间的距离的方法,其计算公式为:d(x, y) = √((x1 - y1)² + (x2 - y2)² + ... + (xn - yn)²) 。
在人脸识别算法中,常用欧氏距离来度量两张人脸图像之间的相似度,即通过比较特征向量之间的欧氏距离来识别身份。
与欧氏距离相似,余弦相似度也是一种用于度量向量之间的相似度的方法,其计算公式为:sim(x, y) = (x·y) / (‖x‖·‖y‖),其中x和y分别为两个向量。
在人脸识别算法中,余弦相似度常用于比较两个特征向量之间的夹角,来度量它们之间的相似度。
二、人脸识别算法中的欧氏距离应用在人脸识别算法中,欧氏距离常被用于度量两张人脸图像之间的相似度。
通过将人脸图像转化为特征向量,并使用欧氏距离来比较这些向量之间的距离,来确定是否为同一人。
举例来说,当系统需要识别一个人脸时,它首先会将该人脸图像提取特征并转化为特征向量,然后与存储在数据库中的特征向量进行比较。
通过计算欧氏距离,系统可以得出两个特征向量之间的距离,从而确定该人脸是否为已知身份。
三、人脸识别算法中的余弦相似度应用除了欧氏距离外,余弦相似度在人脸识别算法中也有着广泛的应用。
与欧氏距离不同,余弦相似度更侧重于计算两个向量之间的夹角,而非距离。
在人脸识别算法中,余弦相似度被用来比较两个特征向量之间的夹角,通过夹角的大小来确定它们之间的相似度。
这种方法能够更好地捕捉到特征向量之间的方向性信息,从而提高识别的准确性。
Opencvpython图像处理-图像相似度计算
Opencvpython图像处理-图像相似度计算⼀、相关概念1. ⼀般我们⼈区分谁是谁,给物品分类,都是通过各种特征去辨别的,⽐如⿊长直、⼤⽩腿、樱桃唇、⽠⼦脸。
王⿇⼦脸上有⿇⼦,隔壁⽼王和⼉⼦很像,但是⼉⼦下巴涨了⼀颗痣和他妈⼀模⼀样,让你确定这是你⼉⼦。
还有其他物品、什么桌⼦带腿、镜⼦反光能在⾥⾯倒影出东西,各种各样的特征,我们通过学习、归纳,⾃然⽽然能够很快识别分类出新物品。
⽽没有学习训练过的机器就没办法了。
2. 但是图像是⼀个个像素点组成的,我们就可以通过不同图像之间这些差异性就判断两个图的相似度了。
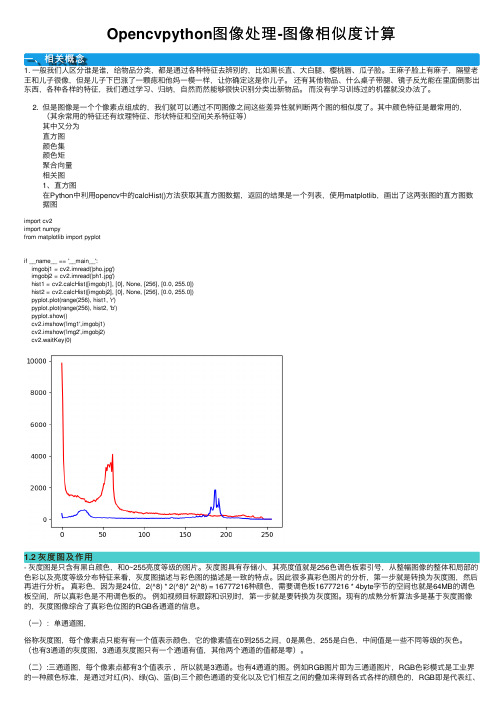
其中颜⾊特征是最常⽤的,(其余常⽤的特征还有纹理特征、形状特征和空间关系特征等)其中⼜分为直⽅图颜⾊集颜⾊矩聚合向量相关图1、直⽅图在Python中利⽤opencv中的calcHist()⽅法获取其直⽅图数据,返回的结果是⼀个列表,使⽤matplotlib,画出了这两张图的直⽅图数据图import cv2import numpyfrom matplotlib import pyplotif __name__ == '__main__':imgobj1 = cv2.imread('pho.jpg')imgobj2 = cv2.imread('ph1.jpg')hist1 = cv2.calcHist([imgobj1], [0], None, [256], [0.0, 255.0])hist2 = cv2.calcHist([imgobj2], [0], None, [256], [0.0, 255.0])pyplot.plot(range(256), hist1, 'r')pyplot.plot(range(256), hist2, 'b')pyplot.show()cv2.imshow('img1',imgobj1)cv2.imshow('img2',imgobj2)cv2.waitKey(0)1.2 灰度图及作⽤- 灰度图是只含有⿊⽩颜⾊,和0~255亮度等级的图⽚。
相似图片搜索原理

相似图片搜索原理
相似图片搜索是一种基于图像内容的检索技术,旨在根据输入的查询图像找到与其相似的其他图像。
其原理主要包括以下几个步骤:
1. 特征提取:通过计算图像的特征向量来描述其内容特征。
这些特征可以是局部的,如SIFT、SURF等,也可以是全局的,如颜色直方图、形状描述子等。
特征提取的目的是将图像从高维空间映射到低维向量空间,以便后续的相似度计算。
2. 相似度计算:通过比较查询图像的特征向量与数据库中其他图像的特征向量来计算它们之间的相似度。
常用的相似度度量方法包括欧氏距离、余弦相似度等。
相似度计算的目的是衡量两个图像之间在内容上的相似程度。
3. 数据库搜索:根据相似度计算的结果,将与查询图像最相似的图像从数据库中按照相似度排序进行检索。
对于大规模的数据库,可能会使用索引结构(如KD-Tree、局部敏感哈希等)
来加速搜索过程。
4. 结果展示:将检索得到的相似图像按照一定的规则展示给用户,通常会将这些图像以缩略图的形式呈现,并给出相似度的排名。
相似图片搜索的原理主要是通过提取图像的特征向量并比较相似度来实现的,并没有直接使用标题文字进行搜索。
相似图片
搜索可以在许多应用场景中发挥作用,如商品推荐、版权保护、图像鉴定等。
相似度量 方法 对比 总结 综述

相似度量方法对比总结综述相似度量是指用于衡量两个对象之间相似程度的方法。
在现实生活中,我们经常需要比较不同对象之间的相似性,比如文本相似度、图像相似度、音频相似度等。
相似度量方法可以帮助我们在各种领域进行对象之间的比较和匹配。
首先,让我们来看一些常用的相似度量方法。
在文本相似度方面,常用的方法包括余弦相似度、Jaccard相似度、编辑距离等。
余弦相似度通过计算两个向量之间的夹角来衡量它们的相似程度,而Jaccard相似度则通过计算两个集合的交集与并集的比值来衡量它们的相似程度。
在图像相似度方面,常用的方法包括结构相似性(SSIM)、均方误差(MSE)等。
这些方法都有各自的特点和适用范围,可以根据具体的应用场景选择合适的方法。
其次,让我们对这些相似度量方法进行对比。
不同的相似度量方法适用于不同的数据类型和应用场景。
比如,余弦相似度适用于文本数据的相似度比较,而SSIM适用于图像数据的相似度比较。
在选择相似度量方法时,需要考虑数据的特点、计算复杂度、准确性等因素。
有些方法可能在某些场景下表现更好,而在其他场景下表现较差。
因此,对不同方法进行对比可以帮助我们选择最合适的方法。
最后,综述一下相似度量方法的应用和发展趋势。
随着大数据和人工智能技术的发展,相似度量方法在各个领域都有着广泛的应用,比如推荐系统、信息检索、图像识别等。
未来,相似度量方法可能会更加注重多模态数据的相似度比较,比如文本和图像的跨模态相似度比较,以及结合深度学习等新技术进行相似度量的研究和应用。
总的来说,相似度量方法在数据分析和人工智能领域具有重要意义,不同的方法适用于不同的场景,通过对不同方法的对比和综述可以更好地理解和应用这些方法。
人脸相似度计算

人脸相似度计算人脸相似度计算是基于人脸识别技术的应用之一,通过比较不同人脸之间的相似程度,判断两个人脸是否属于同一人。
人脸相似度计算在人脸识别、人脸验证、人脸搜索等领域有着广泛的应用,如刷脸支付、人脸解锁等。
人脸相似度的计算过程包括人脸特征提取和相似度量化两个步骤。
首先,人脸相似度计算需要对人脸进行特征提取。
人脸特征提取是将人脸图像转换为一组具有代表性的数值特征的过程。
常见的人脸特征提取方法有主成分分析(PCA)、线性判别分析(LDA)、局部二值模式(LBP)等。
这些方法能够从图像中提取出人脸的特征信息,形成一组数值向量作为人脸的表示。
其次,计算相似度需要对提取出的人脸特征进行量化。
常见的人脸相似度量化方法包括欧式距离、余弦相似度、马氏距离等。
欧式距离是计算两个向量之间的直线距离,余弦相似度则是计算两个向量之间的夹角余弦值,而马氏距离则是考虑到数据的协方差矩阵,在欧式距离的基础上进行了修正。
这些方法能够衡量两个人脸特征之间的差异程度,从而反映出他们的相似度。
除了上述的基本方法,现在还有许多基于深度学习的人脸相似度计算方法。
例如,基于卷积神经网络(CNN)的人脸相似度计算模型能够通过端到端的学习,将人脸图像映射到特征空间,并计算相似度。
这些深度学习方法通常采用大规模的人脸数据集进行训练,能够获取更准确的人脸特征表示,从而提高相似度计算的准确性。
此外,在进行人脸相似度计算时,还需要注意一些问题。
例如,人脸图像的质量会影响相似度的准确性,因此在计算前需要对图像进行预处理,如人脸对齐、光照归一化等。
同时,人脸相似度计算还需要考虑到人脸图像的角度、表情、遮挡等因素对相似度的影响,这些因素可能导致相似度计算的误差。
总而言之,人脸相似度计算是一项重要的人脸识别技术,能够在刷脸支付、人脸解锁等场景中发挥重要作用。
通过人脸特征提取和相似度量化两个步骤,能够判断不同人脸之间的相似程度,从而实现人脸识别和验证。
随着深度学习技术的发展,人脸相似度计算的准确性将会进一步提高,为更多应用场景提供更精确的人脸识别解决方案。
OpenCV实战(1)——图像相似度算法(比对像素方差,感知哈希算法,模板匹配(OCR数字。。。

OpenCV实战(1)——图像相似度算法(⽐对像素⽅差,感知哈希算法,模板匹配(OCR数字。
如果需要处理的原图及代码,请移步⼩编的GitHub地址 传送门: 如果点击有误:https:///LeBron-Jian/ComputerVisionPractice 最近⼀段时间学习并做的都是对图像进⾏处理,其实⾃⼰也是新⼿,各种尝试,所以我这个门外汉想总结⼀下⾃⼰学习的东西,图像处理的流程。
但是动起笔来想总结,⼀下却不知道⾃⼰要写什么,那就把⾃⼰做过的相似图⽚搜索的流程整理⼀下,想到什么说什么吧。
⼀:图⽚相似度算法(对像素求⽅差并⽐对)的学习1.1 算法逻辑1.1.1 缩放图⽚ 将需要处理的图⽚所放到指定尺⼨,缩放后图⽚⼤⼩由图⽚的信息量和复杂度决定。
譬如,⼀些简单的图标之类图像包含的信息量少,复杂度低,可以缩放⼩⼀点。
风景等复杂场景信息量⼤,复杂度⾼就不能缩放太⼩,容易丢失重要信息。
根据⾃⼰需求,弹性的缩放。
在效率和准确度之间维持平衡。
1.1.2 灰度处理 通常对⽐图像相似度和颜⾊关系不是很⼤,所以处理为灰度图,减少后期计算的复杂度。
如果有特殊需求则保留图像⾊彩。
1.1.3 计算平均值 此处开始,与传统的哈希算法不同:分别依次计算图像每⾏像素点的平均值,记录每⾏像素点的平均值。
每⼀个平均值对应着⼀⾏的特征。
1.1.4 计算⽅差 对得到的所有平均值进⾏计算⽅差,得到的⽅差就是图像的特征值。
⽅差可以很好的反应每⾏像素特征的波动,既记录了图⽚的主要信息。
1.1.5 ⽐较⽅差 经过上⾯的计算之后,每张图都会⽣成⼀个特征值(⽅差)。
到此,⽐较图像相似度就是⽐较图像⽣成⽅差的接近成程度。
⼀组数据⽅差的⼤⼩可以判断稳定性,多组数据⽅差的接近程度可以反应数据波动的接近程度。
我们不关注⽅差的⼤⼩,只关注两个⽅差的差值的⼤⼩。
⽅差差值越⼩图像越相似!1.2 代码:import cv2import matplotlib.pyplot as plt#计算⽅差def getss(list):#计算平均值avg=sum(list)/len(list)#定义⽅差变量ss,初值为0ss=0#计算⽅差for l in list:ss+=(l-avg)*(l-avg)/len(list)#返回⽅差return ss#获取每⾏像素平均值def getdiff(img):#定义边长Sidelength=30#缩放图像img=cv2.resize(img,(Sidelength,Sidelength),interpolation=cv2.INTER_CUBIC)#灰度处理gray=cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)#avglist列表保存每⾏像素平均值avglist=[]#计算每⾏均值,保存到avglist列表for i in range(Sidelength):avg=sum(gray[i])/len(gray[i])avglist.append(avg)#返回avglist平均值return avglist#读取测试图⽚img1=cv2.imread("james.jpg")diff1=getdiff(img1)print('img1:',getss(diff1))#读取测试图⽚img11=cv2.imread("durant.jpg")diff11=getdiff(img11)print('img11:',getss(diff11))ss1=getss(diff1)ss2=getss(diff11)print("两张照⽚的⽅差为:%s"%(abs(ss1-ss2))) x=range(30)plt.figure("avg")plt.plot(x,diff1,marker="*",label="$jiames$") plt.plot(x,diff11,marker="*",label="$durant$") plt.title("avg")plt.legend()plt.show()cv2.waitKey(0)cv2.destroyAllWindows() 两张原图: 图像结果如下:img1: 357.03162469135805img11: 202.56193703703704两张照⽚的⽅差为:154.469687654321 实验环境开始设置了图⽚像素值,⽽且进⾏灰度化处理,此⽅法⽐对图像相似对不同的图⽚⽅差很⼤,结果很明显,但是对⽐⽐较相似,特别相似的图⽚不适应。
