初二专题训练17
八年级物理上学期选择题专题训练(可编辑修改word版)

八年级物理上学期选择题专题训练一.单选题(本题包括 100 小题,共 300 分。
)1、某物体在前一半路程中的速度是20米/秒,后一半路程中的速度是30米/秒,则该物体在全路程中的平均速度是:[ ]A.10米/秒B.25米/秒C.24米/秒D.30米/秒2.在暗室里有一束白光,透过红玻璃照在绿布上,绿布呈:[]A.白色B.红色C.绿色D.黑色3.阳光下的树林中,地面上有许多圆形的光斑,这是[ ]A.太阳的像B.树叶的像C.树叶的缝隙D.树叶的影子4.光线从水中斜射入空气中时, 折射角入射角. [ ]A.小于B.等于C.大于D.无法确定5.“漓ft在水中的倒影”这句话中的“影”实际上是[ ]A.ft的影子B.ft的实像C.ft的虚像D.以上说法都不对6.弹簧秤的刻度是均匀的, 是因为在测量范围内: []A.弹簧的长度跟它受到的拉力成正比B.弹簧受到的拉力跟它的伸长成正比C.弹簧的伸长跟它受到的拉力成正比D.弹簧受到的拉力跟它的长度成正比7.甲、乙两物体都做匀速直线运动. 已知甲、乙物体的速度之比为4∶5, 所用时间之比为3∶2, 则甲、乙两物体通过的路程之比为[]A.4∶3B.5∶2C.6∶5D.2∶58.使用最小刻度是毫米的刻度尺,测得下列数据,正确的记录结果为[]A.0.184 米B.1.848 分米C.18.4 厘米D.184.82 毫米9.用拉伸了的塑料卷尺测量某物体的长度, 测量的结果将: []A.比真实值偏大B.比真实值偏小C.和真实值一样D.无法判定10.如图,检查视力时,要求眼睛与视力表间距离为5米,现在视力表AB对面3米处竖有一面镜子MN,那么检查视力时[ ]A.人应面对镜子而坐,且人与镜面之间距离为2.5米B.人应面对镜子而坐,且人与镜面之间距离为2米C.人应面对视力表而坐,且人与视力表间距为3米D.人应面对视力表而坐,且人与视力表间距为2.5米11.下面的物体中,长度接近4厘米的是[ ]A.物理课本的长度B.墨水瓶高度C.钢笔长度D.乒乓球直径12.人从远处走近一直立的穿衣镜的过程中,他在镜中的像大小将[ ]A.逐渐变大B.逐渐变小C.不变D.无法确定13.一个人站在木排上漂流而下,河岸上有树,下列说法正确的是[ ]A.人相对于木排是静止的,相对于水是运动的B.人相对于水是静止的,相对于河岸是运动的C.木排相对于水是运动的,相对于河岸也是运动的D.水相对于人和河岸都是运动的14.下图是光线通过厚玻璃板的折射光路示意图,其中正确的是:[ ]15.甲、乙两个人分别坐在并列的两台升降机上,甲看见楼房的窗户(相对自己)正在匀速上升,乙看见甲正在匀速上升,若以地面为参照物,则[ ]A.甲在匀速上升,乙在下降B.甲在匀速下降,乙在匀速上升C.甲、乙都匀速下降,但乙的速度比甲的速度大D.甲、乙都匀速下降,但甲下降速度比乙大16.甲、乙两个物体在一条直线上运动. 它们在一个小时内所经过的路程相同, 如果甲做匀速直线运动, 则乙做匀速直线运动. [ ]A.一定B.不一定C.肯定不D.无法确定17.关于g=9.8牛顿/千克的物理意义, 下列说法中正确的是: []A.1千克等于9.8牛顿B.1牛顿等于9.8千克C.质量为1千克的物体所受的重力是9.8牛D.当物体所受的重力为9.8牛顿时, 它的质量一定是1千克18.关于速度,下列说法中不正确的是[ ]A.物体通过的路程越长,它的速度越大B.速度越大的物体运动得越快C.路程相同时,速度越大运动时间越短D.平均速度是粗略描述变速运动快慢的19.用同一把尺子先后四次测量一物体的长度,得到以下数据:2.43厘米,2.45厘米,2.47厘米,2.48厘米,则这个物体的平均长度是:[ ]A.2.45厘米B.2.46厘米C.2.458厘米D.2.457厘米20.下列关于声现象的说法中,正确的是[ ]A.悦耳动听的歌声是由歌唱家的声带振动发生的B.声音传播不需要介质,真空也能传声C.声音在钢铁中的传播速度小于在水中的传播速度D.声音在水中的传播速度小于在空气中的传播速度21.如果回声到达人耳比原声晚秒以上,人耳才能把回声跟原声区分开.[ ]A.1秒B.0.1秒C.0.01秒D.0.001秒22.某人在平面镜前3米,若人向平面镜靠近1米,则他与镜中像的距离为[ ]A.1米B.2 米C.3 米D.4 米23.已知某物体的质量是2千克, 计算它受到的重力, 下列各式中正确的是:A.2千克=19.6牛顿B.2千克=2千克×9.8牛顿/千克=19.6牛顿C.G=mg=2×9.8=19.6牛顿D.G=mg=2千克×9.8牛顿/千克=19.6牛顿24.吊车吊着货物匀速上升,则[ ]A.货物受到的重力等于绳子对它的拉力B.货物受到的重力小于绳子对它的拉力C.货物受到的重力大于绳子的对它的拉力D.以上说法都不对25.身高1.8米的人站在水深1米的清水池岸上,那么,此人在水中“倒影”的高度是[ ]A.2.8 米B.1.8 米C.1 米D.0.8 米26.某人站在河边看到水中的鱼和云,他所看到的[ ]A.云是光的反射所形成的虚像B.云是光的折射所形成的虚像C.鱼是光的反射所形成的实像D.鱼是光的折射所形成的实像27.有关弹簧秤,下列说法中正确的是[ ]A.弹簧越大,所受拉力一定越大B.弹簧的长度与所受的拉力成正比C.只要弹簧不断,弹簧的伸长与所受拉力成正比D.在一定范围内,弹簧的伸长与所受拉力成正比28.某物体重1牛顿,这个物体可能是[ ]A.一张稿纸B.一块橡皮C.一支钢笔D.一本初二年级物理书29.甲、乙两辆汽车,以甲车为参照物,乙车向东运动,若以大地为参照物,则乙[ ]A.向东运动B.向西运动C.静止D.无法确定30.下列不是由于光的反射形成的是[ ]A.镜中花B.水中月亮C.桥在水中倒影D.月食的形成31.放大镜是根据的现象制成的. [ ]A.凸透镜成倒立缩小的实像B.凸透镜成倒立放大的实像C.凸透镜成正立放大的虚像D.凹透镜成正立放大的虚像32.一个物体在光滑的斜面上向下滑的过程中,受到的力有[ ]A.重力B.重力、下滑力C.重力、支持力D.重力、摩擦力、支持力33.如图所示,一束光线射向O处的光学元件后会聚于主光轴上的S点,取掉光学元件后,光线会聚于S'点,则该镜一定是[ ]A.凸镜B.凹镜C.凸透镜D.凹透镜34.下面哪一个是实像[]A.通过汽车上的观后镜看到的像B.放映电影时银幕上的像C.平静的水面所映出的明月的像D.照镜子看到的像35.如图所示,木块的长度是: []A.4.8米B.1.8厘米C.1.85厘米D.4.85厘米36.力是物体与物体的相互作用,对于磁铁与附近的铁钉,下列说法中正确的是:[ ]A.施力物体只是磁铁, 受力物体只是铁钉B.只有当磁铁与铁钉接触时, 才会产生力的作用C.磁铁和铁钉虽然没接触, 但也会产生力的作用D.磁铁对铁钉有吸引作用, 而铁钉不会吸引磁铁37.照相机应用了凸透镜哪种成像规律: []A.u>2f, 凸透镜能成缩小实像B.u>f, 凸透镜能成放大虚像C.2f>u>f, 凸透镜能成放大虚像D.u<2f, 凸透镜能成缩小实像38.人站在水平地板上,而人在平面镜中的像和人垂直,则平面镜和水平面的夹角是]A.90°B.65°C.45°D.30°39.下列关于实像与虚像的说法正确的是:[ ]A.光线经折射所成的像是实像,经反射所成的像是虚像B.实像可以成像在光屏上,虚像则不能C.虚像就是影子,实像就是实际光线所成的亮斑D.凸透镜所成像是实像,平面镜所成的像是虚像40.小球沿斜面滚下, 它受到的重力的方向是: []A.沿斜面方向向下B.垂直于斜面向下C.竖直向下D.上述方向都有可能41.物体在凸透镜前20厘米处, 得到倒立, 放大的实像, 现将物体向透镜移近10厘米, 得到的是:[]A.倒立放大的虚像B.正立放大的虚像C.倒立缩小的实像D.倒立等大的实像42.关于物体受到的重力, 下列叙述中正确的是: []A.物体的重力是由物体对支持物的压力或者对悬线拉力而产生的.B.物体所受的重力只有大小, 而无方向.C.质量是1千克的物体, 其重力一定是1千牛顿.D.物体重力大小随它在地球上不同地理位置而不同.43.凸透镜的焦距为f,将一个物体从距透镜5f处逐渐移动到离透镜1.5f处,在这一过程中物体和它像的距离[ ] A. 逐渐减小 B. 逐渐增大 C. 先逐渐减小,后又逐渐增大 D. 先逐渐增大,后又逐渐减少44.下图,是物体在平面镜中的像,其中正确的是[ ]45.用绳子系住水桶,手握绳子从井中提水,手受到竖直向下拉力,此拉力的施力物体是∶[ ]A.地球B.水桶C.绳子D.手46.某同学在“研究凸透镜成像”的实验中,光屏移动到离凸透镜16厘米处,得到烛焰的倒立、放大的像.下列的四块透镜,他使用的是[ ]A.焦距是4厘米的凸透镜B.焦距是8厘米的凸透镜C.焦距是12厘米的凸透镜D.焦距是18厘米的凸透镜47.坐在直升飞机上的人,看到ft和树木在往上运动,若以地面为参照物,则A.直升飞机在向下运动B.直升飞机在向下运动C.直升飞机在空中静止D.无法判断48.光从水中斜射入空气里时,其折射光线应是哪一条?A.oa B.ob C.oc D.od49.一束光线与界面成30°角射到界面上时,发生了反射和折射,已知反射光线与折射光线的夹角是85°折射角是:[ ] A.15° B.35°C.45° D.20°50.下列现象中属于光的折射的是:[ ]A.通过潜望镜观察海面上的船只B.用汽车观后镜观看车后的景物C.看水中物体比它的实际位置浅D.在路灯下出现了人的影子51.下列说法正确的是: [ ]A.平面镜成等大、正立的实像B.幻灯机成放大、正立的虚像C.照相机成倒立、缩小的实像D.放大镜成正立、放大的实像52.采用密绕法测铜丝的直径时,把铜丝在木棍上绕50匝,然后用毫米刻度尺量出50匝铜丝的总宽度L,则可的出一根铜丝的直径d=L/50,用此法先后测量三次,每次都将铜丝重新绕过, 并放刻度尺上不同位置, 结果三次测得的铜丝直径不同, 则误差产生的原因是: []A.只是由于铜丝间绕得紧密程度不同B.只是由于铜丝的粗细不均匀C.只是由于刻度尺的刻度不均匀D.以上三种因素都有可能53.用照相机拍照时,所得到的人和景物的像是[ ]A.缩小倒立的实像B.缩小倒立的虚像C.放大正立的实像D.放大正立的虚像54.在下列各种光学现象中,属于光的折射的是 [ ]A.平静的水面上清楚地映出岸边景物的“倒影”B.在岸边看到池水的深度比实际的深度要浅C.小孔成像D.在汽车观后镜中能看到路旁的景观55 人在河边看到水中的鱼,其位置比鱼的实际深度[ ]A.偏深B.偏浅C.深浅一样D.无法判断56.关于力作用在物体上产生的效果,下列说法中不正确的是[ ]A.改变物体形状B.使物体运动状态发生变化C.改变物体质量D.使物体形状和运动状态同时改变57.人站在竖直放置的平面镜前,距镜3米,则[ ]A.人以1米/秒的速度走向平面镜,像以2米/秒的速度走近平面镜B.人以1米/秒的速度走近平面镜,像以2米/秒的速度靠近人C.人离平面镜越近,人的像就越大D.人离平面镜越远,人的像就越小58.关于小孔成像,下面说法中正确的是:[]A.小孔所成的像一定比物体小B.小孔所成的像一定是虚像C.小孔所成的像是倒立的实像 D.小孔所成的像是正立的实像59.相对于地面来说, 下面的哪个物体, 它的运动状态没有发生变化? [ ]A.在水平面上做匀速圆周运动的小球B.紧急刹车后继续向前滑行的汽车C.点火时,被发射升空的火箭D.匀速上升的电梯60.一个焦距为10厘米的凸透镜, 在物体由离透镜30厘米处移向15厘米的过程中[ ]A.先成放大实像, 后成放大虚像B.始终成虚像C.始终成实像, 且像逐渐变大D.始终成实像, 且像逐渐变小。
2022至2023年年初二后半期期末地理专题训练(河南省新乡市长垣县)

选择题下列条件不属于划分我国四大地理区域依据的是A. 民族分布B. 自然环境C. 人文特点D. 地理位置【答案】A【解析】我国地域辽阔,各地区之间自然环境和社会经济差异很大,根据自然环境条件、农业生产和居民生活、地理位置等特征的差异,将我国划分为四大地理区域,与民族分布无关,故选A。
选择题关于北方地区和南方地区的说法,不正确的是:()A.南方地区的植被以常绿阔叶林为主B.北方地区农田多为旱田C.南方地区1月的平均气温一般高于0℃D.北方民居比南方民居的屋顶坡度大【答案】D【解析】秦岭-淮河一线主要是我国四大区域中,南方地区与北方地区的分界线;一月份0℃等温线通过的地方;800mm等降水线通过的地方;温度带中,暖温带与亚热带分界线;干湿地区中,湿润区与半湿润区分界线;温带季风气候与亚热带季风气候分界线;水稻、小麦的分界线;亚热带常绿阔叶林与温带落叶阔叶林的分界线等。
南方地区的植被以常绿阔叶林为主;北方地区农田多为旱田;南方地区1月的平均气温一般高于0℃。
南方地区雨水多,所以房屋的坡度比北方地区大。
所以本题选择D选项。
选择题坎儿井的水源主要来自()A. 河流水B. 海洋水C. 冰雪融水D. 大气降水【答案】C【解析】坎儿井是新疆古老的引水灌溉工程,规模宏大,被称为“地下长城”,该工程是利用高山冰雪融水,通过暗渠输水到农田,这样可以减少水分的蒸发,可以节约水资源,故选C。
选择题青藏地区的自然特征是()A. 高寒B. 干旱C. 水土流失D. 荒漠化【答案】A【解析】青藏地区是我国四大区域中海拔最高的地区,平均海拔在4000米以上,因海拔高、气温低,突出的自然特征是高寒,气候恶劣,不适合人类居住,农业生产形式是畜牧业,种植业主要分布在河谷地带,故选A。
选择题读“我国局部地区图”,回答下面小题:【1】下列有关图示区域自然资源的叙述,正确的是()①煤炭资源特别丰富②森林资源特别丰富③甘肃、宁夏水能资源丰富④是我国太阳能最丰富的地区A. ①②B. ②③C. ③④D. ①③【2】图中表示太行山和秦岭的字母分别是()A. a、bB. b、cC. c、dD. a、d【答案】【1】D【2】A【解析】试题【1】从图上看,图中所示区域是北方地区,北方地区山西、河北等省煤炭资源特别丰富,①对;图中所示区域几省没有森林资源分布不是很多,②错;从青藏高原到黄土高原再到河套平原是有海拔落差的,水流速度应该说是比较快的,使得甘肃、宁夏水能资源丰富,③对;故选D。
中考数学八年级专题训练50题含答案

中考数学八年级专题训练50题含答案一、单选题1.不等式23x -<的解集是( )A .23x <-B .23x >-C .32x <-D .32x >- 2.下列各式中,一定是二次根式的是()A .BCD 3.下列各组数中,能组成勾股数的是( )A .0.2,0.3,0.4B .1,4,9C .5,12,13D .5,11,124.设a =a 在两个相邻整数之间,则这两个整数是( )A .-1和-2B .-2和-3C .-3和-4D .-4和-5 5.从下列不等式中选择一个与x +1≥2组成不等式组,如果要使该不等式组的解集为x ≥1,那么可以选择的不等式是( )A .x >-1B .x >2C .x <-1D .x <26.如图,将△ABC 绕点B 顺时针旋转50°得△DBE ,点C 的对应点恰好落在AB 的延长线上,连接AD ,下列结论不一定成立的是( )A .AB =DB B .△CBD =80°C .△ABD =△E D .△ABC △△DBE 7.规定一种新的运算“JQx →+∞A B ”,其中A 和B 是关于x 的多项式.当A 的次数小于B 的次数时,JQx →+∞0A B =;当A 的次数等于B 的次数时,JQx →+∞A B的值为A 和B 的最高次项的系数的商;当A 的次数大于B 的次数时,JQx →+∞A B 不存在.例:JQx →+∞21x -=0,JQx →+∞22212312x x x +=+-.若223615(2)11A x xB x x -=-÷--,则JQx →+∞A B的值为( )A .0B .12C .13D .不存在8.在227,π-,0,3.14,,0.333,0.1010010001⋯(两个“1”之间依次多一个“0”)中,无理数的个数是( )A .1B .2C .3D .49.实数a ,b 在数轴上对应点的位置如图所示,则下列结论正确的是( )A .a <﹣bB .|a|>|b|C .|a|<|b|D .﹣a >b 10.下列说法中正确的是( )A .若||a b >,则22a b >B .若a >b ,则11a b <C .若a b >,则22ac bc >D .若,a b c d >>,则a c b d ->- 11.实数a ,b 在数轴上的对应点的位置如图所示,则下列结论中,正确的是( )A .a b >B .a b =C .a b <D .a b =- 12.如图,E ,F 分别是 □ABCD 的边AB ,CD 的中点,则图中平行四边形的个数共有( ).A .2个B .3个C .4个D .5个13.如图,在ABC ∆中,AB 的垂直平分线交AB 于点D ,交BC 于点E .ABC ∆的周长为19,ACE ∆的周长为13,则AB 的长为( )A .3B .6C .12D .1614.下列说法: △已知△ABC 中,AB =6,AC =8,则中线AD 的取值范围是1≤AD≤7;△两边和一角对应相等的两个三角形全等;△如果两个三角形关于某直线成轴对称,那么它们是全等三角形;△一腰上的中线也是这条腰上的高的等腰三角形是等边三角形.其中正确的有( )A .1个B .2个C .3D .4个15.如图,在矩形ABCD 中,AE 平分BAD ∠交BC 于点E ,5,3ED EC ==,则矩形的周长为( )A .18B .20C .21D .22 16.关于x 的方程32211x m x x --=++有增根,则m 的值为( ) A .2 B .7- C .5 D .5-17.两人在直线跑道上同起点、同终点、同方向匀速跑步400米,先到终点的人原地休息.已知甲先出发2秒,在跑步过程中,甲、乙两人之间的距离y (米)与乙出发的时间t (秒)之间的关系如图所示给出以下结论:△8a =;△72b =;△98c =.其中正确的是( )A .△△B .△△△C .△△D .△△18.如图,ABC 是等边三角形,ABD △是等腰直角三角形,90BAD ∠=︒,AE BD ⊥于点E ,连接CD ,分别交、AE AB 于点F 、G ,过点A 作AH CD ⊥交BD 于点H ,1EH =,则下列结论:△15ACD =︒∠;△AFG 是等腰三角形;△ADF BAH △△≌;△2DF =.其中正确的有( )A .△△△B .△△△C .△△△D .△△△19.正方形111A B C O 、2221A B C C 、3332A B C C …按如图所示的方式放置.点1A 、2A 、3A …和点1C 、2C 、3C …别在直线1y x =+和x 轴上,则点2019A 的坐标是( )A .()201820192,2B .()2018201821,2-C .()201920182,2D .()2018201921,2-二、填空题20.如果等腰三角形腰上的高是腰长的一半,那么它顶角的度数是_____.21.“迎面穿梭接力”是北关中学历届校运动会最具吸引力的集体项目之一,单程100米,该比赛项目要求班级超过半数的学生参加,是衡量一个班级整体田径实力的重要项目,取胜的一个至关重要的因素是接力棒交接时不掉棒.今年运动会上,初二21班和初二22班两个班级在比赛中出现了惊心动魄的一幕,21班最后一个参赛同学甲在接棒时掉棒,掉棒的同时22班倒数第二位参赛同学乙距离下一个接棒同学丙还有一段距离,并随后顺利与丙交接棒(交接棒时间忽略不计),最后冲刺中丙反超甲赢得了比赛,在比赛过程中,甲乙丙均匀速前进,两个班跑步中的队员之间的距离y(米)与甲成功接棒后出发的时间x(分钟)之间的关系如图所示,则丙到达终点时,甲距终点的距离是______米.22.如图,平行四边形ABCD中,AC、BD相交于点O,若AD=6,AC+BD=18,则△BOC的周长为_____.23a,小数部分为b,则2a b+_________.24.已知正方形的对角线长为______.1),则点25.如图,在平面直角坐标系中,四边形ABCO是正方形,已知点CA的坐标是______________.26.如图,将5个边长为1cm的正方形按如图所示摆放,点A1,A2,……,An分别是正方形的中心,则5个正方形重叠形成的重叠部分的面积和为______.27.如图,△COD 是△AOB 绕点O 顺时针方向旋转30°后所得的图形,点C 恰好在AB 上,则△A 的度数为______.28.将矩形添加一个适当的条件:_____,能使其成为正方形.29.已知钝角三角形的三边分别为2,3,4,则该三角形的面积为__________. 30.如图,将ABC ∆沿BC 所在的直线平移得到DEF ∆.如果2GC =, 4.5DF =, 那么AG =____.31.一等腰三角形的一条边长为6,一个外角为120° , 则这个三角形的周长为_____. 32.已知直线y =kx ﹣3与y =(3k ﹣1)x +2互相平行,则直线y =kx ﹣3不经过第_____象限.33.菱形的周长是24,两邻角比为1﹕2,较短的对角线长为_________34.已知在△ABC 和△A 1B 1C 1中,AB =A 1B 1,△A =△A 1,要使△ABC △△A 1B 1C 1,还需添加一个条件,这个条件可以是____________________.35.如图,直线4y x =+与y 轴交于1A ,按如图方式作正方形11122213332A B C O A B C C A B C C ⋯,,,,点123A A A ⋯,,在直线4y x =+上,点123C C C ⋯,,,在x 轴上,图中阴影部分三角形的面积从左到右依次记为123n S S S S ⋯,,,,则1S =_________,n S = __(用含n 的代数式表示,n 为正整数).36.已知关于x 的一元一次不等式组21x m n x m-≥⎧⎨-≤⎩的解集为35x ≤≤,则n m 的值是_____.37.若关于x 的方程3101ax x +-=-无解,则a 的值为__________. 38.如图,在平行四边形ABCD 中,对角线AC 、BD 交于点O ,点E 、F 在BD 上,请你添加一个条件_____使四边形AECF 是平行四边形(填加一个即可).39.如图,在正方形ABCD 中,AD =5,点E 、F 是正方形ABCD 外的两点,且AE =FC =3, BE =DF =4,则EF 的长为_______.三、解答题40.已知2a ﹣1的平方为9,b ﹣1的算术平方根是2,c a ﹣b +c 的值.41.已知:如图,△ABC 是等边三角形,点D 、E 分别在边AB 、BC 的延长线上,且AD =BE ,联结DC 、AE .(1)试说明△BCD △△ACE 的理由;(2)如果BE =2AB ,求△BAE 的度数.42小数部分我们不可能全部写出来,而12<<1分.请解答下列问题:(1__________,小数部分是__________;(2a b ,求a b +43.两张矩形纸片ABCD 和CEFG 完全相同,且AB=CE ,AD >AB .操作发现:(1)如图1,点D 在GC 上,连接AC 、CF 、CG 、AG ,则AC 和CF 有何数量关系和位置关系?并说明理由.实践探究:(2)如图2,将图1中的纸片CEFG 以点C 为旋转中心逆时针旋转,当点D 落在GE 上时停止旋转,则AG 和GF 在同一条直线上吗?请判断,并说明理由.44.先阅读短文,然后回答短文后面所给出的问题:对于三个数a 、b 、c 的平均数,最小的数都可以给出符号来表示,我们规定M {a ,b ,c }表示a ,b ,c 这三个数的平均数,m i n {a ,b ,c }表示a ,b ,c 这三个数中最小的数,max {a ,b ,c }表示a ,b ,c 这三个数中最大的数.例如:M {﹣1,2,3}=123433-++=,m i n {﹣1,2,3}=﹣1,max {﹣1,2,3}=3;M {﹣1,2,a }=12133a a -+++=,m i n {﹣1,2,a }=()()111a a a ⎧≤-⎪⎨->-⎪⎩.(1)请填空:max{c﹣1,c,c+1}=;若m<0,n>0,m i n{3m,(n+3)m,﹣mn}=;(2)若m i n{2,2x+2,4﹣2x}=2,求x的取值范围;(3)若M{2,x+1,2x}=m i n{2,x+1,2x},求x的值.45.计算:(1(2)+46.如图,BAD是由BEC在平面内绕点B逆时针旋转60︒而得,且⊥=,,连接DE.求证:BDE≌BCE.AB BC BE CE47.(1)解方程(1)(x+5)=16 (2x-1)=64(2)解下列不等式,并将它解集在数轴上表示出来:48.如图,中,,是上一点,是延长线上一点,且,若与相交于,求证:.答案第1页,共26页 参考答案:1.D【分析】不等式的两边都除以2-,即可得到答案.【详解】解:23x -<,两边都除以2-得:32x >-,故D 正确. 故选:D .【点睛】本题考查的是一元一次不等式的解法,掌握“利用不等式的基本性质解一元一次不等式”是解本题的关键.2.D0a ≥,的式子称为二次根式,利用定义解题即可.【详解】解:A 中根号里面为负数,不是二次根式;B 中是三次根,不是二次根式;C 中未说明1a ≥,可能不是二次根式;D 中210a +>,故一定是二次根式.故选D .【点睛】本题主要考查二次根式的定义,注意0a ≥的条件是否满足.3.C【分析】根据勾股数的定义进行分析,从而得到答案.【详解】A 、不是,因为它们不是正整数;B 、不是,12+42≠92 ;C 、是,满足勾股数的定义;D 、不是,因为52+112≠122;故选:C .【点睛】此题考查了勾股数,解答此题要用到勾股定理的逆定理和勾股数的定义,已知三角形ABC 的三边满足a 2+b 2=c 2,则三角形ABC 是直角三角形.4.D【分析】先确定19的大小,再根据算术平方根的定义、不等式的性质即可得到答案.【详解】△16<19<25,△45<,△54-<-,故选:D.【点睛】此题考查算术平方根的定义、不等式的性质、实数的大小比较.5.A【详解】试题分析:x+1≥2,解得:x≥1,根据大大取大可得另一个不等式的解集一定是x不大于1.故选A.考点:不等式的解集.6.C【分析】利用旋转的性质得△ABC△△DBE,BA=BD,BC=BE,△ABD=△CBE=50°,△C=△E,再由A、B、E三点共线,由平角定义求出△CBD=80°,由三角形外角性质判断出△ABD>△E.【详解】解:△△ABC绕点B顺时针旋转50°得△DBE,△AB=DB,BC=BE,△ABD=△CBE=50°,△ABC△△DBE,故选项A、D一定成立;△点C的对应点E恰好落在AB的延长线上,△△ABD+△CBE+△CBD =180°,.△△CBD=180°-50°-50°=80°,故选项B一定成立;又△ △ABD=△E+△BDE,△△ABD>△E,故选项C错误,故选C.【点睛】本题主要考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.7.C【分析】先对223615211A x xB x x-⎛⎫=-÷⎪--⎝⎭进行计算,然后再根据规定的新运算,解答即可.【详解】解:223615211A x xB x x-⎛⎫=-÷⎪--⎝⎭=()()()325 25111x xxx x x--÷-+-=()()()11251325x x x x x x +--⨯-- =13x x+, △A 的次数等于B 的次数,△JQx →+∞A B =13, 故选:C .【点睛】本题考查了新定义,以及分式的混合运算,理解已知规定的新运算是解题的关键.8.C【分析】无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.【详解】解:在227,π-,0,3.14,,0.333,0.1010010001⋯(两个“1”之间依次多一个“0”)中,227,0,3.14,0.32-,33是有理数, π-, ,0.1010010001⋯(两个“1”之间依次多一个“0”)是无理数,共3个, 故选:C .【点睛】本题考查了有理数、无理数的概念,求一个数的立方根.以下几类无理数应知道:π或含有π的式子;开不尽方的数以及它们与有理数的和、差、积、商也都是无理数;还有如0.070070007⋯(每两个7之间依次多一个0)这样的数也是无理数. 9.C【分析】根据绝对值的定义可求解.【详解】由图可得:﹣1<a <0,1<b <2△|a|<|b|故选:C .【点睛】本题考查了实数与数轴,解决本题的关键是熟练掌握绝对值的定义.10.A【分析】利用两个非负数的平方性质可判断A ,利用不等式性质可判断B ,C ,利用举反例可判断D .【详解】解:A . 若||a b >,则22a b >,故选项A 正确;B . 若a >b >0,则11a b <;若0>a >b ,则11a b <;若a >0>b ,则11a b>,故选项B 不正确;C . 若a b >,c≠0,则22ac bc >;若a b >,c=0则22=ac bc ,故选项C 不正确;D . 若,a b c d >>,例如0>-2,-3>-7,则0-(-3)<-2-(-7),则a c b d ->-不一定成立,故选项D 不正确.故选择A .【点睛】本题考查不等式的性质,掌握不等式的性质以及举反例方法是解题关键. 11.C【分析】根据数轴上点的特点,进行判断即可.【详解】ABC.根据数轴上点a 、b 的位置可知,0a <,0b >,△a b <,故AB 错误,C 正确;根据数轴上点a 、b 的位置可知,a b -<,故D 错误.故选:C .【点睛】本题主要考查了数轴上点的特点,熟练掌握数轴上点表示的数,越向右越大,是解题的关键.12.C【分析】首先根据四边形ABCD 是平行四边形,可得DC△AB ,DC=AB ,再根据E 、F 分别是边AB 、CD 的中点,可得DF=FC=12DC ,AE=EB=12AB ,进而可根据一组对边平行且相等的四边形是平行四边形证明四边形DFBE 和CFAE 都是平行四边形,再根据平行四边形的性质可得DE△FB ,AF△CE ,进而可证出四边形FHEG 是平行四边形.【详解】解:△四边形ABCD 是平行四边形, △DC△AB ,DC=AB ,△E 、F 分别是边AB 、CD 的中点,△DF=FC=DC,AE=EB=AB,△DC=AB,△DF=FC=AE=EB,△四边形DFBE和CFAE都是平行四边形,△DE△FB,AF△CE,△四边形FHEG是平行四边形,故选C.【点睛】此题主要考查了平行四边形的判定和性质,关键是掌握平行四边形的性质定理和判定定理.13.B【分析】根据线段垂直平分线的性质和等腰三角形的性质即可得到结论.【详解】△AB的垂直平分线交AB于点D,△AE=BE,△△ACE的周长=AC+AE+CE=AC+BC=13,△ABC的周长=AC+BC+AB=19,△AB=△ABC的周长-△ACE的周长=19-13=6,故答案为:B.【点睛】本题考查了线段垂直平分线的性质:垂直平分线垂直且平分其所在线段;垂直平分线上任意一点,到线段两端点的距离相等.14.B【分析】根据三角形的三边关系,全等三角形的判定,等边三角形的判定,轴对称的性质一一判断即可.【详解】解:△已知△ABC中,AB=6,AC=8,则中线AD的取值范围是1≤AD≤7,错误,应该是中线AD的取值范围是1<AD<7.△两边和一角对应相等的两个三角形全等,错误,SSA不一定全等.△如果两个三角形关于某直线成轴对称,那么它们是全等三角形,正确.△一腰上的中线也是这条腰上的高的等腰三角形是等边三角形,正确.故选:B.【点睛】本题考查了轴对称的性质,等边三角形的判定,全等三角形的判定等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.15.D【分析】根据勾股定理求出DC=4;证明BE=AB=4,即可求出矩形的周长.【详解】解:△四边形ABCD 是矩形,△△C=90°,AB=CD ,AD△BC ,AD=BC ,△ED=5,EC=3,△DC 2=DE 2-CE 2=25-9=16,△DC=4,AB=4;△AD△BC ,△△AEB=△DAE ;△AE 平分△BAD ,△△BAE=△DAE ,△△BAE=△AEB ,△BE=AB=4,△BC=BE+EC=7,△矩形ABCD 的周长=2(4+7)=22.故选:D .【点睛】该题主要考查了矩形的性质、勾股定理、等腰三角形的判定等知识;解题的关键是灵活运用矩形的性质和等腰三角形的判定.16.D【分析】分式方程去分母转化为整式方程,由分式方程有增根,求出x 的值,代入整式方程求出m 的值即可.【详解】分式方程去分母得:322(1)x m x --=+,解得,4x m =+,由分式方程有增根,得到x+1=0,即x=-1,△4+1m =-解得,m=-5;故选:D .【点睛】此题考查了分式方程的增根,增根问题可按如下步骤进行:△让最简公分母为0确定增根;△化分式方程为整式方程;△把增根代入整式方程即可求得相关字母的值. 17.B【分析】易得乙出发时,两人相距8m ,除以时间2即为甲的速度;由于出现两人距离为0的情况,那么乙的速度较快.乙80s 跑完总路程400可得乙的速度,进而求得80s 时两人相距的距离可得b 的值,同法求得两人距离为0时,相应的时间,让两人相距的距离除以甲的速度,减2即为c 的值.【详解】由函数图象可知,甲的速度为824÷=(米/秒),乙的速度为400805÷=(米/秒),8(54)8∴÷-=(秒),8a ∴=,故△正确;5804(802)400328b =⨯-⨯+=-72=(米)故△正确;4004298c =÷-=(秒)故△正确;∴正确的是△△△.故选B .【点睛】本题考查了一次函数的应用,得到甲乙两人的速度是解决本题的突破点,得到相应行程的关系式是解决本题的关键.18.C【分析】△由等边三角形与等腰直角三角形知△CAD 是等腰三角形且顶角△CAD =150°,据此可判断;△求出△AFG 和△F AG 度数,从而得出△AGF 度数,据此得出答案;△根据ASA 证明△ADF △△BAH 即可判断;△由△BAE =45°,△ADC =△BAH =15°,则△EAH =30°,DF =2EH 即可得出.【详解】解:△△ABC 为等边三角形,△ABD 为等腰直角三角形,△△BAC =60°,△BAD =90°,AC =AB =AD ,△ADB =△ABD =45°,△△CAD 是等腰三角形,且顶角△CAD =150°,△△ADC =15°,故△正确;△AE △BD ,即△AED =90°,△△DAE =45°,△△AFG =△ADC +△DAE =60°,△F AG =45°,△△AGF =75°,△△AFG 三个内角都不相等,△△AFG 不是等腰三角形,故△错误;由AH △CD 且△AFG =60°知△F AH =30°,则△BAH =△ADC =15°,在△ADF 和△BAH 中,△ADF =△BAH ,DA =AB ,△△ADF △△BAH (ASA ),故△正确;△△ABE =△EAB =45°,△ADF =△BAH =15°,△DAF =△ABH =45°,△△EAH =△EAB -△BAH =45°-15°=30°,△AH =2EH ,△EH =1,△ADF △△BAH (ASA )△DF =AH ,△DF =AH =2EH =2,故△正确;故选:C .【点睛】本题考查全等三角形的判定与性质,解题的关键是掌握直角三角形的性质、等腰三角形与等边三角形的性质、全等三角形的判定与性质等知识点的应用.19.B【分析】利用一次函数图象上点的坐标特征及正方形的性质可得出点1234,,,B B B B 的坐标,根据点的坐标的变化可找出变化规律“点n B 的坐标为()n n-12-12,(n 为正整数)”,再代入n=2019即可得出n B 的坐标,然后再将其横坐标减去纵坐标得到n A 的横坐标,n A 和n B 的纵坐标相同.【详解】解:当0x=时,y=x+1=0+1=1,△点A 1的坐标为(0,1).△四边形A 1B 1C 1O 为正方形,△点B 1的坐标为(1,1),点C 1的坐标为(1,0).当x=1时,y=x+1=1+1=2,△点A 2的坐标为(1,2).△A 2B 2C 2C 1为正方形,△点B 2的坐标为(3,2),点C 2的坐标为(3,0).同理,可知:点B 3的坐标为(7,4),点B 4的坐标为(15,8),点B 5的坐标为(31,16),…,△点n B 的坐标为()n n-12-12,(n 为正整数), △点2019B 的坐标为()2019201821,2- ,△点2019A 的坐标为()2019201820182-1-22,,即为()201820182-12, . 故选B .【点睛】本题考查了一次函数图象上点的坐标特征、正方形的性质以及规律型:点的坐标,根据点的坐标的变化找出变化规律是解题的关键.20.30°或150°.【分析】利用等腰三角形的性质和含30度角的直角三角形的性质,分三角形是锐角三角形和钝角三角形,两种情况,即可求解.【详解】解:△如图,△ABC 中,AB =AC ,CD △AB 且CD =12AB , △△ABC 中,CD △AB 且CD =12AB ,AB =AC , △CD =12AC , △△A =30°.△如图,△ABC 中,AB =AC ,CD △BA 的延长线于点D ,且CD =12AB , △△CDA =90°,CD =12AB ,AB =AC , △CD =12AC , △△DAC =30°,△△A =150°.故答案为30°或150°.【点睛】本题考查含30度角的直角三角形,等腰三角形的性质,注意要分三角形是锐角三角形和钝角三角形两种情况.21.10【分析】由图可知甲乙相距10m ,在1s 时两人相遇,当x=2.5s 时乙丙完成交接,然后x=15s时,丙到达终点,进而可根据此信息求出乙的速度,设甲的速度为am/s,然后可求解.【详解】解:由图可知:甲乙相距10m,在1s时两人相遇,当x=2.5s时乙丙完成交接,然后x=15s时,丙到达终点,△乙跑完10m用时2.5s,则速度为:10 2.54÷=m/s,设甲的速度为a m/s,则有:()4110a+⨯=,a=,故甲的速度为6m/s,解得:6-⨯=;则丙到达终点时,甲距终点的距离为:10061510m故答案为10.【点睛】本题主要考查函数图像,关键是根据函数图像得到相关信息,然后求解即可.22.15【分析】根据平行四边形的性质,三角形周长的定义即可解决问题.【详解】解:△四边形ABCD是平行四边形,△AD=BC=6,OA=OC,OB=OD,△AC+BD=18,△OB+OC=9,△△BOC的周长=BC+OB+OC=6+9=15.故答案为:15.【点睛】本题考查平行四边形的性质,三角形的周长等知识,解题的关键是熟练掌握平行四边形的对角线互相平分,属于中考常考题型.23.6【分析】根据题意表示出a和b的值,进而得出答案.【详解】解:3<13<4∴=,33ab=2∴+a b2=33=6故答案为:6.【点睛】本题考查了估计无理数的大小,代数式求值等知识点的应用,解题的关键是求出无理数的取值范围.24.25算出边长,从而求算面积.【详解】△正方形的对角线长为△正方形的边长为5=△正方形的面积为25故答案为:25是解题关键.25.(-【分析】分别过点A 作AD x ⊥轴于点,D CE x ⊥于点E ,由“一线三等角”证明()ADO OEC AAS ≅,结合正方形的性质解得1AD OE DO EC ====,由此解题.【详解】解:如图,分别过点A 作AD x ⊥轴于点,D CE x ⊥于点E ,90AOC ∠=︒90AOD COE ∴∠+∠=︒+90DAO AOD ∠∠=︒DAO COE ∴∠=∠在正方形AOCB 中,ADO OEC AO OC ∠=∠=,()ADO OEC AAS ∴≅,AD OE DO EC ∴== (3,1)C1AD OE DO EC ∴====(A ∴-故答案为:(-.【点睛】本题考查全等三角形的判定与性质、正方形的性质、坐标与象限等知识,是重要考点,难度较易,掌握相关知识是解题关键.26.21cm【分析】过正方形ABCD 的中心O 作OM △CD 于M ,作ON △BC 于N ,则易证△OEM △△OFN ,根据已知可求得一个阴影部分的面积是正方形的面积的14,已知两个正方形可得到一个阴影部分,则n 个这样的正方形重叠部分即为n −1阴影部分的和,即可得出结果.【详解】解:如图,过正方形ABCD 的中心O 作OM △CD 于M ,作ON △BC 于N ,则△EOM =△FON ,OM =ON ,在△OEM 和△OFN 中,OME ONF OM ONEOM FON ∠=∠⎧⎪=⎨⎪∠=∠⎩, △△OEM △△OFN (ASA ),则四边形OECF 的面积就等于正方形OMCN 的面积,如正方形ABCD 的边长是1,则OMCN 的面积是214cm , △得阴影部分面积等于正方形面积的214cm ,△5个这样的正方形重叠部分(阴影部分)的面积和为21414cm ⨯=, 故答案为:21cm . 【点睛】考查了正方形的性质、全等三角形的判定与性质,解决本题的关键是找到规律,难点是求得一个阴影部分的面积.27.75°【分析】由旋转的性质可得AO =CO ,△AOC =30°,由等腰三角形的性质可求解.【详解】解:△△COD 是△AOB 绕点O 顺时针方向旋转30°后所得的图形,△AO =CO ,△AOC =30°,△△A =△ACO =280013︒-︒=75°, 故答案为:75°.【点睛】本题考查了旋转的性质,等腰三角形的性质,掌握旋转的性质是本题的关键. 28.邻边相等(或对角线互相垂直)【分析】根据正方形的性质及判定方法在矩形的基础上只要邻边相等或对角线互相垂直就可以.【详解】解:当邻边相等(或对角线互相垂直)时,矩形就是正方形.故答案为:邻边相等(或对角线互相垂直).【点睛】本题考查正方形的判定,熟练掌握正方形的判定方法是解答的关键.29 【分析】首先利用勾股定理列方程求出AD 的长,再代入求BD ,进而利用三角形的面积公式即可.【详解】解:如图,2AB =,3BC =,4AC =,过点B 作BD AC ⊥于D ,设AD x =,4CD x =-,BD AC ⊥,90ADB BDC ︒∴∠=∠=,222223(4)x x ∴-=--,解得118x =, 118AD ∴=,BD ∴=11422S AC BD ∴=⨯=⨯=,. 【点睛】本题考查了勾股定理,解题的关键是根据题意求出三角形的高.30.2.5【分析】根据平移的性质可得AC DF =,从而由AG AC GC =-求解即可.【详解】由平移的性质可得:45AC DF .==,△45225AG AC GC ..=-=-=,故答案为:2.5.【点睛】本题考查图形平移的性质,理解基本性质是解题关键.31.18【分析】由等腰三角形的一个外角为120°,则这个外角所对的内角为60°,即可判定这个等腰三角形是等边三角形,由此求得该三角形的周长即可.【详解】一个外角为120°,则这个外角所对的内角为60°,又因为是等腰三角形,所以这个三角形为等边三角形,所以周长为6×3=18.故答案为18.【点睛】本题考查了等边三角形的判定与性质,证得这个三角形为等边三角形是解决问题的关键.32.二【分析】根据两直线平行一次项系数相等,可列出关于k 的方程,求出k ,即可判断y=kx-3经过的象限;【详解】△y=kx-3与y=(3k-1)x+2互相平行,△ k=3k-1,解得:k=12, △ y=kx-3=12x-3,经过一、三、四象限,不经过第二象限;故答案为:二.【点睛】本题考查了一次函数图象的性质与系数之间的关系,熟练掌握知识点是解题的关键;33.6【详解】画出图形如下所示:△菱形的周长为24,△菱形的边长为6,△两邻角之比为1:2,△较小角为60°,△△ABC=60°,AB=BC=6,△△ABC 是等边三角形,△AC=6,故答案为:6.34.AC=A 1C 1(或△B=△B 1,△C=△C 1,答案不唯一).【分析】根据全等三角形的判定定理添加即可.【详解】添加AC=A 1C 1后可根据SAS 判定ABC△△A 1B 1C 1,添加△B=△B 1后可根据ASA 判定ABC△△A 1B 1C 1,添加△C=△C 1后可根据AAS 判定ABC△△A 1B 1C 1,故答案为:AC=A 1C 1(或△B=△B 1,△C=△C 1,答案不唯一).【点睛】此题考查全等三角形的判定定理,熟记判定定理并运用解题是关键.35. 8 212n +【分析】设直线4y x =+与x 轴交于H ,求出14OA OH ==,得到145A HO =︒∠,则直线与坐标轴相交构成的三角形是等腰直角三角形,再求出第n 个正方形的边长为12n +,再根据三角形面积公式进行求解即可.【详解】解:设直线4y x =+与x 轴交于H ,当0x =时,4y =,当0y =时,4x =-,△14OA OH ==,△145A HO =︒∠,△直线4y x =+与x 轴的夹角为45°,△直线与坐标轴相交构成的三角形是等腰直角三角形,△14OA =,即第一个正方形的边长为4,△114OC OA ==,△2118A C HC ==,即第二个正方形的边长8,同理可得3316A C =,即第三个正方形的边长为16,…,△可知第n 个正方形的边长为12n +, △41124422S =⨯⨯=, 62128822S =⨯⨯=, 8212161622S =⨯⨯=, …,2211211222222n n n n n S ++++=⨯⨯== 故答案为:8;212n +.【点睛】本题考查了一次函数图象上点的坐标特征,正方形的性质,等腰直角三角形的性质与判定,根据直线解析式判断出等腰直角三角形是解题的关键,也是本题的难点.36.23-【分析】根据不等式组的解集情况列方程求,m n 的值,从而求解.【详解】解:21x m n x m -≥⎧⎨-≤⎩①②, 由△得x m n ≥+,由△得()112x m ≤+, 关于x 的一元一次不等式组21x m n x m -≥⎧⎨-≤⎩的解集为35x ≤≤, ()31152m n m +=⎧⎪∴⎨+=⎪⎩,解得96m n =⎧⎨=-⎩, 6293n m -∴==-. 【点睛】本题考查代数式求值,涉及到解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.37.1或-3.【分析】分式方程去分母转化为整式方程,去分母后所得整式方程无解,或解这个整式方程得到的解使原方程的分母等于0. 【详解】3101ax x +-=-, ()310ax x +-=﹣即:()14a x -=-△当1a =时,整式方程无解,分式方程无解;当1a ≠时,41x a -=- 1x =时,分式的分母为0,方程无解, 即411a --,解得:3a =-, 因此3a =-时,方程无解.故答案为:1或-3.【点睛】本题主要考查解分式方程,去分母后所得整式方程无解,或解这个整式方程得到的解使原方程的分母等于0.38.BE =DF【分析】添加BE =DF ,证明四边形AECF 的对角线互相平分即可.【详解】添加BE =DF ,△四边形ABCD 是平行四边形,△AO =CO ,BO =DO ,△BE =DF ,△BO −BE =DO −DF ,△EO =FO ,△四边形AECF 是平行四边形.故答案为BE =DF .【点睛】本题考查的是平行四边形.熟练掌握平行四边形的判定与性质是解题的关键. 39.【分析】延长EA 交FD 的延长线于点M ,可证明EMF 是等腰直角三角形,而EM=MF=AE+DF=7,所以利用勾股定理即可求出EF 的长.【详解】解:如图所示,延长EA 交FD 的延长线于点M ,△四边形ABCD 是正方形,△AB=BC=CD=AD=5,又△AE=FC=3,BE=DF=4,△222AE BE =AB +,222FC DF =CD +, △ABE 和CDF 皆是直角三角形, 在ABE 和CDF 中,AE=CF BE=DF AB=CD ⎧⎪⎨⎪⎩△ABE△CDF (SSS ),△△EAB=△FCD ,△EBA=△FDC ,△EAB+△EBA=90°,△CDF+△FDC=90°,△△EAB+△CDF=90°,△MAD+△MDA=90°,故△M=90°, △EMF 是直角三角形,△△EAB+△MAD=90°,△MAD +△MDA=90°,△△EAB=△MDA ,在ABE 和DMA 中,AEB=M=90EAB=MDA AB=DA ∠∠︒⎧⎪∠∠⎨⎪⎩△ABE△DMA (AAS ),△AM=BE=4,MD=AE=3,△EM=MF=7,△故答案为:【点睛】本题考查了正方形的性质、全等三角形的判定和性质以及勾股定理的运用,题目的综合性较强,证明出EMF 是等腰直角三角形是解题的关键.40.-3【分析】先依据平方根算术平方根的定义得到2a−1=±3,b−1=4小,于是可得到c 的值.【详解】2a ﹣1的平方为9,△2a ﹣1=±3,解得:a =2或a =﹣1.△b ﹣1的算术平方根是2,△b ﹣1=4,解得b =5.△c△c =3. 当a =2时,a ﹣b +c =2﹣5+3=0;当a =﹣1时,ab +c =﹣1﹣5+3=﹣3.【点睛】本题考查估算无理数的大小,求得a 、b 、c 的值是解题的关键.41.(1)见解析(2)90°【分析】(1)由等边三角形的性质得出AB =BC =AC ,△ABC =△ACB =60°.可证明△BCD △△ACE ;(2)证得AC =CE ,得出△CAE =△E ,可求出△E =30°,由三角形的内角和定理可求出答案.(1)解:△△ABC 是等边三角形,△AB =BC =AC ,△ABC =△ACB =60°.△△DBC =△ECA =120°.△AD =BE ,△AD ﹣AB =BE ﹣BC ,即BD =CE .在△BCD 和△ACE 中,BC CA DBC ECA BD CE =⎧⎪∠=∠⎨⎪=⎩,△△BCD △△ACE (SAS );(2)解△△BE =2BC ,△BC =CE ,△AC =BC ,△AC =CE ,△△CAE =△E ,△△ACB =△CAE +△E =60°,△△E =30°,△△ABE +△E +△BAE =180°,△ABE =60°,△△BAE =180°﹣△ABE ﹣△E =90°.【点睛】本题主要考查等边三角形的性质,三角形的内角和定理,全等三角形的判定和性质,掌握全等三角形的判定方法是解题的关键.42.(1)55;(2)0【分析】(1的取值范围进而得出答案;(2【详解】解:(1)<56∴<,55;故答案为:55;。
初二动点问题解析与专题训练(详细)
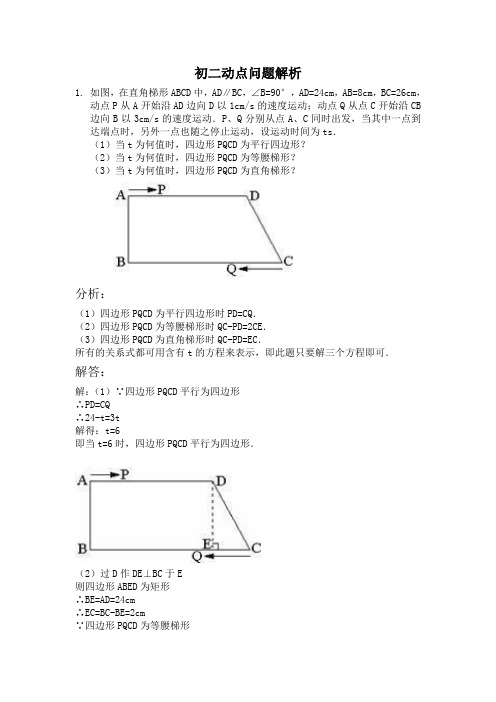
初二动点问题解析1.如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,AB=8cm,BC=26cm,动点P从A开始沿AD边向D以1cm/s的速度运动;动点Q从点C开始沿CB 边向B以3cm/s的速度运动.P、Q分别从点A、C同时出发,当其中一点到达端点时,另外一点也随之停止运动,设运动时间为ts.(1)当t为何值时,四边形PQCD为平行四边形?(2)当t为何值时,四边形PQCD为等腰梯形?(3)当t为何值时,四边形PQCD为直角梯形?分析:(1)四边形PQCD为平行四边形时PD=CQ.(2)四边形PQCD为等腰梯形时QC-PD=2CE.(3)四边形PQCD为直角梯形时QC-PD=EC.所有的关系式都可用含有t的方程来表示,即此题只要解三个方程即可.解答:解:(1)∵四边形PQCD平行为四边形∴PD=CQ∴24-t=3t解得:t=6即当t=6时,四边形PQCD平行为四边形.(2)过D作DE⊥BC于E则四边形ABED为矩形∴BE=AD=24cm∴EC=BC-BE=2cm∵四边形PQCD为等腰梯形∴QC-PD=2CE即3t-(24-t)=4解得:t=7(s)即当t=7(s)时,四边形PQCD为等腰梯形.(3)由题意知:QC-PD=EC时,四边形PQCD为直角梯形即3t-(24-t)=2解得:t=6.5(s)即当t=6.5(s)时,四边形PQCD为直角梯形.点评:此题主要考查了平行四边形、等腰梯形,直角梯形的判定,难易程度适中.1.如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的外角平分线CF于点F,交∠ACB内角平分线CE于E.(1)试说明EO=FO;(2)当点O运动到何处时,四边形AECF是矩形并证明你的结论;(3)若AC边上存在点O,使四边形AECF是正方形,猜想△ABC的形状并证明你的结论.分析:(1)根据CE平分∠ACB,MN∥BC,找到相等的角,即∠OEC=∠ECB,再根据等边对等角得OE=OC,同理OC=OF,可得EO=FO.(2)利用矩形的判定解答,即有一个内角是直角的平行四边形是矩形.(3)利用已知条件及正方形的性质解答.解答:解:(1)∵CE平分∠ACB,∴∠ACE=∠BCE,∵MN∥BC,∴∠OEC=∠ECB,∴∠OEC=∠OCE,∴OE=OC,同理,OC=OF,∴OE=OF.(2)当点O运动到AC中点处时,四边形AECF是矩形.如图AO=CO,EO=FO,∴四边形AECF为平行四边形,∵CE平分∠ACB,∴∠ACE= ∠ACB,同理,∠ACF= ∠ACG,∴∠ECF=∠ACE+∠ACF= (∠ACB+∠ACG)= ×180°=90°,∴四边形AECF是矩形.(3)△ABC是直角三角形∵四边形AECF是正方形,∴AC⊥EN,故∠AOM=90°,∵MN∥BC,∴∠BCA=∠AOM,∴∠BCA=90°,∴△ABC是直角三角形.点评:本题主要考查利用平行线的性质“等角对等边”证明出结论(1),再利用结论(1)和矩形的判定证明结论(2),再对(3)进行判断.解答时不仅要注意用到前一问题的结论,更要注意前一问题为下一问题提供思路,有相似的思考方法.是矩形的判定和正方形的性质等的综合运用.2.如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,已知AD=AB=3,BC=4,动点P 从B点出发,沿线段BC向点C作匀速运动;动点Q从点D出发,沿线段DA向点A作匀速运动.过Q点垂直于AD的射线交AC于点M,交BC于点N.P、Q两点同时出发,速度都为每秒1个单位长度.当Q点运动到A点,P、Q两点同时停止运动.设点Q运动的时间为t秒.(1)求NC,MC的长(用t的代数式表示);(2)当t为何值时,四边形PCDQ构成平行四边形;(3)是否存在某一时刻,使射线QN恰好将△ABC的面积和周长同时平分?若存在,求出此时t的值;若不存在,请说明理由;(4)探究:t为何值时,△PMC为等腰三角形.分析:(1)依据题意易知四边形ABNQ是矩形∴NC=BC-BN=BC-AQ=BC-AD+DQ,BC、AD已知,DQ就是t,即解;∵AB∥QN,∴△CMN∽△CAB,∴CM:CA=CN:CB,(2)CB、CN已知,根据勾股定理可求CA=5,即可表示CM;四边形PCDQ构成平行四边形就是PC=DQ,列方程4-t=t即解;(3)可先根据QN平分△ABC的周长,得出MN+NC=AM+BN+AB,据此来求出t的值.然后根据得出的t的值,求出△MNC的面积,即可判断出△MNC的面积是否为△ABC 面积的一半,由此可得出是否存在符合条件的t值.(4)由于等腰三角形的两腰不确定,因此分三种情况进行讨论:①当MP=MC时,那么PC=2NC,据此可求出t的值.②当CM=CP时,可根据CM和CP的表达式以及题设的等量关系来求出t的值.③当MP=PC时,在直角三角形MNP中,先用t表示出三边的长,然后根据勾股定理即可得出t的值.综上所述可得出符合条件的t的值.解答:解:(1)∵AQ=3-t∴CN=4-(3-t)=1+t在Rt△ABC中,AC2=AB2+BC2=32+42∴AC=5在Rt△MNC中,cos∠NCM= = ,CM= .(2)由于四边形PCDQ构成平行四边形∴PC=QD,即4-t=t解得t=2.(3)如果射线QN将△ABC的周长平分,则有:MN+NC=AM+BN+AB即:(1+t)+1+t= (3+4+5)解得:t= (5分)而MN= NC= (1+t)∴S△MNC= (1+t)2= (1+t)2当t= 时,S△MNC=(1+t)2= ≠×4×3∴不存在某一时刻t,使射线QN恰好将△ABC的面积和周长同时平分.(4)①当MP=MC时(如图1)则有:NP=NC即PC=2NC∴4-t=2(1+t)解得:t=②当CM=CP时(如图2)则有:(1+t)=4-t解得:t=③当PM=PC时(如图3)则有:在Rt△MNP中,PM2=MN2+PN2而MN= NC= (1+t)PN=NC-PC=(1+t)-(4-t)=2t-3∴[ (1+t)]2+(2t-3)2=(4-t)2解得:t1= ,t2=-1(舍去)∴当t= ,t= ,t= 时,△PMC为等腰三角形点评:此题繁杂,难度中等,考查平行四边形性质及等腰三角形性质.考查学生分类讨论和数形结合的数学思想方法.3.如图,在矩形ABCD中,BC=20cm,P,Q,M,N分别从A,B,C,D出发沿AD,BC,CB,DA方向在矩形的边上同时运动,当有一个点先到达所在运动边的另一个端点时,运动即停止.已知在相同时间内,若BQ=xcm(x≠0),则AP=2xcm,CM=3xcm,DN=x2cm.(1)当x为何值时,以PQ,MN为两边,以矩形的边(AD或BC)的一部分为第三边构成一个三角形;(2)当x为何值时,以P,Q,M,N为顶点的四边形是平行四边形;(3)以P,Q,M,N为顶点的四边形能否为等腰梯形?如果能,求x的值;如果不能,请说明理由.分析:以PQ,MN为两边,以矩形的边(AD或BC)的一部分为第三边构成一个三角形的必须条件是点P、N重合且点Q、M不重合,此时AP+ND=AD即2x+x2=20cm,BQ+MC ≠BC即x+3x≠20cm;或者点Q、M重合且点P、N不重合,此时AP+ND≠AD即2x+x2≠20cm,BQ+MC=BC即x+3x=20cm.所以可以根据这两种情况来求解x的值.以P,Q,M,N为顶点的四边形是平行四边形的话,因为由第一问可知点Q只能在点M的左侧.当点P在点N的左侧时,AP=MC,BQ=ND;当点P在点N的右侧时,AN=MC,BQ=PD.所以可以根据这些条件列出方程关系式.如果以P,Q,M,N为顶点的四边形为等腰梯形,则必须使得AP+ND≠AD即2x+x2≠20cm,BQ+MC≠BC即x+3x≠20cm,AP=ND即2x=x2,BQ=MC即x=3x,x≠0.这些条件不能同时满足,所以不能成为等腰梯形.解答:解:(1)当点P与点N重合或点Q与点M重合时,以PQ,MN为两边,以矩形的边(AD或BC)的一部分为第三边可能构成一个三角形.①当点P与点N重合时,由x2+2x=20,得x1= -1,x2=- -1(舍去).因为BQ+CM=x+3x=4(-1)<20,此时点Q与点M不重合.所以x= -1符合题意.②当点Q与点M重合时,由x+3x=20,得x=5.此时DN=x2=25>20,不符合题意.故点Q与点M不能重合.所以所求x的值为-1.(2)由(1)知,点Q只能在点M的左侧,①当点P在点N的左侧时,由20-(x+3x)=20-(2x+x2),解得x1=0(舍去),x2=2.当x=2时四边形PQMN是平行四边形.②当点P在点N的右侧时,由20-(x+3x)=(2x+x2)-20,解得x1=-10(舍去),x2=4.当x=4时四边形NQMP是平行四边形.所以当x=2或x=4时,以P,Q,M,N为顶点的四边形是平行四边形.(3)过点Q,M分别作AD的垂线,垂足分别为点E,F.由于2x>x,所以点E一定在点P的左侧.若以P,Q,M,N为顶点的四边形是等腰梯形,则点F一定在点N的右侧,且PE=NF,即2x-x=x2-3x.解得x1=0(舍去),x2=4.由于当x=4时,以P,Q,M,N为顶点的四边形是平行四边形,所以以P,Q,M,N为顶点的四边形不能为等腰梯形.点评:本题考查到三角形、平行四边形、等腰梯形等图形的边的特点.4.如图,在梯形ABCD中,AD∥BC,∠B=90°,AB=14cm,AD=15cm,BC=21cm,点M 从点A开始,沿边AD向点D运动,速度为1cm/s;点N从点C开始,沿边CB向点B运动,速度为2cm/s、点M、N分别从点A、C出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒.(1)当t为何值时,四边形MNCD是平行四边形?(2)当t为何值时,四边形MNCD是等腰梯形?分析:(1)根据平行四边形的性质,对边相等,求得t值;(2)根据等腰梯形的性质,下底减去上底等于12,求解即可.解答:解:(1)∵MD∥NC,当MD=NC,即15-t=2t,t=5时,四边形MNCD是平行四边形;(2)作DE⊥BC,垂足为E,则CE=21-15=6,当CN-MD=12时,即2t-(15-t)=12,t=9时,四边形MNCD是等腰梯形点评:考查了等腰梯形和平行四边形的性质,动点问题是中考的重点内容.5.如图,在直角梯形ABCD中,AD∥BC,∠C=90°,BC=16,DC=12,AD=21,动点P 从点D出发,沿射线DA的方向以每秒2个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,P、Q分别从点D、C同时出发,当点Q运动到点B时,点P随之停止运动,设运动时间为t(s).(1)设△BPQ的面积为S,求S与t之间的函数关系;(2)当t为何值时,以B、P、Q三点为顶点的三角形是等腰三角形?分析:(1)若过点P作PM⊥BC于M,则四边形PDCM为矩形,得出PM=DC=12,由QB=16-t,可知:s= PM×QB=96-6t;(2)本题应分三种情况进行讨论,①若PQ=BQ,在Rt△PQM中,由PQ2=PM2+MQ2,PQ=QB,将各数据代入,可将时间t求出;②若BP=BQ,在Rt△PMB中,由PB2=BM2+PM2,BP=BQ,将数据代入,可将时间t求出;③若PB=PQ,PB2=PM2+BM2,PB=PQ,将数据代入,可将时间t求出.解答:解:(1)过点P作PM⊥BC于M,则四边形PDCM为矩形.∴PM=DC=12,∵QB=16-t,∴s= •QB•PM= (16-t)×12=96-6t(0≤t≤).(2)由图可知,CM=PD=2t,CQ=t,若以B、P、Q为顶点的三角形是等腰三角形,可以分三种情况:①若PQ=BQ,在Rt△PMQ中,PQ2=t2+122,由PQ2=BQ2得t2+122=(16-t)2,解得;②若BP=BQ,在Rt△PMB中,PB2=(16-2t)2+122,由PB2=BQ2得(16-2t)2+122=(16-t)2,此方程无解,∴BP≠PQ.③若PB=PQ,由PB2=PQ2得t2+122=(16-2t)2+122得,t2=16(不合题意,舍去).综上所述,当或时,以B、P、Q为顶点的三角形是等腰三角形.点评:本题主要考查梯形的性质及勾股定理.在解题(2)时,应注意分情况进行讨论,防止在解题过程中出现漏解现象.6.直线y=- 34x+6与坐标轴分别交于A、B两点,动点P、Q同时从O点出发,同时到达A点,运动停止.点Q沿线段OA运动,速度为每秒1个单位长度,点P沿路线O⇒B⇒A运动.(1)直接写出A、B两点的坐标;(2)设点Q的运动时间为t(秒),△OPQ的面积为S,求出S与t之间的函数关系式;(3)当S= 485时,求出点P的坐标,并直接写出以点O、P、Q为顶点的平行四边形的第四个顶点M的坐标.分析:(1)分别令y=0,x=0,即可求出A、B的坐标;(2))因为OA=8,OB=6,利用勾股定理可得AB=10,进而可求出点Q由O到A 的时间是8秒,点P的速度是2,从而可求出,当P在线段OB上运动(或0≤t≤3)时,OQ=t,OP=2t,S=t2,当P在线段BA 上运动(或3<t≤8)时,OQ=t,AP=6+10-2t=16-2t,作PD⊥OA于点D,由相似三角形的性质,得 PD=48-6t5,利用S= 12OQ×PD,即可求出答案;(3)令S= 485,求出t的值,进而求出OD、PD,即可求出P的坐标,利用平行四边形的对边平行且相等,结合简单的计算即可写出M的坐标.解答:解:(1)y=0,x=0,求得A(8,0)B(0,6),(2)∵OA=8,OB=6,∴AB=10.∵点Q由O到A的时间是 81=8(秒),∴点P的速度是 6+108=2(单位长度/秒).当P在线段OB上运动(或O≤t≤3)时,OQ=t,OP=2t,S=t2.当P在线段BA上运动(或3<t≤8)时,OQ=t,AP=6+10-2t=16-2t,如图,做PD⊥OA于点D,由 PDBO=APAB,得PD= 48-6t5.∴S= 12OQ•PD=- 35t2+245t.(3)当S= 485时,∵ 485>12×3×6∴点P在AB上当S= 485时,- 35t2+245t= 485∴t=4∴PD= 48-6×45= 245,AD=16-2×4=8 AD= 82-(245)2= 325 ∴OD=8- 325= 85 ∴P ( 85, 245) M1( 285, 245),M2(- 125, 245),M3( 125,- 245)点评:本题主要考查梯形的性质及勾股定理.在解题(2)时,应注意分情况进行讨论,防止在解题过程中出现漏解现象.动点问题专题训练1、如图,已知ABC △中,10AB AC ==厘米,8BC =厘米,点D 为AB 的中点. (1)如果点P 在线段BC 上以3厘米/秒的速度由B 点向C 点运动,同时,点Q 在线段CA 上由C 点向A 点运动.①若点Q 的运动速度与点P 的运动速度相等,经过1秒后,BPD △与CQP △是否全等,请说明理由;②若点Q 的运动速度与点P 的运动速度不相等,当点Q 的运动速度为多少时,能够使BPD △与CQP △全等?(2)若点Q 以②中的运动速度从点C 出发,点P 以原来的运动速度从点B 同时出发,都逆时针沿ABC △三边运动,求经过多长时间点P 与点Q 第一次在ABC △的哪条边上相遇?2、直线364y x =-+与坐标轴分别交于A B 、两点,动点P Q 、同时从O 点出发,同时到达A 点,运动停止.点Q 沿线段OA 运动,速度为每秒1个单位长度,点P 沿路线O →B →A 运动.(1)直接写出A B 、两点的坐标;(2)设点Q 的运动时间为t 秒,OPQ △的面积为S ,求出S 与t 之间的函数关系式; (3)当485S =时,求出点P 的坐标,并直接写出以点O P Q、、为顶点的平行四边形的第四个顶点M的坐标.3如图,在平面直角坐标系中,直线l:y=-2x-8分别与x轴,y轴相交于A,B 两点,点P(0,k)是y轴的负半轴上的一个动点,以P为圆心,3为半径作⊙P.(1)连结PA,若PA=PB,试判断⊙P与x轴的位置关系,并说明理由;(2)当k为何值时,以⊙P与直线l的两个交点和圆心P为顶点的三角形是正三角形?4 如图1,在平面直角坐标系中,点O是坐标原点,四边形ABCO是菱形,点A 的坐标为(-3,4),点C在x轴的正半轴上,直线AC交y轴于点M,AB边交y轴于点H.(1)求直线AC的解析式;(2)连接BM,如图2,动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数关系式(要求写出自变量t的取值范围);(3)在(2)的条件下,当t为何值时,∠MPB与∠BCO互为余角,并求此时直线OP与直线AC所夹锐角的正切值.5在Rt △ABC 中,∠C =90°,AC = 3,AB = 5.点P 从点C 出发沿CA 以每秒1个单位长的速度向点A 匀速运动,到达点A 后立刻以原来的速度沿AC 返回;点Q 从点A 出发沿AB 以每秒1个单位长的速度向点B匀速运动.伴随着P 、Q 的运动,DE 保持垂直平分PQ ,且交PQ 于点D ,交折线QB -BC -CP 于点E .点P 、Q 同时出发,当点Q 到达点B 时停止运动,点P 也随之停止.设点P 、Q 运动的时间是t 秒(t >0).(1)当t = 2时,AP = ,点Q 到AC 的距离是 ;(2)在点P 从C 向A 运动的过程中,求△APQ 的面积S 与t 的函数关系式;(不必写出t 的取值范围)(3)在点E 从B 向C 运动的过程中,四边形QBED 能否成为直角梯形?若能,求t 的值.若不能,请说明理由; (4)当DE 经过点C 时,请直接..写出t 的值.6如图,在Rt ABC △中,9060ACB B ∠=∠=°,°,2BC =.点O 是AC 的中点,过点O 的直线l 从与AC 重合的位置开始,绕点O 作逆时针旋转,交AB 边于点D .过点C 作CE AB ∥交直线l 于点E ,设直线l 的旋转角为α.(1)①当α= 度时,四边形EDBC 是等腰梯形,此时AD 的长为 ;②当α= 度时,四边形EDBC 是直角梯形,C BPQ ED图16OEC D αl OC (备用图)此时AD 的长为 ;(2)当90α=°时,判断四边形EDBC 是否为菱形,并说明理由.7如图,在梯形ABCD中,3545AD BC AD DC AB B ====︒∥,,,.动点M 从B 点出发沿线段BC 以每秒2个单位长度的速度向终点C 运动;动点N 同时从C 点出发沿线段CD 以每秒1个单位长度的速度向终点D 运动.设运动的时间为t 秒. (1)求BC 的长.(2)当MN AB ∥时,求t 的值.(3)试探究:t 为何值时,MNC △为等腰三角形.8如图1,在等腰梯形ABCD 中,AD BC ∥,E 是AB 的中点,过点E 作EF BC ∥交CD 于点F .46AB BC ==,,60B =︒∠. (1)求点E 到BC 的距离;(2)点P 为线段EF 上的一个动点,过P 作PM EF ⊥交BC 于点M ,过M 作MN AB ∥交折线ADC 于点N ,连结PN ,设EP x =. ①当点N 在线段AD 上时(如图2),PMN △的形状是否发生改变?若不变,求出PMN △的周长;若改变,请说明理由; ②当点N 在线段DC 上时(如图3),是否存在点P ,使PMN △为等腰三角形?若存在,请求出所有满足要求的x 的值;若不存在,请说明理由.C MA D E BF CAD E BFCA D E BF C图1 图2A D EB FC PNM 图3AD EBFCPN M (第25题)9如图①,正方形ABCD中,点A、B的坐标分别为(0,10),(8,4),点C在第一象限.动点P在正方形ABCD的边上,从点A出发沿A→B→C→D 匀速运动,同时动点Q以相同速度在x轴正半轴上运动,当P点到达D点时,两点同时停止运动,设运动的时间为t秒.(1)当P点在边AB上运动时,点Q的横坐标x(长度单位)关于运动时间t(秒)的函数图象如图②所示,请写出点Q开始运动时的坐标及点P运动速度;(2)求正方形边长及顶点C的坐标;(3)在(1)中当t为何值时,△OPQ的面积最大,并求此时P点的坐标;(4)如果点P、Q保持原速度不变,当点P沿A→B→C→D匀速运动时,OP与PQ能否相等,若能,写出所有符合条件的t的值;若不能,请说明理由.1数学课上,张老师出示了问题:如图1,四边形ABCD 是正方形,点E 是边BC 的中点.90AEF ∠=,且EF 交正方形外角DCG ∠的平行线CF 于点F ,求证:AE =EF .经过思考,小明展示了一种正确的解题思路:取AB 的中点M ,连接ME ,则AM =EC ,易证AME ECF △≌△,所以AE EF =.在此基础上,同学们作了进一步的研究:(1)小颖提出:如图2,如果把“点E 是边BC 的中点”改为“点E 是边BC 上(除B ,C 外)的任意一点”,其它条件不变,那么结论“AE =EF ”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由; (2)小华提出:如图3,点E 是BC 的延长线上(除C 点外)的任意一点,其他条件不变,结论“AE =EF ”仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.11已知一个直角三角形纸片OAB ,其中9024AOB OA OB ∠===°,,.如图,A D F C G EB 图1 A D FC G E B 图2 AD FC G E B 图3将该纸片放置在平面直角坐标系中,折叠该纸片,折痕与边OB 交于点C ,与边AB 交于点D .(Ⅰ)若折叠后使点B 与点A 重合,求点C(Ⅱ)若折叠后点B 落在边OA 上的点为B ',设OB x '=,OC y =,试写出y 关于x 的函数解析式,并确定y 的取值范围;(Ⅲ)若折叠后点B 落在边OA 上的点为B ',且使B D OB '∥,求此时点C 的坐标.12问题解决图(1)A BCD EFM N如图(1),将正方形纸片ABCD 折叠,使点B 落在CD 边上一点E (不与点C ,D 重合),压平后得到折痕MN .当12CE CD =时,求AMBN 的值.类比归纳在图(1)中,若13CE CD =,则AM BN 的值等于 ;若14CE CD =,则AMBN 的值等于 ;若1CE CD n =(n 为整数),则AMBN的值等于 .(用含n 的式子表示) 联系拓广 如图(2),将矩形纸片ABCD 折叠,使点B 落在CD 边上一点E (不与点C D,重合),压平后得到折痕MN ,设()111AB CE m BC m CD n =>=,,则AMBN的值等于 .(用含m n ,的式子表示)1解:(1)①∵1t =秒,∴313BP CQ ==⨯=厘米,图(2) N AB C D EF M∵10AB =厘米,点D 为AB 的中点,∴5BD =厘米.又∵8PC BC BP BC =-=,厘米,∴835PC =-=厘米,∴PC BD =. 又∵AB AC =,∴B C ∠=∠,∴BPD CQP △≌△.②∵P Q v v ≠, ∴BP CQ ≠,又∵BPD CQP △≌△,B C ∠=∠,则45BP PC CQ BD ====,,∴点P ,点Q 运动的时间433BP t ==秒, ∴515443Q CQ v t===厘米/秒. (2)设经过x 秒后点P 与点Q 第一次相遇,由题意,得1532104x x =+⨯, 解得803x =秒.∴点P 共运动了803803⨯=厘米.∵8022824=⨯+,∴点P 、点Q 在AB 边上相遇,∴经过803秒点P 与点Q 第一次在边AB 上相遇2解(1)A (8,0)B (0,6)(2)86OA OB ==,10AB ∴=点Q 由O 到A 的时间是881=(秒)∴点P 的速度是61028+=(单位/秒) 当P 在线段OB 上运动(或03t ≤≤)时,2OQ t OP t ==, 2S t = 当P 在线段BA 上运动(或38t <≤)时,6102162OQ t AP t t ==+-=-,, 如图,作PD OA ⊥于点D ,由PD AP BO AB =,得4865tPD -=, 21324255S OQ PD t t ∴=⨯=-+ (3)82455P ⎛⎫ ⎪⎝⎭,12382412241224555555I M M 2⎛⎫⎛⎫⎛⎫--⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,,,,,3解:(1)⊙P 与x 轴相切.∵直线y =-2x -8与x 轴交于A (4,0),与y 轴交于B (0,-8),∴OA =4,OB =8.由题意,OP =-k ,∴PB =PA =8+k .在Rt △AOP 中,k 2+42=(8+k )2, ∴k =-3,∴OP 等于⊙P 的半径, ∴⊙P 与x 轴相切.(2)设⊙P 与直线l 交于C ,D 两点,连结PC ,PD 当圆心P在线段OB 上时,作PE ⊥CD 于E .∵△PCD 为正三角形,∴DE =12CD =32,PD =3, ∴PE 33.∵∠AOB =∠PEB =90°, ∠ABO =∠PBE ,∴△AOB ∽△PEB ,∴2,AO PEAB PB PB=,∴PB=∴8PO BO PB=-=-∴8)P-,∴8k-.当圆心P在线段OB延长线上时,同理可得P(0,-8),∴k=-8,∴当k-8或k=-8时,以⊙P与直线l的两个交点和圆心P为顶点的三角形是正三角形.∴NG CD BC==.同理,四边形ABNG也是平行四边形.∴54AG BN==.∵90MN BE EBC BNM⊥∴∠+∠=,°.90NG BC MNG BNM EBC MNG⊥∴∠+∠=∴∠=∠,°,.在BCE△与NGM△中90EBC MNGBC NGC NGM∠=∠⎧⎪=⎨⎪∠=∠=⎩,,°.∴BCE NGM EC MG=△≌△,.·································5分∵114AM AG MG AM=--=5,=.4······································································ 6分∴15AMBN=. ·············································································································· 7分类比归纳25(或410);917;()2211nn-+····················································································· 10分联系拓广2222211n m nn m-++················································································································· 12分解:(1)1,85; (2)作QF ⊥AC 于点F ,如图3, AQ = CP = t ,∴3AP t =-.由△AQF ∽△ABC,4BC ==, 得45QF t =.∴45QF t =. ∴14(3)25S t t =-⋅,即22655S t t =-+.(3)能.①当DE∥QB 时,如图4.∵DE ⊥PQ ,∴PQ ⊥QB ,四边形QBED 是直角梯形.此时∠AQP =90°.由△APQ ∽△ABC,得AQ AP AC AB =,即335t t -=. 解得98t =.②如图5,当PQ ∥BC 时,DE ⊥BC ,四边形QBED 是直角梯形. 此时∠APQ =90°. 由△AQP ∽△ABC ,得AQ APAB AC=, 即353t t -=. 解得158t =.(4)52t =或4514t =. ①点P 由C 向A 运动,DE 经过点C .连接QC ,作QG ⊥BC 于点G ,如图6.PC t =,222QC QG CG =+2234[(5)][4(5)]55t t =-+--. 由22PC QC =,得22234[(5)][4(5)]55t t t =-+--,解得52t =.②点P 由A 向C 运动,DE 经过点C ,如图7.22234(6)[(5)][4(5)]55t t t -=-+--,4514t =】解(1)①30,1;②60,1.5;(2)当∠α=900时,四边形EDBC 是菱形. ∵∠α=∠ACB=900,∴BC //ED .∵CE //AB , ∴四边形EDBC 是平行四边形. 在Rt △ABC 中,∠ACB =900,∠B =600,BC =2,∴∠A =300.∴AB =4,AC ∴AO =12AC 在Rt △AOD 中,∠A =300,∴AD =2.∴BD =2.∴BD =BC .又∵四边形EDBC 是平行四边形,∴四边形EDBC 是菱形7解:(1)如图①,过A 、D 分别作AK BC ⊥于K ,DH BC ⊥于H ,则四边形ADHK 是矩形P图4图5C∴3KH AD ==.在Rt ABK △中,sin 454AK AB =︒== 2cos 454242BK AB =︒== 在Rt CDH △中,由勾股定理得,3HC = ∴43310BC BK KH HC =++=++=(2)如图②,过D 作DG AB ∥交BC 于G 点,则四边形ADGB 是平行四边形 ∵MN AB ∥∴MN DG ∥∴3BG AD ==∴1037GC =-= 由题意知,当M 、N 运动到t 秒时,102CN t CM t ==-,.∵DG MN ∥∴NMC DGC =∠∠又C C =∠∠∴MNC GDC △∽△ ∴CN CM CD CG =即10257t t -=解得,5017t = (3)分三种情况讨论:①当NC MC =时,如图③,即102t t =-∴103t =②当MN NC =时,如图④,过N 作NE MC ⊥于E 解法一:由等腰三角形三线合一性质得()11102522EC MC t t ==-=- 在Rt CEN △中,5cos EC t c NC t -==又在Rt DHC △中,3cos 5CH c CD ==∴535t t -=解得258t =解法二:(图①)A D CB K H(图②)ADCB G MNADCB MN(图③)(图④)AD CBM NH E∵90C C DHC NEC =∠=∠=︒∠∠,∴NEC DHC △∽△∴NC ECDC HC=即553t t -=∴258t = ③当MN MC =时,如图⑤,过M 作MF CN ⊥于F 点.1122FC NC t == 解法一:(方法同②中解法一)132cos 1025tFC C MC t ===-解得6017t = 解法二:∵90C C MFC DHC =∠=∠=︒∠∠, ∴MFC DHC △∽△∴FC MC HC DC=即1102235tt -=∴6017t =综上所述,当103t =、258t =或6017t =时,MNC △为等腰三角形8解(1)如图1,过点E 作EG BC ⊥于点G . 1分∵E 为AB 的中点,∴122BE AB ==. 在Rt EBG △中,60B =︒∠,∴30BEG =︒∠.∴112BG BE EG ====, 即点E 到BC(2)①当点N 在线段AD 上运动时,PMN △的形状不发生改变.∵PM EF EG EF ⊥⊥,,∴PM EG ∥.∵EF BC ∥,∴EP GM =,PM EG ==同理4MN AB ==. 如图2,过点P 作PH MN ⊥于H ,∵MN AB ∥,∴6030NMC B PMH ==︒=︒∠∠,∠.∴12PH PM =∴3cos302MH PM =︒=.则35422NH MN MH =-=-=.在Rt PNH △中,PN === ∴PMN △的周长=4PM PN MN ++=.(图⑤) ADCBH N MF图1AD E BF CG图2BC②当点N 在线段DC 上运动时,PMN △的形状发生改变,但MNC △恒为等边三角形.当PM PN =时,如图3,作PR MN ⊥于R ,则MR NR =.类似①,32MR =.∴23MN MR ==. ∵MNC △是等边三角形,∴3MC MN ==.此时,6132x EP GM BC BG MC ===--=--=.当MP MN =时,如图4,这时MC MN MP ===此时,615x EP GM ===-=当NP NM =时,如图5,30NPM PMN ==︒∠∠.则120PMN =︒∠,又60MNC =︒∠,∴180PNM MNC +=︒∠∠.因此点P 与F 重合,PMC △为直角三角形.∴tan301MC PM =︒=. 此时,6114x EP GM ===--=. 综上所述,当2x =或4或(5时,PMN △为等腰三角形. 解:(1)Q (1,0)点P 运动速度每秒钟1个单位长度.(2) 过点B 作BF ⊥y 轴于点F ,BE ⊥x 轴于点E ,则BF =8,4OF BE ==. ∴1046AF =-=.在Rt △AFB中,10AB = 3分 过点C 作CG ⊥x 轴于点G ,与FB 的延长线交于点H . ∵90,ABC AB BC ∠=︒= ∴△ABF ≌△BCH . ∴6,8BH AF CH BF ====. ∴8614,8412OG FH CG ==+==+=.∴所求C 点的坐标为(14,12). 4分 (3) 过点P 作PM ⊥y 轴于点M ,PN ⊥x 轴于点N , 则△APM ∽△ABF . ∴AP AM MP AB AF BF ==. 1068t AM MP∴==. ∴3455AM t PM t ==,. ∴3410,55PN OM t ON PM t ==-==. 设△OPQ 的面积为S (平方单位)∴213473(10)(1)5251010S t t t t =⨯-+=+-(0≤t ≤10) 说明:未注明自变量的取值范围不扣分.图3A D E BFCPN M图4AD E BF CP MN 图5AD E B F (P )CMN GGRG∵310a =-<0 ∴当474710362()10t =-=⨯-时, △OPQ 的面积最大. 此时P 的坐标为(9415,5310) .(4) 当 53t =或29513t =时, OP 与PQ 相等. 解:(1)正确.证明:在AB 上取一点M ,使AM EC =,连接ME . (2分) BM BE ∴=.45BME ∴∠=°,135AME ∴∠=°.CF 是外角平分线,45DCF ∴∠=°,135ECF ∴∠=°. AME ECF ∴∠=∠.90AEB BAE ∠+∠=°,90AEB CEF ∠+∠=°,AME BCF ∴△≌△(ASA ).AE EF ∴=. (2)正确.证明:在BA 的延长线上取一点N .使AN CE =,连接NE . BN BE ∴=.45N PCE ∴∠=∠=°. 四边形ABCD 是正方形,AD BE ∴∥.DAE BEA ∴∠=∠.NAE CEF ∴∠=∠. ANE ECF ∴△≌△(ASA ).AE EF ∴=.) 11解(Ⅰ)如图①,折叠后点B 与点A 重合, 则ACD BCD △≌△.设点C 的坐标为()()00m m >,.则4BC OB OC m =-=-. 于是4AC BC m ==-.在Rt AOC △中,由勾股定理,得222AC OC OA =+, 即()22242m m -=+,解得32m =.∴点C 的坐标为302⎛⎫ ⎪⎝⎭, .(Ⅱ)如图②,折叠后点B 落在OA 边上的点为B ',则B CD BCD '△≌△.由题设OB x OC y '==,,则4B C BC OB OC y '==-=-, 在Rt B OC '△中,由勾股定理,得222B C OC OB ''=+.()2224y y x ∴-=+,即2128y x =-+ 由点B '在边OA 上,有02x ≤≤, ∴ 解析式2128y x =-+()02x ≤≤为所求.当02x ≤≤时,y 随x 的增大而减小,y ∴的取值范围为322y ≤≤.(Ⅲ)如图③,折叠后点B 落在OA 边上的点为B '',且B D OB ''∥. 则OCB CB D ''''∠=∠. 又CBD CB D OCB CBD ''''∠=∠∴∠=∠,,有CB BA ''∥.Rt Rt COB BOA ''∴△∽△.有OB OCOA OB''=,得2OC OB ''=. A DF CGBM AD FGE B N在Rt B OC ''△中,设()00OB x x ''=>,则02OC x =.由(Ⅱ)的结论,得2001228x x =-+,解得000808x x x =-±>∴=-+,∴点C的坐标为()016.由题设,得四边形ABNM 和四边形FENM 关于直线MN 对称.∴MN 垂直平分BE .∴BM EM BN EN ==,. ················································ 1分 ∵四边形ABCD 是正方形,∴902A D C AB BC CD DA ∠=∠=∠=====°,. ∵112CE CE DE CD =∴==,.设BN x =,则NE x =,2NC x =-. 在Rt CNE △中,222NE CN CE =+. ∴()22221x x =-+.解得54x =,即54BN =. ······················································ 3分 在Rt ABM △和在Rt DEM △中,222AM AB BM +=,222DM DE EM +=,∴2222AM AB DM DE +=+. ················································································· 5分设AM y =,则2DM y =-,∴()2222221y y +=-+.解得14y =,即14AM =. ··························································································· 6分∴15AM BN =.················································································································ 7分 方法二:同方法一,54BN =. ···················································································· 3分如图(1-2),过点N 做NG CD ∥,交AD 于点G ,连接BE .∵AD BC ∥,∴四边形GDCN 是平行四边形N图(1-1)A BC DEFMN图(1-2)A BC DEFMG。
初二奥数之等腰三角形的判定

初二奥数之等腰三角形的判定专题17 等腰三角形的判定阅读与思考在学习了等腰三角形性质与判定后,我们可以对等腰三角形的判定、证明线段相等的方法作出归纳总结.1.等腰三角形的判定:⑴从定义入手,证明一个三角形的两条边相等; ⑵从角入手,证明一个三角形的两个角相等. 2.证明线段相等的方法:⑴当所证的两条线段位于两个三角形,通过全等三角形证明; ⑵当所证的两条线段位于同一个三角形,通过等角对等边证明; ⑶寻找某条线段,证明所证的两条线段都与它相等. 善于发现、构造等腰三角形,进而利用等腰三角形的性质为解题服务,是解几何题的一个常用技巧.常见的构造方法有:平分线+平行线、平分线+垂线、中线+垂线.如图所示:例题与求解【例1】如图,在△ABC 中,AB =7,AC =11,点M 是BC 的中点,AD 是∠BAC 的平分线,MF ∥AD ,则CF 的长为____________.(全国初中数学竞赛试题)解题思路:角平分线+平行线易构造等腰三角形,解题的关键是利用条件“中点M ”.【例2】如图,在△ABC 中,∠B =2∠C ,则AC 与2AB 之间的关系是( ) A .AC >2AB B .AC =2AB C .AC ≤2AB D .AC <2AB(山东省竞赛试题)解题思路:如何条件∠B =2∠C ,如何得到2AB ,这是解本题的关键.ABD MFCABC【例3】两个全等的含300,600角的三角板ADE 和三角板ABC ,如图所示放置,E 、A 、C 三点在一条直线上,连结BD ,取BD 中点M ,连结ME ,MC ,试判断△EMC 的形状,并说明理由.(山东省中考试题)解题思路:从△ADE ≌△BAC 出发,先确定△ADB 的形状,为判断△EMC 的形状奠定基础.【例4】如图,已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE =AC ,延长BE 交AC 于F ,求证:AF =EF .(天津市竞赛试题)解题思路:只需证明∠F AE =∠AEF ,利用中线倍长,构造全等三角形、等腰三角形.【例5】如图,在等腰△ABC 中,AB =AC ,∠A =200,在边AB 上取点D ,使AD =BC ,求∠BDC 度数.(“祖冲之杯”竞赛试题)解题思路:由条件知底角为300,这些角并不是特殊角,但它们的差却为600,600使我们联想到等边三角形,由此找到切入口.如图1,以BC 为边在△ABC 内作等边△BCO ;如图②,以AC 为边作等边△ACE .ABCMD EEA BDCFBCADB CA D图1O BCA D图2E能力训练A 级1.已知△ABC 为等腰三角形,由顶点A 所引BC 边的高线恰等于BC 边长的一半,则 ∠BAC =__________.2.如图,在Rt △ABC 中,∠C =900,∠ABC =660,△ABC 以点C 为中点旋转到△A ′B ′C 的位置,顶点B 在斜边A ′B ′上,A ′C 与AB 相交于D ,则∠BDC =_________.3.如图,△ABC 是边长为6的等边三角形,DE ⊥BC 于E ,EF ⊥AC 于F ,FD ⊥AB 于D ,则AD =_______.(天津市竞赛试题)4.如图,一个六边形的六个内角都是1200,其连续四边的长依次是1cm ,9cm ,9cm ,5cm ,那么这个六边形的周长是____________cm .(“祖冲之杯”邀请赛试题)5.如图,△ABC 中,AB =AC ,∠B =360,D 、E 是BC 上两点,使∠ADE =∠AED =2∠BAD ,则图中等腰三角形共有( )A .3个B .4个C .5个D .6个6.若△ABC 的三边长是a ,b ,c ,且满足44422a b c b c =+-,44422b a c a c =+-,44422c a b a b =+-,则△ABC ( ) A .钝角三角形B .直角三角形C .等腰直角三角形D .等边三角形(“希望杯”邀请赛试题)7.等腰三角形一腰上的高等于该三角形某一条边的长度的一半,则其顶角等于( )A .300B .300或1500C .1200或1500D .300或1200或1500(“希望杯”邀请赛试题)8.如图,已知Rt △ABC 中,∠C =900,∠A =300,在直线BC 或AC 上取一点P ,使得△P AB 是等腰三角形,则符合条件的P 点有( )A .2个B .4个C .6个D .8个(江苏省竞赛试题)ACDB B ′A ′(第2题)AB CDEF (第3题)(第4题)9915第5题图 第8题图 第9题图9.如图在等腰Rt △ABC 中,∠ACB =900,D 为BC 中点,DE ⊥AB ,垂足为E ,过点B 作BF ∥AC 交DE 的延长线于点F ,连接CF 交AD 于G .⑴ 求证:AD ⊥CF ;⑵ 连结AF ,度判断△ACF 的形状,并说明理由.10.如图,△ABC 中,AD ⊥BC 于D ,∠B =2∠C ,求证:AB +BD =CD .(天津市竞赛试题)11.如图,已知△ABC 是等边三角形,E 是AC 延长线上一点,选择一点D ,使得△CDE 是等边三角形,如果M 是线段AD 的中点,N 是线段BE 的中点,求证:△CMN 是等边三角形.(江苏省竞赛试题)12.如图1,Rt △ABC 中,∠ACB =900,CD ⊥AB ,垂足为D ,AF 平分∠CAB ,交CD 于点E ,交CB 于点F .BCABACD EBCADFG E B ACDAC ENMB D⑴ 求证:CE =CF ;⑵ 将图1中的△ADE 沿AB 向右平移到△A ′D ′E 的位置,使点E ′落在BC 边上,其他条件不变,如图2所示,试猜想:BE ′与CF 有怎样的数量关系?请证明你的结论.(山西省中考试题)B 级1.如图,△ABC 中,AD 平分∠BAC ,AB +BD =AC ,则∠B :∠C 的值=__________.2.如图,△ABC 的两边AB 、AC 的垂直平分线分别交BC 于D 、E ,若∠BAC +∠DAE =1500,则∠BAC 的度数是____________.3.在等边△ABC 所在平面内求一点P ,使△P AB 、△PBC 、△P AC 都是等腰三角形,具有这样性质的点P 有_________个.4.如图,在△ABC 中,∠ABC =600,∠ACB =450,AD 、CF 都是高,相交于P ,角平分线BE 分别交AD 、CF 于Q 、S ,则图中的等腰三角形的个数是( )A .2B .3C .4D .55.如图,在五边形ABCDE 中,∠A =∠B =1200,EA =AB =BC =12DC =12DE ,则∠D =( ) A .300B .450C .600D .67.50(“希望杯”竞赛试题)6.如图,∠MAN =160,A 1点在AM 上,在AN 上取一点A 2,使A 2A 1=AA 1,再在AM 上取一点A 3,使A BDFE C图1A B D FEC图2A ′E ′D ′ABC D(第1题)(第2题)ABD E CA BD CEF PQS (第4题)A B CED第5题AA 1NMA 2A 3(第6题)A 3A 2=A 2A 1,如此一直作下去,到不能再作为止,那么作出的最后一点是( )A .A 5B .A 6C .A 7D .A 87.若P 为△ABC 所在平面内一点,且∠APB =∠BPC =∠CP A =1200,则点P 叫作△ABC 的费尔马点,如图1.⑴若点P 为锐角△ABC 的费尔马点,且∠ABC =600,P A =3,PC =4,则PB 的值为_____.⑵如图2,在锐角△ABC 外侧作等边△ACB ′,连结BB ′.求证:BB ′过△ABC 的费尔马点P ,且BB ′=P A +PB +PC .(湖州市中考试题)8.如图,△ABC 中,∠BAC =600,∠ACB =400,P 、Q 分别在BC 、AC 上,并且AP 、BQ 分别是∠BAC 、∠ABC 的角平分线,求证:BQ +AQ =AB +BP .(全国初中数学联赛试题)9.如图,在△ABC 中,AD 是∠BAC 的平分线,M 是BC 的中点,过M 作ME ∥AD 交BA 延长线于E ,交AC 于F ,求证:BE =CF =12(AB +AC ). (重庆市竞赛试题)ABCPACBB ′图1图2ABPQC10.在等边△ABC 的边BC 上任取一点D ,作∠DAE =600,DE 交∠C 的外角平分线于E ,那么△ADE 是什么三角形?证明你的结论.(《学习报》公开赛试题)11.如图,在平面直角坐标系中,O 为坐标原点,直线l :12y x m =-+与x 轴、y 轴的正半轴分别相交于点A 、B ,过点C (-4,-4)作平行于y 轴的直线交AB 于点D ,CD =10.⑴求直线l 的解析式;⑵求证:△ABC 是等腰直角三角形;⑶将直线l 沿y 轴负方向平移,当平移恰当的距离时,直线与x ,y 轴分别相交于点A ′、B ′,在直线CD 上存在点P ,使得△A ′B ′P 是等腰直角三角形,请直接写出所有符合条件的点P 的坐标.(宁波市江东区模拟题)12.如图1,在平面直角坐标系中,△AOB 为等腰直角三角形,A (4,4).ABD MCFE BACO Dyx⑴ 求B 点坐标; ⑵ 如图2,若C 为x 轴正半轴上一动点,以AC 为直角边作等腰直角△ACD ,∠ACD =900,连接OD ,求∠AOD 度数;⑶ 如图3,过点A 作y 轴于E ,F 为x 轴负半轴上一点,G 在EF 的延长线上,以EG 为直角边作等腰Rt △EGH ,过A 作x 轴垂线交EH 于点M ,连接FM ,等式AM FMOF=1是否成立?若成立,请证明;若不成立,说明理由.B AOxyB AOxyC DB AO xyEFGH M 图1 图2图3专题17 等腰三角形的判定例1 延长MF ,BA 交于E ,延长FM 至点P ,使MP =MF ,连BP ,则△BMP ≌△CMF ,∴BP =CF .∵AD 平分∠BAC ,AD ∥FM ,∠BAD =∠DAC =∠MFC =∠AFE =∠E =∠P ,∴AE =AF ,BE =BP ,即AB +AE =AB +AF =AB +AC -CF =CF ,∴CF =12(AB +AC )= 12(7+11)=9.例 2 D例 3 提示:△EMC 为等腰直角三角形,连AM ,易证:△ADE ≌△BAC .∴AD =AB , 又∠DAB =90°.又∵M 为BD 中点,∴AM ⊥DB 且DM =BM =AM . 又∵∠MDE =∠MAC =105°,∴△EDM ≌△CAM . ∴EM =MC ,∠DME =∠AMC , ∴∠DME +∠EMA =∠AMC +∠EMA =90°. ∴△EMC 为等腰直角三角形.例4延长AD 至G ,使DG =AD ,连接BG . 由△ADC ≌△GDB ,得AC =BG ,AC ∥BG . ∵BE =AC ,∴BE =BG ,得∠BED =∠BGD , ∴∠F AE =∠BGD =∠BED =∠AEF , 故AF =EF .例5 提示:结合图1,给出解答过程.由图形的轴对称性知:△ABO ≌△ACO ,∴∠BAO =∠CAO =10°,∴∠ABO =∠ACO =20°,∴∠AOB =∠AOC =150°.又∵BO =BC =CO = AD ,∴△ACD ≌△CAO ,∴∠AOC =∠CDA =150°,故∠BDC =30°.A 级1.90°或75°或15°2.72°3.24.375.D6.D 提示:将三式相加7.D8.C9.⑴先证△ACD ≌△CBF ,∴∠CAD =∠BCF .又∵∠CAD +∠CDG =∠BCF +∠CDG =90°, ∴∠CGD =90°,∴AD ⊥CF . ⑵△ACF 为等腰三角形.10.提示:延长DB 至E ,使BE =AB ,连结AE ,证明∠E =∠C ,AC =AE . 11. 提示:证明△DCA ≌△ECB 、△DCM ≌△ECN ,∠NCM =60°. 12. ⑴提示:先证明∠CEF =∠CFE .⑵作EG ⊥AC 于G ,证明△CEG ≌△BE ´D ´,可得CE = BE ´,又CF =CE ,BE ´=CF .B 级1.2:12.110°3.104.D5.C 提示:在五边形内作等边三角形ABF ,则E 、F 、C 在一条直线上.6.B7. 提示:⑴23 ⑵ 在BB ´上取点P ,使∠BPC =120°,再在PB ´上取点E 使PE =PC ,连结CE . 则由△PCE 为等边三角形,可得:PC =CE ,∠PCE =60°,∠CEB ´=120°∵△ACB ´为正三角形,∴可证:△ACP ≌△B ´CE . ∴∠APC =∠B ´EC =120°,P A =EB ´.ABCGDEF∴∠APC =∠BPC =∠CP A =120°,∴P 为△ABC 的费马点.∴BB ´过△ABC 的P ,且BB ´=EB ´+PB +PE =P A +PB +PC .8. 提示:延长AB 至M ,使BM =BP ,连结PM ,则AB +BP =AM ,可证明BQ =QC .∴AQ +QB =AQ +QC =AC ,又由△AMP ≌△ACP 得AM =AC ,故AB +BP =AQ +BQ .9. 提示:延长FM 至P ,使PM =FM ,连结BP ,则△BMP ≌△CMF ,AE =AF ,BE =BP .10. 提示:当D 为BC 的端点,显见△AED 是等边三角形;当D 为BC 边的中点,取AC 的中点F ,连接DF ,易证△CDF 为等边三角形,又△ADF ≌△EDC ,故△ADE 为等边三角形.猜测:当D 为BC 上任意点时,△ADE 也为等边三角形.11.(1)142y x =-+; (2)过点C 作CH ⊥y 轴于H ,证明△AOB ≌△BHC 即可;(3)符合条件的P 点共有5个,分别为()()()()84,12,4,,4,8,4,4,4,43⎛⎫-------- ⎪⎝⎭. 12.提示:(1)B (8,0);(2)如图a ,过A 作AS ⊥OB 于S ,过D 作DT ⊥x 轴于T .∵△OAB 为等腰直角三角形,∴OS =AS =BS ,再由△ASC ≌△CTD ,可得:AS =CT ,SC =TD .∴CT =AS =OS ,∴OT =CS =TD .∴∠TOD =45°,则∠AOD =90°;(3)等式成立,理由如下:如图b ,在AM 上截取AS =OF ,连ES ,可证△EAS ≌△EOF ,可得:ES =EF ,∠AES =∠OEF∴∠SEF =∠AEO =90°,∴∠FEM =∠SEM =45°.又∵EM =EM ,∴△EFM ≌△ESM ,∴FM =SM ,∴AM =AS +SM =OF +FM ,∴1AM FM OF-=. x y T S A B O D C x y C S F A M H O G E 图a 图b。
初二英语找规律专题训练

初二英语找规律专题训练题目一:请找出下列单词中的规律并填入括号中的选项。
1. apple (A) banana (B) orange (C) peach (D)(规律:水果按字母顺序排列,选项对应字母的顺序)2. cat (A) dog (B) bird (C) elephant (D)(规律:动物按体型大小排列,选项对应体型从小到大的顺序)3. Monday (A) Tuesday (B) Wednesday (C) Thursday (D)(规律:星期按顺序排列,选项对应星期的顺序)题目二:请找出下列数字序列中的规律并填入括号中的选项。
1. 2, 4, 6, 8, (A) (B) (C) (D)(规律:每个数字是前一个数字加上2,选项中的数字应分别加上2)2. 3, 6, 9, 12, (A) (B) (C) (D)(规律:每个数字是前一个数字加上3,选项中的数字应分别加上3)3. 1, 4, 9, 16, (A) (B) (C) (D)(规律:每个数字是前一个数字的平方,选项中的数字应分别进行平方)题目三:请找出下列图形序列中的规律并填入括号中的选项。
1. ▢, ▲, ◯, (A) (B) (C) (D)(规律:图形形状按顺序交替循环,选项中的图形应按循环规律继续)2. △, ▽, △, (A) (B) (C) (D)(规律:图形形状按顺序交替循环,选项中的图形应按循环规律继续)3. ■, ■, ■, (A) (B) (C) (D)(规律:图形形状相同,选项中的图形形状应与之前的相同)题目四:请找出下列词语序列中的规律并填入括号中的选项。
1. north (A) south (B) east (C) (D)(规律:方位词按字母顺序排列,选项中的字母应按顺序填入)2. blue (A) red (B) green (C) (D)(规律:颜色按字母顺序排列,选项中的字母应按顺序填入)3. pen (A) pencil (B) eraser (C) (D)(规律:文具按字母顺序排列,选项中的字母应按顺序填入)题目五:请找出下列数列中的规律并填入括号中的选项。
(完整word版)初二数学找规律专题训练

初二数学找规律专题训练一、填空题1.课本中有这样一句话:“利用勾股定理能够作出,,线段(如图所示).”即:OA=1,过 A 作 AA1⊥OA 且 AA1=1,依据勾股定理,得 OA1=;再过 A1作 A1 A2⊥OA1且 A1A2=1,得 OA2=;以此类推,得OA2017=______ .2.3.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1 12,),第次接着运动到点( 2,0),第 3 次接着运动到点( 3,2),第4 次接着运动到点(4,0),,按这样的运动规律,经过第 2017 次运动后,动点P 的坐标是 ______ .4. 正方形B C O,A B2C C,ABCC按如下图搁置,点 A 、A 、A 在直线y=x+1 上,点 C、A11122133321231 C2、 C3在x 轴上,则A n的坐标是 ______ .5. 在如下图的平面直角坐标系中,△OA1B1是边长为2 的等边三角形,作△B2A2B1成中心对称,再作△B2A3B3与△B2A2B1对于点B2成中心对称,,这样作下去,则与△OA1B1对于点 B1△B2015A2016B2016的顶点 A2016的坐标是______.第 4 题第 5 题6. 在直角坐标系中,直线y=x+2与y轴交于点A1A1B1C1O A2B2C2C1 A3B3C1C2,按如图方式作正方形、、,A 、A 、A 在直线 y=x+2 上,点 C、C 、C 在 x 轴上,图中暗影部分三角形的面积从左到右挨次记123123为 S1、S2、 S3、 S n,则 S n的值为 ______ (用含 n 的代数式表示, n 为正整数).7.在平面直角坐标系中,直线l: y=x-1 与 x 轴交于点 A1,如下图挨次作正方形 A1B1C1O、正方形 A2B2C2C1、、正方形 A n B n C n C n-1,使得点 A1、A2、 A3、在直线 l 上,点 C1、C2、C3、在 y 轴正半轴上,则点 B n的坐标是 ______ .8.察看以下图形:已知 a∥b,在第一个图中,可得∠1+∠2=180 °,则依据以上规律,∠1+ ∠2+∠P1 + +∠P n=______ 度.8.察看以下一组式的变形过程,而后回答以下问题:例1:====-1.例2:=-,=-,=-利用以上结论解答以下问题:(1)= ______(2)应用上边的结论,求以下式子的值.+++ +(3)拓展提升,求以下式子的值.+++ +.9.阅读下边的文字,解答问题.大家知道是无理数,而无理数是无穷不循环小数,所以的小数部分我们不行能所有地写出来,可是因为 1<<2,所以的整数部分为1,将减去其整数部分1,差就是小数部分-1,依据以上的内容,解答下边的问题:(1)的整数部分是 _______,小数部分是 ______;(2)1+的整数部分是_______,小数部分是 ____;(3) 若设 2+的整数部分是x,小数部分是y,求 x-y 的值。
初二生物细胞结构专题训练

初二生物细胞结构专题训练
生物细胞是生命的基本单位,了解细胞结构对于理解生物体的组织和功能十分重要。
以下是初二生物细胞结构的专题训练,帮助你巩固对细胞结构的理解。
1. 选择题
1. 细胞是由许多化合物组成的,其中最主要的化合物是:
- A. 碳水化合物
- B. 脂肪
- C. 蛋白质
- D. 水
2. 下面哪个细胞结构是所有细胞都具有的?
- A. 核
- B. 核膜
- C. 细胞膜
- D. 线粒体
3. 下面哪个细胞结构参与细胞呼吸过程?- A. 叶绿体
- B. 核膜
- C. 细胞壁
- D. 线粒体
4. 构成细胞壁的主要物质是:
- A. 蛋白质
- B. 纤维素
- C. 脂质
- D. 脂肪
5. 下面哪个细胞结构具有消化和分解功能?- A. 核
- B. 核膜
- C. 液泡
- D. 核仁
2. 简答题
1. 描述细胞膜的结构和功能。
2. 什么是核和核膜?它们分别有什么功能?
3. 解释线粒体的结构和作用。
4. 什么是叶绿体?它在细胞中起到什么作用?
5. 解释细胞壁的功能和组成。
3. 论述题
请选取一个你感兴趣的生物细胞结构,论述其重要性和在生物体中的功能。
(请使用更多的细节和科学术语进行论述)
以上是初二生物细胞结构专题训练的内容,希望能够帮助你更好地理解细胞的组成和功能。
加油!。
初二语文找规律专题训练

初二语文找规律专题训练1. 初步了解规律在初二语文研究中,找规律是一个非常重要的能力。
通过找规律,我们可以更好地理解和掌握语文知识。
下面是一些帮助你初步了解规律的训练方法:- 阅读经典文学作品,如《红楼梦》、《西游记》等,观察作品中的人物形象、情节发展等是否存在某种规律。
- 阅读报纸、杂志等现实生活中的文章,分析其中的语言表达、结构特点等是否有一定的规律可循。
2. 句子规律训练句子是语文研究中的基本单位,掌握句子规律对于语文研究至关重要。
下面是一些针对句子规律的训练方法:- 阅读文章时,注意观察句子的主语、谓语、宾语、状语等成分之间的关系和顺序,尝试总结句子结构的规律。
- 比较不同文章中句子的长短、种类等,发现其中的共同点和差异,分析其规律。
3. 篇章规律训练篇章是语文研究中的重要组成部分,掌握篇章规律有助于提高阅读理解和写作水平。
下面是一些有助于训练篇章规律的方法:- 通过阅读不同类型的文章,如议论文、说明文、记叙文等,分析其结构特点和篇章组织方式,总结归纳规律。
- 针对特定的篇章类型,进行阅读理解训练,尝试抓住关键信息、理清结构,找出文章的主旨和论点。
4. 联系实际,应用规律研究规律只有在实际应用中才能发挥作用。
下面是一些将规律应用于实际的训练方法:- 在写作练中,尝试运用所学的规律,如句子结构、篇章组织等,提高文章的逻辑性和连贯性。
- 参与语文竞赛或作文比赛,通过和他人的交流和比较,进一步发现和应用规律。
通过以上的专题训练,你将能够更好地掌握初二语文中的找规律技巧,提高语文学习的效果和水平。
加油!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初二专题训练17—正比例函数
内容指要:(1)正比例函数的概念(2)正比例函数的解析式
1、若正比例函数y=(2-3m)x的图象经过点A(x1,y1)和B(x2,y2),且当x1<x2时,y1>y2,则m的取值范围是()
A、m>0
B、m>2
3
C、m<
2
3
D、m<0
2、正比例函数y=(k2+1)x(k为常数,k≠0)一定经过第_____象限()
A、一、三
B、二、四
C、一、四
D、二、三
3、下列各函数中,y是x的正比例函数的是()
A、y=3x2
B、y=3
x
C、y=
3
x
D、y=
1
1
3
x+
4、y=
28
(3)m
m x-
-是正比例函数,则m的值为()
A、±3
B、3
C、﹣3
D、任意实数
5、已知正比例函数y=(2k-3)x,且y随x的增大而减小,则k的取值范围是()
A、k<
3
2
-、 B、k>
3
2
- C、k>
3
2
D、k<
3
2
6、函数y=
23
(2)m
m x-
-是正比例函数,则m=_______.
7、已知一个正比例函数的图象经过点P(2,﹣3),则它的解析式为__________.
8、若y+2与x+3成正比例,且x=1
2
时,y=5,则y=8时,x=____________.
9、若正比例函数y=kx的图象过点(-3,3
2
),则函数y=(k+1)x的图象过第_____象限.
10、已知正比例函数y=
222
(3)m m
m x--
-的图象过点P(2,a),则a的值为_________.
三、解答题
12、点燃蜡烛,蜡烛的燃烧长度与时间成正比例关系,长为21cm的蜡烛,点燃6分钟后,蜡烛变短了3.6cm,设蜡烛点燃x分钟后变短ycm,求:
(1)、用x表示y的函数关系式;
(2)、自变量x的取值范围;
(3)、此蜡烛点燃后,几分钟烧完?
13、甲、乙两名同学进行登山比赛,图中表示甲同学
和乙同学同时从山脚出发,沿相同路线到达山顶的过
程,各自行进的路程随时间变化的图象,根据图象中
的有关数据回答下列问题。
(1)、分别求出甲、乙两同学登山过程中,路程s(km)
与时间t(h)的函数解析式(不要求写出自变量t的
取值范围);
(2)、当甲到达山顶时,乙行进到山路的某点A处,求点A离山顶的距离。
14.在函数y=-3x的图象上取一点P,过P点作PA⊥x轴,已知P点的横坐标为-•2,求△POA的面积(O为坐标原点).
15、已知函数y=()()1
12-
+
+m
x
m当m取什么值时, y是x的正比例函数。
