系统建模与仿真实验报告
系统建模与仿真实验报告

实验1 Witness仿真软件认识一、实验目的熟悉Witness 的启动;熟悉Witness2006用户界面;熟悉Witness 建模元素;熟悉Witness 建模与仿真过程。
二、实验内容1、运行witness软件,了解软件界面及组成;2、以一个简单流水线实例进行操作。
小部件(widget)要经过称重、冲洗、加工和检测等操作。
执行完每一步操作后小部件通过充当运输工具和缓存器的传送带(conveyer)传送至下一个操作单元。
小部件在经过最后一道工序“检测”以后,脱离本模型系统。
三、实验步骤仿真实例操作:模型元素说明:widget 为加工的小部件名称;weigh、wash、produce、inspect 为四种加工机器,每种机器只有一台;C1、C2、C3 为三条输送链;ship 是系统提供的特殊区域,表示本仿真系统之外的某个地方;操作步骤:1:将所需元素布置在界面:2:更改各元素名称:如;3:编辑各个元素的输入输出规则:4: 运行一周(5 天*8 小时*60 分钟=2400 分钟),得到统计结果。
5:仿真结果及分析:Widget:各机器工作状态统计表:分析:第一台机器效率最高位100%,第二台机器效率次之为79%,第三台和第四台机器效率低下,且空闲时间较多,可考虑加快传送带C2、C3的传送速度以及提高第二台机器的工作效率,以此来提高第三台和第四台机器的工作效率。
6:实验小结:通过本次实验,我对Witness的操作界面及基本操作有了一个初步的掌握,同学会了对于一个简单的流水线生产线进行建模仿真,总体而言,实验非常成功。
实验2 单品种流水线生产计划设计一、实验目的1.理解系统元素route的用法。
2.了解优化器optimization的用法。
3.了解单品种流水线生产计划的设计。
4.找出高生产效率、低临时库存的方案。
二、实验内容某一个车间有5台不同机器,加工一种产品。
该种产品都要求完成7道工序,而每道工序必须在指定的机器上按照事先规定好的工艺顺序进行。
MATLAB Simulink系统建模与仿真 实验报告

MATLAB/Simulink 电力系统建模与仿真实验报告姓名:******专业:电气工程及其自动化班级:*******************学号:*******************实验一无穷大功率电源供电系统三相短路仿真1.1 无穷大功率电源供电系统仿真模型构建运行MATLAB软件,点击Simulink模型构建,根据电路原理图,添加下列模块:(1)无穷大功率电源模块(Three-phase source)(2)三相并联RLC负荷模块(Three-Phase Parallel RLC Load)(3)三相串联RLC支路模块(Three-Phase Series RLC Branch)(4)三相双绕组变压器模块(Three-Phase Transformer (Two Windings))(5)三相电压电流测量模块(Three-Phase V-I Measurement)(6)三相故障设置模块(Three-Phase Fault)(7)示波器模块(Scope)(8)电力系统图形用户界面(Powergui)按电路原理图连接线路得到仿真图如下:1.2 无穷大功率电源供电系统仿真参数设置1.2.1 电源模块设置三相电压110kV,相角0°,频率50Hz,接线方式为中性点接地的Y形接法,电源电阻0.00529Ω,电源电感0.000140H,参数设置如下图:1.2.2 变压器模块变压器模块参数采用标幺值设置,功率20MVA,频率50Hz,一次测采用Y型连接,一次测电压110kV,二次侧采用Y型连接,二次侧电压11kV,经过标幺值折算后的绕组电阻为0.0033,绕组漏感为0.052,励磁电阻为909.09,励磁电感为106.3,参数设置如下图:1.2.3 输电线路模块根据给定参数计算输电线路参数为:电阻8.5Ω,电感0.064L,参数设置如下图:1.2.4 三相电压电流测量模块此模块将在变压器低压侧测量得到的电压、电流信号转变成Simulink信号,相当于电压、电流互感器的作用,勾选“使用标签(Use a label)”以便于示波器观察波形,设置电压标签“Vabc”,电流标签“Iabc”,参数设置如下图:1.2.5 故障设置模块勾选故障相A、B、C,设置短路电阻0.00001Ω,设置0.02s—0.2s发生短路故障,参数设置如下图:1.2.6 示波器模块为了得到仿真结果准确数值,可将示波器模块的“Data History”栏设置为下图所示:1.3 无穷大功率电源供电系统仿真结果及分析得到以上的电力系统参数后,可以首先计算出在变压器低压母线发生三相短路故障时短路电流周期分量幅值和冲击电流的大小,短路电流周期分量的幅值为Im=10.63kA,时间常数Ta=0.0211s,则短路冲击电流为Iim=17.3kA。
系统建模与仿真实验二

实验二 动态系统的Simulink 仿真一、实验目的:1、掌握Simulink 使用的基本方法;2、熟悉连续系统仿真设计的基本方法;二、实验内容:1、编写M 脚本文件编写一个M 脚本文件,绘制函数⎪⎩⎪⎨⎧>+-≤<≤=3,630,0,sin )(x x x x x x x y在区间[-5,5]中的图形。
x=-5:0.1:5; % 设定系统输入范围与仿真步长leng=length(x); % 计算系统输入序列长度for i=1:leng % 计算系统输出序列if x(i)<=0 % 逻辑判断y(i)=sin(x(i));else if (x(i)>0&&x(i)<=3)y(i)=x(i);elsey(i)=-x(i)+6;endendendplot(x,y);grid;2、编写和调用M 函数编写一个M 函数,表示出如下函数关系t=0:0.1:3;leng=length(t);for i=1:lengif t(i)<=1;y(i)=t(i).^2;elsey(i)=t(i).^(1/2);endendplot(t,y);grid;⎪⎩⎪⎨⎧>∈=1,]1 ,0[,212t u t uy并用M脚本文件调用该函数,绘制其在[0,3]区间内的图像。
3.一个生长在罐中的细菌的简单模型。
要求给各模块和信号线改名称、改颜色或增加阴影。
假定细菌的出生率和当前细菌的总数成正比,死亡率和当前的总数的平方成正比。
若以x 代表当前细菌的总数,则细菌的出生率可表示为:_birth=ratebx细菌的死亡率可表示为:2death=rate_px细菌总数的总变化率可表示为出生率与死亡率之差。
因此系统可表示为如下的微分方程形式:2px=x-bx假定h;/5==,当前细菌的总数为1000,建立其simulink模型,.0phb/05并绘制细菌总数变化图。
4.根据种群增长曲线的数学方程进行simulink仿真,并正确设置参数,绘制出种群增长的“J”型曲线和“S”型曲线。
系统建模与仿真实验报告extendsim

系统建模与仿真实验报告院系:管理科学与工程学院专业:质量与可靠性工程班级:1005104学号:100510432姓名:谢纪伟实验目录一.问题描述.二.系统数据.三. 建立过程的简单流程图.四.模型实体设计.五. 建立模型.六.运行模型.七.实验改进.八.结果分析.实验报告一.问题描述.电路板生产商要引入一个新产品,需要适当扩大现有生产线的产能,因此对现有生产线进行研究,经提前分析,发现生产过程存在瓶颈,现在对此生产线进行建模,并通过用extendsim建立的模型所得到的数据对现有生产线进行分析,并通过分析得到解决问题的办法。
二.系统数据.1.根据确定的时间表,5种型号电路板按照固定批量送入生产线中,时间表每隔120min重复一次,如下表所示:电路板种类在...min进入批量电路板种类在...min进入批量1 0 20 5 80 252 20 30 1 120 203 40 25 2 140 304 60 30 ………………进料时间表2.第一步操作是通过一台清洁工作站,每一个电路板需要至少36s,至多54s 的时间,一般情况需要48s。
3.清洁后的电路板装入自动插件机中,这台机器最多能同是处理6个电路板,每个板耗时5min。
4.当完成大部分标准插件的工作,电路板被置于一个10m的传送带上,通过波峰焊接机。
传送带上能放下30个电路板,每分钟移动1米。
5.此外,有三个工作站,用来插件机无法完成的非标准元件。
这个操作的耗时量根据板的种类而不同,如下表:电路板种类处理时间(min)电路板种类处理时间(min)1 2.5 4 3.02 2.0 5 2.03 2.5非标准元件的处理时间6.最后一步是高温加速老化试验,在这个过程中,电路板被组合成24个一组,放入烤箱中,循环通电20min。
三.建立过程的简单流程图电路板清洁自动插件波峰焊非标准插件非标准插件非标准插件高温老化离开四.模型实体设计.模拟电路板到达模拟缓冲器模拟插件机模拟convey item模拟非标准插件机三个物体汇合在一个通道将24个电路板组成一个批量对成批的电路板进行高温老化将成批的电路板还原成单独的电路板将加工后的电路板输出五.建立模型.1.定义全局单位时间.搭建模型从选择合适的全局时间单位开始。
仿真实验报告

仿真实验报告
仿真实验报告
实验目的:
本实验旨在通过仿真模拟的方式进行某个系统的测试和分析,以研究系统在不同条件下的性能和功能。
实验装置:
本实验使用仿真软件搭建模型进行实验。
实验装置包括计算机、仿真软件和仿真模型。
实验步骤:
1. 确定实验目标:根据需求,确定本次实验的目标和要求。
2. 建立仿真模型:根据实验要求和系统特点,使用仿真软件搭建仿真模型。
3. 定义实验参数:根据实验目标,定义所需的实验参数和变量。
4. 运行实验:根据实验设计和定义的参数,运行仿真模型,记录实验结果。
5. 数据分析:根据实验结果,进行数据分析和统计。
6. 结果讨论:根据实验数据和分析结果,进行结果讨论,评估系统的性能和功能。
7. 编写实验报告:根据实验过程和结果,编写实验报告,包括实验目的、实验装置、实验步骤、实验结果和结论等内容。
实验结果:
根据实验数据和分析结果,可以得出系统在不同条件下的性能和功能评估。
结论:
根据实验结果,可以对系统的性能和功能进行评估,在实际应用中为系统的优化和改进提供参考。
实验总结:
通过本次实验,深入了解了系统在不同条件下的性能和功能,为系统的优化和改进提供了依据。
同时,也了解了使用仿真软件进行实验的方法和步骤,为日后的实验工作提供了经验。
控制工程实训课程学习总结基于MATLAB的系统建模与仿真实验报告

控制工程实训课程学习总结基于MATLAB 的系统建模与仿真实验报告摘要:本报告以控制工程实训课程学习为背景,基于MATLAB软件进行系统建模与仿真实验。
通过对实验过程的总结,详细阐述了系统建模与仿真的步骤及关键技巧,并结合实际案例进行了实验验证。
本次实训课程的学习使我深入理解了控制工程的基础理论,并掌握了利用MATLAB进行系统建模与仿真的方法。
1. 引言控制工程是一门应用广泛的学科,具有重要的理论和实践意义。
在控制工程实训课程中,学生通过实验来加深对控制系统的理解,并运用所学知识进行系统建模与仿真。
本次实训课程主要基于MATLAB软件进行,本文将对实验过程进行总结与报告。
2. 系统建模与仿真步骤2.1 确定系统模型在进行系统建模与仿真实验之前,首先需要确定系统的数学模型。
根据实际问题,可以选择线性或非线性模型,并利用控制理论进行建模。
在这个步骤中,需要深入理解系统的特性与工作原理,并将其用数学方程表示出来。
2.2 参数识别与估计参数识别与估计是系统建模的关键,它的准确性直接影响到后续仿真结果的可靠性。
通过实际实验数据,利用系统辨识方法对系统的未知参数进行估计。
在MATLAB中,可以使用系统辨识工具包来进行参数辨识。
2.3 选择仿真方法系统建模与仿真中,需要选择合适的仿真方法。
在部分情况下,可以使用传统的数值积分方法进行仿真;而在其他复杂的系统中,可以采用基于物理原理的仿真方法,如基于有限元法或多体动力学仿真等。
2.4 仿真结果分析仿真结果的分析能够直观地反映系统的动态响应特性。
在仿真过程中,需对系统的稳态误差、动态响应、鲁棒性等进行综合分析与评价。
通过与理论期望值的比较,可以对系统的性能进行评估,并进行进一步的优化设计。
3. 实验案例及仿真验证以PID控制器为例,说明系统建模与仿真的步骤。
首先,根据PID控制器的原理以及被控对象的特性,建立数学模型。
然后,通过实际实验数据对PID参数进行辨识和估计。
建模与仿真实验报告

建模与仿真实验报告建模与仿真实验报告引言建模与仿真是一种常用的方法,用于研究和分析复杂系统的行为。
通过建立数学模型并进行仿真实验,我们可以更好地理解系统的运行机制,预测其未来的发展趋势,并为决策提供依据。
本实验报告将介绍我所进行的建模与仿真实验,以及所得到的结果和结论。
1. 实验目标本次实验的目标是研究一个电动汽车的充电过程,并通过建模与仿真来模拟和分析其充电时间和电池寿命。
2. 实验步骤2.1 建立数学模型首先,我们需要建立一个数学模型来描述电动汽车充电过程。
根据电动汽车的充电特性和电池的充电曲线,我们选择了一个二阶指数函数来表示充电速度和电池容量之间的关系。
通过对历史充电数据的分析,我们确定了模型的参数,并进行了合理的调整和验证。
2.2 仿真实验基于建立的数学模型,我们使用MATLAB软件进行了仿真实验。
通过输入不同的充电时间和初始电池容量,我们可以获得充电过程中电池容量的变化情况,并进一步分析充电时间与电池寿命之间的关系。
3. 实验结果通过多次仿真实验,我们得到了一系列充电时间和电池寿命的数据。
根据这些数据,我们可以绘制出充电时间与电池寿命的关系曲线。
实验结果表明,充电时间与电池寿命呈现出一种非线性的关系,即充电时间的增加并不总是能够延长电池的使用寿命。
4. 结果分析通过对实验结果的分析,我们可以得出以下结论:4.1 充电时间的增加并不总是能够延长电池的使用寿命。
虽然在一定范围内增加充电时间可以提高电池的容量,但过长的充电时间会导致电池内部产生过多的热量,从而缩短电池的寿命。
4.2 充电速度对电池寿命的影响较大。
较快的充电速度会增加电池的热量产生,从而缩短电池的寿命;而较慢的充电速度则可以减少电池的热量产生,延长电池的寿命。
4.3 充电时间和电池寿命之间的关系受到电池类型和充电方式等因素的影响。
不同类型的电池在充电过程中表现出不同的特性,因此在实际应用中需要根据具体情况进行充电策略的选择。
系统建模与仿真实验报告

系统建模与仿真实验报告系统建模与仿真实验报告1. 引言系统建模与仿真是一种重要的工程方法,可以帮助工程师们更好地理解和预测系统的行为。
本实验旨在通过系统建模与仿真的方法,对某个实际系统进行分析和优化。
2. 实验背景本实验选择了一个电梯系统作为研究对象。
电梯系统是现代建筑中必不可少的设备,其运行效率和安全性对于整个建筑物的使用体验至关重要。
通过系统建模与仿真,我们可以探索电梯系统的运行规律,并提出优化方案。
3. 系统建模为了对电梯系统进行建模,我们首先需要确定系统的各个组成部分及其相互关系。
电梯系统通常由电梯、楼层按钮、控制器等组成。
我们可以将电梯系统抽象为一个状态机模型,其中电梯的状态包括运行、停止、开门、关门等,楼层按钮的状态则表示是否有人按下。
4. 仿真实验在建立了电梯系统的模型之后,我们可以通过仿真实验来模拟系统的运行过程。
通过设定不同的参数和初始条件,我们可以观察到系统在不同情况下的行为。
例如,我们可以模拟电梯在高峰期和低峰期的运行情况,并比较它们的效率差异。
5. 仿真结果分析通过对仿真实验结果的分析,我们可以得出一些有价值的结论。
例如,我们可以观察到电梯在高峰期的运行效率较低,这可能是由于大量乘客同时使用电梯导致的。
为了提高电梯系统的运行效率,我们可以考虑增加电梯的数量或者改变乘客的行为规则。
6. 优化方案基于对仿真结果的分析,我们可以提出一些优化方案来改进电梯系统的性能。
例如,我们可以建议在高峰期增加电梯的数量,以减少乘客等待时间。
另外,我们还可以建议在电梯内设置更多的信息显示,以便乘客更好地了解电梯的运行状态。
7. 结论通过本次实验,我们深入了解了系统建模与仿真的方法,并应用于电梯系统的分析和优化。
系统建模与仿真是一种非常有用的工程方法,可以帮助我们更好地理解和改进各种复杂系统。
在未来的工作中,我们可以进一步研究和优化电梯系统,并将系统建模与仿真应用于更多的实际问题中。
8. 致谢在本次实验中,我们受益于老师和同学们的帮助与支持,在此表示诚挚的感谢。
系统建模与仿真实验

系统仿真与建模分析实验实验一生态平衡建模实验系统描述:在一个封闭的海岛上,设有两个群体:1. 狐狸(FOXES);2.啮齿动物(RODENTS情况是:1)狐狸出生后,需要八个月成长为成年狐狸,幼年狐狸每只(每月)要吃10 只啮齿动物,若没有吃的就饿死,幼年狐狸的出生率为4,成年狐狸死亡因素有两个,一是每只狐狸每月要吃60 只啮齿动物,若没有吃的就要饿死,二是从仿真时间算起,十年之后,每月要被猎人打死4 只。
2)啮齿动物RODY出生后,三个月即可长成为成年啮齿动物,啮齿动物的出生率为0.8 ,如果幼年啮齿动物的父母死亡,则以短缺扶养和保护而死亡。
成年啮齿动物每月的死亡率有两个原因决定:一个是被狐狸吃掉,一个原因是总数超过100000(十万)只,则以水草不足而饿死。
一、实验目的:通过此实验了解系统动力学的仿真方法,学会用所学的建模理论来对实际问题进行建模,并对实际问题进行分析。
对此生态平衡系统进行仿真实验,改变不同的控制参数,分析实验的结果,得出系统保持生态平衡的条件,为决策者决策提供理论分析基础。
二.实验原理系统动力学(System Dynamics)是美国麻省理工学院J.W福雷斯特(JayW Forrester教授创立的一门新兴学科。
它按照自身独特的方法论建立系统的动态模型,并借助于计算机进行仿真,以处理行为随时间变化的系统的问题。
系统动力学首先强调系统性的观点,以及联系、发展、运动的观点,是研究复杂系统,诸如:社会、经济、环境、人口、生态平衡、产业发展等的有效工具。
系统动力学的研究对象主要是社会经济系统。
社会经济系统的范围十分广泛,凡是涉及到人类的社会活动和经济活动的系统都属于社会系统。
诸如本文要研究的人口系统、资源系统、环境系统、经济系统、科技系统、能源系统,都属于社会经济系统。
系统动力学的基础是通过实验方法认识系统的行为,为管理决策者提供决策的依据。
系统动力学仿真的基本步骤是:(1)明确建模目的一般来说,系统动力学对社会系统进行仿真实验的主要目的是认识和预测系统的结构和设计最佳参数,为制定合理的政策提供依据。
《工程系统建模》实验报告

《工程系统建模与仿真》实验报告实验一扭摆法测定物体的转动惯量实验名称扭摆法测定物体的转动惯量同组成员学号姓名XXXXXX XXXXXXXXX XXXXXXXXX XXXXXXXXX XXXXXXXXX XXXXXXXXX XXXXXXXXX XXXXXXXXX XXXXXXXXX XXX三、实验器材1)转动惯量测试仪2)数字式电子台秤3)游标卡尺4)扭摆及几种有规则的待测转动惯量的物体:金属载物圆盘、塑料圆柱体、木球、验证转动惯量平行轴定理用的金属细杆,杆上有两块可以自由移动的金属滑块。
四、实验原理转动惯量的测量,一般都是使刚体以一定形式运动,通过表征这种运动特征的物理量与转动惯量的关系,进行转换测量。
本实验使物体作扭转摆动,动周期及其它参数的测定计算出物体的转动惯量。
扭摆的构造如图1-1所示,在垂直轴1上装有一根薄片状的螺旋弹簧以产生恢复力矩。
在轴的上方可以装上各种待测物体以降低摩擦力矩。
3为水平仪,用来调整系统平衡。
将物体在水平面内转过一定角度9后,在弹簧的恢复力矩作用下物体就开始绕垂直轴作周期往返扭转运动。
根据虎克定律,弹簧受扭转而产生的恢复力矩M与所转过的角度9成正比,即:M=-K9 ⑴上式中,K为弹簧的扭转常数。
由转动定律M= I卩得:萨M/I ⑵ 令J2=K/I,忽略轴承的摩擦阻力矩,由式⑴、⑵得:d2K 2dt2I上述方程表示扭摆运动具有角简谐振动的特性,角加速度与角位移成正比,且方向相反。
此方程的解为:9=Acos(3+?)。
式中,A为谐振动的角振幅,©为初相位角,①为角速度,此谐振动的周期由于摆2,用垂直轴与支座间装有轴承,为:T- 2J⑶由式(3)可知,只要实验测得物体扭摆的摆动周期,并在I 和K 中任何一个量已知时即可计算出另一个量。
本实验首先用一个规则几何形状的物体,它的转动惯量可以根据它的质量和 几何尺寸用理论公式直接计算得到,再算出本仪器弹簧的扭转常数 K 值。
(完整版)系统建模与仿真实验报告

实验1 Witness仿真软件认识一、实验目的熟悉Witness 的启动;熟悉Witness2006用户界面;熟悉Witness 建模元素;熟悉Witness 建模与仿真过程。
二、实验内容1、运行witness软件,了解软件界面及组成;2、以一个简单流水线实例进行操作。
小部件(widget)要经过称重、冲洗、加工和检测等操作。
执行完每一步操作后小部件通过充当运输工具和缓存器的传送带(conveyer)传送至下一个操作单元。
小部件在经过最后一道工序“检测”以后,脱离本模型系统。
三、实验步骤仿真实例操作:模型元素说明:widget 为加工的小部件名称;weigh、wash、produce、inspect 为四种加工机器,每种机器只有一台;C1、C2、C3 为三条输送链;ship 是系统提供的特殊区域,表示本仿真系统之外的某个地方;操作步骤:1:将所需元素布置在界面:2:更改各元素名称:如;3:编辑各个元素的输入输出规则:4:运行一周(5 天*8 小时*60 分钟=2400 分钟),得到统计结果。
5:仿真结果及分析:Widget:各机器工作状态统计表:分析:第一台机器效率最高位100%,第二台机器效率次之为79%,第三台和第四台机器效率低下,且空闲时间较多,可考虑加快传送带C2、C3的传送速度以及提高第二台机器的工作效率,以此来提高第三台和第四台机器的工作效率。
6:实验小结:通过本次实验,我对Witness的操作界面及基本操作有了一个初步的掌握,同学会了对于一个简单的流水线生产线进行建模仿真,总体而言,实验非常成功。
实验2 单品种流水线生产计划设计一、实验目的1.理解系统元素route的用法。
2.了解优化器optimization的用法。
3.了解单品种流水线生产计划的设计。
4.找出高生产效率、低临时库存的方案。
二、实验内容某一个车间有5台不同机器,加工一种产品。
该种产品都要求完成7道工序,而每道工序必须在指定的机器上按照事先规定好的工艺顺序进行。
MATLAB Simulink系统建模与仿真 实验报告.

MATLAB/Simulink 电力系统建模与仿真实验报告姓名:******专业:电气工程及其自动化班级:*******************学号:*******************实验一无穷大功率电源供电系统三相短路仿真1.1 无穷大功率电源供电系统仿真模型构建运行MATLAB软件,点击Simulink模型构建,根据电路原理图,添加下列模块:(1)无穷大功率电源模块(Three-phase source)(2)三相并联RLC负荷模块(Three-Phase Parallel RLC Load)(3)三相串联RLC支路模块(Three-Phase Series RLC Branch)(4)三相双绕组变压器模块(Three-Phase Transformer (Two Windings))(5)三相电压电流测量模块(Three-Phase V-I Measurement)(6)三相故障设置模块(Three-Phase Fault)(7)示波器模块(Scope)(8)电力系统图形用户界面(Powergui)按电路原理图连接线路得到仿真图如下:1.2 无穷大功率电源供电系统仿真参数设置1.2.1 电源模块设置三相电压110kV,相角0°,频率50Hz,接线方式为中性点接地的Y形接法,电源电阻0.00529Ω,电源电感0.000140H,参数设置如下图:1.2.2 变压器模块变压器模块参数采用标幺值设置,功率20MVA,频率50Hz,一次测采用Y型连接,一次测电压110kV,二次侧采用Y型连接,二次侧电压11kV,经过标幺值折算后的绕组电阻为0.0033,绕组漏感为0.052,励磁电阻为909.09,励磁电感为106.3,参数设置如下图:1.2.3 输电线路模块根据给定参数计算输电线路参数为:电阻8.5Ω,电感0.064L,参数设置如下图:1.2.4 三相电压电流测量模块此模块将在变压器低压侧测量得到的电压、电流信号转变成Simulink信号,相当于电压、电流互感器的作用,勾选“使用标签(Use a label)”以便于示波器观察波形,设置电压标签“Vabc”,电流标签“Iabc”,参数设置如下图:1.2.5 故障设置模块勾选故障相A、B、C,设置短路电阻0.00001Ω,设置0.02s—0.2s发生短路故障,参数设置如下图:1.2.6 示波器模块为了得到仿真结果准确数值,可将示波器模块的“Data History”栏设置为下图所示:1.3 无穷大功率电源供电系统仿真结果及分析得到以上的电力系统参数后,可以首先计算出在变压器低压母线发生三相短路故障时短路电流周期分量幅值和冲击电流的大小,短路电流周期分量的幅值为Im=10.63kA,时间常数Ta=0.0211s,则短路冲击电流为Iim=17.3kA。
建模仿真实习报告

一、实习背景随着建筑行业的发展,建筑信息模型(BIM)技术逐渐成为我国建筑行业的重要组成部分。
为了提升我的专业技能,了解BIM技术的实际应用,我参加了为期一个月的建模仿真实习。
本次实习旨在通过实际操作,掌握BIM建模的基本流程,熟悉相关软件的使用,并了解BIM技术在建筑工程中的应用。
二、实习内容1. BIM基础知识学习实习初期,我重点学习了BIM的基本概念、发展历程、应用领域以及在我国的发展现状。
通过学习,我了解到BIM技术是一种以三维数字技术为基础,对建设工程项目的设计、施工和运营全过程进行管理和优化的方法。
BIM技术具有可视化、协同性、模拟性、优化性和可出图性等特点,在建筑行业具有广泛的应用前景。
2. BIM建模软件学习在实习过程中,我主要学习了Autodesk Revit软件,该软件是目前应用最广泛的BIM建模软件之一。
通过学习,我掌握了Revit软件的基本操作,包括界面布局、建模命令、族创建、参数化设计等。
同时,我还学习了如何利用Revit软件进行建筑模型的创建、编辑、修改和渲染。
3. BIM建模实践在实习过程中,我参与了实际项目的BIM建模工作。
首先,我根据项目图纸和设计要求,创建了建筑模型的基本框架;然后,我利用Revit软件的族库和参数化设计功能,对建筑模型进行了细化和完善;最后,我根据项目需求,对建筑模型进行了渲染和出图。
4. BIM协同工作在实习过程中,我了解到BIM技术在协同工作中的应用。
通过Revit软件,我们可以实现多专业之间的协同设计,提高设计效率。
同时,BIM技术还可以应用于施工阶段的进度管理、成本控制和资源调配等方面。
三、实习收获1. 提升了专业技能通过本次实习,我掌握了BIM建模的基本流程和Revit软件的使用方法,为今后的工作打下了坚实的基础。
2. 增强了团队协作能力在实习过程中,我与团队成员共同完成了BIM建模任务,提高了自己的团队协作能力。
3. 了解了BIM技术在建筑行业中的应用通过实际操作,我深刻认识到BIM技术在建筑行业中的重要作用,为今后的职业发展指明了方向。
建模与仿真 实验报告

建模与仿真实验报告建模与仿真实验报告一、引言建模与仿真是现代科学研究和工程设计中不可或缺的工具。
通过建立数学模型和进行仿真实验,我们可以更好地理解和预测复杂系统的行为,优化设计方案,降低成本和风险。
本实验旨在通过一个实际案例,介绍建模与仿真的基本原理和应用。
二、案例背景我们选择了一个机械系统的案例,以便更好地说明建模与仿真的过程。
该机械系统是一个简化的汽车悬挂系统,由弹簧和减震器组成。
我们的目标是通过建模和仿真,分析不同参数对系统性能的影响,以优化悬挂系统的设计。
三、建模过程1. 系统分析:首先,我们对悬挂系统进行了详细的分析,了解其工作原理和关键参数。
通过研究相关文献和实际数据,我们确定了弹簧刚度和减震器阻尼系数等参数。
2. 建立数学模型:基于系统分析的结果,我们使用牛顿第二定律建立了数学模型。
假设车辆在垂直方向上的运动可以近似为简谐振动,我们得到了如下的微分方程:m * x''(t) + c * x'(t) + k * x(t) = 0其中,m是车辆的质量,x(t)是车辆在垂直方向上的位移,c是减震器的阻尼系数,k是弹簧的刚度。
3. 参数估计:为了进行仿真实验,我们需要估计模型中的参数值。
通过实验测量和理论计算,我们得到了车辆的质量m,减震器的阻尼系数c和弹簧的刚度k的估计值。
四、仿真实验1. 车辆行驶过程仿真:我们使用Matlab/Simulink软件进行了悬挂系统的仿真实验。
通过设定初始条件和参数值,我们模拟了车辆在不同路况下的行驶过程。
通过分析仿真结果,我们可以得到车辆的位移、速度和加速度等关键性能指标。
2. 参数优化:为了优化悬挂系统的设计,我们进行了参数优化实验。
通过调整减震器的阻尼系数和弹簧的刚度,我们比较了不同参数组合下系统性能的差异。
通过与仿真结果的对比,我们可以选择最佳参数组合,以达到最佳的悬挂系统性能。
五、实验结果与讨论通过仿真实验,我们得到了悬挂系统在不同参数下的性能曲线。
系统建模与仿真实验报告extendsim.

系统建模与仿真实验报告院系:管理科学与工程学院专业:质量与可靠性工程班级:1005104学号:100510432姓名:谢纪伟实验目录一.问题描述.二.系统数据.三. 建立过程的简单流程图.四.模型实体设计.五. 建立模型.六.运行模型.七.实验改进.八.结果分析.实验报告一.问题描述.电路板生产商要引入一个新产品,需要适当扩大现有生产线的产能,因此对现有生产线进行研究,经提前分析,发现生产过程存在瓶颈,现在对此生产线进行建模,并通过用extendsim建立的模型所得到的数据对现有生产线进行分析,并通过分析得到解决问题的办法。
二.系统数据.1.根据确定的时间表,5种型号电路板按照固定批量送入生产线中,时间表每隔120min重复一次,如下表所示:电路板种类在...min进入批量电路板种类在...min进入批量1 0 20 5 80 252 20 30 1 120 203 40 25 2 140 304 60 30 ………………进料时间表2.第一步操作是通过一台清洁工作站,每一个电路板需要至少36s,至多54s 的时间,一般情况需要48s。
3.清洁后的电路板装入自动插件机中,这台机器最多能同是处理6个电路板,每个板耗时5min。
4.当完成大部分标准插件的工作,电路板被置于一个10m的传送带上,通过波峰焊接机。
传送带上能放下30个电路板,每分钟移动1米。
5.此外,有三个工作站,用来插件机无法完成的非标准元件。
这个操作的耗时量根据板的种类而不同,如下表:电路板种类处理时间(min)电路板种类处理时间(min)1 2.5 4 3.02 2.0 5 2.03 2.5非标准元件的处理时间6.最后一步是高温加速老化试验,在这个过程中,电路板被组合成24个一组,放入烤箱中,循环通电20min。
三.建立过程的简单流程图电路板清洁自动插件波峰焊非标准插件非标准插件非标准插件高温老化离开四.模型实体设计.模拟电路板到达模拟缓冲器模拟插件机模拟convey item模拟非标准插件机三个物体汇合在一个通道将24个电路板组成一个批量对成批的电路板进行高温老化将成批的电路板还原成单独的电路板将加工后的电路板输出五.建立模型.1.定义全局单位时间.搭建模型从选择合适的全局时间单位开始。
系统建模与仿真报告
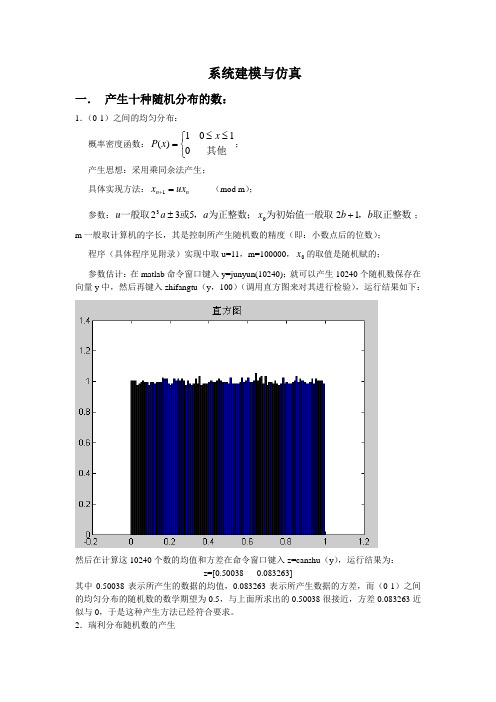
系统建模与仿真一. 产生十种随机分布的数:1.(0-1)之间的均匀分布:概率密度函数:⎩⎨⎧≤≤=其他101)(x x P ;产生思想:采用乘同余法产生; 具体实现方法:n n ux x =+1(mod m );参数:取正整数,为初始值一般取为正整数;,或一般取b b x a a u 1253203+±;m 一般取计算机的字长,其是控制所产生随机数的精度(即:小数点后的位数); 程序(具体程序见附录)实现中取u=11,m=100000,0x 的取值是随机赋的;参数估计:在matlab 命令窗口键入y=junyun(10240);就可以产生10240个随机数保存在向量y 中,然后再键入zhifangtu (y ,100)(调用直方图来对其进行检验),运行结果如下:然后在计算这10240个数的均值和方差在命令窗口键入z=canshu (y ),运行结果为: z=[0.50038 0.083263]其中0.50038表示所产生的数据的均值,0.083263表示所产生数据的方差,而(0-1)之间的均匀分布的随机数的数学期望为0.5,与上面所求出的0.50038很接近,方差0.083263近似与0,于是这种产生方法已经符合要求。
2.瑞利分布随机数的产生概率密度函数:⎪⎩⎪⎨<≥=-000)(222x x ex x P σσ; 产生思想:利用直接抽样法产生;具体实现方法:a .先调用产生(0-1)之间的均匀分布的函数(y=junyun(n))产生一组(0-1)之间均匀分布的随机数保存在向量x 里;b .然后作2ln z y =-;c .另z y σ=,于是向量y 就是要产生的瑞利分布的随机数;参数估计:在matlab 命令窗口键入y=ruili(1,10240);就可以产生10240个随机数保存在向量y 中,然后再键入zhifangtu (y ,100)(调用直方图来对其进行检验),运行结果如下:然后在计算这10240个数的均值和方差在命令窗口键入z=canshu (y ),运行结果为: z=[1.255 0.43138]其中1.255表示所产生的数据的均值,0.43138表示所产生数据的方差,而瑞利分布的数学期望计算式为:12πσσ=其中,代入计算得:1.253,与上面所求出的随机数的平均值1.2555相当接近,瑞利分布方差的计算公式为:224σπ-当1σ=时代入计算得0.42920与0.43138相当接近,于是这种产生方法已经符合要求。
系统建模的仿真实验报告

系统建模的仿真实验报告系统建模的仿真实验报告引言在现代科学与工程领域中,系统建模是一项重要的工作。
通过对系统进行建模,可以帮助我们更好地理解系统的运行原理、优化系统性能以及预测系统的行为。
仿真实验是一种常用的方法,通过模拟系统的运行过程,可以得到系统的各种指标,从而评估系统的性能。
本报告将介绍一个系统建模的仿真实验,并分析实验结果。
一、实验目的本次实验的目的是建立一个模型,模拟一个电梯系统的运行过程,并通过仿真实验来评估该电梯系统的性能。
电梯系统是现代建筑中不可或缺的设施,其运行效率和服务质量直接关系到人们的出行体验。
通过建立模型和仿真实验,我们可以优化电梯系统的设计和运行策略,提高其性能。
二、建模过程1. 系统边界的确定首先,我们需要确定电梯系统的边界。
电梯系统通常包括电梯本身、楼层按钮、电梯控制器等组成部分。
在建模过程中,我们将关注电梯的运行过程和楼层按钮的使用情况。
2. 系统的状态和状态转换接下来,我们需要确定电梯系统的状态和状态转换。
电梯系统的状态可以包括电梯的位置、运行方向、开关门状态等。
状态转换可以根据电梯的运行规则和楼层按钮的使用情况确定。
3. 系统参数的确定在建模过程中,我们还需要确定系统的参数。
电梯系统的参数可以包括电梯的运行速度、电梯的载重量、楼层按钮的响应时间等。
这些参数将直接影响到电梯系统的性能。
三、仿真实验设计基于建立的电梯系统模型,我们设计了一系列的仿真实验,以评估电梯系统的性能。
以下是几个典型的实验设计:1. 不同高峰期的电梯系统性能比较我们选择了不同高峰期的时间段,并模拟了电梯系统在这些时间段内的运行情况。
通过比较不同时间段内电梯的等待时间、运行效率等指标,我们可以评估电梯系统在不同高峰期的性能差异。
2. 不同楼层按钮响应时间的影响我们模拟了不同楼层按钮响应时间的情况,并评估了电梯系统的性能。
通过比较不同响应时间下电梯的等待时间和运行效率,我们可以确定最佳的楼层按钮响应时间。
系统建模与仿真实验报告_冉陈键

实验 4:求
( s 2 2)( s 4)( s 1) 的商及余式。 s3 s 1
实验结果:
3
黑龙江大学电子工程学院《系统建模与仿真实验》指导书
《系统建模与仿真》实验报告二
报告人: 实验题目: 符号计算 实验目的:
1) 2) 3) 掌握反函数的运算、合并同类项、符号表达式的简化; 掌握替换求值、符号的微分 、积分、泰勒展式、留数; 掌握 Laplace 变换及其逆变换。
s s s 6.5 U1 ( s ) 6.5 U 2 ( s ) s 2 s 6.5
2
的 Simulink 结构图,并进行仿真(输入均为单位阶跃函数) 。
7
黑龙江大学电子工程学院《系统建模与仿真实验》指导书
绘制系统的单位阶跃响应和单位脉冲响应。 实验习题 3:已知系统的开环传递函数为 G ( s ) 和奈奎斯特图 5( s 2 5s 6) 实验习题 4:已知系统的传递函数为 G ( s ) 6 ,试判 s 2s 5 8s 4 12 s 3 20s 2 16s 16 断系统的稳定性。
B A. ^ 2 C A^2
4 2 0 2 4 实验 2:找出数组 A 中所有绝对值大于 3 的元素,并在 A 中将其 3 1 1 3 5 换成 0。 实验 3:建立方阵A 1 2 3 2 2 3 9 7 5 1)计算其行列式和逆矩阵; 2)计算其特征值和特征向量。
《系统建模与仿真》实验报告六
报告人: 实验题目: 实验目的:
用 Matlab 作图 Bernoulli―Gaussian 白噪声、对一阶自回归模型、状态空间模型分别绘图。
专业: 模型建立
学 号:
系统模拟实验报告

系统模拟实验报告1. 实验目的本实验的目的是通过系统模拟的方法,对某一特定系统进行分析和研究,并获取系统的性能指标。
通过模拟,我们可以更好地了解系统的工作原理和行为特点,并进行系统的改进和优化。
2. 实验原理与方法2.1 实验原理系统模拟是利用计算机对实际系统进行建模,并通过数学方法进行仿真以推测其行为。
系统模拟实验是为了填补实际测试困难或高成本的需求,以更低的代价快速获取系统性能参数。
2.2 实验方法本实验中,我们选择了一种传统的生产线系统进行模拟。
首先,我们建立了一个生产线模型,定义了各个模块的输入、输出和相互关系。
然后,我们根据实际数据和相关的数学模型来设置模块的参数。
在模拟实验过程中,我们不断调整输入参数,并观察系统的输出行为。
通过对多个参数进行组合测试,我们可以研究不同参数对系统性能的影响,并找到系统的瓶颈和改进方向。
3. 实验步骤与结果3.1 实验步骤在本次实验中,我们认为整个生产线系统可以分为3个模块:原料处理、加工生产和成品包装。
我们首先建立了一个基本模型,然后对每个模块进行了详细规划。
在原料处理模块中,我们设置了原料输入速度、质量控制参数等。
在加工生产模块中,我们设置了每台设备的加工速度和故障概率等参数。
在成品包装模块中,我们设置了包装速度以及包装质量控制等。
3.2 实验结果经过一系列的模拟实验,我们得到了以下结果:1. 原料处理模块中,原料的输入速度对整个系统的生产效率有较大影响。
当输入速度过高时,容易造成设备堵塞现象;当输入速度过低时,容易造成设备闲置。
通过对输入速度的调整,我们找到了一个合适的输入速度范围。
2. 在加工生产模块中,设备的故障概率对系统的正常运行时间有较大影响。
我们发现,当设备故障概率较高时,整个系统的平均正常运行时间显著降低。
通过优化设备维护和改进设备结构,我们可以有效提高系统的可靠性。
3. 在成品包装模块中,包装速度对整个系统的生产效率和包装质量有较大影响。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
上机作业一P111第十题对时间延迟e^-2s用函数pade( )进行三阶近似>>G=tf([12],[1,3,3,1,0]);Gc=tf([2,3],[1,0]);>> tau=2;[n1,d1]=pade(tau,3);G1=tf(n1,d1)Transfer function:-s^3 + 6 s^2 - 15 s + 15------------------------s^3 + 6 s^2 + 15 s + 15>> T=feedback(G1*G*Gc,1)Transfer function:-24 s^4 + 108 s^3 - 144 s^2 - 180 s + 540------------------------------------------------------------------------s^8 + 9 s^7 + 36 s^6 + 79 s^5 + 72 s^4 + 168 s^3 - 129 s^2 - 180 s + 540P112第二十题>> A=[-9,-26,-24,0;1,0,0,0;0,1,0,0;0,1,1,-1];B=[1;0;0;0];C=[0,1,1,2];D=zeros(1); >> G=ss(A,B,C,D);G1=minreal(G)2 states removed.a =x1 x2x1 -7.027 -1.708x2 8.907 1.027b =u1x1 0.2429x2 -0.2461c =x1 x2y1 1.669 1.647d =u1y1 0Continuous-time model.>> G2=tf(G);zpk(G2)Zero/pole/gain:(s+3) (s+1)-----------------------(s+4) (s+3) (s+2) (s+1)G2中的零极点-3,-1并未完全抵消,所以并非最小实现。
P102例题3-33>>u=[0.4398,0.3400,0.3142,0.3651,0.3932,0.5915,0.1197,0.03813,0.4586,0.8699,0.9342,0.2644,0 .1603,0.8729,0.2379,0.6458,0.9669,0.6649,0.8704,0.009927,0.137,0.8188,0.4302,0.8903,0.7349,0 .6973,0.3461,0.166,0.1556,0.1911,0.4225,0.856,0.4902,0.8159,0.4608,0.4574,0.4507,0.4122,0.90 16,0.005584,0.2974,0.04916,0.6932,0.6501,0.983,0.5527,0.4001,0.1988]';y=[0 0.1374 0.2978 0.4886 0.7238 0.9934 1.3430 1.5759 1.7425 1.9793 2.3299 2.7339 2.96503.1091 3.4020 3.5085 3.6735 3.92144.0990 4.3271 4.2963 4.2053 4.2444 4.1705 4.2082 4.23024.2561 4.1900 4.0395 3.8353 3.5940 3.3884 3.3211 3.2067 3.2221 3.1971 3.1945 3.2071 3.2171 3.3789 3.3148 3.2787 3.1353 3.1341 3.1458 3.2882 3.3669 3.4131]';>> t1=arx([y,u],[4,4,1])Discrete-time IDPOL Y model: A(q)y(t) = B(q)u(t) + e(t)A(q) = 1 - 2.696 q^-1 + 2.574 q^-2 - 0.9603 q^-3 + 0.09228 q^-4B(q) = 0.312 q^-1 - 0.4067 q^-2 + 0.1806 q^-3 - 0.01402 q^-4Estimated using ARXLoss function 7.66547e-007 and FPE 1.02206e-006Sampling interval: 1>> identOpening System Identification Tool>> U=iddata(y,u,0.1); T=arx(U,[4,4,1]);H=tf(T);G=H(1);t=0:0.1:0.1*(length(u)-1); lsim(G ,u,t);hold on;plot(t,y,'o')T o : y 1Linear Simulation ResultsTime (sec)A m p l i t u d e上机作业二1.>> A=[0,1;-2,-3];B=[1,0;1,1];C=[2,1;1,1;-2,-1];D=[3,0;0,0;0,1];G1=ss(A,B,C,D);G=tf(G1)Transfer function from input 1 to output...3 s^2 + 12 s + 12#1: -----------------s^2 + 3 s + 22 s + 2#2: -------------s^2 + 3 s + 2-3 s - 6#3: -------------s^2 + 3 s + 2Transfer function from input 2 to output...s + 2#1: -------------s^2 + 3 s + 2s + 1#2: -------------s^2 + 3 s + 2s^2 + 2 s#3: -------------s^2 + 3 s + 22.>>A=[0,1,0;0,0,1;-6,-11,-6];B=[0;0;1];C=[0,0,0];D=[0];>>G1=ss(A,B,C,D);T=[1,1,1;-1,-2,-3;1,4,9];>>G2=ss2ss(G1,T)a =x1 x2 x3x1 7 17.5 4.5x2 -26 -59 -15x3 82 182 46u1x1 1x2 -3x3 9c =x1 x2 x3y1 0 0 0d =u1y1 0Continuous-time model.>> eig(G1)ans =-1.0000-2.0000-3.0000>> eig(G2)ans =-3.0000-1.0000-2.0000>>3.>>A=[-2,2,-1;0,-2,0;1,-4,0];B=[0,1;0,0;1,0];C=[1,0,0;0,1,0];D=zeros(2);Tc=ctrb(A,B)Tc =0 1 -1 -2 2 30 0 0 0 0 01 0 0 1 -1 -2>> rank(Tc)ans =2>> Tb=obsv(A,C)Tb =1 0 00 1 0-2 2 -10 -2 03 -4 20 4 0>> rank(Tb)ans =3Tc的秩为2<3,所以系统不可控;Tb的秩为3=3所以系统可观;综上系统不可控但可观测。
4.A=[1,1,1;0,1,0;1,1,1];B=[0,1;1,0;0,1];C=[1,0,1];D=0; [Ac,Bc,Cc,Tc]=ctrbf(A,B,C)Ac =0 0 00 1.0000 00 -1.4142 2.0000Bc =0 0-1.0000 00 1.4142Cc =0 0 1.4142 Tc =-0.7071 0 0.7071 0 -1.0000 0 0.7071 0 0.7071 >>上机作业三2.G=tf(10,[1,2,10])Transfer function: 10 -------------- s^2 + 2 s + 10>> step(G)Step ResponseTime (sec)A m p l i t u d e01234560.20.40.60.811.21.4>>num=[10]; for zeta=[1,2];den=[1,2*zeta*sqrt(10),10]G=tf(num,den)step(G);hold on;endden =1.0000 6.3246 10.0000Transfer function:10------------------s^2 + 6.325 s + 10den =1.0000 12.6491 10.0000Transfer function:10------------------s^2 + 12.65 s + 100123456789Time (sec)A .系统有零点S=-5的情况 >>f1=figure;f2=figure; den=[1,2,10]; num1=[10]; num2=[2,10];figure(f1);G1=tf(num1,den);step(G1); hold on;figure(f2);G2=tf(num2,den);step(G2) hold on;Time (sec)A m p l i t u d e01234560.511.5增加一个零点对系统的影响:系统的超调量由34.7%增大到43.2%,阶跃响应速度变快,Ts 由3.45减小为3.36。
Time (sec)A m p l i t u d e01234560.20.40.60.811.21.4B .分子分母多项式阶数相等的情况 >>f1=figure;f2=figure; den=[1,2,10]; num1=[10];num2=[1,0.5,10];figure(f1);G1=tf(num1,den);step(G1); hold on;figure(f2);G2=tf(num2,den);step(G2) hold onTime (sec)A m p l i t u d e01234567分子分母阶数相同时对系统的影响:从图中可以看出会使系统的阶跃产生一个反方向的超调 0.69,同时系统的调整时间增大到3.95s 系统响应速度变慢。
Time (sec)A m p l i t u d e012345600.20.40.60.811.21.4C .分子多项式零次项系数为零的情况 >>f1=figure;f2=figure; den=[1,2,10]; num1=[10];num2=[1,0.5,0];figure(f1);G1=tf(num1,den);step(G1); hold on;figure(f2);G2=tf(num2,den);step(G2) hold onTime (sec)A m p l i t u d e0123456分子多项式的零次项系数为零时:系统阶跃响应的终值减小为0,调整时间增加为3.4,超调量为inf ,系统稳定性减弱。
