流体力学与应用-2
流体力学第二章参考答案

流体力学第二章参考答案第二章 流体静力学2-1 将盛有液体的U 形小玻璃管装在作水平加速运动的汽车上(如图示),已知L =30 cm ,h =5cm ,试求汽车的加速度a 。
解:将坐标原点放在U 形玻璃管底部的中心。
Z 轴垂直向上,x 轴与加速度的方向一致,则玻璃管装在作水平运动的汽车上时,单位质量液体的质量力和液体的加速度分量分别为0,0,,0,0x y z x y z g g g ga a a a ===-===代入压力全微分公式得d (d d )p a x g z ρ=-+ 因为自由液面是等压面,即d 0p =,所以自由液面的微分式为d d a x g z =- 积分的:a z x c g=-+,斜率为a g -,即a g h L = 解得21.63m/s 6g a g h L ===2-2 一封闭水箱如图示,金属测压计测得的压强值为p =4.9kPa(相对压强),测压计中心比A 点高z =0.5m ,而A 点在液面以下h =1.5m 。
求液面的绝对压强和相对压强。
解:由0p gh p gz ρρ+=+得相对压强为30() 4.91010009.81 4.9kPa p p g z h ρ=+-=⨯-⨯⨯=-绝对压强0( 4.998)kPa=93.1kPa abs a p p p =+=-+2-3 在装满水的锥台形容器盖上,加一力F =4kN 。
容器的尺寸如图示,D =2m ,d =l m ,h =2m 。
试求(1)A 、B 、A ’、B ’各点的相对压强;(2)容器底面上的总压力。
解:(1)02 5.06kPa 4F F p D A π===,由0p p gh ρ=+得:0 5.06kPa A B p p p ===''0 5.06kPa+10009.82Pa 24.7kPa A B p p p gh ρ==+=⨯⨯=(2) 容器底面上的总压力为2'24.7kPa 77.6kN 4A D P p A π==⨯=2-4 一封闭容器水面的绝对压强p 0=85kPa ,中间玻璃管两端开口,当既无空气通过玻璃管进入容器、又无水进人玻璃管时,试求玻璃管应该伸入水面下的深度h 。
流体力学实验 (2)

流体力学实验
流体力学实验是研究流体运动、流体性质和流体力学现象的实验方法和实验技术。
在流体力学实验中,通常会使用各种仪器设备和测量装置来观测、记录和分析流体的运动状态、流速、压力、温度等重要参数。
流体力学实验的目的可以是验证理论模型、研究流体流动的规律、探究流体与固体的相互作用等。
以下是一些常见的流体力学实验:
1. 流体的静力学实验:通过测量流体中的压力分布,来研究流体静力学的规律,常用的实验方法有水压实验和气压实验。
2. 流体的动力学实验:研究流体运动的规律,常见的实验包括流体的流速测量、流体的流线观测、流体的密度测量等。
3. 流体的粘性实验:用来研究流体粘性特性的实验方法,通常会测量流体的粘度和黏滞阻力。
4. 流体与固体相互作用的实验:研究流体在固体表面上的附着和流动的实验,如流体在管道中的摩擦阻力实验、流体在物体表面的湿润实验等。
5. 流体流动模拟实验:通过模拟实验方法来研究流体流动的现象和规律,常见的方法有模型试验和数值模拟。
流体力学实验通常需要使用精密的仪器设备和仔细的实验操作,以确保实验结果的准确性和可靠性。
实验结果可以为理论研究提供验证和支持,也可以为工程应用提供参考和指导。
流体力学三版第2章课后答案

第一章 流体的基本概念1-1 单位换算:1.海水的密度ρ=1028公斤/米3,以达因/厘米3,牛/米3为单位,表示此海水的重度γ值。
解:2.酒精在0℃时的比重为0.807,其密度ρ为若干公斤/米3 ? 若干克/厘米3 ? 其重度γ为若干达因/厘米3 ? 若干牛/米3 ? 解:l-2 粘度的换算:1.石油在50℃时的重度γ=900达因/厘米3,动力粘度μ=58.86×10-4牛.秒/米2。
求此石油的运动粘性系数ν。
解:2.某种液体的比重为1.046,动力粘性系数μ=1.85厘泊,其运动粘性系数为若干斯? 解:3.求在1大气压下,35℃时空气的动力粘性系数μ及运动粘性系3323333w /8.790/7908/8.9/807 0.807g/cm 807kg/m 1000kg/m cm dy m N s m m kg ==⨯===⨯γ酒精√sm s cm cmdy s cm cm s dy g /104.6/1064 /900/)/980101086.58( 26233224--⨯=⨯=⨯⋅⨯==∴γμν)(/017686.0 /1046.1/1085.1 232w 斯比重s cm cmg cm s g =⨯⋅⨯=⨯=∴-ρμν33235/44.1007/4.10074/8.9/1028 101 ; cm dy m N s m m kg dyN g ==⨯=∴==γργ数ν之值。
解:1-3 相距10毫米的两块相互平行的板子,水平放置,板间充满20℃的蓖麻油(动力粘度μ=9.72泊)。
下板固定不动,上板以1.5米/秒的速度移动,问在油中的切应力τ是多少牛/米2? 解:1-4 直径为150毫米的圆柱,固定不动。
内径为151.24毫米的圆筒,同心地套在圆柱之外。
二者的长度均为250毫米。
柱面与筒内壁之间的空隙充以甘油。
转动外筒,每分钟100转,测得转矩为9.091牛米。
假设空隙中甘油的速度按线性分布,也不考虑末端效应。
《流体力学》第二章流体静力学

p z C g
pa 4 3 真空 1
p2 g
p=0
z1
z3
2
z=0
p 为压强水头 g
z 为位置水头
2.3 重力场中的平衡流体 重要结论
p p0 gh
(1) 在重力作用下的静止液体中,静压强随深度按线性 规律变化,即随深度的增加,静压强值成正比增大。 (2)在静止液体中,任意一点的静压强由两部分组成: 一部分是自由液面上的压强P0;另一部分是该点到自由 液面的单位面积上的液柱重量ρgh。 (3)在静止液体中,位于同一深度(h=常数)的各点的静 压强相等,即任一水平面都是等压面。
2.2 流体平衡微分方程 一、欧拉平衡方程
p dx 1 p dx 1 p dx p 2 3 x 2 2 x 2 6 x 2
2 3
2
3
p dx 1 p dx 1 p dx p 2 3 x 2 2 x 2 6 x 2
dA dA n
dF pdAn
F pdAn
A
流体静压力:作用在某一面积上的总压力; (矢量) 流体静压强:作用在某一面积上的平均压强或某一点的 (标量) 没有方向性 压强。
2.1 平衡流体上的作用力 证明:
z A
pn px
微元四面体受力分析
py
dx C x
dz O dy B y
y
p x p y p z pn
C x
pz
f
↑
z
表 面 力 质 量 力
1 d yd z 2 1 Py p y d zd x 2 1 P p d yd x z z 2 P n pn d A P x px
流体力学-第2章

流体静压强是空间点坐标的标量函数 说明: 1) 静止流体中不同点的压强一般是不等的,同一点的各向静 压强大小相等。 2) 运动状态下的实际流体,流体层间若有相对运动,则由于 粘性会产生切应力,这时同一点上各向法应力不再相等。 流体力学
§2.2
流体平衡微分方程
• 流体平衡微分方程的推导
p ρ= R T
T =T0 − βz
z 5.256 ⇒ p =101.3(1− ) kPa 44300
(2)同温层压强的分布 流体力学 见 P23
三、压强的度量 1、压强的两种计算基准 绝对压强pabs:以无气体分子存在的完全真空为零点起算的压强 相对压强p:以当地同高程的大气压强pa为零点起算的压强 p= pabs - pa • 正压 负压 真空度pv pv= -p = pa - pabs
流体力学
例 2-5 封 闭 水 箱 如 图 , 水 箱 顶 面 安 装 的 压 力 表 读 值 为 p0=10kN/m2,水箱内水深 h =3m,当地大气压pa=98kN/m2。求 水面下2m处的绝对压强和相对压强。 解:
p = p0 + γh = 10 + 9.8 × 2 = 29.6 kPa
p0 3m A 封闭水箱
(2)质量力
ρ dxdydz
X ρ dxdydz
Y ρ dxdydz
Z ρ dxdydz
流体力学
x 方向平衡微分方程
∂p dx ∂p dx (p− ) dydz − ( p + ) dydz + X ρ dxdydz = 0 ∂x 2 ∂x 2
1 ∂p X− =0 ρ ∂x
流体力学
1 ∂p X− =0 ρ ∂x
流体力学教案第2章流体静力学

第二章 流体静力学§2-1作用在流体上的力、表面力、质量力在运动的实际流体中任取一块流体,其体积为V ,表面积为A ,在这块流体上任取一微元面积δA ,作用在其表面上的力为δF ,分解为⎩⎨⎧切向力法向力τδδF F n ,则法向力: AF p A δδδn 0lim →= (N/m 2)切向力:AF A δδτδτ0lim →= (N/m 2)在这块流体上,取一流体微团,其体积为δV,由于地球引力的作用,产生的重力为ρg δV 。
由于流体存在加速度a,根据达朗贝尔原理,虚加的惯性力为-ρδVa。
所以,流体所受的力为:⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧惯性力重力或体积力质量力一般情况不考虑和表面张力摩擦力切向应力压力法向应力表面力)()()()(στP 表面力―是指作用在流体中的所取某部份流体体积表面上的力,也就是该部分体积周围的流体(既可是同一种类的流体,也可是不同种类的流体)或固体通过接触面作用在其上的力。
质量力―是指作用在流体内部所有流体质点上并与流体的体积或质量成正比的力,又称体积力。
通常,单位质量流体的质量力用→f 表示,在笛卡尔直面坐标系中:k j i zyxf f f f →→→→++=流体静力学―研究流体处于静止状态时各种物理量的分布规律及在工程实际中的应用。
所谓流体的静止状态是指流体对选用的坐标系无相对运动的状态。
δF§2-2流体的静压强及其特性在静止的流体中,任取一块流体。
当δA →0时,p 就定义为空间某点的静压强:AP p A δδδlim→=静压强的两个特性:① 流体静压强指向作用面的内法线方向。
② 流体中任意点静压强的大小只是位置的函数,即p=f (x ,y ,z )与其作用面的方向无关,又称作静压强各向同性。
证①:流体中任意点所受的力均可分为切应力和压应力。
因总体静止,0d d =yu, 故切应力0=τ,所以,只存在法向应力,当然垂直于作用面。
又:流体在拉力作用下,要发生运动,因为静止,故只存在压应力。
流体力学课件2-2

四. 压强的度量单位
• 定义式: (N/m2 ; Pa)
1公斤力/米2 = 9.8 N/m2
• 液柱高度:
h = P/γ
(m)
• 大气压:
1标准物理大气压(atm)=1.033公斤力/厘米2=101325帕 1工程大气压(at)=98000帕=10mH20=735.6mmHg
• 大气压与大气压强:
面打孔,接出一端开口与大气相通的玻璃管,即为测压管。
测压管内的静止液面上
p = 0 ,其液面高程即为
pA /
测点处的 z p ,所以
pB /
叫测压管水头。
zA
zB
O
O
• 测静压只须一根测压管
如果容器内的液体是静
止的,一根测压管测得
的测压管水头也就是容
器内液体中任何一点的
pA /
测压管水头。如接上多
O
A
A点相 对压强
A点绝
B
对压强
相对压强基准 B点真空压强
B点绝对压强
绝对压强基准
O
• 今后讨论压强一般指
相对压强,省略下标, 记为 p,若指绝对压强 则特别注明。
压强
大气压强 pa
O
A
A点相 对压强
A点绝
B
对压强
相对压强基准 B点真空压强
B点绝对压强
绝对压强基准
O
方程的物理意义:
三. 位置水头、压强水头、测压管水头
X 0;Y 0; Z g
代入压力差公式
dp (Xdx Ydy Zdz)
积分得: p gz C '
积分常数根据液体自由表面上的边界条件确定:
z z0 ; p p0
C' p0 gz0
流体力学-第二章 基本方程

h
0
xy
z
经流体柱后侧流入的流体质量应为:
流入质量=
h
0
uy
z
同时,经流体柱前侧流出的质量为:
z
流出质量=
h
0
uy
z
x
h
0
uy
z
x
O
x u u x
x
y
u
h y
x
Chen Haishan NIM NUIST
流出质量减去流入质量 =柱体内质量的减少。
柱体内的净流出量
(流入质量减去流出质量 =柱体内质量的增加)
pnx nx pxx ny pyx nz pzx
pny nx pxy ny pyy nz pzy
pnz
nx pxz
ny pyz
nz pzz
Chen Haishan
NIM NUIST
z
pzz
z
pzx
pz pzy
pxz
px
pxx
pxy
pyy
pyx
py
P Pnz n
Pny
y Pnx o
Chen Haishan NIM NUIST
通过体积分,作用于体积为 的流体块上的质量力:
Fd =作用于流体的质量力
Chen Haishan NIM NUIST
② 表面力
表面力:是指流体内部之间或者流体与其他物体之 间的接触面上所受到的相互作用力。
如流体内部的粘性应力和压力、流体与固体接触面 上的摩擦力等。
x y
n n
cosn, cosn,
x y
nxn n y n
z n cosn, z nzn
Chen Haishan NIM NUIST
流体力学-习题2

2-36 如图所示,用倾斜式微压计测量烟道中烟气的真空度,已 知测量管的倾角α=30o。微压计所用工作液体酒精的密度ρ =800 kg/m3,测量管读值n =200mm,当地大气压pa =0.1MPa 。试求 该测点烟气的真空度和绝对压强。 解:
解:
p0 p表 g (h1 h2 )
4900 1000 9.8 (1.5 0.4) 5880Pa
2-22
解: (1)
p pC gH 1 9.8 12 117.6 kPa
(2)
pB g ( H h) 1 9.8 10.2 99.96 kPa
解: 先求水作用在平板上的总压力
F ghC bl 9.8 2 1 2 39.2 kN
再求作用点
hC 2 yC 2 2 2.828 m sin sin 45
bl I xC l2 yD yC 0.118m yC A yC bl 12yC
1 12
2
3
解: 先求水平分力
再求竖向分力
h1 h2 Fx pC A g b(h1 h2 ) 2 22 9. 8 1 (2 2) 78.4 kN 2
h1 (h1 h2 ) Fz gV g bh2 c tan 2 6 9.8 1 2 1 58.8 kN 2 Fz 3 2 2 F Fx Fz 98 kN tan Fx 4
T Fz上 49.55 kN
2-19 如图所示,水管A、B两点高差h1 =0.2m,U形压差计中水 银液面高差h2 =0.2m 。试求A、B两点的压强差。
解:
A
h1
pA 水 g (h1 x h2 ) pB 水 gx 水银 gh2
工程流体力学演示习题-2
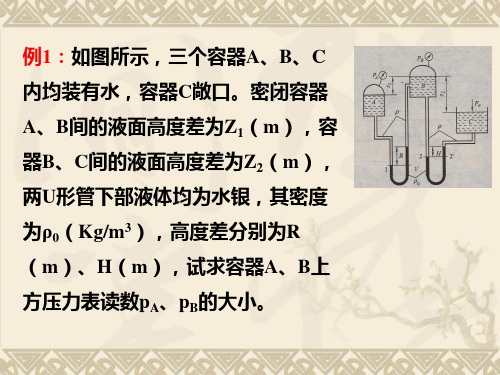
2’,显然面1-1’、2-2’均为等压
面,即:
p1 p1'
p2 p2'
再根据静力学原理,得:
pB 表 gZ2 H pa 0gH
于是
pB 表 pa 0gH gZ2 H
(Pa)
由此可知,容器壁上方的真空表读数为pB(Pa)。
同理,根据 p1 p1' 及静力学原理,得:
pA 表 gR pB 表 gZ1 0 gR
z0
p0
v02 2g
z
p
v2 2g
(1)
液面速度取为零v0=0,液面和孔口均为大气压强 p0=p=0(表压),由(1)式可得:
v 2gz0 z 2gh (2)
解析:(2)式也适用于平行于液面的狭缝出流, 形式上与初始速度为零的自由落体运动一样,这是 不考虑流体粘性损失的结果,液面上流体质元具有 的位能全部转化为小孔出流的动能。
解:在两个水池自由表面间列伯努利方程,
高表面为1-1过水断面,底表面为2-2过水
断面,基准线为管线2的管轴中线。
Z1
p1
1V12
2g
Z2
p2
2V22
2g
hf
(1)
由题意:Z1-Z2=H 1 2 1 V1=V2≈0
所以由(1)式可得:
H h f (2)
由串并联管路特性可知:
h f h f 4 h f 1 h f 5 (3)
解:
设: Hg Hg g
水 水g
酒精 酒精g
取等压面1-1、2-2、3-3,得下列关系式
p1 pA 水 h h1
p2 p1 Hg h1 p A 水 h h1 Hgh1
p3 p2 Hg h2 p A 水 h h1 Hg h1 酒精h1
流体力学习题2

流体力学习题一、判断题:1.由绝热流动的能量方程可知,当没有热交换时,单位质量流体所具有的总能量是一个常数。
()2.当流体与外界有热交换时,这个总能量会增加或减少,这时滞止温度不再是常数,流动是等熵的。
()3.当马赫数小于一时,在等截面管道中亚音速流动作加速流动。
超音速流动作减速流动。
()4.在绝热摩擦管流中,亚音速只能加速至M=1,超音速只能减速至M=1。
()5.从有热交换的能量方程可以看出,对于加热流动dq大于0,亚音速流作加速运动。
()6.对于冷却流动dq小于0,亚音速流作减速运动,超音速流作加速运动。
(T)7.气体的比热由气体本身的性质决定的,所以对某一种气体来说,比热是常数。
()8.液体都具有可压缩性。
()9.一般情况下,液体的压缩性很小,可视为不可压缩流体,只有在水击现象中才考虑流体的压缩性。
()10.如果气体流速很大超过音速的三分之一,可以忽略其压缩性。
()11.不同的加热过程,气体具有不同的比热。
()12.在绝热的可逆过程中,熵将不发生变化。
()13.气体作绝热的且没有摩擦损失的流动时,称为等熵流动。
()14.音波的传播是一个等温过程。
()15.液体的压缩性很小,可视为不可压缩流体。
()16.在可压缩流体中,如果某处产生一个微弱的局部压力扰动,这个和扰动将以波面的形式在流体内播,其传播的速度等于声音的速度。
()17.陆上的交通车辆如果以超音速行驶,路上的行人将听不到疾驶过来的车辆的鸣笛声。
(T)18.在超音速流动中,扰动只能在马赫锥内传播。
()19.亚音速流动在收缩管内不可能加速到超音速。
()20.背压和管道出口压强永远是相等的。
()二、填空题1.一般地说,压强和温度的变化都会引起液体的改变。
2.热力学第一定律是热现象的能量转换及定律。
3.在绝热流动中,单位质量的流体所具有的与之和是一个常数。
4.在可压缩流体中,如果产生一个微弱的局部压力扰动,这个压力扰动将以波面的形式在流体内传播,其传播速度称为。
流体力学-第二章

二、解析法 求解作用在任意平面上的液体总压力
二、解析法 求解作用在任意平面上的液体总压力 作用在dA面积上的液体总压力为 作用在 面积上的液体总压力为 作用在整个受压平面面积为A上的液体总压力为 作用在整个受压平面面积为 上的液体总压力为
作用在任意形状平面上的液体总压力大小, 作用在任意形状平面上的液体总压力大小,等于该平面的淹没 面积与其形心处静压强的乘积, 面积与其形心处静压强的乘积,而形心处的静压强就是整个受 压平面上的平均压强。 压平面上的平均压强。 总压力的方向垂直于平面,并指向平面。 总压力的方向垂直于平面,并指向平面。
ω
旋转
等压面方程
自由表面方程
第五节 一、图解法
作用在平面上的液体总压力来自液体总压力的方向垂直于矩形平面,并指向平面, 液体总压力的方向垂直于矩形平面,并指向平面,液体总压力的 作用线通过静压强分布图体积的重心。 作用线通过静压强分布图体积的重心。液体总压力作用线与矩形 平面相交的作用点D称为压力中心 称为压力中心。 平面相交的作用点 称为压力中心。
三、流体静力学基本方程的物理意义和几何意义 1. 流体静力学基本方程的物理意义
Z:单位重量流体从某一基准面算起所 : 具有的位能,因为是对单位重量而言, 具有的位能,因为是对单位重量而言, 所以称单位位能。 所以称单位位能。
:单位重量流体所具有的压能,称 单位重量流体所具有的压能, 单位压能。 单位压能。
等压面方程
三、等压面 帕斯卡定 律 等压面方程 当流体质点沿等压面移动距离ds时 质量力所作的微功为零。 当流体质点沿等压面移动距离ds时,质量力所作的微功为零。 ds 因为质量力和位移ds都不为零,所以等压面和质量力正交。 ds都不为零 因为质量力和位移ds都不为零,所以等压面和质量力正交。 这是等压面的一个重要特性。 这是等压面的一个重要特性。
大学物理上 第4章 流体-2

作业:15页,T6-T81Q S =∆=常量v 2211v v S S ∆∆+=常量=++221v ρρgh p常量=++221v ρρgh p •• ghB 2=v221221122p ρρ+=+v v 常量=++221v ρρgh p 实例: 喷雾器、水流抽气机、内燃机中汽化器S 2v 2=S 1v 15ABCA p 大C p 大B p 小p <p 021p =v ρv 2=0p p gh ρ'=+(3) 组合皮托管28Pitot tube on a helicopter to measureairspeed Close ‐up of a Pitot tube, showing the stagnation pressure hole and two of the five static circumferential pressure holes.1+ p1. 实验:甘油在竖直圆管中的分层流动分析11甘油、血液⋯理想流体:绝对不可压缩;完全没有黏性⇒较大的黏性黏性与哪些因素有关?第2节黏性流体的运动Motion of Viscous Fluid✶创造了用水银压力计测量狗主动脉血压的方法✶建立了黏滞流动的泊肃叶公式泊肃叶(Poiseuille,1778‐1869)法国医生及生理学家血压测量✶1733年英国牧师黑尔斯(R.S.Hales,1677-1761)完成最早的血压测量。
✶1828年,泊肃叶设计出了“U”形汞压力计。
✶1856年医生们开始用这种方法测量人的血压。
✶1896年,意大利医生罗克西首创了将袖带与血压计连接起来测量血压的方法。
16212()8p p R Lη-=max21v v =2212()(4p p R r Lη-=-v )rv248f LR Rη⇒=π只决定与管的长度、半径和流体的黏度。
+ + 412()8R p p Q Lηπ-=S 1SS 2vf R R生活小常识:为什么自来水龙头开大了以后,水流就变得不透明了?层流湍流20着色水水龙头清水层流状态23湍流会发声,层流不会发声。
经典:流体力学-第二章-水静力学

压力体可分为实压力体和虚压力体
实压力体判定方法: 绘出的压力体图形与实际的水体居于受压曲面同侧(重叠),
为实压力体。方向向下。
虚压力体判定方法: 绘出的压力体图形与实际的水体分居受压曲面两侧(不重叠),
为虚压力体。方向向上。
对于复式断面,先根据压力体的三个面围出压力体,再根据上述原 则判定虚、实。
第二章流体静力学25作用在平面上的静水总压力一用解析法求任意平面上的静水总压力二用压力图法求矩形平面上的静水总压力26作用在曲面上的静水总压力一曲面上静水压力二压力体27浮力与浮潜体的稳定一浮力二潜体的平衡与稳定性三浮体的平衡及稳定性第四讲25作用在平面上的静水总压力工程实践中需要解决作用在结构物表面上的液体静压力的问题
2.合力P对Ox轴取力矩
总压力P对Ox轴的力矩为: P y D g sa ix n y S D g sa i c A n y y D
3.据力矩定理
得:
yD
Ix Sx
Ix yc A
6
yD
Ix Sx
Ix yc A
上式表明:平面上静水总压力作用点D的纵坐标yD等于受压面面积A对Ox 轴的惯性矩与静矩之比。
其中
为图形对形心轴
的静矩,其值应等于零,则得
IyIyca2A
结论:同一平面内对所有相互平行的坐标轴的惯性矩,对形心轴的最小 。 在使用惯性矩移轴公式时应注意a ,b的正负号。
8
故对于本问题有: Ix Ay 2 d A A (y c a )2 d A Ay c 2 d A 2 y cA a d A a A 2 d A Ix Ic y c2 A
2.液体总压力P的铅直分力Pz:
B' F' E'A'
流体力学-第二章-流体静力学ppt课件

1.等加速直线运动容器内液体的相对平衡
由 dp fxdx f ydy fzdz
重力(-g) 惯性力(-a)
fx a (惯性力) f y 0, Z g 边界条件: x 0, z 0, p p0
p dp
x
adx
z gdz
p0
0
0
p p0 ax gz
在自由面: p p0
流体静力学:研究平衡流体的力学规律及其应用
平衡流体互相之间没有相对运动 粘性无从显示
■ 平衡流体上的作用力 ■ 流体的平衡微分方程 ■ 重力场中流体的平衡 ■ 静压强的计算与测量 ■ 平衡流体对壁面的作用力 ■ 液压机械的工作原理 ■ 液体的相对平衡
2.1 平衡流体上的作用力
作用在微团△V上的力可分为两种:质量力 表面力 1.质量力:作用在所研究的流体质量中心,与质量成正比
平行轴定理
I x IC yC2 A
yD
IC
yC2 yC A
A
yC
IC yC A
yC
常见图形的yC和IC
图形名称
yC
h
矩形
2
IC
b h3 12
三角形 半圆
h a 2b 3 a b
h3 36
a2
4ab ab
b2
d
d4
2
64
2d
9 2 64 d 4
3
1152
Fx
Ax
大小、作用点与作用 在平面上的压力相同
(2)垂直方向的作用力
dFz dF sin ghdAsin ghdAz
Fz dFz g Az hdAz gVF
VF——压力体体 ρgVF——压力体重量
Az Ax
Az Ax
工程流体力学-第二章

三、静压力
工程流体力学---第二章 流体静力学
在静止的流体中,不存在切应力。因此,流体中的表面力就是
沿受力面法线方向的正压力或法向力。
F p lim
A0 A
法向力 微元面积
静压力定义
上式中p就是垂直作用于流体单位面积上的力,即物理学中 的压强,称为流体的静压力,简称压力,用p表示,单位为牛 顿(N)。作用于整个面上的力称为总压力。
工程流体力学---第二章 流体静力学 四、流体静压力的两个重要特性
1. 流体静压强垂直于其作用面,其方向指向该作用面的内法线 方向。 (利用静止流体性质进行证明)
☆流体静止时只有法向力,没有切向力,静压力只能沿法线方向; ☆流体不能承受拉力,只能承受压力。
静压力惟一可能的方向就是内法线方向。
工程流体力学---第二章 流体静力学
微元体内流体所受质量力: dxdydz
说明:
微元体内流体所受质量力在x方向的分力: Xdxdydz (1)在流体力学
2. 静止流体中任意一点处流体静压强的大小与作用面的方位无
关,即同一点各方向的流体静压强均相等。
z
Pn
Px dz
Py
Px Py Pz Pn P
O
dx
dy
y
x
Pz
表明:静止流体中任意一点上的流体静压力,无论来自何方均相
等,或者说与作用方向无关。流体静压强不是矢量,而是标量,
仅是坐标的连续函数。即:p= p(x,y,z),由此得静压强的全微分
☆流体静力时,流体质点之间没有相对运动,因此粘滞性在静止 流体中显现不出来。 ☆本章所得到的流体平衡规律对理想流体和实际流体均适用。
流体力学第2章_水静力学--用

流体静力学
§2-1 静水压强及其基本特性 §2-2 液体平衡微分方程及其积分 §2-3 重力作用下静水压强的分布规律 §2-4 几种质量力作用下液体的相对平衡 §2-5 作用于平面上的静水总压力 §2-6 作用于曲面上的静水总压力
流体静力学就是研究平衡流体的力学规律及其应用的科 学。 所谓平衡 或者说静止), 平衡( ),是指流体宏观质点之间没有 所谓平衡(或者说静止),是指流体宏观质点之间没有 相对运动,达到了相对的平衡。 相对运动,达到了相对的平衡。 因此流体处于静止状态包括了两种形式: 因此流体处于静止状态包括了两种形式: 一种是流体对地球无相对运动,叫绝对静止, 一种是流体对地球无相对运动,叫绝对静止,也称 为重力场中的流体平衡。 为重力场中的流体平衡。如盛装在固定不动容器中的液 体。 另一种是流体整体对地球有相对运动, 另一种是流体整体对地球有相对运动,但流体对运动 容器无相对运动,流体质点之间也无相对运动, 容器无相对运动,流体质点之间也无相对运动,这种静 止叫相对静止或叫流体的相对平衡。 止叫相对静止或叫流体的相对平衡。例如盛装在作等加 速直线运动和作等角速度旋转运动的容器内的液体。 速直线运动和作等角速度旋转运动的容器内的液体。
p0
z y
x
h1 z0 1 z1
dp = ρ ( Xdx + Ydy + Zdz )
0
z2 0
(2-4)
返回
2
h2
z
若取图示1 若取图示1、2两点,则得: 两点,则得
Z1 +
p1 p = Z2 + 2 ρg ρg
p0
y
x
h1 z0 1 z1
上式为重力作用下静止液体中的压强分布规律。 上式为重力作用下静止液体中的压强分布规律。 对于流体中的任意点和表面点运用此方程, 对于流体中的任意点和表面点运用此方程, 可得: 可得
流体力学(2)

射流外边界旳交点称为射流极点
四、基本段旳速度分布
在基本段,各横断面旳速度分布都不相同。一方面在射流轴线上,流速沿流 向递减;另一方面,横断面上旳速度由内向外递减至零。
射流基本段旳速度分布可用半经验公式表达为:
u um
1
r Rm
1.5
2
五、初始段旳速度分布
初始段内包括两部分,即关键层和边界层。关键层内各点速度都等于喷射速度 u0
能够看出断面质量平均流速也与断面到喷口旳距离成反比,与喷出口处旳流 速成正比。
五、初始段旳关键长度 s0
初始段旳关键长度为喷口到转折断面旳距离
s0
0.68
R0 a
六、关键旳收缩角 tg R0 1.47a
六、初始段旳s流0 量
任意断面旳关键半径为 r R0 tg s R0 1.47as
关键区旳无量纲流量为
QR Q0
r 2u0 R02 u 0
r R0
2
1
1.47
as R0
2
边界层旳无量纲流量为 Qn 1 Rm u 2rdr Q0 R02u0 r
经过推导可得
Qn Q0
3.74 as R0
0.90
as R0
2
七、初始段旳断面平均流速
u u0
QR Qn / A
Q0 / A0
Rm 0
2rudr
2um Rm2
1u 0 um
r Rm
d
r Rm
2R02u0 Rm2
1u 0 um
r Rm
d
r Rm
因为 2R02u0 Q0
所以:
Q
2Q0
Rm R0
2
um u0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3-3’
p A pB = ( ρ 0 ρ ) g ( R1 + R2 )
2. 液位测量 (1)近距离液位测量装置 压差计读数R反映出容器 压差计读数 反映出容器 内的液面高度。 内的液面高度。
液面越高, 越小 压差计读数R越小 越小, 越小; 液面越高 ,h越小,压差计读数 越小; 当液 面达到最高时, 为零 为零, 亦为零 亦为零。 面达到最高时,h为零,R亦为零。
讨论: 讨论: (1)适用于重力场中静止、连续的同种不可压缩性 )适用于重力场中静止、 重力场中静止 流体; 流体; (2)物理意义: )物理意义: zg ——单位质量流体所具有的位能,J/kg; 单位质量流体所具有的位能,J/kg; 单位质量流体所具有的位能
p
ρ
——单位质量流体所具有的静压能,J/kg。 单位质量流体所具有的静压能,J/kg。 单位质量流体所具有的静压能
解:
p1 = p A + ρgz1 = 13600 × 9.81× 0.1 + 1000 × 9.81× 2.5 = 11183.4 Pa
p2 = ρgz2 = 1000 × 9.81×1.5 = 14715Pa
p2>p1 所以当阀门打开时,容器 中的水将 所以当阀门打开时,容器2中的水将 向容器1中流动 即容器2中液面下降 中流动, 中液面下降h 向容器 中流动,即容器 中液面下降 2,溶 中液面上升h 液1中液面上升 1。 中液面上升
p1 p1
pa
pa
表压
真空度
(2)指示液的选取: )指示液的选取: 指示液与被测流体不互溶,不发生化学反应; 指示液与被测流体不互溶,不发生化学反应; 其密度要大于被测流体密度。 其密度要大于被测流体密度。 应根据被测流体的种类及压差的大小选择指示液。 应根据被测流体的种类及压差的大小选择指示液。
当重新达到平衡时 p1 = p2
A1h1 = A2 h2
p A + ρg ( z1 + h1 ) = ρg ( z2 h2 )
π
4 D h =
2 1 1
π
4
D h
2 2 2
代入已知条件得 h1=0.05m h2=0.31m
思考:若U形压差计安装在倾斜管路中,此时读数 思考: 形压差计安装在倾斜管路中, 形压差计安装在倾斜管路中 R反映了什么? 反映了什么? 反映了什么
p2 p1 z1 R A A’ z2
p1 p 2 = ( ρ 0 ρ ) gR + ρ ( z 2 z 1 ) g
(2)双液体 管压差计 )双液体U管压差计 适用于压差较小的场合。 适用于压差较小的场合。 密度接近但不互溶的两种指示 液A和C ( ρ A > ρ C ) ; 和 扩大室内径与U管内径之比应 扩大室内径与 管内径之比应 大于10 大于 。
p1 p 2 = Rg ( ρ A ρ C )
(3) 倒U形压差计 ) 形压差计 指示剂密度小于被测流体密度, 指示剂密度小于被测流体密度 , 如空气作为指示剂
p1 p 2 = Rg ( ρ ρ 0 ) ≈ Rgρ
(4) 倾斜式压差计 ) 倾斜式压差计 适用于压差较小的情况。 适用于压差较小的情况。 (5) 复式压差计 ) 适用于压差较大的情况。 适用于压差较大的情况。
(3)在静止的、连续的同种流体内,处于同一水平 静止的 连续的同种流体内 处于同一水平 上各点的压强处处相等。压强相等的面称为等压 面 上各点的压强处处相等 。 压强相等的面称为 等压 面。 在同一静止流体中,处在不同位置流体的位能 (4)在同一静止流体中,处在不同位置流体的位能 和静压能各不相同, 但二者可以转换 , 其 总和保持 和静压能 各不相同,但二者可以转换, 各不相同 不变 。 压强具有传递性:液面上方压强变化时, (5)压强具有传递性:液面上方压强变化时,液体 内部各点的压强也将发生相应的变化。 内部各点的压强也将发生相应的变化。
1.2.2 流体静力学基本方程
一、静力学基本方程 设流体不可压缩, ρ 设流体不可压缩, = Const . 重力场中对液柱进行受力分析: 重力场中对液柱进行受力分析: (1)上端面所受总压力 )
P1 = p1 A
p1 G p2 z2 z1 p0
方向向下
(2)下端面所受总压力 ) P2 = p2 A 方向向上 (3)液柱的重力
3. 液封高度的计算 液封作用: 液封作用: 确保设备安全: 确保设备安全 : 当设备 内压力超过规定值时, 内压力超过规定值时 , 气 体从液封管排出; 体从液封管排出; 防止气柜内气体泄漏。 防止气柜内气体泄漏。 液封高度: 液封高度:
4.判断流体流动方向 判断流体流动方向 mm,D 例1-4 两 容 器 直 径 分 别 为D1=1000mm, 2=400 mm, mm,容器 水面上方维持不变的真空度H 容器1水面上方维持不变的真空度 mm,容器 水面上方维持不变的真空度 V=100mm mm Hg,容器 为敞口容器,当阀门 关闭时,两容器的 关闭时, ,容器2 为敞口容器,当阀门F关闭时 m,Z m。试问 水面高度分别为Z 水面高度分别为 1=2.5m, 2=1.5m。试问 m, m。 1. 当阀门开启时, 两液面能否维持不变? 当阀门开启时, 两液面能否维持不变? 2. 若不能维持原状,当重新达到平衡时,液面高度 若不能维持原状,当重新达到平衡时, 各何变化? 各何变化?
所以 整理得
p1 + ρg( m + R ) = p2 + ρgm + ρ 0 gR
p1 p 2 = ( ρ 0 ρ ) gR
若被测流体是气体, 若被测流体是气体,ρ << ρ 0 ,则有
p1 p 2 ≈ Rgρ 0
讨论: 讨论: 形压差计可测系统内两点的压强差, (1)U形压差计可测系统内两点的压强差,当将 形 ) 形压差计可测系统内两点的压强差 当将U形 管一端与被测点连接、另一端与大气相通时, 管一端与被测点连接、另一端与大气相通时,也可测 得流体的表压或真空度——单管压差计 得流体的表压或真空度 单管压差计
G = ρgA( z1 z2 )
方向向下
液柱处于静止时,上述三项力的合力为零: 液柱处于静止时,上述三项力的合力为零:
p2 A p1 A ρgA( z1 z 2 ) = 0
p2 = p1 + ρg( z1 z 2 )
p1
压强形式 能量形式
ρ
+ z1 g =
p2
ρ
+ z2 g
——静力学基本方程 静力学基本方程
1.2 流体静力学
流体力学机理 流体静力学
研究流体在静止时的规律
流体动力学
研究流体在运动时的基本规律
水力学
流体在运动时, 流体在运动时,速度和加速度及其作用 力之间关系
1.2
流体静力学
1.2.1 静压力的特性 1.2.2 流体静力学基本方程
1.2
流体静力学
1.2.1 静压力的特性
流体压力与作用面垂直,并指向该作用面; 流体压力与作用面垂直,并指向该作用面; 任意界面两侧所受压力,大小相等、方向相反; 任意界面两侧所受压力,大小相等、方向相反; 作用于任意点不同方向上的压力在数值上均相同。 作用于任意点不同方向上的压力在数值 例1-1 如附图所示,水在水平管道内流动。为测量流 体在某截面处的压强,直接在该处连接一U形压差计 形压差计, 体在某截面处的压强,直接在该处连接一 形压差计, 指示液为水银, 指示液为水银,读数 R=250mm,h=900mm。已 = , = 。 密度为1000kg/m3 , 水银的密度 密度为 为 13600kg/m3 。 试 计 算 该 截 面 处的压强。 处的压强。
二、静力学基本方程的应用 1. 压强及压强差的测量 (1)U形压差计 ) 形压差计 设指示液的密度为 ρ 0 被测流体的密度为 ρ A与A′面 为等压面,即 p A = p A′ 与 ′ 为等压面,
m R A A’ p1 p2
p A = p1 + ρg ( m + R )
pA′ = p2 + ρgm + ρ 0 gR
h
知当地大气压为101.3kPa,水的 , 知当地大气压为
例1-2
如附图所示,用一复式 形压差计测量某 如附图所示,用一复式U形压差计测量某
种流体流过管路A、 两点的压力差 两点的压力差。 种流体流过管路 、B两点的压力差。已知流体的 密度为ρ,指示液的密度为ρ 且两U形管指示液 密度为 , 指示液的密度为 0 , 且两 形管指示液 之间的流体与管内流体相同。 之间的流体与管内流体相同。已知两个 U形压差计的读数分别 形压差计的读数分别 试推导A、 为 R1 、 R2 , 试推导 、 B两点压力差的计算式 。 两点压力差的计算式。 两点压力差的计算式
