精英新课堂春七级数学下册一次方程组
合集下载
2019年春七年级数学下册第7章一次方程7.2二元一次方程组的解法7.2.3用加减法解二元一次方程组

A )
x=2, D. y=8
x+y=10,① 【解析】 ②-①,得 x=6.把 x=6 代入①,得 y=4.故原 2 x + y = 16. ② x=6, 方程组的解为 y=4.
2x-3y=4,① 3.已知方程组 用加减消去 x 的方法是_____________ ②×2-①×3 , 3x+2y=1.②
解:设一盒牛奶 x 元,一瓶冰茶 y 元.
3x+4y=29, x=5, 由题意,得 解得 x + y = 8.5 , y=3.5.
答:一盒牛奶 5 元,一瓶冰茶 3.5 元.
【点悟】 本题考查了二元一次方程组的应用,解答本题的关键是读懂 题意,设出未知数,找出合适的等量关系,列方程组求解.
由①,得 x=-2y.③ 把③代入②,得 3×(-2y)+4y=6, 解得 y=-3. 将 y=-3 代入③,得 x=6.
x=6, 故原方程组的解为 y=-3.
①+②,得 3x=6,解得 x=2. 将 x=2 代入①,得 y=-1.
x=2, 故原方程组的解为 y=-1.
x=2, ax+by=7, 7.[2018· 随州]已知 是关于 x、y 的二元一次方程组 y=1 ax-by=1
用加减消去 y 的方法是①× _____________ 2+②×3 .
分层作业
[学生用书P34]
3x-2y=5,① 1.用加减法解二元一次方程组 下列四种解法中,正确 3x+4y=-1.②
的是( C ) A.①+②,得 6x-2y+(-4y)=5-1 B.②-①,得 4y-2y=-1+5,所以 y=2 C.②-①,得 4y+2y=-1-5,所以 y=-1 2 D.②-①,得 4y+2y=1-5,所以 y=-3
(1) 你从表格中获取了什么信息? ( 请用自己的语言描述,写出一条即
吉林省长春市七年级数学下册第7章一次方程组7.2二元一次方程组的解法7.2.1二元一次方程组的解法_代入法教案
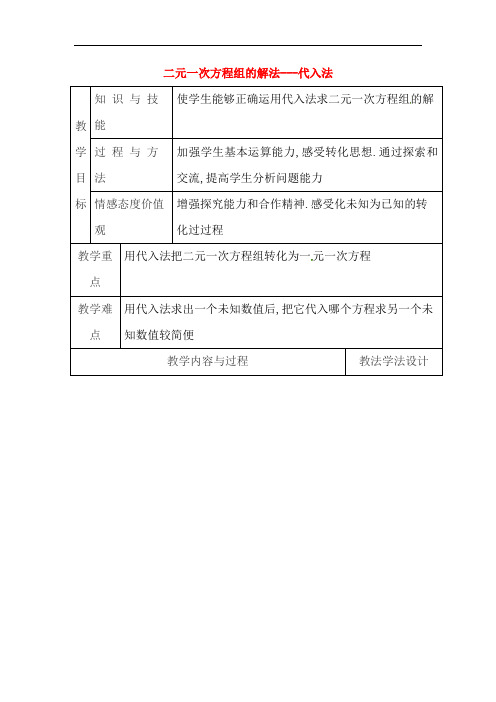
3x 2 y 5① 5 x 2 y 3②
你们想消去那个未知 数
; (2)
3 x y 1① 3 x 4 y 4②
.
3x 2 y 5① 5 x 2 y 3②
中 y 的系数的特点是
________,把这两个方程的两边相_____,可消去未知 数 y. 方程组
探究任务三: ※ 典型例题
x 2 y 1 2x 3y 1
4x y 6 y 2x 2
方程中若有一个方程为 y =k x +b 或 x =k y +b 的形式,则 直接把该方程代入另外一个方程消元; 若没有这种方 程,则先进行变形后再代入。
三、总结提升 ※ 学习小结
1.解二元一次方程组的 思路。 2.掌握代入消元法解二元一次方程组的一般步骤。 加减消元法解方程组基本思路:加减消元----二元 ---一元 主要步骤有: 变形----同一个未知数的系数相同或互为相反数 加减----消去一个元 求解----分别求出两个未知数的值
④
4 x 6 y 2 9 x 6 y 24
其中变形正确的是( A.①② B 4、 (2008 怀化)方程组 ________. 课后作业 P34 页练习 B.③④
) C.①③ D.②④
x y 5, 的解是 x y 3
教 学 反 思
一、课前准备 (预习教材,找出疑惑之处) 复习: 1.什么叫二元一次方程,二元一次方程组 ,二元一次 方程组的解?
2.把 3x+y=7 改写成用 x 的代数式表示 y 的形式。
二、新课导学 ※ 学习探究 探究任务一:通过交流达到理解的目的,同时也解决 本节重点。
回顾上一节课的问题 2,如果设应拆除旧校舍 xm2,建 新校舍 ym2,那么根据题意可列出方程组。 y-x=20000×30% y=4x ① ②
你们想消去那个未知 数
; (2)
3 x y 1① 3 x 4 y 4②
.
3x 2 y 5① 5 x 2 y 3②
中 y 的系数的特点是
________,把这两个方程的两边相_____,可消去未知 数 y. 方程组
探究任务三: ※ 典型例题
x 2 y 1 2x 3y 1
4x y 6 y 2x 2
方程中若有一个方程为 y =k x +b 或 x =k y +b 的形式,则 直接把该方程代入另外一个方程消元; 若没有这种方 程,则先进行变形后再代入。
三、总结提升 ※ 学习小结
1.解二元一次方程组的 思路。 2.掌握代入消元法解二元一次方程组的一般步骤。 加减消元法解方程组基本思路:加减消元----二元 ---一元 主要步骤有: 变形----同一个未知数的系数相同或互为相反数 加减----消去一个元 求解----分别求出两个未知数的值
④
4 x 6 y 2 9 x 6 y 24
其中变形正确的是( A.①② B 4、 (2008 怀化)方程组 ________. 课后作业 P34 页练习 B.③④
) C.①③ D.②④
x y 5, 的解是 x y 3
教 学 反 思
一、课前准备 (预习教材,找出疑惑之处) 复习: 1.什么叫二元一次方程,二元一次方程组 ,二元一次 方程组的解?
2.把 3x+y=7 改写成用 x 的代数式表示 y 的形式。
二、新课导学 ※ 学习探究 探究任务一:通过交流达到理解的目的,同时也解决 本节重点。
回顾上一节课的问题 2,如果设应拆除旧校舍 xm2,建 新校舍 ym2,那么根据题意可列出方程组。 y-x=20000×30% y=4x ① ②
2022春七年级数学下册第7章一次方程组二元一次方程授课课件新版华东师大版ppt

x2的次数不是1.只有②⑤⑥满足.其中⑥已指明
a=0,所以ax2=0,则方程化简后为2x+3y=0.
总结
知1-讲
判断一个方程是否为二元一次方程的方法: 一看原方程是否是整式方程且只含有两个未知数; 二看整理化简后的方程是否具备两个未知数的系数都 不为0且含未知数的项的次数都是1.
知1-讲
例2 (1)已知方程(a+2)x+(b-3)y=9是关于x,y的 二元一次方程,则a的取值范围是__a_≠_-__2__, b的取值范围是__b_≠_3____;
所以x必为偶数. 而由 y 12 - 3x ≥ 0,x≥0,得0≤x≤4,
2 所以x=0或2或4.
当x=0时,y=6;当x=2时,y=3;当x=4时,y=0,
所以原方程的非负整数解为
x y
0, 6
或
x y
2, 或 3
x y
4, 0.
总结
知4-讲
求二元一次方程的整数解的方法:(1)变形:把x看 成常数,把方程变形为用x表示y的形式;(2)划界:根据 方程的解都是整数的特点,划定x的取值范围;(3)试值: 在x的取值范围内逐一试值;(4)确定:根据试值结果得 到二元一次方程的整数解.其求解流程可概述为: 变形 用x表示y 划界 确定x的范围 试值 逐一验证 确定.
总结
知1-讲
在含有字母参数的方程中,如果指明它是二元一 次方程,那么它必定隐含两个条件(1)含未知数的项 的次数都是1且两个未知数的系数都不为0;根据这两 个条件,可分别得到关于这个字母参数的方程或不等 式(以后将学到),由此可求得这个字母参数的值或取 值范围.
知1-练
1 在下列式子:① 2x y 6;② 1 +y 4;③3x+
