2012年普通高等学校招生全国统一考试(安徽卷)理
2012年高考语文古诗词鉴赏详解

2012年高考语文古诗词鉴赏详解古典诗文2012-06-24 12392012年高考语文古诗词鉴赏详解井永战整理全国卷大纲版12.阅读下面这首唐诗,然后回答问题。
(8)落叶修睦注雨过闲田地,重重落叶红。
翻思向春日,肯信有秋风。
几处随流水,河边乱暮空。
只应松自立,二不与君同。
[注]修睦晚唐诗人。
(1)从写落叶的角度看,第二联与一、三两联的不同是如何体现出来的?这样写有什么作用?答(1)(4分)第一、三两联从旁观者的角度描写7秋雨之后落叶的情态,而第二联中“思”与“信”的主体是落叶,使落叶人格化。
第二联插入一、三两联之间,使得全诗富于变化,别具情致。
【解析】本题考查考生鉴赏诗歌的形象和表达技巧的能力。
答出“思”、“信”两字作用的.给2分;答出使全诗富于变化的,给2分。
意思答对即可。
如有其他答案,只要言之成理.也可得一些分。
(2)本诗最后一联为什么要写松?请简要分析。
答【答案】(2)(4分)以松“王”与叶“落”二者的不同构成鲜明对比,采表达对松树不凋的赞叹,强化了对落叶飘零的感慨。
【解析】本题考查考生鉴赏诗歌的形象和表达技巧的能力。
答出构成对比的,给2分能简要分析的,给2分。
意思答对即可。
解答时要联系全诗,借助注释,准确把握。
2012年普通高等学校招生全国统一考试语文新课标试题解析阅读下面这首宋词,完成8~9题。
思远人晏几道红叶黄花秋意晚,千里念行客。
飞云过尽,归鸿无信,何处寄书得。
泪弹不尽临窗滴,就砚旋研墨。
渐写到别来,此情深处,红笺为无色。
8.这首词表达了什么样的感情?“红叶黄花秋意晚”一句对表达这种感情有什么作用?(5分)答9.“就砚旋研墨”与“临窗滴”有什么关系?“红笺为无色”的原因是什么?请简要分析。
(6分)答8.【命题意图】本题考查考生对诗歌思想感情的理解,以及表达技巧的赏析。
【解题思路】解答时要联系全词词句,联系题目、的情况,准确把握。
从题目上——思远人,可以看出这是一首思念怀人之作;在写法上,借秋景、飞云、归鸿等意象来表现这一情感,从词的每一个意象上去思考,联系的思念之情去作答即可。
2012年普通高等学校招生统一考试(安徽卷)含答案

2012年普通高等学校招生统一考试(安徽卷) 12.2010年发行的首套宣纸材质邮票《中国古代书法——行书》,被称为国家名片与国宝艺术的完美集合,彰显了宣纸“纸寿千年,墨润万变”的独特魅力。
图中属于该套邮票的是()13.唐太宗曾对吏部尚书杜如晦说:“今专以言辞刀笔取人,而不悉其行,至后败职,虽刑戮之,而民已敝矣。
”这句话意在强调()A.应严刑处罚失职官员B.选官须注重才学C.官员失职会危害民生D.选官应注重品行15.据有关统计资料,元朝岁收粮赋,河南江北行省占全国总额的21.39%,江浙行者占37.10%,江西行省占9.56%,湖广行省占6.97%。
结合图分析,正确的是()元朝行省图A.长江中下游地区粮赋总额约占全国的3/4B.长江以南各行省粮赋总额占全国一半以上C.长江以北各行省经济均落后于江南各行省D.我国的经济中心开始向长江以南地区转移16.19世纪70年代末,一位英国人写道:“一个重庆商人如果要在上海采办洋货,他可以到一个钱庄……押借一笔款项,……(然后)将订货单子寄予他在上海的代理人;钱庄经理也通知与他有关系的上海钱庄或其分庄,由后者向洋行或其中国的代理人处付予这笔款项。
”可见此时的钱庄()A.已经完全变成了洋行的附庸B.在中外贸易中居于关键地位C.一般不愿支持土货出口业务D.在洋货内销中具有重要作用17.图为民国年间的漫画,画中人物指的是()A.袁世凯B.段祺瑞C.张勋D.溥仪18.下表是依据龚关主编《中华人民共和国经济史》中的相关数据编制的。
该表反映出()表1979~1984年我国城乡居民收入与消费水平平均增长率收入农村(家庭收入) 17.6%城镇(职工货币工资) 8.0%消费水平农村8.9% 城镇 4.5%A.社会主义商品市场体系已建立B.农村经济体制改革成效显著C.城市经济体制改革还没有启动D.城镇居民消费水平低于农村19.西方古典作品《阿提卡之夜》记载,“一个审判官或仲裁官,受命于出庭辩论时[审讯案件],而他们被揭穿在[这个]案件中接受金钱贿赂”,依据《十二铜表法》第九表第三条应被处以死刑。
2012年安徽高考理科综合试卷及答案

2012年普通高等学校招生全国统一考试(安徽卷)理综综合第Ⅰ卷(选择题共120分)本卷共20小题,每小题6分,共120分。
在每小题给出的四个选项中,只有一项是生命题目要求的。
以下数据可供起解题参考:相对原子质量(原子量):H 1 C 12 O 16 S 32 Pb 2071.某同学以新鲜洋葱磷片叶内表皮为材料,经不同处理和染色齐染色,用高倍显微镜观察。
下列描述正确的是A.经吡罗红甲基绿染色,可观察到红色的细胞核B.经吡罗红甲基绿染色,可观察到绿色的细胞质C.经健那绿染色,可观察到蓝绿色颗粒状的线粒体D.经苏丹Ⅲ染色,可观察到橘黄色颗粒状的蛋白质2. 蛙的神经远内、外Na+浓度分别是15mmol/L和120mmol/L。
在腊电位由内负外正转变为内正外负过程中有Na+流入细胞,膜电位恢复过程中有Na+排出细胞。
下列判断正确的是A.Na+流入是被动运输,排出是主动运输B.Na+流入是主动运输,排出是被动运输C.Na+流入和排出都是被动运输D.Na+流入和排出都是主动运输3.脊椎动物在胚胎发育中产生了过量的运动神经元,它们竞争肌细胞所分泌的神经生长因子,只有接受了足够量神经生长因子的神经元才能生存,并与靶细胞建立连接其他的则发生凋亡。
下列叙述正确的是A.脊椎动物细胞凋亡仅发生在胚胎发育时期B.一个存活的神经元只与一个靶细胞建立连接C.神经元凋亡是不受环境影响的细胞编程性死亡D.神经元凋亡是由基因控制的,自动的细胞死亡4.假若某植物种群足够大,可以随机交配,没有迁入和迁出,基因不产生突变。
抗病基因R 对感病基因r为完全显性。
现种群中感病植株rr占1/9,抗病植株RR和Rr各占4/9,抗病植株可以正常开花和结实,而感病植株在开花前全部死亡。
则子一代中感病植株占A 、1/9B 、1/16C 、4/81D 、1/85.图示细胞内某些重要物质的合成过程,该过程发生在A .真核细胞内,一个mRNA 分子上结合多个核糖体同时合成多条肽链B .原核细胞内,转录促使mRNA 在核糖体上移动以便合成肽链C .原核细胞内,转录还未结束便启动遗传信息的翻译D .真核细胞内,转录的同时核糖体进入细胞核启动遗传信息的翻译6.留树保鲜是通过延迟采收保持果实品质的一项技术。
2012年全国高考各地试卷诗歌鉴赏试题解析

2012年全国高考各地试卷诗歌鉴赏试题解析2012年全国统一考试语文题(大纲版)详解12.阅读下面这首唐诗,然后回答问题。
(8)落叶修睦注雨过闲田地,重重落叶红。
翻思向春日,肯信有秋风。
几处随流水,河边乱暮空。
只应松自立,二不与君同。
[注]修睦:晚唐诗人。
(1)从写落叶的角度看,第二联与一、三两联的不同是如何体现出来的?这样写有什么作用?答:(1)(4分)第一、三两联从旁观者的角度描写7秋雨之后落叶的情态,而第二联中“思”与“信”的主体是落叶,使落叶人格化。
第二联插入一、三两联之间,使得全诗富于变化,别具情致。
【解析】本题考查考生鉴赏诗歌的形象和表达技巧的能力。
答出“思”、“信”两字作用的.给2分;答出使全诗富于变化的,给2分。
意思答对即可。
如有其他答案,只要言之成理.也可得一些分。
(2)本诗最后一联为什么要写松?请简要分析。
答:【答案】(2)(4分)以松“王”与叶“落”二者的不同构成鲜明对比,采表达作者对松树不凋的赞叹,强化了对落叶飘零的感慨。
【解析】本题考查考生鉴赏诗歌的形象和表达技巧的能力。
答出构成对比的,给2分:能简要分析的,给2分。
意思答对即可。
解答时要联系全诗,借助注释,准确把握。
2012年普通高等学校招生全国统一考试语文新课标试题解析阅读下面这首宋词,完成8~9题。
思远人晏几道红叶黄花秋意晚,千里念行客。
飞云过尽,归鸿无信,何处寄书得。
泪弹不尽临窗滴,就砚旋研墨。
渐写到别来,此情深处,红笺为无色。
8.这首词表达了什么样的感情?“红叶黄花秋意晚”一句对表达这种感情有什么作用?(5分)答:9.“就砚旋研墨”与“临窗滴”有什么关系?“红笺为无色”的原因是什么?请简要分析。
(6分)答:8.【命题意图】本题考查考生对诗歌思想感情的理解,以及表达技巧的赏析。
【解题思路】解答时要联系全词词句,联系题目、作者的情况,准确把握。
从题目上——思远人,可以看出这是一首思念怀人之作;在写法上,借秋景、飞云、归鸿等意象来表现这一情感,从词的每一个意象上去思考,联系作者的思念之情去作答即可。
2012年高考理综安徽卷(含详细答案)

理科综合能力测试试卷 第1页(共46页)理科综合能力测试试卷 第2页(共46页)绝密★启用前2012年普通高等学校招生全国统一考试(安徽卷)理科综合能力测试本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷第1页至第5页,第Ⅱ卷第6页至第14页。
全卷满分300分。
考生注意事项:1. 答题前,务必在试题卷、答题卡规定的地方填写自己的姓名、座位号,并认真核对答题卡上所粘贴的条形码中的姓名、座位号与本人姓名、座位号是否一致。
务必在答题卡背面规定的地方填写姓名和座位号后两位。
2. 答第Ⅰ卷时,每小题选出答案后,用2B 铅笔把答题卡上所对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
3. 答第Ⅱ卷时,必须使用0.5毫米的黑色墨水签字笔在答题卡上....书写,要求字体工整、笔迹清晰。
作图题可先用铅笔在答题卡...的规定的位置绘出,确认后再用0.5毫米的黑色墨水签字笔描清楚。
必须在题号所指示的答题区域作答,超出答题....区域书写的答案无效,在试题卷、草稿纸上答题无效.......................。
4. 考试结束,务必将试题卷和答题卡一并上交。
可能用到的相对原子质量:H —1 C —12 O —16 S —32 Pb —207第Ⅰ卷(选择题 共120分)本卷共20小题,每小题6分,共120分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 某同学以新鲜洋葱磷片叶内表皮为材料,经不同处理和染色齐染色,用高倍显微镜观察。
下列描述正确的是( )A. 经吡罗红甲基绿染色,可观察到红色的细胞核B. 经吡罗红甲基绿染色,可观察到绿色的细胞质C. 经健那绿染色,可观察到蓝绿色颗粒状的线粒体D. 经苏丹Ⅲ染色,可观察到橘黄色颗粒状的蛋白质2. 蛙的神经远内,外+Na 浓度分别是15 mmol/L 和120 mmol/L 。
在膜电位由内负外正转变为内正外负过程中有+Na 流入细胞,膜电位恢复过程中有+Na 排出细胞。
2012年普通高等学校招生全国统一考试文科数学(安徽卷)

12安徽(文)1.(2012安徽,文1)复数z 满足(z -i )i =2+i ,则z =( ). A .-1-i B .1-i C .-1+3i D .1-2i B 由题意可得,z -i =2i i+=2(2i)i i+=1-2i ,所以z =1-i .2.(2012安徽,文2)设集合A ={x |-3≤2x -1≤3},集合B 为函数y =lg (x -1)的定义域,则A ∩B =( ). A .(1,2) B .[1,2] C .[1,2) D .(1,2] D 由-3≤2x -1≤3得,-1≤x ≤2;要使函数y =lg (x -1)有意义,须令x -1>0, ∴x >1.∴集合A ={x |-1≤x ≤2},B ={x |x >1}, ∴A ∩B ={x |1<x ≤2}.3.(2012安徽,文3)(log 29)·(log 34)=( ). A .14B .12C .2D .4D 原式=(log 232)·(log 322)=4(log 23)·(log 32)=4·lg 3lg 2·lg 2lg 3=4.4.(2012安徽,文4)命题“存在实数x ,使x >1”的否定..是( ). A .对任意实数x ,都有x >1 B .不存在实数x ,使x ≤1 C .对任意实数x ,都有x ≤1 D .存在实数x ,使x ≤1C 该命题为存在性命题,其否定为“对任意实数x ,都有x ≤1”.5.(2012安徽,文5)公比为2的等比数列{a n }的各项都是正数,且a 3a 11=16,则a 5=( ). A .1 B .2 C .4 D .8 A 由题意可得,a 3·a 11=27a =16,∴a 7=4.∴a 5=72a q=242=1.6.(2012安徽,文6)如图所示,程序框图(算法流程图)的输出结果是( ).A .3B .4C .5D .8B 由程序框图依次可得,x =1,y =1→x =2,y =2→x =4,y =3→x =8,y =4→输出y =4.7.(2012安徽,文7)要得到函数y =cos (2x +1)的图象,只要将函数y =cos 2x 的图象( ). A .向左平移1个单位 B .向右平移1个单位 C .向左平移12个单位 D .向右平移12个单位C ∵y =cos (2x +1)=cos 122x ⎡⎤⎛⎫+ ⎪⎢⎥⎝⎭⎣⎦,∴只须将y =cos 2x 的图象向左平移12个单位即可得到y =cos (2x +1)的图象.8.(2012安徽,文8)若x ,y 满足约束条件0,23,23,x x y x y ≥⎧⎪+≥⎨⎪+≤⎩则z =x -y 的最小值是( ).A .-3B .0C .32D .3A 作出可行域如图所示,令z =0,得l 0:x -y =0,平移l 0,当l 0过点A (0,3)时满足z 最小,此时z min =0-3=-3.9.(2012安徽,文9)若直线x -y +1=0与圆(x -a )2+y 2=2有公共点,则实数a 的取值范围是( ). A .[-3,-1] B .[-1,3] C .[-3,1] D .(-∞,-3]∪[1,+∞C 由题意可得,圆的圆心为(a ,0),22221(-1)≤+即|a +1|≤2,解得-3≤a ≤1.10.(2012安徽,文10)袋中共有6个除了颜色外完全相同的球,其中有1个红球、2个白球和3个黑球.从袋中任取两球,两球颜色为一白一黑的概率等于( ). A .15B .25C .35D .45B 记1个红球为A ,2个白球为B 1,B 2,3个黑球为C 1,C 2,C 3,则从中任取2个球,基本事件空间Ω={(A ,B 1),(A ,B 2),(A ,C 1),(A ,C 2),(A ,C 3),(B 1,B 2),(B 1,C 1),(B 1,C 2),(B 1,C 3),(B 2,C 1),(B 2,C 2),(B 2,C 3),(C 1,C 2),(C 1,C 3),(C 2,C 3)},共计15种,而两球颜色为一白一黑的有如下6种:(B 1,C 1),(B 1,C 2),(B 1,C 3),(B 2,C 1),(B 2,C 2),(B 2,C 3),所以所求概率为615=25.安徽,文11)设向量a =(1,2m ),b =(m +1,1),c =(2,m ),若(a +c )⊥b ,则|a |= . 2由题意可得,a +c =(3,3m ).由(a +c )⊥b 得,(a +c )·b =0,即(3,3m )·(m +1,1)=3(m +1)+3m =0, 解之,得m =-12.∴a =(1,-1),|a 212.(2012安徽,文12)某几何体的三视图如图所示,则该几何体的体积等于 .56 由三视图可知,该几何体为底面是直角梯形,且侧棱垂直于底面的棱柱,∴V 柱=12×(2+5)×4×4=56.13.(2012安徽,文13)若函数f (x )=|2x +a |的单调递增区间是[3,+∞),则a = .-6 f (x )=|2x +a |=a 2x a,x ,2a 2x a,x ,2⎧+≥-⎪⎪⎨⎪--<-⎪⎩∵函数f (x )的增区间是[3,+∞), ∴-a 2=3,即a =-6.14.(2012安徽,文14)过抛物线y 2=4x 的焦点F 的直线交该抛物线于A ,B 两点,若|AF |=3,则|BF |= .32设点A (x 1,y 1),B (x 2,y 2),由|AF |=3及抛物线定义可得,x 1+1=3,∴x 1=2.∴A 点坐标为(2,则直线AB 的斜率为k1∴直线AB 的方程为y =x -1). 由2y 4x ,y x 1),⎧=⎪⎨=-⎪⎩消去y 得,2x 2-5x +2=0,解得x 1=2,x 2=12.∴|BF |=x 2+1=32.15.(2012安徽,文15)若四面体ABCD 的三组对棱分别相等,即AB =CD ,AC =BD ,AD =BC ,则 (写出所有正确结论的编号).①四面体ABCD 每组对棱相互垂直 ②四面体ABCD 每个面的面积相等③从四面体ABCD 每个顶点出发的三条棱两两夹角之和大于90°而小于180° ④连接四面体ABCD 每组对棱中点的线段相互垂直平分⑤从四面体ABCD 每个顶点出发的三条棱的长可作为一个三角形的三边长②④⑤ 如图所示,四面体ABCD 中,AB =CD ,AC =BD ,AD =BC ,则△ABC ≌△CDA ≌△DCB ≌△BAD ,故②正确;∵△ABC ≌△CDA ≌△BAD ,∴∠BAD =∠ABC ,∠C AD =∠ACB ,∴∠BAC +∠CAD +∠B AD =∠B AC +∠ACB +∠ABC =180°,故③错; 取AB ,BC ,CD ,DA 的中点M ,N ,P ,Q ,连接MN ,NP ,PQ ,MQ ,由此得,MN =QP =12AC ,NP =MQ =12BD ,∵BD =AC ,∴MN =QP =MQ =NP ,∴四边形MNPQ 为菱形,∴对角线相互垂直平分,故④正确,①错误;而⑤正确,如AB ,AC ,AD 可作为△ABC 的三边.16.(2012安徽,文16)设△ABC 的内角A ,B ,C 所对边的长分别为a ,b ,c ,且有2sin B cos A =sin A cos C +cos A sin C . (1)求角A 的大小;(2)若b =2,c =1,D 为BC 的中点,求AD 的长.解:(1)(方法一)由题设知,2sin B cos A =sin (A +C )=sin B ,因为sin B ≠0,所以cos A =12.由于0<A <π,故A =3π.(方法二)由题设可知,2b ·222b c a 2bc +-=a ·222a b c 2ab +-+c ·222b c a 2bc+-,于是b 2+c 2-a 2=bc ,所以cos A =222b c a 2bc +-=12.由于0<A <π,故A =3π.(2)(方法一)因为2A D =2A B A C 2⎛⎫+ ⎪⎝⎭=14(2A B+2A C +2AB ·AC ) =11421243cos π⎛⎫++⨯⨯⨯⎪⎝⎭=74,所以|AD2从而AD2(方法二)因为a 2=b 2+c 2-2bc cos A =4+1-2×2×1×12=3, 所以a 2+c 2=b 2,B =2π.因为BD2AB =1,所以AD217.(2012安徽,文17)设定义在(0,+∞)上的函数f (x )=ax +1ax+b (a >0).(1)求f (x )的最小值;(2)若曲线y =f (x )在点(1,f (1))处的切线方程为y =32x ,求a ,b 的值.解:(1)(方法一)由题设和均值不等式可知,f (x )=ax +1ax+b ≥2+b ,其中当且仅当ax =1时,等号成立, 即当x =1a时,f (x )取最小值为2+b .(方法二)f (x )的导数f '(x )=a -21ax=222a x 1ax-,当x >1a时,f '(x )>0,f (x )在1,a⎛⎫+∞ ⎪⎝⎭上递增;当0<x <1a时,f '(x )<0,f (x )在10,a ⎛⎫ ⎪⎝⎭上递减.所以当x =1a 时,f (x )取最小值为2+b . (2)f '(x )=a -21ax.由题设知,f '(1)=a -1a =32,解得a =2或a =-12(不合题意,舍去). 将a =2代入f (1)=a +1a+b =32,解得b =-1.所以a =2,b =-1.18.(2012安徽,文18)若某产品的直径长与标准值的差的绝对值不超过1 mm 时,则视为合格品,否则视为不合格品,在近期一次产品抽样检查中,从某厂生产的此种产品中,随机抽取5 000件进行检测,结果发现有50件不合格品,计算这50件不合格品的直径长与标准值的差(单位:mm ),将所得数据分组,得到如下频率分布表:(1)将上面表格中缺少的数据填在相应位置上;(2)估计该厂生产的此种产品中,不合格品的直径长与标准值的差落在区间(1,3]内的概率;(3)现对该厂这种产品的某个批次进行检查,结果发现有20件不合格品,据此估算这批产品中的合格品的件数.(2)由频率分布表知,该厂生产的此种产品中,不合格品的直径长与标准值的差落在区间(1,3]内的概率约为0.50+0.20=0.70;(3)设这批产品中的合格品数为x件,依题意有505000=20x20+,解得x=50002050⨯-20=1 980.所以该批产品的合格品件数估计是1 980件.19.(2012安徽,文19)如图,长方体ABCD-A1B1C1D1中,底面A1B1C1D1是正方形,O是BD的中点,E是棱AA1上任意一点,(1)证明:BD⊥EC1(2)如果AB=2,AE OE⊥EC1,求AA1的长.(1)证明:连接AC,A1C1.由底面是正方形知,BD⊥AC.因为AA1⊥平面ABCD,BD⊂平面ABCD,所以AA1⊥BD.又由AA1∩AC=A,所以BD⊥平面AA1C1C.再由EC1⊂平面AA1C1C知,BD⊥EC1.(2)解:设AA1的长为h,1.在Rt△OAE中,AE AO故OE 222=4.在Rt △EA 1C 1中,A 1E =h A 1C 1=故E 21C =(h 2+(2.在Rt △OCC 1中,OC CC 1=h ,O 21C =h 22, 因为OE ⊥EC 1,所以OE 2+E 21C =O 21C ,即4+(h 2+(2=h 22,解得h =所以AA 1的长为20.(2012安徽,文20)如图,F 1,F 2分别是椭圆C :22x a +22y b =1(a >b >0)的左、右焦点,A 是椭圆C 的顶点,B 是直线AF 2与椭圆C 的另一个交点,∠F 1AF 2=60°.(1)求椭圆C 的离心率;(2)已知△AF 1B 的面积为求a ,b 的值. 解:(1)由题意可知,△AF 1F 2为等边三角形,a =2c ,所以e =12.(2)(方法一)a 2=4c 2,b 2=3c 2直线AB 的方程可为:y x -c ). 将其代入椭圆方程3x 2+4y 2=12c 2,得B 855⎛⎫ ⎪ ⎪⎝⎭.所以|AB 8c 05-=165c .由1A FB S =12|AF 1|·|AB |sin ∠F 1AB =12a ·165c 252=解得a =10,b =(方法二)设|AB |=t .因为|AF 2|=a ,所以|BF 2|=t -a .由椭圆定义|BF 1|+|BF 2|=2a 可知,|BF 1|=3a -t . 再由余弦定理(3a -t )2=a 2+t 2-2at cos 60°可得,t =85a .由1A FB S =12a ·85a 252=,a =10,b =21.(2012安徽,文21)设函数f (x )=x 2+sin x 的所有正的极小值点从小到大排成的数列为{x n }.(1)求数列{x n }的通项公式;(2)设{x n }的前n 项和为S n ,求sin S n . 解:(1)f '(x )=12+cos x =0.令f '(x )=0,则cos x =-12,解得x =2k π±23π(k ∈Z ).由x n 是f (x )的第n 个正极小值点知 x n =2n π-23π(n ∈N *).(2)由(1)可知,S n =2π(1+2+…+n )-23n π=n (n +1)π-2n 3π,所以sin S n =sin 2n n (n 1)3ππ⎡⎤+-⎢⎥⎣⎦.因为n (n +1)表示两个连续正整数的乘积,n (n +1)一定为偶数, 所以sin S n =-sin 2n 3π.当n =3m -2(m ∈N *)时,sin S n =-sin 42m 3ππ⎛⎫- ⎪⎝⎭2当n =3m -1(m ∈N *)时, sin S n =-sin 22m 3ππ⎛⎫- ⎪⎝⎭2当n =3m (m ∈N *)时,sin S n =-sin 2m π=0.综上所述,sin S n=***n 3m 2(m ),2n 3m 1(m ),20,n 3m (m ).N N N ⎧-=-∈⎪⎪⎪⎪=-∈⎨⎪=∈⎪⎪⎪⎩。
2010年普通高等学校招生全国统一考试(安徽卷)——理科综合能力测试(生物部分)
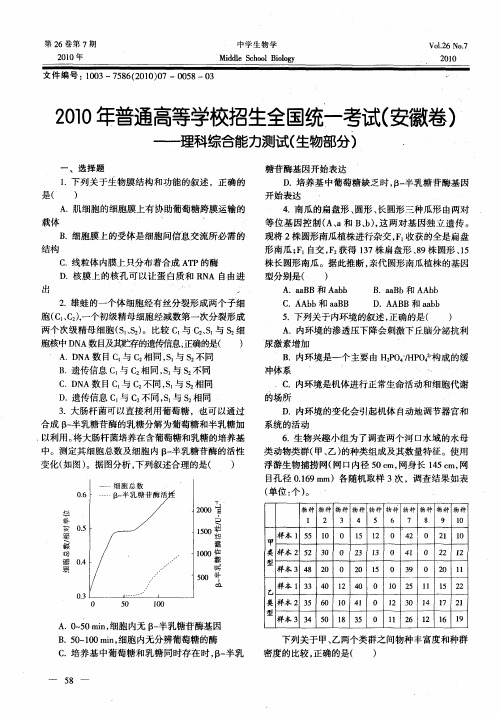
5 下列关于内环境的叙述 , . 正确的是( ) A 内环境的渗透压下降会刺激下丘脑分泌抗利 .
尿 激素 增加 B .内环 境是 一个 主要 由 HzO- 0  ̄ 成 的缓 P HP 2构 / 冲体系 一 一
中。测定其细胞总数及细胞 内 B 半乳糖苷酶的活性 一 变化( 如图) 。据 图分析 , 下列叙述合理的是( )
目孔径 019a )各随机取样 3 ,调查结果如表 . m 6 次 ( 位 : ) 单 个 。
20 0 0
物 种 种 物种 种 种 种 物 物 物 物 物种 种 种 种 物 物 物
型分 别是 ( )
B a b和 A b .aB Ab A a B和 A b .a B ab
2 雄蛙 的一个体细胞经有丝分裂形成两个子细 .
胞 ( 。C) 个初级 精母 细胞经 减数第 一次 分裂 形成 C、 , 一
C A b和 a B .A b aB
D AB .A B和 ab ab
,
D .内环境的变化会引起机体 自 动地调节器官和 系统 的活动
6 生 物兴 趣小 组 为 了调 查 两个 河 口水域 的水母 . 类 动物类 群 ( 、 ) 种类组 成及 其数 量特征 。使 用 甲 乙 的 浮游 生 物捕捞 网( 口内径 5 1, 网 011网身 长 15c 网 3 1 4 m,
D .乙类 群 的丰 富度 小 , 物种 1 0的种群 密度 大
二 、 非 选 择 题
细胞 , 黑点( 表示神经元胞体 , ⑦表示神经纤维。 ●) ①一 按图示 , 肉受到刺激不 由自主地收缩 , 肌 神经 冲动在
神经纤维上 出现的顺序依次为— — ( 填①~ ⑦编 号) 大脑感觉到肌 肉受到刺激 , 。 其信号( 神经冲动 ) 在 神经纤维上 出现的顺序依次为— — ( 填①~ ⑦编
2012年高考文科数学安徽卷(含详细答案)

数学试卷 第1页(共24页)数学试卷 第2页(共24页)数学试卷 第3页(共24页)绝密★启用前2012年普通高等学校招生全国统一考试(全国新课标卷1)数学(文科)适用地区:海南、宁夏、黑龙江、吉林、山西、河南、新疆、云南、河北、内蒙古注息事项:1. 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.答卷前,考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上.2. 回答第Ⅰ卷时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动.用橡皮擦干净后,再选涂其它答案标号.写在本试卷上无效.3. 回答第Ⅱ卷时,将答案写在答题卡上.写在本试卷上无效.4. 考试结束后,将本试卷和答且卡一并交回.第Ⅰ卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合2{|20}A x x x =--<,{|11}B x x =-<<,则( )A .A ⫋B B . AB φ=C . A B =D . B ⫋A 2. 复数3i2iz -+=+的共轭复数是 ( )A . 2i +B . 1i --C . 1i -+D . 2i -3. 在一组样本数据11(,)x y ,22(,)x y ,,(,)n n x y (122,,,,n n x x x ≥不全相等)的散点图中,若所有样本点(,)i i x y (1,2,,)i n =都在直线112y x =+上,则这组样本数据的样本相关系数为( )A . 1-B . 0C . 12D . 14. 设1F 、2F 是椭圆E :22221(0)x y a b a b +=>>的左、右焦点,P 为直线32x a =上一点,21F PF △是底角为30°的等腰三角形,则E 的离心率为( )A . 12B . 23C . 34D . 455. 已知正三角形ABC 的顶点(1,1)A ,(1,3)B ,顶点C 在第一象限,若点(,)x y 在ABC △内部,则z x y =-+的取值范围是( )A . (13,2)-B . (0,13)+C . (31,2)-D . (0,2)6. 如果执行右边的程序框图,输入正整数(2)N N ≥和实数1a ,2a ,,N a ,输出A ,B ,则( )A . AB +为1a ,2a ,,N a 的和B .2A B+为1a ,2a ,,N a 的算术平均数C . A 和B 分别是1a ,2a ,,N a 中最大的数和最小的数D . A 和B 分别是1a ,2a ,,N a 中最小的数和最大的数7. 如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为( )A . 6B . 9C . 12D . 188. 平面α截球O 的球面所得圆的半径为1,球心O 到平面α的距离为2,则此球的体积为( )A .6πB . 43πC . 46πD . 63π9. 已知0ω>,0πϕ<<,直线π4x =和5π4x =是函数()sin()f x x ωϕ=+图象的两条相邻的对称轴,则ϕ=( )A .π4B .π3C .π2D .3π410. 等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线216y x =的准线交于A ,B 两点,||43AB =,则C 的实轴长为( )A .2 B . 22 C . 4D . 8 11. 当102x <≤时,4log xa x <,则a 的取值范围是( )A . 2(0,)2B . 2(,1)2C . (1,2)D . (2,2) 12. 数列{}n a 满足1(1)21nn n a a n ++-=-,则{}n a 的前60项和为( )A . 3 690B . 1 830C . 1 845D . 3 660第Ⅱ卷(非选择题 共90分)本卷包括必考题和选考题两部分.第13~21题为必考题,每个试题考生都必须作答.第22~24题为选考题,考生根据要求作答.二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中的横线上. 13. 曲线(3ln 1)y x x =+在点(1,1)处的切线方程为_________.14. 等比数列{}n a 的前n 项和为n S ,若3230S S +=,则公比q =_________. 15. 已知向量a ,b 夹角为45,且||1=a ,2|10-=|a b ,则|=|b _________.16. 设函数22(1)sin ()1x xf x x ++=+的最大值为M ,最小值为m ,则M m +=_________.姓名________________ 准考证号_____________--------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效--------数学试卷 第4页(共24页)数学试卷 第5页(共24页)数学试卷 第6页(共24页)三、解答题:本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤. 17.(本小题满分12分)已知a ,b ,c 分别为ABC △三个内角A ,B ,C 的对边,3sin cos c a C c A =-. (Ⅰ)求A ;(Ⅱ)若2a =,ABC △的面积为3,求b ,c .18.(本小题满分12分)某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售.如果当天卖不完,剩下的玫瑰花作垃圾处理.(Ⅰ)若花店一天购进17枝玫瑰花,求当天的利润y (单位:元)关于当天需求量n (单位:枝,n ∈N )的函数解析式;(Ⅱ)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:日需求量n 14 15 16 17 18 19 20 频数10201616151310(ⅰ)假设花店在这100天内每天购进17枝玫瑰花,求这100天的日利润(单位:元)的平均数;(ⅱ)若花店一天购进17枝玫瑰花,以100天记录的各需求量的频率作为各需求量发生的概率,求当天的利润不少于75元的概率.19.(本小题满分12分)如图,在三棱柱111ABC A B C -中,侧棱垂直底面,90ACB ∠=,112AC BC AA ==,D 是棱1AA 的中点.(Ⅰ)证明:平面1BDC ⊥平面BDC ;(Ⅱ)平面1BDC 分此棱柱为两部分,求这两部分体积的比.20.(本小题满分12分)设抛物线C :22(0)x py p =>的焦点为F ,准线为l .A 为C 上一点,已知以F 为圆心,FA 为半径的圆F 交l 于B ,D 两点.(Ⅰ)若90BFD ∠=,ABD △的面积为42,求p 的值及圆F 的方程;(Ⅱ)若A ,B ,F 三点在同一直线m 上,直线n 与m 平行,且n 与C 只有一个公共点,求坐标原点到m ,n 距离的比值.21.(本小题满分12分)设函数()e 2xf x ax =--.(Ⅰ)求()f x 的单调区间;(Ⅱ)若1a =,k 为整数,且当0x >时,()()10x k f x x '-++>,求k 的最大值.请考生在第22~24三题中任选一题作答,如果多做,则按所做的第一题计分.22.(本小题满分10分)选修4—1:几何证明选讲如图,D ,E 分别为ABC △边AB ,AC 的中点,直线DE 交ABC △的外接圆于F ,G 两点.若CF AB ∥,证明: (Ⅰ)CD BC =; (Ⅱ)BCD GBD △∽△.23.(本小题满分10分)选修4—4:坐标系与参数方程已知曲线1C 的参数方程是2cos ,3sin x y ϕϕ=⎧⎨=⎩(ϕ为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线2C 的极坐标方程是2ρ=.正方形ABCD 的顶点都在2C 上,且A ,B ,C ,D 依逆时针次序排列,点A 的极坐标为π(2,)3. (Ⅰ)求点A ,B ,C ,D 的直角坐标;(Ⅱ)设P 为1C 上任意一点,求2222||||||||PA PB PC PD +++的取值范围.24.(本小题满分10分)选修4—5:不等式选讲已知函数()|||2|f x x a x =++-.(Ⅰ)当3a =-时,求不等式()3f x ≥的解集;(Ⅱ)若()4|f x x -≤|的解集包含[1,2],求a 的取值范围.(1,2]A B=,集合BA B。
2012高考安徽文综试卷(含答案)

【安徽卷】2012年普通高等学校招生考试文综2012年普通高等学校招生全国统一考试(安徽卷)文科综合能力测试本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷第1页至第8页,第Ⅱ卷第9页至第12页。
全卷满分300分。
考生注意事项:1.答卷前,务必在试题卷、答题卡规定的地方填写自己的姓名、座位号,并认真核对答题卡上所粘贴的条形码中姓名、座位号与本人姓名、座位号是否一致。
务必在答题卡背面规定的地方填写姓名和座位号后两位。
2.答第Ⅰ卷时,每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再涂其他答案标号。
3.答第Ⅱ卷时,必修使用0.5毫米的黑色墨水签字笔在答题卡上书写,要求字体工整、笔迹清晰。
作图题可先用铅笔在答题卡规定的位置绘出,确认后再用0.5毫米的黑色墨水签字笔描清楚。
必须在题号所指示的答题区域作答,超出答题区域书写的答案无效,在试题卷、草稿纸上答题无效。
4.考试结束,务必将试题卷和答题卡一并上交。
第Ⅰ卷(选择题共132分)本卷共33小题,每小题4分,共132分。
在每题给出的四个选项中,只有一项是符合题目要求的。
1.2012年我国经济社会发展要突出把握好稳中求进的工作总基调。
下列选项中符合这一要求且表述正确的是A. 运用经济手段——国内生产总值增长目标略微调低为7.5%B. 运用行政手段——调整金融机构存款准备金率C. 采取积极的财政政策——规范并引导民间融资健康发展D. 采取稳健的货币政策——落实和完善支持小微企业的税收优惠政策2.图1 反映的是在商品价格和其它因素不变时,收入(M)变化引起A商品需求量(X)变化的曲线。
下列判断正确的有①随着收入增加,A商品需求量相应增加②随着收入增加,A商品需求量相应减少③随着收入增加,A商品需求量的增加幅度递增④随着收入增加,A商品需求量的增加幅度递减A. ①③B. ①④C. ②③D. ②④3.读表1,假定其他件不变,2011年某企业生产M 商品的劳动生产率提高的比例和价值总量分别是表1①提升网络参与者的素养②提高政府的行政管理水平③防止网络信息传播扩散④增强公民的民主管理能力A.①②B.①④C. ②③D. ③④5.2012年中国共产党将召开第十八次全国代表大会。
2012年普通高等学校招生全国统一考试生物(安徽卷)

2012年普通高等学校招生全国统一考试理科综合能力测试生物试题(安徽卷)第Ⅰ卷(选择题共120分)本卷共20小题,每小题6分,共120分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.某同学以新鲜洋葱鳞片叶内表皮为材料,经不同处理和染色剂染色,用高倍显微镜观察。
下列描述正确的是()A.经吡罗红甲基绿染色,可观察到红色的细胞核B.经吡罗红甲基绿染色,可观察到绿色的细胞质C.经健那绿染色,可观察到蓝绿色颗粒状的线粒体D.经苏丹Ⅲ染色,可观察到橘黄色颗粒状的蛋白质2.蛙的神经元内、外Na+浓度分别是15 mmol/L和120 mmol/L。
在膜电位由内负外正转变为内正外负过程中有Na+流入细胞,膜电位恢复过程中有Na+排出细胞。
下列判断正确的是()A.Na+流入是被动运输、排出是主动运输B.Na+流入是主动运输、排出是被动运输C.Na+流入和排出都是被动运输D.Na+流入和排出都是主动运输3.脊椎动物在胚胎发育中产生了过量的运动神经元,它们竞争肌细胞所分泌的神经生长因子,只有接受了足够量神经生长因子的神经元才能生存,并与靶细胞建立连接,其他的则发生凋亡。
下列叙述正确的是()A.脊椎动物细胞凋亡仅发生在胚胎发育时期B.一个存活的神经元只与一个靶细胞建立连接C.神经元凋亡是不受环境影响的细胞编程性死亡D.神经元凋亡是由基因控制的、自动的细胞死亡4.假设某植物种群非常大,可以随机交配,没有迁入和迁出,基因不产生突变,抗病基因R对感病基因r为完全显性。
现种群中感病植株rr占19,抗病植株RR和Rr各占49,抗病植株可以正常开花和结实,而感病植株在开花前全部死亡。
则子一代中感病植株占()A.19B.116C.481D.185.图示细胞内某些重要物质的合成过程。
该过程发生在()A.真核细胞内,一个mRNA分子上结合多个核糖体同时合成多条肽链B.原核细胞内,转录促使mRNA在核糖体上移动以便合成肽链C.原核细胞内,转录还未结束便启动遗传信息的翻译D.真核细胞内,转录的同时核糖体进入细胞核启动遗传信息的翻译6.留树保鲜是通过延迟采收保持果实品质的一项技术。
2012年普通高等学校招生全国统一考试(安徽卷)文科综合能力测试试题

姓名:座位号:(在此卷上答题无效)2012年普通高等学校招生全国统一考试(安徽卷)文科综合能力测试本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷第1至第9页,第Ⅱ卷第10至第14页。
全卷满分300分,考试时间150分钟。
考生注意事项:1、答题前,务必在试题卷、答题卡规定填写自己的姓名、座位号,并认真核对答题卡上所粘贴的条形码中姓名、座位号与本人姓名、座位号是否一致。
务必在答题卡背面规定的地方填写姓名和座位号后两位。
2、答第Ⅰ卷时,每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
3、答第Ⅱ卷时,必须使用0.5毫米的黑色墨水签字笔在答题卡上书写,要求字体工整、笔迹清晰。
作图题可先用铅笔在答题卡规定的位置绘出,确认后再用0.5毫米的黑色墨水签字笔描清楚。
必须在题号所指示的答题区域作答,超出书写的答案无效,在试题卷、草稿纸上答题无效。
4、考试结束后,务必将试题卷和答题卡一并上交。
第I卷:选择题(132分)本卷共33小题,每小题4分共132分。
每小题都给出四个选项中,其中只有一个是最符合题意的。
1、2012年我国经济社会发展要突出把握好稳中求进的工作总基调。
下列选项中符合这一要求且表述正确的是A. 运用经济手段——国内生产总值增长目标略微调低为7.5%B. 运用行政手段——调整金融机构存款准备金率C. 采取积极的财政政策——规范并引导民间融资健康发展D. 采取稳健的货币政策——落实和完善支持小微企业的税收优惠政策2、图1 反映的是在商品价格和其它因素不变时,收入(M)变化引起A商品需求量(X)变化的曲线。
下列判断正确的有①随着收入增加,A商品需求量相应增加②随着收入增加,A商品需求量相应减少③随着收入增加,A商品需求量的增加幅度递增④随着收入增加,A商品需求量的增加幅度递减A. ①③B. ①④C. ②③D. ②④3、读表1,假定其他件不变,2011年某企业生产M 商品的劳动生产率提高的比例和价值总量分别是表1A. 50% 40万B. 50% 80万C. 100% 80万D. 200% 160万4、网络给人们的信息交流提供了便利的平台,同时,借助这一平台,谣言也得以迅速传播。
2012年全国高考安徽理科数学试题详细解析

A. 甲的成绩的平均数小于乙的成绩的平均数 B. 甲的成绩的中位数等于乙的成绩的中位数 C. 甲的成绩的方差小于乙的成绩的方差
D. 甲的成绩的极差小于乙的成绩的极差
5.【答案】C 【解析】由条形图易知甲的平均数为 x甲 = 方差为 s
2 甲
4+5+6+7+8 = 6 ,中位数为 6 , 5
( −2 ) + ( −1) =
F A
x
(
)
k=
−2 2 − 0 = −2 2 , 2 −1
直线 AB 的方程为 y = −2 2 x + 2 2 , 联立直线与抛物线方程
y = −2 2 x + 2 2, y = 4 x,
2
可得 2 x − 5 x + 2 = 0 ,
2
1 , 2 1 3 3 9 可得 BF = − ( −1) = , AB = AF + BF = 3 + = , 2 2 2 2
A.3
B.4
C.5
D.6
3.【答案】B 【解析】第一次循环后: x = 2, y = 2 ;第二次循环后: x = 4, y = 3 ;第三次循环后:
x = 8, y = 4 ,跳出循环,输出 y = 4 .
【规律总结】 具有循环结构的流程图问题, 最有效的求解方法之一就是当循环次数比较少时, 把每一次循环之后每个变量的取值都一一列出, 当循环次数比较多时, 利用数列通项把每次 循环之后每个变量的取值一一列出. 4.公比为 2 的等比数列 {an } 的各项都是正数,且 a3 a11 = 16 ,则 log 2 a10 = ( )
2
1 −2 常数项,只要找 2 − 1 展开式中的常数项和含 x 项即可. x
品析高考试题1

需要运用地理原理解答问题?
三、2012地理高考题品析
地 理 思 维 的 综 合 性
自然地理与人文地理的充分结合
(28分)(1)全年温和多雨 温带大陆性气候 (2)从沿海到内陆(干湿度地带) 水分 (3)①土壤肥沃,水分适宜,有利于葡萄生长;②葡萄生长期内光照充足,昼夜温差较大,有利 于糖分的积累;③葡萄成熟后气温低,能够自然冰冻。 (4)①少耕、免(休)耕,退耕还草;②加强牧场生态管理,划区轮牧;③加强水资源管理, 推广节水农业;④合理利用肥料和农药(加强农牧业技术培训与推广等)。 (广东卷) 40. 加拿大地广人稀,西南部地区地形发杂,欧肯那根河谷是世界
命题依据教育部制定的2012年普通高等学校招生全 国统一 考 试新课程标准思想政治、历史、地理科目 考试大纲的有关规定。
命题以能力测试为主导,既注意体现共同基础性, 也注意体现多样选择性, 。。。。。
命题既要体现新课程的理念,又要保证高考的相对 平稳。
二、地理高考的能力要求
获取和解读地理信息的能力
断 洱
层
○
∴
点
层 陡
A
苍
B
陡
1974
坡
∴ ○ 大理古城
1974 湖面 海拔/m 断层陡 坡范围 0 3 6 km
(2)如果在洱海西岸大规模建议住宅, 可能对地理环境产生哪些不利影响?
22
坡
海
答案:占用耕地和湿地,影响农业生产,湿地的功能减弱、效益降低。人口增 下关 多,林地遭破坏,入湖污水增多,生物多样性减少,自然灾害增多,环境质量 图 14 云南苍山洱海地区土地利用类型示意图 下降,不利于大理古城的保护,人地关系恶化。
比较思维与逆向思维的充分应用 发展性课程评价研究系列
2012年普通高等学校招生全国统一考试(安徽卷)数学(理科)

2012年普通高等学校招生全国统一考试(安徽卷)数学(理科)学校:___________姓名:___________班级:___________考号:___________一、选择题(本大题共10小题,共50.0分)1.复数z满足( z-i)(2-i)=5,则z=()A.-2-2iB.-2+2iC.2-2iD.2+2i【答案】D【解析】由题意可得,z-i==2+i,所以z=2+2i.2.下列函数中,不满足f(2 x)=2 f( x)的是()A. f( x)=| x|B. f( x)=x-| x|C. f( x)=x+1D. f( x)=-x【答案】C【解析】∵f(2 x)=2 x+1,而2 f( x)=2 x+2,∴f(2 x)≠2 f( x),只有C不满足.3.如图所示,程序框图(算法流程图)的输出结果是()A.3B.4C.5D.8【答案】B【解析】由程序框图依次可得,x=1,y=1→x=2,y=2→x=4,y=3→x=8,y=4→输出y=4.4.公比为2的等比数列{ a n}的各项都是正数,且a3a11=16,则log2a10=()A.4B.5C.6D.7【答案】B【解析】由题意可得,a3a11=a72=16,∴a7=4.∴a10=a7q3=25.∴log2a10=log225=5.5.甲、乙两人在一次射击比赛中各射靶5次,两人成绩的条形统计图如图所示,则()A.甲的成绩的平均数小于乙的成绩的平均数B.甲的成绩的中位数等于乙的成绩的中位数C.甲的成绩的方差小于乙的成绩的方差D.甲的成绩的极差小于乙的成绩的极差【答案】C【解析】由图可得,,,故A项错;而甲的成绩的中位数为6,乙的成绩的中位数为5,故B项错;,,故C项正确;甲的成绩的极差为4,乙的成绩的极差也为4,故D项错.6.设平面α与平面β相交于直线m,直线a在平面α内,直线b在平面β内,且b⊥m,则“α⊥β”是“a⊥b”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件【答案】A【解析】由面面垂直的性质定理可得,α⊥β,α∩β=m,bβ,b⊥m b⊥α.又∵aα,∴a⊥b,但反之则不成立.7.( x2+2)(-1)5的展开式的常数项是()A.-3B.-2C.2D.3【答案】D【解析】(-1)5的通项为T r+1=()5-r(-1) r=(-1) r.要使( x2+2)(-1)5的展开式为常数,须令10-2 r=2或0,此时r=4或5.故( x2+2)(-1)5的展开式的常数项是(-1)4×+2×(-1)5×=3.8.在平面直角坐标系中,点O(0,0),P(6,8).将向量绕点O按逆时针方向旋转后得向量,则点Q的坐标是()A.(,)B.(,)C.(,-2)D.(,2)【答案】A【解析】设与x轴正半轴的夹角为θ,则,,则由三角函数定义可得,=(cos( θ+),sin( θ+.∵cos( θ+)=×(cosθcos-sinθsin)=,sin( θ+)=×(sinθcos+cosθsin)=,∴=(,),即点Q的坐标为(,).9.过抛物线y2=4 x的焦点F的直线交该抛物线于A,B两点,O为坐标原点.若| AF|=3,则△AOB的面积为…()A. B. C. D.【答案】C【解析】设点A( x1,y1),B( x2,y2),由| AF|=3及抛物线定义可得,x1+1=3,∴x1=2.∴A 点坐标为(2,),则直线AB的斜率.∴直线AB的方程为y=( x-1),即为,则点O到该直线的距离为.由消去y得,2 x2-5 x+2=0,解得x1=2,.∴| BF|=x2+1=,∴.∴.10.6位同学在毕业聚会活动中进行纪念品的交换,任意两位同学之间最多交换一次,进行交换的两位同学互赠一份纪念品.已知6位同学之间共进行了13次交换,则收到4份纪念品的同学人数为()A.1或3B.1或4C.2或3D.2或4【答案】D【解析】6位同学之间互相交换,总共有种,而实际只交换了13次,故有2次未交换.不妨设为甲与乙、丙与丁之间未交换或甲与乙、甲与丙之间未交换,当甲与乙、丙与丁之间未交换时,甲、乙、丙、丁4位同学都收到4份礼物;当甲与乙、甲与丙之间未交换时,只有乙、丙两位同学收到4份礼物,故选D.二、填空题(本大题共5小题,共25.0分)11.若x,y满足约束条件则x-y的取值范围是__________.【答案】[-3,0]【解析】作出可行域如图所示,令z=x-y,当z=0时,得l0:x-y=0.平移l0,当l0过点A(0,3)时满足z最小,此时z min=0-3=-3;当l0过点B(1,1)时,此时z max=1-1=0,故x-y的取值范围为[-3,0].12.某几何体的三视图如图所示,该几何体的表面积是__________.【答案】92【解析】由三视图可知,该几何体为底面是直角梯形且侧棱垂直于底面的棱柱,该几何体的表面积为S=2××(2+5)×4+[2+5+4+]×4=92.13.在极坐标系中,圆ρ=4sinθ的圆心到直线( ρ∈R)的距离是__________.【答案】【解析】由极坐标下圆的方程ρ=4sinθ可得,ρ2=4 ρsinθ,所以x2+ y2=4 y,即x2+( y -2)2=4,表示以(0,2)为圆心,2为半径的圆.又( ρ∈R)表示直线,∴由点到直线的距离公式可得.14.若平面向量a,b满足|2 a-b|≤3,则a·b的最小值是__________.【答案】【解析】∵|2 a-b|≤3,∴4 a 2+ b2≤9+4 a·b.∵4 a2+ b2≥4| a|·| b|≥-4 a·b,∴9+4 a·b≥-4 a·b.∴.15.设△ABC的内角A,B,C所对边的长分别为a,b,c,则下列命题正确的是__________(写出所有正确命题的编号).①若ab>c2,则②若a+ b>2 c,则③若a3+ b3=c3,则④若( a+ b) c<2 ab,则⑤若( a2+ b2) c2<2 a2b2,则【答案】①②③【解析】对于①,由ab>c2可得.故,∴①正确;对于②,由a+ b>2 c可得,故.故.∴,②正确;对于③,由a3+ b3=c3可得,故a2+ b2-c2=a2+ b2-=.又a3+ b3=c3,故c>a,c>b,故,故a2+ b2>c2.故,③正确;对于④,,故.故.∴,④不正确;对于⑤,由( a2+ b2) c2<2 a2b2可得.故.∴,⑤不正确.综上可知,①②③正确.三、解答题(本大题共6小题,共75.0分)16.设函数f( x)=cos(2 x+)+sin2x.(1).求f( x)的最小正周期;(2).设函数g( x)对任意x∈R,有g( x+)=g( x),且当x∈[0,]时,g( x)=-f( x).求g( x)在区间[-π,0]上的解析式.【答案】解:(1)f( x)=cos(2x+)+sin2x=(cos2xcos-sin2xsin)+=,故f( x)的最小正周期为π.(2)当x∈[0,]时,g( x)=-f( x)=sin2x.故①当x∈[,0]时,x+∈[0,].由于对任意x∈R,g( x+)=g( x),从而g( x)=g( x+)=sin[2( x+)]=sin(π+2x)=sin2x.②当x∈[-π,)时,x+π∈[0,).从而g( x)=g( x+π)=sin[2( x+π)]=sin2x.综合①,②得g( x)在[-π,0]上的解析式为【解析】略17.某单位招聘面试,每次从试题库中随机调用一道试题.若调用的是A类型试题,则使用后该试题回库,并增补一道A类型试题和一道B类型试题入库,此次调题工作结束;若调用的是B类型试题,则使用后该试题回库,此次调题工作结束.试题库中现共有n+ m道试题,其中有n道A类型试题和m道B类型试题.以X表示两次调题工作完成后,试题库中A类型试题的数量.(1).求X=n+2的概率;(2).设 m = n ,求 X 的分布列和均值(数学期望).【答案】解:以 A i 表示第 i 次调题调用到 A 类型试题, i =1,2. (1) P ( X = n +2)= P ( A 1 A 2)=.(2) X 的可能取值为 n , n +1, n +2.P ( X = n )=.P ( X = n +1)=,P ( X = n +2)= P ( A 1 A 2)=,从而 X 的分布列是EX = n ×+( n +1)×+( n +2)×= n +1.【解析】 略18.平面图形 ABB 1 A 1 C 1 C 如图1所示,其中 BB 1 C 1 C 是矩形, BC =2, BB 1=4, AB = AC =, A 1 B 1=A 1 C 1=,现将该平面图形分别沿 BC 和 B 1 C 1折叠,使△ ABC与△ A 1 B 1 C 1所在平面都与平面 BB 1 C 1 C 垂直,再分别连接 A 1 A , A 1 B , A 1 C ,得到如图2所示的空间图形.对此空间图形解答下列问题.(1).证明: AA 1⊥ BC ;(2).求 AA 1的长;(3).求二面角 A - BC - A 1的余弦值.【答案】(向量法)(1)证明:取BC,B1C1的中点分别为D和D1,连接A1D1,DD1,AD.由四边形BB1C1C为矩形知,DD1⊥B1C1.因为平面BB1C1C⊥平面A1B1C1,所以DD1⊥平面A1B1C1.又由A1B1= A1C1知,A1D1⊥B1C1.故以D1为坐标原点,可建立如图所示的空间直角坐标系D1-xyz.由题设,可得A1D1=2,AD=1.由以上可知AD⊥平面BB1C1C,A1D1⊥平面BB1C1C,于是AD∥A1D1.所以A(0,-1,4),B(1,0,4),A1(0,2,0),C(-1,0,4),D(0,0,4).故=(0,3,-4),=(-2,0,0),.因此,即AA1⊥BC.(2)解:因为=(0,3,-4),所以,即AA1=5.(3)解:连接A1D.由BC⊥AD,BC⊥AA1,可知BC⊥平面A1AD,BC⊥A1D,所以∠ADA1为二面角A-BC-A1的平面角.因为=(0,-1,0),=(0,2,-4),所以,即二面角A-BC-A1的余弦值为.(或用法向量求解)(综合法)(1)证明:取BC,B1C1的中点分别为D和D1,连接A1D1,DD1,AD,A1D.由条件可知,BC⊥AD,B1C1⊥A1D1.由上可得AD⊥平面BB1C1C,A1D1⊥平面BB1C1C,因此AD∥A1D1,即AD,A1D1确定平面AD1A1D.又因为DD1∥BB1,BB1⊥BC,所以DD1⊥BC.又考虑到AD⊥BC,所以BC⊥平面AD1A1D,故BC⊥AA1.(2)解:延长A1D1到G点,使GD1= AD.连接AG.因为AD GD 1,所以AG DD1BB1.由于BB1⊥平面A1B1C1,所以AG⊥A1G.由条件可知,A1G= A1D1+ D1G=3,AG=4,所以AA1=5.(3)解:因为BC⊥平面AD1A1D,所以∠ADA1为二面角A-BC-A1的平面角.在R t△A1DD1中,DD1=4,A1D1=2,解得sin∠D1DA1=,cos∠ADA1=cos(+∠D1DA1)=,即二面角A-BC-A1的余弦值为.【解析】略19.设函数f( x)=ae x++ b( a>0).(1).求f( x)在[0,+∞)内的最小值;(2).设曲线y=f( x)在点(2,f(2))处的切线方程为,求a,b的值.【答案】解:(1)f′( x)=ae x-,当f′( x)>0,即x>-ln a时,f( x)在(-ln a,+∞)上递增;当f′( x)<0,即x<-ln a时,f( x)在(-∞,-ln a)上递减.①当0<a<1时,-ln a>0,f( x)在(0,-ln a)上递减,在(-ln a,+∞)上递增,从而f( x)在[0,+∞)上的最小值为f(-ln a)=2+ b;②当a≥1时,-ln a≤0,f( x)在[0,+∞)上递增,从而f( x)在[0,+∞)上的最小值为f(0)=a++ b.(2)依题意,解得ae2=2或(舍去).所以,代入原函数可得2++ b=3,即.故,.【解析】略20.如图,点F1(-c,0),F2( c,0)分别是椭圆C:( a>b>0)的左、右焦点,过点F1作x轴的垂线交椭圆C的上半部分于点P,过点F2作直线PF2的垂线交直线于点Q.(1).如果点Q的坐标是(4,4),求此时椭圆C的方程;(2).证明:直线PQ与椭圆C只有一个交点.【答案】(1)解:方法一:由条件知,P(-c,).故直线PF2的斜率为.因为PF2⊥F2Q,所以直线F2Q的方程为.故Q(,2a).由题设知,,2a=4,解得a=2,c=1.故椭圆方程为.方法二:设直线与x轴交于点M.由条件知,P(-c,).因为△PF1F2∽△F2MQ,所以.即,解得| MQ|=2a,所以a=2,c=1.故椭圆方程为.(2)证明:直线PQ的方程为,即.将上式代入椭圆方程得x2+2cx+ c2=0,解得x=-c,.所以直线PQ与椭圆C只有一个交点.【解析】略21.数列{ x n}满足x1=0,x n+1=-x n2+ x n+ c( n∈N*).(1).证明:{ x n}是递减数列的充分必要条件是c<0;(2).求c的取值范围,使{ x n}是递增数列.【答案】(1)证明:先证充分性,若c<0,由于x n+1=+ x n+ c≤x n+ c<x n,故{ x n}是递减数列;再证必要性,若{ x n}是递减数列,则由x2<x1可得c<0.(2)解:假设{ x n}是递增数列.由x1=0,得x2=c,x3=-c2+2c.由x1<x2<x3,得0<c<1.由x n<x n+1=+ x n+ c知,对任意n≥1都有x n<,①注意到-x n+1=-x n-c+=(1--x n)(-x n).②由①式和②式可得1--x n>0,即x n<1-.由②式和x n≥0还可得,对任意n≥1都有-x n+1≤(1-)(-x n).③反复运用③式,得-x n≤(1-) n-1(-x1)<(1-) n-1.x n<1-和-x n<(1-) n-1两式相加,知-1<(1-) n-1对任意n≥1成立.根据指数函数y=(1-) x的性质,得-1≤0,,故0<c≤.若0<c≤,要证数列{ x n}为递增数列,即x n+1-x n=+ c>0.即证x0<对任意n≥1成立.下面用数学归纳法证明当0<c≤时,x n<对任意n≥1成立.当n=1时,x1=0<≤,结论成立.假设当n=k( n∈N*)时结论成立,即x k<.因为函数f( x)=-x2+ x+ c在区间(-∞,]内单调递增,所以x k+1=f( x k)<f()=,这就是说当n=k+1时,结论也成立.故x n<对任意n≥1成立.因此,x n+1=x n-+ c>x n,即{ x n}是递增数列.综上可知,使得数列{ x n}单调递增的c的取值范围是(0,].【解析】略。
普通高等学校招生全国统一考试英语试题(安徽卷,含答案)

普通高等学校招生全国统一考试英语试题(安徽卷,含答案)第Ⅰ卷(选择题共50分)第一部分听力(共两节,满分30分)第二部分英语知识运用(共两节,满分45分)第一节单项填空(共15小题;每小题1分,满分15分)从A、B、C、D四个选项中,选出可以填入空白处的最佳选项,并在答题卡上将该项涂黑。
21. Carl is studying food science at college and hopes to open up meat processing factory of his own one day.A. / ; aB. / ;theC. the ; aD. the ; the本题考查冠词,science是不可数名词,用the表示特指是不可能的,后面的factory是一个可数名词,用a 表示泛指。
22.——May I help you? You seem to be having some problems.—— , thanks. I think I can manage.A. All rightB. No problemC. It’all rightD. There’s no way很多学生会选择答案D ,我想这是有道理的。
A. B. C都表示肯定,即接受帮助,只有D是拒绝。
我没有去过国外,也很少见到老外,所以我不敢轻言答案是哪个,很多学生也应该是这样吧。
我也不知道老外是否会经常用不定式的进行时进行交际,想必出卷教师一定是交际高手吧。
【你说的对,我是遇到问题了,但是谢谢你的好意,我自己可以解决】23. Interest is as to learning as the ability to understand , even more so.A. vitalB. availableC. specificD. SimilarBe vital to 表示:对.....极端重要;something be available to somebody表示:某人可以得到某物,列句:cooperative medical service is available to all the members of the the commune. C答案specific 不能与to 搭配;D 答案 similar to 表示:与.....相似。
2012年高考文科综合试题(安徽卷下 WORD)

美国某州盛产蔬菜和水果,该州通过“北水南调”工程和“水银行”(调剂州内水资源余缺的管理机构)动作,较好地解决了州内水资源供需矛盾。
图10为该州“北水南调”工程示意图,表3为该州“水银行”交易统计表。
完成28-29题。
图1028. 该州实施“北水南调”的地理背景是①自北向南地势逐渐升高②北部地区湿润多雨③农业用地多集中在中部和南部④中部和南部聚落较密集A. ①②③B.②③④C. ①②④D.①③④29.1993年该州“水银行”没有运作,是因为当年中南部地区A.节水技术改进,用水效率提高B. 产业结构调整,用水量减少C. 水价过高,需水方难以承受D. 降水量增加,水资源充足图11为我省平原地区某中学的操场和行道树示意图(晴天8:00前后,东操场大部分被行道树的树荫覆盖)。
完成30-31题。
图1130.为充分利用树荫遮阳,6月某日16:00-16:45该校某班同学上体育课的最佳场地是A. ①B.②C. ③D.④31. 下列日期中,阳光照射行道树产生的阴影在地面转动角度最大的是青藏高原四周多高山。
青海省位于青藏高原东北部,平均海拔3500米以上;柴达木盆地位于青海西北部。
面积约占全省的三分之一。
图12为青海省年降水量分布和年平均气温分区图。
完成32-33题。
图1232.青海省东南边缘降水较多,其水汽主要来自A. ①B.②C. ③D.④33.根据年平均气温分布状况,将青海省划分为Ⅰ、Ⅱ、Ⅲ三个温度区。
三区年平均气温相比A. Ⅰ>Ⅱ > ⅢB.Ⅰ< Ⅱ < ⅢC. Ⅰ< ⅡⅡ> ⅢD.Ⅰ>ⅡⅡ < Ⅲ2012年普通高等学校招生全国统一考试(安徽卷)文科综合能力测试第Ⅱ卷(非选择题共168分)考生注意事项:请用0.5毫米黑色墨水签字笔在答题卡上作答,在试题卷上答题无效。
34.(32分)根据材料和图13,结合所学知识,回答下列问题。
材料一近些年,“干湖之省”湖北针对省情,夯实农业发展基础,调整产业结构,优化产业布局,推动区域协调发展。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2012年普通高等学校招生全国统一考试(安徽卷)
数学(理科)
第Ⅰ卷 (选择题 共50分)
一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.复数z 满足()()52=--i i z ,则=z ( )
A 、i 22--
B 、i 22+-
C 、i 22-
D 、i 22+ 2.下列函数中,不满足()()x f x f 22=的是( ) A 、()x x f = B 、()x x x f -= C 、()1+=x x f D 、()x x f -=
3.如图所示,程序框图(算法流程图)的输出结果是( ) A 、3 B 、4 C 、5 D 、8
4.公比为2的等比数列{}n a 的各项都是正数,且16113=a a ,则=102log a ( ) A 、4 B 、5 C 、6 D 、7
5.甲、乙两人在一次射击比赛中各射靶5次,两人成绩的条形统计图
如图所示,则( )
A 、甲的成绩的平均数小于乙的成绩的平均数
B 、甲的成绩的中位数等于乙的成绩的中位数
C 、甲的成绩的方差小于乙的成绩的方差
D 、甲的成绩的极差小于乙的成绩的极差
6.设平面α与平面β相交于直线m ,直线a 在平面α内,直线b 在平面β内,且m b ⊥,则“βα⊥”是“b a ⊥”的( ) A 、充分不必要条件 B 、必要不充分条件 C 、充分必要条件 D 、既不充分也不必要条件
7.()
5
22112⎪⎭
⎫
⎝⎛-+x x 的展开式的常数项是( )
A 、3-
B 、2-
C 、2
D 、3
8.在平面直角坐标系中,点()0,0O 、()8,6P ,将向量OP 绕点O 按逆时针方向旋转4
3π
后得向量OQ ,则点Q 的坐标是( )
A 、()2,27--
B 、()2,27-
C 、()2,64--
D 、()
2,64-
9.过抛物线x y 42
=的焦点F 的直线交该抛物线于A 、B 两点,O 为坐标原点。
若3=AF ,则
AOB ∆的面积为( )
A 、
22 B 、2 C 、2
23 D 、22 10.6位同学在毕业聚会活动中进行纪念品的交换,任意两位同学之间最多交换一次,进行交换的两
位同学互赠一份纪念品。
已知6位同学之间共进行了13次交换,则收到4份纪念品的同学人数为( ) A 、1或3 B 、1或4 C 、2或3 D 、2或4
第Ⅱ卷 (非选择题 共100分)
二、填空题:本大题共5小题,每小题5分,共25分。
把答案填在答题卡的相应位置。
11.若x 、y 满足约束条件⎪⎩
⎪
⎨⎧≤+≥+≥32320y x y x x ,则y x -的取值范围是 。
12.某几何体的三视图如图所示,该几何体的表面积是 。
13.在极坐标系中,圆θρ
sin 4=的圆心到直线6
π
θ=
(R ∈ρ)的距离
是 。
14.若平面向量a 、b 满足32≤-b a ,则b a ⋅的最小值是 。
15.设ABC ∆的内角
A 、
B 、
C 所对边的长分别为a 、b 、c ,则下列命题正确的是 (写
出所有正确命题的编号)。
(1)若2
c ab >,则3
π
<
C (2)若c b a 2>+,则3
π
<
C
(3)若3
33c b a =+,则2
π
<
C (4)若()ab c b a 2<+,则2
π
>
C
(5)若()
2
22222b a c b a <+,则3
π
>
C
三、解答题:本大题共6小题,共75分。
解答应写出文字说明、证明过程或演算步骤。
解答写在答题卡的指定区域内
16.(本小题满分12分)
设函数()x x x f 2sin 42cos 22+⎪⎭⎫ ⎝
⎛
+=
π。
(1)求()x f 的最小正周期;
(2)设函数()x g 对任意R x ∈,有()x g x g =⎪⎭⎫
⎝
⎛+2π,
且当⎥⎦
⎤
⎢⎣⎡∈2,0πx 时,()()x f x g -=21,求()x g 在区间[]0,π-上的解析式。
17.(本小题满分12分)
某单位招聘面试,每次从试题库中随机调用一道试题。
若调用的是A 类型试题,则使用后该试题回库,并增补一道A 类型试题和一道B 类型试题入库,此次调题工作结束;若调用的是B 类型试题,则使用后该试题回库,此次调题工作结束。
试题库中现共有m n +道试题,其中有n 道A 类型试题和
m 道B 类型试题。
以X 表示两次调题工作完成后,试题库中A 类型试题的数量。
(1)求2+=n X 的概率;
(2)设n m =,求X 的分布列和均值(数学期望)。
18.(本小题满分12分)
平面图形ABB 1A 1C 1C 如图1所示,其中BB 1C 1C 是矩形,BC=2,BB 1=4,AB=AC=2,A 1B 1=A 1C 1=5。
现将该平面图形分别沿BC 和B 1C 1折叠,使△ABC 与△A 1B 1C 1所在平面都与平面BB 1C 1C 垂直,再分别连接A 1A 、A 1B 、A 1C ,得到如图2所示的空间图形。
对此空间图形解答下列问题:
(1)证明:AA 1⊥BC ; (2)求AA 1的长;
(3)求二面角A-BC-A 1的余弦值。
19.(本小题满分13分) 设函数()b ae ae x f x
x
++
=1
(0>a ) (1)求()x f 在[)+∞,0内的最小值;
(2)设曲线()x f y =在点()()2,2f 处的切线方程为x y 2
3
=,求a 、b 的值。
20.(本小题满分13分)
如图,点()0,1c F -、()0,2c F 分别是椭圆C :122
22=+b
y a x (0>>b a )的左、右焦点,过点1
F 作x 轴的垂线交椭圆C 的上半部分于点P ,过点2F 作直线2PF 的垂线交直线c
a x 2
=于点Q 。
(1)如果点Q 的坐标是()4,4,求此时椭圆C 的方程; (2)证明:直线PQ 与椭圆C 只有一个交点。
21.(本小题满分13分)
数列{}n x 满足01=x ,c x x x n n n ++-=+2
1(+∈N n )。
(1)证明:{}n x 是递减数列的充分必要条件是0<c ; (2)求c 的取值范围,使{}n x 是递增数列。
