第二章 关系
离散数学第二章关系

例9 .设A={1,2,3,4} ,B={2,4,6,8,10} 。 R={(1,2),(2,4),(3,6)}。
则 (R) = {1,2,3}A , (R) = {2,4,6}B 。
二.关系的一些关联性质 17
离散数学
定理1. 设R1,R2 A×B是两个关系。若 R1 R2 ,则
(1)保序性: (R1) (R2) ; (2)保序性: (R1) (R2) ;
注:笛卡尔(1596-1650 ),法国数学家, 1637年发表《方法论》之 一《几何学》,首次提出坐标及变量概念。这里是其概念的推广。
定义2. • 二个集合A,B的(二维或二重)叉积定义为 A×B ={(a, b): a A bB} ; •其元素——二元组(a, b)通常称为序偶或偶对(ordered
故 (R1)∩ (R2) = {1,2 }
21
离散数学
所以 (R1)∩ (R2) (R1 ∩ R2) 。
元素aA和集合A1A在关系R A×B下的关联集 (1)a的R-关联集(R-relative set of a):
R(a)={b : bBaRb }B ;
(2) A1的R-关联集(R-relative set of A1): R(A1)={b : bB (aA1)(aRb) }B 。
•当A=B时,即RA×A,则称R是A上的一个二元关 系。
例1 . 设A是西安交通大学全体同学组成的集合。 11
离散数学
R={(a,b) : aAbAa与b是同乡}A×A 于是,R是西安交通大学同学之间的同乡关系。
例2 . 设A是某一大家庭。
R1 = {(a,b) : aAbAa是b的父亲或母亲}A×A R2 = {(a,b) : aAbAa是b的哥哥或姐姐}A×A R3 = {(a,b) : aAbAa是b的丈夫或妻子}A×A 于是,
第2章 关系

f ( x) y ( x, y) f .
f {( a,2), (b,3), (c,3)}.
A到B的关系是不是A到B的函数? R {( a,2), (a,3), (c,3)} ?
结论:不是任何一个集合A到B的关系都可构成 集合A到B的函数。
函数的关系定义
A到B的关系f 满足什么条件成为A到B的函数? ⑴domf=A:A中任意元素都有B中元素与之对应. ⑵对于任意x∈A,若(x, y1)∈f且(x,y2)∈f,则y1=y2 : 一个x∈A只能有唯一的y与之对应。
计算: R S , R S , R, R S , R S .
先求出R和S,再计算。 解: R = {(2, 2), (2, 4), (2, 6), (3, 3), (3, 6), (4, 4), (5, 5), (6, 6)} S = {(2, 3), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6), (4, 5), (4, 6), (5, 6)}
例 A = {a, b}, B = {1, 2, 3},判断下式是否成立。
R {( a,3), (a,2), (b,1), (b,3)} A B ? A B {( a,1), (a,2), (a,3), (b,1), (b,2), (b,3)}.
2.1 关系的概念
空关系
设A,B是集合,R是A到B的二元关系,若R= , 则称R为空关系。
Chapter 2 关系
贾 敏
母 女
母女
母子
父 子 表兄妹
Chapter 2 关系
Chapter 2 关系
三个学生选修了5门课程中部分课程,并且根据 学习情况由任课教师给出了他们的成绩。如何表 达学生、课程和成绩之间的关系?
离散数学第二章
注意:
有些关系既不是对称的也不是反对称的;
0 1 0 1 0 1 0 0 0
可以是既是对称的,也是反对称的
如相等关系
24
定义2.10:在集合X上的关系R,如果有:
x, y R且 y, z R ,则必有 x, z R ,
即非对角线上的1, 对称位置必须是0; 而非对角线上的0 不做要求
判断方法:
1. 如果如果存在a到b的有向边,就不存在b到a的有向边。 (逆命题不成立,即可以两条有向边都不存在); 2. 关系矩阵中,如果 a j ,i 1则ai , j 0,这里i j
(注意:a j ,i 0不一定ai , j 1)
n个
容易证明: n m nm m n i: R R R , R R mn ,m,n均为正整数 0 ii: R 是相等关系,即: R0 ={(x,x)|x∈A} 1 iii: R R
13
逆关系
由于关系中的元素是有序偶,则如果将该有序偶的顺
序颠倒,会得到一个新的关系,称之为逆关系。
~ ~ ~
~
补集的逆关系
~ ~ ~
(5) R S R S , R S R S
注意,这个跟德· 摩根律不一样
(6) R S R S
~
~
~
18
关系的重要性质
定义2.6:在集合X上的关系R,如果对任意 x X , 有 x, x R ,则称R是自反的。
如:整数集合上的相等关系、" " 关系等;
如果 miq mqj 1 即mij 0 ,则 miq mqj 1 即 ai , aq R且 aq , a j R 由传递性的定义可知,如果R为传递的, 必有 ai , a j R ,即应有 mij 1 2 即:当R是A上的传递关系时,如果 M R 中的元素 bij 0 , 则必须有 mij 1 ,反之亦然
第二章 二元关系(集合论讲义)

例 1.1 例 1.2
例 1.3 设 A 是非空集合, ρ ( A) 上的包含关系 ⊆ A 定义如下: ( B, C ) ∈⊆ A 当且仅当 B ⊆ C 。 例 1.4 设 A 是任意集合, A 上的恒等关系 I A 定义如下: I A = {( a, a ) : a ∈ A} 。 例 1.5 上的模 2 同余关系 M 2 定义如下: aM 2b 当且仅当 2 | (a − b) 。
(2) ( R1 ∪ R2 ) (3) ( R1 ∩ R2 ) (4) ( A × B ) (5) ∅
−1
−1
−1
= B× A
=∅
= R −1
−1 −1 = R1−1 − R2 −1 −1
(6) ( R )
−1
(7) ( R1 − R2 )
(8)若 R1 ⊆ R2 ,则 R1 ⊆ R2 复合运算
先看一个例子。兄妹关系为 R1 ,母子关系为 R2 , a 与 b 有兄妹关系, b 与 c 有母子关系, 即 aR1b , bR2 c ,则 a 与 c 有舅甥关系 R3 , R3 称为 R1 与 R2 的复合关系,记为 R3 = R1 R2 。
结点 ai 。如果 ai Ra j ,则画一条从结点 ai 到结点 a j 的带箭头的线段,称该线段为弧(有向 边) ;如果 ai Ra j ,则对应的弧称为自环。如此得到的图形称为 R 的关系图,记为 G ( R) 。 例 2.2 设 A = {1, 2,3, 4,5} , A 上的模 2 同余关系的关系图如图 2.1 所示。
第二章 二元关系
关系一词是大家所熟知的,它是指多个事物之间的一种特定意义的联系。在诸多的关系中, 最基本的是涉及两个对象的关系, 比方说父子关系, 师生关系, 同学关系等, 称为二元关系。 本章的目的是给出二元关系的性质和运算并重点介绍一些特殊类型的二元关系。
数据库原理第二章关系数据库
关系代数小结
❖ 传统的集合运算
▪ 并、差、交、笛卡尔积
❖ 专门的关系运算
▪ 选择、投影、连接、除
❖ 5种基本运算
▪ 并、差、笛卡尔积、投影、选择
二、关系演算
❖ 关系演算是以数理逻辑中的谓词演算为基础的,通过谓词 形式来表示查询表达式。
❖ 根据谓词变元的不同,可将关系演算分为元组关系演算和 域关系演算。前者以元组为变量,简称元组演算;后者以 域为变量,简称域演算。
❖ 元组关系演算
▪ Tuple Relational Calculus ,简称TRC ▪ 元组关系演算语言ALPHA ▪ 元组关系表达式
❖ 域关系运算
▪ Domain Relational Calculus ,简称DRC ▪ 域关系演算语言QUE
1、元组关系演算
❖ 元组关系演算是以元组变量作为谓词变元的基本对象。 ❖ 元组关系演算语言的典型代表是E.F.Codd提出的ALPHA
例2:查询一名男同学的教师号和姓名,并使他的年龄最小。
GET W (1) (Student) : Student. Ssex = ‘男’ up Student.Sage
▪ 所谓的定额查询就是通过在W后面的括号中加上定额数量, 限定查询出元组的个数。
▪ 这里(1)表示查询结果中男同学的个数,取出学生表中第一 个男同学的学号和姓名。
RANGE Course CX SC SCX
GET W (Student.Sname): SCX (SCX.Sno=Student.Sno∧ CX (o=o∧CX.Pcno='6'))
例5:查询选修全部课程的学生姓名。
RANGE SC X Course CX
GET W (Student.SN) : CXSCX (SCX.SNO=Student.SNO∧O=O)
第2章 关系模型

4. 关系模式
关系模式是关系的形式化描述。
最简单的表示为:
关系名(属性名1,属性名2,…,属性名n)
注意:主键要用下划线表明。但有时,关系模式 中并没有表明主键。 例如:Students关系的关系模式为:
Students(Sno,Sname,Ssex,Sbirthdate,Sdept)
一个二维表就是一个关系
字段
属性
元组 学号 1001 1002 1003 姓名 张军 李红 王伟
学生表
记录
年龄 21 22 19
性别 男 女 男
系号 D01 D01 D02
域:关系中一个属性的取值范围。例如,Ssex的取值 范围是{‘M’, ‘F’},代表性别为男性和女性。。
关系示例:
关系的等价术语之间的对应关系
实体(Entity):实体是客观存在的并且相互区分的事务。实体 可以是实际事务,也可以是抽象事件。例如,一个职工、一 个部门等属于实际的事务;一次订货、借阅若干本图书、一 场比赛等活动是比较抽象的事件。 实体集( Entity Set):同型实体的集合称为实体集。例如 全体职工集合,全馆图书等。 实体型( Entity Type):具有相同属性的实体具有共同的 特征和性质,用实体名及其属性名来抽象和刻画同类实体称 为实体型。例如实体型“职工”表示全体职工的概念,并不 具体指职工甲或职工乙。每个职工是职工实体“型”的一个 具体“值”,必须明确区分“型”与“值”的概念。在数据 模型中的实体均是指“型”而言的。以后在不致引起混淆的 情况下,说实体即是实体型。
关系模式即是一个表的表头描述。 表头也称为关系的结构、关系的型等。
除表头一行以外的所有行的集合(即表内 容), 称为关系的值。 一个关系(表),由表头和表内容两部分组 成,表头是相对不变的,而表内容是经常 改变的。如Students表中,当有新学生入 学时,就增加若干行,当学生毕业时,就 要删除若干行,所以表是动态的。
第二章-关系模型PPT课件

数据库系统概念
习题分析与解答
第二章 关系模型
Copyright © by ECNU CS DBLAB All rights reserved.
习题目录
习题2.1 (参阅课本P44) 习题2.3 (参阅课本P44) 习题2.5 (参阅课本P45) 习题2.7 (参阅课本P45) 习题2.9 (参阅课本P45) 习题2.11 (参阅课本P45)
12
❖第二章 关系模型
数据库系统概念
2.5.c. 找出First Bank Corporation所有年收入在10 000美元 以上的员工的姓名和居住的街道、城市。
参考解答: c. ∏person-name,street,city (σcompany-name=“First Bank Corporation”∧salary>10000(works ∞ emplyee))
employee(person_name,street,city) works(person_name,company_name,salary) company(company_name,city) manages(person_name,manager_name)
Copyright © by ECNU CS DBLAB All rights reserved.
Copyright © by ECNU CS DBLAB All rights reserved.
7
❖第二章 关系模型
数据库系统概念
2.3.a. 修改数据库,使Jones现在居住在Newtown
参考解答: a.employee←∏emplyee-name,street,city←“Newtown”(σ employee=“Jones”(employee))∪
高中数学必修知识点总结:第二章_直线与平面的位置关系

第二章直线与平面的位置关系1. 三个公理:<1)公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内公理1作用:判断直线是否在平面内<2)公理2:过不在一条直线上的三点,有且只有一个平面。
公理2作用:确定一个平面的依据。
<3)公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线。
公理3作用:判定两个平面是否相交的依据2.空间的两条直线有如下三种关系:相交直线:同一平面内,有且只有一个公共点;共面直线平行直线:同一平面内,没有公共点;异面直线:不同在任何一个平面内,没有公共点。
3.公理4:平行于同一条直线的两条直线互相平行。
公理4作用:判断空间两条直线平行的依据。
4.等角定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补5.注意点:① a'与b'所成的角的大小只由a、b的相互位置来确定,与O的选择无关,为简便,点O一般取在两直线中的一条上;b5E2RGbCAP② 两条异面直线所成的角θ∈(0, >;③ 当两条异面直线所成的角是直角时,我们就说这两条异面直线互相垂直,记作a⊥b;④ 两条直线互相垂直,有共面垂直与异面垂直两种情形;⑤ 计算中,通常把两条异面直线所成的角转化为两条相交直线所成的角。
6.直线与平面有三种位置关系:<1)直线在平面内——有无数个公共点<2)直线与平面相交——有且只有一个公共点<3)直线在平面平行——没有公共点7.直线与平面平行的判定定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行。
简记为:线线平行,则线面平行。
8.两个平面平行的判定定理:一个平面内的两条交直线与另一个平面平行,则这两个平面平行。
9.定理:一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行。
简记为:线面平行则线线平行。
作用:利用该定理可解决直线间的平行问题。
10.定理:如果两个平面同时与第三个平面相交,那么它们的交线平行。
数据库基础-第二章 关系数据模型与关系运算

2.2 关系代数
数据查询基本运算
❖1.关系属性的指定——投影运算 这个操作是对一个关系进行垂直分割,消去某些列,并 重新安排列的顺序。
i1,i2,,in(R) {t | t ti1,ti2,,tin t1,t2,,tk R}
例子2-3
❖2.关系元组选定——选择运算 选择操作是根据某些条件对关系做水平分割,即选取符合 条件的元组。
R S {t | t R t S}
式中“-”为差运算符,t为元组变量,结果R-S为一个新的与R、S兼
容的关系,该关系是由属于R而且不属于S的元组构成的集合,即 在R中减去与S中相同的那些元组。
关系 R
A
B
C
a1
b1
c1
a1
b2
c2
a2
b2
c1
关系 R∪S
A
B
C
a1
b1
c1
a1
b2
c2
a2
b2 c2
a1
b2
c2
a2
b2
c1
图 2.9 关系 R 和关系 S 及其交运算
2.2 关系代数
2.除法运算
设关系R和S的元数分别为r和s(设r>s>0),那么R÷S是一个(r-s)元的 元组的集合。(R÷S)是满足下列条件的最大关系:其中每个元组t与S中 每个元组u组成的新元组<t,u>必在关系R中。
S# (S) S# (SC)
例2-7 在关系C中增加一门新课程(C13, ML, C3, null): 如果令这门新课程元组所构成的关系为R,则有: R=(C13,ML,C3,null),这时结果为:C∪R。
学生关系:S (S# ,Sn, Sex,Sa ,Sd) ; 课程关系:C (C# ,Cn ,P#,Tn) ; 选课关系:SC (S#, C# ,G),
离散数学基础(洪帆)第二章_关系

二、 两关系矩阵的乘积
定义
设M1是一个(i,j)通路(即第i行、第j列的元素)为
r 的l×m关系矩阵,
(2) r M2是一个(i,j)通路为 ij 的m×n关系矩阵,
(1) ij
则M1与M2乘积记为M1﹒M2是一个l×n的矩阵,
其(i,j)通路为: rij
(r r )
(1) ik (2) kj k=1
1 1 2
2
3
4
3
4
图(1)
图(2)
4. 关系矩阵 定义 设集合A={a1,a2,…,an},B={b1,b2,…,bm} 是由A到B的关系, 则 的关系矩阵 定义为一个n行、m列的矩阵, 记为 M , 且关系矩阵的第i行、第j列的元素 rij
定义如下:
1 若 a i b j rij 0 若 a i 'b j
1 0 1 0
1 1 0 0
1 1 1 1
2.3 关系的复合
一、关系的一般运算:交、并、补、差 例1 设A={4,6,9,10}, 1 和 2 是A上的两个关系:
1 ={(a,b)|(a-b)/2是正整数}, 2 ={(a,b)|(a-b)/3是正整数}
试求:1 2 , 1 2 , 1 , 1 2 , 1 2 ,
例3 设A={a,b,c,d},A上的关系: ={(a,a),(a,b),(b,d),(c,a),(d,c)} 4 试求复合关系 。
2.4 复合关系的关系矩阵和关系图
一、布尔运算 布尔运算只涉及数字0和1, 数字的加法和乘法按照以下方式进行: 0+0=0 0+1=1+0=1+1=1 1· 1=1 1· 0=0· 1=0· 0=0 如:(1· 1)+(0· 1· 1)+(1· 0· 0)+1+0=1
数据库 第二章 关系数据库

关系的描述称为关系模式,在上图中二维表的表头那行
称为关系模式,又称表的框架。
(2)形式化定义 :
R(U,D,Dom,F)
其中:R表示关系名;
U表示组成该关系的属性集合;
D表示U中属性所来自的域;
Dom表示属性向域的映像的集合
F表示属性间数据的依赖关系集合
上一页 下一页 第一页 最末页
退出
第一节 关系数据结构及形式化定义
一、和”关系”相关的概念定义 二、“关系”相关的概念 三、关系数据库中关系的类型 四、数据库中基本关系的性质
上一页 下一页 第一页 最末页
退出
一、和”关系”相关的概念定义
1、域:P47 2、笛卡儿积:P48 3、关系:P48
上一页 下一页 第一页 最末页
退出
域的定义
专业号 001 002
专业名 计算机应用 信息管理
二、DBMS在维护完整性方面具备的功能
1、提供定义完整性约束条件的机制 2、提供完整性检查的方法 3、违约处理
1、实体完整性
(1)定义:Primary key ->主键 (2)检查:
①对基本表插入一条记录 ②对基本表的主码进行更新 (3)违约处理 ① 若主码不唯一则拒绝插入或修改 ②若主码的各个属性有一个为空则拒绝插入或修改
3、参照完整性(Referential Integrity)
(1)外码 (2)参照完整性规则
外码(Foreign Key)
• 外码的定义:设F是基本关系R的一个或一组属性,但 不是R的码,如果F与基本关系S的主码相对应,则 称F为基本关系R的外码。并称R为参照关系,S为被 参照关系。
• 外码举例: 学生(学号,姓名,性别,专业号,年龄) 专业(专业号,专业名)
第2章关系数据库

(2)模型概念单一。 (3)集合操作:操作对象和结果都是元组的集合,即关系。
LOGO
2.1 关系模型的基本概念
2.1.3 关系模型、关系子模式、关系内模式
美国国家标准学会(ANSI)所属标准计划和要求委员 会在1975年公布的研究报告中,把数据库分为三级:模式、 外模式和内模式。对用户而言可以对应分为概念级模式、 一般用户级模式和物理级模式(其体系结构如图2-1)。 关系模型中,概念模式是关系模式的集合,外模式是关系 子模式的集合,内模式是存储模式的集合。
2,…,n}
其中每一个元素(d 1 ,d 2 ,…,d n)称为一个n元组(nTuple),或简称为元组(Tuple)通常元素中的每一个值d i
称为一个分量。
LOGO
2.1 关系模型的基本概念来自❖ 两个集合R和S的笛卡尔积(或只是乘积)是元素对的集合, 该元素对是通过选择R的任何元素作为第一个元素,S的元 素作为第二个元素构成的。该乘积用RS表示。当R和S是 关系时,乘积本质上相同。
LOGO
2.1 关系模型的基本概念
1. 关系模式
关系实质上是一张二维表,表的每一行为一个元组, 每一列为一个属性。一个元组就是该关系所涉及的属性集 的笛卡尔积的一个元素。关系是元组的集合,也就是笛卡 尔积的一个子集。因此关系模式必须指出这个元组集合的 结构,即它由哪些属性构成,这些属性来自哪些域,以及 属性与域之间的映象关系。
•计算机专业
•李喆
•刘德成
•通信专业
•吕景刚
•刘德成
•通信专业
•王弶
•刘德成
•通信专业
•李喆
LOGO
第二章人地关系

可持续发展思想
• 1972年,联合国人类环境会议,人类第一次关于全球环 境战略的国际会议,标志着环境开始纳入国际事务议程; 就环境论环境,并未找到正确的解决办法。 • 1980年,《世界自然保护战略》,从资源保护的角度提 出要实现SD,并认为SD “强调人类通过对生物圈的管
理,使生物圈既能满足当代人的最大持续利益,又能保
可持续发展思想
• 1992年,联合国环境与发展大会,标志着SD被各国普 遍接受;人类已经认识到发展与环境相辅相成,不可 人为割裂开来;人类转变传统发展模式和传统生活方 式的重要里程碑。 • 2002年,联合国可持续发展世界首脑会议。《执行计 划》被认为是关系到全球未来10至20年环境与发展进 程走向的路线图,是国际社会在SD领域积极努力的最 新结晶。
• 地域空间乃是地理学的独特性视角。
从区域差异方面;从空间联系方面。
二、地理学的主要任务
• • 人地关系地域系统的形成过程、结构特点和发展趋向的理论研究; ②人地系统中各子系统相互作用的强度分析、潜力估算、后效评价和风 险分析;
•
• • • •
③人与地两大系统间相互作用和物质、能量传递与转换的机理、功能、 结构和整体调控的途径与对策;
适应论
生态论
巴罗斯 地理学是“人类生态学的科学” 研究人类对自然环境的反映(在人地关系中人是中 心论题,其他现象只是当它们涉及人及其对它们的反 应时,才有必要说明。) 地理学应侧重于分析人类在空间上的关系。
四、和谐论与可持续发展思想
• 20C60S以来,人地关系失调 • 人类活动对自然系统的破坏越来越严重地威胁着人类 未来的生存和发展。人类应摆正自然的位臵,人类活 动不要突破生物圈的承受能力;把自然视为调适的对 象,使“人类事务同自然规律相协调”,走人与自然 关系协调的可持续发展之路。 • “协调论”与“和谐论”的人地关系思想,赋予了古 老的人地关系以崭新的历史意义。
第二章线性自由能关系

第二章 线性自由能关系(LFER )一.线性自由能关系的建立在结构和反应性之间的定量关系研究中,常常可以观察到一个反应系列的速度常数与另一反应系列某些参数之间存在一定的关系,这里所指的反应系列是指据相同的反应机理进行的一组密切相关的反应,通常以下式表示:C k m k A B +=lg lg (1) or C K m k A B +=log log (2)A 、B 分别代表两个反应系列, k 为速度常数, K 为平衡常数在反应系列A 和B 中各个反应之间的变化是相同的,这些变化包括反应物中的取代基的变化,试剂或溶剂的变化等。
一般将其中的反应系列A 作为标准反应或模型反应,它们通常是那些比较熟悉,简单或实验数据充足的反应,如m 、p —取代的苯甲酸乙酯X-C 6H 4COOEt 的碱性水解速度常数的对数(B k )与相应的取代的苯甲酸COOH H XC 46的电离常数的对数(A k log )之间存在着上式所示的线性关系,在这两个反应系列中,变化的都是反应物的取代基X ,其中取代苯甲酸的电离是标准反应。
在实际研究中,通常在每个反应系列中选择一个反应作为整个反应系列的参考反应,如上例中,选X=H 为参考反应,其速度常数和平衡常数分别为0k 和0K ,将上式减去 参考反应的对应式,则得)/lg()/lg(00A A B B k k m k k = (3))/l g ()/l g (00A A B B K K m k k = (4)这样,由标准反应系列的)/lg(0A A k k or )/lg(0A A K K 就定义了反应速度与结构定量关系中的参数。
平衡常数,速度常数分别与标准Gibbs 自由能变化︒∆G 和活化Gibbs 自由能≠∆0G 相关:RT G K 3.2/lg ︒∆-=' (5) RT G NhRT k 3.2/)lg(lg 0≠∆-= (6) 将上述关系代入(1),(2),并考虑到实验在恒温下进行,即得(7)常数+∆=∆≠≠A B G m G 00 (7)或 常数+∆=∆≠00A B G m G因此,两个反应系列之间若存在线性关系(1)或(2),则表明反应系列B 的活化Gibbs 自由能与反应系列A 的活化Gibbs 自由能改变或标准Gibbs 自由能之间存在着线性关系,这种关系可以更一般地表示为(8)常数+∆=∆A B G m G (8)当B G ∆是反应B 的标准自由能改变0B G ∆,则可得到与平衡常数有关的线性关系,ΔG 也可以用其他参数表示,如氧化还原势能和波谱参数(如IR,UV 和NMR 吸收频率等),凡是可以有上述Gibbs 自由能关系得到的各种关系,都称为线性自由能关系(LFER ),本章将主要讨论与速度有关的一些主要LFER 。
第2章 关系代数与关系数据库理论

01 传统的集合运算(举例)
R和S ➢ 具有相同的目n(即两个关系都有n个属性) ➢ 相应的属性取自同一个域
23
01 传统的集合运算(举例)
24
关系代数及其运算
关系的数学定义 关系代数概述 传统的集合运算 专门的关系运算
01
PART ONE
01 专门的关系运算
专门的关系运算包括选择、投影、连接、除等。 为了叙述上的方便,先引入几个记号: (1)设关系模式为R(A1,A2,…,An),它的一个关系设为R, t∈R 表示t是R的一个元组,t[Ai]表示元组t中相应于属性Ai 上的一个分量。 (2)若A={Ai1,Ai2,…,Aik},其中Ai1,Ai2,…,Aik是A1, A2,…,An中的一部分,则A称为字段名或域列。 t[A]=(t[Ai1],t[Ai2],…,t[Aik])表示元组 t 在字段名 A 上诸 分量的集合。 Aഥ 表示{A1,A2,…,An)中去掉{Ai1,Ai2,…, Aik}后剩余的属性组。
10
01 关系的数学定义
➢ 基数(Cardinal number) • 若Di(i=1,2,…,n)为有限集,其基数为 mi(i=1,2,…,n} • 则D1×D2×…×Dn的基数M为:
➢ 笛卡尔积的表示方法 • 笛卡尔积可表示为一个二维表。 • 表中的每行对应一个元组,表中的每列对应一 个域。
11
例1:查询学生的学号和姓名。 ➢πSno,Sname(Student)或π1,2(Student) ➢ 查询结果:
37
01 专门的关系运算
连接(Join) ➢ 连接也称为θ连接 ➢ 连接运算的含义: • 从两个关系的笛卡尔积中选取属性间满足一定条 件的元组 • A和B:分别为R和S上度数相等且可比的属性组 • θ:比较运算符 ➢ 从R和S的笛卡尔积R×S中选取R关系在A属性组上的值 与S关系在B属性组上的值满足比较关系θ的元组。
第二章 形与形的关系
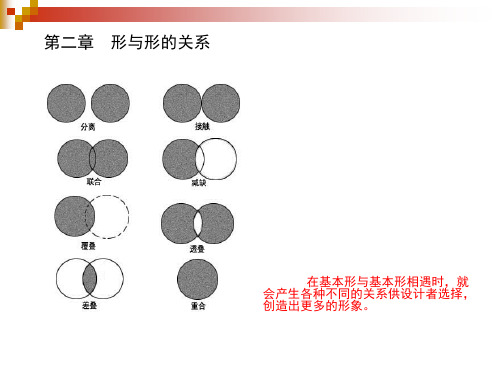
来成为同一个空间平面内的较大的新的形象。 4、减缺:形象与形象相互重叠,覆盖产生了前后上下关系,保留覆盖在 上面的形象,后面被 上面覆盖所留下的剩余形象为减缺的新形象。 5、覆叠:一个形象覆叠在另一个形象上,覆盖在上面的形象不变,而被 覆叠的形象就有所变化,覆叠的位置不同也就产生出不同的形象,并产生 上与下、前与后的空间关系。 6、透叠:形象与形象相互交错重叠,交错重叠部分为交叠。重叠部分具 有透明性,不掩盖形象的轮廓也不定分出前后或者上下的空间关系。 7、差叠:两个形象相互交叠,交叠部分成为新的形象,其余部分被减去。 8、重合:两个相同的形象,不相互交错,其中一个覆盖在另一个上,成 为合二为一,完全重合的形象。
第二章
形与形的关系
在基本形与基本形相遇时,就 会产生各种不同的关系供设计者选择, 创造出更多的形象。
第二章 形与形的关系
不接触,呈现出各自的图形。 2、接触:形和形的边缘恰好相切。 3、联合:形象与形象交错重叠,不分前后上下关系,而把两个形象联合
起
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.4 关系上的闭包运算
• 例:设集合A={a,b,c,d},定义 R={(a,b),(b,a),(b,c),(c,d)},求r(R),s(R),t(R) • 解:
r(R)=RUQ ={(a,a),(b,b),(c,c),(a,b),(b,a),(b,c),(c,d)} % s(R)=RU R ={(a,b),(b,a),(b,c),(c,b),(c,d),(d,c)} t(R)=RUR2UR3UR4 ={(a,b),(b,a),(b,c),(c,d)} U {(a,a),(a,c),(b,b),(b,d)} U {(a,b),(a,d),(b,a),(b,c)} U {(a,a),(a,c),(b,b),(b,d)} ={(a,a),(b,b),(a,b),(a,c),(a,d),(b,a),(b,c),(b,d),(c,d)}
2.2 关系的运算
• 定理(复合运算满足结合律):
– 设R、S、T分别表示从X到Y、Y到Z、Z到U 的关系,则有
(RoS) oT = Ro(SoT) = RoSoT • 定义2.4
设有一个集合X上的关系R,则Rn可定义如下: 1)R1=R 2)Rn+1=RnoR
故,RmoRn=Rm+n
(Rm)n=Rm×n
% R={(a,1),(b,1),(c,1)}
2.2 关系的运算
• 定理
– 设R,S分别是从X到Y及Y到Z的关系,则有 % % 1) R=R % % 2) R ∪ S=R ∪ S % % 3) R ∩ S=R ∩ S 4) R × S=S × R % % 5) (R o S)=S o R
2.3 关系的重要性质
– 在集合X上的关系R,如果有(x,y) ∈R且x≠y, 必有(y,x)∉R,则称R是反对称 反对称的 反对称 • 例:有一些人的集合中“同事”关系是对称的, “父子”关系则是反对称的。 • 在集合X={1,2,3,4}上的关系R: R={(1,2),(2,1),(3,4),(4,2)}既不是对称的也不是反 对称的
2.4 关系上的闭包运算
• 例: 整数集Z上的“<”关系的自反闭包是“≤” 关系;对称闭包是“≠”关系;传递闭包是它本 身。
• 定理:
– 设R是集合X上的关系,则 % r(R)=RUQ,其中Q={(x,x) | x∈X} R ∞ s(R)=RU i UR t(R)= i =1 =RUR2UR3U… 设X是有限集,并设X有n个元素,则 U Ri t(R)= i=1
0 1 MR = 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0
2.2 关系的运算
• 关系的交、并、补、差
– 关系是特殊的集合 – 有关集合的交、并、补、差在关系中也 适用,有关集合运算的一些公式在关系 中也适用
2.2 关系的运算
• 复合运算 • 定义2.3
– 设R是一个从X到Y的关系,S是一个从Y到Z 的关系,则R与S的复合关系: RoS={(x,z) | x∈X,z∈Z,至少存在一个y∈Y有 (x,y)∈R且(y,z)∈S} 计算方法: 1)从定义入手 2)有向图法 3)布尔矩阵 M 'RoS = M R × M s
2.3 关系的重要性质
• 一个集合X上的关系可能具有上述5个性质中的 若干性质. • 全关系是自反的、对称的,传递的 • 空关系是反自反的、对称的、反对称的,传递的 • 例:设集合A={a,b,c,d},判定下列关系具有什么性质
1)R1={(a,a),(b,a)} 反对称的,传递的 2)R2={(c,d)} 反自反的,反对称的,传递的 3)R3={(a,a),(b,b),(c,c)} 自反的,对称的,反对称的,传递的
• 例:集合A={1,2,…,10}的关系
R={(x,y) ∣x+y=10且x,y∈A},则R具有什么性质? 解:R={(1,9),(2,8),(3,7),(4,6),(5,5),(6,4),(7,3),(8,2),(9,1)} R是对称的
2.3 关系的重要性质
• b c c a
2.4 关系上的闭包运算
• 集合A上的二元关系R的闭包运算可以复合,例 如ts(R)=t(s(R))表示R的对称闭包的传递闭包, 可以简称为R的对称传递闭包。tsr(R)则表示R的 自反对称传递闭包。 • 定理:
设R是集合A的二元关系,则有 1) 如果R是自反的,那么s(R)和t(R)也是自反的; 2) 如果R是对称的,那么r(R)和t(R)也是对称的; 3) 如果R是传递的,那么r(R)也是传递的 4) rs(R)=st(R) 5) rt(R)=tr(R) 6) ts(R)⊇st(R)
2.2 关系的运算
• 逆运算
是一种一元运算,其结果组成的关系,称关系的 逆关系.
• 定义2.5
– 设R是一个从X到Y的关系,即R={(x,y) | % x∈X,y∈Y},则从Y到X的关系 R % R = {( y, x) ( x, y ) ∈ R} 称为R的逆关系.
• 例:R={(1,a),(2,b),(3,c)}
2.1 关系的基本概念
• 大型的计算机结构中或一个大型软件结构 中所谓的内部逻辑关系复杂,所指的“逻 辑关系”就是这里的“关系”,只要把这 些结构内的关系搞清,则任何结构的“正 确性”“可靠性”就迎刃而解了.
2.1 关系的基本概念
• 关系的图的表示法 • 一个集合X={x1,x2,…,xn}上的关系可用一 关系图表示之.集合X中元素可用图中结点 R (x ) 表示;关系R的有序偶(xi,xj)可用图中从结 点xi到xj的有向边表示。 • 例: 0 1 0 0 0 0
2.2 关系的运算
• 例:
设R和S是集合X={0,1,2,3}上的关系,有 R={(x,y) | j=i+1 或 j=i/2} S={(x,y) | i=j+2} 求 RoS,SoR
• 解:
R={(0,1),(1,2),(2,3),(0,0),(2,1)} S={(2,0),(3,1)} RoS={(1,0),(2,1)} SoR={(2,1),(2,0),(3,2)}
• • • • • 自反性 反自反性 对称性 反对称性 传递性
2.3 关系的重要性质
• 定义2.6
– 在集合X上的关系R,如对任意x∈X,有 (x,x)∈R,则R是自反 自反的 自反
• 定义2.7
– 在集合X上的关系R,如对任意x∈X,有 (x,x)∉ R,则R是反自反 反自反的 反自反
• 例: • 在整数集Z上的关系,“≤”是自反的,不是反自反的; “<”是反自反的,不是自反的。 • 在集合X={1,2,3,4}上的关系R:R={(1,1),(2,1),(3,4),(4,2)} 既不是自反的也不是反自反的
2.4 关系上的闭包运算
• 例:设有X上的关系R1,R2, 且R1⊇R2,试证 1) r(R1)⊇r(R2) 2) s(R1)⊇s(R2) 3) t(R1)⊇t(R2) • 证明: 1) 因为R1⊇ 2, 所以R1∪E⊇R2∪E, 即r(R1)=r(R2) ⊇R ⊇ % % 2) 因为R1⊇ 2, 所以 R1 ⊇ R 2 ⊇R % % 所以 R1 ∪ R1 ⊇ R 2 ∪ R 2, 即s(R1)=s(R2) 3) 对任意的n∈N, 根据数学归纳法可知: R1 ⊇ R 2 ⇒ R n ⊇ R n 2 1 又因为t(R)=RUR2UR3U…, 所以t(R1)⊇t(R2)
2.1 关系的基本概念
• 如果从X到Y不存在某种关系R,则称这种 关系为空关系 空关系,如果从X的每个元素到Y 空关系 的每个元素之间均具有某种关系,则称此 关系为全关系 全关系. 全关系 • 从X到Y的全关系即X×Y. • 定义2.2
– 由集合X1、X2、…、Xn所确定的的n元关系 元关系是 元关系 X1×X2×…×Xn的一个子集
• 例:
– 在一些人的集合上,“同事”关系是传递的, 但“父子”关系不是传递的 – 整数集Z上的“<”、“≤”都是传递的 – 一些城市所组成的集合上,“线路的连通” 关系是传递的
2.3 关系的重要性质
• 注意:
• 一个关系可以 – 既不是自反的,又不是反自反的; – 即是对称的,又是反对称的; • 根据定义,一个有序偶的第一元素和第二 元素如果可以交换且存在反对称关系的话, 则第一和第二元素应该相同 – 但是传递与非传递不能同时存在 • 传递意为如果有(a,b),(b,c)就应该有(a,c), 如果没有(a,c)就是非传递,一个关系要么 是传递的要么是非传递的,两者只能居其 一,而如果没有(a,b)(b,c)出现的情况也归 为满足传递性。
2.5 次序关系
• 定义2.12
– 集合X上的关系R如果是自反的、反对称的、 传递的,则称R在X上是偏序 偏序的或称R是集合X 偏序 上的偏序关系。而称集合X为R的偏序集 偏序集用 偏序集 (X,R)表示. – 一般用符号“≤”表示偏序 (有时我们用x<y表示x≤y,且x≠y)
第二章 关系
• 本章将研究集合内元素之间的关联 以及集合之间元素的关联,这就是 “关系” • “关系”是很重要的基本数学概念, 它在各数学领域中均有很大的作用, 并且对研究计算机科学中许多问题 都是很好的数学工具
2.1 关系的基本概念
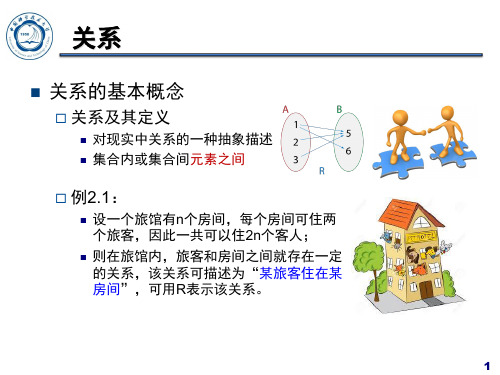
• 定义2.1
– 从集合A到集合B的一个关系 关系R是A与B的笛卡 关系 尔积A×B的一个子集 • 关系R中有序偶第一个客体所允许选取对象的集 合称为关系R的定义域,记以D(R),第二个客体 所允许选取对象集合称为关系R的值域,记以 C(R) • 在特殊情况下,当D(R)=C(R)=M时,M为一集合, 此时称为关系为M上的关系 • 例:实数集R上的“>”关系可以定义为: > = {(x,y) | x∈R, y∈R,且x>y}
c
(a) • 解:
(b)
(c)
