3.8 神经网络训练步骤

合集下载

神经网络的训练步骤和部署方法

神经网络的训练步骤和部署方法
训练一个网络的三要素：结构、算法、权值
网络模型一旦选定，三要素中结构和算法就确定了，接下来要对权值进行调整。

神经网络是将一组训练集（training set）送入网络，根据网络的实际输出与期望输出间的差别来调整权值。

训练模型的步骤：
选择样本集合的一个样本（Ai Bi）（数据标签）
送入网络，计算网络的实际输出Y（此时网络中的权重都是随机的）
计算D=Bi -Y（预测值与实际值的差）
根据误差D调整权值矩阵W
对每个样本重复上述过程，直到对整个样本集来说，误差不超过规定范围。

使用神经网络框架
Caffe是一种开源的软件框架，利用这套框架，我们可以实现新的网络、修改已有的神经网络、训练网络、编写网络使用。

实现新的网络
1 数据打包
2 编写网络结构文件
3 编写网络求解文件
4 开始训练
caffe的文件结构
data 用于存放下载的训练数据
例如安装后会有mnist ilsvrc12 cifar10
docs example 使用的帮助文档和代码样例
使用与部署。

神经网络模型的训练过程及参数调整策略

神经网络模型的训练过程及参数调整策略神经网络作为机器学习领域的重要技术之一，已经在各个领域取得了显著的成就。

但是，神经网络模型的训练过程和参数调整策略在过去被认为是非常复杂和困难的。

本文将介绍神经网络模型的训练过程，并讨论一些参数调整策略，以帮助读者更好地理解和应用神经网络模型。

神经网络模型的训练过程可以分为两个主要阶段：前向传播和反向传播。

在前向传播过程中，输入数据通过从输入层到隐藏层再到输出层的一系列运算，得到神经网络模型的输出结果。

在反向传播过程中，根据输出结果与真实结果的误差，通过调整模型中的参数来最小化误差，并更新模型的权重和偏置。

这个过程将多次迭代执行，直到模型的输出结果能够较好地拟合给定的训练数据。

在神经网络模型的训练过程中，参数调整策略起着至关重要的作用。

下面将介绍一些常用的参数调整策略：1. 学习率调整：学习率是指神经网络模型在每次更新参数时的步长，即网络权重和偏置的调整大小。

过大的学习率可能导致模型发散，而过小的学习率可能导致模型收敛过慢。

因此，合理选择学习率是非常重要的。

常见的学习率调整策略包括固定学习率、逐渐减小学习率和自适应学习率等。

2. 正则化：神经网络模型通常具有大量的参数，容易过拟合训练数据。

为了解决过拟合问题，可以使用正则化技术。

常用的正则化技术包括L1正则化和L2正则化。

L1正则化通过在损失函数中添加参数的绝对值来限制参数的大小，从而促使模型更加稀疏。

L2正则化通过在损失函数中添加参数的平方来限制参数的大小，从而使模型的权重分布更加均匀。

3. 批量规范化：批量规范化是一种常用的用于加速神经网络训练和提高模型性能的技术。

它通过对每个批次的输入数据进行标准化，缩放和平移来稳定模型的训练过程。

批量规范化可以提高网络的收敛速度，减少训练中的梯度消失和梯度爆炸问题。

4. dropout正则化：dropout正则化是一种用于防止神经网络过拟合的技术。

在每次训练迭代中，dropout会随机地关闭一些神经元的连接，从而迫使网络在没有完整信息的情况下进行预测。

神经网络模型中的网络结构优化与训练教程

神经网络模型中的网络结构优化与训练教程神经网络模型是计算机科学领域中一种重要的机器学习方法，具有强大的数据处理和模式识别能力。

在构建神经网络模型时，选择合适的网络结构和进行有效的训练是十分关键的步骤。

本文将介绍神经网络模型中的网络结构优化与训练的教程，帮助读者了解如何优化网络结构和进行有效的训练。

1. 网络结构优化神经网络模型的网络结构包括输入层、隐藏层和输出层。

优化网络结构可以提高模型的性能和泛化能力。

下面将介绍几种常用的网络结构优化方法。

1.1 激活函数选择激活函数可以引入非线性变换，在神经网络中起到关键作用。

常用的激活函数有Sigmoid函数、ReLU函数和Tanh函数等。

在选择激活函数时，需要根据具体的任务需求和数据特点进行选择。

1.2 隐藏层数与神经元个数隐藏层数和神经元个数是网络结构中的重要参数。

增加隐藏层数可以提高网络的表达能力，但也会增加模型的复杂度。

神经元个数的选择要根据数据集的大小和复杂度进行调整，避免过拟合或欠拟合。

1.3 正则化正则化是一种常用的提高模型泛化能力的方法。

常见的正则化方法有L1正则化和L2正则化。

通过加入正则化项，可以降低模型的复杂度，减少过拟合的风险。

1.4 DropoutDropout是一种常用的正则化技术，可以在训练过程中随机地使一部分神经元失活。

这样可以减少神经元之间的依赖关系，增强模型的泛化能力。

2. 训练方法2.1 数据预处理在进行神经网络模型的训练之前，需要对原始数据进行预处理。

常见的预处理方法包括数据归一化、特征缩放和数据平衡等。

数据预处理可以提高训练的效果和模型的稳定性。

2.2 损失函数选择神经网络模型的训练过程中需要选择合适的损失函数。

根据任务的性质，常见的损失函数有均方误差损失函数、交叉熵损失函数和对比损失函数等。

选择合适的损失函数可以使模型更好地拟合数据。

2.3 批量梯度下降法批量梯度下降法是一种常用的训练方法，通过迭代更新模型参数来最小化损失函数。

神经网络训练的技巧和方法(六)

神经网络训练是机器学习领域中的重要技术，它在语音识别、图像识别、自然语言处理等领域有着广泛的应用。

然而，神经网络训练并不是一件容易的事情，需要掌握一定的技巧和方法。

本文将探讨神经网络训练的技巧和方法，帮助读者更好地理解和应用这一技术。

数据预处理数据预处理是神经网络训练的第一步，也是至关重要的一步。

良好的数据预处理可以提高训练的效果。

首先，需要对数据进行标准化处理，使得数据分布在一个较小的范围内，这有助于加快训练速度。

其次，需要对数据进行归一化处理，将数据转化为均匀分布或正态分布，以减小特征之间的差异性。

此外，还需要对数据进行去噪处理，剔除一些噪声数据，以提高训练的准确性。

选择合适的神经网络结构在进行神经网络训练之前，需要选择合适的神经网络结构。

不同的任务和数据集需要不同的网络结构。

例如，对于图像识别任务，常用的网络结构包括LeNet、AlexNet、VGG、GoogLeNet和ResNet等。

而对于自然语言处理任务，常用的网络结构包括RNN、LSTM和Transformer等。

选择合适的网络结构可以提高训练的效果。

合适的损失函数和优化器选择合适的损失函数和优化器也是神经网络训练的关键。

不同的任务需要选择不同的损失函数，例如，对于分类任务，常用的损失函数包括交叉熵损失函数；对于回归任务，常用的损失函数包括均方误差损失函数。

而优化器的选择也很重要，常用的优化器包括SGD、Adam、RMSprop等。

选择合适的损失函数和优化器可以提高训练的效果，加快收敛速度。

超参数调优超参数的选择对神经网络训练也有着重要影响。

常见的超参数包括学习率、批大小、正则化参数等。

学习率是影响训练速度和效果的重要超参数，通常需要进行调优。

批大小也需要进行合理选择，过大的批大小可能导致收敛速度慢，过小的批大小可能导致收敛不稳定。

正则化参数也需要进行调优，以防止过拟合。

数据增强数据增强是提高神经网络训练效果的常用技巧。

通过对原始数据进行一些变换，可以生成更多的训练样本，从而提高网络的泛化能力。

神经网络的训练与优化方法

神经网络的训练与优化方法1.梯度下降（Gradient Descent）梯度下降是神经网络中最常用的优化方法之一、其基本原理是通过不断调整网络参数来降低损失函数的值。

具体而言，梯度下降通过计算参数梯度的负方向来更新参数，以减小损失函数的值。

这个过程可以看作是在参数空间中找到损失函数最小值的下降过程。

2.反向传播算法（Backpropagation）反向传播算法是训练神经网络的关键算法之一、它通过不断计算损失函数对每个参数的梯度来更新参数。

反向传播算法基于链式法则，通过递归计算每一层的梯度来得到整个网络的梯度。

反向传播算法为神经网络提供了高效的梯度计算方法，使得网络可以在大规模数据上进行训练。

3.正则化（Regularization）正则化是一种常用的优化方法，用于防止神经网络过拟合。

过拟合是指模型在训练集上表现很好，但在测试集或实际应用场景中表现较差。

正则化通过在损失函数中引入额外的项来控制网络的复杂程度。

常用的正则化方法包括L1正则化、L2正则化以及Dropout等。

4.优化器（Optimizers）优化器是神经网络训练中常用的工具，用于找到损失函数的最小值。

常见的优化器包括随机梯度下降（SGD）、动量优化器（Momentum）、Nesterov动量优化器、Adagrad、RMSProp和Adam等。

它们的目标都是在每次参数更新时调整学习率以提高训练效果，并加速收敛过程。

5.学习率调整（Learning Rate Adjustment）学习率是指网络在训练过程中每次参数更新的步长。

学习率的选择直接影响网络的训练速度和性能。

通常来说，学习率过大可能导致网络不稳定，学习率过小可能导致网络收敛过慢。

因此，一般会采用学习率衰减或自适应学习率的方法来调整学习率。

常见的学习率调整策略有固定衰减、指数衰减、余弦退火等。

6.批量训练（Batch Training）批量训练是指在训练过程中使用一定数量的样本进行参数更新。

神经网络使用方法及步骤详解

神经网络使用方法及步骤详解随着人工智能的快速发展，神经网络成为了一个热门的研究方向。

神经网络是一种模拟人脑神经元相互连接的计算模型，它可以用来解决各种复杂的问题。

本文将详细介绍神经网络的使用方法及步骤。

一、神经网络的基本原理神经网络由多个神经元组成，这些神经元之间通过连接进行信息传递。

每个神经元都有一个权重，用来调整信号的传递强度。

神经网络通过不断调整权重，从而学习到输入和输出之间的映射关系。

这个过程称为训练。

二、神经网络的训练步骤1. 数据准备：首先，需要准备一组有标签的训练数据。

标签是指输入和输出之间的对应关系。

例如，如果要训练一个神经网络来识别手写数字，那么输入就是一张手写数字的图片，输出就是对应的数字。

2. 网络结构设计：接下来，需要设计神经网络的结构。

神经网络通常包括输入层、隐藏层和输出层。

输入层负责接收输入数据，隐藏层用来提取特征，输出层用来产生结果。

3. 权重初始化：在训练之前，需要对神经网络的权重进行初始化。

通常可以使用随机数来初始化权重。

4. 前向传播：在训练过程中，需要将输入数据通过神经网络进行前向传播。

前向传播是指将输入数据从输入层经过隐藏层传递到输出层的过程。

在每个神经元中，输入数据将与权重相乘，并经过激活函数处理，得到输出。

5. 计算损失：在前向传播之后，需要计算神经网络的输出与标签之间的差距，这个差距称为损失。

常用的损失函数有均方误差和交叉熵等。

6. 反向传播：反向传播是指根据损失来调整神经网络的权重，使得损失最小化。

反向传播通过计算损失对权重的导数，然后根据导数来更新权重。

7. 权重更新：通过反向传播计算得到权重的导数之后，可以使用梯度下降等优化算法来更新权重。

优化算法的目标是使得损失函数最小化。

8. 重复训练：以上步骤需要重复多次，直到神经网络的损失收敛到一个较小的值为止。

三、神经网络的应用神经网络在各个领域都有广泛的应用。

其中，图像识别是神经网络的一个重要应用之一。

神经网络训练步骤

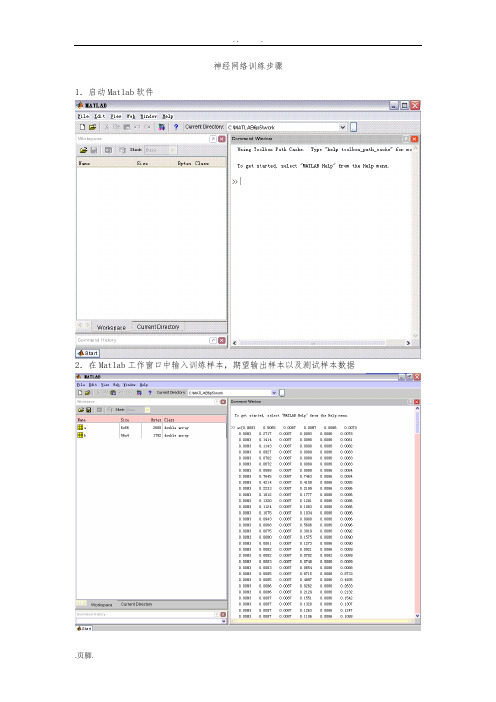
神经网络训练步骤
1．启动Matlab软件
2．在Matlab工作窗口中输入训练样本，期望输出样本以及测试样本数据
3．建立神经网络
在Matlab工作窗口中输入nntool得到神经网络工具箱
4．按import按钮导入输入及目标值
5．按new network按钮建立神经网络
6．在Network Type下拉菜单中选择相应的神经网络
7．在input data的右侧下拉菜单中选择导入的输入样本
8．在Target data的右侧下拉菜单中选择导入的期望输出
9．在Spread constant中选择训练次数
10．按View按钮可以查看具体的神经网络结构
11．按Create按钮，神经网络即建立并训练好
12．选中建立的神经网络然后按simulate按钮即进入仿真状态
13．在input下拉菜单中选择测试样本，然后按Simulate Network按钮进行测试
14．按Export按钮将network1_outputs结果导出到Matlab的工作窗口
15．在Matlab的工作窗口中输入network1_outputs即可得到测试结果。

神经网络训练方法

神经网络训练方法神经网络是一种模拟人脑神经元网络的计算模型，它由输入层、隐藏层和输出层组成。

而神经网络的训练方法主要有监督学习和无监督学习两种。

监督学习是神经网络中最常见的训练方法，它的目标是让神经网络从已知数据中学习到输入和输出之间的映射关系。

具体来说，监督学习通过将输入样本输入到神经网络中，在输出层产生预测结果，然后将预测结果与真实标签进行比较，根据比较结果来调整神经网络的参数，使得预测结果和真实标签之间的差距最小化。

这个调整参数的过程称为反向传播算法(backpropagation)。

反向传播算法的核心思想是通过计算预测结果和真实标签之间的差异来计算损失函数(loss function)，然后通过链式法则来逐层计算每个神经元对损失函数的贡献。

最后根据这些贡献来调整神经网络的参数。

具体来说，反向传播算法首先将损失函数对输出层的权重和偏置求偏导数，然后将这些偏导数传递给隐藏层，再将偏导数传递给输入层，最后根据偏导数的值来调整权重和偏置。

除了反向传播算法，监督学习中还需要选择适当的损失函数。

常见的损失函数包括均方误差(Mean Squared Error, MSE)和交叉熵(Cross Entropy)。

均方误差适用于回归问题，它衡量了预测值与真实值之间的平均差距。

而交叉熵适用于分类问题，它衡量了预测概率分布与真实类别分布之间的差异。

除了监督学习，神经网络还可以使用无监督学习进行训练。

无监督学习不需要真实标签，其目标是从未标注的数据中学习到数据的结构和模式。

常见的无监督学习方法包括自编码器(Autoencoder)和生成对抗网络(Generative Adversarial Network, GAN)。

自编码器是一种包含编码器和解码器的神经网络，它尝试学习到一组潜在表示，可以用来重构输入数据。

自编码器的训练过程可以通过最小化输入数据和重构数据之间的重建误差来完成，其中编码器将输入数据映射到潜在表示，而解码器将潜在表示映射回输入空间。

神经网络模型及训练流程深入解析

神经网络模型及训练流程深入解析神经网络模型是深度学习中最基本的组成部分之一。

它是一种由人工神经元组成的计算模型，可以模拟和处理复杂的非线性关系。

神经网络模型通常包含输入层、隐藏层和输出层，通过层与层之间的连接，实现信息的传递和处理。

一、神经网络模型结构神经网络模型的结构通常是层级的，其中包含多个神经元组成的层。

输入层接收外部的输入数据，隐藏层负责处理输入数据并提取特征，输出层产生最终的预测结果。

隐藏层可以有多个，层数越多越能提取更高级别的特征。

在神经网络模型中，每个神经元与上一层的所有神经元相连接。

每个连接都有一个权重值，表示该连接的重要性。

神经元根据输入数据和连接权重进行加权求和，并通过激活函数将求和结果转换为输出。

常用的激活函数有sigmoid函数、ReLU函数等。

二、神经网络模型的训练流程神经网络模型的训练是通过调整连接权重和偏置值，使得模型的预测结果与真实值尽可能接近的过程。

训练流程通常包括前向传播和反向传播两个阶段。

1. 前向传播首先，将训练数据输入到神经网络模型的输入层。

然后，通过每个神经元将数据传递到隐藏层和输出层，直至得到最终的预测结果。

在传递的过程中，每个神经元根据输入数据和连接权重计算加权求和，并通过激活函数产生输出结果。

2. 反向传播在前向传播的基础上，需要计算损失函数，用于衡量模型预测结果与真实值之间的差异。

常用的损失函数有均方误差、交叉熵等。

通过计算损失函数，可以得到模型对于输入数据的预测误差。

接下来，需要利用误差进行反向传播。

反向传播从输出层向输入层反向计算，通过链式法则更新连接权重和偏置值，使得误差逐渐减小。

通常使用梯度下降算法来更新权重和偏置值，根据梯度的负方向调整参数值。

重复进行前向传播和反向传播多个轮次，直到模型的训练误差达到一个满意的水平为止。

三、常用的神经网络模型1. 前馈神经网络（Feedforward Neural Network）前馈神经网络是最简单的神经网络模型，其中信息只能在一个方向上流动，即从输入层到输出层。

神经网络的构建与训练方法

神经网络的构建与训练方法随着人工智能技术的发展，神经网络已经成为了人工智能领域中最为热门的技术之一。

而神经网络的构建与训练方法也是神经网络技术中最为核心的内容之一。

在这篇文章中，我将为大家详细介绍神经网络的构建与训练方法。

一、神经元模型神经网络是由许多神经元组成的，在构建神经网络之前，我们必须先了解神经元模型。

神经元模型是指神经元的工作原理和输入输出规律，有了这个模型，我们才能建立神经网络。

神经元模型可以采用不同的形式，其中最为常见的是感知器模型。

感知器模型是一种非常简单的神经元模型，它只接受二进制输入，并产生二进制输出。

感知器模型被广泛应用于分类问题中。

二、神经网络结构神经网络结构是指神经网络中神经元之间的连接方式和层数等结构。

神经网络结构的设计十分重要，一定程度上决定了神经网络的性能。

神经网络结构可以分为许多不同的类型，其中最为常见的是前馈神经网络。

前馈神经网络的结构是一层接着一层，每一层之间都是全连接的。

前馈神经网络可以进行多种任务，如分类、回归等。

另外，常见的神经网络结构还包括循环神经网络、卷积神经网络等。

三、神经网络训练算法神经网络的性能取决于神经网络的参数，因此，神经网络需要进行训练，得到最佳的参数。

神经网络训练算法可以分为两种：有监督学习和无监督学习。

有监督学习是指神经网络利用一定的标签信息进行训练。

无监督学习是指神经网络在没有标签信息的情况下进行训练。

常见的有监督学习算法包括反向传播算法、Lee-Carter算法等。

反向传播算法是目前最为常见的神经网络训练算法，它通过正向传播计算神经网络输出，然后通过反向传播计算误差，最后通过梯度下降法更新权重。

常见的无监督学习算法包括自编码器模型、受限玻尔兹曼机等。

自编码器是一种无监督学习算法，它通过学习输入数据的结构，来学习输入数据的自然表示。

四、神经网络的优化神经网络的优化是指如何优化神经网络的性能。

神经网络性能的优化可以从两个方面入手：减小误差和提高泛化能力。

简述神经网络的训练流程

简述神经网络的训练流程英文回答：1. Data Preprocessing.The first step in training a neural network is to preprocess the data. This involves cleaning the data, removing outliers, and normalizing the features.2. Model Selection.Once the data is preprocessed, the next step is to select a neural network model. There are many different types of neural network models, each with its own strengths and weaknesses. The best model for a particular task will depend on the specific data and the desired outcome.3. Hyperparameter Tuning.Once a neural network model has been selected, the nextstep is to tune the hyperparameters. Hyperparameters are settings that control the learning process of the neural network. The optimal values for the hyperparameters will vary depending on the data and the model.4. Training.Once the hyperparameters have been tuned, the next step is to train the neural network. Training involves feeding the neural network data and adjusting the weights of the network so that it can learn to make accurate predictions.5. Evaluation.Once the neural network has been trained, the next step is to evaluate its performance. This involves testing the neural network on a new dataset and measuring its accuracy.6. Deployment.Once the neural network has been evaluated and its performance is satisfactory, the next step is to deploy theneural network. This involves making the neural network available for use by other applications.中文回答：1. 数据预处理。

神经网络训练的技巧和方法

神经网络训练的技巧和方法神经网络是一种受到生物神经系统启发而设计的人工智能模型，它可以通过学习来识别模式、进行预测和做出决策。

神经网络的训练是指通过给定的输入数据和相应的期望输出，调整网络的参数，使得网络能够更好地拟合数据。

在神经网络的训练过程中，有很多技巧和方法可以帮助提高训练的效率和性能。

数据预处理在进行神经网络训练之前，首先需要对数据进行预处理。

数据预处理的目的是使得输入数据更加适合神经网络的学习。

常见的数据预处理方法包括归一化、标准化、降噪和特征选择。

归一化可以将不同特征的取值范围统一到相同的尺度上，从而避免某些特征对网络训练的影响过大。

标准化可以使得数据的均值为0，方差为1，这有助于加速神经网络的收敛过程。

降噪可以去除数据中的噪声，提高网络对输入数据的鲁棒性。

特征选择可以去除冗余的特征，减少网络的复杂度，同时提高网络的泛化能力。

选择合适的损失函数在神经网络的训练过程中，损失函数扮演着非常重要的角色。

损失函数用来衡量网络的预测值与实际值之间的差异，通过最小化损失函数来调整网络的参数。

不同的任务和数据集适合不同的损失函数。

对于分类任务，常用的损失函数包括交叉熵损失函数和sigmoid损失函数；对于回归任务，常用的损失函数包括均方误差损失函数和Huber损失函数。

选择合适的损失函数可以帮助网络更好地拟合数据，提高网络的泛化能力。

合理设置学习率学习率是神经网络训练过程中的一个重要超参数。

学习率决定了网络参数在每次迭代中的更新步长。

如果学习率过大，会导致网络参数在优化过程中不稳定，甚至发散；如果学习率过小，会导致网络收敛速度过慢。

因此，合理设置学习率对于神经网络的训练非常重要。

通常可以通过学习率衰减策略来动态调整学习率，比如指数衰减、余弦退火等方法。

另外，也可以尝试不同的优化算法，比如随机梯度下降、动量法、Adam等，来找到合适的学习率。

使用正则化技术在神经网络的训练过程中，很容易出现过拟合的问题，即网络在训练集上表现良好，但在测试集上表现较差。

神经网络算法的训练过程是怎样的

神经网络算法的训练过程是怎样的在当今的科技世界中，神经网络算法已经成为了一个非常热门的话题。

它在图像识别、语音处理、自然语言处理等众多领域都取得了令人瞩目的成就。

那么，神经网络算法的训练过程到底是怎样的呢？让我们一起来揭开它神秘的面纱。

要理解神经网络算法的训练过程，首先得知道什么是神经网络。

简单来说，神经网络就像是一个非常复杂的数学模型，它由大量的节点（也称为神经元）组成，这些节点通过连接形成一个网络结构。

每个节点都会接收一些输入，并根据一定的规则进行计算，然后输出结果。

神经网络算法的训练，其实就是让这个网络能够学习到如何从输入数据中准确地预测出输出。

这就好比教一个孩子认识各种动物，我们给孩子看很多动物的图片，并告诉他们这是什么动物，经过多次的学习和纠正，孩子就能够逐渐学会自己分辨不同的动物。

训练的第一步是数据准备。

就像给孩子学习用的图片一样，我们需要为神经网络准备大量的有代表性的数据。

这些数据通常会被分为两部分：训练集和测试集。

训练集是用来让神经网络学习的，而测试集则是用来检验学习效果的。

数据准备好之后，接下来就是确定神经网络的结构。

这包括确定神经元的数量、层数，以及它们之间的连接方式等。

就好像盖房子要先设计好框架一样，神经网络的结构决定了它能够学习到什么样的知识和模式。

然后，我们要为神经网络定义一个损失函数。

损失函数就像是一个衡量标准，它用来评估神经网络的输出与真实值之间的差距。

差距越大，损失函数的值就越大；差距越小，损失函数的值就越小。

接下来就是训练的核心步骤——优化。

在这个过程中，神经网络会根据损失函数的值来调整自身的参数，以减小损失。

这就像是孩子在学习过程中不断调整自己的认知方式，以达到更好的学习效果。

优化的方法有很多种，其中最常见的是梯度下降法。

想象一下你在一个山坡上，想要找到最低点，你会朝着坡度最陡的方向走一步，然后再看看位置是不是更低了，如果不是，就调整方向继续走。

神经网络也是这样，通过计算损失函数对每个参数的梯度，来确定参数调整的方向和大小。

神经网络的训练方法和技巧

神经网络的训练方法和技巧神经网络作为一种强大的机器学习模型，在许多领域都取得了巨大的成功。

但是，神经网络的训练和调整需要一定的技巧和方法，以提高其性能和准确度。

本文将介绍一些常用的神经网络训练方法和技巧，帮助您更好地理解和运用神经网络。

首先，我们将介绍梯度下降方法。

梯度下降是最常用的神经网络优化方法之一。

其主要思想是根据损失函数的梯度方向来调整网络的参数，使得损失函数的值不断降低。

在每次迭代中，通过计算损失函数关于参数的偏导数，来更新参数的值。

梯度下降方法有多个变种，包括批量梯度下降（Batch Gradient Descent）、随机梯度下降（Stochastic Gradient Descent）和小批量梯度下降（Mini-batch Gradient Descent）。

这些方法的不同之处在于每次迭代更新参数时所使用的样本数量。

其次，我们将介绍正则化技巧。

正则化是一种用于减小模型过拟合的方法。

过拟合是指模型在训练集上表现良好，但在测试集或新样本上表现较差的现象。

正则化可以通过添加正则化项来调整损失函数，限制参数的取值范围，以防止模型过拟合。

常用的正则化技巧包括L1正则化和L2正则化。

L1正则化通过在损失函数中添加参数的绝对值之和，使得模型更倾向于产生稀疏的权重矩阵。

L2正则化通过在损失函数中添加参数的平方和，使得模型对参数的取值有一个约束，以减小参数的变动范围。

接下来，我们将介绍学习率调度。

学习率是指控制参数更新幅度的因子，它决定了每次迭代中调整参数的幅度大小。

学习率过大可能导致模型无法收敛，学习率过小则会导致模型训练速度过慢。

学习率调度可以根据训练过程中的情况来自适应地调整学习率。

常用的学习率调度方法包括固定学习率、学习率衰减、动量和自适应学习率等。

固定学习率是指在训练过程中保持学习率不变；学习率衰减是指随着训练的进行逐渐减小学习率；动量是指在更新参数时添加一个动量项，加速参数调整过程；自适应学习率可以根据梯度的大小自动调整学习率。

神经网络的训练方法和优化算法

神经网络的训练方法和优化算法神经网络是一种模仿生物神经网络结构和功能的数学模型，它是一个多层逐级处理信息的网络。

神经网络已经被广泛应用于许多领域，如语音识别、图像识别、自然语言处理等。

在应用神经网络之前，需要先对它进行训练，以使该网络能够完成一个特定的任务。

本文将介绍神经网络的训练方法和优化算法。

神经网络的训练方法神经网络的训练是通过不断地调整网络的权重和偏置来实现的。

在训练神经网络之前，需要先定义一个损失函数。

损失函数是用来衡量网络输出结果与实际结果之间的差距的函数。

常用的损失函数包括均方误差(MSE)、交叉熵等。

反向传播算法是一种常用的训练神经网络的方法。

它是基于梯度下降算法的。

梯度下降算法的目标是寻找损失函数的全局最小值或局部最小值，以最小化误差。

反向传播算法是一种基于权重的调整算法。

它通过计算神经网络输出结果的误差，然后将误差反向传播到每个神经元，以调整各层之间的权重和偏置。

改进的反向传播算法随着神经网络的发展，人们提出了许多改进的反向传播算法。

其中最流行的是以下三种：1、动量算法动量算法是一种在梯度下降算法的基础上增加了动量因子的方法。

动量因子是一个介于0和1之间的值。

它起到减少震荡，增加学习速度的作用。

动量算法可以避免梯度下降算法陷入局部最优值。

2、自适应学习率算法自适应学习率算法是一种在反向传播算法中自适应调整学习速率的算法。

它采用Adagrad或RMSProp等自适应学习率算法，根据每个权重和偏置的历史梯度来调整学习速率。

这个算法可以实现自适应优化, 适用于各种复杂的非凸优化问题。

3、Adam算法Adam算法是一种综合了梯度下降算法、动量算法和自适应学习率算法的方法。

它是一种自适应学习率算法，能够自适应的调整每个参数的学习率。

通过Adam算法，可以快速收敛到全局最小值，并且具有较好的鲁棒性。

神经网络的优化算法神经网络的优化算法旨在优化网络的性能，减少网络预测结果与实际结果之间的误差。

神经网络的学习与训练

神经网络的学习与训练神经网络是一种基于数学模型的人工智能算法，它可以通过学习和训练来逐渐提升自身的预测、分类、识别等能力。

在现代社会中，神经网络的应用场景越来越广泛，从图像识别、自然语言处理到股票预测、医疗诊断等领域，都有着广泛的应用。

那么，神经网络的学习与训练是如何实现的呢？首先，神经网络的学习需要依靠大量的数据。

这些数据可以来自于各个领域的数据集，比如ImageNet、MNIST、CIFAR等图像数据集以及开放中文情感分析数据集等自然语言处理数据集。

通过这些数据，神经网络可以逐渐掌握某一领域的特征、规律和规律变化趋势。

在数据准备好之后，就需要定义神经网络的结构了。

神经网络的结构由多个神经元（或称节点）组成，每个神经元都有自己的输入和输出，其中输入通常是来自其他神经元或外部数据源的值，输出则是经过一定计算之后得到的结果。

神经元之间的连接权重则是神经网络的关键所在，它反映了不同神经元之间的关联程度。

同时，每个神经元都有一个激活函数，它可以将输入信号转化为输出信号，这样就形成了一个神经网络。

接下来就是训练神经网络了。

训练神经网络需要使用各种算法，比如基于梯度下降的优化算法、自适应学习速率的优化算法等。

这些算法可以自动地调整神经元之间的连接权重，以最小化输出结果与实际值之间的误差。

一般而言，训练神经网络需要进行多次迭代，每次迭代都会调整权重并更新神经网络的参数，直到误差达到可接受的范围为止。

除此之外，还有许多提升神经网络学习效果的技巧。

比如说，可以使用dropout技术，随机地将某些神经元的输出值置为0，从而防止过拟合；也可以使用卷积神经网络（CNNs）来提升图像识别的效果，因为CNNs可以有效地压缩图像信息，从而提高分类精度等等。

总之，神经网络的学习和训练是一个相对比较复杂的过程，但它给我们带来的强大预测和处理能力是非常可观的。

今后，随着技术的不断提升和应用场景的不断丰富，相信神经网络的应用前景也将越来越广阔。

神经网络的训练的大致流程

# 训练神经网络 with tf.Session() as sess:
# 参数初始化 init_op = tf.global_variables_initializer() sess.run(init_op)
...
# 训练模型。 STEPS = ... # 迭代的更新参数 for i in range(STEPS):
# 准备batch_size个训练数据。一般将所有训练数据打乱之后再选取可以得到更好的优化效果。 current_X, current_Y = ... # 对`tf.GraphKeys.TRAINABLE_VARIABLES`集合中的变量进行优化，使得当前batch下损失最小 sess.run(train_step, feed_dict = {x : current_X, y : current_Y})
博主请问怎么按照co样
神经网络的训练的大致流程
batch_size = n
# 每次读取一小部分数据作为当前的训练数据来执行反向传播算法 x = tf.placeholder(tf.float32, shape=(batch_size, feature_num), name="x-input") y_= tf.placeholder(tf.float32, shape=(batch_size, 1), name='y-input')
# 定义神经网络结构和优化算法 loss = ... # loss = -tf.reduce_mean(y_ * tf.log(tf.clip_by_value(y, 1e-10, 1.0))) learning_rate = 0.001
## cross_entropy(交叉熵)
#定义反向传播算法 train_step = tf.train.AdamOptimizer(learning_rate).minimize(loss) # 优化算法

3.8 神经网络训练步骤

2.6神经网络训练步骤
1．获取训练样本集
获取训练样本集合是训练神经网络的第一步，也是十分重要和关键的一步。它包括训练数据的收集、分析、选择和预处理等。首先要在大量的测量数据中确定出最主要的输人模式。即对测量数据进行相关性分析，找出其中最主要的量作为输人。在确定了主要输人量后，要对其进行预处理，将数据变化到一定的范围，如[−1,1] 或[0,1]等，并剔除野点，同时还可以检验其是否存在周期性、固定变化趋势或其它关系。对数据的预处理分析的目的是使得到的数据便于神经网络学习和训练。
2．选择网络类型与结构
神经网络的类型很多，需要根据任务的性质和要求来选择合适的网络类型。如对函数估计问题，可选用BP网络。当然也可以设计一个新的网络类型，来满足特定任务的需要，但这一般比较困难。通常是从已有的网络类型中选择一种比较简单而又满足要求的网络。网络类型确定后，就要确定网络的结构及参数。以BP 网络为例，就是要确定网络的层数、每层的节点数、节点激活函数、初始权值、学习算法等。如前所述，这些选项有一定的指导原则，但更多的是靠经验和试凑。对具体问题，若输人输出确定后，则网络的输入层和输出层节点数即可确定。关于隐层及其节点数的选择比较复杂。一般原则是：在能正确反映输入输出关系的基础上，应选用较少的隐步是利用获取的训练样本对网络进行反复训练，直至得到合适的映射结果。这里应注意的是，并非训练的次数越多，结果就越能正确反映输入输出的映射关系。这是由于所收集到的样本数据都包含有测量噪声，训练次数过多，网络将噪声也复制了下来，反而影响了它的泛化能力。在训练过程中，网络初始权值的选择可采用随机法产生。为避免产生局部极值，可选取多组初始权值，然后通过检验测试误差来选用一组较为理想的初始权值。

神经网络训练的过程

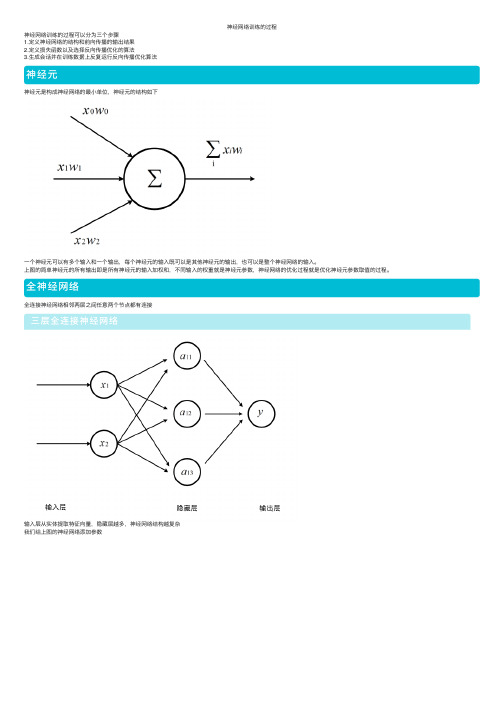
神经⽹络训练的过程神经⽹络训练的过程可以分为三个步骤1.定义神经⽹络的结构和前向传播的输出结果2.定义损失函数以及选择反向传播优化的算法3.⽣成会话并在训练数据上反复运⾏反向传播优化算法神经元神经元是构成神经⽹络的最⼩单位，神经元的结构如下⼀个神经元可以有多个输⼊和⼀个输出，每个神经元的输⼊既可以是其他神经元的输出，也可以是整个神经⽹络的输⼊。

上图的简单神经元的所有输出即是所有神经元的输⼊加权和，不同输⼊的权重就是神经元参数，神经⽹络的优化过程就是优化神经元参数取值的过程。

全神经⽹络全连接神经⽹络相邻两层之间任意两个节点都有连接三层全连接神经⽹络输⼊层从实体提取特征向量，隐藏层越多，神经⽹络结构越复杂我们给上图的神经⽹络添加参数W表⽰神经元的参数，上标为神经⽹络的层数，下标为连接节点标号，W的数值就为当前边上的权重。

隐藏层的a11的值就为对应的输⼊值的加权和输出y就是隐藏层的三个值的加权和线性模型如果模型的输出为输⼊的加权和，输出y和输⼊xi满⾜如下关系，则这个模型就是线性模型wi,b∈R是模型的参数，当输⼊只有⼀个的时候x和y就形成了⼀个⼆维坐标系的⼀条直线。

当有n输⼊时，就是⼀个n+1维空间的平⾯。

在现实世界中，绝⼤部分问题是⽆法线性分割的。

如果我们不运⽤激活函数的话，则输出信号将仅仅是⼀个简单的线性函数。

我们需要激活函数帮助我们理解和学习其他复杂类型的数据。

激活函数去线性化如果将每⼀个神经元的输出通过⼀个⾮线性函数，则整个神经⽹络的模型也就不再是线性的了。

整个⾮线性函数就是激活函数。

损失函数神经⽹络模型的效果及优化的⽬标是通过损失函数来定义的监督学习监督学习的思想就是在已知答案的标注数据集上，模型给出的结果要尽量接近真实的答案。

通过调整神经⽹络中的参数对训练数据进⾏拟合，使得模型对未知的样本提供预测能⼒。

反向传播算法反向传播算法实现了⼀个迭代的过程，每次迭代开始的时候，先取⼀部分训练数据，通过前向传播算法得到神经⽹络的预测结果。

神经网络训练流程表

神经网络训练流程表1. 数据准备
- 收集和清理数据
- 划分数据集(训练集、验证集、测试集)
- 数据预处理(标准化、编码等)
2. 定义网络架构
- 选择网络类型(全连接网络、卷积网络等)
- 确定网络层数和每层的神经元数量
- 选择激活函数(ReLU、Sigmoid等)
3. 构建模型
- 定义网络结构(输入层、隐藏层、输出层)
- 初始化权重和偏置
- 选择损失函数(交叉熵、均方误差等)
- 选择优化器(SGD、Adam等)
4. 训练模型
- 设置训练参数(批大小、学习率、epochs等) - 迭代训练
- 前向传播
- 计算损失
- 反向传播
- 更新权重和偏置
- 监控训练过程(损失曲线、准确率等)
- 保存模型权重
5. 模型评估
- 在验证集或测试集上评估模型性能
- 计算评估指标(准确率、精确率、召回率等)
6. 模型调整(可选)
- 根据评估结果调整模型
- 调整网络架构
- 修改超参数
- 增加训练数据
- 重复训练和评估步骤
7. 模型部署
- 将训练好的模型导出
- 在生产环境中部署模型。

3.8 神经网络训练步骤

神经网络的训练步骤和部署方法

神经网络模型的训练过程及参数调整策略

神经网络模型中的网络结构优化与训练教程

神经网络训练的技巧和方法(六)

神经网络的训练与优化方法

神经网络使用方法及步骤详解

神经网络训练步骤

神经网络 训练方法

神经网络模型及训练流程深入解析

神经网络的构建与训练方法

简述神经网络的训练流程

神经网络训练的技巧和方法

神经网络算法的训练过程是怎样的

神经网络的训练方法和技巧

神经网络的训练方法和优化算法

神经网络的学习与训练

神经网络的训练的大致流程

3.8 神经网络训练步骤

神经网络训练的过程

神经网络训练流程表

神经网络训练方法