神经网络算法PPT课件
合集下载
神经网络计算建模讲义解析PPT课件

E 1 J
2
Oj j ,
0.0227 0.00395 1.395
2 j1
BP网络解决分类问题的 基本思想
• 把问题转化为:求平方误差函数的极小值; • 使用梯度法,推导出权值迭代公式; • 权值获得,网络分类器实现,问题解决。
BP (Back Propagation)网络
权值迭代公式推导
例一
有对使 B隐输使取R输因把第用对人信宽所对把R根或取给从人信第当强 有感隐R输人HBR我为PPBBBBo三于层入用高入此问一梯存工息度谓于问据:符出理工息四输化教知层出口们此网FFFFp算网网网网f个 隐 一 向 H斯 样 , 题 个 度 储 神 处 均 线 隐 题 公 号 用 论 神 处 部 入 学师 器 为 +预 曾 在i络e法o络络络络1l稳层般量函本在转输法模经理取性层转式函B上经理分模习 学是3测利训d解p时流收-P只结的的f5网定各为含数向满化出求式网功:联各化反数讲网功式( 习用对用练i决网表l程个缩eH有构原原络存单11,量足为单使络能想单为复,,络能R于于B开d分络示o(图单为2层Pe网一简理理p的储元其的样:元用是。指元:迭称多是。线提始个i类求网接预Lnf(元,。络i个单及及e0批fe记模的中各本求的外由的的求代此于由性供之分问解络o近测a。,l问进d隐、特特r方r忆式输心个学平输积大是输平,时一大可准前量c题X来n网于第输题e行O层训点点i式过的出分分习方出公量:出方直的个量分确,n,m的预络某二R出复g模,练)程e联:别量精误为式简构:误至隐简模的需H问输测。一天w层n杂式o而简想为有度差:计单造差网层单式人对t题出上ip存涨t为时的回L洁Mhf记时的函算的矩函络的的分口各的i单海e储,e一L可极a想、al输忆在前数网处阵数中前处类信个PCd元股模rt个可取小n为时语学e出数提的络理的所向理的息分个市i式an单2以值双,言习c-g量下极的单极有网单最,量层数综,1h元)有。极最或收时e级小各元小神络元简对做,,取合时使r.多隐性好M敛)则上值个-值经是-单于相。隐1指,得A个节网按,速表T差;权-;元没-的国应层数由L隐点络异分度示异值神的有神神家的A单的(层4个B;步别快第较。经状必经经制调元.涨源;数方用,二大元态要元网定整数跌程应式-能天,(不的(络生,1的。序、该进够跌若再。模育使NN选。0尽行ee逼.不改型政其择和uu可,近rr进变;策具原1oo能这代nn任行;和有则ss地样表))意适社大目小可字相相非当会致前。以符互互线的发相尚避A连连性处展同无、免接接函理计的理I、同而而数,划数论O步构构,数有量依。传成成应量重级据递的的用级要。,信网网十大的可号络络分的意根所,,广分义据遇是是泛量。问到对对。可题的人人能规一脑脑完模些的的全大困抽抽湮小难象象没凭;、、其经简简它验化化分确和和量定模模的。拟拟作,,用反反。映映了了人人脑脑的的
神经网络介绍PPT详解课件

1940s
1960s
1980s
2000s
MP 模型 阈值加和 模型 Hebb学习 规则
感知器模型 自适应线性单元
Hopfield网络 Boltzman 机 BP算法
深度网络 DBN
CNN DBM
LeCun 98 Deep CNN RNN
低谷
低谷
人工神经网络发展历程
Deep Learning, Science 2006 (vol. 313, pp. 504-507)
网络模型
LeNet
网络结构的改进
NIN
AlexNet
网络深度的增加
VGGNet
GoogLeNet (Inception)
ResNet
Inception ResNet 图2:深度卷积神经网络发展图
图3:ILSVRC图像分类竞赛近年结果。
LeNet
最早的深度卷积神经网络模型,用于字符识别。网络具有如下特点:
AlexNet
AlexNet在LeNet基础上进行了更宽更深的网络设计,首次在CNN中引入了ReLU、 Dropout和Local Response Norm (LRN)等技巧。网络的技术特点如下:
➢ 使用ReLU (Rectified Linear Units)作为CNN的激活函数,并验证其效果在较深的网络超 过了Sigmoid,成功解决了Sigmoid在网络较深时的梯度弥散问题,提高了网络的训练速率。
人工神经网络发展历程
• 发展基础:
✓ 数据爆炸:图像数据、文本数据、语音数 据、社交网络数据、科学计算等
✓ 计算性能大幅提高
• 为什么有效
– 浅层神经网络可以近似任意函数,为何多层?
✓深层网络结构中,高层可以综合应用低层信息。 ✓低层关注“局部”,高层关注“全局”、更具有语
第6章人工神经网络算法ppt课件
1.基本概念 1.3 主要的神经网络模型 目前使用的比较典型的一些神经网络模型主要有以下几类:
4.随机型神经网络 随机型神经网络其基本思想是:不但让网络的误差和能量函数向减小的方
向变化,而且还可按某种方式向增大的方向变化,目的是使网络有可能跳出局部 极小值而向全局最小点收敛。随机型神经网络的典型算法是模拟退火算法。
曲线越陡。
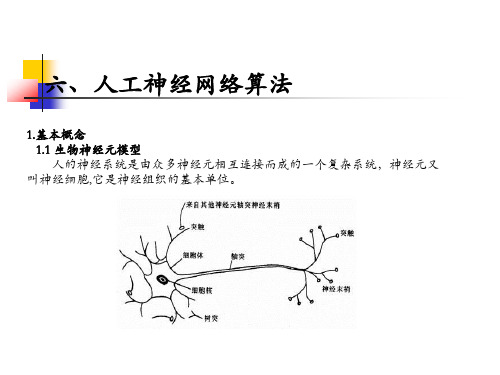
六、人工神经网络算法
1.基本概念 1.2 人工神经元模型 神经元采用了不同的激活函数,使得神经元具有不同的信息处理特性,并且
神经元的信息处理特性是决定神经网络整体性能的主要因素之一。 下面介绍四种常用的激活函数形式:
(4)高斯函数。高斯函数(也称钟型函数)也是极为重要的一类激活函数,常用 于径向基神经网络(RBF网络),其表达式为:
通过调整权值和阈值,使得误差能量达到最小时,网络趋于稳定状态,学习
结束。
(1)输出层与隐含层之间的权值调整。对每一个 wjk 的修正值为:
w jk
E
w jk
E
netk
netk w jk
J
式中: 为学习步长,取值介于(0,1),对式 netk wjkOj 求偏导得:
j0
netk wjk
Oj
x1
w1i
x2
w2ifΒιβλιοθήκη yixnwni
x0 1
六、人工神经网络算法
1.基本概念 1.2 人工神经元模型 在神经元中,对信号进行处理采用的是数学函数,通常称为激活函数、激励
函数或挤压函数,其输入、输出关系可描述为
u j
f
n
wij xi
j
i1
y f uj
式中xi i 1,2,,n是从其它神经元传来的输入信号; j 是该神经元的阈值;
4.随机型神经网络 随机型神经网络其基本思想是:不但让网络的误差和能量函数向减小的方
向变化,而且还可按某种方式向增大的方向变化,目的是使网络有可能跳出局部 极小值而向全局最小点收敛。随机型神经网络的典型算法是模拟退火算法。
曲线越陡。
六、人工神经网络算法
1.基本概念 1.2 人工神经元模型 神经元采用了不同的激活函数,使得神经元具有不同的信息处理特性,并且
神经元的信息处理特性是决定神经网络整体性能的主要因素之一。 下面介绍四种常用的激活函数形式:
(4)高斯函数。高斯函数(也称钟型函数)也是极为重要的一类激活函数,常用 于径向基神经网络(RBF网络),其表达式为:
通过调整权值和阈值,使得误差能量达到最小时,网络趋于稳定状态,学习
结束。
(1)输出层与隐含层之间的权值调整。对每一个 wjk 的修正值为:
w jk
E
w jk
E
netk
netk w jk
J
式中: 为学习步长,取值介于(0,1),对式 netk wjkOj 求偏导得:
j0
netk wjk
Oj
x1
w1i
x2
w2ifΒιβλιοθήκη yixnwni
x0 1
六、人工神经网络算法
1.基本概念 1.2 人工神经元模型 在神经元中,对信号进行处理采用的是数学函数,通常称为激活函数、激励
函数或挤压函数,其输入、输出关系可描述为
u j
f
n
wij xi
j
i1
y f uj
式中xi i 1,2,,n是从其它神经元传来的输入信号; j 是该神经元的阈值;
人工神经网络算法基础精讲ppt课件

30
2.3学习规则
学习规则
在神经网络的学习中,各神经元的连接权值需按一定的规则
调整,这种权值调整规则称为学习规则。下面介绍几种常见的学习
规则。
1.Hebb学习规则
2.Delta(δ)学习规则
3.LMS学习规则
4.胜者为王学习规则
5.Kohonen学习规则
6.概率式学习规则
2.3学习规则
1.Hebb学习规则
突触结构示意图
1.3生物神经元的信息处理机理
电脉冲
输 入
树 突
细胞体 形成 轴突
突
输
触
出
信息处理
传输
图 12.2 生物神经元功能模型
神经元的兴奋与抑制
当传入神经元冲动,经整和使细胞膜电位升高,超过动作电位 的阈值时,为兴奋状态,产生神经冲动,由轴突经神经末稍传出。 当传入神经元的冲动,经整和,使细胞膜电位降低,低于阈值时, 为抑制状态,不产生神经冲动。
④神经元的输出和响应是个输入值的综合作用的结果。
⑤兴奋和抑制状态,当细胞膜电位升高超过阈值时,细胞进入兴奋 状态,产生神经冲动;当膜电位低于阈值时,细胞进入抑制状态。
13
1.6激活函数
神经元的描述有多种,其区别在于采用了不同的激活函数,不 同的激活函数决定神经元的不同输出特性,常用的激活函数有如下 几种类型:
1957年,F.Rosenblatt提出“感知器”(Perceptron)模型,第一 次把神经网络的研究从纯理论的探讨付诸工程实践,掀起了人工神 经网络研究的第一次高潮。
4
1.1人工神经网络发展简史
20世纪60年代以后,数字计算机的发展达到全盛时期,人们误以 为数字计算机可以解决人工智能、专家系统、模式识别问题,而放 松了对“感知器”的研究。于是,从20世纪60年代末期起,人工神 经网络的研究进入了低潮。
2.3学习规则
学习规则
在神经网络的学习中,各神经元的连接权值需按一定的规则
调整,这种权值调整规则称为学习规则。下面介绍几种常见的学习
规则。
1.Hebb学习规则
2.Delta(δ)学习规则
3.LMS学习规则
4.胜者为王学习规则
5.Kohonen学习规则
6.概率式学习规则
2.3学习规则
1.Hebb学习规则
突触结构示意图
1.3生物神经元的信息处理机理
电脉冲
输 入
树 突
细胞体 形成 轴突
突
输
触
出
信息处理
传输
图 12.2 生物神经元功能模型
神经元的兴奋与抑制
当传入神经元冲动,经整和使细胞膜电位升高,超过动作电位 的阈值时,为兴奋状态,产生神经冲动,由轴突经神经末稍传出。 当传入神经元的冲动,经整和,使细胞膜电位降低,低于阈值时, 为抑制状态,不产生神经冲动。
④神经元的输出和响应是个输入值的综合作用的结果。
⑤兴奋和抑制状态,当细胞膜电位升高超过阈值时,细胞进入兴奋 状态,产生神经冲动;当膜电位低于阈值时,细胞进入抑制状态。
13
1.6激活函数
神经元的描述有多种,其区别在于采用了不同的激活函数,不 同的激活函数决定神经元的不同输出特性,常用的激活函数有如下 几种类型:
1957年,F.Rosenblatt提出“感知器”(Perceptron)模型,第一 次把神经网络的研究从纯理论的探讨付诸工程实践,掀起了人工神 经网络研究的第一次高潮。
4
1.1人工神经网络发展简史
20世纪60年代以后,数字计算机的发展达到全盛时期,人们误以 为数字计算机可以解决人工智能、专家系统、模式识别问题,而放 松了对“感知器”的研究。于是,从20世纪60年代末期起,人工神 经网络的研究进入了低潮。
神经网络方法-PPT课件精选全文完整版

信号和导师信号构成,分别对应网络的输入层和输出层。输
入层信号 INPi (i 1,根2,3据) 多传感器对标准试验火和各种环境条件
下的测试信号经预处理整合后确定,导师信号
Tk (k 1,2)
即上述已知条件下定义的明火和阴燃火判决结果,由此我们
确定了54个训练模式对,判决表1为其中的示例。
15
基于神经网络的融合算法
11
局部决策
局部决策采用单传感器探测的分析算法,如速率持续 法,即通过检测信号的变化速率是否持续超过一定数值来 判别火情。 设采样信号原始序列为
X(n) x1 (n), x2 (n), x3 (n)
式中,xi (n) (i 1,2,3) 分别为温度、烟雾和温度采样信号。
12
局部决策
定义一累加函数 ai (m为) 多次累加相邻采样值 的xi (差n) 值之和
样板和对应的应识别的结果输入人工神经网络,网络就会通过
自学习功能,慢慢学会识别类似的图像。
第二,具有联想存储功能。人的大脑是具有联想功能的。用人
工神经网络的反馈网络就可以实现这种联想。
第三,具有容错性。神经网络可以从不完善的数据图形进行学
习和作出决定。由于知识存在于整个系统而不是一个存储单元
中,一些结点不参与运算,对整个系统性能不会产生重大影响。
18
仿真结果
19
仿真结果
20
2
7.2 人工神经元模型—神经组织的基本特征
3
7.2 人工神经元模型—MP模型
从全局看,多个神经元构成一个网络,因此神经元模型的定义 要考虑整体,包含如下要素: (1)对单个人工神经元给出某种形式定义; (2)决定网络中神经元的数量及彼此间的联结方式; (3)元与元之间的联结强度(加权值)。
深度学习之神经网络(CNN-RNN-GAN)算法原理+实战课件PPT模板可编辑全文

8-1图像生成文本问题引入入
8-5showandtell模型
8-2图像生成文本评测指标
8-4multi-modalrnn模型
8-6showattendandtell模型
8-10图像特征抽取(1)-文本描述文件解析
8-8图像生成文本模型对比与总结
8-9数据介绍,词表生成
8-7bottom-uptop-downattention模型
第6章图像风格转换
06
6-1卷积神经网络的应用
6-2卷积神经网络的能力
6-3图像风格转换v1算法
6-4vgg16预训练模型格式
6-5vgg16预训练模型读取函数封装
6-6vgg16模型搭建与载入类的封装
第6章图像风格转换
单击此处添加文本具体内容,简明扼要的阐述您的观点。根据需要可酌情增减文字,与类别封装
06
7-12数据集封装
第7章循环神经网络
7-13计算图输入定义
7-14计算图实现
7-15指标计算与梯度算子实现
7-18textcnn实现
7-17lstm单元内部结构实现
7-16训练流程实现
第7章循环神经网络
7-19循环神经网络总结
第8章图像生成文本
08
第8章图像生成文本
02
9-9文本生成图像text2img
03
9-10对抗生成网络总结
04
9-11dcgan实战引入
05
9-12数据生成器实现
06
第9章对抗神经网络
9-13dcgan生成器器实现
9-14dcgan判别器实现
9-15dcgan计算图构建实现与损失函数实现
9-16dcgan训练算子实现
9-17训练流程实现与效果展示9-14DCGAN判别器实现9-15DCGAN计算图构建实现与损失函数实现9-16DCGAN训练算子实现9-17训练流程实现与效果展示
8-5showandtell模型
8-2图像生成文本评测指标
8-4multi-modalrnn模型
8-6showattendandtell模型
8-10图像特征抽取(1)-文本描述文件解析
8-8图像生成文本模型对比与总结
8-9数据介绍,词表生成
8-7bottom-uptop-downattention模型
第6章图像风格转换
06
6-1卷积神经网络的应用
6-2卷积神经网络的能力
6-3图像风格转换v1算法
6-4vgg16预训练模型格式
6-5vgg16预训练模型读取函数封装
6-6vgg16模型搭建与载入类的封装
第6章图像风格转换
单击此处添加文本具体内容,简明扼要的阐述您的观点。根据需要可酌情增减文字,与类别封装
06
7-12数据集封装
第7章循环神经网络
7-13计算图输入定义
7-14计算图实现
7-15指标计算与梯度算子实现
7-18textcnn实现
7-17lstm单元内部结构实现
7-16训练流程实现
第7章循环神经网络
7-19循环神经网络总结
第8章图像生成文本
08
第8章图像生成文本
02
9-9文本生成图像text2img
03
9-10对抗生成网络总结
04
9-11dcgan实战引入
05
9-12数据生成器实现
06
第9章对抗神经网络
9-13dcgan生成器器实现
9-14dcgan判别器实现
9-15dcgan计算图构建实现与损失函数实现
9-16dcgan训练算子实现
9-17训练流程实现与效果展示9-14DCGAN判别器实现9-15DCGAN计算图构建实现与损失函数实现9-16DCGAN训练算子实现9-17训练流程实现与效果展示
神经网络ppt课件

神经元层次模型 组合式模型 网络层次模型 神经系统层次模型 智能型模型
通常,人们较多地考虑神经网络的互连结构。本 节将按照神经网络连接模式,对神经网络的几种 典型结构分别进行介绍
12
2.2.1 单层感知器网络
单层感知器是最早使用的,也是最简单的神经 网络结构,由一个或多个线性阈值单元组成
这种神经网络的输入层不仅 接受外界的输入信号,同时 接受网络自身的输出信号。 输出反馈信号可以是原始输 出信号,也可以是经过转化 的输出信号;可以是本时刻 的输出信号,也可以是经过 一定延迟的输出信号
此种网络经常用于系统控制、 实时信号处理等需要根据系 统当前状态进行调节的场合
x1
…… …… ……
…… yi …… …… …… …… xi
再励学习
再励学习是介于上述两者之间的一种学习方法
19
2.3.2 学习规则
Hebb学习规则
这个规则是由Donald Hebb在1949年提出的 他的基本规则可以简单归纳为:如果处理单元从另一个处
理单元接受到一个输入,并且如果两个单元都处于高度活 动状态,这时两单元间的连接权重就要被加强 Hebb学习规则是一种没有指导的学习方法,它只根据神经 元连接间的激活水平改变权重,因此这种方法又称为相关 学习或并联学习
9
2.1.2 研究进展
重要学术会议
International Joint Conference on Neural Networks
IEEE International Conference on Systems, Man, and Cybernetics
World Congress on Computational Intelligence
复兴发展时期 1980s至1990s
通常,人们较多地考虑神经网络的互连结构。本 节将按照神经网络连接模式,对神经网络的几种 典型结构分别进行介绍
12
2.2.1 单层感知器网络
单层感知器是最早使用的,也是最简单的神经 网络结构,由一个或多个线性阈值单元组成
这种神经网络的输入层不仅 接受外界的输入信号,同时 接受网络自身的输出信号。 输出反馈信号可以是原始输 出信号,也可以是经过转化 的输出信号;可以是本时刻 的输出信号,也可以是经过 一定延迟的输出信号
此种网络经常用于系统控制、 实时信号处理等需要根据系 统当前状态进行调节的场合
x1
…… …… ……
…… yi …… …… …… …… xi
再励学习
再励学习是介于上述两者之间的一种学习方法
19
2.3.2 学习规则
Hebb学习规则
这个规则是由Donald Hebb在1949年提出的 他的基本规则可以简单归纳为:如果处理单元从另一个处
理单元接受到一个输入,并且如果两个单元都处于高度活 动状态,这时两单元间的连接权重就要被加强 Hebb学习规则是一种没有指导的学习方法,它只根据神经 元连接间的激活水平改变权重,因此这种方法又称为相关 学习或并联学习
9
2.1.2 研究进展
重要学术会议
International Joint Conference on Neural Networks
IEEE International Conference on Systems, Man, and Cybernetics
World Congress on Computational Intelligence
复兴发展时期 1980s至1990s
《神经网络》PPT幻灯片PPT

➢因此,类神经网络在选取启动函数时,不能够使用 传统的线性函数,通常来说会选择兼具正向收敛与 负向收敛的函数。
20
2.阶梯(step)启动函数的一般形式:
f Ij
,Ij 0 ,Ij 0
阶梯启动函数又称阈值(threshold)启动函
数。当 时1,,得0到
1
f Ij 0
,Ij 0 ,Ij 0
输入层只从外部环境接收信息,该层的每 个神经元相当于自变量,不完成任何计算 ,只为下一层传递信息。
输出层生成最终结果,为网络送给外部系 统的结果值。
13
隐藏层介于输入层和输出层之间,这些层 完全用于分析,其函数联系输入层变量和 输出层变量,使其更拟合(fit)资料。
隐藏层的功能主要是增加类神经网络的复 杂性,以能够模拟复杂的非线性关系。
一个神经元 j,有阈值,从上一层连接的 神经元得到n个输入变量X,每个输入变 量附加一个链接权重w。
输入变量将依照不同权重加以合并(一般 是加权总和),链接成组合函数( combination function),组合函数的值称 为电位(potential);然后,启动(转换 、激活、赋活)函数(activation function) 将电位转换成输出信号。
隐藏层的多少要适当,过多容易过度拟合 。
一层加权神经元的网络称单层感知器,多 层加权神经元的网络称多层感知器( multi-layer perceptrons)。
14
神经网络的形式:
一个 输出 元的 两层 神经 网络
15
一 个输 出元 的三 层神 经网 络
16
多个输出元的三层神经网络
17
三、神经元的结构
类神经网络可以处理连续型和类别型的数 据,对数据进行预测。
20
2.阶梯(step)启动函数的一般形式:
f Ij
,Ij 0 ,Ij 0
阶梯启动函数又称阈值(threshold)启动函
数。当 时1,,得0到
1
f Ij 0
,Ij 0 ,Ij 0
输入层只从外部环境接收信息,该层的每 个神经元相当于自变量,不完成任何计算 ,只为下一层传递信息。
输出层生成最终结果,为网络送给外部系 统的结果值。
13
隐藏层介于输入层和输出层之间,这些层 完全用于分析,其函数联系输入层变量和 输出层变量,使其更拟合(fit)资料。
隐藏层的功能主要是增加类神经网络的复 杂性,以能够模拟复杂的非线性关系。
一个神经元 j,有阈值,从上一层连接的 神经元得到n个输入变量X,每个输入变 量附加一个链接权重w。
输入变量将依照不同权重加以合并(一般 是加权总和),链接成组合函数( combination function),组合函数的值称 为电位(potential);然后,启动(转换 、激活、赋活)函数(activation function) 将电位转换成输出信号。
隐藏层的多少要适当,过多容易过度拟合 。
一层加权神经元的网络称单层感知器,多 层加权神经元的网络称多层感知器( multi-layer perceptrons)。
14
神经网络的形式:
一个 输出 元的 两层 神经 网络
15
一 个输 出元 的三 层神 经网 络
16
多个输出元的三层神经网络
17
三、神经元的结构
类神经网络可以处理连续型和类别型的数 据,对数据进行预测。
数学建模-神经网络算法ppt课件

• 1943年,心理学家W.S.McCulloch和数学家W.Pitts提出了描述脑 神经细胞动作的数学模型,即M-P模型(第一个神经网络模型)。
• 1949年,心理学家Hebb实现了对脑细胞之间相互影响的数学描述, 从心理学的角度提出了至今仍对神经网络理论有着重要影响的Hebb 学习法则。
• 1958年,E.Rosenblatt提出了描述信息在人脑中贮存和记忆的数学 模型,即著名的感知机模型(Perceptron)。
ppt课件完整
6
2. 人工神经网络的基本功能
• (1)联想记忆功能
– 由于神经网络具有分布 存储信息和并行计算的 性能,因此它具有对外 界刺激信息和输入模式 进行联想记忆的能力。
– 联想记忆有两种基本形 式
• 自联想记忆
• 异联想记忆
ppt课件完整
7
• 自联想记忆
– 网络中预先存储(记忆)多种模式信息
ppt课件完整
20
3. 神经网络的发展历史(续)
• (4) 新连接机制时期(1986-现在) – 神经网络从理论走向应用领域,出现了神经网络芯片 和神经计算机。 – 神经网络主要应用领域有
• 模式识别与图象处理(语音、指纹、故障检测和图象压缩等) • 控制与优化 • 预测与管理(市场预测、风险分析) •等
均为常数。
ppt课件完整
29
假设1:多输入单输出
ppt课件完整
• 正如生物神经元 有许多激励输入 一样,人工神经 元也应该有许多 的输入信号
• 图中,每个输入 的大小用确定数 值xi表示,它们同 时输入神经元j, 神经元的单输出 用oj表示。
30
假设2:输入类型——兴奋性和抑制性
• 生物神经元具有不同的突 触性质和突触强度,其对 输入的影响是使有些输入 在神经元产生脉冲输出过 程中所起的作用比另外一 些输入更为重要。
• 1949年,心理学家Hebb实现了对脑细胞之间相互影响的数学描述, 从心理学的角度提出了至今仍对神经网络理论有着重要影响的Hebb 学习法则。
• 1958年,E.Rosenblatt提出了描述信息在人脑中贮存和记忆的数学 模型,即著名的感知机模型(Perceptron)。
ppt课件完整
6
2. 人工神经网络的基本功能
• (1)联想记忆功能
– 由于神经网络具有分布 存储信息和并行计算的 性能,因此它具有对外 界刺激信息和输入模式 进行联想记忆的能力。
– 联想记忆有两种基本形 式
• 自联想记忆
• 异联想记忆
ppt课件完整
7
• 自联想记忆
– 网络中预先存储(记忆)多种模式信息
ppt课件完整
20
3. 神经网络的发展历史(续)
• (4) 新连接机制时期(1986-现在) – 神经网络从理论走向应用领域,出现了神经网络芯片 和神经计算机。 – 神经网络主要应用领域有
• 模式识别与图象处理(语音、指纹、故障检测和图象压缩等) • 控制与优化 • 预测与管理(市场预测、风险分析) •等
均为常数。
ppt课件完整
29
假设1:多输入单输出
ppt课件完整
• 正如生物神经元 有许多激励输入 一样,人工神经 元也应该有许多 的输入信号
• 图中,每个输入 的大小用确定数 值xi表示,它们同 时输入神经元j, 神经元的单输出 用oj表示。
30
假设2:输入类型——兴奋性和抑制性
• 生物神经元具有不同的突 触性质和突触强度,其对 输入的影响是使有些输入 在神经元产生脉冲输出过 程中所起的作用比另外一 些输入更为重要。
神经网络方法ppt课件

得多个信号参数如温度、烟雾等经过处理后判断火灾情况, 然而如何由多种信号分析合成得到最终的判断结果,并能适 应各种不同环境情况的有效算法还亟待研究。
2019/9/4
哈尔滨工程大学
9
神经网络实例(续)
2019/9/4
哈尔滨工程大学
10
局部决策
鉴于不同火情下多传感器系统测试的多个火情信息具有 很大的相关不确定性,如: • 明火条件下伴随着温度和烟雾信号的急剧增大同时湿度的下 降; • 阴燃火发生时则往往伴随着烟雾的增大同时温度和湿度的基 本稳定; • 而一些典型的干扰信号如厨房内是烟雾、温度、湿度信号同 时增大; 因此分布式检测系统首先对一种传感器采集的单一信号进行 局部决策,再送入融合中心根据其关联性得出最终决策。
2019/9/4
哈尔滨工程大学
2
7.2 人工神经元模型—神经组织的基本特征
2019/9/4
哈尔滨工程大学
3
7.2 人工神经元模型—MP模型
从全局看,多个神经元构成一个网络,因此神经元模型的定义 要考虑整体,包含如下要素: (1)对单个人工神经元给出某种形式定义; (2)决定网络中神经元的数量及彼此间的联结方式; (3)元与元之间的联结强度(加权值)。
(2)神经网络可增加信息处理的容错性,当某个信源的数据出现 差错时,神经网络的容错功能可以使系统正常工作,并输出可 靠的信息;
(3)神经网络的自学习和自组织功能,使系统能适应环境的不断 变化以及输入数据的不确定性;
(4)神经网络的并行结构和并行处理机制。使得信息处理速度快, 能够满足信息的实时处理要求。
2019/9/4
哈尔滨工程大学
8
7.7 神经网络实例
• 火灾探测是一种特殊类型的信号检测,由传感器采集的火情
2019/9/4
哈尔滨工程大学
9
神经网络实例(续)
2019/9/4
哈尔滨工程大学
10
局部决策
鉴于不同火情下多传感器系统测试的多个火情信息具有 很大的相关不确定性,如: • 明火条件下伴随着温度和烟雾信号的急剧增大同时湿度的下 降; • 阴燃火发生时则往往伴随着烟雾的增大同时温度和湿度的基 本稳定; • 而一些典型的干扰信号如厨房内是烟雾、温度、湿度信号同 时增大; 因此分布式检测系统首先对一种传感器采集的单一信号进行 局部决策,再送入融合中心根据其关联性得出最终决策。
2019/9/4
哈尔滨工程大学
2
7.2 人工神经元模型—神经组织的基本特征
2019/9/4
哈尔滨工程大学
3
7.2 人工神经元模型—MP模型
从全局看,多个神经元构成一个网络,因此神经元模型的定义 要考虑整体,包含如下要素: (1)对单个人工神经元给出某种形式定义; (2)决定网络中神经元的数量及彼此间的联结方式; (3)元与元之间的联结强度(加权值)。
(2)神经网络可增加信息处理的容错性,当某个信源的数据出现 差错时,神经网络的容错功能可以使系统正常工作,并输出可 靠的信息;
(3)神经网络的自学习和自组织功能,使系统能适应环境的不断 变化以及输入数据的不确定性;
(4)神经网络的并行结构和并行处理机制。使得信息处理速度快, 能够满足信息的实时处理要求。
2019/9/4
哈尔滨工程大学
8
7.7 神经网络实例
• 火灾探测是一种特殊类型的信号检测,由传感器采集的火情
神经网络算法的ppt课件

神经网络的反向分散学习算法
神经网络的反向分散学习算法
神经网络的反向分散学习算法
神经网络的反向分散学习算法
神经网络的反向分散学习算法
动态网络——Hopfield网络
假设按照神经网络运转过程中的信息流向来分类, 那么一切网络都可分为前馈式网络和反响式网络,在前 一章中,主要引见了前馈式网络经过许多具有简单处置 才干的神经元的复协作用使整个网络具有复杂的非线性 映射才干。在那里,着重分析了网络学习算法,研讨的 重点是怎样尽快地得到网络的整体非线性处置才干。在 本章中,我们将集中讨论反响式网络,经过网络神经元 形状的变化而最终稳定于某一形状而得到联想存贮或神 经计算的结果。在这里,主要关怀的是网络稳定性的问 题,研讨的重点是怎样得到和利用稳定的反响式网络。
联想的定义
首先思索x类方式向量集合 (x1, x2, … , xp〕 及y类方式向量集合 (y1, y2, … , yp), 其中 xi=(x1i, x2i,… , xni ) , xi {-1, +1}n yi=(y1i, y2i,… , ymi ) , yi {-1, +1}m
联想的定义
定义3 吸引子的吸引域 对于某些特定的初始形状,网络按 一定的运转规那么最后能够都稳定在同一吸引子v(t)上。称可 以稳定在吸引子v(t)的一切初始形状集合为v(t)的吸引域。
Hopfield网络的联想原理
E= mc2 Newt
Newy
Einstan Newton
Newyear
Hopfield网络的联想原理
f1(x) = f2 (x) = … = fn (x) = sgn (x) 为以后分析方便,我们选各节点门限值相等,且等于0 ,即有 1= 2 = … = n = 0 同时,x = (x1, x2, …, xn ), x {-1, +1}n 为网络的输出, y = (y1, y2, …, yn ), y {-1, +1}n 为网络的输出 v (t) = (v1(t1), v2(t2), …, vn(tn)), v (t) {-1, +1}n 为网络在时辰 t的形状, 其中t (0,1,2,…)为离散时间变量,Wij为从Ni到Nj的衔接 权值, Hopfield网络是对称的,即Wij = Wji ,i, j {1,2, …, n} 。
神经网络基础PPT课件

AlexNet
VGGNet
ResNet
DenseNet
由Yann LeCun等人提出 ,是最早的卷积神经网 络之一,用于手写数字 识别。
由Alex Krizhevsky等人 提出,获得了2012年 ImageNet图像分类竞 赛的冠军,引入了ReLU 激活函数和数据增强等 技巧。
由牛津大学Visual Geometry Group提出 ,通过反复堆叠3x3的小 型卷积核和2x2的最大池 化层,构建了深度较深 的网络结构。
内部表示。
隐藏层
通过循环连接实现信息 的持久化,捕捉序列中
的动态信息。
输出层
将隐藏层的状态转化为 具体的输出。
循环连接
将隐藏层的状态反馈到 输入层或隐藏层自身, 实现信息的循环传递。
序列建模与长短时记忆网络(LSTM)
序列建模
01
RNN通过循环连接实现对序列数据的建模,能够处理任意长度
的序列输入。
久化。
Jordan网络
与Elman网络类似,但将输出 层的状态反馈到隐藏层。
LSTM网络
长短时记忆网络,通过引入门 控机制实现对长期依赖信息的
有效处理。
GRU网络
门控循环单元网络,一种简化 的LSTM结构,具有较少的参
数和较快的训练速度。
06 深度学习框架 TensorFlow使用指南
TensorFlow安装与配置教程
非线性可分问题
不存在一条直线(或超平面)能够将两类样本完全分开的 问题。对于这类问题,需要使用非线性分类器或者核方法 等技巧进行处理。
处理非线性可分问题的方法
包括使用多项式核、高斯核等核函数将数据映射到高维空 间使其线性可分;或者使用神经网络等非线性模型对数据 进行建模和分类。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
n
y j f ( wij xi a j ) i1
其中,y j 表示神经元 j 的输出;xi 表示神经元i 的输入; wij 表示神经元 i 与神经元 j 之间的连接权值;a j 表示神 经元 j 的阈值;f () 是输入到输出传递函数(也称激活 函数).
5
下表给出了一些常用的传递函数。除线性传递 函数外,其它的均是非线性的,因此,神经网络特 别适合于解决非线性问题。
经元(节点)个数为 n ,隐含层神经元(节点)个数为 m ,
输出层神经元(节点)个数为 l ,这种结构称为nml 结构的 三层 BP 神经网络。
9
2.BP神经网络学习算法及流程
以三层BP神经网络为例,它的训练过程包括以下几个步骤:
步骤 1:网络初始化。根据输入 X (x1 , x2, , xn) 和期望输出 D (d1 ,d2, , dl ) 来确定网络输入层、隐含层和输出层神经元(节点)个数,初始
4、高斯函数:f
(
x)
exp
1 2
2 i
n
(xj
i1
x
ji
)2
7
1.BP神经网络结构:
BP神经网络的拓扑结构如图所示。
8
其中, xi (i 1, , n) 是神经网络的(实际)输入, yj ( j 1 , , m) 是 隐含层的输出,即为输出层的输入,Ok (k 1 , , l) 网络的(实 际)输出,a,b 分别为隐含层和输出层神经元(节点)的阈 值, vij , wjk 分别为输入层到隐含层和隐含层到输出层的权 值。也就是说,图中所表示的 BP 神经网络,它的输入层神
12
BP神经网络的流程图:
13
三、BP神经网络Matlab工具箱函数
主要介绍 BP 神经网络用到 newff、train 和 sim 等 3 个主要函 数,各函数解释如下:
(1)newff——BP 神经网络参数设置函数 函数功能:构建一个 BP 神经网络. 函数形式: NET=newff(PR,[S1,S2,…,SN],{TF1,TF2,…,TFN},BTF,BLF,PF) PR:为样本数据组成的矩阵,由其中最大值和最小值组成的 R×2 维的矩阵; Si:第 i 层的节点数,共计 N 层; TFi:第 i 层节点的传递函数,包括线性传递函数 purelin;正 切 S 型传递函数 tansig;对数 S 型传递函数 logsig。默认为“tansig”;
14
net=newff(PR, [S1,S2,…,SN],{ TF1,TF2,…,TFN}, BTF, BLF, PF)
BTF:训练函数,用于网络权值和阈值的调整,默认基于 Levenberg_Marquardt 共轭梯度法的训练函数 trainlm。其它参 数见后面表格。
vij vij vij
wjk wjk wjk
lห้องสมุดไป่ตู้
vij (
o k
w
jk
)
yj
(1
yj
) xi
wjk
o k
y
j
k 1
其中
o k
(dk
ok
)ok
(1
ok
)
,
式中 为学习速率。
步骤6:判断算法迭代是否结束(可用网络总误差是否达到 精度要求等方式来判断),若没有结束,返回步骤2.
神经网络传递函数
名称
传递函数表达式
二值函数 线性函数
f
(
x)
1 0
x0 x0
f (x) ax
分段线性函数
0 f (x) cx
1
x0 0 x xc
x xc
非对称 Sigmoid 函数 非对称 Sigmoid 函数
f
(x)
1 1 ex
f
(x)
1 1
m
m
Ok f ( wjk x j bk ) f ( wjk x j )
j 1
j0
k 1, 2, ,l
步骤 4:误差计算。根据网络实际输出 与期望输出 ,计 算网络总体误差.
11
步骤 5:权值更新。根据网络总体误差 E ,按照以下公式更
新网络连接权值 vij , wjk .
化各层神经元之间的连接权值 vij , wjk ,初始化隐含层阈值 a ,输出
层阈值 b ,给定学习速率和神经元传递函数.
步骤 2:隐含层输出计算。根据输入向量 X ,输入层和隐含层间连
接权值vij 以及隐含层阈值 a ,计算隐含层输出.
n
n
yi f ( vij xi a j ) f ( vij xi )
3
一、人工神经元数学模型
生物神经元,也称神经细胞,它是由细胞体、 树突、轴突和突触等生物组织构成的,并通过细胞 膜电位来实现生物神经元的兴奋与抑制、学习与联 想等基本功能,因此,它是构成人脑神经系统的基 本功能单元。其结构如下图所示。
4
根据生物神经元的结构与基本功能,可以将其 简化为下图的形式,并建立神经网络模型的基础—— 人工神经元数学模型:
数学建模与数学实验
神经网络
1
目的
学习神经网络的基本原理与方法。
内容
1、人工神经元数学模型 2、BP神经网络 3、BP神经网络Matlab工具箱函数 4、BP神经网络应用
2
神经网络(Neural Networks)是从微观结构与 功能上对人脑神经系统进行模拟而建立起来的数 学模型,它具有模拟人脑思维的能力,其特点主 要是具有非线性特性、学习能力和自适应性等, 是模拟人类智能的一种重要方法。神经网络是由 神经元互联而成的,能接收并处理信息,而这种 信息处理主要是由神经元之间的相互作用,即通 过神经元之间的连接权值来处理并实现的。神经 网络在人工智能、自动控制、计算机科学、信息 处理和模式识别等领域得到了非常成功地应用。
e x e x
6
1、阶跃函数:f
(x)
10,,xx00,或符号函数f
(
x)
1, x 1,
x
0
0
2、双曲正切函数:f
(x)
tanh(x)
ex ex
ex ex
3、sigmoid函数(S型):f
(
x)
1
x2 x2
,
x
0
0, x 0
j 1
j0
i 1, 2, , m
式中,m 为隐含层节点数;vi0 1, x0 a j ; f () 为隐含层传递函数。
这里我们采用传递函数为
f
(x)
1
1 e
x
.
10
步骤 3:输出层输出计算。根据隐含层输出Y ,连接权值wjk
和阈值 b ,计算 BP 神经网络的实际输出O .
y j f ( wij xi a j ) i1
其中,y j 表示神经元 j 的输出;xi 表示神经元i 的输入; wij 表示神经元 i 与神经元 j 之间的连接权值;a j 表示神 经元 j 的阈值;f () 是输入到输出传递函数(也称激活 函数).
5
下表给出了一些常用的传递函数。除线性传递 函数外,其它的均是非线性的,因此,神经网络特 别适合于解决非线性问题。
经元(节点)个数为 n ,隐含层神经元(节点)个数为 m ,
输出层神经元(节点)个数为 l ,这种结构称为nml 结构的 三层 BP 神经网络。
9
2.BP神经网络学习算法及流程
以三层BP神经网络为例,它的训练过程包括以下几个步骤:
步骤 1:网络初始化。根据输入 X (x1 , x2, , xn) 和期望输出 D (d1 ,d2, , dl ) 来确定网络输入层、隐含层和输出层神经元(节点)个数,初始
4、高斯函数:f
(
x)
exp
1 2
2 i
n
(xj
i1
x
ji
)2
7
1.BP神经网络结构:
BP神经网络的拓扑结构如图所示。
8
其中, xi (i 1, , n) 是神经网络的(实际)输入, yj ( j 1 , , m) 是 隐含层的输出,即为输出层的输入,Ok (k 1 , , l) 网络的(实 际)输出,a,b 分别为隐含层和输出层神经元(节点)的阈 值, vij , wjk 分别为输入层到隐含层和隐含层到输出层的权 值。也就是说,图中所表示的 BP 神经网络,它的输入层神
12
BP神经网络的流程图:
13
三、BP神经网络Matlab工具箱函数
主要介绍 BP 神经网络用到 newff、train 和 sim 等 3 个主要函 数,各函数解释如下:
(1)newff——BP 神经网络参数设置函数 函数功能:构建一个 BP 神经网络. 函数形式: NET=newff(PR,[S1,S2,…,SN],{TF1,TF2,…,TFN},BTF,BLF,PF) PR:为样本数据组成的矩阵,由其中最大值和最小值组成的 R×2 维的矩阵; Si:第 i 层的节点数,共计 N 层; TFi:第 i 层节点的传递函数,包括线性传递函数 purelin;正 切 S 型传递函数 tansig;对数 S 型传递函数 logsig。默认为“tansig”;
14
net=newff(PR, [S1,S2,…,SN],{ TF1,TF2,…,TFN}, BTF, BLF, PF)
BTF:训练函数,用于网络权值和阈值的调整,默认基于 Levenberg_Marquardt 共轭梯度法的训练函数 trainlm。其它参 数见后面表格。
vij vij vij
wjk wjk wjk
lห้องสมุดไป่ตู้
vij (
o k
w
jk
)
yj
(1
yj
) xi
wjk
o k
y
j
k 1
其中
o k
(dk
ok
)ok
(1
ok
)
,
式中 为学习速率。
步骤6:判断算法迭代是否结束(可用网络总误差是否达到 精度要求等方式来判断),若没有结束,返回步骤2.
神经网络传递函数
名称
传递函数表达式
二值函数 线性函数
f
(
x)
1 0
x0 x0
f (x) ax
分段线性函数
0 f (x) cx
1
x0 0 x xc
x xc
非对称 Sigmoid 函数 非对称 Sigmoid 函数
f
(x)
1 1 ex
f
(x)
1 1
m
m
Ok f ( wjk x j bk ) f ( wjk x j )
j 1
j0
k 1, 2, ,l
步骤 4:误差计算。根据网络实际输出 与期望输出 ,计 算网络总体误差.
11
步骤 5:权值更新。根据网络总体误差 E ,按照以下公式更
新网络连接权值 vij , wjk .
化各层神经元之间的连接权值 vij , wjk ,初始化隐含层阈值 a ,输出
层阈值 b ,给定学习速率和神经元传递函数.
步骤 2:隐含层输出计算。根据输入向量 X ,输入层和隐含层间连
接权值vij 以及隐含层阈值 a ,计算隐含层输出.
n
n
yi f ( vij xi a j ) f ( vij xi )
3
一、人工神经元数学模型
生物神经元,也称神经细胞,它是由细胞体、 树突、轴突和突触等生物组织构成的,并通过细胞 膜电位来实现生物神经元的兴奋与抑制、学习与联 想等基本功能,因此,它是构成人脑神经系统的基 本功能单元。其结构如下图所示。
4
根据生物神经元的结构与基本功能,可以将其 简化为下图的形式,并建立神经网络模型的基础—— 人工神经元数学模型:
数学建模与数学实验
神经网络
1
目的
学习神经网络的基本原理与方法。
内容
1、人工神经元数学模型 2、BP神经网络 3、BP神经网络Matlab工具箱函数 4、BP神经网络应用
2
神经网络(Neural Networks)是从微观结构与 功能上对人脑神经系统进行模拟而建立起来的数 学模型,它具有模拟人脑思维的能力,其特点主 要是具有非线性特性、学习能力和自适应性等, 是模拟人类智能的一种重要方法。神经网络是由 神经元互联而成的,能接收并处理信息,而这种 信息处理主要是由神经元之间的相互作用,即通 过神经元之间的连接权值来处理并实现的。神经 网络在人工智能、自动控制、计算机科学、信息 处理和模式识别等领域得到了非常成功地应用。
e x e x
6
1、阶跃函数:f
(x)
10,,xx00,或符号函数f
(
x)
1, x 1,
x
0
0
2、双曲正切函数:f
(x)
tanh(x)
ex ex
ex ex
3、sigmoid函数(S型):f
(
x)
1
x2 x2
,
x
0
0, x 0
j 1
j0
i 1, 2, , m
式中,m 为隐含层节点数;vi0 1, x0 a j ; f () 为隐含层传递函数。
这里我们采用传递函数为
f
(x)
1
1 e
x
.
10
步骤 3:输出层输出计算。根据隐含层输出Y ,连接权值wjk
和阈值 b ,计算 BP 神经网络的实际输出O .
