Matlab软件在牛顿环实验数据处理方法上的创新
基于MATLAB的大学物理可视化研究
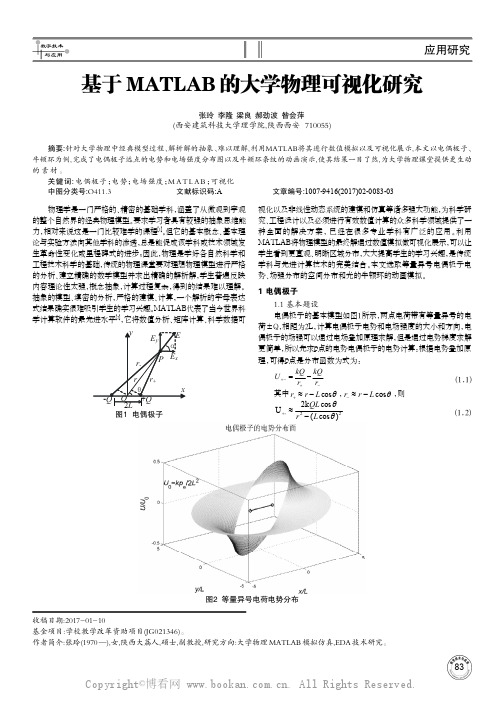
物理学是一门严格的、精密的基础学科,涵盖了从微观到宇观的整个自然界的经典物理模型。
要求学习者具有较强的抽象思维能力,相对来说这是一门比较难学的课程[1]。
但它的基本概念、基本理论与实验方法向其他学科的渗透,总是能促成该学科或技术领域发生革命性变化或里程碑式的进步;因此,物理是学好各自然科学和工程技术科学的基础,传统的物理课堂要对理想物理模型进行严格的分析、建立精确的数学模型并求出精确的解析解,学生普遍反映内容理论性太强,概念抽象,计算过程复杂,得到的结果难以理解。
抽象的模型、缜密的分析,严格的建模、计算,一个解析的字母表达式结果确实很难吸引学生的学习兴趣。
MATLAB代表了当今世界科学计算软件的最先进水平[2],它将数值分析、矩阵计算、科学数据可视化以及非线性动态系统的建模和仿真等诸多强大功能,为科学研究、工程设计以及必须进行有效数值计算的众多科学领域提供了一种全面的解决方案,已经在很多专业学科有广泛的应用。
利用MATLAB将物理模型的最终解通过数值模拟做可视化展示,可以让学生看到更直观、明晰区域分布,大大提高学生的学习兴趣,是传统学科与先进计算技术的完美结合。
本文选取等量异号电偶极子电势、场强分布的空间分布和光的牛顿环的动画模拟。
1 电偶极子1.1 基本题设电偶极子的基本模型如图1所示,两点电荷带有等量异号的电荷±Q,相距为2L,计算电偶极子电势和电场强度的大小和方向,电偶极子的场强可以通过电场叠加原理求解,但是通过电势梯度求解更简单,所以先求p点的电势电偶极子的电势计算:根据电势叠加原理,可得p点是分布函数为式为:-+-+-=r kQ r kQ U (1.1)其中θcos L r r -≈+,θcos L r r -≈-,则22-)cos (cos k 2U θθL r QL -≈+ (1.2)基于MATLAB 的大学物理可视化研究张玲 李隆 梁良 郝劲波 昝会萍(西安建筑科技大学理学院,陕西西安 710055)摘要:针对大学物理中经典模型过程、解析解的抽象、难以理解,利用MATLAB将其进行数值模拟以及可视化展示,本文以电偶极子、牛顿环为例,完成了电偶极子远点的电势和电场强度分布图以及牛顿环条纹的动画演示,使其结果一目了然,为大学物理课堂提供更生动的素材。
用牛顿环测透镜曲率半径的数据处理方法

用牛顿环测透镜曲率半径的数据处理方法步超100104103 机械工程及自动化摘要:牛顿环实验是大学物理实验中非常重要的实验,以单色平行光投射到牛顿环装置上,则由空气膜上下表面反射的光波将互相干涉,形成的干涉条纹为博的等厚各点的轨迹,这种干涉是一种等厚干涉。
处理该实验的测量数据常采用逐差法,最小二乘法,加权平均以及其它方法。
通过介绍用逐差法、线性回归法、加权平均法处理牛顿环测透镜曲率半径数据的方法和过程。
比较三种实验数据处理方法的优缺点,其中加权平均法既考虑了如何克服实验的系统误差,又能按照处理原则去对待非等精度测量,且建立在数理统计理论基础上。
该方法主要是比较相应的权,进而求出加权平均值,得出加权平均法为牛顿环实验数据处理的最佳方法,但加权平均法中要计算的数据较多,公式较多,较传统的方法要复杂的多。
故探讨如何简化加权平均法,利用Matlab软件进行处理。
关键字:牛顿环实验、加权平均法、非等精度实验数据的处理、干涉条纹、加权平均值英文译文:Buchao100104103 Mechanical engineering and automationNewton rings experiment is university physics experiment is very important experiment, deal with the experimentThe test data of the long through "gradual deduction method, the least square method, and the weighted average, and other methods. Through the detailed introduction is used by differential method, linear regression method, the weighted average method to deal with Newton ring the lens curvature radius the method and process of data. Compare three kind of experiment data processing and the advantages and disadvantages of the methods, of which the weighted average method takes into account both the how to overcome the experiment system error, and can according to principles of management to treat the measurement precision, and established in the mathematical statistics theory basis. This method is mainly to compare the corresponding rights, and seek the weighted average, draw the weighted average method for Newton rings experiment data processing the best method, but the weighted average method to compute the data in the more, the formula is more, more traditional method is more complicated. Discusses how to simplify the weighted average method, use of Matlab software for processing.Key word: of Newton ring's experiments, weighted average method, the accuracy of experimental data processing, the interference fringes, weighted average引言:牛顿环是牛顿在1675年所做的著名实验。
Matlab在牛顿环实验数据处理中的应用

图1实验处理程序框架结构Matlab在牛顿环实验数据处理中的应用井晨睿,廖腊梅,亓协兴,马宝红,郑亚利(洛阳师范学院物理与电子信息学院,河南洛阳471934)一、引言牛顿环干涉实验是光波波动性的代表性实验之一。
牛顿环是由凸透镜和玻璃板压制而成,其中凸透镜和玻璃板之间形成了空气薄膜,在不同位置处,由于空气薄膜厚度不同,入射光和反射光之间发生等厚干涉,从而形成了明暗相间的干涉条纹。
实验中通过测量干涉条纹位置读数,可以测定平凸透镜的曲率半径。
在实验过程中,通常需要测量的干涉条纹数目有较多,需要测量的干涉条纹位置读数很多,因此在数据处理的过程中容易出现错误。
基于此本文以Matlab 为平台,开发了数据处理脚本程序,该程序可以实现牛顿环实验中测量数据的快速查错与处理,从而使该实验数据处理的准确性和效率得到了极大地提高。
二、牛顿环实验原理牛顿环由一个曲率半径很大的平凸透镜和一块平玻璃板压制而成。
当单色平行光垂直入射到牛顿环时,空气薄膜上下表面反射的两束光之间发生相互干涉,出现明暗相间的条纹,这种干涉属于等厚干涉[1]。
假设入射光波长为λ,平凸透镜的曲率半径为R ,m 级干涉条纹半径记作r m ,由条件可知,对于第m 级暗条纹半径满足r m =mRλ√(1)假定实验中观测到第m 1和第m 2两个暗环,考虑到干涉级数修正(修正值记作j ),则两个暗环对应的干涉级数分别为m 1+j 和m 2+j 。
根据干涉条件,两个暗环对应的条纹半径应满足r m 1=(m 1+j )Rλ √(2)r m 2=(m 2+j )Rλ√(3)将以上两式两边平方相减,则有r 2m 2-r 2m 1=(m 2-m 1)Rλ(4)从(4)式中可得R =r 2m 2-r 2m 1(m 2-m 1)λ(5)从(5)式可以看出,在已知入射波长以及干涉环序数的情况下,牛顿环半径可以通过测量任意两个暗环半径求解。
由于确定牛顿环表面干涉条纹圆心位置较为麻烦,因此可以通过测量干涉圆环直径得出平凸透镜的曲率半径R ,即R =D 2m 2-D 2m 14(m 2-m 1)λ(6)其中,第m 1,m 2条干涉条纹直径分别记作D m 1,D m 2。
牛顿环干涉matlab

牛顿环干涉matlab牛顿环干涉是一种干涉现象,由英国物理学家艾萨克·牛顿于17世纪时发现。
在牛顿环干涉中,一面平行玻璃板(或一面高透反射膜)被放在半球形凸透镜上,形成一组同心的圆环。
光线从一个点光源入射,穿过平行板或反射后经过半球形凸透镜聚焦到检测屏幕上,形成一组明暗相间的圆环。
这种现象得到了广泛的应用,比如在测量透镜的曲率半径和厚度方面,以及作为一种光学测量的基础。
在计算牛顿环干涉时,matlab可以很好地辅助我们进行精确的计算。
首先,我们需要了解一些牛顿环干涉的理论基础。
1. 光程差:光程差是指,不同路径的光线经过一段距离之后所积累的光程差异。
在牛顿环干涉中,我们可以定义平行玻璃板和半球形透镜之间的距离为d,光线从光源入射到平行玻璃板的距离为D1,从平行玻璃板到透镜的距离为D2,从透镜到检测屏幕的距离为D3。
根据光程差的定义,我们可以得到:d = D1 + D2 + D32. 光程差的公式:当光线从光源入射到平行玻璃板上时,它将发生反射和折射两种现象。
如果我们假设平行玻璃板的折射率为n,反射系数为r,则得到:D1 = (n+1)rλ/2其中,λ是光波长。
类似地,我们可以得到:D2 = (n-1)t其中,t是平行玻璃板的厚度。
由于我们可以假设透镜是理想的,并且距离是非常接近,因此我们可以将从透镜到检测屏幕的距离简单地定义为D3 = f,其中f是透镜的焦距。
根据公式,我们可以得到光程差:Δ = D2 + D3 - D1根据这些公式,我们可以在matlab中进行牛顿环干涉的计算,以获得更加精确和可靠的结果。
这个过程可以通过一些简单而有效的操作来实现。
1. 定义输入参数:首先,我们需要定义光波长、反射系数、折射率、平行玻璃板的厚度以及透镜的焦距等参数。
这些参数需要作为matlab计算过程中的输入,以确保我们得到的结果是准确的。
2. 计算光程差:在计算光程差时,我们需要根据上面提到的公式来进行计算。
牛顿环测透镜曲率半径数据处理方法的分析

牛顿环测透镜曲率半径数据处理方法的分析作者:李晓莉来源:《现代电子技术》2010年第08期摘要:详细介绍用逐差法、线性回归法、加权平均法处理牛顿环测透镜曲率半径数据的方法和过程。
比较三种实验数据处理方法的优缺点,其中加权平均法既考虑了如何克服实验的系统误差,又能按照处理原则去对待非等精度测量,且建立在数理统计理论基础上。
该方法主要是比较相应的权,进而求出加权平均值,利用Matlab软件进行处理,得出加权平均法为牛顿环实验数据处理的最佳方法。
关键词:牛顿环; 逐差法; 线性回归法; 加权平均法中图分类号文献标识码:A文章编号:1004-373X(2010)08-0141-04Analysis of Data Processing in Lens Curvature Radius Measured by Newton′s RingLI Xiao-li(School of Science, Xi’an Shiyou University, Xi’a n 710065, China)Abstract: The methods and procedures of using interative differential method, linear recursive analysis, and weighted average method to process the data of lens curvature of Newton′s Rings are introduced in detail, three experimental dada processing methods are compared. The weighted average method can overcome the experimental systematic distortions, and make a nonprecision measurement according to processing priuciple, and build on the basis of mathematical statistical theory. This method mainly compared the corresponding rights, and then found out the weighted average, used Matlab software processing. It is proved that the weighted average method is optimal for this experiment by theoretic analysis.Keywords: Newton′s ri ngs; interative differential method; linear recursive analysis; weighted average method0 引言“牛顿环”是牛顿在1675年制作天文望远镜时,偶然把一个望远镜的物镜放在平板玻璃上发现的。
Matlab程序编辑在大学物理实验数据处理中的应用

0 引言大学物理实验是高校工科院校必修的一门公共基础实验课,是培养学生实验动手能力和自主创新能力的一门学科,为后继的专业课和实训课打下基础。
很过高校在大学物理实验教学中,仍然采用传统的用坐标纸手工画图,用计算器人工计算的方法。
本文介绍了采用matlab软件编程处理实验数据、画图等,不仅简单便捷,而且提高了数据处理的准确度。
利用计算机辅助大学物理实验教学,提高了学生学习的积极性和创造性。
本文分别以霍尔效应及其应用和测定空气的比热容比实验为例,介绍了matlab软件编程在大学物理实验数据处理中的应用。
Matlab是20世纪80年代美国Mathworks公司推出的一款简单、运算快速、兼程序编辑和画图于一体的计算机软件,它以矩阵作为最基本的编程单位[1]。
内含很多库函数和工具箱,已被很多研究学生和大学生所使用。
在高校推广使用matlab画图和数据处理,已具有良好的基础。
1 利用matlab 软件编程求解霍尔系数霍尔效应实验是大学物理经典实验之一,该实验主要研究两个问题:一、学习用“对称测量法”消除副效应的影响,测量试样的VH -Is曲线[2]。
实验中霍尔电压有如下公式:s sH HI B I BV Rd d==(1)其中1HR ne=(2)称为霍尔系数,在已知Is、B和d的情况下,测出VH,通过以下公式(3)求出霍尔系数。
HHsV d dR kI B B==(3)其中,HsVk I=(4),VH与Is成线性关系,k为该曲线的斜率。
Matlab语言程序如下:clc;clear all;x=[1.00 1.50 2.00 2.50 3.00 4.00];%读入Is测量数据y=[-3.58 -5.38 -7.17 -8.96 -10.75 -14.34]; %读入VH测量数据p=polyfit(x,y,1);%多项式拟合出方程系数xi=0.000:0.0001:5.000;%以0.000为起始点,以0.0001递增到5.000its application experimental data with matlab programming. In the experiment of measuring the specific heat and heat capacity of air, the gross error is eliminated by using the romanesche criterion, and the new measurement column is obtained. Matlab program was used to calculate the mean, the standard deviation of the new sequence and the standard deviation of the arithmetic mean. The application of computer means to the teaching of college physics experiment provides students with a method of data processing and improves students’ data processing ability.Keywords: Matlab; University physics experiment; Data processing图1 霍尔电压和电流的关系实验点与拟合曲线程序执行结果如下:p = -3.5851 0.0020f =-3.5851 x + 0.002y1=-3.5831 -5.3757 -7.1683 -8.9609 -10.7534 -14.3386 fy=0.0031 0.0043 0.0017 0.0009 0.0034 0.0014E1 =0.0025E2 =0.0028RH =-.7413e-2从拟合的图1可以看到,实验数据点都均匀地分布在拟合直线的两侧,与画图的基本要求相符。
基于Matlab的牛顿环白光干涉实验仿真

c 0
( 1 )
式( 1 ) 中, , 和 分别 为 两列相 干光 波到 达
收 稿 日期 : 2 0 1 4 . 0 4 — 0 5
基金项 目: 国家 自然科 学 ̄
( 5 1 1 6 7 0 1 6 ); 青海 师范大学 2 0 1 2年教学改革研究项 目
由于 白光 源难 于控 制 和 白光 的干 涉 场 光 强较 弱 , 白光 的干 涉 现象 观察 有一 定 的难度 。文章 中根 据 色度 学 原理 , 应 用 Ma t l a b仿 真 了实 验 室 中牛 顿 环 的 白光等 厚 干涉 现象 。 j 。
色光 的三基 色 是 指 红 、 绿、 蓝三色 , 任 何 颜 色 的光 可 以通 过 红 、 绿、 蓝 三色按 照不 同的 比例 合成 产生 , 这 是 色度 学 的最 基本 原 理 , 即三基 色原 理 。 因此 , 可将 白光 分解 为红 、 绿、 蓝 三 基色 , 白光 产生 的干涉 条纹 可认 为是 由红 、 绿、 蓝三 基色 的相 干单 色光 波 所 产 生 干 涉 条 纹 的 非 相 干 叠 加 。 由 “ C I E ( 国际 照 明委 员会 ) 1 9 3 1 - R G B系统 ” 的规 定 , 白光 可被分解 为波长分 别为 7 0 0 n m、 5 4 6 . 1 n m、 4 3 5 . 8 n m
板之 间形 成很 薄 的空气 层 。如果 有光 从上 向下 照 射, 那 么从 空气 层 的上 下 表 面 反射 出 的两 束 光线
1 、 2将产 生 干涉 。 由于空气 层 厚 度 相 同 的各 点位 于 以透镜 顶点 O为 圆心 半径 r的 圆周上 , 因此 干 涉条 纹是 以 O 为 圆 心 的 若 干 同心 圆。 当光 源 发 出 的许 多 波长 的 光 发生 干 涉 时 , 就 会 形 成 彩 色 的 干涉 条纹 。这 种 干 涉 现象 的发 现 者 是 牛 顿 , 故 该 装 置被 称 为牛 顿环 J 。
牛顿环干涉实验的 Matlab模拟

3.2 波长 对牛顿环的影响
改变波长 情况下,保持 R=2m , =500nm,如图 5 所示:
图5
R=2m , =500nm
保持 R=2m , =400nm,如图 6 所示:
图6
R=2m , =400nm
通过图 2、图 5、图 6 的比较发现,波长对牛顿环干涉的影响,随着波长的减小,牛顿环向内收 缩,条纹也变的越来越窄。
2d / 2
(1)
k 1,2, k 1,2,
(2k 1 ) / 2 产生暗纹的条件是: (2k) / 2 产生亮纹的条件是:
(2) (3)
对于间隙厚度 d 与条纹半径 r 的关系,由几何关系得:
r 2 R2 (R d )2
1.牛顿环干涉的原理
在编制程序之前, 我们需要对决定干涉条纹特征的光程差、 相位差与干涉条纹半径 r, 光波波长 和平凸透镜的曲率半径 R 之间的关系。装置如图 1 所示:
图1
牛顿环装置图
将一块曲率半径为 R 的平凸透镜凸面朝下放在一块平面透镜上,以平行单色光垂直照射,则经 空气层上下表面反射的两束光线有一光程差,在平凸透镜凸面相遇后,将发生干涉。 当透镜凸面的曲率半径 R 很大时, 相遇时的两反射光线的几何程差为该处空气间隙厚度 d 的两倍, 即 2d。又因这两条相干光线中一条光线来自光密媒质面上的反射,另一条光线来自光疏媒质上的反 射,它们之间有一附加的半波损失,所以在 P 点处得两相干光的总光程差为:
(12)
2.编写程序
为了得到明暗相间的牛顿环干涉条纹,我们需要用 matlab 模拟出光强变化过程,也就是说,我
们编程的重点在于实现对公式 (12)的模拟。设光强的系数 4 I 0 =1,波长 =600nm ,凸透镜曲率半径 R=2m。建立一个大小为 8mm*8mm 具有 400*400 个像素点的视场,视场各点(x,y)到视场中心的距 离可以表示为: r= x 2 y 2 根据公式(12),利用 matlab 编程: R=2; Lamda=632.8e-9; [x,y]=meshgrid(linspace(-0.004,0.004,400)); r2=(x.^2+y.^2); delta=pi*r2/(R*lamda)+pi/2; I=cos(delta).^2; Imshow(I); %牛顿环曲率半径 %波长 %视场范围 %各点到中心的距离 %相位差 %干涉光强 %画图 (13)
牛顿环实验数据处理分析

牛顿环实验数据处理分析一、引言牛顿环实验是光学实验中的经典内容,主要用于研究光的干涉现象以及波动性质。
通过此实验,我们可以深入理解波的叠加原理,验证光的波动性质,并探究光学元件的表面质量对光学现象的影响。
本文将详细阐述牛顿环实验的数据处理和分析方法。
二、实验原理牛顿环实验利用了光的干涉现象。
当两束光波叠加时,如果它们的相位差是2nπ(n为整数),则它们相互增强,形成明亮的干涉条纹;如果相位差是(2n+1)π,则它们相互抵消,形成暗的干涉条纹。
在牛顿环实验中,入射光被分成两束,分别反射和透射于光学元件的表面,然后再重新组合。
三、数据处理方法在进行牛顿环实验后,我们收集了一系列数据,包括每个环的半径、明暗条纹的数量、背景光的强度等。
以下是我们进行数据处理的主要步骤:1、数据清洗:去除异常值和重复值,确保数据的质量和准确性。
2、数据整理:将数据整理成适合进一步分析的格式,如制作表格或绘制图形。
3、数据可视化:利用图表将数据可视化,如条形图、饼图、散点图等,以便更直观地观察和分析数据。
4、数据分析:通过计算平均值、标准差等统计指标,分析数据的分布特征和规律。
5、数据建模:建立数学模型,对数据进行拟合和预测,如使用回归分析、时间序列分析等方法。
6、结果呈现:将分析结果以图表和文字的形式呈现出来,便于理解和应用。
四、数据分析结果通过数据分析,我们可以得出以下1、随着实验的进行,牛顿环的半径逐渐增大,这是因为入射光的波长逐渐减小。
2、明暗条纹的数量逐渐增多,这表明光的干涉现象越来越明显。
3、背景光的强度基本保持不变,这表明实验过程中环境的温度和湿度等参数保持稳定。
4、通过对比实验前后的数据,我们可以发现光学元件的表面质量对干涉现象有明显影响。
表面质量越好,明暗条纹越清晰,干涉现象越明显。
五、结论与展望牛顿环实验是研究光的干涉现象的重要手段,通过对此实验的数据处理和分析,我们可以深入理解光的波动性质和光学元件的表面质量对光学现象的影响。
实验6 干涉的Matlab模拟
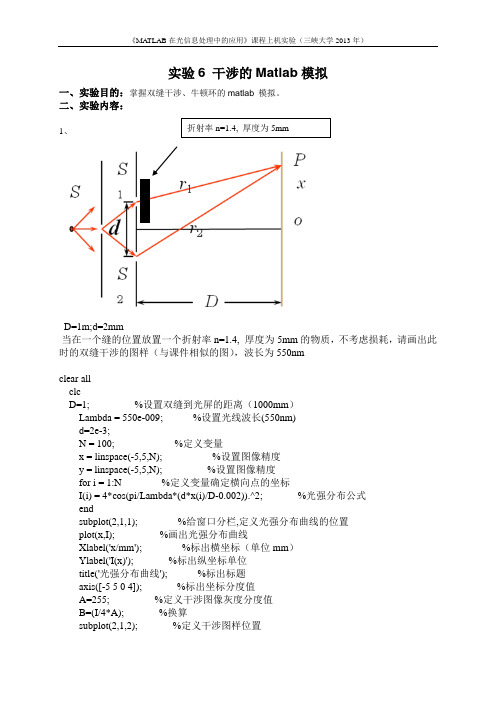
实验6 干涉的Matlab模拟一、实验目的:掌握双缝干涉、牛顿环的matlab 模拟。
二、实验内容:折射率n=1.4, 厚度为5mm1、D=1m;d=2mm当在一个缝的位置放置一个折射率n=1.4, 厚度为5mm的物质,不考虑损耗,请画出此时的双缝干涉的图样(与课件相似的图),波长为550nmclear allclcD=1; %设置双缝到光屏的距离(1000mm)Lambda = 550e-009; %设置光线波长(550nm)d=2e-3;N = 100; %定义变量x = linspace(-5,5,N); %设置图像精度y = linspace(-5,5,N); %设置图像精度for i = 1:N %定义变量确定横向点的坐标I(i) = 4*cos(pi/Lambda*(d*x(i)/D-0.002)).^2; %光强分布公式endsubplot(2,1,1); %给窗口分栏,定义光强分布曲线的位置plot(x,I); %画出光强分布曲线Xlabel('x/mm'); %标出横坐标(单位mm)Ylabel('I(x)'); %标出纵坐标单位title('光强分布曲线'); %标出标题axis([-5 5 0 4]); %标出坐标分度值A=255; %定义干涉图像灰度分度值B=(I/4*A); %换算subplot(2,1,2); %定义干涉图样位置image(x,y,B); %画出干涉图像原形 colormap(gray(A)); %将图样转化为灰度图 Xlabel('x/mm'); %标出横坐标(单位mm ) Ylabel('y/mm'); %标出纵坐标(单位mm ) title('干涉图样'); %标出标题axis([-5 5 0 5]); %标出坐标分度值-5-4-3-2-101234501234x/mm I (x )光强分布曲线x/mmy /m m干涉图样-5-4-3-2-10123450123452、请画出d, D, 波长分别变化(假如对不同波长折射率一样)时候的双缝干涉的强度分布的2维图形。
matlab仿真牛顿环

暗环形成条件为δ0= 2e+λ/2 = (2k+ 1)λ/2 (k= 0,1,2,…)
干涉级次kLeabharlann 大,对应的厚度e也越大,明环和暗环距离中心越远。
相邻明环或暗环之间的厚度差为Δe=λ/2,
可知:相邻明环或暗环的厚度差相同。
设凸透镜的半径为R,光环的半径为r,由于r2=R2-(R-e)2≈ 2Re
解答:
当单色光垂直入射时,在凸透镜下表面
与空气的交界面同时发生反射和透射,
反射光为a,透射光在平板玻璃的上表
面再发生反射,反射光为b。a和b是
同一束光的两部分,因而是相干光,
相遇时就发生干涉。a光反射时没有
半波损失,b光反射时有半波损失。
空气的折射率n= 1,在空气厚度为e的地方,两列光的光程差为δ0= 2e+λ/2,
I=cos(pi*(R.^2+1/2)).^2;%反射光的相对光强
I(R>rm)=0;%最大半径外的光强改为0
c=linspace(0,1,64)'f;%颜色范围
figure%建立图形窗口
h=image(I*64);%画图像
colormap([c*0,c,c*0])%形成绿色图
axisoffequal%隐轴
班级:*******姓名:*******学号:********序号:********
Matlab仿真牛顿环
题目:
如图所示,取一块表面平整的玻璃板,将一半径很大的平凸透镜的凸面与平板玻璃接在一起,平凸透镜的凸面与平板玻璃表面搭出一个空气薄膜。用波长为λ的单色光垂直照射时,可观察到一系列明暗相间的同心圆环,这一现象最先被牛顿观察到,史称牛顿环。牛顿环的干涉条纹的分布规律是什么?如果平凸透镜向上缓慢移动,干涉条纹如何移动?
牛顿环实验数据的处理方法研究

左环的位置 11. 444 ( mm) 右环的位置 21. 355 ( mm) 环的直径 ( mm) 环的级数 ( n) 9. 911 15
左环的位置 11. 561 ( mm) 右环的位置 20. 188 ( mm) 环的直径 ( mm) 8. 627
2 2 x = ( d2 珋 m - d n ) = 23 . 803 ( mm )
槡
) ( x i - x 珋 = 0. 1345 ( mm2 ) n( n - 1 )
δR 珔=
δx 珋 = 167 . 3 ( mm) 4 ( m - n) λ
所以平凸透镜的曲率半径为 : R = ( 0 . 863 ± 0 . 045 ) m, 因 系统的误差可以 为这个实验测量是非等精度的测量逐差法 , , , 这样避免 但是也不能测量非等精度 这个方法虽被经常使
产业与科技论坛 2012 年第 11 卷第 15 期
牛顿环实验数据的处理方法研究
□张 丽 吴 阳 王相和
【内容摘要】 用牛顿环实验中的实测数据 , 比较牛顿环实验的两种数据处理方法 , 通过对这两种方法的理论分析 , 论证了加权平 均法是该实验数据处理的最佳方法 , 提出了借助计算机用 matlab 软件处理牛顿环实验的数据将简化加权平均法 。 【关键词】 牛顿环; 逐差法; 加权平均法; matlab 【基金项目】 本文受大学生科研项目 ( 批准文号: xs11136 ) 资助。 【作者简介】 张丽( 1979. 2 ~ ) , 女, 通化师范学院物理学院讲师 ; 研究方向: 声学与微波 通化师范学院物理学院在读学生 ; 王相和, 通化师范学院物理学院教师 吴阳,
23 11. 611 21. 249 9. 638 13 11. 445 19. 874 8. 429
(仅供参考)牛顿环干涉实验的-Matlab模拟

牛顿环干涉实验的Matlab模拟在光学上,牛顿环是一个等厚干涉现象。
将一块平凸透镜凸面朝下放在一块平面透镜上,将单色光直射向凸镜的平面,入射光和通过平透镜的反射光发生干涉,产生一个个明暗相间的圆环条纹,这些圆环就是牛顿环干涉条纹。
下面我们将通过matlab实现牛顿环干涉的模拟,画出其干涉条纹。
1.牛顿环干涉的原理在编制程序之前,我们需要对决定干涉条纹特征的光程差、相位差与干涉条纹半径r,光波波长λ和平凸透镜的曲率半径R之间的关系。
装置如图1所示:图1 牛顿环装置图将一块曲率半径为R的平凸透镜凸面朝下放在一块平面透镜上,以平行单色光垂直照射,则经空气层上下表面反射的两束光线有一光程差,在平凸透镜凸面相遇后,将发生干涉。
当透镜凸面的曲率半径R很大时,相遇时的两反射光线的几何程差为该处空气间隙厚度d的两倍,即2d。
又因这两条相干光线中一条光线来自光密媒质面上的反射,另一条光线来自光疏媒质上的反射,它们之间有一附加的半波损失,所以在P点处得两相干光的总光程差为:=+∆d(1)2/2λ产生暗纹的条件是:2/=∆k⋅⋅⋅(+2λ)1k(2)=,2,1产生亮纹的条件是:2/∆⋅⋅⋅(k=)2λk(3)=,2,1对于间隙厚度d与条纹半径r的关系,由几何关系得:222)(d R R r --= (4)R r d 2/2= (5)由此可得,牛顿环的明、暗纹半径分别为: 2/2λR k r k )(暗= (6)2/12λR k r k )(亮-= (7)因此通过以上两式,当λ已知时,只要测出第m 级亮环、暗环的半径,就可计算出透镜的曲率半径R ;相反,当R 已知时,即可算出λ。
我们可以通过测量距环中心教远的两个暗环的半径和的平方差来计算曲率半径R 。
结合公式(1)、(5)得出光程差最终表达式:2//2/22λλ+=+=∆R r d (8)观察牛顿环时将会发现,牛顿环中心不是一点,而是一个不甚清晰的暗或亮的圆斑。
其原因是透镜和平玻璃板接触时,由于接触压力引起形变,使接触处为一圆面;又镜面上可能有微小灰尘等存在,从而引起附加的程差。
牛顿环实验的MATLAB仿真

作者: 崔海瑛;吴春梅;赵大伟;王馨玉
作者机构: 大庆师范学院机电工程学院,黑龙江大庆163712
出版物刊名: 大庆师范学院学报
页码: 14-16页
年卷期: 2016年 第3期
主题词: 牛顿环 仿真 MATLAB
摘要:仿真实验是现代实验技术发展的一个重要方向,也是对实验教学的一个重要补充。
利用MATLAB强大的功能技术,可以实现牛顿环干涉实验的仿真。
实验仿真过程直观、动态,实现了仿真实验与实验内容、实验原理、实验操作视频相连接,并展现了不同曲率半径对牛顿环实验干涉图像的影响,以及入射光波长对干涉图像的影响,实验仿真效果良好,为科研和教学提供了新的研究方法。
利用MATLAB模拟分析光源的非单色性对牛顿环的影响

利用MATLAB模拟分析光源的非单色性对牛顿环的影响牛顿环干涉实验具有普遍性,在生产研究中也有广泛的应用[1—3]。
传统的牛顿环实验使用钠光灯作为光源,干涉条纹生成于牛顿环的透镜表面,为定域干涉条纹;用He—Ne激光器作为光源照射牛顿环,则干涉条纹生成于牛顿环反射光束传播空间的任何截面上,为非定域干涉条纹。
在牛顿环实验应用实践中,干涉条纹的可见度对测量精度有很大的影响,而光源的选取影响着条纹的可见度。
本文分别以钠灯和He—Ne激光作为光源,实验观察并理论模拟了两个光源情况下的牛顿环干涉图样;在光的相于性理论指导下,研究了牛顿环条纹生成的原理,并利用MATLAB模拟了钠双黄线的牛顿环干涉图样,分析了光源的非单色性对牛顿环干涉图样可见度的影响。
1 牛顿环干涉实验现象分析牛顿环实验由光源、牛顿环干涉仪、读数显微镜和平板玻璃等组成。
在牛顿环干涉实验中,我们分别选用钠灯和He—Ne激光作为光源,观察到的干涉图样如图1和图2。
从图样可以看到,钠灯光源比激光光源的干涉效果好。
理论上,激光相干性好,牛顿环干涉效果应该比钠灯好。
但是,可以看到实验效果恰好是相反的,激光牛顿环干涉不仅条纹未变清晰,还使得视场中出现了多套干涉条纹(有多个圆心,还有平行条纹)。
通过研究分析发现:在整个实验光路中有多个反射面,平凸透镜的平面和凸面的反射光、凸面和平板玻璃的上表面的反射光、凸面和平板玻璃的下表面的反射光都会发生干涉,此外还有其他的反射面和杂散光的干涉。
对于钠黄光,其相干长度为0.58mm,除了靠近凸面顶点的空气层上下表面反射光的干涉在相干长度以内,其他地方的干涉都是非相干叠加不会产生干涉条纹。
对于激光,其相干长度可以达到几米到几十公里,所有反射面的反射光都参与干涉,还有杂散光的干涉,所以视场中出现多套干涉条纹。
2 牛顿环干涉理论分析2.1扩展单色光源设有一个透明薄膜,由一个准单色的点光源S来照射,薄膜上下两个反射面的反射光在薄膜外P点相遇,如图3。
MATLAB实验牛顿环实验的MATLAB仿真

实验三牛顿环实验的MATLA 仿真、实验目的MATLAB 在光学实验的计算机仿真方面有着重要的应用。
使用MATLA 师以仿真大多数光学实验,例如杨氏双缝干涉实验、牛顿环实验、夫琅和费衍射等, 使得原本抽象的必须借助 实验仪器才能感知的光学现象可以直观而且动态的显示在计算机上,从而获得对某一特定光学现象充分的感性认知,加深我们对抽象光学现象的理解和认识。
这里将以牛顿环实验的 MATLAB^真为例,向大家介绍光学实验的 MATLAB^态仿真的基本方法并通过上机练习以达 到如下几个目的:1. 掌握用imshow 实现光强度二维分布的可视化显示方法;2. 掌握MATLAB^态仿真技术一影片动画技术;、实验原理1.牛顿环干涉原理右图所示为牛顿环装置的示意图。
R 为牛顿环透镜的曲率半径,d 为空气膜的厚度(R»d )。
垂直入射光经空气膜的上下两表面反射后产生干涉,干涉后的光强I =11 12 2」112cos (二)⑴其中I i 和-是两束相干光的光强,可近似认为 I 1 = I 2 = | 0。
=、为两束光相遇时的位相差宀 2兀九(2 d -)⑵由图中的几何关系以及 R …d 条件可得r 2 d⑶2 R(2)、(3)式代入(1)式后有I =2I °sin 2( R-) =sin 2( R-)R 九 R 九点的坐标。
(4)式是实验仿真的基础,对于任意给定点(x,y),如果该点的光强I 取最大值1, 则该点为明条纹所在;若光强I 取最小值0,则是暗纹所在;其他值则介于两者之间。
(4)式给出了牛顿环干涉光强的二维平面分布,那么如何将光强的平面分布(数值)可 视化显示出来?下面介绍一种简单的实现方法。
2. 光强分布的可视化实现上式中为了方便取系数2I o =1。
在直角坐标系中 r 2 = x 2 • y 2,(x,y )代表光强的二维分布人肘光图1对于数据的可视化,MATLAB提供了很多实现方法,比如前面介绍的plot、plot3、surf函数等。
牛顿环MATLAB处理实验报告
21.014 20.915 20.821 20.740 20.655 20.561 20.480 20.415 20.339 20.251];
R=[];theta=0:0.001:2*pi;Ri=[];
R=[];Ri=[];theta=0:0.001:2*pi;
fori=1:20;
D=l(i)-l(41-i);
R=D/2;
Ri=[Ri;R]
figure(1)
x=R*sin(theta);
y=R*cos(theta);
plot(x,y,'-r')
axisequal
holdon
end
Ri
计算结果:
牛顿环
Rm^2-m图像
由上图可知,其斜率的绝对值应为 ,实验所用的钠光波长为:589nm,带入计算得: ,与公式法计算所得结果基本吻合!
Matlab计算程序:
程序二:计算不确定度
clc,clear
l=[27.094 27.012 26.943 26.859 26.780 26.701 26.615 26.523 26.434 26.332...
26.234 26.138 26.030 25.919 25.799 .669 25.540 25.385 25.209 25.018...
22.319 22.154 21.981 21.822 21.691 21.588 21.444 21.330 21.222 21.105...
21.014 20.915 20.821 20.740 20.655 20.561 20.480 20.415 20.339 20.251];
Matlab GUI的牛顿环实验数据处理系统设计

Matlab GUI的牛顿环实验数据处理系统设计
周志玉
【期刊名称】《武夷学院学报》
【年(卷),期】2022(41)3
【摘要】基于Matlab GUI强大的计算、人机交互功能,设计出牛顿环干涉实验数
据处理系统,该系统包括逐差法和最小二乘法两个数据处理应用界面。
系统界面控
件布局合理,操作简单,即时显示运行结果,功能符合逐差法和最小二乘法的数据处理要求。
在界面上分别运行牛顿环实验数据,结果显示,两个处理界面均能快速、直观、准确地计算出凸透镜的曲率半径和不确定度,从而避免繁琐的计算和出现人为失误,
大大提高学生处理牛顿环实验数据的效率。
【总页数】4页(P58-60)
【作者】周志玉
【作者单位】集美大学诚毅学院实验管理中心
【正文语种】中文
【中图分类】O4-39
【相关文献】
1.Matlab软件在牛顿环实验数据处理方法上的创新
2.基于MATLAB GUI的导热
系数测量实验数据处理3.基于MATLAB GUI的声速测量实验仿真\r及数据处理4.Matlab在牛顿环实验数据处理中的应用5.基于Matlab GUI的大学物理实验数
据处理系统设计
因版权原因,仅展示原文概要,查看原文内容请购买。
牛顿环实验最佳方法的对比

牛顿环实验最佳方法的对比曹佳妍;顾菊观;苏婷燕【摘要】牛顿环干涉实验是大学物理实验的一个基本实验,基于学者提出的逐差法计算方法,本文比较了两种逐差方法,运用 Mathematics 软件进行数据处理,得到牛顿环实验的最佳测量方法、最佳计算方法和最佳处理方法。
利用计算机对实验数据进行处理的方法,既培养了学生的计算机应用能力,又为实验数据处理提供了方便,简化了大量烦琐的计算。
%Newton ring interference experiment is a basic experiment in university physics ex-periment.Based on the calculation method of successive difference method proposed by schol-ars,this paper compares the two kinds of successive difference methods,and obtain the best measurement method,optimum calculation method and the best processing method of Newton ring experiment through the data processing with the Mathematics software.Experimental da-ta processing method with the computer can not only raise the computer application ability of the students,but also provides convenience for experimental data processing,which simplifies the complicated calculation.【期刊名称】《物理与工程》【年(卷),期】2015(000)004【总页数】4页(P47-50)【关键词】牛顿环;逐差法;曲率半径;不确定度;数据拟合【作者】曹佳妍;顾菊观;苏婷燕【作者单位】湖州师范学院理学院,浙江湖州 313000;湖州师范学院理学院,浙江湖州 313000;湖州师范学院理学院,浙江湖州 313000【正文语种】中文牛顿环干涉实验是大学物理实验中一个重要的基础性实验,基本实验方法是通过读数显微镜对牛顿环的干涉条纹进行测量,进而计算出平凸透镜的曲率半径[1,3,4].在计算方法的选取上,文献[2,5~10]讨论了逐差法计算方法和不确定度的计算及评定,但是并没有比较直径方法和半径方法等.在数据处理方面有应用C语言和Origin软件进行计算和处理得到平凸透镜曲率半径[7,12-15].本文将通过比较直径计算的两种逐差法,得到最佳测量方法和最佳计算方法;再结合Mathematics进行最小二乘法作图求得平凸透镜的曲率半径,比较理论计算和数据拟合得到的曲率半径得出最佳数据处理方法.该讨论和比较为牛顿环实验测量、计算和数据处理提供了很好的指导.1 直径逐差后平均法测量牛顿环条纹暗环的直径,由公式(1)应用逐差后平均法计算平凸透镜的曲率半径:式(1)是先计算直径的逐差平方差再取平均然后代入公式算出R(其中取m=5).测量直径时按图1进行测量,十字叉丝与某个圆环暗纹的左侧相外切,往右移动叉丝越过中心再与该条纹的右侧相内切,两读数的差值就是该条纹的直径;测量时应注意叉丝只能一直往前移动,不能反转移动,否则会产生很大的误差.图1 测量牛顿环干涉条纹示意图在测量过程中,选取环数为1~50暗环进行测量,测量方法如上所述,每环暗纹测量3次.所有值的单位为mm,测量结果见表1(因篇幅有限,只提供前20环的数据).表1的第3、5、7列是以式(1)计算所得的平凸透镜曲率半径,表1的第8列是每个暗纹3次测量直径的平均值,第9列是以下面式(3)计算所得的平凸透镜曲率半径.表1 每组暗纹直径和平凸透镜的曲率半径10 7.270 2225.293 7.224 2180.092 7.253 2178.000 7.249 2194.459 9 6.920 2224.451 6.881 2195.334 6.900 2174.044 6.900 2197.965 8 6.528 2224.706 6.546 2250.164 6.538 2231.666 6.537 2235.510 7 6.097 2191.010 6.080 2185.983 6.138 2238.140 6.105 2205.001 6 5.660 2224.082 5.644 2231.401 5.658 2181.219 5.654 2212.573 5 5.160 5.147 5.190 5.166 4 4.655 4.634 4.689 4.659 3 4.049 4.041 4.055 4.048 2 3.369 3.347 3.361 3.359 1 2.413 2.357 2.511 2.427曲率半径对应的不确定度公式[16]为表2 各组曲率半径的平均值和不确定度第一组第二组第三组平均值images/BZ_227_1541_2002_1582_2049.png 2200.811 2187.900 2206.064 2198.258不确定度 7.746 5.079 14.118 8.981由表2知,第三组测量数据与前二组相差很大,说明测量时肯定有较大的偶然误差存在,该数据不予考虑.考虑前二项的结果,=2194.356mm,S(R)=6.413mm.2 直径平均后逐差法测量条纹暗环的直径,先算出直径的平均值,再求平均值的平方差后代入式(3)得到R最后再求平均(其中m=5).测量方法与逐差后平均法相同.测量和计算结果见表1,由表1第9列得,3 数据拟合式表明任意两干涉环的直径平方差和干涉级及暗环序数无关,而只与两环的序数差m有关.因此,只要准确测定两个环的直径,由两个直径平均平方后逐差就可算出平凸透镜的曲率半径.该方法也可以应用作图法来确定平凸透镜的曲率半径,由设x =4jλ,理论上y与x成正比,即y=kx+b,其中斜率即为透镜的曲率半径R.由表1对应的D2j和暗纹级次j,按所设以y和x作数据拟合,根据拟合曲线结果得对应的平凸透镜曲率半径R相当于逐差后平均法所得的平凸透镜曲率半径R.图2 以暗纹直径数据拟合得曲率半径图2(a)拟合得到的一次函数y=2198.08x+1.07,即平凸透镜的曲率半径=2198.08mm;图2(b)拟合得到的一次函数y=2198.19x+0.39,即平凸透镜的曲率半径=2198.19mm;图2(c)拟合得到的一次函数y=2199.71x+1.51,即平凸透镜的曲率半径=2199.71mm.以表1数据实验理论计算与数据拟合得到的曲率半径比较见表3,由表3知数据拟合得到的结果比实验理论计算得到的结果的不确定度要小很多,其结果与文献[11,13~15]相一致.因而,实验过程中可以选择数据拟合和实验理论计算来计算平凸透镜的曲率半径,在精度要求不高时两者都可以,但应用计算机处理数据计算方便和省时,计算结果的不确定度较小,因而建议使用计算数据拟合来进行数据处理和计算比较好.表3 以直径方法进行数据拟合结果与实验理论计算结果比较计算方法第一组第二组第三组images/BZ_227_1541_2002_1582_2049.png以images/BZ_227_1541_2002_1582_2049.png为真值的不确定度数据拟合2198.080 2198.190 2199.710 2198.660 0.526逐差后平均法实验计算2200.8112187.900 2206.064 2200.811 5.397平均后逐差法实验计算2198.258 4.5524 结语牛顿环干涉实验中测量直径是最佳测量方法,以平均后逐差法计算是最佳计算方法,以数据拟合进行数据处理是最佳处理方法,3个方法综合应用所得结果不确定度最小,因此,建议牛顿环干涉实验中要想得到最佳结果需要满足以上3个最佳.上述方法对培养学生的动手能力、数据处理能力和计算应用能力是很有效的;在学生实验时间足够和学生开放实验时,可以让学生尝试多种实验测量方法和数据处理方法进行实验对比,对学生科学思想、科学方法和科学素质培养是很有益的途径之一.数据处理和曲线拟合也可应用Matlab和Excel等软件进行处理.参考文献【相关文献】[1]杨述武.普通物理实验(光学部分)[M].北京:高等教育出版社,2000.[2]赵纪平,徐庆强.牛顿环实验数据处理的最佳方法[J].徐州师范大学学报(自然科学版),2001,19(4):48-50.[3]腾敏康.实验误差与数据处理[M].南京:南京大学出版社,1989.[4]任隆良,谷晋骐.物理实验[M].天津:天津大学出版社,2009.[5]李平.牛顿环实验的三种数据处理方法物理实验[J].物理实验,1989,11(3):115-117.[6]虞仲博,屠全良.牛顿环实验等精度测量及其不确定度的评定与表示[J].物理实验,2000,20(5):17-19..[7]苗琦,王明东,等.牛顿环测透镜曲率半径数据分析和结果探讨[J].物理与工程,2010,20(5):32-33,57.[8]刘长发.牛顿环实验方法的改进[J].物理与工程,2006,16(1):34-36.[9]王雅红.不同数据采集方法对牛顿环测曲率半径准确度的影响[J].物理与工程,2005,15(4):36-38.[10]李平.牛顿环实验数据处理方法的回顾与讨论[J].物理与工程,2002,12(12):31-33,62.[11]谭亮,高雄健,等.C语言和Origin7.5软件在实验中的应用[J].物理通报,2013,23(1):77-80.[12]滕坚.牛顿环实验数据处理方法分析[J].物理通报,2006(6):34-36.[13]唐春红,唐曙光,刘扬正.逐差法和Origin8.0软件在牛顿环实验数据处理中的比较[J].物理通报,2013(9):98-100.[14]苗琦,王金苗.Origin软件在牛顿环测透镜曲率半径实验数据处理中的应用[J].大学物理实验,2011,24(2):76-78.[15]王晓雄.利用Origin拟合方法处理牛顿环实验数据[J].大学物理实验,2011,24(4):73-74.[16]陈殿伟,盖啸尘,等.牛顿环实验测量结果不确定度的评定[J].大学物理实验,2007,20(3):72-74.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Matlab 软件在牛顿环实验数据处理方法上的创新
徐少刚 夏雪琴 大学物理实验学A12船舶2
(浙江海洋学院,浙江 舟山 316022)
摘要:本文运用了用Matlab 软件的功能函数对牛顿环测量平凸透镜的曲率半径实验的数据进行处理,简化了数据处理过程,提高了实验结果的准确度;同时也提高了我们大学生应用软件的能力,激发了学习兴趣,提高了教学质量。
关键词:牛顿环;Matlab 软件;最小二乘法;数据处理;创新
牛顿环实验是一个古老而又非常重要的光学实验,一般用它来测量平凸透镜的曲率半径 十分方便,这个实验在我校已开设许多年了。
目前数据处理方法主要有:逐差法和最小二乘法,用人工计算既繁琐又篇幅大,占用了我们学生较多的学习时间,并且往往运算容易出差错,得不到十分理想的实验结果,这样必然会影响我们学生的学习积极性和教学效果。
随着计算机软件的迅速发展,如用Matlab 软件的功能函数进行最小二乘法曲线拟合,得到平凸透镜的曲率半径,而且还能进行误差理论分析,一方面简化了数据处理过程,提高了实验结果的准确度;另一方面提高了我们大学生应用软件的能力,并且对实验数据处理方法上的一种创新,激发了我们大学生对学习大学物理实验的兴趣,提高了教学质量。
1实验原理[1]
在一块平面玻璃上安放上一焦距很大的平凸透镜,使其凸面与平面相接触,在接触点附近就形成一层空气膜。
当用一平行的准单色光垂直照射时,在空气膜上表面反射的光束和下表面反射的光束在膜上表面相遇相干,形成以接触点为圆心的明暗相间的环状干涉图样,称为牛顿环,其如图1。
由干涉条件知,当2(21)22
r K R λλ
δ+=+=时,干涉条纹为
暗条纹。
于是:K r (0,1,2,
)KR K λ=2= 可改为K (0,1,2,
)D KR K λ=2=4
用Matlab 软件作图并处理实验数据,作出2K D ~K 的关系图。
令2K y D = ; x K =;4k R λ= ,
可得到拟合直线方程 y k x b =+,并从其斜率k中求出平凸透镜曲率半径R 的值。
2实验数据记录
已知钠光的波长75.89310m λ-=⨯,仪器误差6
510m -⨯ 8800m R 标=0.
图1牛顿环光路示意图
3 3.1得到y 与x 的数据表
令K L R
D X X =-,x K =,2K y D =,
用Matlab 软件编写程序计算: >>x=[55 50 45 40 35 30 25 20 15 10]
>>c1=[0.032394 0.032112 0.031902 0.031638 0.031338 0.031036 0.030702 0.030318 0.029918 0.02941] % X L 的值
>>c2=[0.021538 0.021786 0.022062 0.022314 0.0226 0.022918 0.023338 0.023602 0.024026 0.024506] % X R 的值
>>c3=c1-c2 %D K =(X L - X R )的值 >>y=c3.^2 % y-D K 2的值
表2由2K D 与K 之间关系得到y 与x 的数据
3.2.1用Matlab 软件最小二乘法公式求出斜率k 、相关系数γ
y kx b =+ 用最小二乘法求出曲线的斜率k 、相关系数γ,
2
()()()
i
i i
x x y y k x x --=
-∑∑ b y k x =- ,()()x x y y γ--=
Matlab 程序: >> a=polyfit(x,y,1)
结果得: k=0.2079e-5,b=0.3307e-5
3.2.2用plot 函数绘y 与x 的拟合图2
Matlab 程序: >>x1=10:5:55;k=2, >> y1=a(1)*x1+a(2);
>> plot(x,y,’*’,x1,y1,’k ’),xlabel(‘P ’),ylabel(‘I ’),grid on, Matlab 拟合图见图2
图2 Matlab 绘y 与x 的拟合图
所以拟合直线方程为:550.2079100.330710y x --=⨯+⨯
4 Matlb 软件最小二乘法误差分析计算 4.1 Matlab 程序:
>> yn=a(1)*x+a(2),xn=(y-a(2))/a(1),
>> sigmayn=sqrt((yn-y)*(yn-y)’/(k*(k-1))), %
K D 的绝对误差Y Δ
>> sigmaxn=sqrt((xn-x)*(xn-x)’/(k*(k-1))), %K 的绝对误差
X Δ
>> xp=mean(x),yp=mean(y),Lxx=(x-xp)*(x-xp)’, % >> Lxy=(x-xp)*(y-yp)’,Lyy=(y-yp)*(y-yp)’,
>> r=Lxy/sqrt(Lxx*Lyy), 线性相关系数r >> R=a(1)/(4*5.893*0.0000001), %曲率半径R >>R0=0.88,deth=(R-R0)/R0, %百分差R E >>y2=0.000107,x2=50,b=a(2),
>>sigmah=R*sqrt((sigmayn/(y2-b))^2+(sigmaxn/x2)^2), %R Δ
>> deth1=sigmah/R, %相对不确定度R E
4.2误差结果得:
sigmayn =9.9912e-007 sigmaxn =0.4807 sigmah =0.012 r =0.9999 R =0.8818 deth =0.0020 death1=0.0136
线性相关系数r =0.9999接近于1,说明k 、b 的值准确性高且可用,拟合直线方程为:550.2079100.330710y x --=⨯+⨯线性拟合度高。
曲率半径的最佳值: R 0.8818m =. 2K D 的绝对误差Y Δ=sigmayn =9.9912e-007,
K 的绝对误差X Δ=sigmaxn =0.4807,R 的绝对误差R Δ=sigmah =0.012。
5实验结论
通过上面用Matlab 软件的功能函数对实验数据进行处理,很快得到如下实验结果:
相对不确定度:1
0.1210100% 1.4%0.882R P E R
-∆⨯=
=⨯=
百分差:
3
3
(881.8880.0)10
100%100%% R880.010
R
R R
E
-
-
-⨯
=⨯⨯
⨯
标
标
-
==0.2
根据上面的数据处理和误差分析可知,Matlab软件的功能函数最小二乘法对牛顿环实验进行数据处理精度高,而且程序运行简便,计算快捷、高效;因此, 大学生在物理实验中用Matlab软件对牛顿环实验进行数据处理,是对传统的数据处理方法上的一种创新,提高了我们大学生学习积极性,同时也提高了大学物理实验的教学质量。
参考文献
[1]竺江峰,鲁晓东,夏雪琴.大学物理实验教程[M].中国水利水电出社.2011.9
[2]陈怀琛,MATLAB及其在理工课程中的应用指南[M] .西安电子科技大学出版社.2001. Innovation Method Matlab Software Processing Experimental
Data in Newton's Ring
Xu Shaogang Xia Xueqin
(Zhejiang Ocean University,Zhoushan 316022)
Abstract:In this paper, using experimental measurement of curvature radius of ring Plano convex lens on Newton with the function of Matlab software of data processing, the data processing process, improve the accuracy of its results;but also improve the ability of our studentsapplication software, stimulate interest in learning,improve teaching quality.
Keywords:Newtonring;Matlab software;least square method;data processing;innovation。
