正态分布图的制作方法
2012-05-07 简单易学 图文并茂 Excel VBA 制作正态分布曲线

<简单易学> <图文并茂>Excel VBA 制作正态分布曲线简介正态分布与Excel测量数据的正态分布,对相关工作有很重要的判定意义;特别是直观的分布曲线,让人对数据质量一目了然。
/view/45379.htm?wtp=tt参看不少文档,没有见到Excel有直接绘制正态分布曲线的函数,故考虑使用VBA编程的方法,实现从测量数据自动生成正态分布曲线的功能。
约定和程序假设有Excel数据表,把测试数据放在第一张表的第一列中:在VBA编辑器中新建一个模块,名字默认,输入如下代码(代码已经包含注释,请自行参看):'*****************************************************Public Sub myDistrib()Dim Aver As Double '平均数Dim Std As Double '标准差Dim Max As Double '最大值Dim Min As Double '最小值Dim Limit As Double '极限值Aver = Application.WorksheetFunction.Average(Selection)Std = Application.WorksheetFunction.StDev(Selection)Max = Application.WorksheetFunction.Max(Selection)Min = Application.WorksheetFunction.Min(Selection)'取极值的三倍作为今后绘图的上下限Limit = Application.WorksheetFunction.Max(Max - Aver, Aver - Min) * 2'在上下限间创建100个单点值step = Limit * 2 / 100Selection.Copy'创建一个新的表生成需要的数据'这是绘制分布曲线需要的数据Worksheets.Add , Worksheets(Worksheets.Count), 1Worksheets(Worksheets.Count).Name = "【正态分布】" & Trim(Str(Sheets.Count)) Range("A1").SelectActiveSheet.Paste[C1] = "平均值"[D1] = Round(Aver, 2)[C2] = "标准差"[D2] = Round(Std, 2)[C3] = "绘图上限(X2)"[D3] = Round(Aver + Limit, 2)[C4] = "绘图下限(X2)"[D4] = Round(Aver - Limit, 2)For I = 1 To 100Cells(I, 6).Value = (I - 1) * step + (Aver - Limit)Cells(I, 7).Value = Application.WorksheetFunction.NormDist(Cells(I, 6).Value, Aver, Std, 0)Next I'这是绘制上下标识和平均值需要的数据[C6] = "最大值"[D6] = Max[E6] = Max[D7] = 0[E7] = [G51][C9] = "最小值"[D9] = Min[E9] = Min[C10] = "绘图上标值"[D10] = 0[E10] = [G51][C12] = "平均值"[D12] = Aver[E12] = Aver[C13] = "绘图上标值"[D13] = 0[E13] = [G51]Columns.AutoFit'绘制图形ActiveSheet.Shapes.AddChart.SelectActiveChart.ChartType = xlXYScatterSmoothNoMarkersActiveChart.SeriesCollection.NewSeriesActiveChart.SeriesCollection(1).XValues = "='【正态分布】4'!$F$1:$F$100" ActiveChart.SeriesCollection(1).Values = "='【正态分布】4'!$G$1:$G$100" ActiveChart.SeriesCollection(1).Name = "=""分布曲线"""ActiveChart.SeriesCollection(2).DeleteActiveChart.SeriesCollection.NewSeriesActiveChart.SeriesCollection(2).XValues = "='【正态分布】4'!$D$6:$E$6" ActiveChart.SeriesCollection(2).Values = "='【正态分布】4'!$D$7:$E$7"ActiveChart.SeriesCollection(2).Name = "=""最大值"""ActiveChart.SeriesCollection.NewSeriesActiveChart.SeriesCollection(3).XValues = "='【正态分布】4'!$D$9:$E$9"ActiveChart.SeriesCollection(3).Values = "='【正态分布】4'!$D$10:$E$10"ActiveChart.SeriesCollection(3).Name = "=""最小值"""ActiveChart.SeriesCollection.NewSeriesActiveChart.SeriesCollection(4).XValues = "='【正态分布】4'!$D$12:$E$12"ActiveChart.SeriesCollection(4).Values = "='【正态分布】4'!$D$13:$E$13"ActiveChart.SeriesCollection(4).Name = "=""平均值"""'调整图形的位置ActiveSheet.Shapes(1).IncrementLeft 185ActiveSheet.Shapes(1).IncrementTop -93.75End Sub'*****************************************************使用方法为:选择Sheet1上,第一列的原始数据;按Alt+F8。
WPS中用excel做正态分析

1.数据录入新建excel文档,录入待分析数据(本例中将数据录入A列,则在后面引用中所有的数据记为A:A);2.计算“最大值”、最小值、极差、分组数、分组组距,公式如下图:3.分组“分组”就是确定直方图的横轴坐标起止范围和每个小组的起止位置。
选一个比最小值小的一个恰当的值作为第一个组的起始坐标,然后依次加上“分组组距”,直到最后一个数据值比“最大值”大为止。
这时的实际分组数量可能与计算的“分组数”有一点正常的差别。
类似如下图二、统计频率“频率”就是去统计每个分组中所包含的数据的个数。
最简单的方法就是直接在所有的数据中直接去统计,但当数据量很大的时候,这种方法不但费时,而且容易出错。
一般来说有两种方法来统计每个小组的数据个数:1.采用“FREQUENCY”函数;2.采用“COUNT IF”让后再去相减。
这里介绍的是“FREQUENCY”函数方法:“Date_array”:是选取要统计的数据源,就是选择原始数据的范围;“Bins_array”:是选取直方图分组的数据源,就是选择分组数据的范围;生成“FREQUENCY”函数公式组,步骤如下:1. 先选中将要统计直方图每个子组中数据数量的区域2.再按“F2”健,进入到“编辑”状态再同时按住“Ctrl”和“Shift”两个键,再按“回车Enter”键,最后三键同时松开,大功告成!三、获取正态分布概率密度正态分布概率密度正态分布函数“NOR MDIST”获取。
在这里是以分组边界值为“X”来计算:Mean=AVERAGE(A:A)(数据算术平均)Standard_dev=STDEV(A:A)(数据的标准方差)Cumulative=0(概率密度函数)向下填充四、制作正态分布图1、选中统计好的折线图每个小组的分布概率密度,用折线图来完成正态分布图;2、选中正态分布概率密度列下所有数据(I2:I14),插入——图标——折线图,3、选好图表类型及配色方案后,单击“下一步”,进入“源数据”对话框,如图4、单击框图上“系列”菜单5、单击“添加”系列,新建系列二,如图6、在系列名称点击框选图标,在表格中选取G1单元格,其自动将“频率”转换成代码,再点击框选图标,返回源数据对话框7、然后在系列“值”栏,清除数据={1}后点击框选图标,在表格中选中频率下所有数据(G2:G14),8、再返回源数据对话框,可以看到原系列二已更名为频率9、单击系列1,将其名称更换为“正态分布概率密度”,即在选中系列1后10、在名称栏中点击框选图标,在表格中选中“I1”单元格后返回“源数据对话框”,11、在分类X轴标志栏,点击框选图标,在表格中选中分组列下所有数据(F2:F14),返回对话框,可以看到对话框中图表横轴发生变化12、然后单击“下一步’,进入图表选项对话框,在标题菜单的“图表标题”中输入“正态分布概率密度曲线”,在分类x轴中输入“分组”,在数据Y轴中输入“概率密度”,如图13、单击完成,图表绘制完成。
正态分布图的制作方法

参考資料:QC 数学の話(大村 平著) 日科技連出版 翻訳完成日期:2009年6月6日 品质管理的基石统计初步(翻訳:李琰) 目录·从互换性到品质管理·QC 是迈向文明社会的技术突破 ·从互换性到品质管理 ·SQC 的成熟与TQC ·数据整理的基本 ·代表值的选出 ·平均值的计算 ·标准偏差的计算 ·正态分布概念引入 ·正态分布的加法与减法 ·正态分布应用举例第1章从统计学的互换性到品质管理20世纪人类历史上发生了3大震撼世界技术的突破。
1,原子能的利用;2,高分子化合物的合成;3,信息技术的飞跃发展。
关于原子能的利用,主要在民生和军事方面得到了广泛的发展。
在人类历史上原子能的出现翻开了历史新的一页,震撼了世界这是众所周知的。
二次世界大战期间在広島,長崎投下的原子弹的爆炸,造成了人类的大量伤亡。
在民生应用方面,随着碳素系列能源的枯竭和CO 2排出的控制, 原子能发电已经得到广泛应用。
另外在高分子化合物合成技术方面,给人类生活带来了极大的影响。
用塑料做成的各种各样建材类,器具类遍布了我们的生活周围。
如果把我们生活中存在的塑料制品全部拿走的话,我们生活就象没有了文字一样,土蹦瓦解。
化肥使粮食增产。
人工纤维的合成,给我们提供了丰富多样的衣着。
合成橡胶,洗剂,粘结剂,调味品等不胜枚举。
还有,信息技术的飞跃发展。
首先让我们只看一下和我们切身利益相关的民生用品,各种各样的业务预约,存款储蓄,通信网和铁道网的管理,天气预报,犯罪搜查等虽然眼睛直接看不到,却支撑着我们的近代生活。
而且各种技术计算,生命科学,人工智能等先端事物已变成了我们生活中的神圣组织。
如果说没有高分子化合物我们的生活会瓦解的话,那么没有信息我们的生活会瘫痪。
基于以上,我们可以说,原子能是能源方面的突破,高分子合成是硬件方面的突破,信息技术是软件方面的突破,3个方面对我们的生活带来了震撼性的影响。
Excel表格中怎么制作正态分布图和正态曲线模板?
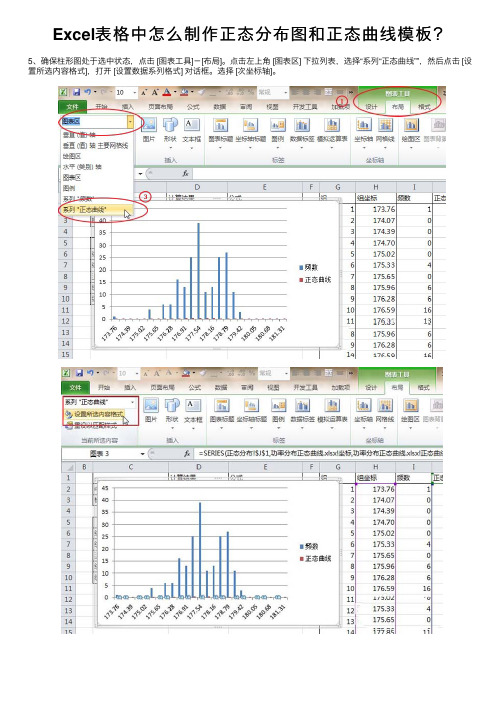
Excel表格中怎么制作正态分布图和正态曲线模板?5、确保柱形图处于选中状态,点击 [图表⼯具]-[布局]。
点击左上⾓ [图表区] 下拉列表,选择“系列“正态曲线””,然后点击 [设置所选内容格式],打开 [设置数据系列格式] 对话框。
选择 [次坐标轴]。
6、 [图表⼯具] 选项组切换到 [设计] 选项卡。
点击 [更改图表类型],打开 [更改图表类型] 对话框。
如图选择拆线图7、柱形图中选中正态曲线,然后在 [图表⼯具] 选项组切换到 [布局] 选项卡。
点击 [设置所选内容格式],打开 [设置数据系列格式] 对话框。
切换到 [线型] ,选择 [平滑线]。
8、⾄此,图形已经画完。
如果只需要柱形分布图,不需要正态曲线,在柱形图中选中正态曲线,按键盘上的Delete键删除就⾏了。
有的专业作图软件中,柱形分布图中柱⼦是紧挨在⼀起的。
要这样设置的话请在柱形图中选中柱⼦,然后 [图表⼯具] 选项组切换到 [布局] 选项卡。
点击 [设置所选内容格式],打开 [设置数据系列格式] 对话框。
分类间距设为0%。
切换到 [边框颜⾊] ,然后选择 [实线] ,颜⾊随便选⼀个,只要和柱⼦不是⼀个颜⾊就可以了。
这⾥选择了⿊⾊。
9、最后,试着修改下“组”和上下限与中⼼值距离的值,图表会⾃动更新。
在第3步中,我们计算了100组的值,所以,只要此处的组不超过100,均可得到正确的图表。
⼀般分组到100的情况极少,所以,第3步预留了100组的数据,以便在更改组时,总能等到正确的图表。
当然,如果你原意,计算1000组也⽆所谓了。
反正你已经学会⽅法了。
以后如果样本数据变更了,直接将A列数据换成新的样本数据,设置下需要的分组和上下限与中⼼值距离的值,正态分布图分分钟钟就出来啦。
⾄于美化嘛,只要更改相关设置就可以了,⽐如开篇那张,当然,你可以把图表美化的更加漂亮,尽情发挥想象⼒吧。
上⼀页12 3下⼀页阅读全⽂。
正态分布曲线
第八步: 每个小块都填上不同的颜色,并标上数值
34 34
13.5
16 2.5
第九步: 所有形状复制一份并填充较深的同色系颜色。 给第一个形状制作擦除进入动画,用动画刷 刷到其他形状上。
34
34 13.5
16 2.5
还在用饼图表示百分比吗?
真是弱爆了!
学着做一个老罗这样的正态分布图吧
第一步: 先画一个矩形
第四步: 用组合形状里面的形状剪除,剪掉正态分布 曲线的下半部分
第五步: 画5个矩形,用【左对齐】,【右对齐】和 【横向分布】排列整齐
ห้องสมุดไป่ตู้
第六步: 复制正态分布曲线四次,获得5条正态分布曲 线
第七步: 正态分布曲线分别和五个矩形进行【组合形 状】【形状交点】
Excel有关正态分布函数NORMSDIST做正态分布图

Excel做正态分布图用正态分布函数NORMSDIST正态分布函数的语法是NORMDIST(x,mean,standard_dev,cumulative)cumulative为一逻辑值,如果为0则是密度函数,如果为1则是累积分布函数。
如果画正态分布图,则为0。
例如均值10%,标准值为20%的正态分布,先在A1中敲入一个变量,假定-50,选中A列,点编辑-填充-序列,选择列,等差序列,步长值10,终止值70。
然后在B1中敲入NORMDIST(A1,10,20,0),返回值为0.000222,选中B1,当鼠标在右下角变成黑十字时,下拉至B13,选中A1B13区域,点击工具栏上的图表向导-散点图,选中第二排第二个图,点下一步,默认设置,下一步,标题自己写,网格线中的勾去掉,图例中的勾去掉,点下一步,完成。
图就初步完成了。
下面是微调把鼠标在图的坐标轴上点右键,选坐标轴格式,在刻度中填入你想要的最小值,最大值,主要刻度单位(x轴上的数值间隔),y轴交叉于(y为0时,x多少)等等。
确定后,正态分布图就大功告成了。
PS:标准正态分布的语法为NORMSDIST(z),均值:分布的均值;标准差:分布的标准差;累积:若1,则为分布函数;若0,则为概率密度函数。
当均值为0,标准差为1时,正态分布函数NORMDIST即为标准正态分布函数NORMDIST。
例3已知考试成绩服从正态分布,,,求考试成绩低于500分的概率。
解在Excel中单击任意单元格,输入公式:“=NORMDIST (500,600,100,1 )”,得到的结果为0.158655,即,表示成绩低于500分者占总人数的15.8655%。
例4假设参加某次考试的考生共有2000人,考试科目为5门,现已知考生总分的算术平均值为360,标准差为40分,试估计总分在400分以上的学生人数。
假设5门成绩总分近似服从正态分布。
解设表示学生成绩的总分,根据题意,,。
第一步,求。
用EXCEL制作直方图和正态分布图
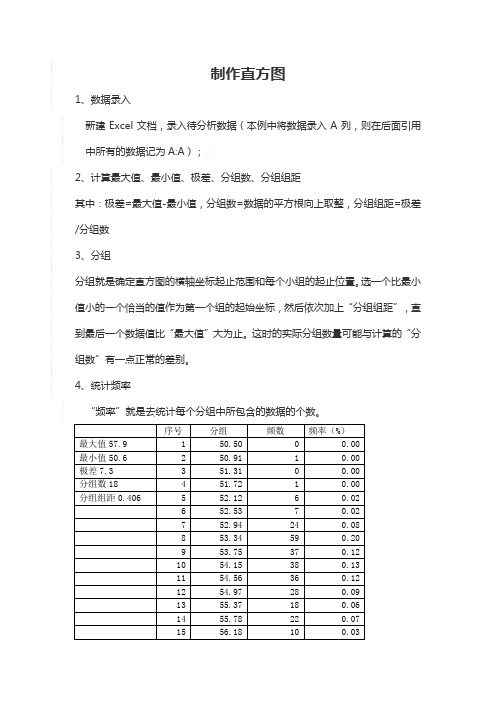
制作直方图
1、数据录入
新建Excel文档,录入待分析数据(本例中将数据录入A列,则在后面引用中所有的数据记为A:A);2
2、计算最大值、最小值、极差、分组数、分组组距
其中:极差=最大值-最小值,分组数=数据的平方根向上取整,分组组距=极差/分组数
3、分组
分组就是确定直方图的横轴坐标起止范围和每个小组的起止位置。
选一个比最小值小的一个恰当的值作为第一个组的起始坐标,然后依次加上“分组组距”,直到最后一个数据值比“最大值”大为止。
这时的实际分组数量可能与计算的“分组数”有一点正常的差别。
4、统计频率
5、制作直方图
选中统计好的直方图每个小组的分布个数的数据源(就是“频率”),用“柱形图”来完成直方图:选中频率列下所有数据(G1:G21),插入→柱形
选中正态分布柱形图→右键→更改系列图表类型,选中“拆线图”,确定。
选中正态分布曲线→右键→设置数据列格式→线型→勾选“平滑线”→关闭。
excel画正态分布曲线图

excel画正态分布曲线图Excel是微软公司出品的办公软件,使用非常广泛。
它不仅可以用来处理各种表格,还可以制作精美的图表。
本文将介绍如何使用Excel来画正态分布曲线图。
首先,我们需要准备一份数据表,该表应包含来自观测值的观测数据。
在Excel中,将数据表格式设置为“简单表格”,然后把数据复制到此表格中。
接下来,在新工作表中插入正态分布曲线图。
打开图表编辑器,点击“图表类型”,然后选择“曲线图”,点击“确定”。
接着,在“数据”标签中,选择“添加数据”,并将Excel中的数据表中的数据复制到此框中。
点击“确定”,曲线图就生成了。
接下来,我们就可以对正态分布曲线图进行美化了。
先把X轴的标题改成“观测值”,Y轴标题改成“概率”,然后把曲线的粗细调整一下,把颜色改成你喜欢的颜色,最后可以把图表的标题改成“正态分布图”,这样就可以得到一幅精美的正态分布图了。
正态分布图有很多用途,它可以帮助用户更好地分析和理解数据。
例如,我们可以使用正态分布图查看一组观测数据的分布规律。
我们可以看到,这些观测值有多少在平均值附近,有多少偏离平均值。
另外,正态分布图还可以用来评估观测数据是否符合正态分布,以及观测数据的变异情况。
最后,我们可以介绍一下使用Excel画正态分布曲线图的优势。
Excel是一款只需要很少的操作就可以搞定的软件,使用它画正态分布曲线图相当容易,而且能得到较高质量的曲线图,并且可以在图表中添加更多的新元素,比如说添加坐标轴的网格线、标题等等,让曲线图变得更为美观。
以上就是本文关于“Excel画正态分布曲线图”的内容,希望本文能够帮助读者学会如何使用Excel来制作正态分布曲线图,深入了解正态分布图的特点以及它的用途,也希望读者在制作这种图表时能够节省时间,得到更好的效果。
excel制作正态分布图

excel有个数据分析工具,里面可以做直方图,但是正态分布图不能直接做。
若要两种图都显示,那么就需要用到函数了。
方法如下:
假若你的数据在A1:A10
1.统计数据个数;任意选个单元格,如B1,输入count(A1:A10);
2.求最大值;如B2中输入:max(A1:A10)
3.求最小值;如B3中输入:min(A1:A10)
4.求平均值;如B4中输入:average(A1:A10)
5.求标准偏差:如B5中输入:stdev(A1:A10)
6.获得数据区间;用最大值减最小值;如B6中输入:B3-B2
7.获得直方图个数;个数的开放加1,如B7中输入:sqrt(B1)+1
8.获得直方图组距;用区间除以(直方图个数-1),如B8中输入B6/(B7-1)
下面就开始作图了:
1.任选个空单元格:如C列第一个单元格C1,令C1等于最小值,即输入=B3
2.在C2中输入=C1+$B$8 (最小值逐渐累加,绝对引用)
3.选中C2,然后向下拉,直到数据大于最大值就可以了;比如你拉到C5了。
4.统计频数,如在D1中输入frequency(A1:A10,C1:C5)确定,然后将选中D1到D5,将光标定位到公式栏,同时按住Ctrl+Shift+Enter
5.统计正态分布的数据,E1中输入normdist(C1,$B$4,$B$5,0)回车;然后选中E1,下拉到E5。
一步一步教你作正态分布图

=NORMDI ST(A2,Av gValue,S DValue,F ALSE) NORMDIS T函数帮助 信息:
=IF((ROU
ND(A2,Ma
in!$C$2)=
控制上限
ROUND(U pValue,M
ain!$C$2))
,MAX(B:B)
*1.15,NA()
=IF((ROU
ND(A2,Ma
in!$C$2)=
目标值
ROUND(T gtValue,M
ain!$C$2))
,MAX(B:B)
*1.15,NA() 定义名称:
数据的小数位数
1
数据个数
298
最大值
479
最小值
406
平均值
441
标准偏差
11.6
目标值
440
控制上限
460
控制下限
420
控制下限
目标值
控制上限
1 2
34正态来自分布图
5
391.4 398.4 405.4 412.4 419.4 426.4 433.4 440.4 447.4 454.4 461.4 468.4 475.4 482.4 489.4
(目的是作
图时易于控
制数据源) =OFFSET
(Calculati
on!$A$1,1
ChartData ,0,COUNT
A(Calculat
ion!$A:$A)
正态分布图做法Excel

不合格区域 合格区域 控制下限 控制上限 目标值
a b
制作步骤:
1 在工作表Data里输入你的原始数据
2 定义名称:
Time
=OFFSET(Data!$A$1,1,0,COUNTA(Data!$A:$A)-1,1)
Data
=OFFSET(Time,0,1)
3 计算下列
数据的小数位数
可选
数据个数
可选
合格区域 =IF(AND(A2>=LowValue,Calculation!A2<=UpValue),B2,NA())
不合格区域 =IF(OR($A2<LowValue,$A2>UpValue),Calculation!B2,NA())
根据控制上下限将图分为合格和不合格区域。函数NA()隐藏数据点
控制下限 =IF(ROUND(A2,Main!$C$2)=ROUND(LowValue,Main!$C$2),MAX(B:B)*1.15,NA()
NORMDIST函数帮助信息:
NORMDIST(x,mean,standard_dev,cumulative)
X 为需要计算其分布的数值。
Mean 分布的算术平均值。
Standard_dev 分布的标准偏差。
Cumulative 为一逻辑值,指明函数的形式。
如果 cumulative 为 TRUE,函数 NORMDIST 返回累积分布函数;如果为 FALSE,返回概率密度函数。
a 这时你的Excel工具菜单会变样。选择“图表”-“图表类型”-设置为面积图 b 选择“格式”-“数据系列”-设置红色底色,边框线为无
一直按向下键,直到名称框里出现“系列“合格区域”” 重复步骤a,b,将该系列设置为底色为绿色,无边框的面积图 一直按向下键,直到名称框里出现“系列“正态分布...”” 将此系列设置为折线图(实际上,该系列可有可无) 一直按向下键,直到名称框里出现“系列“控制下限”” 步骤a,b,将系列设置为折线图表,线形颜色为红色,数据标识无 设置该系列Y值误差为负误差,“百分比=100%”,误差线格式为红色,无标示 同样步骤设置“控制上限” 同样步骤设置“目标值”,颜色为蓝色 第三步,图表修饰 一直按向下键,直到名称框里出现“数值轴主要网格线”,删除 一直按向下键,直到名称框里出现“数值轴”,删除 双击绘图区,底色设置为黑色 一直按向下键,直到名称框里出现“分类轴” 选择“格式”-“坐标轴”-设置 在对话框里-图案-主要刻度线-外部 在对话框里-刻度-一次为1,70,20 一直按向下键,直到名称框里出现“系列“控制下限”” 选择“格式”-“数据系列”-“数据标识”-勾选“系列名称” 选中该数据标识(同样可以用向下键选定)-设置字体颜色为白色,字号为9,去掉“自动缩放”的勾选 一定要去掉“自动缩放”的勾选,否则数据一改变,你的设置又白费了。 将图表区底色设置为灰色,图表标题设置字体和边框都为白色 第四步,如何去掉多余的图例
excel生成正态曲线

excel生成正态曲线
在Excel中生成正态曲线可以通过以下步骤实现。
首先,打开Excel并创建一个新的工作表。
然后按照以下步骤操作:
1. 在一个列中输入一系列代表正态分布的X值。
例如,可以输
入-3、-2.5、-2、-1.5、-1、-0.5、0、0.5、1、1.5、2、2.5、3
等数值。
2. 在另一列中,使用正态分布函数NORM.DIST来计算对应X值
的Y值。
该函数的语法为
=NORM.DIST(x,mean,standard_dev,cumulative),其中x是要计算
的值,mean是正态分布的均值,standard_dev是正态分布的标准差,cumulative是一个逻辑值,用于指定计算累积分布函数还是概率密
度函数。
例如,可以使用=NORM.DIST(A2,0,1,FALSE)来计算X值为
A2的概率密度函数值。
3. 将上述公式拖动或填充到下面的单元格,以计算所有X值对
应的Y值。
4. 选择X和Y值的数据范围,然后插入散点图。
在Excel中,
选择“插入”选项卡,然后选择“散点图”图标。
选择适当的散点图类型,确保X轴是你输入的X值,Y轴是计算得到的Y值。
5. 在生成的散点图上,右键单击数据点,然后选择“添加趋势线”。
在弹出的对话框中,选择“正态分布”作为趋势线类型。
通过上述步骤,你就可以在Excel中生成一个代表正态分布的曲线图表。
这样可以直观地展示正态分布的特征,对于数据分析和可视化非常有帮助。
希望这些步骤能帮助到你。
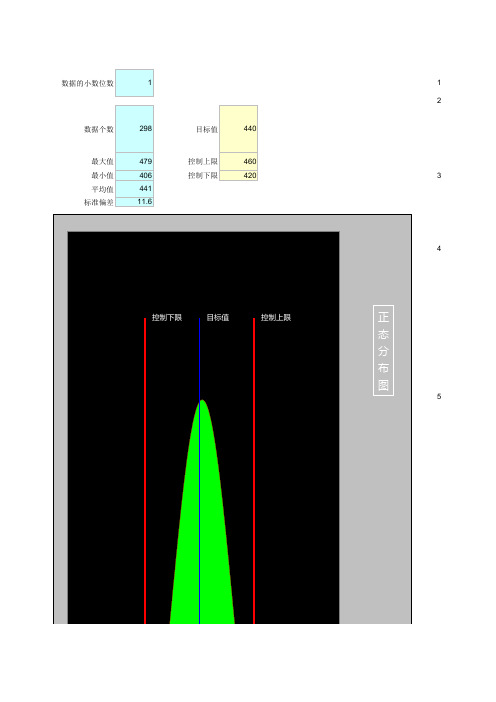
正态分布图做法(输入数据自动生成)
=OFFSET
ChartData3 (ChartLab
el,0,3)
=OFFSET
ChartData4 (ChartLab
el,0,4)
=OFFSET
ChartData5 (ChartLab
el,0,5)
=OFFSET
ChartData6 (ChartLab
el,0,6)
=OFFSET
(Calculati
(目的是作
图时易于控
制数据源) =OFFSET
(Calculati
on!$A$1,1
ChartData ,0,COUNT
A(Calculat
ion!$A:$A)
-1,1)
=OFFSET
ChartData1 (ChartLab
el,0,1)
=OFFSET
ChartData2 (ChartLab
el,0,2)
A2=ROUN D(AvgVal ue340*(Max ValueMinValue) /500,Main! $C$2) A3~A1001 =ROUND( A2+(MaxV alueMinValue) /500,Main! $C$2)
=NORMDI ST(A2,Av gValue,S DValue,F ALSE) NORMDIS T函数帮助 信息:
NORMDIS T 返回累 积分布函 数;如果 为 FALSE, 返回概率 密度函数 。 =IF(AND( A2>=Low Value,Cal culation!A 2<=UpVal ue),B2,NA =IF(OR($ A2<LowV alue,$A2> UpValue), Calculatio n!B2,NA() 根据控制 上下限将 图分为合 格和不合 格区域。 函数NA() 隐藏数据 点 =IF(ROUN D(A2,Main !$C$2)=R OUND(Lo wValue,M ain!$C$2), MAX(B:B) *1.15,NA()
Excel有关正态分布函数NORMSDIST做正态分布图

Excel做正态分布图用正态分布函数NORMSDIST正态分布函数的语法是NORMDIST(x,mean,standard_dev,cumulative)cumulative为一逻辑值,如果为0则是密度函数,如果为1则是累积分布函数。
如果画正态分布图,则为0。
例如均值10%,标准值为20%的正态分布,先在A1中敲入一个变量,假定-50,选中A列,点编辑-填充-序列,选择列,等差序列,步长值10,终止值70。
然后在B1中敲入NORMDIST(A1,10,20,0),返回值为0.000222,选中B1,当鼠标在右下角变成黑十字时,下拉至B13,选中A1B13区域,点击工具栏上的图表向导-散点图,选中第二排第二个图,点下一步,默认设置,下一步,标题自己写,网格线中的勾去掉,图例中的勾去掉,点下一步,完成。
图就初步完成了。
下面是微调把鼠标在图的坐标轴上点右键,选坐标轴格式,在刻度中填入你想要的最小值,最大值,主要刻度单位(x轴上的数值间隔),y轴交叉于(y为0时,x多少)等等。
确定后,正态分布图就大功告成了。
PS:标准正态分布的语法为NORMSDIST(z),均值:分布的均值;标准差:分布的标准差;累积:若1,则为分布函数;若0,则为概率密度函数。
当均值为0,标准差为1时,正态分布函数NORMDIST即为标准正态分布函数NORMDIST。
例3已知考试成绩服从正态分布,,,求考试成绩低于500分的概率。
解在Excel中单击任意单元格,输入公式:“=NORMDIST (500,600,100,1 )”,得到的结果为0.158655,即,表示成绩低于500分者占总人数的15.8655%。
例4假设参加某次考试的考生共有2000人,考试科目为5门,现已知考生总分的算术平均值为360,标准差为40分,试估计总分在400分以上的学生人数。
假设5门成绩总分近似服从正态分布。
解设表示学生成绩的总分,根据题意,,。
第一步,求。
excel怎么用制作对数正态分布的概率密度分布曲线图表?

excel怎么⽤制作对数正态分布的概率密度分布曲线图表?我们在⽇常⽣活中会遇到很多呈对数正态分布的事件,如经破碎的粉尘粒径就呈对数正态分布。
我们可以知道对数正态分布的概率密度曲线为右偏态曲线(取对数前原始数据偏左,取对数后向右偏),单从概率密度曲线难以确定事件的元素是否呈对数正态分布。
验证事件的元素的对数正态分布性,⼀般可借助对数正态分布概率纸进⾏,若在概率纸上绘制的概率密度曲线为线性,那么该事件即呈对数正态分布。
那么,如何借助excel绘制对数正态分布的概率密度线性分布曲线呢?1、⾸先要做的是绘制正态分布刻度。
打开2013版excel,按⾃⼰的需要输⼊⼀系列累积分布值。
在”X轴⽹格值“那⼀列的第⼆个单元格中插⼊公式"NORM.S.INV"。
在弹出的窗⼝的"probability“处选⼀开始输⼊的系列累积分布值,选确定,空格,填充柄下拉,即得到正态刻度数值。
2、往三列第⼆个单元格输⼊0,填充柄填充。
以"X轴⽹格值”为横坐标,以第三列填充的0为纵坐标,做散点图。
作出的散点图如下图⼀,此时正态刻度以在X轴显⽰,接下来要调整坐标轴的格式。
3、选中横坐标轴,右击选“设置坐标轴格式”,在右边窗⼝的“最⼤值”“最⼩值”分别填“3.7194695”“-3.7194695”。
在“纵坐标轴交叉”处选“坐标轴值”,并输⼊数值“-3.7194695”,表⽰纵坐标和横坐标交叉于点(-3.7194695,0)。
调整后坐标如图4、接下来要做的就是要把累积分布值显⽰在横坐标上。
选中横坐标轴,删除。
选中横坐标轴线上的点,右击,选“添加数据标签”。
再⼀次选中轴上的点,右击,选“设置数据标签格式”。
在右边窗⼝“标签包括”先勾选“X值”,再把原有的“Y值”的勾去掉,并在“标签位置”选“靠下”。
完成上述步骤后,显⽰出来的数据为原始的X轴⽹格值,可通过⼿动修改,把想要显⽰的数据输⼊修改即可得到图三效果。
powerpoint制作正态分布曲线教材-精品文档

钱币收藏网,人民币收藏平台 qianbishoucang
学着做一个老罗这样的正态分布图吧
第一步: 先画一个矩形
钱币收藏网,人民币收藏平台 qianbishoucang
第二步: 用编辑顶点功能,把矩形的一条长边变成正 态分布曲线
钱币收藏网,人民币收藏平台 qianbishoucang
第六步: 复制正态分布曲线四次,获得5条正态分布曲 线
钱币收藏网,人民币收藏平台 qianbishoucang
第七步: 正态分布曲线分别和五个矩形进行【组合形 状】【形状交点】
钱币收藏网,人民币收藏平台 qianbishoucang
第八步: 每个小块都填上不同的颜色,并标上数值
钱币收藏网,人民币收藏平台 qianbishoucang
第三步: 再画一个矩形
钱币收藏网,人民币收藏平台 qianbishoucang
第四步: 用组合形状里面的形状剪除,剪掉正态分布 曲线的下半部分
钱币收藏网,人民币收藏平台 qianbishoucang
第五步: 画5个矩形,用【左对齐】,【右对齐】和【 横向分布】排列整齐
34 34 13.5
16 2.5
钱币收藏网,人民币收藏平台 qianbishoucang
第九步: 所有形状复制一份并填充较深的同色系颜色。 给第一个形状制作擦除进入动画,用动画刷 刷到其他形状上。
34 34 13.5
16 2.5
钱币收藏网,人民币收藏平台 qianbishoucang
3.正态分布

u u2
e 2du
2
φ(u)表示从-∞到u值范围内X分布面积
附表1(P245)就是根据此公式和图形制定的
2021/8/8
陈学芬 制作
20
概率密度函数与累积分布函数
1
f(X) F(X) 0.8
0.6 0.4 0.2
0 -4 -3 -2 -1 0 1 2 3 4
X
3.正态曲线下面积的分布规律
曲线下面积分布规律
▪ 总体标准差σ是变异度参数:描述正态分布离散趋势, 越小,分布越集中,曲线形状越“瘦高”;反之越“矮 胖”。
正态曲线由,两个参数共同决定
2021/8/8
陈学芬 制作
7
1.正态分布的概念和特征
三种不同均值的正态分布 σ恒定
-∞
μ1
μ2
μ3
+∞
μ 1<μ 2<μ 3
μ越大,曲线沿横轴越向右移动
2021/8/8
68.27%
95.00%
99.00%
-2.58 -1.96 -1
0
1 1.96 2.58
标准正态分布
面积或概率
-1~1
68.27%
-1.96~1.96
95.00%
-2.58~2.58
99.00%
标准正态曲线 横轴为u值
3.正态曲线下面积的分布规律
将变量值(x)转换为u值后,统计学家按φ(u)公式编制成了附 表1,即标准正态分布表 查表注意事项:
2021/8/8
陈学芬 制作
23
3.正态曲线下面积的分布规律
例 1.求区间(2.58,+∞)的面积。
因为区间(2.58,+∞)和区间(-∞ ,-2.58)对称 所以只需求出(-∞ ,-2.58)的面积即可,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
参考資料:QC 数学の話(大村 平著) 日科技連出版 翻訳完成日期:2009年6月6日 品质管理的基石统计初步(翻訳:李琰) 目录·从互换性到品质管理·QC 是迈向文明社会的技术突破 ·从互换性到品质管理 ·SQC 的成熟与TQC ·数据整理的基本 ·代表值的选出 ·平均值的计算 ·标准偏差的计算 ·正态分布概念引入 ·正态分布的加法与减法 ·正态分布应用举例第1章从统计学的互换性到品质管理20世纪人类历史上发生了3大震撼世界技术的突破。
1,原子能的利用;2,高分子化合物的合成;3,信息技术的飞跃发展。
关于原子能的利用,主要在民生和军事方面得到了广泛的发展。
在人类历史上原子能的出现翻开了历史新的一页,震撼了世界这是众所周知的。
二次世界大战期间在広島,長崎投下的原子弹的爆炸,造成了人类的大量伤亡。
在民生应用方面,随着碳素系列能源的枯竭和CO 2排出的控制, 原子能发电已经得到广泛应用。
另外在高分子化合物合成技术方面,给人类生活带来了极大的影响。
用塑料做成的各种各样建材类,器具类遍布了我们的生活周围。
如果把我们生活中存在的塑料制品全部拿走的话,我们生活就象没有了文字一样,土蹦瓦解。
化肥使粮食增产。
人工纤维的合成,给我们提供了丰富多样的衣着。
合成橡胶,洗剂,粘结剂,调味品等不胜枚举。
还有,信息技术的飞跃发展。
首先让我们只看一下和我们切身利益相关的民生用品,各种各样的业务预约,存款储蓄,通信网和铁道网的管理,天气预报,犯罪搜查等虽然眼睛直接看不到,却支撑着我们的近代生活。
而且各种技术计算,生命科学,人工智能等先端事物已变成了我们生活中的神圣组织。
如果说没有高分子化合物我们的生活会瓦解的话,那么没有信息我们的生活会瘫痪。
基于以上,我们可以说,原子能是能源方面的突破,高分子合成是硬件方面的突破,信息技术是软件方面的突破,3个方面对我们的生活带来了震撼性的影响。
那么为什么以上3个方面可以在20世纪能够获得极大的技术突破呢? 我认为是以下两个方面的原因:1, 抗身抗生物质的发现。
2, 品质管理的普及。
为什么这么说呢?下面阐述理由。
最初的科学文明,把人类从严酷的劳动和疾病中解放出来。
人类为了确保衣食住的安定,做出了很大的QC 数学的話题努力,也取得了很大的进步。
其中被迫做出的最大的苦战是与疾病的搏斗。
但是20世纪链酶素和盘尼西林的出现飞跃性的改善了人们抗疾病的能力。
不治之病和恐慌人们的结核病,痢疾,伤寒,霍乱,鼠疫等多种传染病得到了控制。
一百年前和现在的寿命曲线对比看一下,就会一目了然。
因此抗生物质的发现是20世纪震撼世界的较大的技术突破。
接下来我们讲述品质管理的推荐理由。
生活在现代生活中的我们,被大量的工业品包围。
正是因为工业品的存在,我们才可以享受丰富的现代生活。
而且这些工业制品对我们基本没造成伤害。
电子微波炉过热造成的着火,热水壶把儿的着火,鞋底的脱落,皮带扣的断裂后造成裤子的突然脱落,瓶塞的破裂等以上的品质问题还不至于造成很大的担心。
还有灯泡坏了换一个即可,电池和胶卷等也很容易买到手。
几乎没有我们买不到的东西。
我们可以放心大胆地使用围绕在我们周围的工业制品,但是做到放心使用是一件非常难的事情。
要实现放心使用,我们首先必须做那些事情呢?第一,这些工业制品必须大量生产。
如果没有大量生产,销售价格不可能便宜,当然也不可能遍布全国。
第二,这些大量生产的工业制品必须100%的确保质量。
如果品质不能保证,普及越广就会引起到处出问题。
这是社会所不允许的。
基于以上,也就是说既要大量生产又要100%保证质量。
当然不仅工业制品,农产物,水产物,畜产物等也是一样既要大量生产又要100%保证质量。
那么,怎么做才能使做出的所有的产品都符合品质要求呢?还有,流到市场上的产品都能保证质量吗?然后就出现了一系列的品质管理手法(Quality Control,简称QC)。
QC萌芽于1920年,成熟于20世纪后半期。
均一品质产品的大量的供给生产,是科学文明发展史上的飞跃。
这个飞跃被评价为20世纪文明的技术突破。
这个评价一点也不夸张。
首先,互换性的解说。
黑猩猩用石头敲开果实的皮;有一种啄木的鸟用嘴吸仙人掌球,用嘴趋赶枯木缝中的虫子。
动物使用工具的例子,通过观察可以举很多例子。
但是,不管怎么动物都是在自然现有的物品中选别使用工具。
动物自己不能创造工具,也不能使用部品组装成新的工具。
人类最初和动物一样,可是后来,通过锻打石头制作石器。
把铁棒的头部磨尖制作枪。
还有把尖的石器帮在铁棒的头部制作出了新的工具。
这可以认为是使用两个以上的部品通过组装制作新工具的开始。
然后,人类学会把弓和箭合起来使用。
把两个部品组合后使用确实是人类史上的一大进步。
就是在那时,人类利用智慧,制作出了很多箭可以使用同一个弓,这样的箭相互之间可以相互替换具有融通性。
这种部品之间可以相互替换使用的特性称为互换性。
在概念没有成熟之前,互换性已经被提前使用了。
话虽如此,互换性的概念成熟,基于互换性的基础上,大量生产成为可能在历史上是最近的事情。
17~18世纪伴随着工业革命的发展,大量生产大量消费的时代到来。
没有互换性大量生产是几乎不可能的事情。
在各个场所互换性的利用变成了理所当然的事情。
也就是在那个时候的1763年,法国的将军,为了实现带火炮,弹药的炮兵器材的互换性,发表了他制订的标准化计划。
进入20世纪后,正式的大量生产的时代到来了。
那时谈的最多的话题是美国T型形式的车,从1908年开始近20年间生产了1500万台T型形式的车,该车也被称为“世纪车”。
在日本也引进了海外车型经过日本本国的改进,有一种叫“圆太郎”的车在东京风靡一时,现在的前辈们非常怀念以前的古典的车厢。
在当时T型形式的车因性能好,外观优美曾经很畅销。
不管怎么样T型车当时仍然是有钱人的奢侈品。
到普通大众可以买的起为止,必须进行大副降价。
对于价格下降做出巨大贡献的是,传送带在流水线上的使用。
传送带系统,几乎被所有的制造业导入使用,为20世纪工业发展做出了巨大贡献。
那么,流水线能够成立的第一条件是部品同伴之间具有互换性。
流水线左边传送上过来的部品和流水线上右边流过来的部品可以自由组装。
流水线左边传送上过来的部品和流水线上右边流过来的部品永远可以自由组装,如果不是这样,流水线生产不可能实现。
也就是说,左边部品的同伴之间必须具有互换性,右边部品的同伴之间必须具有互换性。
比如说,部品之间没有互换性,那将是一件非常麻烦的事情。
配对部品在流水线上按一定的节拍流过来,如果某一个部品不能使用,将被返回原处。
当然对该不良品需要进行必要的处理。
也就是说带传送带的流水线生产方式是不可能的。
基于以上原因,用带传送带的流水线生产方式进行大量生产的前提条件是部品的同伴之间具有互换性。
那么通过什么样的手段才能保证部品之间的互换性呢?下面进行举例说明。
让我们想象一下,有一个直径10㎜的轴与一个直径为10㎜的轴套进行配合,并且进行大量生产。
站在生产轴的角度上,总是希望做出来的轴的外直径与10㎜相比不大也不小。
站在做轴套的角度上,总是希望做出来的轴套的孔径与10㎜相比不大也不小。
因为不是神仙,做出来的产品与要求的尺寸一点误差也没有是不可能的事情。
那么按这样的条件做出来的轴和轴套进行配合。
用一个轴与所有的轴套进行配合试一下发现、轴的外径比轴套的孔径大时,轴无法进入到轴套中。
轴的外径比轴套的孔径大的概率50%发生的可能性也是有的。
不得已,只有通过不同的轴与不同的轴套逐个试一遍,也许会提高轴和轴套配合的良品率,那么会需要很多人手,在大量生产的情况下只有边生产边哭了。
如果轴的同伴之间,轴套的同伴之间没有互换性的话,生产会非常狼狈。
因此在加工时要指定尺寸公差(尺寸单位使用mm.)轴的直径10+0.0-0.1 (1.1)轴套的直径10+0.1-0.0 (1.2)总之,轴的外径在9.0~10.0之间波动,轴套的直径在10.0~10.1之间波动。
按以上规格进行加工的话,尺寸最大的轴与尺寸最小的轴套进行配合的话,之间的缝隙用下列公式进行计算:(10-0.0)-(10+0.0)=0 (1.3)轴与轴套之间虽然一点缝隙也没有,努努力还是可以把轴塞到轴套中。
下面我们用外径最小的轴与内径最大的轴套配合,之间的缝隙用下列公式进行计算:(10+0.1)-(10-0.1)=0.2 (1.4)轴与轴套之间会产生0.2的缝隙,但是这点缝隙对使用上不造成影响。
这样的话所有的轴可以配合所有的轴套。
可以说在本例的轴的同伴之间,轴套的同伴之间互换性得到了实现。
另外,(1.1)中的+0.0-0.1部分被成为公差值(tolerance)。
为了实现部品同伴之间的互换性而制订的尺寸变化幅度。
接下来的话题可能会扯的远一些。
现在我们尽量做出来的轴和轴套满足(1.1)和(1.2) 的要求。
做出的大量的制品如果经过测量不满足尺寸规格,对不良品需要剔除,要花相当多的时间和劳力,也就是说要花大量的经费。
这时需要对所做的产品进行检查,比如说我们要加工一个轴要用图1.1样式的检查器具进行检查。
虽然看起来有些古老,但是是最廉价的检查方法。
我们假定我们用无变形,无擦伤,无缺损的原材料制作内径为9.9和10.0的孔,制作出来的轴进入10.0的孔,不能进入到9.9孔内,我们判定该轴为良品。
相反如果生产出来的轴不能进入10.0的孔或进入到9.9孔内我们判定该轴为不良品。
作为10+0.1-0.0孔的检查器具,用10.1的圆棒,10.0的圆棒进行测试,10.1的圆棒进入到孔中或10.0的圆棒不能进入到孔中都判定为不良品。
以上讲述的例子中,为了使轴和轴套具有互换性,对轴和轴套的尺寸进行了管理。
尺寸是产品的重要品质项目之一,用专用的品质管理方法进行管理也言之不过。
前面提到过的话题讲述一下,前面(1.1)的要求进行加工轴时,轴的外径以9.95为目标进行加工。
还有(1.2)的要求进行加工孔时,孔的内径以10.05为目标进行加工。
也就是说,在部品加工时,我们一般按指定的公差中心值进行生产。
在加工时如果有正确的品质管理方法,制作出来的轴和轴套之间的配合偏紧,偏松的几率接近零的话是最理想的。
基于以上,我们可以说大量生产与互换性是表里如一的,互换性与品质管理也是表里如一的。
SQC的成熟与TQC时代在不断的进步,敲响人类最不幸大门的是第二次世界大战的爆发(1939~1945)。
对于二次世界大战的看法多种多样,但是简单一句话概括的话,扩大了殖民地,世界被一分为二。
一个是以美·英为首的战胜国,以日本为主的战败国。
沾满血迹的一场场战争是历史上的悲惨事件。
随着近代工业的崛起,也伴随着战争的发生。
