阵列除法器设计与实现
电路中的除法器设计

电路中的除法器设计在电路设计中,除法器是一种十分重要的组件。
它可以将输入的数字进行除法运算,将商和余数输出。
除法器在计算机和数字信号处理器等电子设备中被广泛使用,因此其设计和优化具有重要意义。
一、除法器的基本原理除法运算是一种复杂的运算,要实现除法器的设计,首先需要了解其基本原理。
除法器的基本原理是通过移位和减法实现的。
在将被除数和除数输入除法器后,除法器将被除数和除数进行比较,并开始迭代过程。
在每一次迭代中,被除数的位数向左移动,直到其高位与除数相等或超过除数。
然后,除法器进行减法操作,将除数减去被除数,结果作为商的一位。
此后,商持续左移,被减数保持不变,重复上述过程,直到所有的商位都得出。
二、除法器的设计策略在除法器的设计中,有几种常见的策略可以考虑。
1. 组合逻辑除法器:这种类型的除法器使用组合逻辑电路实现,通过减法器、比较器和移位器等组件的组合来实现除法运算。
组合逻辑除法器的优点是速度较快,但缺点是占用较多的电路资源。
2. 串行逻辑除法器:与组合逻辑除法器相反,串行逻辑除法器使用顺序逻辑电路实现。
它通过一个时钟信号,逐位地进行计算,因此典型的串行逻辑除法器速度较慢。
但串行逻辑除法器更节省电路资源,因此在一些资源有限的场景中得到了广泛应用。
3. 重复系列除法器:这种除法器通过多个并行的子除法器实现,并行计算多个位的商。
重复系列除法器具有较高的性能,但需要更多的电路资源和功耗。
三、除法器的优化方法为了提高除法器的性能和效率,可以采用一些优化方法。
1. 位级并行思路:通过将除法器分解为多位的子除法器,并行计算多个子除法器,可以大幅提高除法器的速度。
这种方法在重复系列除法器中得到了广泛应用。
2. 乘法相关技巧:利用乘法器计算除法运算,可以加速除法器的运算速度。
通过将除数进行逆运算,转化为乘法操作,可以利用乘法器的高速性能,提升除法器的效率。
3. 进制转换思想:将数字进行二进制到十进制的转换,然后进行简单的除法运算,可以减少运算的复杂程度,提高除法器的运算速度。
阵列除法器的FPGA实现

・ 备与 设旖・ 设
阵列除法器的 F G P A实现
口 孙 亮 周忠海 1廉 月仙 。 军礼 , 2 , , 刘
(. 1 中国海洋大学, 山东 青 岛 2 6 0; . 60 3 2山东省海洋仪器仪表研究所, 山东 青岛 2 60 ; 60 1 3西 日本株式会社. _ 山东 青岛 2 6 0 ) 60 1
口 SUN La g , in  ̄ZHOU Zh n - a , I e xa 。L U J n l o g h i LAN Yu - in , I u —i ’
( . c a i r i f i , n d o 2 6 0 , i ; . s tt f e n g a h sr me tt n S a d n 1O e n Un e s y o n Qi a 6 0 3 Ch a 2 I tueo a o r p i I t v t Ch a g n n i Oc c n u nai , h n o g o
除法器是 电子技术领 域的基础模 块 ,在 电子 电路设 计中
得多 , 但为了提升运算速度 , 就要 以硬件资源 的消耗为代价 。
2 除法 的运 算 的 分析
得到广泛地应用。然而相对于加法和乘法等其他操作 , 除法操 作的效率很低 。出现这种情况 的原 因除了除法本身 的复杂性
外, 还与人们普遍认为除法是不频繁的操作有关 。作为微处理 器的一个重要 的运 算单 元 , 除法器 的运 算速度 、 能 、 性 功耗 等 都会影 响系统 的整体性能 ,所 以对除法效率 的忽视会导致系
【 中图分类号】
T 62 N0
【 文献标 识码】
B Βιβλιοθήκη 【 文章编号】 1 0 — 5 8(0 8 0 — 1 0 0 7 4 3 , 0 ) 4 0 仃一 2 2
除法器设计方法
controlsignals:process(T,I,X,Y)
--状态控制进程
begin
Extern<='0';Done<='0';Ain<='0';Gin<='0';
Gout<='0';AddSub<='0';Rin<="0000";Rout<="0000";
case T is
when "00"=>
update:process(clk)
--同步数据更新进程
begin
if(clk='1'and clk'event) then
state<=nextstate;
if load='1' then
dividend<='0'÷nd_in;
end if;
if su='1' then
dividend(8 downto 4)<=subout;
end proc;
architecture Behavioral of proc is
component upcount
--计数器元件声明
Port ( Clear,Clock : in std_logic;
Q : buffer std_logic_vector(1 downto 0));
end component;
signal subout:std_logic_vector(4 downto 0);
signal dividend:std_logic_vector(8 downto 0);
阵列除法器

沈阳航空工业学院课程设计报告课程设计名称:计算机组成原理课程设计课程设计题目:阵列除法器的设计院(系):计算机学院专业:计算机科学与技术班级:7401101学号:*****************指导教师:***完成日期:2010年1月15日沈阳航空工业学院课程设计报告目录第1章总体设计方案 (1)1.1设计原理 (1)1.2设计思路 (2)1.3设计环境 (3)第2章详细设计方案 (6)2.1顶层方案图的设计与实现 (6)2.1.1创建顶层图形设计文件 (6)2.1.2器件的选择与引脚锁定 (7)2.1.3编译、综合、适配 (8)2.2功能模块的设计与实现 (8)2.3仿真调试 (10)第3章编程下载与硬件测试 (12)3.1编程下载 (12)3.2硬件测试及结果分析 (12)参考文献 (14)附录(电路原理图) (15)第1章总体设计方案1.1 设计原理阵列除法器的功能是利用一个可控加法/减法(CAS)单元所组成的流水阵列来实现的。
它有四个输出端和四个输入端。
当输入线P=0时,CAS作加法运算;当P=1时,CAS作减法运算。
可控加法/减法(CAS)单元的逻辑电路图如图1.1所示。
图1.1可控加法/减法(CAS)单元的逻辑图CAS单元的输入与输出关系可用如下一组逻辑方程来表示:S i=A i ⊕(B i ⊕P) ⨁CC i+1=(A i+C i) ∙(B i ⊕P)+A i C i当P=0时,就得到我们熟悉的一位全加器(FA)的公式:S i=A i ⊕B i ⊕C iC i+1=A i B i+B i C i+A i C i当P=1时,则得求差公式:S i=A i ⨁B i '⨁C iC i+1=A i B i '+B i 'C i+A i C i其中B i '=B i⨁1。
在减法情况下,输入C i称为借位输入,而C i+1称为借位输出。
不恢复余数的除法也称加减交替法。
组成原理课程设计报告-阵列乘法器的设计与实现

沈阳航空航天大学课程设计报告课程设计名称:计算机组成原理课程设计课程设计题目:阵列乘法器的设计与实现院(系):计算机学院专业:计算机科学与技术班级:学号:姓名:指导教师:施国君完成日期:2014年01月10日沈阳航空航天大学课程设计报告目录第1章总体设计方案 (2)1.1设计原理 (2)1.2设计思路 (2)1.3设计环境 (3)第2章详细设计方案 (5)2.1总体方案的设计与实现 (5)2.1.1创建顶层图形设计文件 (5)2.2功能模块的设计与实现 (6)2.2.1输入加法器模块的设计与实现 (6)2.3阵列乘法器的设计与实现 (8)第3章编程下载与硬件测试 (10)3.1编程下载 (10)3.2硬件测试及结果分析 (10)参考文献 (13)附录 (14)第1章 总体设计方案1.1 设计原理以COP2000实验仪、FPGA 实验板为硬件平台,采用Xilinx Foundation F3.1设计工具和COP2000仿真软件,采用自上而下的设计方法,设计并实现阵列乘法器功能。
阵列乘法器的设计原理如图1.1所示,X1,X2,X3,X4, Y1,Y2,Y3,Y4为阵列乘法器的输入端, S1~S8为阵列乘法器的输出端。
图中的排列形式和笔算乘法的位积排列形式相似。
阵列的每一行由乘数Y 的每一位数位控制,而各行错开形成的每一列由被乘数X 的每一位数位控制。
图中方框内的电路由一个与门和一个全加器组成。
由于采用阵列结构,虽然采用加法器数量较多,但内部结构规则,采用超大规模集成电路很容易实现,可大大提高运算速度。
图1.1 阵列乘法器原理图1.2 设计思路阵列乘法器是设计主要包含如下3个部分:S6S5S4S3S2S1乘 积 P = P 40P1P2P3部分积1、加法器的设计与实现;2、阵列乘法器的设计与实现;3、下载与硬件测试;阵列乘法器的设计与实现采用自上而下的设计方法,在这3个部分中分别设计实现相应功能的器件,在连接具体电路时配合相应脉冲和门电路以达到预期效果。
fpga除法运算

fpga除法运算FPGA(Field Programmable Gate Array)是用于数据处理、数字信号处理、调制解调、高速通讯等领域的一种可重构的现场可编程门阵列芯片。
它通过可编程的硬件逻辑资源来实现各种功能,包括了数字电路中的算数逻辑单元(ALU)。
在数字设计中,除法是一种非常重要的算术运算,而FPGA中的除法是属于整数除法。
因为浮点除法很难用硬件实现且复杂度很高,所以FPGA中的除法大多是整数除法。
在FPGA中实现除法有两种方法:1. 直接方法:直接使用除法器,这种方式的局限性比较大。
2. 迭代法:将除法转化为乘法,每次计算一位,比较灵活。
下文将详细介绍迭代法。
迭代法的基本思路是将被除数逐位移位,不断进行减法运算,直到除数小于被除数,就得到了商和余数。
因为每次只需要减去一个二进制数,因此运算速度会比使用除法器快一些。
FPGA中的除法可以使用两种方法:恒定除法和非恒定除法。
1. 恒定除法:被除数和除数的位数是恒定的,即所有数码相乘的结果按照一定规律进行加法运算。
2. 非恒定除法:被除数和除数的位数不确定,需要不断移位和相减以获得余数和商,这需要使用迭代方法。
原理介绍:FPGA中的迭代法除法通常采用的是高斯-约旦算法。
该算法的基本原理是使用几个数码相等的跨度,通过移位和加减运算进行迭代循环,将大数除以小数,得到除数和余数。
这个过程就是高斯-约旦算法,也被称为尾数规制法。
这种算法要求被除数和除数都是非负的,通过对两个正整数之间的无限不循环小数进行近似,将除法问题转化为乘法问题。
算法步骤:1. 消除除数最高位不为1的情况。
2. 对于每一位,将被除数左移一位并减去除数。
如果差值为负数,那么这一位就标记为0,否则标记为1,余数也会减去这个值。
3. 重复以上步骤,直到被除数小于除数,并得到商和余数。
举个例子来说明具体的计算过程:假设被除数为1101,除数为0110,如下所示。
- 首先从除数的最高位开始,找到最高的1(此例中是第二位)。
不恢复余数阵列除法器的FPGA实现

l
I
\
P
l
\
Y
I F l\ A
S i
减法. 也就是说 , 可作为1 图4 个单符号位的n l + 位补码加法/ 减法器 , 若考 虑n 1 C S + 个 A 的所有 输 出端 , 其符 号化 示 意图如 图5 示 . 则 所
圈 3 C S 逻 辑 结构 A的
2 不恢 复余 数 算 法
以定 点小 数 为 例 , 已知 【 和[] 为保 x Y补, 证 商也 是 定 点 小 数 ,故 规 定 I >XI为 了分 YII . 析 算 法 , 此 只考 虑 x Y 为 正 数 的情 况 , 因 和 均
则有 【 = .l …x, = .l " Y, Y 补 X 0 X 2 【 x Y 0 y 2 " [ ] = 0 y' 一
1YY…y, .。 设部 分余数 为 R, 为Q, 执 行下 商 则
列操 作 :
符号 位 ຫໍສະໝຸດ f l f n 图4 单 符号 位 的n l 补码 加/ 法器 +位 减
R= .x…x( 部分 余数 R , 做 减法 ) 00x 求 】 。 先 ,
21 0 0年 5 月
保 定 学 院 学 报
J 0URNAL 0F BA0DI NG UNI VERS T I Y
Ma ,01 y2 0
第2 3卷第 3 期
Vo 2 o3 L 3 N .
文章编 号 :6 42 9 (0 0 0 .0 60 17 .4 4 2 1 )30 5 .4
P
Ci + l
原码的阵列乘、除法运算器教学设计

( 1 ) 出一 道 十进 制 和一 道 二 进 制 的 乘 法 题 目 , 让 学生 在 黑 板 上运 算 , 然 后 总结 , 并 得 出结 论 : n位
另一方面是“ 操作系统” 、 “ 计算机系统结构” 等课程
的基 础 , 在课 程 体 系 中 起 着 承上 启 下 的作 用 。 学生
第3 8卷
第 6期
电气 电子教 学 学报
J O URNAL OF EE E
Vo 1 . 3 8 N o . 6
De C. 201 6
2 0 1 6年 l 2月
原 码 的 阵 列乘 、 除法 运 算 器 教 学 设 计
李社 蕾,杨婷婷 ,刘小飞
(三 亚 学院 理 工学 院 , 海 南 三亚 5 7 2 0 2 2 )
关 专业 的 核 心 专 业 基 础 课 , 它一 方 面 以 “ 模 拟 电 路 ”、 “ 数 字逻 辑 电路 ” 、 “ 汇编语言 法研 究
课 堂上 , 原码 陈列 乘法 器授 课可采 用 出题 、 解题 和 总结 的方 式进 行 。 例如 : 三道 实 例 题 的 授课 过程
Ab s t r ac t :Ac c o r d i n g t o t he c h a r a c t e r i s t i c s o f b r o a d s c o p e a n d a bs t r a c t i o n f o r a r r a y mu l t i p l i e r a n d a r r a y s d i v i d e r i n t h e Co mp u t e r Or g a n i z a t i o n Pr i nc i p l e s c o ur s e,t h e n e w wa y s o f c l a s s r o o m o r g a n i z a t i o n a n d a ra n g e me n t o f t e a c h i n g c o nt e n t i s d e s i g n e d,c l a s s r o o m t e a c h i n g a c t i v i t i e s h a s p r o v e d t ha t t hi s t e a c hi n g d e s i g n i s he l p f u l t o s t ud e n t s u n d e r - s t a n d i n g o f kn o wl e d g e p o i n t s,a n d b r i n g t h e c o nt e n t i n t o t h e i r o wn kn o wl e d g e s y s t e m ,a nd c u l t u r e d l e a r n i n g a b i l i t y
实验三_乘、除法运算器实验报告

实验三乘、除法运算器实验报告姓名:阿迪兰13053004马光明13052046 班级:计算机2班实验三乘、除法运算器实验报告一、实验目的1、掌握移位加算法设计乘法运算单元的基本思想2、掌握阵列算法乘法运算单元的设计方法3、掌握基于状态机的乘法运算单元的设计方法4、掌握基于宏模块的乘除法运算器的设计方法二、实验任务1、完成一个基于阵列的4位无符号乘法运算器的设计;实现代码为:module c01(x, y, out);input [7:0]x, y;output [15:0]out;genvar i, j, k, l;wire [8:0]tmp_sun[7:0], tmp_out[7:0];wire [8:0]tmp_x;assign tmp_x = {1'b0,x};assign out[0] = tmp_x[0] & y[0];generateassign tmp_out[0][0] = 1'b0;for(i=0;i<8;i=i+1)begin:add_bttop_m tm (tmp_x[i+1], y[0], tmp_x[i], y[1], tmp_out[0][i],tmp_sun[0][i], tmp_out[0][i+1]);endassign out[1] = tmp_sun[0][0];assign tmp_sun[0][8] = tmp_out[0][8];for(j=2;j<8;j=j+1)begin:ftffor(k=0;k<8;k=k+1)begin:add_bbbtm_m bm (tmp_sun[j-2][k+1], tmp_x[k], y[j], tmp_out[j-1][k], tmp_sun[j-1][k], tmp_out[j-1][k+1]);endassign out[j] = tmp_sun[j-1][0]assign tmp_sun[j-1][8] = tmp_out[j-1][8];Endfor(l=8;l<16;l=l+1)begin:add_oassign out[l] = tmp_sun[6][8];endendgenerateendmodulemodule top_m(m0, q0, m1, q1, cin, sun, cout);input m0, m1, q0, q1;input cin;output sun, cout;wire x, y;assign x = m0 & q0;assign y = m1 & q1;full_add fa (x, y, cin, sun, cout);endmodulemodule btm_m(sunin, m, q, cin, sun, cout); input sunin, m, q, cin;output sun, cout;wire y;assign y = m & q;full_add fa (sunin, y, cin, sun, cout); endmodulemodule full_add(x, y, cin, sun, cout);input x, y, cin;output reg sun, cout;always@(x, y, cin)beginsun <= x^y^cin;cout <= x&y | x&cin | y&cin;endendmodule2、完成一个基于移位加原理,用状态机实现的4位无符号乘法运算器的设计;实现代码为:module c02input[1:0] x;input[1:0] y;output[3:0] p;wire [3:0] temp;assign temp = {x , y};always @(temp)case temp4'b 0101:p =4'b 0001;4'b 0110: p = 4'b 0010;4'b 0111: p = 4'b 0011;4'b 1001: p = 4'b 0010;4'b 1010: p = 4'b 0100;4'b 1011: p = 4'b 0110;4'b 1101:p = 4'b 0011;4'b 1110: p = 4'b 0110;4'b 1111: p = 4'b 1001;default: p = 4'b 0000;endcase;endmodule;。
fpga小数除法

fpga小数除法FPGA(Field-Programmable Gate Array,现场可编程门阵列)是一种集成电路设备,其可在特定的硬件平台上重新编程实现不同的功能。
由于FPGA具有灵活性高、可重构性强的特点,因此广泛应用于许多领域,如数字信号处理、网络通信、嵌入式系统等。
在FPGA中,除法是一种常见的运算操作。
而小数除法是较为复杂的一种除法运算,因为它需要考虑到小数点的位置和保留的精度。
下面将详细介绍FPGA中的小数除法实现方法。
一、基于二进制数的小数除法FPGA中的小数除法常常使用二进制数进行运算。
首先,将原始的十进制小数转换为二进制表示形式,然后进行二进制数的除法运算。
例如,对于十进制数0.5除以0.25,我们可以将其转换为二进制数1.0除以0.01来计算。
在FPGA中,可以使用二进制除法器(Binary Divider)来实现这种小数除法。
二、定点小数除法在FPGA中,除法运算往往会使用定点数表示法。
定点数是一种固定小数点位置的数表示方法,其中小数点位置是由设计人员在FPGA中指定的。
定点小数的精度由小数点位置决定,小数点的移动可以通过右移或左移操作实现。
在进行定点小数除法之前,首先需要将十进制小数转换为二进制定点小数。
例如,将0.5转换为二进制定点小数,可以表示为0.1。
在FPGA中,可以使用定点数除法器(Fixed-Point Divider)来实现定点小数的除法运算。
三、浮点小数除法浮点数是一种可以表示带有小数的数的科学计数法表示方法。
浮点数通常由符号位、尾数和指数三部分组成。
在FPGA中实现浮点小数除法可以比较复杂,需要使用浮点数除法器(Floating-Point Divider)来完成。
浮点数除法涉及到多个步骤,包括指数对齐、尾数相除、舍入等操作。
浮点数除法器可以根据IEEE 754标准对浮点数进行运算,实现浮点数的精确除法运算。
四、小数除法的应用领域小数除法在FPGA中有广泛的应用领域。
加减交替阵列除法器的设计与仿真实现

加减交替阵列除法器的设计与仿真实现一、引言随着数字电路的发展,除法器在计算机和通信系统中的应用越来越广泛。
加减交替阵列除法器是一种高效的除法器,具有运算速度快、面积小等优点。
本文将详细介绍加减交替阵列除法器的设计与仿真实现。
二、加减交替阵列除法器原理加减交替阵列除法器是一种基于移位和加减运算的快速除法器。
其主要原理如下:1. 将被除数左移n位,得到一个n+1位的数(其中最高位为0)。
2. 对于每个n+1位的数,采用加减交替的方式进行运算。
3. 在第n步时,判断商是否已经求出。
4. 如果商未求出,则返回第1步。
三、加减交替阵列除法器设计1. 系统框图加减交替阵列除法器由以下模块组成:被除数寄存器、商寄存器、余数寄存器、控制单元、计算单元和状态机。
系统框图如下所示:2. 系统模块设计(1)被除数寄存器被除数寄存器用于存储待处理的被除数。
它由一个n位的寄存器和一个移位器组成,可以将被除数左移n位。
(2)商寄存器商寄存器用于存储计算得到的商。
它由一个n位的寄存器和一个移位器组成,可以将商左移1位。
(3)余数寄存器余数寄存器用于存储计算得到的余数。
它由一个n+1位的寄存器和一个移位器组成,可以将余数左移1位。
(4)控制单元控制单元用于控制整个系统的运行。
它根据状态机的输出信号来控制各个模块之间的数据传输和运算。
(5)计算单元计算单元是加减交替阵列除法器最核心的部分,用于进行加减运算。
它由若干个加法器和减法器组成,每个加法器或减法器都能够进行一次加或减运算。
(6)状态机状态机用于控制控制单元的工作状态,并输出相应的信号。
它有以下三种状态:a. 初始化状态:在这个状态下,被除数、商、余数等变量都被初始化。
b. 运行状态:在这个状态下,加减交替阵列除法器按照原理进行运算。
c. 结束状态:在这个状态下,商已经求出,整个系统停止工作。
四、加减交替阵列除法器仿真实现1. 系统仿真为了验证加减交替阵列除法器的正确性,需要对其进行仿真。
fpga小数除法 -回复

fpga小数除法-回复FPGA(现场可编程门阵列)是一种集成电路技术,可以实现可编程硬件逻辑的实时处理。
它在各种领域中得到广泛应用,包括图像处理、数据通信以及数字信号处理等。
在这篇文章中,我们将讨论FPGA 的小数除法功能及其实现。
小数除法是一项基本的数学运算,但在计算机中实现它是具有挑战性的。
传统的微处理器和硬件并不直接支持小数除法,所以通常需要额外的软件算法来实现。
然而,FPGA 具有高度可编程的特性,可以用硬件逻辑直接实现小数除法功能,从而提供更高的计算性能。
下面是实现FPGA 小数除法的基本步骤:1. 确定使用的数据格式:在开始实现小数除法之前,需要确定所使用的数据格式。
常用的格式包括浮点数和定点数。
浮点数用于表示较大的范围和更高的精度,而定点数适用于精确的小数计算。
2. 设计除法器的数据路径:在FPGA 中实现小数除法的关键是设计一个合适的数据路径。
数据路径是各种逻辑电路组件的连接,用于执行特定的计算任务。
在小数除法器的数据路径中,通常包括寄存器、加减器、比较器和移位器等。
3. 实现除法运算步骤:小数除法通常通过迭代运算来实现,其中每个迭代步骤都将部分商和余数逐渐逼近最终结果。
每个步骤的核心操作是将当前余数乘以基数,然后与除数进行比较和运算。
这个过程将一直进行到达到所需的精度。
4. 处理异常情况:在小数除法的实现过程中,需要考虑可能的异常情况。
例如,如果被除数或除数为零,就会引发除以零的错误。
为了确保计算的正确性和稳定性,需要在硬件逻辑中加入异常处理机制。
5. 优化设计:在实现小数除法器后,可以通过优化设计来提高其性能和效率。
一种常见的方法是使用流水线技术,将整个除法过程分为多个阶段,并同时处理多个数据。
这样可以提高整个计算过程的并行性和速度。
需要注意的是,FPGA 小数除法的实现并不是一项简单的任务。
它需要对数字电路和计算机体系结构有深入的了解,并且需要使用专门的设计工具和语言,如VHDL或Verilog。
除法器的工作原理

除法器的工作原理
除法器是一种数字电路,用于执行除法操作。
它的工作原理可以分为以下几个步骤:
1. 导入除数和被除数:除法器接收输入信号,将除数和被除数导入电路中。
2. 对齐操作:除法器需要将除数和被除数进行对齐,使它们的小数点位置相同。
这可能需要移位操作。
3. 比较操作:除法器需要将除数与被除数进行比较,以确定商的各个位。
4. 商的计算:通过重复减法和比较操作,除法器逐位地计算商的各个位。
5. 商的校正:在商的计算过程中,商可能会偏离实际结果。
因此,除法器可能需要进行商的校正,以确保得到正确的商结果。
6. 结果输出:除法器将商和余数输出到指定的输出端口。
这些步骤的具体实现方式可能会因使用的具体除法算法而有所不同。
一些常见的除法算法包括原码除法、补码除法以及余数-商模型除法等。
除法器的设计和实现是数字电路设计中的重
要部分,涉及到逻辑门、多路复用器、触发器等基本电路元件的使用。
计算机组成原理加减交替的阵列除法器实验

计算机组成原理加减交替的阵列除法器实验计算机组成原理是计算机科学中的一门重要课程,而阵列除法器则是其中的重要实验内容之一。
在这个实验中,我们将学习如何利用加减交替的方式来完成除法运算。
阵列除法器是一种计算机硬件,用于执行除法运算。
其核心思想是将被除数不断地与除数进行比较,直到减数小于或等于被除数。
这个过程类似于手算中的竖式除法。
在阵列除法器中,被除数和除数都被表示为二进制数,并通过寄存器进行存储。
被除数和除数都要进行位扩展,保证它们能够进行正常的比较。
除数左移一位相当于乘以2,而右移一位相当于除以2。
在加减交替的过程中,我们先根据除数的最高位,将被除数右移一个位数,并记录下该位数的值,然后使用加法器对被除数进行加减交替操作。
如果被除数大于或等于除数,则表示该位上的商为1,否则商为0。
将得到的商左移一位,然后将被除数和商相减,得到余数。
如果余数小于除数,则表示剩下的所有位数的商都为0。
如果余数大于除数,则使用余数代替被除数,并继续进行加减交替,直到余数小于或等于除数为止。
为了更好地理解这个过程,我们可以通过一个简单的例子来进行说明。
假设我们要计算的是7除以3的结果。
首先将7和3转换为二进制数,得到分别为111和011。
然后进行位扩展,得到1110和0110。
接下来,我们开始进行加减交替的操作。
首先,我们将1110右移一位,得到0111,并将1记录下来。
然后,我们使用加法器对0111和0110进行加减交替操作。
由于0111大于或等于0110,因此我们将得到的商左移一位,得到0010。
然后将0111和0110相减,得到0001。
由于0001小于0110,因此这个过程结束,7除以3的结果为2余1。
通过这个例子,我们可以看到,阵列除法器的加减交替过程虽然比较复杂,但是其本质可以归结为不断地进行位移和加减操作。
掌握了这个原理之后,我们就能够利用阵列除法器来完成更加复杂的除法计算了。
加减交替阵列除法器的设计与仿真实现实验报告

加减交替阵列除法器的设计与仿真实现实验报告一、引言加减交替阵列除法器是一种常用的数字逻辑电路,用于计算两个数的除法运算。
它能够将一个除数和被除数作为输入,输出商和余数。
本实验报告将详细介绍加减交替阵列除法器的设计原理、电路结构以及仿真实现结果。
二、设计原理1. 加减交替阵列除法器的基本原理是通过将除法运算转化为连续的减法和加法运算来实现。
具体步骤如下:- 将除数和被除数输入除法器。
- 如果被除数大于等于除数,则进行减法运算,将结果存储为商,并将被除数减去除数。
- 如果被除数小于除数,则进行加法运算,将结果存储为商,并将被除数加上除数。
- 重复上述过程,直到被除数小于除数为止。
2. 加减交替阵列除法器的电路结构主要由以下几个部分组成:- 除法单元:负责执行减法和加法运算。
- 商和余数寄存器:用于存储每一步的商和余数。
- 控制模块:用于控制除法运算的步骤和判断条件。
三、电路结构加减交替阵列除法器的电路结构如下所示:1. 除法单元:由一个减法器和一个加法器组成,用于执行减法和加法运算。
2. 商和余数寄存器:包括商寄存器和余数寄存器。
商寄存器用于存储每一步的商,余数寄存器用于存储每一步的余数。
3. 控制模块:根据被除数和除数的大小关系,确定执行减法还是加法运算,并控制除法运算的步骤和判断条件。
四、仿真实现我们使用Verilog语言进行仿真实现。
首先,我们定义了除法单元、商和余数寄存器以及控制模块的输入输出端口,并根据设计原理实现了相应的功能。
然后,通过编写测试程序,对设计的加减交替阵列除法器进行了仿真测试。
仿真结果显示,加减交替阵列除法器能够正确执行除法运算,并输出正确的商和余数。
在不同的测试案例中,除法器的运算速度和准确性都得到了验证。
五、实验总结本实验通过对加减交替阵列除法器的设计与仿真实现,深入理解了其工作原理和电路结构。
加减交替阵列除法器在计算中起到了重要的作用,能够高效地完成除法运算。
通过本次实验,我们对数字逻辑电路的设计和仿真有了更深入的了解,并提高了我们的实践能力。
基于加减交替法除法器的FPGA设计与实现

文章编号:1008--0570(2008)09-2-0141-03
基于加减交替法除法器的F P G A设计与实现
FPGA Design and Implementation of add-subtraction alternate algorithm Division
(桂林电子科技大学)潘明许勇
PAN Ming XU Yong
万方数据
复成原来的余数。恢复余数法进行除法运算的缺点是不能预先 知道商应该上0还是1,因此运算步骤不能预先确定,这样会使 控制变得复杂。加减交替法是对恢复余数法的一种改进,其特 点是运算过程中如出现不够减,则不必恢复余数,根据余数符号, 可以继续往下运算,因此步数固定。控制简单。原码加减交替法 的规则是:当余数为正时,商“l”,余数左移一位,减除数;当余
[21鲍吉龙,基于DSP技术的汽车防撞雷达,微计算机信息,2006,4--2 【3】周立功,基于嵌入式系统基础教程,北京航空航天大学出版 社,2005.1
作者简介:柳智鑫(1982一),女汉族),内蒙古赤峰,内蒙古工业
大学硕士研究生,研究方向:汽车车载安全系统的研究:吕芳 (1964一),女(汉族),内蒙古包头市,内蒙古工业大学信息工程 学院,副教授,研究方向:GPS卫星定位系统。
一14万2—方36数0,据L/年邮局订阅号:82.946
图4除法器仿真波形
对原码加减交替除法电路进行编译和综合。综合结果是,共使 用了45个逻辑单元LE。仿真结果表明,该除法器的工作频率 可达85.16MHz。
对除法器进行时序仿真分析,仿真波形如图4所示。图中 被除数(H,g)=45ABH,除数(Y):67H,所进行的运算是45AB— H+67H=ADH。从仿真波形可以看出,当START=0时,被除数 的高位加载到余数寄存器H,低位加载到商寄存器g。当 START=1时,除法器开始运算。&控制运算节拍,每两个CLK 时钟周期为一个节拍周期,在一个节拍周期中完成一位除法 运算。当s0为低电平时,余数寄存器H加载数据;当s。为高 电平时,余数寄存器带进位左移,实现余数x2的操作。这样。 16位除以8位的二进制除法共用了16个时钟周期。运算结束 时,执行结果是:商(D)=ADH,余数(R)=IOH,与理论分析结果 完全~致。
第五讲阵列除法器

• 最上面一行所执行的初始操作经常是减法。因此最上面一行 的 控制线P固定置成“1”。
计算机组成原理
8
• 减法是用2的补码运算来实现的,这时右端各CAS单元上的反 馈线用作初始的进位输入。
• 每一行最左边的单元的进位输出决定着商的数值。 将当前的商反馈到下一行,我们就能确定下一行的操作。 由于进位输出信号指示出当前的部分余数的符号,因此,它将决 定下一行的操作将进行加法还是减法。
余数
r=0.00r3r4r5r6
7
不恢复余数阵列除法器的逻辑原理
计算机组成原理
• 被除数x是一个6位的小数(双倍长度值): x=0.x1x2x3x4x5x6 它是由顶部一行和最右边的对角线上的垂直输入线来提供的。 • 除数y是一个3位的小数 y=0.y1y2y3 它沿对角线方向进入这个阵列。这是因为: 在除法中所需要的部分余数的左移,可以用下列等效的操作 来代替:即让余数保持固定,而将除数沿对角线右移。
不恢复余数阵列除法器;
补码阵列除法器 等等。
计算机组成原理
1
(1) 可控加法/减法(CAS)单元
用于并行除法流水逻辑阵列中。 P=0 做加法运算 P=1 做减法运算
计算机组成原理
2
CAS单元的输入与输出的关系可用如下一组逻辑方程来表示:
Si=Ai⊕(Bi⊕P)⊕Ci Ci+1=(Ai+Ci)· (Bi⊕P)+AiCi
• 当P=0时, 即是我们熟悉的一位全加器(FA)的公式:
Si=Ai⊕Bi⊕Ci Ci+1=AiBi+BiCi+AiCi
• 当P=1时, 则得求差公式:
Si=Ai⊕Bi⊕Ci Ci+1=AiBi+BiCi+AiCi
其中Bi=Bi⊕1。
在减法情况下:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课程设计报告
课程设计名称:计算机组成原理课程设计课程设计题目:阵列除法器设计及实现
院(系):计算机学院
专业:
班级:
学号:
姓名:
指导教师:
完成日期:2016年1月12日
目录
第1章总体设计方案0
1.1设计原理0
1.2设计思路2
1.3设计环境3
第2章详细设计方案4
2.1功能模块的设计及实现4
2.1.1细胞模块的设计及实现5
2.1.2除法器模块的设计及实现7 2.2仿真调试9
参考文献11
附录(电路原理图)
1 2
第1章总体设计方案
1.1 设计原理
在原码除法中,原码除法符号位是单独处理的,商符由两数符号位进行异或运算求得,商值由两数绝对值相除求得。
原码除法中由于对余数的处理不同,又可分为恢复余数法和不恢复余数法(加减交替法)。
在机器操作中通常采用加减交替法,因为加减交替法机器除法时间短,操作规则。
加减交替法的运算规则如下:
(1)当余数为正时,上商1,余数左移一位后减去除数得下一
位余数。
(2)当余数为负时,上商0,余数左移一位后加上除数得下一位
余数。
阵列除法器是一种并行运算部件,采用大规模集成电路制造,及早期的串行除法器相比,阵列除法器不仅所需的控制线路少,而且能提供令人满意的高速运算速度。
阵列除法器有多种形式,如不恢复余数阵列除法器、补码阵列除法器等等。
本实验设计的是加减交替阵列除法器。
本实验利用的细胞单元是一个可控加法/减法CAS单元,利用它组成的流水阵列来实现四位小数的除法。
CAS单元有四个输入端、四个输出端。
其中有一个控制输入端P,当P=0时,CAS作加法运算;
当P=1时,CAS作减法运算。
逻辑结构图如图1.1所示。
图1.1 可控加法/减法(CAS)单元逻辑结构图CAS单元的输入及输出的关系可用如下逻辑方程来表示:Si=Ai⊕(Bi⊕P)⊕Ci
Ci+1=(Ai+Ci)(Bi⊕P)+AiCi
当P=0时,CAS单元就是一个全加器,如下:
Si=Ai⊕B⊕iCi
Ci+1=AiBi+BiCi+AiCi
当P=1时,则得求差公式:
Si=Ai⊕B⊕iCi
Ci+1=AiBi+BiCi+AiCi
其中有Bi=Bi⊕1
在减法中,输入称为借位输入,而称为借位输出。
不恢复余数法的除法即加减交替法。
在不恢复余数的除法阵列中,若前一行输出的符号及被除数的符号是一致的则这一行执行加法,如果不一致则这一行执行减法。
当出现不够减时,部分余数相对被除数来说要改变符号。
这时应该产生一个商位“0”,除数首先沿对角线右移,然后加到下一行的部分余数上,当部分余数不改变它的符号时,即产生商位“1”,下一行的操作应该是减法。
本实验就是要求用加减交替法设计阵列除法器。
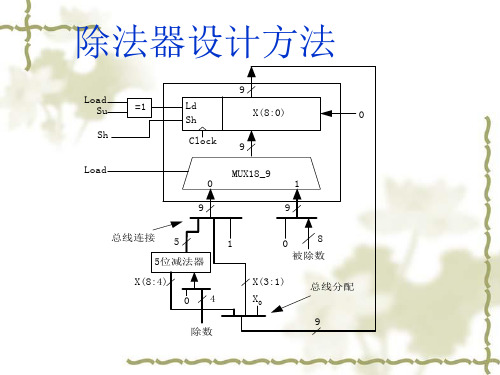
如下图1.2所示的就是用加减交替法设计的阵列除法器,图中每一个方框代表一个CAS 单元,除数为Y0Y1Y2Y3Y4;
被除数为X0X1X2X3X4。
其中X0和Y0是被除数和除数的符号位,均为零,商的符号恒为零,商为0.S1S2S3S4,余数为0.000YU1YU2YU3YU4YU5。
被除数由顶部一行和最右边的对角线上的垂直输入线来提供,除数沿对角线方向进入阵列。
由控制信号P 来决定此行作加法还是除法,当P=0时,CAS作加法运算;当P=1时,CAS作减法运算。
1.2 设计思路
在本实验中要求输入得除数和被除数数据位均为四位,并用加减交替法来设计这个阵列除法器。
这个可以用CAS单元所组成的流水阵列来实现,四位数据位加上一个符号位,一个五位除五位的加减交替除
法阵列由5×5个CAS单元组成,其中两个操作数均为正。
流水逻辑框图如上图1.2所示
1.3 设计环境
(1)硬件环境
•伟福COP2000型计算机组成原理实验仪
COP2000计算机组成原理实验系统由实验平台、开关电源、软件三大部分组成。
实验平台上有寄存器组R0-R3、运算单元、累加器等组成。
COP2000计算机组成原理实验系统各单元部件都以计算机结构模型布局,系统在实验时即使不借助PC 机,也可实时监控数据流状态及正确及否, 实验系统的软硬件对用户的实验设计具有完全的开放特性,系统提供了微程序控制器和组合逻辑控制器两种控制器方式,系统还支持手动方式、联机方式、模拟方式三种工作方式,系统具备完善的寻址方式、指令系统和强大的模拟调试功能。
•COP2000集成调试软件
COP2000集成开发环境是为COP2000实验仪及PC机相连进行高层次实验的配套软件,它通过实验仪的串行接口和PC机的串行接口相连,提供汇编、反汇编、编辑、修改指令、文件传送、调试FPGA实验等功能,该软件在Windows下运行。
(2)EDA环境
•Xilinx foundation f3.1设计软件
Xilinx foundation f3.1是Xilinx公司的可编程期间开发工具,该平台功能强大,主要用于百万逻辑门设计。
该系统由设计入口工具、设计实现工具、设计验证工具三大部分组成。
第2章详细设计方案
2.1 功能模块的设计及实现
阵列除法器的底层设计包括25个CAS模块,这个CAS模块由2个或门、4个及门和3个异或门逻辑组合而成。
2.1.1细胞模块的设计及实现
(1)创建细胞模块设计原理图。
细胞模块原理结构图如图2.1所示。
图2.1 细胞块逻辑框图
(2)创建元件图形符号
为了能在图形编辑器中调用CAS芯片需要把它封装,可利Xilinx foundation f3.1编译器中的如下步骤实现:Tools=>Symbol Wizard=>下一步。
其中XIN、YIN、PIN、CIN为四个输入信号,YUOUT、YOUT、POUT、COUT为四个输出信号。
用其元件图形符号如图2.2所示:
图2.2 细胞元件图形符号
(3)功能仿真
对创建的取补模块进行功能仿真,验证其功能的正确性,可用Xilinx foundation f3.1编译器的Simulator模块实现。
仿真结果如图2.4所示:
图2.3 细胞模块仿真结果
表2.1 细胞模块真值表
输入信号输出信号
YOUT POUT COUT XIN YIN PIN CIN YUOU
T
11110111 00110011 10111011 11101110
00101010 10100011 11011101 00011000 10010001 11000101 00000000 10001000将仿真结果及细胞模块的输入、输出信号真值表相对比可知,细胞模块的仿真结果正确。
2.1.2除法器模块的设计及实现
(1)创建除法器模块设计原理图。
除法器模块原理结构如图2.4所示:
图2.54 除法器原理模块框图
(2)创建元件图形符号
为了能在图形编辑器中调用YANG芯片,需要为除法器模块创建一个元件图形符号,可利Xilinx foundation f3.1编译器中的如下步骤实现:Tools=>Symbol Wizard=>下一步。
其元件图形符号如图2.5所示:
图2.5 选择器元件图形符号
(3)功能仿真
对除法器模块进行功能仿真,验证其功能的正确性,可用Xilinx foundation f3.1编译器的Simulator模块实现。
仿真结果如图2.6
所示:
图2.6 除法器模块仿真结果图
(3)功能仿真
对创建的乘数补码移位寄存器模块进行功能仿真,验证其功能的正确性,可用Xilinx foundation f3.1编译器的Simulator模块实现。
仿真结果如图2.10所示:
2.2 仿真调试
仿真调试主要验证设计电路逻辑功能、时序的正确性,本设计中
主要采用功能仿真方法对设计的电路进行仿真。
(1)建立仿真波形文件及仿真信号选择
功能仿真时,首先建立仿真波形文件,选择仿真信号,对选定的输入信号设置参数,选定的仿真信号和设置的参数如表2. 2所示。
表2.2 仿真信号相关参数表
(2)功能仿真结果及分析
仿真结果分别如图2.6所示,仿真数据结果如表2.2所示。
对比图2.6和表2.2,多组功能仿真结果均正确,进而说明此电路设计的正确性。
参考文献
[1] 曹昕燕.EDA技术实验及课程设计[M].北京:清华大学出版社,2006
[2] 范延滨.微型计算机系统原理、接口及EDA设计技术[M].北京:
北京邮电大学出版社,2006
[3] 王爱英.计算机组成及结构(第三版)[M].北京:清华大学出版社,2006
[4] 白中英.计算机组成原理(第四版)[M].北京:科学出版社,2009
[5] 唐朔飞.计算机组成原理(第二版)[M].北京:高等教育出版社,2008
[6] 江国强.EAD技术习题及实验[M].北京:电子工业出版社,2005
附录(电路原理图)。
