数字信号处理实验(MATLAB版)刘图文 (5)

合集下载

数字信号处理实验报告MATLB第一章

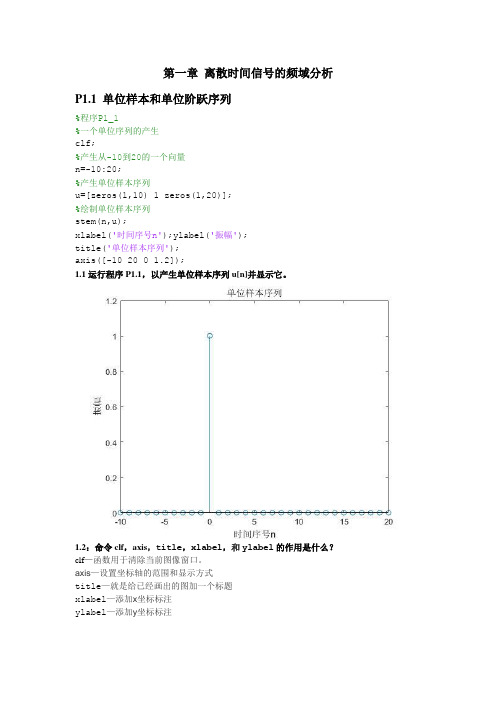
第一章离散时间信号的频域分析P1.1 单位样本和单位阶跃序列%程序P1_1%一个单位序列的产生clf;%产生从-10到20的一个向量n=-10:20;%产生单位样本序列u=[zeros(1,10) 1 zeros(1,20)];%绘制单位样本序列stem(n,u);xlabel('时间序号n');ylabel('振幅');title('单位样本序列');axis([-10 20 0 1.2]);1.1运行程序P1.1，以产生单位样本序列u[n]并显示它。

1.2：命令clf，axis，title，xlabel，和ylabel的作用是什么？clf—函数用于清除当前图像窗口。

axis—设置坐标轴的范围和显示方式title—就是给已经画出的图加一个标题xlabel—添加x坐标标注ylabel—添加y坐标标注1.3修改程序P1.1，以产生带有延时11个样本的延迟单位样本序列ud[n]。

运行修改的程序并显示产生的序列。

%程序%产生并绘制一个单位样本序列延时11clf;%产生从-10到20的一个向量n=-10:20;%产生单位样本序列u=[zeros(1,3) 1 zeros(1,27)];%绘制单位样本序列stem(n,u);xlabel('时间序号n');ylabel('振幅');title('单位样本序列');axis([-10 20 0 1.2]);1.5 修改程序P1.1，以产生带有超前7个样本的延时单位阶跃序列sd[n]。

运行修改后的序并显示产生的序列。

%程序%产生并绘制一个单位样本序列超前7clf;%产生从-10到20的一个向量n=-10:20;%产生单位样本序列u=[zeros(1,3) 1 zeros(1,27)];%绘制单位样本序列stem(n,u);xlabel('时间序号n');ylabel('振幅'); title('单位样本序列');axis([-10 20 0 1.2]);P1.2 指数信号%程序P1_2%生成一个复数指数序列clf;c=-(1/12)+(pi/6)*i;k=2;n=0:40;x=k*exp(c*n);subplot(2,1,1);stem(n,real(x));xlabel('时间序号n');ylabel('振幅');title('实部');subplot(2,1,2);stem(n,imag(x));xlabel('时间序号n');ylabel('振幅');title('虚部');1.6 运行程序P1.2，以产生复数值的指数序列。

数字信号处理MATLAB实验

(8) 用 FFT 分别计算 xa (n)( p 8, q 2) 和 xb(n) (a=0.1,f=0.0625)的自相关函数。
三、思考题
(1)实验中的信号序列 xc(n)和 xd(n)，在单位圆上的 z 变换频谱
和一些，为什么？
会相同吗？如果不同，说明哪一个低频分量更多
(2)对一个有限长序列进行 DFT 等价于将该序列周期延拓后进行
五、与本实验有关的 MATLAB 函数 x=sin（2*pi*f/fs*n）;生成频率为f，采样频率为fs的正弦信号，式
中，n=[0 1 2 … N]。 sum（X）；对于向量X，计算X各元素的和。对于矩阵X，计算X
各列元素之和组成的行向量。 plot（t，y）；画出以向量t为坐标的向量y（行或列）的曲线。向
出该信号，并讨论信号的混叠情况。
（3）令
,其中 f/fs=1/16，即每个周期有 16 个
点。试利用 MATLAB 编程实现：
○1 作 M=4 倍的抽取，使每个周期变成 4 点。
○2 作 L=3 倍的插值，使每个周期变成 48 点。
（4）输入信号 x（n）为归一化频率分别为 f1=0.04，f2=0.3 的正弦信号相加而成，N=50，插因子为 5，抽取因子为 3，给出按有理因子 5/3 做采样率变换的输入输出波形。
（1）简述实验目的及原理。（2）按实验步骤附上试验程序。（3）按实验容附上有关离散信号的波形或关键样本，对音频信号
给出测听的结果。（4）简要回答思考题。五、与本实验相关的 MATLAB 函数 y=decimate(x,M);对信号 x 按整数 M 作抽取，抽取前后作抗混叠低通滤波，结果放在 y 中。 y=interp(x,L); 对信号 x 按整数 L 插零，然后作抗镜像低通滤波，结果放在 y 中。 y=resample(x,L,M);对信号 x 按有理因子 L/M 作采样率转换，结果放在 y 中。

数字信号处理实验(MATLAB版)1章图文 (8)

5
一般电话对声音的要求是最低的，只需传输0.3～3.4 kHz 范围内的频率，采样频率可以取最低的8 kHz，单声道，量化8 位。CD唱片则要求能聆听20 kHz的频率，故采样频率取44.1 kHz，立体声，量化16位。
放音时，量化了的数字信号又通过D/A转换器，把保存起来的数字数据恢复成原来的模拟的语音信号。
6
三、实验任务 (1)用计算机的声音编辑工具录制一段语音信号，生
成.wav文件。录制的语音信号可以由话筒输入，也可以由CD输入。
*提示计算机声音编辑工具的使用方法是：在Windows操作系统下点击【开始】→【程序】→【附件】→【娱乐】→ 【录音机】，将出现如图28-1所示的录音机面板。
7 图28-1 Windows操作系统下的录音机面板
8
(2)理解信号采样率的定义方法。选择3种不同的采样率对同一语音信号进行采样，生成.wav文件，并试听回放效果，进行比较。
*提示在Windows操作系统的录音机【文件】→【属性】下，将显示如图28-2所示的界面，可以选择放音、录音格式。单击【立即转换】，将显示如图28-3所示的界面，可以选择采样速率、量化等级、单声道或立体声等指标。
用计算机的声音编辑工具进行语音信号的录制时，已经利用了计算机上的A/D转换器，将模拟的声音信号变成了离散的量化了的数字信号。
4
把这段语音信号以数据的形式存储起来，可以得到以.wav 作为文件扩展名的文件。Wav格式是Windows下通用的数字音频文件标准。其数据格式为二进制码，编码方式为PCM(脉冲编码调制)。其采样速率从8 kHz到48 kHz，通常三个标准的采样频率分别为44.1 kHz，22.05 kHz，11.025 kHz。量化等级有8位和16位两种，且分为单声道和立体声，使用时可根据需要进行选择。

数字信号处理matlab实验

目录实验一数字信号的产生和频谱分析实验 (2)一.实验目的 (2)二.实验要求 (2)三.实验原理 (2)四.实验步骤 (3)五.流程图 (3)七.实验结果分析 (6)实验二FIR数字滤波器设计 (7)一.试验目的 (7)二.实验要求 (7)三.实验原理和步骤 (7)四.实验流程图 (7)五.实验波形 (8)六.实验结果分析 (11)实验三IIR数字滤波器设计 (11)一.试验目的 (11)二.实验要求 (11)三.实验原理 (12)四.实验流程图 (12)五．实验波形 (13)六.实验结果分析 (14)实验四模拟调制解调 (14)一.试验目的 (14)二.实验要求 (14)三．实验原理 (15)四.实验流程图 (15)五.实验波形 (16)六.实验结果分析 (17)实验五数字调制解调 (17)一.试验目的 (17)二.实验要求 (17)三.实验原理 (18)四.实验流程图 (18)五.实验波形 (18)六.实验结果分析 (20)实验一数字信号的产生和频谱分析实验一.实验目的1.通过仿真掌握采样定理2.掌握利用FFT进行信号谱分析的原理二.实验要求1. 按照采样定理生成CW信号和LFM信号；2. 画出信号时域波形图和频谱图；3. 生成高斯分布的白噪声；4. 生成一定信噪比的带噪信号，并对其进行谱分析。

三.实验原理1.采样定理:在模拟信号数字化时,需要对模拟信号进行采样,当采样频率fs.max大于信号中最高频率fmax的2倍时(fs.max>=2fmax)，采样之后的数字信号完整地保留了原始信号中的信息，否则会发生频谱混叠,造成最后解调出来的信号失真.一般实际应用中保证采样频率为信号最高频率的5～10倍；采样定理又称奈奎斯特定理。

2.快速傅立叶变换(FFT)算法长度为N的序列的离散傅立叶变换为：N点的DFT可以分解为两个N/2点的DFT，每个N/2点的DFT又可以分解为两个N/4点的DFT。

数字信号处理实验报告MATLAB5

第三章离散时间系统的频域分析（3）-Z变换分析目的：学习Z变换的性质及应用。

Q3.46 使用程序P3.1在单位圆生求下面的z变换：% 程序 P3_1% 离散时间傅里叶变换的求取clf;% 计算离散时间傅立叶变换的频率样本w = -4*pi:8*pi/511:4*pi;num = [2 5 9 5 3];den = [5 45 2 1 1];h=freqz(num,den,w);% Plot the DTFTfigure(1)subplot(2,1,1)plot(w/pi,real(h));gridtitle('H(e^{j\omega})的实部')xlabel('\omega /\pi');ylabel('振幅');subplot(2,1,2)plot(w/pi,imag(h));gridtitle('H(e^{j\omega})的虚部')xlabel('\omega /\pi');ylabel('振幅');figure(2)subplot(2,1,1)plot(w/pi,abs(h));gridtitle('|H(e^{j\omega})|幅度谱')xlabel('\omega /\pi');ylabel('振幅');subplot(2,1,2)plot(w/pi,angle(h));gridtitle('相位谱 arg[H(e^{j\omega})]')xlabel('\omega /\pi');ylabel('以弧度为单位的相位');figure(3)h = zplane(num, den);%画出极零图title('极零图')xlabel(''); ylabel('');运行结果为：Q3.47编写一个MATLAB程序，计算并显示零点和极点，计算并显示其因式形式，并产生以z^-1的两个多项式之比的形式表示的z变换的零点图。

Matlab数字信号处理实验报告

数字信号处理实验报告基础实验篇实验一离散时间系统及离散卷积一、实验原理利用Matlab软件计算出系统函数的零极点分布、单位脉冲响应和系统频率响应等的图像并于笔算结果进行比较，找出异同。

编译合适程序能计算取值范围不同的离散卷积。

二、实验目的（1）熟悉MATLAB软件的使用方法。

（2）熟悉系统函数的零极点分布、单位脉冲响应和系统频率响应等概念。

（3）利用MATLAB绘制系统函数的零极点分布图、系统频率响应和单位脉冲响应。

三、实验步骤（1）自编并调试实验程序，并且，给实验程序加注释；（2）按照实验内容完成笔算结果；（3）验证计算程序的正确性，记录实验结果。

（4）至少要求一个除参考实例以外的实验结果，在实验报告中，要描述清楚实验结果对应的系统，并对实验结果进行解释说明。

四、实验源程序及实验结果a=[1,-1,0.9];b=1;x=chongji(-20,120);n=-20:120;h=filter(b,a,x);figure(1)stem(n,h);title('冲击响应');实验1-2运行结果b=[0.0181,0.0543,0.0543,0.0181];a=[1.000,-1.76,1.1829,-0.2781];w=pi*freqspace(500);H=freqz(b,a,w);MH=abs(H);AH=angle(H);subplot(2,1,1);plot(w/pi,MH);grid;axis([0,1,0,1]);xlabel('w(pi)');ylabel('|H|');title('幅度、相位响应');subplot(2,1,2);plot(w/pi,AH);grid;xlabel('w(pi)');ylabel('angle(H)');实验1-3运行结果n=0:30;%输入x(n)和冲激响应h(n) x=zeros(1,length(n)); h=zeros(1,length(n)); x([find((n>=0)&(n<=4))])=1; h([find((n>=0)&(n<=8))])=0.5;figure(1) subplot(3,1,1); stem(n,x);axis([0,30,0,2]); title('输入序列'); xlabel('n'); ylabel('x(n)');subplot(3,1,2); stem(n,h);axis([0,30,0,2]); title('冲激响应序列'); xlabel('n'); ylabel('h(n)');%输出响应y=conv(x,h); subplot(3,1,3); n=0:length(y)-1; stem(n,y);title('输出响应'); xlabel('n'); ylabel('y(n)');实验二离散傅立叶变换与快速傅立叶变换一、实验原理对有限长序列使用离散Fouier 变换(DFT)可以很好的反映序列的频谱特性，而且易于用快速算法在计算机上实现，当序列x(n)的长度为N 时，它的DFT 定义为()()[]()∑==-=1N n nk N W n x n x DFT k X 10-≤≤N k反变换为()()[]()∑==-=-101N n nkN W k X N k X IDFT n x 10-≤≤N n 有限长序列的DFT 是其Z 变换在单位圆上的等距采样，或者说是序列Fourier 变换的等距采样，因此可以用于序列的谱分析。

数字信号处理,matlab实验报告

Matlab实验报告实验一：1.实验Matlab代码：N=25;Q=0.9+0.3*j;WN=exp(-2*j*pi/N);x=zeros(25,1);format long; %长整型科学计数for k0=1:25x(k0,1)=Q^(k0-1);end;for k1=1:25;X1(k1,1)=(1-Q^N)/(1-Q*WN^(k1-1));end;X1;X2=fft(x,32);subplot(3,1,1);stem(abs(X1),'b.');axis([0,35,0,15]);title('N=25,formular');xlabel('n'); subplot(3,1,2);stem(abs(X2),'g.');axis([0,35,0,15]);title('N=32, FFT');xlabel('n');for(a=1:25)X3(a)=X1(a)-X2(a)end;subplot(3,1,3);stem(abs(X3),'r.');title('difference');xlabel('n');实验结果如图：实验结论：可以看出基2时间抽选的FFT算法与利用公式法所得到的DFT结果稍有偏差，但不大，在工程上可以使用计算机利用FFT处理数据。

2.实验Matlab代码：N = 1000; % Length of DFTn = [0:1:N-1];xn = 0.001*cos(0.45*n*pi)+sin(0.3*n*pi)-cos(0.302*n*pi-pi/4);Xk = fft(xn,N);k=[0:1:N-1];subplot(5,1,1);stem(k,abs(Xk(1:1:N)));title('DFT x(n)');xlabel('k');axis([140,240,0,6])subplot(5,1,2);stem(k, abs(Xk(1:1:N)),'r');%画出sin(0.3npi)-cos(0.302npi-pi/4) axis([140,160,0,6]);title('sin(0.3*pi*n)-cos(0.302*pi*n) ');xlabel('k');subplot(5,1,3);stem(k, 1000*abs(Xk(1:1:N)),'g');%画出0.001*cos(0.45npi)axis([220,230,0,6]);title('cos(0.45*pi*n) ');xlabel('k');subplot(5,1,4);stem(k,0.01*abs(Xk(1:1:N)),'k');%画%sin(0.3npi)-cos(0.302npi-pi/4)axis([140,160,0,6]);title('sin(0.3*pi*n)-cos(0.302*pi*n) ');xlabel('k');subplot(5,1,5);stem(k, 10*abs(Xk(1:1:N)),'m');%画出0.001*cos(0.45npi)axis([220,230,0,6]);title('cos(0.45*pi*n) ');xlabel('k');实验结果如图：实验结论：由上图及过程可知，当DFT变换长度为1000时所得到的谱线非常理想。

Matlab数字信号处理实验报告材料

编译合适程序能计算取值范围不同的离散卷积。

二、实验目的（1）熟悉MATLAB软件的使用方法。

（2）熟悉系统函数的零极点分布、单位脉冲响应和系统频率响应等概念。

（3）利用MATLAB绘制系统函数的零极点分布图、系统频率响应和单位脉冲响应。

三、实验步骤（1）自编并调试实验程序，并且，给实验程序加注释；（2）按照实验内容完成笔算结果；（3）验证计算程序的正确性，记录实验结果。

（4）至少要求一个除参考实例以外的实验结果，在实验报告中，要描述清楚实验结果对应的系统，并对实验结果进行解释说明。

四、实验源程序及实验结果实验二离散傅立叶变换与快速傅立叶变换一、实验原理对有限长序列使用离散Fouier 变换(DFT)可以很好的反映序列的频谱特性，而且易于用快速算法在计算机上实现，当序列x(n)的长度为N 时，它的DFT 定义为()()[]()∑==-=1N n nk N W n x n x DFT k X 10-≤≤N k反变换为()()[]()∑==-=-101N n nkN W k X N k X IDFT n x 10-≤≤N n 有限长序列的DFT 是其Z 变换在单位圆上的等距采样，或者说是序列Fourier 变换的等距采样，因此可以用于序列的谱分析。

FFT 是为了减少DFT 运算次数的一种快速算法。

它是对变换式进行一次次分解，使其成为若干较短序列的组合，从而减少运算量。

常用的FFT 是以2为基数的，其长度。

它的效率高，程序简单，使用非常方便，当要变换的序列长度不等于2的整数次方时，为了使用以2为基数的FFT ，可以用末位补零的方法，使其长度延长至2的整数次方。

用FFT 可以实现两个序列的圆周卷积。

在一定的条件下，可以使圆周卷积等于线性卷积。

《数字信号处理》MATLAB编程实验报告

《计算机程序设计基础》实验报告
6
《数字信号处理》实验报告
实验项目实验类别基础性 MATLAB 编程语言环境使用实验学时 4
实验目的及要求
（1）正确进入 MATLAB 工作环境并熟悉其基本结构（2）熟悉其基本操作命令，包括变量的设置、help 命令的使用、结果的保存与调用等（3）编写 M 文件并在环境中运行（4）信号与系统工具包使用
正弦信号程序代码
n=0:0.001:100; y=2*sin(0.1*n+pi/8); plot(n,y), grid on
《计算机程序设计基础》实验报告 3
计算机科学与工程学院 axis([0,100,-3,3])
正弦信号 x1(n)=2 sin(0.1n+pi/8)的图像为
复指数信号程序源代码 clear,t0=0;tf=5;dt=0.05;t1=1; t=t0:dt:tf; st=length(t); alpha=-0.5; w=10; x=exp((alpha+j*w)*t); subplot(1,2,1),plot(t,real(x)),grid on; subplot(1,2,2),plot(t,imag(x)),grid on;
复指数信号
x2 (n) Ae(机程序设计基础》实验报告
4
计算机科学与工程学院
思考题
1.说明点乘（.*）运算和乘法运算（*）有何不同答：每一个符号变量都被认为是一个元素，不论它的表达式多么复杂。因此如果你仅从符号
的视角出发，那所有的乘法都是点乘！就相当于两个数相乘一样，没有点乘还是差乘的分别。但是如果一个矩阵是由符号变量组成的。那么点乘和差乘就有分别了。数值运算和符号运算都是一样的，都要考虑点乘还是差乘

数字信号处理MATLAB实验报告

MATLAB提供了求离散时间系统频响特性的函数freqz，调用freqz的格式主要有两种。一种形式为
[H,w]=freqz(B,A,N)
其中，B与A分别表示的分子和分母多项式的系数向量；N为正整数，默认值为512；返回值w包含范围内的N个频率等分点；返回值H则是离散时间系统频率响应在范围内N个频率处的值。另一种形式为
[H,w]=freqz(B,A,N,’whole’)
与第一种方式不同之处在于角频率的范围由扩展到。
上机练习：
试用MATLAB的residuez函数，求出的部分分式展开和。
b=[2 16 44 56 32];
a=[3 3 -15 18 -12];
[R,P,K]=residuez(b,a)
R =
+
zplane(B,A)
其中，B与A分别表示的分子和分母多项式的系数向量。它的作用是在Z平面上画出单位圆、零点与极点。
与拉氏变换在连续系统中的作用类似，在离散系统中，z变换建立了时域函数与z域函数之间的对应关系。因此，z变换的函数从形式可以反映的部分内在性质。我们仍旧通过讨论的一阶极点情况，来说明系统函数的零极点分布与系统时域特性的关系。
[R,P,K]=residuez(B,A)
其中，B，A分别表示X(z)的分子与分母多项式的系数向量；R为部分分式的系数向量；P为极点向量；K为多项式的系数。若X(z)为有理真分式，则K为零。
离散时间系统的系统函数定义为系统零状态响应的z变换与激励的z变换之比，即
（4-4）
如果系统函数的有理函数表示式为
x=iztrans(z)
上式中的x和Z分别为时域表达式和z域表达式的符号表示，可通过sym函数来定义。
如果信号的z域表示式是有理函数，进行z反变换的另一个方法是对进行部分分式展开，然后求各简单分式的z反变换。设的有理分式表示为

matlab 数字信号实验报告

matlab 数字信号实验报告MATLAB数字信号实验报告摘要：本实验使用MATLAB软件对数字信号进行处理和分析。

首先，我们使用MATLAB生成不同类型的数字信号，并对其进行采样和量化。

然后，我们利用MATLAB对这些数字信号进行滤波、傅里叶变换和频谱分析。

通过本实验，我们可以深入了解数字信号处理的基本原理和方法，并掌握MATLAB在数字信号处理中的应用。

1. 实验目的本实验旨在通过MATLAB软件对数字信号进行处理和分析，加深对数字信号处理原理的理解，掌握MATLAB在数字信号处理中的应用技巧。

2. 实验原理数字信号处理是对数字信号进行处理和分析的技术。

数字信号处理的基本原理包括采样、量化、滤波、傅里叶变换和频谱分析等。

MATLAB是一种强大的工具，可以方便地对数字信号进行处理和分析。

3. 实验内容（1）生成不同类型的数字信号在MATLAB中，我们可以生成不同类型的数字信号，如正弦信号、方波信号和三角波信号等。

通过改变信号的频率、幅度和相位等参数，可以得到不同的数字信号。

（2）采样和量化对生成的数字信号进行采样和量化，得到离散时间信号和离散幅度信号。

（3）滤波利用MATLAB对采样和量化后的数字信号进行滤波处理，去除噪声和干扰，得到清晰的信号。

（4）傅里叶变换和频谱分析对滤波后的数字信号进行傅里叶变换，得到信号的频谱图，分析信号的频率成分和能量分布。

4. 实验结果通过MATLAB对不同类型的数字信号进行处理和分析，得到了清晰的信号波形图和频谱图。

通过对比不同类型的数字信号，我们可以发现它们在频率、幅度和相位等方面的差异。

5. 结论本实验通过MATLAB软件对数字信号进行处理和分析，加深了对数字信号处理原理的理解，掌握了MATLAB在数字信号处理中的应用技巧。

数字信号处理在通信、音频、图像等领域有着广泛的应用，掌握数字信号处理技术对于工程技术人员具有重要的意义。

MATLAB作为一种强大的工具，为数字信号处理提供了便利和高效的解决方案。

《数字信号处理》Matlab实验

《数字信号处理》Matlab 实验一．离散信号的 FFT 分析1.用Matlab 编程上机练习。

已知：N=2^5。

这里Q=0.9+j0.3。

可以推导出，首先根据这个式子计算X(k)的理论值，然后计算输入序列x(n)的32个值，再利用基2时间抽选的FFT 算法，计算x(n)的DFT X(k)，与X(k)的理论值比较（要求计算结果最少6位有效数字）。

解：函数代码：>> function xn()>> format long>> q=0.9+0.3*i;>> wn=exp(-2*pi*i/32);>> xk=(1-q^32)./(1-q*wn.^[0:31])>>xn=q.^[0:31]>> xk1=fft(xn,32)>>diff=xk-xk1具体执行情况：>> function xn()format longq=0.9+0.3*i;wn=exp(-2*pi*i/32);xk=(1-q^32)./(1-q*wn.^[0:31])xk =Columns 1 through 20.5698 + 3.3840i 2.8369 + 8.8597iColumns 3 through 49.3189 - 9.8673i 1.2052 - 3.5439iColumns 5 through 61.8846 -2.0941i 0.8299 - 1.2413i11,011)()()(k k 10nk 10-=--===∑∑-=-=N k QW Q QW W n x k X N NnN N n N N n ，0.9214 - 1.0753i 0.3150 - 0.0644i Columns 9 through 100.9240 - 0.8060i 0.4202 - 0.2158i Columns 11 through 120.8513 - 0.6357i 0.5040 - 0.1701i Columns 13 through 140.6217 - 0.6931i 0.2441 - 0.8978i Columns 15 through 160.9454 - 0.2800i 0.7139 - 0.3158i Columns 17 through 180.6723 - 0.6496i 0.0263 + 0.5093i Columns 19 through 200.5671 + 0.6914i 0.3173 + 0.9841i Columns 21 through 220.8929 + 0.7792i 0.4066 + 0.8452i Columns 23 through 240.5847 + 0.9017i 0.9129 + 0.9283i Columns 25 through 260.0573 + 0.5531i 0.4219 + 0.9562i Columns 27 through 280.3298 + 0.3143i 0.4513 + 0.2638i0.7214 + 0.1879i 0.0933 + 1.7793iColumns 31 through 320.9483 + 1.9802i 0.4932 + 2.6347i>> xn=q.^[0:31]xn =Columns 1 through 21.0000 0.0000 + 0.0000i Columns 3 through 40.0000 + 0.0000i 0.0000 + 0.0000iColumns 5 through 60.0000 + 0.0000i -0.0000 + 0.0000iColumns 7 through 8-0.0000 + 0.0000i -0.0000 + 0.0000iColumns 9 through 10-0.0000 + 0.0000i -0.0000 + 0.0000iColumns 11 through 12-0.0000 - 0.0000i -0.0000 - 0.0000iColumns 13 through 14-0.2000 - 0.4000i -0.3600 - 0.5200iColumns 15 through 16-0.9680 - 0.1760i 0.4816 - 0.3488i0.2381 - 0.2695i 0.2951 - 0.1711i Columns 19 through 200.1169 - 0.4655i 0.4449 - 0.9838i Columns 21 through 220.6955 + 0.2480i 0.5516 + 0.4319i Columns 23 through 240.3669 + 0.5542i 0.9639 + 0.2088i Columns 25 through 260.3049 + 0.9771i -0.5187 + 0.4709i Columns 27 through 28-0.6081 + 0.2682i -0.1278 + 0.5589i Columns 29 through 30-0.4827 + 0.0647i -0.6538 + 0.5134i Columns 31 through 32-0.8425 - 0.4341i -0.1280 - 0.1434i >> xk1=fft(xn,32)xk1 =Columns 1 through 20.5698 + 3.3839i 2.8366 + 8.8599i Columns 3 through 49.3182 - 9.8692i 1.2051 - 3.5439i1.8845 -2.0942i 0.8298 - 1.2413i Columns 7 through 80.9213 - 1.0754i 0.3150 - 0.0645i Columns 9 through 100.9240 - 0.8060i 0.4202 - 0.2158i Columns 11 through 120.8514 - 0.6356i 0.5040 - 0.1701i Columns 13 through 140.6217 - 0.6931i 0.2441 - 0.8977i Columns 15 through 160.9454 - 0.2800i 0.7139 - 0.3159i Columns 17 through 180.6723 - 0.6496i 0.0263 + 0.5093i Columns 19 through 200.5671 + 0.6913i 0.3172 + 0.9840i Columns 21 through 220.8929 + 0.7792i 0.4065 + 0.8452i Columns 23 through 240.5846 + 0.9016i 0.9129 + 0.9283i Columns 25 through 260.0572 + 0.5531i 0.4219 + 0.9563i0.3297 + 0.3144i 0.4512 + 0.2638iColumns 29 through 300.7213 + 0.1879i 0.0932 + 1.7793iColumns 31 through 320.9480 + 1.9802i 0.4928 + 2.6347i>> diff=xk-xk1diff =1.0e-013 *Columns 1 through 20.4625 + 0.8501i 0.9504 - 0.4003iColumns 3 through 40.6010 + 0.4028i 0.4752 + 0.7001iColumns 5 through 60.5502 + 0.8501i 0.4625 + 0.8501iColumns 7 through 80.7751 + 0.9250i 0 + 0.3875i Columns 9 through 100.7751 - 0.4625i 0.3126 - 0.4625iColumns 11 through 12-0.4625 - 0.3126i 0.4625 + 0.3875iColumns 13 through 14-0.9250 + 0.6938i 0.3875 - 0.0781iColumns 15 through 160.3875 - 0.6156i 0 + 0.9641iColumns 17 through 180.9250 - 0.7598i -0.4625 - 0.0422iColumns 19 through 200.4625 + 0.1172i 0.4625 + 0.3094iColumns 21 through 220.9250 + 0.4625i 0.9250 + 0.2313iColumns 23 through 240.3875 + 0.1563i 0.3875 - 0.2313iColumns 25 through 260.8501 -0.9250 - 0.4625iColumns 27 through 280.0127 - 0.7751i 0.7001 - 0.9250iColumns 29 through 300.1626 0.7814 - 0.9250iColumns 31 through 320.4816 + 0.9250i 0.7255 - 0.8501i由以上结果可知，由基2时间抽选的FFT算法所得到的DFT结果与利用公式法所得的理论值稍有偏差，但误差较小，从结果可以看出大概在小数点第15位才开始出现误差，故而用计算机FFT处理数据在精度上是可以接受的。

数字信号处理实验(MATLAB版)刘章图文 (4)

36
程序如下： T0＝［0.5，0.25，0.125，0.125］； %输入不同的Ts 值 N0＝［256，256，256，2048］；%输入不同的N值 forr＝1：4； Ts＝T0(r)；N＝N0(r)；%赋Ts和N值 n＝0：N－1； D＝2*pi/(Ts*N)；%计算模拟频率分辨率 xa＝[ZK(]exp(－0.01*n*Ts).*(sin(2*n*Ts)＋ sin(2.1*n*Ts)＋sin(2.2*n*Ts))； k＝floor(－(N－1)/2：(N－1)/2)；
16
在使用FFT进行DFT的高效运算时，一般不直接用n从n1到
n2的x(n)，而是取
的~x(主n值) 区间(n＝0，1，…，N－1)的数
据，经FFT将产生N个数据，定位在k＝0，1，…，N－1的数字
频率点上，即对应［0，2p］。如果要显示［－p，p］范围的
频谱，则可以使用fftshift(X)进行位移。
20 图14-2 例14-3有限长序列的频谱
21
由图14-2可知，当有限长序列的长度N＝5时，频谱的频率样本点数也为5 的间距非常大，即分辨率很低。即使使用了plot命令的插值功能，显示出的曲线仍是断断续续的，与真实曲线有较大的误差。
改变分辨率的基本方法是给输入序列补零，即增加频谱的密度。注意，这种方法只是改善了图形的视在分辨率，并不增加频谱的细节信息。
11 图14-1 例14-1用FFT求有限长序列的傅里叶变换
12
例14-2 将例13-5已知的两个时域周期序列分别取主值，
得到x1＝［1，1，1，0，0，0
x2＝［0，1，2，3，0，
0］，求时域循环卷积y(n)并用图形表示。
解本例将例13-5使用DFT处理的计算，改为用FFT和IFFT

数字信号处理实验报告MATLAB

数字信号处理实验报告姓名：班级：09电信一班学号：2)]得下图二，图二图一3．将如下文件另存为：sigadd.m文件function [y,n] = sigadd(x1,n1,x2,n2)% 实现y(n) = x1(n)+x2(n)% -----------------------------% [y,n] = sigadd(x1,n1,x2,n2)% y = 在包含n1 和n2 的n点上求序列和,% x1 = 在n1上的第一序列% x2 = 在n2上的第二序列(n2可与n1不等)n = min(min(n1),min(n2)):max(max(n1),max(n2)); % y(n)的长度y1 = zeros(1,length(n)); y2 = y1; % 初始化y1(find((n>=min(n1))&(n<=max(n1))==1))=x1; % 具有y的长度的x1y2(find((n>=min(n2))&(n<=max(n2))==1))=x2; % 具有y的长度的x2y = y1+y2;在命令窗口输入：x1=[1,0.5,0.3,0.4];n1=-1:2;x2=[0.2,0.3,0.4,0.5,0.8,1];n2=-2:3; [y,n] = sigadd(x1,n1,x2,n2)得：y =n=-1:10;x=sin(0.4*pi*n);y=fliplr(x);n1=-fliplr(n);subplot(2,1,1),stem(n,x) subplot(2,1,2),stem(n1,y在命令窗口键入:n=-1:10; x=sin(0.4*pi*n);n (samples)实验结果：1.（1）在命令窗口输入：tic; [am,pha]=dft1(x)N=length(x);w=exp(-j*2*pi/N);for k=1:Nsum=0;for n=1:Nsum=sum+x(n)*w^((k-1)*(n-1));endam(k)=abs(sum);pha(k)=angle(sum);end;toc得到如下结果：am =Columns 1 through 11120.0000 41.0066 20.9050 14.3996 11.3137 9.6215 8.6591 8.1567 8.0000 8.1567 8.6591Columns 12 through 169.6215 11.3137 14.3996 20.9050 41.0066pha =Columns 1 through 110 1.7671 1.9635 2.1598 2.3562 2.5525 2.7489 2.9452 3.1416 -2.9452 -2.7489Columns 12 through 16-2.5525 -2.3562 -2.1598 -1.9635 -1.7671Elapsed time is 0.047000 seconds.（2）在命令窗口输入：tic;[am,pha]=dft2(x)N=length(x);n=[0:N-1];k=[0:N-1];w=exp(-j*2*pi/N);nk=n’*k;wnk=w.^(nk); Xk=x*wnk; am= abs(Xk); pha=angle(Xk); toc得到下图：figure(1)00.10.20.30.40.50.60.70.80.91signal x(n), 0 <= n <= 99（2）在命令窗口键入：n3=[0:1:99];y3=[x(1:1:10) zeros(1,90)]; ％添90个零。

数字信号处理(MATLAB版)上机实验操作

实验一离散时间信号与系统一、实验目的：1、熟悉常见离散时间信号的产生方法；2、熟悉离散时间系统的单位脉冲响应和单位阶跃响应的求解方法；3、熟悉离散时间信号经过离散时间系统的响应的求解方法。

二、实验内容：已知离散时间系统差分方程为y(n)-0.5y(n-1)+0.06y(n-2)=x(n)+x(n-1)，求1、该系统的单位脉冲响应并绘图；2、该系统的单位阶跃响应并绘图；3、已知x(n)=可自己指定用filter函数经过系统的响应并绘图；4、用conv_m函数求系统响应并绘图。

三、实验平台：MA TLAB集成系统四、设计流程：此处写个人自己的设计流程五、程序清单：此处写程序内容六、调试和测试结果：此处写程序的执行结果和实验过程中的调试经过、出现的错误和对应的解决方法七、教师评语与成绩评定此处由老师填写上机操作：实验一离散时间信号与系统实验内容：1．脉冲响应>> b =[1,1]; a = [1,-0.5,0.06];n = [-10:25];>> impz(b,a,n);>> title('Impulse Response'); xlabel('n'); ylabel('h(n)')2.单位阶跃响应>> x = stepseq(0,-10,25); s = filter(b,a,x);Warning: Function call stepseq invokes inexact match d:\MATLAB7\work\STEPSEQ.M.>> stem(n,s)>> title('Step Response'); xlabel('n');ylabel('s(n)')3.>> a=[1,-0.5,0.06];b=[1,1];>> n=-20:120;>> x1=exp(-0.05*n).*sin(0.1*pi*n+pi/3);>> s1=filter(b,a,x1);>> stem(n,s1);;xlabel('n');ylabel('s1(n)');4．>> a=[1,-0.5,0.06];b=[1,1];>> n=-20:120;>> h=impz(b,a,n);>> x1=exp(-0.05*n).*sin(0.1*pi*n+pi/3);>> [y,m]=conv_m(x1,n,h,n);Warning: Function call conv_m invokes inexact match d:\MATLAB7\work\CONV_M.M. >> stem(m,y);title('系统响应');xlabel('m');ylabel('y(m)');实验二离散信号与系统的连续频域分析一、实验目的：1、掌握离散时间信号的DTFT的MATLAB实现；2、掌握离散时间系统的DTFT分析；3、掌握系统函数和频率相应之间的关系。

数字信号处理实验报告MATLAB

实验2 离散时间信号的频谱分析1、实验内容一、编写子函数计算长度为N 的序列x(n) （ 0≤n ≤ N-1）的离散时间傅里叶变换，将频率均匀离散化，一个周期内有M 个点。

要求画出虚部、实部、幅度、相位，并标注坐标轴。

二、对矩形序列x(n)=RN(n)1. 用公式表示x(n)的频谱，求出其幅度谱和相位谱；2. 利用编写的子函数，计算并画出x(n)的频谱1）固定M ，改变N ，观察N 的取值对频谱的最大值、过零点、第一旁瓣幅度与最大值的比值以及相位谱的影响；2）固定N ，改变M ，观察M 的取值对幅度谱和相位谱的影响。

如： M=4，26，100N=4，26，100三、利用子函数，画出信号x(n)=sin(pi*n/5)和 x(n)=cos(pi*n/4)+cos(pi*n/8) （ 0≤n ≤ N -1）的幅度谱和相位谱。

N 分别取为8，16，20，64，75，128，M=256。

观察N 取不同值时信号频谱的相同和不同之处，为什么会有这样的结果。

2、编程原理、思路和公式（1）、给定长度为N 的序列x(n)的离散时间傅里叶变换（DTFT ）的公式为 10()()N jwjwn n X e x n e --==∙∑ 1()()2j w j w n x n X e e d w πππ-=⎰。

可以看出x(n)的DTFT 仍然是一个连续函数，所以需要将数字角频域w 离散化，设一个频率周期内离散点有M 个，则第k 个点所代表的数字角频率2w k M π=。

这样x(n)的DTFT 变成：2210()()()N j k j nk jw M M n X e X e x n eππ--===∙∑ 01k M ≤≤-，（2）、因为0≤.n ≤.N-1, 01k M ≤≤- 设置两层for 循环，用sum 表示累加求和的值，即可实现2210()()()N j k j nk jw MM n X e X e x n eππ--===∙∑（3）对矩形序列x(n)=R4(n)，首先固定M 不变，改变N 的取值。

数字信号处理MATLAB实验代码&图

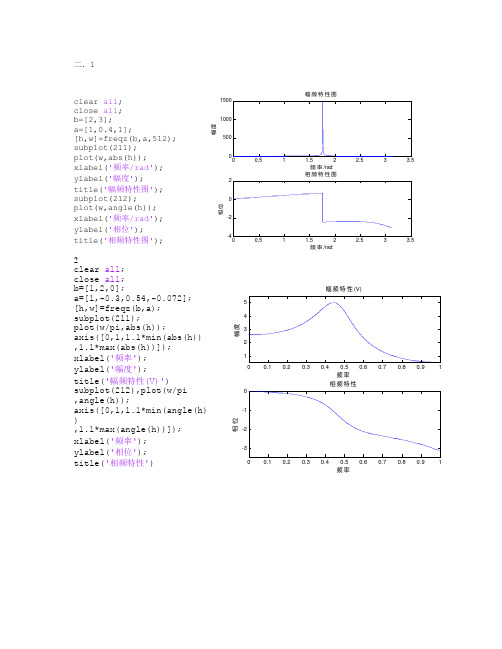
二．1clear all;close all;b=[2,3];a=[1,0.4,1];[h,w]=freqz(b,a,512);subplot(211);plot(w,abs(h));xlabel('频率/rad');ylabel('幅度');title('幅频特性图');subplot(212);plot(w,angle(h));xlabel('频率/rad');ylabel('相位');title('相频特性图');2clear all;close all;b=[1,2,0];a=[1,-0.3,0.54,-0.072]; [h,w]=freqz(b,a);subplot(211);plot(w/pi,abs(h));axis([0,1,1.1*min(abs(h)) ,1.1*max(abs(h))]);xlabel('频率');ylabel('幅度');title('幅频特性(V)')subplot(212),plot(w/pi,angle(h));axis([0,1,1.1*min(angle(h) ),1.1*max(angle(h))]); xlabel('频率');ylabel('相位');title('相频特性')频率/rad幅度幅频特性图频率/rad 相位相频特性图频率幅度幅频特性(V)频率相位相频特性3.clear all; close all;b=[0.187632,0,-0.241242,0,0.241242,0,-0.187632];a=[1,0,0.602012,0,0.495684,0,0.0359244];[h,w]=freqz(b,a);subplot(221),plot(w/pi,abs(h) );axis([0,1,1.1*min(abs(h)),1.1*max(abs(h))]);xlabel('频率');ylabel('幅度');title('幅频响应')subplot(222),plot(w/pi,angle( h));axis([0,1,1.1*min(angle(h)),1.1*max(angle(h))]);xlabel('频率');ylabel('相位');title('相频特性')三．1clear all;close all;z1=[0.3]';p1=[-0.5+0.7j,-0.5-0.7j]';k=1;[b1,a1]=zp2tf(z1,p1,k);subplot(3,2,1),zplane(z1,p1);title('极点在单位圆内 ');subplot(3,2,2),impz(b1,a1,20);z2=[0.3]';p2=[-0.6+0.8j,-0.6-0.8j]';[b2,a2]=zp2tf(z2,p2,k);subplot(3,2,3),zplane(z2,p2);title('极点在单位圆上');subplot(3,2,4),impz(b2,a2,20);z3=[0.3]';p3=[-1+j,-1-j]';[b3,a3]=zp2tf(z3,p3,k);subplot(3,2,5),zplane(z3,p3); title('极点在单位圆外');subplot(3,2,6),impz(b3,a3,20);频率幅度幅频响应-202Real PartImaginaryPart极点在单位圆内051015n (samples)AmplitudeImpulse Response Real PartImaginaryPart极点在单位圆上n (samples)AmplitudeImpulse Response-202Real PartImaginaryPart极点在单位圆外051015n (samples)AmplitudeImpulse Responseclear all;close all;z1=[1,-3]';p1=[2,-4]';k=5;[b1,a1]=zp2tf(z1,p1,k); subplot(211),zplane(z1,p1 );title('零极点分布');subplot(212),impz(b1,a1,2 0);四．1clear all;`close all;xn=[7,6,5,4,3,2];N=length(xn);n=0:N-1;k=0:N-1;Xk=xn*exp(-j*2*pi/N).^(n'*k );x=(Xk*exp(j*2*pi/N).^(n'*k) )/N;subplot(221),stem(n,xn); title('x(n)');subplot(222),stem(n,abs(x)) ;title('IDFT abs(X(k))'); subplot(223),stem(k,abs(Xk) );title('abs(X(k))');subplot(224),stem(k,angle( Xk));title('arg(X(k))');2.clear all;close all;xn=[7,6,5,4,3,2];N=length(xn);m=0:N-1;n=0:3*N-1;k=0:3*N-1;x1=xn(mod(n,N)+1);Xk=x1*exp(-j*2*pi/N).^(n'* k);subplot(221),stem(m,xn);Real PartImaginaryPart零极点分布11n (samples)AmplitudeImpulse Responsex(n)IDFT abs(X(k))abs(X(k))arg(X(k))x(n)IDFT abs(X(k))abs(X(k))angle(X(k))title('x(n)');subplot(222),stem(n,x1);title('IDFT abs(X(k))');subplot(223),stem(k,abs(Xk));title('abs(X(k))');subplot(224),stem(k,angle(Xk));title('angle(X(k))');3.clear all;close all;xn=[7,6,5,4,3,2];N=length(xn);n=0:N-1;w=linspace(-2*pi,2*pi,500);x=xn*exp(-j*n'*w);subplot(311),stem(n,xn,'k');title('x(n)');subplot(312),plot(w,abs(x),'k');axis([-2*pi,2*pi,1.1*min(abs(x)),1.1*max(abs(x))]);title('幅度谱');subplot(313),plot(w,angle(x),'k');axis([-2*pi,2*pi,1.1*min(angle(x)),1.1*max(angle(x))]); title('相位谱');x(n)幅度谱相位谱。

数字信号处理MATLAB实验报告 4

这就是经常称之为傅立叶级数的变换形式。在这里，也是模拟角频率。可以看到，
时域的连续函数造成频率域的非周期谱，频域函数的离散造成时域函数的周期性。结论：周期连续时间函数对应于一非周期离散频域变换函数。
3、非周期离散时间信号 x(n) 的傅立叶变换 X (e j ) 可以表示为

X (e j ) x(n)e jn n
DFT 的性质
两个序列 x1(n) 和 x2 (n) 都是 N 点有限长序列，设
X1(k) DFT[x1],
X 2 (k) DFT[x2 ]
线性
DFT[ax1(n) bx2 ] aX1(k) bX 2 (k), 式中 a，b 为任意常数。
圆周移位
一个有限长序列 x (n) 的圆周移位定义

x x
(n)] (n)]
用 X R (k ) 和 X I (k ) 分别表示实部和虚部序列的 DFT ，即
X R (k) DFT[xr (n)] X I (k) DFT[xi (n)]
而且可以证明得到
X R (k ) X R[(N K )]N X I (k ) X I [(N K )]N 通常称 X R (k) 为 X (k) 的共轭偶部， X I (k) 为 X (k) 的共轭奇部。所以说，对于时域、频域的 DFT 对应关系来说，序列 x(n) 实部对应于 X (k ) 的共轭偶部，序列 x(n) 的虚
其逆变换为
x(n)

1 N
N 1
X (k )WN nk
k 0
k 0,1,2 N 1 n 0,1, N 1
上机练习：
1．试用 Mablab 求其有限长序列 x1(n) (0.8)n (0 n 10) 与