预备知识一

合集下载

2020年预备党员知识题库

2020年预备党员知识题库
1.什么是党的纪律？
党的纪律是党的章程和党的决议确定的党的规定，是党员必须遵守的行为准则，是党内维护党的团结和统一的重要手段。

2.什么是党的民主集中制？
党的民主集中制是中国共产党的根本组织原则，是党的全部工作的基础，是党的纪律的基础。

它要求，党的一切工作都要坚持民主集中制，即党内要坚持民主，集体决策，个别服从；集体要坚持集中，严格执行党的决定，发扬集体主义精神。

3.什么是党的组织原则？
党的组织原则是指党的组织的基本原则，包括党的民主集中制原则、党的统一领导原则、党的分类管理原则、党的群众路线原则、党的政治路线原则、党的思想路线原则、党的组织路线原则等。

中考语文--初中语文文言文万能答题模板1

中考语文--初中语文文言文万能答题模板一、预备知识预备知识一:如何读懂选文(1)先读最后一道题目，了解大致内容和主要事件。

(此题如果要求“选择正确的一项”则除外)(2)然后带着“何人?”、“何时何地做何事?”、“结果怎样?”、“为什么?”等问题。

对文段用心地默读文章，以“事件”为依据对文章分层，理清文章思路。

(3)遇到实在不懂的字词，不必着急，同时必须用?或其他记号来提示自己放放先读下文,也许过后联系上下文进行推导自然能明白，或者可以到题目中去找答案。

预备知识二:官位变迁及官吏行为词1.表被任以官职的征、辟、察、举、召、荐、进、称、补、作、表、为、就2.表官职变化的:(1)表任命的:授、拜、除、封;(2) 表提升的:擢、拔、陟、升、迁。

(3)表调动的:调、徙、转、改、放、出、出官;(4)表降职的:左迁、迁谪、谪、逐、贬、诎(黜)预备知识三:其他高频词汇1.人称代词:第一人称(余吾予);第二人称(尔而女汝乃若);第三人称(之其彼渠厥)2.疑问代词:谁孰何曷胡焉安奚恶3.谦敬词语:请谨窃忝辱敢幸4.修辞词句:更衣山陵崩社稷中道崩殂5.兼词:诸焉盍旃叵二、如何答好每一道题1.文言实词释义题本题往往考查多义实词，古今异义词，通假字,偏义词及词类活用等知识点。

【答题技巧】记住:实词理解题不完全在于考你是否记得实词意思，更主要是考你是否会利用上下文进行推测。

掌握常见的理解和推断实词在文中含义的方法:第一种:从语法搭配的角度辨析词性第二种:从语义搭配的角度推测词义第三种:从语境暗示的角度推断词义第四种:从字形构成的角度推测词义第五种:从词类活用(古今异义)等用法的角度判断词义第六种:从句子结构对称的角度推断词义第七种:从字音字形通假的角度推断词义【相关知识】一词多义的产生:①词的本义。

如“(解)狐乃引弓送而射之”(拉开引。

②词的引申义.如“我君景公引领西望”(伸长)，成语有“引吭高歌”③词的比喻义.如“金城汤池”(比喻牢不可破)。

《预备知识》课件

学术论文：用于撰写学术论文，提高论文质量
个人学习领域
自我提升：通过PPT课件学习新知识、新技能，提升个人能力复习巩固：通过PPT课件复习学过的知识，巩固记忆学习计划：通过PPT课件制定学习计划，明确学习目标学习分享：通过PPT课件分享学习心得、经验，与他人交流学习心得
预备知识 PPT课件的优点
PPT课件制作需要掌握一定的计算机操作技能和设计技巧，如文字排版、图片处理、动画制作等。
PPT课件制作过程中需要注意内容的逻辑性和连贯性，以及视觉效果的吸引力和易读性。
PPT课件制作完成后，可以通过投影仪、电脑等设备进行展示，方便教师和学生进行互动和交流。
PPT课件制作流程
添加标题
添加标题
添加标题
添加标题
Keynote：苹果公司推出的演示文稿制作软件，界面简洁，操作流畅
Prezi：一款在线演示文稿制作工具，以缩放、旋转、平移等特效展示内容，具有较强的视觉冲击力
PPT课件制作技巧
内容选择：选择重点、难点内容进行讲解，避免冗余和重复。布局设计：合理安排幻灯片布局，突出重点内容，使用图表、图片等辅助元素增加视觉效果。文字处理：精炼文字，避免大段文字堆砌，使用标题、段落等格式设置突出层次和重点。动画效果：适当使用动画效果，增强演示的生动性和趣味性，但不要过度使用。
预备知识的分类
基础知识：包括数学、语文、英语等学科的基础知识技能知识：包括计算机、驾驶、烹饪等技能知识社会知识：包括历史、地理、政治等社会知识科学知识：包括物理、化学、生物等科学知识艺术知识：包括音乐、美术、舞蹈等艺术知识生活知识：包括健康、饮食、运动等生活知识

预备知识

而且
Cn Cn
r
nr
排列与组合的区别在于排列与次序有关而组合与次序无关。
例1
从1,2,3,4,5,6这六个数字中任取五个
组成五位数,问共能组成多少个五位数?
从六个不同数中任取五个组成五位数, 显然与次序有关，所以这里须用排列计算，相当于从六个数中任取五个数生成一个排列，共有不同的五位数的个数为：
n· …· =nr种 n· n
r个
3、组合
从n个不同的元素中任取r个元素组成一组 (0 r n )
称为一个组合。所有可能的组合数记为 C r ,
n
则
C
r n
A
r n
r!
n! n ( n 1) ( n r 1) ( n r ) ! r ! r!
n
ቤተ መጻሕፍቲ ባይዱ
特别，当n = r时，C n 1
熟练工人。现从9个工人中选出5人去管理这台机器，
已知这9个工人中有4个是熟练工人，问共有几种选
法？
方法1：
分析： 1）由 9人中有4名熟练工人知，5人中
至少有2个熟练工人的选法可有以下三类：有2 个熟练工人、3个熟练工人、4个熟练工人。须用加法原理计算.
2）每一类选法须分两步进行：先选取熟练工人再选取非熟练工人。用乘法原理计算，所以
r n
(n r )!
特别，当n = r时，称该排列为一个全排列，所有全排列的种数为
An n ( n 1)( n 2) 3 2 1 n !
n
2、有重复排列从n个不同的元素中有重复地取r个元素排成一列 0 r n ，称为一个有重复排列。由乘法原理
得所有不同的排法有

_新教材高中数学第一章预备知识1

1．补集是相对于全集而言的，它与全集不可分割．一方面，若没有定义全集，则不存在补集的说法；另一方面，补集的元素逃不出全集的范围．
2．补集既是集合之间的一种关系，同时也是集合之间的一种运算．求集合 A 的补集的前提是 A 为全集 U 的子集，随着所选全集的不同，得到的补集也是不同的．
1．已知全集 U＝{0，1，2}，且∁UA＝{2}，则 A＝
所以－m≤－2，即 m≥2，所以 m 的取值范围是{m|m≥2}．
[母题探究] 1．(变条件)本例将条件“(∁UA)∩B＝∅”改为“(∁UA)∩B≠∅”，其他条件不变，则 m
的取值范围又是什么？
解：由已知得 A＝{x|x≥－m}，所以∁UA＝{x|x<－m}，又(∁UA)∩B≠∅，所以－m>－2，解得 m<2. 故 m 的取值范围为{m|m<2}． 2．(变条件)本例将条件“(∁UA)∩B＝∅”改为“(∁UB)∪A＝R ”，其他条件不变，则 m 的取值范围又是什么？
A 的元素组成的集合，叫作 U 中子集 A 的补集，记作∁UA. 2．符号：∁UA＝{x|___x_∈__U_，__且___x_∉_A__ }． 3．Venn 图
4．补集的性质 (1)A∪(∁UA)＝__U__； (2)A∩(∁UA)＝__∅__； (3)∁UU＝__∅__，∁U∅＝U，∁U(∁UA)＝__A_； (4)(∁UA)∩(∁UB)＝∁U(A∪B)； (5)(∁UA)∪(∁UB)＝∁U(A∩B)．
解：由已知 A＝{x|x≥－m}，∁UB＝{x|x≤－2 或 x≥4}．
又(∁UB)∪A＝R ，所以－m≤－2，解得 m≥2. 故 m 的取值范围为{m|m≥2}．
由集合的补集求解参数的方法 (1)如果所给集合是有限集，由补集求参数问题时，可利用补集定义求解； (2)如果所给集合是无限集，与集合交、并、补运算有关的求参数问题时，一般利用数轴分析求解．

2020_2021学年新教材高中数学第1章预备知识1集合1.2集合的基本关系学案含解析北师大版必修一

1.2 集合的基本关系学习目标核心素养1.理解集合的包含与相等的含义．(难点) 2．能识别集合的子集、真子集，会判断集合间的关系．(难点、易混点)1．通过对集合之间包含与相等的含义以及子集、真子集概念的学习，培养数学抽象素养．2．借助子集、真子集的应用，培养逻辑推理素养．1．Venn图为了直观地表示集合间的关系，常用平面上封闭曲线的内部表示集合，称为Venn图．2．子集文字叙述对于两个集合A与B，如果集合A中的任何一个元素都属于集合B，即若a∈A，则a∈B，那么称集合A是集合B的子集．符号表示若a∈A⇒a∈B，则A⊆B．图形表示性质(1)任何一个集合都是它本身的子集，即A⊆A．(2)空集是任何集合的子集，即∅⊆A．(3)若A⊆B，B⊆C，则A⊆C．思考1：符号“∈”与“⊆”有何不同？提示：“∈”表示元素与集合的关系，而“⊆”表示集合与集合的关系．3．集合相等对于两个集合A与B，如果集合A是集合B的子集，且集合B也是集合A的子集，那么称集合A与集合B相等，记作A＝B．思考2：如何证明集合相等？提示：证明这两个集合互为子集．4．真子集对于两个集合A与B，如果A⊆B，且A≠B，那么称集合A是集合B的真子集，记作A B.1．设M＝{}1，2，3，N＝{}1，则下列关系正确的是( )A．N∈M B．N MC ．N ⊆MD ．N ⊇MC [由1∈M ，知N ⊆M .]2．已知集合A ＝{x |x 是平行四边形}，B ＝{x |x 是矩形}，C ＝{x |x 是正方形}，D ＝{x |x 是菱形}，则( )A ．A ⊆B B ．C ⊆B C ．D ⊆CD ．A ⊆DB [根据四边形的定义和分类，可知选B.] 3．集合{}0，1的子集有________个．4 [集合{}0，1的子集分别是∅，{}0，{}1，{}0，1.] 4．已知集合{}16⊆{}a 2，a ＋3，7，求实数a 的值．[解] (1)由已知，得16∈{}a 2，a ＋3，7，所以a 2＝16或a ＋3＝16，解得a ＝－4，4或13，当a ＝4时，a ＋3＝7，集合{}a 2，a ＋3，7的元素不满足互异性，所以，实数a 的值为－4，13.集合间的关系的判断【例1】判断下列各组中集合间的关系．(1)A ＝{} |x x 是等腰三角形，B ＝{x |x 是等边三角形}； (2)A ＝{} |x x ()x －1＝0，B ＝{}0，1； (3)A ＝{} |x －1<x <4，B ＝{} |x x <5；(4)A ＝⎩⎨⎧⎭⎬⎫ |x x ＝n ＋12，n ∈Z ，B ＝{x ⎪⎪⎪x ＝12n ＋1，n ∈Z }．[解] (1)因为等边三角形一定是等腰三角形，但等腰三角形不一定是等边三角形，故B A .(2)A ＝B .(3)把集合A 与B 在数轴上表示出来，根据定义易得A B . (4)A ＝⎩⎨⎧⎭⎬⎫ |x x ＝2n ＋12，n ∈Z ，B ＝⎩⎨⎧⎭⎬⎫ |x x ＝n ＋22，n ∈Z ，又{} |x x ＝2n ＋1，n ∈Z {} |x x ＝n ＋2，n ∈Z ，所以AB .判断两集合关系的常用方法(1)化简集合，从元素的属性中寻找两集合间的关系； (2)利用列举法表示各集合，从元素中寻找关系．提醒：在判断集合间的关系时，要注意数轴及Venn 图的应用，它可以直观地帮助我们发现集合间的关系．[跟进训练] 1．设A ＝{}|x x ＝2n －1，n ∈Z ，B ＝{}|x x ＝2n ＋1，n ∈Z ，C ＝{} |x x ＝4n －1，n ∈Z ，判断它们之间的关系．[解] 因为A ＝{} |x x ＝2n －1，n ∈Z ＝{x |x ＝2()n －1＋1，n ∈Z }⊆B ，B ＝{} |x x ＝2n ＋1，n ∈Z ＝{}x |x ＝2()n ＋1－1，n ∈Z ⊆A ，所以A ＝B .因为C ＝{} |x x ＝4n －1，n ∈Z ＝{x |x ＝2×2n －1，n ∈Z }⊆A ，又－3∈A ，但－3C ，所以C A .综上，C A ＝B .子集个数问题【例2】已知{}1，2M ⊆{}1，2，3，4，5，试写出满足条件的所有集合M . [思路点拨] 先分析集合M 中元素的特点，然后分类列举．[解] 集合M 含有元素1，2，且含有3，4，5中的至少一个元素，依据集合元素的个数分类列举如下：含有3个元素：{}1，2，3，{}1，2，4，{}1，2，5；含有4个元素：{}1，2，3，4，{}1，2，3，5，{}1，2，4，5；含有5个元素：{}1，2，3，4，5. 故满足条件的集合M 共有上述7个集合．1．解决此类问题，一般先分析集合元素的特征，然后按集合元素个数分类列举． 2．若一个集合有n 个元素，则它有2n个子集；有2n－1个真子集．[跟进训练]2．已知集合B ＝{}1，2，A ＝{}x |x ⊆B ， (1)写出集合A ；(2)判断B 与A 的关系．[解] (1)集合B 的子集分别是∅，{}1，{}2，{}1，2，所以A ＝{}∅，{}1，{}2，{}1，2；(2)B A .集合间的关系的应用 [探究问题]1．已知{}x |－1≤x ≤1⊆{}x |a ≤x ≤b ，试求a ，b 满足的条件．提示：a ≤－1且b ≥1.2．已知{}x |a ≤x ≤b ⊆{}x |－1≤x ≤1，试求a ，b 满足的条件．提示：对集合{}x |a ≤x ≤b 是否为空集讨论，当{}x |a ≤x ≤b 为空集，即a >b 时，满足题意；当{}x |a ≤x ≤b 非空时，－1≤a ≤b ≤1，故a ，b 满足的条件是a >b 或－1≤a ≤b ≤1.【例3】已知集合A ＝{x |－2≤x ≤7}，B ＝{x |m ＋1＜x ＜2m －1}，且B ⊆A ，求实数m 的取值范围．[思路点拨] 将集合间的关系转化为元素间的关系，由于B 可能为空集，故需分B ＝∅与B ≠∅两种情况讨论．[解] 当B ＝∅时，有m ＋1≥2m －1，得m ≤2，当B ≠∅时，有⎩⎪⎨⎪⎧m ＋1≥－2，2m －1≤7，m ＋1＜2m －1，解得2＜m ≤4.综上得m ≤4.1．对于本例中的集合A ，B ，是否存在实数m 使A ⊆B?[解] 若A ⊆B ，则⎩⎪⎨⎪⎧m ＋1<－22m －1>7 ，该不等式组无解，故实数m 不存在．2．若将本例中的“A ＝{x |－2≤x ≤7}”改为“A ＝{}x |x ≤－2，或x ≥7”，其他条件不变，求实数m 的取值范围．[解] 当B ＝∅时，有m ＋1≥2m －1，得m ≤2，当B ≠∅时，有⎩⎪⎨⎪⎧m ＋1＜2m －1，2m －1≤－2，或⎩⎪⎨⎪⎧m ＋1＜2m －1，m ＋1≥1，解得m ≥6，综上得x ≤2或m ≥6.1．对于B ⊆A ，在未指明B 非空时，应分B ＝∅与B ≠∅两种情况讨论．2. 对于B ≠∅这种情况，在确定参数的取值时，可借助数轴来完成，将两个集合在数轴上表示出来，分清实心点与空心圈，由集合之间的关系，列出关于参数的不等式，解不等式求出参数的取值范围．1．在判断集合间的关系时，要注意数轴及Venn 图的应用，它可以直观的帮助我们发现集合间的关系，这是数形结合思想的应用．2．若一个集合有n 个元素，则它的有2n个子集；有2n－1个真子集． 3．由集合间的关系求参数的取值范围时，要考虑空集是否符合题意．1．思考辨析(正确的画“√”，错误的画“×”) (1)空集是任何集合的真子集．( )(2)任何一个集合不可能是其自身的真子集． ( ) (3)任何一个集合至少有两个子集．( ) (4)若A 不是B 的子集，则A 中至少存在一个元素不属于B . ( )[答案] (1)× (2)√ (3)× (4)√2．集合A ＝{}x ∈N |0≤x <3真子集的个数是( ) A ．3 B ．4 C ．7 D ．8C [因为A ＝{}0，1，2，所以其真子集的个数是23－1＝7.]3．设x ，y ∈R ，A ＝{}()x ，y |y ＝x ，B ＝⎩⎨⎧⎭⎬⎫()x ，y ⎪⎪⎪y x＝1，则集合A ，B 的关系是________．[答案] B A4．已知集合A ＝{x |1≤x ≤2}，B ＝{x |1≤x ≤a ，a ≥1}． (1)若A B ，求实数a 的取值范围； (2)若B ⊆A ，求实数a 的取值范围． [解] (1)当A B 时，a >2. (2)当B ⊆A 时，1≤a ≤2.。

高中数学第一章预备知识1集合1.1集合的概念与表示2集合的表示同步高一第一册数学

第2课时集合(jíhé)的表示
12/9/2021
第一页，共五十四页。
必备知识·自主(zìzhǔ)学习
导思
1.用列举法表示集合要注意哪些问题? 2.用描述法表示集合要注意哪些问题? 3.有限集、无限集、空集的含义是什么? 4.用区间表示集合要注意哪些问题?
1.列举法 (1)方法:把集合中的元素一一列举出来写在花括号“{ }”内. (2)一般形式:{a,b,c,…}. (3)关注点:元素的排列___顺__序可(s以hùn(xkùě)yǐ)不同.
12/9/2021
第三十一页，共五十四页。
2.用描述法表示下列集合: (1)小于10的非负整数(zhěngshù)构成的集合; (2)数轴上与原点的距离大于3的点构成的集合; (3)平面直角坐标系中第二、四象限内的点构成的集合; (4)集合{1,3,5,7,…}.
12/9/2021
第三十二页，共五十四页。
【补偿训练】
已知集合A={x|x=2m-1,m∈Z},B={x|x=2n,n∈Z},且x1,x2∈A,x3∈B,则下列判断(pànduàn)不
正确的是
()
A.x1·x2∈A
B.x2·x3∈B
C.x1+x2∈B
D.x1+x2+x3∈A
【解析】选D.因为集合A表示奇数集,集合B表示偶数集,所以x1,x2是奇数,x3是偶数,
12/9/2021
第十四页，共五十四页。
关键能力·合作(hézuò)学习
类型(lèixíng)一列举法表示集合(数学抽象)
【题组训练】
1.设a,b∈R, 与1，a 表0,示a同b一个集合,则b-a=( )
A.1
B.-1
C.2
D.-2

高一第一章预备知识点

高一第一章预备知识点高一的第一章是预备知识点，为同学们打下学习的基础。

本章主要包括数学、化学、物理、生物、地理、历史、政治等学科的一些基础知识点。

下面将分别介绍各学科的预备知识点。

1. 数学在高一的数学课程中，预备知识点主要集中在数与代数方面。

包括常见的数集与数的运算、分式与有理数、整式与分式、二次根式等等。

同学们需要熟练掌握基本的数学运算法则和公式，并能熟练运用到实际问题中。

2. 化学在化学方面，高一的预备知识点主要包括化学元素、化合物和化学方程式等内容。

同学们需要学习元素周期表，了解各种元素的基本性质和特点，同时还需要掌握化学方程式的书写和化学反应的基本原理。

3. 物理高一的物理预备知识点主要涉及力学和电学方面的内容。

同学们需要掌握牛顿运动定律、力的合成与分解、机械功和机械能、电路的基本组成和性质等。

这些内容是后续学习物理课程的基础，同学们需要牢记。

4. 生物生物方面的预备知识点主要包括基本的细胞结构和生物进化的基础概念。

同学们需要了解细胞的构成、功能和分类，以及生物进化的基本原理和演化过程。

这些知识将有助于后续学习更深入的生物学知识。

5. 地理在地理方面，高一的预备知识点主要涵盖地球与地图的基本概念、自然地理和人文地理的基本内容。

同学们需要了解地球的形状和结构，学习地图的读法和使用方法，还需要了解地球上各种自然地理和人文地理现象的形成原因和影响。

6. 历史历史方面的预备知识点主要包括中国历史的基本轴线和历史时期的划分。

同学们需要了解中国历史的主要事件和人物，学习不同历史时期的社会背景和演变过程。

这些知识将为后续学习具体历史时期提供基础。

7. 政治政治方面的预备知识点主要涉及国家制度与国家管理的基本概念。

同学们需要掌握国家的定义，了解国家组织和管理的基本原则，同时还需要学习国家的基本制度和行政管理的基本方式。

以上就是高一第一章的预备知识点的简要介绍。

同学们在学习这些知识点的过程中，要注重理解和实际应用。

中专预备知识

预备知识第一节数及数的运算一、相反数与绝对值的概念1.相反数（1）定义只有符号不同的两个数叫做互为相反数，如－2008与2008互为相反数.从数轴上看，位于原点两旁，且与原点距离相等的两点所表示的两个数叫做互为相反数.如5与－5是互为相反数.0的相反数是0.也只有0的相反数是它的本身.相反数表示两个数的相互关系，不能单独存在.（2）相反数的表示在一个数的前面添上“－”号就成为原数的相反数.若a表示一个实数，则a的相反数表示为－a.在一个数的前面添上“+”号仍与原数相同.如，＋7=7.特别地，＋0=0，－0=0.（3）特性若a，b互为相反数，则0a ba b+=，则a，b互为相反数.+=，反之若0（4）多重符号化简相反数的意义是简化多重符号的依据.如-（-1）是－1的相反数，而－1的相反数为+1，所以-(-1)=+1=1.多重符号化简的结果是由“－”号的个数决定的.如果“－”号是奇数个，则结果为负；如果是偶数个，则结果为正.可简写为“奇负偶正”.2.绝对值（1）定义数轴上表示数a的点与原点的距离叫做数a的绝对值，记作a.根据定义得，一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；零的绝对值是零．（2）性质一个实数的绝对值是一个非负数，即0a ≥，因此，在实数范围内，绝对值最小的数是零．两个相反数的绝对值相等．二、分数运算1.加减当两数分母相同时，有p q p q m m m±±=；当两数分母不同时，有p q pn qm m n mn ±±=. 2.乘除分数乘分数，分子的积作为分子，分母的积作为分母.即p q p q m n m n⋅⋅=⋅. 分数除分数，把除式的分子、分母颠倒位置后，与被除式相乘.即p q p n p n m n m q m q⋅÷=⋅=⋅. 三、二次根式及其运算1.二次根式的定义(0)a ≥的式子叫做二次根式.”叫做二次根号.当0a >时，a 0>；当0a =00=；a 不能为负.2(0)a a = ≥2.二次根式的运算（1）乘除(0,0)a b ≥≥.===二次根式的除法规定为ba b a =(0,0)a b > ≥.===如果二次根式的被开方数不含分母且不含能开的尽方的因数或因式，则称为最简二次根式.（2）加减二次根式加减时，可以先将二次根式化成最简二次根式，再将被开方数相同的二次根式进行合并.例如，-==课堂练习：1.计算.（1）125736-+ （2）4192-+ （3）37()58⨯- （4）32838()45⨯⨯- （5）3244÷ （6）572()4153⨯÷- 2.计算.（1 （2）（3）3.已知xy =1x y -=，则(1)(1)x y +-的值是多少？第二节代数式及其运算一、代数式1.代数式用基本的运算符号把数、表示数的字母连接而成的式子叫做代数式.一个代数式中可能有几种运算，但不含表示关系的符号，如等号、不等号．如31(4)2x -，等都是代数式，而32>，2πS r =等都不是代数式．特别地，单独的一个数和字母也是代数式．如：2，y 等都是代数式．用数值代替代数式里的字母，计算后所得的结果叫做代数式的值．2.整式数与字母乘积表示的代数式叫做单项式，单项式中的数字因数叫做单项式的系数.单独一个数或一个字母也是单项式.一个单项式中，所有字母的指数的和叫做这个单项式的次数.几个单项式的和叫做多项式.在多项式中，每个单项式叫做多项式的项，其中不含字母的项叫做常数项.一个多项式有几项就叫做几项式.多项式中，次数最高的项的次数，就是这个多项式的次数.单项式和多项式统称为整式.代数式包含整式.二、整式的运算1.同类项所含字母相同，并且相同字母的指数也分别相同的项叫做同类项.如33x 与37x -就是同类项.同类项的系数相加，所得的结果作为系数，字母和字母的指数不变，叫做合并同类项.2.整式的加减几个整式相加减，通常用括号把每一个整式括起来，再用加减号连接；然后去括号，合并同类项. 例如，2211312()()2323x x y x y --+-+ 22123122323x x y x y =-+-+ 23x y =-+.3.整式的乘除单项式相乘(除)，把它们的系数、相同字母分别相乘(除)，对于只在一个单项式(被除式)里含有的字母，则连同它的指数作为积(商)的一个因式.例如，3342(5)(2)[(5)(2)]()()10a b ab a a b b a b --=-⨯-⋅⋅=.4234321284(284)7x y x y x y xy --÷=÷⋅=.多项式乘(除)以单项式，先把这个多项式的每一项乘(除)以这个单项式，再把所得的积(商)相加．例如，32(1263)3a a a a -+÷321236333a a a a a a =÷-÷+÷2421a a =-+.多项式与多项式相乘，先用一个多项式的每一项乘以另一个多项式的每一项，再把所得的积相加．例如，(31)(2)x x +-33(2)11(2)x x x x =⋅+⋅-+⋅+⨯-2352x x =--.三、因式分解把一个多项式化为几个整式的积的形式，这种变形叫做把这个多项式因式分解，也作分解因式.常用的因式分解法有提公因式法，公式法和十字相乘法.1.提公因式法各项都含有的公共的因式叫做这个多项式各项的公因式.如ma mb mc +-的公因式为m .如果一个多项式的各项有公因式，可以把这个公因式提出来，从而将多项式化成两个因式乘积的形式，这种分解因式的方法叫做提公因式法.例如，323222228168828(2)a b ab c ab a ab bc ab a bc +=⋅+⋅=+.2.公式法常用的公式有（1）平方差公式：22()()a b a b a b -=+-.例如，2294(32)(32)a b a b a b -=+-.（2）完全平方公式：2222()a ab b a b ++=+，2222()a ab b a b -+=-. 例如，22244(2)x xy y x y -+=-.（3）立方和公式：3322()()a b a b a ab b +=+-+.例如，33228(2)(44)x y x y x xy y +=+-+.（4）立方差公式：3322()()a b a b a ab b -=-++.3.十字相乘法形如2()x p q x pq +++的多项式可运用十字相乘法分解，即2()()()x p q x p q x p x q+++=++. 例如，22710(25)25(2)(5)x x x x x x ++=+++⨯=++.课堂练习：1.计算.（1）22232(43)b a a a b a ---+++ （2）22221()()2a b c d ab c ÷ （3）3222(462)(2)a b a b ab ab -+÷- （4）2(2)()2(2)x y x y x xy +---2.分解因式.（1）2a ab - （2）2441a a ++（3）2222()()x a b y b a --- （4）22222()4a b a b +-（5）xy y x 81622-+ （6）26x x +-（7）2232x x +- （8）3827x -第三节方程与方程组一、二元一次方程与二元一次方程组方程中含有两个未知数（x 和y ），并且未知数的指数都是1，这样的方程叫做二元一次方程.如20x y +=，37x y -+=等.使二元一次方程两边的值相等的两个未知数的值，叫做二元一次方程的解.一般情况下，二元一次方程有无数的解.把两个二元一次方程合在一起，就组成二元一次方程组.二元一次方程组的两个方程的公共解，叫做二元一次方程组的解.求二元一次方程组的解可以利用代入消元法或加减消元法.由二元一次方程组中一个方程，将一个未知数用含另一个未知数的式子表示出来，再代入另一个方程，实现消元，进而求得这个二元一次方程组的解.这种方法叫做代入消元法.例1.用代入消元法解方程组33814x y x y -=⎧⎨-=⎩.解：由3x y -=得3x y =+，代入3814x y -=，得3(3)814y y +-=，解方程，得1y =-，把1y =-代入3x y =+，得2x =，所以此方程组的解为21x y =⎧⎨=-⎩. 两个二元一次方程中同一未知数的系数相反或相等时，将两个方程的两边分别相加或相减，能消去这个未知数，得到一个一元一次方程.这种方法叫做加减消元法.例2.用加减消元法解方程组257325x y x y +=⎧⎨+=⎩.解：将原方程组变成615216410x y x y +=⎧⎨+=⎩，两方程相减得1111x =，即1x =，再将1x =代入325x y +=中，得1y =，所以此方程组的解为11x y =⎧⎨=⎩.二、一元二次方程等号两边都是整式，只含有一个未知数，并且未知数的最高次数是2的方程，叫做一元二次方程，一般形式为20ax bx c ++=，(0)a ≠.解一元二次方程可以利用配方法、公式法或因式分解法.对于一元二次方程20ax bx c ++=，(0)a ≠，通过配成完全平方的形式来求解一元二次方程的方法叫做配方法.例3.利用配方法求解方程2810x x -+=.解：移项，得281x x -=-，配方，得2228414x x -+=-+，化简为2(4)15x -=，由此可得4x -=所以14x =24x =对于一元二次方程20ax bx c ++=，(0)a ≠，当240b ac -≥时，将a ，b ，c代入式子x =，就得到方程的根.这个式子叫做一元二次方程的求根公式，利用求根公式解一元二次方程的方法叫做公式法.例4.利用求根公式解方程2210x x --=.解：a =2，b =-1，c =-1，因为224(1)42(1)90b ac -=--⨯⨯-=>，所以134x ±==，即11x =，212x =-. 特别地，当240b ac -=时，一元二次方程有两个相等的实根；当240b ac -<时，一元二次方程没有实根.对于一元二次方程20ax bx c ++=，(0)a ≠，利用因式分解使方程化成两个一次式的乘积等于0的形式，再使两个一次式分别等于0进行求解.这种方法叫做因式分解法.例5.利用因式分解法解方程223x x +=.解：因式分解，得(3)(1)0x x +-=，于是，30x +=或10x -=，即13x =-，21x =.三、分式方程分母中含有未知数的方程叫做分式方程.解分式方程的基本思路是将分式方程化为整式方程，具体做法是将方程两边同乘最简公分母，去掉分母再去求解.但是，注意将整式方程的解代入最简公分母，若最简公分母的值不为0，则整式方程的解是原方程的解；否则，此解不是原分式方程的解.例6.解方程233x x=-. 解：方程两边同乘(3)x x -，得239x x =-，解得，9x =.通过检验，9x =时(3)0x x -≠，9是原分式方程的解.课堂练习：1.解下列二元一次方程组.（1）422x y x y +=⎧⎨-=⎩ （2）32102310x y x y +=⎧⎨+=⎩（3）2553285x y x y +=⎧⎨+=⎩2. 解下列一元二次方程.（1）21(2)402x +-= （2）0662=++x x （3）24810x x -+= （4）(1)(2)24x x x ++=+3. 关于x 的一元二次方程20x px q ++=的两根分别为13x =，21x =，求这个一元二次方程.4.解下列分式方程.（1）311x x =- （2）256x x x x -=-- （3）6710453x x -=-+ （4）214111x x x +-=-- 第四节一元一次不等式与一元一次不等式组一、一元一次不等式及不等式的性质1.一元一次不等式形如0ax b +>的式子叫做一元一次不等式，其中0a ≠，且“>”可换成其他形式的不等号.使不等式成立的x 的取值范围叫做不等式的解集.2.不等式的性质（1）不等式两边加（或减）同一个数（或式子），不等号的方向不变.（2）不等式两边乘（或除以）同一个正数，不等号的方向不变.（3）不等式两边乘（或除以）同一个负数，不等号的方向改变. 利用不等式的性质，可以逐步求出不等式的解集.例1.求350x +>的解集.解：不等式两边同时减5，得35x >-，两边同时再除以3，得53x >-，所以原不等式的解集为53x >-. 二、一元一次不等式组把两个一元一次不等式合起来，组成一个一元一次不等式组.两个一元一次不等式解集的公共部分，叫做不等式组的解集.例2.解不等式组212541x x x x ->+⎧⎨+<-⎩. 解：解第一个不等式，得3x >，解第二个不等式，得2x >，两个解集的公共部分，即原不等式组的解集为3x >.课堂练习：1.解下列一元一次不等式.（1）2331x x -+>+ （2）52x x -+≤（3）2(3)7x +< （4）1132x x ++> 2.解下列一元一次不等式组.（1）235324x x +<⎧⎨->⎩ （2）()43321311522x x x x -<+⎧⎪⎨->-⎪⎩（3）()4321213x xxx-<-⎧⎪⎨++>⎪⎩（4）()2 1.55261x xx x+⎧⎪⎨->-⎪⎩≤。

预备知识

用区间表示为： (, 1 ) 2
本节作业：第22页 1（2、3）
【1-1-7】
(7) x x ( y 0) yy
【1-1-4】
三、区间与邻域 1、区间：
表示数轴上某一段点的集合。包括区间端点、区间长度等，区间包括开区间、闭区间、半开半闭区间，还区分有限区间、无限区间。
(a,b) {x a x b}
另外，还有下列常见的区间：
[a,b],(a,b],[a,b),(, ),(, a),(, a],(a, ),[a, )
OM () {x x M} (, M ) U(M , ), M 0
【1-1-6】
4、理解举例
解不等式 x 2 x 1，并用区间表示该不等式的解集。
解：根据绝对值的几何意义，上述不等式表示的实际上是到点—2的距离小于到点1的所有点的集合，因此从数轴上满足上述要求的点集为
{x x 1} 2
注：无穷大不是一个很大的数，而是一个变化趋势，它表达的是不管给定多么大一个数，它都比这个数还要大，因此在区间的端点上，都不能包含无穷大，无穷大只能是开。
【1-1-5】
2、邻域
(1)点x0的邻域 : 在数轴上到点x0的距离小于 ( 0)的点的集合, 记作
O (x0 ) (x0 , x0 ), 其中x0称为邻域的中心, 称为邻域的半径
注：不等式的加法必须是同方向的相加，才能得出相同方向的不等式。【1-1-3】
(5) x y x y
证明： x x y y x y y x y x y
y yxx yx x x y xy
x y x y x y x y x y
(6) xy x y
{x a x a}
【1-1-2】
3、绝对值的基本性质：对x, y R,则有如下一些常用结论

28' §3.2 古典概型预备知识(一)

5、某班级有男学生 5 人，女学生 4 人 (1)从中任选一人去领奖, 有多少种不同的选法？ (2)从中任选男、女学生各一人去参加座谈会，有多少种不同的选法？
王新敞
奎屯新疆
6、甲厂生产的收音机外壳形状有 3 种，颜色有 4 种，乙厂生产的收音机外壳形状有 4 种，颜色有 5 种，这两厂生产的收音机仅从外壳的形状和颜色看，共有所少种不同的品种？ 7、从 1,2,3,4 这 4 个数字中，每次取出 2 个数字组成一个两位数. （1）若两位数中的数字不允许重复使用，则能得到多少个不同的两位数？（2）若两位数中的数字允许重复使用，则能得到多少个不同的两位数？ 8、用 1,5,9,13 中任意一个数作分子，4,8,12,16 中任意一个数作分母，可组成多少个不同的分数？可组成多少个不同的真分数？
4
扬大附中导学案必修三第三章概率主备：高源辅备：刘跃武编号：
28′
反思感悟：
§3.2 * 古典概型预备知识（二）
班级：高二（）班姓名：时间：月日
一、教学目标
1．理解排列、组合的概念，正公式，为古典概型的学习做好知识准备。
三、问题探究
例 1、（1）写出从 a, b, c, d 这 4 个字母中，取出 2 个字母的所有排列，并用树形图表示；（2）写出从 a, b, c, d 这 4 个字母中，取出 3 个字母的所有排列，并用树形图表示。
5
扬大附中导学案必修三第三章概率主备：高源辅备：刘跃武编号：
28′
1
扬大附中导学案必修三第三章概率主备：高源辅备：刘跃武编号：的选法。
28′
反思感悟：
三、问题探究：
例 1、书架的第 1 层放有 4 本不同的计算机书，第 2 层放有 3 本不同的文艺书，第 3 层放有 2 本不同的体育书。（1）从书架上任取 1 本书，有多少种不同的取法？（2）从书架的第 1、2、3 层各取 1 本书，有多少种不同的取法？

随机过程-1预备知识

• 概率空间的性质
设(, F,P)为概率空间，则
(4) P()= 0
(5)P(B\A)= P(B) -P(A) , (AB)
(6)
lim n
P(
An
)

P P
n1 n1
An An
, ,
A1 A1

A2 An A2 An
• 显然，这样建立的概率满足三条公理。
17
• 例2 为依次抛掷三枚硬币的试验建立概率模型。 • 解用“1”表示正面向上，“0”表示反面向上，
样本空间为：
• {(1,1,1),(1,1,0),(1,0,1),(1,0,0),(0,1,1),
(0,1,0),(0,0,1),(0,0,0)}
• 如果上述8种结果出现的可能性相同，根据可加性和归一性，每个结果的概率为 1/8.
概率实例：
• 例1 给掷一枚硬币的试验建立概率模型。 • 解：掷一枚硬币，有两个可能的结果：正
面和反面。若用 1 表示正面，2 表示反面，则样本空间为： {1, 2 } • 事件为： {1 , 2 }, {1}, {2 }, • 根据定义和性质，得到
P({1,2 }) 1, P() 0
（2）若AF, 则\AF （对立事件）

（3）若AiF,i=1,2…，则 AiF （可列
并事件）
i 1
称F为-代数，（， F ）为可测空间
例投掷一次骰子试验，ei表示出现i点， ={e1,e2,e3,e4,e5,e6} F ={，{e1,e2,e3}，{e4,e5,e6}， }
• 定义1.2概率空间：设(,F)为可测空间,映
射P：F R，A|P(A)满足

第1章预备知识

P
1.2.2
几乎必然收敛
几乎必然收敛又称为以概率 1 收敛. 定义 1.2.2 (几乎必然收敛) 随机变量序列 {Xn , n = 1, 2, · · · }, 当 P (limn→∞ Xn = a.s. X ) = 1 时，说它几乎必然 (以概率为 1) 收敛于一个随机变量 X，记为： Xn → X . a.s. 注：等价地，若对 ∀ > 0，有 P (limn→∞ |Xn − X | < ) = 1，则 Xn → X . 下面介绍另一个 a.s. 收敛的定义. a.s. 定理 1.2.4 Xn → X 当且仅当对 ∀ > 0， limm→∞ P (supn m |Xn − X | ) = 1. 注：若 ∀ > 0， limn→∞ P (|Xn − X | ) = 1，则 Xn → X . 由上面定理知几乎必然收敛强于依概率收敛. 定理 1.2.5 (强大数定律) 假设 X1 , X2 , · · · , Xn 是独立同分布的随机变量序列，且有 E |X1 | < ∞, 则当 n → ∞ 时，有 ¯n = 1 X n
σ2 P ¯n → = 0, 即 X µ. nε2 定理 1.2.1 (弱大数定律) 假设 X1 , X2 , · · · , Xn 是独立同分布随机变量，且 E |X1 | < ∞，则当 n → ∞ 时有 n P ¯n = 1 X Xi → E (X1 ). n
i=1
第1 章
预备知识
3
注：(1) 更一般的情况下，{Xn , n = 1, 2, · · · } 是独立随机变量序列，并且 E (Xi ) = µi ，有 n n 1 1 P Xi − µi → 0. n n
i=1 i=1

预备知识

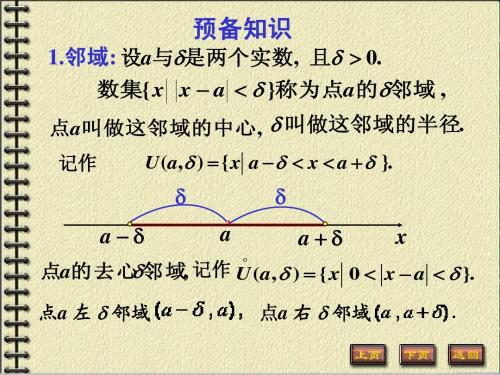
(5) 反三角函数
反正弦函数 y = arcsin x
y = arcsin x
反余弦函数 y = arccos x
y = arccos x
反正切函数 y = arctan x
y = arctan x
反余切函数 y = arccot x
y =arccot x
幂函数,指数函数对数函数幂函数指数函数,对数函数三角函数和反指数函数对数函数,三角函数和反三角函数统称为基本初等函数基本初等函数. 三角函数统称为基本初等函数
x<1 x + 2, , ϕ( x ) = 2 x≥1 x − 1,
x<0 , x≥0
解
e ϕ ( x ) , ϕ( x ) < 1 f [ϕ( x )] = ϕ( x ), ϕ( x ) ≥ 1
10 当ϕ( x ) < 1时,
或 x < 0, ϕ( x ) = x + 2 < 1,
3、由函数 y = e u，u = x 2 复合而成的函数为 ______ .
4、函数 y = sin ln 2 x 由 __________ 复合而成 .
5、若 f ( x ) 的定义域为 [ 0 ， ] ，则 f（x 2）的定义域 1 为 __________ ，f (sin x ) 的定义域为 __________ ， f ( x + a )(a > 0) 的定义域为 ___________ ， f ( x + a ) + f ( x − a ) (a > 0) 的定义域为 _________ .
二、应用图形的“叠加 ”作函数 y = x + sin x 的图形 . 应用图形的“

新教材高中数学第一章预备知识1集合1-1集合的概念与表示第1课时集合的概念课件北师大版必修第一册

2.(多选题)下列关系正确的是( BD )
A.0∈N+
B.(√2 − √7)∉Q
C.0∉Q
D.8∈Z
3.已知集合S中的元素a,b是一个四边形的两条对角线的长,那么这个四边
形一定不是(
)
A.梯形 B.平行四边形
C.矩形 D.菱形
答案 C
解析因为集合中的元素具有互异性,所以a≠b,即四边形对角线不相等,故选
可能只含有一个元素.
本节要点归纳
1.知识清单:
(1)元素与集合的概念、元素与集合的关系;
(2)集合中元素的三个特性及应用;
(3)常用数集的表示.
2.方归纳:分类讨论.
3.常见误区:忽视集合中元素的互异性.
学以致用•随堂检测全达标
1.(2022湖北襄阳月考)判断下列各组对象可以组成集合的是(
)
(1)1
N+;
(2)-3
N;
1
(3)3
Q;
(4)√3
1
(5)-2
(6)π
Q;
R;
R+.
答案 (1)∈ (2)∉
(3)∈ (4)∉ (5)∈
(6)∈
重难探究•能力素养全提升
探究点一集合的概念
【例1】给出下列各组对象:
①我们班比较高的同学;②无限接近于0的数的全体;③比较小的正整数的
全体;④平面上到点O的距离等于1的点的全体;⑤正三角形的全体;⑥ √的
第一章
第1课时集合的概念
课标要求
1.通过实例,了解集合的含义.
2.掌握集合中元素的三个特征.
3.理解元素与集合的“属于”关系.
4.记住常用数集及其记法.
内
容

新教材高中数学第一章预备知识1集合集合的概念与表示第2课时集合的表示素养作业北师大版必修第一册

第一章 §1 1.1 第2课时A 组·素养自测一、选择题1．用列举法表示集合{x |x 2－3x ＋2＝0}为( C ) A ．{(1,2)} B ．{(2,1)} C ．{1,2}D ．{x 2－3x ＋2＝0}[解析] 解方程x 2－3x ＋2＝0得x ＝1或x ＝2．用列举法表示为{1,2}． 2．直线y ＝2x ＋1与y 轴的交点所组成的集合为( B ) A ．{0,1}B ．{(0,1)}C ．⎩⎨⎧⎭⎬⎫－12，0 D ．⎩⎨⎧⎭⎬⎫⎝ ⎛⎭⎪⎫－12，0[解析] 解方程组⎩⎪⎨⎪⎧y ＝2x ＋1，x ＝0，得⎩⎪⎨⎪⎧x ＝0，y ＝1.故该集合为{(0,1)}．3．已知x ∈N ,则方程x 2＋x －2＝0的解集为( C ) A ．{x |x ＝2} B ．{x |x ＝1或x ＝－2} C ．{x |x ＝1}D ．{1,－2}[解析] 方程x 2＋x －2＝0的解为x ＝1或x ＝－2．由于x ∈N ,所以x ＝－2舍去．故选C ．4．若A ＝{－1,3},则可用列举法将集合{(x ,y )|x ∈A ,y ∈A }表示为( D ) A ．{(－1,3)} B ．{－1,3}C ．{(－1,3),(3,－1)}D ．{(－1,3),(3,3),(－1,－1),(3,－1)}[解析] 因为集合{(x ,y )|x ∈A ,y ∈A }是点集或数对构成的集合,其中x ,y 均属于集合A ,所以用列举法可表示为{(－1,3),(3,3),(－1,－1),(3,－1)}．5．下列集合中,不同于另外三个集合的是( B ) A ．{x |x ＝1} B ．{x |x 2＝1} C ．{1}D ．{y |(y －1)2＝0}[解析] 因为{x |x ＝1}＝{1},{x |x 2＝1}＝{－1,1},{y |(y －1)2＝0}＝{1},所以B 选项的集合不同于另外三个集合．6．下列说法：①集合{x ∈N |x 3＝x }用列举法可表示为{－1,0,1}；②实数集可以表示为{x |x 为所有实数}或{R }；③一次函数y ＝x ＋2和y ＝－2x ＋8的图象交点组成的集合为{x ＝2,y ＝4},正确的个数为( D )A ．3B ．2C ．1D ．0[解析] 由x 3＝x ,得x (x －1)(x ＋1)＝0,解得x ＝0或x ＝1或x ＝－1．因为－1∉N ,故集合{x ∈N |x 3＝x }用列举法可表示为{0,1},故①不正确．集合表示中的“{}”已包含“所有”“全体”等含义,而“R ”表示所有的实数组成的集合,故实数集正确表示应为{x |x 为实数}或R ,故②不正确．联立方程组可得⎩⎪⎨⎪⎧y ＝x ＋2，y ＝－2x ＋8，解得⎩⎪⎨⎪⎧x ＝2，y ＝4，∴一次函数与y ＝－2x ＋8的图象交点为(2,4),∴所求集合为{(x ；y )|x ＝2且y ＝4},故③不正确．二、填空题7．已知A ＝{(x ,y )|x ＋y ＝4,x ∈N ,y ∈N },用列举法表示A 为__{(0,4),(1,3),(2,2),(3,1),(4,0)}__．[解析] ∵x ＋y ＝4,x ∈N ,y ∈N , ∴x ＝4－y ∈N ,∴⎩⎪⎨⎪⎧x ＝0，y ＝4，⎩⎪⎨⎪⎧x ＝1，y ＝3，⎩⎪⎨⎪⎧x ＝2，y ＝2，⎩⎪⎨⎪⎧x ＝3，y ＝1，⎩⎪⎨⎪⎧x ＝4，y ＝0.∴A ＝{(0,4),(1,3),(2,2),(3,1),(4,0)}．8．集合{1,2,3,2,5,…}用描述法表示为．[解析] 注意到集合中的元素的特征为n ,且n ∈N *,所以用描述法可表示为{x |x ＝n ,n ∈N *}．9．已知集合A ＝{x |2x ＋a ＞0},且1∉A ,则实数a 的取值范围是__(－∞,－2]__． [解析] 因为1∉A ,则应有2×1＋a ≤0, 所以(－∞,－2]．三、解答题10．用适当的方法表示下列集合：(1)方程组⎩⎪⎨⎪⎧2x －3y ＝143x ＋2y ＝8,的解集；(2)方程x 2－2x ＋1＝0的实数根组成的集合； (3)平面直角坐标系内所有第二象限的点组成的集合； (4)二次函数y ＝x 2＋2x －10的图象上所有的点组成的集合； (5)二次函数y ＝x 2＋2x －10的图象上所有点的纵坐标组成的集合．[解析] (1)解方程组⎩⎪⎨⎪⎧2x －3y ＝14，3x ＋2y ＝8，得⎩⎪⎨⎪⎧x ＝4，y ＝－2，故解集可用描述法表示为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫(x ，y )⎪⎪⎪⎩⎪⎨⎪⎧x ＝4y ＝－2，,也可用列举法表示为{(4,－2)}． (2)方程x 2－2x ＋1＝0的实数根为1,因此可用列举法表示为{1},也可用描述法表示为{x |x 2－2x ＋1＝0}．(3)集合的代表元素是点,可用描述法表示为{(x ,y )|x ＜0且y ＞0}．(4)二次函数y ＝x 2＋2x －10的图象上所有的点组成的集合中,代表元素为点,可用描述法表示为{(x ,y )|y ＝x 2＋2x －10}．(5)二次函数y ＝x 2＋2x －10的图象上所有点的纵坐标组成的集合中,代表元素为y ,是实数,可用描述法表示为{y |y ＝x 2＋2x －10}．B 组·素养提升一、选择题 1．方程组⎩⎪⎨⎪⎧x －y ＝2，x ＋2y ＝－1的解集是( C )A ．{x ＝1,y ＝－1}B ．{1}C ．{(1,－1)}D ．{(x ,y )|(1,－1)}[解析] 方程组的解集中元素应是有序数对形式,排除A,B,而D 的集合表示方法有误,排除D ．2．用列举法可将集合{(x ,y )|x ∈{1,2},y ∈{1,2}}表示为( D ) A ．{1,2} B ．{(1,2)} C ．{(1,1),(2,2)}D ．{(1,1),(1,2),(2,1),(2,2)}[解析] x ＝1,y ＝1；x ＝1,y ＝2；x ＝2,y ＝1；x ＝2,y ＝2．∴集合{(x ,y )|x ∈{1,2},y ∈{1,2}}表示为{(1,1),(1,2),(2,1),(2,2)},故选D ． 3．(多选题)大于4的所有奇数构成的集合可用描述法表示为( BD ) A ．{x |x ＝2k －1,k ∈N } B ．{x |x ＝2k ＋1,k ∈N ,k ≥2} C ．{x |x ＝2k ＋3,k ∈N }D ．{x |x ＝2k ＋5,k ∈N }[解析] 选项A,C 中,集合内的最小奇数不大于4． 4．(多选题)下列各组中M ,P 表示不同集合的是( ABD ) A ．M ＝{3,－1},P ＝{(3,－1)} B ．M ＝{(3,1)},P ＝{(1,3)}C ．M ＝{y |y ＝x 2＋1,x ∈R },P ＝{x |x ＝t 2＋1,t ∈R } D ．M ＝{y |y ＝x 2－1,x ∈R },P ＝{(x ,y )|y ＝x 2－1,x ∈R }[解析] 选项A 中,M 是由3,－1两个元素构成的集合,而集合P 是由点(3,－1)构成的集合；选项B 中,(3,1)与(1,3)表示不同的点,故M ≠P ；选项D 中,M 是二次函数y ＝x 2－1,x ∈R 的所有因变量组成的集合,而集合P 是二次函数y ＝x 2－1,x ∈R 图象上所有点组成的集合．故选ABD ．二、填空题5．若集合A ＝{x |ax 2＋2x ＋1＝0,a ∈R }中只有一个元素,则实数a 的值是__0或1__． [解析] 集合A 中只有一个元素,有两种情况：当a ≠0时,由Δ＝0,解得a ＝1,此时A ＝{－1},满足题意；当a ＝0时,x ＝－12,此时A ＝⎩⎨⎧⎭⎬⎫－12,满足题意．故集合A 中只有一个元素时,a 的值是0或1．6．设A ,B 为两个实数集,定义集合A ＋B ＝{x |x ＝x 1＋x 2,x 1∈A ,x 2∈B },若A ＝{1,2,3},B ＝{2,3},则集合A ＋B 中元素的个数为__4__．[解析] 当x 1＝1时,x 1＋x 2＝1＋2＝3或x 1＋x 2＝1＋3＝4；当x 1＝2时,x 1＋x 2＝2＋2＝4或x 1＋x 2＝2＋3＝5；当x 1＝3时,x 1＋x 2＝3＋2＝5或x 1＋x 2＝3＋3＝6．∴A ＋B ＝{3,4,5,6},共4个元素．三、解答题7．已知集合A ＝⎩⎨⎧⎭⎬⎫x ∈N ⎪⎪⎪86－x ∈N ,试用列举法表示集合A ．[解析] 由题意可知6－x 是8的正约数,当6－x ＝1时,x ＝5；当6－x ＝2时,x ＝4；当6－x ＝4时,x ＝2；当6－x ＝8时,x ＝－2,而x ≥0,∴x ＝2,4,5,即A ＝{2,4,5}．8．已知集合A ＝{x |ax 2－3x ＋2＝0}． (1)若A 中只有一个元素,求集合A ；(2)若A 中至少有一个元素,求a 的取值范围．[解析] (1)因为集合A 是方程ax 2－3x ＋2＝0的解集,则当a ＝0时,A ＝⎩⎨⎧⎭⎬⎫23,符合题意；当a ≠0时,方程ax 2－3x ＋2＝0应有两个相等的实数根,则Δ＝9－8a ＝0,解得a ＝98,此时A ＝⎩⎨⎧⎭⎬⎫43,符合题意．综上所述,当a ＝0时,A ＝⎩⎨⎧⎭⎬⎫23,当a ＝98时,A ＝⎩⎨⎧⎭⎬⎫43．(2)由(1)可知,当a ＝0时,A ＝⎩⎨⎧⎭⎬⎫23符合题意；当a ≠0时,要使方程ax 2－3x ＋2＝0有实数根, 则Δ＝9－8a ≥0,解得a ≤98且a ≠0．9 8．综上所述,若集合A中至少有一个元素,则a≤。

高中数学预备知识

高中数学预备知识
1、数的基本概念：数的定义、正数、负数、整数、有理数、无理数、绝对值。

2、因式分解：分解因式、合并因式。

3、分数：定义、运算、约分、真分数、假分数、分数的乘法、分数的除法。

4、指数：定义、运算、科学计数法、幂的乘法、幂的除法。

5、根式：定义、运算、合并根式、分解根式。

6、平方根：定义、运算、合并平方根、分解平方根。

7、立方根：定义、运算、合并立方根、分解立方根。

8、比例：定义、比例的运算、比例的等价。

9、比例的应用：比例的判断、比例的解决。

10、方程：定义、一元一次方程的解法、一元二次方程的解法。

11、不等式：定义、不等式的解法、不等式的应用。

12、函数：定义、函数的概念、函数的表示法、函数的性质、函数的图像。

13、直线：定义、直线的性质、直线的方程、直线的图像。

14、圆：定义、圆的性质、圆的方程、圆的图像。

15、概率：定义、概率的计算、概率的应用。

《预备知识》课件

总结词
企业培训案例，展示如何将预备知识应用于实际工作场景。
详细描述
企业培训案例可以提供关于如何在实际工作场景中应用预备知识的具体实例。这些案例可以帮助学习者更好地理解预备知识在工作中的重要性和应用方式，并提供实用的培训方法和技巧。
教育机构的教学案例
总结词
教育机构的教学案例，提供不同教育背景下预备知识的应用情况。
工程学
工程学与《预备知识》中的许多应用密切相关，通过学习工程学可以更好地将理论知识应用于实际工程中。
持续关注学科动态
学术会议
参加学术会议能够了解最新的研究成果和动态，与同行交流心得和经验，不断更新自己的知识和技能。
学术期刊
定期阅读学术期刊能够了解最新的学术进展和趋势，掌握学科发展的方向和重点。
参加培训课程
STEP 01
培训机构
STEP 02
在职培训
参加专业培训机构提供的培训课程，系统学习预备知识。
STEP 03
学术交流
参加学术会议、研讨会等交流活动，与同行交流学习心得。
参加公司或组织提供的在职培训，提升专业技能和知识水平。
请教他人
导师指导
专家咨询
向导师请教，接受导师的指导和帮助。
《预备知识》ppt课件
• 预备知识的重要性 • 预备知识的获取途径 • 预备知识的应用场景 • 预备知识的积累方法 • 预备知识的拓展方向 • 预备知识的案例分析
目录
PartBiblioteka 01预备知识的重要性为后续课程做准备
确保学生具备足够的基础知识，以便更好地理解和掌握后续课程的内容。
帮助学生减少在后续课程中可能遇到的困难和障碍。
为学生提供一个平滑的学习过渡，使他们能够更好地适应课程的节奏和难度。

_新教材高中数学第一章预备知识1

N ，但不能表示为{x|x 为所有自然数}或{N }．
1．用描述法表示函数 y＝3x＋1 图象上的所有点的是
A．{x|y＝3x＋1}
B．{y|y＝3x＋1}
C．{(x，y)|y＝3x＋1}
D．{y＝3故可表示为{(x，y)|y＝3x＋1}，故选 C. 答案：C 2．用描述法表示不等式 4x－5＜7 的解集为________．
用描述法表示集合的注意点 (1)写清楚集合中的代表元素，如数或点等； (2)说明该集合中元素的共同特征，如满足的方程、不等式、函数或几何图形等； (3)所有描述的内容都要写在花括号内，用于描述内容的语言力求简洁、准确； (4)“{}”有“所有”“全体”的含义，因此自然数集可以表示为{x|x 为自然数}或
第一
章
预备知识
§1 集合 1．1 集合的概念与表示
第 2 课时集合的表示
语言是人与人之间相互联系的一种方式，同样的祝福又有着不同的表示方法．例如，简体中文中的“生日快乐”，用繁体中文为“生日快樂”，英文为“Happy Birthday”……
[问题] 对于一个集合，有哪些不同的表示方法呢？
知识点一列举法把集合中的元素__一__一__列__举__出来写在花括号“_{_}_”内表示集合的方法，
用区间表示数集的方法 (1)区间左端点值小于右端点值； (2)区间两端点之间用“，”隔开； (3)含端点值的一端用中括号，不含端点值的一端用小括号； (4)以“－∞”，“＋∞”为区间的一端时，这端必须用小括号．
1．区间(－3，2]用集合可表示为 A．{－2，－1，0，1，2}
[跟踪训练] B．{x|－3＜x＜2}
即kΔ≠＝0，（－8）2－4×k×16<0，解得 k>1.
综上，实数 k 的取值集合为{k|k＝0 或 k≥1}．

预备知识一

2020年预备党员知识题库

中考语文--初中语文文言文万能答题模板1

《预备知识》课件

预备知识

_新教材高中数学第一章预备知识1

2020_2021学年新教材高中数学第1章预备知识1集合1.2集合的基本关系学案含解析北师大版必修一

高中数学第一章预备知识1集合1.1集合的概念与表示2集合的表示同步高一第一册数学

高一第一章预备知识点

中专预备知识

预备知识

28' §3.2 古典概型预备知识(一)

随机过程-1预备知识

第1章预备知识

预备知识

新教材高中数学第一章预备知识1集合1-1集合的概念与表示第1课时集合的概念课件北师大版必修第一册

新教材高中数学第一章预备知识1集合 集合的概念与表示第2课时集合的表示素养作业北师大版必修第一册

高中数学预备知识

《预备知识》课件

_新教材高中数学第一章预备知识1

新教材高中数学第一章预备知识1集合集合的概念与表示第2课时集合的表示素养作业北师大版必修第一册