Matlab实验报告5
MATLAB实验报告

MATLAB实验报告一、实验目的本次 MATLAB 实验旨在深入了解和掌握 MATLAB 软件的基本操作和应用,通过实际编程和数据处理,提高解决问题的能力,培养编程思维和逻辑分析能力。
二、实验环境本次实验使用的是 MATLAB R2020a 版本,运行在 Windows 10 操作系统上。
计算机配置为英特尔酷睿 i5 处理器,8GB 内存。
三、实验内容(一)矩阵运算1、矩阵的创建使用直接输入、函数生成和从外部文件导入等方式创建矩阵。
例如,通过`1 2 3; 4 5 6; 7 8 9` 直接输入创建一个 3 行 3 列的矩阵;使用`ones(3,3)`函数创建一个 3 行 3 列元素全为 1 的矩阵。
2、矩阵的基本运算包括矩阵的加减乘除、求逆、转置等。
例如,对于两个相同维度的矩阵`A` 和`B` ,可以进行加法运算`C = A + B` 。
3、矩阵的特征值和特征向量计算通过`eig` 函数计算矩阵的特征值和特征向量,加深对线性代数知识的理解和应用。
(二)函数编写1、自定义函数使用`function` 关键字定义自己的函数,例如编写一个计算两个数之和的函数`function s = add(a,b) s = a + b; end` 。
2、函数的调用在主程序中调用自定义函数,并传递参数进行计算。
3、函数的参数传递了解值传递和引用传递的区别,以及如何根据实际需求选择合适的参数传递方式。
(三)绘图功能1、二维图形绘制使用`plot` 函数绘制简单的折线图、曲线等,如`x = 0:01:2pi; y = sin(x); plot(x,y)`绘制正弦曲线。
2、图形的修饰通过设置坐标轴范围、标题、标签、线条颜色和样式等属性,使图形更加清晰和美观。
3、三维图形绘制尝试使用`mesh` 、`surf` 等函数绘制三维图形,如绘制一个球面`x,y,z = sphere(50); surf(x,y,z)`。
(四)数据处理与分析1、数据的读取和写入使用`load` 和`save` 函数从外部文件读取数据和将数据保存到文件中。
基于matlab的实验报告

基于matlab的实验报告实验报告:基于MATLAB 的实验一、实验目的通过使用MATLAB 软件,掌握如何进行数据分析、图像处理、算法实现等一系列实验操作,提高实验者的实践能力和动手能力。
二、实验原理MATLAB 是一种在科学计算和技术开发领域广泛应用的计算机软件。
它能进行矩阵计算、绘制函数和数据图像、实现算法以及进行数据分析等。
通过掌握MATLAB 的使用,能够快速、高效地解决各种科学和工程问题。
三、实验内容1. 数据分析:使用MATLAB 的数据分析工具进行数据的导入、处理和分析。
2. 图像处理:利用MATLAB 的图像处理工具包对图像进行滤波、增强、分割等操作。
3. 算法实现:使用MATLAB 实现常用的算法,如排序、搜索、图像压缩等。
四、实验步骤1. 数据分析:(1)使用MATLAB 的读取数据函数将数据导入MATLAB 环境中。
(2)利用MATLAB 的数据处理函数进行数据清洗和预处理。
(3)使用MATLAB 的统计工具进行数据分析,如求平均值、标准差等。
(4)利用MATLAB 的绘图函数将分析结果可视化。
2. 图像处理:(1)使用MATLAB 的读取图像函数将图像导入MATLAB 环境中。
(2)利用MATLAB 的图像处理工具包进行滤波操作,如均值滤波、中值滤波等。
(3)使用MATLAB 的图像增强函数对图像进行锐化、变换等操作。
(4)利用MATLAB 的图像分割算法对图像进行分割。
3. 算法实现:(1)使用MATLAB 编写排序算法,如冒泡排序、快速排序等。
(2)使用MATLAB 编写搜索算法,如二分查找、线性搜索等。
(3)使用MATLAB 实现图像压缩算法,如离散余弦变换(DCT)。
五、实验结果实验中,我们使用MATLAB 完成了数据分析、图像处理和算法实现的一系列实验操作。
通过数据分析,我们成功导入了数据并对其进行了清洗和预处理,最后得到了数据的统计结果。
在图像处理方面,我们对图像进行了滤波、增强和分割等操作,最终得到了处理后的图像。
matlab仿真实验报告

matlab仿真实验报告Matlab仿真实验报告引言:Matlab是一种广泛应用于科学和工程领域的数值计算软件,它提供了强大的数学和图形处理功能,可用于解决各种实际问题。
本文将通过一个具体的Matlab 仿真实验来展示其在工程领域中的应用。
实验背景:本次实验的目标是通过Matlab仿真分析一个电路的性能。
该电路是一个简单的放大器电路,由一个输入电阻、一个输出电阻和一个放大倍数组成。
我们将通过Matlab对该电路进行仿真,以了解其放大性能。
实验步骤:1. 定义电路参数:首先,我们需要定义电路的各个参数,包括输入电阻、输出电阻和放大倍数。
这些参数将作为Matlab仿真的输入。
2. 构建电路模型:接下来,我们需要在Matlab中构建电路模型。
可以使用电路元件的模型来表示电路的行为,并使用Matlab的电路分析工具进行仿真。
3. 仿真分析:在电路模型构建完成后,我们可以通过Matlab进行仿真分析。
可以通过输入不同的信号波形,观察电路的输出响应,并计算放大倍数。
4. 结果可视化:为了更直观地观察仿真结果,我们可以使用Matlab的图形处理功能将仿真结果可视化。
可以绘制输入信号波形、输出信号波形和放大倍数的变化曲线图。
实验结果:通过仿真分析,我们得到了以下实验结果:1. 输入信号波形与输出信号波形的对比图:通过绘制输入信号波形和输出信号波形的变化曲线,我们可以观察到电路的放大效果。
可以看到输出信号的幅度大于输入信号,说明电路具有放大功能。
2. 放大倍数的计算结果:通过对输出信号和输入信号的幅度进行计算,我们可以得到电路的放大倍数。
通过比较不同输入信号幅度下的输出信号幅度,可以得到放大倍数的变化情况。
讨论与分析:通过对实验结果的讨论和分析,我们可以得出以下结论:1. 电路的放大性能:根据实验结果,我们可以评估电路的放大性能。
通过观察输出信号的幅度和输入信号的幅度之间的比值,可以判断电路的放大效果是否符合设计要求。
matlab实验报告总结精选

matlab实验报告总结电气工程学院自动化102班 2012年12月21日实验一 MATLAB环境的熟悉与基本运算一、实验目的1.熟悉MATLAB开发环境2.掌握矩阵、变量、表达式的各种基本运算二、实验基本知识1.熟悉MATLAB环境MATLAB桌面和命令窗口、命令历史窗口、帮助信息浏览器、工作空间浏览器、文件和搜索路径浏览器。
2.掌握MATLAB常用命令变量与运算符变量命名规则如下:变量名可以由英语字母、数字和下划线组成变量名应以英文字母开头长度不大于31个区分大小写MATLAB中设置了一些特殊的变量与常量,列于下表。
MATLAB运算符,通过下面几个表来说明MATLAB的各种常用运算符表2 MATLAB算术运算符表3 MATLAB关系运算符表4 MATLAB逻辑运算符表5 MATLAB特殊运算的一维、二维数组的寻访表6 子数组访问与赋值常用的相关指令格式的基本运算表7 两种运算指令形式和实质内涵的异同表的常用函数表8 标准数组生成函数表9 数组操作函数三、实验内容1、新建一个文件夹2、启动,将该文件夹添加到MATLAB路径管理器中。
3、保存,关闭对话框4、学习使用help命令,例如在命令窗口输入help eye,然后根据帮助说明,学习使用指令eye5、学习使用clc、clear,观察command window、command history和workspace等窗口的变化结果。
6、初步程序的编写练习,新建M-file,保存,学习使用MATLAB的基本运算符、数组寻访指令、标准数组生成函数和数组操作函数。
注意:每一次M-file的修改后,都要存盘。
练习A:help rand,然后随机生成一个2×6的数组,观察command window、command history和workspace等窗口的变化结果。
学习使用clc、clear,了解其功能和作用。
答:clc是清除命令窗体内容 clear是清除工作区间输入C=1:2:20,则C表示什么?其中i=1,2,3,?,10。
matlab实验五循环结构程序设计实验报告

实验五:循环结构程序设计实验报告一、实验目的1. 了解循环结构的基本概念和原理;2. 掌握使用Matlab进行循环结构程序设计的方法;3. 提高编程能力和问题解决能力。
二、实验内容1. 学习while循环和for循环的基本语法和用法;2. 设计并编写一些基于循环结构的Matlab程序;3. 分析程序运行结果并进行总结。
三、实验原理循环结构是程序设计中的重要组成部分,它可以让一段代码重复执行多次,从而简化程序的编写。
在Matlab中,循环结构主要有while 循环和for循环两种形式。
while循环在执行循环体前判断条件是否为真,只有条件为真时才会执行循环体;for循环则是指定循环的次数,每次迭代时执行一次循环体。
四、实验步骤与结果1. 编写一个使用while循环的程序,实现1~100的累加。
程序代码如下:```matlabsum = 0;i = 1;while i <= 100sum = sum + i;i = i + 1;enddisp(sum);```运行程序后,得到的结果为5050。
2. 编写一个使用for循环的程序,实现1~10的阶乘。
程序代码如下:```matlabresult = 1;for i = 1:10result = result * i;enddisp(result);```运行程序后,得到的结果为xxx。
五、实验总结通过本次实验,我深刻理解了循环结构的基本概念和原理,掌握了使用Matlab进行循环结构程序设计的方法。
在编写循环程序的过程中,我发现循环结构可以大大简化程序的编写,并且能够高效地处理重复性任务。
我也进一步提高了自己的编程能力和问题解决能力。
本次实验使我对Matlab中的循环结构有了更加深入的了解,我相信这对我的编程能力和日后的学习工作都将大有裨益。
六、实验感想和改进意见通过本次实验,我深刻认识到循环结构在程序设计中的重要性和灵活性。
循环结构能够帮助我们简化程序的编写,提高代码的重用性和可读性,因此在实际的程序设计中,合理地运用循环结构能够大大提高程序的效率和逻辑清晰度。
实验五+MATLAB数值计算(含实验报告)

实验五 MATLAB 数值计算一、实验目的1.掌握求数值导数和数值积分的方法。
2.掌握代数方程数值求解的方法。
3.掌握常微分方程数值求解的方法。
二、实验的设备及条件计算机一台(带有MATLAB7.0以上的软件环境)。
设计提示1.参考本节主要内容,学习并理解相关函数的含义及调用方法。
三、实验内容1.线性系统方程:分别使用左除(\)和求逆(inv )求解下面系统方程的解:⎪⎩⎪⎨⎧=+=+=++377251463c b b a c b a2. 数值积分:使用quad 和trapz 求解⎰-503/dx xe x 的数值积分,并与其解析解9243/5+--e 相比较;3. 请完成教材P154页中实验指导环节的实验内容第2题4. 请完成教材P155页中思考练习的第3题(1),并绘制解在该求解区间(即[0,5])上的图像;。
5、请完成教材P164页实验指导环节的实验内容第5题。
(提示:该函数的符号导数,可以通过函数diff 求得。
首先定义符号变表达式,如求sin(x)的一阶符号导数,可以先定义f=’sin(x)’;df=diff(f);可求得df=cos(x)。
其中df 即为函数f 的一阶符号导数)。
四、实验报告要求(包含预习报告要求和最终报告要求)1.实验名称2.实验目的3.实验设备及条件4.实验内容及要求5.实验程序设计指程序代码。
6.实验结果及结果分析实验结果要求必须客观,现象。
结果分析是对实验结果的理论评判。
7.实验中出现的问题及解决方法8. 思考题的回答五、实验报告的提交方式Word文档,命名方式:实验号_你的学号_姓名例如本次实验:实验一_000000001_张三.doc(信息101提交报告邮箱):E_mail: *******************(网络工程101提交作业邮箱):E_mail: *******************(注意网络班的M是大写的)下一次课前提交,过期不收!六、参考文献参考教材和Matlab帮助文件。
matlab 实验报告

matlab 实验报告Matlab 实验报告引言:Matlab(Matrix Laboratory)是一种强大的科学计算软件,它为科学家、工程师和研究人员提供了一个强大的计算环境。
本实验报告旨在介绍我对Matlab的实验结果和使用体验,以及对其优点和局限性的思考。
一、Matlab的基本功能和特点Matlab是一种高级编程语言和开发环境,它具有广泛的数学和工程计算功能。
通过Matlab,我可以进行矩阵运算、数值计算、数据可视化、算法开发等一系列操作。
Matlab的语法简洁易懂,可以快速实现复杂的计算任务。
此外,Matlab还提供了大量的工具箱,如信号处理、控制系统、图像处理等,使得各种领域的科学研究和工程应用变得更加便捷。
二、实验结果与应用案例在本次实验中,我选择了一个经典的数值计算问题——求解非线性方程。
通过Matlab的数值计算能力,我可以使用不同的迭代方法来求解方程的根。
在实验中,我使用了牛顿迭代法、二分法和割线法来求解方程。
通过对比这些方法的收敛速度和精度,我得出了不同方法的优缺点。
在实际应用中,Matlab可以广泛应用于信号处理、图像处理、数据分析等领域。
例如,在信号处理中,我可以使用Matlab的信号处理工具箱来进行滤波、频谱分析等操作。
在图像处理中,我可以利用Matlab的图像处理工具箱进行图像增强、边缘检测等操作。
这些应用案例充分展示了Matlab在科学计算和工程应用中的重要性和灵活性。
三、Matlab的优点1. 强大的计算功能:Matlab提供了丰富的数学和工程计算函数,可以高效地进行复杂的计算任务。
2. 简洁的语法:Matlab的语法简洁易懂,使得编程变得更加高效和便捷。
3. 丰富的工具箱:Matlab提供了大量的工具箱,覆盖了各种领域的科学计算和工程应用需求。
4. 可视化能力强:Matlab提供了丰富的绘图函数,可以直观地展示数据和计算结果。
四、Matlab的局限性1. 高昂的价格:Matlab是一款商业软件,其价格较高,对于个人用户而言可能不太容易承受。
matlab实验报告

matlab实验报告Matlab实验报告实验题目:利用Matlab进行数据处理与分析实验目的:通过使用Matlab进行数据处理与分析的实践,掌握Matlab的基本操作和数据处理的方法。
实验内容:1. 数据读取:从文件中读取原始数据,并进行初步的观察和分析。
2. 数据清洗:对原始数据进行清洗,包括去除空值、异常值等。
3. 数据可视化:利用Matlab的绘图函数,将数据可视化呈现,以方便对数据进行进一步的分析和理解。
4. 数据分析:对清洗后的数据进行统计分析,包括求平均值、方差、相关系数等。
5. 模型建立:根据数据分析的结果,建立合适的数学模型,并使用Matlab进行参数估计和模型验证。
6. 结果验证:利用实验数据和模型进行实验结果的对比,验证模型的准确性和可靠性。
实验步骤:1. 准备实验数据:从实验样本中获得原始数据,并将其存储为文本文件。
2. 使用Matlab导入数据:使用Matlab的数据导入函数,将文本文件中的数据导入到Matlab的工作空间中。
3. 数据分析与处理:使用Matlab的数据处理函数,对导入的数据进行清洗和处理,去除异常值和空值,并进行初步的数据观察和分析。
4. 数据可视化:利用Matlab的绘图函数,绘制数据的直方图、散点图、折线图等,以展示数据的分布和趋势。
5. 数据统计分析:使用Matlab的统计分析函数,对处理后的数据进行统计分析,包括计算平均值、方差、相关系数等。
6. 模型建立与验证:根据数据分析的结果,建立合适的数学模型,并使用Matlab进行参数估计和模型验证。
7. 结果对比和讨论:将实验结果与模型预测结果进行对比,并进行结果的讨论和分析。
8. 实验结论:总结实验结果并给出结论。
实验结果:根据实验数据的分析和处理,得出如下结论:1. 数据呈现正态分布,符合正态性假设。
2. 数据之间存在显著的正相关关系,相关系数为0.8,结果具有统计学意义。
3. 建立的数学模型与实验数据拟合良好,模型预测结果与实验结果吻合度高。
MATLAB上机实验报告

MATLAB上机实验报告实验一、实验目的--------------------------------------------------------------------------------------------------------3二、实验内容--------------------------------------------------------------------------------------------------------3三、实验步骤--------------------------------------------------------------------------------------------------------31. M 文件的编辑----------------------------------------------------------------------------------------------32. 程序流程控制结构---------------------------------------------------------------------------------------31) for 循环结构-----------------------------------------------------------------------------------------42) while 循环结构----------------------------------------------------------------------------------------5练习-----------------------------------------------------------------------------------------------------------53)if-else-end分支结构---------------------------------------------------------------------------------54)switc-case结构----------------------------------------------------------------------------------------63. 子函数和参数传递------------------------------------------------------------------------------------------6练习-----------------------------------------------------------------------------------------------------------74. 局部变量和全局变量--------------------------------------------------------------------------------------8 MATLAB上机练习6.1 M 文件--------------------------------------------------------------------------------------------8(1)脚本文件-----------------------------------------------------------------------------------------------------8(2)函数文件-----------------------------------------------------------------------------------------------------9(3)函数调用-----------------------------------------------------------------------------------------------------9 6.2 MATLAB 的程序控制结构( 1) for 循环----------------------------------------------------------------------------------------------------9(2) while 循环----------------------------------------------------------------------------------------------------12(3)if语句---------------------------------------------------------------------------------------------------------12(4)switch 语句-------------------------------------------------------------------------------------------------13(5)try 语句-----------------------------------------------------------------------------------------------------14(6)程序流的控制--------------------------------------------------------------------------------------------14 6.3 数据的输入与输出-----------------------------------------------------------------------------------14(1)键盘输入语句------------------------------------------------------------------------------------------14(2)屏幕输出语句---------------------------------------------------------------------------------------------14 6.4 MATLAB文件操作(1)fopen 语句-----------------------------------------------------------------------------------------------------15(2) fclose 语句-----------------------------------------------------------------------------------------------------15 6.5 面向对象编程--------------------------------------------------------------------------------------------15(1)创建类目录----------------------------------------------------------------------------------------------------15(2) 建立类的数据结构-----------------------------------------------------------------------------------------15(3)创建类的基本方法---------------------------------------------------------------------------------------------16 6.6 MATLAB 程序优化-----------------------------------------------------------------------------------------17 6.7程序调试------------------------------------------------------------------------------------------------------17 6.8 习题----------------------------------------------------------------------------------------------------------17实验五MATLAB 程序设计一、实验目的掌握MATLAB 程序设计的主要方法,熟练编写MATLAB 函数。
MATLAB实验报告

班级:通信班姓名:彭羊平学号: 222008315222033实验一:matlab的基本操作一、实验目的:1、了解MATLAB的集成环境,熟悉其基本操作。
2、了解MATLAB的基础知识,包括矩阵的建立、简单操作、逻辑操作和关系运算。
3、熟悉基本的数学函数和逻辑函数。
4、在命令窗口输入命令完成一些简单的功能,为MATLAB程序设计奠定基础。
二、实验内容:1、利用diag等函数产生下列矩阵:然后利用reshape函数将它们变换成行向量。
2、利用rand函数产生(0,1)间均匀分布的10*10随机矩阵A,然后统计A中大于等于0.6的元素的个数。
3、有一矩阵A,找出矩阵中值大于1的元素,并将它们重新排列成列向量B。
4、在一测量矩阵A(6*6),存在有奇异值(假设大于100的值为奇异值),编程实现删去奇异值所在的行。
三、实验结果:1、程序如下:a=fliplr(diag([8,-7,2])+diag([5,3],-1))a=reshape(a,1,9)b=diag([2,5,8])+diag([4],2)+diag([7],-2) b=reshape(b,1,9)结果如下:2、程序如下:A=rand(10)A=A>0.6sum(sum(A))结果如下:3、程序如下:A=fix(5*rand(5))a=A>1;K=find(a);for k=1:length(K)B(k)=A(K(k));endB=B'结果如下:4、程序如下:A=fix(100*rand(8))+5 B=A>100;k=find(any(B'))A(k,:)=0结果如下:班级:通信班姓名:彭羊平学号: 222008315222033实验二: matlab绘图(1)一、实验目的:1、了解MATLAB图形系统和各种图形函数。
2、熟悉MATLAB的基本图形操作,具备MATLAB画图能力。
3、熟悉各种数学函数,并通过图形函数画出。
(完整word)Matlab实验报告
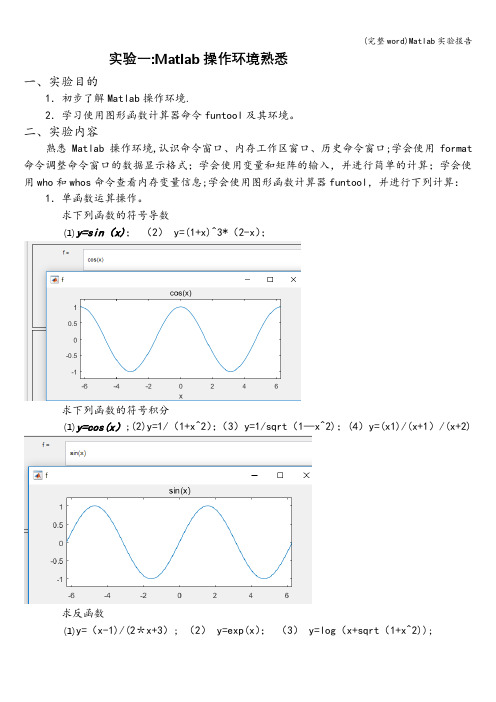
实验一:Matlab操作环境熟悉一、实验目的1.初步了解Matlab操作环境.2.学习使用图形函数计算器命令funtool及其环境。
二、实验内容熟悉Matlab操作环境,认识命令窗口、内存工作区窗口、历史命令窗口;学会使用format 命令调整命令窗口的数据显示格式;学会使用变量和矩阵的输入,并进行简单的计算;学会使用who和whos命令查看内存变量信息;学会使用图形函数计算器funtool,并进行下列计算:1.单函数运算操作。
求下列函数的符号导数(1)y=sin(x);(2) y=(1+x)^3*(2-x);求下列函数的符号积分(1)y=cos(x);(2)y=1/(1+x^2);(3)y=1/sqrt(1—x^2);(4)y=(x1)/(x+1)/(x+2)求反函数(1)y=(x-1)/(2*x+3); (2) y=exp(x);(3) y=log(x+sqrt(1+x^2));代数式的化简(1)(x+1)*(x-1)*(x-2)/(x-3)/(x—4);(2)sin(x)^2+cos(x)^2;(3)x+sin(x)+2*x—3*cos(x)+4*x*sin(x);2.函数与参数的运算操作。
从y=x^2通过参数的选择去观察下列函数的图形变化(1)y1=(x+1)^2(2)y2=(x+2)^2(3) y3=2*x^2 (4) y4=x^2+2 (5) y5=x^4 (6) y6=x^2/2 3.两个函数之间的操作求和(1)sin(x)+cos(x) (2) 1+x+x^2+x^3+x^4+x^5乘积(1)exp(—x)*sin(x) (2) sin(x)*x商(1)sin(x)/cos(x); (2) x/(1+x^2); (3) 1/(x—1)/(x—2); 求复合函数(1)y=exp(u) u=sin(x) (2) y=sqrt(u) u=1+exp(x^2)(3) y=sin(u) u=asin(x) (4) y=sinh(u) u=-x实验二:MATLAB基本操作与用法一、实验目的1.掌握用MATLAB命令窗口进行简单数学运算。
(最新版)MATLAB实验报告

实验一典型环节的MATLAB仿真一、实验目的1.熟悉MATLAB桌面和命令窗口,初步了解SIMULINK功能模块的使用方法。
2.通过观察典型环节在单位阶跃信号作用下的动态特性,加深对各典型环节响应曲线的理解。
3.定性了解各参数变化对典型环节动态特性的影响。
二、SIMULINK的使用MATLAB中SIMULINK是一个用来对动态系统进行建模、仿真和分析的软件包。
利用SIMULINK功能模块可以快速的建立控制系统的模型,进行仿真和调试。
1.运行MATLAB软件,在命令窗口栏“>>”提示符下键入simulink命令,按Enter 键或在工具栏单击按钮,即可进入如图1-1所示的SIMULINK仿真环境下。
2.选择File菜单下New下的Model命令,新建一个simulink仿真环境常规模板。
3.在simulink仿真环境下,创建所需要的系统。
以图1-2所示的系统为例,说明基本设计步骤如下:1)进入线性系统模块库,构建传递函数。
点击simulink下的“Continuous”,再将右边窗口中“Transfer Fen”的图标用左键拖至新建的“untitled”窗口。
2)改变模块参数。
在simulink仿真环境“untitled”窗口中双击该图标,即可改变传递函数。
其中方括号内的数字分别为传递函数的分子、分母各次幂由高到低的系数,数字之间用空格隔开;设置完成后,选择OK,即完成该模块的设置。
3)建立其它传递函数模块。
按照上述方法,在不同的simulink的模块库中,建立系统所需的传递函数模块。
例:比例环节用“Math”右边窗口“Gain”的图标。
4)选取阶跃信号输入函数。
用鼠标点击simulink下的“Source”,将右边窗口中“Step”图标用左键拖至新建的“untitled”窗口,形成一个阶跃函数输入模块。
5)选择输出方式。
用鼠标点击simulink下的“Sinks”,就进入输出方式模块库,通常选用“Scope”的示波器图标,将其用左键拖至新建的“untitled”窗口。
matlab 实验报告

matlab 实验报告Matlab实验报告引言:Matlab是一种强大的数值计算和可视化软件,广泛应用于科学、工程和经济等领域。
本实验报告将介绍我在使用Matlab进行实验过程中的一些经验和结果。
实验一:矩阵运算在这个实验中,我使用Matlab进行了矩阵运算。
首先,我创建了一个3x3的矩阵A和一个3x1的矩阵B,并进行了矩阵相乘运算。
通过Matlab的矩阵乘法运算符*,我得到了一个3x1的结果矩阵C。
接着,我对矩阵C进行了转置操作,得到了一个1x3的矩阵D。
最后,我计算了矩阵C和矩阵D的点积,并将结果输出。
实验二:数据可视化在这个实验中,我使用Matlab进行了数据可视化。
我选择了一组实验数据,包括时间和温度两个变量。
首先,我将数据存储在一个矩阵中,并使用Matlab的plot函数将时间和温度之间的关系绘制成曲线图。
接着,我使用Matlab的xlabel、ylabel和title函数添加了横轴、纵轴和标题。
最后,我使用Matlab的legend函数添加了图例,以便更好地理解图表。
实验三:数值积分在这个实验中,我使用Matlab进行了数值积分。
我选择了一个函数f(x)进行积分计算。
首先,我使用Matlab的syms函数定义了符号变量x,并定义了函数f(x)。
接着,我使用Matlab的int函数对函数f(x)进行积分计算,并将结果输出。
为了验证结果的准确性,我还使用了Matlab的diff函数对积分结果进行了求导操作,并与原函数f(x)进行了比较。
实验四:信号处理在这个实验中,我使用Matlab进行了信号处理。
我选择了一个音频文件,并使用Matlab的audioread函数读取了该文件。
接着,我使用Matlab的fft函数对音频信号进行了傅里叶变换,并将结果绘制成频谱图。
为了进一步分析信号的特征,我还使用了Matlab的spectrogram函数绘制了信号的时频图。
通过对信号的频谱和时频图的观察,我可以更好地理解信号的频率和时域特性。
控制系统计算机仿真(matlab)实验五实验报告
实验五 控制系统计算机辅助设计一、实验目的学习借助MATLAB 软件进行控制系统计算机辅助设计的基本方法,具体包括超前校正器的设计,滞后校正器的设计、滞后-超前校正器的设计方法。
二、实验学时:4 学时 三、实验原理1、PID 控制器的设计PID 控制器的数学模型如公式(5-1)、(5-2)所示,它的三个特征参数是比例系数、积分时间常数(或积分系数)、微分时间常数(或微分系数),因此PID 控制器的设计就是确定PID 控制器的三个参数:比例系数、积分时间常数、微分时间常数。
Ziegler (齐格勒)和Nichols (尼克尔斯)于1942提出了PID 参数的经验整定公式。
其适用对象为带纯延迟的一节惯性环节,即:s e Ts Ks G τ-+=1)( 5-1式中,K 为比例系数、T 为惯性时间常数、τ为纯延迟时间常数。
在实际的工业过程中,大多数被控对象数学模型可近似为式(5-1)所示的带纯延迟的一阶惯性环节。
在获得被控对象的近似数学模型后,可通过时域或频域数据,根据表5-1所示的Ziegler-Nichols 经验整定公式计算PID 参数。
表控制器的参数。
假定某被控对象的单位阶跃响应如图5-4所示。
如果单位阶跃响应曲线看起来近似一条S 形曲线,则可用Ziegler-Nichols 经验整定公式,否则,该公式不适用。
由S 形曲线可获取被控对象数学模型(如公式5-1所示)的比例系数K 、时间常数T 、纯延迟时间τ。
通过表5-1所示的Ziegler-Nichols 经验整定公式进行整定。
如果被控对象不含有纯延迟环节,就不能够通过Ziegler-Nichols 时域整定公式进行PID 参数的整定,此时可求取被控对象的频域响应数据,通过表5-1 所示的Ziegler-Nichols 频域整定公式设计PID 参数。
如果被控对象含有纯延迟环节,可通过pade 命令将纯延迟环节近似为一个四阶传递函数模型,然后求取被控对象的频域响应数据,应用表5-1求取PID 控制器的参数。
matlab实验报告

matlab实验报告Matlab实验报告引言:Matlab(Matrix Laboratory)是一种高级的计算机编程语言和环境,主要用于数值计算、数据分析和可视化。
它的功能强大,被广泛应用于科学研究、工程设计和教学实验等领域。
本实验报告将介绍我在使用Matlab进行实验过程中的一些经验和收获。
一、Matlab的基本语法和数据类型Matlab的语法与其他编程语言相比较简单,但仍然需要掌握一些基本的语法规则。
例如,Matlab中的变量命名不区分大小写,但建议使用小写字母来命名变量。
Matlab支持多种数据类型,包括数值型、字符型、逻辑型等。
在实验中,我常常使用数值型数据进行计算和分析。
二、Matlab中的矩阵运算矩阵运算是Matlab的重要特性之一,它使得处理大量数据变得更加高效和简便。
我在实验中经常使用矩阵运算来进行数据的处理和分析。
例如,我可以使用矩阵乘法来计算两个矩阵的乘积,或者使用矩阵的转置来进行数据的重排和变换。
Matlab还提供了丰富的矩阵运算函数,如求逆矩阵、特征值分解等,这些函数大大简化了复杂计算的过程。
三、Matlab的数据可视化Matlab提供了强大的数据可视化功能,可以帮助我们更直观地理解和展示数据。
在实验中,我常常使用Matlab绘制曲线图、散点图和柱状图等,以便更清晰地观察数据的分布和趋势。
Matlab的绘图函数丰富多样,可以根据不同的需求选择合适的图形类型和样式。
此外,Matlab还支持图像处理和三维可视化等高级功能,这些功能在科学研究和工程设计中有着广泛的应用。
四、Matlab的编程和调试Matlab不仅是一种计算工具,还是一种编程语言。
通过编写脚本和函数,我们可以实现更复杂的计算和操作。
在实验中,我常常使用Matlab编写自定义函数来实现特定的功能。
编程过程中,我注意到Matlab的调试功能非常强大,可以帮助我们找出代码中的错误和问题。
Matlab提供了断点调试、变量监视和错误提示等功能,这些功能对于提高代码的可靠性和效率非常有帮助。
matlab实验报告

matlab实验报告实验名称:MATLAB数值分析实验报告摘要:本实验通过使用MATLAB软件,实现了一些数值分析中重要的算法,包括线性方程组求解、非线性方程求根、数值积分与微分以及常微分方程求解。
在算法实现的过程中,通过观察输出结果验证了算法的正确性和可靠性,并探讨了一些算法实现中需要注意的问题。
1.线性方程组求解线性方程组求解是数值分析中的重要算法之一,是很多数学问题的基础。
本实验中使用了三种求解线性方程组的算法:高斯消元法、LU分解法和共轭梯度法。
在实验中,我们需要注意选取矩阵的条件数,使用一些特殊矩阵,如对角矩阵、三对角矩阵和希尔伯特矩阵等来验证算法的正确性。
2.非线性方程求根非线性方程求根是MATLAB中一个非常实用的函数,能够快速解决大量的非线性方程。
本实验中,我们更深入地探讨了二分法、牛顿法和割线法等算法,通过实现代码,实现了对非线性方程的求解。
同时,对不同的算法进行比较,从而选择合适的算法。
3.数值积分与微分数值积分与微分是宏观物理中需要用到的重要数学问题之一。
本实验中,我们使用了梯形法、辛普森法和龙贝格法等多种数值积分算法实现了函数的数值积分。
同时,也对数值微分的误差和稳定性进行了研究和探讨。
4.常微分方程求解常微分方程求解是MATLAB中最常用的功能之一。
本实验中,我们实现了欧拉法、龙格-库塔法等常微分方程求解算法。
并不断尝试对算法进行改进,提高其效率和精度。
实验结果表明,使用MATLAB实现数值分析算法是非常可靠和高效的。
同时,也需要注意在算法实现中注意问题和选择合适的算法。
matlab 模拟 实验报告

matlab 模拟实验报告《利用Matlab模拟的实验报告》摘要:本实验利用Matlab软件对某一特定系统进行了模拟实验。
通过对系统的建模和仿真,我们得出了一些有价值的结论,并对系统的性能进行了评估。
本文将详细介绍实验的目的、方法、结果和分析,以及对实验结果的讨论和总结。
1. 引言Matlab是一种强大的数学建模和仿真工具,广泛应用于工程、科学和技术领域。
利用Matlab进行系统仿真可以帮助我们更好地理解系统的行为和性能,优化系统设计,并预测系统在不同条件下的表现。
本实验旨在利用Matlab对某一特定系统进行仿真,以验证系统的性能和稳定性。
2. 实验目的本实验的主要目的是利用Matlab对某一特定系统进行建模和仿真,分析系统的动态响应和稳定性,并评估系统的性能。
具体来说,我们将通过仿真实验探讨系统的频率响应、阶跃响应和脉冲响应,以及系统的稳定性和鲁棒性。
3. 实验方法首先,我们对系统进行了建模,包括系统的传递函数、状态空间模型等。
然后,利用Matlab软件进行仿真实验,分别对系统的频率响应、阶跃响应和脉冲响应进行了分析。
最后,我们对仿真结果进行了统计和评估,得出了一些有价值的结论。
4. 实验结果与分析通过Matlab的仿真实验,我们得到了系统的频率响应曲线、阶跃响应曲线和脉冲响应曲线。
通过对这些曲线的分析,我们可以得出系统的动态特性和稳定性。
同时,我们还对系统的性能进行了评估,包括系统的超调量、调节时间等指标。
5. 结果讨论与总结通过对实验结果的讨论和总结,我们得出了一些结论和建议。
我们对系统的性能和稳定性进行了评估,发现系统在某些条件下存在一些问题,提出了一些建议和改进措施。
同时,我们也对Matlab软件在系统仿真中的应用进行了总结和展望。
结论本实验利用Matlab对某一特定系统进行了建模和仿真,得出了一些有价值的结论。
通过对系统的动态响应和稳定性进行分析,我们发现了系统存在的一些问题,并提出了一些建议和改进措施。
MATLAB上机实验实验报告

MATLAB上机实验一一、实验目的初步熟悉MATLAB 工作环境,熟悉命令窗口,学会使用帮助窗口查找帮助信息; 命令窗口二、实验内容1 熟悉MATLAB 平台的工作环境;2 熟悉MATLAB 的5 个工作窗口;3 MATLAB 的优先搜索顺序;三、实验步骤1. 熟悉MATLAB 的5 个基本窗口①Command Window 命令窗口②Workspace 工作空间窗口③Command History 命令历史记录窗口④Current Directory 当前目录窗口⑤Help Window 帮助窗口1 命令窗口Command Window;在命令窗口中依次输入以下命令:>>x=1>> y=1 2 34 5 67 8 9;>> z1=1:10,z2=1:2:5;>> w=linspace1,10,10;>> t1=ones3,t2=ones1,3,t3=ones3,1>> t4=ones3,t4=eye4x =1z1 =1 2 3 4 5 6 7 8 9 10t1 =1 1 11 1 11 1t2 =1 1 1t3 =111t4 =1 1 11 1 11 1 1t4 =1 0 0 00 1 0 00 0 1 00 0 0 1思考题:①变量如何声明,变量名须遵守什么规则、是否区分大小写;答:1变量声明1.局部变量每个函数都有自己的局部变量,这些变量只能在定义它的函数内部使用;当函数运行时,局部变量保存在函数的工作空间中,一旦函数退出,这些局部变量将不复存在;脚本没有输入输出参数,由一系列MATLAB命令组成的M文件没有单独的工作空间,只能共享调用者的工作空间;当从命令行调用,脚本变量存在基本工作空间中;当从函数调用,脚本变量存在函数空间中;2.全局变量在函数或基本工作空间内,用global声明的变量为全局变量;例如声明a为全局变量:>>global a声明了全局变量的函数或基本工作空间,共享该全局变量,都可以给它曲赋值;如果函数的子函数也要使用全局变量,也必须用global声明;3.永久变量永久变量用persistent声明,只能在M文件函数中定义和使用,只允许声明它的函数存取;当声明它的函数退出时,MATLAB不会从内存中清除它,例如声明a为永久变量:>>persistent a2变量命名规则如下:始于字母,由字母、数字或下划线组成;区分大小写;可任意长,但使用前N个字符;N与硬件有关,由函数namelengthmax返回,一般N=63;不能使用关键字作为变量名关键字在后面给出;避免使用函数名作为变量名;如果变量采用函数名,该函数失效;3区分大小写②试说明分号、逗号、冒号的用法;答:分号:加上分号“;”其作用是将计算机结果存入内存,但不显示在屏幕上,反之,语句结尾若不加“;”,则表示在语句执行后,在将计算结果存入内存的同时,还将运算结果显示出来;逗号:分割列表冒号:从什么到什么,比如1:10意思是——1到10③linspace 称为“线性等分”函数,说明它的用法;可使用help命令,格式如下:>>help linspace④说明函数ones 、zeros 、eye 的用法;答;1ones函数:全部元素都为1的常数矩阵; 2zeros函数:全部元素都为0的矩阵; 3eye函数:单位矩阵;4linspace函数:如a=linspacen1,n2,n3,表示在线性空间上,行矢量的值从n1到n22 工作空间窗口Workspace;单击工作空间窗口右上角的按钮,将其从MATLAB 主界面分离出来;①在工作空间查看各个变量,或在命令窗口用who, whos注意大小写查看各个变量;②在工作空间双击变量,弹出Array Editor 窗口数组编辑器窗口,即可修改变量;③使用save 命令把工作空间的全部变量保存为文件;>>save④输入下列命令:>>clear all %清除工作空间的所有变量观察工作空间的变量是否被清空;使用load 命令把刚才保存的变量载入工作空间;>>load⑤清除命令窗口命令:>>clc3 历史命令窗口Command History;打开历史命令窗口,可以看到每次运行MATLAB 的时间和曾在命令窗口输入过的命令,练习以下几种利用历史命令窗口重复执行输入过的命令的方法;①在历史命令窗口中选中要重复执行的一行或几行命令,右击,出现快捷菜单,选择Copy,然后再Paste 到命令窗口;②在历史命令窗口中双击要执行的一行命令,或者选中要重复执行的一行或几行命令后,用鼠标将其拖动到命令窗口中执行;③在历史命令窗口中选中要重复执行的一行或几行命令,右击,出现快捷菜单,选择Evaluate Selection,也可以执行;④或者在命令窗口使用方向键的上下键得到以前输入的命令;例如,按方向键“↑”一次,就重新将用户最后一次输入的命令调到MATLAB 提示符下;重复地按方向上键“↑”,就会在每次按下的时候调用再往前一次输入的命令;类似地,按方向键“↓”的时候,就往后调用一次输入的命令;按方向键“←”或者方向键“→”就会在提示符的命令中左右移动光标,这样用户就可以用类似于在字处理软件中编辑文本的方法编辑这些命令;4 当前目录命令窗口Current Directory;MATLAB 的当前目录即是系统默认的实施打开、装载、编辑和保存文件等操作时的文件夹;打开当前目录窗口后,可以看到用“save”命令所保存的文件是保存在目录C:\MATLAB6p5\work 下;5 帮助窗口Help Window;单击工具栏的图标,或选择菜单View|Help,或选择菜单Help|MATLAB Help 都能启动帮助窗口;①通过Index 选项卡查找log2函数的用法,在Search index for 栏中输入需要查找的词汇“log2”,在左下侧就列出与之最匹配的词汇条目,选择“log21”,右侧的窗口就会显示相应的内容;②也可以通过Search 选项卡查找log2 函数的用法;Search 选项卡与Index 选项卡不同,Index 只在专用术语表中查找,而Search 搜索的是整个HTML 帮助文件;2. MATLAB 的数值显示格式设置屏幕显示方式有紧凑Compact和松散Loose两种,其中Loose 为默认方式;>>a=ones1,30>>format compact>>a数字显示格式有short、long、short e、long e 等,请参照教材的列表练习一遍;>>format long>>pi>>format short>>pi>>format long>>pi>>format +>>pi>>-pi3. 变量的搜索顺序在命令窗口中输入以下指令:>>pi>>sinpi;>>exist'pi'>>pi=0;>>exist'pi'>>pi>>clear pi>>exist'pi'>>pi思考题:① 3 次执行exist'pi'的结果一样吗如果不一样,试解释为什么答:不一样,pi原来是库存函数,但是如果被赋值则系统默认被赋予的值为pi后来的值,但是当执行clear pi之后所赋的值被清空,因此pi的值又成为②圆周率pi 是系统的默认常量,为什么会被改变为0答:pi原来是库存函数,但是如果被赋值则系统默认被赋予的值为pi后来的值,但是当执行clear pi之后所赋的值被清空,因此pi的值又成为实验二 MATLAB语言基础一、实验目的基本掌握MATLAB向量、矩阵、数组的生成及其基本运算区分数组运算和矩阵运算、常用的数学函数;交接字符串的操作;二、实验内容1 向量的生成和运算;2 矩阵的创建、引用和运算;3 多维数组的创建及运算;4 字符串的操作;三、实验步骤1.向量的生成和运算1 向量的生成直接输入法:A =2 3 4 5 6>> B=1;2;3;4;5B =12345冒号生成发:>> A=1:2:10 ,B=1:10 ,C=10:-1:1A =1 3 5 7 9B =1 2 3 4 5 6 7 8 9 10C =10 9 8 7 6 5 4 3 2 1函数法:Linspace 是线性等分函数,logspace 是对数等分函数;>> A=linspace1,10 ,B=linspace1,30,10A =Columns 1 through 9Columns 10 through 18Columns 19 through 27Columns 28 through 36Columns 37 through 45Columns 46 through 54Columns 55 through 63Columns 64 through 72Columns 73 through 81Columns 82 through 90Columns 91 through 99Column 100B =Columns 1 through 9Column 10>> A=logspace0,4,5A =1 10 100 1000 10000练习:使用logspace 创建1-4 的有10个元素的行向量;答案:>> A=logspace1,10,4piA =+010Columns 1 through 9Columns 10 through 122 向量的运算维数相同的行向量只见可以相加减,维数相同的列向量也可以相加减,标量可以与向量直接相乘除;>> A=1 2 3 4 5, B=3:7,A =1 2 3 4 5B =3 4 5 6 7>> AT=A', BT=B',AT =12345BT =34567>> E1=A+B, E2=A-BE1 =4 6 8 10 12E2 =-2 -2 -2 -2 -2 >> F=AT-BT,F =-2-2-2-2-2>> G1=3A, G2=B/3,G1 =3 6 9 12 15G2 =向量的点积与叉积运算;>> A=ones1,10;B=1:10; BT=B';>> E1=dotA,BE1 =55>> E2=ABTE2 =55>> clear>> A=1:3,B=3:5,A =1 2 3B =3 4 5>> E=crossA,BE =-2 4 -22.矩阵的创建、引用和运算1 矩阵的创建和引用矩阵是由nm 元素构成的矩阵结构,行向量和列向量是矩阵的特殊形式;直接输入法:>> A=1 2 3;4 5 6A =1 2 3 4 5 6 >> B= 1 4 72 5 83 6 9B =1 4 72 5 83 6 9 >> A1ans =1>> A4:endans =5 36 >> B:,1ans =123>> B:ans =123456789>> B5ans =5抽取法>> clear>> A=1 2 3 4;5 6 7 8;9 10 11 12;13 14 15 16A =1 2 3 45 6 7 89 10 11 1213 14 15 16>> B=A1:3,2:3B =2 36 710 11>> C=A1 3,2 4C =2 410 12>> A1 3;2 4ans =1 95 13函数法:>> A=ones3,4A =1 1 1 11 1 1 11 1 1 1>> B=zero3Undefined function or method 'zero' for input arguments of type 'double'. >> B=zeros3B =0 0 00 0 00 0 0>> C=eyes3,2Undefined function or method 'eyes' for input arguments of type 'double'. >> C=eye3,2C =1 00 10 0>> D=magic3D =8 1 63 5 74 9 2拼接法>> clear>> A=ones3,4A =1 1 1 11 1 1 1>> B=zeros3B =0 0 00 0 00 0 0>> C=eye4C =1 0 0 00 1 0 00 0 1 00 0 0 1>> D=A BD =1 1 1 1 0 0 0 1 1 1 1 0 0 0 1 1 1 1 0 0 0 >> F=A;CF =1 1 1 11 1 1 11 1 1 10 1 0 0 0 0 1 0 0 0 0 1 拼接函数和变形函数法:>> clear>> A=0 1;1 1A =0 11 1>> B=2ones2B =2 22 2>> cat 1,A,B,Aans =0 11 12 22 20 11 1>> cat 2 A,B,Acat 2 A,B,AError: Unexpected MATLAB expression.>> cat2,A,B,Aans =0 1 2 2 0 11 12 2 1 1>> repmatA,2,2ans =0 1 0 11 1 1 10 1 0 11 1 1 1>> repmatA,2ans =0 1 0 11 1 1 10 1 0 11 1 1 1练习:使用函数法、拼接法、拼接函数法和变形函数法,按照要求创建以下矩阵:A为43⨯的3⨯的单位矩阵、D为33⨯的0矩阵/C为33⨯的全1矩阵、B为3魔方阵、E由C 和D纵向拼接而成,F抽取E的2---5行元素生成、G由F经变形为46⨯的大3⨯的矩阵而得、以G为子矩阵用复制函数repmat生成8矩阵H;答案:>> A=ones3,4A =1 1 1 11 1 1 11 1 1 1>> B=zeros3,3B =0 0 00 0 00 0 0>> C=eye3C =1 0 00 1 00 0 1>> D=magic3D =8 1 63 5 74 9 2>> E=C;DE =1 0 00 1 00 0 18 1 63 5 74 9 2>> F=2:5,:F=2:5,:Error: Expression or statement is incorrect--possibly unbalanced , {, or . >> F=E2:5,:F =0 1 00 0 18 1 63 5 7>> G=respaceE,3,4Undefined command/function 'respace'.>> G=respaceF,3,4Undefined command/function 'respace'.>> G=reshapeF,3,4G =0 3 1 10 1 5 68 0 0 7>> H=repmatG,2,2H =0 3 1 1 0 3 1 1 0 1 5 6 0 1 5 6 8 0 0 7 8 0 0 7 0 3 1 1 0 3 1 1 0 1 5 6 0 1 5 6 8 0 0 7 8 0 0 7 2)矩阵的运算矩阵的加减、数乘与乘法已知矩阵:>> A=1 23 -1,A =1 23 -1>> B=-1 01 2B =-1 01 2>> A+Bans =0 24 1>> 2Aans =2 46 -2>> 2A-3Bans =5 43 -8>> ABans =1 4-4 -2矩阵的逆矩阵>> format rat;A=1 0 1;2 1 2;0 4 61 0 12 1 2 0 4 6 >> A1=invAA1 =-1/3 2/3 -1/6 -2 1 0 4/3 -2/3 1/6 >> AA1ans =1 0 0 0 1 0 0 0 1 矩阵的除法>> a=1 2 1;3 1 4;2 2 1,b=1 1 2,d=b'a =1 2 1 3 1 42 2 1b =1 1 2112>> c1=binva,c2=b/ac1 =6/7 3/7 -4/7 c2 =6/7 3/7 -4/7 >> c3=invad, c4=a\bc3 =12/7-4/7Error using ==> mldivideMatrix dimensions must agree.>> c3=invad, c4=a\dc3 =12/7-4/7c4 =12/7-4/7练习:按下列要求求出各种的矩阵运算的值求矩阵的秩、特征值和特征向量、矩阵的乘幂与开方;矩阵的指数与对数矩阵的提取与翻转答案:>> A=6 3 4 3-2 5 7 -48 -1 -3 -7A =6 3 4 3-2 5 7 -48 -1 -3 -7>> B=rankAB =3>> rb=rankArb =3>> X,Lamda=eigAError using ==> eigMatrix must be square.>> X,Lamda=eigsAError using ==> eigsA must be a square matrix or a function which computes Ax. >> C=6 3 4-2 5 78 -1 -3C =6 3 4-2 5 78 -1 -3>> X,Lamda=eigsCX =Lamda =0 00 00 0>> X,Lamda=eigCX =Lamda =0 0 0 0 0 0 >> X,Lamda=eigCX =Lamda =0 0 0 0 0 0 >> D=A^2Error using ==> mpower Matrix must be square. >> D=C^2D =34 12 626 22 34>> E=sqrtmCE =+ - -+ - -- + +>> F=expmCF =+004>> G=logmCWarning: Principal matrix logarithm is not defined for A with nonpositive real eigenvalues. A non-principal matrix logarithm is returned.> In funm at 153In logm at 27G =+ - -- + + >> H=fliplrCH =4 3 6 75 -2 -3 -1 8 >> I=triuCI =6 3 4 0 57 0 0 -3 >> J=trilCJ =6 0 0 -2 5 0 8 -1 -3 >> K=diagCK =65-33.多维数组的创建及运算1)多维数组的创建>> A1=1,2,3;4 5 6;7,8,9;A2=reshape10:18,3,3 A2 =10 13 1611 14 1712 15 18>> T1:,:,1=ones3;T1:,:,2=zeros3T1:,:,1 =1 1 11 1 11 1 1T1:,:,2 =0 0 00 0 00 0 0>> T2=ones3,3,2T2:,:,1 =1 1 11 1 11 1 1T2:,:,2 =1 1 11 1 11 1 1>> T3=cat3,A1,A2,T4=repmatA1,1,1,2T3:,:,1 =1 2 34 5 67 8 9T3:,:,2 =10 13 1611 14 1712 15 18T4:,:,1 =1 2 34 5 67 8 9T4:,:,2 =1 2 34 5 67 8 92)多维数组的创建数组运算用小圆点加在运算符的前面表示,以区分矩阵的运算;特点是两个数组相对应的元素进行运算;>> A=1:6;B=ones1,6;>> C1=A+B,C2=A-BC1 =2 3 4 5 6 7C2 =0 1 2 3 4 5 >> C3=A.B,C4=B./A,C5=A.\BC3 =1 2 3 4 5 6C4 =C5 =关系运算或逻辑运算的结果都是逻辑值;>> I=A>3,C6=AII =0 0 0 1 1 1C6 =4 5 6>> A1=A-3,I2=A1&AA1 =-2 -1 0 1 2 3 I2 =1 1 0 1 1 1>> I3=~II3 =1 1 1 0 0 0 4.字符串的操作1 字符串的创建>> S1='Ilike MATLAB'S1 =Ilike MATLAB>> S2='I''m a stuent.'S2 =I'm a stuent.>> S3=S2,'and',S1S3 =I'm a MATLAB2)求字符串长度>> lengthS1ans =12>> sizeS1ans =1 123)字符串与一维数值数组的相互转换>> CS1=absS1CS1 =73 108 105 107 101 32 77 65 84 76 65 66>> CS2=doubleS1CS2 =73 108 105 107 101 32 77 65 84 76 65 66>> charCS2ans =Ilike MATLAB>> setstrCS2ans =Ilike MATLAB练习:用char 和向量生成的方法创建如下字符串AaBbCc......XxYyZz.>> S1=65:90;S2=97:122;>> C=S1;S2;>> C=C:';>> S3=doubleC;charS3ans =AaBbCcDdEeFfGgHhIiJjKkLlMmNnOoPpRrSsTtUuVvWwXxYyZz实验三 MALTAB数值运算一、实验目的掌握MATLAB的数值运算及其运算中所用到的函数,掌握结构数组和细胞数组的操作;二、实验内容1)多项式运算;2)多项式插值和拟合;3)数值为积分;4)结构数组和细胞数组;三、实验步骤1、多项式运算1)多项式表示;在MATLAB中,多项式表示成向量的形式;如:432S S S+-+在MATLAB中表示为359>> s=1 3 -5 0 92)多项式的加减法相当于向量的加减法,但必须注意阶次要相同;如不同,低阶次的要补0;如多项式23547+-++相加;s s s s++与多项式432239s s>> s1=0 0 2 3 11>> s2=1 2 -5 4 7>> s3=s1+s2答;s1 =0 0 2 3 11s2 =1 2 -5 4 7s3 =1 2 -3 7 183)多项式的乘、除法分别用函数conv和的deconv实现; >> s1=2 3 11>> s2=1 3 -5 4 7>> s3=convs1,s2>> s4=deconvs3,s1答;s1 =2 3 11s2 =1 3 -5 4 7s3 =2 9 10 26 -29 65 77s4 =1 3 -5 4 74)多项式求根用函数roots;>> s1=2 4 2>> rootss1答;s1 =2 4 2ans =-1-15)多项式求值用函数polyval>> s1=2 4 1 -3>> polyvals1,3>> x=1:10>> y=polyvals1,x答;s1 =2 4 1 -3ans =90x =1 2 3 4 5 6 7 8 9 10y =Columns 1 through 84 31 90 193 352 579 886 1285 Columns 9 through 10练习:求23(1)(3)(1)21s s ss s+++++的“商”及余数;>> s1=1 0 1;s2=1 3;s3=1 1;>> s4=1 0 2 1;>> q,r=deconvconvconvs1,s2,s3,s4答;q =1 4r =0 0 2 -5 -12、多项式插值和拟合有一组实验数据如附表1-1所示;附表1-1分别用拟合二阶至三阶和插值线性和三次样条的方法来估算X=时Y的值;以下是实现一阶拟合的语句;>> x=1:10>> y=16 32 70 142 260 436 682 1010 1342 1960>> p1=polyfitx,y,1 %一阶拟合>> y1=polyvalp1, %计算多项式P1在x=的值答;x =1 2 3 4 5 6 7 8 9 10y =Columns 1 through 816 32 70 142 260 436 682 1010Columns 9 through 101342 1960p1 =y1 =+0033、数值微积分1)差分使用diff函数实现;>> x=1:2:9>> diffx答;x =1 3 5 7 9ans =2 2 2 22)可以用因变量和自变量差分的结果相处得到数值微分;>> x=linspace0,2pi,100;>> y=sinx;>> plotx,y>> y1=diffy./diffx;>> plotx1:end-1,y1答;3)cumsum函数求累计积分,trapz函数用梯形法求定积分,即曲线的面积;>> x=ones1,10>> cumsumx>> x=linspace0,pi,100;>> y=sinx;>> trapzx,y>> p=cumsumy;>> p100pi/100-1答;x =1 1 1 1 1 1 1 1 1 1ans =1 2 3 4 5 6 7 8 9 10ans =ans =练习:图A1是瑞士地图,为了算出其国土面积,首先对地图作如下测量:以由西向东方向为X轴,由南向北方向为Y 轴,选择方便的原点,并将从最西边界点到最东边界点在X轴上的区间适当划分为若干段,在每个分点的Y方向测出南边界点和北边界点的Y坐标Y1和Y2,这样就得到表1,根据地图比例尺回到18mm相当于40Km,试由测量数据计算瑞士国km比较;地图的数据见附表1-2单位mm;土近似面积,与其精确值412282附表1-2X 7 13 34 48 56 61 91Y1 44 45 47 50 50 38 30 30 34 36 34 41 45 46续表提示:由高等数学的知识,一条曲线的定积分是它与x轴所围成的面积,那么两条曲线所围成的面积可由两条曲线的定积分相减得到;4、结构数组与细胞数组1)机构数组的创建;>> ='Jack';>> student2.n>> ='Lucy';>> student或者用struct函数创建;>> student=struct'number',{'001','002'},'name',{'Jack','Lucy'};答;student =1x2 struct array with fields:numbername2)机构数组的操作;>> student1.subject= %添加subject域并赋予空值>> student1.score=>> filednamesstudeng>>fieldnamesstudeng>>fieldnamesstudent>> getfieldstudent,{2},'name'>> student=rmfieldstudent,'subject' %删除subject域>> student=setfieldstudent,{1},'score',90;>> student2.score=88; %比较和上一条语句是否效果一样答;student =1x2 struct array with fields:numbernamesubjectstudent =1x2 struct array with fields:numbernamesubjectscoreUndefined function or variable 'studeng'.练习:创建一结构数组stusorce,其域为:No,Name,English,Math,Chinese,Total,Average;结构数组的大小为2×2;3)细胞数组的创建;>> A={'How are you',ones3;1 2;3 4,{'cell'}}; %直接创建>> B1,1={'Hello world'}; %由各个细胞元素创建>> B1,2={magic3};>> B2,1={1 2 3 4};答或者用cell函数先创建空的细胞数组,然后再给各个元素赋值c=cell1,2;>> c1,1={'Hello world'};>> c1,2={magic3};>> c1,3={1 2 3 4};4)细胞数组的操作;>> ans1=A1,1>> ans2=A1,1>> whos ans1 ans2>> celldispA>> a1=A{2,1}1,2>> a2 a3=dealA{1:2}答;ans1 ='How are you'ans2 ='How are you'Name Size Bytes Class Attributesans1 1x1 84 cellans2 1x1 84 cellA{1,1} =How are youA{2,1} =1 23 4A{1,2} =1 1 11 1 11 1 1A{2,2}{1} =cella1 =2a2 =How are youa3 =1 23 4实验四 MALTAB符号运算一、实验目的掌握符号变量和符号表达式的创建,掌握MALTAB的symbol工具箱的一些基本运用;二、实验内容1)符号变量、表达式、方程及函数的表示; 2)符号微积分运算;3)符号表达式的操作和转换;4)符号微分方程求解;三、实验步骤1、符号运算的引入在数值运算中如果求x xxπsinlim→,则可以不断让的让x趋近0,一球的表达式趋近什么数,但终究不能令x=0,因为在数值运算中0不是能作除数的;MATLAB的符号运算能解决这内问题;输入如下命令:>> f=sym'sinpix/x'>> limitf,'x',0答;f =sinpix/xans =pi2、符号常量、符号变量、符号表达式的创建1)使用sym创建输入以下命令,观察Workspace中A、B、f是什么内性的数据,占用多少字节的内存空间;>> A=sym'1' %符号常量>> B=sym'x' %符号变量>> f=sym'2x^2+3x-1' %符号表达式>> clear>> f1=sym'1+2' %有单引号,表示字符串>> f2=sym1+2 %无单引号>> f2=sym1+2>> f4=sym'2x+3' %为什么出错>> x=1>> f4=sym2x+3答;A =1B =x2x^2+3x-1f1 =1+2f2 =3f2 =3f4 =2x+3x =1f4 =5通过看MATLAB的帮助可知,sym的参数可以使字符串或是数值类型,无论是哪种类型都会生成符号类型数据; 2)使用syms创建>> clear>> syms x y z>> x,y,z>> f1=x^2+2x+1>> f2=expy+expz^2>> f3=f1+f2答;x =xy =yz =zf1 =x^2+2x+1f2 =expy+expz^2f3 =x^2+2x+1+expy+expz^23、符号矩阵创建>> syms a1 a2 a3 a4>> A=a1 a2;a3 a4>> A1,A3答;A =a1, a2a3, a4ans =a1a24、符号算术运算1)符号向量相乘、相除符号量相成和数值量相乘一样,分成矩阵乘和数组乘;>> a=sym5;b=sym7;>> c1=ab>> c2=a/b>> a=sym5;B=sym3 4 5;>> C1=aB,C2=a\B>> syms a b>> A=5 a;b 3;B=2a b;2b a;>> C1=AB,C2=A.B>> C3=A\B,C4=A./B答;c1 =35c2 =5/7C1 =15, 20, 25C2 =3/5, 4/5, 1C1 =10a+2ab, 5b+a^22ab+6b, b^2+3aC2 =10a, ab2b^2, 3aC3 =2ab-3/-15+ab, a^2-3b/-15+ab2ba-5/-15+ab, -5a-b^2/-15+abC4 =5/2/a, a/b1/2, 3/a2)符号数值任意精度控制和运算任意精度的VPA运算可以使用命令digits设定默认的精度和vpa对指定对象以新的精度进行计算来实现; >> a1=sym'2sqrt5+pi'>> a=sym'2sqrt5+pi'>> b=sym2sqrt5+pi>> digits>> vpaa>> digits15>> c1=vpaa,56>> c2=vpab,56答a1 =2sqrt5+pia =2sqrt5+pib =Digits = 32ans =ans =c1 =c2 =注意观察c1和c2的数值类型,c1和c2是否相等;3) 符号类型与数值类型的转换使用命令sym 可以把数值型对象转换成有理数性符号对象,命令vpa 可以讲数值型对象转换为任意精度的VPA 型符号对象;使用double,numeric 函数可以将有理数型和VPA 型符号对象转换成数值对象.>> clear>> a1=sym'2sqrt5+pi'>> b1=doublea1 %符号转数值>> b2=isnumericb1 %判断是否转换成了数值>> a2=vpaa1,70 %数值转符号答;a1 =2sqrt5+pib1 =b2 =1a2 =85、 符号表达式的操作和转换1独立变量的确定原则独立变量的确定原则:在符号表达式中默认变量是惟一的;MATLAB 会对单个英文小写字母除i 、j 外进行搜索,且以x 为首选独立变量;如果表达式中字母不唯一,且无x,就选在字母表最接近x 的字母;如果有相连的字母,则选择在字母表中较后的那一个;例如:'*3'z y +中,y 是默认独立变量;)'*sin('b t a +,t 是默认独立变量;输入以下命令,观察并分析结果;>> clear>> f=sym'a+b+i+j+x+y+xz'>> findsymf>> findsymf,1>> findsymf,2>> findsymf,3>> findsymf,4>> findsymf,5>> findsymf,6答;f =a+b+i+j+x+y+xzans =a, b, j, x, xz, yans =xans =x,xzans =x,xz,yans =x,xz,y,jans =x,xz,y,j,bans =x,xz,y,j,b,a2符号表达式的化简符号表达式化简主要包括表达式美化pretty 、合并同类项collcet 、多项式展开expand 、因式分解factor 、化简simple 或simplify 等函数;①合并同类项collect;分别按x 的同幂项和e 指数同幂项合并表达式: 2(1)()t t x xe x e --+++;>> syms x t;>> f=x^2+x^exp-t+1x+exp-t;>> f1=collectf>> f2=collectf,'exp-t'答;f1 =x^3+exp-tx^2+x^exp-t+1x+x^exp-t+1exp-tf2 =x^2+x^exp-t+1exp-t+x^2+x^exp-t+1x②对显示格式加以美化pretty;针对上例,用格式美化函数可以使显示的格式更符合数学书写习惯;>> prettyf1>> prettyf2答;f1 =x^3+exp-tx^2+x^exp-t+1x+x^exp-t+1exp-tf2 =x^2+x^exp-t+1exp-t+x^2+x^exp-t+1x>> prettyf1prettyf23 2 exp-t exp-tx + exp-t x + x + 1 x + x + 1 exp-t2 exp-t 2 exp-tx + x + 1 exp-t + x + x + 1 x注意与直接输出的f1和f2对比;③多项式展开expand;展开12x-成x不同次幂的多项式.(1)>> syms x>> f=x-1^12;>> expandf>> prettyexpandf答;ans =1+x^12-12x^11+66x^10-220x^9+495x^8-792x^7+924x^6-792x^5+495x^4-220x^3+66x^2-12x 12 11 10 9 8 7 6 51 + x - 12 x + 66 x - 220 x + 495 x - 792 x + 924 x - 792 x4 3 2+ 495 x - 220 x + 66 x - 12 x④因式分解factor;将表达式121x-做因式分解;>> syms x;f=x^12-1;>> prettyfactorf答;ans =1+x^12-12x^11+66x^10-220x^9+495x^8-792x^7+924x^6-792x^5+495x^4-220x^3+66x^2-12x 12 11 10 9 8 7 6 51 + x - 12 x + 66 x - 220 x + 495 x - 792 x + 924 x - 792 x4 3 2+ 495 x - 220 x + 66 x - 12 x>> syms x;f=x^12-1;prettyfactorf2 2 2 4 2x - 1 1 + x + x 1 + x 1 - x + x 1 + x x - x + 1⑤化简simple或simplify;将函数f=;>> clear>> syms x;f=1/x^3+6/x^2+12/x+8^1/3;>> g1=simplef>> g2=simplifyf答;g1 =2x+1/xg2 =2x+1^3/x^3^1/36、符号表达式的变量替换subs函数可以对符号表达式中的符号变量进行替换>> clear>> f=sym'x+y^2+4x+10'>> f1=subsf,'x','s' %使用s替换x>> f2=subsf,'x+y','z'答;f =x+y^2+4x+10f1 =s+y^2+4s+10f2 =z^2+4x+107、符号极限、符号积分与微分1)求极限函数的调用格式limitF,x,a %返回符号对象F当x→a时的极限limitF,a %返回符号对象F当独立变量→a时的极限limitF %返回符号对象F当独立变量→0a=0时的极限limitF,x,a,’right’ %返回符号对象F当x→a时的右极限limitF,x,a,’left’ %返回符号对象F当x→a时的左极限例一:>> clear>> f=sym'sinx/x+ax'>> limitf,'x',0 %以x为自变量求极限>> limitf,'a',0 %以a为自变量求极限>> limitf %在默认情况下以x为自变量求极限>> findsymf %得到变量并且按字母表顺序排列答‘f =sinx/x+axans =1ans =sinx/xans =1ans =a, x例二:>> clear>> f=sym'sqrt1+1/n;>> limitf,n,inf %求n趋于无穷大时的极限2)求积分函数的调用格式intF %求符号对象F关于默认变量的不定积分intF,v %求符号对象F关于指定变量v的不定积分intF,a,b %求符号对象F关于默认变量的从a到b的定积分intF,v,a,b %求符号对象F关于指定变量的从a到b的定积分3)求微分方程的调用格式diffF %求符号对象F关于默认变量的微分diffF,v %求符号对象F关于指定变量v的微分diffF,n %求符号对象F关于默认变量的n阶微分,n为自然数1、2、3……diffF,v,n %求符号对象F关于指定变量v的n阶微分8、符号方程求解1常规方程求解函数的调用格式g=solveeq %求方程或表达式或字串eq关于默认变量的解g=solveeq,var %求方程或表达式或字串eq关于指定变量var的解g=solveeq1,eq2,….,eqn,var1,var2,…,varn %求方程或表达式或字串eq1,eq2,eq3,……eqn关于指定变量组var1,var2,……,varn的解求一元二次方程20++=的解;其求解方法有多种形式:ax bx c①seq=solve'ax^2+bx+c'②seq=solve'ax^2+bx+c=0'③eq=’ax^2+bx+c’;④eq=’ax^2+bx+c=0’;seq=solveeq⑤sym x a b ceq=ax^2+bx+cseq=solveeq2常微分方程求解求解常微分方程的函数是dsolve;应用此函数可以求得常微分方程组的通解,以及给定边界条件或初始条件后的特解;常微分方程求解函数的调用格式:r=dsolve’eq1,eq2,…’,’cond1,cond2,…’,’v’r=dsolve’eq1’,’eq2’,…,’cond1’,’cond2’,…,’v’说明:①以上两式均可给出方程eq1,、qeq2对应初始条件cond1、cond2之下的一v 作为解变量的各微分方程的解; ②常微分方程解的默认变量为t;③第二式中最多可接受的输入式是12个;④微分方程的表达方法;在用MATLAB 求解常微分方程时,用大写字母Dy 表示dxdy ,用D2y 表示22d y dx ,依此类推; 边界条件以类似于ya=b 给出;其中y 为因变量,a 、b 为常数.如果初始条件给的不够,求出的解为含有C1、C2等待定常数的通解;例一 求微分方程x dx dy 2=的通解. 练习:1求222132lim x x x x →--+; 2求函数()cos 2sin 2f x x x =-的积分;求函数()g x =3计算定积分60(sin 2)x dx π+⎰ 4求下列线性方程组的解5求解但y0=2,在z0=7时,微分方程组的解;实验五 MATLAB 程序设计一、实验目的掌握MATLAB 程序设计的主要方法,熟练编写MATLAB 函数.二、 实验内容1M 文件的编辑;。
matlab实验报告

matlab实验报告实验名称熟悉matlab环境课程名称数值分析学生姓名乔幸帅学号 331201000018专业信号与信息处理一、实验目的本次实验的目的是在理论基础的学习前提下熟悉matlab的基本操作,学会matlab的基本绘图以及函数的编写,为学习数值分析这门课奠定基础,并为以后在其他学习和工程使用中打下基础。
二、实验内容1.熟悉matlab的三种指令输入方式2.学会简单的绘图命令3.用matlab编程学会创建函数三、实验步骤3.1 matlab的三种指令输入方式3.1.1 在指令框中直接输入指令并查看结果,如图所示:3.1.2 创建M文件写入指令并运行○1点击matlab的FILE按键选中NEW-Script创建一个如图所示:○2在M文件中输入想要运行的程序并保存○3点击debug中的Run按键运行程序显示结果如图:012345678910matlab Notebook的启动点击matlab左下角的start按钮,点击里面的notebook选项即可新建一个类似word的文档,在里面输入程序,并在Notebook下拉菜单选择Define Input Cell,继续选择Ealuate Input Cell,即得结果如图所示3.2 matlab的简单绘图绘制图像的最基本函数是plot(),其基本调用格式是plot(x,y)如果要绘制多个图像可以使用subplot函数,即在同一个窗口绘制多个子图。
用subplot函数花多个子图。
t=0:pi/100:2*pi;y1=sin(t);y2=cos(t);y3=sin(t)+cos(t);y4=sin(t).*cos(t);subplot(2,2,1)plot(t,y1)xlabel('\itt\rm/s');ylabel('y_1=sin(t)');subplot(2,2,2)plot(t,y2)xlabel('\itt\rm/s'); ylabel('y_2=cos(t)'); subplot(2,2,3) plot(t,y3) gridxlabel('\itt\rm/s'); ylabel('y_3=sin(t)+cos(t)'); subplot(2,2,4) plot(t,y4) gridxlabel('\itt\rm/s'); ylabel('y_4=sin(t)*cos(t)'); 程序运行结果如图所示2468-1-0.500.51t /sy 1=s i n (t )02468-1-0.500.51t /sy 2=c o s (t )2468-2-1012t /sy 3=s i n (t )+c o s (t )02468-0.50.5t /sy 4=s i n (t )*c o s (t )3.3 用 matlab 编写函数MATLAB 的 M 函数是由 function 语句引导的,其基本格式如下: function [返回变量列表] = 函数名 (输入变量列表)[例子]:假设我们想生成一个 n*m 阶的 Hilbert 矩阵, 它的第 i 行第 j 列的元素值为 1/(i+j-1)。
MATLAB上机实验实验报告

MATLAB上机实验实验报告实验名称:用MATLAB实现多项式拟合及插值一、实验目的:通过使用MATLAB实现多项式拟合及插值的方法,掌握MATLAB软件的基本操作和函数应用,进一步了解多项式拟合及插值的原理和实现过程。
二、实验原理:多项式拟合及插值是一种常见的数值分析方法,通过对已知数据点集合的拟合或插值,构造出一个多项式函数,用于近似表示原始数据。
1.多项式拟合:通过最小二乘法原理,选择一个合适的多项式函数,使得拟合出的多项式与已知数据点之间的误差最小。
拟合函数可以是一次、二次或高阶多项式。
2.多项式插值:通过已知数据点的横纵坐标值,构造一个满足这些点的多项式函数。
插值函数可以是一次、二次或高阶多项式。
插值函数经过每个已知数据点。
三、实验步骤:1.数据准备:选择一组已知数据,包含横纵坐标值。
数据点的个数可以根据具体情况自行确定。
2.多项式拟合:使用MATLAB中的polyfit函数,根据已知数据点进行多项式拟合。
根据拟合结果,获取拟合的多项式系数。
3.多项式插值:使用MATLAB中的polyfit函数,根据已知数据点进行多项式插值。
通过plot函数绘制原始数据点的散点图和插值多项式的曲线图。
可以尝试不同阶数的多项式插值。
4.结果分析:根据实验结果,分析拟合与插值的效果。
对比拟合结果与原始数据的误差大小,评估拟合的准确性。
对比插值结果与原始数据的差异,评估插值的精确度。
五、实验总结:通过这次实验,我熟练掌握了使用MATLAB实现多项式拟合及插值的方法。
在实验中,我了解了多项式拟合的原理,以及如何利用最小二乘法求取多项式拟合的系数。
同时,我也学会了如何使用MATLAB中的polyfit函数实现多项式拟合和插值。
通过实验结果的分析,我对拟合和插值的实际应用和效果有了更加深入的认识。
[1]MATLAB官方文档[2]高等数值分析教程以上为MATLAB上机实验实验报告,共计1200字。
