数据结构中栈的介绍

合集下载

数据结构-栈与队列

栈 1.6栈的应用
运算符的优先级关系表在运算过程中非常重要，它是判定进栈、出栈的重要依据。
θ1
θ2
+
-
+
>
>
-
>
>
*
>
>
/
>
>
(
<
<
)
>
>
#
<
<
*
/
(
)
#
<
<
<
>
>
<
<
<
>
>
>
>
<
>
>
>
>
<
>
>
<
<
<
=
>
>
>
>
<
<
<
=
栈
1.6栈的应用
下面以分析表达式 4+2*3-12/(7-5)为例来说明求解过程，从而总结出表达式求值的算法。求解中设置两个栈：操作数栈和运算符栈。从左至右扫描表达式：# 4+2*3-12/(7-5) #，最左边是开始符，最右边是结束符。表达式求值的过程如下表所示：
1.4栈的顺序存储结构
设计进栈算法——Push 函数。首先，判断栈是否已满，如果栈已满，就运用 realloc 函数重新开辟更大的栈空间。如果 realloc 函数返回值为空，提示溢出，则更新栈的地址以及栈的当前空间大小。最终，新元素入栈，栈顶标识 top 加 1。

stack的知识点

stack的知识点1. 栈的定义和特点栈（Stack）是一种具有特殊限制的线性数据结构，它的特点是“后进先出”（Last In First Out，LIFO）。

栈在计算机科学中有着广泛的应用，是一种非常重要的数据结构。

2. 栈的基本操作栈的基本操作包括入栈（push）和出栈（pop）两个操作。

•入栈操作：将元素添加到栈的顶部，使其成为新的栈顶元素。

•出栈操作：移除栈顶的元素，并返回被移除的元素。

除了入栈和出栈操作外，栈还支持其他操作，如获取栈顶元素（top）、判断栈是否为空（empty）、获取栈的大小（size）等。

3. 栈的实现方式栈可以使用数组或链表来实现。

•数组实现：使用数组来存储栈中的元素，通过一个指针来指示栈顶元素的位置。

入栈操作将元素添加到数组的末尾，出栈操作将指针向前移动一位。

•链表实现：使用链表来存储栈中的元素，每个节点包含一个数据元素和一个指向下一个节点的指针。

入栈操作将新元素插入链表的头部，出栈操作将头节点移除。

4. 栈的应用场景栈在计算机科学中有许多应用场景，以下是一些常见的应用场景。

•函数调用栈：在函数调用时，参数、局部变量和返回地址等信息会被压入栈中，函数返回时再从栈中弹出这些信息。

•表达式求值：栈可以用于解析和计算数学表达式，如中缀表达式的转换和后缀表达式的计算。

•括号匹配：栈可以用于检查表达式中的括号是否匹配，如圆括号、方括号和花括号等。

•浏览器的前进和后退功能：浏览器使用栈来记录用户访问的网页历史，通过栈的出栈和入栈操作实现前进和后退功能。

5. 栈的复杂度分析栈的入栈和出栈操作都只涉及到栈顶元素，所以这两个操作的时间复杂度都是O(1)。

而获取栈顶元素、判断栈是否为空和获取栈的大小等操作也都可以在O(1)时间内完成。

6. 总结栈是一种非常重要的数据结构，具有广泛的应用场景。

它的特点是“后进先出”，支持入栈和出栈等基本操作。

栈可以使用数组或链表来实现，常见的应用场景包括函数调用栈、表达式求值、括号匹配和浏览器的前进后退功能等。

栈和队列数据结构的特点

栈和队列数据结构的特点栈和队列是常用的数据结构，它们在程序设计和算法实现中有着重要的作用。

下面将分别介绍栈和队列的特点。

一、栈（Stack）的特点：1.先进后出（FILO）：栈是一种只允许在栈顶进行插入和删除操作的线性数据结构。

元素的插入和删除都只能在栈顶进行，最后插入的元素是第一个被删除的元素。

2.后进先出（LIFO）：栈中最后一个进栈的元素是第一个出栈的元素。

3.只能在栈顶进行操作：栈的操作局限于栈顶，在栈顶可以执行的操作有入栈和出栈操作，其他位置的元素无法直接访问和操作。

4.压入和弹出操作：在栈中，我们只能在栈的一端（通常是栈顶）进行数据的插入和删除操作，分别称为“压入”和“弹出”。

5.递归的应用：栈的结构特点使得它在递归算法的实现中非常有用。

递归函数调用时，每次进入一层递归都需要保存当前的状态，包括参数、局部变量等信息，在递归返回时再恢复状态。

6.存储空间的限制：栈的存储空间是有限的，当栈的元素数量超过了栈的容量时，就会发生栈溢出错误。

7.实现方式：栈可以使用数组或链表来实现。

栈的典型应用场景包括函数调用、表达式求值、括号匹配、迷宫求解等。

二、队列（Queue）的特点：1.先进先出（FIFO）：队列是一种只允许在队尾插入操作，在队头删除操作的线性数据结构。

最先插入的元素是第一个被删除的元素，最后插入的元素是最后被删除的元素。

2.队头和队尾操作：队列的操作局限于队头和队尾，在队头可以执行的操作有删除，称为“出队”操作；在队尾可以执行的操作有插入，称为“入队”操作。

3.可用空间有限：队列的存储空间是有限的，当队列的元素数量超过了队列的容量时，就会无法再插入新的元素，即发生队列溢出错误。

4.实现方式：队列可以使用数组或链表来实现。

若使用链表实现的队列，可实现动态调整队列的大小。

队列的典型应用场景包括多线程任务调度、缓冲队列、消息队列等。

栈和队列都是特殊的线性数据结构，它们各自的特点使它们在不同的应用场景下得到广泛的应用。

栈的总结以及体会

栈的总结以及体会
栈是一种常用的数据结构，常用于程序的调用栈、表达式求值、深度优先搜索等场景。

栈的特点是先进后出，只允许在栈顶进行操作。

以下是对栈的总结和体会：
1. 实现方式：栈可以通过数组或链表来实现。

数组实现简单，但需要指定固定大小；链表实现可以动态调整大小，但需要额外的内存空间来保存指针信息。

2. 基本操作：栈的基本操作包括入栈（push）、出栈（pop）、获取栈顶元素（top）、判空（isEmpty）等。

操作的时间复杂
度均为O(1)。

3. 应用场景：栈在计算机科学中有广泛的应用。

例如，程序调用栈用于存储函数的局部变量和返回地址；表达式求值中使用栈来转换中缀表达式为后缀表达式，并利用后缀表达式进行运算；深度优先搜索中使用栈来维护待访问的节点。

4. 栈的优点：由于栈的特点，它在某些场景下能够提供高效的解决方案。

例如，在递归算法中，通过使用栈来保存递归的中间结果，可以避免递归的重复计算，提升算法的性能；在编译器的语法分析阶段，可以使用栈来验证括号的匹配情况，确保代码的正确性。

5. 栈的缺点：栈的大小一般是有限制的，当数据量超过栈的容量时，会导致栈溢出。

此外，由于栈是一个内存上的顺序结构，数据的存储是连续的，对于大型数据结构，可能会出现内存分
配不足的问题。

总而言之，栈是一种简单、高效的数据结构，广泛应用于计算机科学的各个领域。

熟练掌握栈的基本操作和相关应用场景，能够帮助我们更好地理解和解决实际问题。

栈和队列先进先出和后进先出的数据结构

栈和队列先进先出和后进先出的数据结构栈和队列是常用的数据结构，它们分别以先进先出（FIFO）和后进先出（LIFO）的方式来组织和管理数据。

在许多编程语言中，栈和队列被广泛应用于解决各种问题。

本文将从定义、特点、应用和实现这几个方面来介绍栈和队列。

一、定义栈（Stack）是一种只允许在固定一端进行插入和删除操作的线性数据结构。

这一端被称为栈顶，而另一端被称为栈底。

栈的特点是先进后出。

队列（Queue）是一种先进先出的线性数据结构，允许在一端进行插入操作，而在另一端进行删除操作。

插入操作在队列的尾部进行，删除操作则在队列的头部进行。

二、特点2.1 栈的特点（1）插入和删除操作只能在栈顶进行，保证数据的顺序。

（2）栈是一种后进先出（LIFO）的数据结构，也就是最后插入的元素最先被删除。

（3）栈只能在栈顶进行插入和删除操作，不允许在中间或者底部进行操作。

2.2 队列的特点（1）插入操作只能在队列的尾部进行，保证数据的顺序。

（2）删除操作只能在队列的头部进行，始终删除最先插入的元素。

（3）队列是一种先进先出（FIFO）的数据结构，也就是最先插入的元素最早被删除。

三、应用3.1 栈的应用（1）函数调用和递归：栈被用于保存函数调用时的局部变量和返回地址。

（2）表达式求值：使用栈来实现中缀表达式转换为后缀表达式，然后计算结果。

（3）括号匹配：通过栈检查括号是否配对合法。

（4）浏览器的前进和后退：把浏览器的访问记录保存在栈中，方便前进和后退操作。

3.2 队列的应用（1）任务调度：使用队列管理任务，在现有任务执行完毕后按照先后顺序执行新任务。

（2）缓存管理：常用的缓存淘汰策略是先进先出，即最早进入缓存的数据最早被淘汰。

（3）消息队列：实现进程间的异步通信，提高系统的并发性和可扩展性。

（4）打印队列：打印任务按照先后顺序排队执行，保证打印的顺序。

四、实现栈和队列可以通过数组或链表来实现。

使用数组实现的栈和队列称为顺序栈和顺序队列，而使用链表实现的栈和队列称为链式栈和链式队列。

信息学奥赛知识点(十二)—栈和队列

栈和队列是信息学竞赛中经常涉及的数据结构，它们在算法和程序设计中有着广泛的应用。

掌握栈和队列的基本原理和操作方法，对于参加信息学竞赛的同学来说是非常重要的。

本文将深入探讨栈和队列的相关知识点，帮助大家更好地理解和掌握这两种数据结构。

一、栈的定义与特点栈是一种先进后出（LIFO）的数据结构，它的特点是只允许在栈顶进行插入和删除操作。

栈可以用数组或链表来实现，常见的操作包括压栈（push）、出栈（pop）、获取栈顶元素（top）等。

栈的应用非常广泛，比如在计算机程序中，函数的调用和返回值的存储就是通过栈来实现的。

二、栈的基本操作1. 压栈（push）：将元素压入栈顶2. 出栈（pop）：将栈顶元素弹出3. 获取栈顶元素（top）：返回栈顶元素的值，但不把它从栈中移除4. 判空：判断栈是否为空5. 获取栈的大小：返回栈中元素的个数三、栈的应用1. 括号匹配：利用栈来检查表达式中的括号是否匹配2. 表达式求值：利用栈来实现中缀表达式转换为后缀表达式，并进行求值3. 迷宫求解：利用栈来实现迷宫的路径搜索4. 回溯算法：在深度优先搜索和递归算法中，通常会用到栈来保存状态信息四、队列的定义与特点队列是一种先进先出（FIFO）的数据结构，它的特点是只允许在队尾进行插入操作，在队首进行删除操作。

队列同样可以用数组或链表来实现，常见的操作包括入队（enqueue）、出队（dequeue）、获取队首元素（front）、获取队尾元素（rear）等。

队列在计算机领域也有着广泛的应用，比如线程池、消息队列等都可以用队列来实现。

五、队列的基本操作1. 入队（enqueue）：将元素插入到队列的末尾2. 出队（dequeue）：从队列的头部删除一个元素3. 获取队首元素（front）：返回队列的头部元素的值4. 获取队尾元素（rear）：返回队列的尾部元素的值5. 判空：判断队列是否为空6. 获取队列的大小：返回队列中元素的个数六、队列的应用1. 广度优先搜索算法（BFS）：在图的搜索中，通常会用队列来实现BFS算法2. 线程池：利用队列来实现任务的调度3. 消息队列：在分布式系统中，常常会用队列来进行消息的传递4. 最近最少使用（LRU）缓存算法：利用队列实现LRU缓存淘汰在信息学竞赛中，栈和队列的相关题目经常出现，并且有一定的难度。

栈的共享数据结构

栈的共享数据结构栈（Stack）是一种数据结构，用于在计算机科学中管理和组织数据。

它遵循先进后出（LIFO）的原则，即最后进入堆栈的元素最先出来。

栈可以通过数组或链表实现，但无论如何实现，栈都具有一些共享的数据结构。

在栈的实现中，通常有两个主要操作：push（入栈）和pop（出栈）。

push操作将一个元素添加到栈的顶部，而pop操作则从栈顶移除元素。

此外，栈还有一个peek操作，它返回栈顶的元素，但不对栈做任何修改。

对于栈的实现，有两种常见的共享数据结构，它们是数组和链表。

1.数组实现栈：数组实现栈时，最简单的方式是使用固定大小的数组。

我们需要一个指针来跟踪栈顶元素在数组中的位置。

当执行push操作时，只需将元素添加到当前栈顶指针的下一个位置，并更新栈顶指针。

当执行pop操作时，只需将栈顶指针向下移一位，并返回该位置的元素。

限制性固定大小的数组实现栈的一个问题是可能会溢出。

当栈已满时，尝试push新元素将导致溢出。

为了解决这个问题，通常我们会使用动态大小的数组。

当栈满时，我们会先创建一个更大的数组，并将现有元素复制到新数组，然后继续push新元素。

数组实现栈的优点是简单且常数时间（O(1)）的push和pop操作。

然而，其缺点是动态分配内存时可能会导致性能下降。

2.链表实现栈：链表实现栈的常见方法是使用单链表。

我们需要一个指针来跟踪栈顶元素，同时该指针将指向单链表的头。

当执行push操作时，我们只需要创建一个新节点，并将其插入到链表的头部。

当执行pop操作时，只需将栈顶指针指向下一个节点，并返回当前节点的值。

链表实现栈的优点是可以动态添加节点而无需担心溢出问题。

除此之外，链表实现栈的内存分配比数组实现更灵活，因为它只在需要时分配新节点。

与数组实现相比，链表实现栈的缺点是可能导致内存分配更频繁，并且每个节点需要存储额外的指针。

除了数组和链表之外，栈的共享数据结构还可以使用动态数组（Vector）或双链表（Double Linked List）等其他数据结构来实现。

栈的概念理解

栈的概念理解栈是一种数据结构，它是一种特殊的线性表，只能在表的一端进行插入和删除操作，该一端被称为栈顶，另一端被称为栈底。

栈的特点是后进先出（Last In First Out, LIFO）。

在栈中，最后插入的元素最先弹出，而最先插入的元素最后弹出。

这就好像是一堆盘子，你只能在最上面放盘子和拿盘子，不能随意放在下面的盘子上。

栈的这种特性使得它非常适合解决一些具有“倒序”需求的问题。

栈的基本操作包括入栈和出栈。

入栈（Push）是指将元素放入栈顶；出栈（Pop）是指从栈顶弹出元素。

除此之外，还有一些常用的操作，比如获取栈顶元素（Top）、判断栈是否为空（Empty）、获取栈中元素的个数（Size）等。

栈的实现可以用数组或链表来完成。

使用数组实现的栈叫作顺序栈，使用链表实现的栈叫作链式栈。

对于顺序栈，我们需要定义一个数组和一个整数来表示栈。

数组用于存储栈中的元素，整数用于记录栈顶元素的下标。

一开始，栈为空，栈顶下标可以初始化为-1。

插入元素时，需要判断栈是否已满，如果已满则无法插入；如果未满，将元素放入栈顶，同时栈顶下标加1。

删除元素时，需要判断栈是否为空，如果为空则无法删除；如果不为空，将栈顶元素弹出，并将栈顶下标减1。

对于链式栈，我们需要定义一个结构体来表示栈中的节点。

节点包括一个数据域和一个指向下一个节点的指针域。

和顺序栈类似，链式栈也需要一个指针来表示栈顶元素。

插入元素时，需要创建一个新节点，并将栈顶指针指向该节点，新节点的指针域指向原来的栈顶元素。

删除元素时，需要判断栈是否为空，如果为空则无法删除；如果不为空，将栈顶节点删除，并将栈顶指针指向下一个节点。

栈的应用非常广泛。

在计算机科学中，栈是一种重要的数据结构，它被用于实现函数调用、表达式求值、编译器的语法分析、操作系统的进程管理等。

在编程中，我们可以使用栈来解决一些具有“倒序”性质的问题，比如字符串反转、括号匹配、计算逆波兰表达式等。

此外，栈还被用于图的深度优先搜索（DFS）算法中的节点遍历顺序。

栈的输入输出规则

栈的输入输出规则介绍栈（Stack）是一种常见的数据结构，其特点是先进后出，类似于现实生活中的一摞盘子。

栈的输入输出规则主要指的是对栈进行入栈和出栈操作时的规则和顺序。

本文将详细探讨栈的输入输出规则，包括栈的定义、基本操作、规则分类以及应用场景。

栈的定义栈是一种线性数据结构，只能在栈的一端进行插入和删除操作，该端被称为栈顶（Top），另一端称为栈底（Bottom）。

栈的操作遵循“先进后出”的原则，即最后进栈的元素最早出栈，最先进栈的元素最后出栈。

基本操作栈的基本操作包括入栈（Push）和出栈（Pop）。

以下是对这两个操作的详细描述：入栈（Push）入栈操作将一个新元素添加到栈的栈顶位置。

具体步骤如下： 1. 检查栈是否已满，若已满则无法进行入栈操作。

2. 若栈未满，则将新元素放置在栈顶位置。

3. 更新栈顶指针的位置。

出栈（Pop）出栈操作将栈顶元素移除，并返回该元素的值。

具体步骤如下： 1. 检查栈是否为空，若为空则无法进行出栈操作。

2. 若栈不为空，则将栈顶元素移除。

3. 更新栈顶指针的位置。

4. 返回出栈的元素值。

规则分类根据栈的输入输出规则，通常将栈的规则分类为以下几种类型：FILO（First In Last Out）规则是栈的最基本规则，也是最常见的规则。

按照FILO规则，最后插入的元素首先被移除。

这是因为栈的特点是栈顶元素只能通过出栈操作移除，而栈底元素必须经过多次出栈操作才能被移除。

FIFO规则FIFO（First In First Out）规则是栈的一种特例，与FILO规则相反。

按照FIFO规则，最先插入的元素首先被移除。

但由于栈的性质是先进后出，所以栈并不符合FIFO规则。

FIFO规则通常用于队列（Queue）数据结构中。

LIFO规则LIFO（Last In First Out）规则与FILO规则类似，但稍有差别。

按照LIFO规则，最后插入的元素首先被移除。

LIFO规则常用于描述栈的输入输出顺序。

名词解释栈

名词解释栈栈（stack）在计算机科学中是限定仅在表尾进行插入或删除操作的线形表。

栈是一种数据结构，它按照后进先出的原则存储数据，先进入的数据被压入栈底，最后的数据在栈顶，需要读数据的时候从栈顶开始弹出数据（最后一个数据被第一个读出来）。

栈是只能在某一端插入和删除的特殊线性表。

用桶堆积物品，先堆进来的压在底下，随后一件一件往堆。

取走时，只能从上面一件一件取。

堆和取都在顶部进行，底部一般是不动的。

栈就是一种类似桶堆积物品的数据结构，进行删除和插入的一端称栈顶，另一堆称栈底。

插入一般称为进栈（PUSH），删除则称为退栈（POP）。

栈也称为后进先出表（LIFO表）。

在程序中，堆用于动态分配和释放程序所使用的对象。

在以下情况中调用堆操作：1.事先不知道程序所需对象的数量和大小。

2.对象太大，不适合使用堆栈分配器。

堆使用运行期间分配给代码和堆栈以外的部分内存。

传统上，操作系统和运行时库随附了堆实现。

当进程开始时，操作系统创建称为进程堆的默认堆。

如果没有使用其他堆，则使用进程堆分配块。

语言运行时库也可在一个进程内创建单独的堆。

（例如，C运行时库创建自己的堆。

）除这些专用堆外，应用程序或许多加载的动态链接库(DLL)之一也可以创建并使用单独的堆。

Win32提供了一组丰富的API用于创建和使用专用堆。

有关堆函数的优秀教程，请参阅MSDN平台SDK节点。

当应用程序或DLL创建专用堆时，这些堆驻留于进程空间中并且在进程范围内是可访问的。

某一给定堆分配的任何数据应为同一堆所释放。

（从一个堆分配并释放给另一个堆没有意义。

）在所有虚拟内存系统中，堆位于操作系统的虚拟内存管理器之上。

语言运行时堆也驻留在虚拟内存之上。

某些情况下，这些堆在操作系统堆的上层，但语言运行时堆通过分配大的块来执行自己的内存管理。

绕开操作系统堆来使用虚拟内存函数可使堆更好地分配和使用块。

典型的堆实现由前端分配器和后端分配器组成。

前端分配器维护固定大小块的自由列表。

栈与队列LIFO和FIFO的数据结构

栈与队列LIFO和FIFO的数据结构栈与队列：LIFO和FIFO的数据结构数据结构是计算机科学中非常重要的概念，它可以帮助我们组织和管理数据，提高算法的效率和性能。

其中，栈和队列是两种常见的数据结构，分别以LIFO（Last In, First Out）和FIFO（First In, First Out）的方式进行数据的存取和处理。

本文将对栈和队列的定义、特性以及应用进行详细介绍。

一、栈的定义和特性栈是一种线性数据结构，具有后进先出（LIFO）的特性。

它可以通过两个主要操作来实现：入栈（push）和出栈（pop）。

入栈操作将数据元素添加到栈顶，而出栈操作则将栈顶的元素移除。

栈的特性使得它具有一些独特的应用场景。

首先，栈被广泛应用于程序运行时的函数调用过程中。

每当一个函数被调用时，相关的信息（如局部变量、返回地址等）将被入栈保存，在函数返回时再通过出栈操作恢复。

其次，栈也可用于实现逆波兰表达式的计算，其中运算符和操作数通过栈的入栈和出栈操作进行处理。

二、队列的定义和特性队列也是一种线性数据结构，具有先进先出（FIFO）的特性。

它支持两个主要操作：入队（enqueue）和出队（dequeue）。

入队操作将元素添加到队列的末尾，而出队操作则将队列的首个元素移除。

类似于栈，队列也有其特定的应用场景。

首先，队列广泛应用于多线程和多进程的协调，例如任务调度、消息传递等。

其次，队列还被用于实现广度优先搜索算法，其中待搜索的节点被按层级顺序排列。

三、栈和队列的比较和应用场景尽管栈和队列都是线性数据结构，但它们的特性差异决定了它们的适用场景也不同。

1. 栈的应用场景栈的后进先出特性使得它适合于需要反向迭代的场景。

例如，在计算机程序中，栈被用于实现递归函数的迭代，以及进行深度优先搜索算法等。

2. 队列的应用场景队列的先进先出特性使得它适合于需要顺序处理的场景。

例如，在操作系统中，队列被广泛用于进程调度、磁盘输入输出等。

数据结构-栈

数据结构-栈⼀、栈1. 1. 为什么要学习栈？栈是什么？为什么要学习它？现在先来说说栈的辉煌作⽤吧！在计算机领域中，栈是⼀种不可忽略的概念，⽆论从它的结构上，还是存储数据⽅⾯，它对于学习数据结构的⼈们来说，都是⾮常重要的。

那么就会有⼈问，栈究竟有什么作⽤，让我们这么重视它？⾸先，栈具有⾮常强⼤的“记忆”功能，它可以保存对你有作⽤的数据，也可以被叫做保存现场；其次，当咱们调⽤⼀个带参函数时候，被调⽤的函数的形参，在编译器编译的时候，这些形参都需要⼀定的空间存放他们，这时计算机就会默认帮你保存到栈中了！1. 2. 栈的定义栈的作⽤，这是⼀个咱们⽣活中处处⽤到，但是却⼜没发现的⼀种现象，例如当你拿个篮⼦去买苹果，那么你最先挑选的苹果就是在篮⼦的最底下，最后挑选的苹果就在篮⼦的最上边，那么这就造成了这么⼀种现象：先拿进篮⼦的苹果，要最后才能取出来；相反，最后拿进篮⼦的苹果，就能最先取出来！栈是限定只能在表尾进⾏插⼊和删除的线性表。

我们把允许插⼊和删除的⼀端称作栈顶(Top)，另⼀端称作栈底(bottom)。

不含任何数据元素的栈被称作空栈，栈也被称为先进后出的线性表(具有线性关系)。

⽽栈的特殊性，就是在表中想进⾏插⼊和删除的操作，只能在栈顶进⾏。

这也就使得了：栈底是⾮常稳定的，因为先进来的元素都被放在了栈底。

栈的插⼊操作：叫做进栈，也叫作压栈，⼊栈。

栈的删除操作：叫做出栈，也叫弹栈。

1. 3. 进栈出栈变化形式现在请⼤家思考这样的⼀个问题：最先进栈的元素，是不是只能最后才能出来呢？答案是不⼀定的，这个问题就要细分情况了。

栈对线性表的插⼊和删除的位置进⾏了限制，并没有对元素的进出时间进⾏限制，这也就是说，在不是所有元素都进栈的情况下，事先进去的元素也可以先出站，只要确保⼀点：栈元素是从栈顶出栈就可以了！举例来说，现在有3个整型数元素1、2、3依次进栈，会有哪些出栈次序呢？第⼀种：1、2、3依次进，再3、2、1依次出栈。

数据结构中栈的介绍

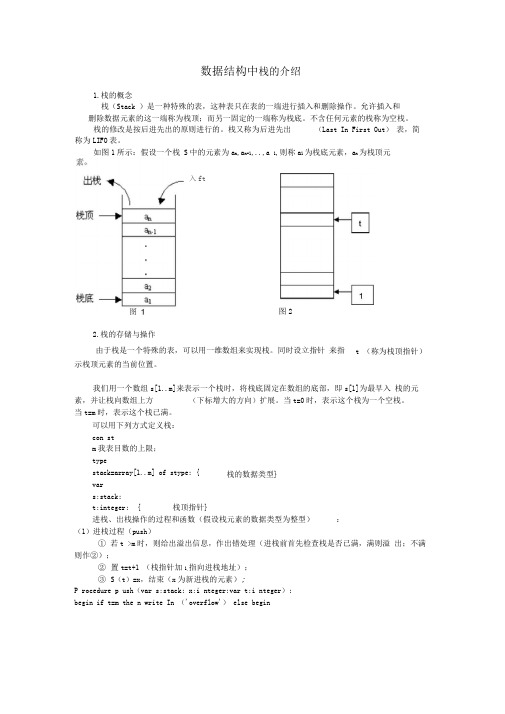
数据结构中栈的介绍1.栈的概念栈（Stack ）是一种特殊的表，这种表只在表的一端进行插入和删除操作。

允许插入和删除数据元素的这一端称为栈顶；而另一固定的一端称为栈底。

不含任何元素的栈称为空栈。

栈的修改是按后进先出的原则进行的。

栈又称为后进先出（Last In First Out ）表，简称为LIFO 表。

如图1所示：假设一个栈 S 中的元素为a n ,a n-1,..,a 1,则称a 1为栈底元素，a n 为栈顶元由于栈是一个特殊的表，可以用一维数组来实现栈。

同时设立指针来指示栈顶元素的当前位置。

我们用一个数组s[1..m]来表示一个栈时，将栈底固定在数组的底部，即s[1]为最早入栈的元素，并让栈向数组上方（下标增大的方向）扩展。

当t=0时，表示这个栈为一个空栈。

当t=m 时，表示这个栈已满。

可以用下列方式定义栈：con stm 我表目数的上限； typestack=array[1..m] of stype; { var s:stack;t:integer; { 栈顶指针}进栈、出栈操作的过程和函数（假设栈元素的数据类型为整型）：（1）进栈过程（push ）① 若t >m 时，则给出溢出信息，作出错处理（进栈前首先检查栈是否已满，满则溢出；不满则作②）；② 置t=t+1 （栈指针加1,指向进栈地址）； ③ S （t ）=x ，结束（x 为新进栈的元素）;P rocedure p ush （var s:stack; x:i nteger;var t:i nteger ）; begin if t=m the n write In （'overflow'） else begint （称为栈顶指针）栈的数据类型}入ft2.栈的存储与操作图2t:=t+1;s[t]:=x; end end;⑵退栈函数(pop )① 若t < 0,则给出下溢信息，作出错处理(退栈前先检查是否已为空栈，空则下溢;不空则作②)；② x=s(t),(退栈后的元素赋给 x ); ③ t=t-1，结束(栈指针减1,指向栈顶)。

栈的工作原理

栈的工作原理栈是一种常见的数据结构，它的工作原理可以类比为我们日常生活中的堆叠物品，比如书籍、盘子等。

在计算机科学中，栈是一种具有特定操作规则的数据结构，它遵循"先进后出"（Last In First Out，简称LIFO）的原则。

本文将详细介绍栈的工作原理及其应用场景。

一、栈的定义和特点栈是一种线性数据结构，它由一系列相同类型的元素组成，这些元素按照线性顺序排列。

栈的特点是只能在一端插入和删除元素，这一端称为栈顶，相对的另一端称为栈底。

二、栈的基本操作栈的基本操作包括入栈（Push）和出栈（Pop）。

入栈操作将一个新元素放入栈顶，使其成为新的栈顶元素；出栈操作将栈顶元素删除，并返回该元素的值。

三、栈的应用场景1.函数调用和递归在函数调用中，每次函数调用时，都会将函数的返回地址、参数和局部变量等信息存储在栈中，以便在函数执行完毕后能够返回到调用处。

递归函数的执行过程也是通过栈来实现的，每次递归调用都会将当前的状态保存在栈中。

2.表达式求值栈在表达式求值中也有重要的应用。

当我们计算一个表达式时，需要根据运算符的优先级来确定计算的顺序，而栈可以帮助我们保存运算符的优先级，确保表达式的正确计算顺序。

3.括号匹配栈在括号匹配中也发挥着重要的作用。

当我们遇到左括号时，将其入栈；当遇到右括号时，将栈顶的左括号出栈并判断是否匹配。

如果匹配，则继续处理后面的字符；如果不匹配，则表示括号不匹配，可以提前结束。

4.浏览器的前进和后退在浏览器中，我们可以通过点击前进和后退按钮来切换页面，这就是一个典型的栈的应用场景。

浏览器会将每个访问的页面存储在一个栈中，每次点击前进按钮时，会将当前页面入栈；每次点击后退按钮时，会将当前页面出栈。

四、栈的实现方式栈可以通过数组或链表来实现。

使用数组实现的栈称为顺序栈，它的优点是访问速度快，但容量固定；使用链表实现的栈称为链式栈，它的优点是容量可动态调整，但访问速度相对较慢。

栈和堆的概念

栈和堆的概念1.引言在计算机科学中，栈和堆是两个常见的数据结构和内存管理概念。

它们在程序执行、变量分配和内存管理方面起着重要作用。

本文将介绍栈和堆的概念，并探讨它们的特点和应用。

2.栈的概念2.1定义栈（Stack）是一种后进先出（Last In First Out，LIFO）的数据结构。

它类似于现实生活中的一叠盘子，只能在最顶层进行操作。

栈具有两个基本操作：入栈（Push）和出栈（Pop）。

入栈将元素放入栈的顶部，出栈则从栈的顶部移除元素。

2.2特点-后进先出：栈中最后进入的元素将首先被移除。

-有限容量：栈的容量有限，当栈已满时无法再进行入栈操作。

-快速访问：由于栈的特殊结构，对于栈中的元素可以快速进行访问和操作。

2.3应用-函数调用：在函数调用过程中，局部变量和函数参数被存储在栈中。

每次函数调用时，相关的数据被压入栈中，函数返回时再从栈中弹出。

-表达式求值：在数学表达式求值过程中，栈常被用于保存运算符和操作数的顺序。

-递归算法：递归算法通常使用栈来保存每一层递归的状态。

3.堆的概念3.1定义堆（Heap）是一种动态内存分配方式，也是一种数据结构。

堆的内存空间可以在程序运行时进行动态分配和释放。

与栈不同，堆的数据访问没有限制顺序，可以任意读取或写入堆中的数据。

3.2特点-动态分配：堆的内存空间可以在程序运行时动态分配，而不受固定容量的限制。

-无序性：堆中的数据可以以任意顺序进行读写，没有先进先出或后进先出的限制。

-存储复杂的数据结构：由于堆的灵活性，它可以存储复杂的数据结构，如树、图等。

3.3应用-动态内存分配：堆经常用于动态分配内存空间，例如在编程中使用new或malloc函数来动态创建对象或数组。

-数据库管理：数据库中的数据通常存储在堆中，以便在需要时进行动态增加或删除。

-图形处理：堆经常用于图形处理算法，如最短路径、最小生成树等。

4.栈和堆的区别4.1分配方式栈的分配方式是静态的，大小固定，并且由编译器自动管理。

栈的概念与特点

栈的概念与特点栈是一种数据结构，它可以用来存储数据和实现一些特定的操作。

栈的概念和特点可以通过以下几个方面来阐述。

首先，栈是一种线性数据结构，其特点是数据元素按照线性顺序排列，且只能在一端进行操作。

这一端通常称为栈顶，另一端称为栈底。

栈的结构类似于我们平常使用的一对叠盘子，只能从上面取盘子或者放盘子。

其次，栈的特点是“后进先出”，即最后一个入栈的元素最先出栈，而最先入栈的元素最后出栈。

这与我们日常生活中的一些场景相符，比如堆积东西或书籍时，我们通常会先放上面的物品，而需要使用时则先取出上面的物品。

这种特点在计算机科学中应用广泛，有助于解决一些问题。

再次，栈只能在一端进行操作，即在栈的顶部进行插入元素、删除元素或者查看栈顶元素等操作。

这种特点决定了在栈中只有栈顶元素可见，其他元素是不可见的。

这也是栈的一个重要特性，它限制了对栈内数据的访问方式，在某些情况下能够提高程序的效率。

此外，栈还具有一种重要的性质，即拥有“局部性原理”。

局部性原理指的是在程序执行过程中，往往会存在一些临时的变量或者子程序的调用，这些变量或者子程序的执行过程通常是连续的，也就是说它们的连续执行是非常频繁的。

而栈的特点正好满足了这一需求，可以将这些临时变量或者子程序的返回地址存储在栈中，以实现快速的跳转和恢复。

另外，栈还具有动态分配内存空间的能力。

在使用栈时，一般会预先确定栈的最大容量，但实际使用时可能需要动态地分配栈的空间。

这是因为在程序执行过程中，数据的个数或者大小是不确定的，可能会有增加或者减少的情况。

而栈可以通过动态地改变栈顶指针的位置来实现空间的动态分配和释放。

此外，栈还可以通过递归来实现一些复杂的问题。

递归是一种函数调用自身的方法，它可以通过栈的特点实现函数的嵌套调用和返回。

递归在解决一些具有递归结构的问题时非常有用，并且可以通过栈的特性来实现递归的过程管理和结果返回。

除了以上几个方面，栈还有一些其他的应用场景，比如括号匹配、表达式求值、函数调用和返回等。

栈和队列区别及应用场景

栈和队列区别及应用场景栈（Stack）和队列（Queue）是两种常见的数据结构，它们在计算机科学领域有广泛的应用。

本文将从定义、特点和基本操作等方面详细介绍栈和队列的区别，并分析它们各自的应用场景。

一、栈的定义及特点：栈是一种线性数据结构，其特点是“先进后出”（Last In First Out，LIFO）。

即在栈中最后一个进入的元素，也是第一个出栈的元素。

栈的基本操作包括入栈和出栈。

入栈（Push）是将一个元素追加到栈的顶部，出栈（Pop）是将栈顶元素移除。

栈的应用场景：1.函数调用：在函数调用时，每遇到一个新的函数调用就将当前的上下文（包括局部变量和返回地址）压入栈中，当函数调用完毕后，再弹出栈顶元素，恢复上一个函数的上下文。

2.表达式求值：栈可以用于进行中缀表达式到后缀表达式的转换，并通过栈来计算后缀表达式的值。

3.递归：递归算法的实现中通常会使用栈来保存递归调用的上下文。

4.撤销操作：在很多应用程序中，比如文本编辑器和图像处理软件中，通过栈来存储用户操作，以便可以撤销之前的操作。

5.浏览器历史记录：浏览器通常使用栈来实现历史记录的功能，每当用户浏览一个新的页面时，就将该页面的URL入栈，当用户点击后退按钮时，再依次出栈。

6.二叉树的遍历：用栈可以实现二叉树的深度优先遍历，具体的实现是使用非递归的方式进行前序、中序、后序遍历。

二、队列的定义及特点：队列也是一种线性数据结构，其特点是“先进先出”（First In First Out，FIFO）。

即在队列中最先进入的元素，也是第一个出队列的元素。

队列的基本操作包括入队和出队。

入队（Enqueue）是将元素放入队列的尾部，出队（Dequeue）是将队列的头部元素移除。

队列的应用场景：1.广度优先搜索：在图论中，广度优先搜索（Breadth First Search，BFS）通常会使用队列来实现，按照层次的顺序进行搜索。

2.缓冲区：队列可以用作缓冲区，在生产者和消费者模型中，生产者将数据放入队列的尾部，消费者从队列的头部取出数据进行处理。

数据结构栈和队列知识点总结

数据结构栈和队列知识点总结一、栈的基本概念栈是一种线性数据结构，具有后进先出（LIFO）的特点。

栈有两个基本操作：入栈（push）和出栈（pop）。

入栈指将元素压入栈中，出栈指将最近压入的元素弹出。

二、栈的实现方式1. 数组实现：利用数组来存储元素，通过一个变量来记录当前栈顶位置。

2. 链表实现：利用链表来存储元素，每个节点包含一个数据域和一个指向下一个节点的指针。

三、应用场景1. 表达式求值：使用两个栈分别存储操作数和运算符，按照优先级依次进行计算。

2. 函数调用：每当调用一个函数时，就将当前函数的上下文信息压入调用栈中，在函数返回时再弹出。

3. 浏览器历史记录：使用两个栈分别存储浏览器前进和后退的网页地址。

四、队列的基本概念队列是一种线性数据结构，具有先进先出（FIFO）的特点。

队列有两个基本操作：入队（enqueue）和出队（dequeue）。

入队指将元素加入到队列尾部，出队指从队列头部删除元素。

五、队列的实现方式1. 数组实现：利用数组来存储元素，通过两个变量分别记录队列头和队列尾的位置。

2. 链表实现：利用链表来存储元素，每个节点包含一个数据域和一个指向下一个节点的指针。

六、应用场景1. 广度优先搜索：使用队列来保存待访问的节点，按照层次依次访问。

2. 线程池：使用队列来保存任务，线程从队列中取出任务进行处理。

3. 缓存淘汰策略：使用队列来维护缓存中元素的顺序，根据一定策略选择删除队首或队尾元素。

七、栈和队列的比较1. 栈是一种后进先出的数据结构，而队列是一种先进先出的数据结构。

2. 栈只能在栈顶进行插入和删除操作，而队列可以在两端进行操作。

3. 栈可以用于回溯、函数调用等场景，而队列适合于广度优先搜索、缓存淘汰等场景。

八、常见问题及解决方法1. 栈溢出：当栈空间不够时，会发生栈溢出。

解决方法包括增加栈空间大小、减少递归深度等。

2. 队列空间浪费：当使用数组实现队列时，可能会出现队列空间不足的情况。

简述栈的工作原理

简述栈的工作原理栈是一种常见的数据结构，它具有后进先出（LIFO）的特性。

栈的工作原理是通过两个基本操作实现的：压入（push）和弹出（pop）。

在栈中，数据项只能从栈的顶部进行访问和操作，而不能从中间或底部进行操作。

栈的工作原理可以用一个生活中常见的场景来解释。

想象一下，你在家里叠放了一堆盘子。

当你要拿走盘子时，你只能从盘子堆的顶部拿走一个盘子。

同样，当你要放置一个盘子时，你只能将其放在盘子堆的顶部。

这就是栈的工作原理。

栈的实现可以使用数组或链表。

无论使用哪种方式，栈的基本操作都是一样的。

下面我们来具体了解一下栈的工作原理。

栈有一个指针，称为栈顶指针（top），用于指示栈的顶部元素。

初始时，栈为空，栈顶指针指向一个特殊的位置，通常是-1或null。

当我们执行压入操作时，即向栈中添加一个元素，栈顶指针会向上移动一个位置，指向新添加的元素。

这个过程称为入栈。

入栈操作可以多次执行，每次都会将元素添加到栈的顶部。

当我们执行弹出操作时，即从栈中移除一个元素，栈顶指针会向下移动一个位置，指向栈中的下一个元素。

这个过程称为出栈。

出栈操作也可以多次执行，每次都会将栈顶的元素移除。

通过不断执行入栈和出栈操作，我们可以在栈中保存和访问一系列元素。

栈的大小可以根据需要进行动态调整。

除了入栈和出栈操作，栈还提供了其他一些常用的操作，例如查看栈顶元素（top）和判断栈是否为空。

查看栈顶元素可以通过获取栈顶指针所指向的元素来实现。

判断栈是否为空可以通过检查栈顶指针的位置是否为初始值来实现。

栈在计算机科学中有广泛的应用。

例如，在编程语言中，栈被用于存储函数调用的上下文信息。

每当一个函数被调用时，相关的信息（如参数、局部变量等）会被压入栈中，函数执行完成后再从栈中弹出这些信息。

这样可以保证函数调用的顺序和嵌套关系得到正确处理。

栈还可以用于实现算法中的一些重要操作。

例如，深度优先搜索（DFS）算法使用栈来存储待访问的节点，以及回溯算法使用栈来回溯之前的选择。