最新代数式专题练习(解析版)
列代数式专项练习60题(有答案)

列代数式专项练习60题(有答案)1.正方体棱长为a,体积为V,则V与a之间的关系式为_________ ,当a=4cm时,V= _________ cm3.2.一个数比a的3倍的平方小3,则这个数是_________ .3.体校里男学生人数是m,女学生人数是n,教练人数和学生人数的比是1:20,则教练人数是_________ .4.某商品的进价是x元,售价是132元,则此商品的利润是_________ .5.“x的2倍与y的3倍的差”列式为_________ .6.在负整数a后添上3,使其位数增加一位,则这个数可表示为_________ .7.若一个数比x的2倍小3,则这个数可表示为_________ .8.“比a的3倍小2的数”用整式表示是_________ .9.“x与y的和”用代数式可以表示为_________ .10.用代数式表示“a的3倍与4的和”为_________ .11.某校共有学生x人,其中女生占总数的m%,则男生人数为_________ 人.12.某商品进价是m元,提价30%后标价,又打九折出售,则该商品的利润是_________ .13.一个笼子里的鸡a只,兔b只,则笼子里的鸡和兔的脚共有_________ 只.14.某工厂的产值由a万元增加了20%,达到_________ 万元.15.一台a元的电视机,降价20%后的价格为_________ 元.16.某工厂今年的产值是a万元,比去年增加了20%,则去年的产值是_________ .17.苹果每千克p元,若苹果超过10千克以上,则全部9折优惠,买15千克应付_________ 元.18.张红在一次考试中,得数学a分,语文b分,则张红这二科的平均成绩是_________ 分.19.科学家在南极考察时,拾到一块不规则的矿石,科学家用一把刻度尺,一只圆柱体的玻璃杯和足量的水,就测出了这块矿石的体积.如果玻璃杯的内直径为r,把矿石完全浸没在水中,测出杯中水面上升的高度为h,则这块矿石的体积是_________ .20.一件商品原价为a元,先涨价5元后,再按8.5折出售,那么现售价用代数式表示为_________ .21.如图,正方形的边长为2,分别以正方形的两个相对顶点为圆心,以正方形的一边为半径画弧,则阴影部分的面积是_________ .22.如图是数值转换器的示意图,如果输入的数字用x表示,那么输出的数字可以用代数式_________ 表示.23.小亮从一列火车的第m节车厢起,一直数到第2m节车厢,他数过的车厢节数是_________ .24.小明在考试前到文具店里买了2支2B的铅笔和一副三角板,2B的铅笔每支x元,三角板每副3元,小明总共应付_________ 元(用含x的代数式表示).25.三毛早上从报社以每份0.4元的价格购进了a份报纸.以每份0.5元的价格出售,一天共售b份报纸,剩余的报纸以每份0.2元的价格退回报社,回家后三毛发现这一天的辛苦还是赚到了钱,那么三毛这天赚了_________ 元.26.n(n≥2)个球队进行单循环赛(参加比赛的每个队都与其他所有的队各赛一场),总的比赛场数是_________ .27.绥阳某商店的一种商品每件进价为a元,按进价提高30%标价,再按标价的8折出售,那么打折后,每件商品的售价是_________ 元.28.“圆形方孔钱”是中国古钱币的突出代表.如图,一枚圆形方孔钱的外圆直径为a,中间方孔边长为b,则图示阴影部分面积为_________ .30.如图,两个长方形的一部分重叠在一起,重叠部分是边长为3的正方形,则阴影部分的面积是_________ .31.三角形三边的长分别是(2x+1)厘米,(3x﹣2)厘米,(8﹣2x)厘米,求这个三角形的周长,如果x=3,三角形的周长是多少?32.晓霞的爸爸开了一个超市,一天,她爸爸分别以P元进了A、B两种商品,后来A商品提价20%,B商品降价10%,这样在某一天中,A商品卖了10件,B商品卖了20件,问这一天里超市作这两种买卖是赚了还是赔了?并说明理由.33.列代数式:(1)比a与b的积的2倍小5的数;(2)a与b的平方差;(3)被5除商是a,余数是2的数.34.我国出租车收费标准因地而异,A市为:起步价10元,3km后每千米加价1.2元;B市为:起步价8元,3km 后每千米加价1.4元;(1)试分别写出在A,B两城市坐出租车x(x>3)km所付的车费;(2)求在A,B两城市坐出租车x(x>3)km的差价是多少元?35.如图,大正方形的边长为a,小正方形的边长为2,求阴影部分的面积.36.窗户的形状如图,其上部是半圆形,下部是长方形.已知窗户的下部宽为xm,窗户长方形部分高度为1.5xm.计算:(1)窗户的面积S;(2)窗框的总长L.37.“十一”黄金周期间,小刚拿着妈妈给的800元钱到重百商场购买运动服和运动鞋,他来到自己喜欢的“阿迪、(1)200~500元(含500元)的部分打9折;(2)500~800元(含800元)的部分打8折;(3)800元以上的部分打7折(商品金额可累计),他又看到运动服标价a元/件(400≤a≤500),运动鞋标价b元/双(300≤b≤400);(1)算他单独买一件运动服需多少钱;(用含a的代数式表示)(2)计算他一次性买一件运动服和一双运动鞋共需多少钱.(用含a、b的代数式表示)38.为了节约用水,某市决定调整居民用水收费方法,规定:如果每户每月用水不超过20吨,每吨水收费3元,如果每户每月用水超过20吨,则超过部分每吨水收费3.8元;小红看到这种收费方法后,想算算她家每月的水费,但是她不清楚家里每月的用水是否超过20吨.(1)如果小红家每月用水15吨,水费是多少.如果每月用水35吨,水费是多少;(2)如果字母x表示小红家每月用水的吨数,那么小红家每月的水费该如何用x的代数式表示呢.39.某轮船顺水航行4小时,逆水航行2.5小时,已知轮船在静水中的速度为m千米/小时,水流速度为y千米/小时.轮船共航行了多少千米?40.一轮船航行于甲、乙两港口之间,在静水中的航速为m千米/小时,水流速度为12千米/小时,(1)则轮船顺水航行5小时的行程是多少?(2)轮船逆水航行4小时的行程是多少?(3)轮船顺水航行5小时和逆水航行4小时的行程相差多少?41.某公园的成人票价是20元,儿童票价是8元,甲旅行团有x名成人和y名儿童;乙旅行团的成人数是甲旅行团的2倍,儿童人数是甲旅行团的.(1)求两个旅行团的门票总费用是多少?(2)当x=10人,y=6人时,求两个旅行团的门票总费用是多少元?42.小明想把一长是60cm,宽为40cm的长方形硬纸片做成一个无盖的长方体盒子,于是在长方形的四个角各剪去一个相同小正方形(如图).(1)若设这些小正方形的边长为xcm,求图中阴影部分小长方形的面积.(2)当x=5时,求这个盒子的体积.43.某礼堂第1排a个座位,后面每排比第一排多1个座位,用含a的代数式表示:(1)第2排有多少个座位?第5排有多少个座位?第10排有多少个座位?(2)前10排共有多少个座位?(3)第11排比第5排多多少个座位?44.如图,正方形ABCD的边长为a,长方形AEFD的长AE为b,(1)用代数式表示图中阴影部分的面积;(2)求当a=5cm,b=7cm时,阴影部分的面积.45.一个三位数,个位上的数是十位上的数的平方,百位上的数比十位上的数的4倍多1.将十位上的数设为x.(1)列式表示这个三位数;(2)这个三位数是多少?46.学校组织初一年级全体同学参加植树造林劳动.全体同学分三队,第一队植树x棵,第二队植的树比第一队植树的两倍少80棵,第三队植的树比第二队植树多了10%.(1)求全体同学一共植树多少棵?(用含x的式子表示)(2)若x=100棵,求全体同学共植树多少棵?47.攀枝花市出租车收费标准为:起步价5元(其中包含2千米),2千米后每千米价1.8元.则某人乘坐出租车x 千米的付费为多少元.(用代数式表示)48.龙港某企业有甲、乙两种经营收入,2010年甲种年收入是乙种年收入的1.5倍,预计2011年甲种年收入将减少20%,而乙种年收入将增加40%,记2010年乙种年收入为a万元.(1)2010年该企业甲种年收入为_________万元;(2)2011年该企业甲种年收入为_________万元;乙种年收入为_________万元.(3)当a=100万元时,请问该企业2011年总收入比2010年总收入是增加,还是减少?增加或减少了多少?请说明理由.49.用代数式表示下列图形中阴影部分的面积.(1)S阴影=_________;(2)S阴影=_________.50.学校需要到印刷厂印刷n份材料,甲印刷厂的收费标准是每份材料收0.2元的印刷费,另收500元的制版费;乙印刷厂的收费标准是每份材料收0.4元印刷费,不收制版费.(1)两个印刷厂的收费各是多少元?(用含n的代数式来表示)(2)学校要印2600份材料,若不考虑其他因素,选择哪家印刷厂比较合算?试说明理由.51.一辆汽车以每小时80千米的速度行驶,从A城市到B城市需要t小时,按题意解决下列问题(1)如果汽车行驶的速度每小时增加v千米,那么从从A城市到B城市还需要多少小时.(2)如果某次因紧急情况,从B城市返回到A城市的平均速度比原来每小时增加12千米,那么预计返回比原来可提前多少时间.52.一种笔记本售价为2.3元/本,如果买100本以上(不含100本),售价为2.2元/本.(1)列式表示买n本笔记本所需的钱数;(2)按照售价规定,会不会出现多买比少买反而付钱少的情况?(3)如果需要100本笔记本,怎样购买更省钱?并说明理由.53.甲、乙两家商场以同样的价格出售同样的电器,但各自推出的优惠方案不同.甲商场规定:凡超过1000元的电器,超出的金额按90%收取;乙商场规定:凡超过500元的电器,超出的金额按95%收取.某顾客购买的电器价格是x元.(1)当x=850时,该顾客应选择在_________商场购买比较合算;(2)当x>1000时,分别用代数式表示在两家商场购买电器所需付的费用;(3)当x=1700时,该顾客应选择哪一家商场购买比较合算?说明理由.54.列代数式:(1)a的3倍与b的和;(2)a与b的差的平方;(3)被5除商是x,余数是2的数.55.如图,将一张长方形大铁皮切割(切痕为虚线)成九块,其中有两块是边长都为a厘米的大正方形,两块是边长都为b厘米的小正方形,且a>b.(1)这张长方形大铁皮长为_________厘米,宽为_________厘米(用含a、b的代数式表示);(2)①求这张长方形大铁皮的面积(用含a、b的代数式表示);②若最中间的小长方形的周长为22厘米,大正方形与小正方形的面积之差为33厘米2,试求a和b的值,并求这张长方形大铁皮的面积;(3)现要从切块中选择5块,恰好焊接成一个无盖的长方体盒子,共有哪几种方案可供选择(画出示意图)?按哪种方案焊接的长方体盒子的体积最大?试说明理由.(接痕的大小和铁皮的厚度忽略不计)56.在正常情况下,某出租车司机每天驾车行驶t小时,且平均速度为v千米/小时.已知他在A日比正常情况少行驶2小时,平均速度比正常情况慢5千米/小时,他在B日比正常情况多行驶2小时,平均速度比正常情况快5千米/小时,(1)求A日出租车司机比正常情况少行驶多少千米?(用含v,t的代数式表示)(2)已知A日出租车司机比正常情况少行驶120千米,求B日出租车司机比正常情况多行驶多少千米?57.已知我市出租车收费标准如下:乘车路程不超过3km的一律收费7元;超过3km的部分按每千米加1.8元收费.(1)如果有人乘计程车行驶了m千米(m>3),那么他应付多少车费?(列代数式)(2)游客甲乘出租车行驶了4km,他应付车费多少元?(3)某游客乘出租车从西区大润发到文昌楼,付了车费10.6元,试估算从西区大润发到文昌楼大约有多少公里?58.如图为一梯级的纵截面,一只老鼠沿长方形的两边A→B→D路线逃跑,一只猫同时沿梯级(折线)A→C→D的路线去捉,结果在距离C点0.6米的D处,捉住了老鼠.请将下表中的语句“译成”数学语言(写出代数式).设梯级(折线)A→C的长度x米AB+BC的长为A→C→D的长为A→B→D的长为设猫捉住老鼠所用时间为t秒猫的速度老鼠的速度59.某地公交公司推出刷卡月票制,即持有这种月票的乘客通过刷卡扣除每次的车票.某人买了50元的这种月票卡,如果此人乘车的次数用m表示,每次乘车的余额用n表示,它们之间的关系如下表:乘车次数m 月票余额n/元1 50﹣0.82 50﹣1.63 50﹣2.44 50﹣3.2……回答下列问题:(1)如果此人乘车的次数m,那么月票余额是_________元.(2)此人最多能乘车几次?简单说明理由.60.一本小说共m页,一位同学第一天看了全书的少6页,第二天看了剩下的多6页,第三天把剩下的全部看完,该同学第三天看了多少页?若m=900,则第三天看了多少页?列代数式专项练习60题参考答案:1.∵正方体边长为a,∴它的体积是V=a3.当a=4cm时,V=4 3=64cm3.故答案为:a3,64.2.由题意得:(3a)2﹣3=9a2﹣3,故答案为:9a2﹣3.3.设没分为x人,则教练有x人,学生有20x人,由题意,得∴20x=m+n,∴x=,∴教练有人.故答案为:人4.∵某商品的进价是x元,售价是132元,∴此商品的利润=售价﹣进价=132﹣x(元).故答案为(132﹣x)元.5.x的2倍是2x,y的3倍是3y,则x的2倍与y的3倍的差为:2x﹣3y.故答案是:2x﹣3y.6.在负整数a后添上3,使其位数增加一位,则这个数可表示为10a﹣3.故答案为10a﹣3.7.一个数比x的2倍小3,则这个数可表示为2x﹣3.故填:2x﹣38.由题意得:3a﹣2,故答案为:3a﹣2.9.“x与y的和”用代数式可以表示为:x+y.故答案为x+y10.先求a的3倍是3a,再求与4的和为3a+4.故答案为:3a+4.11.由题意得:x﹣m%x,故答案为:(x﹣m%x).12.∵某商品进价是m元,提价30%后标价,又打九折出售,∴此商品的售价为0.9×1.3m=1.17m(元),∴该商品的利润是1.17m﹣m=0.17m(元).故答案为0.17m13.∵鸡有两只脚,兔有四只脚,又∵鸡有a只,兔有b只,∴鸡和兔的脚共有:2a+4b.故答案为:2a+4b14.根据题意得产值由a万元增加了20%,达到的产值15.∵电视机的原价为a元,∴降价20%后的价格为(1﹣20%)a=0.8a(元).故答案为0.8a16.∵今年比去年增加了20%,∴今年的产值占去年的1+20%=120%,∴去年的产值=a÷120%=a万元.故答案为:a万元.17.15×0.9p=13.5p.故答案是:13.5p.18.二科的平均成绩是:(a+b).故答案是:(a+b).19.根据圆柱的体积公式可得这块矿石的体积为:.故填:20.根据一件商品原价为a元,先涨价5元,则价格变为:a+5,再按8.5折出售,依题意得:(a+5)×0.85.故答案为:0.85(a+5)21.S阴影=2S扇形﹣S正方形=2×﹣22=π×22﹣22=2(π﹣2).故填2(π﹣2)22.根据示意图可得:2x﹣3.故答案为2x﹣3.23.根据题意列得:他数过的车厢有(2m﹣m+1)即(m+1)节.故答案为:m+1.故选D24.因为2支2B铅笔2x元,一副三角板3元,所以小明总共应付(2x+3)元.故答案为:2x+325.∵每份0.4元的价格购进了a份报纸,∴这些报纸的成本是0.4a元,∵每份0.5元的价格出售,一天共售b份报纸,∴共买了0.5b元,∵剩余的报纸以每份0.2元的价格退回报社,∴退回了0.2(a﹣b)元,他一天工赚到的钱数为:0.5b+0.2(a﹣b)﹣0.4a=0.3b26.n支球队举行单循环比赛,比赛的总场数为:n(n ﹣1).故答案为:n(n﹣1)27.根据题意得:a•(1+30%)×80%=1.04a;故答案为:1.04a.28.圆的面积为π×()2=,中间正方形的面积为b2,∴图中阴影部分面积为:﹣b2.故答案为:﹣b2.29.∵由题意可得计算过程如下:( x×2+y2)÷2,∴当x=5,y=﹣2时,( x×2+y2)÷2=(5×2+4)÷2=7.故答案为:730.阴影部分的面积是:ab+cd﹣2×32=ab+cd﹣18;故答案为:ab+cd﹣18.31.三角形的周长是2x+1+3x﹣2+8﹣2x=3x+7,当x=3时,原式=3x+7=3×3+7=16.32.在一天的两种商品的买卖中,超市不赚不赔.∵10件A商品一共卖了10×(1+20%)P=12P(元),20件B商品一共卖了20×(1﹣10%)P=18P(元),∴这30件商品一共卖了12P+18P=30P(元),∵30P﹣30P=0,∴超市不赚不赔33.(1)2ab﹣5.(2)a2﹣b2.(3)5a+234.(1)A:10+1.2(x﹣3)=1.2x+6.4;B:8+1.4(x﹣3)=1.4x+3.8;(2)A与B的差价=(1.2x+6.4)﹣(1.4x+3.8)=2.6﹣0.2x.35.阴影部分的面积=GF•DG+GF•CG=GF•CD=×2•a.=a.36.①S==(m2)(4分);②L===(m)37.(1)由题意得,单独买一件运动服需要的钱数为:200+(200﹣a)×0.9即20+0.9a.(2)∵700≤a+b≤900,而打折却有7折和8折两种方式,∴当700≤a+b≤800时,应付费:200+300×0.9+(a+b﹣500)×0.8即为70+0.8a+0.8b(元);当800<a+b≤900时,应付费:200+300×0.9+300×0.8+(a+b﹣800)×0.7即为150+0.7a+0.7b(元)38.(1)每月用水15吨时,水费为:15×3=45元(1分)每月用水35吨时,水费为:3.8(35﹣20)+60=117元…(2分)(2)①如果每月用水x≤20吨,水费为:3x元(4分)②如果每月用水x>20吨,水费为:3.8(x﹣20)+60或3.8x﹣16元39.根据题意得:4(m+y)+2.5(m﹣y)=6.5m+1.5y.轮船共航行了(6.5m+1.5y)千米.40.(1)根据题意得:(m+12)×5=5m+60(千米);答:轮船顺水航行5小时的行程是(5m+60)千米.(2)根据题意得:(m﹣12)×4=4m﹣48(千米)答:轮船逆水航行4小时的行程是(4m﹣48)千米.(3)根据题意得:5m+60﹣(4m﹣48)=m+108(千米)答:轮船顺水航行5小时和逆水航行4小时的行程相差(m+108)千米.41.(1)由题意得:甲旅行团门票总费用:20x+8y;乙旅行团门票总费用:20×2x+8×y=40x+4y;(2)甲旅行团门票总费用:20x+8y=20×10+8×6=248(元);乙旅行团门票总费用:40x+4y=40×10+4×6=424(元),248+424=672(元).答:两个旅行团的门票总费用是672元42.(1)剩余部分的面积为:(60×40﹣4x2)cm2;(2)盒子的体积为:x(60﹣2x)(40﹣2x)cm3;当x=5时,原式=5(60﹣10)(40﹣10)=7500cm3;答:盒子的体积为7500立方厘米43.(1)∵第1排a个座位,后面每排比第一排多1个座位,(2)根据题意得:a+(a+1)+(a+2)+…+(a+9)=10a+(1+9)×9÷2=10a+45答:前10排共有10a+45个座位;(3)∵第11排有(a+10)个座位,第5排有(a+4)个座位,∴第11排比第5排多的座位数是:(a+10)﹣(a+4)=6(个);则第11排比第5排多6个座位44.(1)阴影部分的面积为:a(b﹣a)(3分);(2)当a=5cm,b=7cm时,原式=5×(7﹣5)=10cm2 45.(1)100(4x+1)+10x+x2(1分)=400x+100+10x+x2=x2+410x+100(2分);(2)当x=0时,x2+410x+100=100,当x=1时,x2+410x+100=511,当x=2时,x2+410x+100=924,当x取3,4,…,9时,4x+1>9,不合题意.由上可知,这个三位数是100或511或924.(4分)46.(1)∵第一队植树x棵,第二队植的树比第一队的2倍少80棵,∴第二队的植树棵数为:2x﹣80,∵第三队植的树比第二队植树多了10%.∴第三队的植树棵数为:(2x﹣80)(1+10%),所以三个队共植树:x+2x﹣80+(2x﹣80)(1+10%)=x﹣168,(2)当x=100棵时,全体同学共植树:x﹣168=×100﹣168=352(棵)47.根据题意可知:当x≤2,支出费用为:5元,若某人乘坐出租车x(x>2)千米的付费=5+1.8×(x﹣2),整理得:应付费用为:1.4+1.8x48.(1)1.5a(1分)(2)1.5a(1﹣20%);a(1+40%)各(1分)(3)2010年总收入250万元,(1分)2011年总收入260万元,(1分)260﹣250=10万元.(1分)答:该企业2011年总收入比2010年总收入增加了10万元49.(1)阴影部分的面积:;(2)阴影部分的面积:,故答案为ab ,.(2)学校要印2600份材料,在甲厂印费用=0.2×2600+500=1020(元);在乙厂印费用=0.4×2600=1040元,∵1020<1040,∴在甲厂印刷比较合算51.1)A城市与B城市之间的距离:80t,从A城市到B 城市的时间:小时,答:需要小时.(3分)(2)由题意:t ﹣=t ﹣=t ﹣=(7分)答:可以提前小时到达52.(1)当n≤100时,买n本笔记本所需的钱数是:2.3n,当n>100时,买n本笔记本所需的钱数是:2.2n;(2)因为2.3n>2.2n,所以会出现多买比少买付钱少的情况;(3)如果需要100本笔记本,购买101本笔记本,比较省钱53.(1)根据题意可得:当x=850时,在甲商场没有优惠,在乙商场有优惠,费用是:500+(850﹣500)×95%=8332.5(元),故在乙商场买合算;(2)当x>1000时:在甲商场的费用是:1000+(x﹣1000)×90%=0.9x+100;在乙商场的费用是:500+(x﹣500)×95%=0.95x+25;(3)把x=1700代入(2)中的两个代数式:0.9x+100=0.9×1700+100=1630,0.95x+25=0.95×1700+25=1635,∵1635>>1630,∴选择甲商场合算54.(1)3a+b,(2)(a﹣b)2,(3)5x+2.55.(1)(2a+b)、(a+2b)…(2分)(2)①依题意可得:(2a+b)(a+2b)=2a2+4ab+ab+2b2=(2a2+5ab+2b2)cm2…(4分)②依题意得a2﹣b2=33即(a+b)(a﹣b)=33又2(a+b)=22即a+b=11①∴a﹣b=3②…(6分)由①②式可求得解得:a=7,b=4当a=7,b=4时,2a2+5ab+2b2=2×72+5×7×4+2×42=270答:这张长方形大铁皮的面积是270cm2.…(8分)(3)共有下列四种方案可供选择:V2=a2bV3=a2bV4=ab2…(12分)∴V1=V4,V2=V3∴V1﹣V2=ab2﹣a2b=ab(b﹣a)∵a>b∴V1=V4<V2=V3∴方案②与③的体积最大.56.(1)由已知得:A日出租车司机比正常情况少行驶:vt﹣(t﹣2)(v﹣5)=2v+5t﹣10(米);(2)由已知得:B日出租车司机比正常情况多行驶(t+2)(v+5)﹣vt=2v+5t+10(米)①,又由(1)和已知的得:2v+5t﹣10=120,将2v+5t=130代入①得140(米).答:B日出租车司机比平时多行驶140千米57.(1)由题意得:应付的车费为:7+(m﹣3)×1.8=1.8m+1.6(元)即他应付1.8m+1.6元车费;(2)由(1)知,如果有人乘计程车行驶了m千米(m >3),那么他应付1.8m+1.6元车费,此时甲乘出租车行驶了4km,所以1.8×4+1.6=8.8(元),即他应付车费8.8元;(3)由(1)知,如果有人乘计程车行驶了m千米(m >3),那么他应付1.8m+1.6元车费,此时游客付了10.6元,则可列出方程为:1.8m+1.6=10.6解得:m=5,即从西区大润发到文昌楼大约有5公里58.AB+BC的长=A→C的长,为x,∵CD=0.6米,∴A→C→D的长=x+0.6,A→B→D的长=x﹣0.6,猫的速度=,老鼠的速度=.故答案为:x;x+0.6;x﹣0.6;;.59.(1)此人乘车的次数m,则月票余额是:50﹣0.8m;(2)50﹣0.8m≥0,故答案为:(1)(50﹣0.8m).60.∵一本小说共m 页,一位同学第一天看了全书的少6页,∴第一天看了m﹣6,剩下m ﹣(m﹣6)=m+6,∵第二天看了剩下的多6页,∴第二天看了,剩下:,当m=900时,(页).。
专题02 代数式(解析版)

2022-2023学年七年级数学上册章节同步实验班培优题型变式训练(北师大版)专题02 代数式【题型1】代数式表示数、图形的规律1.(2022·河北廊坊·七年级期末)如图.用棋子按规律摆出下列一组图形,据此规律,第2022个,图形棋子的枚数为( )A.6065B.6068C.6069D.6071【答案】B【分析】由所给的图形不难看出第n个图形所棋子枚数是:3n+2,从而可求解.【详解】解:∵第1个图形棋子枚数为:5=3×1+2,第2个图形棋子枚数为:5+3=3×2+2,第3个图形棋子枚数为:5+3+3=3×3+2,∴第n 个图形棋子枚数为:3n +2,∴第2022个图形棋子枚数为:3×2022+2=6068,故B 正确.故选:B .【点睛】此题考查图形的变化规律,找出图形之间的联系,得出规律是解题的关键.【变式1-1】2.(2022·黑龙江大庆·期中)观察下面一系列等式:23181-=´,22531682-==´,22752483-==´,22973284,-==´…分析其规律,并用含有a 的字母表示这个规律__________.【答案】()()2221218a a a+--=【分析】根据题意观察式子,发现等式的左边为连续的两个奇数的平方差,右边为8与从1开始的自然数的乘积,据此用代数式表示即可求解.【详解】解:23181-=´,22531682-==´,22752483-==´,22973284,-==´…分析其规律,可得()()2221218a a a +--=.故答案为:()()2221218a a a +--=.【点睛】本题考查了用代数式表示式子的规律,发现规律是解题的关键.【题型2】代数式的书写方法1.(2021·福建·晋江市磁灶中学七年级期中)下列代数式书写规范的是( )A .2m n ´B .526abC .a b ¸D .3xD、该选项正确.故选D.【点睛】本题考查了代数式的书写要求,解决本题的关键是掌握代数式的书写要求.要求:(1)数与字母,字母与字母相乘,乘号可以省略,也可写成“.”;(2)数字要写在前面;(3)带分数一定要写成假分数;(4)在含有字母的除法中,一般不用“÷”号,而写成分数的形式.【变式2-1】2.(2022·全国·七年级课时练习)将下列各式按照列代数式的规范要求重新书写:(1)a×5,应写成_______ ;(2)S÷t应写成_________;(3)123a a b´´-´,应写成______;(4)413x, 应写成______.【题型3】代数式表示的实际意义1.(2022·内蒙古通辽·七年级期末)下列赋予4m实际意义的叙述中不正确的是()A.若一个两位数中的十位数字和个位数字分别为4和m,则4m表示这个两位数B.若正方形的边长为m厘米,则4m表示这个正方形的周长(单位:厘米)C.若葡萄的价格是4元/千克,则4m表示买m千克葡萄的金额(单位:元)D.若一辆汽车行驶的速度是m千米/小时,则4m表示该汽车4小时行驶的路程(单位:千米)【答案】A【分析】根据两位数的表示=十位数字×10+个位数字;正方形周长=边长×4;金额=单价×重量;路程=速度×时间进行分析即可.【详解】解:A、若一个两位数中的十位数字和个位数字分别为4和m,则(4×10+m)表示这个两位数,原说法不正确,故此选项符合题意;B、若正方形的边长为m厘米,则4m表示这个正方形的周长,原说法正确,故此选项不符合题意;C、若葡萄的价格是4元/千克,则4m表示买m千克葡萄的金额,原说法正确,故此选项不符合题意;D、若一辆汽车行驶的速度是m千米/小时,则4m表示该汽车4小时行驶的路程,原说法正确,故此选项不符合题意;故选:A.【点睛】本题主要考查代数式,解题的关键是掌握代数式的书写规范和实际问题中数量间的关系.【变式3-1】2.(2022·江苏·七年级)某超市的苹果价格如图,试说明代数式100﹣9.8x的实际意义__.【答案】用100元买每斤9.8元的苹果x斤余下的钱【分析】根据题意结合图片得出代数式100﹣9.8x的实际意义.【详解】解:代数式100﹣9.8x 的实际意义为:用100元买每斤9.8元的苹果x 斤余下的钱.故答案为:用100元买每斤9.8元的苹果x 斤余下的钱.【点睛】此题主要考查了代数式,结合题意利用图片得出是解题关键.【题型4】求代数式的值1.(2021·湖北·公安县教学研究中心七年级阶段练习)已知|2|a =-,则a -5=( )A .3-B .3C .7-D .7【答案】A【分析】由绝对值的意义求出a 的值,再代入a -5中计算即可.【详解】∵|2|a =-,∴2a =,∴a -5=2-5=-3.故选A .【点睛】本题考查求一个数的绝对值,代数式求值.掌握正数和0的绝对值是它本身,负数的绝对值是它的相反数是解题关键.【变式4-1】2.(2021·江西·宜春九中七年级阶段练习)已知150y x -++--=,则x y +=__________.一.选择题1.(2022·全国·七年级专题练习)某商店促销的方法是将原价x 元的衣服以(0.8x ﹣10)元出售,意思是( )A .原价减去10元后再打8折B .原价打8折后再减去10元C .原价减去10元后再打2折D .原价打2折后再减去10元【答案】B【分析】根据先算乘法可知先打折,再减价.【详解】解:将原价x 元的衣服以(0.8x ﹣10)元出售,意思是原价打8折后再减去10元,故选:B .【点睛】本题考查代数式的实际意义.理解运算中乘为打折,减是减价是解题关键.2.(2021·湖南·宁远县教研室七年级期中)下列式子中不是代数式的是( )A .32a b +B .52+C .1a b +=D .1b a +【答案】C【分析】根据代数式的定义:用基本运算符号(基本运算包括加减乘除、乘方和开方)把数或表示数的字母连接起来的式子,由此可排除选项.【详解】解:A 、是代数式,故不符合题意;B 、是代数式,故不符合题意;C 、中含有“=”,不是代数式,故符合题意;D 、是代数式,故不符合题意;故选C .【点睛】本题主要考查代数式的定义,熟练掌握代数式的定义是解题的关键.3.(2022·全国·七年级专题练习)下列各式中,符合整式书写规则的是( )A .5x ´B .72xyC .124xyD .1x y-¸【答案】B【分析】利用代数式的书写要求分别判断得出答案.【详解】解:A 、5x ´不符合代数式的书写要求,应为5x ,故此选项不符合题意;4.(2022.湖北.利川市思源实验学校七年级阶段练习)小王利用计算机设计了一个程序,输入和输出的数据如下表:输入 (1)2345…输出…1225310417526…那么,当输入数据8时,输出的数据是( )A .861B .863C .865D .8675.(2021·全国·七年级单元测试)已知3257x y -+=,那么多项式15102x y -+的值为( )A .8B .10C .12D .35【答案】C【分析】由多项式3257x y -+=,可求出322x y -=,从而求得1510x y -的值,继而可求得答案.【详解】解:∵3257x y -+=∴322x y -=∴151010x y -=∴1510+2x y -10+212==故选C .【点睛】本题考查了求多项式的值,关键在于利用“整体代入法”求代数式的值.6.(2019·海南·中考真题)当m =-1时,代数式2m+3的值是( )A .-1B .0C .1D .2【答案】C【分析】将=1m -代入代数式即可求值;【详解】解:将=1m -代入232(1)31m +=´-+=;故选C .【点睛】本题考查代数式求值;熟练掌握代入法求代数式的值是解题的关键.二、填空题7.(2018·上海·中考真题)某商品原价为a 元,如果按原价的八折销售,那么售价是_____元.(用含字母a 的代数式表示).【点睛】本题考查了销售问题、列代数式,弄清题意,列出符合题意的代数式是解题的关键.8.(2020·河北·模拟预测)若4x y +=,a ,b 互为倒数,则1()52x y ab ++的值是_________9.(2019·广东·中考真题)已知23x y =+,则代数式489x y -+的值是_____.【答案】21【分析】由已知可得x-2y=3,继而对所求的式子进行变形后,利用整体代入思想即可求得答案.【详解】∵x=2y+3,∴x-2y=3,∴4x-8y+9=4(x-2y)+9=4×3+9=21,故答案为21.【点睛】本题考查了代数式求值,正确的进行变形是解题的关键.10.(2022·全国·七年级课时练习)某书店新进了一批图书,甲、乙两种书的进价分别为4元/本、5元/本.现购进m 本甲种书和n 本乙种书,共付款Q 元.(1)用含m ,n 的代数式表示Q =______;(2)若共购进3510´本甲种书及3310´本乙种书,Q =______(用科学记数法表示).【答案】 4m +5n 43.510´【分析】(1)根据题意列代数式即可;(2)根据题意列出算式进行化简即可.【详解】解:(1)由题意,得Q =4m +5n ;(2)Q =4×3510´+5×3310´=20×310+15×310=35×310=43.510´.故答案为:4m +5n ,43.510´.【点睛】本题考查了整式中的列代数式,科学记数法的运算,正确地理解能力和计算能力是解决问题的关键.三、解答题11.(2021·全国·七年级单元测试)如图所示,有长为l 的篱笆,利用它和一面墙围城长方形园子,在园子的长边上开了1米的门,园子的宽为t .(1)用关于l ,t 的代数式表示园子的面积.(2)当l =100m ,t =30m 时,求园子的面积.【答案】(1)()12S l t t =+-;(2)21230m 【分析】(1)表示出长,利用长方形的面积列出算式即可;(2)把l =100m ,t =30m 代入(1)求得答案即可;【详解】解:(1)宽为t,长为:l +1-2t 面积为:()12S l t t =+-(2)当l =100m ,t =30m 时S=()()12100123030l t t +-=+-´´=1230故园子的面积为21230m 【点睛】本题考查根据实际,列出代数式,再代入求值,关键在于找到等量关系.12.(2022·全国·七年级专题练习)(1)观察下面的点阵图与等式的关系,并填空:第1个点阵2213112++=+第2个点阵13531++++=______+______第3个点阵++++++=______+______.1357531(2)通过猜想,写出第n个点阵相对应的等式.【答案】(1)22,32,32,42(2)1+3+5+…+(2n﹣1)+(2n+1)+(2n﹣1)+…+5+3+1=n2+(n+1)2【分析】(1)根据点阵图即可求解;(2)根据(1)中的3个等式得出规律,进而写出第n个点阵相对应的等式.【详解】(1)第1个点阵1+3+1=12+22,第2个点阵1+3+5+3+1=22+32,第3个点阵1+3+5+7+5+3+1=32+42.故答案为22,32,32,42;(2)根据(1)中的3个等式,可以发现,第n个点阵的对角点最多有2n+1个,而且等号右侧是22++,n n(1)∴第n个点阵相对应的等式为:1+3+5+…+(2n﹣1)+(2n+1)+(2n﹣1)+…+5+3+1=n2+(n+1)2.【点睛】本题考查了规律型:图形的变化类,要求学生通过观察,分析、归纳发现其中的规律.13.(2022·全国·七年级专题练习)用同样大小的两种不同颜色(白色.灰色)的正方形纸片,按如图方式拼成长方形.[观察思考]第(1)个图形中有212=´张正方形纸片;´+==´张正方形纸片;第(2)个图形中有2(12)623´++==´张正方形纸片;第(3)个图形中有2(123)1234第(4)个图形中有2(1234)2045´+++==´张正方形纸片;……以此类推(1)[规律总结]第(5)个图形中有__________张正方形纸片(直接写出结果).(2)根据上面的发现我们可以猜想:123n ++++=L __________.(用含n 的代数式表示)(3)[问题解决]根据你的发现计算:101102103200++++L .14.(2022·全国·七年级专题练习)特殊值法,又叫特值法,是数学中通过设题中某个未知量为特殊值,从而通过简单的运算,得出最终答案的一种方法.例如:已知:432432106a x a x a x a x a x ++++=,则:①取0x =时,直接可以得到00a =;②取1x =时,可以得到432106a a a a a ++++=;③取1x =-时,可以得到432106a a a a a -+-+=-;④把②,③的结论相加,就可以得到4222a a +020+=a ,结合①00a =的结论,从而得出420a a +=.请类比上例,解决下面的问题:已知654326543210(1)(1)(1)(1)(1)(1)4a x a x a x a x a x a x a x -+-+-+-+-+-+=.求:(1)0a 的值;(2)6543210++++++a a a a a a a 的值;(3)642a a a ++的值.【答案】(1)4(2)8(3)0【分析】(1)观察等式可发现只要令x =1即可求出a 0;(2)观察等式可发现只要令x =2即可求出a 6+a 5+a 4+a 3+a 2+a 1+a 0的值;(3)令x =2即可求出等式①,令x =0即可求出等式②,两个式子相加即可求出来.(1)解:当1x =时,∵654326543210(1)(1)(1)(1)(1)(1)4a x a x a x a x a x a x a x -+-+-+-+-+-+=,∴0414a =´=;(2)解:当2x =时,∵654326543210(1)(1)(1)(1)(1)(1)4a x a x a x a x a x a x a x -+-+-+-+-+-+=,∴65432108a a a a a a a +++++=+;(3)解:当2x =时,∵654326543210(1)(1)(1)(1)(1)(1)4a x a x a x a x a x a x a x -+-+-+-+-+-+=,∴65432108a a a a a a a +++++=+①;当0x =时,∵654326543210(1)(1)(1)(1)(1)(1)4a x a x a x a x a x a x a x -+-+-+-+-+-+=,∴65432100+-++=--a a a a a a a ②;用①+②得:406282222++=+a a a a ,∴642040a a a a ++=-=.【点睛】本题主要考查代数式求值问题,合理理解题意,整体思想求解是解题的关键.15.(2019·贵州贵阳·中考真题)如图是一个长为a ,宽为b 的矩形,两个阴影图形都是一对底边长为1,且底边在矩形对边上的平行四边形.(1)用含字母a ,b 的代数式表示矩形中空白部分的面积;(2)当a =3,b =2时,求矩形中空白部分的面积.【答案】(1)S =ab ﹣a ﹣b +1;(2)矩形中空白部分的面积为2;【分析】(1)空白区域面积=矩形面积-两个阴影平行四边形面积+中间重叠平行四边形面积;(2)将a=3,b=2代入(1)中即可;【详解】(1)S =ab ﹣a ﹣b +1;(2)当a=3,b=2时,S=6﹣3﹣2+1=2;【点睛】本题考查阴影部分面积,平行四边形面积,代数式求值;能够准确求出阴影部分面积是解题的关键.。
代数式典型例题专项练习30题(有答案)

.代数式专项练习30题(有答案)一.选择题(共5小题)1.在1,a,a+b,,x2y+xy2,3>2,3+2=5中,代数式有()A .3个B.4个C.5个D.6个2.下列各式:﹣x+1,π+3,9>2,,,其中代数式的个数是()A .5 B.4 C.3 D.23.下列各式:①1x;②2•3;③20%x;④a﹣b÷c;⑤;⑥x﹣5;其中,不符合代数式书写要求的有()A .5个B.4个C.3个D.2个4.在下列的代数式的写法中,表示正确的一个是()A.“负x的平方”记作﹣x2B.“a除以2b 的商”记作C.“x的3倍”记作x3 D.“y与的积”记作5.下列说法正确的是()A.x是代数式,0不是代数式B.表示a与b的积的代数式为a+bC.a、b两数和的平方与a、b两数积的2倍的和为(a+b)2+2abD.意义是:a与b的积除y的商二.填空题(共13小题)6.代数式“5x”,可解释为:“小明以5千米/时的速度走了x小时,他一共走了5x千米”.请你对“5x”再给出一个身边生活中的解释:_________ .7.叙述下列代数式的意义.(1)(x+2)2可以解释为_________ .(2)某商品的价格为n元.则80%n可以解释为_________ .8.一个三位数的百位数字是2,十位数字与个位数字组成的两位数为x,用代数式表示这个三位数为_________ .9.x表示一个两位数,y表示一个三位数,把x放在y的右边组成一个五位数,则这个五位数可以表示为_________ .10.m个数的平均数为a,n个数的平均数为b,这m+n个数的平均数为_________ .11.一本书共n页,小华第一天读了全书的,第二天读了剩下的,则未读完的页数是_________ .(用含n的式子表示)12.(1)已知a﹣b=3,则3a﹣3b= _________ ,5﹣4a+4b= _________ .(2)已知x+5y﹣2=0,则2x+3+10y= _________ .(3)已知3x2﹣6x+8=0,则x2﹣2x+8= _________ .13.若a,b互为倒数,c,d互为相反数,则3c+3d﹣9ab= _________ .14.已知代数式ax3+bx,当x=﹣1时,代数式的值为5;则当x=1时,ax3+bx的值是_________ .15.任意写出x3y的3个同类项:_________ ,_________ ,_________ .16.已知7x m y3和﹣是同类项,则(﹣n)m= _________ .17.若单项式3x4y n与﹣2x2m+3y3的和仍是单项式,则(4m﹣n)n= _________ .18.已知x5y n与﹣3x2m+1y3n﹣2是同类项,则m+n= _________ .三.解答题(共12小题)19.如图,池塘边有一块长为18米,宽为10米的长方形土地,现在将其余三面留出宽都是x米的小路,中间余下的长方形部分做菜地,用代数式表示:(1)菜地的长a= _________ 米,宽b= _________ 米;(2)菜地的面积S= _________ 平方米;(3)求当x=1米时,菜地的面积.20.已知﹣3x4+m y与x4y3n是同类项,求代数式m100+(﹣3n)99﹣mn的值.21.已知关于多项式mx2+4xy﹣x﹣2x2+2nxy﹣3y合并后不含有二次项,求n m的值.22.若关于x、y的方程6x+5y﹣2﹣3Rx﹣2Ry+4R=0合并同类项后不含y项,求R的值.23.k为何值时,多项式x2﹣2kxy﹣3y2+6xy﹣x﹣y中,不含x,y的乘积项.24.去括号,合并同类项(1)﹣3(2s﹣5)+6s;(2)3x﹣[5x﹣(x﹣4)];(3)6a2﹣4ab﹣4(2a2+ab);(4)﹣3(2x2﹣xy)+4(x2+xy﹣6)25.先去括号,后合并同类项:(1)x+[﹣x﹣2(x﹣2y)];(2);(3)2a﹣(5a﹣3b)+3(2a﹣b);(4)﹣3{﹣3[﹣3(2x+x2)﹣3(x﹣x2)﹣3]}.26.观察下列各等式,并回答问题:;;;;…(1)填空:= _________ (n是正整数);(2)计算:….27.观察下面一列数,探求其规律:(1)请问第7个,第8个,第9个数分别是什么数?(2)第2004个数是什么如果这列数无限排列下去,与哪个数越来越接近?28.如图,每个正方形点阵均被一直线分成两个三角形点阵,根据图中提供的信息,用含n的等式表示第n个正方形点阵中的规律_________ .29.下列是幼儿园小朋友用火柴棒拼出的一列图形.仔细观察,找出规律,解答下列各题:(1)第4个图中共有_________ 根火柴,第6个图中有_________ 根火柴;(2)第n个图形中共有_________ 根火柴(用含n的式子表示);(3)请计算第2008个图形中共有多少根火柴.30.如图,用同样规格的黑白两色正方形瓷砖铺设矩形地面,请观察下列图形,探究并解答下列问题.(1)在第1个图中,共有白色瓷砖_________ 块.(2)在第2个图中,共有白色瓷砖_________ 块.(3)在第3个图中,共有白色瓷砖_________ 块.(4)在第10个图中,共有白色瓷砖_________ 块.(5)在第n个图中,共有白色瓷砖_________ 块.代数式典型例题30题参考答案:1.解:在1,a,a+b,,x2y+xy2,3>2,3+2=5中,代数式有1,a,a+b,,x2y+xy2,共5个.故选C2.解:题中的代数式有:﹣x+1,π+3,共3个.故选C.3.解:①1x分数不能为假分数;②2•3数与数相乘不能用“•”;③20%x,书写正确;④a﹣b÷c不能出现除号;⑤,书写正确;⑥x﹣5,书写正确,不符合代数式书写要求的有①②④共3个.故选:C4.解:“负x的平方”记作(﹣x)2;“x的3倍”记作3x;“y与的积”记作y.故选B5.解:A、x是代数式,0也是代数式,故选项错误;B、表示a与b的积的代数式为ab,故选项错误;C、正确;D、意义是:a与b的和除y的商,故选项错误.故选C6.解:答案不唯一,如买一支钢笔5元,买x支钢笔共5x元7.解:(1)(x+2)2可以解释为正方形的边长为x+2,则它的面积为(x+2)2;(2)某商品的价格为n元.则80%n可以解释为这件商品打八折后的价格.故答案为:(1)正方形的边长为x+2,则它的面积为(x+2)2;(2)这件商品打八折后的价格8.解:根据题意得此三位数=2×100+x=200+x9.解:两位数x放在一个三位数y的右边相当于y扩大了100倍,那么这个五位数为(100y+x)10.解:这m+n个数的平均数=.故答案为:.11.解:小华第一天读了全书的,还剩下(1﹣)n=n;第二天读了剩下的,即(1﹣)n×=n.则未读完的页数是n12.解:(1)∵a﹣b=3,∴3a﹣3b=3,5﹣4a+4b=5﹣4(a﹣b)=5﹣4=1;(2)∵x+5y﹣2=0,∴x+5y=2,∴2x+3+10y=2(x+5y)+3=2×2+3=7;(3)∵3x2﹣6x+8=0,∴x2﹣2x=﹣,∴x2﹣2x+8=﹣+8=.故答案为:(1)3,1;(2)7;(3)13.解:因为a,b互为倒数,c,d互为相反数,所以ab=1,c+d=0,所以3c+3d﹣9ab=3(c+d)﹣9ab=0﹣9=﹣9,故答案为:﹣914.解:由题意知:﹣a﹣b=5所以a+b=﹣5;则当x=1时,ax3+bx=a+b=﹣515.解:开放题,答案无数个,只要所写同类项,所含字母相同且相同字母的指数也相同即可,同类项与字母的顺序无关.如5x3y,12x3y,20x3y.故答案为:5x3y,12x3y,20x3y16.解:由同类项的定义可知m=2,n=3,代入(﹣n)m,结果为9.答:(﹣n)m值是917.解:两个单项式的和是单项式,则它们是同类项,则2m+3=4,m=;n=3.则(4m﹣n)n=(4×﹣3)3=﹣1.答:(4m﹣n)n=﹣118.解:x5y n与﹣3x2m+1y3n﹣2是同类项,2m+1=5,n=3n﹣2,m=2,n=1,m+n=2+1=3,故答案为:319.解:(1)∵其余三面留出宽都是x米的小路,∴由图可以看出:菜地的长为18﹣2x米,宽为10﹣x米;(2)由(1)知:菜地的长为18﹣2x米,宽为10﹣x米,所以菜地的面积为S=(18﹣2x)•(10﹣x);(3)由(2)得菜地的面积为:S=(18﹣2x)•(10﹣x),当x=1时,S=(18﹣2)(10﹣1)=144m2.故答案分别为:(1)18﹣2x,10﹣x;(2)(18﹣2x)(10﹣x);(3)144m220.解:∵﹣3x4+m y与x4y3n是同类项,∴4+m=4,3n=1,∴m=0,n=,∴m100+(﹣3n)99﹣mn=0+(﹣1)﹣0=﹣121.解:∵多项式mx2+4xy﹣x﹣2x2+2nxy﹣3y合并后不含有二次项,即二次项系数为0,即m﹣2=0,∴m=2;∴2n+4=0,∴n=﹣2,把m、n的值代入n m中,得原式=422.解:∵6x+5y﹣2﹣3Rx﹣2Ry+4R=0合并同类项后不含y项,∴5﹣2R=0,解得R=2.523.解:原式=x2+(﹣2k+6)xy﹣3y2﹣y,∵不含x,y的乘积项,∴x,y的乘积项的系数为0,∴﹣2k+6=0,∴2k=6,∴k=3.∴当k=3时,已知多项式不含x,y的乘积项24.(1)﹣3(2s﹣5)+6s=﹣6s+15+6s=15;(2)3x﹣[5x﹣(x﹣4)]=3x﹣[5x﹣x+4]=3x﹣5x+x﹣4=﹣x+4;(3)6a2﹣4ab﹣4(2a2+ab)=6a2﹣4ab﹣8a2﹣2ab=﹣2a2﹣6ab;(4)﹣3(2x2﹣xy)+4(x2+xy﹣6)=﹣6x2+3xy+4x2+4xy﹣24=﹣2x2+7xy﹣2425.(1)x+[﹣x﹣2(x﹣2y)]=x﹣x﹣2x+4y=﹣2x+4y;(2)原式=a﹣a﹣﹣+b2=;(3)2a﹣(5a﹣3b)+3(2a﹣b)=2a﹣5a+3b+6a﹣3b=3a;(4)﹣3{﹣3[﹣3(2x+x2)﹣3(x﹣x2)﹣3]},=﹣3{9(2x+x2)+9(x﹣x2)+9},=﹣27(2x+x2)﹣27(x﹣x2)﹣27,=﹣54x﹣27x2﹣27x+27x2﹣27,=﹣81x﹣2726.解:(1)﹣;(2)原式=1﹣+﹣++…+﹣=1﹣=27.解:(1)∵第n个数是(﹣1)n,∴第7个,第8个,第9个数分别是﹣,,﹣.(2),最后与0越来越接近28.解:通过图案观察可知,当n=1时,点的个数是12=1;当n=2时,点的个数是22=4;当n=3时,点的个数是32=9;当n=4时,点的个数是42=16,…∴第n个正方形点阵中有n2个点,∴第n个正方形点阵中的规律是=n2.29.解:根据图案可知,(1)第4个图案火柴有3×4+1=13;第6个图案中火柴有3×6+1=19;(2)当n=1时,火柴的根数是3×1+1=4;当n=2时,火柴的根数是3×2+1=7;当n=3时,火柴的根数是3×3+1=10;所以第n个图形中火柴有3n+1.(3)当n=2008时,3n+1=3×2008+1=602530.解:(1)在第1个图中,共有白色瓷砖1×(1+1)=2块,(2)在第2个图中,共有白色瓷砖2×(2+1)=6块,(3)在第3个图中,共有白色瓷砖3×(3+1)=12块,(4)在第10个图中,共有白色瓷砖10×(10+1)=110块,(5)在第n个图中,共有白色瓷砖n(n+1)块。
3.2 代数式(练习)(解析版)

第三章代数式3.2代数式一、单选题1.下列说法正确的是()A .212x π的次数是3B .12是单项式C .24x -的系数为4D .3是单项式()3x y -的系数A .273xB .14a ⨯C .126p -D .2y ÷zA .2231x xy --是二次三项式B .1x -+不是单项式C .223xy π-的系数是23π-D .222xyb -的次数是6【详解】解:A .2231x xy --是二次三项式故选项正确,不符合题意;A .a 2B .2aC .2aD .a +2A .若葡萄的价格是4元/千克,则4a 表示买a 千克该种葡萄的金额B .若a 表示一个正方形的边长,则4a 表示这个正方形的周长C .一辆汽车以a 千米/小时的速度行驶,从A 城到B 城需4小时,则4a 表示A ,B 两城之间的路程D .若4和a 分别表示一个两位数中的十位数字和个位数字,则4a 表示这个两位数【详解】解:A .若葡萄的价格是4元/千克,则4a 表示买a 千克葡萄的金额,原说法正确,故此选项不符合题意;B .若a 表示一个正方形的边长,则4a 表示这个正方形的周长,原说法正确,故此选项不符合题意;C .一辆汽车以a 千米/小时的速度行驶,从A 城到B 城需4小时,则4a 表示A ,B 两城之间的路程,原说法正确,故此选项不符合题意;D .若4和a 分别表示一个两位数中的十位数字和个位数字,则40+a 表示这个两位数,原说法错误,故此选项符合题意;故选:D .6.下列各式中,不是整式的是()A .3a B .12x C .0D .x +y【详解】解:A 、3a 是整式,不符合题意;57x 9x ……A .(2n -1)n x B .(2n +1)n x C .(n -1)n x D .(n +1)n x 【详解】解:依题意,得第n 项为(2n -1)xn ,故选:A .8.如果整式252n x x --+是关于x 的二次三项式,那么n 等于()A .3B .4C .5D .6【详解】解:∵多项式252n x x --+是关于x 的二次三项式,∴n -2=2,解得n =4,故选:B .9.给出下列判断:①单项式32510x ⨯的系数是5;②2x xy y -+是二次三项式;③多项式2223721a b a b ab -+-+的次数是9;④几个有理数相乘,当负因数有奇数个时,积为负.其中正确的判断有()A .1个B .2个C .3个D .4个【详解】①单项式32510x ⨯的系数是3510⨯,故结论错误;②2x xy y -+是二次三项式,故结论正确;③多项式2223721a b a b ab -+-+的次数是4,故结论错误;④几个有理数相乘,当负因数有奇数个时,积为负.若任意一个有理数为0,则积为0,故结论错误.综上所述,只有②一个结论是正确的.故选:A .10.下列代数式212,,3,,84a b x m m x π-++-,其中整式有()A .1个B .2个C .3个D .4个11.多项式3x 2y 2﹣2xy 213-xy 的二次项系数为_____.12.下列各式:0,1x -,F =ma ,m +2>m ,2x 2﹣3x +11,B≠12,3,﹣y ,6π,其中代数式的有_____个.【详解】解:∵﹣x ,x 3,﹣x 5,x 7,﹣x 9,…,∴第n 个单项式是(﹣1)nx 2n ﹣1,∴第15个单项式是(﹣1)15x2×15﹣1∴第15个单项式是﹣x 29,故答案为:﹣x 29.14.在代数式a ,π,43ab ,a ﹣b ,2a b +,x 2+x +1,5,2a ,1x x +中,整式有__个;单项式有__个,次数为2的单项式是_;系数为1的单项式是_.是五次四项式.【详解】解:∵多项式()4223n x m x y xy +++﹣是五次四项式,∴1=520n m ++≠,,解得,=42n m ≠,﹣,故答案为:=42n m ≠,﹣.三、解答题16.观察下列各式:﹣a ,12a 2,﹣14a 3,18a 4,﹣116a 5,132a 6,…(1)写出第2014个和2015个单项式;(2)写出第n 个单项式.①a 2b +ab ﹣b 2,②2a b +,③23xy ,④3x y -+,⑤0,⑥2x ,⑦2x (1)单项式;(2)多项式;(3)整式.【答案】(1)③⑤⑦(2)①②(3)①②③⑤⑦18.把下列各代数式的序号填入相应集合的括号内:①2a 2b +213ab ;②1a b -;③0;④223m n +;⑤﹣25mn ;⑥2x ﹣3y =5;⑦2a +6abc +3k 单项式集合:{};多项式集合:{};二项式集合:{}.【详解】解:单项式集合:{③,⑤,……};多项式集合:{①,④,⑦,……};二项式集合:{①,③,……}。
列代数式专项练习60题(有答案)ok

列代数式专项练习60题(有答案)1.正方体棱长为a,体积为V,则V与a之间的关系式为_________ ,当a=4cm时,V= _________ cm3.2.一个数比a的3倍的平方小3,则这个数是_________ .3.体校里男学生人数是m,女学生人数是n,教练人数和学生人数的比是1:20,则教练人数是_________ .4.某商品的进价是x元,售价是132元,则此商品的利润是_________ .5.“x的2倍与y的3倍的差”列式为_________ .6.在负整数a后添上3,使其位数增加一位,则这个数可表示为_________ .7.若一个数比x的2倍小3,则这个数可表示为_________ .8.“比a的3倍小2的数”用整式表示是_________ .9.“x与y的和”用代数式可以表示为_________ .10.用代数式表示“a的3倍与4的和”为_________ .11.某校共有学生x人,其中女生占总数的m%,则男生人数为_________ 人.12.某商品进价是m元,提价30%后标价,又打九折出售,则该商品的利润是_________ .13.一个笼子里的鸡a只,兔b只,则笼子里的鸡和兔的脚共有_________ 只.14.某工厂的产值由a万元增加了20%,达到_________ 万元.15.一台a元的电视机,降价20%后的价格为_________ 元.16.某工厂今年的产值是a万元,比去年增加了20%,则去年的产值是_________ .17.苹果每千克p元,若苹果超过10千克以上,则全部9折优惠,买15千克应付_________ 元.18.张红在一次考试中,得数学a分,语文b分,则张红这二科的平均成绩是_________ 分.19.科学家在南极考察时,拾到一块不规则的矿石,科学家用一把刻度尺,一只圆柱体的玻璃杯和足量的水,就测出了这块矿石的体积.如果玻璃杯的内直径为r,把矿石完全浸没在水中,测出杯中水面上升的高度为h,则这块矿石的体积是_________ .20.一件商品原价为a元,先涨价5元后,再按8.5折出售,那么现售价用代数式表示为_________ .21.如图,正方形的边长为2,分别以正方形的两个相对顶点为圆心,以正方形的一边为半径画弧,则阴影部分的面积是_________ .22.如图是数值转换器的示意图,如果输入的数字用x表示,那么输出的数字可以用代数式_________ 表示.23.小亮从一列火车的第m节车厢起,一直数到第2m节车厢,他数过的车厢节数是_________ .24.小明在考试前到文具店里买了2支2B的铅笔和一副三角板,2B的铅笔每支x元,三角板每副3元,小明总共应付_________ 元(用含x的代数式表示).25.三毛早上从报社以每份0.4元的价格购进了a份报纸.以每份0.5元的价格出售,一天共售b份报纸,剩余的报纸以每份0.2元的价格退回报社,回家后三毛发现这一天的辛苦还是赚到了钱,那么三毛这天赚了_________ 元.26.n(n≥2)个球队进行单循环赛(参加比赛的每个队都与其他所有的队各赛一场),总的比赛场数是_________ .27.绥阳某商店的一种商品每件进价为a元,按进价提高30%标价,再按标价的8折出售,那么打折后,每件商品的售价是_________ 元.28.“圆形方孔钱”是中国古钱币的突出代表.如图,一枚圆形方孔钱的外圆直径为a,中间方孔边长为b,则图示阴影部分面积为_________ .29.右下图是一个数值转换机的示意图.若输入的x是5,y是﹣2,则输出的结果是_________ .30.如图,两个长方形的一部分重叠在一起,重叠部分是边长为3的正方形,则阴影部分的面积是_________ .31.三角形三边的长分别是(2x+1)厘米,(3x﹣2)厘米,(8﹣2x)厘米,求这个三角形的周长,如果x=3,三角形的周长是多少?32.晓霞的爸爸开了一个超市,一天,她爸爸分别以P元进了A、B两种商品,后来A商品提价20%,B商品降价10%,这样在某一天中,A商品卖了10件,B商品卖了20件,问这一天里超市作这两种买卖是赚了还是赔了?并说明理由.33.列代数式:(1)比a与b的积的2倍小5的数;(2)a与b的平方差;(3)被5除商是a,余数是2的数.34.我国出租车收费标准因地而异,A市为:起步价10元,3km后每千米加价1.2元;B市为:起步价8元,3km 后每千米加价1.4元;(1)试分别写出在A,B两城市坐出租车x(x>3)km所付的车费;(2)求在A,B两城市坐出租车x(x>3)km的差价是多少元?35.如图,大正方形的边长为a,小正方形的边长为2,求阴影部分的面积.36.窗户的形状如图,其上部是半圆形,下部是长方形.已知窗户的下部宽为xm,窗户长方形部分高度为1.5xm.计算:(1)窗户的面积S;(2)窗框的总长L.37.“十一”黄金周期间,小刚拿着妈妈给的800元钱到重百商场购买运动服和运动鞋,他来到自己喜欢的“阿迪、达斯”专柜前看到该品牌打出的优惠条件:标价200元以内(含200元)不打折;标价200元以上的按如下方式打折:(1)200~500元(含500元)的部分打9折;(2)500~800元(含800元)的部分打8折;(3)800元以上的部分打7折(商品金额可累计),他又看到运动服标价a元/件(400≤a≤500),运动鞋标价b元/双(300≤b≤400);(1)算他单独买一件运动服需多少钱;(用含a的代数式表示)(2)计算他一次性买一件运动服和一双运动鞋共需多少钱.(用含a、b的代数式表示)38.为了节约用水,某市决定调整居民用水收费方法,规定:如果每户每月用水不超过20吨,每吨水收费3元,如果每户每月用水超过20吨,则超过部分每吨水收费3.8元;小红看到这种收费方法后,想算算她家每月的水费,但是她不清楚家里每月的用水是否超过20吨.(1)如果小红家每月用水15吨,水费是多少.如果每月用水35吨,水费是多少;(2)如果字母x表示小红家每月用水的吨数,那么小红家每月的水费该如何用x的代数式表示呢.39.某轮船顺水航行4小时,逆水航行2.5小时,已知轮船在静水中的速度为m千米/小时,水流速度为y千米/小时.轮船共航行了多少千米?40.一轮船航行于甲、乙两港口之间,在静水中的航速为m千米/小时,水流速度为12千米/小时,(1)则轮船顺水航行5小时的行程是多少?(2)轮船逆水航行4小时的行程是多少?(3)轮船顺水航行5小时和逆水航行4小时的行程相差多少?41.某公园的成人票价是20元,儿童票价是8元,甲旅行团有x名成人和y名儿童;乙旅行团的成人数是甲旅行团的2倍,儿童人数是甲旅行团的.(1)求两个旅行团的门票总费用是多少?(2)当x=10人,y=6人时,求两个旅行团的门票总费用是多少元?42.小明想把一长是60cm,宽为40cm的长方形硬纸片做成一个无盖的长方体盒子,于是在长方形的四个角各剪去一个相同小正方形(如图).(1)若设这些小正方形的边长为xcm,求图中阴影部分小长方形的面积.(2)当x=5时,求这个盒子的体积.43.某礼堂第1排a个座位,后面每排比第一排多1个座位,用含a的代数式表示:(1)第2排有多少个座位?第5排有多少个座位?第10排有多少个座位?(2)前10排共有多少个座位?(3)第11排比第5排多多少个座位?44.如图,正方形ABCD的边长为a,长方形AEFD的长AE为b,(1)用代数式表示图中阴影部分的面积;(2)求当a=5cm,b=7cm时,阴影部分的面积.45.一个三位数,个位上的数是十位上的数的平方,百位上的数比十位上的数的4倍多1.将十位上的数设为x.(1)列式表示这个三位数;(2)这个三位数是多少?46.学校组织初一年级全体同学参加植树造林劳动.全体同学分三队,第一队植树x棵,第二队植的树比第一队植树的两倍少80棵,第三队植的树比第二队植树多了10%.(1)求全体同学一共植树多少棵?(用含x的式子表示)(2)若x=100棵,求全体同学共植树多少棵?47.攀枝花市出租车收费标准为:起步价5元(其中包含2千米),2千米后每千米价1.8元.则某人乘坐出租车x 千米的付费为多少元.(用代数式表示)48.龙港某企业有甲、乙两种经营收入,2010年甲种年收入是乙种年收入的1.5倍,预计2011年甲种年收入将减少20%,而乙种年收入将增加40%,记2010年乙种年收入为a万元.(1)2010年该企业甲种年收入为_________万元;(2)2011年该企业甲种年收入为_________万元;乙种年收入为_________万元.(3)当a=100万元时,请问该企业2011年总收入比2010年总收入是增加,还是减少?增加或减少了多少?请说明理由.49.用代数式表示下列图形中阴影部分的面积.(1)S阴影=_________;(2)S阴影=_________.50.学校需要到印刷厂印刷n份材料,甲印刷厂的收费标准是每份材料收0.2元的印刷费,另收500元的制版费;乙印刷厂的收费标准是每份材料收0.4元印刷费,不收制版费.(1)两个印刷厂的收费各是多少元?(用含n的代数式来表示)(2)学校要印2600份材料,若不考虑其他因素,选择哪家印刷厂比较合算?试说明理由.51.一辆汽车以每小时80千米的速度行驶,从A城市到B城市需要t小时,按题意解决下列问题(1)如果汽车行驶的速度每小时增加v千米,那么从从A城市到B城市还需要多少小时.(2)如果某次因紧急情况,从B城市返回到A城市的平均速度比原来每小时增加12千米,那么预计返回比原来可提前多少时间.52.一种笔记本售价为2.3元/本,如果买100本以上(不含100本),售价为2.2元/本.(1)列式表示买n本笔记本所需的钱数;(2)按照售价规定,会不会出现多买比少买反而付钱少的情况?(3)如果需要100本笔记本,怎样购买更省钱?并说明理由.53.甲、乙两家商场以同样的价格出售同样的电器,但各自推出的优惠方案不同.甲商场规定:凡超过1000元的电器,超出的金额按90%收取;乙商场规定:凡超过500元的电器,超出的金额按95%收取.某顾客购买的电器价格是x元.(1)当x=850时,该顾客应选择在_________商场购买比较合算;(2)当x>1000时,分别用代数式表示在两家商场购买电器所需付的费用;(3)当x=1700时,该顾客应选择哪一家商场购买比较合算?说明理由.54.列代数式:(1)a的3倍与b的和;(2)a与b的差的平方;(3)被5除商是x,余数是2的数.55.如图,将一张长方形大铁皮切割(切痕为虚线)成九块,其中有两块是边长都为a厘米的大正方形,两块是边长都为b厘米的小正方形,且a>b.(1)这张长方形大铁皮长为_________厘米,宽为_________厘米(用含a、b的代数式表示);(2)①求这张长方形大铁皮的面积(用含a、b的代数式表示);②若最中间的小长方形的周长为22厘米,大正方形与小正方形的面积之差为33厘米2,试求a和b的值,并求这张长方形大铁皮的面积;(3)现要从切块中选择5块,恰好焊接成一个无盖的长方体盒子,共有哪几种方案可供选择(画出示意图)?按哪种方案焊接的长方体盒子的体积最大?试说明理由.(接痕的大小和铁皮的厚度忽略不计)56.在正常情况下,某出租车司机每天驾车行驶t小时,且平均速度为v千米/小时.已知他在A日比正常情况少行驶2小时,平均速度比正常情况慢5千米/小时,他在B日比正常情况多行驶2小时,平均速度比正常情况快5千米/小时,(1)求A日出租车司机比正常情况少行驶多少千米?(用含v,t的代数式表示)(2)已知A日出租车司机比正常情况少行驶120千米,求B日出租车司机比正常情况多行驶多少千米?57.已知:我市出租车收费标准如下:乘车路程不超过3km的一律收费7元;超过3km的部分按每千米加1.8元收费.(1)如果有人乘计程车行驶了m千米(m>3),那么他应付多少车费?(列代数式)(2)游客甲乘出租车行驶了4km,他应付车费多少元?(3)某游客乘出租车从西区大润发到文昌楼,付了车费10.6元,试估算从西区大润发到文昌楼大约有多少公里?58.如图为一梯级的纵截面,一只老鼠沿长方形的两边A→B→D路线逃跑,一只猫同时沿梯级(折线)A→C→D的路线去捉,结果在距离C点0.6米的D处,捉住了老鼠.请将下表中的语句“译成”数学语言(写出代数式).设梯级(折线)A→C的长度x米AB+BC的长为A→C→D的长为A→B→D的长为设猫捉住老鼠所用时间为t秒猫的速度老鼠的速度59.某地公交公司推出刷卡月票制,即持有这种月票的乘客通过刷卡扣除每次的车票.某人买了50元的这种月票卡,如果此人乘车的次数用m表示,每次乘车的余额用n表示,它们之间的关系如下表:乘车次数m 月票余额n/元1 50﹣0.82 50﹣1.63 50﹣2.44 50﹣3.2……回答下列问题:(1)如果此人乘车的次数m,那么月票余额是_________元.(2)此人最多能乘车几次?简单说明理由.60.一本小说共m页,一位同学第一天看了全书的少6页,第二天看了剩下的多6页,第三天把剩下的全部看完,该同学第三天看了多少页?若m=900,则第三天看了多少页?参考答案:1.∵正方体边长为a,∴它的体积是V=a3.当a=4cm时,V=4 3=64cm3.故答案为:a3,64.2.由题意得:(3a)2﹣3=9a2﹣3,故答案为:9a2﹣3.3.设没分为x人,则教练有x人,学生有20x人,由题意,得∴20x=m+n,∴x=,∴教练有人.故答案为:人4.∵某商品的进价是x元,售价是132元,∴此商品的利润=售价﹣进价=132﹣x(元).故答案为(132﹣x)元.5.x的2倍是2x,y的3倍是3y,则x的2倍与y的3倍的差为:2x﹣3y.故答案是:2x﹣3y.6.在负整数a后添上3,使其位数增加一位,则这个数可表示为10a﹣3.故答案为10a﹣3.7.一个数比x的2倍小3,则这个数可表示为2x﹣3.故填:2x﹣38.由题意得:3a﹣2,故答案为:3a﹣2.9.“x与y的和”用代数式可以表示为:x+y.故答案为x+y10.先求a的3倍是3a,再求与4的和为3a+4.故答案为:3a+4.11.由题意得:x﹣m%x,故答案为:(x﹣m%x).12.∵某商品进价是m元,提价30%后标价,又打九折出售,∴此商品的售价为0.9×1.3m=1.17m(元),∴该商品的利润是1.17m﹣m=0.17m(元).故答案为0.17m13.∵鸡有两只脚,兔有四只脚,又∵鸡有a只,兔有b只,∴鸡和兔的脚共有:2a+4b.故答案为:2a+4b14.根据题意得产值由a万元增加了20%,达到的产值15.∵电视机的原价为a元,∴降价20%后的价格为(1﹣20%)a=0.8a(元).故答案为0.8a16.∵今年比去年增加了20%,∴今年的产值占去年的1+20%=120%,∴去年的产值=a÷120%=a万元.故答案为:a万元.17.15×0.9p=13.5p.故答案是:13.5p.18.二科的平均成绩是:(a+b).故答案是:(a+b).19.根据圆柱的体积公式可得这块矿石的体积为:.故填:20.根据一件商品原价为a元,先涨价5元,则价格变为:a+5,再按8.5折出售,依题意得:(a+5)×0.85.故答案为:0.85(a+5)21.S阴影=2S扇形﹣S正方形=2×﹣22=π×22﹣22=2(π﹣2).故填2(π﹣2)22.根据示意图可得:2x﹣3.故答案为2x﹣3.23.根据题意列得:他数过的车厢有(2m﹣m+1)即(m+1)节.故答案为:m+1.故选D24.因为2支2B铅笔2x元,一副三角板3元,所以小明总共应付(2x+3)元.故答案为:2x+325.∵每份0.4元的价格购进了a份报纸,∴这些报纸的成本是0.4a元,∵每份0.5元的价格出售,一天共售b份报纸,∴共买了0.5b元,∵剩余的报纸以每份0.2元的价格退回报社,∴退回了0.2(a﹣b)元,他一天工赚到的钱数为:0.5b+0.2(a﹣b)﹣0.4a=0.3b26.n支球队举行单循环比赛,比赛的总场数为:n(n ﹣1).故答案为:n(n﹣1)27.根据题意得:a•(1+30%)×80%=1.04a;故答案为:1.04a.28.圆的面积为π×()2=,中间正方形的面积为b2,∴图中阴影部分面积为:﹣b2.故答案为:﹣b2.29.∵由题意可得计算过程如下:( x×2+y2)÷2,∴当x=5,y=﹣2时,( x×2+y2)÷2=(5×2+4)÷2=7.故答案为:730.阴影部分的面积是:ab+cd﹣2×32=ab+cd﹣18;故答案为:ab+cd﹣18.31.三角形的周长是2x+1+3x﹣2+8﹣2x=3x+7,当x=3时,原式=3x+7=3×3+7=16.32.在一天的两种商品的买卖中,超市不赚不赔.∵10件A商品一共卖了10×(1+20%)P=12P(元),20件B商品一共卖了20×(1﹣10%)P=18P(元),∴这30件商品一共卖了12P+18P=30P(元),∵30P﹣30P=0,∴超市不赚不赔33.(1)2ab﹣5.(2)a2﹣b2.(3)5a+234.(1)A:10+1.2(x﹣3)=1.2x+6.4;B:8+1.4(x﹣3)=1.4x+3.8;(2)A与B的差价=(1.2x+6.4)﹣(1.4x+3.8)=2.6﹣0.2x.35.阴影部分的面积=GF•DG+GF•CG=GF•CD=×2•a.=a.36.①S==(m2)(4分);②L===(m)37.(1)由题意得,单独买一件运动服需要的钱数为:200+(200﹣a)×0.9即20+0.9a.(2)∵700≤a+b≤900,而打折却有7折和8折两种方式,∴当700≤a+b≤800时,应付费:200+300×0.9+(a+b﹣500)×0.8即为70+0.8a+0.8b(元);当800<a+b≤900时,应付费:200+300×0.9+300×0.8+(a+b﹣800)×0.7即为150+0.7a+0.7b(元)38.(1)每月用水15吨时,水费为:15×3=45元(1分)每月用水35吨时,水费为:3.8(35﹣20)+60=117元…(2分)(2)①如果每月用水x≤20吨,水费为:3x元(4分)②如果每月用水x>20吨,水费为:3.8(x﹣20)+60或3.8x﹣16元39.根据题意得:4(m+y)+2.5(m﹣y)=6.5m+1.5y.轮船共航行了(6.5m+1.5y)千米.40.(1)根据题意得:(m+12)×5=5m+60(千米);答:轮船顺水航行5小时的行程是(5m+60)千米.(2)根据题意得:(m﹣12)×4=4m﹣48(千米)答:轮船逆水航行4小时的行程是(4m﹣48)千米.(3)根据题意得:5m+60﹣(4m﹣48)=m+108(千米)答:轮船顺水航行5小时和逆水航行4小时的行程相差(m+108)千米.41.(1)由题意得:甲旅行团门票总费用:20x+8y;乙旅行团门票总费用:20×2x+8×y=40x+4y;(2)甲旅行团门票总费用:20x+8y=20×10+8×6=248(元);乙旅行团门票总费用:40x+4y=40×10+4×6=424(元),248+424=672(元).答:两个旅行团的门票总费用是672元42.(1)剩余部分的面积为:(60×40﹣4x2)cm2;(2)盒子的体积为:x(60﹣2x)(40﹣2x)cm3;当x=5时,原式=5(60﹣10)(40﹣10)=7500cm3;答:盒子的体积为7500立方厘米43.(1)∵第1排a个座位,后面每排比第一排多1个座位,(2)根据题意得:a+(a+1)+(a+2)+…+(a+9)=10a+(1+9)×9÷2=10a+45答:前10排共有10a+45个座位;(3)∵第11排有(a+10)个座位,第5排有(a+4)个座位,∴第11排比第5排多的座位数是:(a+10)﹣(a+4)=6(个);则第11排比第5排多6个座位44.(1)阴影部分的面积为:a(b﹣a)(3分);(2)当a=5cm,b=7cm时,原式=5×(7﹣5)=10cm2 45.(1)100(4x+1)+10x+x2(1分)=400x+100+10x+x2=x2+410x+100(2分);(2)当x=0时,x2+410x+100=100,当x=1时,x2+410x+100=511,当x=2时,x2+410x+100=924,当x取3,4,…,9时,4x+1>9,不合题意.由上可知,这个三位数是100或511或924.(4分)46.(1)∵第一队植树x棵,第二队植的树比第一队的2倍少80棵,∴第二队的植树棵数为:2x﹣80,∵第三队植的树比第二队植树多了10%.∴第三队的植树棵数为:(2x﹣80)(1+10%),所以三个队共植树:x+2x﹣80+(2x﹣80)(1+10%)=x﹣168,(2)当x=100棵时,全体同学共植树:x﹣168=×100﹣168=352(棵)47.根据题意可知:当x≤2,支出费用为:5元,若某人乘坐出租车x(x>2)千米的付费=5+1.8×(x﹣2),整理得:应付费用为:1.4+1.8x48.(1)1.5a(1分)(2)1.5a(1﹣20%);a(1+40%)各(1分)(3)2010年总收入250万元,(1分)2011年总收入260万元,(1分)260﹣250=10万元.(1分)答:该企业2011年总收入比2010年总收入增加了10万元49.(1)阴影部分的面积:;(2)阴影部分的面积:,故答案为ab ,.(2)学校要印2600份材料,在甲厂印费用=0.2×2600+500=1020(元);在乙厂印费用=0.4×2600=1040元,∵1020<1040,∴在甲厂印刷比较合算51.1)A城市与B城市之间的距离:80t,从A城市到B 城市的时间:小时,答:需要小时.(3分)(2)由题意:t ﹣=t ﹣=t ﹣=(7分)答:可以提前小时到达52.(1)当n≤100时,买n本笔记本所需的钱数是:2.3n,当n>100时,买n本笔记本所需的钱数是:2.2n;(2)因为2.3n>2.2n,所以会出现多买比少买付钱少的情况;(3)如果需要100本笔记本,购买101本笔记本,比较省钱53.(1)根据题意可得:当x=850时,在甲商场没有优惠,在乙商场有优惠,费用是:500+(850﹣500)×95%=8332.5(元),故在乙商场买合算;(2)当x>1000时:在甲商场的费用是:1000+(x﹣1000)×90%=0.9x+100;在乙商场的费用是:500+(x﹣500)×95%=0.95x+25;(3)把x=1700代入(2)中的两个代数式:0.9x+100=0.9×1700+100=1630,0.95x+25=0.95×1700+25=1635,∵1635>>1630,∴选择甲商场合算54.(1)3a+b,(2)(a﹣b)2,(3)5x+2.55.(1)(2a+b)、(a+2b)…(2分)(2)①依题意可得:(2a+b)(a+2b)=2a2+4ab+ab+2b2=(2a2+5ab+2b2)cm2…(4分)②依题意得a2﹣b2=33即(a+b)(a﹣b)=33又2(a+b)=22即a+b=11①∴a﹣b=3②…(6分)由①②式可求得解得:a=7,b=4当a=7,b=4时,2a2+5ab+2b2=2×72+5×7×4+2×42=270答:这张长方形大铁皮的面积是270cm2.…(8分)(3)共有下列四种方案可供选择:V2=a2bV3=a2bV4=ab2…(12分)∴V1=V4,V2=V3∴V1﹣V2=ab2﹣a2b=ab(b﹣a)∵a>b∴V1=V4<V2=V3∴方案②与③的体积最大.56.(1)由已知得:A日出租车司机比正常情况少行驶:vt﹣(t﹣2)(v﹣5)=2v+5t﹣10(米);(2)由已知得:B日出租车司机比正常情况多行驶(t+2)(v+5)﹣vt=2v+5t+10(米)①,又由(1)和已知的得:2v+5t﹣10=120,将2v+5t=130代入①得140(米).答:B日出租车司机比平时多行驶140千米57.(1)由题意得:应付的车费为:7+(m﹣3)×1.8=1.8m+1.6(元)即他应付1.8m+1.6元车费;(2)由(1)知,如果有人乘计程车行驶了m千米(m >3),那么他应付1.8m+1.6元车费,此时甲乘出租车行驶了4km,所以1.8×4+1.6=8.8(元),即他应付车费8.8元;(3)由(1)知,如果有人乘计程车行驶了m千米(m >3),那么他应付1.8m+1.6元车费,此时游客付了10.6元,则可列出方程为:1.8m+1.6=10.6解得:m=5,即从西区大润发到文昌楼大约有5公里58.AB+BC的长=A→C的长,为x,∵CD=0.6米,∴A→C→D的长=x+0.6,A→B→D的长=x﹣0.6,猫的速度=,老鼠的速度=.故答案为:x;x+0.6;x﹣0.6;;.59.(1)此人乘车的次数m,则月票余额是:50﹣0.8m;(2)50﹣0.8m≥0,解得m≤62.5,∴此人最多能乘车62次.故答案为:(1)(50﹣0.8m).60.∵一本小说共m 页,一位同学第一天看了全书的少6页,∴第一天看了m﹣6,剩下m ﹣(m﹣6)=m+6,∵第二天看了剩下的多6页,∴第二天看了,剩下:,当m=900时,(页).列代数式----11。
数学七年级上册 代数式专题练习(解析版)

一、初一数学代数式解答题压轴题精选(难)1.某超市在十一长假期间对顾客实行优惠,规定如下:________元:小明妈妈一次性购300元的衣服,她实际付款________元:如果他们两人合作付款,则能少付________元. (2)小芳奶奶在该超市一次性购物x元生活用品,当x大于或等于500时,她们实际付款________元(用含x的式子表示,写最简结果)(3)如果小芳奶奶两次购物货款合计900元,第一次购物的货款为a元(200<a<300),两次购物小芳奶奶实际付款多少元?(用含a的式子表示)(4)如何能更省钱,请给出一些建议.【答案】(1)190;280;10(2)(0.8x+60)(3)解:100+0.9(a-100)+100+0.9×(500-100)+0.8(900-a-500)=(0.1a+790)元. 答:两次购物小芳奶奶实际付款(0.1a+790)元。
(4)解:一次性购物能更省钱。
【解析】【解答】(1)解:小明的爷爷一次性购200元的保健食品,他实际付款100+0.9×(200-100)=190元:小明妈妈一次性购300元的衣服,她实际付款100+0.9×(300-100)=280元:如果他们两人合作付款,则能少付190+280-[100+0.9×(200+300-100)]=10元.故答案为:190;280;10( 2 )解:小芳奶奶在该超市一次性购物x元生活用品,当x大于或等于500时,她们实际付款100+360+0.8(x-500)=(0.8x+60)元.故答案为:(0.8x+60)【分析】(1)根据优惠办法"少于100元不予优惠,超过100元但低于500元,超过100元部分给予九折优惠"可球得实际付款;(2)由"少于100元不予优惠,超过100元但低于500元,超过100元部分给予九折优惠,超过500元的,超过500元部分给予八折优惠"可列出代数式;(3)分别求出两次购物小芳奶奶实际付款的钱数,相加即可求解;(4)通过计算可知一次性购物能更省钱.2.从2开始,连续的偶数相加时,它们的和的情况如下表:12=1×222+4=6=2×332+4+6=12=3×442+4+6+8=20=4×552+4+6+8+10=30=5×6……S和n之间有什么关系?用公式表示出来,并计算以下两题:(1)2a+4a+6a+…+100a;(2)126a+128a+130a+…+300a.【答案】(1)解:依题可得:S=n(n+1).2a+4a+6a+…+100a,=a×(2+4+6+…+100),=a×50×51,=2550a.(2)解:∵2a+4a+6a+…+126a+128a+130a+…+300a,=a×(2+4+6+…+300),=a×150×151,=22650a.又∵2a+4a+6a+…+124a,=a×(2+4+6+…+124),=a×62×63,=3906a,∴126a+128a+130a+…+300a,=22650a-3906a,=18744a.【解析】【分析】(1)根据表中规律可得出当n个连续偶数相加时,它们的和S=n(n+1);由此计算即可得出答案.(2)根据(1)中公式分别计算出2a+4a+……+300a和2a+4a+……+124a的值,再用前面代数式的值减去后面代数式的值即可得出答案.,3.如图,在数轴上有两点A、B,点A表示的数是8,点B在点A的左侧,且AB=14,动点P从点A出发,以每秒4个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.(1)写出数轴上点B表示的数:________ ;点P表示的数用含t的代数式表示为________ .(2)动点Q从点B出发沿数轴向左匀速运动,速度是点P速度的一半,动点P、Q同时出发,问点P运动多少秒后与点Q的距离为2个单位?(3)若点M为线段AP的中点,点N为线段BP的中点,在点P的运动过程中,线段MN 的长度是否会发生变化?若变化,请说明理由;若不变,求出线段MN的长.【答案】(1)解:8-14=-6;因此B点为-6;故答案为:-6;解:因为时间为t,则点P所移动距离为4t,因此点P为8-4t ;故答案为:8-4t(2)解:由题意得,Q 的速度为4÷2=2(秒)则点Q为-6-2t,又点P为8-4t;所以①P在Q的右侧时8-4t-(-2t-6)=2解得x=6②P在Q左侧时-2t-6-(8-4t)=2解得x=8答:动点P、Q同时出发,问点P运动6或8秒后与点Q的距离为2个单位.故答案为:6或8秒(3)解:①当P在A,B之间时,线段AP=8-(8-4t)=4t;线段BP=8-4t-(-6)=14-4t因点M为线段AP的中点,点N为线段BP的中点所以MP=AP=2t;NP=BP=7-2tMN=MP+NP=2t+7-2t=7②当P在P的左边时线段AP=8-(8-4t)=4t;线段BP=(-6)-(8-4t)=4t-14因点M为线段AP的中点,点N为线段BP的中点所以MP=AP=2t;NP=BP=2t-7MN=MP-NP=2t-(2t-7)=7因此在点P的运动过程中,线段MN的长度不变, MN=7【解析】【分析】(1)①由数轴上两点之间距离的规律易得B的值为8-14=16;②因为时间为t,则点P所移动距离为4t,因此易得P为8-4t(2)由题易得:Q 的速度为4÷2=2(秒)则点Q为-6-2t,又点P为8-4t;分别讨论P在Q 左侧或右侧的情况,由此列方程,易得结果为6或8秒;(3)结合(1)(2)易得当P在AB间以及P在B左边时的两种情况;当P在A,B之间时,线段AP=8-(8-4t)=4t;线段BP=8-4t-(-6)=14-4t;当P在P的左边时线段AP=8-(8-4t)=4t;线段BP=(-6)-(8-4t)=4t-14;利用中点性质,易得结果不变,为7.4.已知:a、b、c满足a=-b,|a+1|+(c-4)2=0,请回答问题:(1)请求出a、b、c的值;(2)a、b、c所对应的点分别为A、B、C,P为数轴上一动点,其对应的数为x,若点P 在线段BC上时,请化简式子:|x+1|-|1-x|+2|x-4|(请写出化简过程);(3)若点P从A点出发,以每秒2个单位长度的速度向右运动,试探究当点P运动多少秒时,PC=3PB?【答案】(1)解:因为,所以a+1=0,c-4=0,即a=-1,c=4. 因为a=-b,a=-1,所以b=-a=-(-1)=1. 综上所述,a=-1,b=1,c=4(2)解:因为点P在线段BC上,b=1,c=4,所以 . 因为,所以x+1>0,, . 0时,;当时,;当时, . 因此,当点P在线段BC上(即 )时,== = .(3)解:设点P的运动时间为t秒. 因为点P从A点出发,以每秒2个单位长度的速度向右运动,所以AP=2t. 因为点A对应的数为-1,点C对应的数为4,所以AC=4-(-1)=5. PB. 故点P不可能在点C的右侧. 因此,PC=AC-AP. 因为AP=2t,AC=5,所以PC=AC-AP=5-2t. 分析本小题的题意,点P与点B的位置关系没有明确的限制,故本小题应该对以下两种情况分别进行求解. ①点P在点B的左侧,如下图. 因为点A对应的数为-1,点B对应的数为1,所以AB=1-(-1)=2. 因为AP=2t,AB=2,所以PB=AB-AP=2-2t. 因为PC=3PB,PC=5-2t,PB=2-2t,所以5-2t=3(2-2t). 解这个关于t的一元一次方程,得. ②点P在点B的右侧,如下图.因为AP=2t,AB=2,所以PB=AP-AB=2t-2. 因为PC=3PB,PC=5-2t,PB=2t-2,所以5-2t=3(2t-2). 解这个关于t的一元一次方程,得 .综上所述,当点P运动或秒时,PC=3PB.【解析】【分析】(1)因|a+1|0;(c-4)20,所以由题意得a+1=0,c-4=0,即a=-1,c=4,所以b=1.(2)结合(1),由题意得,所以原式去绝对值化简得原式=x+1-(x-1)+2(4-x)=-2x+10.(3)结合(1),由题意得AP=2t,PC=5-2t;然后分情况讨论P在B点左右两侧两种情况。
代数式知识点及专项训练(含答案解析)

代数式知识点及分类训练(含答案解析)知识点一:代数式的定义1. 用基本的运算符号把数或表示数的字母连接而成的式子叫做代数式。
如:16n ,2a+3b ,34 ,n,(a+b)2等式子;代数式不含有等号或不等号,单独的2一个数或一个字母也是代数式。
知识点二:代数式的规范书写1. 数字与数字相乘用“×”;数字与字母、字母与字母相乘乘号, 通常用“·”表示或省略不写;2. 字母与数字相乘,数字因式应放在字母因式之前(之前/之后),带分数与字母相乘,带分数要化为假分数3. 代数式中的除号一般用“分数线”表示;4. 几个字母相乘时,一般按字母顺序排列。
5. 如果字母前面的数字是1,通常省略不写.知识点三:列代数式在解决实际问题时,常常先把问题中与数量有关的词语用代数式表示出来,即列出代数式,使问题变得简洁,更具一般性.1.重点:用字母表示数与数之间的关系;2.比谁的几倍多(少)几的问题;3.比谁的几分之几多(少)几的问题;4.折扣问题:例:八折是乘0.8,八五折是乘0.855.提价与降价问题:例:一个商品原价a,先提价20%,在降价20%,即a(1+20%)(1-20%)6.路程问题:掌握公式:s=vt7.出租车计费问题:分类讨论思想,将总路程切割成不同的段(例:前三公里收费7元,之后每公里1.6元,公里数x,总费用y)y={7 x≤3 1.6(x−3)+7 x>38.已知各数位上的数字,表示数的问题:字母乘10表示在十位上,乘100表示在百位上。
9.特定字母的意义:C:周长 S:面积 V:体积 r:半径 d:直径s:路程 t:时间 v:速度n:正整数知识点三:代数式的值1. 用数值代表代数式里的字母,按照代数式中的运算关系计算得出的结果叫做代数式的值。
2. 代数式的值的求解步骤:一是代入,二是计算。
在过程中一要弄清楚运算符号,二要注意运算顺序.在计算时,要注意按代数式指明的运算进行.3. 求代数式的值的方法3.1 直接代入法:将字母的值直接代入代数式中求值3.2 转换代入法:按指定的程序代入计算3.3 整体代入法:即整体思想:把“整体”看作一个新字母代入计算【知识点1:代数式的概念】1. 下列式子中,符合代数式书写格式的是( )A .813a 2b 3B .−y xC .xy ·5D .−1c【答案】B【解析】选项A 正确的书写格式是253a 2b 3,选项B 的书写格式是正确的,选项C 正确的书写格式是5xy ,选项D 正确的书写格式是-c.故选:B .2. 下列式子中,不属于代数式的是( )A .a+3B .mn 2C .√6D .x >y 【答案】D .【解析】A 、是代数式,故本选项错误;B 、是代数式,故本选项错误;C 、是代数式,故本选项错误;D 、不是代数式,故本选项正确;故选D .3. 下列各式符合代数式书写规范的是( )A .a bB . a×3C . 2m ﹣1个D . 125m 【答案】A .【解析】A 、符合代数式的书写,故A 选项正确;B 、a×3中乘号应省略,数字放前面,故B 选项错误;C 、2m ﹣1个中后面有单位的应加括号,故C 选项错误;D 、125m 中的带分数应写成假分数,故D 选项错误.4. 判断下列各式中哪些是代数式,哪些不是代数式?0,10x−1,F =ma ,m+2>m ,2x 2﹣3x+11,112,13≠12,6x 2+y 23,﹣y ,6π. 【答案】代数式的有:0,10x−1,2x2﹣3x+11,112,6x 2+y 23,﹣y ,6π.不是代数式的有:F =ma ,m+2>m ,13≠12.【解析】根据代数式的概念选择5. 指出下列各式哪些是代数式,哪些不是代数式?①0;②a+b=3;③b;④x+2>4;⑤1x ;⑥2mn;⑦1+x;⑧x 3.【答案】①、③、⑤、⑥、⑦、⑧是代数式,②、④不是代数式【解析】②a+b=3,④x+2>4中的“=”“>” 它们不是运算符号,因此②④都不是代数式;①0,③b,都是代数式,因为单个数字和字母是代数式;⑤1x ,⑦1+x,⑧x3,都是除、加、乘方等运算符号连接起来的,因此是代数式;综上,①、③、⑤、⑥、⑦、⑧是代数式,②、④不是代数式.6. 下列哪些是代数式?哪些不是代数式?(1)3x+y ;(2)a ≠0;(3)s=πr 2;(4)ab a+b ;(5)-1>-2;(6)65;(7)m.【答案】代数式有(1),(4),(6),(7);不是代数式的有(2),(3),(5).【解析】根据代数式的概念,用运算符号把数字与字母连接而成的式子叫做代数式.单独的一个数或一个字母也是代数式.代数式有:3x+y ,ab a+b ,65,m.不是代数式的有:a ≠0,s=πr 2,-1>-2.7. 指出下列各式中,哪些是代数式,哪些不是代数式?(1)2x-1;(2)a=1;(3)S=πR 2;(4)π;(5)72;(6)12>13.【答案】(2)(3)是等式不是代数式;(6)不是等式不是代数式;(1)(4)(5)是代数式.【解析】根据代数式的概念,用运算符号把数字与字母连接而成的式子叫做代数式.单独的一个数或一个字母也是代数式.解:(2)(3)是等式不是代数式;(6)不是等式不是代数式;(1)(4)(5)是代数式.【知识点2:列代数式】1.购买1个单价为a元的面包和3瓶单价为b元的饮料,所需钱数为()A.(a+b)元B.3(a+b)元C.(3a+b)元D.(a+3b)元【答案】D.【解析】求购买1个面包和2瓶饮料所用的钱数,我们需要用一个面包的价钱加上3瓶饮料的价钱即可,即(a+3b)元,故选D.2.x减去y的平方的差,用代数式表示正确的是().A.(x-y)2B.x2-y2C.x2-yD.x-y2【答案】D【解析】本题主要考查了列代数式,关键是正确理解文字语言中的关键词;y的平方为y2,所以x减去y的平方的差为x-y2,故选D.3.根据题意列式:(1)x的平方的3倍与5的差,用代数式表示为 .(2)操作电脑时,甲4小时打x个字,乙3小时打y个字,甲乙两人每小时共打个字.【答案】(1)3x2-5 (2)(x4+y3)【解析】(1)本题主要考查了列代数式,关键是正确理解文字语言中的关键词;x的平方为x2,它的3倍为3x2,所以再与5的差为3x2-5;(2)已知甲4小时打x个字,则甲每小时打x4个字;乙3小时打y个字,则乙每小时打y3个字,所以甲、乙两人每小时共同打(x4+y3)个字4.校园里刚栽下1.8m高的小树苗,以后每年长0.3m,则n年后是 m.【答案】(0.3n+1.8);【解析】解决问题的关键是读懂题意,找到关键描述语,找到所求的量的等量关系。
2.1.1 代数式(一)(解析版)
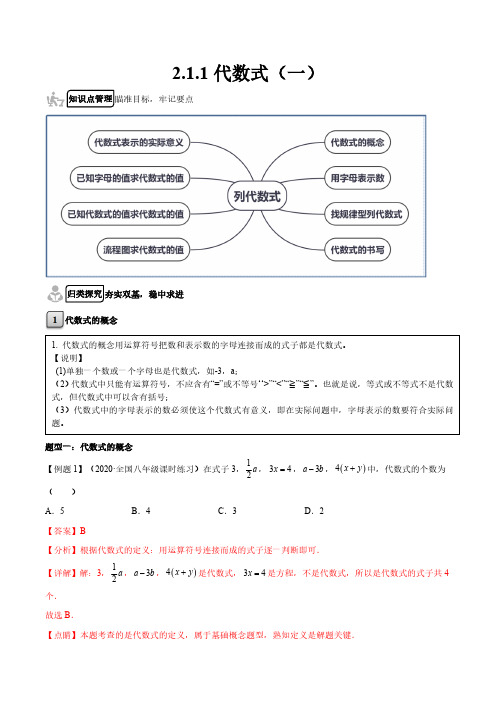
2.1.1代数式(一)代数式的概念题型一:代数式的概念【例题1】(2020·全国八年级课时练习)在式子3,12a ,34x =,3ab -,()4x y +中,代数式的个数为()A .5B .4C .3D .2【答案】B【分析】根据代数式的定义:用运算符号连接而成的式子逐一判断即可.【详解】解:3,12a ,3ab -,()4x y +是代数式,34x =是方程,不是代数式,所以是代数式的式子共4个.故选B .【点睛】本题考查的是代数式的定义,属于基础概念题型,熟知定义是解题关键.变式训练【变式1-1】(2018·河北沧州市·七年级期末)下列说法正确的是( )A .2a 是代数式,1不是代数式B .代数式2a b -表示2﹣a 除bC .当x =4时,代数式413x -的值为0D .零是最小的整数【答案】C【分析】根据代数式的定义、代数式表示的意义、代数式求值等知识点判断各项【详解】2a 是代数式,单独的数字也是代数式,故A 不正确;代数式2a b -表示2-a 除以b ,故B 不正确;当x=4时,代数式413x -的值为0,故C 正确;零是绝对值最小的整数,故D 不正确.故选C .【点睛】此题主要考查代数式的定义、代数式表示的意义、代数式求值等知识点.用数值代替代数式里的字母解题的关键【变式1-2】(2019·上海市西延安中学七年级月考)下列各式中,代数式有()个(1)a+b=b+a;(2)1;(3)2x-1 ;(4)23x x +;(5) s = πr 2;(6) -6k A .2B .3C .4D .5【答案】C【分析】根据代数式的定义即可求解.【详解】(1)a+b=b+a 为等式,故错误;(2)1为代数式,正确;(3)2x-1为代数式,正确;(4)23x x +为代数式,正确;(5) s = πr 2为等式,故错误;(6) -6k 为代数式,正确故选C.【点睛】此题主要考查代数式的识别,解题的关键是熟知代数式的定义.【变式1-3】(2020·正安县思源实验学校七年级期中)下列式子①23´②210x -=③y ④s vt =⑤ 3.14π>⑥1a ⑦()()x y x y +-⑧452x x +,其中代数式有( )A .3个B .4个C .5个D .6个【答案】C【分析】代数式是运算符号把数和表示数的字母连接而成的式子,据此确定解答即可.【详解】解:代数式是运算符号把数和表示数的字母连接而成的式子,所以以上八个式子中,是代数式的有①③⑥⑦⑧五个.故选:C【点睛】本题考查了代数式的定义,准确理解代数式的定义是解题关键.题型二:用字母表示数【例题2】三个连续整数中,中间一个是m ,则最大的一个是()A .m+1B .m+2C .m+3D .m+4【答案】A【分析】根据三个连续的自然数两两之间相差1,可知中间一个是m ,那么最大的一个数就是m+1.【详解】解:三个连续的自然数两两之间相差1,中间一个是m ,最大的一个数就是m+1.故选A .【点睛】明确相邻的两个自然数之间相差1是解决此题关键.变式训练【变式2-1】下列说法正确的是( )A .-a 一定是负数B .a 的倒数是1aC .2a 一定是分数D .a 2一定是非负数【答案】D【解析】【分析】本题考查的是负数、倒数、分数、非负数的定义,根据负数、倒数、分数、非负数的定义依次判断各项即可.A 、当a 是负数时,-a 是正数,故本选项错误;B 、当a 是0时,a 没有倒数,故本选项错误;C 、当a=4时,a 2=2,是整数,故本选项错误; D 、2a 一定是非负数,本选项正确,故选D.【点睛】本题考查了用字母表示数,解题的关键是掌握好负数、倒数、分数、非负数的定义.【变式2-2】a +1的相反数是()A .-a +1B .-(a +1)C .a -1D .11a +【答案】B【详解】1a +的相反数是:(1)a -+.点睛:表示一个式子的相反数只需把这个式子用括号括起来,再在括号前面添上一个“-”即可.【变式2-3】(2019·山东)甲数比乙数的3倍大2,若甲数为x ,则乙数为( )A .3x -2B .3x+2C .23x +D .23-x 【答案】D【分析】本题主要考查列代数式,根据甲数比乙数的3倍大2,可知甲数减去2是乙数的3倍,再除以3即可得到结果.【详解】根据题意,得乙数为23x -.选D.【点睛】本题考查了列代数式,解题的关键是正确理解文字语言中的关键词,从而明确其中的运算关系,正确地列出代数式.题型三:找规律型列代数式【例题3】(2020·江西省于都中学七年级期中)观察如图所示图形,则第n 个图形中三角形的个数是( )A .2n +2B .4n +4C .4nD .4n -4【分析】由已知的三个图可得到一般的规律,即第n个图形中三角形的个数是4n,根据一般规律解题即可.【详解】解:根据给出的3个图形可以知道:第1个图形中三角形的个数是4,第2个图形中三角形的个数是8,第3个图形中三角形的个数是12,从而得出一般的规律,第n个图形中三角形的个数是4n.故选C.【点睛】此题考查了学生由特殊到一般的归纳能力.解此题时要注意寻找各部分间的联系,找到一般规律.变式训练【变式3-1】(2020·广州市育才中学七年级期中)用棋子摆出下列一组“口”字,按照这种方法摆下去,则第n个“口”字需要用棋子( )A.(4n﹣4)枚B.4n枚C.(4n+4)枚D.n2枚【答案】B【分析】观察图形可知,构成每个“口”字的棋子数量,等于构成边长为(n+1)的正方形所需要的棋子数量减去构成边长为(n+1-2)的正方形所需要的棋子数量.【详解】解:由图可知第n个“口”字需要用棋子的数量为(n+1)2-(n+1-2)2=4n,故选择B.【点睛】本题考查了规律的探索.【变式3-2】(2020·广东七年级期末)下列图案由边长相等的黑、白两色正方形按一定的规律拼接而成,依此规律,第n个图形中白色正方形的个数为( )A .4n +1B .4n ﹣1C .3n ﹣2D .3n +2【答案】D 【分析】第一个图形中有5个白色正方形;第2个图形中有531+´个白色正方形;第3个图形中有532+´个白色正方形;…由此得出第n 个图形中有53(1)32nn +´+﹣=个白色正方形.【详解】解:第一个图形中有5个白色正方形;第2个图形中有531+´个白色正方形;第3个图形中有532+´个白色正方形;…第n 个图形中有53(1)32nn +´+﹣=个白色正方形.故选:D 。
代数式典型例题专项练习30题(有答案)

. . . .代数式专项练习30题(有答案)一.选择题(共5小题)1.在1,a,a+b,,x2y+xy2,3>2,3+2=5中,代数式有()A .3个B.4个C.5个D.6个2.下列各式:﹣x+1,π+3,9>2,,,其中代数式的个数是()A .5 B.4 C.3 D.23.下列各式:①1x;②2•3;③20%x;④a﹣b÷c;⑤;⑥x﹣5;其中,不符合代数式书写要求的有()A .5个B.4个C.3个D.2个4.在下列的代数式的写法中,表示正确的一个是()A.“负x的平方”记作﹣x2B.“a除以2b的商”记作C.“x的3倍”记作x3 D.“y与的积”记作5.下列说确的是()A.x是代数式,0不是代数式B.表示a与b的积的代数式为a+bD.意义是:a与b的积除y的商二.填空题(共13小题)6.代数式“5x”,可解释为:“小明以5千米/时的速度走了x小时,他一共走了5x千米”.请你对“5x”再给出一个身边生活中的解释:_________ .7.叙述下列代数式的意义.(1)(x+2)2可以解释为_________ .(2)某商品的价格为n元.则80%n可以解释为_________ .8.一个三位数的百位数字是2,十位数字与个位数字组成的两位数为x,用代数式表示这个三位数为_________ .9.x表示一个两位数,y表示一个三位数,把x放在y的右边组成一个五位数,则这个五位数可以表示为_________ .10.m个数的平均数为a,n个数的平均数为b,这m+n个数的平均数为_________ .11.一本书共n页,小华第一天读了全书的,第二天读了剩下的,则未读完的页数是_________ .(用含n的式子表示)12.(1)已知a﹣b=3,则3a﹣3b= _________ ,5﹣4a+4b= _________ .(2)已知x+5y﹣2=0,则2x+3+10y= _________ .13.若a,b互为倒数,c,d互为相反数,则3c+3d﹣9ab= _________ .14.已知代数式ax3+bx,当x=﹣1时,代数式的值为5;则当x=1时,ax3+bx的值是_________ .15.任意写出x3y的3个同类项:_________ ,_________ ,_________ .16.已知7x m y3和﹣是同类项,则(﹣n)m= _________ .17.若单项式3x4y n与﹣2x2m+3y3的和仍是单项式,则(4m﹣n)n= _________ .18.已知x5y n与﹣3x2m+1y3n﹣2是同类项,则m+n= _________ .三.解答题(共12小题)19.如图,池塘边有一块长为18米,宽为10米的长方形土地,现在将其余三面留出宽都是x米的小路,中间余下的长方形部分做菜地,用代数式表示:(1)菜地的长a= _________ 米,宽b= _________ 米;(2)菜地的面积S= _________ 平方米;(3)求当x=1米时,菜地的面积.21.已知关于多项式mx2+4xy﹣x﹣2x2+2nxy﹣3y合并后不含有二次项,求n m的值.22.若关于x、y的方程6x+5y﹣2﹣3Rx﹣2Ry+4R=0合并同类项后不含y项,求R的值.23.k为何值时,多项式x2﹣2kxy﹣3y2+6xy﹣x﹣y中,不含x,y的乘积项.24.去括号,合并同类项(1)﹣3(2s﹣5)+6s;(2)3x﹣[5x﹣(x﹣4)];(3)6a2﹣4ab﹣4(2a2+ab);(4)﹣3(2x2﹣xy)+4(x2+xy﹣6)25.先去括号,后合并同类项:(1)x+[﹣x﹣2(x﹣2y)];(2);(3)2a﹣(5a﹣3b)+3(2a﹣b);(4)﹣3{﹣3[﹣3(2x+x2)﹣3(x﹣x2)﹣3]}.26.观察下列各等式,并回答问题:;;;;…(1)填空:= _________ (n是正整数);(2)计算:….27.观察下面一列数,探求其规律:(1)请问第7个,第8个,第9个数分别是什么数?(2)第2004个数是什么如果这列数无限排列下去,与哪个数越来越接近?28.如图,每个正方形点阵均被一直线分成两个三角形点阵,根据图中提供的信息,用含n的等式表示第n个正方形点阵中的规律_________ .29.下列是幼儿园小朋友用火柴棒拼出的一列图形.(1)第4个图中共有_________ 根火柴,第6个图中有_________ 根火柴;(2)第n个图形中共有_________ 根火柴(用含n的式子表示);(3)请计算第2008个图形中共有多少根火柴.30.如图,用同样规格的黑白两色正方形瓷砖铺设矩形地面,请观察下列图形,探究并解答下列问题.(1)在第1个图中,共有白色瓷砖_________ 块.(2)在第2个图中,共有白色瓷砖_________ 块.(3)在第3个图中,共有白色瓷砖_________ 块.(4)在第10个图中,共有白色瓷砖_________ 块.(5)在第n个图中,共有白色瓷砖_________ 块.代数式典型例题30题参考答案:1.解:在1,a,a+b,,x2y+xy2,3>2,3+2=5中,代数式有1,a,a+b,,x2y+xy2,共5个.故选C2.解:题中的代数式有:﹣x+1,π+3,共3个.故选C.3.解:①1x分数不能为假分数;②2•3数与数相乘不能用“•”;③20%x,书写正确;④a﹣b÷c不能出现除号;⑤,书写正确;⑥x﹣5,书写正确,不符合代数式书写要求的有①②④共3个.故选:C4.解:“负x的平方”记作(﹣x)2;“x的3倍”记作3x;“y与的积”记作y.故选B5.解:A、x是代数式,0也是代数式,故选项错误;B、表示a与b的积的代数式为ab,故选项错误;C、正确;D、意义是:a与b的和除y的商,故选项错误.故选C7.解:(1)(x+2)2可以解释为正方形的边长为x+2,则它的面积为(x+2)2;(2)某商品的价格为n元.则80%n可以解释为这件商品打八折后的价格.故答案为:(1)正方形的边长为x+2,则它的面积为(x+2)2;(2)这件商品打八折后的价格8.解:根据题意得此三位数=2×100+x=200+x9.解:两位数x放在一个三位数y的右边相当于y扩大了100倍,那么这个五位数为(100y+x)10.解:这m+n个数的平均数=.故答案为:.11.解:小华第一天读了全书的,还剩下(1﹣)n=n;第二天读了剩下的,即(1﹣)n×=n.则未读完的页数是n12.解:(1)∵a﹣b=3,∴3a﹣3b=3,5﹣4a+4b=5﹣4(a﹣b)=5﹣4=1;(2)∵x+5y﹣2=0,∴x+5y=2,∴2x+3+10y=2(x+5y)+3=2×2+3=7;(3)∵3x2﹣6x+8=0,∴x2﹣2x=﹣,∴x2﹣2x+8=﹣+8=.故答案为:(1)3,1;(2)7;(3)因为a,b互为倒数,c,d互为相反数,所以ab=1,c+d=0,所以3c+3d﹣9ab=3(c+d)﹣9ab=0﹣9=﹣9,故答案为:﹣914.解:由题意知:﹣a﹣b=5所以a+b=﹣5;则当x=1时,ax3+bx=a+b=﹣515.解:开放题,答案无数个,只要所写同类项,所含字母相同且相同字母的指数也相同即可,同类项与字母的顺序无关.如5x3y,12x3y,20x3y.故答案为:5x3y,12x3y,20x3y16.解:由同类项的定义可知m=2,n=3,代入(﹣n)m,结果为9.答:(﹣n)m值是917.解:两个单项式的和是单项式,则它们是同类项,则2m+3=4,m=;n=3.则(4m﹣n)n=(4×﹣3)3=﹣1.答:(4m﹣n)n=﹣118.解:x5y n与﹣3x2m+1y3n﹣2是同类项,2m+1=5,n=3n﹣2,m=2,n=1,m+n=2+1=3,故答案为:319.解:(1)∵其余三面留出宽都是x米的小路,(2)由(1)知:菜地的长为18﹣2x米,宽为10﹣x米,所以菜地的面积为S=(18﹣2x)•(10﹣x);(3)由(2)得菜地的面积为:S=(18﹣2x)•(10﹣x),当x=1时,S=(18﹣2)(10﹣1)=144m2.故答案分别为:(1)18﹣2x,10﹣x;(2)(18﹣2x)(10﹣x);(3)144m220.解:∵﹣3x4+m y与x4y3n是同类项,∴4+m=4,3n=1,∴m=0,n=,∴m100+(﹣3n)99﹣mn=0+(﹣1)﹣0=﹣121.解:∵多项式mx2+4xy﹣x﹣2x2+2nxy﹣3y合并后不含有二次项,即二次项系数为0,即m﹣2=0,∴m=2;∴2n+4=0,∴n=﹣2,把m、n的值代入n m中,得原式=422.解:∵6x+5y﹣2﹣3Rx﹣2Ry+4R=0合并同类项后不含y项,∴5﹣2R=0,解得R=2.523.解:原式=x2+(﹣2k+6)xy﹣3y2﹣y,∵不含x,y的乘积项,∴x,y的乘积项的系数为0,∴﹣2k+6=0,∴2k=6,∴k=3.∴当k=3时,已知多项式不含x,y的乘积项24.(1)﹣3(2s﹣5)+6s=﹣6s+15+6s=15;(2)3x﹣[5x﹣(x﹣4)]=3x﹣[5x﹣x+4]=3x﹣5x+x﹣4=﹣x+4;(3)6a2﹣4ab﹣4(2a2+ab)=6a2﹣4ab﹣8a2﹣2ab=﹣2a2﹣6ab;(4)﹣3(2x2﹣xy)+4(x2+xy﹣6)=﹣6x2+3xy+4x2+4xy﹣24=﹣2x2+7xy﹣2425.(1)x+[﹣x﹣2(x﹣2y)]=x﹣x﹣2x+4y=﹣2x+4y;(2)原式=a﹣a﹣﹣+b2=;(3)2a﹣(5a﹣3b)+3(2a﹣b)=2a﹣5a+3b+6a﹣3b=3a;(4)﹣3{﹣3[﹣3(2x+x2)﹣3(x﹣x2)﹣3]},=﹣3{9(2x+x2)+9(x﹣x2)+9},=﹣27(2x+x2)﹣27(x﹣x2)﹣27,=﹣54x﹣27x2﹣27x+27x2﹣27,=﹣81x﹣2726.解:(1)﹣;(2)原式=1﹣+﹣++…+﹣=1﹣=27.解:(1)∵第n个数是(﹣1)n,∴第7个,第8个,第9个数分别是﹣,,﹣.(2),最后与0越来越接近28.解:通过图案观察可知,当n=1时,点的个数是12=1;当n=2时,点的个数是22=4;当n=3时,点的个数是32=9;当n=4时,点的个数是42=16,…∴第n个正方形点阵中有n2个点,∴第n个正方形点阵中的规律是=n2.29.解:根据图案可知,(1)第4个图案火柴有3×4+1=13;第6个图案中火柴有3×6+1=19;(2)当n=1时,火柴的根数是3×1+1=4;当n=2时,火柴的根数是3×2+1=7;当n=3时,火柴的根数是3×3+1=10;所以第n个图形中火柴有3n+1.(3)当n=2008时,3n+1=3×2008+1=602530.解:(1)在第1个图中,共有白色瓷砖1×(1+1)=2块,(2)在第2个图中,共有白色瓷砖2×(2+1)=6块,(3)在第3个图中,共有白色瓷砖3×(3+1)=12块,(4)在第10个图中,共有白色瓷砖10×(10+1)=110块,(5)在第n个图中,共有白色瓷砖n(n+1)块。
最新苏科版数学七年级上册 代数式专题练习(解析版)

一、初一数学代数式解答题压轴题精选(难)1.已知整式P=x2+x﹣1,Q=x2﹣x+1,R=﹣x2+x+1,若一个次数不高于二次的整式可以表示为aP+bQ+cR(其中a,b,c为常数).则可以进行如下分类①若a≠0,b=c=0,则称该整式为P类整式;②若a≠0,b≠0,c=0,则称该整式为PQ类整式;③若a≠0,b≠0,c≠0.则称该整式为PQR类整式;(1)模仿上面的分类方式,请给出R类整式和QR类整式的定义,若,则称该整式为“R类整式”,若,则称该整式为“QR类整式”;(2)说明整式x2﹣5x+5为“PQ类整式;(3)x2+x+1是哪一类整式?说明理由.【答案】(1)解:若a=b=0,c≠0,则称该整式为“R类整式”.若a=0,b≠0,c≠0,则称该整式为“QR类整式”.故答案是:a=b=0,c≠0;a=0,b≠0,c≠0(2)解:因为﹣2P+3Q=﹣2(x2+x﹣1)+3(x2﹣x+1)=﹣2x2﹣2x+2+3x2﹣3x+3=x2﹣5x+5.即x2﹣5x+5=﹣2P+3Q,所以x2﹣5x+5是“PQ类整式”(3)解:∵x2+x+1=(x2+x﹣1)+(x2﹣x+1)+(﹣x2+x+1),∴该整式为PQR类整式.【解析】【分析】(1)根据题干条件,可得若a=b=0,c≠0,则称该整式为“R类整式”;若a=0,b≠0,c≠0,则称该整式为“QR类整式”.(2)根据"PQ类整式"定义,由x2﹣5x+5=﹣2(x2+x﹣1)+3(x2﹣x+1) = ﹣2P+3Q,据此求出结论.(3)由x2+x+1=(x2+x﹣1)+(x2﹣x+1)+(﹣x2+x+1)= PQR,据此判断即可.2.如图,阶梯图的每个台阶上都标着一个数,从下到上的第1个至第4个台阶上依次标着-5,-2,1,9,且任意相邻四个台阶上数的和都相等.(1)求前4个台阶上数的和是多少?(2)求第5个台阶上的数是多少?(3)应用求从下到上前31个台阶上数的和.发现试用含k(k为正整数)的式子表示出数“1”所在的台阶数.【答案】(1)解:由题意得前4个台阶上数的和是-5-2+1+9=3(2)解:由题意得-2+1+9+x=3,解得:x=-5,则第5个台阶上的数x是-5(3)解:应用:由题意知台阶上的数字是每4个一循环,∵31÷4=7…3,∴7×3+1-2-5=15,即从下到上前31个台阶上数的和为15;发现:数“1”所在的台阶数为4k-1【解析】【分析】(1)由台阶上的数求出台阶上数的和即可;(2)根据题意和(1)的值,求出第5个台阶上的数x的值;(3)根据题意知台阶上的数字是每4个一循环,得到从下到上前31个台阶上数的和,得到数“1”所在的台阶数为4k-1.3.已知x1, x2, x3,…x2016都是不等于0的有理数,若y1= ,求y1的值.当x1>0时,y1= = =1;当x1<0时,y1= = =﹣1,所以y1=±1(1)若y2= + ,求y2的值(2)若y3= + + ,则y3的值为________;(3)由以上探究猜想,y2016= + + +…+ 共有________个不同的值,在y2016这些不同的值中,最大的值和最小的值的差等于________.【答案】(1)解:∵ =±1, =±1,∴y2= + =±2或0(2)±1或±3(3)2017;4032【解析】【解答】解:(2)∵ =±1, =±1, =±1,∴y3= + + =±1或±3.故答案为±1或±3,( 3 )由(1)(2)可知,y1有两个值,y2有三个值,y3有四个值,…,由此规律可知,y2016有2017个值,最大值为2016,最小值为﹣2016,最大值与最小值的差为4032.故答案分别为2017,4032.【分析】(1)根据题意先求出=±1,=±1,就可求出y2的3个值。
最新中考数学复习专项练习--代数式求值(含解析)

代数式求值(含解析)一、单选题1.如图,若输入x的值为﹣5,则输出的结果y为()A. -6B. 5C. -5D. 62.已知a﹣b=2,则代数式2a﹣2b﹣3的值是()A. 1B. 2C. 5D. 73.设某代数式为A,若存在实数x0使得代数式A的值为负数,则代数式A可以是()A. |3﹣x|B. x2+xC. D. x2﹣2x+14.若,,则代数式的值是()A. 2B. -2C. 1D. -15.已知2y﹣x=2,则2x﹣4y的值为()A. 4B. -4C. 8D. -86.已知,则的值是()A. B.C. D.7.已知x2﹣2x﹣5=0,则2x2﹣4x的值为()A. -10B. 10C. ﹣2或10D. 2或﹣108.设a,b是非零有理数,且(a+b)2=0,则的值为()A. B. 3C. 1D. -19.已知:a﹣3b=2,则6﹣2a+6b的值为()A. 2B. -2C. 4D. -410.已知代数式的值是5,则代数式的值是()A. 6B. -6C. 11D. -911.已知=3,则代数式的值是()A. B.C. D.12.若3x=6,2y=4则5x+4y 的值为()A. 18B. 15C. 9D. 613.如果a﹣2b=﹣3,则代数式5﹣a+2b的值是()A. -1B. 8C. 2D. -214.当x=1时,代数式ax5+bx3+1的值为6,则x=﹣1时,ax5+bx3+1的值是()A. ﹣6B. ﹣5C. 4D. ﹣4二、填空题15.若x的值满足2x2+3x+7=8,则4x2+6x﹣9=________16.当a=3,b=﹣1时,代数式的值是________.17.若3a2﹣a﹣2=0,则5+2a﹣6a2=________.18.若2a﹣3b2=5,则6﹣2a+3b2=________.19.若,则________。
三、计算题20.先化简,再求值:3(x+2)2﹣2(x﹣2)(x+2),其中x=﹣.21.先化简,再求值:(x+1)(x-1)-(x+1)2,其中x=-222.先化简再求值:,其中a=-,b=-2.23.已知:a﹣b=2,ab=1,求(a﹣2b)2+3a(a﹣b)的值.四、解答题24.当x=-,y=5时,求代数式6x2﹣y+3的值25.某服装厂生产一种西装和领带,西装每套定价200元,领带每条定价40元.厂方在开展促销活动期间,向客户提供两种优惠方案:①买一套西装送一条领带;②西装和领带都按定价的90%付款.现某客户要到该服装厂购买西装20套,领带x条(x>20).(1)若该客户按方案①购买,需付款多少元(用含x的代数式表示);若该客户按方案②购买,需付款多少元(用含x的代数式表示);(2)若x=30,通过计算说明此时按哪种方案购买较为合算?五、综合题26.阅读理解:由面积都是1的小正方格组成的方格平面叫做格点平面.而纵横两组平行线的交点叫做格点.如图1中,有9个格点,如果一个正方形的每个顶点都在格点上,那么这个正方形称为格点正方形.(1)探索发现:按照图形完成下表:格点正方形内格点数格点正方形面积关于格点正方形的面积S,从上述表格中你发现了什么规律?(2)继续猜想:类比格点正方形的概念,如果一个长方形的每个顶点都在格点上,那么这个长方形称为格点长方形,对于格点长方形的面积,你认为也有类似(1)中的规律吗?试以图5中格点长方形为例来说明.27.化简求值:(1)已知x=-1,求x2+3x-1的值;(2)已知,求值.答案解析部分一、单选题1.如图,若输入x的值为﹣5,则输出的结果y为()A. -6B. 5C. -5D. 6【答案】D【考点】代数式求值【解析】【解答】解:已知x=﹣5<0,∴y=﹣x+1=﹣(﹣5)+1=6.故选D.【分析】由已知输入x的值为﹣5,所以由图示得y=﹣x+1,求出y.2.已知a﹣b=2,则代数式2a﹣2b﹣3的值是()A. 1B. 2C. 5D. 7【答案】A【考点】代数式求值【解析】【解答】解:∵a﹣b=2,∴2a﹣2b﹣3=2(a﹣b)﹣3=2×2﹣3=1.故选:A.【分析】直接利用已知a﹣b=2,再将原式变形代入a﹣b=2求出答案.3.设某代数式为A,若存在实数x0使得代数式A的值为负数,则代数式A可以是()A. |3﹣x|B. x2+xC. D. x2﹣2x+1【答案】B【考点】代数式求值【解析】【解答】解:对于任意的x,都有|3﹣x|≥0,,x2﹣2x+1=(x﹣1)2≥0,因为x2+x=(x+0.5)2﹣0.25,所以对于任意的x的取值,代数式A的值可以为正数、负数或0,即存在实数x0使得代数式A的值为负数.故选:B.【分析】首先根据对于任意的x,都有|3﹣x|≥0,,x2﹣2x+1=(x﹣1)2≥0,所以对于任意的实数x0,代数式A的值都为非负数;然后判断出x2+x=(x+0.5)2﹣0.25,对于任意的x的取值,代数式A的值可以为正数、负数或0,即存在实数x0使得代数式A的值为负数,据此解答即可.4.若,,则代数式的值是()A. 2B. -2C. 1D. -1【答案】D【考点】代数式求值【解析】【分析】 ,把,代入上式即可。
中考数学专题练习 代数式(含解析)-人教版初中九年级全册数学试题

代数式一、选择题1.一个代数式减去x2﹣y2等于x2+2y2,则这个代数式是()A.﹣3y2B.2x2+y2C.3y2﹣2x2D.3y22.若3x=4,9y=7,则3x﹣2y的值为()A.B.C.﹣3 D.3.下列各组代数式中,属于同类项的是()A.b与B.a2b与a2cC.22与34D.p与q4.下列计算正确的是()A.3x2﹣x2=3 B.3a2﹣2a2=1 C.3x2+5x3=8x5D.3a2﹣a2=2a25.如果a=255,b=344,c=433,则a、b、c的大小关系是()A.a>c>b B.b>a>c C.b>c>a D.c>b>a6.一个两位数,十位数字是x,个位数字是y,如果在它们中间加上一个0得到的数是()A.10x+y B.100x+y C.100y+x D.x+10y7.如果=0,则下列等式成立的是()A.a=b=0 B.a=b C.a+b=0 D.ab=08.设A、B均为实数,且,,则A、B的大小关系是()A.A>B B.A=B C.A<B D.A≥B9.下列多项式属于完全平方式的是()A.x2﹣2x+4 B.x2+x+C.x2﹣xy+y2 D.4x2﹣4x﹣110.如图所示,下列每个图是由若干盆花组成的形如三角形的图案,每条边(包括两个顶点)有n 盆花,每个图案花盆总数是S,按此推断S与n的关系式为()A.S=3n B.S=3(n﹣1)C.S=3n﹣1 D.S=3n+1二、填空题11.一台电视机的成本价为a元,销售价比成本价增加25%,因库存积压,所以就按销售价的70%出售,那么每台实际售价为元.12.已知=0 则a+b=.13.如果最简二次根式与是同类二次根式,则a=.14.把a3+ab2﹣2a2b分解因式的结果是.15.观察下列各式:,,,设n表示正整数,用关于n的等式表示这个规律是.三、解答下列各题16.如图,一块直径为a+b的圆形钢板,从中挖去直径分别为a与b的两个圆,求剩下的钢板的面积.17.已知A=a+2,B=a2﹣a+5,C=a2+5a﹣19,其中a>2.(1)求证:B﹣A>0,并指出A与B的大小关系;(2)指出A与C哪个大?说明理由.18.已知a、b、c为△ABC三边,利用因式分解说明b2﹣a2+2ac﹣c2的符号.19.某餐厅中1X餐桌可坐六人,有以下两种摆放方式(如图1和2).一天中午,餐厅要接待98位顾客共同就餐,但餐厅只有25X这样的餐桌,若你是这个餐厅的经理,你应该选择哪种拼接方式来摆餐桌?请说明理由.20.计算:.代数式参考答案与试题解析一、选择题1.一个代数式减去x2﹣y2等于x2+2y2,则这个代数式是()A.﹣3y2B.2x2+y2C.3y2﹣2x2D.3y2【考点】整式的加减.【分析】先根据题意列出式子,再去括号后合并同类项即可.【解答】解:这个代数式是(x2+2y2)+(x2﹣y2)=x2+2y2+x2﹣y2=2x2+y2,故选B.【点评】本题考查了整式的加减的应用,解此题的关键是能根据题意列出算式.2.若3x=4,9y=7,则3x﹣2y的值为()A.B.C.﹣3 D.【考点】同底数幂的除法;幂的乘方与积的乘方.【分析】由3x=4,9y=7与3x﹣2y=3x÷32y=3x÷(32)y,代入即可求得答案.【解答】解:∵3x=4,9y=7,∴3x﹣2y=3x÷32y=3x÷(32)y=4÷7=.故选A.【点评】此题考查了同底数幂的除法与幂的乘方的应用.此题难度适中,注意将3x﹣2y变形为3x÷(32)y是解此题的关键.3.下列各组代数式中,属于同类项的是()A.b与B.a2b与a2cC.22与34D.p与q【考点】同类项.【分析】根据字母相同且相同的字母的指数也相同是同类项,可得答案.【解答】解:A、相同字母的指数不同,故A不是同类项;B、字母不同,故B不是同类项;C、常数也是同类项,故C是同类项;D、字母不同,故D不是同类项;故选:C.【点评】本题考查了同类项,注意常数也是同类项.4.下列计算正确的是()A.3x2﹣x2=3 B.3a2﹣2a2=1 C.3x2+5x3=8x5D.3a2﹣a2=2a2【考点】合并同类项.【分析】先判断是否是同类项,如果是同类项,根据合并同类项法则合并即可.【解答】解:A、结果是2x2,故本选项错误;B、结果是a2,故本选项错误;C、不是同类项,不能合并,即结果是3x2+5x3,故本选项错误;D、结果是2a2,故本选项正确;故选D.【点评】本题考查了合并同类项法则的应用,注意:合并同类项时,把同类项的系数相加作为结果的系数,字母和字母的指数不变.5.如果a=255,b=344,c=433,则a、b、c的大小关系是()A.a>c>b B.b>a>c C.b>c>a D.c>b>a【考点】幂的乘方与积的乘方.【分析】a=(25)11=3211,b=(34)11=8111,c=(43)11=6411,从而可得出a、b、c的大小关系.【解答】解:∵a=(25)11=3211,b=(34)11=8111,c=(43)11=6411,∴b>c>a.故选C.【点评】本题考查了幂的乘方和积的乘方,解答本题关键是掌握幂的乘方法则.6.一个两位数,十位数字是x,个位数字是y,如果在它们中间加上一个0得到的数是()A.10x+y B.100x+y C.100y+x D.x+10y【考点】列代数式.【分析】中间加上一个0得到的数是三位数.百位数字是x,十位数字是0,个位数字是y,这个数表示为(100x+y),由此得出答案.【解答】解:百位数字是x,十位数字是0,个位数字是y,这个数表示为(100x+y).故选:B.【点评】此题考查列代数式,关键是正确理解文字语言中的关键词,从而明确其中的运算关系,正确地列出代数式.7.如果=0,则下列等式成立的是()A.a=b=0 B.a=b C.a+b=0 D.ab=0【考点】立方根.【分析】根据立方根的和为0,可得被开方数互为相反数,可得答案.【解答】解:∵=0,∴a+b=0.故选:C.【点评】本题考查了立方根,立方根的和为0,被开方数的和为0.8.设A、B均为实数,且,,则A、B的大小关系是()A.A>B B.A=B C.A<B D.A≥B【考点】实数大小比较.【分析】根据算术平方根的定义得出A是一个非负数,且m﹣3≥0,推出3﹣m≤0,得出B≤0,即可得出答案,【解答】解:∵,∴A是一个非负数,且m﹣3≥0,∴m≥3,∵,∵3﹣m≤0,即B≤0,∴A≥B,故选D.【点评】本题考查了算术平方根的定义,平方根和立方根,实数的大小比较等知识点,题目比较好,但有一定的难度.9.下列多项式属于完全平方式的是()A.x2﹣2x+4 B.x2+x+C.x2﹣xy+y2 D.4x2﹣4x﹣1【考点】完全平方式.【分析】根据完全平方公式的公式结构对各选项分析判断利用排除法求解.【解答】解:A、x2﹣2x+4不是完全平方式,故本选项错误;B、x2+x+=(x+)2,故本选项正确;C、x2﹣xy+y2,不是完全平方式,故本选项错误;D、4x2﹣4x﹣1,不是完全平方式,故本选项错误.故选B.【点评】本题是完全平方公式的应用;两数的平方和,再加上或减去它们积的2倍,就构成了一个完全平方式.10.如图所示,下列每个图是由若干盆花组成的形如三角形的图案,每条边(包括两个顶点)有n 盆花,每个图案花盆总数是S,按此推断S与n的关系式为()A.S=3n B.S=3(n﹣1)C.S=3n﹣1 D.S=3n+1【考点】根据实际问题列一次函数关系式;规律型:图形的变化类.【分析】由图可知:第一图:有花盆3个,每条边有2盆花,那么3=3×(2﹣1);第二图:有花盆6个,每条边有3盆花,那么6=3×(3﹣1);第三图:有花盆9个,每条边有4盆花,那么9=3×(4﹣1);…由此可知S与n的关系式为S=3(n﹣1).【解答】解:根据图案组成的是三角形的形状,则其周长等于边长的3倍,但由于每个顶点重复了一次.所以S=3n﹣3,即S=3(n﹣1).故选B.【点评】本题是一道找规律的题目,这类题型在中考中经常出现.本题要注意给出的图片中所包含的规律,然后根据规律列出函数关系式.二、填空题11.一台电视机的成本价为a元,销售价比成本价增加25%,因库存积压,所以就按销售价的70%出售,那么每台实际售价为元.【考点】列代数式.【分析】每台实际售价=销售价×70%.根据等量关系直接列出代数式即可.【解答】解:a(1+25%)×70%=70%(1+25%)a=元.【点评】解决问题的关键是读懂题意,找到所求的量的等量关系.注意销售价比成本价增加25%后,再按销售价的70%出售.12.已知=0 则a+b=.【考点】分式的值为零的条件;非负数的性质:绝对值;非负数的性质:偶次方;二次根式有意义的条件.【专题】计算题.【分析】分式的值为零,则分子为零,且分母不为零、二次根式的被开方数是非负数;据此列出关于a、b的方程组,通过解该方程组即可求得a、b的值.【解答】解:根据题意,得,解得,,则a+b=2+=;故答案是:.【点评】本题考查了分式的值为零的条件、非负数的性质以及二次根式有意义的条件.若分式的值为零,需同时具备两个条件:(1)分子为0;(2)分母不为0.这两个条件缺一不可.13.如果最简二次根式与是同类二次根式,则a= 5 .【考点】同类二次根式;最简二次根式.【分析】根据最简二次根式和同类二次根式的定义,列方程求解.【解答】解:∵最简二次根式与是同类二次根式,∴3a﹣8=17﹣2a,解得:a=5.【点评】此题主要考查最简二次根式和同类二次根式的定义.14.把a3+ab2﹣2a2b分解因式的结果是a(a﹣b)2.【考点】提公因式法与公式法的综合运用.【分析】先提取公因式a,再利用完全平方公式继续进行二次因式分解.【解答】解:a3+ab2﹣2a2b,=a(a2+b2﹣2ab),=a(a﹣b)2.【点评】本题主要考查提公因式法分解因式和完全平方公式分解因式,进行二次因式分解是解本题的关键.15.观察下列各式:,,,设n表示正整数,用关于n的等式表示这个规律是.【考点】规律型:数字的变化类.【分析】通过观察可以看出两个数的和等于两个数的积,分数的分母比分子小一,而相乘的整数和相加的整数也比分母大一,由此规律得出答案即可.【解答】解:由所给的各式可知,不妨设分母为n,则分子为n+1,另一个因数和加数也为n+1,因此可知律为.故答案为:.【点评】此题考查数字的变化规律,找出式子之间的联系,由特殊找出一般规律解决问题.三、解答下列各题16.如图,一块直径为a+b的圆形钢板,从中挖去直径分别为a与b的两个圆,求剩下的钢板的面积.【考点】整式的混合运算.【分析】剩下钢板的面积等于大圆的面积减去两个小圆的面积,利用圆的面积公式列出关系式,化简即可.【解答】解:S剩下=S大圆﹣S小圆1﹣S小圆2=π•()2﹣π•()2﹣π•()2==;答:剩下的钢板的面积是.【点评】此题考查了整式的混合运算,涉及的知识有:圆的面积公式,完全平方公式,去括号、合并同类项法则,熟练掌握公式及法则是解本题的关键.17.已知A=a+2,B=a2﹣a+5,C=a2+5a﹣19,其中a>2.(1)求证:B﹣A>0,并指出A与B的大小关系;(2)指出A与C哪个大?说明理由.【考点】因式分解的应用;整式的加减.【专题】分类讨论.【分析】计算B﹣A后结论,从而判断A与B的大小;同理计算C﹣A,根据结果来比较A与C的大小.【解答】解:(1)B﹣A=(a﹣1)2+2>0,所以B>A;(2)C﹣A=a2+5a﹣19﹣a﹣2,=a2+4a﹣21,=(a+7)(a﹣3).因为a>2,所以a+7>0,从而当2<a<3时,A>C;当a=3时,A=C;当a>3时,A<C.【点评】本题考查了整式的减法、十字相乘法分解因式,渗透了求差比较大小的思路及分类讨论的思想.18.已知a、b、c为△ABC三边,利用因式分解说明b2﹣a2+2ac﹣c2的符号.【考点】因式分解的应用;三角形三边关系.【分析】原式后三项提取﹣1变形后,利用完全平方公式分解因式,再利用平方差公式分解因式;由a,b及c为三角形的三边,利用两边之和大于第三边即可判断出因式分解后积的正负.【解答】解:原式=b2﹣(a2+c2﹣2ac)=b2﹣(a﹣c)2=(a+b﹣c)(﹣a+b+c);∵a,b,c为△ABC的三边长,∴(a+b﹣c)(﹣a+b+c)中,(a+b﹣c)>0,(﹣a+b+c)>0,∴(a+b﹣c)(﹣a+b+c)>0.【点评】此题考查了因式分解的应用,以及三角形的三边关系,灵活运用完全平方公式及平方差公式是解本题的关键.19.某餐厅中1X餐桌可坐六人,有以下两种摆放方式(如图1和2).一天中午,餐厅要接待98位顾客共同就餐,但餐厅只有25X这样的餐桌,若你是这个餐厅的经理,你应该选择哪种拼接方式来摆餐桌?请说明理由.【考点】规律型:图形的变化类.【分析】能够根据桌子的摆放发现规律,分别求出n=25时,两种不同的摆放方式对应的人数,即可作出判断.【解答】解:∵第一种中,只有一X桌子是6人,后边多一X桌子多4人.即有nX桌子时是6+4(n ﹣1)=4n+2.第二种中,有一X桌子是6人,后边多一X桌子多2人,即6+2(n﹣1)=2n+4.∴当n=25时,4n+2=4×25+2=102>98,当n=25时,2n+4=2×25+4=54<98,所以,选用第一种摆放方式.【点评】此题主要考查了图形的变化类,关键是通过归纳与总结,得到其中的规律.20.计算:.【考点】分式的乘除法.【分析】分式的除法计算首先要转化为乘法运算,然后对式子进行化简,化简的方法就是把分子、分母进行分解因式,然后进行约分.【解答】解:原式==.【点评】在完成此类化简题时,应先将分子、分母中能够分解因式的部分进行分解因式.有些需要先提取公因式,通过分解因式,把分子分母中能够分解因式的部分,分解成乘积的形式,然后找到其中的公因式约去.。
人教版七年级上册《3.1列代数式表示数量关系》2024年同步练习卷(1)+答案解析

人教版七年级上册《3.1列代数式表示数量关系》2024年同步练习卷(1)一、选择题:本题共3小题,每小题3分,共9分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.某校购进价格a元的排球100个,价格b元的篮球50个,则该校一共需支付()A. B. C. D.2.在下列表达式中,不能表示代数式“6a”意义的是()A.6个a相乘B.a的6倍C.6个a相加D.6的a倍3.在式子,,,,中,符合代数式书写要求的有()A.1个B.2个C.3个D.4个二、填空题:本题共4小题,每小题3分,共12分。
4.列式表示:产量由akg增长,就达到______5.苹果每千克a元,梨每千克b元,则整式表示购买______。
6.购买单价为a元的牛奶3盒,单价为b元的面包4个,共需______元;用含a,b的代数式表示全校学生总数是x,其中女生人数占总数的,则女生人数是______,男生人数是______;巧克力糖的单价为每千克a元,奶糖的单价为每千克b元,将m千克巧克力糖和n千克奶糖混合,这样得到的混合糖的平均单价是每千克______元.7.在下列各题的横线上填上适当的代数式:三个连续整数,中间一个数是n,其余两个数分别是______,______;三个连续奇数,中间一个是,其余两个数分别是______,______;一个两位数的个位数字是a,十位数字是b,用代数式表示这个两位数是______;一个三位数的百位数字是a,十位数字是b,个位数字是c,用代数式表示这个三位数是______.三、解答题:本题共5小题,共40分。
解答应写出文字说明,证明过程或演算步骤。
8.本小题8分下列各式哪些是代数式?哪些不是代数式?;;;;;米;9.本小题8分下列代数式可以表示什么?;10.本小题8分在某地,人们发现在一定温度下,某种蟋蟀叫的次数与温度之间有如下的近似关系:用蟋蟀叫的次数n除以7,然后再加上3,就近似地得到该地当时的温度用代数式表示该地当时的温度;当蟋蟀叫的次数为是100时,该地当时的温度约为多少?精确到个位11.本小题8分体育委员带了500元钱去买体育用品,已知一个足球a元,一个篮球b元,说明代数式表示的意义.12.本小题8分某超市出售一种商品,其原价为a元,现有三种调价方案:方案一,先提价,再降价;方案二,先提价,再降价;方案三,先降价,再提价用这三种方案调价,结果是否一样?在方案三中,若先降价,要想恢复原价,需提价百分之几?列方程解决答案和解析1.【答案】A【解析】【分析】本题考查了列代数式,根据数量之间的关系,利用含a,b的代数式表示出需付总金额是解题的关键.由总价=单价数量,可用含a,b的代数式表示出需付金额,此题得解.【解答】解:依题意,需付元.故选:2.【答案】A【解析】解:代数式“6a”意义是6与a相乘,故B、C、D正确;A、6个a相乘表示为:,故命题错误.故选代数式“6a”意义是6与a相乘,根据乘法的意义即可判断.本题考查了代数式的意义,理解乘法的意义是关键.3.【答案】C【解析】解:应写为,应写为,符合代数式书写要求的有三个,故选:代数式是由运算符号加、减、乘、除、乘方、开方把数或表示数的字母连接而成的式子.单独的一个数或者一个字母也是代数式.本题考查了代数式的相关知识,解题关键在于熟记该定义.4.【答案】【解析】解:故答案为:根据产量=原产量+增长的产量,列式即可.本题考查了列代数式,理解题意,找出基本数量关系是解决问题的关键.5.【答案】2千克苹果和1千克梨的钱数【解析】解:苹果每千克a元,表示2千克苹果的钱数,则整式表示购买2千克苹果和1千克梨的钱数,故答案为:2千克苹果和1千克梨的钱数。
人教版七年级上册《3.1列代数式表示数量关系》2024年同步练习卷(2)+答案解析

人教版七年级上册《3.1列代数式表示数量关系》2024年同步练习卷(2)一、选择题:本题共3小题,每小题3分,共9分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.下列各式,,,,其中代数式的个数是()A.5B.4C.3D.22.下面判断语句中正确的是()A.不是代数式B.的意义是a的平方与b的平方的和C.a与b的平方差是D.a,b两数的倒数和为3.下列代数式的书写正确的是()A. B. C. D.二、填空题:本题共5小题,每小题3分,共15分。
4.购买单价为a元的笔记本5本和单价为b元的铅笔6支应付款______元.5.某种电视机每台定价为a元,商店在节日搞促销活动,降价,那么促销期间每台电视机实际售价为______元用含a的代数式表示6.甲、乙二人一起加工零件.甲平均每小时加工a个零件,加工2小时;乙平均每小时加工b个零件,加工3小时.甲、乙二人共加工零件______个.7.一个篮球a元,一个足球b元,班长用500元买了3个篮球,2个足球,还剩______元.8.某机关单位2015年3月的三公经费为a万元,为响应省委提倡节俭的号召,开始减少三公经费,4月份比3月份减少,5月份又比4月份减少,则5月份的三公经费是______万元用含a的式子表示三、解答题:本题共3小题,共24分。
解答应写出文字说明,证明过程或演算步骤。
9.本小题8分请你结合生活实际,设计具体情境,解释下列代数式的意义:;10.本小题8分一种树苗的高度与生长年数之间的关系如下表所示:树苗原高是生长年数a树苗高度1115213031454填写第4年树苗可能达到的高度.请用含a的代数式表示树苗高度用你得到的代数式求生长了20年的树苗可能达到的高度.11.本小题8分新学期,两摞规格相同的数学课本整齐的叠放在讲台上,请根据图中所给出的数据信息,解答下列问题:每本书的高度为______cm,课桌的高度为______cm;当课本数为本时,请写出同样叠放在桌面上的一摞数学课本高出地面的距离用含x的代数式表示;桌面上有56本与题中相同的数学课本,整齐叠放成一摞,若从中取走14本,求余下的数学课本高出地面的距离.答案和解析1.【答案】D【解析】解:题中的代数式有:,,共2个.故选:根据代数式的概念,用运算符号把数字与字母连接而成的式子叫做代数式.单独的一个数或一个字母也是代数式.本题考查了代数式的概念,掌握代数式的概念是关键.2.【答案】D【解析】解:A、是代数式;B、的意义是a与b的和的平方;C、a与b的平方差是;D、a,b两数的倒数和为,正确.故选:根据代数式的定义以及代数式的含义判断各项.注意单独的一个数或一个字母也是代数式.注意代数式的定义与代数式的含义,会用数学语言叙述代数式的含义.3.【答案】D【解析】解:A、正确的书写格式是,故选项错误;B、正确的书写格式是3x,故选项错误;C、正确的书写格式是,故选项错误;D、书写正确.故选:根据代数式的书写要求判断各项.考查了代数式的书写要求:在代数式中出现的乘号,通常简写成“”或者省略不写;数字与字母相乘时,数字要写在字母的前面;在代数式中出现的除法运算,一般按照分数的写法来写.带分数要写成假分数的形式.4.【答案】【解析】解:购买单价为a元的笔记本5本和单价为b元的铅笔6支应付款:元,故答案为:根据题意可以列出相应的代数式,从而可以解答本题.本题考查列代数式,解答本题的关键是明确题意,列出相应的代数式.5.【答案】【解析】解:促销期间每台电视机实际售价为,故答案为:根据题意列出促销期间每台电视机实际售价的代数式即可.此题考查列代数式,找出题目蕴含的数量关系是解决问题的关键.6.【答案】【解析】解:甲、乙二人共加工零件个.故答案为:用甲2小时加工的零件数加上乙3小时加工的零件数即可.此题考查列代数式,找出题目蕴含的数量关系是解决问题的关键.7.【答案】【解析】解:由题意可得:还剩元.故答案为:直接利用剩余钱数=总钱数-买篮球花的钱数-买足球花的钱数,进而得出答案.此题主要考查了列代数式,正确表示出所要花的钱数是解题关键.8.【答案】【解析】解:5月份的产值为:万元.故答案为:根据4月份、5月份与3月份的三公经费的百分比的关系列式计算即可得解.本题考查了列代数式,理解各月之间的三公经费百分比的关系是解题的关键.9.【答案】解:汽车每小时行驶a千米,行驶30千米所用时间为小时.小明家去年产粮食x千克,今年增产,则今年的产量为千克.【解析】此式为分式,根据分式的特点与实际生活相联系.根据代数式表示的是比x增加赋予实际意义即可.此题考查了代数式的实际意义,同学们应当在日常学习中加以积累,观察生活.10.【答案】解:第4年树苗可能达到的高度是160cm,填表如下:生长年数a树苗高度1115213031454160根据表格中的数据可得;当时,,因此,这种树苗生长20年后可能达到的高度是【解析】对于,观察表格中的数据不难发现,每一年树苗高度比上一年增加15cm;对于,根据上述规律,可得生长a年,树苗生长的高度为15a,结合树苗的原高,即可得到高度h的表达式;对于,把代入所得的关系式中进行计算即可得解,试试吧!本题考查的是列代数式,掌握数量关系是解决此题的关键.11.【答案】【解析】解:书的厚度为:;课桌的高度为:;故答案为:;85;本书的高度为,课桌的高度为85,高出地面的距离为;当时,让高摞书距离地面的距离减去低摞书距离地面的距离后除以3即为每本数的高度;让低摞书的高度减去3本书的高度即为课桌的高度;高出地面的距离=课桌的高度本书的高度,把相关数值代入即可;把代入得到的代数式求值即可.考查列代数式及代数式求值问题;得到课桌的高度及每本书的厚度是解决本题的突破点.。
代数式专训05 运用字母表示数-思维转换(解析版)

代数式专训05 运用字母表示数-思维转换一、单选题1.下列各式:2m ,0,-2n ,b a ,221,,x x y a b ab x +-+=中,代数式有( ) A .4个B .5个C .6个D .7个 【答案】C【分析】根据代数式的定义解答即可.【解析】解:2m ,0,-2n ,b a ,221,x x y x+-是代数式; a b ab +=是等式.故选:C .【点睛】本题考查了代数式的识别,一般地,用运算符号加、减、乘、除、乘方、开方把数或者表示数的字母连接起来,所得到的式子叫做代数式.含“=”、“>”、“<”、“≥”、“≤”的式子都不是代数式. 2.下列说法错误的是( )A .数轴上原点表示的数是0B .31ab a -+是二次三项式C .–a 一定是负数D .所有的有理数都可以用数轴上的点表示【答案】C【分析】由数轴的三要素判断A ,由多项式的项与次数判断B ,由用字母表示数判断C ,由有理数的特点及数轴上的点可判断D .【解析】解:数轴上的原点表示的数为0,所以A 正确, 31ab a -+是二次三项式,所以B 正确,a -不一定表示负数,可以表示正数与0,所以C 错误,所有的有理数都可以用数轴上的点表示,所以D 正确.故选C .【点睛】本题考查的是命题的真假,掌握基础知识及举反例是解题的关键.3.a 表示有理数,则下列说法正确的是( )A .a 表示正数B .-a 表示负数C .|a|表示正数D .-a 表示a 的相反数【答案】D【分析】根据用字母表示数的意义对各选项逐一判断即可.【解析】A.a 可以表示正数,0,负数.故A 错误;B. -a 表示正数,0,负数.故B 错误;C.当a=0时,|a|=0,0既不是正数也不是负数,当a≠0时,|a|>0,故|a|≥0,即|a|表示非负数,故C 错误;D. -a 表示a 的相反数,故D 正确.故选D.【点睛】本题考查了用字母表示数的意义,正确理解字的含义是解题的关键.4.下列说法中正确的个数是( )(1)-a 表示负数;(2)多项式2223721a b a b ab -+-+的次数是3;(3)单项式229xy -的系数为-2; (4)若||=-x x ,则0x <.A .0个B .1个C .2个D .3个【答案】A【分析】根据用字母表示数、多项式的次数是多项式中最高次项的次数、单项式的系数是单项式的数字部分、绝对值的性质解答即可.【解析】-a 既可以表示负数也可以表示正数和0,故A 错误;多项式2223721a b a b ab -+-+的次数是4,故B 错误; 单项式229xy -的系数为29-,故C 错误; 若||=-x x ,则x≤0,故D 错误.故选:A【点睛】本题考查的是用字母表示数、多项式的次数、单项式的系数、绝对值的性质,掌握各知识点的定义或性质是关键.5.粗心的小倩在放学回家后,发现把数学练习册忘在教室了,担心教室关门,于是她跑步到学校取了练习册,再步行回家(取书时间忽略不计).已知跑步速度为x ,步行速度为y ,则她往返一趟的平均速度是( )A .xB .yC .2x y +D .2xy x y+ 【答案】D 【分析】设从学校到家路程为s ,然后表示出从家到学校所用时间,再表示出从学校到家所用时间,然后利用总路程除以总时间可得平均速度.【解析】设从学校到家路程为s , 平均速度是:22s s sy sx s s x y xy xy ⎛⎫⎛⎫÷+=÷+ ⎪ ⎪⎝⎭⎝⎭()22s x y xy s xy x y+=÷=+; 故选:D .【点睛】此题主要考查了列代数式,关键是掌握平均速度=路程÷时间.6.下列判断错误的是( )A .多项式2524x x -+是二次三项式B .单项式2343a b c -的系数是3-,次数是9C .式子5m +,ab ,()261a -,2-,s z 都是代数式 D .若a 为有理数,则9a 一定大于a【答案】D【分析】根据多项式与单项式的基本概念判断A 、B ,根据代数式的定义判断C ,根据字母可以表示任何数判断D.【解析】A. 多项式2524x x -+是二次三项式,正确,不符合题意;B. 单项式2343a b c -的系数是3-,次数是9,正确,不符合题意;C. 式子5m +,ab ,()261a -,2-,s z都是代数式,正确,不符合题意; D. 若a 为有理数,则9a 一定大于a ,若a=0,则9=a a ,D 判断错误,符合题意.故选D.【点睛】本题考查多项式、单项式、代数式的基本概念,以及用字母表示数,熟记基本概念是解题的关键. 7.有一个两位数,个位数字是n ,十位数字是m ,则这个两位数可表示为( )A .mnB .10m n +C .10n m +D .m n +【分析】因为m 代表十位这个数字的大小,根据代数式的表示即可.【解析】解:m 代表十位数字的大小,n 代表个位数字的大小,所以这个两位数为10m+n故选B【点睛】本题考查了用字母表示数及列代数式,解题的关键是掌握代数式的表达方式.8.已知2131=+a ,2262=+a ,23103=+a ,24154=+a ……n a ,则20202010-=a a ( )A .2020B .4039C .6060D .8079【答案】C 【分析】先由已知等式,得出规律:()2121n a n n n =++++++23322n n ++=,则133n n a a n +-=+,将2019n =代入,即可求出结果.【解析】解:()2121n a n n n =++++++()()21112n n n +++⎡⎤⎣⎦=+ ()()2212n n n ++=+ 223222n n n +++= 23322n n ++=. ()()2213131233222n n n n n n a a +++++++-=- ()()223131332n n n n +++--= 2236333332n n n n n ++++--= 662n +=2019n =时,()20202019320191a a -=+32020=⨯6060=.故选:C .【点睛】此题主要考查了规律型:数字的变化类及有理数的混合运算,解题时首先观察,分析归纳出题目中隐含的规律,然后利用规律把题目变形,从而使计算变得比较简便.二、填空题9.已知方程35x ﹣15y =1,用含x 的式子表示y ,则y =_____. 【答案】35x -【分析】把x 看做已知数求出y 即可.【解析】解:方程31155x y -=, 去分母得:35x y -=,解得:35y x =-.故答案为:35x -.【点睛】本题考查代数式的表示,二元一次方程的解法等知识,是基础考点,难度较易,掌握相关知识是解题关键.10.如果一个圆的半径是a (cm),那么这个圆的周长是___cm ,面积是____cm 2.【答案】2πa πa 2【分析】根据圆的周长公式和面积公式表示出圆的周长和面积即可.【解析】解:根据圆的周长公式和面积公式得:圆的周长为2πa ;圆的面积为πa 2.故答案为2πa ,πa 2.【点睛】本题考查了列代数式,掌握圆的周长公式和面积公式是解答本题的关键.11.一个没有关紧的水龙头一天滴水约0.09 m 3,n 个这样的水龙头一天滴水约____m 3.【答案】0.09n【分析】直接用0.09乘以n 即可得出答案.【解析】一个没有关紧的水龙头一天滴水约0.09 m 3,n 个这样的水龙头一天滴水约0.09n m 3,故答案为:0.09n .【点睛】本题主要考查用字母表示数,读懂题意是解题的关键.12.一个两位数的个位上的数字是1,十位上的数字比个位上的数字大a ,则这个两位数是______.【答案】10a+11【分析】先表示出十位上的数字,然后再表达出这个两位数的大小【解析】∵个位数是1,十位数比个位数大a∴十位数是1+a∴这个两位数为:10(a+1)+1=10a+11故答案为:10a+11【点睛】本题考查用字母表示数字,解题关键是:若十位数字为a ,则应表示为10a13.字母表示图中阴影部分的面积为_____.【答案】2214a a π- 【分析】图中阴影部分的面积=正方形的面积−圆形的面积.【解析】其中正方形的边长是a ,圆的半径是2a . ∴S 阴=a 2−π•(2a )2=2214a a π-. 故答案为:2214a a π-. 【点睛】此题要能从图中看出阴影部分的面积是哪些图形组合成的,然后再利用已知面积的图形差求阴影的面积:阴影部分的面积=正方形的面积−圆形的面积.14.如图,ABC ∆的BC 边长为x ,BC 边上的高是8,当x 每增加1时,ABC ∆的面积就增加________.【答案】4∆增加后的面积减去增加前的面积计算即可.【分析】根据ABC∆增加后的面积=(x+1)×8÷2=4(x+1),增加前的面积=8x÷2=4x,【解析】ABC∴4(x+1)-4x=4,故答案为:4.【点睛】本题考查了三角形面积公式的代数式表示,代数式的加减计算,掌握代数式的表示是解题的关键.15.一种商品每件成本价是a元,按成本增加20%定价出售,后由于库存积压,又按定价的90%出售,则该商品现在的售价是__________元.【答案】1.08a【分析】先列出开始的售价,再列出后来的售价即可.【解析】解:由题意可知,开始的售价为(1+20%)a元,所以后来的售价为90%×(1+20%)a=1.08a元..故答案为1.08a.【点睛】本题考查列代数式,解答本题的关键是明确题意,列出相应的代数式.16.某音像社对外出租光盘的收费方法是:每张光盘在租出后的头两天每天收0.80元,以后每天收0.50元.那么一张光盘在租出n天(n是大于2的自然数)应收租金___元.【答案】0.5n+0.6【分析】先求出出租后的头两天的租金,然后用n-2求出超出2天的天数,进而求出超出两天后的租金,然后将两部分租金相加即可解答.【解析】由题意可得,应收租金为:()⨯+-⨯n0.8220.5=1.6+0.5n-1=0.5n+0.6故答案为:0.5n+0.6【点睛】本题考查了列代数式,仔细辨别题意,分清数量关系是解题的关键.17.今年五月份,由于禽流感的影响,我市鸡肉的价格下降了10%,设鸡肉原来的价格为a 元/千克,则五月份的价格为________元/千克.【答案】0.9a【分析】因为原来鸡肉价格为a 元/千克,现在下降了10%,所以现在的价格为(1-10%)a ,即0.9a 元/千克.【解析】∵原来鸡肉价格为a 元/千克,现在下降了10%,∴五月份的价格为a-10%a=(1-10%)a=0.9a ,故答案为0.9a .18.若一支圆珠笔的笔芯的价格为0.9元,买一些笔芯需付款0.9x 元,则x 表示的实际意义是______.【答案】这些笔芯共x 支【分析】根据题意解答即可.【解析】解:一支圆珠笔的笔芯的价格为0.9元,买一些笔芯需付款0.9x 元,则x 表示的是笔的支数, 即:x 表示的实际意义是:这些笔芯共x 支【点睛】本题考查了对未知数的含义的理解.三、解答题19.小李家住房结构如图所示,小李打算把卧室和客厅铺上木地板.(1)请问他至少需要买多少平方米的木地板?(用字母表示)(2)若3x =米,2y =米时,并且每平方米木地板的价格是150元,则他至少需要准备多少元钱?【答案】(1)12xy ;(2)10800元【分析】(1)根据长方形的面积公式用字母列式即可得到答案;(2)由(1)可得需要木地板的代数式,将x=3,y=2代入之后再乘以150计算即可.【解析】解:(1)由图中可知,卧室的宽为2y ,长为4x-2x=2x ,客厅的长为4y ,宽为2x ,所以小李至少需要买木地板:2y×2x+4y×2x=12xy平方米,答:他至少需要买12xy平方米的木地板;(2)由(1)可知小李需要买12xy平方米的地板,将x=3,y=2代入有12×3×2=72平方米,因为每平方米木地板的价格是150元,所以需要至少准备:72×150=10800元钱,答:他至少需要准备10800元钱.【点睛】本题考查的是用代数式的知识,根据长方形的面积公式正确的是写出代数式是解题的关键. 20.果园里有苹果树x棵,桃树y棵,且x>y.请用含字母x,y的式子表示下列数量关系:(1)苹果树比桃树多多少棵?(2)苹果树和桃树共有多少棵?【答案】(1)(x-y)棵;(2)(x+y)棵【分析】(1)用x,y的差表示苹果树比桃树多多少棵;(2)用x,y的和表示苹果树和桃树共有多少棵. 【解析】解:由已知可得:(1)苹果树比桃树多(x-y)棵;(2)苹果树和桃树共有(x+y)棵.故答案为:(1)(x-y)棵;(2)(x+y)棵【点睛】本题考核知识点:列含有字母的式子.解题关键点:理解已知中的数量关系.21.某根弹簧下端所挂物体的质量不超过25 g时,弹簧的长度随着物体质量的增加而增加.下表记录的是这根弹簧挂不同质量的物体时弹簧的长度.所挂物体质量/g 0 1 2 3 4 …弹簧长度/cm 10 10.1 10.2 10.3 10.4 …请你根据表中的数据进行分析,当弹簧下端挂质量为x(0≤x≤25)g的物体时,弹簧的长度是多少厘米? 【答案】(10+0.1x)cm.【分析】弹簧的长度随物体的质量的增加而增加,物体的质量每增加1g,则弹簧的长度就增加0.1cm,考虑到弹簧不挂物体时的长度是10cm ,即可解题.【解析】解:根据表中的数据可以看出,当所挂物体质量为0 g 时,弹簧的长度为10 cm ,说明弹簧的原长为10 cm.随着所挂物体质量的增加,弹簧的长度也在增加,并且物体每增加1 g ,弹簧的长度就增加0.1 cm ,所以当所挂物体质量为x (0≤x ≤25) g 时,弹簧的长度为(10+0.1x ) cm.22.工程队计划每天修路a 米,20天可以修完,实际只用了15天,实际每天修路多少米?(1)用式子表示实际每天修路是多少米?(2)根据多个式子,求240a =时,实际每天修路多少米?【答案】(1)20a÷15(2)320米 【分析】(1)根据据路的总长度=计划每天修路的长度×计划的天数求出路的总长度,再依据实际每天修路的长度=总长度÷实际所用的天数列出代数式即可;(2)把a=20代入(1)中的代数式求值即可.【解析】(1)∵路的总长度为20a 米,∴实际每天修路的长度为20a÷15米.答:实际每天修路的长度为20a÷15米. (2)把a=240代入20a÷15得,20a÷15=20×240÷15=320(米).答:实际每天修路320米.【点睛】本题考查了列代数式及求代数式的值,明确各数量间的等量关系,并能根据它们列出代数式是解决本题的关键.23.甲乙两数和的2倍为n ,甲乙两数之和为多少? 【答案】2n 【分析】设甲乙两数之和为x ,则2x n = ,解得2n x =,即两数之和为2n . 【解析】由题意得,甲乙两数之和为2n . 24.某工程甲独做需x 天,乙独做需y 天,求两人合作需几天完成? 【答案】xy x y+ 【分析】由题可知,甲每天完成工程的1x ,乙每天完成工程的1y ,则两人合作每天完成工程的11x y + ,所以需要111x y⎛⎫÷+⎪⎝⎭天才能完成.【解析】1÷(11x y+)=xyx y+.25.平行四边形高a,底b,求面积.【答案】ab【分析】平行四边形的面积=底×高.【解析】由平行四边形的面积公式得,面积为ab.26.同学们,你们还记得“青蛙绕口令”吗?若有a只青蛙,则用绕口令怎么说?请你用今天所学的知识解决这个问题.【答案】见解析【分析】用字母表示数,关键是根据数量关系式把未知量当作已知的量来解答,列数量关系式时首先要弄清语句中各数量的意义及相互关系;本题中由于青蛙的嘴数和只数相等,眼睛数是只数的2倍,腿数是只数的4倍,跳下水的声音数与只数相等,即可用表示出a只青蛙的情况.【解析】由于青蛙的嘴数和只数一样,眼睛数是只数的2倍,腿数是青蛙眼睛数的2倍,腿数是青蛙只数的4倍.当有a只青蛙时,则青蛙的嘴数是a张,眼睛数是2a只,腿数是4a条.故绕口令为“a只青蛙a张嘴,2a 只眼睛4a条腿,扑通a声跳下水点睛:本题考点是探求规律,解题关键是仔细观察,细致分析,局部找规律,整体找联系.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、初一数学代数式解答题压轴题精选(难)1.如图所示,在边长为a米的正方形草坪上修建两条宽为b米的道路.(1)为了求得剩余草坪的面积,小明同学想出了两种办法,结果分别如下:方法①:________ 方法②:________请你从小明的两种求面积的方法中,直接写出含有字母a,b代数式的等式是:________(2)根据(1)中的等式,解决如下问题:①已知:,求的值;②己知:,求的值.【答案】(1)(a-b)2;a2-2ab+b2;(a-b)2=a2-2ab+b2(2)解:①把代入∴,∴②原式可化为:∴∴∴【解析】【解答】解:(1)方法①:草坪的面积=(a-b)(a-b)= .方法②:草坪的面积= ;等式为:故答案为:,;【分析】(1)方法①是根据已知条件先表示出矩形的长和宽,再根据矩形的面积公式即可得出答案;方法②是正方形的面积减去两条道路的面积,即可得出剩余草坪的面积;根据(1)得出的结论可得出;(2)①分别把的值和的值代入(1)中等式,即可得到答案;②根据题意,把(x-2018)和(x-2020)变成(x-2019)的形式,然后计算完全平方公式,展开后即可得到答案.2.如图,在数轴上点A表示数a,点C表示数c,且多项式x3﹣3xy29﹣20的常数项是a,次数是c.我们把数轴上两点之间的距离用表示两点的大写字母一起标记,比如,点A与点B之间的距离记作AB.(1)求a,c的值;(2)若数轴上有一点D满足CD=2AD,则D点表示的数为________;(3)动点B从数1对应的点开始向右运动,速度为每秒1个单位长度.同时点A,C在数轴上运动,点A,C的速度分别为每秒2个单位长度,每秒3个单位长度,运动时间为t 秒.①若点A向右运动,点C向左运动,AB=BC,求t的值;②若点A向左运动,点C向右运动,2AB-m×BC的值不随时间t的变化而改变,直接写出m的值.【答案】(1)解:∵多项式x3﹣3xy29﹣20的常数项是a,次数是c.∴a=-20,c =30(2)-70或(3)解:①如下图所示:当t=0时,AB=21,BC=29. 下面分两类情况来讨论: a.点A,C在相遇前时,点A,B之间每秒缩小1个单位长度,点B,C每秒缩小4个单位长度. 在t=0时,BC -AB=8, 如果AB=BC,那么AB-BC=0,此时t= 秒, b.点A,C在相遇时,AB=BC,点A,C之间每秒缩小5个单位长度,在t=0时,AC=50,秒, c.点A,C在相遇后,BC 大于AC,不符合条件. 综上所述,t= ②当时间为t时,点A表示得数为-20+2t,点B表示得数为1+t,点C表示得数为30+3t,2AB-m×BC=2[(1+t)-(-20+2t)]-m[(30+3t)-(1+t)],=(6-2m)t+(42-29m),当6-2m=0时,上式的值不随时间t的变化而改变,此时m=3.【解析】【解答】解:(2)分三种情况讨论,•当点D在点A的左侧,∵CD=2AD,∴AD=AC=50,点C点表示的数为-20-50=-70,‚当点D在点A,C之间时,∵CD=2AD,∴AD= AC= ,点C点表示的数为-20+ =- ,ƒ当点D在点C的右侧时,AD>CD与条件CD=2AD相矛盾,不符合题意,综上所述,D点表示的数为-70或 ;【分析】(1)根据多项式 x3﹣3xy29﹣20的常数项是a,次数是c.就可得出a、c的值。
(2)分三种情况:当点D在点A的左侧;当点D在点A,C之间时;当点D在点C的右侧时,根据CD=2AD,及点A、C表示的数,就可求出点D表示的数。
(3)① 根据题意画出图形,当t=0时,AB=21,BC=29 ,分情况讨论:a.点A,C在相遇前时; b.点A,C在相遇时,AB=BC ,分别求出符合题意的t的值即可;②当时间为t 时,点A表示得数为-20+2t,点B表示得数为1+t,点C表示得数为30+3t,建立方程求出m的值即可。
3.如图,老王开车从A到D,全程共72千米.其中AB段为平地,车速是30千米/小时,BC段为上山路,车速是22.5千米/小时,CD段为下山路,车速是36千米/小时,已知下山路是上山路的2倍.(1)若AB=6千米,老王开车从A到D共需多少时间?(2)当BC的长度在一定范围内变化时,老王开车从A到D所需时间是否会改变?为什么?(给出计算过程)【答案】(1)解:若AB=6千米,则BC=22千米,CD=44千米,从A到D所需时间为:=2.4(小时)(2)解:从A到D所需时间不变,(答案正确不回答不扣分)设BC=d千米,则CD=2d千米,AB=(72﹣3d)千米,t===2.4(小时)【解析】【分析】(1)根据题意可以求出AB,BC,CD的长,然后根据路程除以速度等于时间,即可分别算出老王开车行三段的时间,再求出其和即可;(2)从A到D所需时间不变,设BC=d千米,则CD=2d千米,AB=(72﹣3d)千米,,然后根据路程除以速度等于时间,即可分别表示出老王开车行三段的时间,再根据异分母分式加法法则求出其和,再整体代入即可得出结论;4.从2022年4月1日起龙岩市实行新的自来水收费阶梯水价,收费标准如下表所示:月用水量不超过15吨的部分超过15吨不超过25吨的部分超过25吨的部分收费标准2.23.34.4(元/吨)(2)某用户8月份用水量为24吨,求该用户8月份应缴水费是多少元.(3)若某用户某月用水量为m吨,请用含m的式子表示该用户该月所缴水费.【答案】(1)解:2.2×10=22元,答:该用户4月份应缴水费是22元,(2)解:15×2.2+(24﹣15)×3.3=62.7元,答:该用户8月份应缴水费是 62.7元(3)解:①当m≤15时,需交水费2.2m元;②当15<m≤25时,需交水费,2.2×15+(m﹣15)×3.3=(3.3m﹣16.5)元,③当m>25时,需交水费2.2×15+10×3.3+(m﹣25)×4.4=(4.4m﹣44)元.【解析】【分析】(1)先根据月用水量确定出收费标准,再进行计算即可;(2) 8月份应缴水费为:不超过15吨的水费+超出的9吨的水费;(3)分①m≤15吨,②15<m≤25吨,③m>25吨三种情况,根据收费标准列式进行计算即可得解。
5.糖业是我省重要的生物资源产业.我省某糖业集团今年4月收购甘蔗后入榨甘蔗250万吨,榨糖率为12%.经市场调查知5月份糖的销售价为2940/吨,若糖业集团在5月销售4月生产的糖,产销率为60%;又知糖业集团若在6月、7月两个月内销售4月生产的糖,销售价将在5月的基础上每月比上月降低6%、糖销量将在5月的基础上每月比上月增加9%.(1)问2005年4月糖业集团生产了多少吨糖?(2)若糖业集团计划只在7月销售4月生产的糖,请求出该糖业集团7月销售4月生产的糖的销售额是多少?(精确到万元)(注:榨糖率=(产糖量/入榨甘蔗量)×100%,产销率=(糖销量/产糖量)×100%,销售额=销售单价×销售数量).【答案】(1)解:2005年4月糖业集团产糖250×12%=30(万吨)=300000(吨)(2)解:设7月份的糖价为x元/吨,则据已知条件有x=2597.784(元/吨);设7月份的糖销量为y吨,则据已知条件得:y=30×0.60×(1+9%)2=21.3858(万吨)设7月份销售4月份产糖的销售额为w元,则据题意得:w=2597.784×21.3858≈55556(万元).答:糖业集团7月份销售4月份产糖的销售额约为55556万元.【解析】【分析】(1)根据产糖量等于入搾甘蔗量乘以搾糖率即可求解;(2)由题意先求出7月份的糖价=2940(1-6%)2=2597.784元/吨,再求出7月份的糖销量=30×0.60×(1+9%)2=21.3858(万吨),最后根据销售额等于销售单价乘以销售量即可解答。
6.甲、乙两家体育用品商店出售同样的乒乓球拍和乒乓球,乒乓球拍每副定价20元,乒乓球每盒定价5元.现两家商店搞促销活动,甲店的优惠办法是:每买一副乒乓球拍赠一盒乒乓球;乙店的优惠办法是:按定价的9折出售.某班需购买乒乓球拍4副,乒乓球若干盒(不少于4盒).(1)用代数式表示(所填式子需化简):当购买乒乓球的盒数为x盒时,在甲店购买需付款________元;在乙店购买需付款________元.(2)当购买乒乓球盒数为10盒时,到哪家商店购买比较合算?说出你的理由.(3)当购买乒乓球盒数为10盒时,你能给出一种更为省钱的购买方案吗?试写出你的购买方案,并求出此时需付款几元?【答案】(1)(5x+60);(4.5x+72)(2)解:当x=10时,甲店需付费5×10+60=110元;乙店需付费4.5×10+72=117元,∴到甲商店比较合算(3)解:可在甲店购买4副乒乓球拍子,在乙店购买(10﹣4)盒乒乓球,所需费用为:4×20+(10﹣4)×5×0.9=80+27=107元【解析】【解答】解:(1)甲店需付费:4×20+(x﹣4)×5=80+5x﹣20=(5x+60)元;乙店需付费:(4×20+x×5)×0.9=(4.5x+72)元;故答案为(5x+60);(4.5x+72);【分析】(1)甲店需付费:4副乒乓球拍子费用+(x﹣4)盒乒乓球费用;乙店需付费:(4副乒乓球拍子费用+x盒乒乓球费用)×0.9,把相关数值代入求解即可;(2)把x=10代入(1)得到的式子计算,比较结果即可;(3)可在甲店购买乒乓球拍子,在乙店购买乒乓球.7.已知(其中是各项的系数,是常数项),我们规定的伴随多项式是,且. 如,则它的伴随多项式.请根据上面的材料,完成下列问题:(1)已知,则它的伴随多项式 ________.(2)已知,则它的伴随多项式 ________;若,x=________(3)已知二次多项式,并且它的伴随多项式是,若关于的方程有正整数解,求的整数值.【答案】(1)5x4(2)10x-27;x=4;(3)解:∵∴g(x)=2(a+3)x+16=(2a+6)x+16,由g(x)=-2x,得(2a+6)x+16=-2x,化简整理得:(2a+8)x=-16,∵方程有正整数解,,∴,∵a为整数,∴a+4=-1或-2或-4或-8,∴a=-5或-6或-8或-12.【解析】【解答】解:(1)∵,∴g(x)=5x4;故答案为:5x4;( 2 )解:∵ = ,∴g(x)=10x-27,由g(x)=13,得10x-27=13,解得:x=4;故答案为:10x-27;x=4;【分析】(1)由题意可知n=5,根据题中的新定义确定出g(x)即可;(2)先变形为 = ,再根据题中的新定义确定出g(x),并求出所求x的值即可;(3)确定出f(x)的伴随多项式g(x)=(2a+6)x+16,由g(x)=-2x得,再根据方程有正整数解,确定出整数a的值即可.8.将7张相同的长方形纸片(如图1)按图2所示的方式不重叠地放在长方形ABCD内,未被覆盖的部分恰好可以分割为两个长方形,面积分别为S1和S2.已知小长方形纸片的长为a,宽为b,且a>b.(1)当a=9,b=2,AD=30时,S1-S2=________.(2)当AD=30时,用含a,b的式子表示S1-S2.(3)若AB长度不变,AD变长,将这7张小长方形纸片按照同样的方式放在新的长方形ABCD内,而且S1-S2的值总保持不变,则a,b满足的关系是________.【答案】(1)48(2)解:S1-S2=a(30-3b)-4b(30-a)=30a-120b+ab(3)a=4b【解析】【解答】(1)解:当a=9,b=2,AD=30时,S1=a(30-3b)=9×(30-3×2)=216S2=4b(30-a)=4×2×(30-9)=168S1-S2=216-168=483)解:设AD=m,S1-S2=(am-3ab)-(4bm-4ab)=am-4bm+ab若S1-S2的值总保持不变,则S1-S2的值与m的取值无关,所以有am-4bm=0则a=4b.【分析】(1)观察图形,分别求出S1和S2的面积,再求差即可;(2)用含a、b的代数式分别表示S1和S2的面积,再求差即可;(3)设AD=m, 用含a、b、m的代数式分别表示S1和S2的面积差,再去括号合并同类项,根据题意S1-S2的值总保持不变,即可解答.9.如图所示,图甲由长方形①,长方形②组成,图甲通过移动长方形②得到图乙.(1)S甲=________,S乙=________(用含a、b的代数式分别表示);(2)利用(1)的结果,说明a2、b2、(a+b)(a﹣b)的等量关系;(3)现有一块如图丙尺寸的长方形纸片,请通过对它分割,再对分割的各部分移动,组成新的图形,画出图形,利用图形说明(a+b)2、(a﹣b)2、ab三者的等量关系.【答案】(1)(a+b)(a-b);a2-b2(2)由两个图形的面积相等可知,(a+b)(a-b)=a2-b2。
