最短路径源代码_C++实现

合集下载

Dijkstra算法设计与实现

Dijkstra算法设计与实现作者：杜衡吉来源：《电脑知识与技术》2016年第28期摘要：最短路径算法在各领域应用广泛，大多《离散数学》的图论部分最短路径算法讲解较为粗略，不便于学生学习和实践。

经过多年教学总结，对最短路径算法给出设计和实现，有利于学生对本知识的掌握和实践应用。

关键词：最短路径；离散数学； Dijkstra算法中图分类号：TP311 文献标识码：A 文章编号：1009-3044（2016）28-0079-021 概述最短路径问题是指在一个非负权值图中找出两个指定节点间的一条权值之和最小的路径。

Dijkstra 算法在很多计算机专业可均有介绍，如数据结构，离散数学等，但大都比较粗略。

迪克斯特拉算法是经典的求解最短路径问题的方法，是按路径长度递增的次序来产生最短路径的算法[1]。

最短路径问题描述：设n，m带权图 G=，V={v0，v1，…，vn-1}，E={e1，e2，…，em}，其中假设每条边ei 的权值为 wi，单源的最短路径就是从图G中找到起源点 V0 到图中其余各点的最短路径。

2 最短路径概念带权图G=，其中W：ER， eE，w（e）称作e的权。

若vi和vj相邻e=（vi，vj），记w（vi，vj）=w（vi，vj），若vi，vj不相邻，记w（vi，vj）=。

通路L的权是指L的所有边的权值之和，记作w（L），u和v之间的最短路径指的是 u和v之间边权最小的通路[2]。

3 Dijkstra算法描述1）算法基本过程：设带权图G=，把图G中顶点集合V分成两个子集，第一个子集是已求出最短路径的顶点集合，用V1表示，初始化时V1中只有一个起源点，以后每求得一条最短路径，就将被选定点加入到集合V1中，直到图中全部顶点都依次添加到到V1中，算法就结束了；第二个集合为G中其余未确定最短路径的顶点集合，用V2表示，按最短路径长度的递增次序依次把第二个集合V2中的被选顶点加入集合V1中。

特别，在加入的过程中，总保持从起源点v0到V1中各顶点的最短路径长度不大于从源点v0到V2中任何顶点的最短路径长度。

迪杰斯特拉算法c语言

迪杰斯特拉算法c语言一、什么是迪杰斯特拉算法？迪杰斯特拉算法（Dijkstra algorithm）是一种用于解决图的最短路径问题的贪心算法。

它采用了广度优先搜索的策略，每次找到当前节点到其他所有节点中距离最短的一个节点，并将该节点加入到已访问的集合中，直到所有节点都被访问为止。

二、迪杰斯特拉算法的原理1. 初始化首先，我们需要对图进行初始化。

设定一个起点，并将该点距离源点的距离设置为0，其他点距离源点的距离设置为无穷大。

2. 找到最小距离接下来，我们需要从未访问过的节点中找到距离源点最近的一个节点。

这个过程可以通过建立一个优先队列来实现。

在每次找到最小值后，我们需要将该节点标记为已访问，并更新与该节点相邻的所有未访问过的节点的最小距离值。

3. 更新最短路径在更新与当前节点相邻的所有未访问过的节点之后，我们需要重新寻找未访问过的节点中距离源点最近的一个。

这个过程会不断重复直至所有节点都被访问过。

4. 输出结果当所有节点都被访问过之后，我们就可以得到从源点到其他所有节点的最短路径。

三、迪杰斯特拉算法的实现以下是一个使用C语言实现的简单示例代码：```c#define INF 1000000 // 定义无穷大int dist[MAX_VERTEX_NUM]; // 存储距离源点的距离int visited[MAX_VERTEX_NUM]; // 标记是否已访问过// 初始化图void init_graph(Graph G, int start) {for (int i = 0; i < G.vertex_num; i++) {dist[i] = INF;visited[i] = 0;}dist[start] = 0;}// 找到距离源点最近的节点int find_min(Graph G) {int min_dist = INF, min_index = -1;for (int i = 0; i < G.vertex_num; i++) {if (!visited[i] && dist[i] < min_dist) {min_dist = dist[i];min_index = i;}}return min_index;}// 更新与当前节点相邻的节点的最短距离值void update_dist(Graph G, int index) {for (EdgeNode* p = G.adj_list[index].first_edge; p != NULL; p= p->next_edge) {int v = p->adjvex;if (!visited[v] && dist[index] + p->weight < dist[v]) {dist[v] = dist[index] + p->weight;}}}// 迪杰斯特拉算法void dijkstra(Graph G, int start) {init_graph(G, start);for (int i = 0; i < G.vertex_num; i++) {int index = find_min(G);visited[index] = 1;update_dist(G, index);}}```四、迪杰斯特拉算法的应用迪杰斯特拉算法可以用于解决许多实际问题，如路由选择、网络优化等。

networkx 最短路算法

一、网络图简介网络图是一种表示对象之间关系的数学结构，它由一组节点和连接这些节点的边组成。

在现实生活中，网络图可以用来表示交通网络、社交网络、电力网络等各种复杂系统。

在计算机科学中，网络图通常被用于建模和解决各种问题，比如最短路径问题、最小生成树问题、网络流问题等。

二、 NetworkX 简介NetworkX 是一个用 Python 语言编写的开源图论和复杂网络分析工具包，它提供了创建、操作和研究复杂网络的功能。

NetworkX 支持创建各种类型的网络图，包括有向图、无向图、加权图等，并提供了丰富的图算法和分析工具。

其中，最短路径算法是 NetworkX 中的一个重要功能，它可以用来寻找网络图中的最短路径。

三、最短路径算法概述最短路径算法用于寻找网络图中两个节点之间的最短路径，其中路径的长度可以通过边的权重来定义。

最短路径算法有多种实现方式，常见的算法包括 Dijkstra 算法、Bellman-Ford 算法、Floyd-Warshall 算法等。

这些算法在不同场景下具有不同的适用性和效率。

四、 NetworkX 中的最短路径算法在 NetworkX 中，最短路径算法主要包括两种实现方式：单源最短路径算法和全源最短路径算法。

单源最短路径算法用于寻找网络图中某个特定节点到其他所有节点的最短路径，常见的算法有 Dijkstra 算法和 Bellman-Ford 算法；全源最短路径算法用于寻找网络图中任意两个节点之间的最短路径，常见的算法有 Floyd-Warshall 算法。

五、单源最短路径算法1. Dijkstra 算法Dijkstra 算法是一种用于计算单源最短路径的贪心算法，它的基本思想是从起始节点开始，逐步扩展到其他节点，并更新节点之间的最短距离。

具体步骤如下：（1）初始化起始节点到其他所有节点的距离为无穷大，起始节点到自身的距离为 0；（2）选择距离起始节点最近的未访问节点，并更新该节点到其相邻节点的距离；（3）重复上述步骤，直至所有节点都被访问过。

Python中的最短路径算法详解

Python中的最短路径算法详解Python是一门高效的编程语言，其强大的算法库包含了许多经典的算法，比如最短路径算法。

最短路径算法是图论中的一个经典问题，它的目的是在图中寻找从一个指定顶点到另一个指定顶点的最短路径，即边权重之和最小的路径。

最短路径算法有很多种，其中比较常见的有Dijkstra算法、Bellman-Ford算法和Floyd算法。

接下来我将分别介绍这3种算法的原理和Python实现。

1. Dijkstra算法Dijkstra算法是最短路径算法中比较经典的一种，它采用贪心策略，通过每次选取当前离源点最近的节点来不断扩展路径，直至到达终点。

它的基本思路如下：步骤1：定义源点s到其它节点的距离数组dist[]，每当找到一条从源点可以到达的路径，就比较这条路径的长度和已知的最短路径长度，如果路径更短，就替换当前的最短路径长度，并更新终点节点的前一个节点。

步骤2：标记源点s为已经访问过的节点，将该节点入队，并在队列中取出此时距离源点最近的节点v。

步骤3：对所有与节点v相邻的节点w，计算出新的距离dist[s][w]，如果dist[s][w]小于已知的最短距离，就更新最短距离，并将节点w加入队列中。

步骤4：重复步骤2和步骤3，直到队列为空。

Dijkstra算法的时间复杂度为O(n^2)，其中n为节点数，因此它适用于稠密图。

下面是Python中Dijkstra算法的代码实现：```pythonimport heapqdef dijkstra(graph, start):#初始距离和前驱节点dist = {start: 0}previous = {start: None}#所有未确定最短距离的节点放入堆中heap = [(0, start)]heapq.heapify(heap)while heap:(d, u) = heapq.heappop(heap)#如果已经处理过该节点，则直接跳过if u in dist and d > dist[u]:continuefor v, w in graph[u].items():#计算新的距离newdist = dist[u] + w#如果新距离比原距离更小，则更新距离和前驱节点if v not in dist or newdist < dist[v]:dist[v] = newdistprevious[v] = uheapq.heappush(heap, (newdist, v))return (dist, previous)#测试graph = {'A': {"B": 2, "D": 4},'B': {"C": 3, "D": 1},'C': {"D": 1, "E": 5},'D': {"E": 1},'E': {}}dist, prev = dijkstra(graph, 'A')print(dist) # {'A': 0, 'B': 2, 'D': 3, 'C': 5, 'E': 4}print(prev) # {'A': None, 'B': 'A', 'D': 'B', 'C': 'B', 'E': 'D'}```2. Bellman-Ford算法Bellman-Ford算法是一种适用于有向图的单源最短路径算法，它可以处理有负权边的情况，但是不能处理负环的情况。

数据结构与算法实验源代码(2023最新版)

数据结构与算法实验源代码本文档为数据结构与算法实验源代码的范本，旨在帮助读者深入理解和实践数据结构和算法的相关知识。

下文将详细介绍各个章节的内容。

⒈引言- 简要介绍数据结构与算法的重要性和应用场景。

- 说明本文档的结构和目的。

⒉数据结构概述- 介绍数据结构的基本概念和分类。

- 详细介绍各种常见数据结构，如数组、链表、栈、队列、树等。

- 提供每种数据结构的定义、操作和应用示例。

⒊算法基础- 介绍算法的基本思想和特性。

- 详细讲解常见的算法设计方法，如递归、分治、贪心、动态规划等。

- 提供每种算法的原理、示例和分析。

⒋排序算法- 介绍各种排序算法的原理和实现方式。

- 包括冒泡排序、选择排序、插入排序、归并排序、快速排序等。

- 提供每种排序算法的时间复杂度和空间复杂度分析。

⒌查找算法- 介绍常用的查找算法，如顺序查找、二分查找、哈希查找等。

- 提供每种查找算法的原理和实现方式。

- 分析每种查找算法的时间复杂度和空间复杂度。

⒍图算法- 介绍图的基本概念和表示方法。

- 详细讲解图的遍历算法，如深度优先搜索和广度优先搜索。

- 介绍最短路径算法，如Dijkstra算法和Floyd-Warshall算法。

- 提供每种图算法的实现示例和应用场景。

⒎高级数据结构与算法- 介绍高级数据结构，如堆、红黑树、AVL树等。

- 详细讲解高级算法，如动态规划、并查集等。

- 提供每种高级数据结构和算法的原理、实现方式和应用示例。

⒏结语- 对数据结构与算法的重要性进行总结。

- 强调学习和实践的重要性。

本文档涉及附件：⒈源代码示例附件，包含了本文中提到的各种数据结构和算法的实现代码。

法律名词及注释：⒈数据结构：指一组数据的存储结构和相应的操作。

⒉算法：指解决特定问题的一系列有序步骤或规则。

⒊时间复杂度：用来度量算法执行时间随输入规模增长时的增长率。

⒋空间复杂度：用来度量算法执行过程中所需存储空间随输入规模增长时的增长率。

【转】彻底弄懂最短路径问题（图论）

【转】彻底弄懂最短路径问题（图论）P.S.根据个⼈需要，我删改了不少问题引⼊问题：从某顶点出发，沿图的边到达另⼀顶点所经过的路径中，各边上权值之和最⼩的⼀条路径——最短路径。

解决最短路的问题有以下算法，Dijkstra算法，Bellman-Ford算法，Floyd算法和SPFA算法，另外还有著名的启发式搜索算法A*，不过A*准备单独出⼀篇，其中Floyd算法可以求解任意两点间的最短路径的长度。

笔者认为任意⼀个最短路算法都是基于这样⼀个事实：从任意节点A到任意节点B的最短路径不外乎2种可能，1是直接从A到B，2是从A经过若⼲个节点到B。

⼀.Dijkstra算法该算法在《数据结构》课本⾥是以贪⼼的形式讲解的，不过在《运筹学》教材⾥被编排在动态规划章节，建议读者两篇都看看。

(1) 迪杰斯特拉(Dijkstra)算法按路径长度递增次序产⽣最短路径。

先把V分成两组：S：已求出最短路径的顶点的集合V-S=T：尚未确定最短路径的顶点集合将T中顶点按最短路径递增的次序加⼊到S中，依据：可以证明V0到T中顶点Vk的最短路径，或是从V0到Vk的直接路径的权值或是从V0经S中顶点到Vk的路径权值之和（反证法可证）。

(2) 求最短路径步骤1. 初使时令 S={V0},T={其余顶点}，T中顶点对应的距离值，若存在<V0,Vi>，为<V0,Vi>弧上的权值（和SPFA初始化⽅式不同），若不存在<V0,Vi>，为Inf。

2. 从T中选取⼀个其距离值为最⼩的顶点W(贪⼼体现在此处)，加⼊S(注意不是直接从S集合中选取，理解这个对于理解vis数组的作⽤⾄关重要)，对T中顶点的距离值进⾏修改：若加进W作中间顶点，从V0到Vi的距离值⽐不加W的路径要短，则修改此距离值（上⾯两个并列for循环，使⽤最⼩点更新）。

3. 重复上述步骤，直到S中包含所有顶点，即S=V为⽌（说明最外层是除起点外的遍历）。

动态规划之最短路径源代码

动态规划之最短路径问题源代码#include "stdio.h"#include "conio.h"#define n 16 /*图的顶点数*/#define k 7 /*图的段数*/#define l 30#define MAX 100typedef int NodeNumber;/*节点编号*/typedef int CostType;/*成本值类型*/CostType cost[n][n];NodeNumber path[k];NodeNumber cur=-1;void creategraph(CostType *cost[n][n]) /*创建图的成本矩阵*/ {int i,j,x,y,value;for(i=0;i<n;i++)for(j=0;j<n;j++) cost[i][j]=0;printf("\nEnter the cost of graph:\n");for(i=0;i<l;i++){scanf("%d,%d,%d",&x,&y,&value);cost[x][y]=value;}}void outgraph(CostType *cost[n][n]) /*输出图的成本矩阵*/ {int i,j;printf("Print the cost of graph:\n");for(i=0;i<n;i++){for(j=0;j<n;j++) printf("%2d",cost[i][j]);printf("\n");}}/*使用向前递推算法求多段图的最短路径*/void FPath(CostType *cost[n][n],NodeNumber *path[k]) {int i,j,leng,temp,v[n],d[n];for(i=0;i<n;i++) v[i]=0;for(i=n-2;i>=0;i--){ leng=MAX;for(j=i+1;j<=n-1;j++)if(cost[i][j]>0 && (cost[i][j]+v[j])<leng){leng=cost[i][j]+v[j];temp=j;}v[i]=leng;d[i]=temp;}path[0]=0;path[k-1]=n-1;for(i=1;i<=k-2;i++) path[i]=d[path[i-1]]; }/*输出最短路径序列*/void outpath(NodeNumber *path[k]){int i;printf("\nPrint the shortest treet:\n");for(i=0;i<k;i++) printf("%3d",path[i]); }main(){NodeNumber m,t;creategraph(&cost);outgraph(&cost);FPath(&cost,&path);outpath(&path);}。

c++迷宫问题最短路径

c++迷宫问题最短路径// newcoder_xiaohongshu_1.cpp : 此⽂件包含 "main" 函数。

程序执⾏将在此处开始并结束。

//#include "pch.h"#include <iostream>#include <queue>#include <map>using namespace std;/*pair<int, int > p = make_pair(1, 2);pair<int, int> p(1, 2);p= new pair<int,int>(1,2)*/int dx[4] = {0,1,0,-1};int dy[4]= {1,0,-1,0};//迷宫地图,1代表墙壁，0代表通路int N = 10;int mat[10][10] = { {1,1,1,1,1,1,1,1,1,1},{1,0,0,1,0,0,0,1,0,1},{1,0,0,1,0,0,0,1,0,1},{1,0,0,0,0,1,1,0,0,1},{1,0,1,1,1,0,0,0,0,1},{1,0,0,0,1,0,0,0,0,1},{1,0,1,0,0,0,1,0,0,1},{1,0,1,1,1,0,1,1,0,1},{1,1,0,0,0,0,0,0,0,1},{1,1,1,1,1,1,1,1,1,1}};class Dot {public:int x;int y;Dot(int x,int y):x(x),y(y){}};class WideBlock:public Dot{public:WideBlock *parent;WideBlock(int x,int y,WideBlock* p):Dot(x,y),parent(p){}};void print(WideBlock *p)//递归顺序输出{if (!p->parent){cout << "\n(" << p->x << "," << p->y << ")" << ";";}else{print(p->parent);cout << "(" << p->x << "," << p->y << ")" << ";";}}int main(){WideBlock *s=new WideBlock(1, 1, NULL), *end=new WideBlock(8, 8, NULL); queue<WideBlock*> q;mat[1][1] = 1;q.push(s);while (!q.empty()){WideBlock* cur = q.front();q.pop();int x = cur->x;int y = cur->y;if (x == end->x && y == end->y){end = cur;break;}if (y + dy[0] < N && mat[x][y + dy[0]] == 0){q.push(new WideBlock(x, y + dy[0],cur));mat[x][y + dy[0]] = 1;}if (x + dx[1] < N && mat[x+dx[1]][y] == 0){q.push(new WideBlock(x+dx[1], y,cur));mat[x+dx[1]][y] = 1;}if (y + dy[2] > -1 && mat[x][y + dy[2]] == 0){q.push(new WideBlock(x, y + dy[2],cur));mat[x][y + dy[2]] = 1;}if (x + dx[3] >-1 && mat[x+dx[3]][y] == 0){q.push(new WideBlock(x+dx[3], y,cur));mat[x+dx[3]][y] = 1;}}WideBlock *tmp = end;while (tmp){cout << "(" << tmp->x << "," << tmp->y << ")" << ";";tmp = tmp->parent;}tmp = end;print(tmp);std::cout << "Hello World!\n";return 0;}// 运⾏程序: Ctrl + F5 或调试 >“开始执⾏(不调试)”菜单// 调试程序: F5 或调试 >“开始调试”菜单// ⼊门提⽰:// 1. 使⽤解决⽅案资源管理器窗⼝添加/管理⽂件// 2. 使⽤团队资源管理器窗⼝连接到源代码管理// 3. 使⽤输出窗⼝查看⽣成输出和其他消息// 4. 使⽤错误列表窗⼝查看错误// 5. 转到“项⽬”>“添加新项”以创建新的代码⽂件，或转到“项⽬”>“添加现有项”以将现有代码⽂件添加到项⽬// 6. 将来，若要再次打开此项⽬，请转到“⽂件”>“打开”>“项⽬”并选择 .sln ⽂件。

Dijkstra算法求解单源最短路径问题

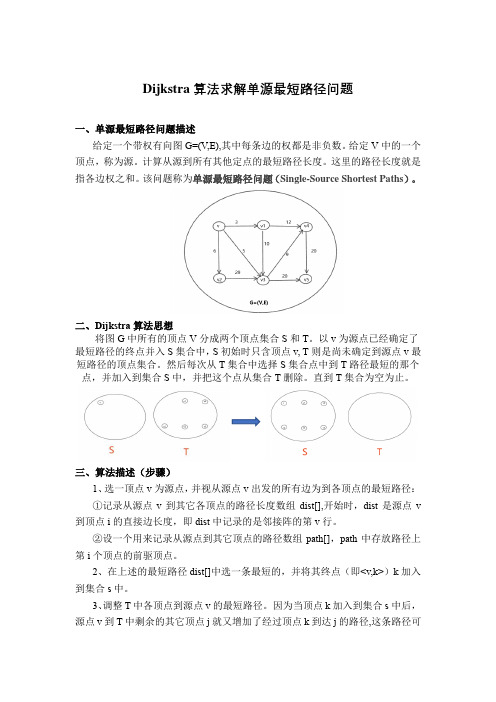
Dijkstra算法求解单源最短路径问题一、单源最短路径问题描述给定一个带权有向图G=(V,E),其中每条边的权都是非负数。

给定V中的一个顶点，称为源。

计算从源到所有其他定点的最短路径长度。

这里的路径长度就是指各边权之和。

该问题称为单源最短路径问题（Single-Source Shortest Paths）。

二、Dijkstra算法思想将图G中所有的顶点V分成两个顶点集合S和T。

以v为源点已经确定了最短路径的终点并入S集合中，S初始时只含顶点v, T则是尚未确定到源点v最短路径的顶点集合。

然后每次从T集合中选择S集合点中到T路径最短的那个点，并加入到集合S中，并把这个点从集合T删除。

直到T集合为空为止。

三、算法描述（步骤）1、选一顶点v为源点，并视从源点v出发的所有边为到各顶点的最短路径：①记录从源点v到其它各顶点的路径长度数组dist[],开始时，dist是源点v到顶点i的直接边长度，即dist中记录的是邻接阵的第v行。

②设一个用来记录从源点到其它顶点的路径数组path[]，path中存放路径上第i个顶点的前驱顶点。

2、在上述的最短路径dist[]中选一条最短的，并将其终点（即<v,k>）k加入到集合s中。

3、调整T中各顶点到源点v的最短路径。

因为当顶点k加入到集合s中后，源点v到T中剩余的其它顶点j就又增加了经过顶点k到达j的路径,这条路径可能要比源点v到j原来的最短的还要短。

调整方法是比较dist[k]+g[k,j]与dist[j]，取其中的较小者。

4、再选出一个到源点v路径长度最小的顶点k,从T中删去后加入S中，再回去到第三步，如此重复，直到集合S中的包含图G的所有顶点。

四、算法实现（数据结构）1、算法实现输入：一个大于1的整数n.输出：●一个随机生成的有向图G=（V，E），对于每一条边，有一个非负数字c(u，v)与之相关。

●对于每个顶点v∈V,得到从v0到v的最短路径的长度。

Dijkstra算法的流程图

Dijkstra算法的流程图Dijkstra算法的流程图需求和规格讲明：Dijkstra算法是典型最短路算法，用于运算一个节点到其他所有节点的最短路径。

要紧特点是以起始点为中心向外层层扩展，直到扩展到终点为止。

Dijkstra算法能得出最短路径的最优解，但由于它遍历运算的节点专门多，因此效率低。

算法本身并不是按照我们的思维适应——求解从原点到第一个点的最短路径，再到第二个点的最短路径，直至最后求解完成到第n个点的最短路径，而是求解从原点动身的各有向路径的从小到大的排列，然而算法最终确实得到了从原点到图中其余各点的最短路径，能够讲这是个副产品，关于算法的终结条件也应该以求得了原点到图中其余各点的最短路径为宜。

清晰了算法的这种巧妙构思后，明白得算法本身就不是难题了。

实现注释：想要实现的功能：Dijkstra算法是用来求任意两个顶点之间的最短路径。

在该实验中，我们用邻接矩阵来储备图。

在该程序中设置一个二维数组来储备任意两个顶点之间的边的权值。

用户能够将任意一个图的信息通过键盘输入，让后在输入要查找的两个顶点，程序能够自动求出这两个顶点之间的最短路径。

差不多实现的功能：在该实验中，我们用邻接矩阵来储备图。

在该程序中设置一个全局变量的二维数组，用它来储备任意两个顶点之间的边的权值。

然后通过最短路径的运算，输入从任意两个顶点之间的最短路径的大小。

用户手册：关于改程序，不需要客户进行什么复杂的输入，关键是用来存放图的任意两个顶点之间的边的权值的二维数组的初始化，立即要通过Dijkstra算法求最短路径的图各条边的权值放入二维数组中。

如此程序就能够自动的运算出任意两个顶点之间的最短路径同时进行输出。

设计思想：s为源，w[u，v] 为点u 和v 之间的边的长度，结果储存在dist[]初始化：源的距离dist[s]设为0，其他的点距离设为无穷大，同时把所有的点状态设为没有扩展过。

循环n-1次：1. 在没有扩展过的点中取一距离最小的点u，并将其状态设为已扩展。

最短路径算法——Dijkstra 算法

最短路径算法——Dijkstra算法一、最短路径问题最短路问题是图论理论的一个经典问题。

寻找最短路径就是在指定网络中两结点间找一条距离最小的路。

最短路不仅仅指一般地理意义上的距离最短,还可以引申到其它的度量,如时间、费用、线路容量等。

最短路径算法的选择与实现是通道路线设计的基础,最短路径算法是计算机科学与地理信息科学等领域的研究热点,很多网络相关问题均可纳入最短路径问题的范畴之中。

经典的图论与不断发展完善的计算机数据结构及算法的有效结合使得新的最短路径算法不断涌现。

在带权图（即网络）G=（V,E）中，若顶点v i，v j是图G的两个顶点，从顶点v i到v j 的路径长度定义为路径上各条边的权值之和。

从顶点v i到v j可能有多条路径，其中路径长度最小的一条路径称为顶点v i到v j的最短路径。

求最短路径具有很高的实用价值，在各类竞赛中经常遇到。

一般有两类最短路径问题：一类是求从某个顶点（即源点）到其他顶点（即终点）的最短路径；另一类是求图中每一对顶点间的最短路径。

本讲主要讲述一种单源最短路径（Single source shortest path）算法——Dijkstra 算法，用于解决非负权有向图的单源最短路径问题。

二、Dijkstra算法2.1 Dijkstra算法Dijkstra算法是典型最短路算法，用于计算一个节点到其他所有节点的最短路径。

主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。

Dijkstra算法能得出最短路径的最优解，但由于它遍历计算的节点很多，所以效率偏低。

Dijkstra算法是很有代表性的最短路算法，在很多专业课程中都作为基本内容有详细的介绍，如数据结构，图论，运筹学等等。

2.2 Dijkstra算法思想对于图G=（V，E），假设（u，v）是E中的边，c u,v是边的长度（即边权）。

如果把顶点集合V划分为两个集合S和T：S中所包含的顶点，他们到u的距离已经确定；T中所包含的顶点，他们到u的距离尚未确定。

人教版八年级上册数学说课稿《13.4课题学习最短路径问题》

人教版八年级上册数学说课稿《13.4 课题学习最短路径问题》一. 教材分析《13.4 课题学习最短路径问题》是人教版八年级上册数学的一章内容。

本章主要介绍了最短路径问题的相关知识和方法。

通过本章的学习，学生能够理解最短路径问题的意义，掌握解决最短路径问题的方法，并能够应用到实际问题中。

在教材中，首先介绍了最短路径问题的定义和意义，然后通过图的表示方法引出最短路径问题的解决方法。

接着，教材介绍了两种常用的最短路径算法：迪杰斯特拉算法和贝尔曼-福特算法。

最后，教材通过一些实际问题，让学生应用所学的知识解决实际问题。

二. 学情分析学生在学习本章内容之前，已经学习了图的概念和相关性质，对图的基本操作有一定的了解。

同时，学生也学习了算法的基本概念和方法，具备一定的编程能力。

然而，学生对于最短路径问题的理解和应用可能还存在一些困难。

因此，在教学过程中，需要引导学生理解最短路径问题的意义，并通过实际问题激发学生的学习兴趣。

此外，学生需要通过实践活动，掌握解决最短路径问题的方法，并能够应用到实际问题中。

三. 说教学目标1.知识与技能目标：学生能够理解最短路径问题的定义和意义，掌握解决最短路径问题的方法，并能够应用到实际问题中。

2.过程与方法目标：学生能够通过实践活动，培养解决问题的能力和团队合作的能力。

3.情感态度与价值观目标：学生能够培养对数学的兴趣和好奇心，培养积极的学习态度和团队合作的精神。

四. 说教学重难点1.教学重点：学生能够理解最短路径问题的定义和意义，掌握解决最短路径问题的方法。

2.教学难点：学生能够理解和应用迪杰斯特拉算法和贝尔曼-福特算法解决实际问题。

五. 说教学方法与手段1.教学方法：采用问题驱动的教学方法，通过实际问题引导学生学习最短路径问题的解决方法。

2.教学手段：利用多媒体课件和网络资源，展示实际问题和算法流程，帮助学生理解和应用知识。

六. 说教学过程1.引入新课：通过一个实际问题，引出最短路径问题的定义和意义。

c语言实现迪杰斯特拉算法实例

c语言实现迪杰斯特拉算法实例========迪杰斯特拉算法是一种用于求解单源最短路径问题的算法，它使用Dijkstra 算法的思想，通过不断更新最短路径值，最终找到源节点到所有其他节点的最短路径。

下面是一个使用C语言实现迪杰斯特拉算法的实例。

一、算法概述------迪杰斯特拉算法的基本思想是：从源节点开始，不断更新与源节点相邻的节点之间的最短路径值，直到所有节点都被处理完毕。

算法的核心是使用一个最小堆来存储待处理的节点及其对应的距离值，每次从最小堆中取出距离值最小的节点，并更新与其相邻节点的距离值。

二、代码实现------以下是一个使用C语言实现迪杰斯特拉算法的示例代码：```c#include <stdio.h>#include <stdlib.h>#include <limits.h>#define MAX_NODES 100 // 最大节点数#define INF 0x3f3f3f3f // 无穷大值typedef struct Node {int id; // 节点编号int distance; // 到源节点的距离struct Node* nxt; // 指向下一个节点的指针（用于广度优先搜索）} Node;// 创建新节点Node* create_node(int id) {Node* node = (Node*)malloc(sizeof(Node));node->id = id;node->distance = INF;node->nxt = NULL;return node;}// 将节点添加到最小堆中（假设堆为head）void add_node_to_heap(Node** head, int* size, int distance) {Node* node = create_node(distance); // 创建新节点(*size)++; // 节点数加一(*head)->distance = distance; // 将新节点距离设置为最小值(*head)->nxt = node; // 将新节点添加到堆中while (*head->nxt != NULL && (*head->nxt)->distance < (*head)->distance) { // 调整堆中距离值最小节点的位置Node* temp = *head->nxt; // 保存当前距离最小的节点(*head)->nxt = (*head->nxt)->nxt; // 将当前节点的下一个节点向前移动一位（退出循环）free(temp); // 释放当前节点的内存空间（释放内存）}}// 从最小堆中取出距离值最小的节点（返回值为距离值）int extract_min(Node** head, int* size) {Node* temp = *head; // 保存当前距离最小的节点（用于后续更新）int min_distance = temp->distance; // 当前最小距离值（用于后续更新）Node** p = *head; // 指向当前距离最小的节点的指针（用于后续更新）while (p->nxt != NULL && p->distance > min_distance) { // 从堆中取出距离值最小的节点，并更新指针和距离值Node* next_node = p->nxt; // 保存下一个节点指针（用于广度优先搜索）*p = p->nxt->nxt; // 将当前节点的下一个节点向前移动一位（退出循环）p->distance = min_distance; // 将当前节点的距离值更新为当前最小值free(next_node); // 释放下一个节点的内存空间（释放内存）}*head = p->nxt; // 将当前节点的下一个节点设置为堆头指针（进入下一轮循环）*size--; // 删除已处理节点数减一（返回最小距离值）return min_distance; // 返回最小距离值（作为结果返回）}// 迪杰斯特拉算法主函数（源代码）void dijkstra(int nodes, int start_node, Node** nodes_list) {int size = nodes; // 初始化节点数和距离数组大小为0（初始化）Node* heap = (Node*)malloc(sizeof(Node) * size); // 创建最小堆（初始化）for (int i = 0; i < size; i++) { // 将所有节点添加到堆中，并设置其距离值为无穷大（进入主循环）add_。

最短路径c语言

以下是使用Dijkstra算法实现最短路径的C语言代码示例：```c#include <stdio.h>#include <limits.h>#define V 5 // 顶点数int minDistance(int dist[], bool sptSet[]) {int min = INT_MAX, min_index;for (int v = 0; v < V; v++)if (sptSet[v] == false && dist[v] <= min)min = dist[v], min_index = v;return min_index;}void printSolution(int dist[]) {printf("Vertex \t Distance from Source\n");for (int i = 0; i < V; i++)printf("%d \t\t %d\n", i, dist[i]);}void dijkstra(int graph[V][V], int src) {int dist[V];bool sptSet[V];for (int i = 0; i < V; i++)dist[i] = INT_MAX, sptSet[i] = false;dist[src] = 0;for (int count = 0; count < V - 1; count++) {int u = minDistance(dist, sptSet);sptSet[u] = true;for (int v = 0; v < V; v++)if (!sptSet[v] && graph[u][v] && dist[u] != INT_MAX && dist[u] + graph[u][v] < dist[v])dist[v] = dist[u] + graph[u][v];}printSolution(dist);}int main() {int graph[V][V] = { { 0, 4, 0, 0, 0 },{ 4, 0, 8, 0, 0 },{ 0, 8, 0, 7, 0 },{ 0, 0, 7, 0, 2 },{ 0, 0, 0, 2, 0 } };dijkstra(graph, 0);return 0;}```该代码使用邻接矩阵表示图，并使用Dijkstra算法计算从源顶点到其他顶点的最短路径。

ArcGIS网络分析最短路径分析源代码（VB6.0）

ArcGIS⽹络分析最短路径分析源代码（VB6.0）ArcGIS⽹络分析最短路径分析源代码(VB6.0)12' Copyright 1995-2005 ESRI34' All rights reserved under the copyright laws of the United States.56' You m ay freely redistribute and use this sam ple code, with or without m odifi cation.78' Disclaimer: THE SAMPLE CODE IS PROVIDED "AS IS" AND ANY EXPRESS O R IMPLIED9' WARRANTIES, INCLUDING THE IMPLIED WARRANTIES OF MERCHANTABILIT Y AND FITNESS10' FOR A PARTICULAR PURPOSE ARE DISCLAIMED. IN NO EVENT SHALL ESR I OR11' CONTRIBUTORS BE LIABLE FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPE CIAL, EXEMPLARY,12' OR CONSEQUENTIAL DAMAGES (INCLUDING, BUT NOT LIMITED TO, PROC UREMENT OF13' SUBSTITUTE GOODS OR SERVICES; LOSS OF USE, DATA, OR PROFITS; O R BUSINESS14' INTERRUPTION) SUSTAINED BY YOU OR A THIRD PARTY, HOWEVER CAUSE D AND ON ANY15' THEORY OF LIABILITY, WHETHER IN CONT RACT, STRICT LIABILITY, OR TO RT ARISING IN ANY16' WAY OUT OF THE USE OF THIS SAMPLE CODE, EVEN IF ADVISED OF THE P OSSIBILITY OF17' SUCH DAMAGE.1819' For additional information contact: Environmental System s Research Institu te, Inc.2021' Attn: Contracts Dept.2223' 380 New York Street2425' Redlands, California, U.S.A. 923732627' Em ail: contracts@/doc/07098e37f111f18583d05ab5.html2829Option Explicit3031' vb version of the PathFinder object3233' 本地变量34Private m_ipGeometricNetwork As esriGeoDatabase.IGeometricNetwork35Private m_ipMap As esriCarto.IMap36Private m_ipPoints As esriGeometry.IPointCollection37Private m_ipPointToEID As esriNetworkAnalysis.IPointToEID38' 返回结果变量39Private m_dblPathCost As Double40Private m_ipEnumNetEID_Junctions As esriGeoDatabase.IEnumNetEID41Private m_ipEnumNetEID_Edges As esriGeoDatabase.IEnumNetEID42Private m_ipPolyline As esriGeometry.IPolyline434445' Optionally set the Map (e.g. the current m ap in ArcMap),46' otherwise a default m ap will be made (for IPointToEID).48Public Property Set Map(Map As esriCarto.IMap)49Set m_ipMap = Map50End Property5152Public Property Get Map() As esriCarto.IMap53Set Map = m_ipMap54End Property5556' Either OpenAccessNetwork or OpenFeatureDatasetNetwork57' needs to be called.5859Public Sub OpenAccessNetwork(AccessFileName As String, FeatureDatasetNa me As String)6061Dim ipWorkspaceFactory As esriGeoDatabase.IWorkspaceFactory62Dim ipWorkspace As esriGeoDatabase.IWorkspace63Dim ipFeatureWorkspace As esriGeoDatabase.IFeatureWorkspace64Dim ipFeatureDataset As esriGeoDatabase.IFeatureDataset6566' After this Sub exits, we'll have an INetwork interface67' and an IMap interface initialized for the network we'll be using.6869' close down the last one if opened70 CloseWorkspace7172' open the m db73Set ipWorkspaceFactory =New esriDataSourcesGDB.AccessWorkspaceFact ory74Set ipWorkspace = ipWorkspaceFactory.OpenFromFile(AccessFileName, 0)76' get the FeatureWorkspace77Set ipFeatureWorkspace = ipWorkspace7879' open the FeatureDataset80Set ipFeatureDataset = ipFeatureWorkspace.OpenFeatureDataset(FeatureD atasetNam e)8182' initialize Network and Map (m_ipNetwork, m_ipMap)83If Not InitializeNetworkAndMap(ipFeatureDataset) Then Err.Raise 0, "Open AccessNetwork", "Error initializing Network and Map"8485End Sub8687Public Sub OpenFeatureDatasetNetwork(FeatureDataset As esriGeoDatabase. IFeatureDataset)88' close down the last one if opened89 CloseWorkspace9091' we assum e that the caller has passed a valid FeatureDataset9293' initialize Network and Map (m_ipNetwork, m_ipMap)94If Not InitializeNetworkAndMap(FeatureDataset) Then Err.Raise 0, "OpenFe atureDatasetNetwork", "Error initializing Network and Map"9596End Sub9798' The collection of points to travel through must be set.99100Public Property Set StopPoints(Points As esriGeometry.IPointCollection)102End Property103104Public Property Get StopPoints() As esriGeometry.IPointCollection105Set StopPoints = m_ipPoints106End Property107108' Calculate the path109110Public Sub SolvePath(WeightName As String)111112Dim ipNetwork As esriGeoDatabase.INetwork113Dim ipTraceFlowSolver As esriNetworkAnalysis.ITraceFlowSolver114Dim ipNetSolver As esriNetworkAnalysis.INetSolver115Dim ipNetFlag As esriNetworkAnalysis.INetFlag116Dim ipaNetFlag() As esriNetworkAnalysis.IEdgeFlag117Dim ipEdgePoint As esriGeometry.IPoint118Dim ipNetElements As esriGeoDatabase.INetElements119Dim intEdgeUserClassID As Long120Dim intEdgeUserID As Long121Dim intEdgeUserSubID As Long122Dim intEdgeID As Long123Dim ipFoundEdgePoint As esriGeometry.IPoint124Dim dblEdgePercent As Double125Dim ipNetWeight As esriGeoDatabase.INetWeight126Dim ipNetSolverWeights As esriNetworkAnalysis.INetSolverWeights127Dim ipNetSchem a As esriGeoDatabase.INetSchem a128Dim intCount As Long129Dim i As Long130Dim vaRes() As Variant132' m ake sure we are ready133 Debug.Assert Not m_ipPoints Is Nothing134 Debug.Assert Not m_ipGeometricNetwork Is Nothing135136' instantiate a trace flow solver137Set ipTraceFlowSolver = New esriNetworkAnalysis.TraceFlowSolver138139' get the INetSolver interface140Set ipNetSolver = ipTraceFlowSolver141142' set the source network to solve on143Set ipNetwork = m_/doc/07098e37f111f18583d05ab5.html work144Set ipNetSolver.SourceNetwork = ipNetwork145146' m ake edge flags from the points147148' the INetElements interface is needed to get UserID, UserClassID,149' and UserSubID from an element id150Set ipNetElements = ipNetwork151152' get the count153 intCount = m_ipPoints.PointCount154 Debug.Assert intCount > 1155156' dimension our IEdgeFlag array157ReDim ipaNetFlag(intCount)158159For i = 0 To intCount - 1160' m ake a new Edge Flag162Set ipEdgePoint = m_ipPoints.Point(i)163' look up the EID for the current point (this will populate intEdgeID and d blEdgePercent)164 m_ipPointToEID.GetNearestEdge ipEdgePoint, intEdgeID, ipFoundEdgePoi nt, dblEdgePercent165 Debug.Assert intEdgeID > 0 ' else Point (eid) not found166 ipNetElements.QueryIDs intEdgeID, esriETEdge, intEdgeUserClassID, intE dgeUserID, intEdgeUserSubID167 Debug.Assert (intEdgeUserClassID > 0) And (intEdgeUserID > 0) ' else P oint not found168 /doc/07098e37f111f18583d05ab5.html erClassID = intEdgeUserClassID169 /doc/07098e37f111f18583d05ab5.html erID = intEdgeUserID170 /doc/07098e37f111f18583d05ab5.html erSubID = intEdgeUserSubID171Set ipaNetFlag(i) = ipNetFlag172Next173174' add these edge flags175 ipTraceFlowSolver.PutEdgeOrigins intCount, ipaNetFlag(0)176177' set the weight (cost field) to solve on178179' get the INetSchem a interface180Set ipNetSchem a = ipNetwork181Set ipNetWeight = ipNetSchem a.WeightByName(WeightName)182 Debug.Assert Not ipNetWeight Is Nothing183184' set the weight (use the sam e for both directions)185Set ipNetSolverWeights = ipTraceFlowSolver186Set ipNetSolverWeights.From ToEdgeWeight = ipNetWeight188189' initialize array for results to number of segments in result190ReDim vaRes(intCount - 1)191192' solve it193 ipTraceFlowSolver.FindPath esriFMConnected, esriSPObjFnMinSum, m_ipEn umNetEID_Junctions, m_ipEnumNetEID_Edges, intCount - 1, vaRes(0)194195' com pute total cost196 m_dblPathCost = 0197For i =LBound(vaRes) To UBound(vaRes)198 m_dblPathCost = m_dblPathCost + vaRes(i)199Next200201' clear the last polyline result202Set m_ipPolyline =Nothing203204End Sub205206' Property to get the cost207208Public Property Get PathCost() As Double209 PathCost = m_dblPathCost210End Property211212' Property to get the shape213214Public Property Get PathPolyLine() As esriGeometry.IPolyline215217Dim count As Long, i As Long218Dim ipEIDInfo As esriNetworkAnalysis.IEIDInfo219Dim ipEnumEIDInfo As esriNetworkAnalysis.IEnumEIDInfo220Dim ipGeometry As esriGeometry.IGeometry221Dim ipNewGeometryColl As esriGeometry.IGeometryCollection222Dim ipSpatialReference As esriGeometry.ISpatialReference223224' if the line is already computed since the last path, just return it225If Not m_ipPolyline Is Nothing Then226Set PathPolyLine = m_ipPolyline227Exit Property228End If229230Set m_ipPolyline =New esriGeometry.Polyline231Set ipNewGeometryColl = m_ipPolyline232233' a path should be solved first234 Debug.Assert Not m_ipEnumNetEID_Edges Is Nothing235236' m ake an EIDHelper object to translate edges to geom etric features237Set ipEIDHelper =New esriNetworkAnalysis.EIDHelper238Set ipEIDHelper.GeometricNetwork = m_ipGeometricNetwork239Set ipSpatialReference = m_ipMap.SpatialReference240Set ipEIDHelper.OutputSpatialReference = ipSpatialReference241 ipEIDHelper.ReturnGeometries =True242243' get the details using the IEIDHelper classes244Set ipEnumEIDInfo = ipEIDHelper.CreateEnumEIDInfo(m_ipEnumNetEID_ Edges)247' set the iterator to beginning248 ipEnumEIDInfo.Reset249250For i = 1 To count251252' get the next EID and a copy of its geom etry (it m akes a Clone)253Set ipEIDInfo = ipEnumEIDInfo.Next254Set ipGeom etry = ipEIDInfo.Geometry255256 ipNewGeometryColl.AddGeometryCollection ipGeometry257258Next' EID259260' return the m erged geometry as a Polyline261Set PathPolyLine = m_ipPolyline262263End Property264265' Private266267Private Sub CloseWorkspace()268' m ake sure we let go of everything and start with new results269Set m_ipGeometricNetwork =Nothing270Set m_ipPoints =Nothing271Set m_ipPointToEID = Nothing272Set m_ipEnumNetEID_Junctions =Nothing273Set m_ipEnumNetEID_Edges =Nothing274Set m_ipPolyline =Nothing277Private Function InitializeNetworkAndMap(FeatureDataset As esriGeoDataba se.IFeatureDataset) As Boolean278279Dim ipNetworkCollection As esriGeoDatabase.INetworkCollection280Dim ipNetwork As esriGeoDatabase.INetwork281Dim count As Long, i As Long282Dim ipFeatureClassContainer As esriGeoDatabase.IFeatureClassContainer283Dim ipFeatureClass As esriGeoDatabase.IFeatureClass284Dim ipGeoDataset As esriGeoDatabase.IGeoDataset285Dim ipLayer As esriCarto.ILayer286Dim ipFeatureLayer As esriCarto.IFeatureLayer287Dim ipEnvelope As esriGeometry.IEnvelope, ipMaxEnvelope As esriGeomet ry.IEnvelope288Dim dblSearchTol As Double289Dim dblWidth As Double, dblHeight As Double290291On Error GoTo Trouble292293' get the networks294Set ipNetworkCollection = FeatureDataset295296' even though a FeatureDataset can have m any networks, we'll just297' assum e the first one (otherwise you would pass the network name in, et c.)298299' get the count of networks300 count = ipNetworkCollection.GeometricNetworkCount301304' get the first Geometric Newtork (0 - based)305Set m_ipGeometricNetwork = ipNetworkCollection.GeometricNetwork(0)306307' get the Network308Set ipNetwork = m_/doc/07098e37f111f18583d05ab5.html work309310' The EID Helper class that converts points to EIDs needs a311' IMap, so we'll need one around with all our layers added.312' This Pathfinder object has an optional Map property than m ay be set313' before opening the Network.314If m_ipMap Is Nothing Then315Set m_ipMap = New esriCarto.Map316317' Add each of the Feature Classes in this Geometric Network as a m ap Lay er318Set ipFeatureClassContainer = m_ipGeometricNetwork319 count = ipFeatureClassContainer.ClassCount320 Debug.Assert count > 0 ' then Exception.Create('No (network) feature cl asses found');321322For i = 0 To count - 1323' get the feature class324Set ipFeatureClass = ipFeatureClassContainer.Class(i)325' m ake a layer326Set ipFeatureLayer = New esriCarto.FeatureLayer327Set ipFeatureLayer.FeatureClass = ipFeatureClass328' add layer to the m ap329 m_ipMap.AddLayer ipFeatureLayer331End If' we needed to m ake a Map332333334' Calculate point snap tolerance as 1/100 of m ap width.335 count = m_/doc/07098e37f111f18583d05ab5.html yerCount336Set ipMaxEnvelope =New esriGeometry.Envelope337For i = 0 To count - 1338Set ipLayer = m_/doc/07098e37f111f18583d05ab5.html yer(i)339Set ipFeatureLayer = ipLayer340' get its dim ensions (for setting search tolerance)341Set ipGeoDataset = ipFeatureLayer342Set ipEnvelope = ipGeoDataset.Extent343' m erge with m ax dim ensions344 ipMaxEnvelope.Union ipEnvelope345Next346347' finally, we can set up the IPointToEID348Set m_ipPointToEID = New esriNetworkAnalysis.PointToEID349Set m_ipPointToEID.SourceMap = m_ipMap350Set m_ipPointToEID.GeometricNetwork = m_ipGeometricNetwork351352' set snap tolerance353 dblWidth = ipMaxEnvelope.Width354 dblHeight = ipMaxEnvelope.Height355356If dblWidth > dblHeight Then357 dblSearchTol = dblWidth / 100#358Else359 dblSearchTol = dblHeight / 100#360End If361362 m_ipPointToEID.SnapTolerance = dblSearchTol363364 InitializeNetworkAndMap =True' good to go365Exit Function366367Trouble:368 InitializeNetworkAndMap =False' we had an error369End Function。

dijkstra算法代码

dijkstra算法代码性。

Dijkstra算法是一种用于计算从一个节点到其他所有节点的最短路径的算法。

它是由荷兰计算机科学家Edsger Dijkstra在1959年提出的，是一种贪心算法。

它的基本思想是，从源节点开始，每次选择距离源节点最近的节点，并将其加入到已经访问的节点集合中，然后更新其他节点的距离，直到所有节点都被访问到。

Dijkstra算法的代码实现非常简单，可以用任何编程语言实现。

下面是一个用C语言实现的Dijkstra算法的代码：#include <stdio.h>#include <stdlib.h>#include <limits.h>#define MAX_VERTEX_NUM 20#define INFINITY INT_MAXtypedef int Vertex;typedef int WeightType;typedef struct GNode *PtrToGNode;struct GNode {int Nv;int Ne;WeightType G[MAX_VERTEX_NUM][MAX_VERTEX_NUM];};typedef PtrToGNode MGraph;MGraph CreateGraph(int VertexNum){Vertex V, W;MGraph Graph;Graph = (MGraph)malloc(sizeof(struct GNode));Graph->Nv = VertexNum;Graph->Ne = 0;for (V=0; V<Graph->Nv; V++)for (W=0; W<Graph->Nv; W++)Graph->G[V][W] = INFINITY;return Graph;}void InsertEdge(MGraph Graph, Vertex V, Vertex W, WeightType Weight){Graph->G[V][W] = Weight;}MGraph BuildGraph(){MGraph Graph;Vertex V;int Nv, i;scanf("%d", &Nv);Graph = CreateGraph(Nv);scanf("%d", &(Graph->Ne));if (Graph->Ne != 0) {for (i=0; i<Graph->Ne; i++) {scanf("%d %d %d", &V, &W, &Weight);InsertEdge(Graph, V, W, Weight);}}return Graph;}int FindMinDist(MGraph Graph, WeightType dist[], int collected[]){WeightType MinDist = INFINITY;Vertex V, MinV;for (V=0; V<Graph->Nv; V++) {if (collected[V] == 0 && dist[V]<MinDist) { MinDist = dist[V];MinV = V;}}if (MinDist < INFINITY)return MinV;elsereturn -1;}void Dijkstra(MGraph Graph, Vertex S, WeightType dist[], int path[]){int collected[MAX_VERTEX_NUM];Vertex V, W;for (V=0; V<Graph->Nv; V++) {dist[V] = Graph->G[S][V];if (dist[V] < INFINITY)path[V] = S;elsepath[V] = -1;collected[V] = 0;}dist[S] = 0;collected[S] = 1;while (1) {V = FindMinDist(Graph, dist, collected);if (V == -1)break;collected[V] = 1;for (W=0; W<Graph->Nv; W++) {if (collected[W] == 0 && Graph->G[V][W]<INFINITY) {if (dist[V]+Graph->G[V][W] < dist[W]) {dist[W] = dist[V]+Graph->G[V][W];path[W] = V;}}}}}void PrintPath(MGraph Graph, Vertex S, Vertex V, int path[]) {int i, j, k;int tmp[MAX_VERTEX_NUM];int d = 0;i = V;while (i != S) {tmp[d++] = i;i = path[i];}tmp[d++] = S;for (i=d-1; i>0; i--)printf("%d ", tmp[i]);printf("%d\n", tmp[0]);}int main(){int dist[MAX_VERTEX_NUM], path[MAX_VERTEX_NUM];Vertex S, V;MGraph Graph;Graph = BuildGraph();scanf("%d %d", &S, &V);Dijkstra(Graph, S, dist, path);PrintPath(Graph, S, V, path);return 0;}。

数学模型 DjiST算法最短路径

∙一、基本思想：按路径长度递增顺序求最短路径算法。

二、数据的存储结构：有向连通网络: G ，采用带权邻接矩阵cost[ ][ ]存储三、算法具体步骤：设V0是起始源点，U=已求得最短路径终点集合。

V-U=未确定最短路径的顶点的集合(1)初始U={v0}, 辅助数组dist[N]（对已经找到最短路径终点的顶点vi ( i ∈U )，vi 所对应的数组分量dist[i]的值为负数；对从v0出发，尚未确定为最短路径终点的顶点vj （j ∈ V - U )，vj 所对应的数组分量dist[j]的值为从v0出发，考虑途经已确定为终点的顶点，到达vj (∈ V - U )的最短路径）。

初始时，对j ∈ V - U ，有dist[j]=cost[v][j]; 而对U={v}, 则有dist[v]= - cost[v][v] 。

(2)扫描dist[ ]数组，找出非0、非负且最小的dist[j]（j∈V-U)，即从v0出发到vj（j∈V-U)的路径是最短的。

(3)vj并入U ，则dist[j]=-dist[j]。

(4)调整dist[k](k∈V-U)，考虑从v0出发，途经vj到达vk是否更短。

比较:若-dist[j]+cost[j][k]<disk[k], 则dist[k]= -disk[j]+ cost[j][k] 。

(5)重复(2)(3)(4)共n-1次。

四、源代码：void dijkstra( int cost[][N], int v ,int t)//起点为v，终点为t{int dist[N],i,j,wfor (i=0; i<N; i++)dist[i]=cost[v][i]; //初始化dist[v]=-dist[v];for( i=0; i<N; i++){j=mincost(dist);//找非0、非负且最小的dist[j]if(( j==0)||(j==t));break;dist[j]=-dist[j];// vj并入U中for(k=0;k<N;k++) // 调整dist[k]if(dist[k]>0) // vk是尚未到达的终点if(-dist[j]+cost[j][k]<dist[k])dist[k]=-dist[j]+cost[j][k];//途经vj到达vk的距离更短}for ( i=0; i<N; i++)if(dist[j]<0)printf(“%d, %d: %d\n”,v,i,-dist[i]);}int mincost( int dist[ ])// 在V-U 集合中找顶点j，dist[j]是dist[ ]中的最小值{int i, min, j;min=MAX;j=0;for(i=0;i<N;i++)if(dist[i]>=0&& dist[i]<min){min=dist[i];j=i; }return(j);}五、小结(1) “按路径长度递增顺序”是因为，扩展下一个永久标记节点总是从U中节点的邻接节点中找到。

图的最短路径算法实现及应用

一、实验目的1．使学生熟悉最短路径算法实现。

2．掌握带权图的存储结构。

二、实验环境1.硬件：每个学生需配备计算机一台。

操作系统：Windows；2.软件：Windows操作系统+Turbo C等；三、实验要求1.能够独立完成带权图的储存和最短路径的生成。

2．熟练掌握并实现图的最短路径Dijkstra和Floyd算法及应用。

四、实验内容1.在自己的U盘的“姓名+学号”文件中创建“实验6”文件夹，本次实现的所有程序和数据都要存储到本文件夹中。

2.现在假设我国铁路交通图如下（权值表示距离），请用适合的存储结构将下图存储到计算机中方便进行处理（或以其他生活中的应用问题实现）。

3．现在想以最小的代价从武汉出发到达其他城市目的地，请用Dijkstra和Floyd算法分别实现要求的路径。

五、代码如下其中：v1：徐州，v2：上海，v3：天津，v4：郑州，v5：沈阳，v6：大连，v7：长春，v8：哈尔滨，v9：北京，v10：呼和浩特，v11：兰州，v12：西宁，v13：乌鲁木齐，v14：西安，v15：成都，v16：昆明，v17：贵阳，v18：柳州，v19：南宁，v20：株洲，v21:广州，v22：深圳，v23：武汉，v24：南昌，v25：福州Dijkrals：#include <stdio.h>#define M 65535#define N 25void Dijkstra(int Cost[][N], int v0, int Distance[], int prev[]){int s[N];int mindis,dis;int i, j, u;for(i=0; i<N; i++){Distance[i] = Cost[v0][i];s[i] = 0;if(Distance[i] == M)prev[i] = -1;elseprev[i] = v0;}Distance[v0] = 0;s[v0] = 1;for(i=1; i < N; i++){mindis = M;u = v0;for (j=0; j < N; j++)if(s[j]==0 && Distance[j]<mindis){mindis = Distance [j];u = j;}s[u] = 1;for(j=0; j<N; j++)if(s[j]==0 && Cost[u][j]<M){dis = Distance[u] +Cost[u][j]; if(Distance[j] > dis){Distance[j] = dis;prev[j] = u;}}}}void PrintPrev(int prev[],int v0,int vn) {int tmp = vn;int i, j;int tmpprv[N];for(i=0; i < N; i++)tmpprv[i] = 0;tmpprv[0] = vn+1;for(i =0, j=1; j < N ;j++){if(prev[tmp]!=-1 && tmp!=0){tmpprv[i] = prev[tmp]+1;tmp = prev[tmp];i++;}else break;}for(i=N-1; i >= 0; i--){if(tmpprv[i] != 0){printf("V%d", tmpprv[i]);if(i)printf("-->");}}printf("-->V%d", vn+1);}int main(){char *Vertex[N]={"徐州", "上海", "天津", "郑州", "沈阳","大连","长春","哈尔滨","北京","呼和浩特","兰州","西宁","乌鲁木齐","西安","成都","昆明","贵阳","柳州","南宁","株洲","广州","深圳","武汉","南昌","福州"};int Cost[N][N]={{0, 651, 674, 349, M, M, M, M, M, M, M, M, M, M, M, M, M, M, M, M, M, M, M, M, M},{651 ,0, M, M, M, M, M, M, M, M, M, M, M, M, M, M, M, M, M, M, M, M, M, 825, M},{674, M, 0, M, 704, M, M, M,137, M, M, M, M, M, M ,M,M,M,M,M,M,M,M,M,M},{349, M, M, 0, M, M, M, M,695, M, M, M, M,511, M, M, M, M, M, M, M, M ,534, M, M},{M, M, 704, M, 0,397,305, M, M, M, M, M, M ,M,M ,M, M, M, M, M, M, M, M, M, M},{M, M, M, M,397,0,M, M, M, M, M, M, M, M, M, M, M, M, M, M, M, M, M, M, M },{M, M, M, M,305,M,0,242,M, M, M, M, M, M, M, M, M, M, M, M, M, M, M, M ,M},{M, M, M, M, M, M,242,0,M, M, M, M, M, M, M, M, M, M, M, M,M, M, M,M,M},{M, M,137,695,M, M, M,M,0 ,668,M,M,M, M, M, M, M, M, M,M, M, M, M, M,M},{M, M, M, M, M, M, M, M, 668, 0, 1145, M, M, M, M, M, M,M, M, M,M, M, M, M, M},{M, M, M, M, M, M, M, M, M, 1145, 0, 216, 1892, 676, M, M, M,M, M, M,M, M, M, M, M},{M, M, M, M, M, M, M, M, M, M, 216, 0, M, M, M, M, M,M, M, M,M,M, M, M, M},{M, M, M, M, M, M, M, M, M, M, 1892, M,0, M, M, M, M,M, M, M,M, M, M, M, M},{M, M, M, 511, M, M, M, M, M, M, 676, M, M, 0, 842, M, M,M, M, M,M, M, M, M, M},{M, M, M, M, M, M, M, M, M, M, M, M, M, 842, 0, 1100, 967,M, M, M,M, M, M, M, M},{M, M, M, M, M, M, M, M, M, M, M, M, M, M, 1100, 0,639,M, M, M,M, M, M, M, M},{M, M, M, M, M, M, M, M, M, M, M, M, M, M, M, 639, 0,607, M, 902,M, M, M, M, M},{M, M, M, M, M, M, M, M, M, M, M, M, M, M, M, M, 607,0, 255, 672,M, M, M, M, M},{M, M, M, M, M, M, M, M, M, M, M, M, M, M, M, M, M,255, 0, M,M, M, M, M, M},{M, M, M, M, M, M, M, M, M, M, M, M, M, M, M, M, 902,672, M, 0,M, M, 409, 367, M},{M, M, M, M, M, M, M, M, M, M, M, M, M, M, M, M, M,M, M, 675,0, 140, M, M, M},{M, M, M, M, M, M, M, M, M, M, M, M, M, M, M, M, M,M, M, M,140, 0, M, M, M},{M, M, M, 534, M, M, M, M, M, M, M, M, M, M, M, M, M,M, M, 409,M, M, 0, M, M},{M,825 ,M, M, M, M, M, M, M, M, M, M, M, M, M, M, M,M, M, 367,M, M, M, 0, 622},{M, M, M, M, M, M, M, M, M, M, M, M, M, M, M, M, M,M, M, M,M, M, M, 622, 0},};int Distance[N];int prev[N];int i;Dijkstra(Cost, 0, Distance, prev);for(i=0; i < N; i++){printf("%s-->%s:%d\t", Vertex[0], Vertex[i], Distance[i]);PrintPrev(prev, 0, i);printf("\n");}return 0;}Floyd算法：#include <iostream>#include <cstring>#include <stack>#include <queue>using namespace std;const int MAX = 65535;class Graph{private:int** G;int** dist;int** path;int Nv;public:Graph(int nv, int ne){this->Nv = nv;G = new int*[nv+1];dist = new int*[nv+1];path = new int*[nv+1];for(int i = 0 ; i < nv+1 ; i++){G[i] = new int[nv+1];dist[i] = new int[nv+1];path[i] = new int[nv+1];memset(path[i],-1,sizeof(path[0][0])*(nv+1));for(int j = 0 ; j < nv+1 ; j++){this->G[i][j] = this->dist[i][j] = MAX;}this->G[i][i] = this->dist[i][i] = 0;}cout<<"请输入边与权重:"<<endl;for(int i = 0 ; i < ne ; i++){int v1,v2,weight;cin>>v1>>v2>>weight;this->G[v1][v2] = this->G[v2][v1] = weight;this->dist[v1][v2] = this->dist[v2][v1] = weight;}}bool Floyd(){for(int k = 1 ; k < this->Nv+1 ; k++){for(int i = 1 ; i < this->Nv+1 ; i++){for(int j = 1 ; j < this->Nv+1 ; j++){if(this->dist[i][k] + this->dist[k][j] < this->dist[i][j]){this->dist[i][j] = this->dist[i][k] +this->dist[k][j];if(i == j && this->dist[i][j] < 0){return false;}this->path[i][j] = k;}}}}return true;}void Find(queue<int> &q ,int start,int end){int mid = this->path[start][end];if(mid == -1){return;}Find(q,start,mid);q.push(mid);Find(q,mid,end);}void Print_Path(int start,int end){queue<int> queue;queue.push(start);this->Find(queue,start,end);queue.push(end);cout<<queue.front();queue.pop();while(!queue.empty()){cout<<"->"<<queue.front();queue.pop();}cout<<endl;}void Print_Floyd(){int i,j,k;for(int i = 1 ; i < this->Nv+1 ; i++){for(int j = 1 ; j < this->Nv+1 ; j++){cout<<this->path[i][j]<<" ";}cout<<endl;}cout<<" length path"<<endl;for(i = 1 ; i < this->Nv+1 ; i++){for(j = i+1 ; j < this->Nv+1 ; j++){cout<<i<<"->"<<j<<" ";cout<<this->dist[i][j]<<" ";this->Print_Path(i,j);}cout<<endl;}}};int main(){cout<<"请输入顶点数与边长数:"<<endl;int nv,ne;cin>>nv>>ne;Graph graph(nv,ne);if(graph.Floyd()){cout<<"各个顶点的最短路径为："<<endl;graph.Print_Floyd();}return 0;}六、运行结果截图Dijkstra：Floyd算法：七、实验总结与体会Floyd算法是解决给定的加权图中顶点间的最短路径的一种算法，可以正确处理有向图或负权的最短路径问题，同时也被用于计算有向图的传递闭包。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

if(!final[w]&&min<0x7fffffff&&G.arcs[v][w]<0x7fffffff&&(min+G.arcs[v][w]<D[w]))
{
D[w]=min+G.arcs[v][w];
for(j=0;j<G.vexnum;++j)
printf("最短路径数组p[i][j]如下:\n");
for(i=0;i<G.vexnum;++i)
{
for(j=0;j<G.vexnum;++j)
printf("%2d",p[i][j]);
printf("\n");
}
printf("%s到各顶点的最短路径长度为：\n",G.vexs[0]);
for(i=0;i<G.vexnum;++i)
if(i!=0)
{
if(D[i]-0x7fffffff)printf("%s-%s:%d\n",G.vexs[0],G.vexs[i],D[i]);
else printf("%s-%s:无路\n",G.vexs[0],G.vexs[i]);
P[w][j]=P[v][j];
P[w][w]=1;
}
}
}
int main()
{
int i,j;
MGraph G;
PathMatrix p;
ShortPathTable D;
CreateDN(G);
ShortestPath_DIJ(G,0,p,D);//求有向图的0顶点到其余顶点v的最短路径p[v]及其带权长度D[v]
i=LocateVex(G,va);
j=LocateVex(G,vb);
G.arcs[i][j]=w;
}
}
typedef int PathMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
typedef int ShortPathTable[MAX_VERTEX_NUM];
}
//system("PAUSE");
return 0;
}
{
min=0x7fffffff;
for(w=0;w<G.vexnum;++w)
if(!final[w]&&D[w]<min)
{
v=w;
min=D[w];
}
final[v]=1;
for(w=0;w<G.vexnum;++w)
for(j=0;j<G.vexnum;++j)
G.arcs[i][j]=0x7fffffff;
printf("请输入边的两个顶点v1---v2和权值w如下：\n",G.arcnum);
for(k=0;k<G.arcnum;++k)
{
scanf("%s%s%d%*c",va,vb,&w);
struct MGraph
{
VertexType vexs[MAX_VERTEX_NUM];
AdjMatrix arcs;
int vexnum,arcnum;
};
int LocateVex(MGraph G,VertexType u)
{
int i;
for(i=0;i<G.vexnum;++i)
void ShortestPath_DIJ(MGraph G,int v0,PathMatrix P,ShortPathTable D)
{
int v,w,i,j,min;
int final[MAX_VERTEX_NUM];
for(v=0;v<G.vexnum;++v)
{
final[v]=0;
D[v]=G.arcs[v0][v];
for(w=0;w<G.vexnum;++w)
P[v][w]=0;
if(D[v]<0x7fffffff)
P[v][v0]=P[v][v]=1;
}
D[v0]=0;
final[v0]=1;
for(i=1;i<G.vexnum;++i)
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#define MAX_NAME 10
#define MAX_VERTEX_NUM 26
typedef char VertexType[MAX_NAME];
typedef int AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
if(strcmp(u,G.vexs[i])==0)
return i;
return -1;
}
void CreateDN(MGraph &G)
{
int i,j,k,w;
VertexType va,vb;
printf("请输入有向网G的顶点数和弧数\n");
scanf("%d %d",&G.vexnum,&G.arcnum);
printf("请输入%d个顶点的值: \n", G.vexnum);
for(ቤተ መጻሕፍቲ ባይዱ=0;i<G.vexnum;++i)
scanf("%s",G.vexs[i]);
for(i=0;i<G.vexnum;++i)