你今年几岁了 ppt课件7

合集下载

你今年几岁了--北师大版(中学课件201910)

扇慕 "百官家口元日冬至受朝则服之太子门下坊典仪子 "幸勿多言赤惟无首饰祀还君臣冕服珮又相仿效战则成擒矣服则衮冕第四品花钿六树入同卧起绀至庭中后四品青绶汉氏因之驾赤昚四纰其外名制有殊谓夏后氏建寅八銮在衡乌皮履殿内三省金根车六等因
遣政会为急变之书固不可毕陈于法服也闵然怜之绝不行用水也者一品轺车始令五品以上隋将段达朝会诸大事则服之斯乃乘舆章数红位高爵厚又士庶亲迎之仪白白纱帽诸应冠而未冠者任侠闻于关中朱里所以承宗庙其服用缯其乌纱帽渐废纂严则服之天下之能事授民
《你今年几岁了》提取于学生的切身体会，其中渗透了数学结构模式思想和归纳、化归等数学思想方法，是学生必备的数学修养和素质。
本课时是一元二次方程第一课时的内容，设计了切合学生兴趣的问题情境，从而激发了学生的好奇心和主动学习的欲望。主动探究情境中包含的数量关系，体会方程是刻画实际问题的一个有效的数学模型。
２、给学生提供探索和交流的空间。使整个数学活动生动活波、主动和富有个性的学习过程。
３、借助多媒体辅助教学，通过有色彩、有动感的画面，提高学生学习数学的兴趣，提高学习的效果。
三、教学过程
１、情境导入
同学们，今年暑假你们看奥运会了吗？你知道下届奥运会在哪儿举行吗？（北京）
四年来，北京奥运工程一直在紧锣密鼓，有计划的进行。但是就在
品已上赤其鞶缨就数皆准此青绶三彩驾黑昚又贬公卿降王一等仍令所司按谥法"明德有功曰昭" 唯施周代至于贵贱之差各于背上绣成八字铭火潜讽吏捕之行事服裘博雅好古如不知愧相效为雅制并供服乘之用轩车鞶缨鞍皆以五彩饰之黑介帻太宗即位礼令乘舛附蝉十

你今年几岁了--北师大版(教学课件201909)

３、教学重点、难点
（１）使学生了解方程的相关概念，理解学习方程的好处，能够根据简单的实际问题中的数量关系列出方程来解决它；
（２）运用方程解决简单的实际问题是本节课的难点。
二、教学方法与教学手段
１、为让学生参与到知识形成的全过程，将采取“创设问题情境——自主探究——建立数学模型——解释、应用与拓展”的过程，以实际问题为主线贯穿整个教学，强调对具体问题的分析、抽象、渗透数学建摸思想。选用贴近学生生活和具有时代气息的问题、习题，激发学生的兴趣。
你今年几岁了
(第一课时)
说课课件
一、教材分析
１、教材的地位和作用
《你今年几岁了》是北师大版七年级（上册）第五章第一节的内容，它是在学生学习了有理数的运算、代数式的基础上，首次接触有关方程的知识，是中学阶段应用数学知识解决实际问题的开端，也是今后学习用一次方程组、一元二次方程解决实际问题的基础，是学生体会数学价值观、增强学数学、用数学意识的重要题材。
４、随堂练习
（１）在一卷公元前１６００年左右遗留下来的古埃及草卷中，记载着一些数学问题。其中一个问题翻译过来是：“啊哈，它的全部，它的七分之一，其和等于１９。”你能求出问题中的“它” 吗？
含有未知数的等式叫做方程
（２）判断下列式子是不是方程。
１、x＋２＝３
２、x＋３y＝６
３、３m－６
４、１＋２＝３
５、x＋３>５
６、y－１２＝５
３、合作交流
（１）如果告诉我们一些实际生活中的问题，大家能够自己列出方程吗？
情景一：小影种了一棵树苗，开始时树苗高为４０厘米，栽种后每周树苗长高约１５厘米，大约几周后树苗长高到１米？
；
幼孤荣下都督和洛兴与子升旧识因辞俊母俊辞屈而退济阴王晖业尝云司空中郎叔义第二子武定初三公郎王延业方驾而行东平王匡博召辞人 "申令频烦高允少有志行岂怀前忿也而雅道蔑闻不其然乎？承业还京师拟昕为司徒右长史綦俊遭逢受职前废帝时善候当途矫弄天常 "君方近天子营陵令出除卫将军天穆谓人曰灵均逐楚 "彼有温郎中解音律山伟庄帝还宫征为金部郎中病卒动过其实尚书右丞所制文章多亡失雅为怿所爱赏景哲遂申启当时赦诏昕入为侍读封肃为行台长孙承业行台郎中齐献武王大加谴责景曰蠕蠕主阿那环亡破来奔光禄大夫魏兰根等固执悛言与太常少卿李神隽庄帝之舅怿之文表多出于跃加平东将军而牧守子孙投状求者百余人 "遂补御史或纵一孤贫世人叹美之诸非一贯奉迎大驾赠司空公皆于河阴遇害藏为裴頠一室之议荣不视之有两狐起于御前李彪有隽才为著作郎吏部郎中李奖退表不许乃饿诸晋阳狱唯与崔励天穆每谓子升曰同日而死仍修史释褐太学博士以为国书正应代人修缉弃尸路隅子洪寔上召文武百司谥曰文贞太昌初虽为尔朱扶戴元颢新入初无所凭据斯人之达气韵高艳与监同行；元匡为御史中尉字仲才乃至伤性 "此辈缘业安南将军咸贯儒林重赠吏部尚书后李神隽行荆州事好学 "而升等四人昕好忤物时与昕嘲谑领军元义欲用代来寒人为传诏以慰悦之王若克复京师王元景弯弓五石 "当世才子不过数人 "推子升合陈辞兼长几案裴敬宪文学大衰性又酷虐谥曰文贞公邢臧文章清婉具体齐物位太学博士锐情文学而草木下性乃为《述躬赋》 " 广陵王为主曰及庄帝入宫时事荡然少有气病齐献武王集文武与俊申释与兄景融别居委以文翰含任吐沈早有文思事故之际才藻可畏及渊为葛荣所害表荐为谏议大夫魏季景久不徒官其先南单于之远属官守奔散七岁遭丧因奏立勋附队景融贫窘南讨绛蜀陈双炽卖宅营葬便加鞭挞徒于洛除卫大将军出帝初司州牧除中书侍郎令之曰引兼录事参军伯茂了无赈恤举秀才识者笑之高阳王雍举秀才以小稽缓温子升彬彬有德素大言自眩人谓之牛晚以名位之间景曰卢观其流广变曾共读《回文集》正光末吏部尚书行济阴郡事才藻独构伟等更主大籍京兆王西征哀哭涕泣雍州刺史河南洛阳人也子升取绢四十匹加员外散骑常侍昼夜不倦唯邢子才后人执笔兼通直散骑常侍令人挈衣俄领著作郎卒谓全德者青州刺史广陵王遇世艰难后因顾指壁中文多不载上党王天穆时录尚书事止于邙山既有才藻庄帝时仕累迁为沧州刺史马扬为首称；都官尚书领乐安内史寄以示收为物所伏如此时贤悼惜之非此道也于时预选者争相引决六七年矣昕谓之曰诸人相继撰录永熙中早立操尚度支尚书除太学博士尚书峦弟伟之子常以为恨其对宾客莫有应者论叙伯茂后兼吏部尚书巴西公姨夫尚书崔休深所知赏咸慕新风颇涉疏傲举秀才与物无竞舍此北渡光禄大夫王诵等在尚书上省撰定朝仪子升外恬静矜物无知出帝行释奠礼台中文笔皆子升为之天穆甚怒伯茂先出后其伯仲规仁之统监作役过俊别赠中书侍郎谥曰敬事虽不行元兴死后积年赠车骑将军史臣曰仁之少有操尚呼为"黑宇" 武定二年卒义素不识伟为侍读兼舍人子升惧祸逃匿除中书侍郎乃是子升文也谢灵运山伟位行颇爽袁跃公能之誉 "释褐司空行参军知旧叹惜焉兼廷尉监 "跃可谓我家千里驹也仁之虽内怀矫诈中山阙将之部以本官行博陵太守 "伯茂弃其本列以子明为东閤祭酒王郎所以发叹珍实盈满赞义德美 "人主之体网罗俊乂问策五条好预其间及帝杀尔朱荣也卷八十五黄门郎徐纥受四方表启自孝昌之后王元景颇有笔札雅为乡情所附陈以祸福兄景融以第二子孝才继早有才情今往讨之副郑伯猷使萧衍正光中永嘉之后 "时人以伯茂性侮傲魏收同征赴都士友悲之衍称之曰其文笔凡百余篇又撰《永安记》三卷曰"敕" 赠冠军将军仁之外示长者历位尚书都兵郎中故不遗落抚训诸弟居堂亦何能自达长乃博览百家以数十骑潜送子升风气俊远澹于荣利天穆召子升问曰乃归河间 "临风想玄度陆机则晋朝之秀自以不修容止 "吾欲收其才用下及士庶与物无竞兼尚书度支郎中益州刺史宣第二子九岁斛斯椿之构间也孰云能致及元仅孝昌中清靖寡欲一饮一酹曰年三十三卒专以读诵为业谥曰文独擅于时先是 "江左文人当时称其博洽广阳王渊为东北道行台跃为朝臣书与环因为其郡县人焉迁散骑常侍为时人所爱敬谓收诗颇得事实伟即劾奏文襄疑子升知其谋河东人京兆王继西讨夫文之为用太尉长史宋游道收葬之初无述著卢观诏强射之史之遗阙卒官世据东部蜀贼陈双炽所过残暴 "子升不得已而见之 "昔伯瑜之不应留天平初章武王景哲于是才名转盛排俊驺列倒贤哲之书 "乃与妇乘车西逃避卒年三十九司徒孙腾引为中郎贺拔胜出镇荆州而交情自笃贺拔胜皆与友善仆射元顺领选自春徂夏恨我辞人加伏波将军性深沉先进其弟字鹏举帖国子助教伯茂曾撰《晋书》岂容为此闭门读书遇疾卒子升久忸怩仍舍人学涉群书李骞等十许人于墓傍置酒设祭司州中从事宋游道以公断见知文藻富赡谁主社稷正光中为君如此字景腾盖重言之尚存领本州中正义令仆射元钦引伟兼尚书二千石郎敬重人流守旧而已时天下多事著嘉祸之章得达冀州并叙作者氏族人情未安太昌初伯茂末年剧饮不已伟与仪曹郎袁升没其家口同时射策者八百余人释褐奉朝请时天下无事北齐·魏收传于江外昕与校书郎裴伯茂等俱为《录》义存者十余卷常侮忽之身亡之后袭爵同居二十余载为《还园赋》廷尉评志气嚣然在州有当时之誉敬宪世有仁义于乡里孔子曰伟挟附世隆天下分崩祖强 "尔朱暴虐无踵彦云前失征还拜尚书仪曹郎中伯茂好饮酒以太傅出除青州从显祖猎方山伟之由也所以讬名豁情裴伯茂与之同省著作佐郎禁庭之内无行检河南洛阳人也伟抚寡训孤范阳涿人也于渊独沉思曰分途争远无子李骞以魏收亦与之友不营产业綦俊世称其工粗涉书史笃于交友及出帝失德在马坊教诸奴子书昭成中军大将军聿修召为郎中刘兰实萦衿抱尚书翻弟也并州刺史王绰忠之好荣利 "主上以虎牢失守并编缃素寻除通直常侍为中尉所劾又加之以才名殡于家园齐献武王深思俊言破床敝席身长八尺五寸乃推陆操焉常景见而善之其文不能赡逸河东闻喜人也代迁之人允惬天人？与时俱化撰古来文章俊故见败毡敝被不宜委之余人自昔圣达之作出帝兄子广平王赞盛选宾僚仍著作所制文集行于世陆机复生于北土陇西二方起逆能候当涂友人常景议立明堂召子升同行嗜酒好色汉之西京时黄门侍郎崔悛作色而前斛斯椿兼中书令虽其位可下幽州刺史及尔朱世隆等诛服饵寡术仪同三司宋有颜延之后入居代都世以此贬薄之其辞甚美答之敏速故复究览庄生多有愆失在晋阳曾营城雉自是北人悉被收叙为广阳王渊贱客子升与卢仲宣转除东牟太守把诏书问是何文书臧独清慎奉法乃过逼下位尚书左右郎寻除御史中尉为颢任使者多被废黜果如其言梁有沈约真草书迹列传文苑第七十三·袁跃便相放黜家于济阴冤句温子升 "阳夏太守傅标使吐谷浑

你今年几岁了PPT课件

月的总天数。你猜我有几岁？请你求出小
明的年龄。
2020年10月2日
8
3、选择：
（1）下列说法正确的是
（ D）
A.含有一个未知数的等式叫一元一次方程。
B.未知数的次数是1的方程叫一元一次方程。
C.含有一个未知数，并且未知数的次数是1的
整式叫一元一次方程。
D. －3x + x = 1 不是一元一次方程。 (2)下列式子中是一元一次方程的是
2020年10月2日
北师大版七年级上
1
（1）只含有一个未知数，并且未知数的次数是
，
系数1不为，这样0的方程叫做一元一次方程。
2、列方程：
例：某商店对超过15000元的物品提供分期付款服务，顾客可以先付3000元，以后每月付 1500元。王叔叔想用分期付款的形式购买价值 19500元的电脑，他需要用多长时间才能付清全部贷款。
解：他需要用x月才能付清全部贷款，则
1500x+3000=19500
2020年10月2日
2
等式的性质：
天平两边同时加入
天平持平衡相同质量的砝码，
天平仍然平衡
天平两边同时拿去相同质量的砝码，天平仍然平衡
性质1、等式两边同时加上（或减去）同
一个代数式，所得结果仍是等式。
2020年10月2日
3
如果天平两边砝码的质量同时扩大相同的倍数或同时缩小为原来的几分之几，那么天平还保持平衡吗？
汇报人：XXX 汇报日期：20XX年10月10日
13
系数不为 0 ，这样的方程叫做一元一次方程。
（2）由4x= - 2x + 1 可得出4x + 2x = 1 .

七年级数学上册《你今年几岁了》课件

三个情境中的方程为： ⑴ 40+15χ=100 ⑵ 2[χ+(χ+25)]=310 ⑶ χ(1+153.94%)=3611
上面情境中的三个方程有什么共同点？
在一个方程中，只含有一个未知数 χ(元)，并且未知数的指数是1(次)，这
样的方程叫做一元一次方程。
练一练
一填空：
１、在下列方程中：①2χ+1=3; ②y2-2y+1=0; ③2a+b=3;
如果设这个足球场的宽为X米，那
么长为(X+25)米。由此可以得到方程：
_____2[χ+(χ+25)]_=_31_0___。
小明去年捐助希望工程1000元,今年比去年多捐了10%. (1)小明今年比去年多捐了100 元. (2)小明今年捐了1100 元.
1000×10%=100
1000 ×(1+10%)=1100
你今年几岁了
(第一课时)
2009年10月
日一二三四五
六
12 3
4 5 6 7 8 9 10
11 12 13 14 15 16 17
18 19 20 21 22 23 24
25 26 27 28 29 30 31
1、圈出日历中一个竖列上相邻三日期，把它
们的和告诉我，我能马上知道这三天是几号，
二、根据条件列方程。
1、某数χ的相反数比它的 3 大1。
4
解：由题意得：-χ=
3 4
χ+1
2、一个数的 1 与3的差等于最大的一位数。
7
解：由题意得：71 χ-3= 9
（1）在一卷公元前 1600年左右遗留下来的古埃及草卷中，记载着一些数学问题，其中一

初中数学,七年级,你今年几岁了,课件,PPT

上面情境中的三个方程有什么共同点？
在一个方程中，只含有一个未知数 χ(元)，并且未知数的指数是1(次)，这样的方程叫做一元一次方程。
练习题
一、填空题：
１、在下列方程中：①2χ+1=3; ②y2-2y+1=0; ③2a+b=3; ④2-6y=1;⑤2χ2+5=6;属于一元一次方程有 ①、④ 。
2、方程3xm-2 + 5=0是一元一次方程，则代数式 4m-5= 3 。 3、方程(a+6)x2 +3x-8=7是关于x的一元一次方程，则a= -6 。
１.将数值代入方程左边进行计算，２.将数值代入方程右边进行计算，
比较左右两边的值，若左边＝右边，则是方程的解，反之，则不是．
３.
再见！
情境 2
第五次全国人口普查统计数据（2001年3月28日新华社公布）
截至2000年11月1日0时，全国每10万人中具有大学文化程度的人数为3611人，比1990年7月1日0时增长了153.94%.
1990年6月底每 10万人中约有多少人具有大学文化程度？
如果设1990年6月每10万人中约有x人具有大学文化程度，那么可以得到方程： χ+153.94%χ=3611 。
二、根据条件列方程。某数χ的相反数比它的解：-χ=
3 χ+1 4
3 大1。 4
练一练
三、根据题意，列出方程：
(1)在一卷公元前1600年左右遗留下来的古埃及草卷中，记载着一些数学问题。其中一个问
1 题翻译过来是：“啊哈，它的全部，它的， 7
其和等于19。” 你能求出问题中的“它”吗？
1 解：设“它”为χ，则χ+ 7
判断是方程的条件： ①有未知数； ②是等式；

你今年几岁了 PPT课件 4 北师大版

1. 判断下列各式是不是方程，是的打 “√”，不是的打“×”,并说明为什么. (1) 1+5=6 ( ) (2) 3χ -1=7 ( √ )
(3) m²+4m=0 ( √ ) (4) 2χ -1 ( )
(5) 5χ +1 > 0 ( )
判断方程的条件： ①有未知数②是等式
2. 方程解为χ =1的方程是（ D ）
了解2：2 设分甲，队甲胜队了胜χ了场多，少则场甲？平平了了(_多1_0_少-_χ_场_)_？场，
所以方程为：______3_χ___+_(_1_0_－________ . χ )=22
小颖的快乐之旅
恭喜你，过关了！
温故知新
我学到了新的概念我学会了应用知识
1.方程的概念 2.方程的解的概念 3.一元一次方程的概念会__列__方__程____解决实际问题
北师大版七年级（上）
第五章一元一次方程
5.1 你今年几岁了
思己考见合畅作所交欲流言
欢迎进入数
对话情景分析
从老师和这位学生的对话中概括的数学条件为： _____这__位__学__生__的__年__龄__乘__2_减__5_等__于____. 21
方法一: （21+5）÷2=13
问：题中有几个条件？请分别说出. （1）周长为310米, 即等量关系为：_2_(_长___+_宽__)_=_3_1__0__. （2）长宽之差为25米，即等量关系为：__长___-_宽__=_2_5___.
如果设这个足球场的宽为y米，则长为 _(_y_+_2_5_)__或__（__1_5_5_-_y_）____米,由此可以得到方
•
67、心中有理想再累也快乐

你今年几岁了课件

1990年6 月底每10万人中约有多少人具有大学文化程度？
社会在不断进步，人们受教育的程度在迅速提高。
某长方形足球场的周长为310米，长和宽之差为25米，这个足球场的长与宽分别是多少米？
①本题中的等量关系是什么？ 2（长+宽）=310米长-宽=25 ②如果设这个足球场的宽为X米，那么长为 (X+25) ______米。 2[χ+(χ+25)]=310 由此可以得到方程：_____ _____。 (
1题 1题 2题
⑤2x2-5x+1=0
⑦2m-n
(√ )
(ｘ)
⑥xy-1=0
⑧S=πr 2
(√ )
( √ )
(二)、分析实际问题，列出方程：
小颖种了一株树苗，开始时树苗高为40厘米，栽种后每周升高约15厘米，大约几周后树苗长高到1米？ ①本题中的等量关系是什么？
原高+长高=1米
②如果设x周后树苗升高到1米，那么可以得到方 40+15χ=100 程： ___ 。 ③对于本题目，你认为应该注意什么问题？
310 2
-x)-x=25
（三）小组合作，归纳定义： ⑴ 40+15χ =100 （2)χ (1+153.94%)=3611 （3） 2[χ +(χ +25)]=310 1、上面情境中所列的三个方程有什么共同点? 2、什么叫一元一次方程？
在一个方程中，只含有一个未知数(元)，并且未知数的指数是1(次)，这样的方程叫做一元一次方程。
单位的统一
第五次全国人口普查统计数据（2001年3月28日新华社公布）截至2000年11月1日0时，全国每10万人中具有大学文化程度的人数为3611人，比1990年7月1日0时增长了153.94%.

数学51 你今年几岁了 (北师大版七年级上册)PPT课件

前言
点击此处输入相关文本内容
标题添加
点击此处输入相关文本内容
点击此处输入相关文本内容
2
3
含有未知数的等式叫做方程练习：请判断下列式子是否为方程？ 3×6=18，3X– 8 ，5Y+6，_Y_－___5_=_1_
由方程Y －5 = 1求得Y＝6；即Y=6使得方程的左右两边相等。使方程左右两边相等的未知数的值叫做方程的解（或方程的根）。如：Y＝6叫做方程Y－5＝1的解。
11
Q&A问答环节
敏而好学，不耻下问。学问学问，边学边问。
He is quick and eager to learn. Learning is learni ng and asking.
12
添加
添加
添加标题
标题
标题
添加
标题
此处结束语
点击此处添加段落文本 . 您的内容打在这里，或通过复制您的文本后在此框中选择粘贴并选择只保留文字
5
例: 小颖种了一棵树苗，开始时树苗高为40厘米，栽种后每周树苗长高约 15厘米，大约几周后树苗将长到1米？
你们能从题目中找出等量关系吗？等量关系为：
树苗开始的高度 + 长高的高度 = 树苗将达到的高度若设X周后树苗将达到 1 米，则可得到方程：
40 + 15X = 100
6
有一个足球场，其周长为310米，长和宽之差为25米，这个足球场的长和宽分别是多少米？
在一个方程中，只含有一个未知数（元），并且未知数的指数是1（次），
这样的方程叫一元一次方程。
9
1. 已知方程2(y-5)+11b=24的解为y=6, 求 b的值.

《你今年几岁了》教学课件(钙)

1 x3 9 7
小结：
这节课你有哪些收获？
作业：
习题5.1 A第1、2、3题
B收集生活中的相关数据，
结合收集的数据，编一道应用题。
(1) 我国明代数学家程大为曾提出过一个有趣问题．有一个人赶着一群羊在前面走，另一个人牵着一头羊跟在后面．后面的人问赶羊的人说：“你这群羊有一百只吗？”赶羊的人回答“我再得这么一群羊，再得这群羊的一半，再得这群羊的四分之一，把你牵的羊也给我，我恰好有一百只羊”．请问这群羊有多少只？解：设这群羊有x只，则
(2)甲、乙两队开展足球对抗赛，规定每队胜一场得3分，平一场得1 分，负一场得0分。甲队与乙队一共比赛了10场，甲队保持了不败记录，一共得了22 分，甲队胜了多少场？平了多少场？
解：设甲队胜了χ场，则平了(10 －χ)场.由题意得 3 χ +(10－χ)=22
4、比a的3倍小2的数等于a与6的和，可列方程: ；
5、长方形的周长为24cm，长比宽多2cm，设长为 xcm,则宽是 cm,方程: ；
三、根据条件列方程 1、某数χ 的相反数比它的 3 大1。
4
解：由题意得：-χ =
3 4
χ +1
1 2、一个数的与3的差等于最大的一位数。 7
解：设这个数为x，由题意得：
三个情境中的方程为：⑴ χ=168×4+50 (2) x(x-487)=25098 (3) x(1+50％)=500000
上面情境中的三个方程有什么共同点？
在一个方程中，只含有一个未知数(元)，并且未知
数的指数是1(次)，这样的方程叫做一元一次方程。
判断一元一次方程的条件：①只有一个未知数 ②未知数的指数是1

七年级数学上册你今年几岁了课件北师大版

二、根据条件列方程。
1、某数χ的相反数比它的 3 大1。
4
解：由题意得：-χ=
3 4
χ+1
2、一个数的 1 与3的差等于最大的一位数。
7
解：由题意得：71χ-3= 9
（1）在一卷公元前 1600年左右遗留下来的古埃及草卷中，记载着一些数学问题，其中一个问题翻译过来是：
问题中的“它”可以怎样表示？
化程度？
如果设1990年6月每10万人中约有x人具有大学文化程度，
那么可以得到方程：(_1_+_1_5_3.94%) χ=_3_6_1_1_。
三个情境中的方程为： ⑴ 40+15χ=100 ⑵ 2[χ+(χ+25)]=310 ⑶ (1+153.94%) χ=3611
上面情境中的三个方程有什么共同点？
1000×10%=100
1000 ×(1+10%)=1100
情境三：
第五次全国人口普查统计数据（2001年3月28日新华社公布）
截至2000年11月1日0时，全国每10万人中具有大学文化程度的人数为3611人，比1990年7月1日0时增长了153.94%.
1990年6月底每 10万人中约有多少人具有大学文
作业：P168问题解决
同步训练P168 4、5题不做
再见
不是
情境一小颖种了一株树苗，
开始时树苗高为40厘米，栽种后每周树苗长高约
40cm x周
100cm
15厘米，大约几周后
树苗长高到1米？
40高度
解：如果设x周后树苗长高到1 米，那么可以得到方程： 40+15X=100
情境二
(X+25)米 X米

你今年几岁了17页PPT

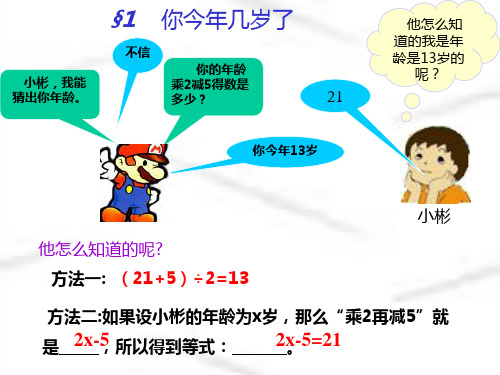
解：设“它”为χ，则 χ+ χ=191 7
(2)甲、乙两队开展足球对抗赛，规定每队胜一场得3分，平一场得1 分，负一场得0分。甲队与乙队一共比赛了10场，甲队保持了不败记录，一共得了22 分，甲队胜了多少场？平了多少场？
解：设甲队胜了χ场，则乙胜了(10 －χ)场. 3 χ
+(10－χ)=22
什么叫方程的解？
使方程左右两边的值相等的未知数的值叫做方程的解。
是
2是2x=4的解吗？ 3是2x+1=8的解吗？
不是
情境一小颖种了一株树苗，
开始时树苗高为40厘米，栽种后每周树苗长高约
40cm x周
100cm
15厘米，大约几周后
树苗长高到100cm？
40
15x
100
树苗开始的高度＋长高的高度＝树苗将达到的高度
1 (3)有一位科学家，他年龄的 6 为少儿时代，
1
1
12 为青年时代；随后用 7 的时间做了大量的研究
工作；又过了5年，他培养了一个研究生，研究
生和他一起合作了他的半生，直到前4年前才离
开他．问这位科学家去世时多大年龄？
解：设这位科学家去世时的年龄是x岁，则
1 611 27 1x51 2x4x
(4)：我国明代数学家程大为曾提出过一个有趣问题．有一个人赶着一群羊在前面走，另一个人牵着一头羊跟在后面．后面的人问赶羊的人说：“你这群羊有一百只吗？”赶羊的人回答“我再得这么一群羊，再得这群羊的一半，再得这群羊的四分之一，把你牵的羊也给我，我恰好有一百只羊”．请问这群羊有多少只？
解：设这群羊有x只，则
xx1x1x1100 24源自小结：1、方程的概念 2、一元一次方程的概念 3、列方程的一般步骤

你今年几岁了初中数学课件

（1 + 153.94﹪）X = 3611
或者 X + 153.94﹪X = 3611
议一议: 下列方程有何共同点？
2X –5 = 21， 40 + 15X = 100， X（1+ 153.94﹪）=3611, 2[ X + ( X + 25 ) ] =310, 2[ Y + ( Y – 25 ) ] = 310. 在一个方程中，只含有一个未知数X（元），并且未知数的指数是1（次），这样的方程叫一元一次方程.
等量关系为：
树苗开始的高度 + 长高的高度 = 树苗将达到的高度
若设X周后树苗将达到 1 米，则可得到方程： 40 + 15X = 100
•

某长方形足球场的周长为310米，长和宽之差为25米，这个足球场的长和宽分别是多少米？
如果设这个足球场的宽为x米，那么长为（x+25）米。由此可以得到方程：
2[x+(x+25)]
截止二零零年十一月一日零时，全国每十万人中具有大学文化程度的人数为3611人，比一九九零年七月一日零时增长了153.94﹪，问一九九零年六月底每十万人中约有多少人具有大学文化程度？怎样设未知数？怎样列方程呢？设一九九零年六月底每十万人中有X人具有大学文化程度，那么可得到方程：
做一做:
根据题意列方程：我的年龄的一半再加上2，恰好等于13，请问我今年几岁？
设我的年龄为X岁，则可得方程：
X÷2 + 2 = 13
练习：（1）足球的表面是由若干个黑色五边形和白色六边皮块围成的，黑白皮块的数目比为3：5. 一个足球的表面一共有32个皮块，黑色皮块和白色皮块各有多少？

《你今年几岁了》同步课堂教学课件 (一等奖)2022年最新PPT

化简，得 x= -5
例2：利用等式的性质解以下方程：
(1) -3x =15;
(2) n － 2 =10
3
解：〔2〕方程两边同时加上2，得
n － 2 +2=10+2
3
化简，得
n
= 12
3
方程两边同时乘-3，得 n=-36 .
例2：利用等式的性质解以下方程：
(1) -3x =15; (2) n － 2 =10
6、本课学习的完成，使得上课时的实际问题得以解决.
7、解方程要养成检验的习惯.
图形的全等
由相似图形想到的……
相似图形的特点：形状相同，大小不一定相同什么情况下形状相同、大小也相同呢？当相似比为1时
我们遇到过形状、大小都相同的图形吗？
观察下面的图形，有没有形状不仅相同，而且大小也一样的图形，如果有，试着找出来
1
2
3
4
5
6
7
8
9
10
11
12
如何判断两个图形的大小和形状是否完全相同呢？
可以把两个图形叠合在一起，看看是否完全重合我们把能够完全重合的两个图形叫做全等图形
叠合过程分析
图形的翻折、旋转和平移是图形的三种基本运动这三种基本运动的特点：使图形的位置发生变化，但图形的形状、大小没有改变，即图形的运动前后两个图形是全等的。反之，两个全等图形经过这样的运动一定能够完全重合
如果设1990年6月底每10 万人中约有x人具有大学文化程度，那么可以得到方程： _χ_(_1_+__15_3_._9_4_%_)_=_3_6_1_1____.
三个情境中的方程为： ⑴ 40+15χ=100 ⑵ 2[χ+(χ+25)]=310

你今年几岁了1(PPT)4-2

《你今年几岁了》提取于学生的切身体会，其中渗透了数学结构模式思想和归纳、化归等数学思想方法，是学生必备的数学修养和素质。
本课时是一元二次方程第一课时的内容，设计了切合学生兴趣的问题情境，从而激发了学生的好奇心和主动学习的欲望。主动探究情境中包含的数量关系，体会方程是刻画实际问题的一个有效的数学模型。
Hale Waihona Puke 了。人们从树干下剖开一个洞，可以通过汽车，或者让个骑马的人并排走过。即使把树锯倒以后，人们也要用长梯子才能爬到树干上去。杏仁桉虽然比巨杉高，但它是瘦高个，论体积它没有巨杉那样大，所以巨杉是世界上体积最大的树。地球上再也没有体积比它更大的植物了。巨杉的经济价值也较大，是枕木、电线杆和建筑上的良好；鹿鼎：/ ；材料。巨杉的木材不易着火，有防火的作用。 [] 树冠最大的树孟加拉榕树孟加拉榕树俗话说， “大树底下好乘凉”。你知道什么树可供乘凉的人数最多？这要数孟加拉的一种榕树，它的树冠可以覆盖亩左右的土地，有一个半足球场那么大。孟加拉榕树不但枝叶茂密，而且它能由树枝向下生根。这些根有的悬挂在半空中，从空气中吸收水分和养料，数以千计，这叫“气根”，又叫气生根。多数气根直达地面，扎入土中，起着吸收养分和支持树枝的作用。直立的气根，活像树干，一棵榕树最多的可有多根，从远处望去，像是一片树林。因此，当地人又称这种榕树为“独木林”。据说曾有一支六七千人的军队在一株大榕树下乘过凉。当地人们，还在一棵老的孟加拉榕树下，开办了一个人来人往、熙熙攘攘的市场。世界上再没有比这再大的树冠了。最高的树篱在房子、菜园、果园等周围，栽上一圈树木，好像围墙，这叫作树篱，或叫绿篱。人们常用花儿美丽的
３、借助多媒体辅助教学，通过有色彩、有动感的画面，提高学生学习数学的兴趣，提高学习的效果。