山西省2019-2020学年第一学期八年级期中质量评估试题·生物(苏教版)·试题+答案
山西省2019-2020学年第一学期八年级期末质量评估试题·生物(苏教版)·试题及答案

19. 营群体生活的动物常常具有社会行为,群体内部往往有分工与合作。下列属于社会行
为的是
A. 两只狗为争夺骨头而争斗
%%%%%%B. 蜜蜂跳“8”字舞
C. 田鼠在洞内堆放粮食
%%%%%%%%%%%%D. 母鸽哺育幼鸽
20. 习近平总书记说“绿水青山就是金山银山”,倡导人们从身边小事做起,转变生活方
式,实现人与地球的和谐相处。下列不符合这一理念的是
将该选项涂黑。每小题 2 分,共 40 分)
1. 浮萍是一种漂浮在水面上的水生植物,叶近圆形,叶背面垂生丝状根,种子外面有果皮
包被,果实近陀螺状。请你根据这些特征分析,浮萍属于
A. 藻类植物
B. 苔藓植物
C. 被子植物
D. 裸子植物
2. 小明对生物学非常感兴趣,在课余时间观察了多种植物并做了详细记录。下面是他记
A. 真菌细胞没有叶绿体,营寄生生活或腐生生活
B. 真菌细胞与动物细胞相比,不同之处是真菌细胞具有细胞壁
C. 有些真菌是我国的传统药材,如灵芝
D. 真菌细胞与细菌细胞都具有细胞核
9. 马和驴杂交可产下骡,但在分类上马和驴同科不同属;俗话说“风马牛不相及”,但在分
类上马和牛同纲不同目。下列说法正确的是
八年级生物 (苏教版) 第 3 页 (共 8 页)
14. 据媒体报道,1996 年我国考古学家在辽宁省发现一对古生物化石,经过研究发现是一
对雌雄孔子鸟化石,体型与鸡的大小相近,上下颌没有牙齿,有清晰的羽毛印迹。下列
分析错误的是
A. 孔子鸟化石揭示了不同生物之间的进化关系
B. 现在发现的化石都是高等生物化石
C. 孔子鸟化石为研究鸟类进化提供了新证据
D. 越复杂、越高等的生物化石出现在越新近形成的地层中
太原市2019_2020学年第一学期八年级期中考试英语(解析)

2019~2020学年第一学期八年级阶段性测评(期中)英语试题解析(试卷)满分:100分答题时间:90分钟第I卷听力测试(共20分)I.听力(共四节,满分20分)略II.单项选择(每小题1分,满分10分)21.答案:B解析:考察点为人称代词的使用。
横杠后为名词,需要形容词性物主代词。
22.答案:C解析:考察点为最高级的常用句型之一。
one of the +最高级+名词复数,表示最..的..之一。
23.答案:A解析:考察点为连词的使用。
翻译为虽然中国女排队伍遇到了很多困难,他们仍旧在世界杯拿到了金牌。
24.答案:C解析:考察点为动词词义辨析。
问句为你怎么看王菲的新歌我和我的祖国,答句为它很棒,它真的赢得了我的心。
25.答案:B解析:考察点为情景交际。
问句为你怎么看待攀登者,答句后半句为她很好,所以根据情景,选B我喜欢它。
26.答案:B解析:考察点为形容词词义辨析。
翻译为随着5G时代的到来,更多有创造力的想法将会改变我们的生活。
27.答案:A解析:考察点为固定搭配词义辨析。
翻译为我真的很想成为班上的好学生。
这取决于你学习的态度。
如果你努力做,那么你将能够成功。
A选项为取决于,B选项为相似,C选项为准备好。
28.答案:C解析:考察点为副词的词义辨析。
翻译为我清晰地记得我第一次在天安门前看升国旗仪式的那一天。
A 为迅速地,B为仔细地,C为清晰地。
29.答案:C解析:考察点为情态动词的使用。
翻译为你如何能交到真心朋友呢?你必须真的在乎他人,并且成为一个倾听者。
30.答案:B解析:考察点为名词的词义辨析和固定搭配的积累。
翻译为我们谈论了传统中国文化。
我的同学最喜欢北京京剧。
其中固定搭配为have a discussion about sth. 谈论关于某事。
III.补全对话(每小题1分,满分5分)31.答案:B解析:此空为寒暄,选B。
32.答案:C解析:由回答语I went to Beijing.可知,此空提问假期去何地,选C。
山西省2019-2020学年第一学期八年级期中质量评估试题·数学(人教版)·试题+答案
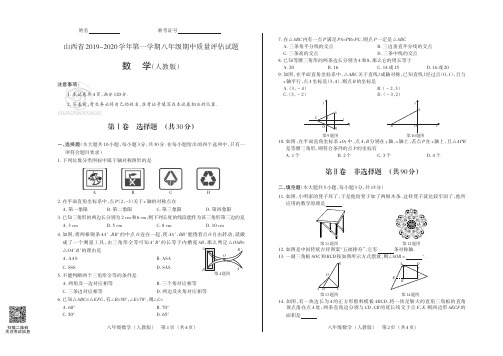
∴∠DAC=∠CEA=∠CDE-∠ACD=60°-45°=15°, …………………………………… 4 分
∴∠ACE=150°, ……………………………………………………………………… 5 分
∴∠BCE=60°,………………………………………………………………………… 6 分
∴△CBE 为等边三角形 . …………………………………………………………… 7 分
21. 证明:∵CA=CB,CE=CA,
∴BC=CE, …………………………………………………………………………… 1 分
∴∠CAE=∠CEA,……………………………………………………………………… 2 分
∵CD 平分∠ACB 交 AE 于 D,且∠CDE=60°,
∴∠ACD=∠DCB=45°, ……………………………………………………………… 3 分
C. 8 cm
D. 10 cm
4. 如图,将两根钢条 AA′ 、BB′ 的中点 O 连在一起,使 AA′ ,BB′ 能绕着点 O 自由转动,就做
成了一个测量工具,由三角形全等可知 A′ B′ 的长等于内槽宽 AB,那么判定△OAB≌
△OA ′ B ′ 的理由是 A. AAS
B. ASA
A
B′
O
C. SSHale Waihona Puke 5. 不能判断两个三角形全等的条件是
E
点 E 为△ABC 外一点,CE=CA,且 CD 平分∠ACB 交 AE 于点
D,∠CDE=60°. 求证:△CBE 为等边三角形 .
A
22.(本题 12 分)如图,在△ABC 中,已知点 D 在线段 BA 的延长线
DM C
第 21 题图 D
上,过 AC 的中点 F 作线段 GE 交∠DAC 的平分线于点 E,交 BC 于点 G,且 AE⫽BC. (1)求证:△ABC 是等腰三角形;
山西省2019-2020学年第一学期八年级期中质量评估试题·英语(牛津版)·试题

沿此线折叠一、情景反应(每小题1分,共5分)本题共5个小题,每小题你将听到一组对话。
请你从每小题所给的A、B、C三幅图片中,选出的出的你的所的听的到的的的信的息的息的关的关的的一项,并在答题卡上将该项涂黑。
A B C1.A B C2.A B C3.4.A BCA B C5.二、对话理解(每小题1分,共5分)本题共5个小题,每小题你将听到一组对话和一个问题。
请你从每小题所给的A、B、C三个选项中,选出一个最佳选项,并在答题卡上将该项涂黑。
6.A.Eric. B.David. C.Peter.7.A.In a hospital. B.In a supermarket. C.In a restaurant.8.A.Action movies. edies. C.Cartoons.9.A.Anna. B.Sophie. C.Maria.10.A.Adam is not good at English.B.Adam’s Englsih is worse than Henry’s.C.Adam’s English is the best in his class.三、语篇理解(每小题1分,共5分)本题你将听到一篇短文。
请你根据短文内容和所提出的5个问题,从每小题所给的A、B、C三个选项中,选出一个最佳选项,并在答题卡上将该项涂黑。
11.When did the girl go to Australia?A.In October.B.In November.C.In December.12.What did the girl think of the trip?A.Fantastic.B.Terrible.C.Boring.13.How did they go to the middle of Australia?A.By plane.B.By bus.C.By car.14.Where did they live at night?A.In tents.B.In hotels.C.In a farmer’s house.15.What is the girl talking about?A.A special day in Sydney.B.A family trip to Australia.C.A bad week in Australia.山西省2019-2020学年第一学期八年级期中质量评估试题英语(牛津版)八年级英语(牛津版)第2页(共12页)八年级英语(牛津版)第1页(共12页)注意事项:1.本试卷分听力和笔试两部分。
山西省2020-2021学年第一学期九年级期中质量评估试题

⼭西省2020-2021学年第⼀学期九年级期中质量评估试题⼭西省2020-2021学年第⼀学期九年级期中质量评估试题·数学(华师版·公⽴)试题学校:___________姓名:___________班级:___________考号:___________⼀、单选题1x 的取值范围是() A .2x ≤ B .2x ≥ C .2x <- D .2x -≤ 2.中国象棋是有着三千多年历史的益智游戏.如图是某局象棋游戏的残局,若在该棋盘上建⽴平⾯直⾓坐标系,使表⽰棋⼦“兵”和“炮”的点的坐标分别为()1,3-,()1,3,则表⽰棋⼦“卒”的点的坐标为()A .()2,1B .()2,1-C .()2,1-D .()2,1-- 3.下列⼆次根式是最简⼆次根式的是()A B C D 4.⼀元⼆次⽅程x 2﹣3x =0的两个根是()A .x 1=0,x 2=﹣3B .x 1=0,x 2=3C .x 1=1,x 2=3D .x 1=1,x 2=﹣3 5.如图,在ABC 中,点D ,E 分别是边AB ,BC 的中点.若ABC 的周长是12,则DBE 的周长是()A .4B .5C .6D .7 6.下列⼀元⼆次⽅程中,有两个不相等实数根的是()A .2104x x -+=B .2390x x ++=C .2250x x -+=D .25130x x -=7,所以看上去就⽐较美,则它的宽为()A BC .D 8.如图,直线123////l l l ,直线AC 分别交1l ,1l ,3l 于点A ,B ,C ;直线DF 分别交1l ,1l ,3l 于点D ,E ,F .若23BC AB =,则DE DF的值为()A .32B .23C .35D .259.⼀元⼆次⽅程x 2-8x -1=0配⽅后可变形为()A .(x +4)2=17B .(x +4)2=15C .(x -4)2=17D .(x -4)2=15 10.我国古代数学《九章算术》中有⼀道“井深⼏何”的问题:“今有井径五尺,不知其深,⽴五尺⽊于井上,从⽊末望⽔岸,⼊径四⼨(1尺等于10⼨),问井深⼏何?”根据题意画出如图⽰意图,则井深为()A .56.5尺B .57.5尺C .6.25尺D .1.25尺⼆、填空题11.已知矩形的⾯积为36,则另⼀边长为______.12.若⼀元⼆次⽅程ax 2﹣bx ﹣2020=0有⼀根为x =﹣1,则a+b =_____. 13.如图,D 是ABC 的边BC 上⼀点,4AB =,2AD =,DAC B ∠=∠.如果ABD △的⾯积为6,那么ACD △的⾯积为_______.14.我国疫情防控⼯作进⼊了⼀个新的阶段——“常态化”,戴⼝罩仍然是切断病毒传播的主要措施.某药店⼋⽉份销售⼝罩500包,⼋⾄⼗⽉份共销售⼝罩1820包.设该店九、⼗⽉份销售⼝罩的⽉平均增长率为x ,则可列⽅程为_______.15.如图,ABC 是等腰直⾓三⾓形,且2AC BC ==,AD 是ABC 的中线,过点C 作CE AD ⊥交AD 于点F ,交AB 于点E ,则EF 的长为_______.三、解答题16.计算:(1))21|1(2)17.解⽅程:(1)210240x x -+=;(2)25440x x --=.18.如图,在正⽅形⽹格中建⽴平⾯直⾓坐标系,已知点()0,0O ,()1,3A -,()4,0B ,连接OA ,OB ,AB .(1)若将OAB 向上平移4个单位长度,再向右平移5个单位长度,得到111O A B △,点O ,A ,B 的对应点分别为1O ,1A ,1B ,画出111O A B △并写出顶点1A 的坐标;(2)画出22OA B △,使22OA B △与OAB 关于原点对称,点A ,B 的对应点分别为2A ,2B ;(3)以点O 为位似中⼼,在给定的⽹格中将OAB 放⼤2倍得到33OA B ,点A ,B 的对应点分别为3A ,3B ,画出33OA B 并直接写出33A B 的长度.19.请阅读下列材料,并解决问题:海伦—秦九韶公式海伦(约公元50年),古希腊⼏何学家,在数学史上以解决⼏何测量问题闻名,在他的著作《度量》⼀书中证明了⼀个利⽤三⾓形的三条边的边长直接求三⾓形⾯积的公式:假设在平⾯内,有⼀个三⾓形的三条边长分别为a ,b ,c ,记2a b c p ++=,那么这个三⾓形的⾯积S =秦九韶(约1202—1261),我国南宋时期的数学家,曾提出利⽤三⾓形的三边求⾯积的秦九韶公式S =从中可以看出中国古代已经具有很⾼的数学⽔平.通过公式变形,可以发现海伦公式和秦九韶公式实质是同⼀公式,所以海伦公式也称海伦—秦九韶公式.问题:在ABC 中,4BC =,5AC =,6AB =,请⽤海伦—秦九韶公式求ABC 的⾯积. 20.如图所⽰,某景区计划在⼀个长为36m ,宽为20m 的矩形空地上修建⼀个停车场,其中阴影部分为三块相同的矩形停车区域,它们的⾯积之和为2336m ,空⽩部分为宽度相等的⾏车通道,问⾏车通道的宽度是多少?21.如图是⼀块三⾓形钢材ABC ,其中边60cm BC =,⾼40cm AD =,把它加⼯成正⽅形零件,使正⽅形的⼀边在BC 上,其余两个顶点分别在AB ,AC 上,这个正⽅形零件的边长是多少?22.已知甲种苹果每箱价格⽐⼄种苹果每箱价格贵10元,每天平均销售甲种苹果70箱,⼄种苹果60箱,销售总额为5900元.(1)求甲、⼄两种苹果每箱的价格;(2)在销售中发现,每箱苹果价格每下调1元,这两种苹果每天均可多销售5箱,为了促销,村⾥决定把两种苹果单价都下调m 元()10m <,在不考虑其他因素的情况下,求m 为多少时,每天的销售额为7460元.23.综合与实践将矩形ABCD 和Rt CEF △按如图1的⽅式放置,已知点D 在CF 上(2CF CD >),90FCE ∠=?,连接BF ,DE .特例研究(1)如图1,当AD CD =,CE CF =时,线段BF 与DE 之间的数量关系是_______;直线BF 与直线DE 之间的位置关系是_______;(2)在(1)条件下中,将矩形ABCD 绕点C 旋转到如图2的位置,试判断(1)中结论是否仍然成⽴,并说明理由;探究发现(3)如图3,当2CF CE =,2CB CD =时,试判断线段BF 与DE 之间的数量关系和直线BF 与直线DE 之间的位置关系,并说明理由;知识应⽤(4)如图4,在(3)的条件下,连接BE ,FD ,若22CE CD ==,请直接写出22BE FD +的值.。
山西省2019-2020学年第二学期八年级阶段一质量评估试题及答案·物理(人教版)

所受重力的示意图。
22. 踢毽子是一种人们喜爱的健身运动,踢毽子,又叫“打鸡”,起源 于汉代,盛行于南北朝和隋唐,有盘踢、拐踢、蹦踢、磕踢四种用 脚的方法。请利用学过的知识解释,踢毽子时,毽子离开脚后, 为什么毽子能落在很远处。 温馨提示:23 小题,解题过程要有必要的文字说明、计算公式和演算步骤,只写最后结 果不得分。
将该项涂黑。每小题 3 分,共 30 分)
1. 生活中,用手托起一枚鸡蛋所用的力最接近
A. 0.1 N
B. 0.5 N
C. 1 N
D. 5 N
2. 如图所示,一只蜘蛛吐丝悬挂在天花板上,蜘蛛受到拉力的施力物体为
A. 地球
B. 天花板
C. 蛛丝
D. 蜘蛛
3. 小明在探究力的作用效果与什么因素有关时,他将一薄钢条的下端固定,分别用不同
C. 茶杯受到向下的弹力是因为桌面发生了形变
D. 桌面受到向下的弹力是因为茶杯发生了形变
9. 看足球比赛时某同学突发奇想,如果在空中飞行的足球所受一切外力突然消失,关于
足球的运动情况,下列判断正确的是
A. 做匀速直线运动
B. 停在空中静止不动
C. 飞行路径不受影响
D. 竖直下落
10. 春晚杂技表演中,杂技演员被抛到空中后仍能继续向上运动一段距离,这是由于
A. 演员在空中受到惯性的作用
B. 演员在空中受到抛力的作用
C. 演员抛到空中后仍具有惯性
D. 演员在空中不受任何力作用
八年级物理 (人教版) 第 2 页 (共 6 页)
第Ⅱ卷 非选择题 (共 70 分)
二、实验探究(本大题共 5 个小题,11 小题 8 分,12 小题 14 分,13 小题 10 分,14 小题 8 分,15
山西省2019-2020学年第一学期八年级期末质量评估试题·语文·试题及答案

一、读·书(12分)1.对联是汉语独有的文学样式,书法是中华民族文化的瑰宝,二者结合更有无穷的魅力。
请赏读下面这副对联,并用楷体将其内容正确、规范、美观地书写在田字格内。
(2分)2.读古诗文,将空缺处的原句书写在横线上。
(10分)(1)白头搔更短,▲。
(《春望》杜甫)(2)▲?心远地自偏。
(《饮酒(其五)》陶渊明)(3)▲,自将磨洗认前朝。
(《赤壁》杜牧)(4)争渡,争渡,▲。
(《如梦令》李清照)(5)▲,望峰息心;▲,窥谷忘反。
(《与朱元思书》吴均)(6)李贺在《雁门太守行》中用“▲,▲”两句诗,表达誓死报国的忠心。
(7)李清照的《渔家傲》中用充满浪漫主义的笔调描绘了一幅海天相接的辽阔图画的句子是:“▲,▲。
”二、读·思(38分)(一)北京时间9月28日下午15点57分,在与塞尔维亚女排的对战中,(A )中国女排提前一轮获得2019年女排世界杯冠军。
中国女排成为女排世界杯历史上唯一一个五冠王。
中国女排让球迷折服,让中国沸腾。
3∶0横扫日本女排,干净利落;3∶2逆转巴西女排,惊心动魄;3∶0完胜美国女排,势如破竹。
(B )中国女排顽强拼搏的意志和团结协作的精神充分显示了郎平教练善打硬仗的风格和及时调整战略的果敢。
中国女排打出了勇气和自信,燃爆了中国,惊艳了世界。
3.结合上面语段,下列表述有误的一项是(2分)A.“勇气和自信”“燃爆了中国”“惊艳了世界”三个短语结构一致。
B.画线A 句的主干是“女排获得冠军”。
C.“3∶0横扫日本女排,干净利落;3∶2逆转巴西女排,惊心动魄;3∶0完胜美国女排,势如破竹。
”这句话运用了排比的修辞,表达了对中国女排的由衷赞美。
D.画线B 句的宾语中心语是“风格和果敢”。
4.名著阅读。
有一次,他趴在地上,用放大镜观察蚂蚁搬死苍蝇,一连看了三四个小时,以至周围挤满了人,他都不曾发现。
有人骂他“怪人”,可他全然不觉,就像没听见一样。
(1)“他”指的是:▲;以上文字出自他的著作:▲。
山西省太原市2019-2020学年八年级上学期期中数学试卷 (有解析)

山西省太原市2019-2020学年八年级上学期期中数学试卷一、选择题(本大题共10小题,共30.0分)1.在实数12,−√3,−3.14,0,π2,2.616116111,√643中,无理数有()A. 1个B. 2个C. 3个D. 4个2.√144的平方根是()A. ±12B. 12C. ±2√3D. 2√33.下列各组数中能作为直角三角形三边长的是()①9,12,15;②13,12,6;③9,12,14;④12,16,20A. ①④B. ①②C. ③④D. ②④4.下列化简或计算正确的是()A. √(−√3)2=−√3B. √1149=1+17=87C. (√6−√3)2=9−2√3D. √24÷(−12√6)=−45.笑笑在平面直角坐标系中画的一次函数y=kx+b的图象经过第一、三、四象限,则k的值可能是()A. 4B. 0C. −1D. −26.已知点M(1,a)和点N(2,b)是一次函数y=−2x+1图象上的两点,则a与b的大小关系是()A. a>bB. a=bC. a<bD. 以上都不对7.已知Rt△ABC中,∠C=90°,a,b,c分别为∠A,∠B,∠C所对的边,若a+b=14cm,c=10cm,则Rt△ABC的面积是()A. 24cm2B. 36cm2C. 48cm2D. 60cm28.已知一次函数y=kx+3(k≠0)的图象经过点A,且函数值y随x的增大而增大,则点A的坐标可能是()A. (−2,−4)B. (1,2)C. (−2,4)D. (2,−1)9.已知锐角三角形的边长是2,3,x,那么第三边x的取值范围是()A. 1<x<√5B. √5<x<√13C. √13<x<√15D. √5<x<√1510.如图,长方体的底面边长分别为2cm和4cm,高为5cm.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径长为()A. 8cmB. 10cmC. 12cmD. 13cm二、填空题(本大题共5小题,共10.0分)11. 化简:−a√−1a化成最简二次根式为____.12. 点A(m,m +5)在函数y =−2x +1的图象上,则m =____. 13. 计算√16的结果是________.14. 《九章算术》中有这样一个问题,大意是:一个竹子高1丈,折断后竹子顶端落在离竹子底端3尺处(其中的丈、尺是长度单位,1丈=10尺).折断处离地面的高度是多少?设折断处离地面的高度是x 尺,根据题意可列方程为______.15. 如图,在等腰△ABC 中,AB =AC =13,BC =10,N 为线段AB 上的任意一点,∠BAC 的平分线交BC 于点D ,M 是AD 上的动点,连结BM 、MN ,则BM +MN 的最小值是________.三、计算题(本大题共1小题,共12.0分) 16. 计算:(1)√3−2√12÷6√13(2)(3√2−√18)÷11√22四、解答题(本大题共7小题,共48.0分)17. 如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:(1)在网格中建立平面直角坐标系,使A点坐标为(−2,4),B点坐标为(−4,2);(2)在(1)建立的平面直角坐标系中,C点坐标是(1,−1),画出△ABC关于关于y轴对称的△A′B′C′.18.学完勾股定理之后,同学们想利用升旗的绳子、卷尺测算出学校旗杆的高度.小明发现旗杆上的绳子垂到地面还多了1m,当他把绳子的下端拉开5m后,发现下端刚好接触地面,请你帮小明求出旗杆的高度.19.已知直线y=−2x+b与x轴交于点A(−3,0),求直线与y轴的交点坐标.DC.20.如图,D为△ABC的BC边上的一点,AB=10,AD=6,DC=2AD,BD=23(1)求BD的长;(2)求△ABC的面积.21.在“美丽广西,清洁乡村”活动中,李家村村支书提出两种购买垃圾桶方案:方案1:买分类垃圾桶,需要费用3000元,以后每月的垃圾处理费用250元;方案2:买不分类垃圾桶,需要费用1000元,以后每月的垃圾处理费用500元.设方案1的购买费和每月垃圾处理费共为y1元,方案2的购买费和每月垃圾处理费共为y2元,交费时间为x个月.(1)直接写出y1,y2与x之间的函数关系式;(2)如图在同一平面直角坐标系内,画出函数y1,y2的图象;(3)在垃圾桶使用寿命相同的情况下,哪种方案更省钱?22.阅读下列材料,并解答问题:√2+√4=√4−√22=2−√22;√4+√6=√6−√42=√6−22;√6+√8=√8−√62=2√2−√62;8+10=√10−√82=√10−2√22;……(1)直接写出第⑤个等式______;(2)用含n(n为正整数)的等式表示你探索的规律;(3)利用你探索的规律,求√2+√4√4+√6√6+√8+⋯√198+√200的值.23.如图,直线y=kx+b与x轴、y轴分别交于点A,B,且OA,OB的长(OA>OB)是方程x2−10x+24=0的两个根,P(m,n)是第一象限内直线y=kx+b上的一个动点(点P不与点A,B重合).(1)求直线AB的解析式.(2)C是x轴上一点,且OC=2,求△ACP的面积S与m之间的函数关系式;(3)在x轴上是否有在点Q,使以A,B,Q为顶点的三角形是等腰三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.-------- 答案与解析 --------1.答案:B解析:本题主要考查了无理数的定义,无限不循环小数叫做无理数.根据无理数的定义对各选项进行分析判断即可.解:∵√643=4,12,−3.14,2.616116111,0是有理数,π2,−√3是无理数,∴无理数有2个. 故选B .2.答案:C解析:解:∵√144=12,12的平方根是±√12=±2√3. ∴√144的平方根是±2√3. 故选:C .先化简,再根据平方根的定义,解答即可.本题考查了平方根,解决本题的关键是熟记平方根的定义.3.答案:A解析:欲求证是否为直角三角形,这里给出三边的长,只要验证两小边的平方和等于最长边的平方即可. 本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.解:①92+122=152,故是直角三角形,故正确; ②62+122=180≠132,故不是直角三角形,故错误; ③92+122=225≠142,故不是直角三角形,故错误; ④122+162=202,故是直角三角形,正确. 故选A .4.答案:D解析:解:A、原式=|−√3|=√3,所以A选项错误;B、原式=√5049=5√27,所以B选项错误;C、原式=6−6√2+3=9−6√2,所以C选项错误;D、原式=−2√24÷6=−4,所以D选项正确.故选D.根据二次根式的性质对A、B进行判断;根据完全平方公式对C进行判断;根据二次根式的除法法则对D进行判断.本题考查了二次根式的性质及计算.5.答案:A解析:本题考查的是一次函数图象与系数的关系,根据k>0,b<0⇔y=kx+b的图象在一、三、四象限解答.解:∵一次函数y=kx+b的图象经过第一、三、四象限,∴k>0,故选:A.6.答案:A解析:解:∵k=−2<0,∴y随x的增大而减小,∵1<2,∴a>b.故选:A.根据一次函数的增减性,k<0,y随x的增大而减小解答.本题考查了一次函数图象上点的坐标特征,利用一次函数的增减性求解更简便.7.答案:A解析:本题考查了勾股定理,这里不要去分别求a,b的值,熟练运用完全平方公式的变形和勾股定理.要求Rt△ABC的面积,只需求出两条直角边的乘积.根据勾股定理得a2+b2=c2=100,求出ab的值,进而得到三角形的面积.解:∵a+b=14,∴(a+b)2=196,∴2ab=196−(a2+b2)=96,∴12ab=24cm2故选A.8.答案:A解析:解:∵y随x的增大而增大,∴k>0.A、当x=−2时,y=−2k+3<3,选项A正确;B、当x=1时,y=k+3>3,选项B错误;C、当x=−2时,y=−2k+3<3,选项C错误;D、当x=2时,y=2k+3>3,选项D错误.故选:A.由y随x的增大而增大,利用一次函数的性质可得出k>0,再利用一次函数图象上点的坐标特征验证四个选项中的点是否在函数图象上,此题得解.本题考查了一次函数图象上点的坐标特征以及一次函数的性质,利用一次函数的性质找出k>0是解题的关键.9.答案:B解析:本题主要考查了锐角三角形的三边关系定理以及勾股定理等知识,熟练掌握这些知识是解题的关键,根据勾股定理可知x的平方取值范围在2与3的平方和与平方差之间.解:因为32−22=5,32+22=13,所以5<x2<13,即√5<x<√13,且3−2<x<2+3,即1<x<5,∴√5<x<√13故选B.10.答案:D解析:本题的是平面展开−最短路径问题,解答此类问题时要先根据题意把立体图形展开成平面图形后,再确定两点之间的最短路径.一般情况是两点之间,线段最短.在平面图形上构造直角三角形解决问题.要求长方体中两点之间的最短路径,最直接的做法就是将长方体展开,然后利用两点之间线段最短解答.解:如图所示:∵长方体的底面边长分别为2cm和4cm,高为5cm.∴PA=4+2+4+2=12cm,QA=5cm,∴PQ2=PA2+AQ2=169,∴PQ=13cm.故选D.11.答案:√−a解析:本题考查最简二次根式的定义,最简二次根式必须满足两个条件:被开方数不含分母;被开方数不含能开得尽方的因数或因式.根据二次根式的性质,可得答案.解:由题意,a<0,所以−a√−1a =−a√−aa2=−a×√−a|a|=√−a,最简二次根式为√−a,故答案为√−a.12.答案:−43解析:解:把点A(m,m+5)代入y=−2x+1得:m+5=−2m+1,解得:m=−43,故答案为:−43.把点A(m,m+5)代入y=−2x+1得到关于m的一元一次方程,解之即可.本题考查了一次函数图象上点的坐标特征,正确掌握代入法是解题的关键.13.答案:4解析:本题考查了算术平方根.掌握算术平方根的定义是解题的关键.根据算术平方根的定义即可求解.解:√16=4.故答案为4.14.答案:x2+32=(10−x)2解析:解:1丈=10尺,设折射处高地面的高度为x尺,则斜边为(10−x)尺,根据勾股定理得:x2+32=(10−x)2.故答案为:x2+32=(10−x)2.杆子折断后刚好构成一直角三角形,设杆子折断处离地面的高度是x尺,则斜边为(10−x)尺.利用勾股定理解题即可.此题考查了勾股定理的应用,解题的关键是利用题目信息构造直角三角形,从而运用勾股定理解题.15.答案:12013解析:本题考查了轴对称−最短路线问题、勾股定理及等腰三角形的性质,过C作CN⊥AB于N,交AD于M,连接BM,根据两点之间线段最短和垂线段最短得出此时BM+MN最小,由于C和B关于AD 对称,则BM+MN=CN,根据勾股定理求出CN,即可求出答案.解:过C作CN⊥AB于N,交AD于M,连接BM,则BM+MN最小(根据两点之间线段最短;点到直线垂直距离最短),由于C和B关于AD对称,则BM+MN=CN,∵等腰△ABC中,AD平分∠CAB,∴AD⊥BC,BD=CD=5,在Rt△ADC中,AD=√AC2−CD2=√132−52=12∴AD是BC的垂直平分线(三线合一),∴C和B关于直线AD对称,∴CM =BM ,即BM +MN =CM +MN =CN , ∵CN ⊥AB ,∴∠CNB =90∘∴12AB×CN=12×10×12, ∴CN =12013.∴BM +MN 的最小值是12013. 故答案为12013.16.答案:解:(1)原式=√3−2×16×√12×3=√3−2;(2)原式=(3√2−√24)÷11√22=11√24÷11√22=12.解析:(1)先根据二次根式的除法法则运算,然后化简即可;(2)先把二次根式化为最简二次根式,然后合并后利用二次根式的除法法则运算.本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后合并同类二次根式即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.17.答案:解:(1)平面直角坐标系如图所示.(2)如图所示:△A′B′C′即为所求.解析:(1)根据A ,B 两点坐标确定平面直角坐标系即可.(2)分别作出A ,B ,C 的对应点A′,B′,C′即可.本题考查作图轴对称变换,平面直角坐标系等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.18.答案:解:设旗杆AB的高为xm,则绳子AC的长为(x+1)m在Rt△ABC中,AB2+BC2=AC2∴x2+52=(x+1)2解得x=12∴AB=12∴旗杆的高为12m.解析:此题考查了学生利用勾股定理解决实际问题的能力,关键是利用勾股定理即可求得AB的长.根据题意设旗杆AB的高为xm,则绳子AC的长为(x+1)m,再利用勾股定理即可求得AB的长,即旗杆的高.19.答案:解:∵直线y=−2x+b与x轴交于点A(−3,0),∴b=−6,∴直线的解析式为y=−2x−6,∴直线与y轴的交点坐标为(0,−6).解析:本题考查一次函数的性质,函数解析式与坐标轴上点的坐标的特征.利用函数解析式和坐标轴上点的坐标特征即可解决问题.20.答案:解:(1)∵AD=6,DC=2AD,∴DC=12,∵BD=2DC,3∴BD=8;(2)在△ABD中,AB=10,AD=6,BD=8,∵AB2=AD2+BD2,∴△ABD为直角三角形,即AD⊥BC,∵BC=BD+DC=8+12=20,AD=6,×20×6=60.∴S△ABC=12解析:(1)由DC=2AD,根据AD的长求出DC的长,进而求出BD的长即可;(2)在直角三角形ABD中,由AB,AD以及BD的长,利用勾股定理的逆定理判断得到三角形为直角三角形,即可求出三角形ABC面积.此题考查了勾股定理的逆定理,熟练掌握勾股定理的逆定理是解本题的关键.21.答案:解:(1)对于方案1:买分类垃圾桶,需要费用3000元,以后每月的垃圾处理费用250元,交费时间为x个月,则y1与x之间的函数关系式为y1=250x+3000;同样,对于方案2可得y2与x之间的函数关系式为y2=500x+1000.;(2)如图所示:(3)①由250x+3000<500x+1000,得x>8,所以当使用寿命大于8个月时,方案1更省钱;②由250x+3000=500x+1000,得x=8,所以当使用寿命等于8个月时,两种方案费用相同;③由250x+3000>500x+1000,得x<8,所以当使用寿命小于8个月时,方案2更省钱.解析:本题主要考查利用一次函数的模型解决实际问题的能力.解题的关键是根据题意列出函数关系式,再结合图象求解.注意要把所有的情况都考虑进去,分情况讨论问题是解决实际问题的基本能力.(1)根据总费用=购买垃圾桶的费用+每月的垃圾处理费用×月份数,即可求出y1、y2与x的函数关系式;(2)根据一次函数的性质,运用两点法即可画出函数y1、y2的图象;(3)观察图象可知:当使用时间大于8个月时,方案1省钱;当使用时间小于8个月时,方案2省钱;当使用时间等于8个月时,方案1与方案2一样省钱.22.答案:解:√10+√12=√12−√102=2√3−√102√n+√n+2=√n+2−√n2(n为正整数);(3)原式=2−√22+√6−22+√8−√62+⋯+√200−√1982=√200−√22=9√22.解析:解:10+12=√12−√102=2√3−√102;√n+√n+2=√n+2−√n2(n为正整数);(3)见答案.故答案为√10+√12=√12−√102=2√3−√102;(1)利用分母有理化写出第⑤个等式;(2)根据前面5个等式的数字变化规律,用含n 的代数式表示上述规律;(3)先分别分母有理化,然后合并即可.本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.23.答案:解:(1)x 2−10x +24=0,解得:x =4或6,故点A 、B 的坐标分别为:(6,0)、(0,4),把点A 、B 的坐标代入一次函数表达式:y =kx +b 得:{6k +b =0b =4,解得:{k =−23b =4, 故直线AB 的表达式为:y =−23x +4;(2)设点P(m,−23m +4),当点C 在x 正半轴时,OC =2,AC =4,S =12×4×(−23m +4)=−43m +8; 当点C 在x 轴负半轴时,同理可得:S =−83m +16,故S =−83m +16或S =−43m +8(0<m <6);(3)设点Q(s,0),则AB 2=52,AQ 2=(6−s)2,BQ 2=s 2+16,①当AB =AQ 时,52=(6−s)2,解得:s =6±2√3;②当AB =BQ 时,同理可得:s =±6(舍去6);③当AQ =BQ 时,同理可得:s =53,综上,点Q 的坐标为:(6+2√13,0)或(6−2√13,0)或(−6,0)或(53,0).解析:(1)x 2−10x +24=0,解得:x =4或6,故点A 、B 的坐标分别为:(6,0)、(0,4),把点A 、B 的坐标代入一次函数表达式,即可求解;(2)设点P(m,−23m +4),当点C 在x 正半轴时,OC =2,AC =4,S =12×4×(−23m +4)=−43m +8;当点C 在x 轴负半轴时,同理可得:S =−83m +16;(3)分AB =AQ 、AB =BQ 、AQ =BQ 三种情况,分别求解即可.本题考查的是一次函数综合运用,涉及到勾股定理的运用、面积的计算等,其中(2)、(3),都要注意分类求解,避免遗漏.。
山西省2019-2020学年第一学期八年级期中质量评估试题·英语(人教版)·试题

八年级英语 (人教版) 第 4 页 (共 12 页)
七、 完形填空(每小题 1 分,共 8 分)
请阅读下面短文,理解其大意,然后从每小题所给的 A、B、C 三个选项中,选出一个
能填入空白处的最佳选项,并在答题卡上将该项涂黑。
Let’s Have a Field Day
Do you know what a“field day” is? You may know this 36 : “The newspaper is
22. Some of us want to use mobile phones, _________ our teachers don’t think we are old
enough.
A. and
B. but
C. if
23. The radio said it would rain in tnot to eat out with his
school year. Usually, it is a time when students can relax and have fun with all their friends.
A Field Day is organized(组织) by the teachers. It
usually 38 on the last or second鄄to鄄last day of the
A. By plane.
B. By bus.
C. By car.
14. Where did they live at night?
A. In tents.
B. In hotels.
C. In a farmer’s house.
15. What is the girl talking about?
太原市2019_2020学年第一学期八年级期中考试物理(试卷)

8. 图 5 是小明“探究声音产生原因”的实验,用悬线下的轻质小球紧靠正在发声的音叉,发现小球多次被 弹开.下列说法正确的是 A.音叉发声是由于小球的跳动产生的 B.小球的跳动说明声音能够传递信息 C.小球的跳动说明空气能够传声 D.用小球的跳动反映音叉的振动
-2 -
二、填空与作图题(本大题共 6 个小题,每空 1 分,每图 2 分,共 18 分)
11. 图 7 是太原二青会开幕式上气势磅礴的太钢威风锣鼓“击鼓而歌”的场景,鼓声是由鼓面
在空气中以
的形式传播到现场观众耳中,靠近音箱的观众用手堵着耳中,这是
在
处减弱噪声的.
产生,它
12. 我国设计的玉兔二号月球车,已于 2019 年 1 月 3 日成功着陆月球背面,如图 8 所示.此车设计的最大速
火”)的原因了.
-5 -
21. 随着生活水平的日益提高,不少场所的装修会考虑学吸音效果.小明同学想比较几
种常见装修材料的吸音性能,他找来厚度相同的三种小块材料(聚酯棉、软木和
泡沫),进行了图 16 所示实验:桌面上放一个玻璃杯,在玻璃杯下分别放上待测
试的小块材料,将悬挂在细线下的小球拉到一定高度释放去敲击玻璃杯,仔细比
(4)若小车被释放前就开始计时,测得的平均速度比真实值偏
.
20. 小明和小华用规格完全相同的器材,设计了探究“水沸腾过程中温度变化规律”的实验,装置如图 15 甲
所示.图 15 乙是两名同学正确操作后,根据实验数据绘制的水温随时间变化的图象.请你解答下列问题:
山西省太原市2019-2020学年八年级上学期期中数学试卷 (有解析)

山西省太原市2019-2020学年八年级上学期期中数学试卷一、选择题(本大题共10小题,共30.0分)1.实数√7的相反数是()A. √7B. ±√7C. −√7D. −72.下列几组数能作为直角三角形的三边长的是()A. 2,2,√8B. √3,2,√5C. 9,12,18D. 12,15,203.下列计算正确的是()3=−3 C. √(−4)2=−4 D. √93=3A. √4=±2B. √−274.如图是雷达探测到的6个目标,若目标B用(30,60°)表示,目标D用(50,210°)表示,则表示为(40,120°)的目标是()A. 目标AB. 目标CC. 目标ED. 目标F5.一次函数y=3x+2的图象不经过()A. 第一象限B. 第二象限C. 第三象限D. 第四象限6.在实数,3.141592,−2.020020002....中,无理数有()A. 2个B. 3个C. 4个D. 5个7.平面直角坐标系中点(−2,1)关于y轴对称的点的坐标为()A. (−2,−1)B. (2,1)C. (−1,2)D. (1,−2)8.已知点M(1,a)和点N(2,b)是一次函数y=−2x+n图象上的两点,则a与b的大小关系是()A. a≤bB. a<bC. a≥bD. a>b9.如图,点A,B在数轴上对应的实数分别为m,n,则A,B间的距离是()A. m+nB. m−nC. n−mD. |m+n|10.如图,棱长为1的正方体木块上有一只蚂蚁,它从顶点A出发沿着正方体表面爬到顶点G处,则它爬行的最短路程是()A. 3B. √5C. √2+1D. 2二、填空题(本大题共5小题,共10.0分)11.计算(√2+1)(√2−1)的结果为______.12.若一个正比例函数的图象经过A(3,−6),B(m,−4)两点,则m的值为______.13.若正三角形的边长为2√5cm,则这个正三角形的面积是______cm2.14.比较大小:3√3−13(填“>”,“<”或“=”).15.如图,Rt△ABC中,∠ACB=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=3,BC=4,则OC的长为______.三、计算题(本大题共3小题,共24.0分)16.计算:(√2−√3)2+2√13×3√2.17.先阅读下面的解题过程,然后解答:化简√7+2√12.解:∵(√4)2+(√3)2=7,√4×√3=√12,∴√7+2√12=√(√4)2+2√3×√4+(√3)2=√(√4+√3)2=√4+√3.根据上述方法化简:√13−2√42.18.在下面的正方形网格中,每个小正方形的边长为1,正方形的顶点称为格点,请在图中以格点为顶点,画出一个周长为2√5+2√10的△ABC,并求它的面积.四、解答题(本大题共5小题,共36.0分)19.如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(2,−1),B(1,−2),C(3,−3)(1)将△ABC向上平移4个单位长度得到△A1B1C1,请画出△A1B1C1;(2)请画出与△ABC关于y轴对称的△A2B2C2;(3)请写出A1、A2的坐标.20. 已知一次函数y =−23x +5的图象与x 轴、y 轴分别交于A 、B 两点,求出点A 、B 的坐标,并画出这个一次函数的图象.21. 如图是一束平行的阳光从教室窗户射入的平面示意图,小强同学测量出BC =1m ,NC =43m ,BN =53m ,AC =4.5m ,MC = 6m ,求MA 的长.22.暑假期间,某剧院举行专场音乐会,成人票每张20元,学生票每张5元,影剧院制定了两种优惠方案,方案1:购买一张成人票赠送一张学生票;方案2:按总价的90%收款.向阳中学4名老师带领若干名(不少于4人)学生听音乐会,设学生人数为x,付款总金额为y(元).(1)分别建立两种优惠方案中y与x的函数关系式;(2)确定最节省钱的购票方案.x的图象交于点A,点P(t,0)是x正半轴上23.如图,一次函数y=−x+7的图象与正比例函数y=34的一个动点.(1)点A的坐标为(______,______);(2)如图1,连接PA,若△AOP是等腰三角形,求点P的坐标:x和y=−x+7的图象于点B,C.是否存在正实(3)如图2,过点P作x轴的垂线,分别交y=34OA,若存在求出t的值;若不存在,请说明理由.数,使得BC=32-------- 答案与解析 --------1.答案:C解析:本题主要考查相反数的定义,根据相反数的定义解答即可.解:实数√7的相反数是−√7.故选C.2.答案:A解析:解:A.22+22=(√8)2,能作为直角三角形的三边长,故本选项符合题意.B.(√3)2+22≠(√5)2,不能作为直角三角形的三边长,故本选项不符合题意.C.92+122≠182,不能作为直角三角形的三边长,故本选项不符合题意.D.152+122≠202,不能作为直角三角形的三边长,故本选项不符合题意.故选A.分别计算较小两数的平方和,看是否等于最大数的平方,若等于就是直角三角形,否则就不是直角三角形.本题考查勾股定理的逆定理,关键知道两个较小边的平方和等于较大边的平方,这个三角形就是直角三角形.3.答案:B解析:本题考查了算术平方根、立方根,解决本题的根据是熟记算术平方根、立方根的定义.根据算术平方根、立方根的定义,即可解答.解:A.√4=2,故计算错误;3=−3,故计算正确;B.√−27C.√(−4)2=4,故计算错误;3不能化简,故计算错误;D.√9故选B.4.答案:B解析:解:∵目标B用(30,60°)表示,目标D用(50,210°)表示,∴第一个数表示距观察站的圈数,第二个数表示度数,∴表示为(40,120°)的目标是:C.故选:B.根据位置的表示方法,第一个数表示距观察站的圈数,第二个数表示度数写出即可.本题考查了坐标位置的确定,读懂题目信息,理解有序数对的两个数表示的实际意义是解题的关键.5.答案:D解析:解:∵k=3>0,b=2>0,∴直线y=3x+2经过一、二、三象限,不经过第四象限.故选:D.一次函数y=kx+b的图象经过第几象限,取决于k和b.当k>0,b>O时,图象过1,2,3象限,据此作答.本题考查一次函数的k>0,b>0的图象性质.一次函数的图象经过第几象限,取决于x的系数和常数项.6.答案:C解析:本题主要考查了无理数的定义,注意带根号的要开不尽方才是无理数,无限不循环小数为无理数.如π,√6,0.8080080008…(每两个8之间依次多1个0)等形式.根据无理数的定义,无理数就是无限不循环小数,据此即可判断.3,−2.020020002……,解:无理数有:−√3,,√9故选C.7.答案:B解析:解:点(−2,1)关于y轴的对称点的坐标是(2,1),故选:B.根据关于y轴对称点的坐标特点:横坐标互为相反数,纵坐标不变;即点(x,y)关于y轴的对称点的坐标是(−x,y).此题主要考查了关于x轴、y轴对称的点的坐标规律,比较容易,关键是熟记规律:(1)关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数.(2)关于y轴对称点的坐标特点:横坐标互为相反数,纵坐标不变.8.答案:D解析:解:∵点M(1,a)和点N(2,b)是一次函数y=−2x+n图象上的两点,∴a=−2+n,b=−4+n,∴a−b=(−2+n)−(−4+n)=2>0,∴a>b,故选:D.把点M和点N的坐标代入一次函数的解析式,求出a、b的值,比较即可.本题考查的是一次函数图象上点的坐标特征,掌握一次函数图象上点的坐标满足一次函数的解析式是解题的关键.9.答案:C解析:本题考查了实数与数轴:实数与数轴上的点是一一对应关系.任意一个实数都可以用数轴上的点表示.用B点表示的数减去A点表示的数即可得到A,B间的距离.解:A,B间的距离=n−m.故选C.10.答案:B解析:解:如图所示:AG=√22+12=√5.故选:B.根据图形是正方体得出最短路径只有一种情况,利用勾股定理求出即可.此题主要考查了平面展开图最短路径问题以及勾股定理的应用,得出正确的展开图是解决问题的关键.11.答案:1解析:解:原式=(√2)2−1=2−1=1.故答案为1.利用平方差公式计算.本题考查了二次根式的混合运算:先把各二次根式化为最简二次根式,在进行二次根式的乘除运算,然后合并同类二次根式.12.答案:2解析:解:设正比例函数的解析式为y=kx(k≠0),∵该正比例函数图象经过点A(3,−6),∴−6=3k,解得:k=−2,∴正比例函数的解析式为y=−2x.∵点B(m,−4)在正比例函数y=−2x的图象上,∴−4=−2m,解得:m=2.故答案为:2.由点A的坐标即可求出正比例函数的解析式,再利用一次函数图象上点的坐标特征可求出m的值,此题得解.本题考查了一次函数图象上点的坐标特征,牢记直线上任意一点的坐标都满足函数关系式y=kx+ b是解题的关键.13.答案:5√3解析:解:作三角形ABC的高AD,∵等边三角形ABC,AD⊥BC,∴BD=CD=√5,在Rt△ABD中,由勾股定理得:AD=√AB2−BD2=√15,∴S△ABC=12BC×AD=12×2√5×√15=5√3,故答案为:5√3.作三角形ABC的高AD,根据等腰三角形的性质求出BD的长,根据勾股定理求出AD,根据三角形的面积公式求出即可.本题考查了等边三角形的性质,勾股定理,三角形的面积等知识点的应用,关键是求出三角形ABC 的高,题型较好,难度不大.14.答案:>解析: 此题主要考查了实数大小比较的方法,要熟练掌握,解答此题的关键是判断出√3−13−13的差的正负.首先求出两个数的差是多少;然后根据求出的差的正负,判断出√3−13,13的大小关系即可.解:√3−13−13 =√3−1−13 =√3−23<0 , ∴√3−13<13. 故答案为>.15.答案:7√22解析:本题考查了正方形的性质的运用,全等三角形的判定及性质的运用,勾股定理的运用,解答时作辅助线,构建全等三角形和等腰直角三角形是关键.过点O 作OM 垂直于CA 于点M ,作ON 垂直于CB 于点N ,易证四边形MCNO 是矩形,利用已知条件再证明△AOM≌△BON ,因为OM =ON ,AM =BN ,所以CO 平分∠ACB ;进而求出CN 的长,根据勾股定理即可求出OC 的长.解:过点O 作OM 垂直于CA 于点M ,作ON 垂直于CB 于点N ,∴∠OMC =∠ONC =90°,∵∠ACB =90°∴四边形MCNO 是矩形,∴∠MON =90°,∵正方形ABDE 对角线交于点O ,∴OA =OB ,∠AOB =90°,∴∠MON −∠AON =∠AOB −∠AON ,∴∠AOM =∠NOB ,∵∠OMA =∠ONB =90°,在△AOM和△BON中,{∠AOM=∠BON∠OMA=∠ONB=90°OA=OB,∴△AOM≌△BON(AAS),∴OM=ON,AM=BN,∴∠ACO=∠BCO=45°,∴矩形MCNO是正方形,∵AC=3,BC=4,∴CN=CM=AC+BC2=72,∵∠OCN=45°,由勾股定理得:OC=7√22.故答案为:7√22.16.答案:解:原式=2−2√6+3+2√33×3√2=5−2√6+2√6=5.解析:先利用完全平方公式计算,再利用二次根式的乘法法则运算,然后合并即可.本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.17.答案:解:∵(√6)2+(√7)2=13,√6×√7=√42,∴√13−2√42=√(√6)2−2(√6×√7)+(√7)2=√(√6−√7)2=√7−√6.解析:本题主要考查了算术平方根的概念.根据算术平方根的概念计算此题.18.答案:解:∵(√10)2+(√10)2=(2√5)2∴该三角形是腰为√10的等腰直角三角形,如图:△ABC 是一个周长为2√5+2√10三角形,△ABC 的面积=3×4−12×2×4−12×1×3−12×1×3=5.解析:根据勾股定理在方格中作出三角形的三条边,根据直角三角形的面积公式、矩形的面积公式计算即可.本题考查的是勾股定理的应用,根据勾股定理作出三角形的三条边是解题的关键.19.答案:解:(1)如图所示:△A 1B 1C 1,即为所求;(2)如图所示:△A 2B 2C 2,即为所求;(3)A 1(2,3),A 2(−2,−1).解析:(1)直接利用平移的性质得出对应点位置进而得出答案;(2)直接利用轴对称的性质得出对应点位置进而得出答案;(3)利用所画图象得出对应点坐标.此题主要考查了轴对称变换以及平移变换,正确得出对应点位置是解题关键.20.答案:解:当x =0时,y =−23x +5=5,∴点B 的坐标为(0,5);当y =−23x +5=0时,x =152,∴点A 的坐标为(152,0).画出函数图象,如图所示.解析:本题考查了一次函数图象上点的坐标特征以及一次函数的图象,解题的关键是:利用一次函数图象上点的坐标特征求出点A 、B 的坐标.分别将x =0、y =0代入一次函数解析式中求出与之对应的y 、x 的值,由此即可得出点A 、B 的坐标,连点、成线,即可画出一次函数的图象. 21.答案:解:∵BC =1米,NC =43米,BN =53米,∴BC 2=1,NC 2=169,BN 2=259,∴BC2+NC2=BN2,∴AC⊥MC,在直角△ACM中,∵AC=4.5m,MC=6m,∴MA2=AC2+CM2=56.25,∴MA=7.5m.解析:本题考查的是勾股定理及其逆定理的应用,先根据题意判断出AC⊥MC是解答此题的关键.先根据勾股定理的逆定理判断出△BCN的形状,再由勾股定理即可得出结论.22.答案:解:(1)按优惠方案1可得y1=20×4+(x−4)×5=5x+60(x≥4),按优惠方案2可得y2=(5x+20×4)×90%=4.5x+72(x≥4);(2)因为y1−y2=0.5x−12(x≥4),①当y1−y2=0时,得0.5x−12=0,解得x=24,∴当购买24张票时,两种优惠方案付款一样多.②当y1−y2<0时,得0.5x−12<0,解得x<24,∴4≤x<24时,y1<y2,优惠方案1付款较少.③当y1−y2>0时,得0.5x−12>0,解得x>24,当x>24时,y1>y2,优惠方案2付款较少.解析:(1)首先根据优惠方案①:付款总金额=购买成人票金额+除去4人后的学生票金额;优惠方案②:付款总金额=(购买成人票金额+购买学生票金额)×打折率,列出y关于x的函数关系式,(2)根据(1)的函数关系式求出当两种方案付款总金额相等时,购买的票数.再就三种情况讨论.本题考查了一次函数的运用.解决本题的关键是根据题意正确列出两种方案的解析式,进而计算出临界点x的取值,再进一步讨论.23.答案:4 3解析:解:(1)解{y=−x+7y=34x得{x=4y=3,∴点A的坐标为(4,3),故答案为:(4,3);(2)∵A(4,3),∴OA=√32+42=5,当OP=OA=5时,△AOP是等腰三角形,∴P(5,0),当AP=OA=5时,△AOP是等腰三角形,则OP=8,∴P(8,0);当OP=PA时,△AOP是等腰三角形,则点P在OA的垂直平分线上,如图1,设OA的垂直平分线交OA于H,∴OH=12OA=52,过A作AG⊥x轴于G,∴△OPH∽△OAG,∴OHOG =OPOA,∴524=OP5,∴OP=258,∴P(258,0),综上所述,P(5,0)或(8,0)或(258,0);(3)∵P(t,0),∴B(t,34t),C(t,−t+7),∵BC=32OA,∴−t+7−34t=32×5或34t+t−7=32×5,解得:t=−27或t=587,∵t>0,∴t=587.(1)解方程组即可得到结论;(2)根据勾股定理得到OA=√32+42=5,当OP=OA=5时,△AOP是等腰三角形,当AP=OA=5时,△AOP是等腰三角形,当OP=PA时,△AOP是等腰三角形,于是得到结论;(3)由P(t,0),得到B(t,34t),C(t,−t+7),根据BC=32OA,解方程即可得到结论.本题考查了一次函数的综合题,解方程组求点的坐标,等腰三角形的性质,相似三角形的判定和性质,正确的识别图形是解题的关键.。
山西省2019-2020学年第一学期九年级期中质量评估试题·道德与法治(公立)·答案

一、选择题(每小题3分,共36分)题号123456789101112答案A C A B C B D B B B A A二、简答题(共20分)13.(1)①为中华民族谋复兴②人民日益增长的美好生活需要和不平衡不充分的发展之间的矛盾③科技创新④人民代表大会制度⑤1999年⑥坚持爱国和爱党、爱社会主义高度统一(每空1分,共6分)(2)①区域发展不平衡;城镇化水平不高;城乡发展不平衡不协调;等等。
(任答两点即可,每点1分,共2分)②乡村振兴战略、创新驱动发展战略、西部大开发战略,等等。
(任答两个即可,每个1分,共2分)14.(1)中国人民政治协商会议第十三届全国委员会第二次会议和中华人民共和国第十三届全国人民代表大会第二次会议。
(或中国人民政治协商会议和全国人民代表大会)(1分)(2)保障人民的合法权益,激发人民的创造活力;有助于推动经济社会持续健康发展,实现人民安居乐业、社会和谐稳定、国家繁荣昌盛。
(每点1分,共2分)(3)首先,要有社会责任感和主人翁意识;其次,要以理性、公正、客观的态度全面、深刻、辩证地看问题;最后,要立场正确、逻辑清晰地做出“投与不投”“投谁不投谁”的决定,从而在实践中提升自己参与民主生活的能力,提升自己的政治素养。
(每点1分,共3分)15.①该校中学生用自己的零花钱或压岁钱送爱心早餐,弘扬和传承了中华优秀传统美德和伟大中华民族精神,他们这种关爱社会、关爱他人的社会责任感和勤于奉献的优秀品质是我们学习的楷模,我要为他们的行为点赞!②美德的力量在于践行,推进社会公德、职业道德、家庭美德、个人品德建设,我们青少年责无旁贷;倡导向上向善、孝老爱亲、忠于祖国、忠于人民,我们青少年必须身体力行;从小事做起,实现自己的人生价值。
③创造和谐、美好社会人人有责,我们要用自己力所能及的行动营造“我为人人,人人为我”的良好社会风尚等。
(或者从亲社会行为、社会实践能力的培养和锻炼方面表述也可)(任答两点即可,每点1分,共2分)16.选新闻一。
山西省太原市2019-2020学年八年级(上)期中阶段性测评物理试题
2019~2020学年第一学期八年级阶段性测评物理试卷(考试时间:下午4:15-5:45)说明:本试卷为闭卷笔答,答题时间90分钟,满分100分。
题号一二三四五总分得分一、选择题(本大题共10个小题,每小题3分共30分.在每小题给出的四个选项中,只有一项符合题目要求,请将其字母标号填入下表相应的位置)题号12345678910答案1.如图是篮球运动员姚明在恐龙馆参观时的场景。
他旁边恐龙模型的高度最可能是A.1mB.2mC.4mD.10m2.央视综合频道推出了用流行音乐演绎经典诗词、经典文学作品的大型音乐节目——《经典咏流传》.听众能分辨不同乐器发出的声音,是根据声音的A.音色B.音调C.响度D.声速3.下列物体正在做匀速直线运动的是A.刚刚开动的汽车B.在平直轨道上匀速行驶的动车C.被抛到空中又落向地面的石块D.从树上自由下落的苹果4.在如图所示的四种物态变化的实例中,属于凝华现象的是A.冰雪消融B.壶嘴冒“白气”C.草叶上形成“白霜”D.将手烘干5.如图所示,用刻度尺测量长度的操作正确的是6.《乘坐自动扶梯的礼仪规范》中提到:搭乘自动扶梯时“右侧站立,左侧急行“,这不仅是国际大都市的文明规则,也是城市文明程度的象征。
如果以扶梯为参照物,下列说法正确的是A.地而是静止的B.右侧站立的人是运动的C.扶梯是运动的D.左侧急行的人是运动的7.在观察碘的升华现象时,将少量熔点为13.7℃的碘颗粒装入如图的密封锤形玻璃泡内。
为加快碘的升华且防止碘熔化,下列最合适的加热方式是(酒精灯外焰温度约800℃)A.没入开水中加热B.用酒精灯外焰加热C.放入冰水混合物中D.置于常温下的空气中8.入图是小明“探究声音产生原因”的实验,用悬线下的轻质小球紧靠正在发声的音叉,发现小球多次被弹开。
下列说法正确的是A.音又发声是由于小球的跳动产生的B.小球的跳动说明声音能够传递信息C.小球的跳动说明空气能够传声D.用小球的跳动反映音叉的振动9.下列场景与所蕴含物理知识的对应关系正确的是A.春季,农民伯伯用地膜覆盖农田育苗——降低液体温度减慢蒸发B.夏季,手拿着一瓶冰冻矿泉水,冰减少,手感到凉——熔化吸热C.秋季,东北街道的树枝上挂着一层霜——霜是非晶体D.冬季,戴着眼镜从室外走进室内,镜片模糊不清——液化吸热10.甲、乙两同学沿平直路面步行,他们运动的路程随时间变化的规律如图所示。
太原市2019_2020学年第一学期八年级期中考试数学(试卷分析)
2019-2020学年第一学期八年级阶段性测评数学试卷分析一、整卷分析本次考试试题一共分为三大题型,如下表所示:二、逐题分析15勾股定理的应用难216二次根式的运算中1217坐标变换易518勾股定理及逆定理的应用易619一次函数图象上点坐标的特征易520勾股定理的应用中521一次函数的实际应用中522二次根式的化简中923一次函数的综合应用难13三、知识点分析期中考试涉及的知识点思维导图呈现如下:期中考试涉及的各知识点分值分析如下:二次根式的化简11二次根式的运算17第三章位置与坐标5坐标的变换5第四章一次函数34一次函数的表示方法3一次函数图像与性质8一次函数的简单应用10一次函数综合应用13四、重难点及易错点分析本次试卷整体难度适中,易:中:难=6:3:1,重点考查勾股定理的应用,实数的运算和一次函数的应用,其中易错题和难题主要有以下几题:1.选择题10题,考查勾股定理的应用,需要找到一条最短路径,为易错题,学生不易于找到最短路径;2.填空题15题,考查勾股定理的应用的两条线段和的最短问题,并结合了轴对称,学生不易找到对称点,难以作答为难题;3.解答题22题阅读材料题,考查二次根式的化简,材料较长,学生提取信息能力比较薄弱,规定时间内缺乏耐心去分析题目;4.解答题23题点第(1)问坐标的求法中需要用到全等三角形的判定,学生不易想到这一点,第(2)问涉及全等三角形的分类讨论,学生对于全等模型不熟悉,考虑不全面,为难题.五、考后教学建议1.对试卷整体分析,常规试题体现“基础性”,所以建议大家一定要掌握基础知识,训练基本技能,领悟数学基本思想,积累基本活动经验;2.对知识点的考查体现了“综合性”,所以建议学生一定要多角度思考问题,加强数学材料阅读题的训练,培养学生的推理能力;3.对实际应用问题体现了“应用性”,应鼓励学生运用所学知识解决实际问题,要做到学以致用,培养学生的应用意识、创新意识和实践能力;4.总的指导思想“狠抓基础,注重过程,渗透思想,突出能力,强调应用,着重创新”.2019-2020学年第一学期八年级阶段性测试数学试卷解析一、选择题(本题共10个小题,每小题3分,共30分)1.下列实数中的无理数是()A .8B .9C .21-D .327【答案】A【考点】无理数的概念【解析】A .228=,是个无理数B .39=,是有理数C .21-是分数,也是有理数D .3273=,是有理数【难度星级】★2.有理数4的平方根是()A .2B .2±C .2D .2±【答案】D【考点】平方根的概念【解析】∵()422=±∴4的平方根是2±【难度星级】★3.下列各组数中,能作为直角三角形三边长的是()A .2,3,5B .6,8,10C .8,15,17D .1,2,3【答案】C【考点】勾股定理逆定理【解析】∵22217158=+∴8,15,17能作为直角三角形三边长【难度星级】★4.下列计算结果正确的是()A .32-23=B .2312=÷C .()6322=D .()-22-2=【答案】B【考点】二次根式运算【解析】A .222-23=B .2312=÷C .()12322=D .()22-2=∴B 正确【难度星级】★5.已知一次函数b kx y +=(k ,b 为常数)的图象经过平面直角坐标系的第一、二、三象限,则下列结论一定正确的是()A .0>kb B .0<kb C .0->b k D .0<b k +【答案】A【考点】一次函数的图象与性质【解析】∵一次函数的图象经过平面直角坐标系的第一、三象限∴0>k 又∵函数图像经过第二象限∴0>b ∴0>kb 【难度星级】★6.在平面直角坐标系中,已知一次函数5-+=x y 的图象经过()1,3y A -,()22y B ,两点,则1y ,2y 的大小关小关系为()A .21y y <B .21y y >C .21y y =D .无法确定【答案】B【考点】一次函数的图象与性质【解析】∵一次函数表达式中01-<=k ,∴y 随x 的增大而减小∵-3<2,∴21y y >故选B【难度星级】★7.如图,在ABC Rt ∆中,︒=∠90BAC ,以ABC Rt ∆的三边为边分别向外作等边三角形BC A 'Δ,C AB '∆,'ABC ∆,若BC A 'Δ,'ABC ∆的面积分别是10和4,则'ABC ∆的面积是()A .4B .6C .8D .9【答案】B【考点】勾股定理【解析】根据勾股定理可得64-10-'Δ'Δ'===ΔC AB BC A ABC S S S 故选B【难度星级】★8.对于一次函数b kx y +=(k ,b 为常数),下表中给出5组自变量及其对应的函数值,其中只有1个函数值计算有误,则这个错误..的函数值是()x…-10123…y…-214810…A .1B .4C .8D .10【答案】C【考点】一次函数的表示方法【解析】∵由表格中的数据可得,x 每增加1,y 就增加3,∴x 由1增加到2时,y 应该由4增加到7.故C 错误【难度星级】★9.为比较613+与613+的大小,小亮进行了如下分析:作一个直角三角形,使其两直角边的长分别为13与6,则由勾股定理可求得其斜边长为.根据“三角形三边关系”,可得613613++>.小亮的这一做法体现的数学思想是()A .分类讨论思想B .方程思想C .类比思想D .数形结合思想【答案】D【考点】数学思想【解析】∵将二次根式比较大小转化成了“三角形三边关系”∴数形结合思想【难度星级】★10.棱长分别为8cm ,6cm 的两个正方体如图放置,点A ,B ,E 在同一直线上,顶点G 在棱BC 上,点P 是棱11F E 的中点.一只蚂蚁要沿着正方体的表面从点A 爬到点P ,它爬行的最短距离是()A .()cm 1053+B .cm 135C .cm277D .()cm3582+【答案】C【考点】勾股定理的应用【解析】将两个正方体展开,由图可知,沿着左面和上面展开时,路线太长.所以下面只讨论沿着前面和上面、前面和右面两种展开图的路线.①沿着前面和右面展开,得到如下展开图:则展开图中,m EP BE AB AP c 71368''=++=++=,cm PP 6'=,在'ΔAPP Rt 中由勾股定理得:cm PP AP AP 135325617''2222==+=+=.②沿着前面和上面展开,得到如下展开图:则展开图中,m BE AB AE c 4168=+=+=,cm P E EE EP 93611=+=+=,在APE Rt Δ中由勾股定理得:cmPE AE AP 2779142222=+=+=∵cm cm 277135>∴最短距离是cm277【难度星级】★★二、填空题(本大题含5个小题,每小题2分,共10分)把答案写在题中横线上.11.把45化成最简二次根式为.【答案】35【考点】二次根式的化简【解析】45=59=95=35⨯⨯.【难度星级】★12.已知点()6,P m 在一次函数153y x =-+的图象上,则点P 的坐标为.【答案】()6,3【考点】一次函数的图象与性质【解析】因为点P 在一次函数图象上,所以将6x =代入153y x =-+中,解得16533y =-⨯+=,则3m =,P 点的坐标为()6,3.【难度星级】★13.在平整的路面上,某型号汽车紧急刹车后仍将滑行s m,一般地有经验公式2300v s =,其中v 表示刹车前汽车的速度(单位:h km /).一次行驶中汽车紧急刹车后滑行的距离12s m =,则这辆汽车刹车前的速度v =h km /.【答案】60【考点】算术平方根的应用【解析】由题可知,刹车后滑行的距离12s m =,将12s =代入方程2300v s =中可求得60v =±,由于0v ≥,所以60v =,则刹车前的速度60v =h km /.【难度星级】★14.《算法统宗》中有一道“荡秋千”的问题,其译文为:“有一架秋千,当它静止时,踏板上一点A 离地1尺,将它往前推送10尺(水平距离)时,点A 对应的点B 就和某人一样高.若此人的身高为5尺,秋千的绳索始终拉得很直,试问绳索有多长?”根据上述条件,秋千绳索长为_______尺.【答案】292(或14.5)【考点】勾股定理的应用【解析】由题意可得右图所示图形,过点B 作BE OC ⊥于点E由题意可得:OB OA =,10BE =,5BD =,1AC =∴4AE =设OB OA x ==∴4OE x =-在RT OBE ∆中,由勾股定理可得222OB OE BE =+即222(4)10x x -+=化简得:8116x =292x =∴秋千绳索长为292(或14.5)尺.【难度星级】★★15.如图,在ABC ∆中,8AB AC ==,4BC =,AD BC ⊥于点D ,点P 是线段AD 上一个动点,过点P 作PE AB ⊥于点E ,连接PB ,则PB PE +的最小值为___________.【答案】15【考点】等腰三角形的性质,勾股定理及轴对称最值问题【解析】∵AB AC=∴ABC ∆为等腰三角形∵AD BC⊥∴点,B C 关于直线AD 对称∴PB PE PC PE +=+又∵PE AB⊥∴当,P,C E 三点共线且CE AB ⊥时PB PE +最小过点C 作CF AB ⊥于点F ∵AB AC =,AD BC ⊥∴1==22BD DC BC =在Rt ABD ∆中,由勾股定理可得222AD AB BD =-∴215AD =∴1122ABC S AD BC AB ∆=⨯=⨯∴CF =【难度星级】★★★16.计算:(本题含4个小题,每小题3分,共12分)(1)2775-;(2)()2323-;(3)57535÷⎪⎪⎭⎫⎝⎛-;(4)18329871225-+.【考点】二次根式的运算【难度星级】★★【解析】(1)解:2775-=3335-=32(2)解:()2323-=()()223323223+⨯⨯-=36618+-=6621-(3)解:57535÷⎪⎪⎭⎫⎝⎛-=5735535÷-÷=777-=776(4)解:183********—+=222225-+=22317.(本题5分)如图,在平面直角坐标系中,ABC ∆的三个顶点的坐标分别为A (3,-1),B (4,2),C (2,4).(1)请在如图的坐标系中画出ABC ∆;(2)在如图的坐标系中,画出ABC ∆关于y 轴对称的C B A '''∆,并直接写出C B A '''∆三个顶点的坐标.【考点】点坐标的变换【难度星级】★★【解析】(1)如图所示,ABC ∆即为所求.............................................................2分(2)如图所示,C B A '''∆即为所求..........................................................4分C B A '''∆三个顶点坐标:A '(-3,-1),B '(-4,2),C '(-2,4)...........................................................................................................................5分18.(本题6分)在一次综合实践活动中,老师让同学们测量公园里凉亭A ,B 之间的距离(A ,B 之间有水池,无法直接测量),智慧小组的同学们在公园里选了凉亭C ,D ,测得m CD AD 10==,︒=∠90D ,40BC=m ,135BCD=∠︒.请你根据上述数据求出A ,B 之间的距离.【考点】勾股定理的实际应用【难度星级】★【解析】解:连接AC在ACD Rt ∆中,由勾股定理得:m CD AD AC 21022=+=.......................................2分∵︒=∠90D ,CDAD =∴︒=∠=∠45DAC DCA ∵︒=∠+∠=∠135ACB DCA BCD ∴︒=∠-∠=∠90DCA DCB ACB .................................................................................2分在ACB Rt ∆中由勾股定理得:m C AC AB 230B 22=+=..............................................................2分19.(本题5分)如图,已知一次函数321-=x y 的图像与x 轴,y 轴分别交于A ,B 两点,点C (-4,n )在该函数的图像上,连接OC .求点A ,B 的坐标和OAC ∆的面积.【考点】一次函数图像的性质【难度星级】★【解析】解:当0=x 时,3-=y ∴点B 的坐标为(0,-3)............................................................................................2分当0=y 时,0321=-x 解得:6=x ∴点A 的坐标为(6,0)...............................................................................................4分当4-=x 时,()53421-=--⨯=y ∴5-=n∴155621=-⨯⨯=∆OAC S ..........................................................................................5分20.(本题5分)如图,在ABC ∆中,6AC =,8BC =,10AB =.点C 在y 轴的正半轴上,边AB 在x 轴上(点A 在点B 的左侧).(1)求点C 的坐标;(2)点D 是BC 边上一点,点E 是AB 边上一点,且点E 和点C 关于AD 所在直线对称.直接写出点D 的坐标.【考点】勾股定理的应用【难度星级】★★★【解析】(1)在ABC ∆中,∵6AC =,8BC =,10AB =,∴2222226810AC BC AC+=+==∴ACB ∆为直角三角形,且︒=∠90ACB .....................................2分由题意得︒=∠90BOC ∴BC AC OC AB ABC S ⋅=⋅=∆2121∴86211021⨯⨯=⨯⨯OC ∴245OC =又∵点C 在y 轴的正半轴上∴C (0,245).............................................................3分(2)∵点E 和点C 关于AD 所在直线对称,∴6AC AE ==,CD DE=又∵AD AD =∴AED ACD ∆∆≌∴︒=∠=∠90ACD AED ∴︒=∠90BED ,4BE =,设DE CD x ==则8DB x=-在BED Rt ∆中∵222DE BE BD+=∴()22248x x +=-∴3x =在AOC Rt ∆中∵222AO OC AC +=∴518524622=⎪⎭⎫ ⎝⎛-=AO ∴125OE =D (3,512).................................................................5分21.(本题5分)2019年10月1日是中华人民共和国成立70周年纪念日,红色旅游成为旅游热点.小王要和朋友们去某红色景点旅游,其门票为零售价为80元/张.国庆节期间,景点推出优惠活动,方案1:门票一律九折优惠;方案2:对10人以内(含10人)购门票不优惠,超过10人超出部分八折优惠.设小王一行参加旅游的人数为x (人),购买门票费用为y (元).(1)小王分别写出方案1和方案2购买门票的费用y (元)与旅游人数x (人)之间的函数表达式如下,请你将空缺部分补充完整:=1y (x >0);⎩⎨⎧≤=)>()<(10100802x x x y (2)小王一行共有40人一起去该景点旅游,通过计算,请判断选择哪种方案更省钱?【考点】一次函数的应用【难度星级】★★【解析】(1)由题意得:方案1:90801⨯=y %x x 72=(x >0)..................1分方案2:808010802⨯+⨯=y %(10-x )64160x =+(x >10)................2分(2)当40=x 时,288040721=⨯=y (元)..................................3分272016040642=+⨯=y (元)............................................4分∵2880>2720,∴12>y y ,∴方案2更省钱....................................5分22.(本题9分)阅读材料:材料一:两个含有二次根式的非零代数式相乘,如果它们的积不含二次根式,那么这两个代数式互为有理化因式.例如:333=⨯,426)26)(26(=-=+-,我们称3的一个有理化因式是3,26-的一个有理化因式是26+.材料二:如果一个代数式的分母中含有二次根式,通常可将分子、分母同乘分母的有理化因式,使分母中不含根号,这种变形叫做分母有理化.例如:33333131=⨯⨯=,22624)26(8)26)(26()26(8268+=+=+-+=-.请你仿照材料中的方法探索并解决下列问题:(1)13的有理化因式为____________,57+的有理化因式为_____________;(均写出一个即可)(2)将下列各式分母有理化:①153;②35211-;(要求:写出变形过程)(3)请从下列A,B 两题中任选一题作答,我选择________题.A.计算:201920181...431321211++++++++的结果为______________________.B.计算:20192017201720192...7557253352332+++++++的结果为_________________________.【答案】(1)13,57-...................................................................................2分(2)①515151531515153153==⨯⨯=...................................................................4分②35211)352(11)352)(352()352(1135211+=+=+-+=-....................................6分(3)A.12019- B.201920191-...........................................9分【考点】二次根式化简【难度星级】★★★【解析】(1)∵131313=⨯,∴13的有理化因式为13.∵257)57)(57(=-=-+,∴57+的有理化因式为57-.(2)①515151531515153153==⨯⨯=②35211)352(11)352)(352()352(1135211+=+=+-+=-(3)A.201920181...431321211++++++++...)43)(43(43)32)(32(32)21)(21(21+-+-+-+-+-+-=)20192018)(20192018(20192018-+-+120192018...143132121--++--+--+--=120192018...433221--++-+-+-=120191--=12019-=B.20192017201720192...7557253352332+++++++...)7557)(7557()7557(2)5335)(5335()5335(2)33)(33()33(2+-+-+-+-+-+-=)2019201720172019)(2019201720172019(2019201720172019(2-+-+201920172019201720172019357557155335333⨯-+-+-+-=2019201920172017...77555533331-+-+-+-=201920191-=23.(本题13分)如图1,已知直线33+=x y 与y 轴,x 轴分别交于A ,B 两点,过点B 在第二象限内作AB BC ⊥且AB BC =,连接AC .(1)求点C 的坐标;(2)如图2,过点C 作直线x CD ∥轴交AB 于D ,交y 轴于点E .请从下列A ,B 两题中任选一题作答,我选择_____题.A.①求线段CD 的长;②在坐标平面内,是否存在点M (除点B 外),使得以点M ,C ,D 为顶点的三角形与BCD ∆全等?若存在,请直接写出所有符合条件的点M 的坐标;若不存在,请说明理由.B.①如图3,在图2的基础上,过点D 作AC DF ⊥于点F ,求线段DF 的长;②在坐标平面内,是否存在点M (除点F 外),使得以点M ,C ,D 为顶点的三角形与FCD ∆全等?若存在,请直接写出所有符合条件的点M 的坐标;若不存在,请说明理由.【答案】(1))1,4(-C(2)A.①310=CD ②存在,)2,1(1-M 或)2,311(2-M 或)0,311(3-M B.①352=DF ②存在,)37,310(1-M 或,(313102--M 或,(31343--M 【考点】一次函数的综合应用.【难度星级】★★★★★【解析】解:(1)过点C 作轴x CP ⊥,交x 轴于点P ........................................................................1分∵轴x CP ⊥,ABBC ⊥∴90=∠CPB , 90=∠ABC ∴ 90=∠+∠BCP CBP , 90=∠+∠ABO CBP ∴ABO BCP ∠=∠.....................................................................2分由题可知90=∠AOB ∴AOBCPB ∠=∠在BCP ∆与ABO ∆中,⎪⎩⎪⎨⎧=∠=∠∠=∠AB BC AOB BPC ABO BCP ∴BCP ∆≌()AAS ABO ∆.........................................................................................................3分∴AO BP =,OBCP =当0=x 时,3303=+⨯=y ∴A (0,3)...............................................................................................................................4分当0=y 时,033=+x 解得1-=x ∴B (-1,0)...................................................................................................5分∴3=AO ,1=BO ∴1=CP ,3=BP ∴4=+=OB BP OP ∴)1,4(-C ...................................................................................................................................6分(2)A. ∵x CD //轴∴点C ,点D 的纵坐标相同∴当1=y 时,133=+x 解得32-=x (7)分∴)1,32(-D ∵)1,4(-C ∴310)4(32=---=CD .........................................................................................................9分②存在........................................................................................................................................10分∵点B 与1M 关于CD 对称,)0,1(-B ,点C ,点D 的纵坐标为1∴)2,1(1-M 作CD 的中垂线与x 轴交于点G∵点B 与3M 关于CD 的中垂线372324-=⎪⎭⎫ ⎝⎛-+-=x 对称∴343713=+-==BG G M ∴311373433=+=+=OG G M O M ∴)0,311(3-M ∵3M 与2M 关于CD 对称∴)2,311(2-M ∴)2,1(1-M 或)2,311(2-M 或)0,311(3-M ......................................................................13分B.①∵()()⎪⎭⎫ ⎝⎛--1,32,1,4,3,0D C A ∴2=AE ,4=CE ,310=CD 在ACE Rt ∆中,由勾股定理得52422222=+=+=CE AE AC ...............................................................................7分在ACD ∆中,由DF AC AE CD ⋅=⋅2121得DF ⨯⨯=⨯⨯5221231021∴352=DF ...................................................9分②存在....................................................10分过点F 作CD FQ ⊥交CD 于点Q∵AC AB =,BCAB ⊥∴ 45=∠CAB ∵ACDF ⊥∴352==DF AF ∴35435252=-=FC 在CDF ∆中,由FD CF FQ CD ⋅=⋅⋅2121得352354310⨯=⨯FQ ∴34=FQ 在FDQ Rt ∆中,由勾股定理得:32343522222=-=-=)()(FQ DF DQ ∴343232=+=QE ∴,(3734-F ∵点F 与1M 关于CD 的中垂线372324-=⎪⎭⎫ ⎝⎛-+-=x 对称∴37,310(1-M ∵1M 与2M ,点F 与3M 关于CD 对称∴),(313102--M 、),(31343--M ∴符合条件的M 点的坐标为)37,310(1-M 或),(313102--M 或),(31343--M ............13分。
山西省2019-2020学年第一学期七年级期中质量评估试题·生物(苏教版)·试题

七年级生物 (苏教版) 第 1 页 (共 6 页)
5. 下图是光学显微镜的一些镜头,其中譹 訛譺 訛譻 訛是目镜镜头,譼 訛譽 訛譾 訛是物镜镜头,下列镜头 组合中,观察到的细胞数量最多的是
譹訛
譺訛
譻訛
譼訛
譽訛
譾訛
A. 譹訛和譼 訛
B. 譹 訛和譾訛
ห้องสมุดไป่ตู้
譻 訛
幼苗,这个过程与细胞的
、
譹 訛
和
过程有关。
(2)番茄属于绿色开花植物,因此它具有
譼 訛
譺訛
大器官。图中属于番茄营养器官的是[ ]、
[ ]和譽訛。其中譽訛能从土壤中吸收
譽 訛
和
。
(3)譺訛在结构层次上属于
。当我们做糖拌西红柿时,需要将它的表皮去掉,这
是因为表皮属于
组织,具有
作用,不易咀嚼。将去皮的番茄放在
观察到白亮的视野。
譾訛
(2)他将写有字母“b”的载玻片放在载物台上,用压片夹压
住后,先转动粗准焦螺旋使镜筒缓缓下降,这时他的眼睛要注视
,以防
压碎载玻片。然后反向转动粗准焦螺旋使镜筒上升,他通过目镜观察的正确方法
七年级生物 (苏教版) 第 4 页 (共 6 页)
应是下图中的
。
目 镜
A
目 镜
B
目 镜
C
七年级生物 (苏教版) 第 5 页 (共 6 页)
沙漠等地区。在 1787 年,有一个叫飞利浦的船长带了一些仙人掌到澳大利亚种植,
由于澳大利亚的自然环境非常适合仙人掌的生长,而且没有天敌的存在,仙人掌便
在澳大利亚快速地蔓延开来,严重地影响其他生物的生长,成为当地的一大灾难,后
山西省2019-2020学年第一学期八年级期中质量评估试题·语文·试题+答案

记得有一年,我拾麦子的成绩也许是有点“超常”。 到了中秋节母亲不知从哪里弄了 点月饼,给我掰了一块,我就蹲在一块石头旁边,大吃起来。 在当时,对我来说,月饼可真 是神奇的好东西,龙肝凤髓也难以比得上的,我难得吃上一次。 我当时并没有注意,母亲 是否也在吃。 现在回想起来,她根本一口也没有吃。 不但是月饼,连其他“白的”,母亲从来 都没有尝过,都留给我吃了。她大概是毕生就与红色的高粱饼子为伍。到了灾年,连这个也 吃不上,那就只有吃野菜了。
6. 请为这则新闻拟写一个标题。
(3 分)
7. 上面图片是记者抓拍的比赛时杨丽射门瞬间的照片,请你根据以下材料用新闻特写的
手法将图片内容描写出来。
(10 分)
写作提示:①描写生动形象,有感染力;②至少使用两种修辞;③不少于 100 字。
材料:所谓特写,本是摄影、电视、电影的一种常用手法,指拍摄人或物的某一部
界军人运动会女子足球比赛 17 日在这里开赛。 在对阵韩国
队的比赛中,中国女队凭借整体实力优势以 3∶0 赢得开门红。
开场不到 7 分钟, 中国队的杨丽便踢进首粒进球。 第
52 分钟,杨丽在队友的配合下再进一球。 补时阶段,中国队
获得点球机会,张睿点球补射入网。 最终,中国队以 3∶0 取胜。
中国女队主教练赵争春赛后表示, 本场比赛中国队正
二、读·思(38 分)
(一)
“学而时习之”是一种很好的学习方法。 学习了三个单元后,老师为了让同学们熟练
太原市2019_2020学年第一学期八年级期中考试数学(解析)

C.y1=y2
D.无法确定
7. 如图,在 Rt△ABC 中,∠BAC=90°,以 Rt△ABC 的三边为边分别向外作等边三角形 ABC , ABC ,
ABC ,若 ABC , ABC 的面积分别是 10 和 4,则 ABC 的面积是( )。
A.4
B.6
C.8
【考点】勾股树 【难度星级】★ 【答案】B
不优惠,超过 10 人超出部分八折优惠.设小王一行参加旅游的人数为 x
(人),购买门票费用为 y(元).
(1)小王分别写出方案 1 和方案 2 购买门票的费用 y(元)与旅游人数 x(人)之间的函数表达式如下,
请你将空缺部分补充完整:
y1=
(x>0);
y2=
80
x(0
x
10) (x
10)
(2)小王一行共有 40 人一起去该景点旅游,通过计算,判断选择哪种方案更省钱?
-6 -
19. (本题 5 分) 如图,已知一次函数 y 1 x 3 的图象与 x 轴,y 轴分别交于 A,B 两点.点 C(4 ,n) 在该函数的图象上, 2 连接 OC.求点 A,的坐标和△OAC 的面积.
【考点】一次函数与面积 【难度星级】★ 【答案】见解析 【解析】令 x=0,的 y=-3∴B(0,-3)
【考点】一次函数的应用 【难度星级】★★ 【答案】(1)72x; 64x+160
(2)当 x=40 时,y1=72×40=2880 当 x=40 时,y2=64×40+160=2620 ∵2880>2620 故方案 2 更合算
-8 -
22. (本题 9 分) 阅读材料: 材料一:两个含有二次根式的非零代数式相乘,如果它们的积不含二次根式,那么这两个代数式 互为有理化因式. 例 如 : 3 3 3,( 6 2)( 6 2) 6 2 4 , 我 们 称 3 的 一 个 有 理 化因 式 是 3 ,
太原市2019_2020学年第一学期八年级期中考试数学(试卷)

板上有一点 A 离地 1 尺,将它往前推算 10 尺(水平距离)时,点 A 对应的点 B 就和
某人一样高.若此人的身高为 5 尺,秋千的绳索始终拉得很直,试问绳索有多长?”根
据上述条件,秋千绳索长为
尺.
15. 如图,在△ABC 中,AB=AC=8,BC=4,AD⊥BC 于点 D,点 P 是线段 AD 上一个动点,过点 P 作点
(人),购买门票费用为 y(元).
(1)小王分别写出方案 1 和方案 2 购买门票的费用 y(元)与旅游人数 x(人)之间的函数表达式如下,
请你将空缺部分补充完整:
y1=
(x>0);
y2=
80
x(0
x
10) (x
10)
(2)小王一行共有 40 人一起去该景点旅游,通过计算,判断选择哪种方案更省钱?
2019~2020 学年度第一学期八年级阶段性测评
数学试卷
一、选择题(本大题共 10 个小题,每小题 3 分,共 30 分)在每小题给出的四个选项中,只有一项是符合
题目要求,请将其字母序号填入下表相应位置)
题号 1
2
3
4
5
6
7
8
9
10
答案
1. 下列实数中的无理数是( )
A. 8
B. 9
C. 1 2
21. (本题 5 分)
2019 年 10 月 1 日式中华人民共和国成立 70 周年纪念日,红色旅游成
为旅游热点.小王要和朋友们去某红色景点旅游,其门票零售价为 80
元/张.国庆节期间,景点推出优惠活动,
方案 1:门票一律九折优惠;方案 2:对 10 人以内(含 10 人)购门票
不优惠,超过 10 人超出部分八折优惠.设小王一行参加旅游的人数为 x
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
;
最后将 A 组馒头片烤干。
(2)通过 A 与 B 的对照实验,小明想探究的问题是:
?
(3)A 与 B 的对照实验中,实验变量是
;分析实验结果,小明得出的结论是:
。
(4)为了探究温度对霉菌生活的影响,小明设计的 C 组实验与
组实验形成对
照,C 组中①、②的条件依次是
、
;预期实验结果③是:
。
(5)通过小明的实验,请你说出一种防止食品发霉的方法:
类飞行无关的特征是
A. 身体大多呈流线型
B. 体表被羽毛
C. 前肢变成翼
D. 鸟卵具有坚硬的卵壳
11. 丰富多彩的生物世界中有一种神奇的微生物,它的结构非常简单,只由蛋白质外壳和
内部的遗传物质组成,没有细胞结构。从生物分类角度来说,它属于
A. 病毒
B. 真菌
C. 细菌
%%%%%%D. 植物
八年级生物 (苏教版) 第 2 页 (共 8 页)
15. 袁隆平和李振声院士分别是水稻和小麦遗传育种学家,他们的科研成果大大提高了
我国水稻和小麦的产量。在分类学上,水稻和小麦同科不同属,水稻和大豆同门不同
纲。下列说法正确的是
A. 生物分类单位中最小的分类单位是科
B. 水稻和大豆的亲缘关系比与小麦近
C. 水稻和小麦的共同特征比与大豆的多
D. 小麦和大豆之间没有共同特征
。
八年级生物 (苏教版) 第 8 页 (共 8 页)
山西省 2019-2020 学年第一学期八年级期中质量评估试题
生物(苏教版)参考答案和评分标准
一、选择题(每小题 2 分,共 40 分)
题 号 1 2 3 4 5 6 7 8 9 10 选项 A D A C A C B B D D 题 号 11 12 13 14 15 16 17 18 19 20 选项 A B B C C C C D D D
B. 利用乳酸菌制作醋
C. 肺炎是由肺炎双球菌引起的
D. 肺结核是由结核杆菌引起的
14. 下列有关如图所示四种生物的叙述,错误的是 ··
甲
乙
丙
丁
A. 甲是细菌,与其他三种生物的细胞结构不同
B. 乙是青霉,细胞具有细胞壁、细胞膜、细胞质、细胞核等结构
C. 丙是蘑菇,能自己制造有机物
D. 丁是酵母菌,是单细胞真菌
环境 未污染区 污染区
实验 放出数量(只) 重新捕回数量(只)
重捕率 放出数量(只) 重新捕回数量(只)
重捕率
灰色桦尺蛾 496 62
12.5% 201 32
15.9%
黑色桦尺蛾 473 30 6.3% 601 205
34.1%
对不同地区两种桦尺蛾重捕率差异的最好解释是
A. 未污染区黑色桦尺蛾的数量多于灰色桦尺蛾的数量
哺育幼体。
(4)D 的幼体与 E 都生活在水中,用
呼吸,但 D 可以在陆地上生活,主要用
呼吸,同时
也具有辅助呼吸的作用。
(5)动物界中种类最多、数量最大、分布最广的是
动物,如图中的
(用
字母表示)。
(6)上述动物中,体温恒定的是
(用字母表示)。
22.(16 分)科学家根据亲缘关系的远近,用生物“进化树”(如图)表示生物进化的主要历
,植株比较矮小;③表示
植物,也生活在阴湿的环境,但体内具
有
组织,能较好地适应陆地生活。
(4)④和⑤表示种子植物的两大类,④表示
植物,种子裸露没有果皮包被,
常见的植物有
(举一例即可)等;⑤表示
植物,能适应各种生活
环境。
(5)图中左侧表示动物进化的大致历程,由图可知鸟类和⑦
动物都是由古代
的⑥
动物进化而来的。
珙桐在分类上属于
A. 苔藓植物
%%%%B. 蕨类植物
C. 裸子植物
%%%%D. 被子植物
3. 小明家附近两年前建了一个化工厂,最近他发现,原来生活在阴湿环境中的一些像绿
“地毯”的ห้องสมุดไป่ตู้物消失了,这些消失的植物类群最可能是
A. 苔藓植物
%%%%%%%%%%%%%%%%%%%%%%%%%%%%B. 藻类植物
图1
%%%图 2
%%%%图 3
(1)藏羚羊、中华白海豚和“小鸟天堂”的小鸟们体内都有脊柱, 因此在分类上属于
动物;其中藏羚羊和
的亲缘关系较近,都属于
动物。
(2)除资料中提到的国家一级保护动物外,请再举两例:
、
。
(3)导致藏羚羊濒临灭绝边缘的主要原因是
;中华白海豚数量急剧减少的原
因有
、
等。
(4)栖息在“小鸟天堂”的鸟类多达 40 多种,这体现了生物多样性中的
多
样性。
(5)青 藏 铁 路 、深 湛 铁 路 和 港 珠 澳 大 桥 的 设 计 和 建 造 都 体 现 了 人 与 自 然 和 谐 共 处
的生态理念。请你列举出保护生物多样性的措施(至少答出三种):
;
;
。
八年级生物 (苏教版) 第 7 页 (共 8 页)
24.(14 分)在温暖潮湿的环境中,馒头上可能长出霉菌。根据这一现象,小明设计实验探 究霉菌生活的环境。他的实验过程如下,请分析实验并回答:
八年级生物 (苏教版) 第 1 页 (共 8 页)
5. 近年来,随着生态文明的建设,在渤海、黄海等海水中发现了“桃花鱼”(如下图)。通过
研究发现, “桃花鱼”的身体中央有消化腔,有口无肛门。
下列动物中与“桃花鱼”亲缘关系最近的是
A. 水螅
B. 涡虫
C. 蛔虫
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%D. 沙蚕
16. 每年 5 月 22 日是“国际生物多样性日”。下列有关生物多样性的叙述正确的是
A. 生物多样性就是遗传多样性
B. 生物多样性包括环境多样性
C. 物种多样性是由遗传物质的多样性决定的
D. 生态系统多样性指生物种类的丰富程度
八年级生物 (苏教版) 第 3 页 (共 8 页)
17. 绘画艺术家常常以各种动物作为绘画素材,如齐白石的《虾》寓意淡泊明志;宋守友的
6. 下列各项中,属于扁形动物特征的是
①消化道有口无肛门 ②身体由许多体节组成 ③身体扁平 ④没有呼吸系统 ⑤具有
外骨骼
A. ①②③
B. ②④⑤
%%C. ①③④
D. ①③⑤
7. 下列关于动物的叙述中,正确的是
A. 软体动物都可以食用
B. 线形动物有口有肛门
C. 环节动物都生活在土壤中
%%D. 节肢动物都具有贝壳
二、非选择题(共 60 分) 21.(除标注外,每空 1 分,共 15 分) (1)软体 乌贼(或章鱼、鲍、泥螺、牡蛎、文蛤、蛤蜊、蛏等) B、F(答对一个给 1 分,2 分) (2)环节 疏松土壤(或提高土壤肥力、生产优良的蛋白质饲料、净化环境等,2 分) (3)哺乳 乳汁 (4)鳃 肺 皮肤 (5)节肢(或昆虫) F (6)C 22.(除标注外,每空 1 分,共 16 分) (1)原始海洋 (2)多细胞藻类(或藻类) 水 (3)苔藓 根 蕨类 输导 (4)裸子 杉(或柏、松、苏铁等) 被子 (5)哺乳 爬行 (6)水生到陆生(2 分) 简单到复杂(2 分) 八年级生物 (苏教版) 答案 第 1 页 (共 2 页)
B. 原始的大气成分和现在的大气成分是相同的
C. 米勒模拟原始地球环境进行实验,产生了原始的生命
D. 原始生命是地球上生物的共同祖先
19. 英国的曼彻斯特地区生活着灰色和黑色两种桦尺蛾,都喜欢栖息于树干上,它们是由
一种桦尺蛾发展而来的。科学家在相同时间内,采用同样的方法,对未污染区和污染
区的两种桦尺蛾进行放出和重新捕回的实验,结果如下表:
(6)从进化树可以看出生物进化的总体趋势是:生活环境由
,结构由
,
分类地位由低等到高等。
23.(15 分)阅读资料,根据资料内容分析回答下列问题:
资料一:藏羚羊(图 1)是我国青藏高原特有的动物,是国家一级保护动物。由于它的
八年级生物 (苏教版) 第 6 页 (共 8 页)
羊绒比金子还贵重,因而遭到疯狂的偷猎。到 20 世纪 90 年代,藏羚羊已濒临灭绝的 边缘。经过保护,藏羚羊的数目已有回升。2001 年青藏铁路开工建设,在施工过程中 采取了严禁惊扰藏羚羊的措施,为藏羚羊迁徙设置了专门的通道。经过一段时间的适 应期,藏羚羊已逐渐适应了青藏铁路的存在。 资料二:2018 年 7 月 1 日,深湛铁路(图 2)开通运营,这条高铁被称为“最温柔的高 铁”。深湛铁路江茂段穿越著名景区“小鸟天堂”,铁路部门耗资 1.87 亿元,建造全封 闭声音屏障,让时速 200 千米的深湛铁路江茂段列车以“静音模式”通过“小鸟天堂”, 使小鸟与铁路和谐共处。 资料三:2018 年 10 月 24 日港珠澳大桥(图 3)开始通车,大桥穿越中华白海豚自然保 护海域约 29 平方公里。中华白海豚属于国家一级保护动物,由于鱼类等食饵减少,加 之航行的船只增多,水域污染以及误捕等原因,其数量急剧减少。在建造港珠澳大桥 的过程中采用各种措施,使其对中华白海豚的影响降到最低。
组别
A
B
C
处理方法
将烤干的馒头片置 将湿润的馒头片置 将①的馒头片置于 于 25 ℃温暖环境里 于 25 ℃温暖环境里 ②环境里
3 天后实验结果
不发霉
发霉
③
(1)实验前,小明先将新鲜的馒头片分成
(选填“不等量的”或“等量的”)A、B、
C 三组;然后将馒头片置于高压蒸锅内隔水蒸 30 分钟,这样处理的目的是
动物,此类动物分布广泛,
如海洋中的
(举一例即可);根据体内有无脊柱将上述动物分成两组,其中
与 A 同组的有 ______(用字母表示)。
