北航研究生算法答案
北航研究生算法(208精心整理)

一:判断题1、一个正确的算法,对于每个合法输入,都会在有限的时间内输出一个满足要求的结果。
(对)2、NP完全问题比其他所有NP问题都要难。
(错)3、回溯法用深度优先法或广度优先法搜索状态空间树。
(错,仅深度优先)4、在动态规划中,各个阶段所确定的策略就构成一个策略序列,通常称为一个决策。
(错)5、P类和NP类问题的关系用P⊂NP来表示是错误的。
(错)6、若近似算法A求解某极小化问题一实例的解为Sa,且已知该问题的最优解为Sa/3,则该近似算法的性能比为3。
(错)7、通常来说,算法的最坏情况的时间复杂行比平均情况的时间复杂性容易计算。
(对)8、若P2多项式时间转化为(polynomial transforms to)P1,则P2至少与P1一样难。
(错)9、快速排序算法的平均时间复杂度是O(nlogn),使用随机化快速排序算法可以将平均时间复杂度降得更低。
(错)10、基于比较的寻找数组A[1,…,n]中最大元素的问题下届是Ω(n/3)。
(错)11、O(f(n))+O(g(n))=O(min{f(n),g(n)})(错)12、若f(n)=Ω(g(n)),g(n)=Ω(h(n)),则f(n)=Ω(h(n))(对)13、若f(n)=O(g(n)),则g(n)=Ω(f(n))(对)14、贪婪技术所做的每一步选择所产生的部分解,不一定是可行性的。
(错)15、LasVegas算法只要给出解就是正确的。
(对)16、一个完全多项式近似方案是一个近似方案{Aε},其中每一个算法Aε在输入实例I的规模的多项式时间内运行。
(错)二:简答1、二叉查找树属于减治策略的三个变种中的哪一个的应用?什么情况下二叉查找树表现出最差的效率?此时的查找和插入算法的复杂性如何?答:减治策略有3个主要的变种,包括减常量、减常数因子和减可变规模。
(1) 二叉查找树属于减可变规模变种的应用。
(2) 当先后插入的关键字有序时,构成的二叉查找树蜕变为单支树,树的深度等于n,此时二叉查找树表现出最差的效率,(3) 查找和插入算法的时间效率都属于Θ(n)。
北航16秋(算法与数据结构)作业3答案100分

北航《算法与数据结构》在线作业三一、单选题(共25 道试题,共100 分。
)1. 对下面四个序列用快速排序的方法进行排序,以序列的第一个元素为基础进行划分。
在第一趟划分过程中,元素移动次数最多的序列是()。
A. 82,75,70,16,10,90,68,23B. 23,10,16,70,82,75,68,90C. 70,75,68,23,10,16,90,82D. 70,75,82,90,23,16,10,68正确答案:D2. 设一数列的顺序为1,2,3,4,5,6,通过栈结构不可能排成的顺序数列为()。
A. 3,2,5,6,4,1B. 1,5,4,6,2,3C. 2,4,3,5,1,6D. 4,5,3,6,2,1正确答案:B3. 线性表是一个具有n个()的有限序列。
A. 表元素B. 字符C. 数据元素D. 数据项正确答案:C4. 链表不具有的特点是()。
A. 不必事先估计存储空间B. 可随机访问任一元素C. 插入删除不需要移动元素D. 所需空间与线性表长度成正比正确答案:B5. 对于线性表基本运算,以下结果是正确的是A. 初始化INITIATE(L),引用型运算,其作用是建立一个空表L=ФB. 求表长LENGTH(L),引用型运算,其结果是线性表L的长度C. 读表元GET(L,i), 引用型运算。
若1<=i<=LENGTH(L),其结果是线性表L的第i个结点;否则,结果为0D. 定位LOCATE(L,X), 引用型运算.若L中存在一个或多个值与X相等的结点,运算结果为这些结点的序号的最大值;否则运算结果为0正确答案:B6. 队列的插入操作是在()进行。
A. 队首B. 队尾C. 队前D. 队后正确答案:B7. 下列有关图遍历的说法中不正确的是()。
A. 连通图的深度优先搜索是个递增过程B. 图的广度优先搜索中邻接点的寻找具有“先进先出”的特征C. 非连通图不能用深度优先搜索法D. 图的遍历要求每个顶点仅被访问一次正确答案:C8. 若由森林转化得到的二叉树是非空的二叉树,则二叉树形状是()。
北航14秋《算法与数据结构》在线作业一答案

、单选题(共1. 若给定的关键字集合为A. 10B. 10C. 10D. 152.A.B.C.D.3.A. O(logB. O(n)C. O(1)D. O(nlog4.A.B.C.D. 图状结构满分:4 分得分:45. 一组记录的排序码为(46,79,56,38,40,84),则利用堆排序的方法建立的初始堆为()。
A. 79,46,56,38,40,80B. 84,79,46,38,40,56C. 84,79,56,46,40,38D. 84,56,79,40,46,38满分:4 分得分:46. 在一个顺序队列中,队首指针指向队首元素的()位置。
A. 后一个B. 前一个C. 当前D. 不确定满分:4 分得分:47. 计算机的算法必须具备输入,输出和()五个特性。
A. 可行性,可移植性和可扩充性B. 可行性,确定性和有穷性C. 确定性,有穷性和稳定性D. 易读性,稳定性和安全性满分:4 分得分:48. 下列关于栈的叙述正确的是()。
A. 栈是非线性结构B. 栈是一种树状结构C. 栈具有先进先出的特征D. 栈具有后进先出的特征满分:4 分得分:49. 在含n个顶点和e条边的无向图的邻接矩阵中,零元素的个数为()。
A. eB. 2eC. n的平方-eD. n的平方-2e满分:4 分得分:410. 以下二叉树说法错误的是A. 完全二叉树上结点之间的父子关系可由它们编号之间的关系来表达B. 在三叉链表上,二叉树的求双亲运算很容易实现C. 在二叉链表上,求根,求左、右孩子等很容易实现D. 在二叉链表上,求双亲运算的时间性能很好满分:4 分得分:411. 在一棵二叉树中,第4层上的结点数最多为()。
A. 8B. 15C. 16D. 31满分:4 分得分:412. 非空的循环单链表head的尾节点(由p所指向)满足()。
A. p->next=NULLB. p=NULLC. p->next=headD. p=head满分:4 分得分:413. 强连通分量是()极大连通子图。
北航计算机研究生课程_算法设计与分析__Assignment_1

一、解:设第k月的需求量为Nk(k=1,2,3,4)状态变量Xk:第k月初的库存量,X1=X5=0,0≤Xk≤Nk+…+N4决策变量Uk:第k月的生产量,max{0,Nk-Xk}≤Uk≤min{6,Nk+…+N4 - Xk}状态转移方程:X k+1 = Uk + Xk – Nk第k月的成本Vk = 0.5*(Xk - Nk) Uk=03 + Uk + 0.5*(Uk + Xk - Nk) Uk≠0设F k(Xk)是由第k月初的库存量Xk开始到第4月份结束这段时间的最优成本则F k(Xk) = min{Vk + F k+1(X k+1)} 1≤k≤4= min{ 3 + Uk + 0.5*(Uk + Xk - Nk) + F k+1(Uk + Xk - Nk) } Uk≠0min{ 0.5*(Xk - Nk) + F k+1(Xk - Nk) } Uk=0 F5(X5)=0四个月内的最优成本为F1(X1)=F1(0)详细计算步骤如下:(1)k=4时4(2)k=3时(3)k=2时(4)k=1时由以上计算可得,4个月的总最优成本为F1(0) = 20.5(千元)二、解:1、变量设定阶段k:已遍历过k个结点,k=1,2…6,7。
K=1表示刚从V1出发,k=7表示已回到起点V1状态变量Xk=(i,Sk):已遍历k个结点,当前位于i结点,还未遍历的结点集合为Sk。
则X1=(1,{2,3,4,5,6}),X6=(i,Φ),X7=(1,Φ)决策变量Uk=(i,j):已遍历k个结点,当前位于i结点,下一个结点选择j。
状态转移方程:X k+1 = T(Xk,Uk) = (j,Sk-{j})第k阶段的指标函数Vk = D[i,j]。
最优指标函数Fk(Xk) = Fk(i,Sk):已遍历k个结点,当前从i结点出发,访问Sk中的结点一次且仅一次,最后返回起点V1的最短距离。
则Fk(i,Sk) = min{ D[i,j] + F k+1(j,Sk-{j}) } 1≤k≤6F7(X7) = F7(1,Φ) = 02、分析:(1)k=6时,F6(i,Φ) = min{D[i,1] + F7(X7)} = D[i,1] i=2,3,4,5,63、伪代码和时间复杂度为方便计算,结点编号改为0到5.(1)用一张二维表格F[][]表示F(i,Sk),行数是n,列数是2n-1。
北航计算机研究生课程算法设计与分析HomeWork_1

一、已知下列递推式:C(n) = 1 若n =1= 2C (n/2) + n – 1 若n ≥ 2请由定理1 导出C(n)的非递归表达式并指出其渐进复杂性。
定理1:设a,c 为非负整数,b,d,x 为非负常数,并对于某个非负整数k, 令n=c k ,则以下递推式f(n) =d 若 n=1=af(n/c)+bn x 若 n>=2的解是f(n)= bnx log c n + dn x 若 a=c x f(n)= x x x ax xn c a bc n c a bc d c log 若 a ≠c x解:令F(n) = C(n) – 1则 F(n) = 0 n=1F(n) = 2C(n/2) + n – 2 n>=2= 2[F(n/2) + 1] + n – 2= 2F(n/2) + n利用定理1,其中:d=0,a=2,c=2,b=1,x=1,并且a=cx 所以 F(n) = nlog 2n所以 C(n) = F(n) + 1 = nlog 2n + 1C(n)的渐进复杂性是O(nlog 2n)二、由于Prim 算法和Kruskal 算法设计思路的不同,导致了其对不同问题实例的效率对比关系的不同。
请简要论述:1、如何将两种算法集成,以适应问题的不同实例输入;2、你如何评价这一集成的意义?答:1、Prim 算法基于顶点进行搜索,所以适合顶点少边多的情况。
Kruskal 从边集合中进行搜索,所以适合边少的情况。
根据输入的图中的顶点和边的情况,边少的选用kruskal 算法,顶点少的选用prim 算法2、没有一个算法是万能的,没有一个算法是对所有情况都适合的。
这一集成体现了针对具体问题选用最适合的方法,即具体问题具体分析的哲学思想。
三、分析以下生成排列算法的正确性和时间效率:HeapPermute (n)//实现生成排列的Heap 算法//输入:一个正正整数n和一个全局数组A[1..n]//输出:A中元素的全排列if n = 1write Aelsefor i ←1 to n doHeapPermute(n-1)if n is oddswap A[1]and A[n]else s wap A[i]and A[n]解:n=1时,输出a1n=2时,输出a1a2,a2a1n=3时,(1)第一次循环i=1时,HeapPermute(2)将a1a2做完全排列输出,记为[a1a2]a3,并将A变为a2a1a3,并交换1,3位,得a3a1a2(2)第二次循环i=2时,HeapPermute(2)输出[a3a1]a2,并将A变为a1a3a2,交换1,3位,得a2a3a1(3)第三次循环i=3时,HeapPermute(2)输出[a2a3]a1,并将A变为a3a2a1,交换1,3位,得a1a2a3,即全部输出完毕后数组A回到初始顺序。
北航991真题答案

一.单项选择题1 选C 前三步操作相同,主要看第四步,先分析前三步做了什么,一二的操作是修改p的前后节点,而p是需要插入的节点,所以还要修改的是q和原本q的后面一个节点2 选D,队列为空的情况3 选A,排除带括号的,括号外的为x4 选D,8层的完全二叉树,第7层为2^6个节点,64个节点,非叶节点为54个,第8层为108个节点,前7层为2^7-1个,127个,共127+108=235,一个有几种情况?3种,7层的完全二叉树,一种234,快速方法,不用计算,因为肯定多于70多,又必是奇数5 选B,送分题6 选D,连通可能有回路,一般无向图不讨论拓扑排序7 选A 0 99中进行查找49,24,11,5,2,0算出了六次,一共七次,用满二叉树来计算,一个6层的满二叉树为63个元素,7层的是127个元素8 选C9 选D,插入排序是不是?10 选A,倒数第二个找到之后,最后一个数不需要进行排序二简答题1 见笔记本2 递归调用自身的,堆栈3 初始点,遍历方法,边的顺序4 不细讲,算一下,选择排序是10000 + ···+9991,快速排序差不多为n*Logn,即10000*log10000,堆是log10000三综合题1 ABCFED | ABFCED从A开始,没有指向A的边,把图画出来即可2 先从层序开始,根节点为A,在中序中C为A的左子树序列,DFBE是右子树序列。
再看A的左子树DFBE在层序中B为第一个,所以B为子树的根节点,再回到中序,DF 在B的前面,所以为左子树,E为右子树。
再分析子树DF,DF在层序中D为第一个,所以D为根节点,而中序中F在D的右边所以F为D的右孩子3 17填在位置5,27填在位置04 求数组的最大值,可以写得详细点四、算法设计题利用堆栈结构,我写是四不像,没有先后顺序,可以进行修改,改成前序typedef int ElementType;//多余的一行,但能使程序可以编译typedef struct BinaryNode{struct BinaryNode*lchild;ElementType data;struct BinaryNode*rchild;}Node,*BinaryTree;Node*searchBroNode(BinaryTree T,Node*q) {Node*Stack[100];int top = -1;Stack[++top] = T;while(top != -1){Node*current = Stack[top--];if(current->lchild == q)return current->rchild;elseif(current->lchild)Stack[++top] = current->lchild;if(current->rchild != q)return current->lchild;elseif(current->rchild)Stack[++top] = current->rchild;}return NULL;}五、单项选择题1.选B2 选C,由于i会导致全部都变为double3 选A4 选C,A必须有输入项,B规定位数没用,输入项必须是变量,或者说地址5 选D,可以这么想,循环继续进行下去的条件是s不等于100且k小于3,则结束条件就是s等于100或者k大于等于36 选A,j++是先执行完这条语句然后再j++,所以循环结束j大于等于4,j++就是57 选B,D还有什么反例?return8 选B9 选D10 选C,“123456”可以看成const char *11 选C,A是比较地址,B是判断两个是否相等12 选B,第一个都是参数的数量,与参数名无关,第二个参数是字符串数组,标准形式是char*argv[ ],等同于char**13 选A,所有变量都是传递值,但是传地址是传什么?传地址也是传地址的值,所以说传地址实际上也是传值14 选D15 选C,这是一个指针数组,数组存放的是int类型的指针,需要区别的是D,D是数组指针,所以选C,原因在于[ ]的优先级高于*16 选D,a三个元素分别的值是{1001,20},{1002,19},{1003,21},只有第2个结构体的age是1002,所以是B,D,B是1001,D是正确答案17 选C,强制类型转换需要带括号18 选D,了解宏定义是什么,宏定义再预处理阶段做处理19 选A,C最完善,但正常不需要这样20 选B,指向结尾所以是a,同时是可读写所以是a+六、填空题1 1,1跟结合性有关,b=1,a=0,运算顺序,b--,重点a+b其中b已经减1了,然后是<=,!=,最后是||2 5 来看一下f是在,干什么,大致跟长度有关,最后s指向字符串开头,p指向’\0’,用一个字符串长度为1的字符串作例子,则返回1,所以返回字符串长度3 11 7 i=(2*M)=>> i=(2*N+1) =>> i=(2*5+1),所以i=11,j=(1+1*M) =>> j=(1+1*5+1) =>> j=74 123456 这道题的疑问就是有没有空格七、程序设计题#include <stdio.h>int main(int argc,char *argv[]){int a,n;scanf("%d %d",&a,&n);int sum = 0;int temp = 0;int i;for(i = 0;i < n;i++){temp = temp * 10 + a;sum += temp;}printf("%d\n",sum);return 0;}八、程序设计题。
(完整word版)北航研究生算法设计与分析Assignment_2

用分支定界算法求以下问题:某公司于乙城市的销售点急需一批成品,该公司成品生产基地在甲城市。
甲城市与乙城市之间共有n 座城市,互相以公路连通。
甲城市、乙城市以及其它各城市之间的公路连通情况及每段公路的长度由矩阵M1 给出。
每段公路均由地方政府收取不同额度的养路费等费用,具体数额由矩阵M2 给出。
请给出在需付养路费总额不超过1500 的情况下,该公司货车运送其产品从甲城市到乙城市的最短运送路线。
具体数据参见文件:m1.txt: 各城市之间的公路连通情况及每段公路的长度矩阵(有向图); 甲城市为城市Num.1,乙城市为城市Num.50。
m2.txt: 每段公路收取的费用矩阵(非对称)。
思想:利用Floyd算法的基本方法求解。
程序实现流程说明:1.将m1.txt和m2.txt的数据读入两个50×50的数组。
2.用Floyd算法求出所有点对之间的最短路径长度和最小费用。
3.建立一个堆栈,初始化该堆栈。
4.取出栈顶的结点,检查它的相邻的所有结点,确定下一个当前最优路径上的结点,被扩展的结点依次加入堆栈中。
在检查的过程中,如果发现超出最短路径长度或者最小费用,则进行”剪枝”,然后回溯。
5.找到一个解后,保存改解,然后重复步骤4。
6.重复步骤4、5,直到堆栈为空,当前保存的解即为最优解。
时间复杂度分析:Floyd算法的时间复杂度为3O N,N为所有城市的个数。
()该算法的时间复杂度等于DFS的时间复杂度,即O(N+E)。
其中,E为所有城市构成的有向连通图的边的总数。
但是因为采用了剪枝,会使实际运行情况的比较次数远小于E。
求解结果:算法所得结果:甲乙之间最短路线长度是:464最短路线收取的费用是:1448最短路径是:1 3 8 11 15 21 23 26 32 37 39 45 47 50C源代码(注意把m1.txt与m2.txt放到与源代码相同的目录下,下面代码可直接复制运行):#include<stdlib.h>#include<stdio.h>#include<time.h>#include<string.h>#define N 50#define MAX 52void input(int a[N][N],int b[N][N]);void Floyd(int d[N][N]);void fenzhi(int m1[N][N],int m2[N][N],int mindist[N][N],int mincost[N][N]);int visited[N],bestPath[N];void main(){clock_t start,finish;double duration;int i,j,mindist[N][N],mincost[N][N],m1[N][N],m2[N][N]; /* m1[N][N]和m2[N][N]分别代表题目所给的距离矩阵和代价矩阵*/// int visited[N],bestPath[N];FILE *fp,*fw;// system("cls");time_t ttime;time(&ttime);printf("%s",ctime(&ttime));start=clock();for(i=0;i<N;i++){visited[i]=0;bestPath[i]=0;}fp=fopen("m1.txt","r"); /* 把文件中的距离矩阵m1读入数组mindist[N][N] */if(fp==NULL){printf("can not open file\n");return;}for(i=0;i<N;i++)for(j=0;j<N;j++)fscanf(fp,"%d",&mindist[i][j]);fclose(fp); /* 距离矩阵m1读入完毕*/fp=fopen("m2.txt","r"); /* 把文件中的代价矩阵m2读入数组mincost[N][N] */if(fp==NULL){printf("can not open file\n");return;}for(i=0;i<N;i++)for(j=0;j<N;j++)fscanf(fp,"%d",&mincost[i][j]);fclose(fp); /* 代价矩阵m2读入完毕*/input(m1,mindist); /* mindist[N][N]赋值给m1[N][N],m1[N][N]代表题目中的距离矩阵*/input(m2,mincost); /* mincost[N][N]赋值给m2[N][N],m2[N][N]代表题目中的代价矩阵*/for(i=0;i<N;i++) /* 把矩阵mindist[i][i]和mincost[i][i]的对角元素分别初始化,表明城市到自身不连通,代价为0 */{mindist[i][i]=9999;mincost[i][i]=0;}Floyd(mindist); /* 用弗洛伊德算法求任意两城市之间的最短距离,结果存储在数组mindist[N][N]中*//*fw=fopen("1.txt","w");for(i=0;i<N;i++){for(j=0;j<N;j++)fprintf(fw,"%4d ",mindist[i][j]);fprintf(fw,"\n");}fclose(fw);// getchar();//*/Floyd(mincost); /* 用弗洛伊德算法求任意两城市之间的最小代价,结果存储在数组mincost[N][N]中*//*fw=fopen("2.txt","w");for(i=0;i<N;i++){for(j=0;j<N;j++)fprintf(fw,"%4d ",mincost[i][j]);fprintf(fw,"\n");}fclose(fw);// getchar();//*/fenzhi(m1,m2,mindist,mincost); /* 调用分支定界的实现函数,寻找出所有的可行路径并依次输出*/finish=clock();duration = (double)(finish - start) / CLOCKS_PER_SEC;printf( "%f seconds\n", duration );//*/}void Floyd(int d[N][N]) /* 弗洛伊德算法的实现函数*/{int v,w,u,i;for(u=0;u<N;u++){for(v=0;v<N;v++){for(w=0;w<N;w++)if(d[v][u]+d[u][w]<d[v][w]){//printf("v,w,u,d[v][u],d[u][w],d[v][w] %d %d %d %d %d %d",v+1,w+1,u+1,d[v][u],d[u][w],d[v][ w]);getchar();d[v][w]=d[v][u]+d[u][w];}}}}void input(int a[N][N],int b[N][N]) /* 把矩阵b赋值给矩阵a */{int i,j;for(i=0;i<N;i++)for(j=0;j<N;j++)a[i][j]=b[i][j];}void fenzhi(int m1[N][N],int m2[N][N],int mindist[N][N],int mincost[N][N]){int stack[MAX],depth=0,next,i,j; /* 定义栈,depth表示栈顶指针;next指向每次遍历时当前所处城市的上一个已经遍历的城市*/int bestLength,shortestDist,minimumCost,distBound=9999,costBound=9999;int cur,currentDist=0,currentCost=0; /* cur指向当前所处城市,currentDist和currentCost分别表示从甲城市到当前所处城市的最短距离和最小代价,currentDist和currentCost初值为0表示从甲城市出发开始深度优先搜索*/stack[depth]=0; /* 对栈进行初始化*/stack[depth+1]=0;visited[0]=1; /* visited[0]=1用来标识从甲城市开始出发进行遍历,甲城市已被访问*/while(depth>=0) /* 表示遍历开始和结束条件,开始时从甲城市出发,栈空,depth=0;结束时遍历完毕,所有节点均被出栈,故栈也为空,depth=0 *//* 整个while()循环体用来实现从当前的城市中寻找一个邻近的城市*/{cur=stack[depth]; /* 取栈顶节点赋值给cur,表示当前访问到第cur号城市*/ next=stack[depth+1]; /* next指向当前所处城市的上一个已经遍历的城市*/for(i=next+1;i<N;i++) /* 试探当前所处城市的每一个相邻城市*/{if((currentCost+mincost[cur][N-1]>costBound)||(currentDist+mindist[cur][N-1]>=distBound)){ /* 所试探的城市满足剪枝条件,进行剪枝*///printf("here1 %d %d %d %d %d %d %d\n",cur,currentCost,mincost[cur][49],costBound,curre ntDist,mindist[cur][49],distBound); getchar();//printf("%d %d %d %d %d %d",cur,i,m1[cur][i],currentCost,mincost[cur][49],costBound); getchar();continue;}if(m1[cur][i]==9999) continue; /* 所试探的城市不连通*/if(visited[i]==1) continue; /* 所试探的城市已被访问*/if(i<N) break; /* 所试探的城市满足访问条件,找到新的可行城市,终止for循环*/ }if(i==N) /* 判断for循环是否是由于搜索完所有城市而终止的,如果是(i==N),进行回溯*/{// printf("here");getchar();depth--;currentDist-=m1[stack[depth]][stack[depth+1]];currentCost-=m2[stack[depth]][stack[depth+1]];visited[stack[depth+1]]=0;}else /* i!=N,表示for循环的终止是由于寻找到了当前城市的一个可行的邻近城市*/{//printf("%d %d %d %d %d %d\n",cur,i,m1[stack[depth]][i],m2[stack[depth]][i],currentCost,curre ntDist);//getchar();currentDist+=m1[stack[depth]][i]; /* 把从当前所处城市到所找到的可行城市的距离加入currentDist */currentCost+=m2[stack[depth]][i]; /* 把从当前所处城市到所找到的可行城市的代价加入currentCost */depth++; /* 所找到的可行城市进栈*/stack[depth]=i; /* 更新栈顶指针,指向所找到的可行城市*/stack[depth+1]=0;visited[i]=1; /* 修改所找到的城市的访问标志*/if(i==N-1) /* i==N-1表示访问到了乙城市,完成了所有城市的一次搜索,找到一条通路*/{// printf("here\n");for(j=0;j<=depth;j++) /* 保存当前找到的通路所经过的所有节点*/ bestPath[j]=stack[j];bestLength=depth; /* 保存当前找到的通路所经过的所有节点的节点数*/shortestDist=currentDist; /* 保存当前找到的通路的距离之和*/minimumCost=currentCost; /* 保存当前找到的通路的代价之和*///costBound=currentCost;distBound=currentDist; /* 更新剪枝的路径边界,如果以后所找到的通路路径之和大于目前通路的路径之和,就剪枝*/if(minimumCost>1500) continue; /* 如果当前找到的通路的代价之和大于1500,则放弃这条通路*/printf("最短路径:%3d,路径代价:%3d,所经历的节点数目:%3d,所经历的节点如下:\n",shortestDist,minimumCost,bestLength+1); /* 输出找到的通路的结果*/bestPath[bestLength]=49;for(i=0;i<=bestLength;i++) /* 输出所找到的通路所经过的具体的节点*/ printf("%3d ",bestPath[i]+1);(完整word版)北航研究生算法设计与分析Assignment_2 printf("\n");depth--; /* 连续弹出栈顶的两个值,进行回溯,开始寻找新的可行的通路*/currentDist-=m1[stack[depth]][stack[depth+1]];currentCost-=m2[stack[depth]][stack[depth+1]];visited[stack[depth+1]]=0;depth--;currentDist-=m1[stack[depth]][stack[depth+1]];currentCost-=m2[stack[depth]][stack[depth+1]];visited[stack[depth+1]]=0;// getchar();}}}}。
北航研究生矩阵论课后参考答案

矩阵论课后参考答案:第1章 线性代数引论习题1.12(1)解:由定义知n m C n m ⋅=⨯)dim(故可知其基为n m ⋅个n m ⨯阶矩阵,简单基记为在矩阵上的某一元素位置上为1,其他元素为0 ,如下⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡000000000001 ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡00000010000(2)解:对约束A A T =分析可知,其为一个上下对称的矩阵(对称阵),则其维数为2)1(1)1()dim(+=++-+=n n n n V 其基为2)1(+n n 个n n ⨯阶的矩阵,故基可写为 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡000000001,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡000000010010 ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡10000000000(3)解:同上理,对A A T -=分析可知其为一个上下成负对称的矩阵,且对角元全为0,则其维数为 2)1(2)1)1)((1(1)2()1()dim(-=+--=++-+-=n n n n n n V其基为2)1(-n n 个n n ⨯阶的矩阵,故基可写为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-0000000000010010 ,⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-000000010000010, ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-01100000000000003解:由题可得},,,{212121ββααspan W W =+ 不难看出其秩为3,则3)dim(21=+W W 设21W W x ∈,则存在2121,,,l l k k 有 22112211ββααl l k k x +=+=则 ⎪⎩⎪⎨⎧=--=-+=+++=---0703020221222121212121l l k l k k l l k k l l k k ,故有⎪⎩⎪⎨⎧-==-=21222134l l l k l k 即)4,3,2,5()4(21222211-=-=+=l l k k x αααα 所以1)dim(21=W W 8(先补充定理:定理:设n 元齐次线性方程组的系数矩阵A 的秩n r A r <=)(,则齐次线性方程组的基础解析存在,并且基础解系所含线性无关的解向量的个数等于r n -)证:1)对任意的21V V B ∈,则有0=AB 且0)(=-B I A 成立,故0=B 所以{0}21=V V 。
北京航空航天大学 《算法导论》期末参考题(有一部分考到了)

一、选择题1.算法分析中,记号O表示(B),记号Ω标售(A),记号Θ表示(D)A 渐进下界B 渐进上界C 非紧上界D 紧渐进界E 非紧下界2.以下关于渐进记号的性质是正确的有:(A)A f(n) =Θ(g(n)),g(n) =Θ(h(n))⇒f(n) =Θ(h(n))B f(n) =O(g(n)),g(n) =O(h(n)) ⇒h(n) =O(f(n))C O(f(n))+O(g(n)) = O(min{f(n),g(n)})D f(n) = O(g(n)) ⇔g(n) = O(f(n))3. 记号O的定义正确的是(A)。
A O(g(n)) = { f(n) | 存在正常数c和n0使得对所有n≥n0有:0≤ f(n) ≤ cg(n) };B O(g(n)) = { f(n) | 存在正常数c和n0使得对所有n≥n0有:0≤cg(n) ≤ f(n) };C O(g(n)) = { f(n) | 对于任何正常数c>0,存在正数和n0 >0使得对所有n≥n0有:0 ≤f(n)<cg(n) };D O(g(n)) = { f(n) | 对于任何正常数c>0,存在正数和n0 >0使得对所有n≥n0有:0 ≤cg(n) < f(n) };4. 记号Ω的定义正确的是(B)。
A O(g(n)) = { f(n) | 存在正常数c和n0使得对所有n≥n0有:0≤ f(n) ≤ cg(n) };B O(g(n)) = { f(n) | 存在正常数c和n0使得对所有n≥n0有:0≤ cg(n) ≤ f(n) };C (g(n)) = { f(n) | 对于任何正常数c>0,存在正数和n0 >0使得对所有n≥n0有:0 ≤f(n)<cg(n) };D (g(n)) = { f(n) | 对于任何正常数c>0,存在正数和n0 >0使得对所有n≥n0有:0 ≤cg(n) < f(n) };5. T(n)表示当输入规模为n时的算法效率,以下算法效率最优的是( C )A T(n)= T(n – 1)+1,T(1)=1B T(n)= 2n2C T(n)= T(n/2)+1,T(1)=1D T(n)= 3nlog2n6. 动态规划算法的基本要素为(C)A 最优子结构性质与贪心选择性质B 重叠子问题性质与贪心选择性质C 最优子结构性质与重叠子问题性质D 预排序与递归调用7.下列不是动态规划算法基本步骤的是( A )。
免费15秋北航《算法与数据结构》在线作业一答案满分

免费15秋北航《算法与数据结构》在线作业一答案满分北航《算法与数据结构》在线作业一单选题一、单选题(共 25 道试题,共 100 分。
)1. 计算机的算法是()。
A. 计算方法B. 排序方法C. 对特定问题求解步骤的一种描述D. 调度算法-----------------选择:C2. 已知二叉树后序遍历序列是dabec,中序遍历序列是debac,它的前序遍历序列是()。
A. acbedB. decabC. deabcD. cedba-----------------选择:D3. 一个有顺序表有255个对象,采用顺序搜索法查表,平均搜索长度为()。
A. 128B. 127C. 126D. 255-----------------选择:A4. 一般地,一个存储结构包括以下三个主要部分。
以下说法错误的是A. 存储结点每个存储结点可以存放一个或一个以上的数据元素B. 数据元素之间关联方式的表示也就是逻辑结构的机内表示C. 附加设施,如为便于运算实现而设置的“哑结点”等等D. 一种存储结构可以在两个级别上讨论。
其一是机器级,其二是语言级-----------------选择:A5. 对线性表进行二分查找时,要求线性表必须()。
A. 以顺序方式存储B. 以链接方式存储C. 以顺序方式存储,且结点按关键字有序排序D. 以链接方式存储,且结点按关键字有序排序-----------------选择:C6. 3个结点可构成()个不同形态的二叉树。
A. 2B. 3C. 4D. 5-----------------选择:D7. 串的逻辑结构与()的逻辑结构不同。
A. 线性表B. 栈C. 队列D. 树-----------------选择:D8. 若从二叉树的任一节点出发到根的路径上所经过的节点序列按其关键字有序,则该二叉树是()。
A. 二叉排序树B. 哈夫曼树C. 堆D. AVL树-----------------选择:C9. 通常要求同一逻辑结构中的所有数据元素具有相同的特性,这意味着A. 数据元素具有同一特点B. 不仅数据元素所包含的数据项的个数要相同,而且对应数据项的类型要一致C. 每个数据元素都一样D. 数据元素所包含的数据项的个数要相等-----------------选择:B10. 在一个长度为n的顺序存储的线性表中,向第i个元素(1≤i≤n+1)之前插入一个新元素时,需要从前向后依次后移()个元素。
北航研究生数值分析作业第二题

北航研究生数值分析作业第二题北航研究生数值分析作业第二题:一、算法设计方案1.按照题目给出的矩阵定义对矩阵A赋初值:对应的函数为a_init();2.对矩阵A进行householder变换,使其拟上三角化:对应的函数为householder();3.输出拟上三角化后的A:对应的函数为aout(int);4.对拟上三角化后的矩阵A使用带双步位移的QR分解法逐次迭代(最大迭代次数L=500),逐个求出其特征值,对应的函数为eigen_a();中间包含两个子程序:calc_mk()和qr_analyze(),分别用来计算矩阵M k和对M k进行QR 分解并得到A k+1;5.输出QR分解过程完毕后的A及求得的特征向量:对应的函数为aout()和eigenvalout();6.对于在第三步中求得的每个实特征值,使用带原点平移的反幂法求出其对应的特征向量,对应的函数为eigenvec();其中包含一个解方程(A-μI)=y k-1的程序段。
这部分也用迭代完成,仍然将最大迭代次数L设置为500;7.输出矩阵A的特征向量,结束计算:对应的函数为eigenvecout()。
算法编译环境:vlsual c++6.0二、源程序如下:#include#include#define N 10 //矩阵阶数;#define EPSL 1.0e-12 //迭代的精度水平;#define L 500 //迭代最大次数;#define OUTPUTMODE 1 //输出格式:0--输出至屏幕,1--输出至文件double a[N][N], a2[N][N], eigen[N][N]; //声明矩阵A;double sa_re[N] = {0}, sa_im[N] = {0}; //声明矩阵的特征值数组;double u_init[N] = {2,1,2,1,2,1,2,1,2,1}; //定义反幂法中使用的初始向量u;//主程序开始;int main(){FILE *p;void a_init();void householder();void equal_zero(double matrix[N][N], int);void eigenvec();int eigen_a();void aout(int);void eigenvalout(int);void eigenvecout(int);if(OUTPUTMODE){p = fopen("Result.txt", "w+");fprintf(p, "计算结果:\n");fclose(p);}a_init(); //对矩阵A进行初始化;householder(); //对矩阵A进行拟上三角化;equal_zero(a, N); //对矩阵A的元素进行归零处理,消除误差;aout(OUTPUTMODE); //输出A;if(eigen_a()) printf("迭代超过最大次数,特征值求解结果可能不正确。
算法设计与分析_北京航空航天大学中国大学mooc课后章节答案期末考试题库2023年

算法设计与分析_北京航空航天大学中国大学mooc课后章节答案期末考试题库2023年1.对如下所示连通无向图【图片】,其最小生成树的权重为【图片】参考答案:232.对如下所示有向图,从【图片】点开始进行深度优先搜索(DFS),搜索时按照字典序遍历某一节点的相邻节点。
在得到的深度优先搜索树中,包含如下哪些类别的边(多选)【图片】参考答案:树边_前向边_后向边_横向边3.在0-1背包问题中,若背包容量为20,5个物品的体积分别为【图片】,价格分别为【图片】。
则该背包能容纳物品的最大总价格为____参考答案:254.设计动态规划算法的一般步骤为____参考答案:问题结构分析→递推关系建立→自底向上计算→最优方案追踪5.给定两个序列分别为“algorithm”和“glorhythm”。
则以下分别为两序列的最长公共子序列和最长公共子串的选项是____参考答案:gorthm thm6.在最长公共子串问题的递推式中,【图片】表示____参考答案:和中以和结尾的最长公共子串的长度7.在支持插入、删除、替换三种操作的最小编辑距离问题中,用【图片】数组来记录编辑方案。
则【图片】数组中的"L","U","LU"分别代表哪种操作___参考答案:插入删除替换/空操作8.字符串“algorithm”到字符串“altruistic”的最小编辑距离为___参考答案:69.数组【图片】中的逆序对个数为____参考答案:510.在上题中,均不在搜索树中的边有哪些____(多选)参考答案:_11.在扇形图(Fan Graph)【图片】中,其邻接表和结构如下第一张图所示。
从顶点【图片】开始进行广度优先搜索(BFS),搜索时按照邻接表顺序遍历某一节点的相邻节点。
得到搜索树如下第二张图,该搜索树并未画全,应从虚线中选择____补全。
(多选)【图片】【图片】参考答案:①_②12.同上题,在扇形图(Fan Graph)【图片】中,其邻接表和结构如下图所示。
北航硕士研究生数值分析大作业一

数值分析—计算实习作业一学院:17系专业:精密仪器及机械姓名:张大军学号:DY14171142014-11-11数值分析计算实现第一题报告一、算法方案算法方案如图1所示。
(此算法设计实现完全由本人独立完成)图1算法方案流程图二、全部源程序全部源程序如下所示#include <iostream.h>#include <iomanip.h>#include <math.h>int main(){double a[501];double vv[5][501];double d=0;double r[3];double uu;int i,k;double mifayunsuan(double *a,double weiyi);double fanmifayunsuan(double *a,double weiyi);void yasuo(double *A,double (*C)[501]);void LUfenjie(double (*C)[501]);//赋值语句for(i=1;i<=501;i++){a[i-1]=(1.64-0.024*i)*sin(0.2*i)-0.64*exp(0.1/i);}//程序一:使用幂方法求绝对值最大的特征值r[0]=mifayunsuan(a,d);//程序二:使用幂方法求求平移λ[0]后绝对值最大的λ,得到原矩阵中与最大特征值相距最远的特征值d=r[0];r[1]=mifayunsuan(a,d);//比较λ与λ-λ[0]的大小,由已知得if(r[0]>r[1]){d=r[0];r[0]=r[1];r[1]=d;}//程序三:使用反幂法求λr[2]=fanmifayunsuan(a,0);cout<<setiosflags(ios::right);cout<<"λ["<<1<<"]="<<setiosflags(ios::scientific)<<setprecision(12)<<r[0]<<endl;cout<<"λ["<<501<<"]="<<setiosflags(ios::scientific)<<setprecision(12)<<r[1]<<endl;cout<<"λ[s]="<<setiosflags(ios::scientific)<<setprecision(12)<<r[2]<<endl;//程序四:求A的与数u最接近的特征值for(k=1;k<40;k++){uu=r[0]+k*(r[1]-r[0])/40;cout<<"最接近u["<<k<<"]"<<"的特征值为"<<setiosflags(ios::scientific)<<setprecision(12)<<fanmifayunsuan(a,uu)<<endl;}//程序五:谱范数的条件数是绝对值最大的特征值除以绝对值最小的特征值的绝对值cout<<"cond(A)2="<<fabs(r[0]/r[2])<<endl;//程序六:A的行列式的值就是A分解成LU之U的对角线的乘积yasuo(a,vv);LUfenjie(vv);uu=1;for(i=0;i<501;i++){uu=uu*vv[2][i];}cout<<"Det(A)="<<uu<<endl;return 1;}double mifayunsuan(double *a,double weiyi){int i,k;double b=0.16;double c=-0.064;double ee,w,v1,v2,mm,sum;double u[501];double y[505]={0};for(i=0;i<501;i++)u[i]=1;//给u赋初值if (weiyi!=0){for (i=0;i<501;i++)a[i]-=weiyi;}ee=1;k=0;//使得初始计算时进入循环语句while(ee>1e-12){mm=0;for(i=0;i<501;i++){mm=mm+u[i]*u[i];}w=sqrt(mm);for(i=0;i<501;i++){y[i+2]=u[i]/w;//注意此处编程与书上不同,之后会解释它的巧妙之处1 }for(i=0;i<501;i++){u[i]=c*y[i]+b*y[i+1]+a[i]*y[i+2]+b*y[i+3]+c*y[i+4];//1显然巧妙之处凸显出来}sum=0;for(i=0;i<501;i++){sum+=y[i+2]*u[i];}v1=v2;v2=sum;//去除特殊情况,减少漏洞if(k==0){k++;}else{ee=fabs(v2-v1)/fabs(v2);}}if (weiyi!=0){for (i=0;i<501;i++)a[i]+=weiyi;}//还原A矩阵return (v2+weiyi);}double fanmifayunsuan(double *a,double weiyi){int i,k;double b=0.16;double c=-0.064;double ee,w,v1,v2,mm,sum;double u[501];double y[501];double C[5][501];void yasuo(double *A,double (*C)[501]);void LUfenjie(double (*C)[501]);void qiuU(double (*C)[501],double *y,double *u);//把A阵压缩到C阵中for(i=0;i<501;i++)u[i]=1;//给u赋初值if (weiyi!=0){for (i=0;i<501;i++)a[i]-=weiyi;}yasuo(a,C);LUfenjie(C);ee=1;k=0; //使得初始计算时进入循环语句while(ee>1e-12){mm=0;for(i=0;i<501;i++){mm=mm+u[i]*u[i];}w=sqrt(mm);for(i=0;i<501;i++){y[i]=u[i]/w;}qiuU(C,y,u);sum=0;for(i=0;i<501;i++){sum+=y[i]*u[i];}v1=v2;v2=sum;//去除特殊情况,减少漏洞if(k==0){k++;}else{ee=fabs(1/v2-1/v1)/fabs(1/v2);}}if (weiyi!=0){for (i=0;i<501;i++)a[i]+=weiyi;}//还原A矩阵return (1/v2+weiyi);}void yasuo(double *A,double (*C)[501]){double b=0.16;double c=-0.064;int i;for(i=0;i<501;i++){C[0][i]=c;C[1][i]=b;C[2][i]=A[i];C[3][i]=b;C[4][i]=c;}}void LUfenjie(double (*C)[501]){int k,t,j;int r=2,s=2;double sum;int minn(int ,int );int maxx(int ,int );for(k=0;k<501;k++){for(j=k;j<=minn(k+s,501-1);j++){if(k==0)sum=0;else{sum=0;for(t=maxx(k-r,j-s);t<k;t++){sum=sum+C[k-t+s][t]*C[t-j+s][j];}}C[k-j+s][j]=C[k-j+s][j]-sum;}for(j=k+1;j<=minn(k+r,501-1);j++){if(k<501-1){if(k==0)sum=0;else{sum=0;for(t=maxx(j-r,k-s);t<k;t++){sum=sum+C[j-t+s][t]*C[t-k+s][k];}}C[j-k+s][k]=(C[j-k+s][k]-sum)/C[s][k];}}}}void qiuU(double (*C)[501],double *y,double *u){int i,t;double b[501];double sum;int r=2,s=2;int minn(int ,int );int maxx(int ,int );for(i=0;i<501;i++){b[i]=y[i];}for(i=1;i<501;i++){sum=0;for(t=maxx(0,i-r);t<i;t++){sum=sum+C[i-t+s][t]*b[t];}b[i]=b[i]-sum;}u[500]=b[500]/C[s][500];for(i=501-2;i>=0;i--){sum=0;for(t=i+1;t<=minn(i+s,500);t++){sum=sum+C[i-t+s][t]*u[t];}u[i]=(b[i]-sum)/C[s][i];}}int minn(int x,int y){int min;if(x>y)min=y;elsemin=x;return min;}int maxx(int b,int c){int max;if(b>c){if(b>0)max=b;elsemax=0;}else{if(c>0)max=c;elsemax=0;}return max;}三、特征值以及的值λ[1]=-1.070011361502e+001 λ[501]=9.724634098777e+000λ[s]=-5.557910794230e-003最接近u[1]的特征值为-1.018293403315e+001最接近u[2]的特征值为-9.585707425068e+000最接近u[3]的特征值为-9.172672423928e+000最接近u[4]的特征值为-8.652284007898e+000最接近u[5]的特征值为-8.0934********e+000最接近u[6]的特征值为-7.659405407692e+000最接近u[7]的特征值为-7.119684648691e+000最接近u[8]的特征值为-6.611764339397e+000最接近u[9]的特征值为-6.0661********e+000最接近u[10]的特征值为-5.585101052628e+000最接近u[11]的特征值为-5.114083529812e+000最接近u[12]的特征值为-4.578872176865e+000最接近u[13]的特征值为-4.096470926260e+000最接近u[14]的特征值为-3.554211215751e+000最接近u[15]的特征值为-3.0410********e+000最接近u[16]的特征值为-2.533970311130e+000最接近u[17]的特征值为-2.003230769563e+000最接近u[18]的特征值为-1.503557611227e+000最接近u[19]的特征值为-9.935586060075e-001最接近u[20]的特征值为-4.870426738850e-001最接近u[21]的特征值为2.231736249575e-002最接近u[22]的特征值为5.324174742069e-001最接近u[23]的特征值为1.052898962693e+000最接近u[24]的特征值为1.589445881881e+000最接近u[25]的特征值为2.060330460274e+000最接近u[26]的特征值为2.558075597073e+000最接近u[27]的特征值为3.080240509307e+000最接近u[28]的特征值为3.613620867692e+000最接近u[29]的特征值为4.0913********e+000最接近u[30]的特征值为4.603035378279e+000最接近u[31]的特征值为5.132924283898e+000最接近u[32]的特征值为5.594906348083e+000最接近u[33]的特征值为6.080933857027e+000最接近u[34]的特征值为6.680354092112e+000最接近u[35]的特征值为7.293877448127e+000最接近u[36]的特征值为7.717111714236e+000最接近u[37]的特征值为8.225220014050e+000最接近u[38]的特征值为8.648666065193e+000最接近u[39]的特征值为9.254200344575e+000cond(A)2=1.925204273902e+003 Det(A)=2.772786141752e+118四、现象讨论在大作业的程序设计过程当中,初始向量的赋值我顺其自然的设为第一个分量为1,其它分量为0的向量,计算结果与参考答案存在很大差别,计算结果对比如下图2所示(左侧为正确结果,右侧为错误结果),导致了我花了很多的时间去检查程序算法。
北航算法和数据结构作业1答案

单项选择题第1题一个深度为L的满K叉树有如下性质:第L层上的结点都是叶子结点,其余各层上每个结点都有K棵非空子树。
如果按层次顺序从1开始对全部结点编号,问编号为n的结点的父结点(若存在)的编号是多少?()A、2n-1B、Kn-1C、KD、1+2+3+…+K答案:B第2题下一段程序实现的功能是打印以h为头节点的单链表中的所有节点,哪一段程序是正确的:()。
A、p = h while ( p != NULL ) {printf(p->data) p = p->next}B、while ( h != NULL ) {printf(h->data)h = h->next}C、p = h while ( p!= NULL ) {p = p->next printf(p->data)}D、p = h while ( p->next!= NULL ) {p = p->next printf(p->data)}答案:A第3题文件的基本组织方式有:()。
A、顺序组织、索引组织、散列组织和链接方式B、磁盘组织、磁带组织C、数据库组织D、关键字与非关键字答案:A第4题设n为正整数。
试确定下列程序段中带标号@的语句的频度。
X=91; Y=100; While(y>0) @If(x>100){ X=x–10; Y=y–1; }else x=x+1; :()。
A、无穷多次B、1100C、9100D、100答案:B多项选择题第5题下述陈述中哪一项是正确的():A、文件是由记录组成的集合B、记录是文件存取的基本单位C、文件是由数据项组成的D、数据项有时也被称之为字段答案:B|D第6题下列排序算法中哪些是不稳定的():A、昌泡排序B、选择排序C、快速排序D、堆排序答案:B|C|D判断题第7题在单向链表中,在X指向的结点后插入结点,对应的方法与X是否是头指针无关。
北航研究生 算法设计与分析大作业一
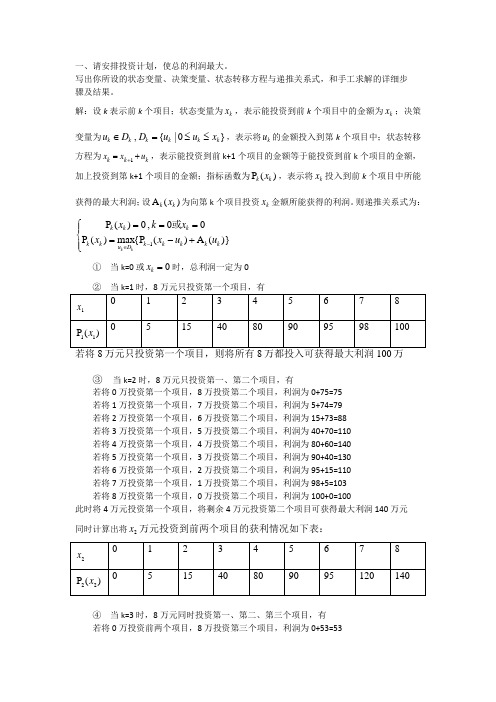
一、请安排投资计划,使总的利润最大。
写出你所设的状态变量、决策变量、状态转移方程与递推关系式,和手工求解的详细步 骤及结果。
解:设k 表示前k 个项目;状态变量为k x ,表示能投资到前k 个项目中的金额为k x ;决策变量为}0|{ , k k k k k k x u u D D u ≤≤=∈,表示将k u 的金额投入到第k 个项目中;状态转移方程为k k k u x x +=+1,表示能投资到前k+1个项目的金额等于能投资到前k 个项目的金额,加上投资到第k+1个项目的金额;指标函数为)(P k k x ,表示将k x 投入到前k 个项目中所能获得的最大利润;设)(A k k x 为向第k 个项目投资k x 金额所能获得的利润。
则递推关系式为:⎪⎩⎪⎨⎧+-====-∈)}(A )({P max )(P 00 , 0)(P 1k k k k k D u kk k k k u u x x x k x k k 或① 当k=0或0=k x 时,总利润一定为0③ 当k=2时,8万元只投资第一、第二个项目,有若将0万投资第一个项目,8万投资第二个项目,利润为0+75=75若将1万投资第一个项目,7万投资第二个项目,利润为5+74=79 若将2万投资第一个项目,6万投资第二个项目,利润为15+73=88 若将3万投资第一个项目,5万投资第二个项目,利润为40+70=110 若将4万投资第一个项目,4万投资第二个项目,利润为80+60=140 若将5万投资第一个项目,3万投资第二个项目,利润为90+40=130 若将6万投资第一个项目,2万投资第二个项目,利润为95+15=110 若将7万投资第一个项目,1万投资第二个项目,利润为98+5=103 若将8万投资第一个项目,0万投资第二个项目,利润为100+0=100此时将4万元投资第一个项目,将剩余4万元投资第二个项目可获得最大利润140万元 同时计算出将2x 万元投资到前两个项目的获利情况如下表:④ 当k=3时,8万元同时投资第一、第二、第三个项目,有 若将0万投资前两个项目,8万投资第三个项目,利润为0+53=53若将1万投资前两个项目,7万投资第三个项目,利润为5+52=57若将2万投资前两个项目,6万投资第三个项目,利润为15+51=66若将3万投资前两个项目,5万投资第三个项目,利润为40+50=90若将4万投资前两个项目,4万投资第三个项目,利润为80+45=125若将5万投资前两个项目,3万投资第三个项目,利润为90+40=130若将6万投资前两个项目,2万投资第三个项目,利润为95+26=121若将7万投资前两个项目,1万投资第三个项目,利润为120+4=124若将8万投资前两个项目,0万投资第三个项目,利润为140+0=140此时将4万元投资第一个项目,将剩余4万元投资第二个项目,第三个项目投资0元,可获得最大利润140万元。
北航研究生数值分析编程大作业1

数值分析大作业一、算法设计方案1、矩阵初始化矩阵[]501501⨯=ij a A 的下半带宽r=2,上半带宽s=2,设置矩阵[][]5011++s r C ,在矩阵C 中检索矩阵A 中的带内元素ij a 的方法是:j s j i ij c a ,1++-=。
这样所需要的存储单元数大大减少,从而极大提高了运算效率。
2、利用幂法求出5011λλ,幂法迭代格式:011111111nT k k k k k k kk T k k k u R u u y u u Ay y u ηηβ--------⎧∈⎪⎪=⎪=⎨⎪=⎪⎪=⎩非零向量 当1210/-≤-k k βββ时,迭代终止。
首先对于矩阵A 利用幂法迭代求出一个λ,然后求出矩阵B ,其中I A B λ-=(I 为单位矩阵),对矩阵B 进行幂法迭代,求出λ',之后令λλλ+'='',比较的大小与λλ'',大者为501λ,小者为1λ。
3、利用反幂法求出ik s λλ,反幂法迭代格式:011111111nTk k k k k k kk T k k k u R u u y u Au y y u ηηβ--------⎧∈⎪⎪=⎪=⎨⎪=⎪⎪=⎩非零向量 当1210/-≤-k k βββ时,迭代终止,1s k λβ=。
每迭代一次都要求解一次线性方程组1-=k k y Au ,求解过程为:(1)作分解LU A =对于n k ,...,2,1=执行[][]s k n r k k k i c c c c c n s k k k j c cc c k s ks k t k s k r i t t s t i k s k i k s k i js j t k s j r k t t s t k j s j k j s j k <+++=-=++=-=+++----=++-++-++-++----=++-++-++-∑∑);,min(,...,2,1/)(:),min(,...,1,:,1,11),,1max(,1,1,1,11),,1max(,1,1,1(2)求解y Ux b Ly ==,(数组b 先是存放原方程组右端向量,后来存放中间向量y))1,...,2,1(/)(:/:),...,3,2(:,1),min(1.1.11),1max(,1--=-===-=+++-++-+--=++-∑∑n n i c x c b x c b x n i b c b b i s t n s i i t t s t i i i ns n n ti r i t t s t i i i使用反幂法,直接可以求得矩阵按模最小的特征值s λ。
北航研究生数理统计答案完全版

n
令
ˆ 于是, 的极大似然估计
⑵ 似然函数
1 。 x x0
L( x0 ; x1 , x 2 , , x n ) n e
( xi x0 )
i 1
n
n e n ( x0 x ) , xi x0 0 ( i 1 , 2,, n )
当 已知时,为 x 0 的单调递增函数,于是由极大似然估计定义可知,
书后部分习题解答整理版
即 ~ t (n 1) .
5. (P35.28) 设 x1 , x 2 ,…, x m 和 y1 , y 2 ,…, y n 分别是从 N ( 1 , 2 ) 和 N ( 2 , 2 ) 总 体中抽取的独立样本, 和 是两个实数,试求
( x 1 ) ( y 2 )
北航研究生数理统计 课后答案完全版
北京航空航天大学
研究生应用数理统计
书后部分习题解答整理版
P{ xi2 1.44} P{ (
i 1
10
xi 2 1.44 ) } 0.09 i 1 0.3 10 x 1 P{ ( i ) 2 16} i 1 0.3 1 0.9 0.1
2 1m
2
2 (n 1) S 2 n
2
( x 1 ) ( y 2 )
2 (m 1) S12m (n 1) S 2 n mn2
2
m
2
n
~ t (m n 2) 。
6. ( P80.1)设总体 X 服从两点分布 B(1, ) , 0 1 , x1 , x 2 ,…, x n 为简单随机样 本,⑴ 求 q( ) Var ( x ) ;⑵ 求 q( ) 的频率估计。
北航算法分析研究生课程3

• Algorithm B
To find a minimum-weight spanning tree T in a weighted, connected network G with N vertices and M edges.
[Initialize] Label all vertices ―unchosen‖; set T ← a network with N vertices and no edges; choose an arbitrary vertex and label it ―chosen‖. Step 1. [Iterate] While there is an unchosen vertex do step 2 od; STOP. Step 2. [Pick a lightest edge] Let (U, V) be a lightest edge between any chosen vertex U and any unchosen vertex V; label V as ―chosen‖; and set T ← T + (U, V). Step 0.
Does it work?
• There are several questions we should ask about this algorithm;
1. Does it always STOP? 2. When it STOPs, is T always a spanning tree of G? 3. Is T guaranteed to be a minimum-weight spanning tree? 4. Is it self-contained (or does it contain hidden, or implicit, sub-algorithms)? 5. Is it efficient?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
判断题:1-5: T F F F F 6-10: F T F F F 11-16: F TT F T F问答题:1.(1)属于减可变规模变种的应用。
(2)当节点个数等于二叉查找树的高度时表现出最差的效率。
(3)此时查找和插入算法在最坏情况的时间复杂度都是O(n)。
2.(1)伪多项式时间算法是一种在L 值的多项式时间内运行的算法,其中L 是输入实例中的最大数值。
(2)Monte Carlo 算法每次都能得到问题的解,但不保证所得解的准确性;Las Vegas 算法是每次不一定得到问题的解,只要得到的解一定是正确的解;可以在Monte Carlo 算法后加上一个验证算法,如果正确就得到解,如果错误就不能生成问题的解,这样Monte Carlo 算法便转化为了Las Vegas 算法。
3. AVL 树和2-3树能够维持树的平衡,避免树的退化,它们在最坏情况下插入和查找的时间复杂度均为O(log 2n)。
4. 0/1背包问题的一个多项式等价判定问题是给定价值为V1, V2, …, Vn ,重量为W1, W 2, …, Wn 的n 个项和两个整数v*和w*,问是否存在一个子集S ,使得,且。
若存在0/1背包问题的多项式算法,则可用其在多项式时间内求解该判定问题,令背包容量等于W*,求出0/1背包问题的最优子集S ,则可以通过判断S 是否满足来确定判定问题的解。
若存在该判定问题的多项式算法,则可以在可能的价值范围内进行二分搜索,在各搜索点上解判定问题以确定0/1背包问题的最优解,令V= 可在O(log(V)) 时间内求得解。
5. 属于NP 问题。
因为可以在多项式的时间验证一个候选路径是否符合条件。
分治题:1. // num : 逆序数num =0;Merge (Type a [], Type left , Type mid , Type right ) {Type b[]; k=left; i = left , j =mid+1;while ( i <= mid && j <= right ) {if (a [i ]> a [j ]) {num += mid –i + 1;b[k++]=a[j++]; }else { b[k++]=a[i++]; }}while(i<=mid)()*i s v i v ∈≥∑()*i sw i w ∈≤∑()*i s v i v ∈≥∑()i nv i ≤∑b[k++]=a[i++];while(j<=right)b[k++]=a[j++];for(i=left; i<=right ; i++)a[i]=b[i];}MergeSort(Type a[], Type left, Type right){if(left < right){mid =(left + right)/2;MergeSort(a, left,mid);MergeSort(a, mid +1, right);Merge(a, left,mid, right);}}算法思路:以归并排序为基础,在两两集合合并的时候如果前一个集合的元素a[i]>a[j],那么说明需要调整次序,逆序数num=num+mid-i。
时间复杂度的迭代公式为11;(n)2(n/2)(n)n1;nTT O=⎧=⎨+>⎩因此算法的时间复杂度为T(n)=O(nlogn);蛮力法的时间复杂度为O(n2),当n数目较大时,分治法计算规模远小于蛮力法。
2.蛮力算法时间复杂度:O(n2);空间复杂度:O(1)/***对长度为len的数组A,找出它的多数元素*/majority(A[], len) {HeapSort(A); // 对数组A中元素按从小到大顺序进行堆排序i = 0;flag = false;while i < len {tmp = A[i]count = 1;while i + count < len && A[i+count] == tmp {count++;}if count > len/2 {print(tmp+“是多数元素”)flag = true;break;}i + = count;}if flag == falseprint(“没有多数元素”)}采用减治的思想每一个减去一个元素,时间复杂度为O(nlgn),蛮力法的时间复杂度为O(n2)。
,动态规划题:1,项目投资k为项目的编号1,2,3;状态变量:Xk为投资项目k到n的总的投资金额。
(其中n为项目总数。
)决策变量:Uk为项目k的投资金额,gk(Uk)为项目k投资Uk后的收益。
允许决策集合:Dk(Xk)={ Uk|0<=Uk<=Xk}状态转移方程:Xk+1=Xk-Uk递推关系式为:fk(Xk)=max{ gk(Uk)+fk+1(Xk-Uk)} k=1,,,n-1。
fn(Xn)=gn(Xn)其中fk(Xk)表示投资项目k到n总投资额Xk后的收益。
最后的结果为f1(X1);在本题中n=3,X1=8,并且0<=Xk<=8。
手工求解过程:1其中x1=8,u1=4,u2=4,u3=0.2 产品需求的每个月的需求量为N1=2,N2=3,N3=2,N4=4;状态变量:每个月初的库存量为Xk, 则0<=Xk<=min{(k-1)*6-(N1+..N(k-1)),Nk+ (4)(k=2,3,4);X1=0;决策变量:每个月的生产量为Yk,则max{0,Xk-Nk}<Yk<min{6,Nk+..+N4-Xk}; k=1,2,3,4;设每个月的费用为Vk;Vk=3+Yk+0.5*(Yk+Xk-Nk)Yk≠0;0.5*(Xk-Nk) Yk=0;状态转移方程式:X(k+1)=Xk+Yk-Nk;设fk(Xk)是第k个月且月初库存量为Xk开始到第4个月结束这段时间的最优成本。
递推关系式为:fk(Xk)=min{Vk+f(k+1)(X(k+1))} k=1,2,3,4;f5(X5)=0;则四个月内最优成本为f1(X1)=f1(0);则四个月的总最优成本为C1(0)=20.5千元由上可得出:第1月产量为5;第2月产量为0;第3月产量为6;第4月产量为0;1.分支定界题1.(1)由题意得,50个站点的原始网络为一个无向完全图,总的边数为50*49/2=1225条。
因此,以边为节点,建一个1225层的二叉搜索树。
对所有的边按照敷设费用从小到大排序,编号为1,2……1225.对第i层(即第i个结点)的分支对应于是否把第i条边添加到解集中。
沿左支前进表示选择该条边;沿右支前进表示不选择该边。
(2)遍历搜索树的原则:前进:在当前层,选择最有可能达到最优的节点进行扩展,且要满足欲加入的边满足网络无环。
总地井数目小于等于UMAX,跨区线路总数据不超过DMAX,当前SMST费用小于上界。
分支:左支表示将该边加入到解集中,右支表示不将该边加入到解集中。
回溯:当当前挑选的边使解不可行或已经找到一个解时回溯。
当从左分支回溯到顶点时,接着由右分支向下进行;当从右分支回溯到顶点时,接着回溯到该结点的父结点。
剪枝:在搜索树的每个结点,除了可行性检查(即总地井数目小于等于UMAX,跨区线路总数据小于等于DMAX,线路是否无环)当前构造的SMST总费用若大于目前已求解的花费,则以当前结点为根的子树被剪枝。
停止:当该二叉树所有结点都被访问过时,可以找到一个最优解。
(3)代价下界:是在当前已选择的边的情况下,不考虑任何限制条件,可以用修改的Kruskals算法构件的最小生成树的总花费代价。
因为加上任何约束条件的可行解的花费均大于等于最小生成树的费用代价,所以改下界是正确且有效的。
代价上界:目前已经得到的一个解的总花费。
因为任何一个解的花费代价都大于等于最优解的费用代价,所以该上界是正确的且有效的。
(4)伪代码;Void Bran_and_Bound(){Int feeLowBound=INF;//初始化最小费用界;A[]=init();Tree=buildTree();//根据边集合构造二叉搜索树While(true){If(currentminU()<=UMAX//总地井数目小于等于UMAX&¤tminD()<=DMAX//跨区线路总数据小于等于DMAX&¤tminfee()<=feeLowBound//当前路径最小花费&&hasnocircle())//没有环{if(findachem)//若能找到一个方案,则必小于lowBound{FeeLowBound=currentminfee();//更新界Record(route);//记录路径Backward();//回溯}else{//前进MoveToNextChild();Continue;}}else{backward();//剪枝}}}2、(1)由题意得,以国家为结点,共有52个国家,所以定义了52层的二叉搜索树,选择A为根节点,且记录在已选择的结点国家的顺序集合中,再从从未被选择过的节点中选择与顺序集合中最后一个国家结点直接相连通的国家作为下一层结点。
沿左支前进表示选择该国家,并把该国家结点加入已选择的顺序集合中;沿右支前进表示不选择该国家。
(2)前进:仍有子结点,且到达该结点时交易时间小于t,到该结点为至的总交纳税费小于等于所给定的界。
分支:对每个结点的选择与否进行分支,左支表示将该国家结点加入到解集中,右支表示不将该国家结点加入解集。
回溯:在当前选择的国家结点使解不可行(两个国家无直接通信或交易时间>=t)或者已经找到一个可行解时,进行回溯。
当从左分支回溯到顶点时,接着由右分支向下进行;当从右分支回溯到顶点时,接着回溯到该结点的父结点。
剪枝:在搜索树的每个结点,除了可行性检查(交易时间<t)还有至当前结点为止的最少缴纳税费大于目前已求解的税费,则以当前结点为根的子树被剪枝。
(3)所交的税费的下界:不考虑世界约束的条件,在已选择的国家结点的情况下,由A国到B国经各个中转国所缴纳最少税费(相当于最短路径问题)因为加上时间限制,实际所求的解均大于等于该下界,因此该下界正确且有效。
所交的税费的上界:目前已得到的一个解的总缴纳税费。
因为任何一个解的总税费均大于等于最优解,即最小总税费,所以该上界是正确且有效的。
(4)伪代码:Void Branch_and_Bound(){Int feeLowBound=INF;//初始化最小税费界Tree=buildTree();//根据52个国家建立二叉搜索树While(true){If(currentTime()<t//交易时间小于t&¤tminfee()<feeLowBound)//当前为止缴纳税费小于已知解的税费{If(findachem)//若找到一个方案,则必小于lowBound{FeeLowBound=currentminfee();//更新界Record(route);//记录路径Backward();//回溯}else{//前进moveToChild();continue;}}else{backward();//剪枝}}}。
